Adaptive Equivalent Factor-Based Energy Management Strategy for Plug-In Hybrid Electric Buses Considering Passenger Load Variations
Abstract
1. Introduction
1.1. PHEB Energy Management Strategy
1.2. Electric Bus Charging Technology
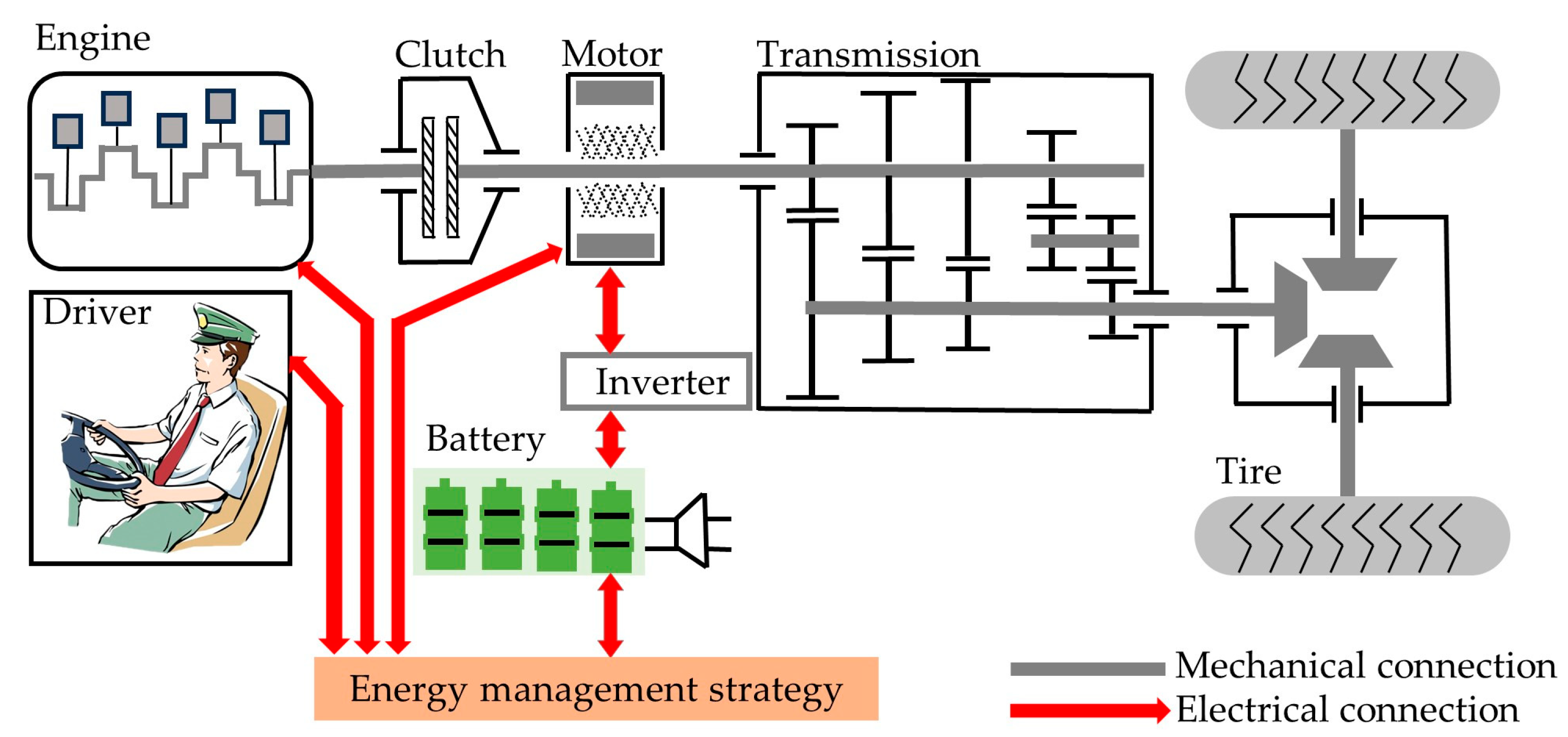
2. Modeling of the Powertrain System for PHEBs
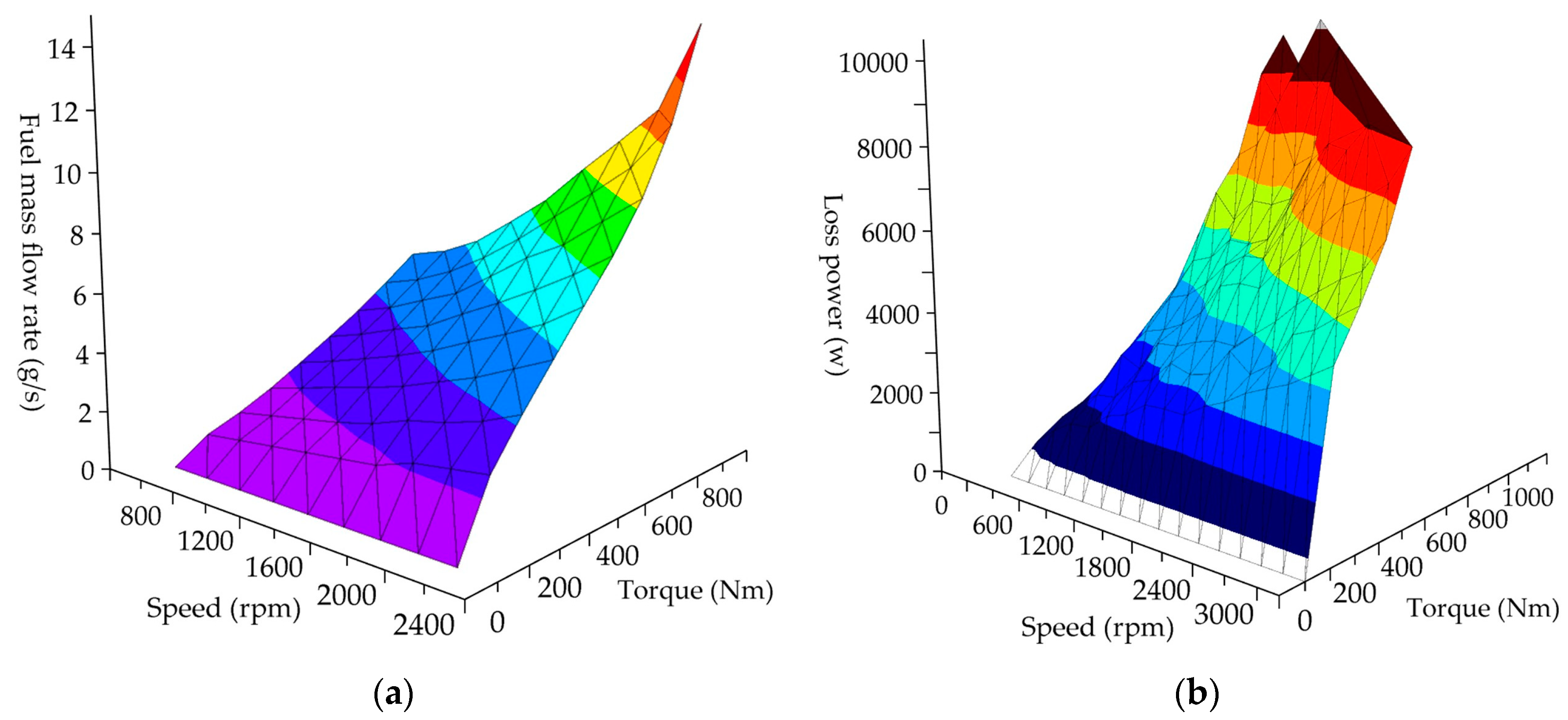
2.1. Engine Model
- —engine’s fuel consumption rate (g/kWh);
- —engine torque (Nm);
- —engine speed (rpm).
- —fuel consumption rate of the engine per unit time (g/s).
2.2. Motor Model
- —motor power loss (w);
- —motor torque (Nm);
- —motor speed (rpm).
- —motor output power (w);
- —motor speed (rad).
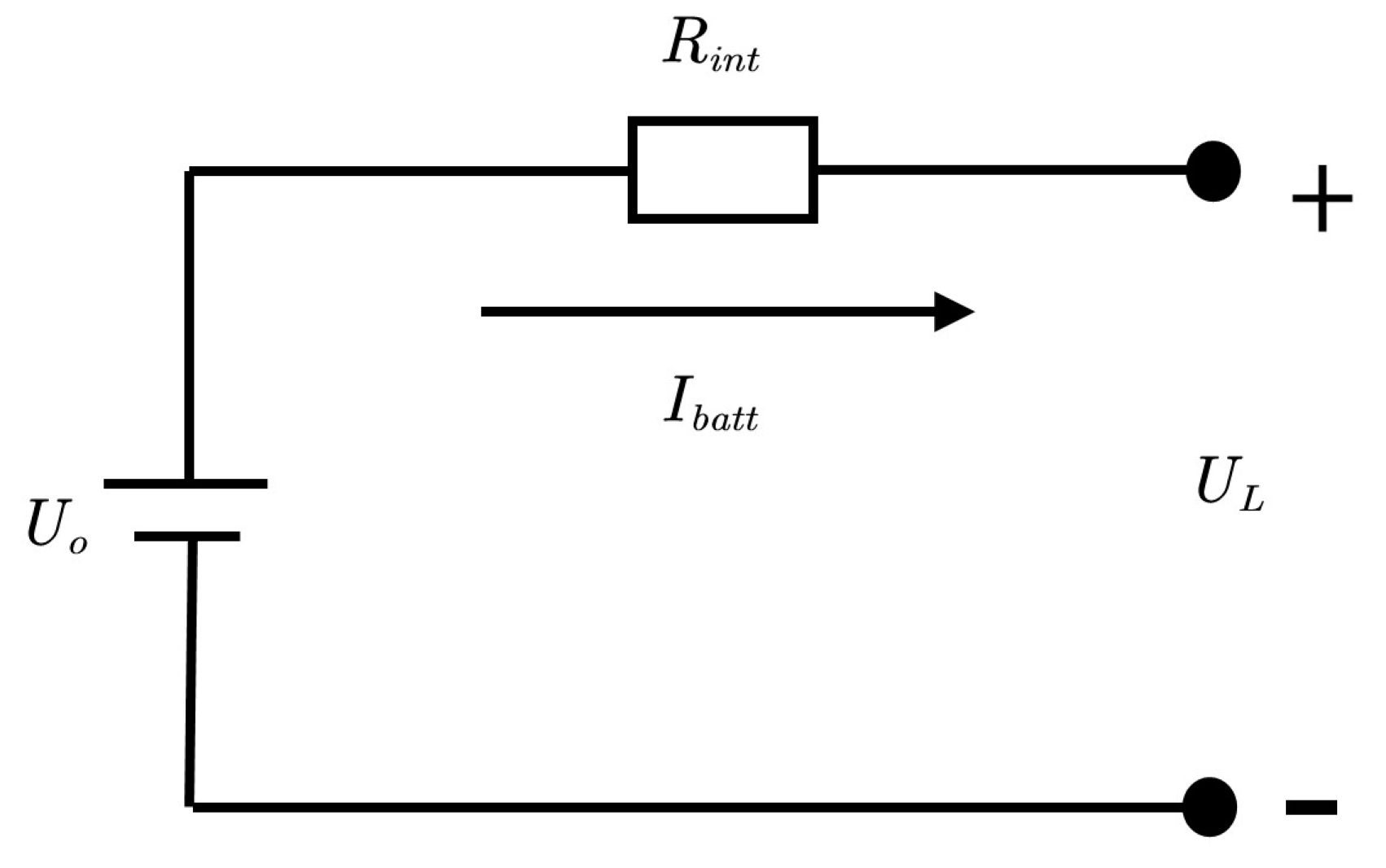
2.3. Battery Model
- —battery load voltage (V);
- —battery open-circuit voltage (V);
- —battery current (A);
- —battery internal resistance ().
- —total battery pack’s load voltage (V);
- —number of series connected battery.
- —initial SOC value;
- —battery capacity (Ah).
2.4. PHEB Longitudinal Dynamics Model
- —air resistance (N);
- —coefficient of air resistance;
- —air density (g/m3);
- —frontal area of the entire vehicle (m2);
- —vehicle speed (m/s);
- —rolling resistance (N);
- —coefficient of rolling resistance;
- —gradient angle (rad);
- —gradient resistance (N);
- —acceleration resistance (N)
- —rotational mass conversion factor;
- —vehicle acceleration (m/s2).
- —driving force at the wheels (N);
- —combined torque provided by the engine and motor in the process of driving the vehicle (N·m);
- —transmission ratio;
- —main gearbox ratio;
- —driveline efficiency;
- —wheel radius (m).
2.5. Driver Model
- —difference between the actual vehicle speed and the reference speed (m/s);
- —reference speed (m/s);
- —actual vehicle speed (m/s);
- —pedal opening, ;
- —proportional control coefficient;
- —integral control coefficient.
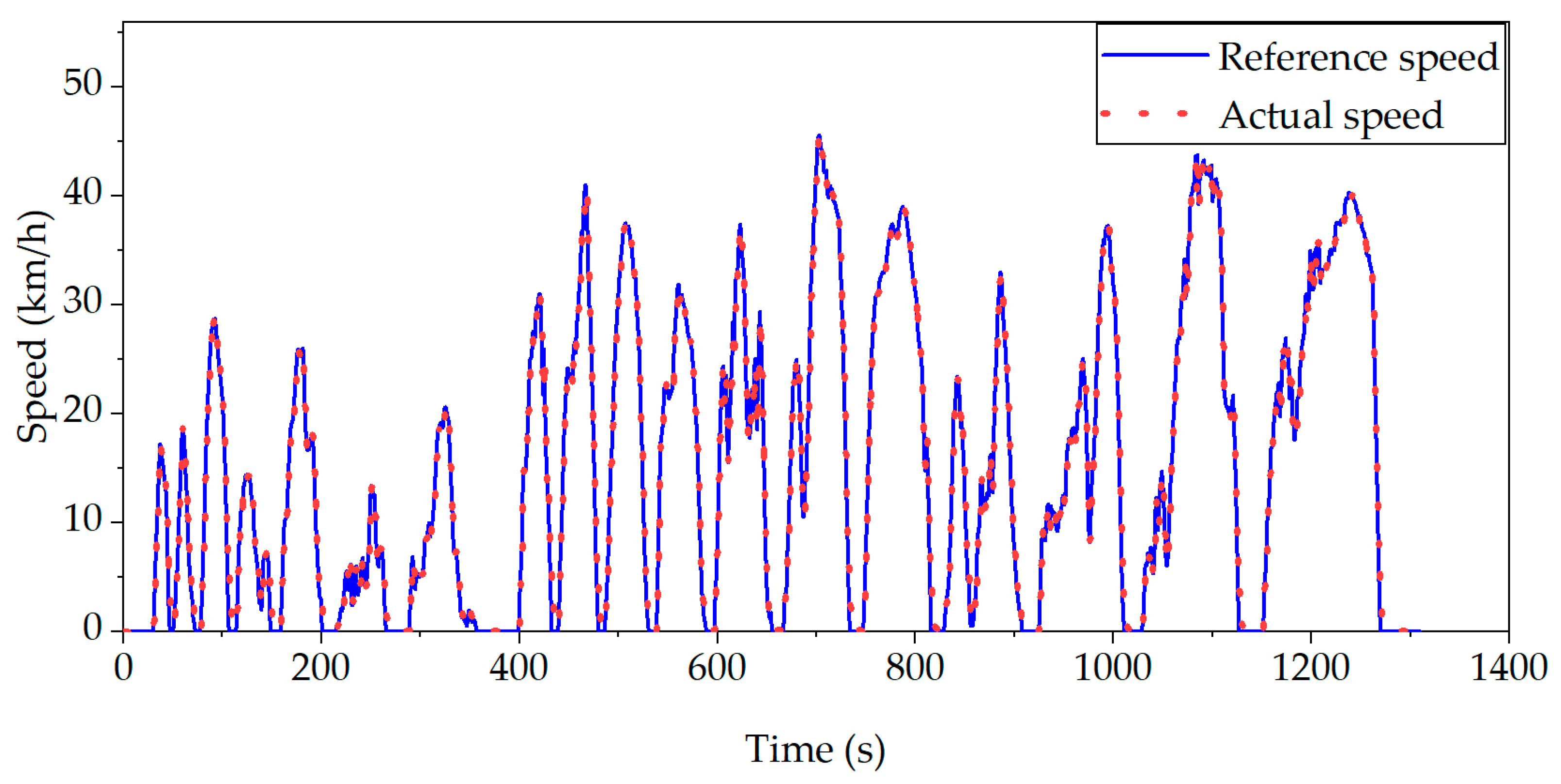
2.6. Model Validation
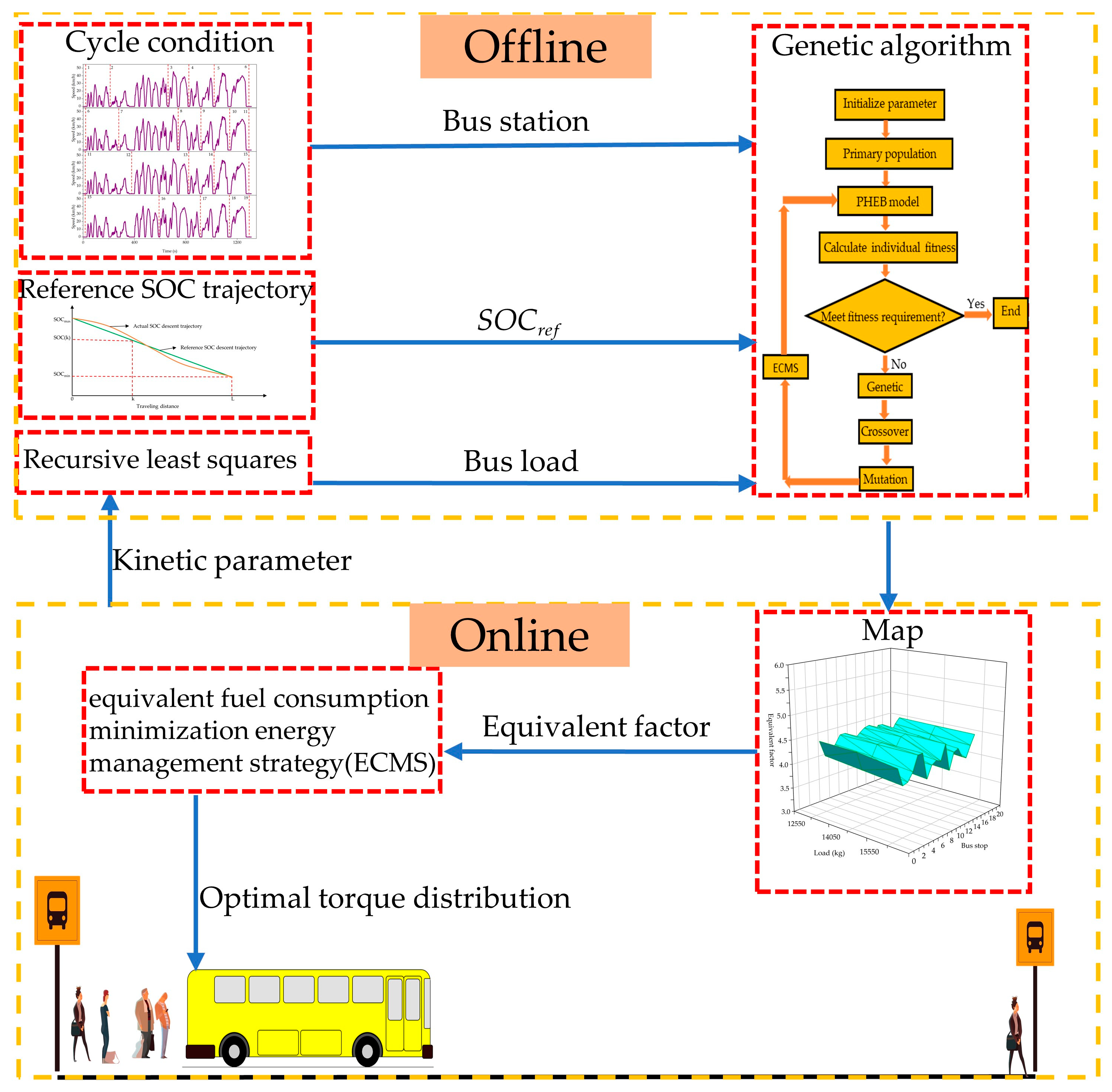
3. Materials and Methods
3.1. Research on Dynamic Programming Algorithm
- —state variable;
- —control variable.
- —PHEB torque demand (Nm).
- G—minimum total fuel consumption;
- —fuel consumption for the kth stage.
- —state variable at the (k + 1)th stage.
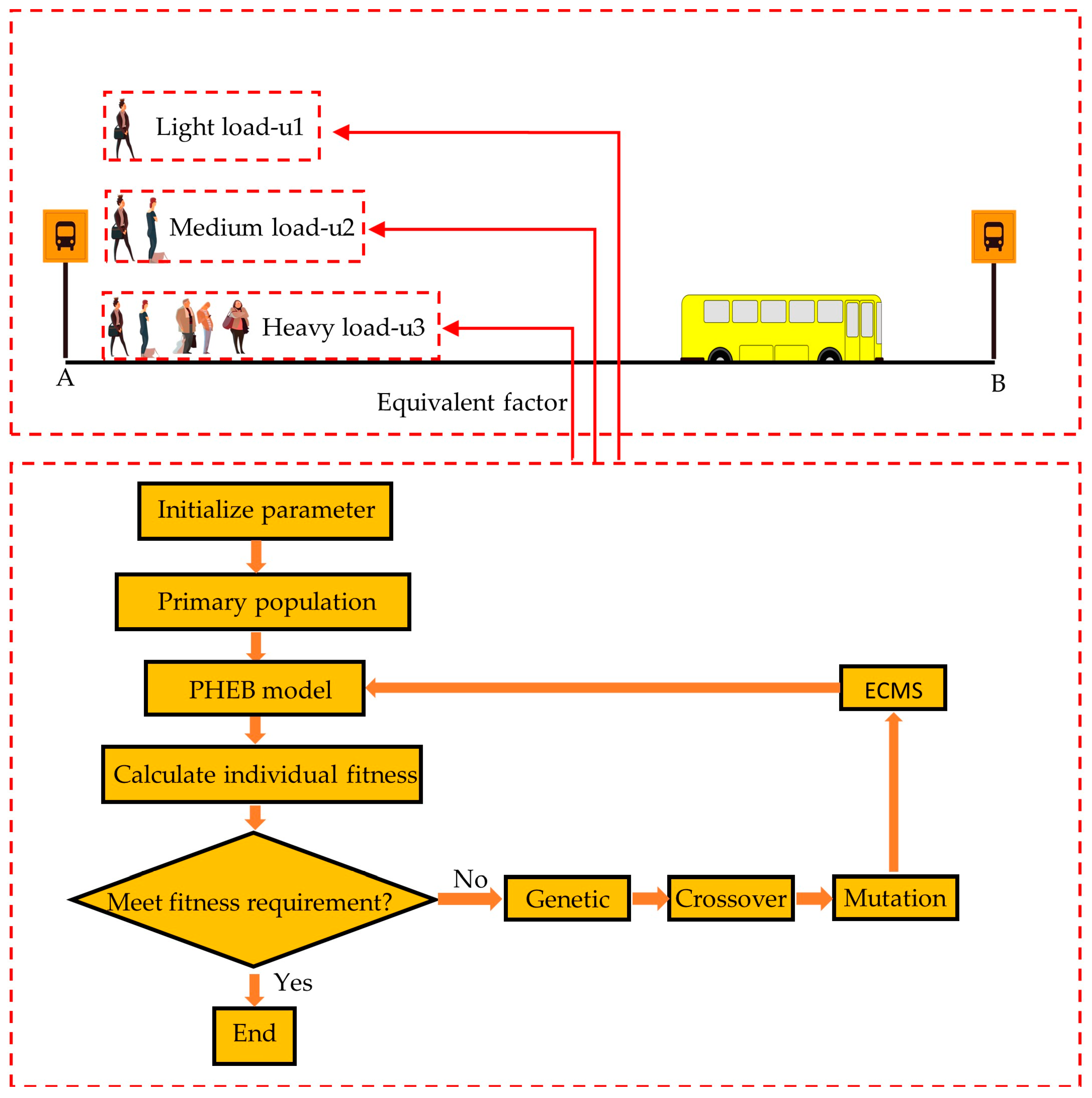
3.2. Research on Load Identification Method
- —process output;
- —process input;
- —estimated parameters;
- —process noise, which is white noise.
- and ()—observed parameters;
- —estimated parameter.
3.3. Research on Equivalent Fuel Consumption Minimization Strategy
- —state variable;
- —common state between power consumption and fuel, i.e., the equivalent coefficient;
- —control variable;
- —differential of the state variable;
- —engine fuel consumption (g/s).
- —battery pack load voltage;
- —battery pack resistance ().
- —equivalent factor;
- —calorific value of the fuel (J/kg).
- —battery output power (w).
- —total equivalent fuel consumption (g/s);
- —equivalent fuel consumption corresponding to the battery (g/s);
3.4. Research on Genetic Algorithm
- Fit—the fitness of individual;
- —scale factor, ;
- —penalty functions, as shown in Equations (38) and (39);
- —reference SOC value;
- —actual SOC value;
- —reference SOC value at the end of the simulation;
- —actual SOC value at the end of the simulation.
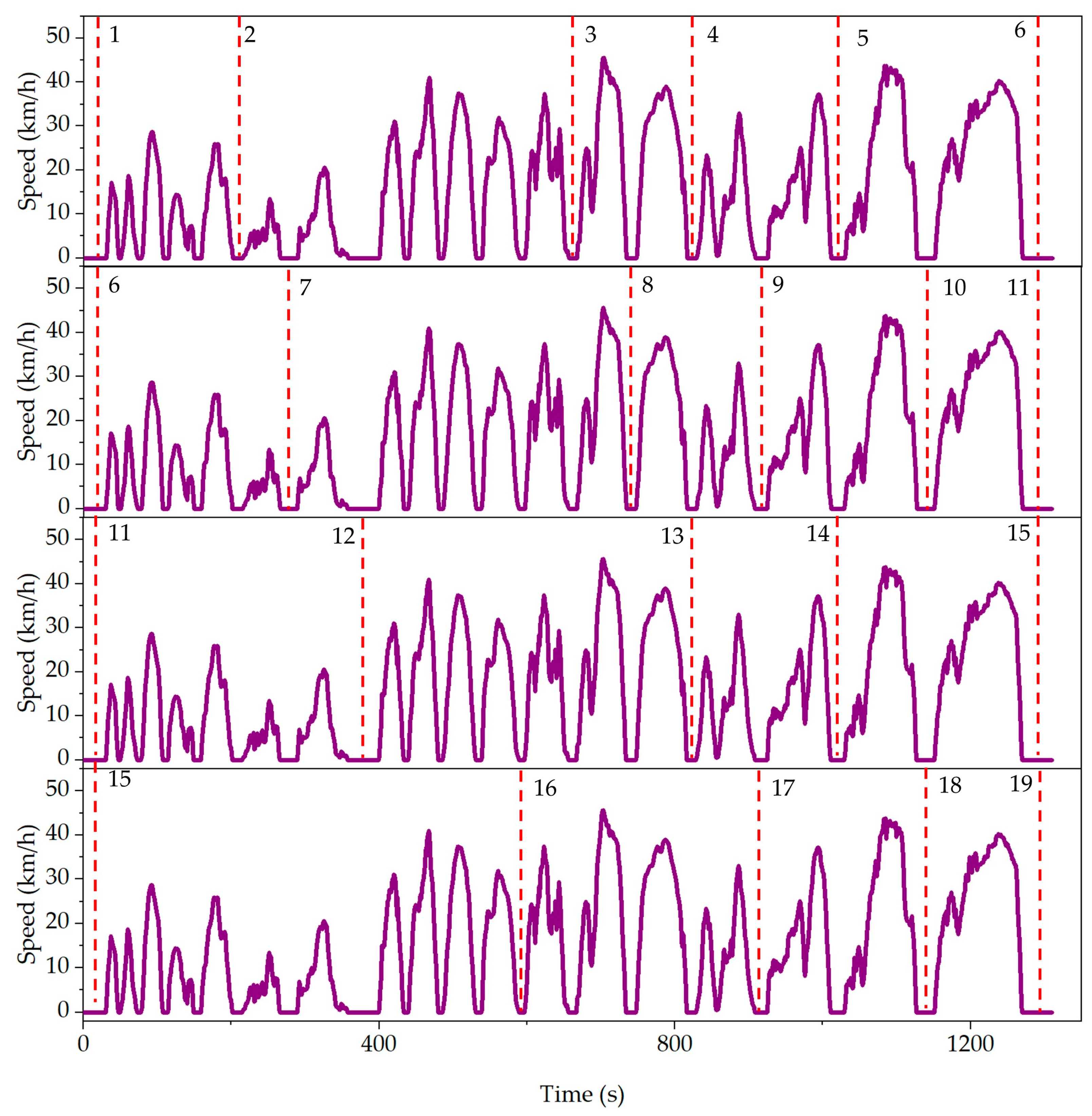
3.5. Research on Division of Bus Stations
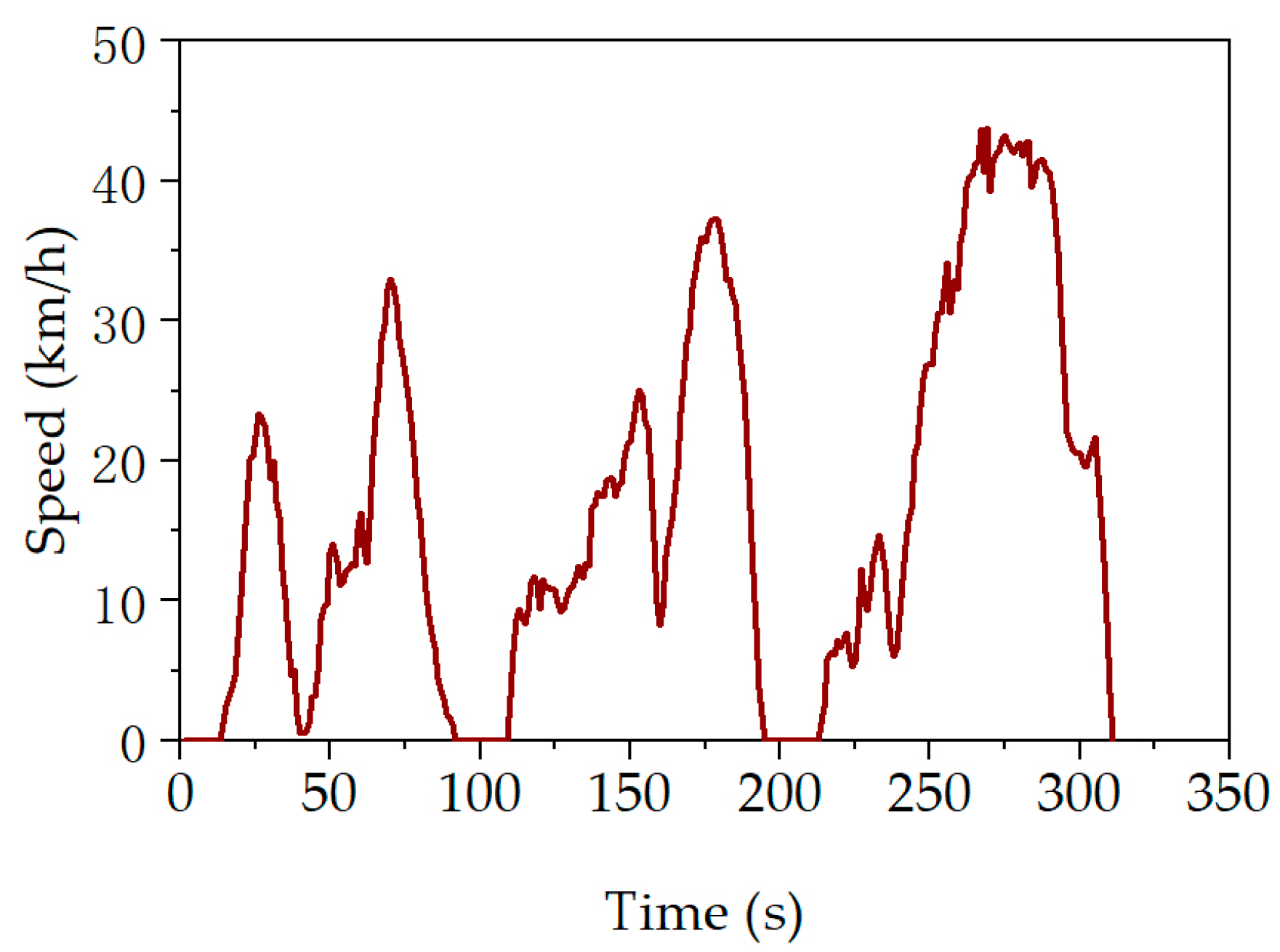
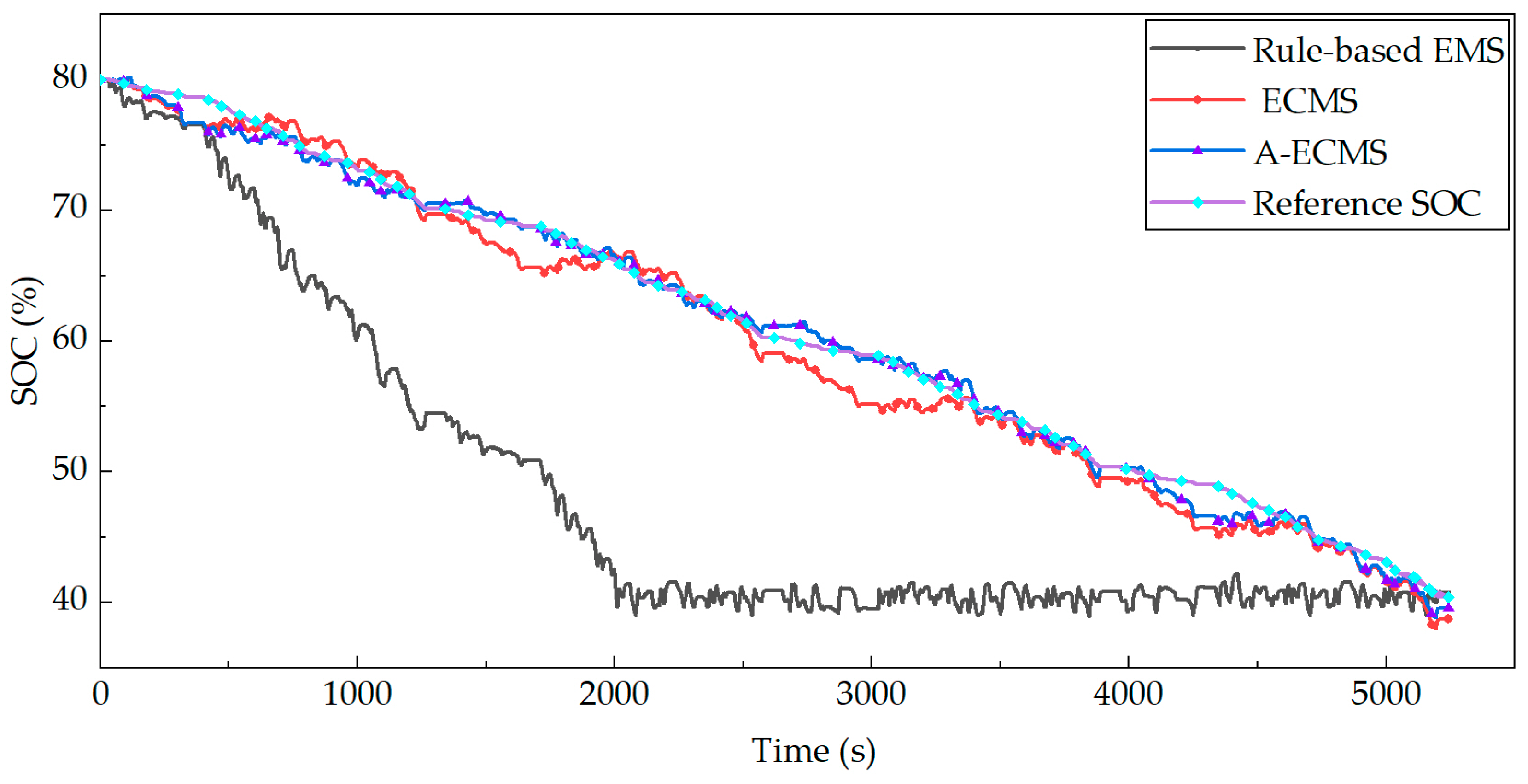
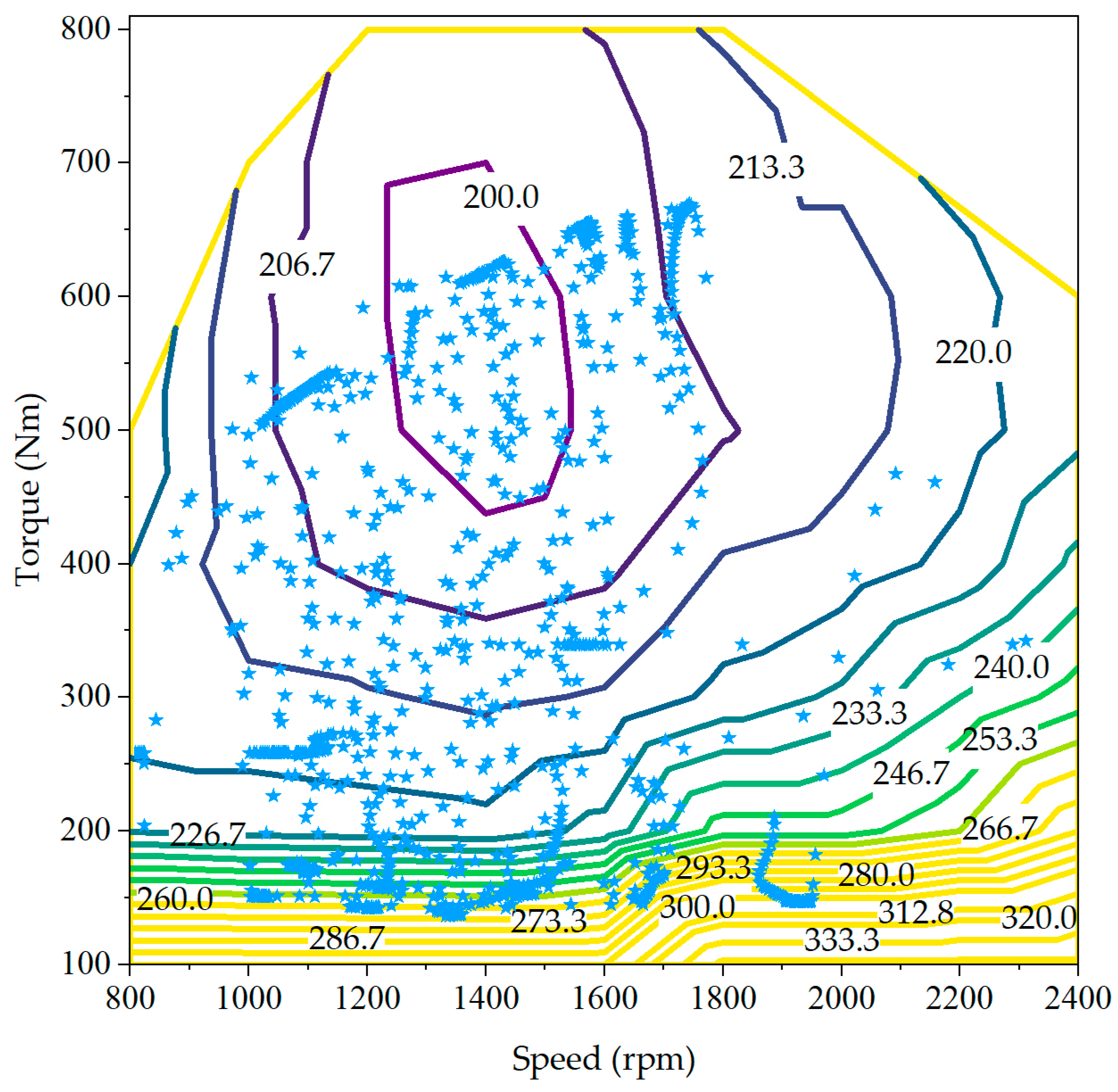
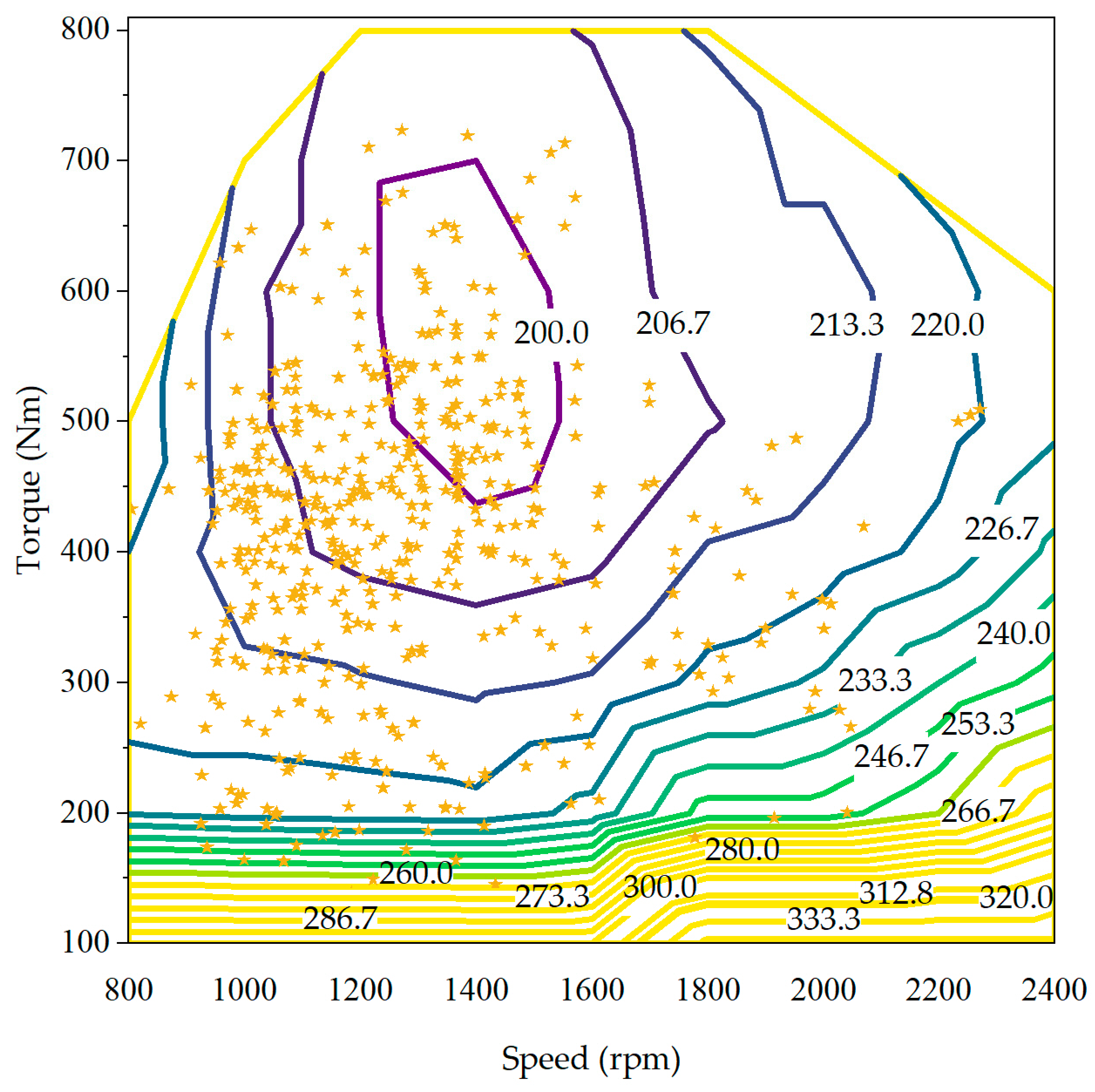
4. Results and Discussion
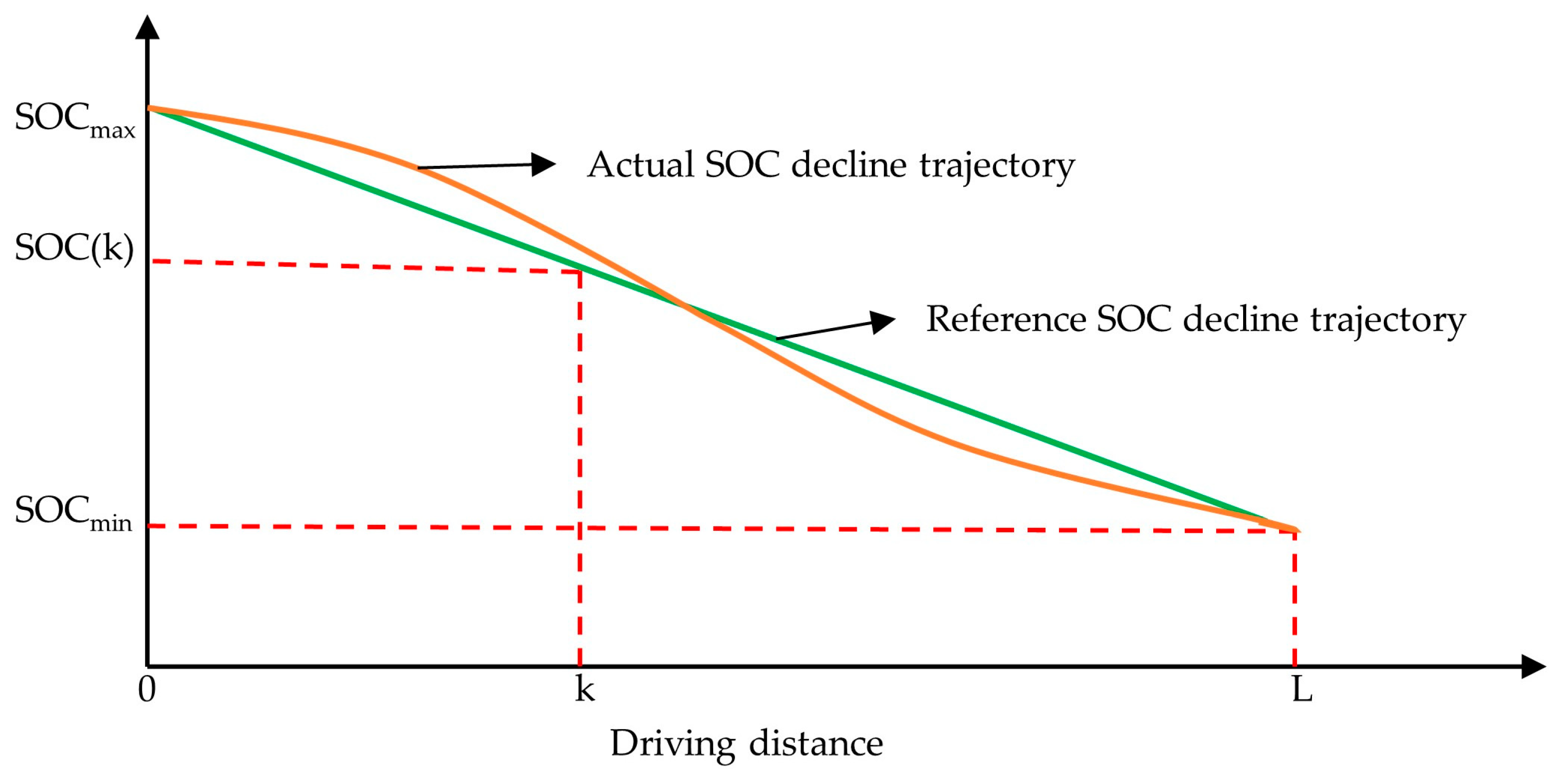
4.1. Obtaining Reference SOC Trajectory Based on Dynamic Programming Algorithm
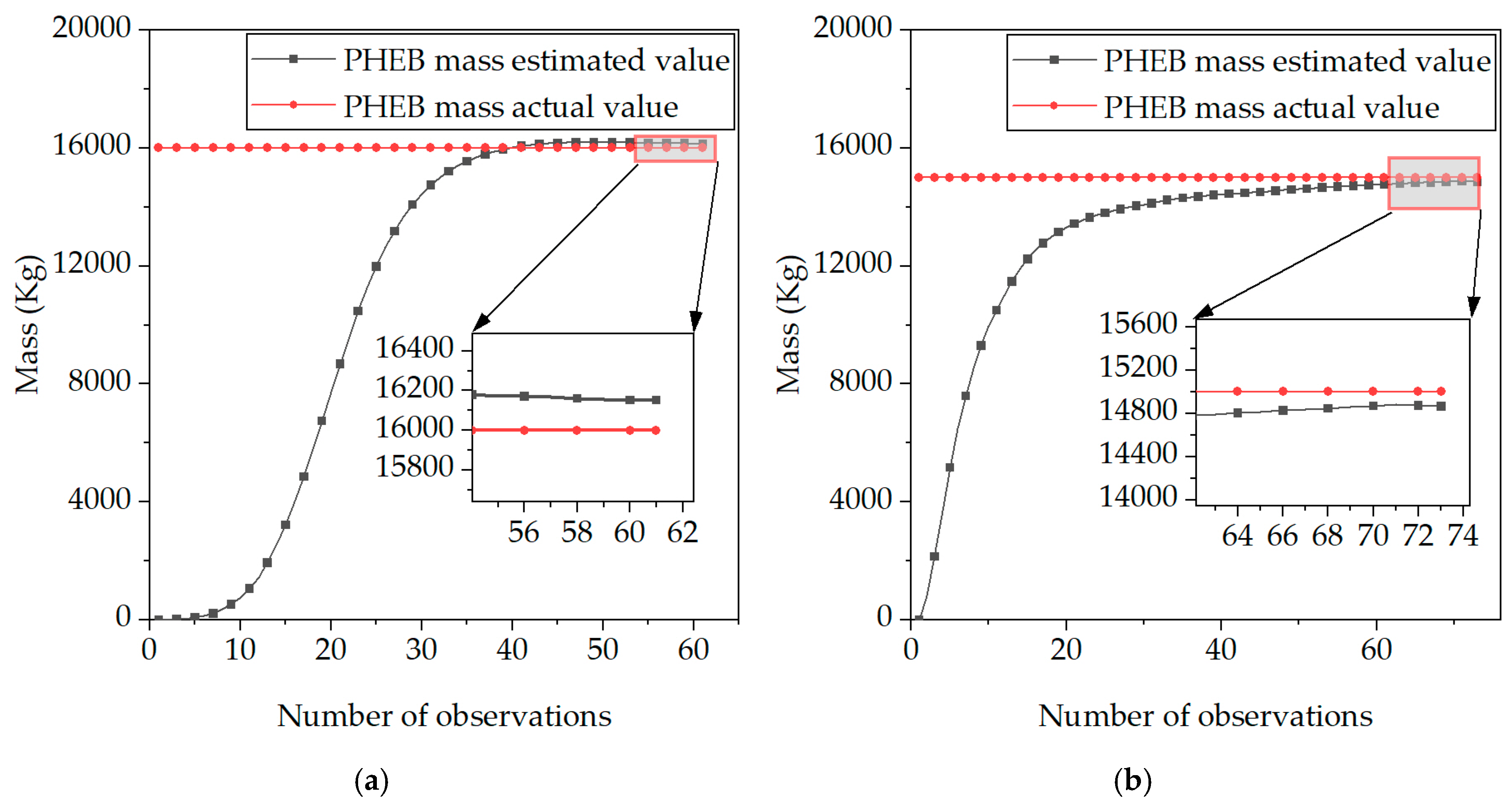
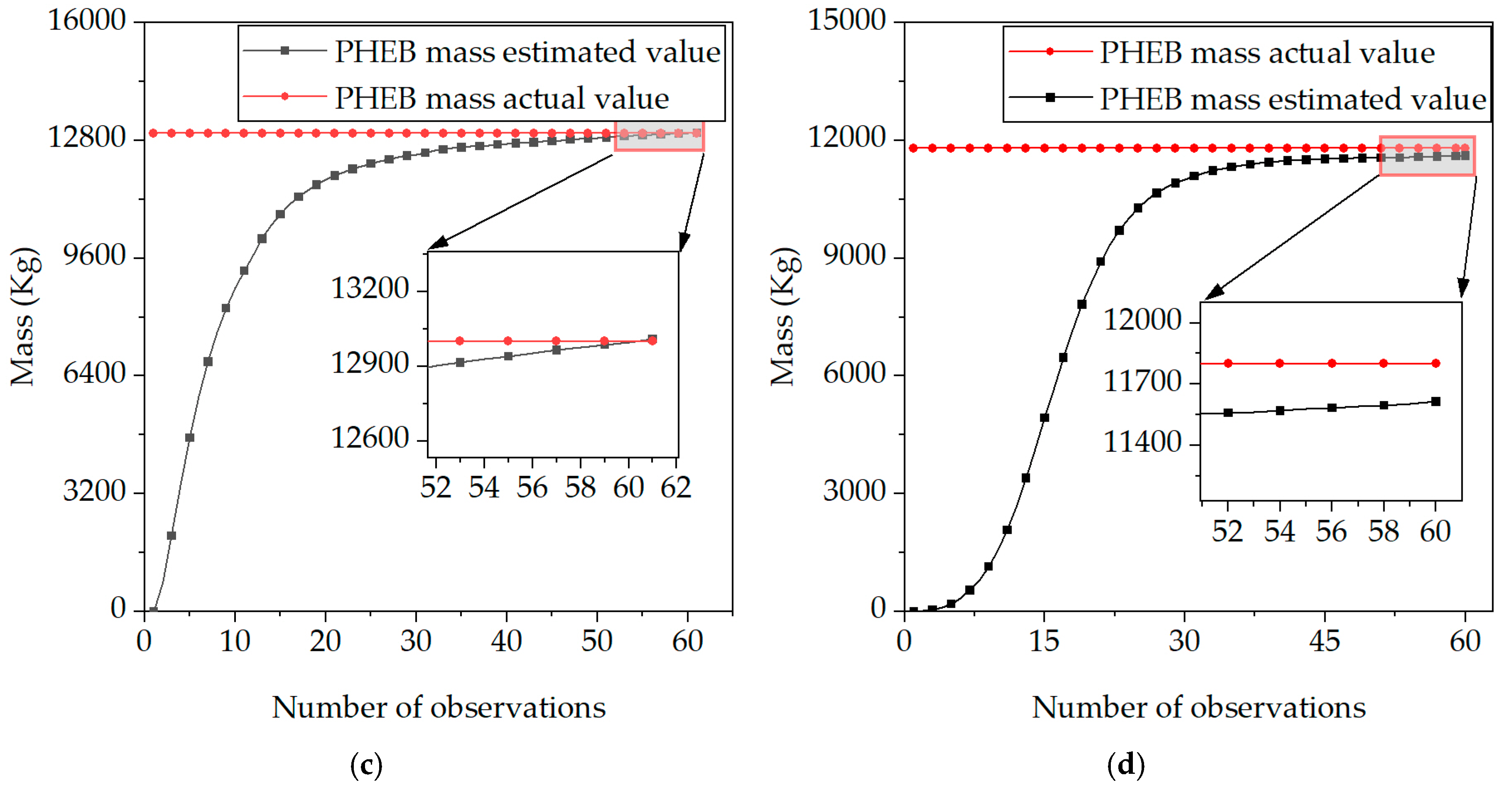
4.2. Analysis of Load Identification Results Based on RLS
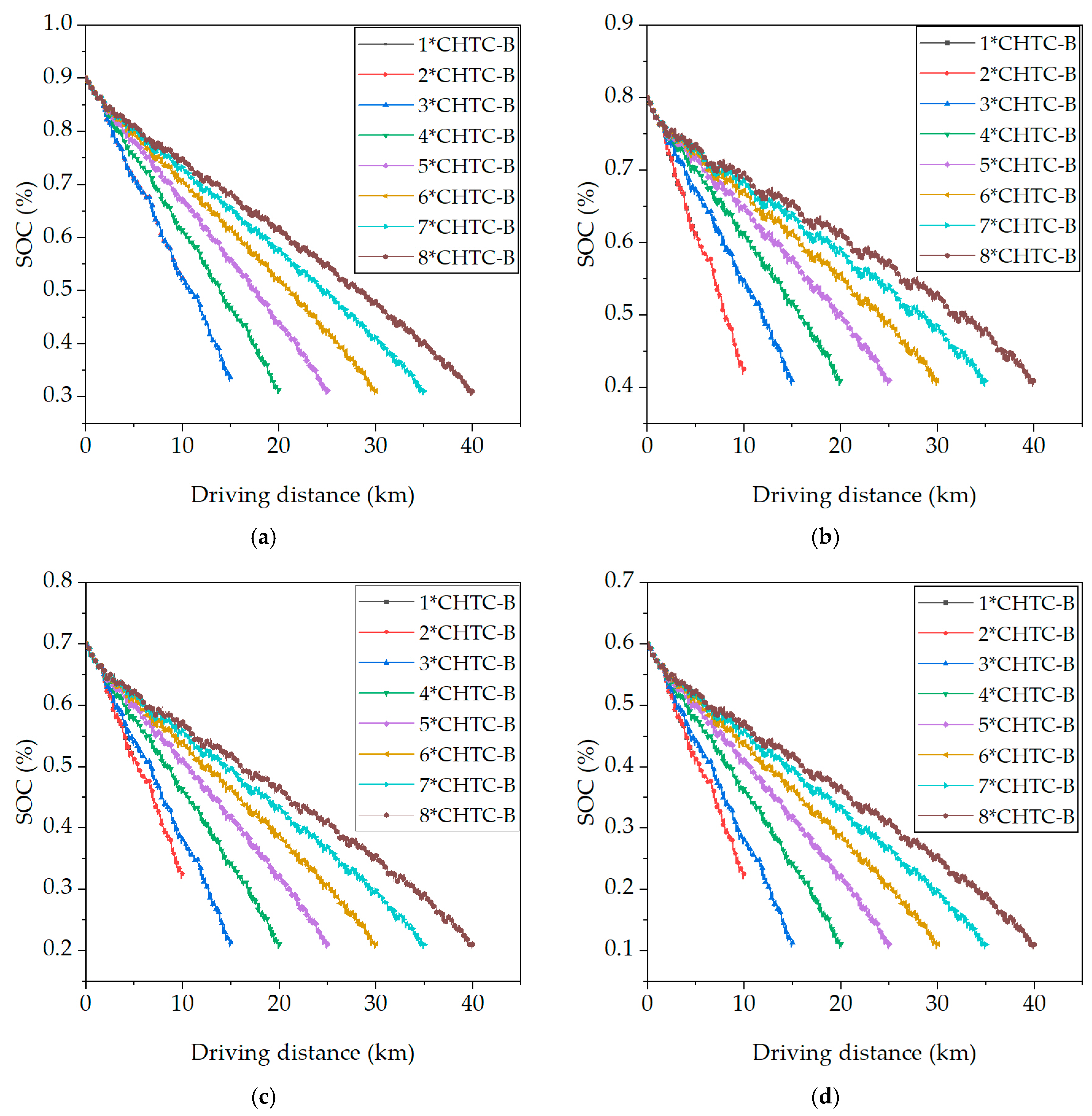
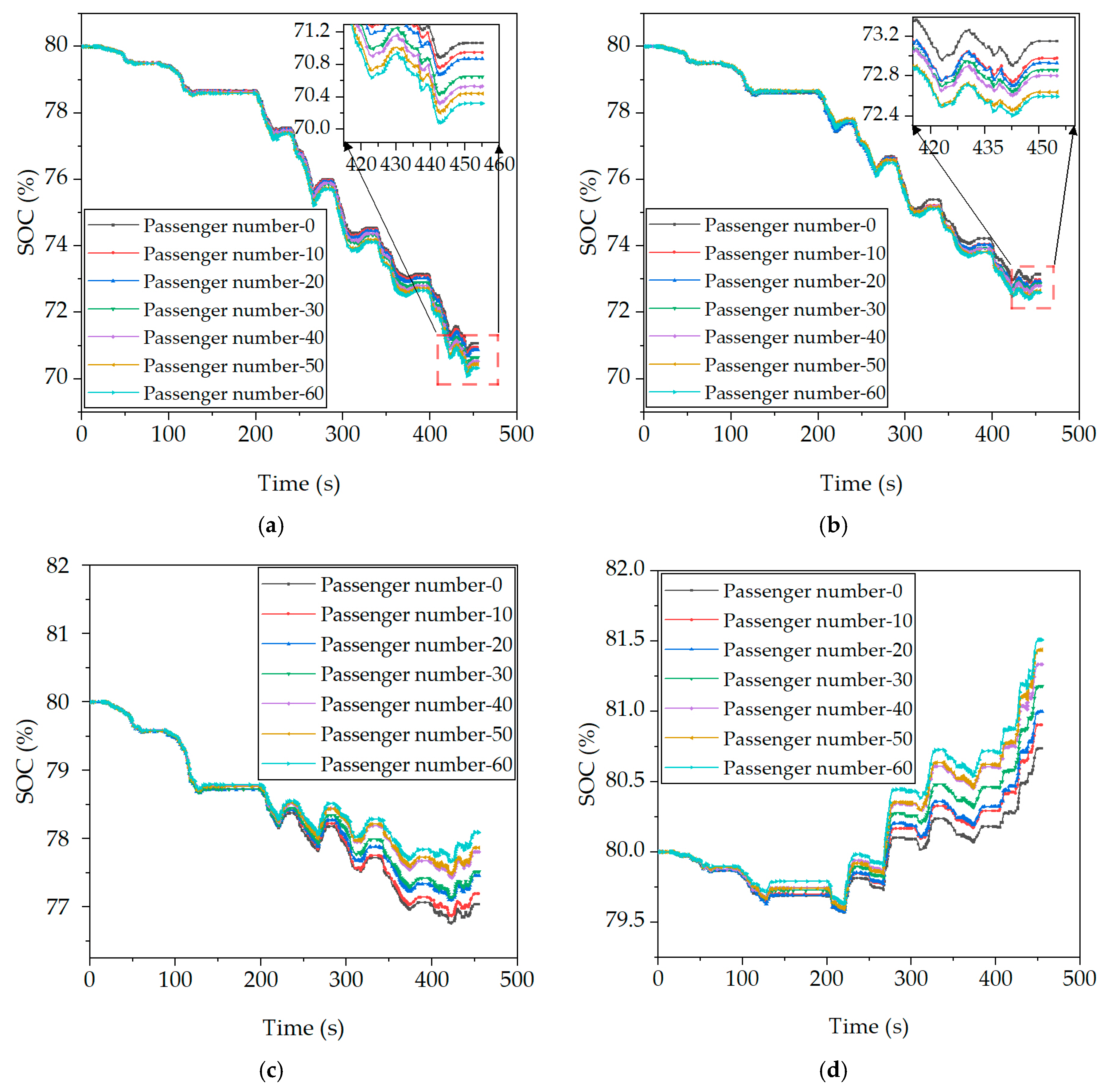
4.3. Analysis of Influence of Load Variations on SOC
4.4. Establishment of Passenger Load–Bus Station Equivalent Factor Map
4.5. Effectiveness Simulation Analysis of A-ECMS
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EMS | energy management strategy |
| PHEB | plug-in hybrid electric bus |
| ECMS | equivalent fuel consumption minimization energy management strategy |
| A-ECMS | adaptive equivalent fuel consumption minimization energy management strategy |
| DP | dynamic programming |
| RLS | recursive least squares |
| SOC | state of charge |
| GA | genetic algorithm |
| EV | pure electric vehicle |
| PHEV | plug-in hybrid electric vehicle |
| HEV | hybrid vehicle |
| PMP | Pontryagin’s minimum principle |
| DNN | deep neural network |
| LS | least squares |
| Nomenclatures | |
| engine’s fuel consumption rate (g/kWh) | |
| engine torque (Nm) | |
| engine speed (rpm) | |
| fuel consumption rate of the engine per unit time (g/s) | |
| motor power loss (kW) | |
| motor torque (Nm) | |
| motor speed (rpm) | |
| motor output power (w) | |
| motor speed (rad) | |
| battery load voltage (V) | |
| battery open-circuit voltage (V) | |
| battery current (A) | |
| battery internal resistance (Ω) | |
| total battery pack’s load voltage (V) | |
| battery capacity (Ah) | |
| air resistance (N) | |
| air density (g/m3) | |
| frontal area of the entire vehicle (m2) | |
| rolling resistance (N) | |
| gradient angle (rad) | |
| gradient resistance (N) | |
| acceleration resistance (N) | |
| driving force at the wheels (N) | |
| combined torque provided by the engine and motor in the process of driving the vehicle (N. m) | |
| wheel radius (m) | |
| difference between the actual vehicle speed and the reference speed (m/s) | |
| reference speed (m/s) | |
| actual vehicle speed (m/s) | |
| PHEB torque demand (Nm) | |
| battery pack resistance () | |
| calorific value of the fuel (J/kg) | |
| total equivalent fuel consumption (g/s) | |
| equivalent fuel consumption corresponding to the battery (g/s) | |
References
- Iris, Ç.; Lam, J.S.L. Optimal energy management and operations planning in seaports with smart grid while harnessing renewable energy under uncertainty. Omega 2021, 103, 102445. [Google Scholar] [CrossRef]
- Wang, Z.; Dridi, M.; El Moudni, A. Co-optimization of eco-driving and energy management for connected HEV/PHEVs near signalized intersections: A review. Appl. Sci. 2023, 13, 5035. [Google Scholar] [CrossRef]
- Li, Z.; Khajepour, A.; Song, J. A comprehensive review of the key technologies for pure electric vehicles. Energy 2019, 182, 824–839. [Google Scholar] [CrossRef]
- Pu, S.; Chu, L.; Hu, J.; Li, S.; Hou, Z. An Equivalent Consumption Minimization Strategy for a Parallel Plug-In Hybrid Electric Vehicle Based on an Environmental Perceiver. Sensors 2022, 22, 9621. [Google Scholar] [CrossRef] [PubMed]
- Guzzella, L.; Sciarretta, A. Vehicle Propulsion Systems, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2007; p. 22. [Google Scholar]
- Martinez, C.M.; Hu, X.; Cao, D.; Velenis, E.; Gao, B.; Wellers, M. Energy management in plug-in hybrid electric vehicles: Recent progress and a connected vehicles perspective. IEEE Trans. Veh. Technol. 2017, 66, 4534–4549. [Google Scholar] [CrossRef]
- Li, Y.; Tao, J.; Xie, L.; Zhang, R.; Ma, L.; Qiao, Z. Enhanced Q-learning for real-time hybrid electric vehicle energy management with deterministic rule. Meas. Control 2020, 53, 1493–1503. [Google Scholar] [CrossRef]
- Wirasingha, S.G.; Emadi, A. Classification and review of control strategies for plug-in hybrid electric vehicles. IEEE Trans. Veh. Technol. 2011, 60, 111–122. [Google Scholar] [CrossRef]
- Hao, L.; Wang, Y.; Bai, Y.; Zhou, Q. Energy management strategy on a parallel mild hybrid electric vehicle based on breadth first search algorithm. Energy Convers. Manag. 2021, 243, 114408. [Google Scholar] [CrossRef]
- Khayyam, H.; Bab-Hadiashar, A. Adaptive intelligent energy management system of plug-in hybrid electric vehicle. Energy 2014, 69, 319–335. [Google Scholar] [CrossRef]
- Banvait, H.; Anwar, S.; Chen, Y. A rule-based energy management strategy for plug-in hybrid electric vehicle (PHEV). In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3938–3943. [Google Scholar]
- Chaos, X. Research on Range-Extended Electric Vehicle Energy Management Strategy Based on Adaptive ECMS. Master’s Thesis, Zhejiang University, Hangzhou, China, 2021. [Google Scholar]
- Won, J.S.; Langari, R. Fuzzy torque distribution control for a parallel hybrid vehicle. Expert Syst. 2002, 19, 4–10. [Google Scholar] [CrossRef]
- Ming, L.V.; Ying, Y.; Liang, L.; Yao, L.; Zhou, W. Energy management strategy of a plug-in parallel hybrid electric vehicle using fuzzy control. Energy Procedia 2017, 105, 2660–2665. [Google Scholar] [CrossRef]
- Rault, J.; Richalet, A.; Testud, J.L.; Papon, J. Model predictive heuristic control: Application to industrial processes. Automatica 1978, 14, 413–428. [Google Scholar]
- Zhang, J. Research on Energy Management Strategy of Plug-In Hybrid Electric Bus Based on Model Predictive Control. Master’s Thesis, Beijing Institute of Technology University, Beijing, China, 2016. [Google Scholar]
- Chen, X.L. Model Predictive Control Based Energy Management for Connected Hybrid Electric Vehicles. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2022. [Google Scholar]
- Xiaohu, Y.; Rong, Y.; Shenglan, T.; Xionghou, Y.; Liang, F. MPGA-based-ECMS for energy optimization of a hybrid electric city bus with dual planetary gear. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 1889–1909. [Google Scholar]
- Chen, Z.; Liu, Y.; Zhang, Y.; Lei, Z.; Chen, Z.; Li, G. A neural network-based ECMS for optimized energy management of plug-in hybrid electric vehicles. Energy 2022, 243, 122727. [Google Scholar] [CrossRef]
- Gu, B.; Rizzoni, G. An adaptive algorithm for hybrid electric vehicle energy management based on driving pattern recognition. In Proceedings of the ASME 2006 International Mechanical Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006; pp. 249–258. [Google Scholar]
- Musardo, C.; Rizzoni, G.; Guezennec, Y.; Staccia, B. A-ECMS: An adaptive algorithm for hybrid electric vehicle energy management. Eur. J. Control 2005, 11, 509–524. [Google Scholar] [CrossRef]
- Zhang, S. Study on Adaptive Equivalent Fuel Consumption Energy Management Strategy for Plug-In Hybrid Electric Vehicles. Master’s Thesis, Jilin University, Changchun, China, 2017. [Google Scholar]
- Hou, S.; Yin, H.; Ma, Y.; Gao, J. Energy management strategy of hybrid electric vehicle based on ECMS in intelligent transportation environment. IFAC-PapersOnLine 2021, 54, 157–162. [Google Scholar] [CrossRef]
- Sun, C.; Sun, F.; He, H. Investigating adaptive-ECMS with velocity forecast ability for hybrid electric vehicles. Appl. Energy. 2017, 185, 1644–1653. [Google Scholar] [CrossRef]
- Tian, X.; Cai, Y.; Sun, X.; Zhu, Z.; Xu, Y. An adaptive ECMS with driving style recognition for energy optimization of parallel hybrid electric buses. Energy 2019, 189, 116151. [Google Scholar] [CrossRef]
- Lin, C.C.; Peng, H.; Grizzle, J.W.; Kang, J.M. Power management strategy for a parallel hybrid electric truck. IEEE Trans. Control Syst. Technol. 2003, 11, 839–849. [Google Scholar]
- Patil, R.M.; Kelly, J.C.; Filipi, Z.; Fathy, H.K. A framework for the integrated optimization of charging and power management in plug-in hybrid electric vehicles. IEEE Trans. Veh. Technol. 2013, 62, 2402–2412. [Google Scholar] [CrossRef]
- Zheng, C.; Xu, G.; Jeong, J.; Cha, S.W. A power management strategy for hybrid buses using measured driving route information. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference, Coimbra, Portugal, 27–30 October 2014; pp. 1–5. [Google Scholar]
- Yang, C.; Du, S.; Li, L.; You, S.; Yang, Y.; Zhao, Y. Adaptive real-time optimal energy management strategy based on equivalent factors optimization for plug-in hybrid electric vehicle. Appl. Energy 2017, 203, 883–896. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiao, X.; Li, L.; Yang, C.; Zhang, L.; Song, J. A hybrid dynamic programming-rule based algorithm for real-time energy optimization of plug-in hybrid electric bus. Sci. China Technol. Sci. 2014, 57, 2542–2550. [Google Scholar] [CrossRef]
- Zheng, C.; Cha, S.W. Real-time application of Pontryagin’s Minimum Principle to fuel cell hybrid buses based on driving characteristics of buses. Int. J. Precis. Eng. Manuf.-Green Tech. 2017, 4, 199–209. [Google Scholar] [CrossRef]
- Li, M.; Yan, M.; He, H.; Peng, J. Data-driven predictive energy management and emission optimization for hybrid electric buses considering speed and passengers prediction. J. Clean. Prod. 2021, 304, 127139. [Google Scholar] [CrossRef]
- Yan, M.; He, H.; Jia, H.; Li, M.; Xue, X. Model predictive control of the air-conditioning system for electric bus. Energ. Procedia 2017, 105, 2415–2421. [Google Scholar] [CrossRef]
- He, H.; Yan, M.; Sun, C.; Peng, J.; Li, M.; Jia, H. Predictive air-conditioner control for electric buses with passenger amount variation forecast☆. Appl. Energy. 2018, 227, 249–261. [Google Scholar] [CrossRef]
- Zhou, X.; Zou, L.; Ma, Y.; Gao, Z.; Wu, Y.; Yin, J.; Xu, X. The current research on electric vehicle. In Proceedings of the 2016 Chinese Control and Decision Conference, Chengdu, China, 28–30 May 2016; pp. 5190–5194. [Google Scholar]
- Kuang, X. Management Strategy Research on Wired and Wireless Charging of Electric Vehicles. Ph.D. Thesis, University of Electronic Science and Technology, Chengdu, China, 2019. [Google Scholar]
- Hao, M.J. Method for Deployment of Wireless Charging Facilities for Electric Bus Routes under Bus-Only Lane Conditions. Master’s Thesis, Jilin University, Changchun, China, 2022. [Google Scholar]
- Li, S.; Mi, C.C. Wireless power transfer for electric vehicle applications. IEEE J. Emerg. Sel. Topics Power Electron. 2014, 3, 4–17. [Google Scholar]
- Zhang, M. Design of Dynamic Wireless Charging System for Electric Vehicles and Research on Charging Control Strategy. Master’s Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Galigekere, V.P.; Pries, J.; Onar, O.C.; Su, G.J.; Anwar, S.; Wiles, R.; Wilkins, J. Design and implementation of an optimized 100 kW stationary wireless charging system for EV battery recharging. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition, Portland, OR, USA, 23–27 September 2018; pp. 3587–3592. [Google Scholar]
- Dai, Z. Scania’s New Wireless Bus System to be Tested in Sweden. Commer. Veh. 2015, 1, 62. [Google Scholar]
- Nahum, O.E.; Hadas, Y. Multi-objective optimal allocation of wireless bus charging stations considering costs and the environmental impact. Sustainability 2020, 12, 2318. [Google Scholar] [CrossRef]
- Ahmadian, A.; Sedghi, M.; Aliakbar-Golkar, M. Fuzzy load modeling of plug-in electric vehicles for optimal storage and DG planning in active distribution network. IEEE Trans. Veh. Technol. 2016, 66, 3622–3631. [Google Scholar] [CrossRef]
- Schäuble, J.; Kaschub, T.; Ensslen, A.; Jochem, P.; Fichtner, W. Generating electric vehicle load profiles from empirical data of three EV fleets in Southwest Germany. J. Clean. Prod. 2017, 150, 253–266. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Gao, Z.Y.; Zheng, J.F.; Du, H.M. Charging station location problem of plug-in electric vehicles. J. Transp. Geogr. 2016, 52, 11–22. [Google Scholar] [CrossRef]
- Chau, C.K.; Elbassioni, K.; Tseng, C.M. Drive mode optimization and path planning for plug-in hybrid electric vehicles. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3421–3432. [Google Scholar] [CrossRef]
- Zhang, F. Research on Control Strategy Optimization of Parallel Hybrid Electric Bus in Vehicular ad Hoc Network Environment. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2018. [Google Scholar]
- Song, P.X. Research on Duty Cycle Prediction and Intelligent Energy Management Strategy for Plug-In Hybrid Electric Buses. Ph.D. Thesis, Jilin University, Changchun, China, 2021. [Google Scholar]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Wang, X.M. Research on Powertrain Matching and Control Optimization of Plug-In Hybrid City Buses. Ph.D. Thesis, Beijing Institute of Technology University, Beijing, China, 2015. [Google Scholar]
- Pelletier, S.; Jabali, O.; Laporte, G. The electric vehicle routing problem with energy consumption uncertainty. Transp. Res. Part B Methodol. 2019, 126, 225–255. [Google Scholar] [CrossRef]
- LI, Y.F. Research on Heavy Vehicle Mass Identification and Road Grade Estimation Method. Master’s Thesis, Jilin University, Changchun, China, 2012. [Google Scholar]
- Chen, W.M. Research on Online Parameter Identification of Permanent Magnet Synchronous Motors. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2020. [Google Scholar]
- Wehbi, L.; Bektaş, T.; Iris, Ç. Optimising vehicle and on-foot porter routing in urban logistics. Transp. Res. Part D Transp. Environ. 2022, 109, 103371. [Google Scholar] [CrossRef]
- Basso, R.; Kulcsár, B.; Sanchez-Diaz, I. Electric vehicle routing problem with machine learning for energy prediction. Transp. Res. Part B Methodol. 2021, 145, 24–55. [Google Scholar] [CrossRef]




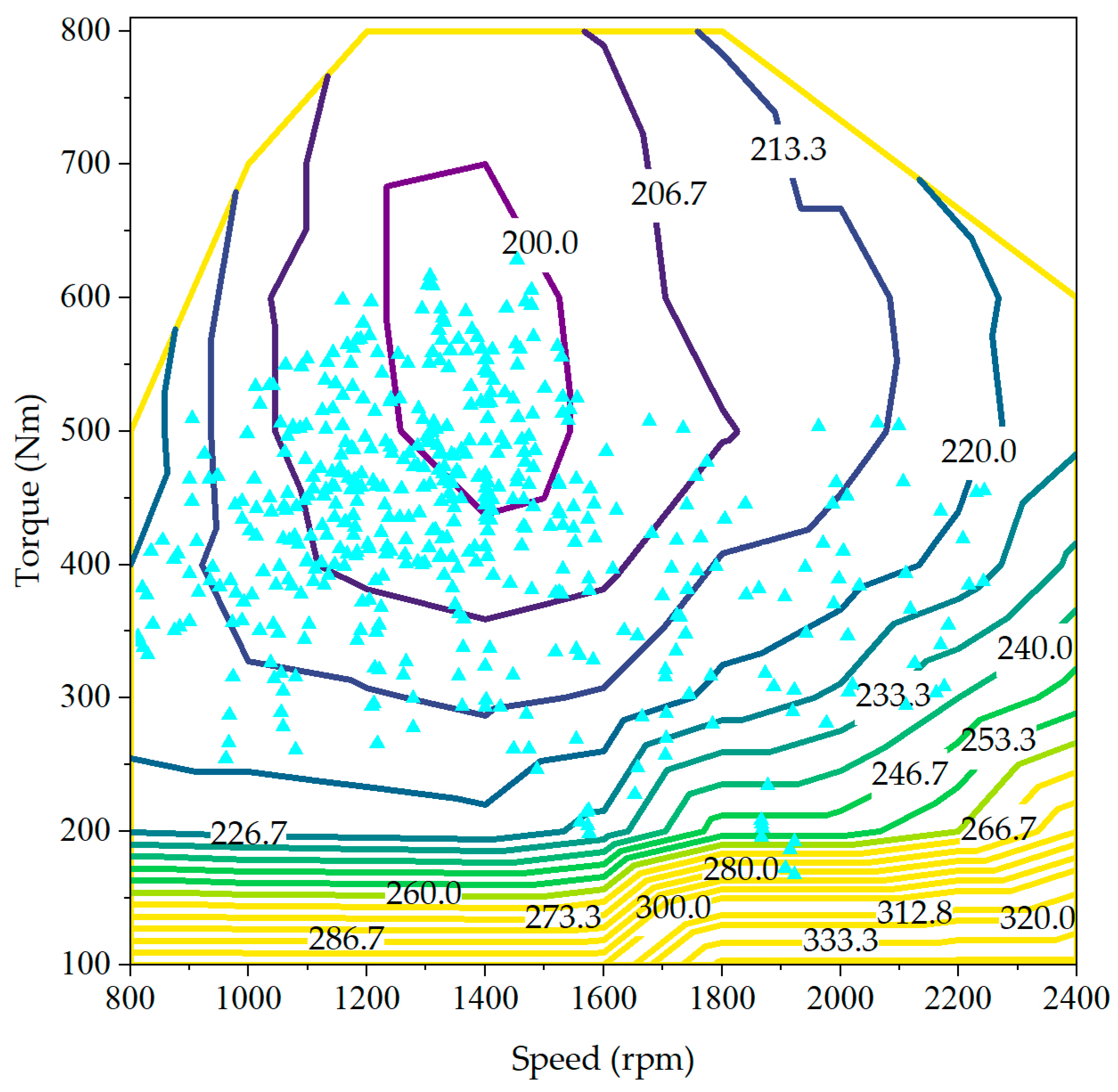

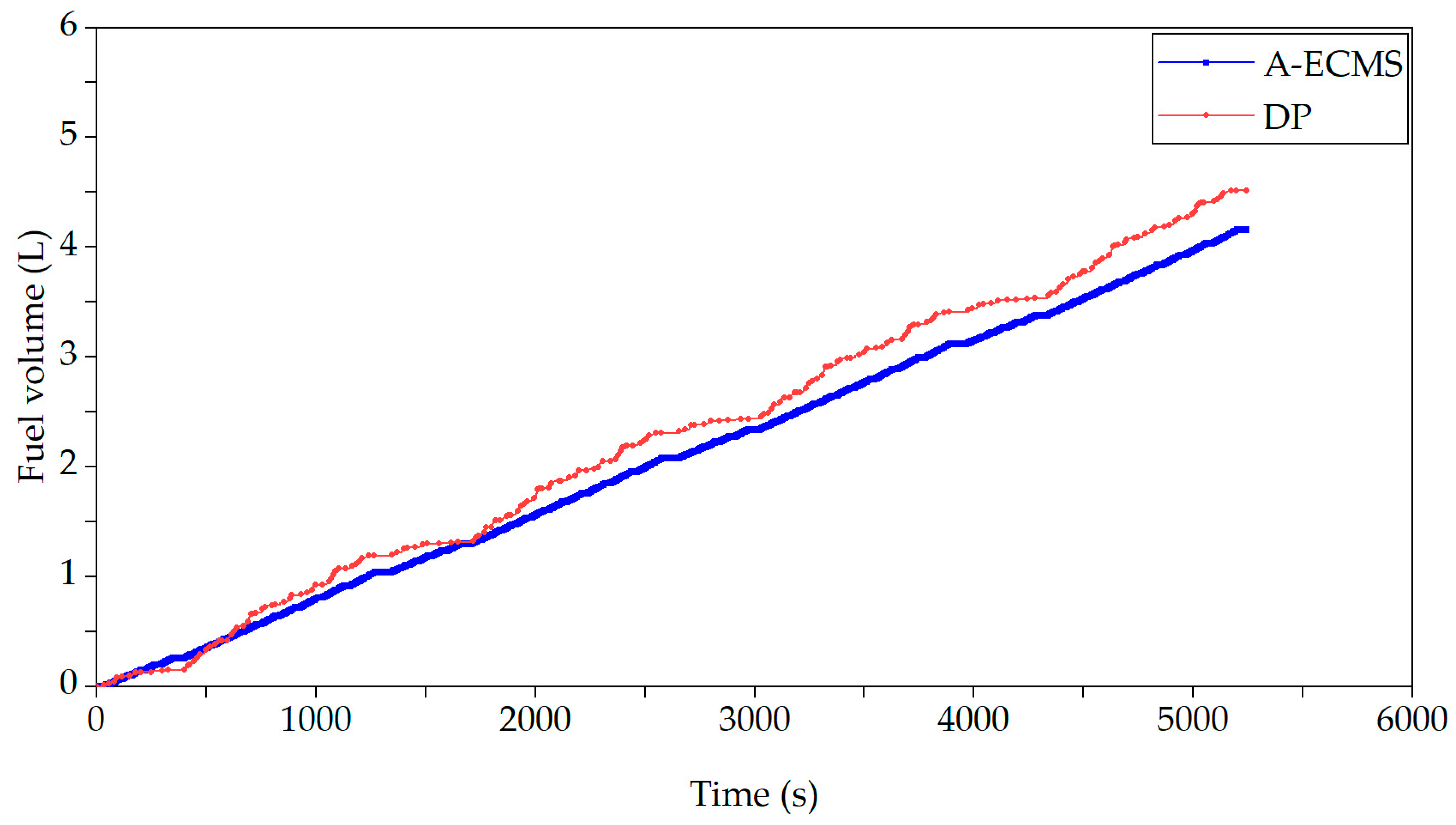
| Parameters | Values |
|---|---|
| Over mass/kg | 11,800 |
| Full load mass/kg | 16,300 |
| Peak engine power/kW | 150 |
| Peak engine torque/Nm | 800 |
| Peak motor power/kW | 160 |
| Peak motor torque/Nm | 1000 |
| Battery capacity/Ah | 50 |
| Equivalent Factor | Fitness |
|---|---|
| 4.96 | 29.11 |
| 5.67 | 40.35 |
| 5.09 | 35.35 |
| 3.33 | 217.9 |
| 4.41 | 19.66 |
| 4.62 | 24.46 |
| 5.46 | 37.66 |
| 5.48 | 38.88 |
| 4.74 | 22.25 |
| 5.09 | 35.35 |
| Equivalent Factor | Fitness |
|---|---|
| 4.51 | 3.145 |
| 4.51 | 3.145 |
| 4.51 | 3.145 |
| 4.51 | 3.145 |
| 4.51 | 3.145 |
| 4.51 | 3.145 |
| 4.51 | 3.145 |
| 4.51 | 3.145 |
| 4.51 | 3.145 |
| 4.51 | 3.145 |
| Bus Station | Load | Optimal Equivalent Factor |
|---|---|---|
| 1 | Heavy | 4.38 |
| 2 | Medium | 4.10 |
| 3 | Light | 4.23 |
| 4 | Medium | 4.30 |
| 5 | Light | 4.52 |
| 6 | Light | 4.51 |
| 7 | Heavy | 3.96 |
| 8 | Light | 4.34 |
| 9 | Light | 4.44 |
| 10 | Light | 4.52 |
| 11 | Heavy | 4.52 |
| 12 | Medium | 4.02 |
| 13 | Heavy | 4.29 |
| 14 | Heavy | 4.33 |
| 15 | Medium | 4.22 |
| 16 | Light | 4.22 |
| 17 | Medium | 4.35 |
| 18 | Heavy | 4.50 |
| EMS | Fuel Consumption (L/100 km) | Electricity Consumption (kWh/100 km) |
|---|---|---|
| Rule-based EMS | 25.1 | 32.75 |
| ECMS | 23.15 | 35.5 |
| A-ECMS | 22.55 | 36.55 |
| DP | 21.83 | -- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, P.; Song, W.; Meng, A.; Li, H. Adaptive Equivalent Factor-Based Energy Management Strategy for Plug-In Hybrid Electric Buses Considering Passenger Load Variations. Energies 2024, 17, 1283. https://doi.org/10.3390/en17061283
Song P, Song W, Meng A, Li H. Adaptive Equivalent Factor-Based Energy Management Strategy for Plug-In Hybrid Electric Buses Considering Passenger Load Variations. Energies. 2024; 17(6):1283. https://doi.org/10.3390/en17061283
Chicago/Turabian StyleSong, Pengxiang, Wenchuan Song, Ao Meng, and Hongxue Li. 2024. "Adaptive Equivalent Factor-Based Energy Management Strategy for Plug-In Hybrid Electric Buses Considering Passenger Load Variations" Energies 17, no. 6: 1283. https://doi.org/10.3390/en17061283
APA StyleSong, P., Song, W., Meng, A., & Li, H. (2024). Adaptive Equivalent Factor-Based Energy Management Strategy for Plug-In Hybrid Electric Buses Considering Passenger Load Variations. Energies, 17(6), 1283. https://doi.org/10.3390/en17061283





