Two Types of Asymmetric Switched-Capacitor Five-Level Single-Phase DC-AC Inverters for Renewable Energy Applications
Abstract
1. Introduction
1.1. Motivations
1.2. Statement of the Related Works
1.3. Contributions
2. Operating Principles of the Proposed Inverters
2.1. Symbol Definitions and Circuit Assumptions
- (1)
- Vin is the input voltage, vo is the output voltage, N is the reference point of zero potential, and Ro is the output resistance;
- (2)
- Lo1 and Lo2 are filter inductors, Co is a filter capacitor, and C1 to C4 are clamping capacitors;
- (3)
- iL is the current flowing through inductors Lo1 and Lo2, iCo is the current flowing through capacitor Co, and io is the output current;
- (4)
- S1 to S8 are switches and D1 to D4 are diodes;
- (5)
- Assuming that the values of the clamping capacitors are large enough, the voltages across them can be reviewed as constant values;
- (6)
- All components are assumed to be ideal.
2.2. Operating Principles for Two Proposed Types of Circuits
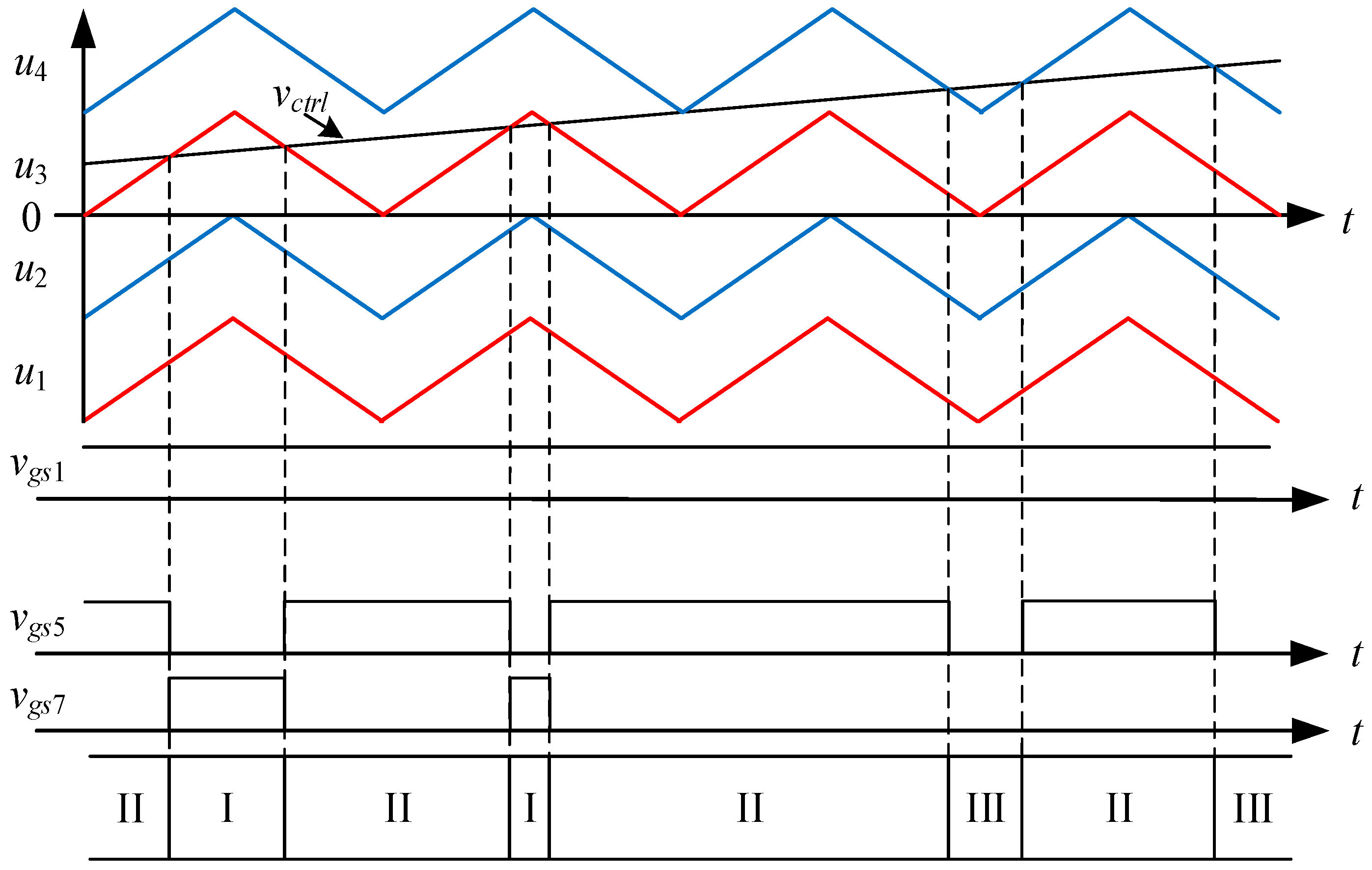
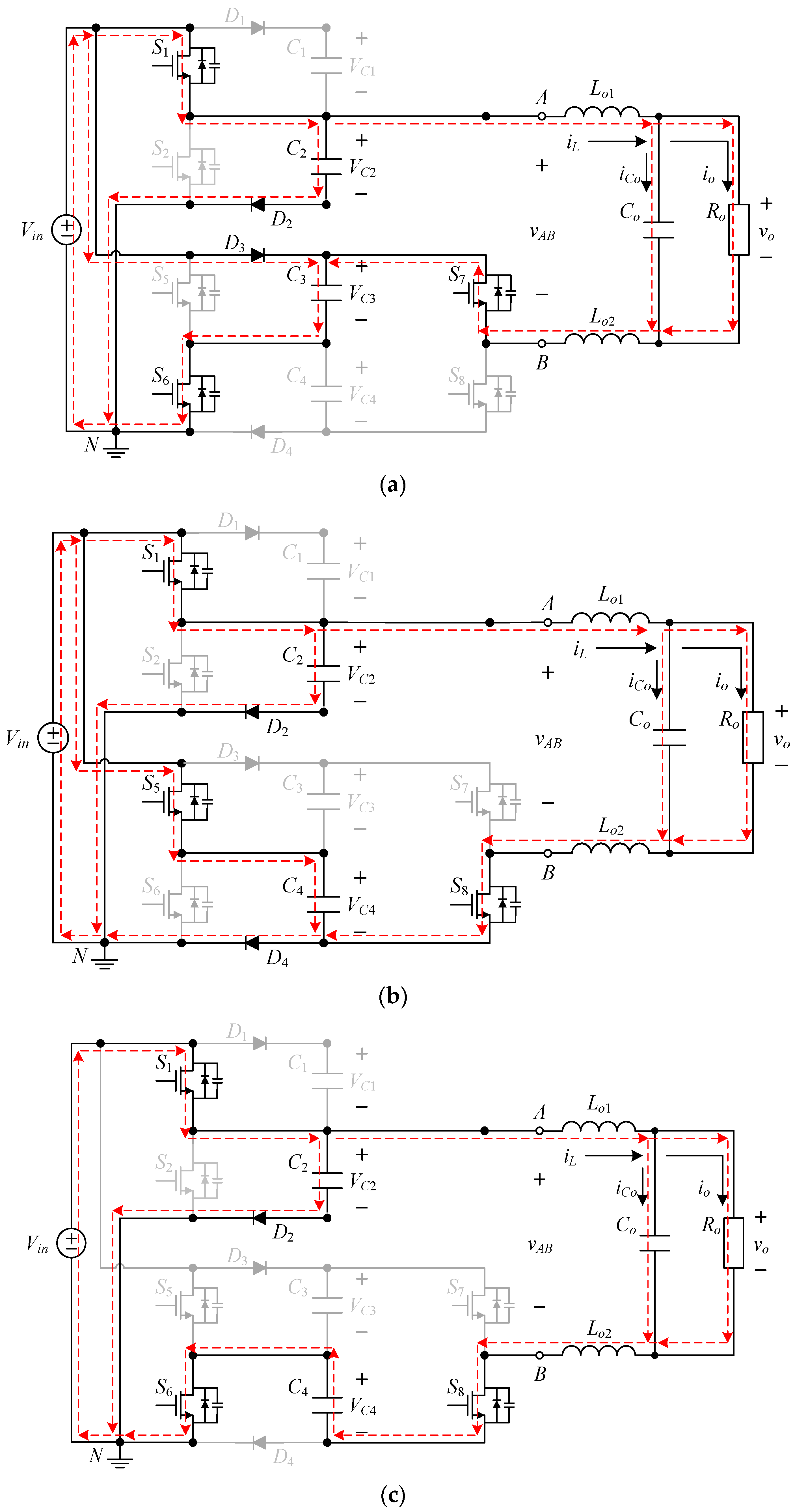
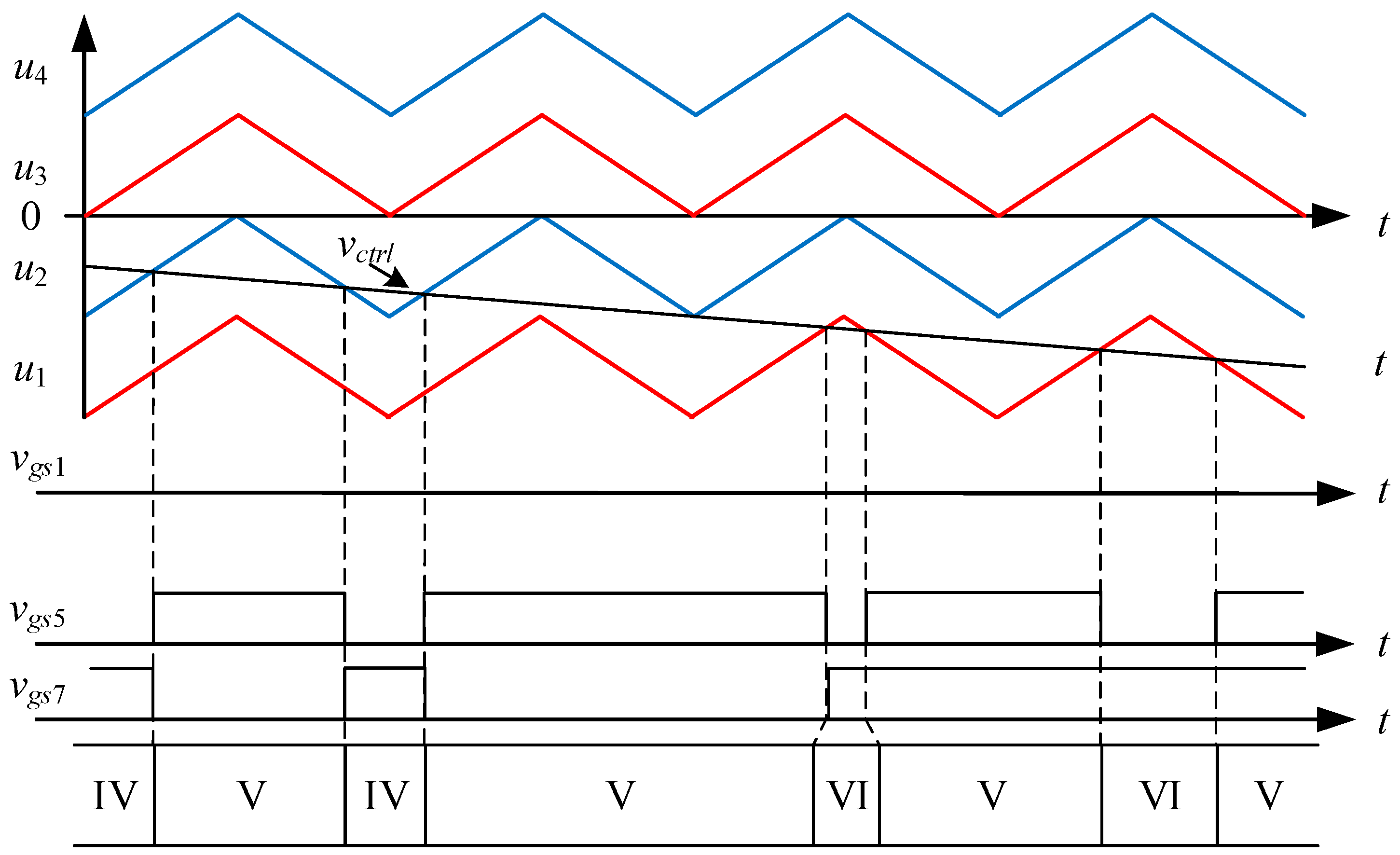
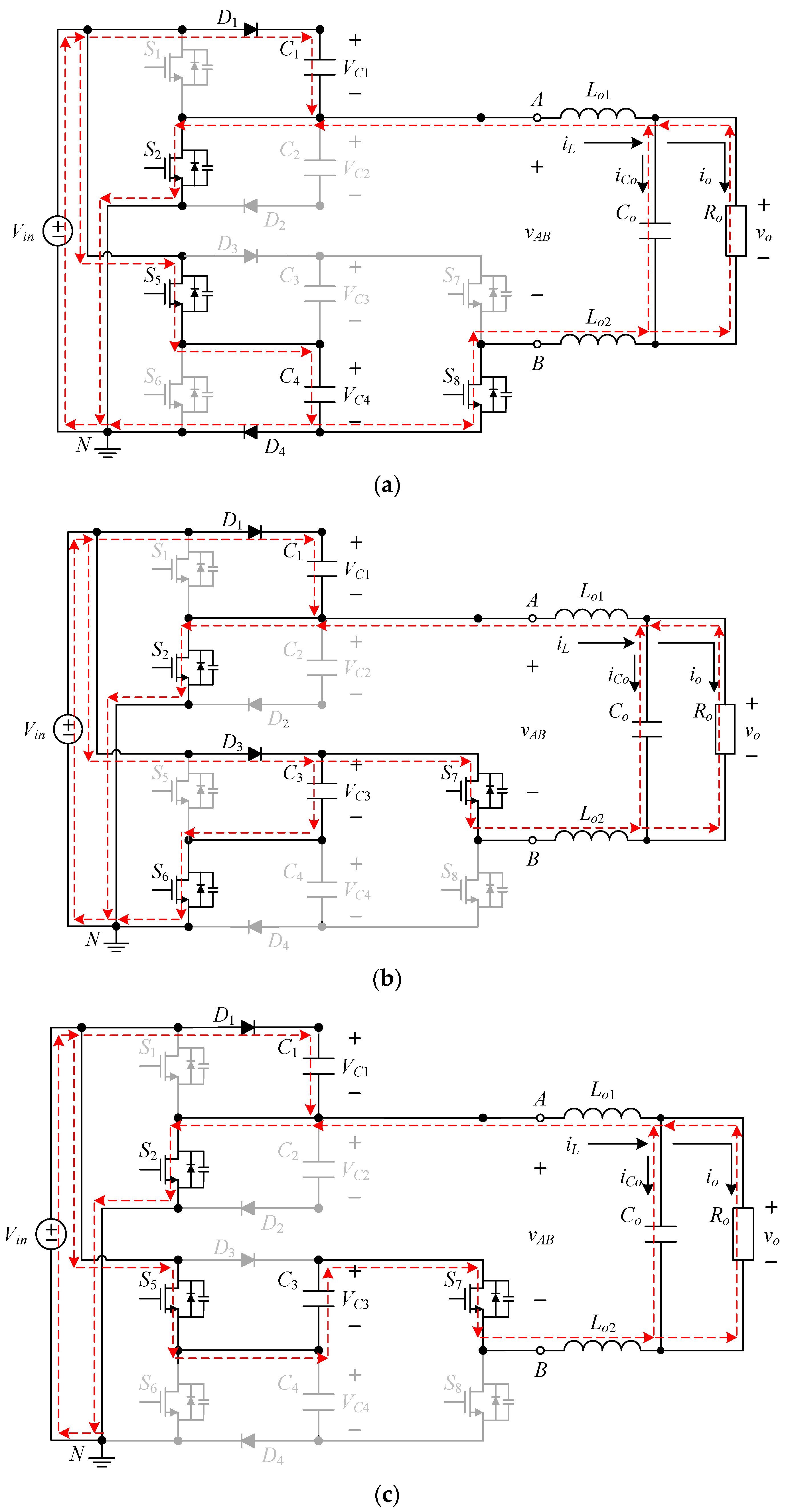
2.2.1. Type-1 Circuit
2.2.2. Type-2 Circuit
2.3. Converter Component Operating Behavior
3. System Design
3.1. System Configuration
3.2. Design of Clamping Capacitor
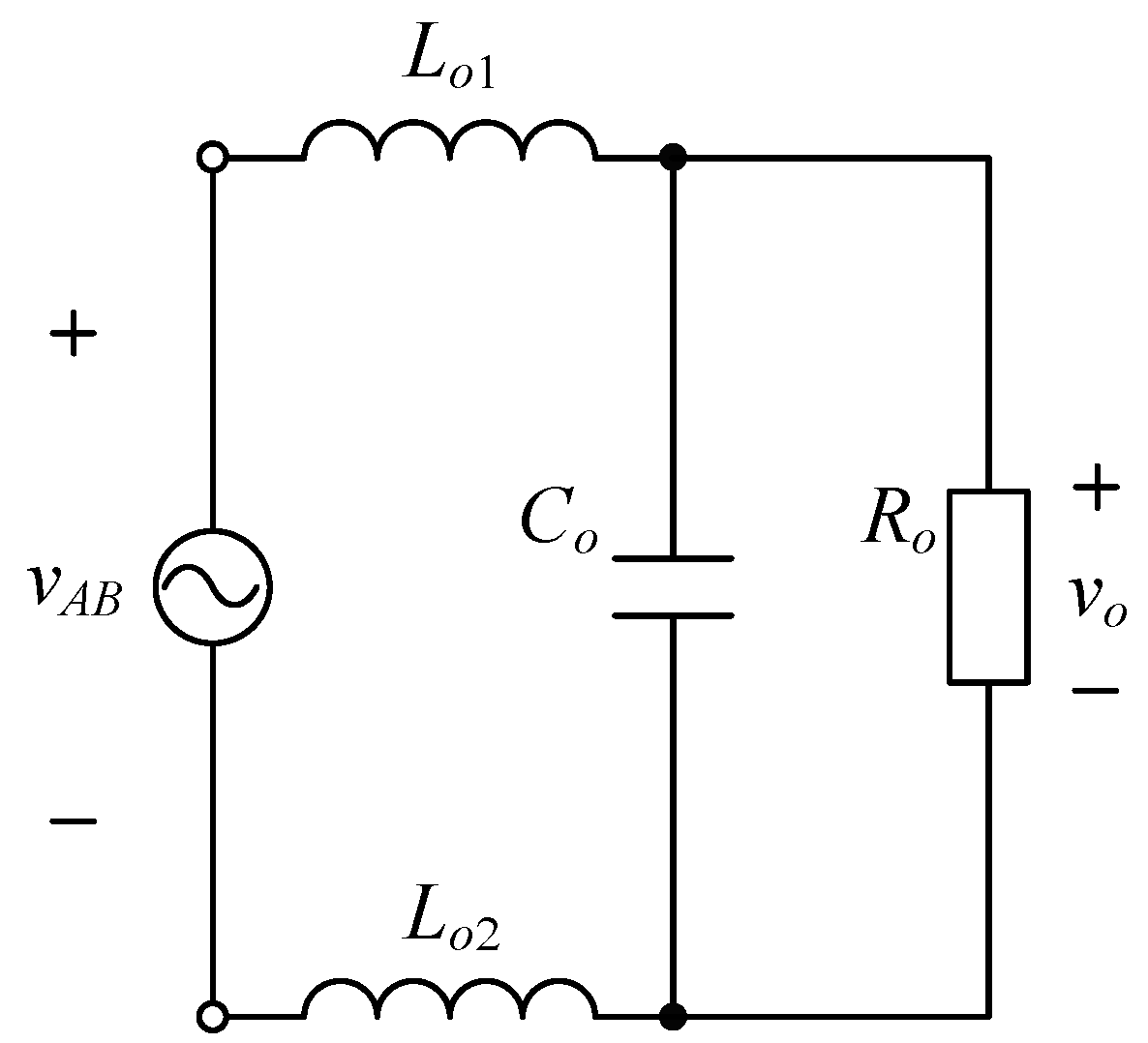
3.3. Design of High Frequency Low-Pass Filter
4. Verification Based on Simulation and Experiment
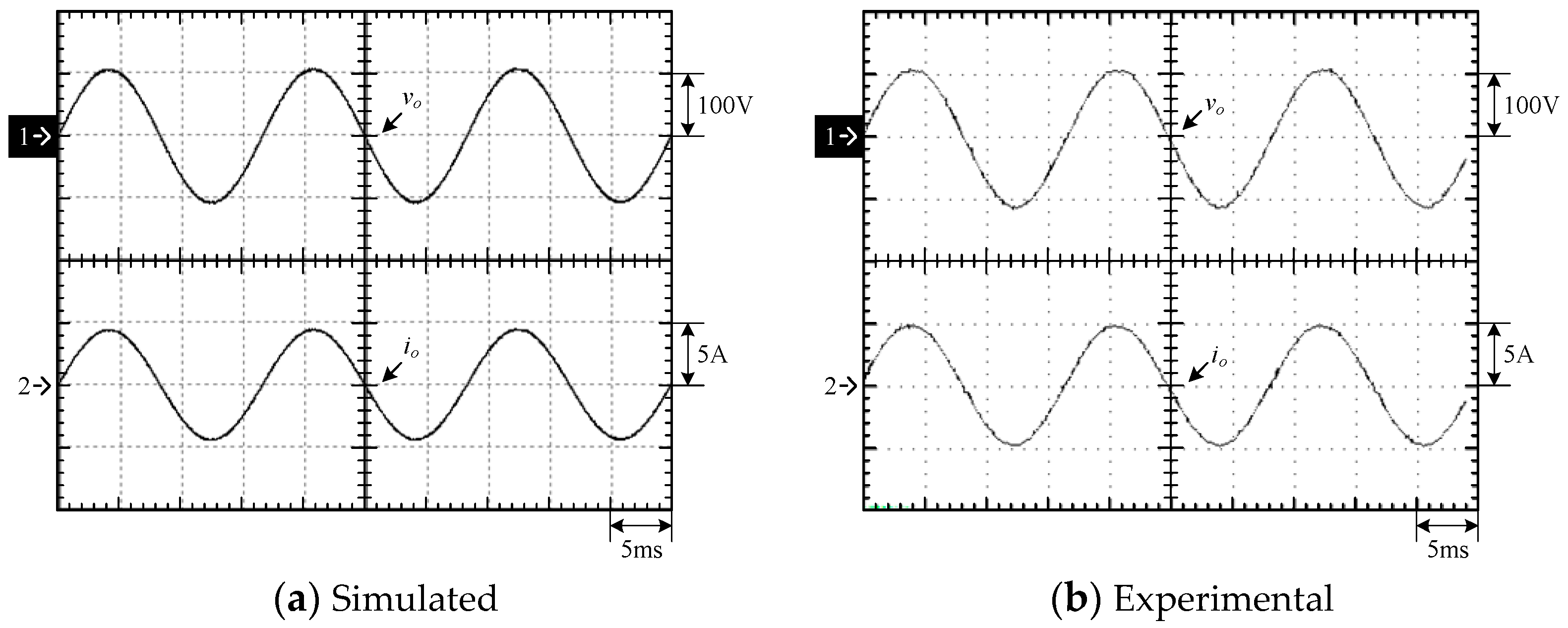
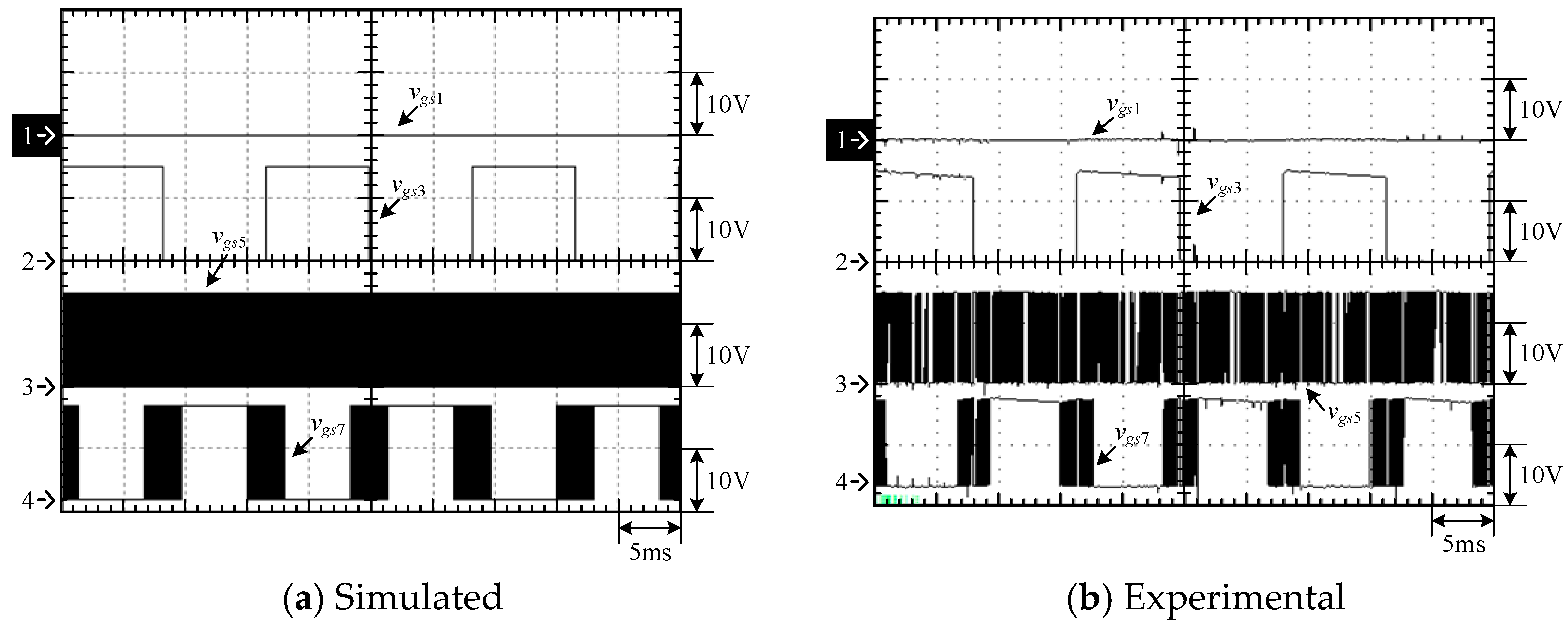
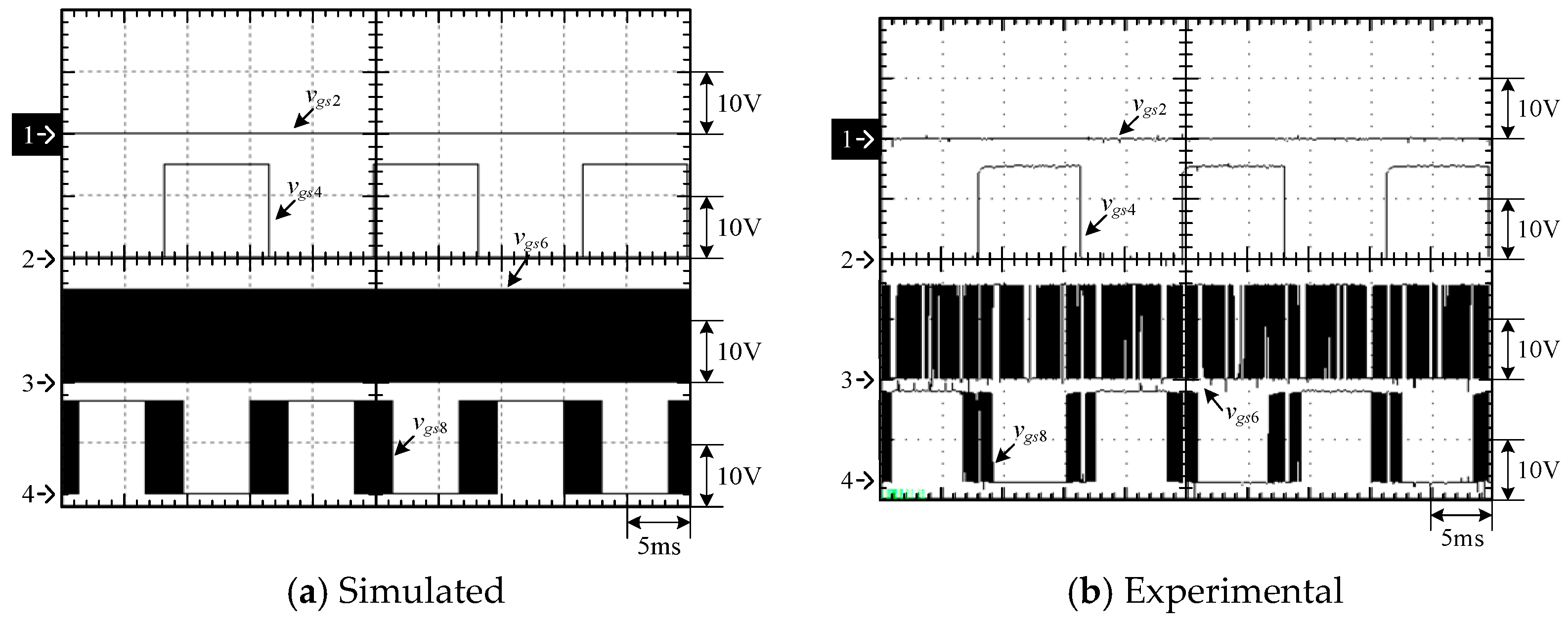
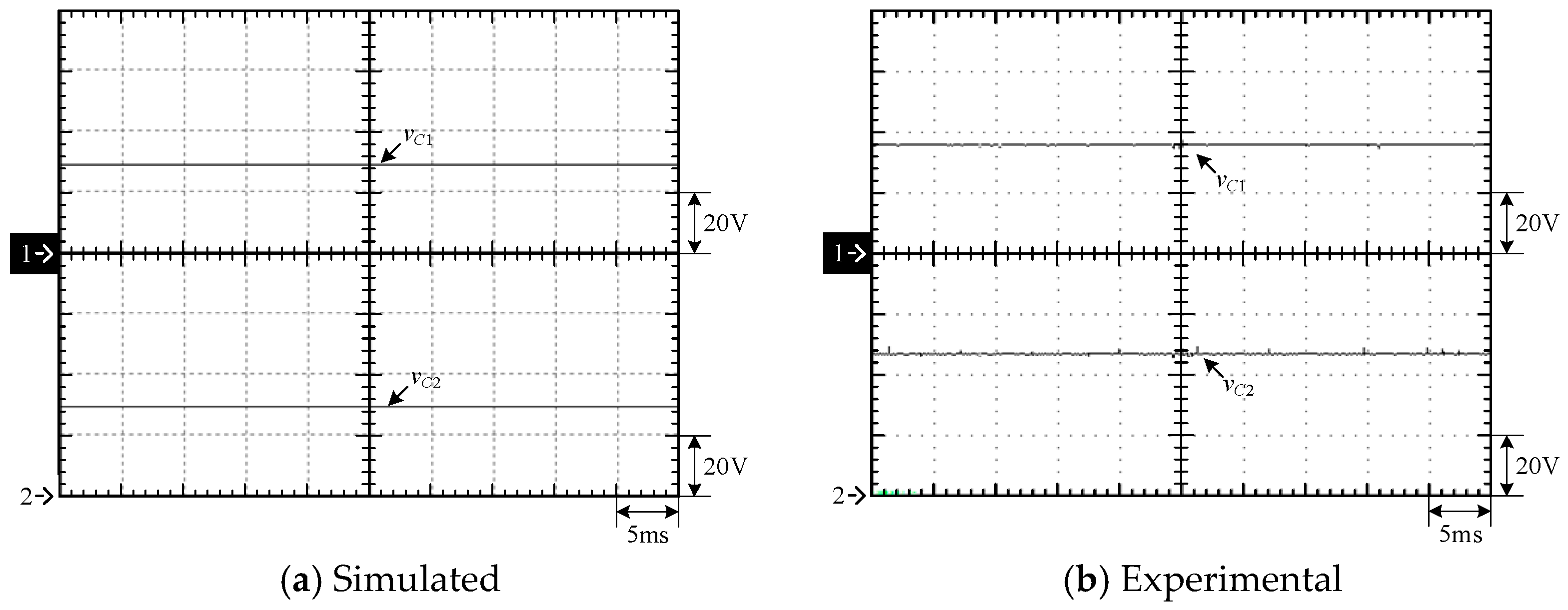
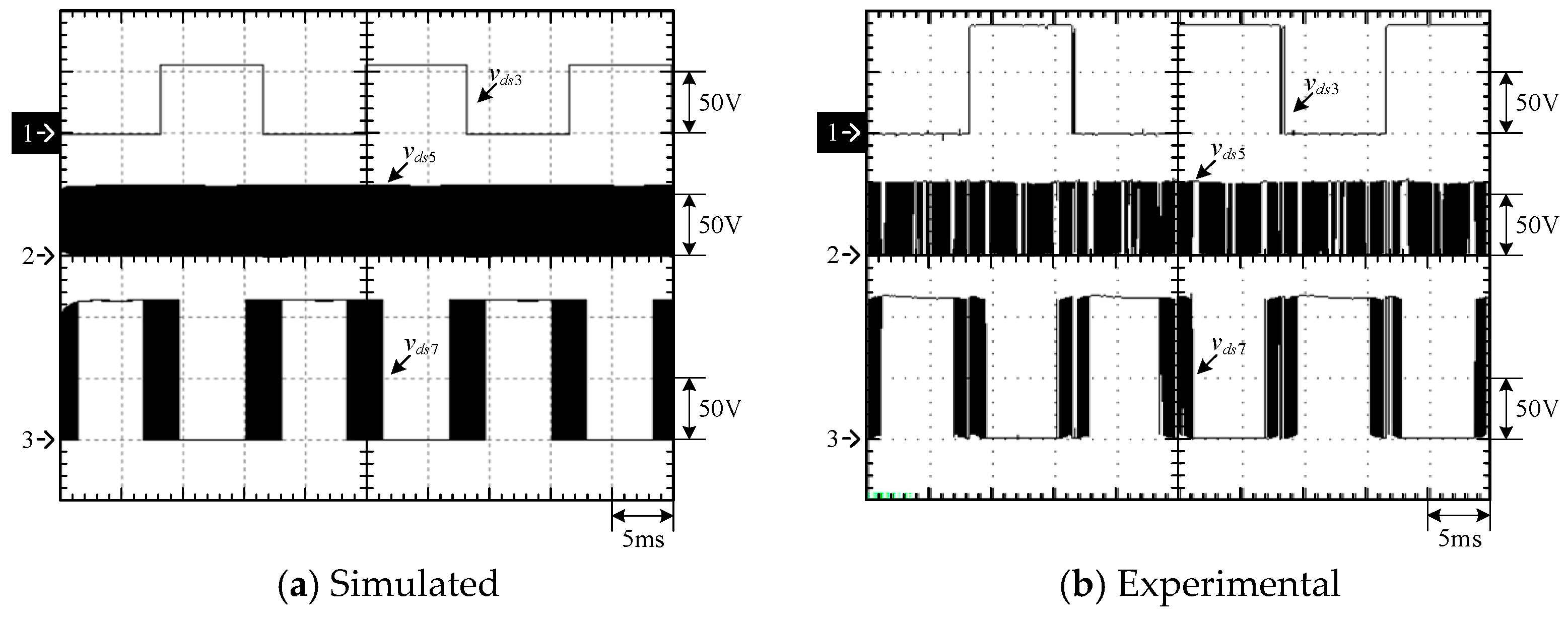
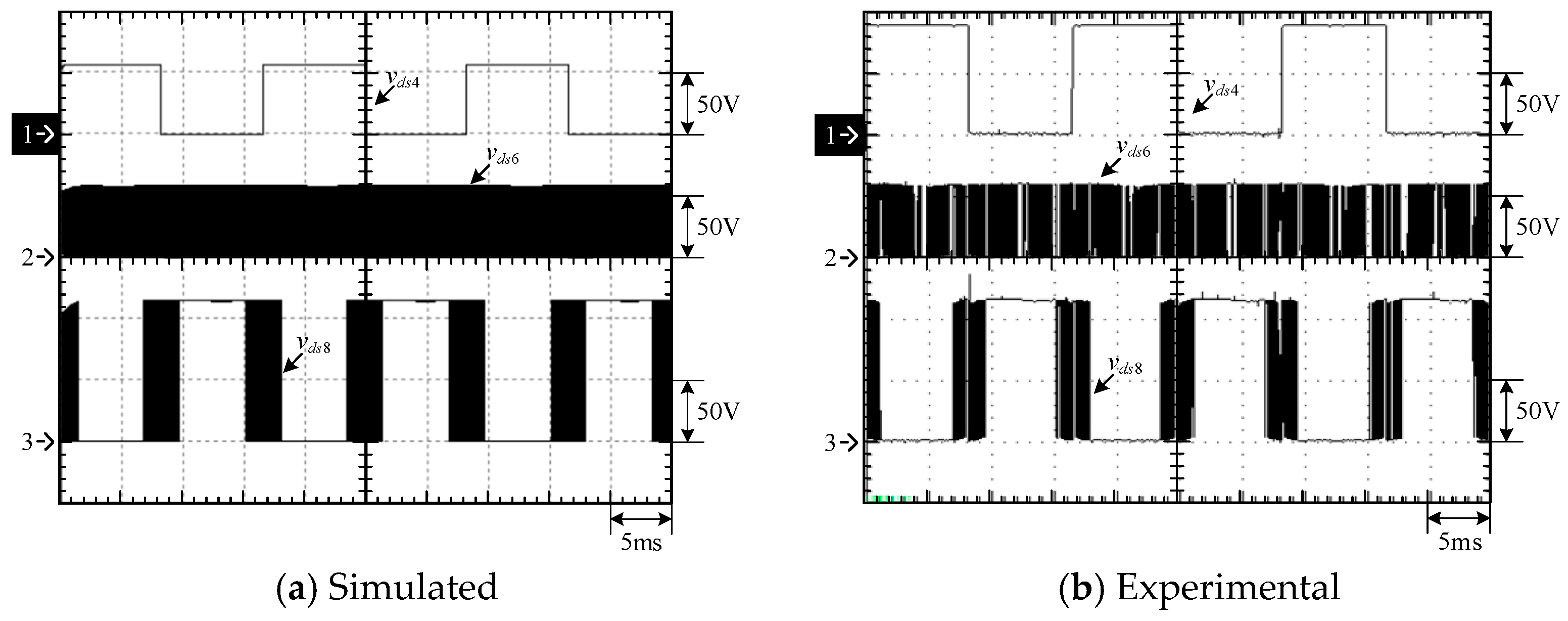
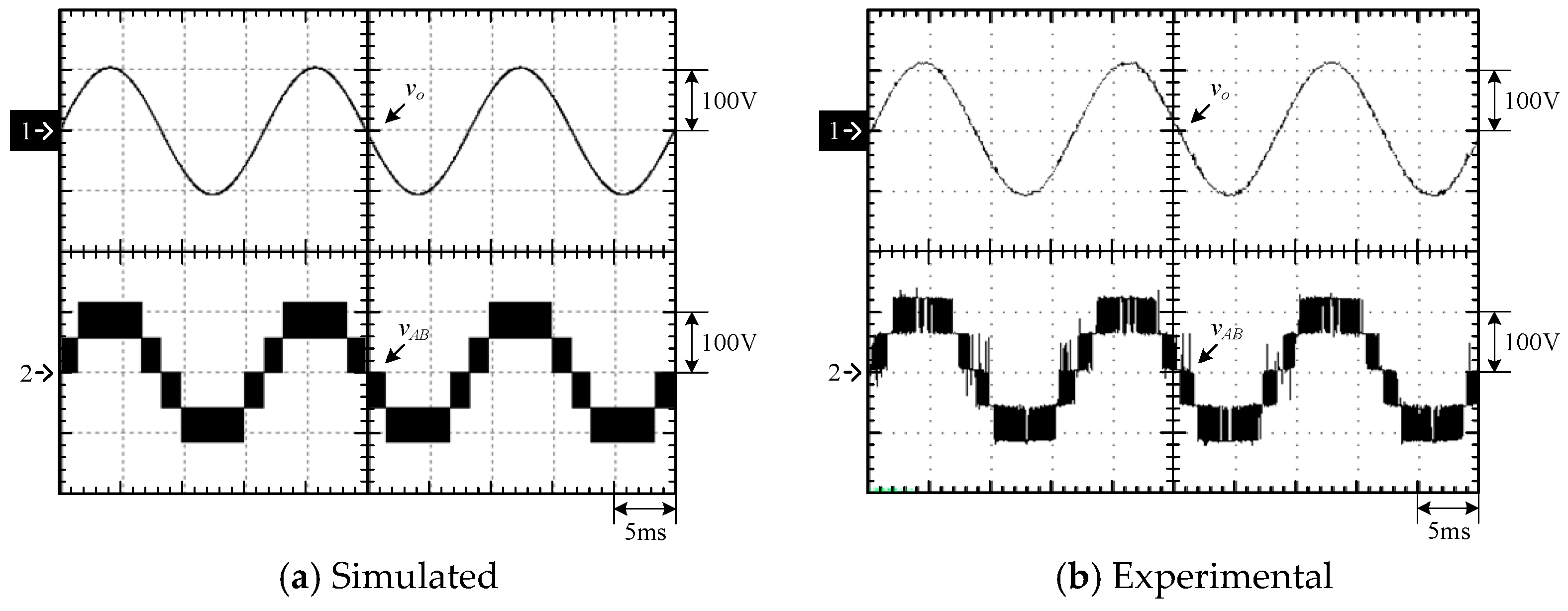
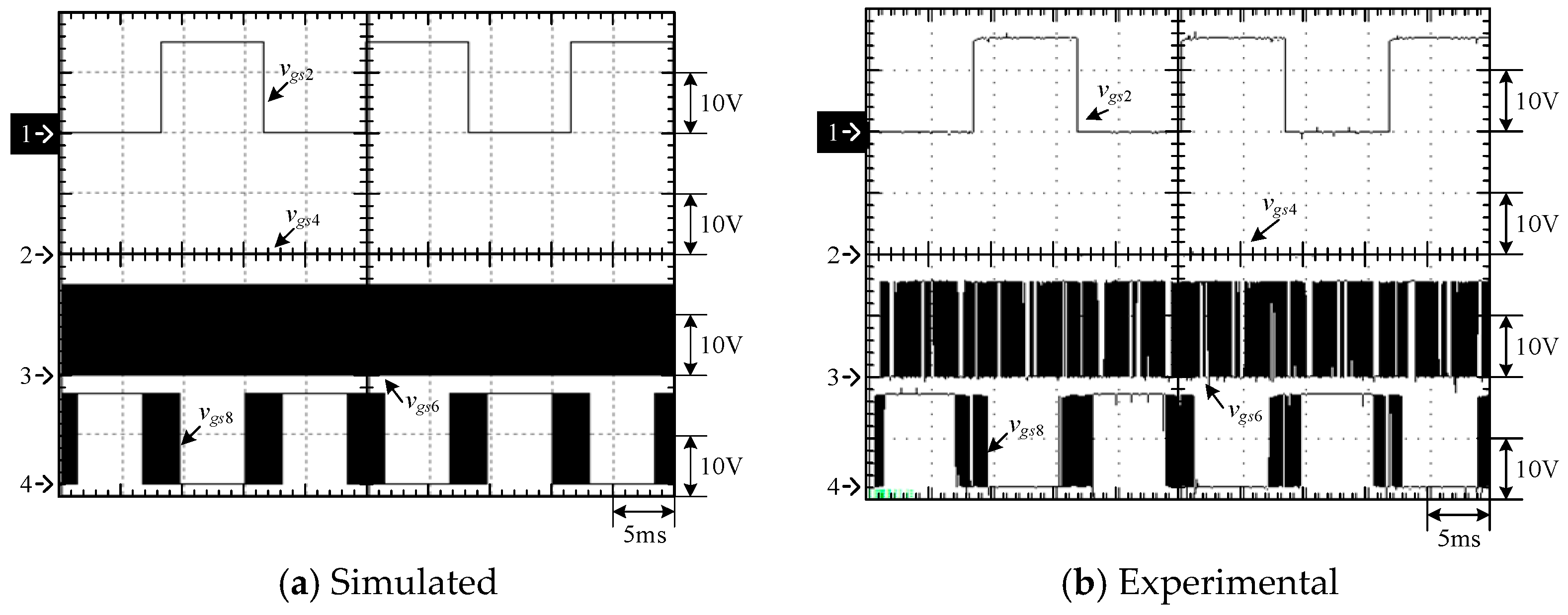
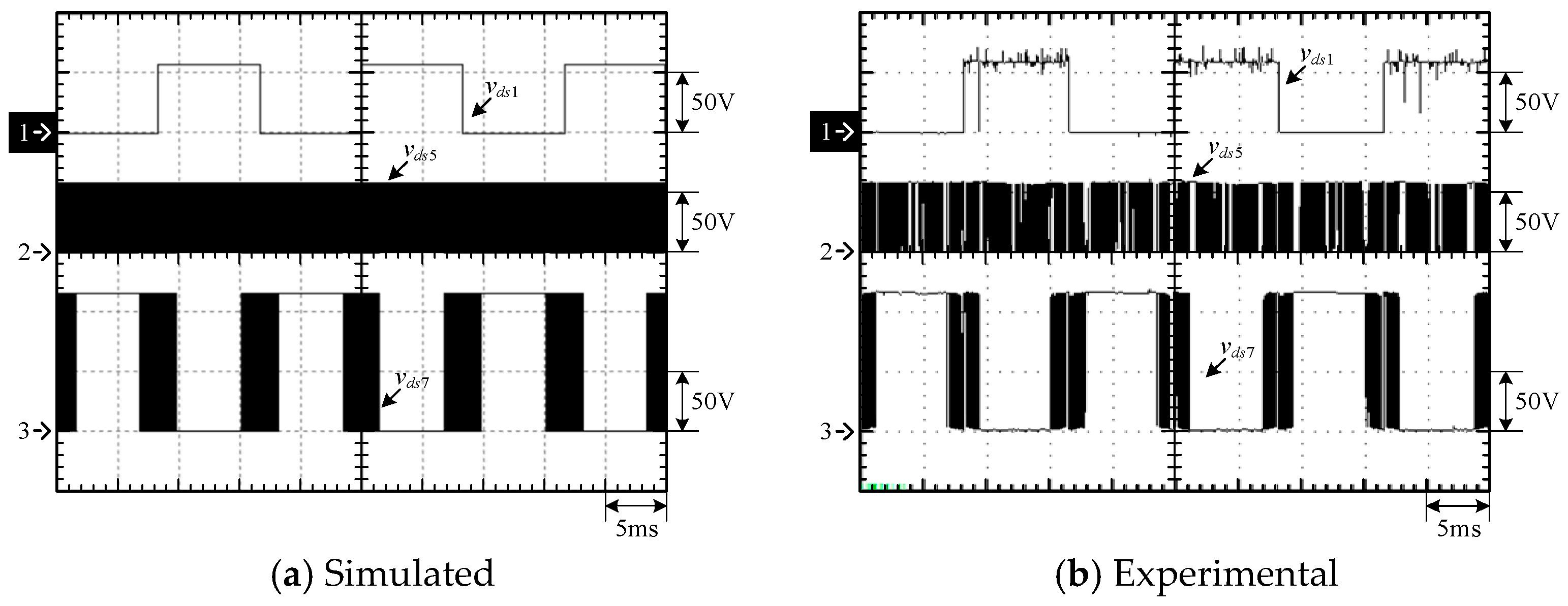
4.1. Simulated and Experimental Waveforms of Type-1 Circuit
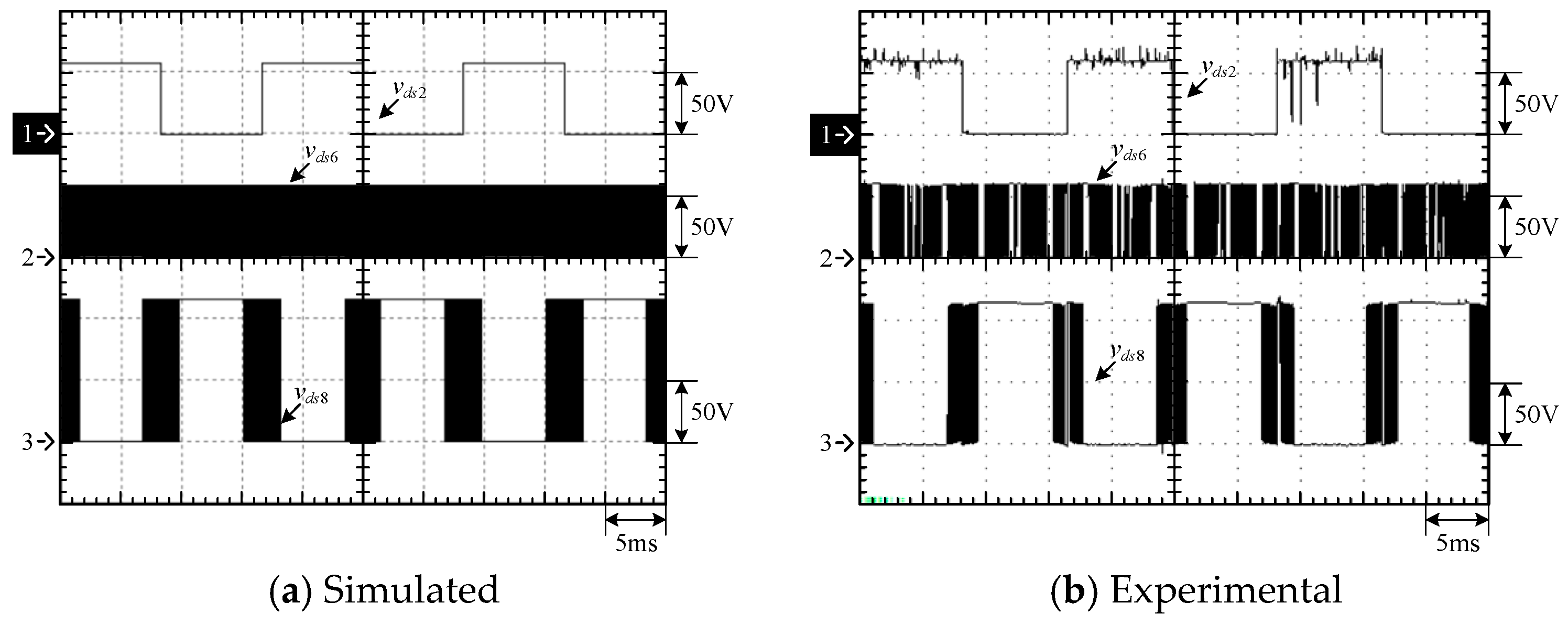
4.2. Simulated and Experimental Waveforms s of Type-2 Circuit
4.3. Waveform Comparison of the Two Types
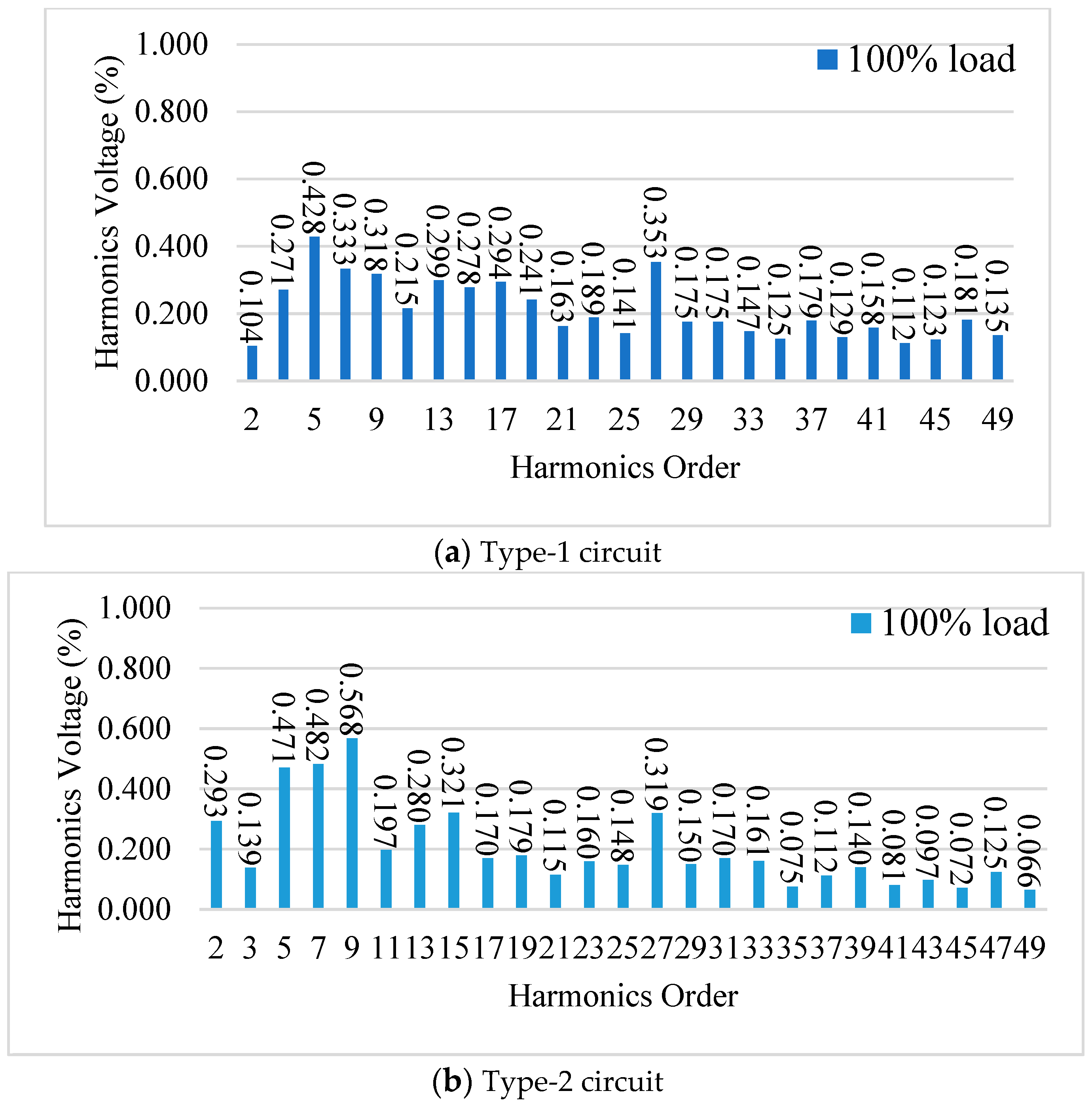
4.4. Harmonic Distribution and Efficiency of Two Types
4.5. Comparison between the Recent Related MLIs
5. Conclusions
6. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sen, P.; Jha, V.; Sahoo, A.K. Inrush current minimization in reduced device count multilevel inverter interfacing PV system. In Proceedings of the IEEE International Conference on Energy, Power and Environment: Towards Clean Energy Technologies, Shillong, India, 5–7 March 2021; pp. 1–6. [Google Scholar]
- Ui-Min, C.; June-Seok, L. Single-phase five-level IT-type NPC inverter with improved efficiency and reliability in photovoltaic systems. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 5226–5239. [Google Scholar]
- Shi, S.; Lo, K.L. An overview of wind energy development and associated power system reliability evaluation methods. In Proceedings of the 48th International Universities’ Power Engineering Conference (UPEC), Dublin, Ireland, 2–5 September 2013; pp. 1–6. [Google Scholar]
- Shi, X.; Shi, X.; Dong, W.; Zang, P.; Jia, H.; Wu, J.; Wang, Y. Research on energy storage configuration method based on wind and solar volatility. In Proceedings of the 10th International Conference on Power and Energy Systems (ICPES), Chengdu, China, 25–27 December 2020; pp. 464–468. [Google Scholar]
- Grigoras, G.; Bizon, N.; Enescu, F.M.; Guede, J.M.L.; Salado, G.F.; Brennan, R.; Dinka, M.O.; Alalm, M.G. ICT based smart management solution to realize water and energy savings through energy efficiency measures in water distribution systems. In Proceedings of the 10th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Iasi, Romania, 28–30 June 2018; pp. 1–4. [Google Scholar]
- Abe, B.T.; Shrivastava, P.; Moloi, K. A review of energy consumption in water supply systems. In Proceedings of the 2019 IEEE AFRICON, Accra, Ghana, 25–27 September 2019; pp. 1–4. [Google Scholar]
- Radwan, J.; Zaid, A.I.O. Geothermal energy in palestine practical applications. In Proceedings of the 2015 Power Generation System and Renewable Energy Technologies (PGSRET), Islamabad, Pakistan, 10–11 June 2015; pp. 1–4. [Google Scholar]
- Assad, M.E.H.; Shamsi, A.A.; Almheiri, M.; Alhefeiti, H.; Alshawab, M.; Shabi, M.A.; AlMallahi, M.N. Design of incubator powered by geothermal energy. In Proceedings of the Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 21–24 February 2022; pp. 1–4. [Google Scholar]
- Rosli, R.; Dimla, E. A review of tidal current energy resource assessment: Current status and trend. In Proceedings of the 5th International Conference on Renewable Energy: Generation and Applications (ICREGA), Al Ain, United Arab Emirates, 25–28 February 2018; pp. 34–40. [Google Scholar]
- Warak, P.; Goswami, P. Overview of generation of electricity using tidal energy. In Proceedings of the IEEE STPEC’20, Nagpur, India, 25–26 September 2020; pp. 1–6. [Google Scholar]
- Farhad, M.H.; Malek, A.B.M.A.; Hasanuzzman, M.; Rahim, N.A. Technical review on biomass conversion processes into required energy form. In Proceedings of the IEEE CEAT’13, Langkawi, Malaysia, 18–20 November 2013; pp. 208–213. [Google Scholar]
- Zhen, X.; Luo, M.; Bai, Y.; Zhang, X.; Li, S.; Tan, C. Rresearch on cogeneration system of heat and electricity biogas based on solar energy and biomass energy. In Proceedings of the 3rd International Conference on Advanced Electrical and Energy Systems (AEES), Lanzhou, China, 23–25 September 2022; pp. 502–507. [Google Scholar]
- Subbulakshmy, R.; Palanisamy, R.; Alshahrani, S.; Saleel, C.A. Implementation of non-isolated high gain interleaved DC-DC converter for fuel cell electric vehicle using ann-based mppt controller. Sustainability 2024, 16, 1335. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Electro-thermal model-based design of bidirectional on-board chargers in hybrid and full electric vehicles. Electronics 2022, 11, 112. [Google Scholar] [CrossRef]
- Fengjiang, W.; Xiaoguang, L.; Fan, F.; Hoay, B.G. Modified cascaded multilevel grid-connected inverter to enhance European efficiency and several extended topologies. IEEE Trans. Ind. Inform. 2015, 11, 1358–1365. [Google Scholar]
- Benedetti, D.; Agnelli, J.; Gagliardi, A.; Dini, P.; Saponara, S. Design of an off-grid photovoltaic carport for a full electric vehicle recharging. In Proceedings of the IEEE EEEIC/I&CPS Europe’20, Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar]
- Rasool, H.; Verbrugge, B.; Zhaksylyk, A.; Tran, T.M.; El Baghdadi, M.; Geury, T.; Hegazy, O. Design optimization and electrothermal modeling of an off-board charging system for electric bus applications. IEEE Access 2021, 9, 84501–84519. [Google Scholar] [CrossRef]
- Ramachandran, T.; Mourad, A.-H.I.; Hamed, F. A Review on Solar Energy Utilization and Projects: Development in and around the UAE. Energies 2022, 15, 3754. [Google Scholar] [CrossRef]
- Ramachandran, T.; Mourad, A.-H.I.; ElSayed, M.S.A. Nb2CTx-Based MXenes Most Recent Developments: From Principles to New Applications. Energies 2023, 16, 3520. [Google Scholar] [CrossRef]
- Bp Statistical Review of World Energy. 2022. Available online: https://www.bp.com/content/dam/bp/business-sites/en/global/corporate/pdfs/energy-economics/statistical-review/bp-stats-review-2022-full-report.pdf (accessed on 23 May 2023).
- IEEE 1547; Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: Piscataway, NJ, USA, 2018.
- IEEE 519; Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems. IEEE: Piscataway, NJ, USA, 2014.
- IEC 60038; Standard Voltages. IEC: Geneva, Switzerland, 2009.
- IEC 61000-3-2; Electromagnetic Compatibility (EMC)-Part3-2: Limits-Limits for Harmonic Current Emissions (Equipment Input Current ≤ 16 A Per Phase). IEC: Geneva, Switzerland, 2005.
- IEC 61000-3-3; Electromagnetic Compatibility (EMC)-Part 3-3: Limits-Limitation of Voltage Changes, Voltage Fluctuations and Flicker in Public Low-Voltage Supply Systems, for Equipment with Rated Cur Rent ≤ 16 A Per Phase and Not Subject to Conditional Connection. IEC: Geneva, Switzerland, 2013.
- IEC 62109-1; Safety of Power Converters for Use in Photovoltaic Power Systems-Part 1: General Requirements. IEC: Geneva, Switzerland, 2010.
- Dargahi, V.; Abarzadeh, M.; Corzine, K.A.; Enslin, J.H.; Sadigh, A.K.; Rodriguez, J.; Blaabjerg, F.; Maqsood, A. Fundamental circuit topology of duo-active-neutral-point-clamped, duo-neutral-point-clamped, and duo-neutral-point-piloted multilevel converters. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 1224–1242. [Google Scholar] [CrossRef]
- Koshti, A.K.; Rao, M.N. A brief review on multilevel inverter topologies. In Proceedings of the IEEE ICDMAI’17, Pune, India, 24–26 February 2017; pp. 1–7. [Google Scholar]
- Lopez-Sanchez, M.J.; Pool, E.I.; Cruz-Chan, R.; Escobar, G.; Martinez-Garcia, J.F.; Valdez-Fernandez, A.A.; Villanueva, C. A single phase asymmetrical NPC inverter topology. In Proceedings of the IEEE CIEP’16, Guanajuato, Mexico, 20–23 June 2016; pp. 253–258. [Google Scholar]
- Woldegiorgis, D.; Mantooth, A. Five-level hybrid T-type inverter topology with mixed Si+SiC semiconductor device configuration. In Proceedings of the IEEE ECCE’21, Singapore, 24–27 May 2021; pp. 991–996. [Google Scholar]
- Ye, M.; Wei, Q.; Li, S.; Ren, W.; Song, G. Research on balance control strategy of single capacitor clamped five-level inverter clamping capacitor. IET Power Electron. 2021, 14, 280–289. [Google Scholar] [CrossRef]
- Shieh, J.-J.; Hwu, K.-I.; Chen, S.-J. Perspective of voltage-fed single-phase multilevel dc-ac inverters. Energies 2023, 16, 898. [Google Scholar] [CrossRef]
- Reza, B.; Mojtaba, F.; Sze, S.L.; Frede, B.; Siwakoti, Y.P. Switched-capacitor multilevel inverters: A comprehensive review. IEEE Trans. Power Electron. 2022, 37, 11209–11243. [Google Scholar]
- Lee, S.S.; Lim, C.S.; Siwakoti, Y.P.; Lee, K.-B. Dual-T-type five-level cascaded multilevel inverter with double voltage boosting gain. IEEE Trans. Power Electron. 2020, 35, 9522–9529. [Google Scholar] [CrossRef]
- Wang, H.; Kou, L.; Liu, Y.-F.; Sen, P.C. A seven-switch five-level active-neutral-point-clamped converter and its optimal modulation strategy. IEEE Trans. Power Electron. 2017, 32, 5146–5161. [Google Scholar] [CrossRef]
- Siwakoti, Y.P. A new six-switch five-level boost-active neutral point clamped (5L-boost-ANPC) inverter. In Proceedings of the IEEE APEC’18, San Antonio, TX, USA, 4–8 March 2018; pp. 2424–2430. [Google Scholar]
- Naderi, R.; Sadigh, A.K.; Smedley, K.M. Dual flying capacitor active-neutral-point-clamped multilevel converter. IEEE Trans. Power Electron. 2016, 31, 6476–6484. [Google Scholar] [CrossRef]
- Babaei, E.; Laali, S.; Bayat, Z. A single-phase cascaded multilevel inverter based on a new basic unit with reduced number of power switches. IEEE Trans. Ind. Electron. 2015, 62, 922–929. [Google Scholar] [CrossRef]
- Dhanamjayulu, C.; Khasim, S.R.; Padmanaban, S.; Arunkumar, G.; Holm-Nielsen, J.B.; Blaabjerg, F. Design and implementation of multilevel inverters for fuel cell energy conversion system. IEEE Access 2020, 8, 183690–183707. [Google Scholar] [CrossRef]
- Valderrama, G.E.; Guzman, G.V.; Pool-Mazun, E.I.; Ray, P.; Lopez-Sanchez, M.J.; Zuniga, J.M.S. A single-phase asymmetrical T-Type five-level transformerless PV inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 140–150. [Google Scholar] [CrossRef]
- Grigoletto, F.B. Multilevel common-ground transformerless inverter for photovoltaic applications. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 831–842. [Google Scholar] [CrossRef]
- Saket, S.K.; Chaturvedi, P.; Yadeo, D. A new fault tolerant single phase 5-level inverter topology. In Proceedings of the IEEE IICPE’18, Jaipur, India, 13–15 December 2018; pp. 1–5. [Google Scholar]
- Barah, S.S.; Behera, S. An optimize configuration of H-bridge multilevel inverter. In Proceedings of the IEEE ICPEE’21, Bhubaneswar, India, 2–3 January 2021; pp. 1–4. [Google Scholar]
- Missula, J.V.; Adda, R.; Tripathy, P. Averaged modeling and SRF-based closed-loop control of single-phase ANPC inverter. IEEE Trans. Power Electron. 2021, 36, 13839–13854. [Google Scholar] [CrossRef]
- Lee, S.S.; Yang, Y.; Siwakoti, Y.P. A novel single-stage five-level common-ground-boost-type active neutral-point-clamped (5l-cgbt-anpc) inverter. IEEE Trans. Power Electron. 2021, 36, 6192–6196. [Google Scholar] [CrossRef]
- Bogineni, J.; Nakka, J. A novel reduced switch single-phase five-level inverter. Int. J. Circuit Theory Appl. 2022, 50, 2793–2809. [Google Scholar] [CrossRef]
- Wang, K.; Zheng, Z.; Li, Y.; Liu, K.; Shang, J. Neutral-point potential balancing of a five-level active neutral-point-clamped inverter. IEEE Trans. Ind. Electron. 2013, 60, 1907–1918. [Google Scholar] [CrossRef]
- Saketi, S.K.; Chaturvedi, P.; Yadeo, D.; Atkar, D. A hybrid five-level inverter configuration with improved reliability and reduced number of components. Int. J. Circuit Theory Appl. 2022, 11, 4104–4130. [Google Scholar] [CrossRef]
- Wang, B.; Li, Z.; Bai, Z.; Krein, P.T.; Ma, H. A redundant unit to form T-Type three-level inverters tolerant of IGBT open-circuit faults in multiple legs. IEEE Trans. Power Electron. 2020, 35, 24–939. [Google Scholar] [CrossRef]
- Hwu, K.I.; Yau, Y.T. Applying one-comparator counter-based PWM control strategy to DC-AC converter with voltage reference feedforward control considered. In Proceedings of the IEEE APEC’11, Fort Worth, TX, USA, 6–11 March 2011; pp. 1811–1815. [Google Scholar]
- Code of Federal Regulations Part 15—Radio Frequency Devices—eCFR. Available online: https://www.ecfr.gov/current/title-47/chapter-I/subchapter-A/part-15 (accessed on 3 June 2023).
- HJC Corp. 2023. Available online: https://hjchelmet.tradekorea.com/company.do (accessed on 15 June 2023).
- Ahmed, W.; Sarkar, B. Management of next-generation energy using a triple bottom line approach under a supply chain framework. Resour. Conserv. Recycl. 2019, 150, 104431. [Google Scholar] [CrossRef]
- Habib, M.S.; Asghar, O.; Hussain, A.; Imran, M.; Mughal, M.P.; Sarkar, B. A robust possibilistic programming approach toward animal fat-based biodiesel supply chain network design under uncertain environment. J. Clean. Prod. 2021, 278, 122403. [Google Scholar] [CrossRef]
- Garai, A.; Sarkar, B. Economically independent reverse logistics of customer-centric closed-loop supply chain for herbal medicines and biofuel. J. Clean. Prod. 2022, 334, 129977. [Google Scholar] [CrossRef]
- Guchhait, R.; Sarkar, B. Increasing growth of renewable energy: A state of art. Energies 2023, 16, 2665. [Google Scholar] [CrossRef]



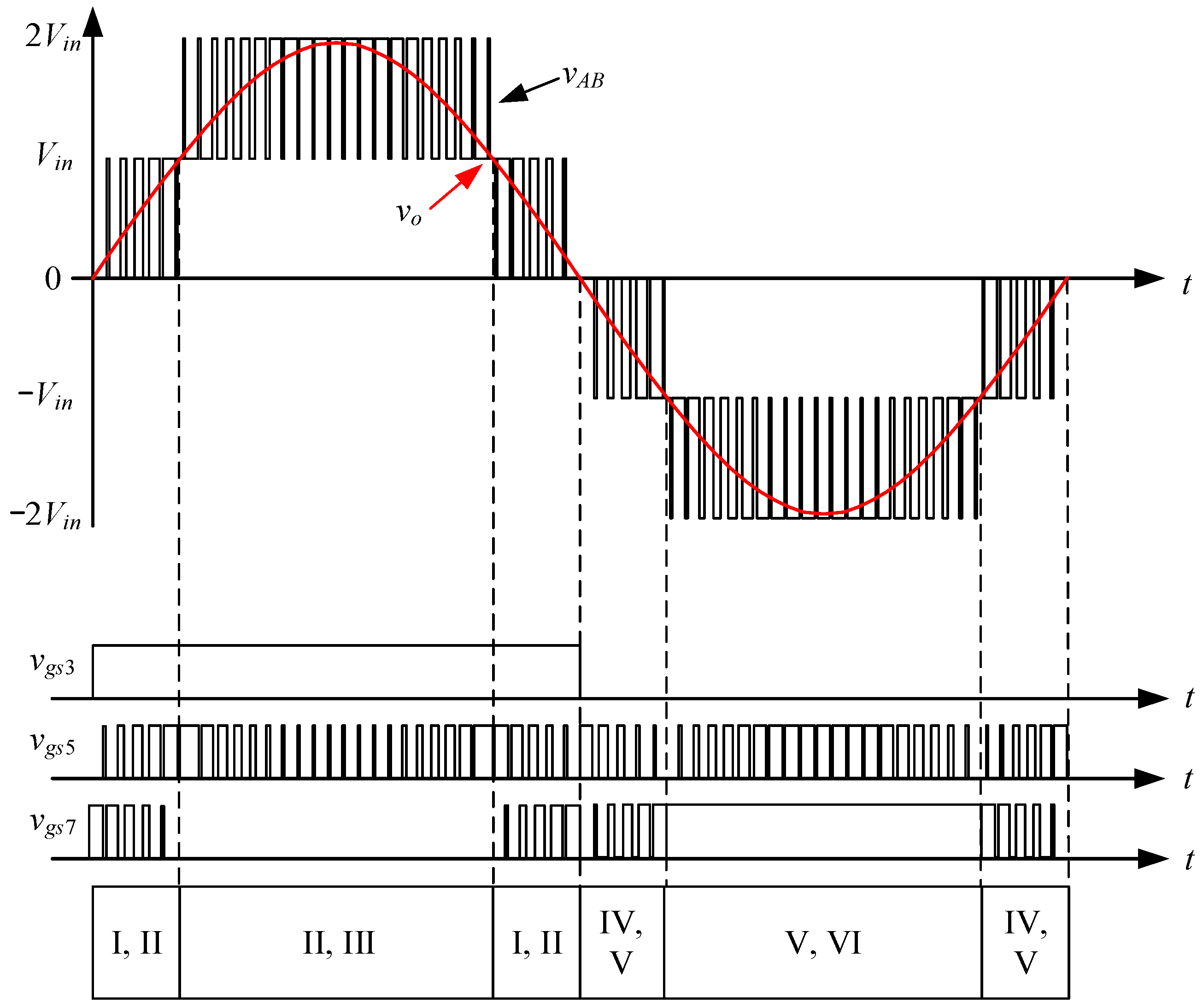
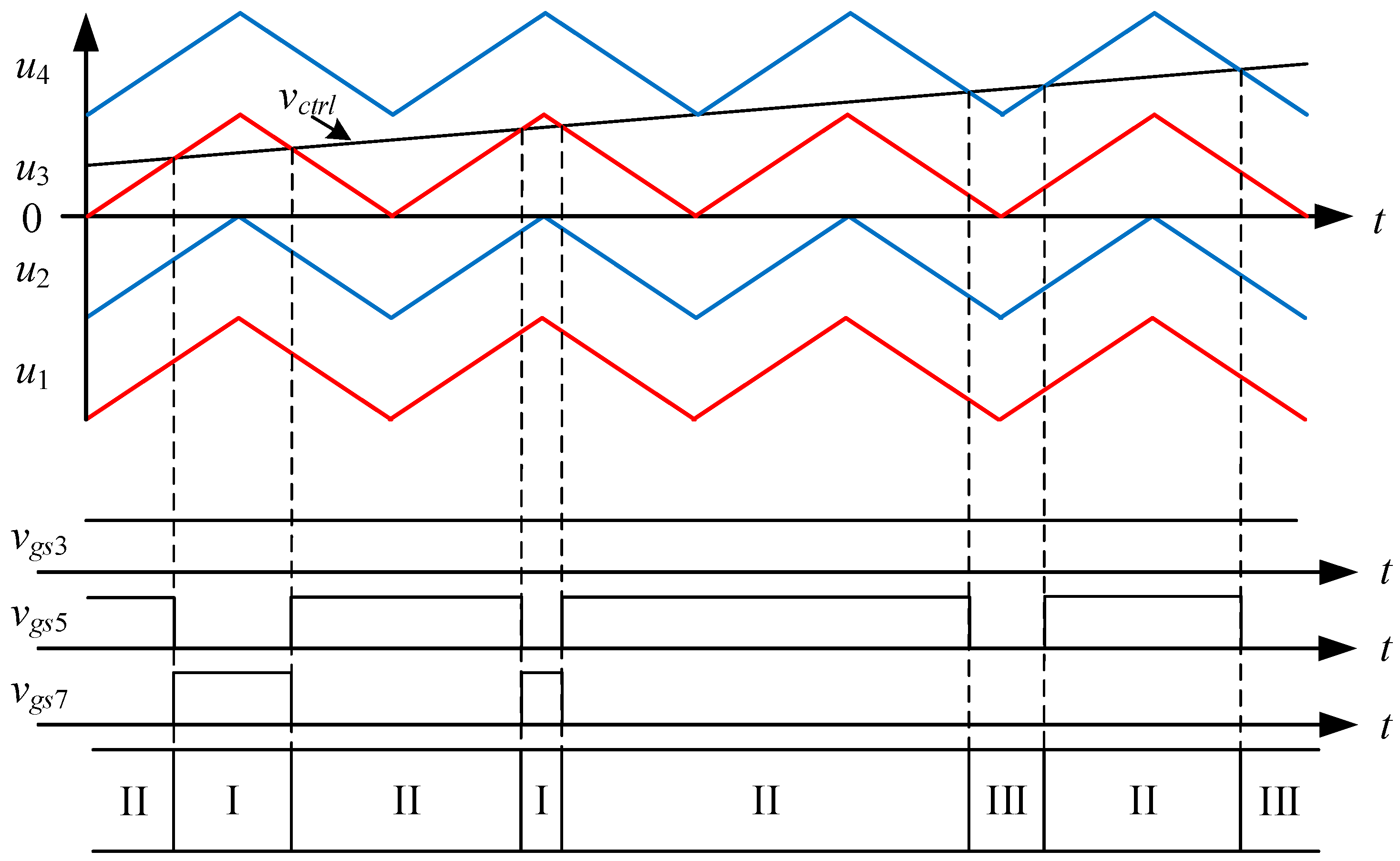

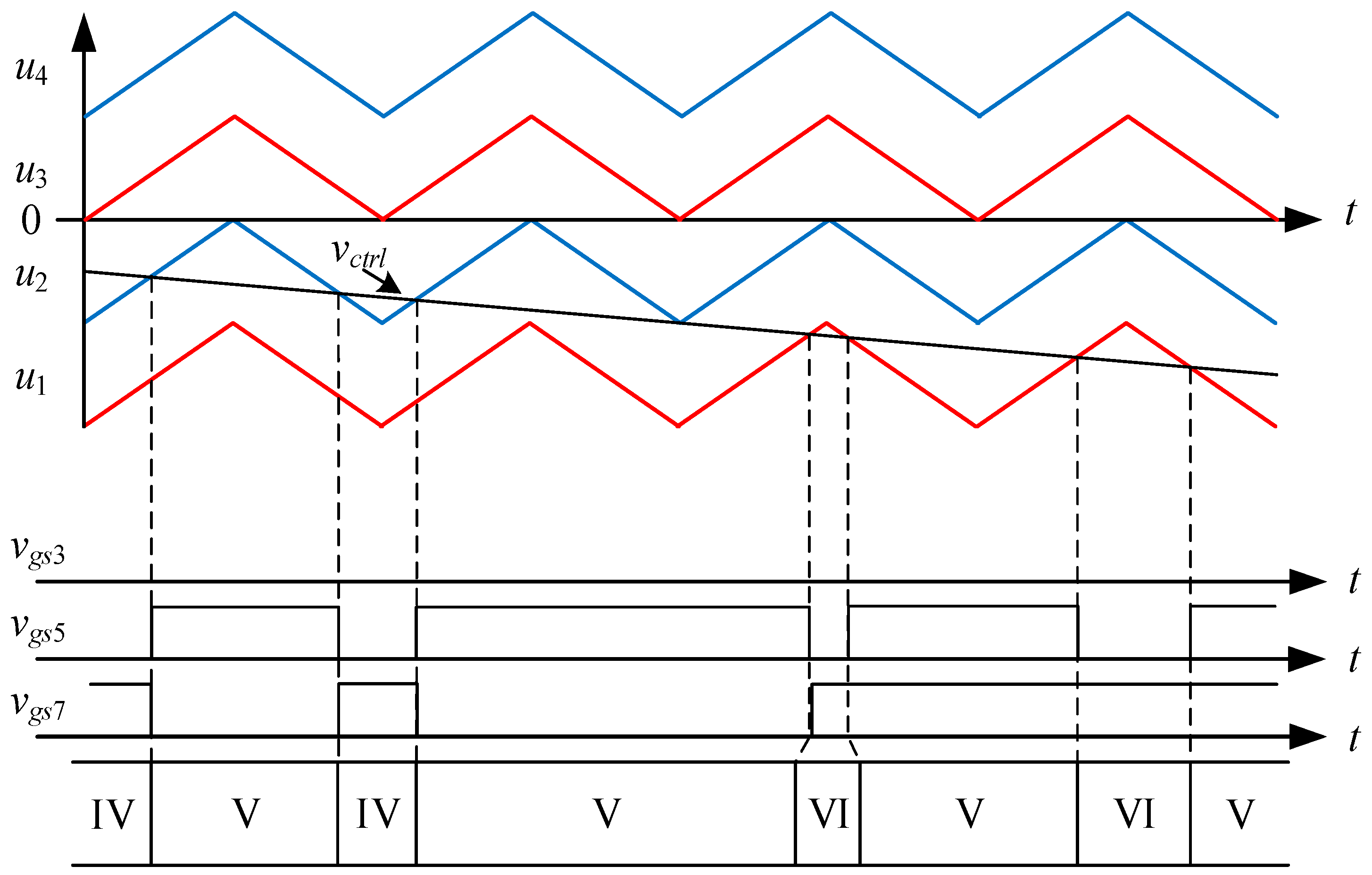

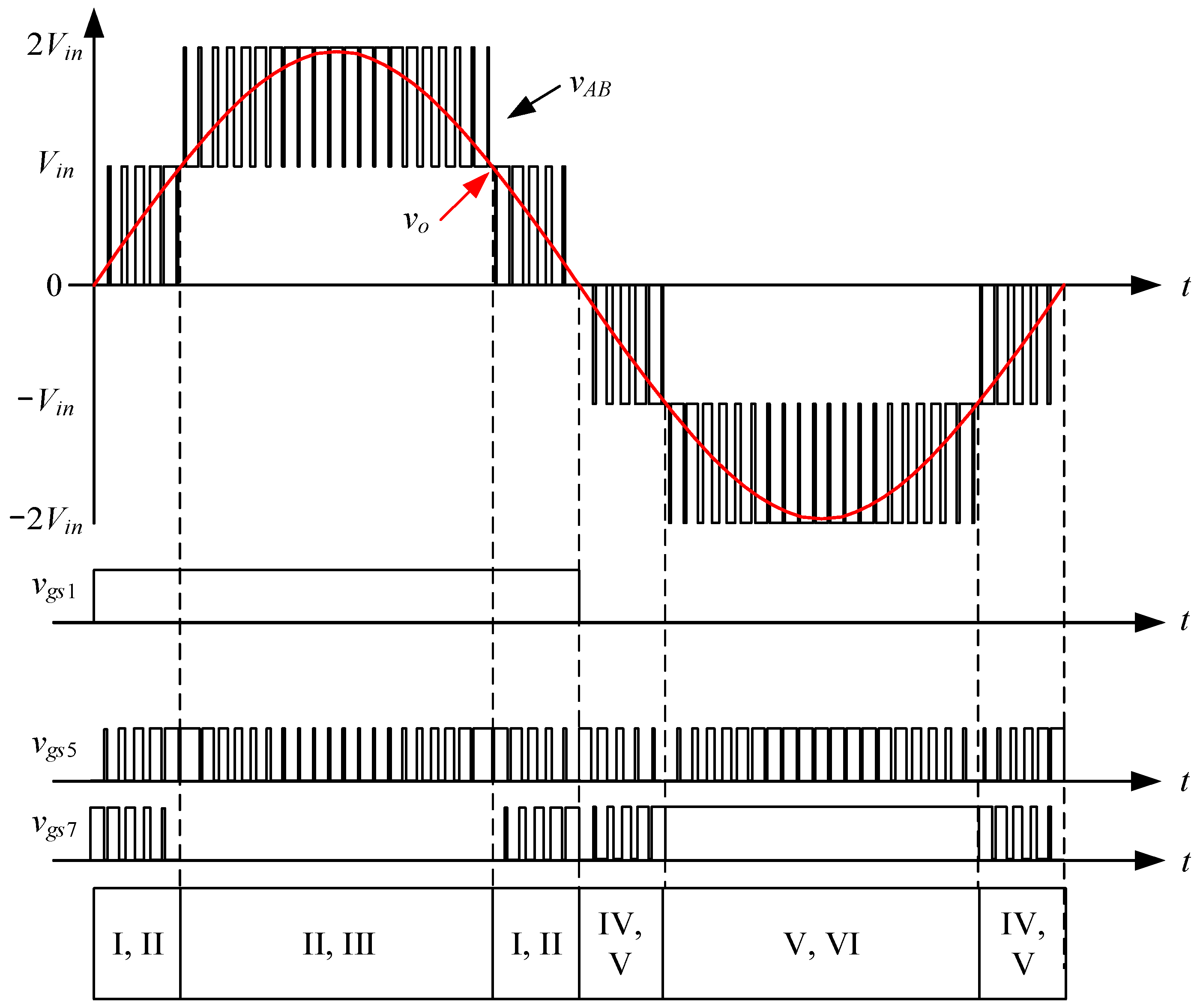









| Reference Number | Voltage Gain | Circuit Features | |
|---|---|---|---|
| Main | Additional | ||
| [2] | 0.75 | T-Type | Diode Clamp plus Bidirectional Switches |
| [34] | 0.5 | T-type | Active Clamp plus Flywheeling Capacitor |
| [35] | 2.0 | T-Type | Front-End Buck-Boost Converter |
| [36] | 1.0 | NPC | Floating Capacitor |
| [37] | 0.5 | Multi-Switches | Floating Capacitor |
| [38] | 2.0 | Cascade-HB | 3 DC Sources |
| [39] | 2.0 | Multi-Switches | 2 DC Sources |
| [40] | 1.0 | T-Type | H-Bridge |
| [41] | 2.0 | SC | T-Type |
| [42] | 2.0 | T-Type | 2 DC Sources plus Bidirectional Switches |
| [43] | 2.0 | HB | Cascaded-HB |
| [31] | 0.5 | FC | Active Clamp |
| [44] | 10.0 | Multi-Switches | Boost Converter plus Floating Capacitor |
| [45] | 2.0 | Multi-Switches | Flywheeling Capacitor |
| [46] | 1.0 | HB | Multi-Switches |
| [47] | 2.0 | NPC | HB |
| [48] | 1.0 | FC | HB |
| [49] | 0.5 | T-type | T-type |
| Circuit | States | Switches | Capacitors | AC Output | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | C1 | C2 | C3 | C4 | vAN | vBN | vAB | ||
| Type-1 | 1 | --- | --- | 1 | 0 | 0 | 1 | 1 | 0 | --- | --- | C | --- | 1 Vin | 1 Vin | 0 Vin |
| 2 | --- | --- | 1 | 0 | 1 | 0 | 0 | 1 | --- | --- | --- | C | 1 Vin | 0 Vin | 1 Vin | |
| 3 | --- | --- | 1 | 0 | 0 | 1 | 0 | 1 | --- | --- | C | D | 1 Vin | −1 Vin | 2 Vin | |
| 4 | --- | --- | 0 | 1 | 1 | 0 | 0 | 1 | --- | --- | --- | C | 0 Vin | 0 Vin | 0 Vin | |
| 5 | --- | --- | 0 | 1 | 0 | 1 | 1 | 0 | --- | --- | C | --- | 0 Vin | 1 Vin | −1 Vin | |
| 6 | --- | --- | 0 | 1 | 1 | 0 | 1 | 0 | --- | --- | D | C | 0 Vin | 2 Vin | −2 Vin | |
| Type-2 | 1 | 1 | 0 | --- | --- | 0 | 1 | 1 | 0 | --- | C | C | --- | 1 Vin | 1 Vin | 0 Vin |
| 2 | 1 | 0 | --- | --- | 1 | 0 | 0 | 1 | --- | C | --- | C | 1 Vin | 0 Vin | 1 Vin | |
| 3 | 1 | 0 | --- | --- | 0 | 1 | 0 | 1 | --- | C | C | D | 1 Vin | −1 Vin | 2 Vin | |
| 4 | 0 | 1 | --- | --- | 1 | 0 | 0 | 1 | C | --- | --- | C | 0 Vin | 0 Vin | 0 Vin | |
| 5 | 0 | 1 | --- | --- | 0 | 1 | 1 | 0 | C | --- | C | --- | 0 Vin | 1 Vin | −1 Vin | |
| 6 | 0 | 1 | --- | --- | 1 | 0 | 1 | 0 | C | --- | D | C | 0 Vin | 2 Vin | −2 Vin | |
| Inverter Type | Level Voltage | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 |
|---|---|---|---|---|---|---|---|---|---|
| Diode Neutral-Point-Clamped (Figure 1a, [29]) | 0 Vin | 0 | 0 | 1 | 1 | 0 | 1 | --- | --- |
| 0.5 Vin | 0 | 1 | 1 | 0 | 0 | 1 | --- | --- | |
| 1 Vin | 1 | 1 | 0 | 0 | 0 | 1 | --- | --- | |
| −0.5 Vin | 1 | 1 | 0 | 0 | 1 | 0 | --- | --- | |
| −1 Vin | 0 | 1 | 1 | 0 | 1 | 0 | --- | --- | |
| T-type Neutral-Point-Clamped (Figure 1b, [30]) | 0 Vin | 0 | 0 | 1 | 1 | 0 | 1 | --- | --- |
| 0.5 Vin | 0 | 1 | 1 | 0 | 0 | 1 | --- | --- | |
| 1 Vin | 1 | 1 | 0 | 0 | 0 | 1 | --- | --- | |
| 0 Vin | 1 | 1 | 0 | 0 | 1 | 0 | --- | --- | |
| −0.5 Vin | 0 | 1 | 1 | 0 | 1 | 0 | --- | --- | |
| −1 Vin | 0 | 0 | 1 | 1 | 1 | 0 | --- | --- | |
| Flywheel Capacitor (Figure 1c, [31]) | 0 Vin | 0 | 0 | 1 | 1 | 0 | 1 | --- | --- |
| 0.5 Vin | 1 | 0 | 1 | 0 | 0 | 1 | --- | --- | |
| 1 Vin | 1 | 1 | 0 | 0 | 0 | 1 | --- | --- | |
| 0 Vin | 0 | 1 | 0 | 1 | 0 | 1 | --- | --- | |
| 0.5 Vin | 1 | 1 | 0 | 0 | 1 | 0 | --- | --- | |
| −0.5 Vin | 0 | 1 | 0 | 1 | 1 | 0 | --- | --- | |
| −1 Vin | 1 | 0 | 1 | 0 | 1 | 0 | --- | --- | |
| −0.5 Vin | 0 | 0 | 1 | 0 | 1 | 0 | --- | --- | |
| Proposed (Type-1) | 0 Vin | --- | --- | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 Vin | --- | --- | 1 | 0 | 1 | 0 | 0 | 1 | |
| 2 Vin | --- | --- | 1 | 0 | 0 | 1 | 0 | 1 | |
| 0 Vin | --- | --- | 0 | 1 | 1 | 0 | 0 | 1 | |
| −1 Vin | --- | --- | 0 | 1 | 0 | 1 | 1 | 0 | |
| −2 Vin | --- | --- | 0 | 1 | 1 | 0 | 1 | 0 | |
| Proposed (Type-2) | 0 Vin | 1 | 0 | --- | --- | 0 | 1 | 1 | 0 |
| 1 Vin | 1 | 0 | --- | --- | 1 | 0 | 0 | 1 | |
| 2 Vin | 1 | 0 | --- | --- | 0 | 1 | 0 | 1 | |
| 0 Vin | 0 | 1 | --- | --- | 1 | 0 | 0 | 1 | |
| −1 Vin | 0 | 1 | --- | --- | 0 | 1 | 1 | 0 | |
| −2 Vin | 0 | 1 | --- | --- | 1 | 0 | 1 | 0 |
| Input Voltage (Vin) | 58 V |
| Output AC Voltage (vo) | 75 Vrms |
| Output Frequency (fline) | 60 Hz |
| Rated Power (Po,rated) | 250 W |
| Switching Frequency (fs) | 58.6 kHz |
| [2] | [43] | [31] | [45] | [46] | [47] | [48] | [49] | [50] | Proposed (Type-1) | Proposed (Type-2) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of Levels | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| Number of Switches | 8 | 6 | 8 | 7 | 6 | 14 | 10 | 10 | 14 | 6 | 6 |
| Number of Diodes | 2 | 0 | 0 | 0 | 0 | 12 | 0 | 0 | 12 | 4 | 4 |
| Number of Capacitors | 2 | 1 | 3 | 2 | 2 | 0 | 5 | 1 | 2 | 4 | 4 |
| Voltage Gain | 0.75 | 1 | 0.5 | 10 | 1 | 1 | 2 | 1 | 0.5 | 2 | 2 |
| Number of DC Power Sources | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Two-Terminal Output | Yes | Yes | Yes | No | Yes | No | No | Yes | No | Yes | Yes |
| Rated-Load Power (W) | 1000 | 25 | 300 | 400 | 1250 | 1450 | 250 | 250 | 1450 | 250 | 250 |
| Input Voltage (V) | 400 | 24 | 128 | 40 | 350 | 400 | 100 | 200 | 400 | 58 | 58 |
| Peak Output Voltage (V) | 311 | 21.6 | 64 | 400 | 350 | 400 | 200 | --- | 141 | 106 | 106 |
| Rated-load THD (%) | --- | 33.27 | 3.86 | 35.11 | 1.55 | 1.58 | --- | 24.41 | 2.15 | 0.71 | 0.78 |
| Peak Efficiency (%) | 97.09 | 95.21 | --- | 97.50 | 98.70 | --- | --- | --- | --- | 96.87 | 95.80 |
| Control Strategy | UP-PWM/ OLC-PWM | PS-PWM | PS-PWM/PD-PWM | SPWM | PD-PWM | PD-SPWM | SPWM | LS-SPWM | PD-SPWM | LS-SPWM | LS-SPWM |
| Full Modularization | Yes | Yes | No | Yes | No | No | Yes | Yes | Yes | Yes | Yes |
| Abbreviation | Full Name |
|---|---|
| OLC-PWM | One-Leg Clamping-PWM |
| UP-PWM | Unipolar-PWM |
| PS-PWM | Phase Shifted-PWM |
| PD-PWM | Phase Disposition-PWM |
| SPWM | Sinusoidal Pulse Width Modulation |
| LS-SPWM | Level Shifted-SPWM |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shieh, J.-J.; Hwu, K.-I.; Chen, S.-J. Two Types of Asymmetric Switched-Capacitor Five-Level Single-Phase DC-AC Inverters for Renewable Energy Applications. Energies 2024, 17, 983. https://doi.org/10.3390/en17050983
Shieh J-J, Hwu K-I, Chen S-J. Two Types of Asymmetric Switched-Capacitor Five-Level Single-Phase DC-AC Inverters for Renewable Energy Applications. Energies. 2024; 17(5):983. https://doi.org/10.3390/en17050983
Chicago/Turabian StyleShieh, Jenn-Jong, Kuo-Ing Hwu, and Sheng-Ju Chen. 2024. "Two Types of Asymmetric Switched-Capacitor Five-Level Single-Phase DC-AC Inverters for Renewable Energy Applications" Energies 17, no. 5: 983. https://doi.org/10.3390/en17050983
APA StyleShieh, J.-J., Hwu, K.-I., & Chen, S.-J. (2024). Two Types of Asymmetric Switched-Capacitor Five-Level Single-Phase DC-AC Inverters for Renewable Energy Applications. Energies, 17(5), 983. https://doi.org/10.3390/en17050983








