Modular Circuit Synthesis Oriented Modelling Approach for Non-Isolated DC-DC Converters in DCM

Abstract

The continued and envisioned large-scale integration of renewable energy sources as a reaction to rising global temperatures and climate change will need a readily available DC grid to increase commissioning and operating efficiency. The effective operation of these grids is predicated on the correct control of its main control points. A plethora of DC-DC converters that find use in DC microgrids act as the main control points. DC-DC converters are non-linear and can operate in different modes with completely unique characteristics. To utilise classical control techniques, laborious equivalent linear models are derived for DC-DC converters using averaging modelling schemes. The application and limitations of these modelling techniques are well captured in the available literature. The most common limitation of the available modelling schemes is that more focus is dedicated to converter attributes like order, functionality and operating mode, even when optimal power flow and voltage regulation within the DC network are of more interest. Structure-based modelling techniques like the use of basic building blocks nullify converter attributes in the modelling process which translates to modelling efficiency. In light of the merits seen with the use of basic building blocks when modelling converters in CCM, the current study extends these merits to converters operation in DCM. Similar to modelling converters in CCM, modelling techniques that are available in the literature continue to consider converter attributes in the modelling process for DCM operation. Moreover, the two modes of operation are treated as unique entities and often modelled in a non-unified manner, which compromise modelling efficiency since the same converter can operate in a different state solely based on loading. The aim is to increase modelling efficiency but also nullify operating mode in the modelling process. The same basic building blocks are now modelled as two-port networks for DCM operation and adopted based on the exact configuration of a specified converter to compute its steady-state and dynamic models. All the advantages seen when modelling converters in CCM using basic building blocks are retained and augmented when considering DCM operation. Thus, any converter with well-defined basic building blocks can be easily modelled solely based on the connection of constituent basic building blocks.

1. Introduction

The need to replace fossil fuel-based energy generation with environmentally friendly generation schemes warrants the large-scale integration of renewable energy-sources (RES) [1]. The compatibility of most RES like solar PV with DC networks warrants an equivalent overhaul of the grid from AC to DC in order to increase operating efficiency [2,3]. Unlike AC transformers, DC-DC converters not only play a vital role of scaling voltages, they are also involved in power extraction [4,5], power conditioning [6], power quality improvement [7] and power transfer among other roles in a typical DC network. As such, correct control of these converters can be tied to the overall performance of a DC grid. DC-DC converters are also known as switch-mode power supplies due to their switching nature. This switching nature makes them non-linear systems [8]. As such, in order to utilise well-developed linear control techniques like PID, equivalent linear models must be derived for these converters. Of course, if the small ripple assumption inherent in averaging modelling techniques ceases to be valid, non-linear control techniques like sliding mode control should be considered [9]. For instances wherein the small ripple assumption is valid, the derivation of a linear model for an inherently non-linear system is labour intensive [8,9,10]. Moreover, these converters can operate in two distinct modes, i.e., continuous conduction mode (CCM) and discontinuous conduction mode (DCM).

There are unique merits associated with each operating mode. For instance, converters operating in DCM have merits of reducing reverse recovery issues in diodes [11]. Furthermore, the dynamics of a converter can be simplified when operated in DCM, which has the advantage of reducing control complexity [11,12]. As such, a converter can be designed to operate in DCM [13]. It was shown in [14] that DCM operation of converters can enhance performance, e.g., inherent power factor improving capabilities. Soft switching can also be achieved through DCM operation [15,16]. Furthermore, DCM operation has also been shown to prevent transformer saturation [17]. On the other hand, high power operation might be more suited for converters operating in CCM. The equivalent linear model for either mode of operation is unique, even for the same converter [18,19]. Currently, the prominent techniques used to derive equivalent linear models for DC-DC converters include the state-space averaging [20], switching flow graph [21] and circuit averaging [22], among others. The available literature treats CCM and DCM as separate entities in the modelling process [18,19,23]. Additionally, converter order [24] and functionality [20,22,25] have also been used as discriminants in the modelling process for both CCM and DCM. However, the same converter can operate in both states solely based on loading conditions. As such, this approach shifts the entire focus to a specific converter even when the converter operates as a minute component of a DC microgrid. On the other hand, fourth-order converters have no unique form of operating in DCM; the consideration of a prominent DCM operating state is one in which the two inductor currents have non-zero minimum values [13]. Furthermore, if an inductor is sandwiched between two steady voltage sources its current dynamics become restricted, i.e., it cannot exhibit any substantial dynamics. Thus, a fourth-order converter can exhibit DCM with only one inductor, e.g., conventional boost converter with input LC filter.

Given the high number of DC-DC converters that are deployed across a DC network, the authors in [26] argue that modelling schemes based on fundamental converter structures are advantageous in that they offer reduced computational effort. These modelling schemes include circuit averaging performed on converter cells which allow for models of a group of converters to be derived based on the analysis of networks realised through port-connection permutations of a pre-modelled converter cell [27]. In this way, modelling inherently non-linear systems reduces to the analysis of equivalent linear circuits. It should be borne in mind that the subsequent analysis of the resultant linear network can also pose increased computational effort especially for higher order systems. Using converter cells, one would have to consider at least 14 converter cells for modelling all the converters of interest. This approach still appears to be placing large emphasis on a small group of converters. Moreover, subsequent analysis of the linear converter realised from inserting converter cell model on a specific converter still poses increased computational effort, especially for higher order networks. Modelling schemes like the layer scheme [28], the graft scheme [29], basic building blocks (BBBs) [30], tapped inductor switcher (TIS) [31,32] or PWM switch [33], are also examples of structure-based modelling schemes which reduce computational effort. The graft and layer scheme mainly consider basic converters, which limits its utility for analysing most of the prominent converter topologies employed in DC microgrids; the TIS’s parameters heavily depend on the analysis of the original circuit of interest which fails to reduce computational effort. The PWM switch works well for most converters, but not all converters can be modelled as a single-pole double-throw switch, e.g., a Zeta converter. On the other hand, the use of BBB is more versatile in that three BBB types and a filter block are sufficient to realise all the converters in [27], which are made up of 14 converter cells. Moreover, other converters like the current-fed and voltage-fed DC-DC converters can be realised from BBBs [30].

The use of basic-building blocks (BBB) in modelling converters was employed in [26]. The authors show the operating principle of a BBB-based modelling scheme for converters in CCM. Generally, DCM models of converters are computationally demanding compared to their CCM equivalent. This is due to the three switching states with three accompanying sub-circuits, as well as the dependence of transfer characteristics on the load and circuit parameters [11,12,13,34]. Maksimovic et al. [35] show that a DCM model of a converter can be computed from its CCM model based on a feedback configuration. The work shows that if the main plant model in the proposed feedback structure is made up of the CCM model, the DCM model can easily be derived once the relevant feedback gains are computed. The presented feedback structure gives a graphical description of the additional computational effort associated with deriving DCM models.

For the envisaged large-scale integration of RES and the accompanying DC network, control philosophy will be more focused on optimal power flow (OPF), power quality and voltage regulation of the network [36]. Such a philosophy can only be justified when the component level control is guaranteed [36]. In DC networks, DC-DC converters act as the main control points and present component level control [26,36]. Given the fact that these converters are deployed in very large numbers in a typical DC network, any modelling technique that relies on converter attributes like order, functionality and operating mode, would prove cumbersome. In such a setup, these converters are merely building blocks of a very large system. As such, a suitable modelling technique should also treat DC-DC converters as building blocks and be independent of converter attributes or operating mode. Such a modelling scheme will not only increase modelling efficiency, it will also lend itself well in highlighting common converter traits.

The use of converter BBBs in synthesising converters was first proposed in [30]. The authors show that three BBBs and a filter block are sufficient to synthesise most non-isolated DC-DC converters. The presented idea highlighted that DC-DC converters can be synthesised based on a unique connection of one or more BBBs. Subsequently, the analysis of these BBBs was presented in [26] to unify the modelling of prominent non-isolated DC-DC converters in CCM. In this work, the authors showed that model computation of any model of interest can be attained based on how the constituent BBBs are connected, i.e., how the converter is synthesised. The main merits of the presented modelling scheme were: (i) the modelling scheme is independent of converter order and functionality, (ii) expressions for transfer functions of interest can be generalised, (iii) the modularity of BBBs reduces computational requirements, (iv) the two-port network representation of the BBB models limits the matrix size to a 2 × 2 which further reduces computational effort. However, DCM operation was not considered in the study. Currently, the literature continues to use converter order and functionality as discriminants in the modelling process when modelling converters operating in DCM [13,18].

The continued use of converter order, functionality or operating mode as discriminants in the modelling process is counter-productive since it focuses more on component level dynamics, when the main issue is on the performance of the larger DC grid. In this work, the merits of modelling converters based on BBB models are extended to converters operating in DCM. In addition to the modelling technique being independent of converter functionality and order, it will be shown that once the BBBs are modelled as two-port networks, the modelling procedure becomes independent of converter operating mode. Moreover, the DCM switch and diode models will be shown to be the same for both second- and fourth-order converters which allows modelling converters in DCM to also be independent of converter order. The current work presents and highlights a modular modelling scheme, since it recognises that new converter topologies that are more suited to perform specialised tasks in DC microgrids will continually be proposed, e.g., the newly proposed non-isolated, high step-up DC-DC converter with reduced input current ripple [37]. As such, a modelling scheme that is modular will improve modelling efficiency for new converters with known BBBs. Additionally, modularity in the modelling scheme can nullify the need for a deeper understanding of the operation of any converter with known BBBs when computing models. This can be useful for instances when multidisciplinary groups work on the same project and the control group wants to test their control algorithm without necessarily knowing more about the plant (DC-DC converters) in this case.

To highlight the full range of the modelling scheme when there are modelling converters operating in DCM, the same group of converters considered for CCM operation in [26] will be considered. Thus, the converters considered in this study are: (i) the conventional buck, boost and buck-boost converters, (ii) the same conventional buck, boost and buck-boost converters with input and output filters, and (iii) the Cuk, Zeta and Sepic converters.

The remainder of this paper is structured as follows: a review of the use of BBB in synthesising converters is conducted in Section 2. The proposed generalised modelling scheme for CCM and DCM operation is presented in Section 3. The application of the proposed modelling scheme on non-conventional converters is presented in Section 4. An example-based illustration of utilising the proposed modelling scheme is presented in Section 5. Section 6 and Section 7, respectively, present the discussions and conclusions of the study.

2. Review of BBB-Based Converter Synthesis

The main idea behind the use of BBBs for converter synthesis is presented in [30]. A total of three BBB types and a filter block are presented as shown in Figure 1. It was further shown that these BBB are sufficient to synthesise all the converters presented in [27]. Additionally, both current and voltage-fed DC-DC converters can be synthesised from these BBB. The synthesis of converters using BBBs provides more versatility in converter synthesis, in that they encompass almost all the main parts found in switch-mode power supplies which creates flexibility in the synthesis process. For the same reasons given in the paper dealing with modelling converters in CCM [26], only converters that find common use in practical applications will be considered. As such, converters considered in this study are the ones listed in Section 1. This range of converters encompass both second- and fourth-order converters and all the main voltage scaling functions. Thus, they present a sufficient range of converters to validate the attributes of the modelling technique listed in Section 1. For the range of converters considered in this study, only Type 1, Type 2 and the filter block are sufficient to synthesise all the converters of interest (e.g. Figure 2). It should be borne in mind that the filter block represents a general structure of a filter. Thus, the filter can be a simple inductive filter, CL, LC or capacitive filter. The LCL filter represents the full filtering capability of the block. The applicable conditions for synthesising a practical converter still hold for any of the BBBs as discussed in [30], i.e.,:

• All the terminal currents of the BBB should be DC, if it is to be used independently to synthesise a converter.
• A BBB has distinct operating modes for the switching elements in order to ensure proper operation.

3. Modelling Concept Development

3.1. Modelling Generalised Circuit

It was shown in the paper dealing with the modelling of converters in CCM [26] that the converters considered in this study can be described as a cascade connection of BBBs as shown in Figure 3. Thus, a converter will have one BBB connected to the input port and another BBB connected to the output port. The input port is made up of the source voltage and the output port is made up of a parallel connection of a capacitor and a resistor, which, respectively, represent voltage filtering and active power consumption. It should be borne in mind that Figure 3 only shows and generalises the connection type and number of BBBs making up the set of converters considered in this study as listed in Section 1. It will be shown in Section 4 that connection type and the number of BBBs are objectively identified for any given converter.

Similar to the BBB oriented modelling scheme for converters operating in CCM [26], the modelling scheme for DCM operation will also consider each BBB’s small-signal and steady-state models independently, such that the computation of a model for a particular converter only relies on the connection of the BBBs making up the converter. Since the converters considered in this study can all be synthesised through a cascade connection of BBBs, it means that the derivation of the resultant converter models can be generalised. Moreover, it was shown in [26], that modelling BBBs as two-port networks can further simplify the modelling process by generalising transfer functions of interest as shown in Generalised Power Stage Models section. It should be noted that the generalised transfer functions are derived using transmission parameters for the equivalent two-port network of the BBBs. A generalised two-port model in terms of transmission parameters is shown in (1a) and (1b) for dynamic and steady-state operation, respectively. The transmission parameters are a natural choice due to the cascade connection of the constituent BBBs, which means the choice of the two-port parameters will always be based on the connection of BBBs, e.g., an input-shunt, output-series connection of BBBs will work well with g-parameters. The dependence of the natural choice for two-port parameters on the connection of BBBs will be shown through examples in Section 5. The available literature does capture the relevant merits and demerits of two-port parameters and network connection [28,38]. Figure 3 provides a graphical representation of the modelling procedure, i.e., (1) the input and output BBBs are modelled independently, (2) the connection of the input and output BBB dictates the type of parameters used for the two-port network and, (3) the generalised transfer functions are derived. The modelling process is the same for both steady-state and dynamic small-signal models. The BBBs are modelled using circuit averaging modelling scheme to retain the graphical representation of the BBB’s circuit components.

To enable the generalisation of the modelling procedure for CCM and DCM operation, the same notation will be used to distinguish the input side BBB’s transmission parameters from those of the output side BBB; superscripts ‘i’ and ‘o’ will be used to denote input and output, respectively. Using this notation, (2a) and (2b) will, respectively, denote small-signal and steady-state transmission parameters for the input side BBB, while (3a) and (3b) represent small-signal and steady-state transmission parameters for the output side BBB.

$$\left[\begin{array}{c}{\tilde{v}}_1(s)\\ {\tilde{i}}_1(s)\end{array}\right]=\left[\begin{array}{cc}A(s)& B(s)\\ C(s)& D(s)\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2(s)\\ {-\tilde{i}}_2(s)\end{array}\right]+\left[\begin{array}{c}{\tilde{v}}_{ind}^T\left(s\right)\\ {\tilde{i}}_{ind}^T\left(s\right)\end{array}\right]\tilde{\delta }(s)$$

(1a)

where:

• ${\tilde{v}}_1(s)\to$ AC input voltage of a given BBB;
• ${\tilde{i}}_1(s)\to$ AC input current of a given BBB;
• ${\tilde{v}}_2(s)\to$ AC output voltage of a given BBB;
• ${\tilde{i}}_2(s)\to$ AC output current of a given BBB;
• ${\tilde{v}}_{ind}^T\left(s\right)\to$ AC input voltage of a given BBB due to the presence of independent sources for Transmission parameters;
• ${\tilde{i}}_{ind}^T\left(s\right)\to$ AC input current of a given BBB due to the presence of independent sources for Transmission parameters;
• $\tilde{\delta }\left(s\right)\to$ AC excursions of the active switch duty ratio.

  $$\left[\begin{array}{c}{V}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]\left[\begin{array}{c}{V}_2\\ -I_2\end{array}\right]+\left[\begin{array}{c}{V}_{ind}^T\\ I_{ind}^T\end{array}\right]$$

  (1b)

  $$\left[\begin{array}{c}{\tilde{v}}_1^{(i)}(s)\\ {\tilde{i}}_1^{(i)}(s)\end{array}\right]=\left[\begin{array}{cc}{A}^{(i)}(s)& B^{(i)}(s)\\ C^{(i)}(s)& D^{(i)}(s)\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2^{(i)}(s)\\ {-\tilde{i}}_2^{(i)}(s)\end{array}\right]+\left[\begin{array}{c}{\tilde{v}}_{ind}^{T(i)}\left(s\right)\\ {\tilde{i}}_{ind}^{T(i)}\left(s\right)\end{array}\right]\tilde{\delta }(s)$$

  (2a)

  $$\left[\begin{array}{c}{V}_1^i\\ I_1^i\end{array}\right]=\left[\begin{array}{cc}{A}^{(i)}& B^{(i)}\\ C^{(i)}& D^{(i)}\end{array}\right]\left[\begin{array}{c}{V}_2^i\\ -I_2^i\end{array}\right]+\left[\begin{array}{c}{V}_{ind}^{T\left(i\right)}\\ I_{ind}^{T\left(i\right)}\end{array}\right]$$

  (2b)

  $$\left[\begin{array}{c}{\tilde{v}}_1^{(o)}(s)\\ {\tilde{i}}_1^{(o)}(s)\end{array}\right]=\left[\begin{array}{cc}{A}^{(o)}(s)& B^{(o)}(s)\\ C^{(o)}(s)& D^{(o)}(s)\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2^{(o)}(s)\\ {-\tilde{i}}_2^{(o)}(s)\end{array}\right]+\left[\begin{array}{c}{\tilde{v}}_{ind}^{T(o)}\left(s\right)\\ {\tilde{i}}_{ind}^{T(o)}\left(s\right)\end{array}\right]\tilde{\delta }(s)$$

  (3a)

  $$\left[\begin{array}{c}{V}_1^o\\ I_1^o\end{array}\right]=\left[\begin{array}{cc}{A}^{(o)}& B^{(o)}\\ C^{(o)}& D^{(o)}\end{array}\right]\left[\begin{array}{c}{V}_2^o\\ -I_2^o\end{array}\right]+\left[\begin{array}{c}{V}_{ind}^{T\left(o\right)}\\ I_{ind}^{T\left(o\right)}\end{array}\right]$$

  (3b)

From Figure 3, it can be shown that the input voltage and current of the input BBB are the same as the converter’s input voltage and current (4a), and the output voltage and current of the output BBB are the same as the converter’s output voltage and current (4b). Additionally, it can also be proved that the output voltage and current of the input BBB are the same as the input voltage and current of the output BBB for small-signal (5a) and steady-state (5b) analysis from which (6a) and (6b) are the result. Equation (6a,b) represents the generalised network of Figure 3 as a two-port network based on transmission parameters. These equations are sufficient for deriving both small-signal and steady-state models of the generalised network.

$$\left[\begin{array}{c}{\tilde{v}}_1^{(i)}(s)\\ {\tilde{i}}_1^{(i)}(s)\end{array}\right]\equiv \left[\begin{array}{c}{\tilde{v}}_{in}(s)\\ {\tilde{i}}_{in}(s)\end{array}\right]$$

(4a)

$$\left[\begin{array}{c}{\tilde{v}}_2^{(o)}(s)\\ {-\tilde{i}}_2^{(o)}(s)\end{array}\right]\equiv \left[\begin{array}{c}{\tilde{v}}_{out}(s)\\ {\tilde{i}}_{out}(s)\end{array}\right]$$

(4b)

$$\left[\begin{array}{c}{\tilde{v}}_2^{(i)}(s)\\ {-\tilde{i}}_2^{(i)}(s)\end{array}\right]=\left[\begin{array}{c}{\tilde{v}}_1^{(o)}(s)\\ {\tilde{i}}_1^{(o)}(s)\end{array}\right]$$

(5a)

$$\left[\begin{array}{c}{V}_2^i\\ -I_2^i\end{array}\right]=\left[\begin{array}{c}{V}_1^o\\ -I_1^o\end{array}\right]$$

(5b)

$$\left[\begin{array}{c}{\tilde{v}}_{in}(s)\\ {\tilde{i}}_{in}(s)\end{array}\right]=\left[\begin{array}{cc}A\left(s\right)& B\left(s\right)\\ C\left(s\right)& D\left(s\right)\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_{out}(s)\\ {\tilde{i}}_{out}(s)\end{array}\right]+\left[\begin{array}{c}{\tilde{v}}_{ind}^T\left(s\right)\\ {\tilde{i}}_{ind}^T\left(s\right)\end{array}\right]\tilde{\delta }\left(s\right)$$

(6a)

where:

$$A\left(s\right)=A^{\left(i\right)}\left(s\right)A^{\left(o\right)}\left(s\right)+B^{(i)}(s)C^{(o)}(s)$$

$$B\left(s\right)={A^{\left(i\right)}\left(s\right)B}^{\left(o\right)}\left(s\right)+B^{(i)}(s)D^{(o)}(s)$$

$$C\left(s\right)=C^{\left(i\right)}\left(s\right)A^{\left(o\right)}\left(s\right)+D^{(i)}(s)C^{(o)}(s)$$

$$D\left(s\right)=C^{\left(i\right)}\left(s\right)B^{\left(o\right)}\left(s\right)+D^{(i)}(s)D^{(o)}(s)$$

$${\tilde{v}}_{ind}^T\left(s\right)=\left\{A^{\left(i\right)}\left(s\right){\tilde{v}}_{ind}^{T(o)}\left(s\right)+B^{\left(i\right)}\left(s\right){\tilde{i}}_{ind}^{T(o)}\left(s\right)\right\}+{\tilde{v}}_{ind}^{T(i)}\left(s\right)$$

$${\tilde{i}}_{ind}^T\left(s\right)=\left\{C^{\left(i\right)}\left(s\right){\tilde{v}}_{ind}^{T(o)}\left(s\right)+D^{\left(i\right)}\left(s\right){\tilde{i}}_{ind}^{T(o)}\left(s\right)\right\}+{\tilde{i}}_{ind}^{T(i)}\left(s\right)$$

$$\left[\begin{array}{c}{V}_{in}\\ I_{in}\end{array}\right]=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]\left[\begin{array}{c}{V}_{out}\\ I_{out}\end{array}\right]+\left[\begin{array}{c}{V}_{ind}^T\\ I_{ind}^T\end{array}\right]$$

(6b)

where:

$$A=A^{(i)}{A}^{(o)}+{B^{(i)}C}^{(o)}$$

$$B=A^{(i)}{B}^{(o)}+{B^{(i)}D}^{(o)}$$

$$C=C^{(i)}{A}^{(o)}+D^{(i)}{C}^{(o)}$$

$$D=C^{(i)}{B}^{(o)}+D^{(i)}{D}^{(o)}$$

$$V_{ind}^T=\left\{A^{\left(i\right)}{V}_{ind}^{\left(o\right)}+B^{\left(i\right)}{I}_{ind}^{\left(o\right)}\right\}+V_{ind}^{(i)}$$

$$I_{ind}^T=\left\{C^{\left(i\right)}{V}_{ind}^{\left(o\right)}+D^{\left(i\right)}{I}_{ind}^{\left(o\right)}\right\}+I_{ind}^{(i)}$$

$${{{\tilde{v}}_2^{\left(o\right)}\left(s\right)=-\tilde{i}}_2^{(o)}(s)Z}_{Load}\left(s\right)$$

(7a)

$$V_2^o=-I_2^o{Z}_{Load}$$

(7b)

$$Z_{Load}\left(s\right)=\frac{R_L{Z}_C\left(s\right)}{R_L+Z_C\left(s\right)}$$

(7c)

Generalised Power Stage Models

The small-signal models of interest will be the audio-susceptibility transfer function (8), control-to-output voltage transfer function (9), input impedance (10), and output impedance (11). The steady-state model will mainly constitute the voltage gain (12). All the models represented by (8)–(12) are independent of the converter topology, and thus generalises the modelling procedure when the coefficients of the matrices in (6a) and (6b) are known.

$${\left.\frac{{\tilde{v}}_{out}\left(s\right)}{{\tilde{v}}_{in}\left(s\right)}\right|}_{\tilde{\delta }\left(s\right)=0}=\frac{Z_{Load}\left(s\right)}{A\left(s\right)Z_{Load}\left(s\right)+B\left(s\right)}$$

(8)

$${\left.\frac{{\tilde{v}}_{out}\left(s\right)}{\tilde{\delta }\left(s\right)}\right|}_{{\tilde{v}}_{in}\left(s\right)=0}=\frac{-{{\tilde{v}}_{ind}^T\left(s\right)Z}_{Load}\left(s\right)}{A\left(s\right)Z_{Load}\left(s\right)+B\left(s\right)}$$

(9)

$${\left.Z_{in}\left(s\right)=\frac{{\tilde{v}}_{in}\left(s\right)}{{\tilde{i}}_{in}\left(s\right)}\right|}_{\tilde{\delta }\left(s\right)=0}=\frac{A\left(s\right)Z_{Load}\left(s\right)+B\left(s\right)}{C\left(s\right)Z_{Load}\left(s\right)+D\left(s\right)}$$

(10)

$${\left.Z_{out}\left(s\right)=\frac{{\tilde{v}}_{out}\left(s\right)}{{-\tilde{i}}_{out}\left(s\right)}\right|}_{\begin{array}{c}{\tilde{v}}_{in}\left(s\right)=0\\ \tilde{\delta }\left(s\right)=0,\end{array}}=\frac{B\left(s\right)Z_{Load}\left(s\right)}{A\left(s\right)Z_{Load}\left(s\right)+B\left(s\right)}$$

(11)

$${\left.\frac{V_{out}}{V_{in}}\right|}_{V_{ind}=I_{ind}=0}=\frac{z_{Load}}{Z_{Load}A+B}$$

(12)

After deriving the generalised transfer functions (8)–(12), the modelling procedure can now be described as follows: (1) the input and output BBBs are modelled independently, (2) the connection of the input and output BBB dictates the type of parameters used for the two-port network and, (3) generalised transfer functions are used to compute models of interest.

3.2. Modelling Type 1 BBB

It was shown in the paper on modelling converters in CCM [26] that for each BBB type, different elements connect to the input and output ports. As such, the two-port models will vary based on element connection relative to the input and output ports. Due to the nature of transmission parameters, an interchange of elements from the input port to the output port will simply result in inverse transmission parameters; thus, that only leaves the element connected to the rail line to dictate the nature of the transmission parameters. Figure 4 shows possible two-port definitions for the Type 1 BBB.

Small-Signal and Steady State Circuit Models of Type 1 BBB

In this section, the circuit averaging approach is adopted to compute small-signal and steady-state circuit models of the various port definitions of Type 1 BBB. The circuit models in Figure 5a–c and Figure 6a–c are derived for each port definition in Figure 4a–c. In Figure 5a–c, the switch and diode circuit models in Figure 4a–c are replaced with their averaged models. It can be seen from Figure 4a that the active switch ‘S₁’ is replaced with a parallel combination of an equivalent resistor and an independent current source, as shown in Figure 5a. The diode ‘S₂’ in Figure 4a is replaced with a parallel combination of an equivalent resistor, a dependent current source and an independent current source, as shown in Figure 5a. The same active switch and diode averaged models are used for the remaining port definitions, i.e., Figure 4b,c. The use of resistors, and current sources in Figure 5a–c is a direct result of analysing the equivalent waveforms for the switches when the converter operates in DCM. For these definitions, the voltage directly across the active switch is designated with double subscripts ‘V₁₁’ and the voltage directly across the diode as measured from the cathode to the anode is also designated with double subscripts ‘V₂₂’. When the averaged circuit models for the various port definitions in Figure 5a–c are considered as two-port networks, the corresponding matrix coefficients defining transmission parameters are shown in

Table 1. DCM small-signal and steady-state models for Type 1 BBB.

BBB Variant	Model State	ABCD Constants
Type 1: Switch to rail	Small-signal (1a)	$\left[\begin{array}{c}{\tilde{v}}_1(s)\\ {\tilde{i}}_1(s)\end{array}\right]=\left[\begin{array}{cc}\frac{r_1+sL}{{r_1+r}_1{r}_2{g}_2}& \frac{{r_{1}r}_2+sL\left(r_1+r_2+r_1{r}_2{g}_2\right)}{r_1+r_1{r}_2{g}_2}\\ \frac{1}{{r_1+r}_1{r}_2{g}_2}& \frac{r_1+r_2+r_1{r}_2{g}_2}{r_1\left(1+r_2{g}_2\right)}\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2(s)\\ {-\tilde{i}}_2(s)\end{array}\right]+\left[\begin{array}{c}\frac{\left\{j_1\left(r_1+{r_{1}r}_2{g}_2\right)-j_2{r}_2\right\}\left\{r_1+sL\right\}-j_1{r}_1\left\{r_1+{r_{1}r}_2{g}_2\right\}}{r_1+{r_{1}r}_2{g}_2}\\ \frac{j_1\left(r_1+r_1{r}_2{g}_2\right)-j_2{r}_2}{r_1+{r_{1}r}_2{g}_2}\end{array}\right]\tilde{\delta }(s)$
	Steady-State (1b)	$\left[\begin{array}{c}{V}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}\frac{r_1}{{r_1+r}_1{r}_2{g}_2}& \frac{{r_{1}r}_2}{r_1+r_1{r}_2{g}_2}\\ \frac{1}{{r_1+r}_1{r}_2{g}_2}& \frac{r_1+r_2+r_1{r}_2{g}_2}{r_1\left(1+r_2{g}_2\right)}\end{array}\right]\left[\begin{array}{c}{V}_2\\ -I_2\end{array}\right]+\left[\begin{array}{c}0\\ 0\end{array}\right]$
Type 1: Diode to rail	Small-signal (1a)	$\left[\begin{array}{c}{\tilde{v}}_1(s)\\ {\tilde{i}}_1(s)\end{array}\right]=\left[\begin{array}{cc}\frac{r_1+r_2+r_1{r}_2{g}_2}{r_2+r_1{r}_2{g}_2}& \frac{{r_{1}r}_2+sL\left(r_1+r_2+r_1{r}_2{g}_2\right)}{r_2+r_1{r}_2{g}_2}\\ \frac{1}{{r_2+r}_1{r}_2{g}_2}& \frac{r_2+sL}{r_2\left(1+r_1{g}_2\right)}\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2(s)\\ {-\tilde{i}}_2(s)\end{array}\right]+\left[\begin{array}{c}-r_1\frac{j_1+j_2}{1+g_2{r}_1}\\ \frac{j_1{r}_1{g}_2-j_2}{1+r_1{g}_2}\end{array}\right]\tilde{\delta }(s)$
	Steady-State (1b)	$\left[\begin{array}{c}{V}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}\frac{r_1+r_2+r_1{r}_2{g}_2}{r_2+r_1{r}_2{g}_2}& \frac{r_1}{1+r_1{g}_2}\\ \frac{1}{{r_2+r}_1{r}_2{g}_2}& \frac{1}{1+r_1{g}_2}\end{array}\right]\left[\begin{array}{c}{V}_2\\ -I_2\end{array}\right]+\left[\begin{array}{c}0\\ 0\end{array}\right]$
Type 1: Inductor to rail	Small-signal (1a)	$\left[\begin{array}{c}{\tilde{v}}_1(s)\\ {\tilde{i}}_1(s)\end{array}\right]=\left[\begin{array}{cc}\frac{r_1+sL}{sL-{r_{1}r}_2{g}_2}& \frac{{r_{1}r}_2+sL\left(r_1+r_2+r_1{r}_2{g}_2\right)}{{sL-r}_1{r}_2{g}_2}\\ \frac{1}{{sL-r}_1{r}_2{g}_2}& \frac{r_2+sL}{{sL-r}_1{r}_2{g}_2}\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2(s)\\ {-\tilde{i}}_2(s)\end{array}\right]+\left[\begin{array}{c}\frac{{j_{2}r}_1{r}_2-sL\left\{{j_{1}r}_1{r}_2{g}_2-j_2{r}_2+j_1{r}_1\right\}}{{sL-r}_1{r}_2{g}_2}\\ \frac{j_2{r}_2{-j_{1}r}_1{r}_2{g}_2}{{sL-r}_1{r}_2{g}_2}\end{array}\right]\tilde{\delta }(s)$
	Steady-State (1b)	$\left[\begin{array}{c}{V}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}\frac{1}{-r_2{g}_2}& \frac{1}{-g_2}\\ \frac{1}{{-r}_1{r}_2{g}_2}& \frac{1}{{-r}_1{g}_2}\end{array}\right]\left[\begin{array}{c}{V}_2\\ -I_2\end{array}\right]+\left[\begin{array}{c}0\\ 0\end{array}\right]$
Parameter definitions
$r_1=\frac{V_{11}}{I_{11}}=\frac{2L}{D^2{T}_{sw}}=R_e;$ $r_2=\frac{V_{22}}{I_{22}};$ $g_2=\frac{2V_{11}}{V_{22}{R}_e};$ $j_1=\frac{2V_{11}}{D{R}_e};$ $j_2=\frac{2V_{11}^2}{V_{22}D{R}_e};$ $I_{22}=\frac{V_{11}^2}{V_{22}{R}_e}$

. In Table 1, both the small-signal and steady-state coefficients of (1a) and (1b) are shown.

3.3. Modelling Type 2 BBB

The Type 2 BBB also appears in various connection forms relative to the input and output ports. The conditions set for BBBs when synthesising converters, as listed in Section 2, highlight that for any BBB to realise a practical DC-DC converter all the port terminals should have DC current signals. It can be observed from Figure 1b,c that the two Type 2 BBB variants both fail to meet this condition. As such, any of the Type 2 BBB variants shown in Figure 1 cannot independently realise a practical converter; they have to be combined with other BBB types to realise a practical converter. Figure 7 shows a lumped Type 2 BBB proposed in [26]. This lumped Type 2 BBB considers the fact that averaged models for the diode or active switch utilise dependent sources which will pose computational complexity if presented in two separate circuits. As such, this lumped Type 2 BBB presents a minimum circuit configuration necessary to have parameters of dependent sources on the same structure. More information pertinent to the realisation of the lumped Type 2 BBB can be found in [26].

The same argument given for the Type 1 BBB still holds for the lumped Type 2 BBB, i.e., a simple exchange of elements from one port to another will simply result in inverse transmission parameters, which leaves the elements connected to the rail to dictate the uniqueness of the matrix coefficients of (1a) and (1b) for each variant of the lumped Type 2 BBB. Figure 7 shows all possible element connections to the rail. For the range of converters considered in this study, it will be shown that the lumped Type 2 BBB only needs to be cascaded with a filter block to realise a practical converter. As highlighted in [26], the introduction of the lumped Type 2 BBB shows close ties between the Cuk and Sepic converters from a synthesis point of view. This is not the same for the classification adopted in [27], wherein both the Cuk and Sepic converters are shown to have unique converter cells.

Small-Signal and Steady-State Circuit Models of Type 2 BBB

Similar to the analysis carried out in Small-Signal and Steady State Circuit Models of Type 1 BBB section, the small-signal and steady-state equivalent circuits for the lumped Type 2 BBB variants are computed using the circuit averaging technique. For each of the lumped Type 2 port definitions, an equivalent small-signal circuit model is shown in Figure 8. Moreover, the corresponding steady-state equivalent circuit model is shown in Figure 9. Ultimately, each equivalent circuit model in Figure 8 is considered as a two-port network and the corresponding matrix coefficients are given in

Table 2. DCM small-signal and steady-state models for the lumped Type 2 BBB.

BBB Variant	Model State	ABCD Constants
Lumped Type 2 BBB: Switch and diode to rail	Small-signal (1a)	$\left[\begin{array}{c}{\tilde{v}}_1(s)\\ {\tilde{i}}_1(s)\end{array}\right]=\left[\begin{array}{cc}\frac{{s^{2}C}_1{L}_1\left[{r_1+r}_2+g_2{r}_1{r}_2\right]+s\left[C_1{r}_1{r}_2+L_1\right]+r_1}{s{C}_1{r}_1{r}_2-g_2{r}_1{r}_2}& \frac{\left[{{s^{2}C}_1{L}_1{r}_1+sL}_1+r_1\right]}{r_1\left(C_{1}s-g_2\right)}\\ \frac{s{C}_1\left[g_2{r}_1{r}_2+r_1{+r}_2\right]+1}{s{C}_1{r}_1{r}_2-g_2{r}_1{r}_2}& \frac{{1+sC}_1{r}_1}{r_1\left(C_{1}s-g_2\right)}\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2(s)\\ {-\tilde{i}}_2(s)\end{array}\right]+\left[\begin{array}{c}\frac{{s^{2}C}_1{L}_1{r}_1{r}_2\left[j_1+j_2\right]{+sL}_1\left[j_2{r}_2-g_2{j}_1{r}_1{r}_2\right]+j_2{r}_1{r}_2}{s{C}_1{r}_1{r}_2-g_2{r}_1{r}_2}\\ \frac{{sC}_1{r}_1{r}_2\left[j_1+j_2\right]+j_2{r}_2-g_2{j}_1{r}_1{r}_2}{s{C}_1{r}_1{r}_2-g_2{r}_1{r}_2}\end{array}\right]\tilde{\delta }(s)$
	Steady-State (1b)	$\left[\begin{array}{c}{V}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}\frac{1}{-g_2{r}_2}& \frac{-1}{g_2}\\ \frac{1}{-g_2{r}_1{r}_2}& \frac{-1}{g_2{r}_1}\end{array}\right]\left[\begin{array}{c}{V}_2\\ -I_2\end{array}\right]+\left[\begin{array}{c}0\\ 0\end{array}\right]$
Lumped Type 2 BBB: inductor and switch to rail	Small-signal (1a)	$\left[\begin{array}{c}{\tilde{v}}_1(s)\\ {\tilde{i}}_1(s)\end{array}\right]=\left[\begin{array}{cc}\frac{1+{s^{2}C}_1{L}_1}{{s^{2}C}_1{L}_1\left[1+g_2{r}_2\right]+g_2{r}_2}& \frac{{s^{2}C}_1{L}_1{r}_2+s{L}_1+r_2}{{s^{2}C}_1{L}_1\left[1+g_2{r}_2\right]+g_2{r}_2}\\ \frac{1+{s^{2}C}_1{L}_1+s{C}_1{r}_1}{{s^{2}C}_1{L}_1\left[r_1+g_2{r}_1{r}_2\right]+g_2{r}_1{r}_2}& \frac{s^2\left[r_1+r_2+g_2{r}_1{r}_2\right]+s\left[L_1+C_1{r}_1{r}_2\right]+r_2}{{s^{2}C}_1{L}_1\left[r_1+g_2{r}_1{r}_2\right]+g_2{r}_1{r}_2}\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2(s)\\ {-\tilde{i}}_2(s)\end{array}\right]+\left[\begin{array}{c}\frac{-j_2{r}_2\left[1+{s^{2}C}_1{L}_1\right]}{{s^{2}C}_1{L}_1\left[1+g_2{r}_2\right]+g_2{r}_2}\\ \frac{{s^{2}C}_1{L}_1\left[j_1{r}_1-j_2{r}_2+g_2{j}_1{r}_1{r}_2\right]{-sC}_1{j}_2{r}_1{r}_2+g_2{j}_1{r}_1{r}_2-j_2{r}_2}{{s^{2}C}_1{L}_1\left[r_1+g_2{r}_1{r}_2\right]+g_2{r}_1{r}_2}\end{array}\right]\tilde{\delta }(s)$
	Steady-State (1b)	$\left[\begin{array}{c}{V}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}\frac{1}{g_2{r}_2}& \frac{1}{g_2}\\ \frac{1}{g_2{r}_1{r}_2}& \frac{1}{g_2{r}_1}\end{array}\right]\left[\begin{array}{c}{V}_2\\ -I_2\end{array}\right]+\left[\begin{array}{c}0\\ 0\end{array}\right]$
Lumped Type 2 BBB: Inductor and diode to rail	Small-signal (1a)	$\left[\begin{array}{c}{\tilde{v}}_1(s)\\ {\tilde{i}}_1(s)\end{array}\right]=\left[\begin{array}{cc}\frac{{s^{2}C}_1{L}_1\left[r_1+r_2+g_2{r}_2\right]+s\left[C_1{r}_2{r}_1+L_1\left[1+g_2-{r_{1}g}_2\right]\right]+r_1}{{s^{2}C}_1{L}_1\left[r_2+g_2{r}_1{r}_2\right]+g_2{r}_1{r}_2}& \frac{{s^{2}C}_1{L}_1{r}_1+s{L}_1+r_1}{{s^{2}C}_1{L}_1\left[1+g_2{r}_1\right]+g_2{r}_1}\\ \frac{1+{s^{2}C}_1{L}_1+s{C}_1{r}_2}{{s^{2}C}_1{L}_1\left[r_2+g_2{r}_1{r}_2\right]+g_2{r}_1{r}_2}& \frac{1+{s^{2}C}_1{L}_1}{{s^{2}C}_1{L}_1\left[1+g_2{r}_1\right]+g_2{r}_1}\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2(s)\\ {-\tilde{i}}_2(s)\end{array}\right]+\left[\begin{array}{c}\frac{{{-s}^{2}C}_1{L}_1{r}_1\left[j_1+j_2\right]+s{L}_1\left[g_2{j}_1{r}_1-j_2\right]-j_2{r}_1}{{s^{2}C}_1{L}_1\left[1+g_2{r}_1\right]+g_2{r}_1}\\ \frac{\left[C_1{L}_1{s}^2+1\right]\left[j_1{g}_2{r}_1-j_2\right]}{{s^{2}C}_1{L}_1\left[1+g_2{r}_1\right]+g_2{r}_1}\end{array}\right]\tilde{\delta }(s)$
	Steady-State (1b)	$\left[\begin{array}{c}{V}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}\frac{1}{g_2{r}_2}& \frac{1}{g_2}\\ \frac{1}{g_2{r}_1{r}_2}& \frac{1}{g_2{r}_1}\end{array}\right]\left[\begin{array}{c}{V}_2\\ -I_2\end{array}\right]+\left[\begin{array}{c}0\\ 0\end{array}\right]$
Parameter definitions
$r_1=\frac{V_{11}}{I_{11}}=\frac{2L}{D^2{T}_{sw}}=R_e;L=\frac{L_1{L}_2}{L_1+L_2};$ $r_2=\frac{V_{22}}{I_{22}};$ $g_2=\frac{2V_{11}}{V_{22}{R}_e};$ $j_1=\frac{2V_{11}}{D{R}_e};$ $j_2=\frac{2V_{11}^2}{V_{22}D{R}_e};$ $I_{22}=\frac{V_{11}^2}{V_{22}{R}_e}$

. The format of (1a) and (1b) is adopted for the matrix coefficients in Table 2.

3.4. DCM Equivalent Circuit Model Parameter Definitions

The bottom of Table 1 and Table 2 show all the parameter definitions as derived for the equivalent circuits in Figure 5 and Figure 8. These parameter definitions are relevant for Type 1 BBB and Type 2 BBB, respectively. It will be noted from these parameter definitions that for Type 1 BBB, the inductance in $R_e$ is the BBB inductance. On the other hand, for the lumped type 2 BBB, the inductance in $R_e$ is a parallel combination of the inductances in the final circuit network, as shown in (13). To further simplify the computation of any model, the parameters are defined in terms of average DC voltages across semiconductor devices. These voltages can easily be defined in terms of input and/or output voltage.

$$L=\frac{L_1{L}_2}{L_1+L_2}$$

(13)

3.5. Modelling the Filter Block

Finally, the last BBB to be considered is the filter block. It was mentioned that the filter block is generically represented as an LCL filter which represents the highest filtering capability. An LC filter is realised by setting absent components in a given filter circuit to zero. Similarly, an L, C, or CL filter can also be realised by assigning a zero value to any absent element in a given filter configuration. It should be noted that this BBB does not contain non-linear components as shown in Figure 1e. As such, there is no need to derive averaged models for this BBB.

Small-Signal and Steady-State Circuit Models of the Filter Block BBB

Since the filter block does not contain any non-linear component, its small-signal and steady-state models are the same as those derived for CCM operation. The equivalent steady-state and small-signal circuit models for the filter block in Figure 10a are shown in Figure 10b. The subsequent consideration of the equivalent circuit mode of Figure 10b as a two-port network yields the matrix coefficients captured in

Table 3. DCM small-signal and steady-state models for the filter block.

BBB Variant	Model State	ABCD Constants
Generalised LCL filter block	Small-signal (1a)	$\left[\begin{array}{c}{\tilde{v}}_1(s)\\ {\tilde{i}}_1(s)\end{array}\right]=\left[\begin{array}{cc}{C}_1{L}_1{s}^2+1& C_1{L}_1{L}_2{s}^3+s\left(L_1+L_2\right)\\ {sC}_1& C_1{L}_2{s}^2+1\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2(s)\\ {-\tilde{i}}_2(s)\end{array}\right]$
	Steady-state (1b)	$\left[\begin{array}{c}{V}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{V}_2\\ -I_2\end{array}\right]+\left[\begin{array}{c}0\\ 0\end{array}\right]$

.

4. Non-Conventional Converters

In this section, the presented modelling scheme based on BBBs is shown to be directly applicable to non-conventional converters with well-defined BBBs. For non-conventional converters, the modelling burden is the same as that for conventional converters, i.e., (1) identify the constituent BBBs and, (2) identify the accompanying connection. Thus, once the constituent BBBs have been identified, each BBB will be modelled as a two-port network. The parameters of the two-port network need not be transmission parameters, which have been shown to be more suited for cascaded systems [38], based on the connection of constituent BBBs; different yet equivalent parameters can be used. The current- and voltage-fed full-bridge DC-DC converters are considered to demonstrate a practical adoption of the proposed modelling scheme for non-conventional converters.

4.1. Modelling the Voltage-Fed Full-Bridge DC-DC Converter

The circuit diagram of a voltage-fed full-bridge DC-DC converter is shown in Figure 11. From Figure 11, a refined diagram of the same circuit is shown in Figure 12. It can be clearly seen from this figure that the circuit of a voltage-fed DC-DC converter is made up of two Type 1 BBBs in a shunt-series connection. The shunt connection is on the input side and the series connection is on the output side. For such a connection, the most suitable two-port network parameters to easily model the circuit will be the g-parameters as justified in the literature [28,38]. It should be noted that the computation of the equivalent two-port network parameters, given one set of parameters, is independent of the original network. As such, given the transmission parameters in Table 1, the computation of g-, h-, z-, y-, or inverse of transmission parameters is independent of the diagrams in Figure 5. An example of the transformation of the transmission parameters to equivalent g-parameters is shown in (14). The transformation matrices are captured in the available literature [38].

$$\left[\begin{array}{c}{\tilde{i}}_1(s)\\ {\tilde{v}}_2(s)\end{array}\right]=\left[\begin{array}{cc}\frac{C(s)}{A(s)}& \frac{-det(T)}{A(s)}\\ \frac{1}{A(s)}& \frac{B(s)}{A(s)}\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_1(s)\\ {\tilde{i}}_2(s)\end{array}\right]+\left[\begin{array}{c}\frac{A\left(s\right){\tilde{i}}_{ind}^T(s) - C(s){\tilde{v}}_{ind}^T(s)}{A(s)}\\ \frac{-{\tilde{v}}_{ind}^T(s)}{A(s)}\end{array}\right]\tilde{\delta }(s)$$

(14)

where: $det\left(T\right)=A\left(s\right)D\left(s\right)-B(s)C(s)$.

The validity of using g-parameters for the constituent BBB of the full-bridge DC-DC converter and the accompanying application of the two-port models considering specific terminal voltage polarities of the identified BBBs are covered in the first paper that deals with modelling DC-DC converters operating in CCM using converter BBBs. Interested readers can look at [26] for a more detailed description. The analysis shown in [26] shows that the equivalent g-parameter-based two-port model for the voltage-fed DC-DC converter BBBs can be given as shown in (15) and (16). The superscripts ‘u’ and ‘l’ in (15) and (16) are used to discriminate parameters of the red BBB from those of the black BBB in Figure 12.

$$\left[\begin{array}{c}{\tilde{i}}_1^{(u)}(s)\\ {\tilde{v}}_2^{(u)}(s)\end{array}\right]=\left[\begin{array}{cc}{g}_{11}^{(u)}& g_{12}^{(u)}\\ g_{21}^{(u)}& g_{22}^{(u)}\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_1^{(u)}(s)\\ {\tilde{i}}_2^{(u)}(s)\end{array}\right]+\left[\begin{array}{c}{\tilde{i}}_{1,ind}^{g(u)}(s)\\ {\tilde{v}}_{2,ind}^{g(u)}(s)\end{array}\right]\tilde{\delta }(s)$$

(15)

$$\left[\begin{array}{c}{\tilde{i}}_1^{(l)}(s)\\ {\tilde{v}}_2^{(l)}(s)\end{array}\right]=\left[\begin{array}{cc}{g}_{11}^{(l)}& -g_{12}^{(l)}\\ {-g}_{21}^{(l)}& g_{22}^{(l)}\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_1^{(l)}(s)\\ {\tilde{i}}_2^{(l)}(s)\end{array}\right]+\left[\begin{array}{c}{\tilde{i}}_{1,ind}^{g(l)}(s)\\ {-\tilde{v}}_{2,ind}^{g(l)}(s)\end{array}\right]\tilde{\delta }(s)$$

(16)

The resultant two-port representation of the complete circuit of Figure 12 in terms of g-parameters is shown in (17) and (18) for dynamic and steady-state operation, respectively. These represent a two-port model of a voltage-fed full-bridge DC-DC converter.

$$\left[\begin{array}{c}{\tilde{i}}_1(s)\\ {\tilde{v}}_2(s)\end{array}\right]=\left[\begin{array}{cc}{g}_{11}(s)& g_{12}(s)\\ g_{21}(s)& g_{22}(s)\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_1(s)\\ {\tilde{i}}_2(s)\end{array}\right]+\left[\begin{array}{c}{\tilde{i}}_{ind}^g(s)\\ {\tilde{v}}_{ind}^g(s)\end{array}\right]\tilde{\delta }(s)$$

(17)

where:

$$g_{11}(s)=g_{11}^{(u)}+g_{11}^{(l)}$$

$$g_{12}(s)=g_{12}^{(u)}+\left(-g_{12}^{(l)}\right)$$

$$g_{21}(s)=g_{21}^{(u)}+\left({-g}_{21}^{(l)}\right)$$

$$g_{22}(s)=g_{22}^{(u)}+g_{22}^{(l)}$$

$${\tilde{i}}_{ind}^g(s)={\tilde{i}}_{1,ind}^{g\left(u\right)}\left(s\right)+{\tilde{i}}_{1,ind}^{g(l)}(s)$$

$${\tilde{v}}_{ind}^g(s)={\tilde{v}}_{2,ind}^{g\left(u\right)}\left(s\right)+\left({-\tilde{v}}_{2,ind}^{g(l)}(s)\right)$$

$$\left[\begin{array}{c}{I}_1\\ V_2\end{array}\right]=\left[\begin{array}{cc}{g}_{11}& g_{12}\\ g_{21}& g_{22}\end{array}\right]\left[\begin{array}{c}{V}_1\\ I_2\end{array}\right]+\left[\begin{array}{c}{I}_{ind}^g\\ V_{ind}^g\end{array}\right]$$

(18)

Similar to a two-port model representation shown in (6a) in terms of transmission parameters, generalised equations for the transfer functions of interest can be derived for the two-port model shown in (17) in terms of g-parameters. Control-to-output voltage transfer function and the audio-susceptibility transfer function are shown in (19) and (20) in terms of g-parameters, respectively.

$${\left.\frac{{\tilde{v}}_{out}\left(s\right)}{\tilde{\delta }\left(s\right)}\right|}_{{\tilde{v}}_{in}\left(s\right)=0}=\frac{{{\tilde{v}}_{ind}^g(s)Z}_{Load}\left(s\right)}{Z_{Load}\left(s\right)+g_{22}\left(s\right)}$$

(19)

$${\left.\frac{{\tilde{v}}_{out}\left(s\right)}{{\tilde{v}}_{in}\left(s\right)}\right|}_{\tilde{\delta }\left(s\right)=0}=\frac{g_{21}\left(s\right)Z_{Load}\left(s\right)}{Z_{Load}\left(s\right)+g_{22}\left(s\right)}$$

(20)

4.2. Modelling the Current-Fed Full-Bridge DC-DC Converter

Similarly, two Type 1 BBBs in a series-shunt connection can be identified as the main constituent BBBs for the current-fed DC-DC converter. The series connection is on the input side and the shunt connection is on the output side. For this connection, it can be shown that h-parameters are more suited for modelling the constituent BBBs as two-port networks. As mentioned in Section 4.1, the transformation from transmission parameters to h-parameters can be easily completed using well defined matrices from the literature as shown in (21). The resultant two-port representation of the complete circuit of Figure 13 in terms of h-parameters is shown in (22) for dynamic operation. These represent the complete two-port model of a current-fed full-bridge DC-DC converter. The corresponding control-to-output voltage transfer function and audio-susceptibility transfer function are shown in (23) and (24), respectively.

$$\left[\begin{array}{c}{\tilde{v}}_1(s)\\ {\tilde{i}}_2(s)\end{array}\right]=\left[\begin{array}{cc}\frac{B(s)}{D(s)}& \frac{det(T)}{D(s)}\\ \frac{-1}{D(s)}& \frac{C(s)}{D(s)}\end{array}\right]\left[\begin{array}{c}{\tilde{i}}_1(s)\\ {\tilde{v}}_2(s)\end{array}\right]+\left[\begin{array}{c}\frac{D\left(s\right){\tilde{v}}_{ind}^T(s) - B(s){\tilde{i}}_{ind}^T(s)}{D(s)}\\ \frac{{\tilde{i}}_{ind}^T(s)}{D(s)}\end{array}\right]\tilde{\delta }(s)$$

(21)

$$\left[\begin{array}{c}{\tilde{v}}_1(s)\\ {\tilde{i}}_2(s)\end{array}\right]=\left[\begin{array}{cc}{h}_{11}(s)& h_{12}(s)\\ h_{21}(s)& h_{22}(s)\end{array}\right]\left[\begin{array}{c}{\tilde{i}}_1(s)\\ {\tilde{v}}_2(s)\end{array}\right]+\left[\begin{array}{c}{\tilde{i}}_{ind}^h(s)\\ {\tilde{v}}_{ind}^h(s)\end{array}\right]\tilde{\delta }(s)$$

(22)

$${\left.\frac{{\tilde{v}}_{out}\left(s\right)}{\tilde{\delta }\left(s\right)}\right|}_{{\tilde{v}}_{in}\left(s\right)=0}=\frac{{\left[h_{21}\left(s\right){\tilde{v}}_{ind}^h\left(s\right)-h_{11}\left(s\right){\tilde{i}}_{ind}^h(s)\right]Z}_{Load}\left(s\right)}{Z_{Load}\left(s\right)\left[h_{22}\left(s\right)h_{11}\left(s\right)-h_{21}\left(s\right)h_{12}\left(s\right)\right]+h_{11}\left(s\right)}$$

(23)

$${\left.\frac{{\tilde{v}}_{out}\left(s\right)}{{\tilde{v}}_{in}\left(s\right)}\right|}_{\tilde{\delta }\left(s\right)=0}=\frac{{{-h}_{21}\left(s\right)Z}_{Load}\left(s\right)}{Z_{Load}\left(s\right)\left[h_{22}\left(s\right)h_{11}\left(s\right)-h_{21}\left(s\right)h_{12}\left(s\right)\right]+h_{11}\left(s\right)}$$

(24)

5. Examples

In this section, the accuracy of the proposed modelling scheme is validated through examples. The aim is to show the application of the modelling scheme on a range of converters. This range of converters is selected to represent most of the common combinations of the BBBs. Since a given converter element can appear more than once on the same converter, e.g., two inductors appear in a Cuk converter, component numbering will be essential. In this section, components will be numbered from left to right in the order they appear. This coincides with the direction of power flow from input to output. The converters considered in this section encompass both second- and fourth-order converters. This is a deliberate selection to show how model order and functionality are nullified in the modelling process.

5.1. Modelling the Conventional Buck-Boost Converter

5.1.1. Model Derivation

The constituent BBB for a conventional buck-boost converter is a Type 1 BBB. The two-port model in terms of transmission parameters for this Type 1 BBB is given in (25). The generic model of a cascaded system shown in (6a) considers two BBBs for a single converter. To conform to this representation, the conventional converter can be considered to be cascaded with connecting wires whose two-port model results in a 2 × 2 identity matrix as shown in (26). Once the two BBBs are condensed in the form of (6a), the transfer function of interest will be computed using the generalised expressions in (9) to result in (27). Similarly, the audio-susceptibility transfer function will be computed using (8) to result in (28).

$$\left[\begin{array}{c}{\tilde{v}}_1^{(i)}(s)\\ {\tilde{i}}_1^{(i)}(s)\end{array}\right]=\left[\begin{array}{cc}\frac{r_1 + s{L}_1}{s{L}_1 - {r_{1}r}_2{g}_2}& \frac{{r_{1}r}_2 + s{L}_1\left(r_1 + r_2 + r_1{r}_2{g}_2\right)}{{s{L}_1 - r}_1{r}_2{g}_2}\\ \frac{1}{{s{L}_1 - r}_1{r}_2{g}_2}& \frac{r_2 + s{L}_1}{{s{L}_1 - r}_1{r}_2{g}_2}\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2^{(i)}(s)\\ {-\tilde{i}}_2^{(i)}(s)\end{array}\right] + \left[\begin{array}{c}\frac{{j_{2}r}_1{r}_2 - s{L}_1\left\{{j_{1}r}_1{r}_2{g}_2 - j_2{r}_2 + j_1{r}_1\right\}}{{s{L}_1 - r}_1{r}_2{g}_2}\\ \frac{j_2{r}_2{ - j_{1}r}_1{r}_2{g}_2}{{s{L}_1 - r}_1{r}_2{g}_2}\end{array}\right]\tilde{\delta }(s)$$

(25)

$$\left[\begin{array}{c}{\tilde{v}}_1^{(o)}(s)\\ {\tilde{i}}_1^{(o)}(s)\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2^{(o)}(s)\\ {-\tilde{i}}_2^{(o)}(s)\end{array}\right]+\left[\begin{array}{c}0\\ 0\end{array}\right]\tilde{\delta }(s)$$

(26)

5.1.2. Model Validation

To validate the accuracy of the transfer functions derived using the proposed modelling scheme, the equivalent bode plots of the transfer functions in (27) and (28) are plotted against an independently derived bode plots based on the AC sweep function in PSim 2021b. The two plots are shown on the same axis in Figure 14 for the control-to-output voltage transfer function and Figure 15 for the audio-susceptibility transfer function. Congruency of the two plots is used to assess accuracy. Numerical values of the circuit elements used for deriving bode plots are shown in

Table 4. Buck-boost converter parameters.

Component	Value
$V_{in}$	50 V
$R_o$	80 Ω
$F_{sw}$	20 kHz
$D$	0.35
$L; C$	150 µH; 100 µF

.

$${\left.\frac{{\tilde{v}}_o\left(s\right)}{\tilde{\delta }\left(s\right)}\right|}_{{\tilde{v}}_{in}\left(s\right)=0}=\frac{R_L\left\{sL\left[{j_{1}r}_1+{j_{1}r}_1{r}_2{g}_2-{j_{2}r}_2\right]-{j_{2}r}_1{r}_2\right\}}{{R_{L}s}^{2}LC\left(r_1+r_2+r_1{r}_2{g}_2\right)+\left\{L\left(r_1+r_2+r_1{r}_2{g}_2\right)+C{R}_L{r}_1{r}_2+R_{L}L\right\}s+r_1{r}_2+R_L{r}_1}$$

(27)

$${\left.\frac{{\tilde{v}}_o\left(s\right)}{{\tilde{v}}_{in}\left(s\right)}\right|}_{\tilde{\delta }\left(s\right)=0}=\frac{R_L\left[sL-g_2{r}_1{r}_2\right]}{{R_{L}s}^{2}LC\left(r_1+r_2+r_1{r}_2{g}_2\right)+\left\{L\left(r_1+r_2+r_1{r}_2{g}_2\right)+C{R}_L{r}_1{r}_2+R_{L}L\right\}s+r_1{r}_2+R_L{r}_1}$$

(28)

5.2. Modelling the Conventional Buck Converter with Input Filter

5.2.1. Model Derivation

The constituent BBBs for a conventional buck converter with input filter are the filter block and a Type 1 BBB. The two-port models in terms of transmission parameters for the filter block is given in (29) and that for the Type 1 BBB is given in (30). Once the two BBBs are combined in the form of (6a), the transfer function of interest will be computed using the generalised expressions in (9) to result in (31). Similarly, the audio-susceptibility transfer function will be computed using (8) to result in (32).

$$\left[\begin{array}{c}{\tilde{v}}_1^{(i)}(s)\\ {\tilde{i}}_1^{(i)}(s)\end{array}\right]=\left[\begin{array}{cc}{C}_1{L}_1{s}^2+1& {sL}_1\\ {sC}_1& 1\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2^{(i)}(s)\\ {-\tilde{i}}_2^{(i)}(s)\end{array}\right]+\left[\begin{array}{c}0\\ 0\end{array}\right]\tilde{\delta }(s)$$

(29)

$$\left[\begin{array}{c}{\tilde{v}}_1^{(o)}(s)\\ {\tilde{i}}_1^{(o)}(s)\end{array}\right]=\left[\begin{array}{cc}\frac{r_1 + r_2 + r_1{r}_2{g}_2}{r_2 + r_1{r}_2{g}_2}& \frac{{r_{1}r}_2 + s{L}_2\left(r_1 + r_2 + r_1{r}_2{g}_2\right)}{r_2 + r_1{r}_2{g}_2}\\ \frac{1}{{r_2 + r}_1{r}_2{g}_2}& \frac{r_2 + s{L}_2}{r_2\left(1 + r_1{g}_2\right)}\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2^{(o)}(s)\\ {-\tilde{i}}_2^{(o)}(s)\end{array}\right] + \left[\begin{array}{c} - r_1\frac{j_1 + j_2}{1 + g_2{r}_1}\\ \frac{j_1{r}_1{g}_2 - j_2}{1 + r_1{g}_2}\end{array}\right]\tilde{\delta }(s)$$

(30)

5.2.2. Model Validation

Similarly, to validate the accuracy of the transfer functions derived using the proposed modelling scheme, the equivalent bode plots of the transfer functions in (31) and (32) are plotted against independently derived bode plots based on the AC sweep function in PSim. The two plots are shown on the same axis in Figure 16 for the control-to-output voltage transfer function and Figure 17 for the audio-susceptibility transfer function. The congruency of the plots is used in a similar manner to assess the accuracy of the proposed modelling scheme. The numerical values of the circuit elements used for deriving bode plots are shown in

Table 5. Buck converter with input filter parameters.

Component	Value
$V_{in}$	50 V
$R_o$	80 Ω
$F_{sw}$	20 kHz
$D$	0.35
$L_1;L_2;C_1;C_2$	500 µH; 300 µH; 20 µF; 31.25 µF

.

$${\left.\frac{{\tilde{v}}_o\left(s\right)}{\tilde{\delta }\left(s\right)}\right|}_{{\tilde{v}}_{in}\left(s\right)=0}=\frac{R_L{C}_1{L}_1{r}_1{r}_2\left(j_1+j_2\right)s^2+{R_{L}L}_1{r}_2\left[j_2-j_1{r}_1{g}_2\right]s+R_L{r}_1{r}_2\left(j_1+j_2\right)}{{∆}_1}$$

(31)

$${\left.\frac{{\tilde{v}}_o\left(s\right)}{{\tilde{v}}_{in}\left(s\right)}\right|}_{\tilde{\delta }\left(s\right)=0}=\frac{R_L\left(r_2+r_1{r}_2{g}_2\right)}{{∆}_1}$$

(32)

where:

$$\begin{array}{ll}\hfill {∆}_1=R_L{C}_1{C}_2{L}_1{L}_2& \left(r_1+r_2+g_2{r}_1{r}_2\right)s^4\hfill \\ & +\left\{C_1{L}_1{L}_2\left(r_1+r_2+g_2{r}_1{r}_2\right)+R_L{C}_2{L}_1{L}_2+R_L{C}_1{C}_2{L}_1{r}_1{r}_2\right\}{s}^3\hfill \\ & +\{R_L{C}_2{L}_2\left(r_1+r_2+g_2{r}_1{r}_2\right)+R_L{C}_1{L}_1\left(r_1+r_2+g_2{r}_1{r}_2\right)+C_2{L}_1{R}_L{r}_2\hfill \\ & +L_1{C}_1{r}_1{r}_2+L_1{L}_2\}{s}^2\hfill \\ & +\left\{R_L\left[C_2{r}_1{r}_2+L_1\right]+L_2\left(r_1+r_2+g_2{r}_1{r}_2\right)+L_1{r}_2\right\}s+r_1{r}_2\hfill \\ & +R_L\left(r_1+r_2+g_2{r}_1{r}_2\right)\hfill \end{array}$$

5.3. Modelling the Sepic Converter

5.3.1. Model Derivation

The constituent BBBs for a Sepic converter are the filter block and a Type 2 BBB. The two-port models in terms of transmission parameters for the filter block is given in (33) and that for the Type 2 BBB is given in (34). Once the two BBBs are combined in the form of (6a), the transfer function of interest will be computed using the generalised expressions in (9) to result in (35) for the control-to-output voltage transfer function. Similarly, the audio-susceptibility transfer function will be computed using (8) to result in (36).

$$\left[\begin{array}{c}{\tilde{v}}_1^{(i)}(s)\\ {\tilde{i}}_1^{(i)}(s)\end{array}\right]=\left[\begin{array}{cc}1& s{L}_1\\ 0& 1\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2^{(i)}(s)\\ {-\tilde{i}}_2^{(i)}(s)\end{array}\right]+\left[\begin{array}{c}0\\ 0\end{array}\right]\tilde{\delta }(s)$$

(33)

$$\left[\begin{array}{c}{\tilde{v}}_1^{(o)}(s)\\ {\tilde{i}}_1^{(o)}(s)\end{array}\right]=\left[\begin{array}{cc}\frac{1 + {s^{2}C}_1{L}_2}{{s^{2}C}_1{L}_2\left[1 + g_2{r}_2\right] + g_2{r}_2}& \frac{{s^{2}C}_1{L}_2{r}_2 + s{L}_2 + r_2}{{s^{2}C}_1{L}_2\left[1 + g_2{r}_2\right] + g_2{r}_2}\\ \frac{1 + {s^{2}C}_1{L}_2 + s{C}_1{r}_1}{{s^{2}C}_1{L}_2\left[r_1 + g_2{r}_1{r}_2\right] + g_2{r}_1{r}_2}& \frac{{s^{2}C}_1{L}_2\left[r_1 + r_2 + g_2{r}_1{r}_2\right] + s\left[L_2 + C_1{r}_1{r}_2\right] + r_2}{{s^{2}C}_1{L}_2\left[r_1 + g_2{r}_1{r}_2\right] + g_2{r}_1{r}_2}\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2^{(o)}(s)\\ {-\tilde{i}}_2^{(o)}(s)\end{array}\right] + \left[\begin{array}{c}\frac{ - j_2{r}_2\left[1 + {s^{2}C}_1{L}_2\right]}{{s^{2}C}_1{L}_2\left[1 + g_2{r}_2\right] + g_2{r}_2}\\ \frac{{s^{2}C}_1{L}_2\left[j_1{r}_1 - j_2{r}_2 + g_2{j}_1{r}_1{r}_2\right]{ - sC}_1{j}_2{r}_1{r}_2 + g_2{j}_1{r}_1{r}_2 - j_2{r}_2}{{s^{2}C}_1{L}_2\left[r_1 + g_2{r}_1{r}_2\right] + g_2{r}_1{r}_2}\end{array}\right]\tilde{\delta }(s)$$

(34)

5.3.2. Model Validation

Similarly, to validate the accuracy of the transfer functions derived using the proposed modelling scheme, the equivalent bode plots of the transfer functions in (35) and (36) are plotted against independently derived bode plots based on the AC sweep function in PSim. The two plots are shown on the same axis in Figure 18 for the control-to-output voltage transfer function and Figure 19 for the audio-susceptibility transfer function. The congruency of the plots is used in a similar manner to assess the accuracy of the proposed modelling scheme. Numerical values of the circuit elements used for deriving bode plots are shown in

Table 6. Sepic converter parameters.

Component	Value
$V_{in}$	50 V
$R_o$	80 Ω
$F_{sw}$	20 kHz
$D$	0.35
$L_1;L_2;C_1;C_2$	600 µH; 150 µH; 30 µF; 50µF

.

$${\left.\frac{{\tilde{v}}_o\left(s\right)}{\tilde{\delta }\left(s\right)}\right|}_{{\tilde{v}}_{in}\left(s\right)=0}=\frac{R_L\left\{{{s^{3}C}_1{L}_1{L}_2\left[j_2{r}_2 - j_1{r}_1 - g_2{j}_1{r}_1{r}_2\right] + s^{2}C}_1\left[j_2{L}_1{r}_1{r}_2 + j_2{L}_2{r}_1{r}_2\right]{ + sL}_1\left[j_2{r}_2 - g_2{j}_1{r}_1{r}_2\right] + j_2{r}_1{r}_2\right\}}{{∆}_2}$$

(35)

$${\left.\frac{{\tilde{v}}_o\left(s\right)}{{\tilde{v}}_{in}\left(s\right)}\right|}_{\tilde{\delta }\left(s\right)=0}=\frac{R_L\left[{s^{2}C}_1{L}_2\left[r_1+g_2{r}_1{r}_2\right]+g_2{r}_1{r}_2\right]}{{∆}_2}$$

(36)

where:

$$\begin{array}{ll}{{∆}_2=s}^4{R}_L{C}_1{C}_2{L}_1& L_2\left(r_1+r_2+g_2{r}_1{r}_2\right)\\ & +s^3\{C_1{L}_1{L}_2\left(r_1+r_2+g_2{r}_1{r}_2\right)+R_L{C}_1{L}_1{L}_2\\ & +R_L{C}_2\left[C_1{L}_2{r}_1{r}_2+L_1\left(L_2+C_1{r}_2{r}_1\right)\right]\}\\ & +s^2\{R_L{C}_2\left(L_2{r}_1+L_1{r}_2\right)+L_1\left[C_1{r}_1{r}_2+L_2\right]+C_1{L}_1{R}_L{r}_1\\ & +C_1{L}_2{r}_2{r}_1+C_1{L}_2{R}_L{r}_1\}+s\left\{R_L\left[C_2{r}_1{r}_2+L_1\right]+L_2{r}_1+L_1{r}_2\right\}\\ & +r_1{r}_2+R_L{r}_1\end{array}$$

5.4. Modelling the Cuk Converter

5.4.1. Model Derivation

The constituent BBB for a Cuk converter is a Type 2 BBB and a filter block made up of a series inductor. The two-port model in terms of transmission parameters for the Type 2 BBB is given in (37). The two-port models in terms of transmission parameters for the filter block is given in (38). Once the two BBBs are combined in the form of (6a), the transfer function of interest will be computed using the generalised expressions in (9) to result in (39) for the control-to-output voltage transfer function. Similarly, the audio-susceptibility transfer function will be computed using (8) to result in (40).

$$\left[\begin{array}{c}{\tilde{v}}_1(s)\\ {\tilde{i}}_1(s)\end{array}\right]=\left[\begin{array}{cc}\frac{{s^{2}C}_1{L}_1\left[{r_1 + r}_2 + g_2{r}_1{r}_2\right] + s\left[C_1{r}_1{r}_2 + L_1\right] + r_1}{s{C}_1{r}_1{r}_2 - g_2{r}_1{r}_2}& \frac{\left[{{s^{2}C}_1{L}_1{r}_1 + sL}_1 + r_1\right]}{r_1\left(C_{1}s - g_2\right)}\\ \frac{s{C}_1\left[g_2{r}_1{r}_2 + r_1{ + r}_2\right] + 1}{s{C}_1{r}_1{r}_2 - g_2{r}_1{r}_2}& \frac{{1 + sC}_1{r}_1}{r_1\left(C_{1}s - g_2\right)}\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2(s)\\ {-\tilde{i}}_2(s)\end{array}\right] + \left[\begin{array}{c}\frac{{s^{2}C}_1{L}_1{r}_1{r}_2\left[j_1 + j_2\right]{ + sL}_1\left[j_2{r}_2 - g_2{j}_1{r}_1{r}_2\right] + j_2{r}_1{r}_2}{s{C}_1{r}_1{r}_2 - g_2{r}_1{r}_2}\\ \frac{{sC}_1{r}_1{r}_2\left[j_1 + j_2\right] + j_2{r}_2 - g_2{j}_1{r}_1{r}_2}{s{C}_1{r}_1{r}_2 - g_2{r}_1{r}_2}\end{array}\right]\tilde{\delta }(s)$$

(37)

$$\left[\begin{array}{c}{\tilde{v}}_1(s)\\ {\tilde{i}}_1(s)\end{array}\right]=\left[\begin{array}{cc}1& s{L}_2\\ 0& 1\end{array}\right]\left[\begin{array}{c}{\tilde{v}}_2(s)\\ {-\tilde{i}}_2(s)\end{array}\right]$$

(38)

$${\left.\frac{{\tilde{v}}_o\left(s\right)}{\tilde{\delta }\left(s\right)}\right|}_{{\tilde{v}}_{in}\left(s\right)=0}=\frac{R_L\left\{-{s^{2}C}_1{L}_1{r}_1{r}_2\left[j_1+j_2\right]{-sL}_1\left[j_2{r}_2-g_2{j}_1{r}_1{r}_2\right]-j_2{r}_1{r}_2\right\}}{{∆}_3}$$

(39)

$${\left.\frac{{\tilde{v}}_o\left(s\right)}{{\tilde{v}}_{in}\left(s\right)}\right|}_{\tilde{\delta }\left(s\right)=0}=\frac{R_L\left[s{C}_1{r}_1{r}_2-g_2{r}_1{r}_2\right]}{{∆}_3}$$

(40)

where:

$$\begin{array}{ll}{∆}_3=s^4{R}_L{C}_1{C}_2{L}_1& L_2\left(r_1+r_2+g_2{r}_1{r}_2\right)\\ & +s^3\{C_1{L}_1{L}_2\left(r_1+r_2+g_2{r}_1{r}_2\right)+R_L{C}_2{L}_2\left[C_1{r}_1{r}_2+L_1\right]\\ & +C_1{C}_2{L}_1{R}_L{r}_2{r}_1\}\\ & +s^2\{R_L{L}_1{L}_2\left(r_1+r_2+g_2{r}_1{r}_2\right)+L_2\left[C_1{r}_1{r}_2+L_1\right]+C_2{L}_2{R}_L{r}_1\\ & +C_1{L}_1{r}_2{r}_1+C_2{L}_1{R}_L{r}_2\}\\ & +s\left\{R_L\left[C_1{r}_1{r}_2+L_1\right]+L_2{r}_1+L_1{r}_2+R_L{C}_2{r}_1{r}_2\right\}+r_1{r}_2+R_L{r}_1\end{array}$$

5.4.2. Model Validation

Similarly, to validate the accuracy of the transfer functions derived using the proposed modelling scheme, the equivalent bode plots of the transfer functions in (39) and (40) are plotted against independently derived bode plots based on the AC sweep function in PSim. The two plots are shown on the same axis in Figure 20 for the control-to-output voltage transfer function and Figure 21 for the audio-susceptibility transfer function. The congruency of the plots is used in a similar manner to assess the accuracy of the proposed modelling scheme. The numerical values of the circuit elements used for deriving bode plots are shown in

Table 7. Cuk converter parameters.

Component	Value
$V_{in}$	50 V
$R_o$	80 Ω
$F_{sw}$	20 kHz
$D$	0.35
$L_1;L_2;C_1;C_2$	150 µH; 150 µH; 100 µF; 100µF

.

6. Discussions

This section discusses the accuracy of the derived models and highlights the merits of the proposed modelling scheme in comparison to existing schemes. Furthermore, a more focused assessment of the proposed scheme is completed in relation to the earlier work dealing with modelling converters operating in CCM [26].

To assess the accuracy of the proposed modelling scheme, the models derived using the proposed modelling scheme are graphically represented in terms of equivalent bode plots against baseline bode plots. The baseline bode plots are derived for each of the four converters considered in Section 5 using an AC sweep function in PSim. This function derives bode plots based on a continuous direct injection of sinusoidal signals on the switching circuit. The injected sinusoids increase in amplitude with an increase in frequency. This is completed due to the common tendency of systems to attenuate in magnitude at higher frequencies.

The accuracy of the models derived using the proposed modelling scheme is the same as that of models derived using other modelling schemes [8,20]. This is the case because the proposed modelling scheme still employs averaging and perturbation as the main steps in modelling circuit parameters. It is well documented in the available literature that averaged models have accuracy limited to about a third of the switching frequency [8]. The bode plots in Section 5 are also drawn for a frequency range that is just above a third of the switching frequency. For a switching frequency of 20 kHz, a frequency limit of 6.67 kHz represents the upper accuracy limit. In addition to accuracy plots shown in Section 5 in terms of bode plots, it can be shown that the actual transfer functions derived in Section 5 are exactly the same as those derived using other modelling techniques like the averaged switch scheme employed in [18]. Thus, the transfer function shown in (27) and (28) for a conventional buck-boost converter are exactly the same as those shown in (25) and (24) in [18], respectively. The main merit of the proposed scheme is modelling efficiency from modularity and less dependency on converter attributes like order, functionality or operating mode.

The numerical values shown in Table 4, Table 5, Table 6 and Table 7 were used for validating the accuracy of the proposed modelling scheme. It can be seen from all the bode plots in Section 5 that the proposed modelling scheme accurately captures the dynamic characteristics of the respective converters. The main accuracy index is based on the congruency of equivalent bode plots with the PSim derived bode plots. It should be noted that limitations in the simulation software can easily influence the congruency of the plots. The AC sweep function on a switching circuit is affected by attributes like time step, number of data points, time taken to reach steady-state and, the selection of amplitude range for the injected signal. Thus, the accuracy of the plots should be quantified with a clear consideration of practical considerations of common limitations.

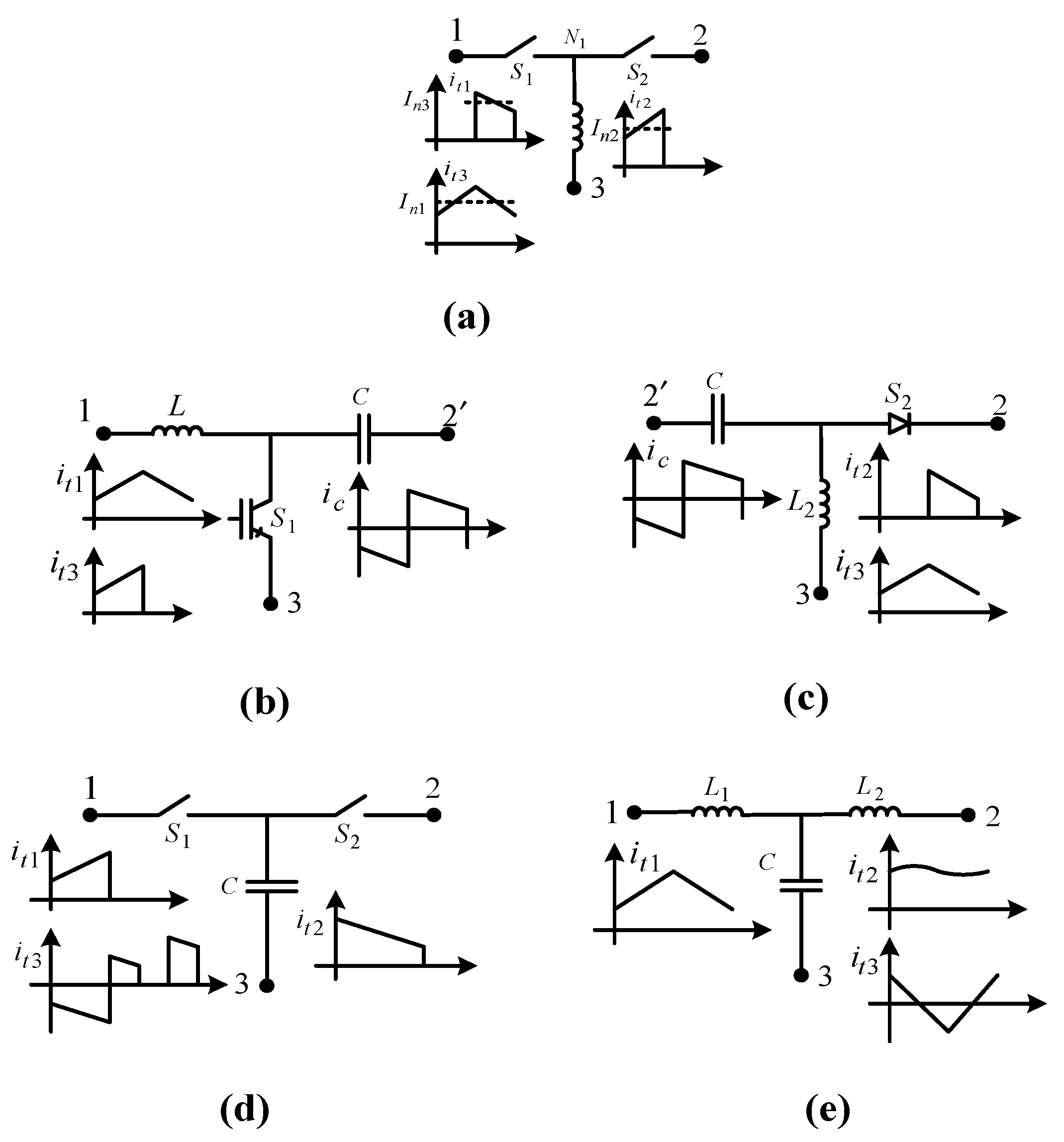
The main merit of the proposed modelling scheme is the inherent modularity which reduces modelling complexity and nullifies converter attributes like converter order and functionality in the modelling process. Moreover, operating mode is also nullified once the correct coefficients are identified. The modelling process is carried out based largely on how a given circuit is synthesised. It should be noted that the identification of constituent BBBs and accompanying connection for a given converter is an objective process. The two-port models of any of the BBBs in Figure 5, Figure 6, Figure 7 and Figure 8 need to only be derived once from which they can be directly applied to any converter with the same BBB. Thus, the modelling task is mainly on using the correct predefined coefficients as defined in the relevant tables. This means that if the buck-boost converter is operating in DCM, the coefficients will be read from Table 1 of this paper and if it is operating in CCM the coefficients will be read from Table 2 in [26]. Once the correct coefficients are identified, the generalised transfer function expressions in (8)–(12) are applicable irrespective of operating mode.

The proposed technique simplifies, through the generalisation of the necessary transfer functions, the computation of input and output impedances in DC-DC converters. These impedance transfer functions are needed to establish stability in cascaded converters. The commissioning of DC distribution systems will establish instability concerns from the resultant interactions between converters [39,40]. Thus, a technique that simplifies the computation of input and output transfer functions in any mode of operation is useful. The use of BBBs in analysing DC-DC converters is not limited to modelling dynamic and steady-state performance. It was shown in [41] that the use of BBBs provides a seamless approach to the analysis of current stresses in a variety of converters. The common attribute in any analysis process based on BBBs is that the converter is refined to its constituent BBBs, which represent the basic form of the converter. It is the analysis of these basic converter forms that provides modularity in the analysis. Furthermore, the identification of BBBs and the accompanying connection makes it easy to extract insight on converter synthesis. In this way, converter similarities and differences are emphasised to inform and simplify analysis. The consideration of BBBs as two-port networks greatly simplifies the subsequent modelling process by limiting matrix sizes to 2 × 2 for all the modelling steps. The complementary generalisation of the main transfer functions (8)–(12) further simplifies the modelling procedure by avoiding cumbersome algebra associated with expressing equations in standard form. To this end, the proposed modelling technique has been shown to nullify converter order, functionality and operating mode in the modelling procedure.

A direct comparison of the proposed modelling scheme, with a competing structure-based modelling scheme like the layer or grafts schemes, shows that unlike the other schemes, the proposed modelling scheme is not limited to conventional converters since it can seamlessly be applied in any converter with well-defined BBB as shown in Section 4. Moreover, the proposed modelling scheme requires less computational effort due to the use of standardised two-port models. The standardised models and accompanying transfer functions enables users with less than average knowledge of the plant (DC-DC converters) to compute models. This will lend itself well in scenarios wherein the controller design group wants to test the control scheme without necessarily knowing more about the plant.

Given the common practice of modifying existing converters to derive new converters, well-defined BBBs will almost always appear in most converters. Thus, the inherent modularity of the proposed modelling scheme will continue to simplify the modelling process.

7. Conclusions

This paper presents and evaluates the use of BBBs to compute small-signal and steady-state models of prominent converters. All the converters considered in this study were shown to be made up of various combinations of any of the two BBB types and a filter block. An extension of the CCM modelling scheme based on a circuit synthesis-oriented combination of BBBs modelled as two-port networks is proposed to cover converters operating in DCM. This extension seamlessly caters for two forms of DCM operation in fourth-order converters, i.e., (1) non-zero minimum inductor current values and (2) one idle inductor current dynamic case as described in Section 1 and shown in Section 5. Similar to the use of BBB in modelling converters in CCM, the merit of modularity in the modelling process is retained. Moreover, the merits of nullifying converter attributes like order and functionality in the modelling process are also retained. A byproduct of the extension shows that converter operating mode is also nullified in the modelling process. All of the listed merits validate the suitability of the proposed modelling scheme for adoption in component level modelling of DC microgrids. The suitability of the proposed modelling scheme for modelling converters in a DC microgrid setup is also validated through the ability of generalising input and output impedance transfer functions which is useful for stability studies. The main merit is the seamless adoption of the modelling scheme in modelling any converter with well-defined BBBs, with little to no knowledge of the inner workings of the specified converter, e.g., the full-bridge DC-DC converter in Section 4. The theoretically computed models are drawn on the same plot as the PSim switched plots to validate accuracy of the proposed modelling scheme. The congruency of the theoretical plots and the PSim plots graphically validates the accuracy. Future work will entail the adoption of the proposed modelling scheme in any newly proposed converter with well-defined BBBs.