Eddy–Viscosity Reynolds-Averaged Navier–Stokes Modeling of Air Distribution in a Sidewall Jet Supplied into a Room
Abstract
1. Introduction
1.1. Turbulence Models
- Turbulence kinetic energy k, which is a measure of the portion of energy flow that arises from velocity fluctuations:
- Turbulence energy dissipation rate ε, which is a measure of the conversion of turbulent kinetic energy into heat per unit time:where , , and are constants, and represent buoyant forces, and expresses the production of turbulence caused by viscous forces:
- Turbulence kinetic energy k:
- Turbulence vorticity ω:where is the turbulence generation rate, and are terms accounting for thermal buoyancy. , , , , are constants in the model.
1.2. Impact of Turbulence Model on CFD Results
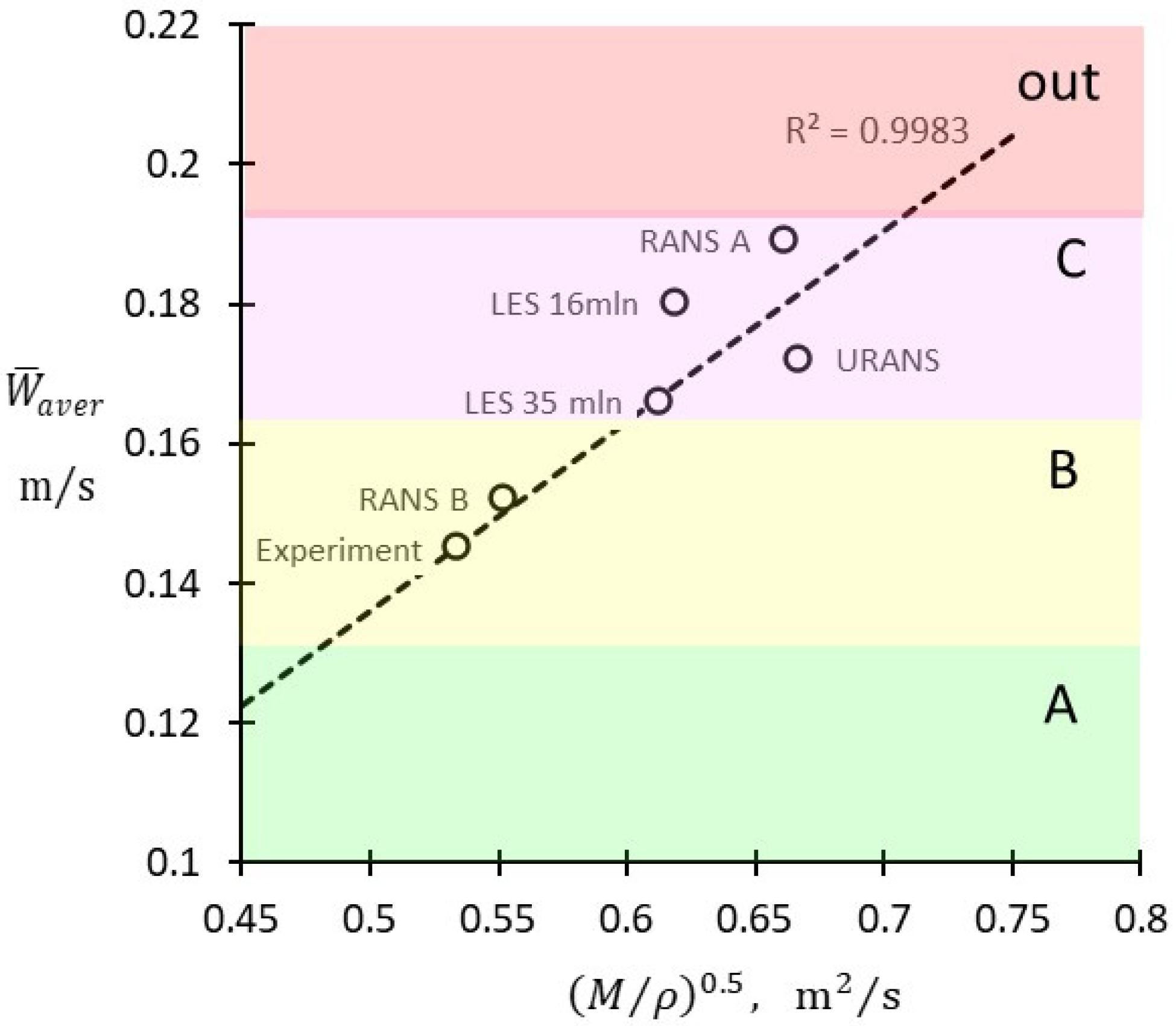
1.3. Methods of CFD Validation
Average Speed in Occupied Zone Versus Jet Momentum Flux
1.4. Recommended Turbulence Models
2. Methods
2.1. Benchmark of a Room with a Sidewall Jet
2.2. Numerical Method
2.3. Local, Gross, and Integral Parameters
3. Results
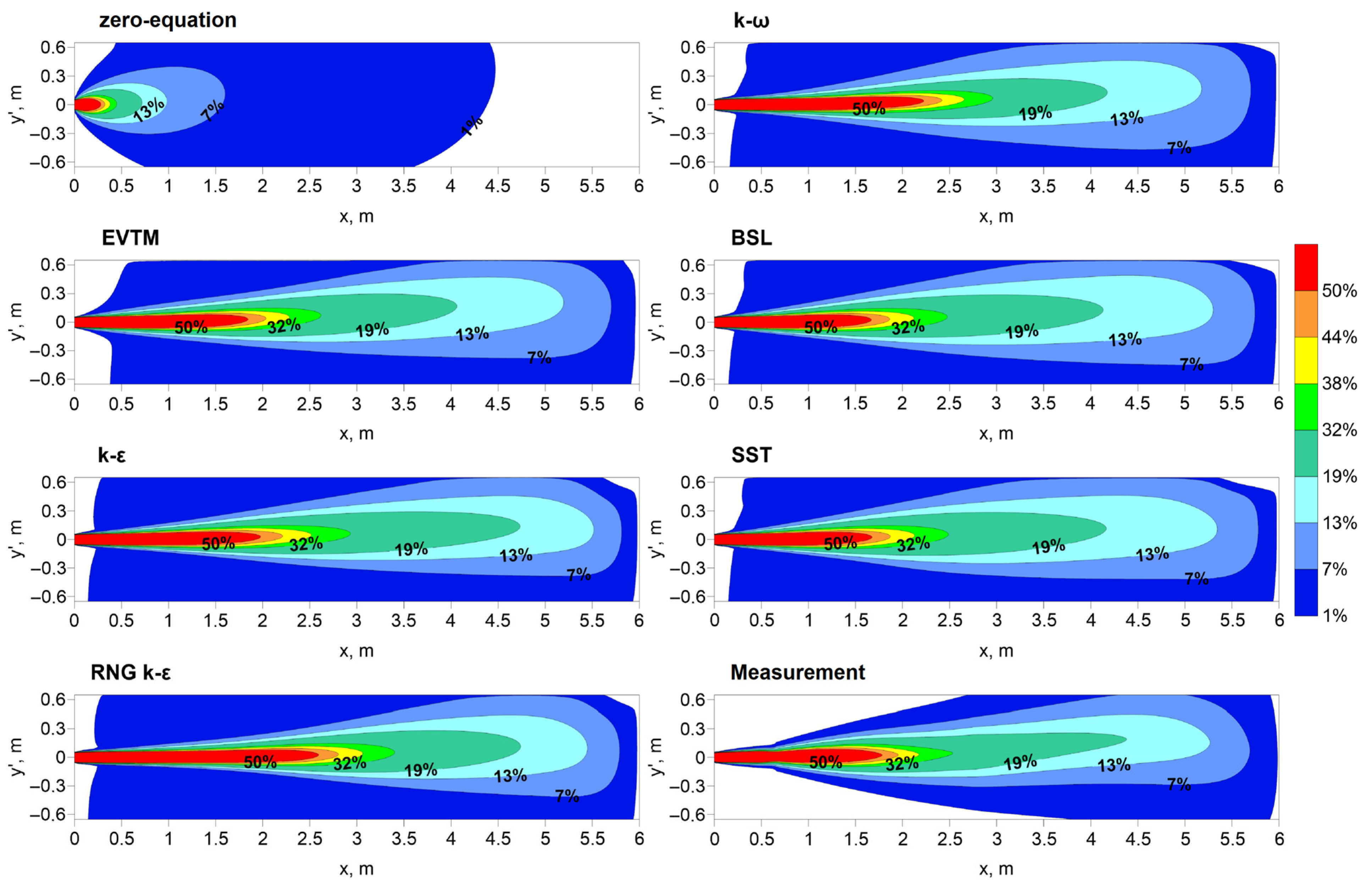
3.1. Maps and Profiles of Mean Axial Velocity Component
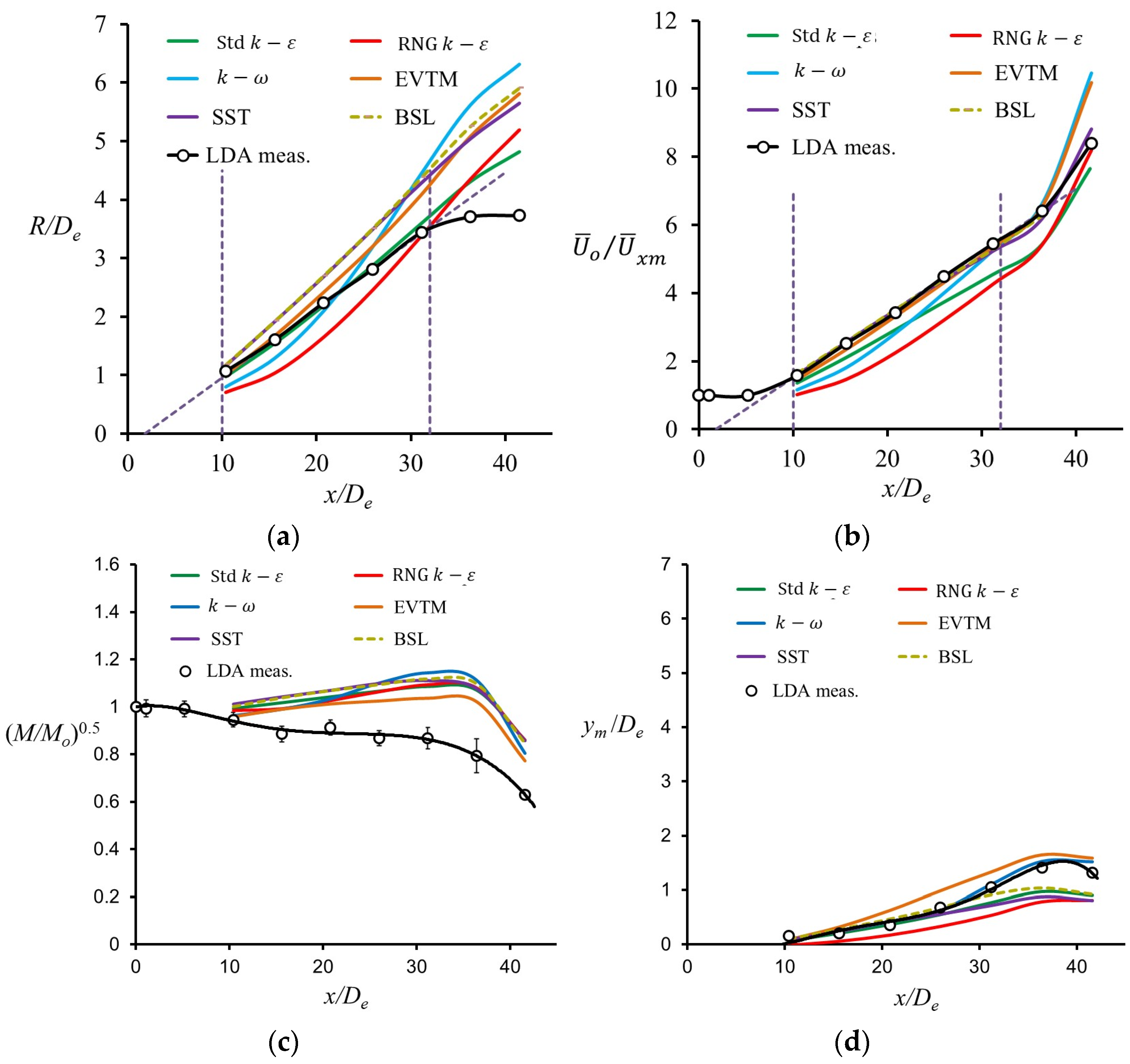
3.2. Gross and Integral Parameters in the Quasi-Free Jet Zone
4. Discussion
- The self-similarity of the mean velocity distribution, as given in Equation (11);
- The linear spread of the jet, as provided in Equation (15);
- The fact that they are inversely proportional to distance velocity decay, as given in Equation (20).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | jet spread coefficient (-) |
| B | boolean variable (-) |
| D | diameter (m) |
| H | upper limit value (-) |
| k | turbulence kinetic energy (m2/s2) |
| K | coefficient (-) |
| M | mean motion momentum flux in the axial direction (kg·m/s2) |
| n | number of samples (-) |
| r | radial distance from the jet axis (m) |
| R | radial width of the jet profile (m) |
| U | velocity (m/s) |
| W | speed (m/s) |
| x, y, z | Cartesian coordinates (m) |
| Greek symbols: | |
| ε | turbulence energy dissipation rate (m2/s3) |
| υ | viscosity coefficient (m2/s) |
| ρ | density (kg/m3) |
| ω | turbulence vorticity (1/s) |
| Subscripts: | |
| e | equivalent |
| i | axis of coordinate system, i = x, y, z |
| m | molecular, maximum |
| M | momentum |
| o | inlet, origin |
| t | turbulent |
References
- ANSI/ASHRAE Standard 55; Thermal Environmental Conditions for Human Occupancy. ANSI: Washington, DC, USA, 2023.
- ISO 7730:2005 (En); Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria. ISO: Geneva, Switzerland, 2005.
- Hussein, T.; Löndahl, J.; Thuresson, S.; Alsved, M.; Al-Hunaiti, A.; Saksela, K.; Aqel, H.; Junninen, H.; Mahura, A.; Kulmala, M. Indoor Model Simulation for COVID-19 Transport and Exposure. Int. J. Environ. Res. Public Health 2021, 18, 2927. [Google Scholar] [CrossRef]
- Cravero, C.; Marsano, D. Simulation of COVID-19 Indoor Emissions from Coughing and Breathing with Air Conditioning and Mask Protection Effects. Indoor Built Environ. 2022, 31, 1242–1261. [Google Scholar] [CrossRef]
- Awbi, H.B. Ventilation of Buildings; Taylor & Francis: London, UK, 2003; ISBN 978-0-415-27056-4. [Google Scholar]
- Jackman, P.J. Air Movement in Rooms with Side-Wall Mounted Grilles: A Design Procedure; Heating & Ventilation Research Association: London, UK, 1970. [Google Scholar]
- ANSI/ASHRAE Standard 113-2005; Method of Testing for Room Air Diffusion. ANSI: Washington, DC, USA, 2005.
- Yang, B.; Melikov, A.K.; Kabanshi, A.; Zhang, C.; Bauman, F.S.; Cao, G.; Awbi, H.; Wigö, H.; Niu, J.; Cheong, K.W.D.; et al. A Review of Advanced Air Distribution Methods—Theory, Practice, Limitations and Solutions. Energy Build. 2019, 202, 109359. [Google Scholar] [CrossRef]
- Stern, F.; Wilson, R.V.; Coleman, H.W.; Paterson, E.G. Verification and Validation of CFD Simulations; Defense Technical Information Center: Fort Belvoir, VA, USA, 1999. [Google Scholar]
- Chen, Q.; Srebric, J. A Procedure for Verification, Validation, and Reporting of Indoor Environment CFD Analyses. HVAC&R Res. 2002, 8, 201–216. [Google Scholar] [CrossRef]
- Chen, Q. Editorial: Computer Simulations and Experimental Measurements of Air Distribution in Buildings: Past, Present, and Future. HVAC&R Res. 2007, 13, 849–851. [Google Scholar] [CrossRef]
- Xiao, H.; Cinnella, P. Quantification of Model Uncertainty in RANS Simulations: A Review. Prog. Aerosp. Sci. 2019, 108, 1–31. [Google Scholar] [CrossRef]
- Cravero, C.; De Domenico, D.; Marsano, D. Uncertainty Quantification Analysis of Exhaust Gas Plume in a Crosswind. Energies 2023, 16, 3549. [Google Scholar] [CrossRef]
- Xia, L.; Zou, Z.-J.; Wang, Z.-H.; Zou, L.; Gao, H. Surrogate Model Based Uncertainty Quantification of CFD Simulations of the Viscous Flow around a Ship Advancing in Shallow Water. Ocean Eng. 2021, 234, 109206. [Google Scholar] [CrossRef]
- Ansys CFX|Industry-Leading CFD Software. Available online: https://www.ansys.com/products/fluids/ansys-cfx (accessed on 24 April 2023).
- Piomelli, U. Large Eddy Simulations in 2030 and beyond. Phil. Trans. R. Soc. A 2014, 372, 20130320. [Google Scholar] [CrossRef]
- Zhai, Z.J.; Zhang, Z.; Zhang, W.; Chen, Q.Y. Evaluation of Various Turbulence Models in Predicting Airflow and Turbulence in Enclosed Environments by CFD: Part 1—Summary of Prevalent Turbulence Models. HVAC&R Res. 2007, 13, 853–870. [Google Scholar]
- Zhang, Z.; Zhang, W.; Zhai, Z.J.; Chen, Q.Y. Evaluation of Various Turbulence Models in Predicting Airflow and Turbulence in Enclosed Environments by CFD: Part 2—Comparison with Experimental Data from Literature. HVAC&R Res. 2007, 13, 871–886. [Google Scholar]
- Chen, Q.; Xu, W. A Zero-Equation Turbulence Model for Indoor Airflow Simulation. Energy Build. 1998, 28, 137–144. [Google Scholar] [CrossRef]
- Wang, M.; Chen, Q. Assessment of Various Turbulence Models for Transitional Flows in an Enclosed Environment (RP-1271). HVAC&R Res. 2009, 15, 1099–1119. [Google Scholar]
- Meslem, A.; Dia, A.; Beghein, C.; El Hassan, M.; Nastase, I.; Vialle, P.-J. A Comparison of Three Turbulence Models for the Prediction of Parallel Lobed Jets in Perforated Panel Optimization. Build. Environ. 2011, 46, 2203–2219. [Google Scholar] [CrossRef]
- Hussain, S.; Oosthuizen, P.H.; Kalendar, A. Evaluation of Various Turbulence Models for the Prediction of the Airflow and Temperature Distributions in Atria. Energy Build. 2012, 48, 18–28. [Google Scholar] [CrossRef]
- Stamou, A.; Katsiris, I. Verification of a CFD Model for Indoor Airflow and Heat Transfer. Build. Environ. 2006, 41, 1171–1181. [Google Scholar] [CrossRef]
- Serra, N. Revisiting RANS Turbulence Modelling Used in Built-Environment CFD Simulations. Build. Environ. 2023, 237, 110333. [Google Scholar] [CrossRef]
- Srebric, J.; Chen, Q. Simplified Numerical Models for Complex Air Supply Diffusers. HVAC&R Res. 2002, 8, 277–294. [Google Scholar] [CrossRef]
- Cao, S.-J.; Meyers, J. Influence of Turbulent Boundary Conditions on RANS Simulations of Pollutant Dispersion in Mechanically Ventilated Enclosures with Transitional Slot Reynolds Number. Build. Environ. 2013, 59, 397–407. [Google Scholar] [CrossRef]
- Tapsoba, M.; Moureh, J.; Flick, D. Airflow Patterns in a Slot-Ventilated Enclosure Partially Loaded with Empty Slotted Boxes. Int. J. Heat Fluid Flow 2007, 28, 963–977. [Google Scholar] [CrossRef]
- Koskela, H.; Maula, H. A CFD Model of a Swirl Diffuser for Heating and Cooling Modes. Int. J. Vent. 2013, 12, 159–166. [Google Scholar] [CrossRef]
- Susin, R.M.; Lindner, G.A.; Mariani, V.C.; Mendonça, K.C. Evaluating the Influence of the Width of Inlet Slot on the Prediction of Indoor Airflow: Comparison with Experimental Data. Build. Environ. 2009, 44, 971–986. [Google Scholar] [CrossRef]
- Gurgul, S.; Fornalik-Wajs, E. On the Measure of the Heat Transfer Performance of RANS Turbulence Models in Single Round Jet Impingement. Energies 2023, 16, 7236. [Google Scholar] [CrossRef]
- Chen, B.; Liu, S.; Liu, J.; Jiang, N.; Chen, Q. Application of Data-Driven RANS Model in Simulating Indoor Airflow. Indoor Air 2022, 32, e13123. [Google Scholar] [CrossRef] [PubMed]
- Hurnik, M.; Ivanov, N.; Zasimova, M.; Popiolek, Z. Local and Gross Parameters of Air Distribution in a Room with a Sidewall Jet: CFD Validation Based on Benchmark Test. Build. Environ. 2022, 207, 108509. [Google Scholar] [CrossRef]
- Kang, L.; van Hooff, T. Influence of Inlet Boundary Conditions on 3D Steady RANS Simulations of Non-Isothermal Mechanical Ventilation in a Generic Closure. Int. J. Therm. Sci. 2022, 182, 107792. [Google Scholar] [CrossRef]
- Thysen, J.-H.; van Hooff, T.; Blocken, B.; van Heijst, G.J.F. CFD Simulations of Two Opposing Plane Wall Jets in a Generic Empty Airplane Cabin: Comparison of RANS and LES. Build. Environ. 2021, 205, 108174. [Google Scholar] [CrossRef]
- Sánchez, M.N.; Giancola, E.; Blanco, E.; Soutullo, S.; Suárez, M.J. Experimental Validation of a Numerical Model of a Ventilated Façade with Horizontal and Vertical Open Joints. Energies 2020, 13, 146. [Google Scholar] [CrossRef]
- Morozova, N.; Trias, F.X.; Capdevila, R.; Pérez-Segarra, C.D.; Oliva, A. On the Feasibility of Affordable High-Fidelity CFD Simulations for Indoor Environment Design and Control. Build. Environ. 2020, 184, 107144. [Google Scholar] [CrossRef]
- Khayrullina, A.; van Hooff, T.; Blocken, B.; van Heijst, G. Validation of Steady RANS Modelling of Isothermal Plane Turbulent Impinging Jets at Moderate Reynolds Numbers. Eur. J. Mech. B/Fluids 2019, 75, 228–243. [Google Scholar] [CrossRef]
- Lestinen, S.; Wesseling, M.; Kosonen, R.; Koskela, H.; Müller, D. Airflow Characteristics under Planar Opposed Ventilation Jets in a Controlled Indoor Environment. E3S Web Conf. 2019, 111, 01029. [Google Scholar] [CrossRef]
- Kosutova, K.; van Hooff, T.; Blocken, B. CFD Simulation of Non-Isothermal Mixing Ventilation in a Generic Enclosure: Impact of Computational and Physical Parameters. Int. J. Therm. Sci. 2018, 129, 343–357. [Google Scholar] [CrossRef]
- Kobayashi, T.; Sugita, K.; Umemiya, N.; Kishimoto, T.; Sandberg, M. Numerical Investigation and Accuracy Verification of Indoor Environment for an Impinging Jet Ventilated Room Using Computational Fluid Dynamics. Build. Environ. 2017, 115, 251–268. [Google Scholar] [CrossRef]
- Moureh, J.; Yataghene, M. Large-Eddy Simulation of an Air Curtain Confining a Cavity and Subjected to an External Lateral Flow. Comput. Fluids 2017, 152, 134–156. [Google Scholar] [CrossRef]
- van Hooff, T.; Blocken, B.; Tominaga, Y. On the Accuracy of CFD Simulations of Cross-Ventilation Flows for a Generic Isolated Building: Comparison of RANS, LES and Experiments. Build. Environ. 2017, 114, 148–165. [Google Scholar] [CrossRef]
- Achari, A.M.; Das, M.K. Application of Various RANS Based Models towards Predicting Turbulent Slot Jet Impingement. Int. J. Therm. Sci. 2015, 98, 332–351. [Google Scholar] [CrossRef]
- Hurnik, M.; Blaszczok, M.; Popiolek, Z. Air Distribution Measurement in a Room with a Sidewall Jet: A 3D Benchmark Test for CFD Validation. Build. Environ. 2015, 93, 319–330. [Google Scholar] [CrossRef]
- Miltner, M.; Jordan, C.; Harasek, M. CFD Simulation of Straight and Slightly Swirling Turbulent Free Jets Using Different RANS-Turbulence Models. Appl. Therm. Eng. 2015, 89, 1117–1126. [Google Scholar] [CrossRef]
- Heschl, C.; Inthavong, K.; Sanz, W.; Tu, J. Evaluation and Improvements of RANS Turbulence Models for Linear Diffuser Flows. Comput. Fluids 2013, 71, 272–282. [Google Scholar] [CrossRef]
- Andersson, H.; Cehlin, M.; Moshfegh, B. A Numerical and Experimental Investigation of a Confluent Jets Ventilation Supply Device in a Conference Room. Energies 2022, 15, 1630. [Google Scholar] [CrossRef]
- Hurnik, M.; Blaszczok, M.; Popiolek, Z. Air Speed and Velocity Measurements in a Room with a Sidewall Jet. Data Brief 2015, 5, 213–217. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Blocken, B. LES over RANS in Building Simulation for Outdoor and Indoor Applications: A Foregone Conclusion? Build. Simul. 2018, 11, 821–870. [Google Scholar] [CrossRef]
- Ansys CFX-Solver Modeling Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2024.



| Zero Equation Model | ||
| One-Equation Model | EVTM model | |
| Two-Equation Models | k-ε model | Standard k-ε |
| RNG k-ε | ||
| k-ω model | Wilcox k-ω | |
| BSL k-ω | ||
| SST | ||
| Authors (Year) [Ref.] | Type of Airflow in Room | Method/Turbulence Model | Validation Method | Conclusion/Preferred Method and Turbulence Model |
|---|---|---|---|---|
| Gurgul and Fornalik-Wajs (2023) [30] | Impinging round jet | SST k-ω, RNG k-ε, Intermittency Transition Model (SST k-ω), Transition SST, v2-f | Comparison of calculated local Nusselt number distribution with literature experimental data and inlet velocity profile with DNS simulation | SST k-ω, SST k-ω, and Intermittency Transition models have the best agreement with experimental and numerical data |
| Chen et al. (2022) [31] | Forced, natural, and mixed convection | RANS/Data-driven RNG k-ε, conventional RNG k-ε LES/WALE, and Smagorinsky–Lilly subgrid scale | Artificial neural network was used to determine the coefficient of high-order terms; RANS validated with LES | Data-driven model is more accurate than conventional RNG k-ε |
| Hurnik et al. (2022) [32] | Sidewall jet, recirculating flow in an occupied zone | URANS/Standard k-ε, wall-modeled LES/S-Omega subgrid-scale model | Comparison of local, gross, and integral parameters in the jet zone, and cumulative distribution of mean air speed in the occupied zone with LDA 1 and LVTA 2 | LES is in better agreement with measurements than RANS and URANS |
| Kang and van Hooff (2022) [33] | Non-isothermal side-wall jet | RANS/Standard k-ε, Realizable k-ε, RNG k-ε, LRN k-ε, RSM (SW), RSM (BSL), and SST k-ω | Comparison of measured with three-hot-wire anemometer and predicted dimensionless velocity magnitude, air temperature, and turbulence kinetic energy | SST k-ω is the optimal turbulence model for CFD calculations in a room with a non-isothermal supplied jet |
| Thysen et al. (2021) [34] | Two opposing plane wall jets in an empty airplane cabin | RANS/RNG k-ε, LRN k-ε, SST k-ω LES/WALE, and kinetic energy subgrid scale | Comparison of measured with PIV 3 and predicted contour maps, mean decay of dimensionless maximum velocity, and jet growth profiles | RANS is in acceptable agreement with measurements; SST k-ω performs better than the k-ε; LES performed much better than RANS |
| Sánchez et al. (2020) [35] | Ventilated façade | Sparlat–Allmaras, Standard k-ε, RNG k-ε, REA k-ε, Standard k-ω, SST k-ω | Comparison of measured with PIV 3 vertical velocity component profiles | RNG k-ε model is in the best agreement with measurements |
| Morozowa et al. (2020) [36] | Differentially heated cavity, mixed convection | Direct numerical simulation (DNS) No-model LES/WALE and S3PQ URANS/Standard k-ε and SST-k-ω | Comparison of calculated global, integral airflow quantities: Nusselt number, stratification, kinetic energy, enstrophy, and average temperature, with reference values obtained in DNS simulation | LES and no-model predict global, integral airflow quantities with higher accuracy than URANS |
| Khayrullina et al. (2019) [37] | Impinging plane jets | RANS/Standard k-ε, Realizable k-ε, RNG k-ε, SST k-ω and Reynolds stress model | Comparison of velocity distributions predicted and measured using PIV 3 | The differences in the validation metric are negligibly small. It is impossible to distinguish the best model |
| Lestinen et al. (2019) [38] | Two plane opposed jets | URANS/SST k-ω, hybrid RANS-LES—detached eddy simulation (DES), hybrid RANS-LES stress-blended eddy simulation (SBES)/SST-k-ω RANS was merged with LES | Comparison of velocity distributions predicted and measured using LVTA 2 | There are no final conclusions regarding the preferred turbulence model |
| Kosutova et al. (2018) [39] | Non-isothermal mixing ventilation in an enclosure with a heated floor | RANS/RNG k-ε, Low Reynolds number k-ε, SST k-ω, Std k-ω and RSM | Comparison of velocity distributions predicted and measured using LDA 1 and temperature distributions predicted and measured using thermocouples | Low-Reynolds-number k-ε performed best in velocity prediction. Temperature was most accurately reproduced by SST k-ω |
| Kobayashi et al. (2017) [40] | Impinging jet | RANS/Standard k-ε, RNG k-ε, SST k-ω, and Low-Re SST k-ω | Comparison of measured and predicted vertical profiles of velocity, turbulent kinetic energy, and temperature; velocity measured with hot wire and ultrasonic anemometers | SST k-ω is optimal for accuracy and computational economy |
| Moureh and Yataghene (2017) [41] | Air curtain | RANS/Standard k-ε, LES/Dynamic Smagorinsky subgrid scale | Comparison of velocity distributions predicted and measured using LDA 1 and PIV 3 | LES predicts jet characteristics better than RANS k-ε, but LES strongly underestimates the jet deviation outwards in comparison with PIV 3 |
| van Hooff et al. (2017) [42] | Cross ventilation | RANS/Standard k-ε, RNG k-ε, Realizable k-ε, SST k-ω, RSM LES/Dynamic Smagorinsky subgrid scale | Comparison of measured with constant temperature anemometry system and predicted parameters: mean velocity, turbulent kinetic energy, ventilation flow rate, and spreading width | RANS models fail to reproduce turbulent kinetic energy, LES better reproduces velocity, turbulence kinetic energy and volume flow rate |
| Achari and Das (2015) [43] | Impinging plane jet | RANS/Standard k-ε, Low Reynolds number k-ε proposed by Launder and Sharma (LS) and Yang and Shih (YS), standard k-ω | Comparison of calculated velocity component profiles with literature experimental data | Low-Reynolds-number k-ε Yang and Shih (YS) performed best |
| Hurnik et al. (2015) [44] | Sidewall jet, recirculating flow in the occupied zone | RANS/Standard k-ε with enhanced wall treatment | Comparison of predicted local, gross, and integral parameters in the jet and occupancy zones with LDA and LVTA measurements | Reproduction of the jet momentum is necessary for accurate air speed modeling in the occupied zone |
| Miltner et al. (2015) [45] | Straight and slightly rotating turbulent free jets | RANS/One-equation, Standard k-ε, RNG k-ε, Realizable k-ε, Standard k-ω, SST and RSM | Comparison of velocity distributions predicted and measured using LDA | The best results of validation in terms of axial and tangential velocity components and turbulence intensity are obtained with RSM |
| Boundary Condition | Value/Description |
|---|---|
| Analysis type | Steady state |
| Supply air speed | 5.16 m/s |
| Inlet turbulence intensity | 5% |
| Heat transfer | Isothermal |
| Air temperature | 23 °C |
| Outlet relative pressure | 1 Pa |
| Outlet pressure profile blend | 0.05 |
| Outlet pressure averaging | Average over whole outlet |
| Boundary condition | No slip wall |
| Wall roughness | Smooth wall |
| Reference domain pressure | 101,325 Pa |
| Discretization Grid Variant | Mesh Edge Length | Refinement Mesh Edge Length | Number of Elements |
|---|---|---|---|
| G1 | 0.3 m | - | 4.10 × 104 |
| G2 | 0.1 m | - | 4.95 × 105 |
| G3 | 0.1 m | 0.01 m (refinement radius 0.6 m) | 3.51 × 107 |
| Definition | Equation | # |
|---|---|---|
| Jet spread | (15) | |
| velocity profile | (16) | |
| in PSM (constant) | (17) | |
| Boundary momentum flux | (18) | |
| Conservation of momentum flux | (19) | |
| (20) |
| a | KM | ||
|---|---|---|---|
| LDA | 1.8 | 0.117 | 88.4% |
| LES [32] | 2.2 | 0.130 | 100.6% |
| k-ω | 4.6 | 0.138 | 103.4% |
| Std k-ε | 2.0 | 0.118 | 104.0% |
| RNG k-ε | 4.0 | 0.105 | 102.9% |
| EVTM | 3.0 | 0.137 | 100.6% |
| BSL | 1.9 | 0.143 | 106.4% |
| SST | 2.5 | 0.148 | 106.5% |
| Turbulence Model | Linear Jet Spread | Inverse Changes of Maximum Velocity | “Gaussian” Radial Profile of Velocity | ∆(xo/De) | δ(a) | δ(KM) |
|---|---|---|---|---|---|---|
| LDA | + | + | + | 0.0 | 0.0% | 0.0% |
| LES [25] | + | + | + | 0.4 | 11.1% | 13.8% |
| k-ω | − | − | − | 2.8 | 17.9% | 17.0% |
| Std k-ε | + | + | + | 0.2 | 0.9% | 17.6% |
| RNG k-ε | − | − | − | 2.2 | −10.3% | 16.4% |
| EVTM | + | + | + | 1.2 | 17.1% | 13.8% |
| BSL | + | + | + | 0.1 | 22.2% | 20.4% |
| SST | + | + | + | 0.7 | 26.5% | 20.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hurnik, M.; Ciuman, P.; Popiolek, Z. Eddy–Viscosity Reynolds-Averaged Navier–Stokes Modeling of Air Distribution in a Sidewall Jet Supplied into a Room. Energies 2024, 17, 1261. https://doi.org/10.3390/en17051261
Hurnik M, Ciuman P, Popiolek Z. Eddy–Viscosity Reynolds-Averaged Navier–Stokes Modeling of Air Distribution in a Sidewall Jet Supplied into a Room. Energies. 2024; 17(5):1261. https://doi.org/10.3390/en17051261
Chicago/Turabian StyleHurnik, Maria, Piotr Ciuman, and Zbigniew Popiolek. 2024. "Eddy–Viscosity Reynolds-Averaged Navier–Stokes Modeling of Air Distribution in a Sidewall Jet Supplied into a Room" Energies 17, no. 5: 1261. https://doi.org/10.3390/en17051261
APA StyleHurnik, M., Ciuman, P., & Popiolek, Z. (2024). Eddy–Viscosity Reynolds-Averaged Navier–Stokes Modeling of Air Distribution in a Sidewall Jet Supplied into a Room. Energies, 17(5), 1261. https://doi.org/10.3390/en17051261






