External Multi-Gap Lightning Arrester Modeling Using the Integration Method
Abstract
1. Introduction
- A new methodology is proposed to model the disruptive effect in an external air gap using the integration method.
- The adjustment of the model parameters is carried out by defining an optimisation problem.
- The proposed methodology is validated using experimental measurements for a case study. Furthermore, the results are compared with those obtained by other authors using different methodologies.
- Based on experimental measurements, the proposed methodology is applied to model a three-electrode-gap or multi-gap device and the capability of the model to predict the time-to-breakdown under different voltages is evaluated.
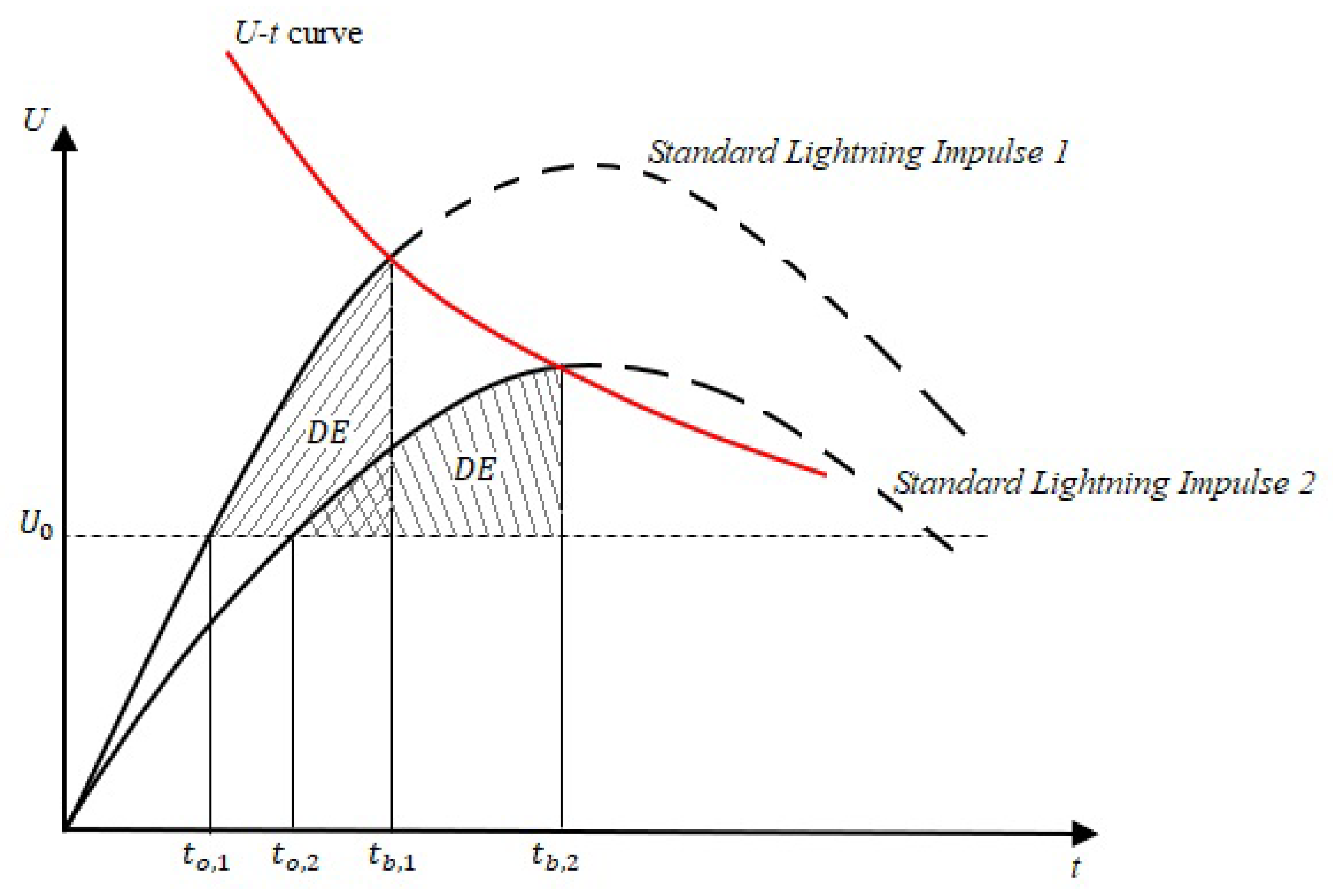
2. Air Gap Modeling
Integration Method Formulation
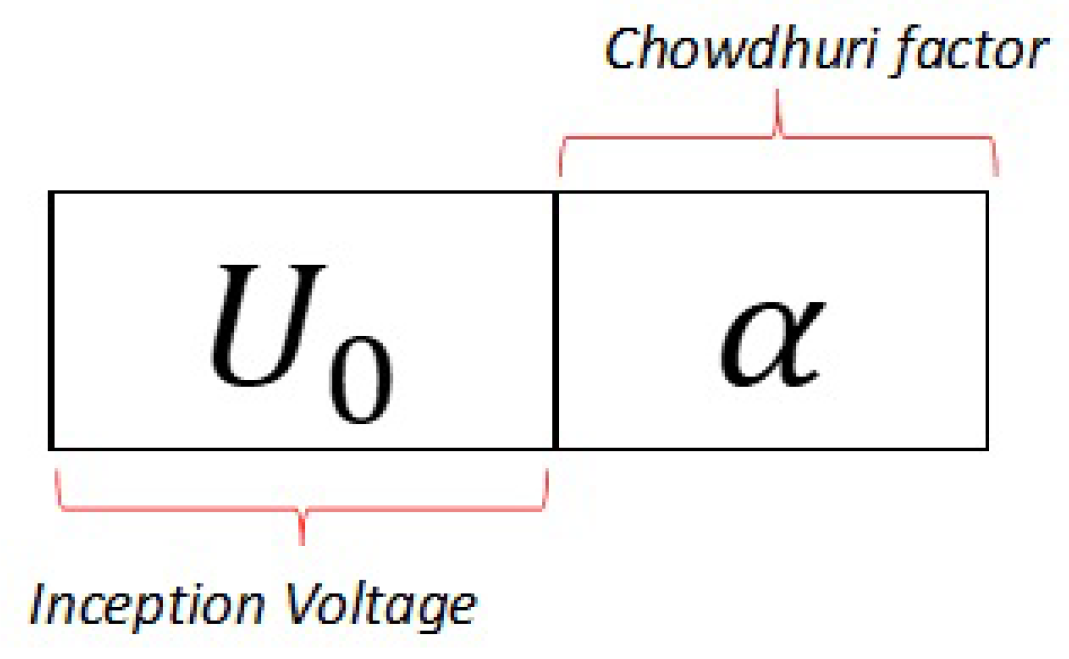
3. Proposed Methodology
4. Case Studies
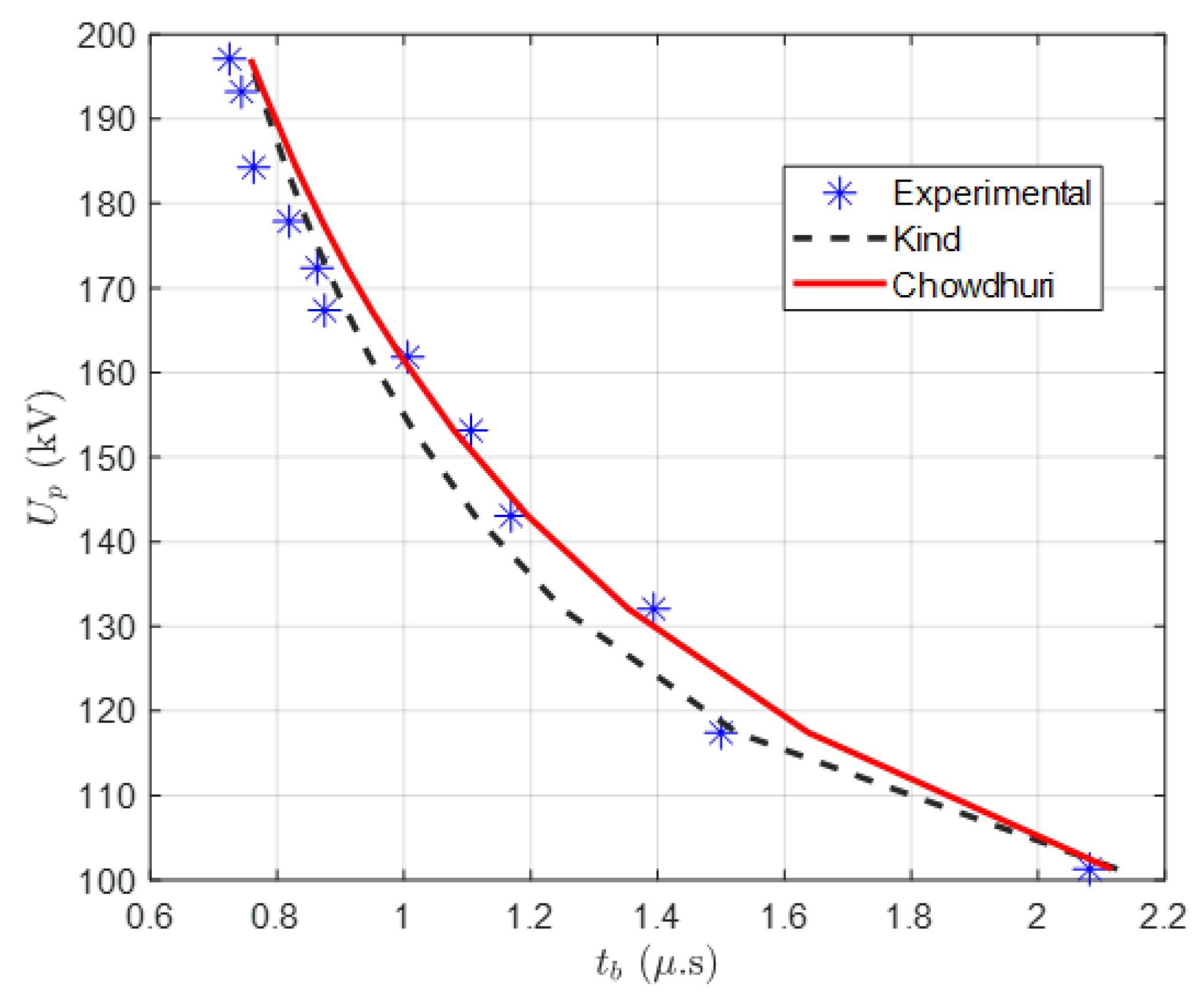
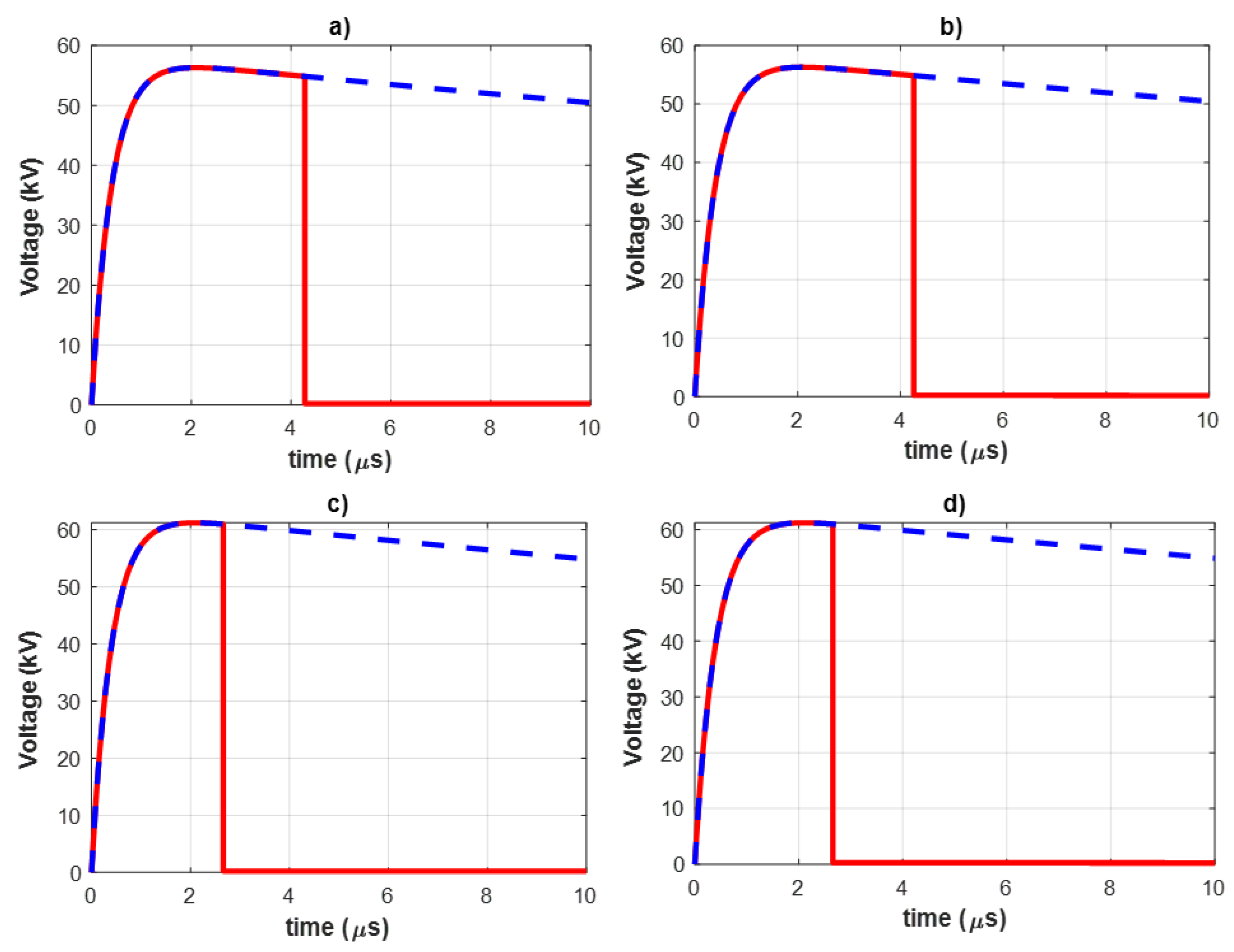
5. Results and Analyses
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Agudelo, L.; López-Lezama, J.M.; Muñoz-Galeano, N. Vulnerability assessment of power systems to intentional attacks using a specialized genetic algorithm. Dyna 2015, 82, 78–84. [Google Scholar] [CrossRef]
- López-Lezama, J.M.; Cortina-Gómez, J.; Muñoz-Galeano, N. Assessment of the Electric Grid Interdiction Problem using a nonlinear modeling approach. Electr. Power Syst. Res. 2017, 144, 243–254. [Google Scholar] [CrossRef]
- Torres Sánchez, H. El Rayo: Mitos, Leyendas, Ciencia y Tecnología; UNIBIBLOS; Universidad Nacional de Colombia, Facultad de Ingeniería: Bogotá, Colombia, 2002. [Google Scholar]
- Sakshaug, E. Influence of Rate-of-Rise on Distribution Arrester Protective Characteristics. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 519–526. [Google Scholar] [CrossRef]
- van der Mescht, M.; van der Mescht, C.; van Schalkwyk, W.D. Protection of Medium Voltage Pole-mount Installations against Lightning. In Proceedings of the 2022 36th International Conference on Lightning Protection (ICLP), Cape Town, South Africa, 2–7 October 2022; pp. 741–744. [Google Scholar] [CrossRef]
- Aranguren, H.D.; Tovar, C.; Inampues, J.; Lopez, J.; Soto, E.; Torres, H. Lightning effects on distribution transformers and reliability of power distribution systems in Colombia. Ing. Investig. 2015, 35, 28–33. [Google Scholar] [CrossRef]
- Georgilakis, P.S.; Kagiannas, A.G. A novel validated solution for lightning and surge protection of distribution transformers. Int. J. Electr. Power Energy Syst. 2014, 63, 373–381. [Google Scholar] [CrossRef]
- Piantini, A.; Janiszewski, J.M.; de Carvalho, T.O.; Obase, P.F.; dos Santos, G.J.G. Lightning-caused transformer failures in distribution systems. In Proceedings of the 2014 International Conference on Lightning Protection (ICLP), Shanghai, China, 11–18 October 2014; pp. 955–960. [Google Scholar] [CrossRef]
- Andreotti, A.; Araneo, R.; Mahmood, F.; Piantini, A.; Rubinstein, M. An Analytical Approach to Assess the Influence of Shield Wires in Improving the Lightning Performance Due to Indirect Strokes. IEEE Trans. Power Deliv. 2021, 36, 1491–1498. [Google Scholar] [CrossRef]
- Arevalo, L.; Mejia, A.; Diaz, O. Design and construction of surge protection devices for rural distribution transformers based on the hygroscopic properties of sand. In Proceedings of the 2007 International Symposium on Lightning Protection (IX SIPDA), Foz do Iguazu, Brazil, 26–30 November 2007; pp. 1–8. [Google Scholar]
- Heine, P.; Lehtonen, M.; Niskanen, J.; Oikarinen, A. Limiting the number of the most severe voltage sags in rural medium voltage networks. In Proceedings of the 2008 Power Quality and Supply Reliability Conference, Parnu, Estonia, 27–29 August 2008; pp. 99–104. [Google Scholar] [CrossRef]
- Lahti, K.K.; da Silva, D.A. Possibilities to protect pole-mounted distribution transformers by means of externally gapped MO arresters. In Proceedings of the 2014 ICHVE International Conference on High Voltage Engineering and Application, Poznan, Poland, 8–11 September 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Khanmiri, D.T.; Ball, R.; Mosesian, J.; Lehman, B. Degradation of low voltage metal oxide varistors in power supplies. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 2122–2126. [Google Scholar] [CrossRef]
- Wang, M.; Ren, X.; Zhou, Q.; Li, Z.; Yang, H.; Jiang, H.; Yan, Y.; Ruan, X.; Yu, W.; Jin, L.; et al. High improvement of degradation behavior of ZnO varistors under high current surges by appropriate Sb2O3 doping. J. Eur. Ceram. Soc. 2021, 41, 436–442. [Google Scholar] [CrossRef]
- IEC60099-8; Metal-Oxide Surge Arresters with External Series Gap (EGLA) for Overhead Transmission and Distribution Lines of A.C. Systems above 1 kV. International Electrotechnical Commission—IEC: London, UK, 2017.
- Woodworth, J. Externally gapped line arrester a comprehensive review. In Proceedings of the IEEE PES T&D 2010, New Orleans, LA, USA, 19–22 April 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Giraudet, F. Various Benefts for Line Surge Arrester Application and Advantages of Externally Gapped Line Arresters. In Proceedings of the 2019 International Conference on High Voltage Engineering and Technology (ICHVET), Hyderabad, India, 7–8 February 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Mansoor, A.; Martzloff, F.; Phipps, K. Gapped arresters revisited: A solution to cascade coordination. IEEE Trans. Power Deliv. 1998, 13, 1174–1181. [Google Scholar] [CrossRef]
- IEC 60099-4:2014; Surge Arresters—Part 4: Metal-Oxide Surge Arresters without Gaps for A.C. Systems. International Electrotechnical Commission—IEC: London, UK, 2014.
- Woodworth, J. Externally gapped line arresters a critical design review. In Proceedings of the 2014 IEEE PES T&D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Plummer, C.; Goedde, G.; Pettit, E.; Godbee, J.; Hennessey, M. Reduction in distribution transformer failure rates and nuisance outages using improved lightning protection concepts. IEEE Trans. Power Deliv. 1995, 10, 768–777. [Google Scholar] [CrossRef]
- Martinez, M.; Wanderley, E.; Nunes, A. Externally Gapped Distribution Arresters to Solve TOV Issues. In Proceedings of the 2013 INMR World Congress, Vancouver, BC, Canada, 8–11 September 2013; pp. 1–10. [Google Scholar] [CrossRef]
- Khodsuz, M. Externally gapped line arrester performance in high voltage transmission line using frequency grounding system: Absorbed energy and expected life assessment. IET Sci. Meas. Technol. 2022, 16, 426–440. [Google Scholar] [CrossRef]
- Omar, A.I.; Mohsen, M.; Abd-Allah, M.A.; Salem Elbarbary, Z.M.; Said, A. Induced Overvoltage Caused by Indirect Lightning Strikes in Large Photovoltaic Power Plants and Effective Attenuation Techniques. IEEE Access 2022, 10, 112934–112947. [Google Scholar] [CrossRef]
- Burrage, L.; Shaw, J.; McConnell, B. Distribution transformer performance when subjected to steep front impulses. IEEE Trans. Power Deliv. 1990, 5, 984–990. [Google Scholar] [CrossRef]
- Ahmadi, M.E.; Niasati, M.; Barzegar-Bafrooei, M.R. Enhancing the lightning performance of overhead transmission lines with optimal EGLA and downstream shield wire placement in mountainous areas: A complete study. IET Sci. Meas. Technol. 2019, 14, 564–575. [Google Scholar] [CrossRef]
- Arias, J. Análisis teórico experimental de la efectividad del sistema de protección contra descargas atmosféricas del transformador de distribución rural de energía en Colombia. Master’s Thesis, Universidad Nacional de Colombia, Bogotá, Colombia, 2003. [Google Scholar]
- Liu, X.; Rong, J. The Application of Multi-Gap Arresters in 10–35kV Overhead Transmission Line. In Proceedings of the 2019 11th Asia-Pacific International Conference on Lightning (APL), Hong Kong, China, 12–14 June 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Guo, T.; Zhou, W.; Su, Z.; Li, H.; Yu, J. A Multigap Structure for Power Frequency Arc Quenching in 10-kV Systems. IEEE Trans. Plasma Sci. 2016, 44, 2622–2631. [Google Scholar] [CrossRef]
- Brignone, M.; Delfino, F.; Procopio, R.; Rossi, M.; Rachidi, F. Evaluation of Power System Lightning Performance—Part II: Application to an Overhead Distribution Network. IEEE Trans. Electromagn. Compat. 2017, 59, 146–153. [Google Scholar] [CrossRef]
- Mestriner, D.; Brignone, M.; Procopio, R.; Nicora, M.; Fiori, E.; Piantini, A.; Rachidi, F. An Efficient Methodology for the Evaluation of the Lightning Performance of Overhead Lines. IEEE Trans. Electromagn. Compat. 2021, 63, 1137–1145. [Google Scholar] [CrossRef]
- Khadka, N.; Bista, A.; Bista, D.; Sharma, S.; Adhikary, B. Direct Lightning Impact Assessment on a Rural Mini-Grid of Nepal. In Proceedings of the 2021 35th International Conference on Lightning Protection (ICLP) and XVI International Symposium on Lightning Protection (SIPDA), Colombo, Sri Lanka, 20–26 September 2021; Volume 1, pp. 1–7. [Google Scholar] [CrossRef]
- Working Group 3.4.11 on Surge Arrester Modeling. Modeling of metal oxide surge arresters. IEEE Trans. Power Deliv. 1992, 7, 302–309. [Google Scholar] [CrossRef]
- Pinceti, P.; Giannettoni, M. A simplified model for zinc oxide surge arresters. IEEE Trans. Power Deliv. 1999, 14, 393–398. [Google Scholar] [CrossRef]
- Unahalekhaka, P. Simplified Modeling of Metal Oxide Surge Arresters. Energy Procedia 2014, 56, 92–101. [Google Scholar] [CrossRef]
- Christodoulou, C.; Ekonomou, L.; Mitropoulou, A.; Vita, V.; Stathopulos, I. Surge arresters’ circuit models review and their application to a Hellenic 150kV transmission line. Simul. Model. Pract. Theory 2010, 18, 836–849. [Google Scholar] [CrossRef]
- IEC TR 60071-4; Insulation Co-Ordination–Part 4: Computational Guide to Insulation Co-Ordination and Modelling of Electrical Networks. International Electrotechnical Commission—IEC: London, UK, 2004.
- Darveniza, M. The generalized integration method for predicting impulse volt-time characteristics for non-standard wave shapes-a theoretical basis. IEEE Trans. Electr. Insul. 1988, 23, 373–381. [Google Scholar] [CrossRef]
- Witzke, R.L.; Bliss, T.J. Co-ordination of Lightning Arrester Location with Transformer Insulation Level. Trans. Am. Inst. Electr. Eng. 1950, 69, 964–975. [Google Scholar] [CrossRef]
- Jones, A.R. Evaluation of the Integration Method for Analysis of Nonstandard Surge Voltages [includes discussion]. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1954, 73, 984–990. [Google Scholar] [CrossRef]
- Witzke, R.L.; Bliss, T.J. Surge Protection of Cable-Connected Equipment. Trans. Am. Inst. Electr. Eng. 1950, 69, 527–542. [Google Scholar] [CrossRef]
- CIGRE WG 33.01. Guide to Procedures for Estimating the Lightning Performance of Transmission Lines; Technical Brochures 063; CIGRE: Paris, France, 1991. [Google Scholar]
- Anderson, J.G. Lightning Performance of Transmission Lines. In Transmission Line Reference Book; Electric Power Research Institute: Palo Alto, CA, USA, 2017; p. 1194. [Google Scholar]
- Kind, D.; Kurrat, M.; Kopp, T.H. Voltage-time characteristics of air gaps and insulation coordination—Survey of 100 years research. In Proceedings of the 2016 33rd International Conference on Lightning Protection (ICLP), Estoril, Portugal, 25–30 September 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Trotsenko, Y.; Brzhezitsky, V.; Masluchenko, I. Circuit simulation of electrical breakdown in air using Kind’s equal-area criterion. Technol. Audit. Prod. Reserv. 2017, 3, 44–49. [Google Scholar] [CrossRef][Green Version]
- Chowdhuri, P.; Mishra, A.; McConnell, B. Volt-time characteristics of short air gaps under nonstandard lightning voltage waves. IEEE Trans. Power Deliv. 1997, 12, 470–476. [Google Scholar] [CrossRef]
- Ancajima, A.; Carrus, A.; Cinieri, E.; Mazzetti, C. Breakdown characteristics of air spark-gaps stressed by standard and short-tail lightning impulses: Experimental results and comparison with time to sparkover models. J. Electrost. 2007, 65, 282–288. [Google Scholar] [CrossRef]
- Silva, A.R.; Piantini, A.; Silva, D.A.d.; Shigihara, M. Breakdown of 15 kV Insulators Under Bipolar Oscillating Impulse Voltage. In Proceedings of the 2018 34th International Conference on Lightning Protection (ICLP), Rzeszow, Poland, 2–7 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Venkatesan, S.; Usa, S. Impulse Strength of Transformer Insulation with Nonstandard Waveshapes. IEEE Trans. Power Deliv. 2007, 22, 2214–2221. [Google Scholar] [CrossRef]
- Inthoulath, K.; Banmongkol, C. A simulation of breakdown characteristics of suspension insulators under standard lightning impulse voltages. In Proceedings of the TENCON 2014—2014 IEEE Region 10 Conference, Bangkok, Thailand, 22–25 October 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Shigihara, M.; Piantini, A.; Ramos, M.; Braz, C.; Mazzetti, C.; Ancajima, A. Comparison of different procedures to predict the volt-time curves of 15kV insulators. Electr. Power Syst. Res. 2017, 153, 82–87. [Google Scholar] [CrossRef]
- IEC 60060-1:2010; High-Voltage Test Techniques–Part 1: General Definitions and Test Requirements. International Electrotechnical Commission—IEC: London, UK, 2010.
- The MathWorks Inc. MATLAB Version: 9.13.0 (R2022b); The MathWorks Inc.: Natick, MA, USA, 2022. [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder–Mead Simplex Method in Low Dimensions. Siam J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- IEEE Std 4-2013 (Revision of IEEE Std 4-1995)—Redline; IEEE Standard for High-Voltage Testing Techniques—Redline. Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2013; pp. 1–500.
- Pérez Posada, A.F.; Villegas, J.G.; López-Lezama, J.M. A Scatter Search Heuristic for the Optimal Location, Sizing and Contract Pricing of Distributed Generation in Electric Distribution Systems. Energies 2017, 10, 1449. [Google Scholar] [CrossRef]
- Ancajima, A.; Carrus, A.; Cinieri, E.; Mazzetti, C. Behavior of MV Insulators Under Lightning-Induced Overvoltages: Experimental Results and Reproduction of Volt–Time Characteristics by Disruptive Effect Models. IEEE Trans. Power Deliv. 2010, 25, 221–230. [Google Scholar] [CrossRef]
- Ancajima, A.; Carrus, A.; Cinieri, E.; Mazzetti, C. Optimal selection of disruptive effect models parameters for the reproduction of MV insulators volt-time characteristics under standard and non standard lightning impulses. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 760–765. [Google Scholar] [CrossRef]
- Rodríguez-Serna, J.M.; Albarracín-Sánchez, R. Numerical Simulation of Temperature and Pressure Changes due to Partial Discharges in Spherical Cavities within Solid Dielectrics at Different Ageing Conditions. Energies 2019, 12, 4771. [Google Scholar] [CrossRef]
- Høidalen, H. ATPDraw™ The Graphical Preprocessor to ATP. 2023. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=9f3c41d43a0b20a045aad260e2eb83bca7eb6890 (accessed on 1 February 2024).



| Statistical Measures | Value |
|---|---|
| (kV) | 58.451 [57.706, 59.196] |
| (kV) | 2.702 [2.268, 3.343] |
| Level | (kV) | Tests | Disruptions | Relative Frequency |
|---|---|---|---|---|
| 1 | 50.2 | 15 | 1 | 0.067 |
| 2 | 51.9 | 15 | 1 | 0.067 |
| 3 | 54.1 | 15 | 4 | 0.267 |
| 4 | 56.3 | 15 | 7 | 0.467 |
| 5 | 57.6 | 15 | 11 | 0.733 |
| 6 | 59.8 | 15 | 14 | 0.933 |
| 7 | 61.2 | 15 | 15 | 1 |
| Parameter | Case Study 1 | Case Study 2 | ||
|---|---|---|---|---|
| Kind | Chowdhuri | Kind | Chowdhuri | |
| (kV) | 74.880 | 73.052 | 49.710 | 47.567 |
| k/ | 1 | 0.125 | 1 | 0.399 |
| 3.369 × | 8.364 × | 1.953 × | 2.242 × | |
| O.F | 0 | 8.102 × | 1.288 × | 1.003 × |
| GA generations | 39 | 163 | 1207 | 125 |
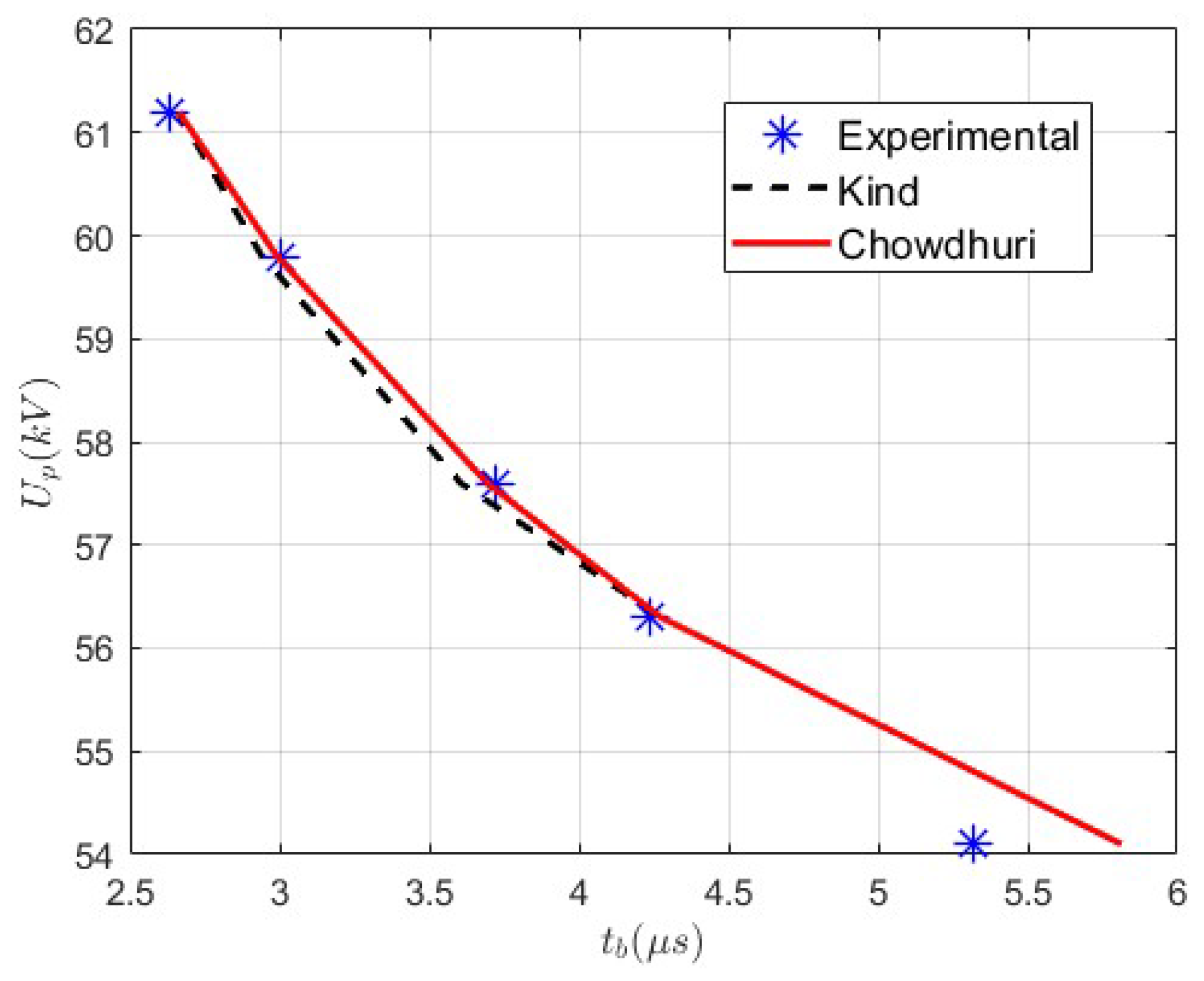
| (kV) | (μs) | (%) | (%) | ||
|---|---|---|---|---|---|
| Curve | Kind | Chowdhuri | |||
| 54.1 | 5.319 | - | 5.813 | - | 9.281 |
| 56.3 | 4.236 | 4.274 | 4.274 | 0.889 | 0.889 |
| 57.6 | 3.719 | 3.606 | 3.694 | 3.026 | 0.659 |
| 59.8 | 3.002 | 2.941 | 2.992 | 2.030 | 0.331 |
| 61.2 | 2.630 | 2.661 | 2.663 | 1.167 | 1.243 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Serna, J.M.; Villa-Acevedo, W.M.; López-Lezama, J.M. External Multi-Gap Lightning Arrester Modeling Using the Integration Method. Energies 2024, 17, 1241. https://doi.org/10.3390/en17051241
Rodríguez-Serna JM, Villa-Acevedo WM, López-Lezama JM. External Multi-Gap Lightning Arrester Modeling Using the Integration Method. Energies. 2024; 17(5):1241. https://doi.org/10.3390/en17051241
Chicago/Turabian StyleRodríguez-Serna, Johnatan M., Walter M. Villa-Acevedo, and Jesús M. López-Lezama. 2024. "External Multi-Gap Lightning Arrester Modeling Using the Integration Method" Energies 17, no. 5: 1241. https://doi.org/10.3390/en17051241
APA StyleRodríguez-Serna, J. M., Villa-Acevedo, W. M., & López-Lezama, J. M. (2024). External Multi-Gap Lightning Arrester Modeling Using the Integration Method. Energies, 17(5), 1241. https://doi.org/10.3390/en17051241







