Multiple Factors Coupling Probability Calculation Model of Transmission Line Ice-Shedding
Abstract
1. Introduction
2. Materials and Methods
2.1. Definition of Transmission Line Ice-Shedding
2.2. Analysis of Key Factors Influencing Ice-Shedding on Transmission Lines
2.2.1. Ice and Icing Prediction on Transmission Lines
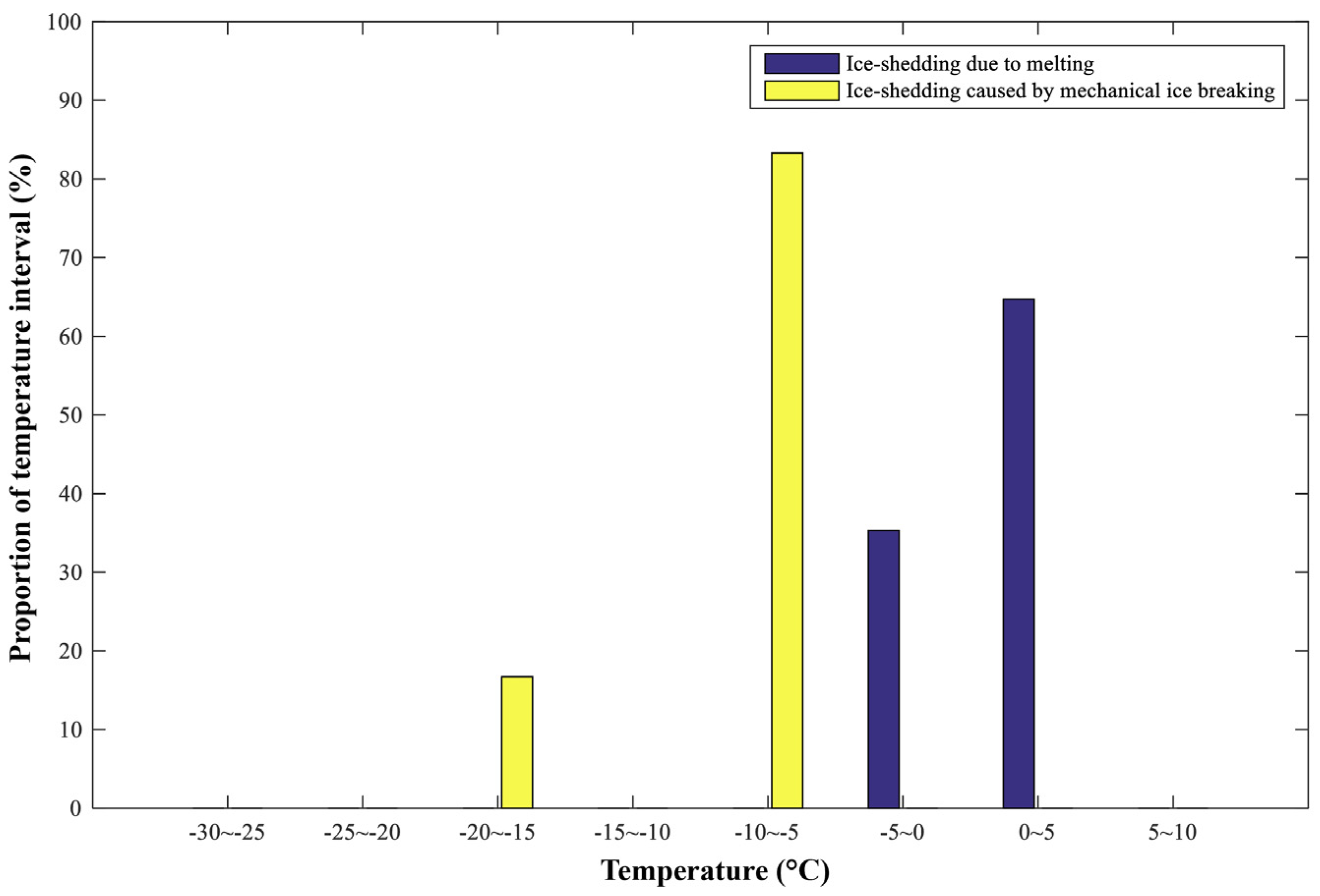
2.2.2. External Environmental Factors
2.2.3. Transmission Line Flashover Faults Caused by Ice-Shedding
3. Probability Calculation Model of Transmission Line Ice-Shedding
3.1. Marginal Probability Distribution of Influence Factors on Transmission Line Ice-Shedding
3.2. Calculation of Multiple-Factor Joint Cumulative Probability Distribution of Transmission Line Ice-Shedding
3.3. Calculation of Transmission Line Ice-Shedding Failure Probability
4. Case Study
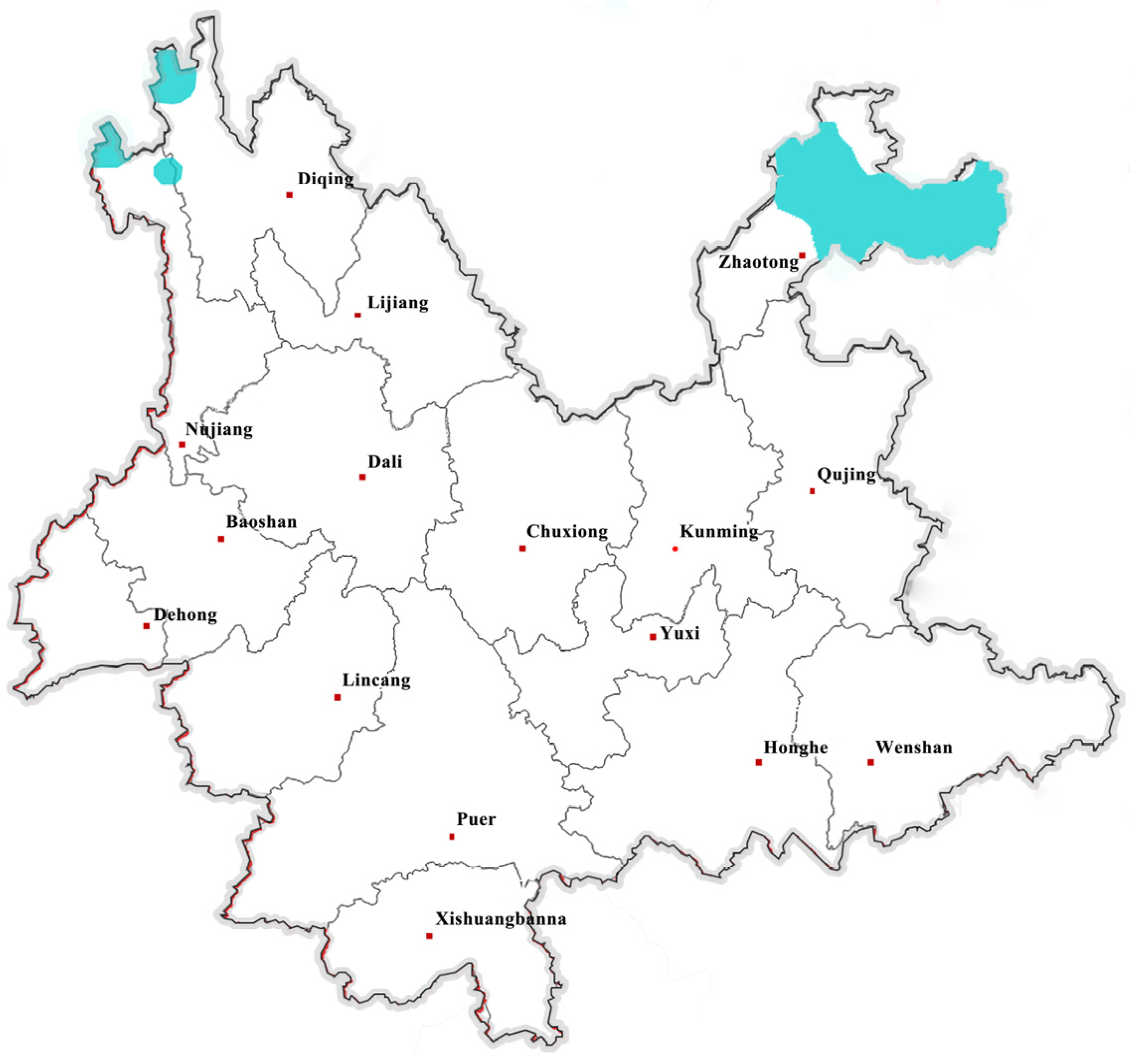
4.1. Study Area and Data Sources
4.2. Ice-Shedding Calculation Results Due to Both Melting and Mechanical Breakage
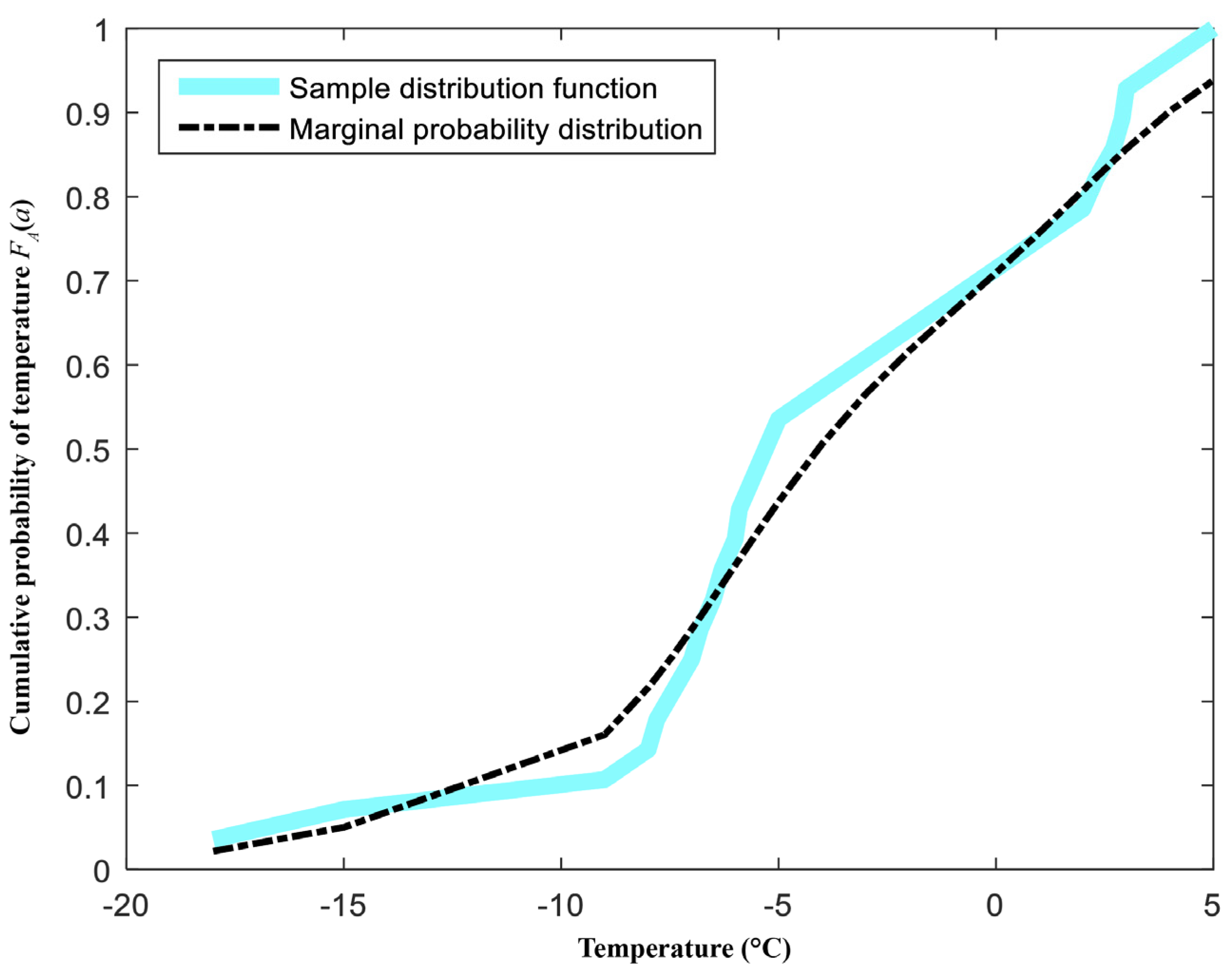
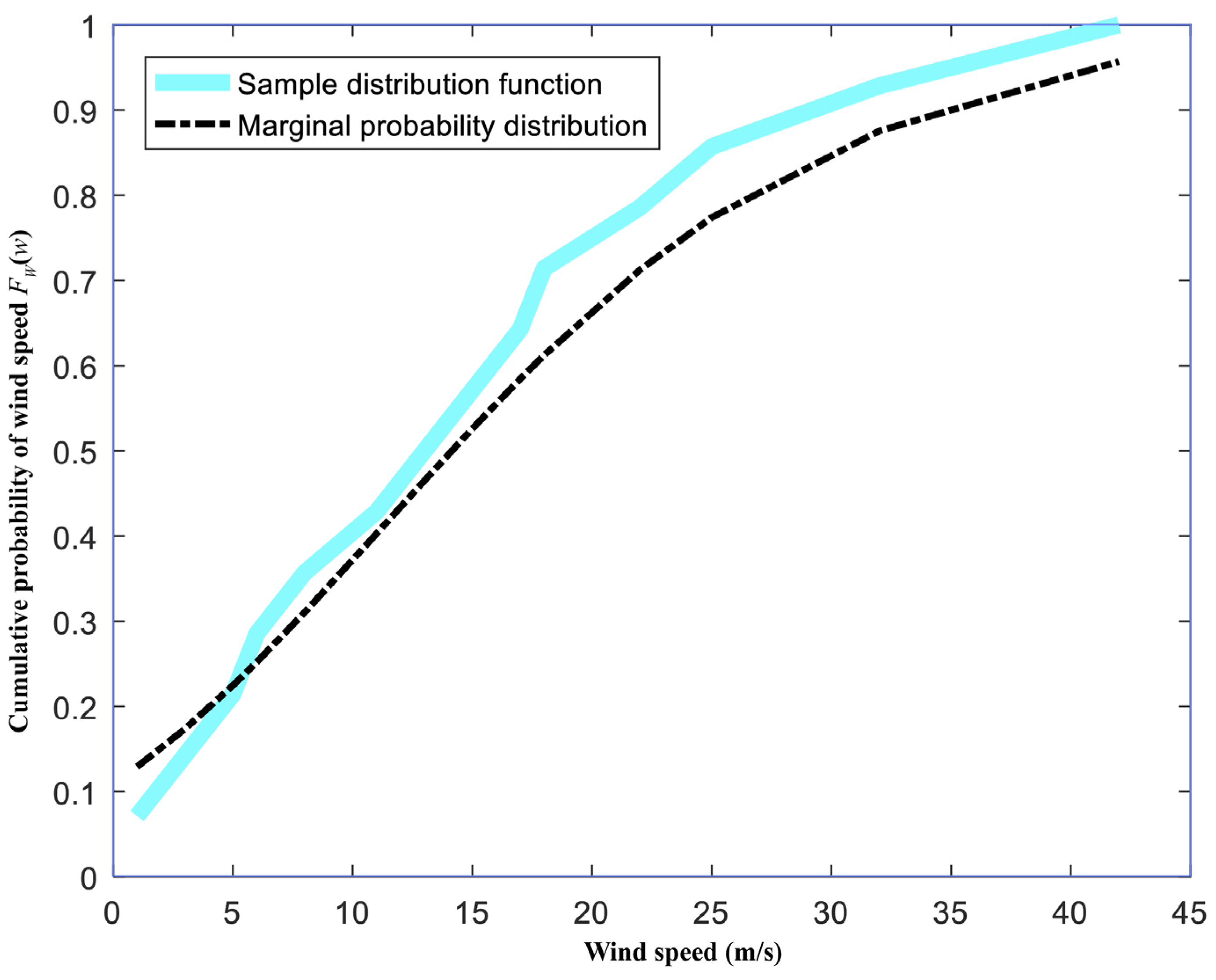
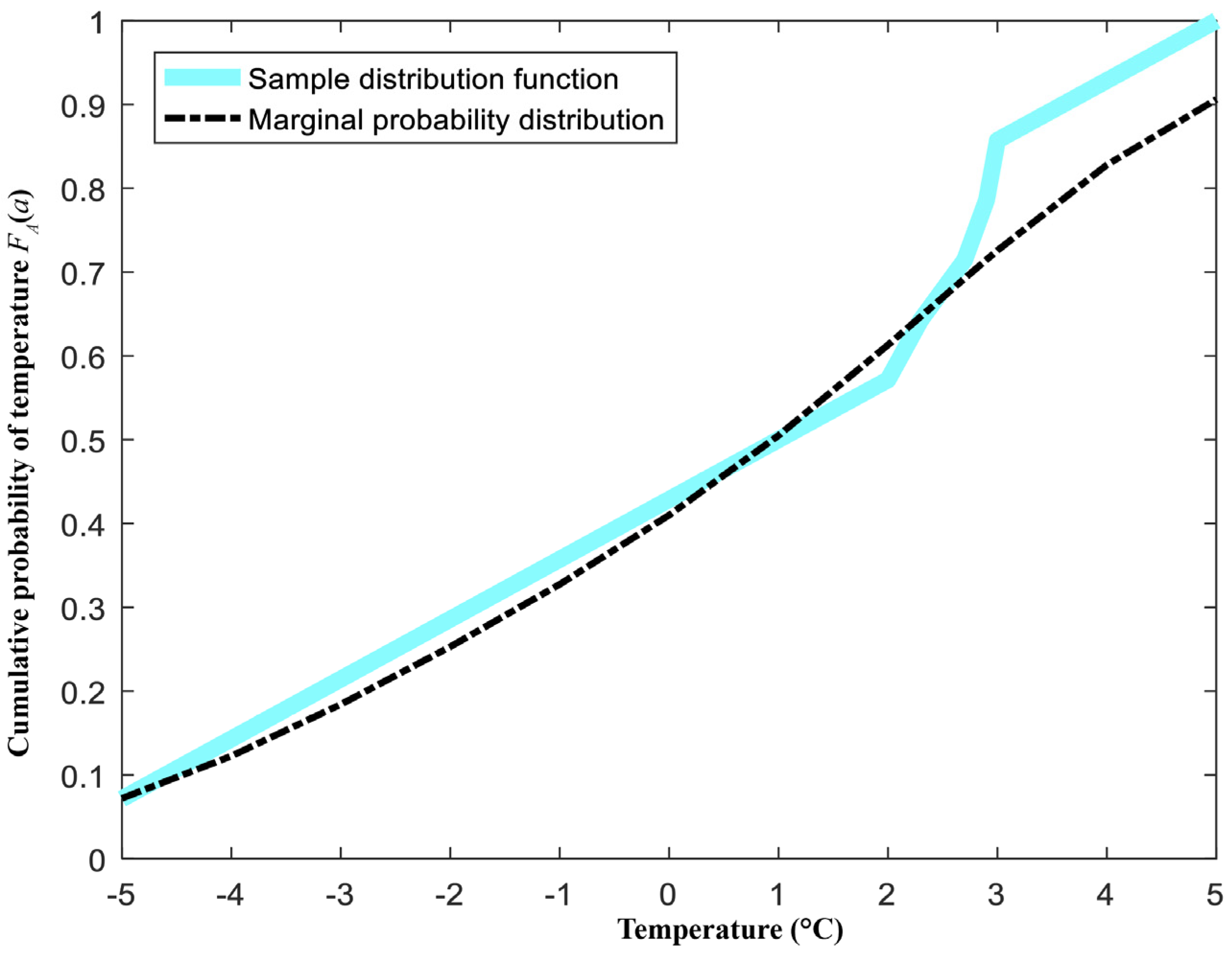
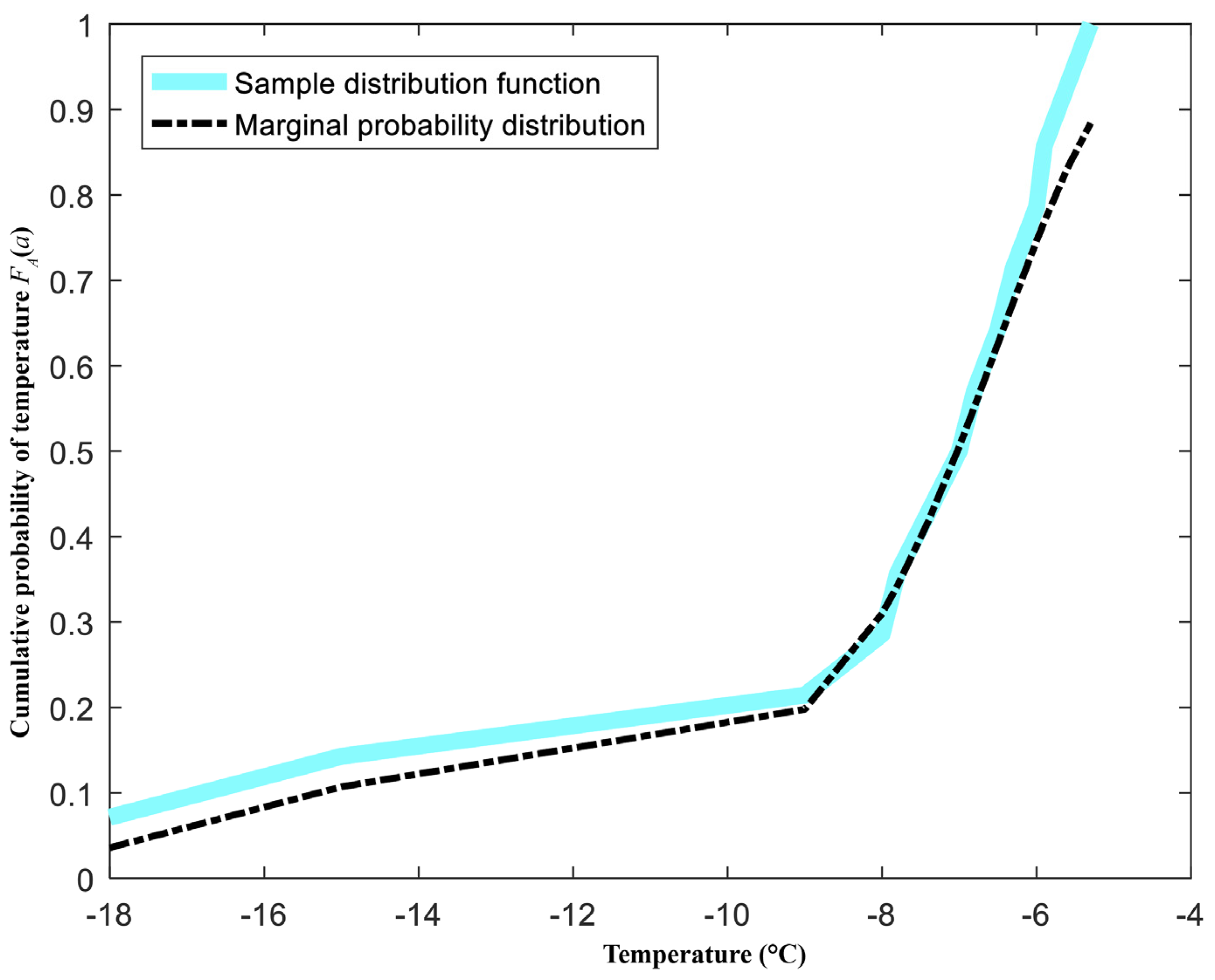
4.2.1. Calculation Results for the Marginal Probability Distribution of Influence Factors in Transmission Line Ice-Shedding
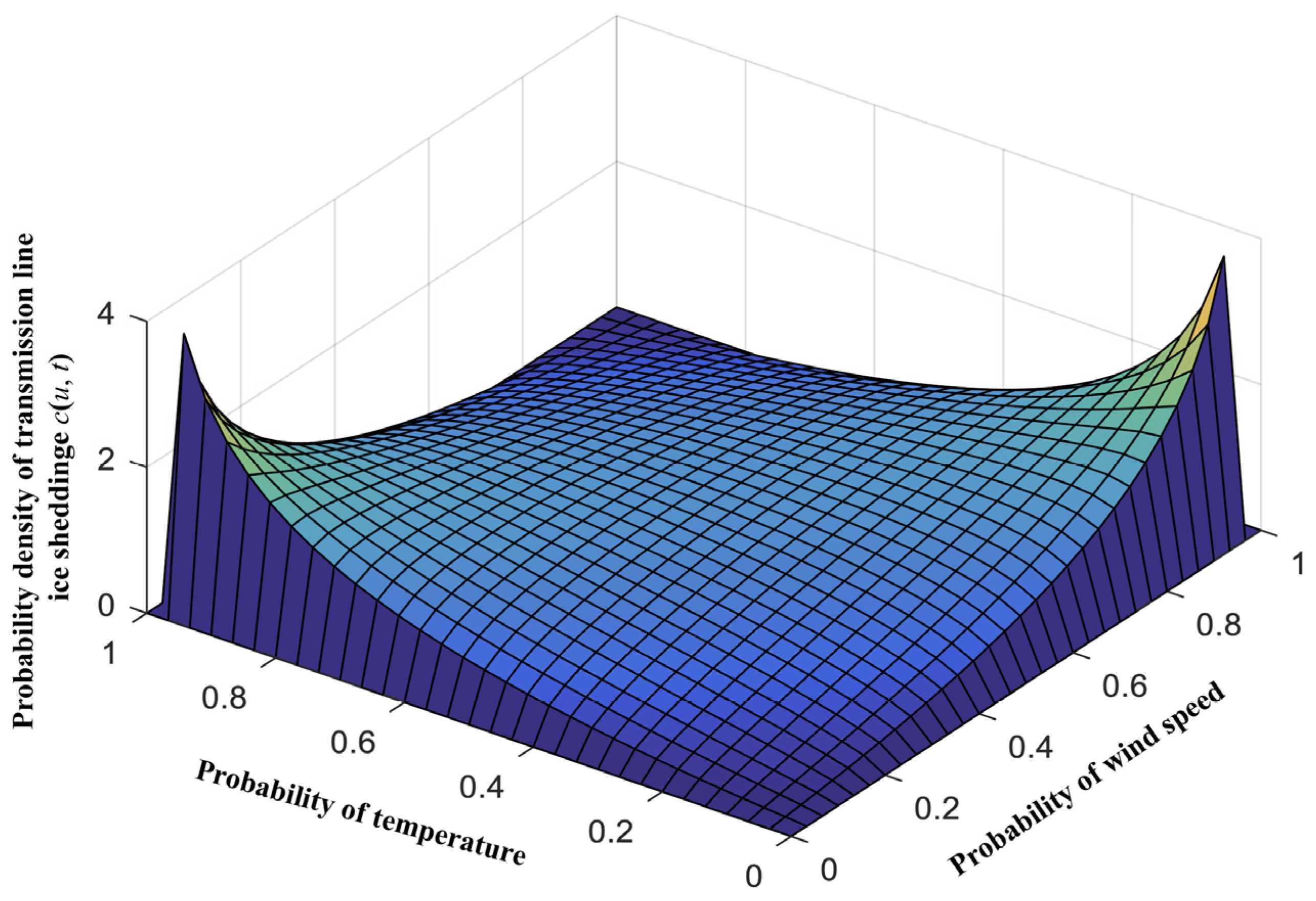
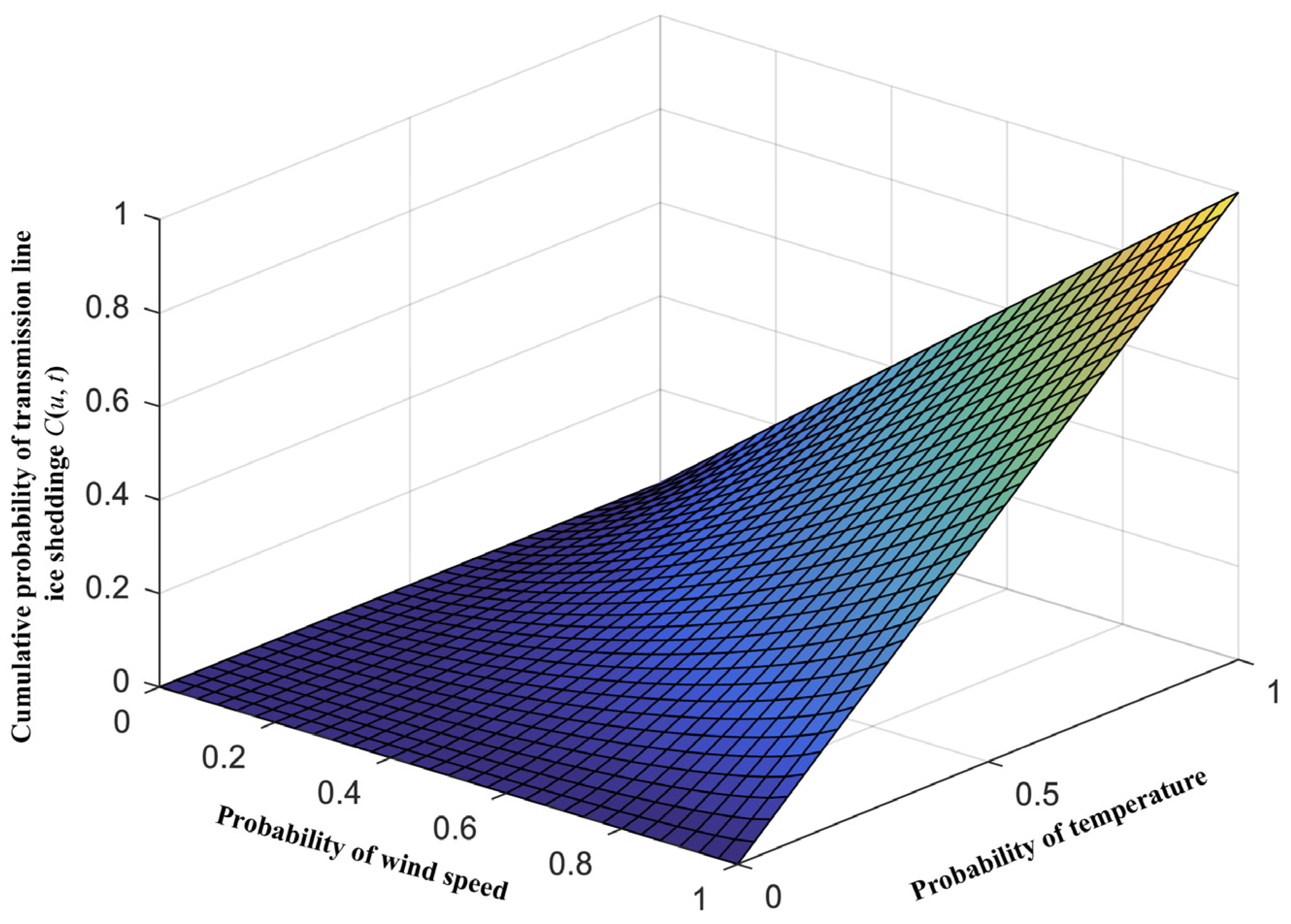
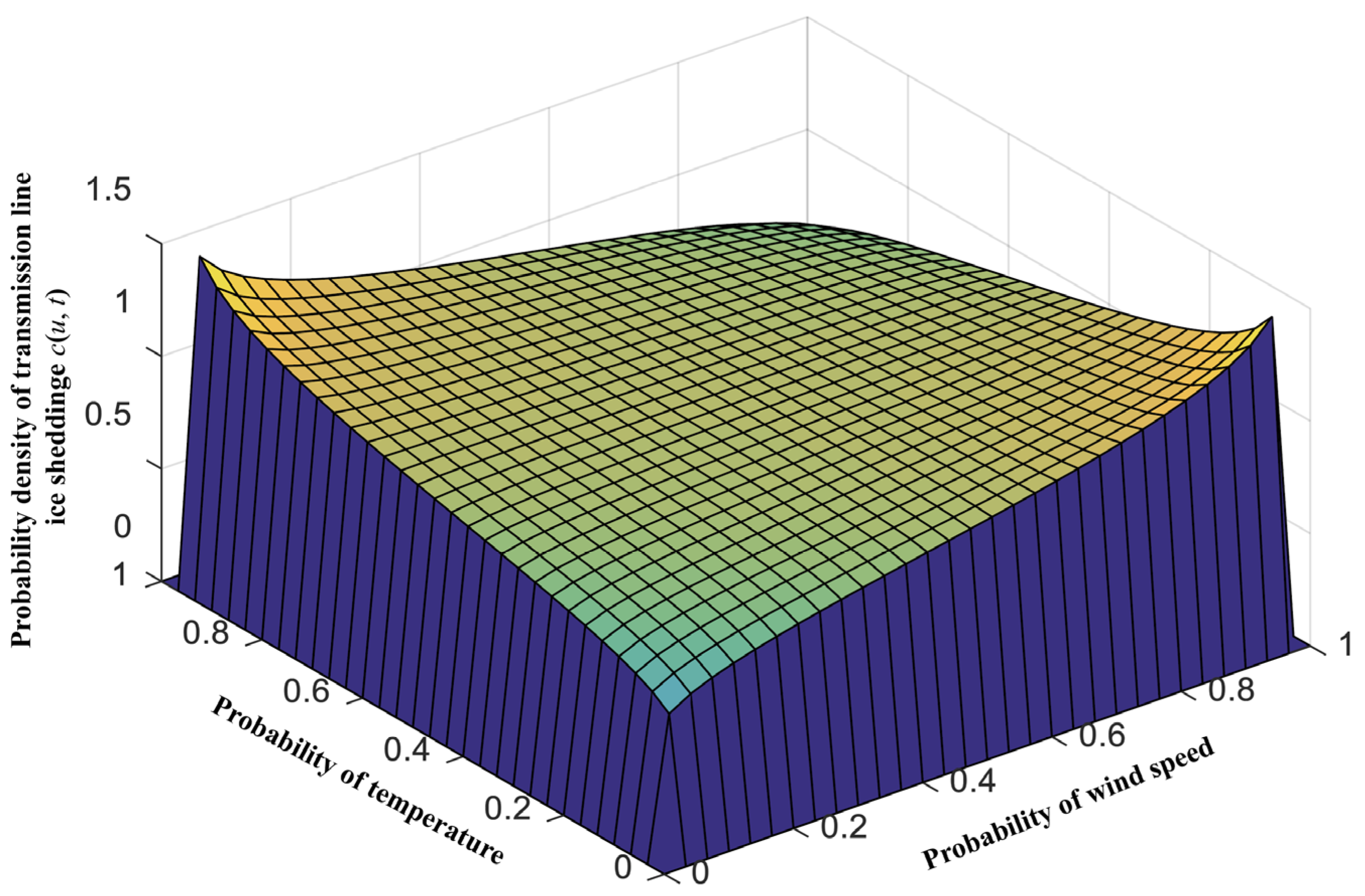
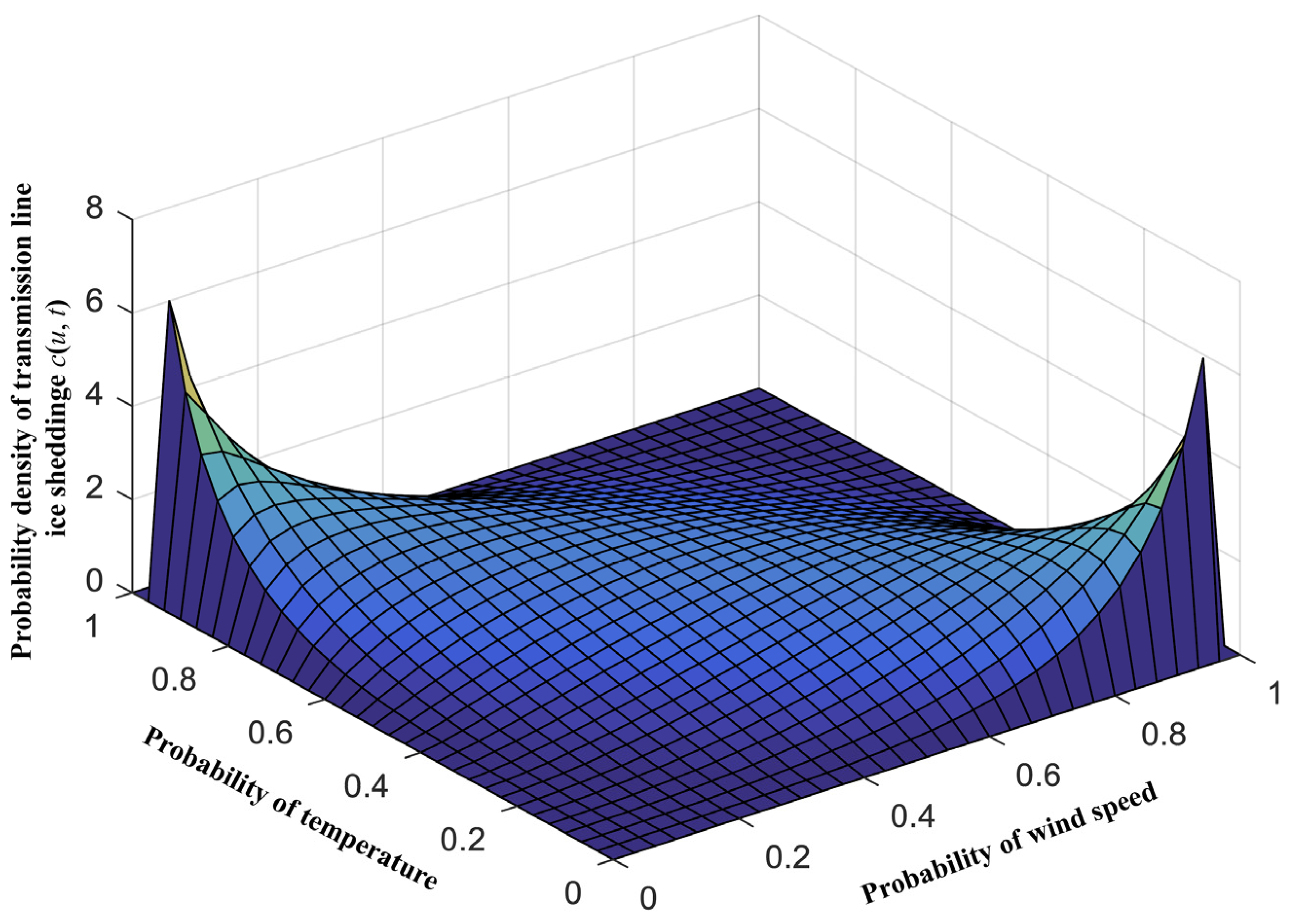
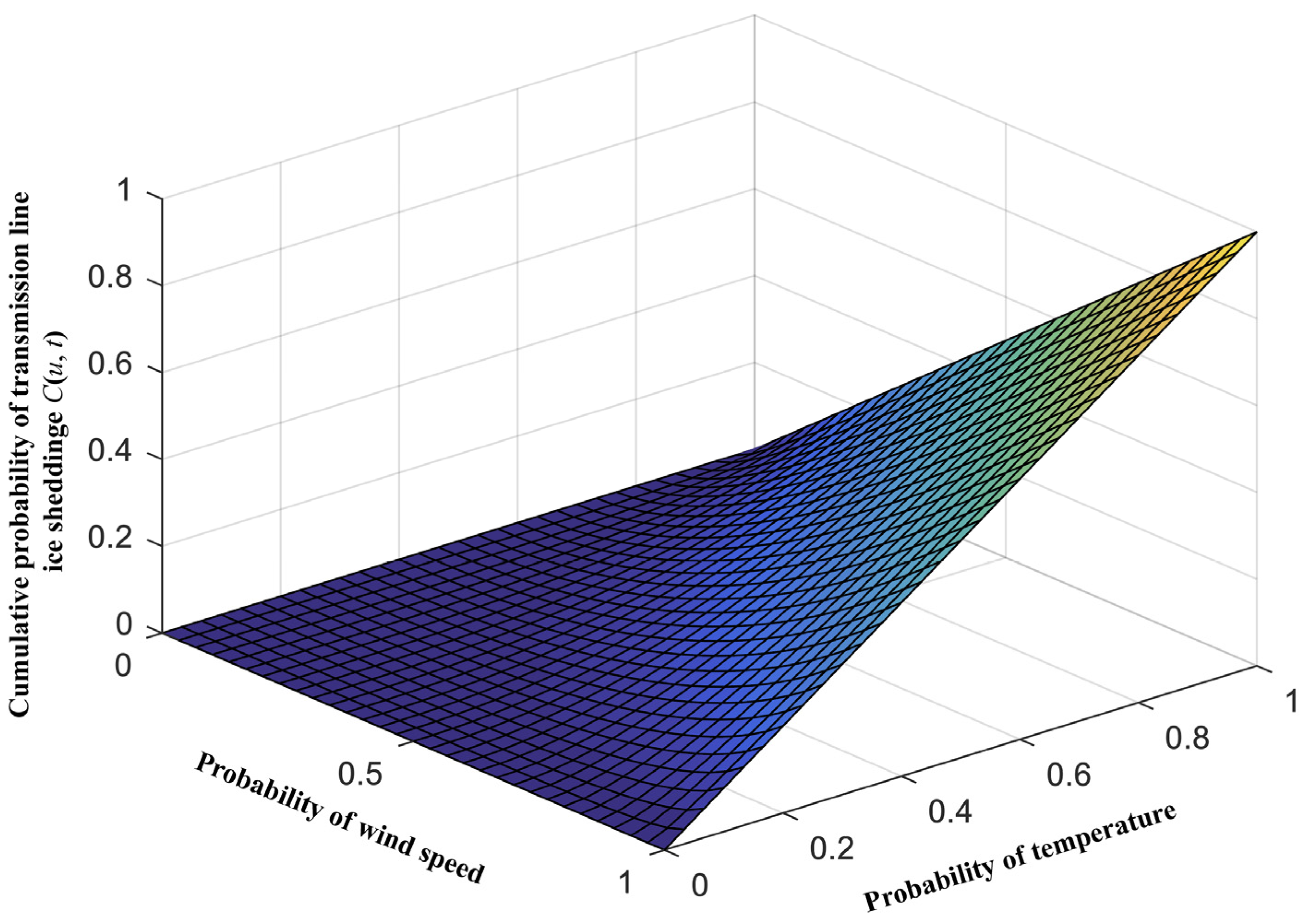
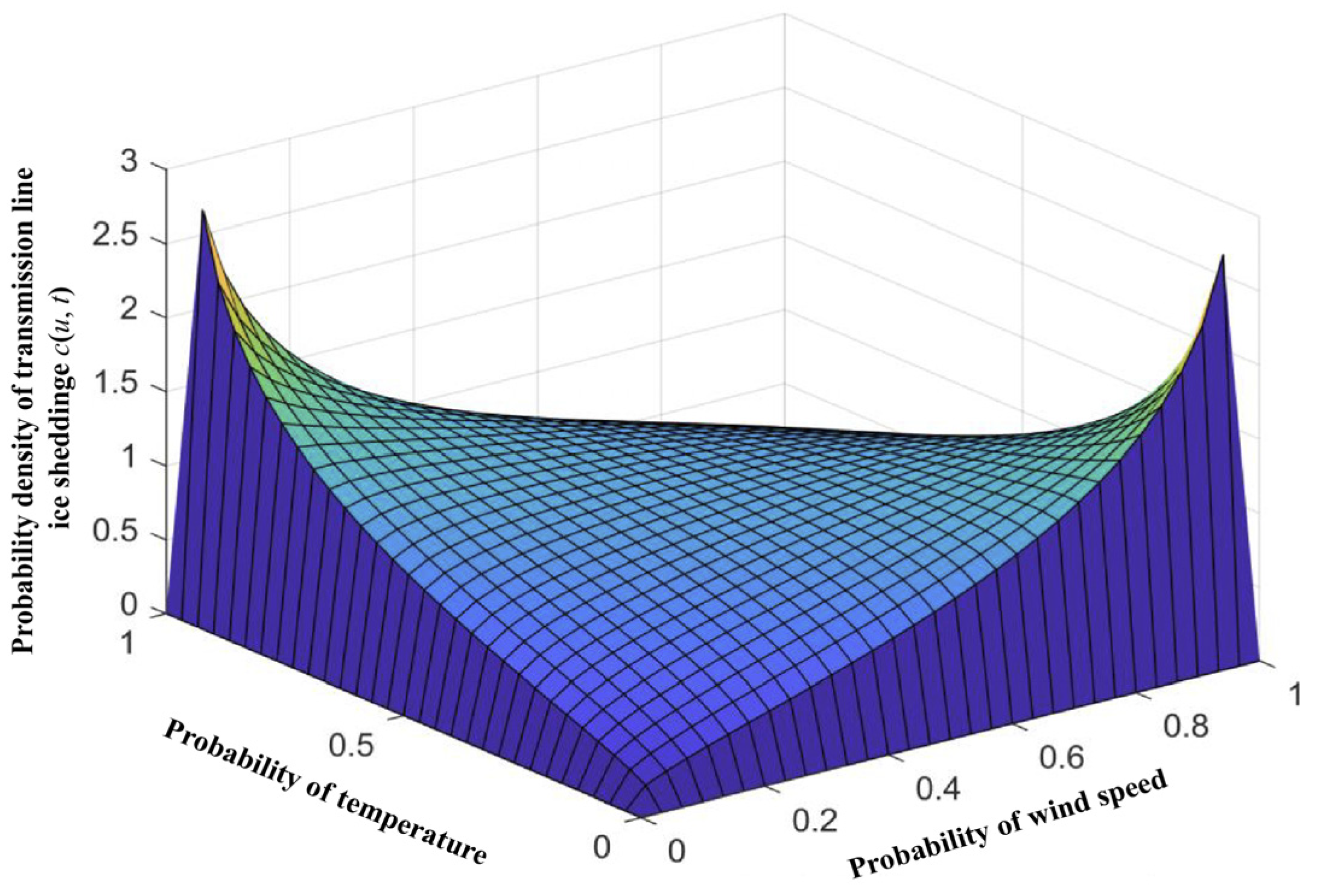
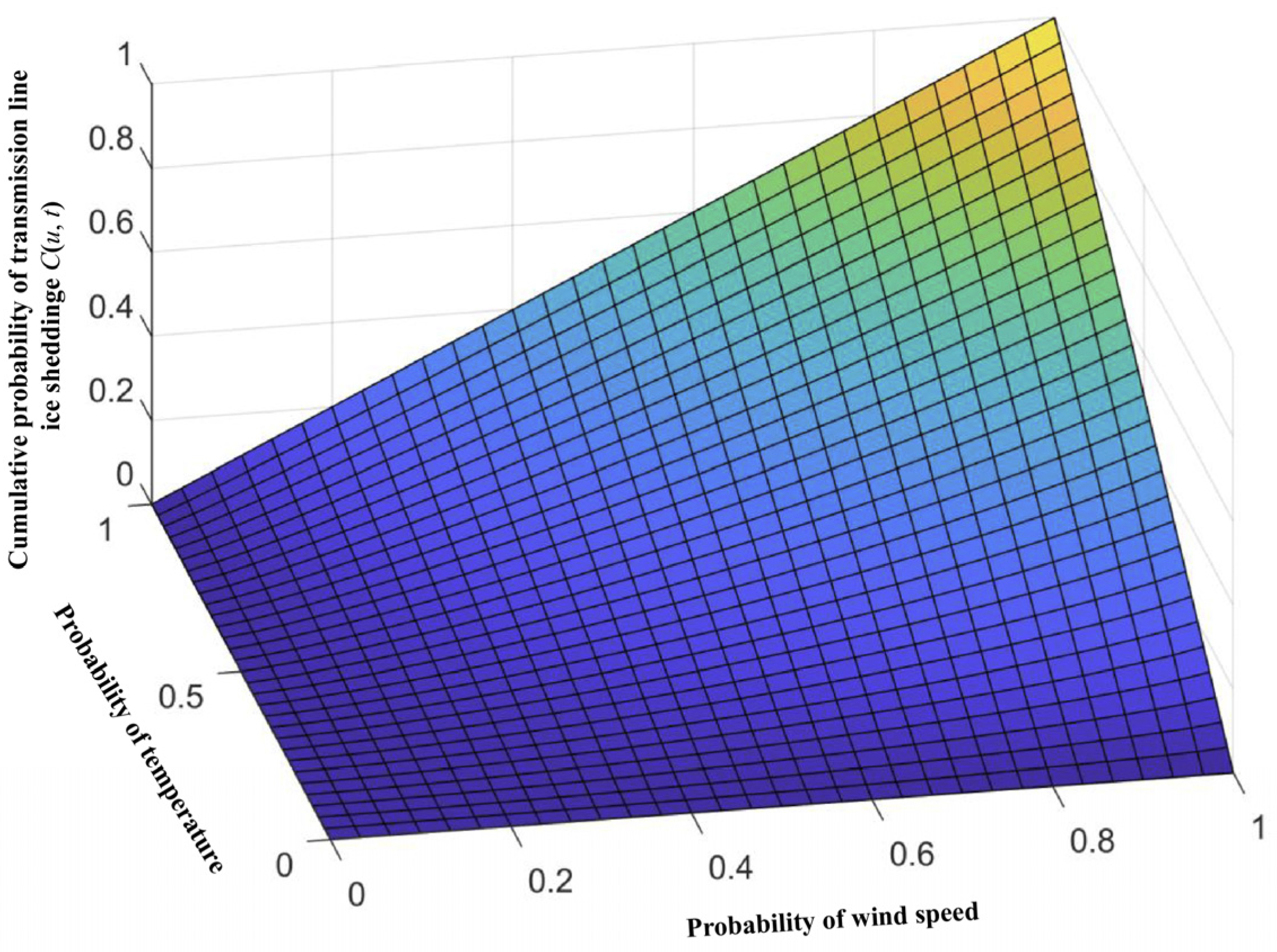
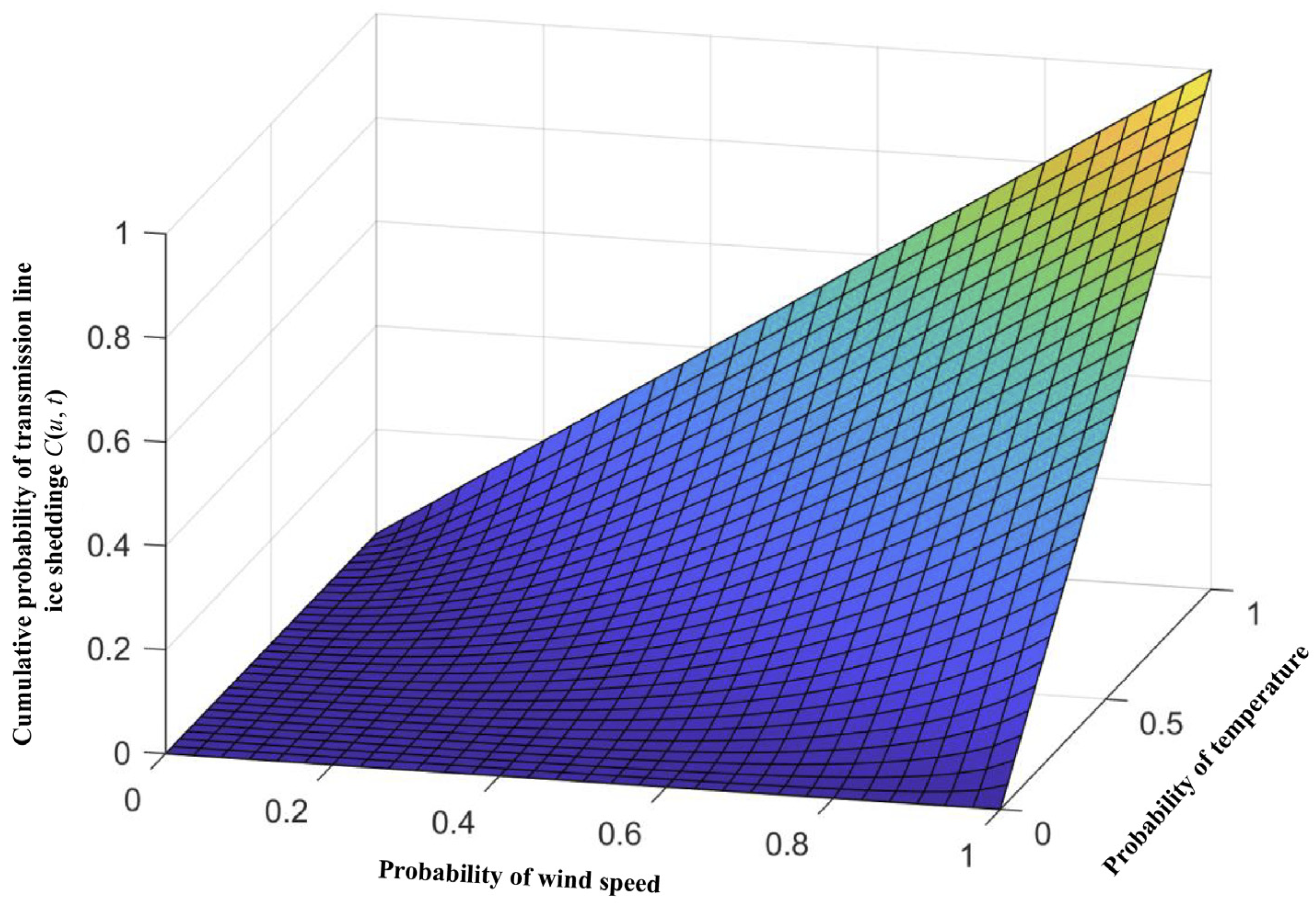
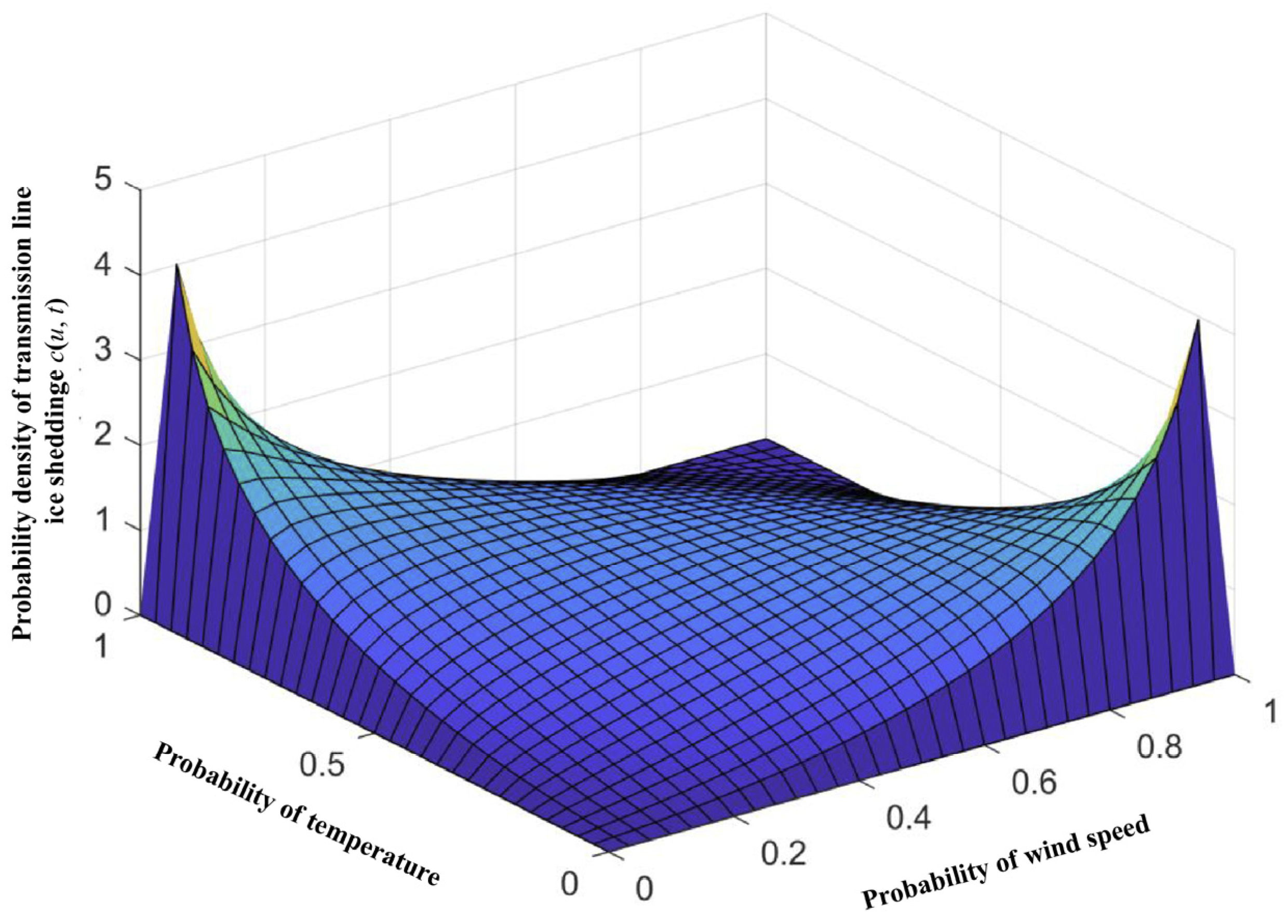
4.2.2. Calculated Multiple-Factor Joint Probability Distribution of Transmission Line Ice-Shedding
4.2.3. Calculation of Transmission Line Ice-Shedding Failure Probability
- By substituting the values of u and t into Formula (5), the joint probability value at this wind speed and temperature can be calculated to be 40.77%.
4.3. Calculated Ice-Shedding Results Due to Melting Alone
4.3.1. Calculated Results for the Marginal Probability Distributions of the Influence Factors in Transmission Line Ice-Shedding
4.3.2. Calculated Multiple-Factor Joint Probability Distributions of Transmission Line Ice-Shedding
4.3.3. Calculation of Transmission Line Ice-Shedding Failure Probability
4.4. Ice-Shedding Calculation Results Due to Mechanical Breakage Alone
4.4.1. Calculated Marginal Probability Distributions of the Influence Factors of Transmission Line Ice-Shedding
4.4.2. Calculated Multiple-Factor Joint Probability Distribution of Transmission Line Ice-Shedding
4.4.3. Calculation of Transmission Line Ice-Shedding Failure Probability
4.5. Ice-Shedding Calculation Results under Different Type of Ice
4.5.1. Calculated Multiple-Factor Joint Probability Distributions of Transmission Line Glaze Ice-Shedding
4.5.2. Calculated Multiple-Factor Joint Probability Distributions of Transmission Line Hard Rime Ice-Shedding
4.5.3. Calculated Multiple-Factor Joint Probability Distributions of Transmission Line Soft Rime Ice-Shedding
4.5.4. Calculation of Transmission Line Ice-Shedding Failure Probability
5. Comparison and Discussion
5.1. Comparison of Different Type of Ice-Shedding
5.2. Comparison of Probability Calculation Results for Different Icing Types and Different Ice-Shedding Mechanisms
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, J.; Jiang, Z.; Lei, H.; Zhang, H.; Peng, J.; Li, B.; Fang, Z. Analysis of Hunan Power Grid Ice Disaster Accident in 2008. Auto Electr. Power Syst. 2008, 32, 16–19. [Google Scholar]
- Savadjiev, K.; Farzaneh, M. Study of icing rate and related meteorological parameter distributions during atmospheric icing events. In Proceedings of the 11th International Offshore and Polar Engineering Conference, Stavanger, Norway, 17–22 June 2001; Volume 1, pp. 665–670. [Google Scholar]
- Savadjiev, K.; Farzaneh, M. Modeling of icing and ice shedding on overhead power lines based on statistical analysis of meteorological data. IEEE Trans. Power Deliv. 2004, 19, 715–721. [Google Scholar] [CrossRef]
- Wagner, T. Modelling of Wind Borne Ice Accretion on Power Transmission Lines. Ph.D. Thesis, Technische University, Braunschweig, Germany, 2010. [Google Scholar]
- Hou, L.; Wang, L.; Zhu, P.; Guan, Z. Dynamic Behavior Computation of Ice Shedding of UHV Overhead Transmission Lines. Proc. Chin. Soc. Electr. Eng. 2008, 28, 1–6. [Google Scholar]
- Liang, C. Research on Ice Shedding from 220 kV-Double-Circle Transmission Line in Heavy Icing Area. Master’s Thesis, North China Electric Power University, Baoding, China, 2017. [Google Scholar]
- Wu, C. Study on Jump Height after Ice-shedding and Galloping Oscillation Characteristics of Transmission Lines. Ph.D. Thesis, Chongqing University, Chongqing, China, 2017. [Google Scholar]
- Zhao, Y.; Li, L.; Deng, W. Transmission lines ice-shedding numerical simulation jump-height after ice shedding horizontal amplitude. Water Res. Power 2013, 31, 211–215. [Google Scholar]
- Xu, G. Numerical Simulation Study of Iced Conductor on Dynamic Response of Ice-Shedding on Transmission Lines. Master’s Thesis, Xi’an Technology University, Xi’an, China, 2016. [Google Scholar]
- Yan, B.; Chen, K.; Xiao, H.; Li, L.; Yi, W. Horizontal amplitude of iced conductor after ice-shedding under wind load. Chin. J. Appl. Mech. 2013, 30, 913–919. [Google Scholar]
- Deng, W. Numerical Simulation Research of Unbalanced Tension of Ice-Shedding on Transmission Lines. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2013. [Google Scholar]
- Long, H. Modeling on Transmission Tower-line System and Simulation Research on the Jumping of Transmission Line after Ice-shedding. Master’s Thesis, Hunan University of Science and Technology, Xiangtan, China, 2015. [Google Scholar]
- Li, H.; Wu, Y.; Fu, X.; Du, W. Dynamic Response of Transmission Lines Following Ice Shedding via a Three-Dimensional Motion Capture System. Int. J. Struct. Stab. Dyn. 2022, 22, 2250175. [Google Scholar] [CrossRef]
- Ye, Z.; Wu, C.; Liu, X.; Huang, F. Numerical Simulation of the Dynamic Responses of Electric Power Fitting of Transmission Lines after Ice Shedding. Shock Vib. 2022, 2022, 3675271. [Google Scholar] [CrossRef]
- Li, J.; Wang, B.; Sun, J.; Wang, S.; Zhang, X.; Fu, X. Collapse Analysis of a Transmission Tower-Line System Induced by Ice Shedding. Front. Phys. 2021, 9, 712161. [Google Scholar] [CrossRef]
- Huang, G.; Yan, B.; Guo, Y.; Zhang, B.; Wu, G. Experimental study on dynamic response characteristics of isolated-span transmission lines after ice-shedding. High Volt. 2023, 8, 196–208. [Google Scholar] [CrossRef]
- Lou, W.; Zhang, Y.; Xu, H.; Huang, M.; Zhang, B.; Bian, R. Field experiments on ice-accretion and ice-shedding processes of power transmission lines based on a conductor segment model. China Civil Eng. J. 2022, 55, 27–35. [Google Scholar]
- Li, H.; Wu, Y. Experimental study on dynamic responses of transmission lines caused by ice shedding. China Civil Eng. J. 2019, 52, 35–46, 100. [Google Scholar]
- Huang, G.; Yan, B.; Wen, N.; Wu, C.; Li, Q. Study on jump height of transmission lines after ice-shedding by reduced-scale modeling test. Cold Reg. Sci. Technol. 2019, 165, 102781. [Google Scholar] [CrossRef]
- Wang, L.; Cao, L.; Mei, H.; Huang, T.; Gao, Y. Simulation Research on Suppressing Measures Against Severe Ice-shedding Jump of UHVAC Double-circuit Transmission Lines on the Same Tower. High Volt. Eng. 2018, 44, 1475–1482. [Google Scholar]
- Xie, Y.; Huang, L.; Wang, D.; Ding, H.; Yin, X. Modeling and analysis of progressive ice shedding along a transmission line during thermal de-icing. Math. Probl. Eng. 2019, 2019, 4851235. [Google Scholar] [CrossRef]
- Yang, F.; Yang, J.; Li, Z.; Han, J.; Fu, D. Ice shedding and vibration suppression of a transmission line system. J. Vib. Shock 2010, 29, 20–25. [Google Scholar]
- Li, L.; Zhang, X.; Yin, P. Control for Jumping Response Induced by Ice-Shedding of Transmission Lines. J. Vib. Shock 2008, 27, 61–64, 80, 192. [Google Scholar]
- Yin, P.; Li, L.; Zhang, X. Investigation on Control of Jumping Induced by Transmission Line Ice-Shedding. Adv. Power Syst. Hydroelectr. Eng. 2008, 24, 3–7. [Google Scholar]
- Huang, W. Study on Tower-Line System Ice-Shedding Jump and Vibration Reduction. Master’s Thesis, Hunan University of Science and Technology, Xiangtan, China, 2016. [Google Scholar]
- Song, C. Dynamic Properties and Vibration Control on Wire-Breaking and Ice-Shedding of Transmission Tower-Line System. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2013. [Google Scholar]
- Wu, J.; Xu, C. Major Chinese cities’ solar radiant intensities in winter. J. Harbin Inst. Technol. 2003, 35, 1236–1239. [Google Scholar]
- Zhang, S. FEM Simulations on Temperature Rising and Mechanical Responses of Transmission Lines under Increasing Current Capacity. Master’s Thesis, Huazhong University of Science & Technology, Wuhan, China, 2014. [Google Scholar]
- Yan, M.; Zhou, Z.; Wen, J.; Guo, C.; Lu, J. Assessment Method for Power Grid Icing Risk Based on Short-term Icing Forecasting. Auto. Electr. Power Syst. 2016, 40, 168–175. [Google Scholar]
- Lu, J.; Guo, J.; Hu, J.; Yang, L.; Feng, T. Analysis of ice disasters on ultra-high-voltage direct-current transmission lines. Nat. Hazards 2017, 86, 203–217. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Y.; Zou, Q.; Ye, L.; Zhu, S.; Zhang, H. Study on optimization and combination strategy of multiple daily runoff prediction models coupled with physical mechanism and LSTM. J. Hydrol. 2023, 624, 129969. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Wang, D.; Yan, B.; Huang, G.; Huang, X.; Li, M. Simplified formula for jump height of transmission lines after ice-shedding. J. Chongqing Univ. (Nat. Sci. Ed.) 2020, 43, 64–71. [Google Scholar]
- GB/T 35706-2017; Technical Rule for Ice Mapping of Power Grid. Standards Press of China: Beijing, China, 2017.






| ID | Tower Number | Voltage Level | Temperature (°C) | Wind Speed (m/s) | Ice Thickness (mm) | >Critical Icing Thickness? | Wind Speed in the Marginal Probability Distribution u | Temperature in the Marginal Probability Distribution t | Copula Function Parameter θ | Probability of Ice-Shedding Failure | Observed Ice-Shedding or Not |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 46# | 220 kV | 4 | 17.5 | 12 | Yes | 0.4916 | 0.9018 | −4.0246 | 40.77% | Yes |
| 2 | 2# | 220 kV | 3 | 18.8 | 16 | Yes | 0.5257 | 0.8569 | −4.0246 | 40.21% | Yes |
| 3 | 128# | 220 kV | −2 | 25.2 | 15 | Yes | 0.6703 | 0.6165 | −4.0246 | 32.91% | Yes |
| 4 | 23# | 220 | 2 | 20.5 | 13 | Yes | 0.5682 | 0.8075 | −4.0246 | 39.93% | Yes |
| 5 | 1508# | ±800 | −1.5 | 26.5 | 20 | Yes | 0.6943 | 0.6402 | −4.0246 | 36.79% | Yes |
| 6 | 75# | 220 kV | −5 | 12.5 | 12 | Yes | 0.3533 | 0.4374 | −4.0246 | 6.05% | No |
| 7 | 267# | 500 kV | −1 | 6.5 | 5 | No | 0.1970 | 0.6633 | −4.0246 | 6.43% | No |
| 8 | 211# | 500 kV | 2 | 10.5 | 15 | Yes | 0.2984 | 0.8075 | −4.0246 | 17.81% | No |
| 9 | 1760# | ±500 kV | −2 | 11.2 | 6 | No | 0.3174 | 0.6165 | −4.0246 | 10.34% | No |
| 10 | 24# | 220 kV | −3 | 8.5 | 13 | Yes | 0.2458 | 0.5653 | −4.0246 | 5.91% | No |
| ID | Tower Number | Voltage Level | Temperature (°C) | Wind Speed (m/s) | Ice Thickness (mm) | > Critical Icing Thickness? | Wind Speed in the Marginal Probability Distribution u | Temperature in the Marginal Probability Distribution t | Copula Function Parameter θ | Probability of Ice-Shedding Failure | Observed Ice-Shedding or Not |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 46# | 220 kV | 4 | 17.5 | 12 | Yes | 0.5985 | 0.8279 | −1.3117 | 47.42% | Yes |
| 2 | 2# | 220 kV | 3 | 18.8 | 16 | Yes | 0.6338 | 0.7258 | −1.3117 | 43.12% | Yes |
| 3 | 128# | 220 kV | −2 | 25.2 | 15 | Yes | 0.7776 | 0.2528 | −1.3117 | 17.44% | Yes |
| 4 | 23# | 220 | 2 | 20.5 | 13 | Yes | 0.6772 | 0.6130 | −1.3117 | 38.24% | Yes |
| 5 | 1508# | ±800 | −1.5 | 26.5 | 20 | Yes | 0.8004 | 0.2893 | −1.3117 | 20.93% | Yes |
| 6 | 75# | 220 kV | −5 | 12.5 | 12 | Yes | 0.4496 | 0.0719 | −1.3117 | 2.20% | No |
| 7 | 267# | 500 kV | −1 | 6.5 | 5 | No | 0.2665 | 0.3273 | −1.3117 | 6.06% | No |
| 8 | 211# | 500 kV | 2 | 10.5 | 15 | Yes | 0.3873 | 0.6130 | −1.3117 | 20.08% | No |
| 9 | 1760# | ±500 kV | −2 | 11.2 | 6 | No | 0.4091 | 0.2528 | −1.3117 | 7.47% | No |
| 10 | 24# | 220 kV | −3 | 8.5 | 13 | Yes | 0.3257 | 0.1840 | −1.3117 | 3.98% | No |
| ID | Tower Number | Voltage Level | Temperature (°C) | Wind Speed (m/s) | Ice Thickness (mm) | > Critical Icing Thickness? | Wind speed in the Marginal Probability Distribution u | Temperature in the Marginal Probability Distribution t | Copula Function Parameter θ | Probability of Ice-Shedding Failure | Observed Ice-Shedding or Not |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 46# | 220 kV | 4 | 17.5 | 12 | Yes | 0.3808 | 1.0000 | −6.6384 | 38.08% | Yes |
| 2 | 2# | 220 kV | 3 | 18.8 | 16 | Yes | 0.4106 | 1.0000 | −6.6384 | 41.06% | Yes |
| 3 | 128# | 220 kV | −2 | 25.2 | 15 | Yes | 0.5496 | 1.0000 | −6.6384 | 54.96% | Yes |
| 4 | 23# | 220 | 2 | 20.5 | 13 | Yes | 0.4491 | 1.0000 | −6.6384 | 44.91% | Yes |
| 5 | 1508# | ±800 | −1.5 | 26.5 | 20 | Yes | 0.5755 | 1.0000 | −6.6384 | 57.55% | Yes |
| 6 | 75# | 220 kV | −5 | 12.5 | 12 | Yes | 0.2676 | 0.9253 | −6.6384 | 20.84% | No |
| 7 | 267# | 500 kV | −1 | 6.5 | 5 | No | 0.1502 | 1.0000 | −6.6384 | 15.02% | No |
| 8 | 211# | 500 kV | 2 | 10.5 | 15 | Yes | 0.2253 | 1.0000 | −6.6384 | 22.53% | No |
| 9 | 1760# | ±500 kV | −2 | 11.2 | 6 | No | 0.2398 | 1.0000 | −6.6384 | 23.98% | No |
| 10 | 24# | 220 kV | −3 | 8.5 | 13 | Yes | 0.1859 | 0.9995 | −6.6384 | 18.55% | No |
| ID | Tower Number | Voltage Level | Temperature (°C) | Wind Speed (m/s) | Ice Thickness (mm) | >Critical Icing Thickness? | Ice Type | Wind Speed in the Marginal Probability Distribution u | Temperature in the Marginal Probability Distribution t | Copula Function Parameter θ | Probability of Ice-Shedding Failure | Observed Ice-Shedding or Not |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 46# | 220 kV | 4 | 17.5 | 12 | Yes | glaze | 0.6169 | 0.9412 | −3.3042 | 56.43% | Yes |
| 2 | 2# | 220 kV | 3 | 18.8 | 16 | Yes | glaze | 0.6785 | 0.8824 | −3.3042 | 57.11% | Yes |
| 3 | 128# | 220 kV | −2 | 25.2 | 15 | Yes | hard rime | 0.7032 | 0.8530 | −6.9068 | 55.79% | Yes |
| 4 | 23# | 220 | 2 | 20.5 | 13 | Yes | soft rime | 0.4881 | 0.9998 | −4.2731 | 48.79% | Yes |
| 5 | 1508# | ±800 | −1.5 | 26.5 | 20 | Yes | soft rime | 0.6441 | 0.9411 | −4.2731 | 58.86% | Yes |
| 6 | 75# | 220 kV | −5 | 12.5 | 12 | Yes | hard rime | 0.3088 | 0.7448 | −6.9068 | 11.87% | No |
| 7 | 267# | 500 kV | −1 | 6.5 | 5 | No | soft rime | 0.0996 | 0.9603 | −4.2731 | 8.64% | No |
| 8 | 211# | 500 kV | 2 | 10.5 | 15 | Yes | glaze | 0.3393 | 0.6826 | −3.3042 | 15.58% | No |
| 9 | 1760# | ±500 kV | −2 | 11.2 | 6 | No | soft rime | 0.1979 | 0.9218 | −4.2731 | 15.59% | No |
| 10 | 24# | 220 kV | −3 | 8.5 | 13 | Yes | hard rime | 0.2479 | 0.8320 | −6.9068 | 12.80% | No |
| ID | Tower Number | Voltage Level | Temperature (°C) | Wind Speed (m/s) | Ice Thickness (mm) | Critical Icing Thickness? | Probability of Ice-Shedding Failure | Observed Ice-Shedding or Not |
|---|---|---|---|---|---|---|---|---|
| 1 | 46# | 220 kV | 4 | 17.5 | 12 | Yes | 47.42% | Yes |
| 2 | 2# | 220 kV | 3 | 18.8 | 16 | Yes | 43.12% | Yes |
| 3 | 128# | 220 kV | −2 | 25.2 | 15 | Yes | 54.96% | Yes |
| 4 | 23# | 220 | 2 | 20.5 | 13 | Yes | 44.91% | Yes |
| 5 | 1508# | ±800 | −1.5 | 26.5 | 20 | Yes | 57.55% | Yes |
| 6 | 75# | 220 kV | −5 | 12.5 | 12 | Yes | 20.84% | No |
| 7 | 267# | 500 kV | −1 | 6.5 | 5 | No | 15.02% | No |
| 8 | 211# | 500 kV | 2 | 10.5 | 15 | Yes | 22.53% | No |
| 9 | 1760# | ±500 kV | −2 | 11.2 | 6 | No | 23.98% | No |
| 10 | 24# | 220 kV | −3 | 8.5 | 13 | Yes | 18.55% | No |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, H.; Zhou, F.; Ma, Y.; Ma, Y.; Qiu, P.; Guo, J. Multiple Factors Coupling Probability Calculation Model of Transmission Line Ice-Shedding. Energies 2024, 17, 1208. https://doi.org/10.3390/en17051208
Pan H, Zhou F, Ma Y, Ma Y, Qiu P, Guo J. Multiple Factors Coupling Probability Calculation Model of Transmission Line Ice-Shedding. Energies. 2024; 17(5):1208. https://doi.org/10.3390/en17051208
Chicago/Turabian StylePan, Hao, Fangrong Zhou, Yi Ma, Yutang Ma, Ping Qiu, and Jun Guo. 2024. "Multiple Factors Coupling Probability Calculation Model of Transmission Line Ice-Shedding" Energies 17, no. 5: 1208. https://doi.org/10.3390/en17051208
APA StylePan, H., Zhou, F., Ma, Y., Ma, Y., Qiu, P., & Guo, J. (2024). Multiple Factors Coupling Probability Calculation Model of Transmission Line Ice-Shedding. Energies, 17(5), 1208. https://doi.org/10.3390/en17051208







