A Refined Wind Power Forecasting Method with High Temporal Resolution Based on Light Convolutional Neural Network Architecture
Abstract
1. Introduction
- (1)
- The input method of grouping the original input features is proposed, which provides more refined input feature information for the model through two channels with different combinations of input features.
- (2)
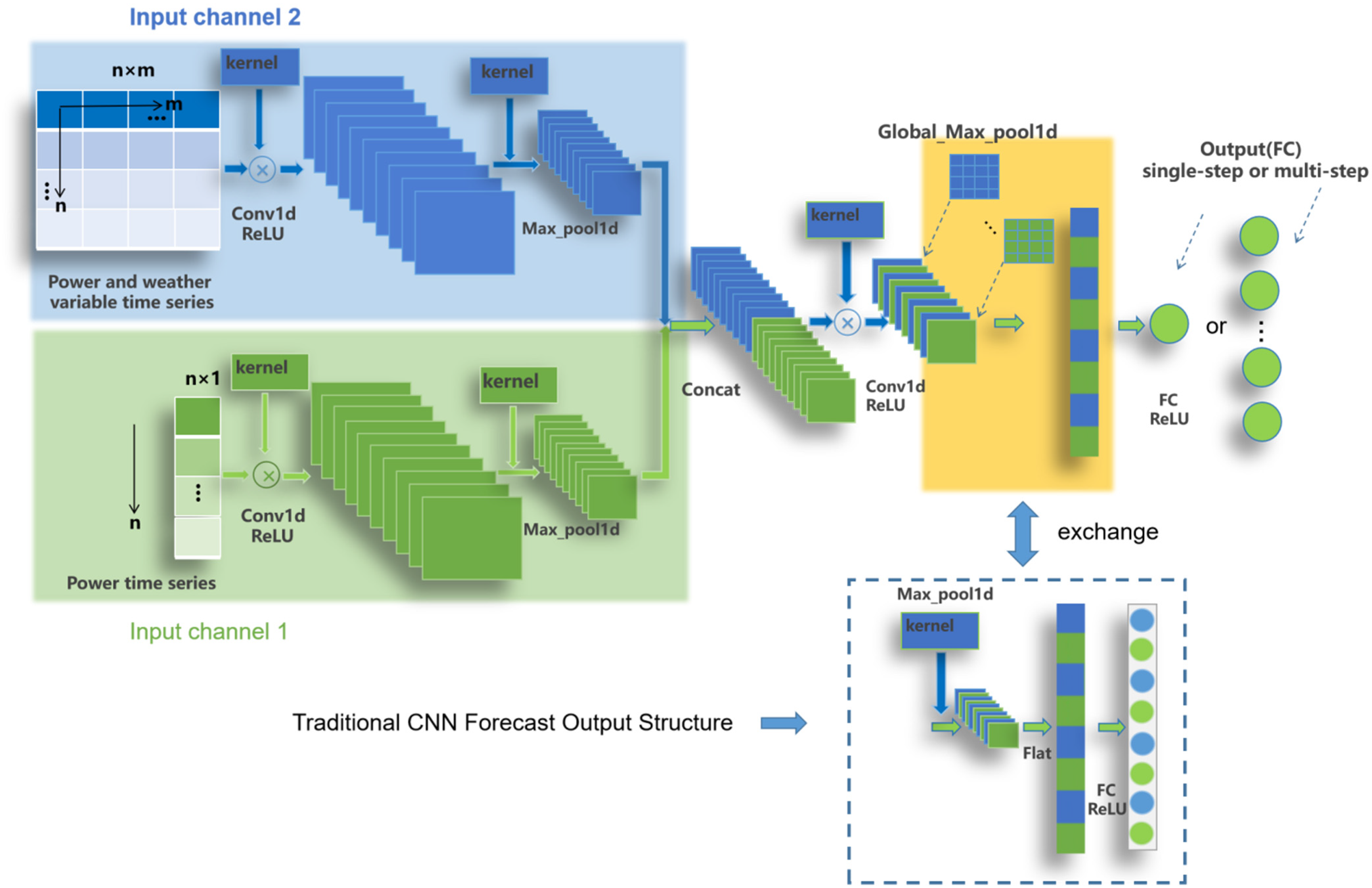
- Two parallel sets of convolutional neural networks are used to extract different kinds of feature constraint relationships: one targeted to extract local constraint relationships between wind power sequence elements, and the other considers local constraints between wind speed, wind direction, and wind power while extracting local constraint relationships between wind power sequence elements.
- (3)
- The light global maximum pooling approach replaces the traditional CNN’s flattening combined with the FC forecasting approach, which directly downscales the 3D feature data of the front layer, eliminating the data flattening operation and the introduction of more FC layers, which greatly improves the model’s computational efficiency.
- (4)
- Single-step and multi-step second-level high-resolution wind power forecasting experiments are carried out simultaneously to meet the demand for different time-scale forecasting results in high time resolution application scenarios of the power system, and the performance of the model on different average wind speed intervals is also investigated.
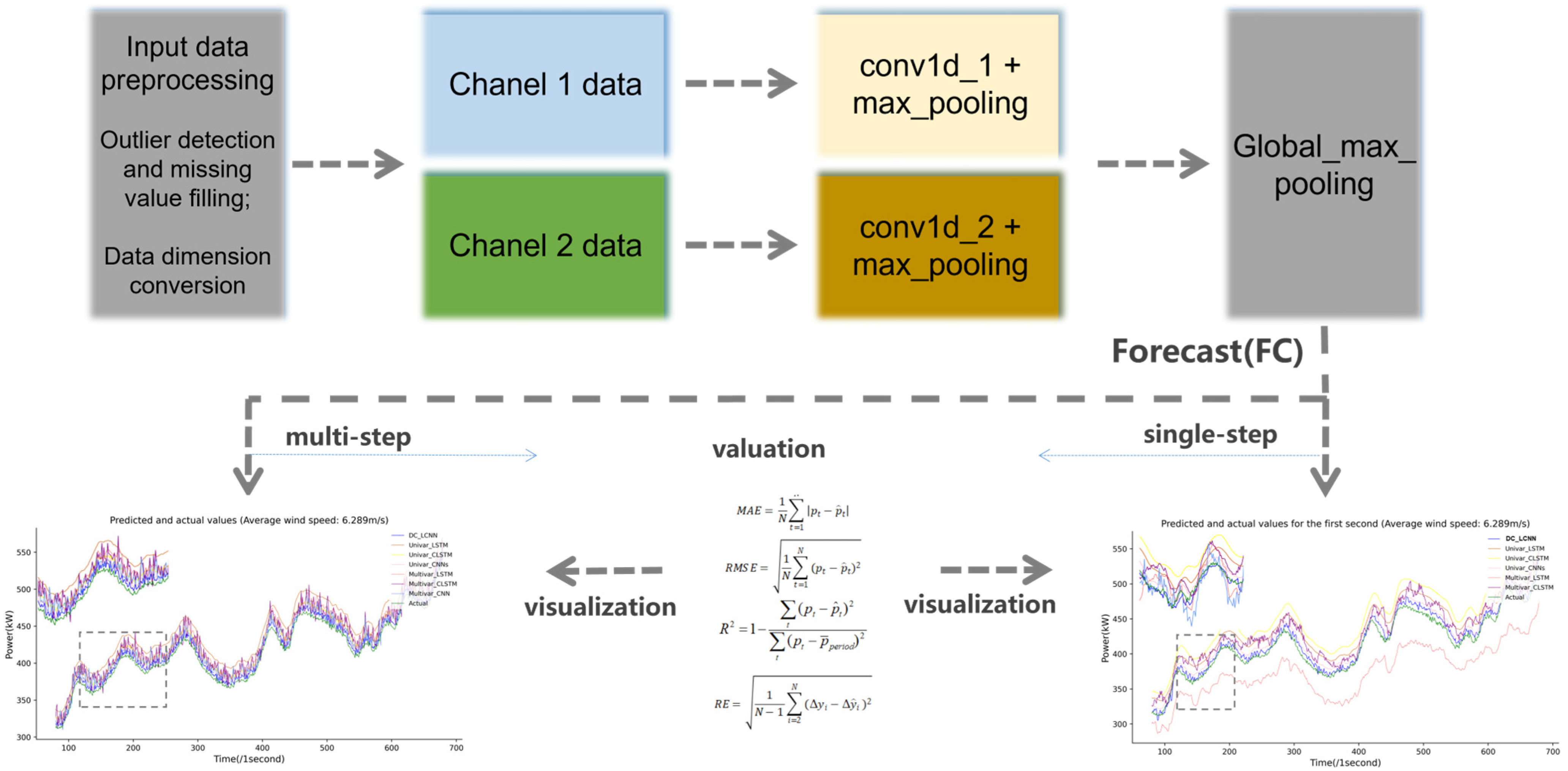
2. Proposed Methodology
- 1.
- Data Preprocessing
- 2.
- Input Layer
- 3.
- Forecasting model
- 4.
- Performance evaluation and visualization
2.1. 1D Convolutional Neural Network
2.2. Proposed Light Convolutional Neural Network Architecture
3. Evaluation Indexes
4. Case Study
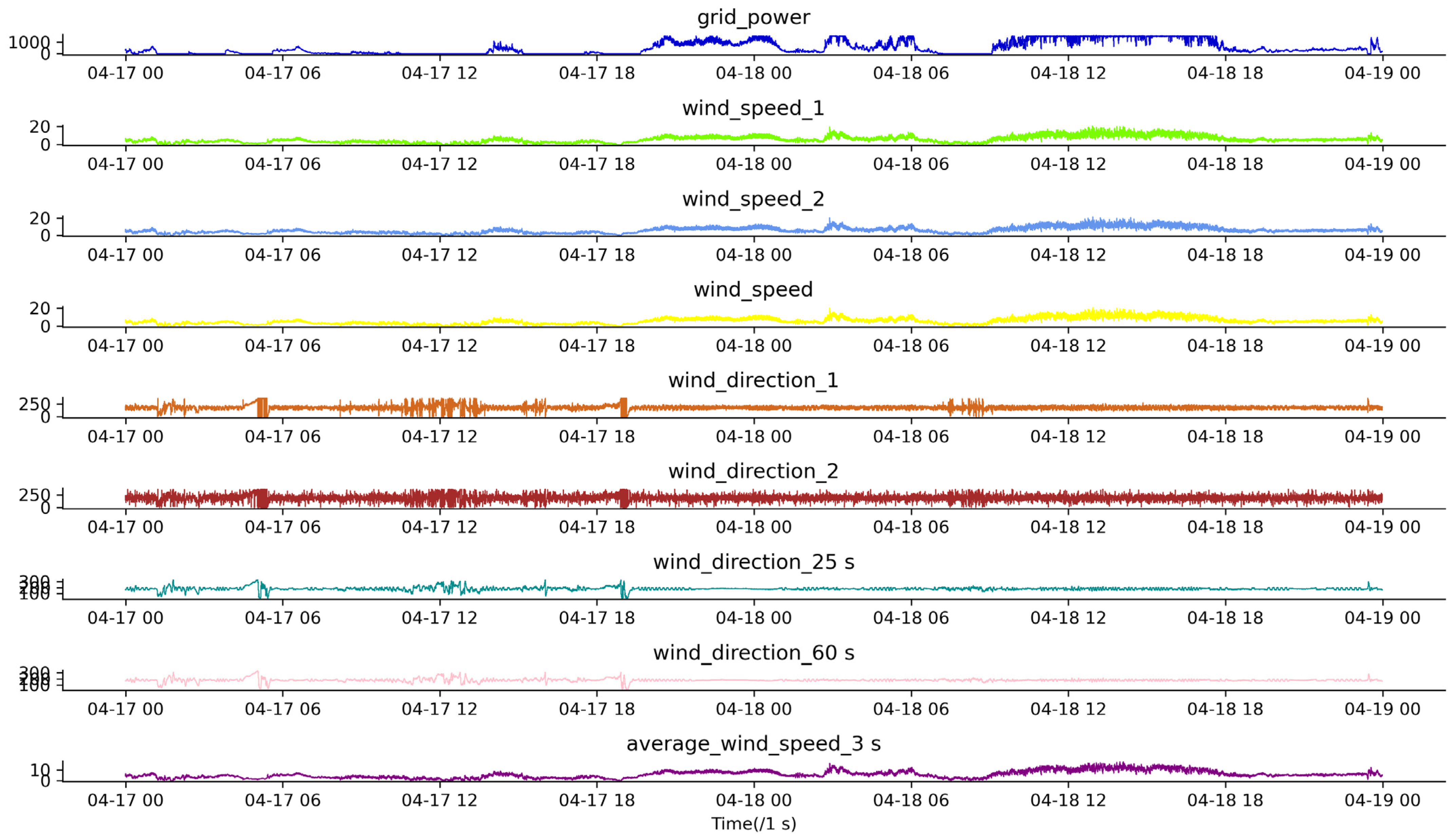
4.1. Experimental Data
4.2. Experimental
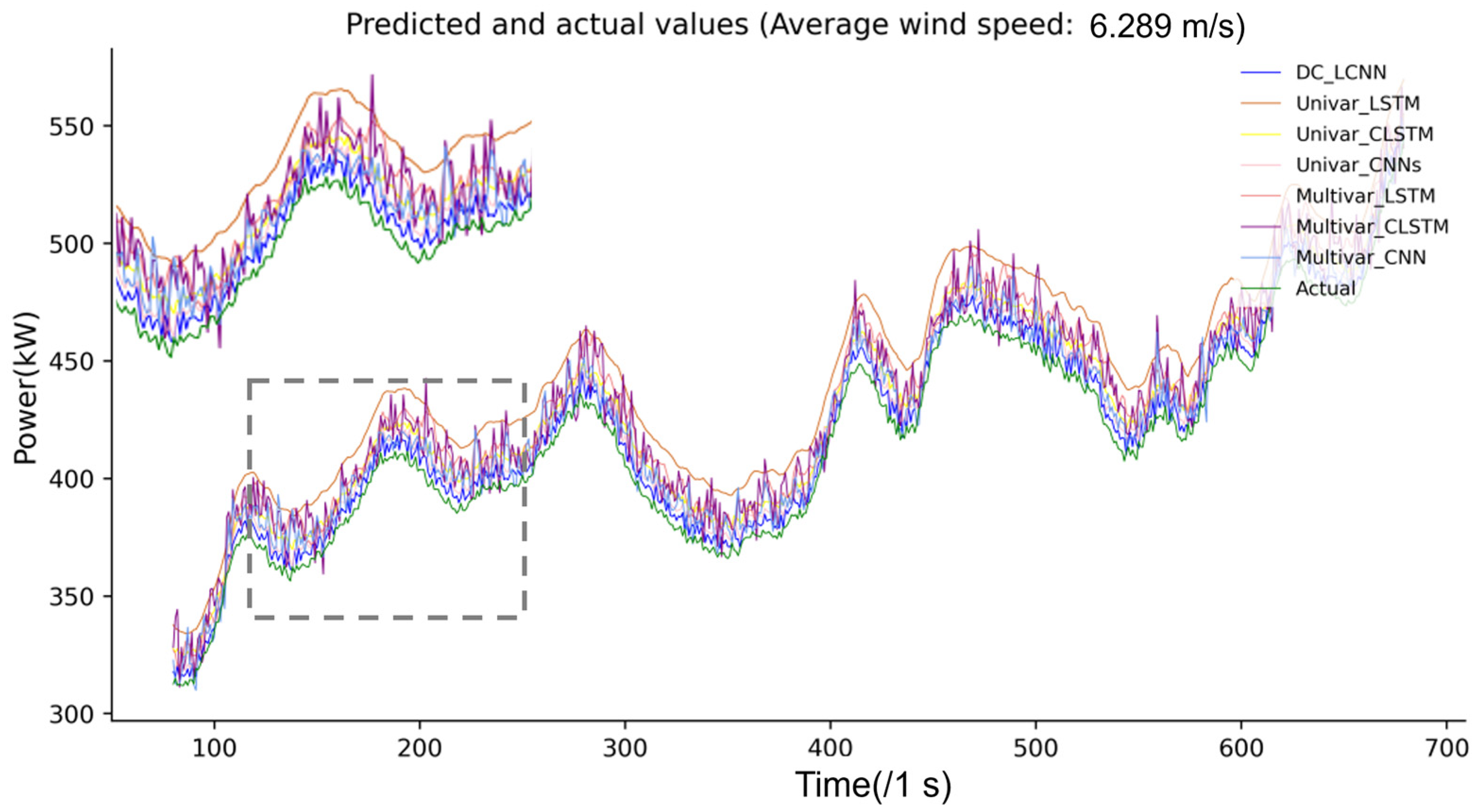
4.2.1. Experiments on Single-Step Second Wind Power Forecasting Task
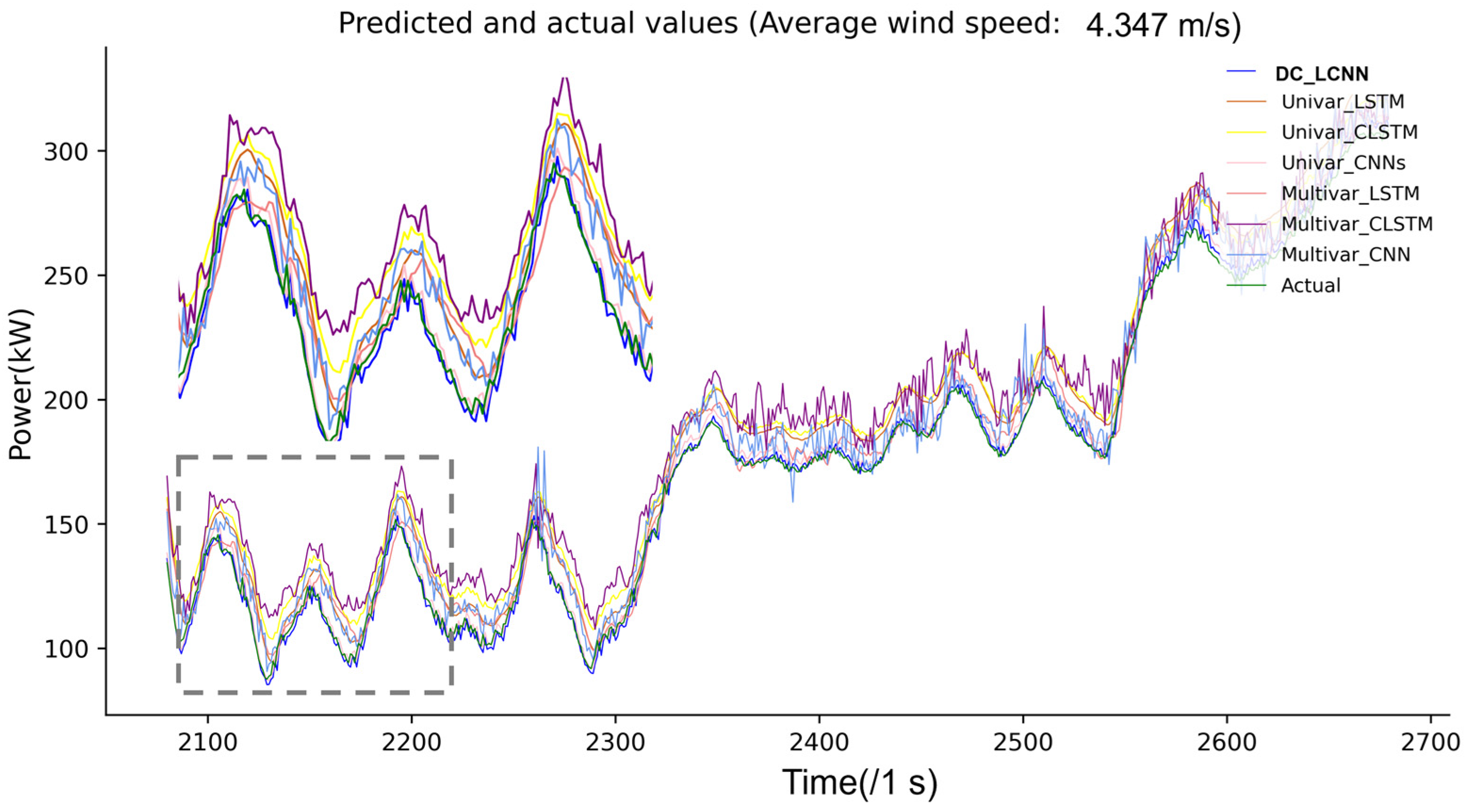
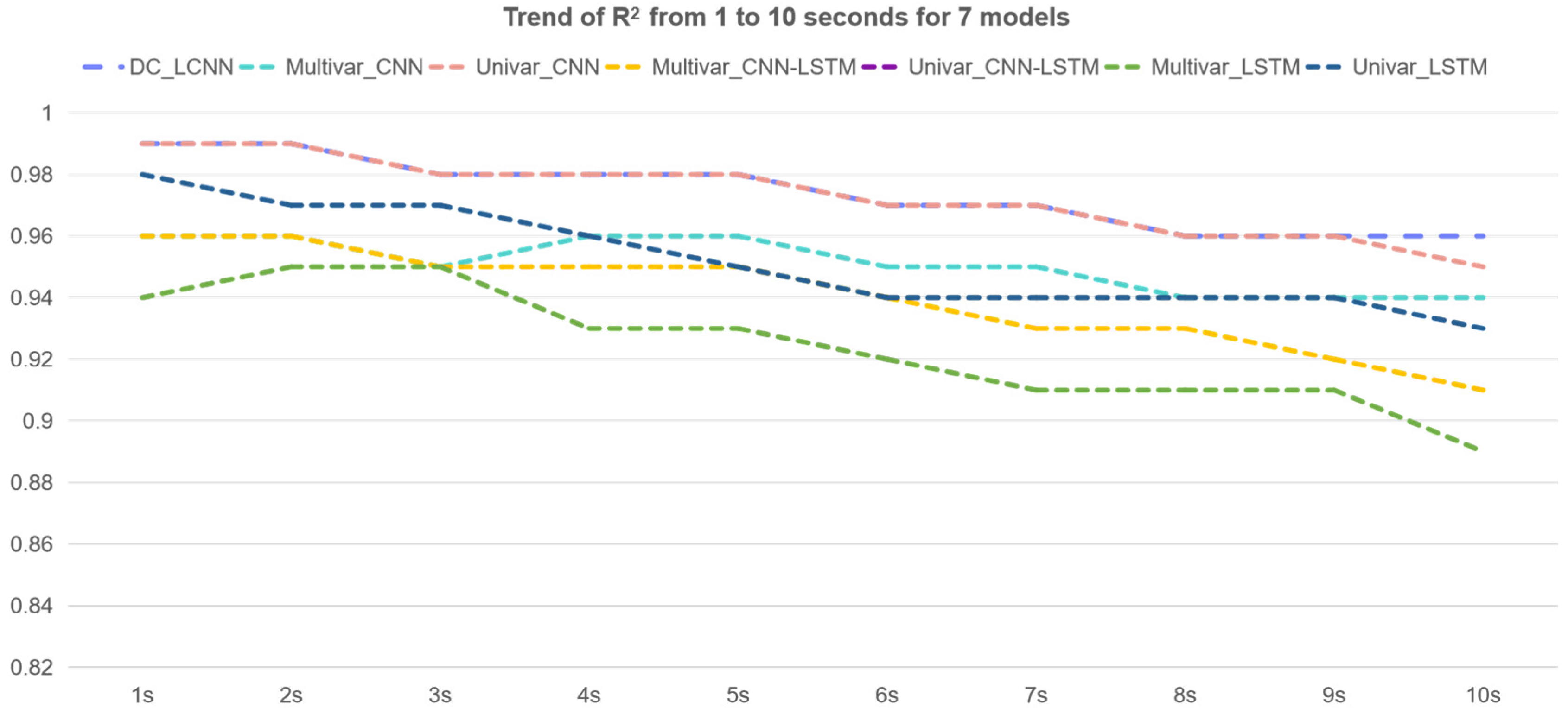
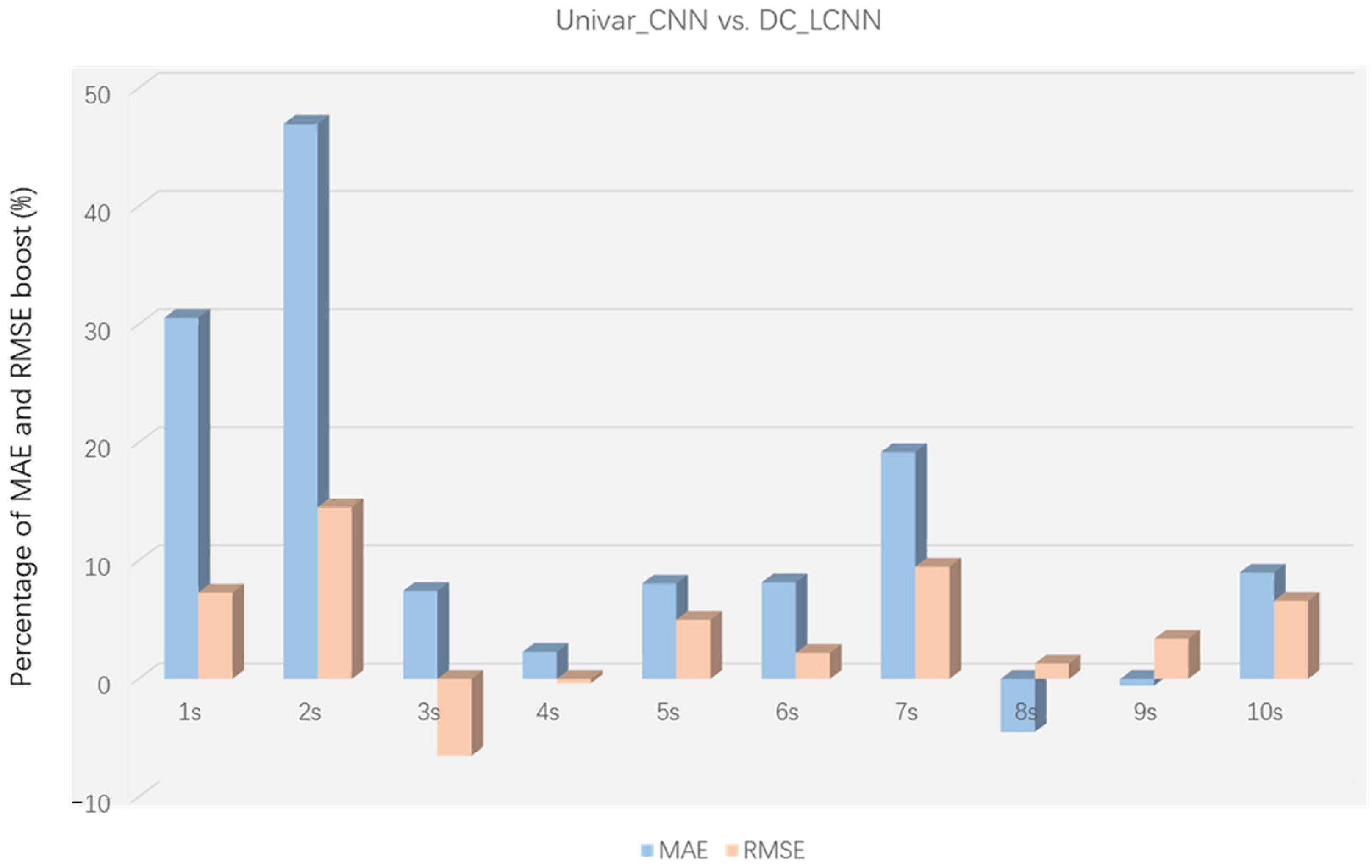
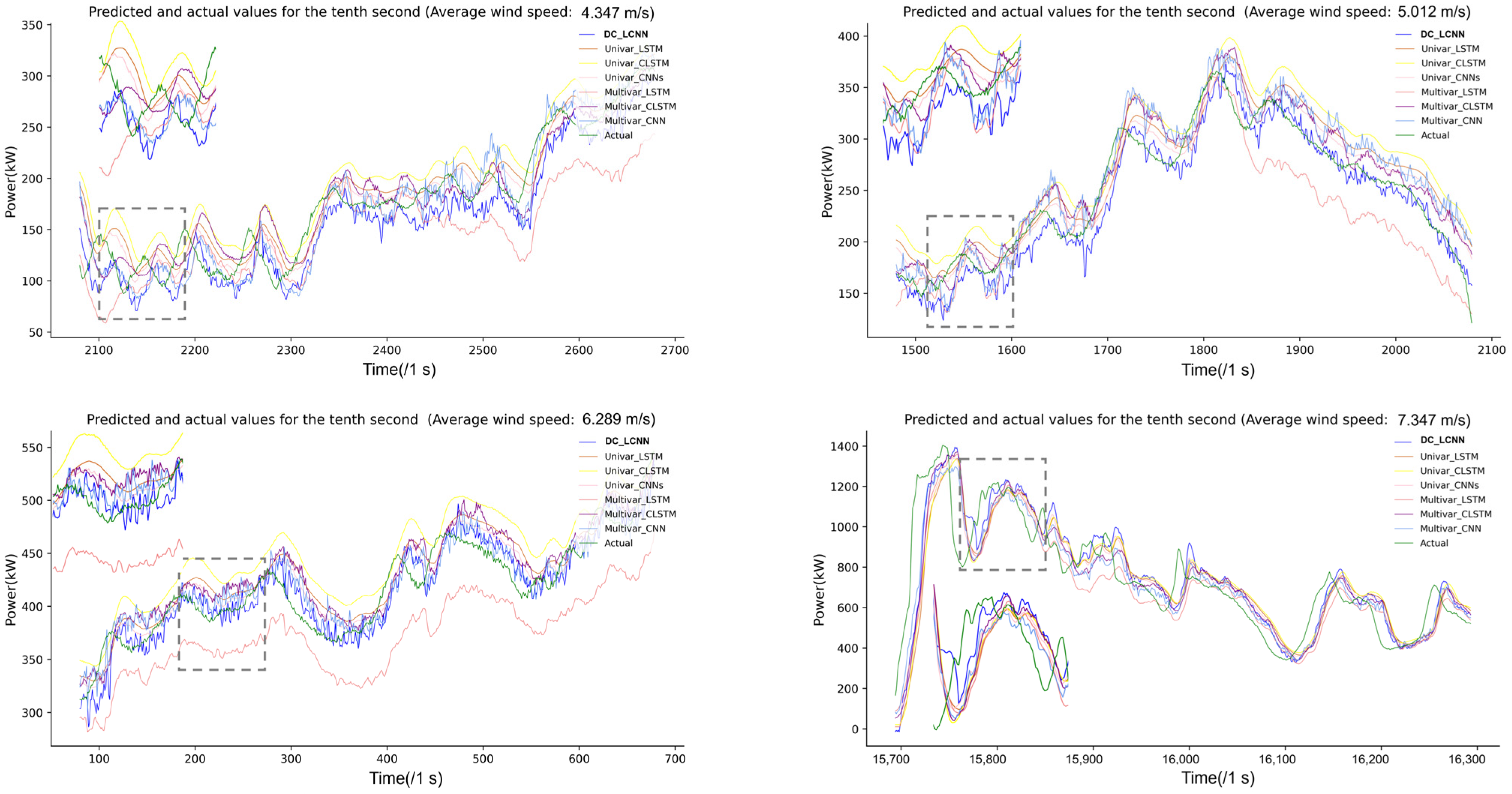
4.2.2. Multi-Step Second Wind Power Forecasting Task Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chandran, V.; Patil, C.K.; Manoharan, A.M.; Ghosh, A.; Sumithra, M.; Karthick, A.; Rahim, R.; Arun, K. Wind power forecasting based on time series model using deep machine learning algorithms. Mater. Today Proc. 2021, 47, 115–126. [Google Scholar] [CrossRef]
- Dolatabadi, A.; Jadidbonab, M.; Mohammadi-Ivatloo, B. Short-term scheduling strategy for wind-based energy hub: A hybrid stochastic/IGDT approach. IEEE Trans. Sustain. Energy 2019, 10, 438–448. [Google Scholar] [CrossRef]
- Hu, T.; Wu, W.; Guo, Q.; Sun, H.; Shi, L.; Shen, X. Very short-term spatial and temporal wind power forecasting: A deep learning approach. CSEE J. Power Energy Syst. 2020, 6, 434–443. [Google Scholar]
- Zhao, W.; Wei, Y.-M.; Su, Z. One day ahead wind speed forecasting: A resampling-based approach. Appl. Energy 2016, 178, 886–901. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Q.; Wang, J.; Liu, Z.; Shahidehpour, M.; Xue, Y. Combined Active and Reactive Power Control of Wind Farms based on Model Predictive Control. IEEE Trans. Energy Convers. 2017, 32, 1177–1187. [Google Scholar] [CrossRef]
- Gazafroudi, A.S. Assessing the impact of load and renewable energies’ uncertainty on a hybrid system. Int. J. Energy Power Eng. 2016, 5, 1–8. [Google Scholar] [CrossRef][Green Version]
- Jung, J.; Broadwater, R.P. Current status and future advances for wind speed and power forecasting. Renew. Sustain. Energy Rev. 2014, 31, 762–777. [Google Scholar] [CrossRef]
- Li, Z.; Han, J.; Song, Y. On the forecasting of high-frequency financial time series based on ARIMA model improved by deep learning. J. Forecast. 2020, 39, 1081–1097. [Google Scholar] [CrossRef]
- Biyun, C.; Suifeng, W.; Yongjun, Z.; Ping, H. Wind power prediction model considering smoothing effects. In Proceedings of the 2013 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC 2013), Kowloon, Hong Kong, 8–11 December 2013; pp. 1–4. [Google Scholar]
- Hu, J.; Heng, J.; Wen, J.; Zhao, W. Deterministic and probabilistic wind speed forecasting with de-noising-reconstruction strategy and quantile regression based algorithm. Renew. Energy 2020, 162, 1208–1226. [Google Scholar] [CrossRef]
- Ma, L.; Luan, S.; Jiang, C.; Liu, H.; Zhang, Y. A review on the forecasting of wind speed and generated power. Renew. Sustain. Energy Rev. 2009, 13, 915–920. [Google Scholar]
- Shi, Z.; Liang, H.; Dinavahi, V. Direct interval forecast of uncertain wind power based on recurrent neural networks. IEEE Trans. Sustain. Energy 2018, 9, 1177–1187. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.-W.; Li, Y.-F. Wind speed forecasting method based on deep learning strategy using empirical wavelet transform, long short term memory neural network and Elman neural network. Energy Convers. Manag. 2018, 156, 498–514. [Google Scholar] [CrossRef]
- Ren, X.; Zhang, F.; Zhu, H.; Liu, Y. Quad-kernel deep convolutional neural network for intra-hour photo-voltaic power forecasting. Appl. Energy 2022, 323, 119682. [Google Scholar] [CrossRef]
- Moharm, K.; Eltahan, M.; Elsaadany, E. Wind speed forecast using LSTM and biLSTM algorithms over gabal el-zayt wind farm. In Proceedings of the 2020 International Conference on Smart Grids and Energy Systems (SGES), Perth, Australia, 23–26 November 2020; pp. 922–927. [Google Scholar]
- Yu, R.; Gao, J.; Yu, M.; Lu, W.; Xu, T.; Zhao, M.; Zhang, J.; Zhang, R.; Zhang, Z. LSTM-EFG for wind power forecasting based on sequential correlation features. Future Gener. Comput. Syst. 2019, 93, 33–42. [Google Scholar] [CrossRef]
- Xin, Z.; Liu, X.; Zhang, H.; Wang, Q.; An, Z.; Liu, H. An enhanced feature extraction based long short-term memory neural network for wind power forecasting via considering the missing data reconstruction. Energy Rep. 2024, 11, 97–114. [Google Scholar] [CrossRef]
- Sun, Y.; He, J.; Ma, H.; Yang, X.; Xiong, Z.; Zhu, X.; Wang, Y. Online chatter detection considering beat effect based on Inception and LSTM neural networks. Mech. Syst. Signal Process. 2023, 184, 109723. [Google Scholar] [CrossRef]
- Yang, T.; Li, B.; Xun, Q. LSTM-attention-embedding model-based day-ahead prediction of photovoltaic power output using Bayesian optimization. IEEE Access 2019, 7, 171471–171484. [Google Scholar] [CrossRef]
- Shu, X.; Zhang, L.; Sun, Y.; Tang, J. Host–parasite: Graph LSTM-in-LSTM for group activity recognition. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 663–674. [Google Scholar] [CrossRef]
- Wang, H.-Z.; Li, G.-Q.; Wang, G.-B.; Peng, J.-C.; Jiang, H.; Liu, Y.-T. Deep learning based ensemble approach for probabilistic wind power forecasting. Appl. Energy 2017, 188, 56–70. [Google Scholar] [CrossRef]
- Acikgoz, H.; Budak, U.; Korkmaz, D.; Yildiz, C. WSFNet: An efficient wind speed forecasting model using channel attention-based densely connected convolutional neural network. Energy 2021, 233, 121121. [Google Scholar] [CrossRef]
- Houran, M.A.; Bukhari, S.M.S.; Zafar, M.H.; Mansoor, M.; Chen, W. COA-CNN-LSTM: Coati optimization algorithm-based hybrid deep learning model for PV/wind power forecasting in smart grid applications. Appl. Energy 2023, 349, 121638. [Google Scholar] [CrossRef]
- Nguyen, T.H.T.; Phan, Q.B. Hourly day ahead wind speed forecasting based on a hybrid model of EEMD, CNN-Bi-LSTM embedded with GA optimization. Energy Rep. 2022, 8, 53–60. [Google Scholar] [CrossRef]
- Li, N.; Dong, J.; Liu, L.; Li, H.; Yan, J. A novel EMD and causal convolutional network integrated with Transformer for ultra short-term wind power forecasting. Int. J. Electr. Power Energy Syst. 2023, 154, 109470. [Google Scholar] [CrossRef]
- Yuan, P.; Jiao, Y.; Li, J.; Xia, Y. A densely connected causal convolutional network separating past and future data for filling missing PM2.5 time series data. Heliyon 2024, 10, e24738. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Liu, Y.; Li, Q.; Wang, T.; Chu, F. Short-term multi-step wind power forecasting based on spatio-temporal correlations and transformer neural networks. Energy Convers. Manag. 2023, 283, 116916. [Google Scholar] [CrossRef]
- Zhu, J.; Su, L.; Li, Y. Wind power forecasting based on new hybrid model with TCN residual modification. Energy AI 2022, 10, 100199. [Google Scholar] [CrossRef]
- Gong, M.; Yan, C.; Xu, W.; Zhao, Z.; Li, W.; Liu, Y.; Li, S. Short-term wind power forecasting model based on temporal convolutional network and Informer. Energy 2023, 283, 129171. [Google Scholar] [CrossRef]
- Islam, M.; Barua, P.; Rahman, M.; Ahammed, T.; Akter, L.; Uddin, J. Transfer learning architectures with fine-tuning for brain tumor classification using magnetic resonance imaging. Healthc. Anal. 2023, 4, 100270. [Google Scholar] [CrossRef]
- Mirza, A.F.; Mansoor, M.; Usman, M.; Ling, Q. Hybrid Inception-embedded deep neural network ResNet for short and medium-term PV-Wind forecasting. Energy Convers. Manag. 2023, 294, 117574. [Google Scholar] [CrossRef]
- Zhang, F.; Li, P.C.; Gao, L.; Liu, Y.Q.; Ren, X.Y. Application of autoregressive dynamic adaptive (ARDA) model in real-time wind power forecasting. Renew. Energy 2021, 169, 129–143. [Google Scholar] [CrossRef]







| The Layers for DC_LCNN | Parameters of Each Layer |
|---|---|
| Conv1D_1(Input 1) | Filters = 32, kernel size = 2, stride = 1, activation = ‘relu’, padding = ‘same’ |
| MaxPooling1D_1 | Kernel size = 2, stride = 1 |
| Conv1D_2(Input 2) | Filters = 32, kernel size = 2, stride = 1, activation = ‘relu’, padding = ‘same’ |
| MaxPooling1D_2 | Kernel size = 2, stride = 1 |
| Dropout_2 | Rate = 0.1 |
| Conv1D_3 | Filters = 32 (single-step forecasting), filters = 10 (multi-step forecasting), kernel size = 2, stride = 1, activation = ‘relu’, padding = ‘same’ |
| Global_MaxPooling1D_1 | - |
| Dense | Neurons = 1 (single-step forecasting); neurons = 10 (multi-step forecasting) |
| Others | Epoches = 150; EarlyStopping:monitor = ‘mse’; batch size = 24, patience = 5; min_delta = 0.0001 |
| Models | The Layers | Parameters of Each Layer |
|---|---|---|
| Univar_LSTM and Multivar_LSTM | LSTM | Neurons = 32 (single-step forecasting); neurons = 20 (multi-step forecasting); activation = ‘relu’; return_sequences = True |
| Flatten | - | |
| Dense | Neurons = 128 (single-step forecasting); neurons = 400 (multi-step forecasting); activation = ‘relu’; kernel_regularizer = l2 (0.0001) | |
| Dense | Neurons = 1 (single-step forecasting); neurons = 10 (multi-step forecasting) | |
| Univar_CNN-LSTM and Multivar_CNN-LSTM | Conv1D | Filters = 32; kernel size = 2; stride = 1; activation = ‘relu; padding = ‘same’ |
| MaxPooling1D | Kernel size = 2; stride = 1 | |
| LSTM | Neurons = 128 (single-step forecasting); neurons = 320 (multi-step forecasting); activation = ‘relu’; return_sequences = True | |
| Flatten | - | |
| Dense | Neurons = 128 (single-step forecasting); neurons = 320 (multi-step forecasting); activation = ‘relu’; kernel_regularizer = l2 (0.0001) | |
| Dense | Neurons = 1 (single-step forecasting); neurons = 10 (multi-step forecasting) | |
| Univar_CNN | Conv1D_1 | Filters = 32; kernel size = 2; stride = 1; activation = ‘relu’; padding = ‘same’ |
| MaxPooling1D_1 | Kernel size = 2; stride = 1 | |
| Conv1D_2 | Filters = 32; kernel size = 2; stride = 1; activation = ‘relu’; padding = ‘same’ | |
| MaxPooling1D_2 | kernel size = 2; stride = 1 | |
| Flatten | - | |
| Dense | Neurons = 64 (single-step forecasting); neurons = 160 (multi-step forecasting); activation = ‘relu’; kernel_regularizer = l2 (0.0001) | |
| Dense | Neurons = 1 (single-step forecasting); neurons = 10 (multi-step forecasting) | |
| Multivar_CNN | Conv1D_1 | Filters = 32; kernel size = 2; stride = 1; activation = ‘relu’; padding = ‘same’ |
| MaxPooling1D_1 | Kernel size = 2; stride = 1 | |
| Conv1D_2 | Filters = 32; kernel size = 2; stride = 1; activation = ‘relu’; padding = ‘same’ | |
| MaxPooling1D_2 | Kernel size = 2; stride = 1 | |
| Flatten | - | |
| Dropout | Rate = 0.1 | |
| Dense | Neurons = 64 (single-step forecasting); neurons = 160 (multi-step forecasting); activation = ‘relu’; kernel_regularizer = l2 (0.0001) | |
| Dense | Neurons = 1 (single-step forecasting); neurons = 10 (multi-step forecasting) | |
| Other public parameters | Epoches = 150; EarlyStopping:monitor = ‘mse’; batch size = 120 (single-stepforecasting); batch size = 120 (multi-stepforecasting); patience = 5; min_delta = 0.0001 | |
| Model | MAE (kW) | RMSE (kW) | R2 |
|---|---|---|---|
| DC1_LCNN | 8.959 | 9.779 | 1 |
| DC2_LCNN | 13.862 | 19.233 | 0.98 |
| DC_LCNN | 4.625 | 6.061 | 1 |
| Model | MAE (kW) | RMSE (kW) | R2 |
|---|---|---|---|
| DC_CNN (FC) | 8.959 | 9.779 | 1 |
| DC_LCNN | 4.625 | 6.061 | 1 |
| Model | Training Time (s) | Forecast Time (s) | Forecast Time for Each Step (s) |
|---|---|---|---|
| DC_CNN (FC) | 161.768 | 1.235 | 1.235/17,280 |
| DC_LCNN | 80.696 | 0.916 | 0.916/17,280 |
| Model | MAE (kW) | RMSE (kW) | Maximum Absolute Error (kW) |
|---|---|---|---|
| Persistence | 3.258 | 5.920 | 153.60 |
| DC_LCNN | 4.625 | 6.061 | 86.32 |
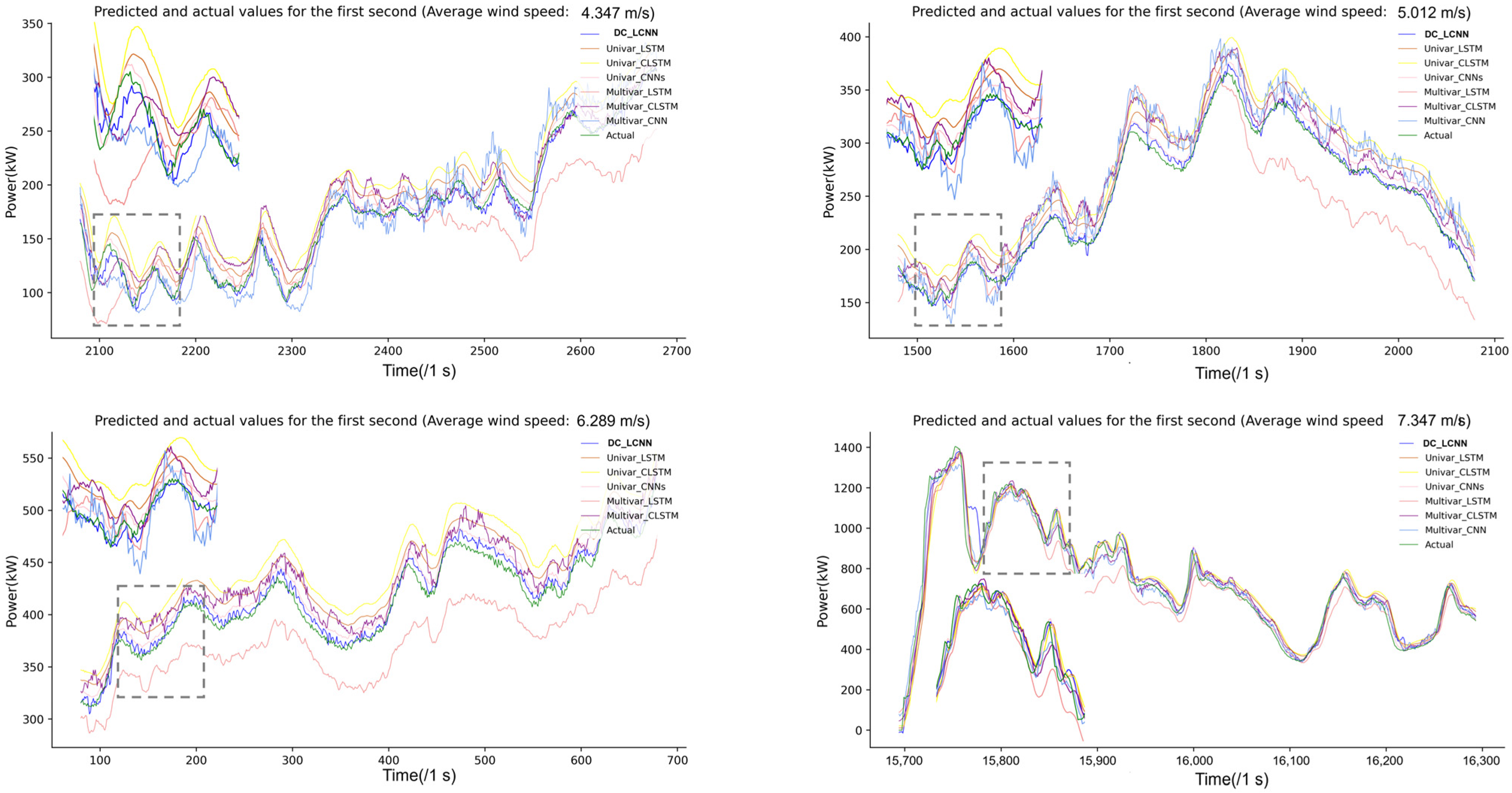
| Model | MAE (kW) (Figure 4a,b) | RMSE (kW) (Figure 4a,b) | MAE (kW) (Figure 4c,d) | RMSE (kW) (Figure 4c,d) |
|---|---|---|---|---|
| Persistence | 13.32 | 20.91 | 66.36 | 88.48 |
| DC_LCNN | 10.16 | 14.17 | 49.17 | 62.27 |
| Indexes | Univar_LSTM | Multivar_LSTM | Univar_CNN-LSTM | Multivar_CNN-LSTM | Univar_CNN | Multivar_CNN | DC_LCNN |
|---|---|---|---|---|---|---|---|
| MAE | 22.99 | 15.40 | 14.23 | 17.11 | 7.776 | 11.57 | 4.625 |
| RMSE | 24.81 | 17.86 | 14.89 | 19.27 | 8.97 | 17.49 | 6.06 |
| R2 | 0.98 | 0.99 | 0.99 | 0.99 | 1.0 | 0.99 | 1.0 |
| RE | 4.52 | 4.89 | 4.62 | 10.24 | 4.91 | 7.84 | 4.47 |
| Models | Indexes | Time Steps (s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| DC1_LCNN | MAE | 9.023 | 10.66 | 12.12 | 13.82 | 19.44 | 13.77 | 15.91 | 18.86 | 20.84 | 20.52 |
| RMSE | 14.27 | 18.40 | 21.30 | 21.86 | 30.82 | 28.34 | 29.91 | 34.95 | 38.50 | 38.90 | |
| R2 | 0.99 | 0.99 | 0.98 | 0.98 | 0.97 | 0.97 | 0.97 | 0.95 | 0.95 | 0.93 | |
| DC2_LCNN | MAE | 21.92 | 26.38 | 27.71 | 21.84 | 35.65 | 39.36 | 40.77 | 35.43 | 34.92 | 35.68 |
| RMSE | 31.15 | 39.18 | 39.62 | 37.24 | 49.56 | 48.93 | 49.82 | 49.94 | 49.12 | 50.73 | |
| R2 | 0.96 | 0.95 | 0.95 | 0.95 | 0.92 | 0.92 | 0.91 | 0.92 | 0.92 | 0.91 | |
| DC_LCNN | MAE | 7.311 | 7.617 | 13.65 | 13.69 | 12.29 | 16.29 | 14.30 | 18.94 | 19.34 | 19.62 |
| RMSE | 11.68 | 14.88 | 21.21 | 21.57 | 22.43 | 27.59 | 27.45 | 32.68 | 33.59 | 35.83 | |
| R2 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.97 | 0.97 | 0.96 | 0.96 | 0.96 | |
| Models | Indexes | Time Steps (s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| DC_LCNN (FC) | MAE | 30.20 | 15.54 | 24.50 | 23.46 | 29.09 | 22.38 | 32.77 | 26.10 | 35.44 | 31.88 |
| RMSE | 31.95 | 21.77 | 28.78 | 29.57 | 35.22 | 31.88 | 40.97 | 38.04 | 45.84 | 45.09 | |
| R2 | 0.97 | 0.98 | 0.97 | 0.97 | 0.96 | 0.97 | 0.94 | 0.95 | 0.93 | 0.93 | |
| DC_LCNN | MAE | 7.311 | 7.617 | 13.65 | 13.69 | 12.29 | 16.29 | 14.30 | 18.94 | 19.34 | 19.62 |
| RMSE | 11.68 | 14.88 | 21.21 | 21.57 | 22.43 | 27.59 | 27.45 | 32.68 | 33.59 | 35.83 | |
| R2 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.97 | 0.97 | 0.96 | 0.96 | 0.96 | |
| Model | Training Time (s) | Forecast Time (s) | Forecast Time for Each Step (s) |
|---|---|---|---|
| DC_CNN (FC) | 246.478 | 1.420 | 1.420/17,280 |
| DC_LCNN | 158.923 | 0.981 | 0.981/17,280 |
| Models | Indexes | Time Steps (s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| Univar_LSTM | MAE | 22.04 | 22.76 | 23.66 | 23.84 | 23.45 | 25.56 | 25.31 | 25.90 | 26.99 | 26.99 |
| RMSE | 25.68 | 28.16 | 30.55 | 32.49 | 34.07 | 37.35 | 38.85 | 41.12 | 43.54 | 44.89 | |
| R2 | 0.98 | 0.97 | 0.97 | 0.96 | 0.95 | 0.94 | 0.94 | 0.94 | 0.94 | 0.93 | |
| RE | 4.41 | 4.73 | 4.96 | 5.11 | 5.20 | 5.28 | 5.36 | 5.40 | 5.43 | 5.47 | |
| Multivar_LSTM | MAE | 33.87 | 30.13 | 30.35 | 35.04 | 32.46 | 34.71 | 36.02 | 36.52 | 34.65 | 39.35 |
| RMSE | 43.35 | 38.61 | 39.70 | 46.73 | 43.99 | 47.98 | 50.43 | 52.01 | 50.23 | 56.54 | |
| R2 | 0.94 | 0.95 | 0.95 | 0.93 | 0.93 | 0.92 | 0.91 | 0.91 | 0.91 | 0.89 | |
| RE | 4.94 | 5.29 | 5.48 | 5.55 | 5.62 | 5.69 | 5.74 | 5.8 | 5.8 | 5.87 | |
| Univar_CNN- LSTM | MAE | 32.25 | 31.13 | 33.02 | 32.53 | 32.65 | 32.87 | 35.32 | 34.87 | 34.03 | 37.87 |
| RMSE | 34.97 | 35.16 | 37.93 | 39.04 | 40.07 | 42.35 | 45.38 | 46.74 | 47.79 | 51.67 | |
| R2 | 0.96 | 0.96 | 0.95 | 0.95 | 0.94 | 0.94 | 0.93 | 0.93 | 0.92 | 0.91 | |
| RE | 4.49 | 4.74 | 4.94 | 5.13 | 5.19 | 5.37 | 5.38 | 5.40 | 5.46 | 5.52 | |
| Multivar_CNN-LSTM | MAE | 18.94 | 19.03 | 17.71 | 20.76 | 21.01 | 21.11 | 22.99 | 22.93 | 23.55 | 26.19 |
| RMSE | 24.77 | 26.21 | 26.67 | 30.06 | 31.84 | 33.66 | 36.65 | 37.85 | 40.40 | 43.30 | |
| R2 | 0.98 | 0.98 | 0.98 | 0.97 | 0.97 | 0.96 | 0.95 | 0.95 | 0.94 | 0.94 | |
| RE | 6.17 | 6.37 | 6.54 | 6.62 | 6.58 | 6.58 | 6.47 | 6.57 | 6.45 | 6.49 | |
| Univar_CNN | MAE | 10.53 | 14.37 | 14.75 | 13.97 | 13.37 | 17.74 | 17.70 | 18.08 | 19.23 | 21.56 |
| RMSE | 12.60 | 17.41 | 19.83 | 21.65 | 23.62 | 28.20 | 30.33 | 33.11 | 34.78 | 38.36 | |
| R2 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.97 | 0.97 | 0.96 | 0.96 | 0.95 | |
| RE | 4.22 | 4.64 | 5.10 | 5.27 | 5.30 | 5.40 | 5.49 | 5.49 | 5.64 | 5.68 | |
| Multivar_CNN | MAE | 22.46 | 22.24 | 25.00 | 21.92 | 22.74 | 23.84 | 24.84 | 28.51 | 27.70 | 26.88 |
| RMSE | 33.14 | 32.78 | 36.57 | 34.36 | 34.57 | 37.26 | 39.06 | 42.24 | 42.80 | 43.51 | |
| R2 | 0.96 | 0.96 | 0.95 | 0.96 | 0.96 | 0.95 | 0.95 | 0.94 | 0.94 | 0.94 | |
| RE | 9.87 | 10.09 | 10.29 | 10.19 | 10.12 | 10.40 | 10.33 | 9.89 | 9.90 | 9.80 | |
| DC_LCNN | MAE | 7.311 | 7.617 | 13.65 | 13.69 | 12.29 | 16.29 | 14.30 | 18.94 | 19.34 | 19.62 |
| RMSE | 11.68 | 14.88 | 21.21 | 21.57 | 22.43 | 27.59 | 27.45 | 32.68 | 33.59 | 35.83 | |
| R2 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.97 | 0.97 | 0.96 | 0.96 | 0.96 | |
| RE | 4.13 | 4.59 | 4.96 | 5.05 | 5.20 | 6.25 | 5.21 | 5.39 | 5.75 | 5.74 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Ren, X.; Liu, Y. A Refined Wind Power Forecasting Method with High Temporal Resolution Based on Light Convolutional Neural Network Architecture. Energies 2024, 17, 1183. https://doi.org/10.3390/en17051183
Zhang F, Ren X, Liu Y. A Refined Wind Power Forecasting Method with High Temporal Resolution Based on Light Convolutional Neural Network Architecture. Energies. 2024; 17(5):1183. https://doi.org/10.3390/en17051183
Chicago/Turabian StyleZhang, Fei, Xiaoying Ren, and Yongqian Liu. 2024. "A Refined Wind Power Forecasting Method with High Temporal Resolution Based on Light Convolutional Neural Network Architecture" Energies 17, no. 5: 1183. https://doi.org/10.3390/en17051183
APA StyleZhang, F., Ren, X., & Liu, Y. (2024). A Refined Wind Power Forecasting Method with High Temporal Resolution Based on Light Convolutional Neural Network Architecture. Energies, 17(5), 1183. https://doi.org/10.3390/en17051183






