Battery Management in Electric Vehicle Routing Problems: A Review

Abstract

The adoption of electric vehicles (EVs) has gained significant momentum in recent years as a sustainable alternative to traditional internal combustion engine vehicles. However, the efficient utilization of batteries in EVs, coupled with the growing demand for sustainable transportation, has posed complex challenges for battery management in the context of electric vehicle routing problems in a broad sense, which includes vehicle routing problems, team orienteering problems, and arc routing problems, all of them using EVs. This paper presents a comprehensive review of the state-of-the-art approaches, methodologies, and strategies for battery management in each of the aforementioned optimization problems. We explore the relevant factors influencing battery performance and the interplay between routing, charging, and energy management in the context of EVs. The paper also discusses the advances in optimization algorithms, vehicle-to-grid integration, and intelligent decision-making techniques aimed at enhancing the range, reliability, and sustainability of EV operations. Key findings indicate a paradigm shift towards addressing uncertainties, dynamic conditions, and synchronization challenges inherent in large-scale and dynamic routing problems within the context of EVs that require efficient battery management.

1. Introduction

In numerous countries worldwide, the adoption of EVs is driven by the pursuit of sustainable and environmentally conscious transportation and citizens’ mobility [1]. These vehicles offer a promising alternative to traditional internal combustion engine vehicles (CVs), aligning seamlessly with global objectives to reduce carbon emissions and enhance energy efficiency [2]. However, the integration of EVs into daily transportation and mobility operations, presents significant challenges, particularly within the context of electric vehicle routing problems (EVRPs) [3]. The limitations posed by the low energy density of batteries and the efficient utilization of limited available resources can be counted among these difficulties [4]. The low energy density of batteries limits the range and endurance of EVs, constraining their practicality for long-distance travel and necessitating frequent recharging. Malik et al. [5] listed the primary variables that impacted an electric battery’s range: increasing vehicle mass as energy density rose, temperature, air resistance, rolling resistance, battery cooling charge, traffic, speed, and cabin air conditioning. Numerous scholars worked on intelligent algorithm-based function-monitoring and control schemes. Since it was not feasible to directly examine their essential microscopic physical factors, they provided the foundation for extending the driving ranges of electric batteries [6]. Furthermore, the intermittent nature of renewable energy sources such as solar and wind increases the challenge of matching energy supply with demand. However, addressing these challenges through innovative approaches to resource management and utilization can produce substantial benefits [7]. Efficient utilization of limited resources, such as optimizing charging and discharging schedules for EVs based on grid demand and energy pricing, can enhance overall system reliability and resilience.

Simultaneously, in the pursuit of sustainability, cities worldwide are experiencing a growing adoption of EVs for citizens’ mobility [8] and last-mile logistics [9]. Governmental initiatives in regions such as Europe, North America, and Asia endorse zero-emission technologies, despite challenges such as driving range anxiety, extended recharging durations, insufficient infrastructure, and limited financial incentives hindering widespread EV acceptance in urban environments [10]. In urban settings, fleet-based activities related to freight transportation and citizens’ mobility necessitate efficient coordination to reduce costs, operational times, energy consumption, and environmental impacts. This coordination is often modeled as mathematical optimization problems, including vehicle routing problems (VRPs) [11,12,13], arc routing problems (ARPs) [14,15], and team orienteering problems (TOPs) [16,17], which are NP-hard even in basic forms. Heuristic-based algorithms [18] and simulation-based approaches are crucial tools for addressing real-life instances compounded by operational complexities, including driving range constraints and lengthy recharging times. 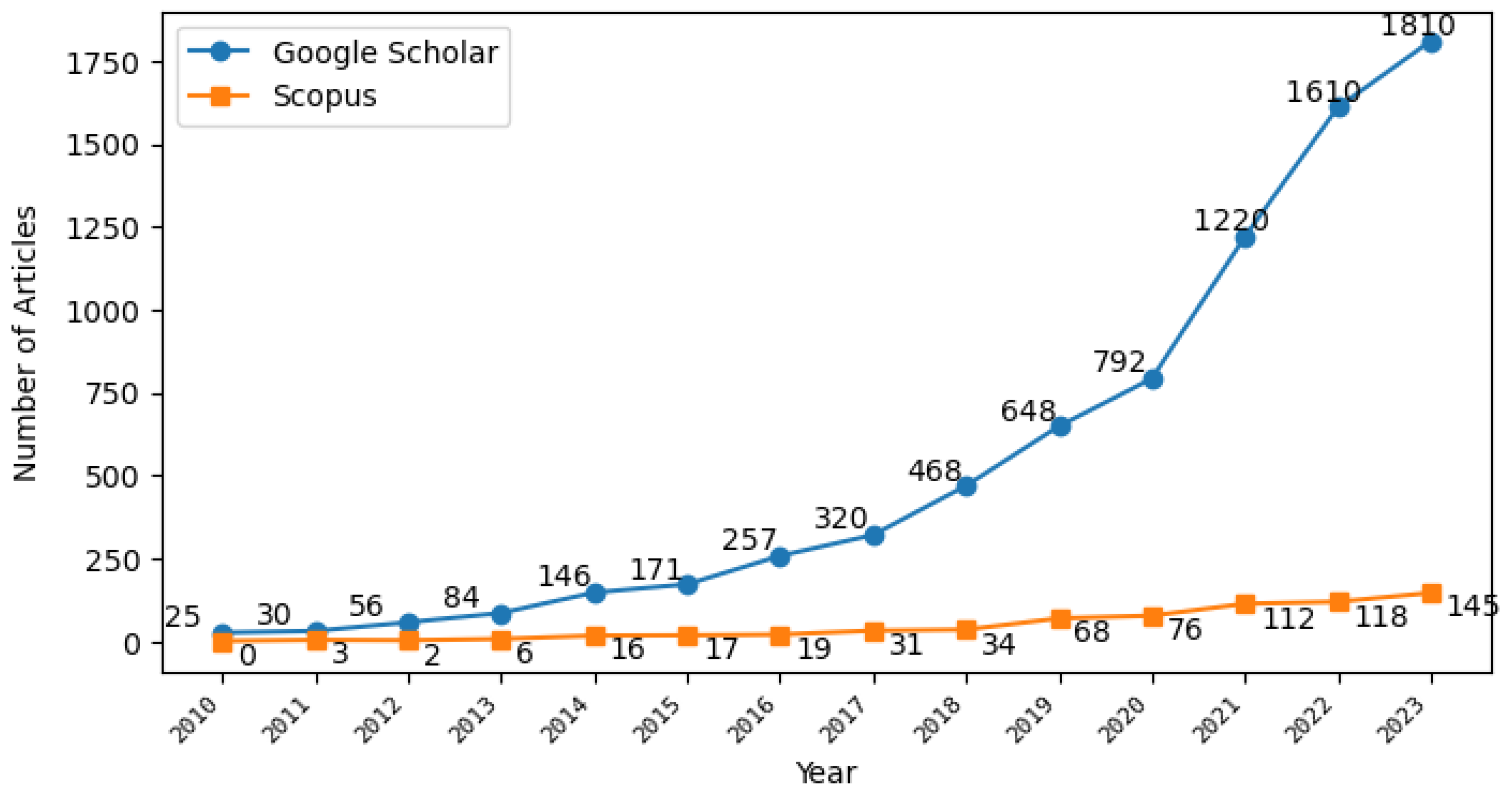To assess the increasing interest in EVRPs, Figure 1 illustrates the annual number of published documents in Google Scholar and Scopus databases containing the expression ‘electric vehicle’ AND ‘routing problem’ in their title or abstract. The time series highlights a continuous rise in interest within the scientific community over the last decade.

This paper explores cutting-edge approaches, methodologies, and strategies dedicated to battery management within EVRPs. In response to the increasing demand for sustainable transportation and mobility, the development of efficient concepts, strategies, and algorithmic solutions becomes indispensable. Hence, the paper analyzes key factors influencing battery performance within EVs, examining the relationship between routing decisions, charging infrastructure, and energy management. Moreover, recent advancements in optimization algorithms, the integration of vehicle-to-grid systems, and intelligent decision-making techniques are also discussed. The manuscript not only identifies critical gaps in the existing knowledge but also outlines promising future directions for research. The main contributions include a detailed literature review on various electric vehicle routing problems. Thus, our research extends to the connection between sustainable transportation and the expanding utilization of electric vehicles.

As can be observed in the studies by Zhou and Zhao [19] or Kucukoglu et al. [3], the majority of review papers on electric vehicle routing problems have been exclusively focused on EVRPs, creating gaps in the literature regarding other types of challenges related to routing and electric vehicles. As a result, our research contributes with a comprehensive review of electric vehicle routing problems, encompassing not only EVRPs but also various models of electric arc routing problems (EARPs) and electric team orienteering problems (ETOPs). This includes a thorough discussion of the algorithms employed for their resolution. In contrast to most of the reviews, such as those mentioned earlier, particular emphasis is placed on models under uncertainty or dynamic conditions, reflecting the increasing necessity for the development of more realistic models. Strategies such as synchronized routing or agile optimization are also discussed, providing researchers with insights into novel approaches applicable to numerous emerging problems.

The remainder of the paper is structured as follows. Section 2 offers an exploration of various EVRPs. This section serves as a foundational overview, establishing the context for the subsequent discussions on routing challenges specific to EVs. The challenges in routing based on electric vehicles are examined in Section 3. Section 4 discusses battery logistics, providing a comprehensive analysis of the logistical considerations surrounding the efficient utilization and management of batteries in the context of EVs. This includes an exploration of key factors influencing battery performance and the interplay between routing decisions, charging infrastructure, and energy management. Section 5, Section 6 and Section 7 form a trilogy of comprehensive reviews, addressing the EVRP, ETOP, and EARP, respectively. Each section dissects the existing literature, synthesizing the state-of-the-art approaches, methodologies, and strategies specific to the corresponding routing problem. The subsequent sections, namely Section 8, Section 9, Section 10 and Section 11, analyze electric routing under different conditions and paradigms. From simheuristics to learning-based approaches, agile optimization, and synchronized routing, each section explores novel strategies and techniques aimed at optimizing electric routing efficiency. Section 12 provides a glimpse into the future trends in the domain of electric vehicle routing. It explores emerging concepts, technologies, and methodologies that could define the future of electric routing problems. Finally, Section 13 summarizes the findings from each section and provides some future research lines.

2. Different Routing Problems in Transportation

Routing problems refer to a class of optimization problems concerned with finding the most efficient routes or sequences of visits for vehicles tasked with delivering goods or services. These problems typically involve determining optimal paths through a network of nodes (e.g., customers, locations) while satisfying various constraints such as vehicle capacity, time windows, and distance or time limitations. The scientific literature contains a variety of problem families, depending on the particulars of the transportation activity. VRPs, ARPs, and TOPs are some of the most prevalent. Even in their most basic forms, these problems are NP-hard and can model scenarios involving both road and aerial EVs. Therefore, in this paper, we will concentrate our review on these three problem families, aiming to provide insights into their formulation, solution methods, and applications in the context of EVs and battery management. We provide a short explanation on each of the routing combinatorial optimization problems that are considered in this article: the EVRP, the EARP, and the ETOP.

2.1. The Vehicle Routing Problem with EVs

Starting with the VRP, this is a well-known challenge that consists in finding optimal routes for a fleet of vehicles, while meeting the demands of customers [20]. Therefore, in VRP problem-solving, the objective is to design routes for cargo vehicles with minimal transportation costs, facilitating the distribution of goods between a central depot and a set of customers. Each customer, assigned to a single product, places demands on the depot, where a fleet of capacitated vehicles (which are typically considered homogeneous) are stationed. These vehicles visit customers to fulfill their demands, eventually returning to the central depot once all customers are served. The optimization goal is minimizing distribution costs, such as travel distance or time-based expenses, to efficiently serve all customers without surpassing the loading capacity of the vehicles. Key constraints include ensuring each route starts and ends at the depot, each customer is visited precisely once by a single vehicle, and the total demand within a route does not exceed the vehicle’s capacity. 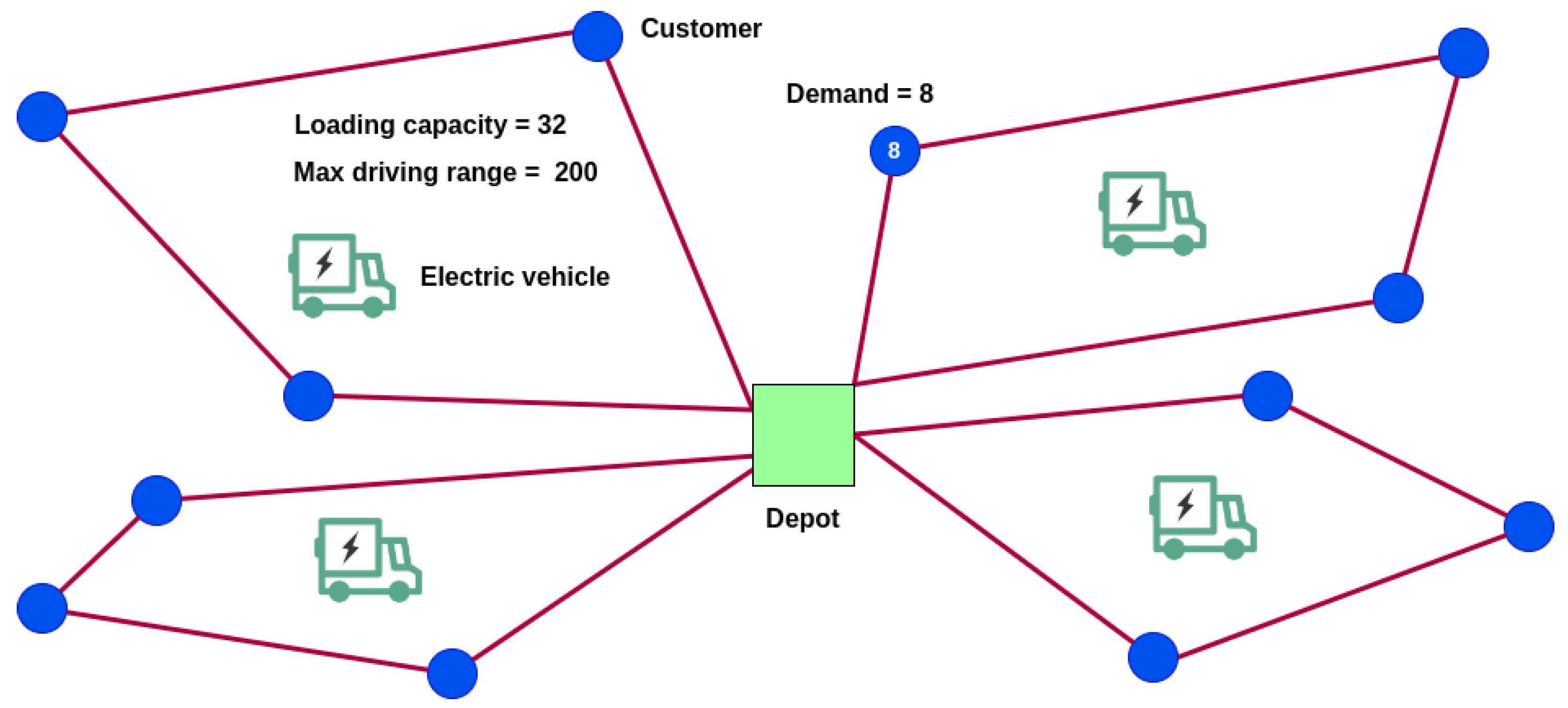Figure 2 provides a representation of a simple EVRP scenario, featuring a single depot, multiple customers with specific demands, a homogeneous fleet of EVs with a maximum loading capacity and maximum driving range due to battery constraints, and associated travel costs between any pair of nodes. EVRPs involve planning routes tailored for electric commercial vehicles in the logistics services sector. The fundamental constraints of these EVRPs mainly revolve around managing the variable energy levels upon reaching a customer, initiating routes with a full charge, identifying permissible charging points, and accounting for travel, charging, and service times. To extend the mathematical model of the VRP to the EVRP, new constraints must be incorporated into the original problem. The model is based on the one described by Dantzig and Ramser [21], represented as an undirected graph $G=(V,E)$. Additional constraints ensure that exactly m vehicles depart from the depot and that each client is visited exactly once. Further constraints are introduced to eliminate sub-tours. To model this problem with EVs, an additional constraint needs to be added to the model. This constraint restricts the total travel distance throughout the tour to the EV’s maximum battery capacity $L_h$. This constraint can be observed in Equation (1), where $c_{ij}$ refers to the battery cost of traveling from node i to node j, and $x_{ij}^h$ is a binary variable, that takes value 1 if vehicle h traverses the edge $(i,j)\in E$.

$$\begin{array}{cc}\hfill & \sum _{(i,j)\in E}{x}_{ij}^h·c_{ij}\le L_h\forall h\in \{1,2,\dots ,m\}\hfill \end{array}$$

(1)

2.2. The Team Orienteering Problem with EVs

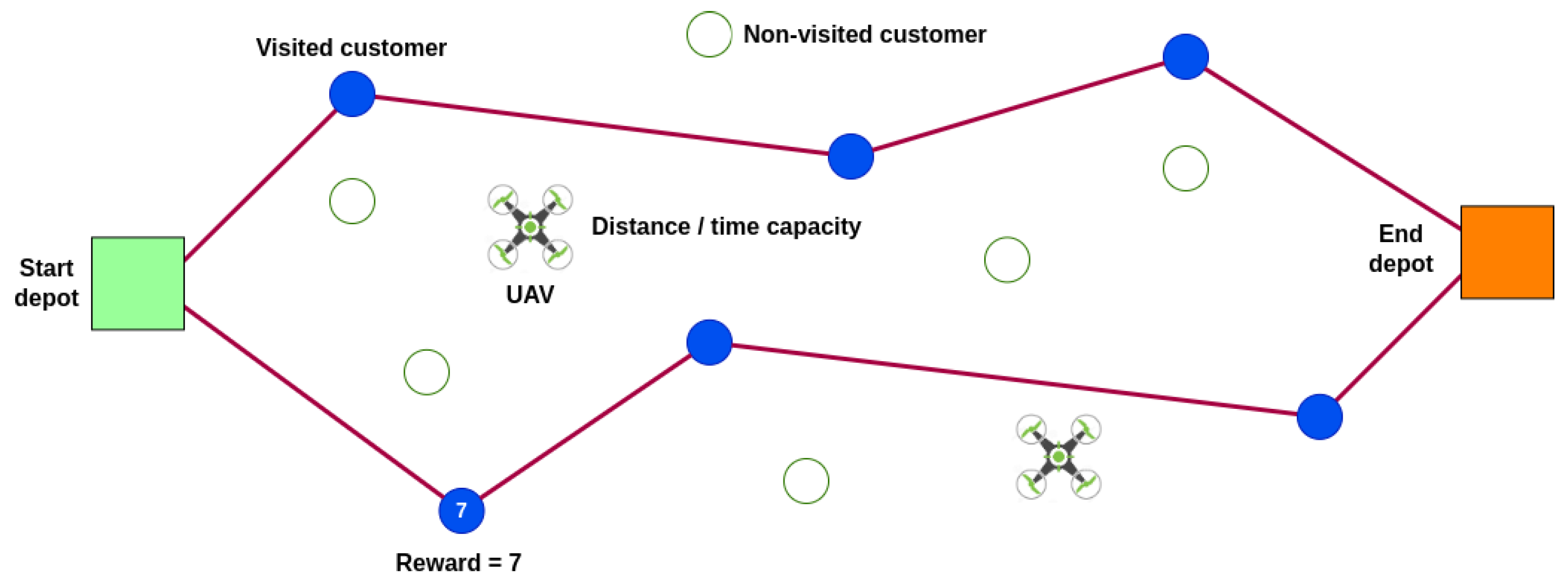
In contrast to VRPs, where visiting all customers is obligatory, in a TOP the necessity to skip certain customers arises frequently. This is driven by restrictions on fleet size and the maximum allowable route length. Each customer in a typical TOP contributes a reward, collected upon the initial visit. Consequently, solving a TOP involves maximizing the total reward collected by a fixed fleet of vehicles as they visit a set of customers. Unlike the basic version of VRPs, cargo constraints are typically not considered in the basic version of TOPs. When employing EVs, operational constraints stem from their limited driving range. As a consequence, not all customers can be visited, as depicted in Figure 3, which illustrates a basic ETOP. Regarding this problem, a similar process is employed to transform the TOP into an ETOP. The model, based on the one described by Lin [22] incorporates a maximum time per route restriction in addition to the constraints of an EVRP. Contrary to the VRP, the TOP is modeled as a directed graph $G=(N,A)$, where N stands for the set of nodes and A represents the set of arcs. Given that this maximum time restriction does not need to be related to the vehicle’s maximum traversable distance, the constraint given by Equation (2) needs to be considered.

$$\begin{array}{cc}\hfill & \sum _{(i,j)\in A}{x}_{ij}^h·c_{ij}\le L_h\forall h\in \{1,2,\dots ,m\}\hfill \end{array}$$

(2)

The integration of unmanned aerial vehicles (UAVs) in cargo transportation by parcel delivery companies has introduced a new dimension to TOP systems. UAVs, constrained by load capacity and battery-driven driving range, pose operational challenges that necessitate careful route planning to avoid failures. Addressing questions of battery recharge locations and timing, a concern not exclusive to UAVs but pertinent to all types of EVs has become a critical aspect of TOP operations [23].

2.3. The Arc Routing Problem with EVs

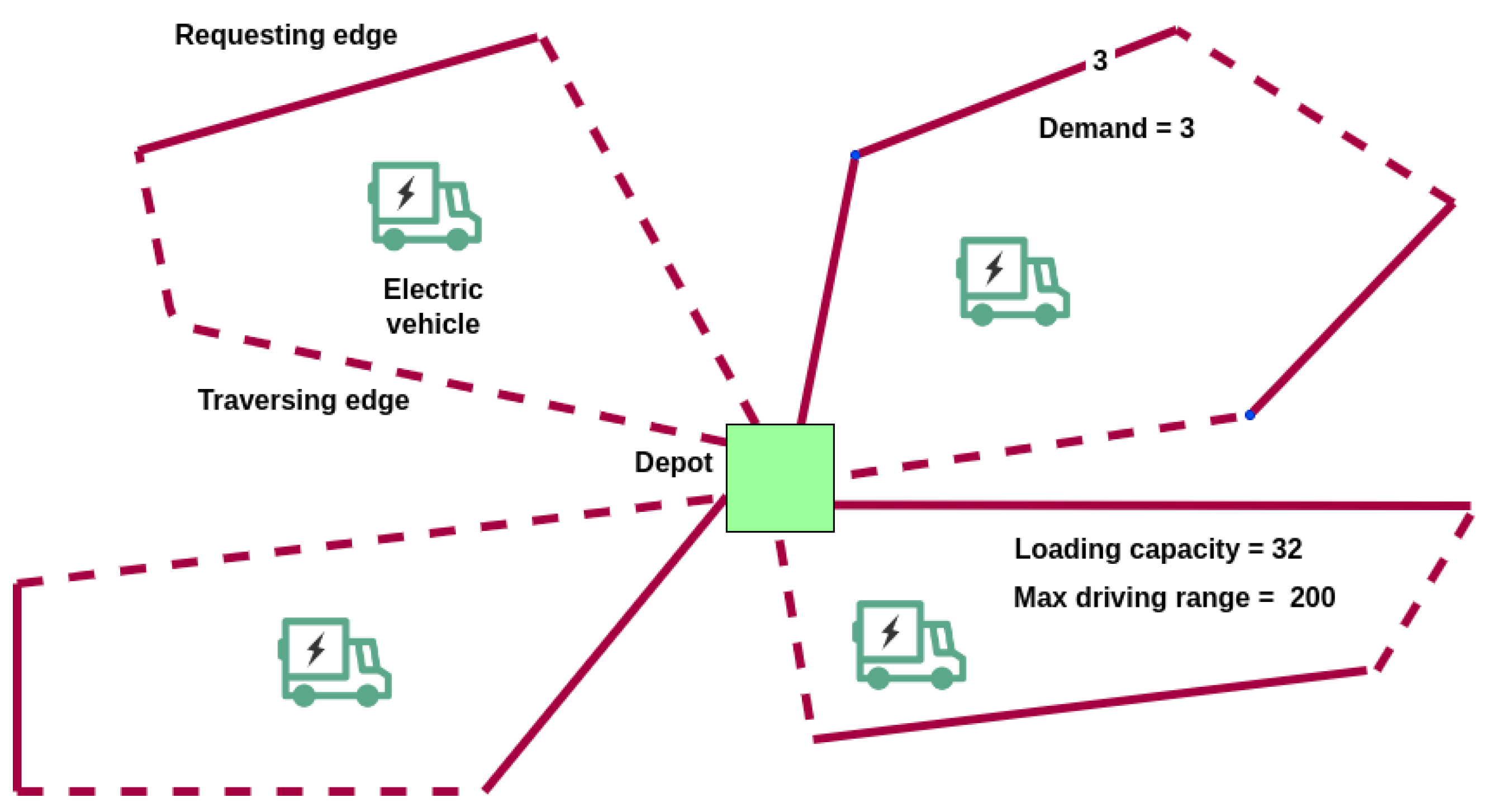
The ARP can be modeled on an undirected or a directed graph, where a subset of requesting edges or arcs holds positive demand that requires fulfillment by a fleet of capacitated vehicles, typically treated as homogeneous. The remaining edges, designated as traversing edges, bear null demand. Hence, the visitation of these traversing edges is non-mandatory and they are only used in case they allow a vehicle to visit a requesting edge. In Figure 4, an illustration of a simple EARP is presented. The goal of the EARP lies in finding a set of routes that cover the demands of all requesting edges (arcs), aiming to minimize overall costs. These costs can be delineated in terms of expenditures, traveled distance, or time. Each route is covered by a single capacitated EV, commencing and concluding the journey at a singular depot. The return journey can utilize the same edges (arcs) employed during the outward trip or opt for different ones. It is imperative that the total demand from all requesting edges (arcs) within each route does not surpass the capacity of the assigned vehicle. Furthermore, every edge (arc) with a positive demand must be serviced exactly once. In addition, EVs have to consider a finite driving range, typically quantified in terms of time or distance, which must be adhered to. To transform the ARP into an EARP, whenever this problem is represented with an undirected graph, the constraint given by Equation (1) needs to be added to the problem. Likewise, in the case of a directed graph, the constraint given by Equation (2) would be added. The basic model can be found in Van Bevern et al. [24].

3. Challenges in Routing Based on Electric Vehicles

One of the most significant challenges EVs face in comparison to conventional vehicles is their limited driving, which restricts their utility as transportation tools [25]. Not only battery capacity plays an important role there, but weather conditions and even the so-called range anxiety can impact the distance an EV user is able or willing to travel [26,27]. Moreover, recharging stations are not as integrated into the transport network as they should be, largely due to the historical dominance that traditional combustion vehicles have had in the market, which makes EV users deviate from their destination and take longer routes in order to recharge their vehicles. This effect is called distance inconvenience, and although these situations make EVs less effective and more difficult to refuel in comparison to traditional vehicles, considerable effort has been put into addressing these issues, driven by the increasing demand for EVs.

Given their possible scarcity, determining the location of new recharging stations is a critical problem needed to address, to incentivize and enhance the use of EVs, but numerous variables come into play when planning one. For instance, it is essential to take into account the type of facility or its capacity. Additionally, the location of the recharging station should vary depending on factors such as the number of planned stations or even traffic patterns, making this problem inherently complex to solve. It is considered a specific case of the facility location problem, and most models either aim to minimize the maximum cost of travel, which is referred to as the center problem, or minimize the average cost of travel, known as the median problem. Depending on the refueling demand, the challenges associated with determining recharging station locations can be categorized into flow-based and node-based models [28]. Flow-based models operate under the assumption that EV drivers who travel for distances longer than their driving range need to recharge the battery during the journey. Consequently, recharging stations have to be strategically located so that the distance between two consecutive charging stations does not exceed the driving range of the EV. On the other hand, node-based models are more suitable for people who prefer to recharge their EVs near their home or workplace while they are resting, working, or engaging in other activities. Thus, for example, Ahangar et al. [29] conducted a case study in one district of Tehran and implemented a bi-objective mixed-integer linear mathematical model solved by the Lagrangian relaxation method where limited budget, disruption in charging stations and customer dissatisfaction (measured by the traveling distance to charge EVs) are considered. However, node-based and flow-based models are not the only two approaches used to model this problem as can be seen in Jung et al. [30], where the authors propose a method based on vehicle trajectory to solve the problem for electric taxis routing. Those two studies highlight the adaptability and diversity of methods used to tackle the challenges associated with the different features of EVs and recharging infrastructure planning.

Moreover, it is also important to consider that the arrival time of the EVs to the stations and their level of charge is not usually known, resulting in significant variations in the time EVs spend there and creating problems related to the scheduling and capacity of the station. For instance, García-Álvarez et al. [31] propose hybrid metaheuristics and a memetic algorithm to solve the scheduling problem for a large set of EVs, both the dynamic and the static problem. For the metaheuristic part, a greedy randomized adaptive search procedure (GRASP) is used. Results show that these methods outperform others like genetic algorithms (GAs) and a method based on priority rules (EVS). According to our findings, there are a lot of variables that need to be taken into account when planning new stations. Still, in order to improve routing problems of non-conventional vehicles, stations should offer easy public access and be situated at safe and highly visible locations [32]. This will raise public awareness of the benefits of EVs and bring confidence to users about the reliability of the recharging network.

4. Battery Logistics

Ever since lithium-ion batteries were first brought to market, incredible progress has been made in terms of increasing energy density, lowering costs, and raising overall performance. The development of EVs, which present a viable option for lowering dependence on gas and reducing vehicle emissions, has been aided by these developments in battery technology. As a result, almost all of the big manufacturers have started producing EVs, and several countries have plans to get rid of CVs over the next few decades. 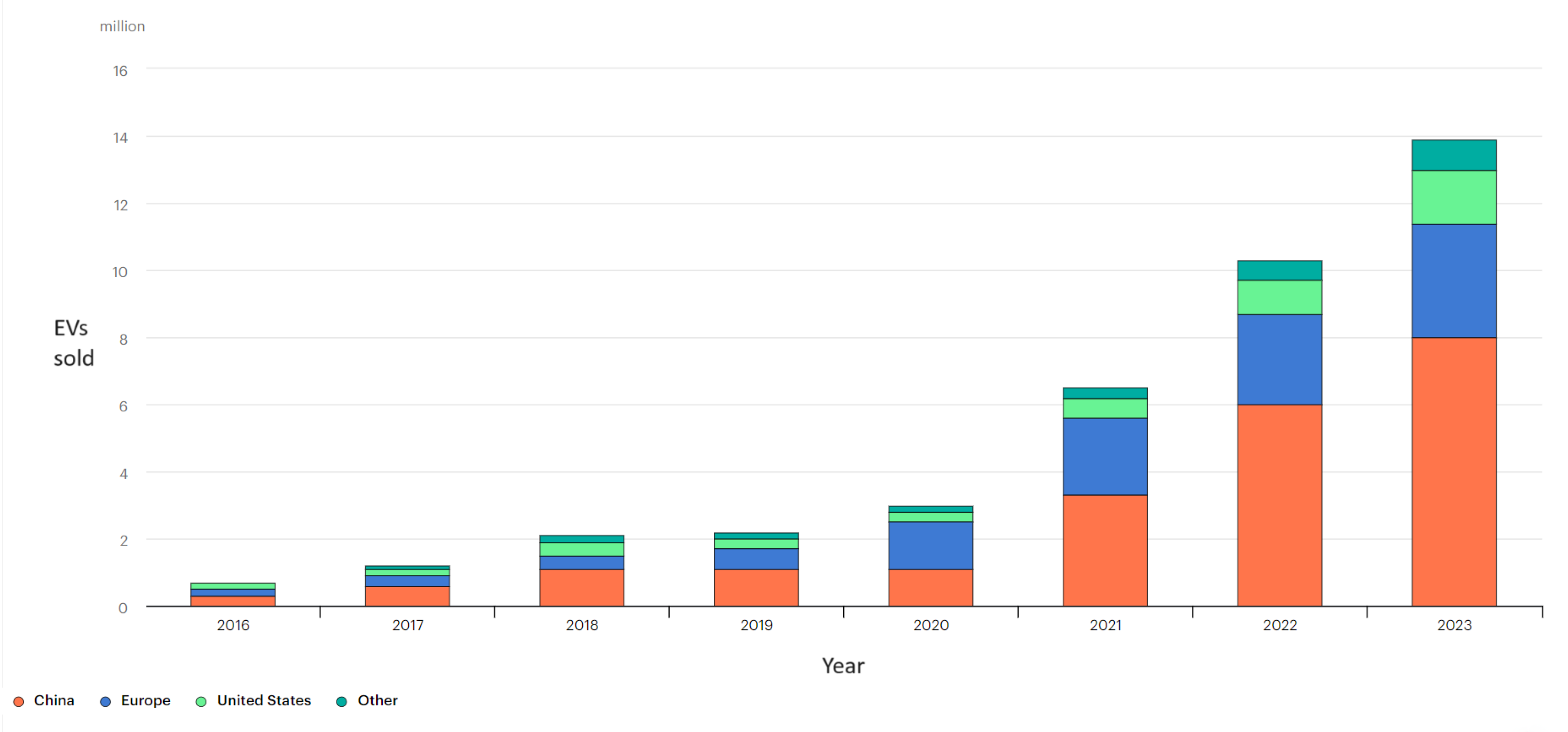Figure 5 shows the evolution in the sales of EVs by country, provided by the International Energy Agency. However, there are still a lot of challenges to overcome, especially in the area of battery technology [33]. This section delves into the essential prerequisites and difficulties of battery logistics in EVs to provide a thorough grasp of the variables influencing the direction of EVs in the future.

As previously explained, EVs face challenges related to their limited driving range compared to conventional vehicles. This is a significant concern for potential EV customers, as it directly impacts the practicality and usability of these vehicles. The driving range of an EV is mainly determined by the battery’s energy density, which refers to the amount of energy stored per unit volume or weight. In EVs, batteries with higher energy densities are essential for driving longer distances. Lithium-ion batteries (LIBs), currently one of the most common battery technologies used in EVs, have relatively high energy densities. However, these energy densities are still significantly lower than that of gasoline, necessitating a large number of batteries to achieve a comparable driving range [34]. As the energy densities of LIBs approach a limit, the development of next-generation batteries with even higher energy densities becomes imperative for effectively increasing driving range. Various solutions have been explored to surpass the energy densities of LIBs [35]. However, these alternative designs face challenges such as safety concerns or poor cyclability, which currently limit their application in EVs. Another significant challenge of EVs compared to CVs is their high upfront purchase price, which remains a significant barrier to widespread adoption. The cost of the battery, which sets a large portion of the EV’s total price, is a major contributor to this expense [36]. Over the years, there has been a dramatic reduction in battery costs to achieve cost parity with CVs. One approach to cost reduction is the use of high-energy-density materials, which require smaller amounts of material. However, transitioning to materials with higher energy densities poses challenges related to safety and cyclability. Another avenue for cost reduction is the replacement of expensive materials like cobalt with more affordable alternatives. However, eliminating them presents its own set of challenges, as it impacts battery safety and cycle life. In addition, managing manufacturing costs is crucial in reducing the overall cost of a battery system [37]. Each battery production involves numerous process steps, with some steps requiring long processing times and affecting yield rates. Furthermore, EVs encounter the issue of battery degradation over time, resulting in a gradual decline in the vehicle’s driving range until repair or replacement becomes necessary. This issue is absent in CVs, thus contributing to a reduced lifespan for EVs compared to CVs. Some studies have focused on assessing the environmental impact of this phenomenon, considering that EVs produce no greenhouse gas emissions during operation. However, the production of batteries and a significant portion of their components is more environmentally harmful compared to equivalent components of CVs. An extensive study on this topic is available in the work by Zhang et al. [38], where the authors explore the life cycle environmental impact of EVs and other types of vehicles across various indexes. Batteries can also be significantly impacted by environmental conditions, which play a crucial role in determining their performance and longevity. As electrochemical systems, batteries are influenced by factors such as temperature, which can significantly impact their charging/discharging rates and degradation mechanisms. Balancing these effects becomes challenging as batteries must maintain consistent performance across a range of temperatures. Since EVs may encounter diverse environmental conditions throughout their operational lifespan, maintaining battery performance under varying temperatures is important. Effective thermal management systems are essential in achieving this goal by regulating battery temperature within an optimal range. However, efficiently cooling or heating batteries when necessary presents challenges due to limitations such as limited contact area and heat transfer rates. Moreover, recharging time is a crucial factor influencing the adoption of EVs, leading to the classification of recharging stations into two groups: fast and slow charging stations. Fast charging stations can replenish EVs in a relatively short amount of time but at the expense of reducing the lifespan of the batteries. In contrast, slow charging stations preserve better the battery but require a significant amount of time to fully complete a recharge. Recharging stations can also be categorized into three levels: level 1 stations have a charging power less than 5 kW, while those of level 2 are considered fast charging facilities and operate on a range from 5 to 50 kW. Both of them can completely refuel an EV in 2 to 8 h, which may not be optimal for users requiring a driving range beyond the maximum capacity of their vehicles. Lastly, level 3 stations are considered super-fast stations and have a charging power greater than 50 kW [39]. While these may be the preferred option for users in need of quicker recharges, it is essential to consider that such high-speed charging could potentially lead to a reduction in the lifespan of the battery, posing a trade-off between charging speed and long-term battery health.

These stations typically have limited capacity, meaning only a small number of vehicles can be charged simultaneously, while others have to wait in queues. Different routes, battery capacity or departure time can result in EVs reaching the stations at different times, posing challenges in managing these variations. Moreover, charging stations can produce an increase in the peak load of the electric network, threatening the power system’s security. Thereby, some strategies are needed to mitigate this issue, suggesting that the creation of new charging stations should be coupled with an improvement of the power supply system [28]. Following this perspective, Yu et al. [40] defined a critical short circuit ratio as the short circuit ratio when the system voltage is in a critical state. They utilized this concept to differentiate between weak and strong systems, a distinction that will be essential in the near future as EVs become more prevalent. A potential solution to the charging stations problem involves replacing the existing depleted or nearly depleted battery with a fully recharged one. This process is known as battery swapping and could be completed in less than 10 min, which is faster than a significant amount of recharging stations [41]. Battery swap stations offer several advantages: for instance, the depleted batteries can be charged at night slowly, extending the battery lifespan and minimizing electricity costs. Furthermore, they enable a refueling process comparable to conventional vehicles, while also providing centralized grid-support services, potentially enhancing the adoption of EVs. As we have explained before, batteries are one the most contaminant parts of EVs. Thus, having the station recharge the batteries at the most optimal moment, and taking care of them from bring-up to recycling when the battery is not functional can reduce one of the worst environmental impacts EVs have. Moreover, this solution can also help us to deal with reduced driving range due to battery degradation, since the station could potentially replace the battery once it is degraded enough. However, the capacity of the battery swap station could also become a problem, as not having enough chargers or ready batteries can lead to changing a depleted battery to a non-fully recharged one. This can force the user to stop at a non-planned station, with the consequences previously stated. Another potential solution was investigated by Jaman et al. [42], where researchers investigated various topologies and control strategies for integrated onboard charger systems in EVs, analyzing their component count, switching frequency, efficiency, controllability, and reliability. They evaluated performance indices such as setting time and rise time for charging and traction operations, while also exploring the feasibility of level 3 charging stations. Additionally, the study discussed power density trends in commercial integrated charging systems, offering insights for researchers and engineers in the automotive industry. While considerable progress is required in this domain, the current outlook suggests that in the meantime battery swap stations are better suited for EVs in the public transportation sector, while regular users are better with a mix of battery swap stations and recharging stations due to irregular demand, as highlighted by Zhan et al. [43]. Nevertheless, this solution suffers from the lack of battery standards for EVs, which complicates the feasibility of establishing widespread battery swap infrastructure.

5. Review of the Electric Vehicle Routing Problem

In the EVRP the constraints of the VRP are modified based on new considerations regarding electric vehicles, such as their limited battery capacity. These modifications give rise to new operational challenges for the problem. Various variants of the EVRP have been considered, encompassing aspects like time windows, homogeneous or heterogeneous fleets, partial or total recharge stations, and the incorporation of stochastic, fuzzy, or dynamic variables. Different techniques have been employed to address this problem, including exact methods and heuristics. However, due to the problem’s complexity, exact methods can only handle small-sized instances. Consequently, diverse heuristics and metaheuristics have been developed. In this section, a review of various articles is presented, highlighting a range of approaches when dealing with this problem. Thus, Almouhanna et al. [44] proposed a fast multi-start heuristic and a metaheuristic to address the location routing problem with constrained distances. The heuristic integrates biased-randomization techniques to Tillman’s heuristic for the VRP, while the metaheuristic combines biased-randomization with variable neighborhood search (BR-VNS). Experimental results indicate that the multi-start biased-randomized Heuristic is able to generate high-quality solutions in almost real-time, while the BR-VNS provided even better solutions with higher computational times.

Real-life problems do not usually behave in a deterministic manner. Therefore, one approach to extending the EVRP is by incorporating uncertainty. Keskin et al. [45] addressed a VRP with time windows and stochastic queuing times at recharging stations. In this variant, a homogeneous fleet of EVs might have to wait at recharging stations due to limited chargers available. In addition to this, queue waiting times at stations follow known probability distributions and are determined once the EV arrives at a station. In this paper, the goal is to minimize the sum of energy cost, vehicle acquisition cost and driver wages, while satisfying different constraints regarding electric vehicles, such as battery capacity or their cargo capacity and time windows. In addressing the issue, they introduced a two-stage heuristic approach based on simulation, employing adaptive large neighborhood search (ALNS). During the initial stage, routes were established while considering the anticipated waiting times at stations. Once the actual waiting time was revealed, if the time window of a customer was violated, the second stage corrects the solution. They finally tested it on both small and large literature instances, obtaining good results in both computational times and quality of the solution. A different approach was taken by Zhang et al. [46], who presented an ALNS algorithm to solve a fuzzy EVRP with time windows. The model included a single depot, stations allowing partial recharge and a homogeneous fleet of EVs. Battery energy consumption, service time and travel time are considered uncertain and, therefore, addressed with fuzzy variables. A Variable Neighborhood descent (VND) algorithm is also applied to further improve the solution’s quality. Numerical experiments finally validated the performance of the proposed method, showing its effectiveness. Another aspect to consider in EVRPs is the fleet type. Typically, a homogeneous fleet is considered for its simplicity in modeling, but considering a heterogeneous fleet offers a more realistic approach. Erdem and Koç [47] presented a hybrid metaheuristic combining GAs and a VND to solve a variant of the home healthcare routing problem, where a group of healthcare workers performed a number of jobs using EVs. In this problem, multi-depot and heterogeneous fleet were considered, using EVs with different battery capacities, energy consumption and recharging rates. Time windows were also considered, in addition to preferences, competencies, connected activities, different charging methods, including partial or full charge strategies and an objective function aimed to minimize the total travel time. To solve the problem the authors proposed a hybrid metaheuristic, where the GA diversifies the solution space and the VND intensifies the solution. Finally, computational experiments were made, first for parameter tuning and a comparative test afterward. It is shown in the paper that having a time limit of 3600 s, the metaheuristic achieved the same solutions as the ones obtained using the CPLEX commercial solver and better solutions in those instances where CPLEX reached the time limit, while having much lower computational times. Following the same context, while electric vehicles are a much cleaner option than conventional vehicles, they often struggle to compete in terms of cost. Nevertheless, due to the environmental impact, several companies are starting to include EVs in their delivery operations. Goeke and Schneider [48] proposed an EVRP with time windows and a mixed fleet, where a mix of conventional vehicles and EVs was considered. Non-linear energy consumption and variable recharging times are considered, depending on the vehicle’s speed, battery level and cargo load. An ALNS enhanced by a local search was developed to address the problem and numerical studies showed that considering the actual load significantly improved the quality of the solutions generated.

Yet another important consideration in addressing an EVRP is the factor of dynamism. When dealing with a real-life problem, several aspects can change with time. In this regard, Wang et al. [49] discussed a dynamic electric vehicle routing problem, where the demand of the customers could change over time. They considered a homogeneous fleet of EVs with fixed load capacities and limited driving ranges. No charging stations were considered, so each EV was required to return to the depot for full charging. A memetic algorithm (MA) with an adaptive local search method was proposed to solve the problem, being compared afterward in computer experiments with another eight algorithms, including GAs and MAs with different local search methods. Finally, other aspects can be considered, such as battery consumption or charging time. Xiao et al. [50], investigated an EVRP with time windows where they considered an energy consumption rate per unit of distance as a function dependent on speed and load—as battery consumption in an EV rises as their speed increases. The objective function’s purpose was to minimize total cost, considering a fixed cost per EV and driver, the cost produced by battery usage and drivers’ wage rate, taking into account the constraints occasioned by EVs and time windows. To provide a solution to this problem, a mixed-integer linear programming (MILP) model was developed, optimally solving it with CPLEX for up to 25 customers and being partially optimized for large instances of up to 100 customers utilizing a dynamic heuristic. The heuristic was named as dynamic partial optimization with iterative neighborhood search. Comparative tests based on simulations were made, showing that the proposed algorithm obtained either the best-known solution or a near-optimal solution with much lower computing time when compared to CPLEX. Similarly, Montoya et al. [51] considered an EVRP with a nonlinear charging function. A hybrid metaheuristic was proposed, combining an iterated local search and a heuristic concentration, achieving better solutions than those obtained by the Gurobi commercial solver.

Table 1. Summary and classification of revised EVRP references.

Reference	Problem Characteristics	Solution Approach
Almouhanna et al. [44]	ELRP, HoF, DP	H, MH
Keskin et al. [45]	EVRP, TW, HoF, SP	H
Zhang et al. [46]	EVRP, TW, HoF, FP	MH
Erdem and Koç [47]	HHRP, TW, HeF, DP	MH
Goeke and Schneider [48]	EVRP, TW, MF, DP	MH
Wang et al. [49]	EVRP, HoF, DyP	MH
Xiao et al. [50]	EVRP, TW, HoF, DP	EM, H
Montoya et al. [51]	EVRP, HoF, DP	MH

Note: ELRP = electric location routing problem, EVRP = electric vehicle routing problem, HHRP = home health routing problem, TW = time windows, HoF = Homogeneous Fleet, HeF = heterogeneous fleet (of EVs), MF = mixed fleet (of CVs and EVs), DP = deterministic problem, SP = stochastic problem, FP = fuzzy problem, DyP = dynamic problem, EM = exact method, H = heuristic, MH = metaheuristic.

shows a summary of the EVRP articles, categorized according to their problem characteristics and their solution approach. Regarding problem characteristics, the use of time windows, homogeneous or heterogeneous fleet and whether it is considered as a deterministic, stochastic, fuzzy or dynamic problem. According to the second criterion, solution approaches considered are heuristics, metaheuristics and exact methods.

6. Review of the Electric Team Orienteering Problem

The rising popularity of EVs for cargo transportation in recent years has also resulted in their use in TOP applications. For such applications, effective operational planning is essential to prevent undesired and typically costly route failures [52]. This is natural as every route is constrained due to the limited driving range caused by battery usage, and not every client can be visited. In addition, new considerations about where and when to recharge the batteries are among the issues that have arisen. In particular, all EV types face this difficulty [23].

In single-vehicle orienteering problems (OP), Lee and Park [53] introduced a tour planning service focused on selecting a maximum number of places to visit, considering the time interval during which tourists waited for their vehicles to charge without participating in any activity. They assumed each spot had a charging station. To address this problem, they proposed a GA. Their experiments showed that $95\%$ of the selected spots could be visited without causing waiting times for tourists. Similarly, Wang et al. [54] considered an EV tour planning with time windows. In addition, the study introduced EV recharging limitations to ascertain the battery’s condition at each visit. This way, researchers determined whether or not the following visit was feasible considering battery usage. Heuristic-based strategies were used to address this problem and the Taiwanese road network was used to test the different heuristic strategies. More recently, an EV that traveled from an origin depot to a destination depot while maximizing reward along its path was addressed by Juan et al. [55]. The vehicle came across a variety of charging stations in diverse areas with station type, weather, congestion, and battery condition as dynamic aspects that influenced rewards. The study developed a hybrid strategy that integrated simulation and reinforcement learning to navigate this dynamic environment. Computational experiments showed that the methodology could produce route plans that performed better than arbitrary choices. In the context of surveillance operations, Pěnička et al. [56] examined an OP using a UAV for data-gathering missions in military operations. In this regard, the UAV was outfitted with sensors to collect data from a list of predefined targets. This problem took into account the possibility of gathering the data (i.e., reward) from a nearby neighborhood sensing the distance surrounding the target places. To address this problem, a VNS metaheuristic was proposed. Similar to the previous study, Dasdemir et al. [57] discussed route planning for a reconnaissance mission involving a UAV in a radar-monitored region. The UAV had to visit several targets, each with data that could be collected in a certain amount of time. Target selection, visit order, and trajectory decisions were all included in the route construction, which took into account a number of goals including safety, mission duration, and information gathering. For smaller instances, the study suggested a mixed-integer programming model. For larger instances, the authors suggested a hybrid algorithm that combines exact methods with heuristics. A case study based on a Colorado terrain was included, followed by a discussion of practical issues related to UAV route planning.

In multiple-vehicle OPs or TOPs, Mufalli et al. [58] discussed the assignment of sensors to UAVs and their routing to maximize intelligence gain. One base was available where the UAVs could start from and return to. The UAVs could only travel a certain distance before needing to come back due to limited battery. The authors took into account that adding sensors would make the UAVs heavier and reduce their travel distance. They came up with a detailed plan to solve this problem using both a complex mathematical model solved with CPLEX 12.2 software and simpler strategies that used local search methods. These strategies were enhanced by column generation for larger missions, where efficiency was critical. In the context of smart cities, Reyes-Rubiano et al. [52] studied the routing of a set of UAVs to deliver goods to customers in a space that was shared by different types of vehicles. In their case, the problem was modeled with random rewards and a variable service time for visiting each customer which depended on the collected reward. In addition, UAV batteries could require more time than the estimated time needed to travel the routes. To address this problem, a simheuristic algorithm was proposed. Results showed that solutions given by the simheuristic algorithm outperformed the ones given by the deterministic version in uncertainty scenarios. Likewise, Saeedvand et al. [59] presented a hybrid technique for solving a TOP with time windows for rescue operations, combining a learning algorithm with an evolutionary multi-objective approach. Humanoid robots made up the fleet, and their five goals were to maximize overall energy, maximum energy consumption for a single robot, task rewards, job completion time, and missed deadline penalties. Every robot completed a set of tasks to serve a route, making money each time a task was completed within its designated time frame. Similar to other studies, every robot had a finite amount of energy, meaning that the assigned tasks were to be finished before the energy ran out. The learning algorithm sought to update robot plans so that they could quickly and accurately make decisions. In Xu et al. [60], an alternative use of EVs in TOP systems was described where energy-critical sensors needed to be charged by mobile chargers. The ability to visit every sensor was restricted since these mobile chargers had limited energy capacity. A separate cost was assigned to each node to account for the energy consumption of the mobile charger during sensor charging, in addition to the travel cost. The research also considered several vehicle types based on how much power each one had and how far they could fly. Moreover, a sensor may be visited by several vehicles, which would reduce the marginal profit. The researchers presented an approximation algorithm to solve this problem, which was later improved to handle vehicles of the same type. Recently, Sundar et al. [61] proposed a concurrent multi-threaded branch-and-price algorithm with acceleration schemes to solve an ETOP. In this case, the study focused on fixed-wing drones which introduced additional constraints to the problem. Among these were kinematic restrictions that limited the drones’ ability to make quick turns, which ultimately limited the minimum turn radius. These limitations were addressed with the introduction of branching mechanisms. While the approach successfully found optimal solutions for most problem instances, the use of exact approaches, as proposed in their study, limited the ability to find real-time solutions—a crucial requirement in many dynamic systems.

Table 2. Summary and classification of ETOP references.

Paper	Problem Characteristics	Solution Approach
Lee and Park [53]	SV, HoF, DP	MH
Wang et al. [54]	SV, HoF, DP, TW	EM, H
Juan et al. [55]	SV, HoF, DyP	H
Pěnička et al. [56]	SV, HoF, DP	MH
Dasdemir et al. [57]	SV, HoF, DP	EM, H
Mufalli et al. [58]	MV, HeF, DP, TW	EM, H
Reyes-Rubiano et al. [52]	MV, HoF, SP	MH
Saeedvand et al. [59]	MV, HeF, DP, TW	MH
Xu et al. [60]	MV, HeF, DP	AM
Sundar et al. [61]	MV, HoF, DP	EM

Note: SV = single vehicle, MV = multi vehicle, HoF = homogeneous fleet, HeF = heterogeneous fleet, DP = deterministic problem, SP = stochastic problem, DyP = dynamic problem, TW = time windows, EM = exact method, AM = approximate method, H = heuristic, MH = metaheuristic.

summarizes the revised ETOP papers according to the following criteria: (i) the problem characteristics being addressed; and (ii) the solving method used to solve the problem. The first criterion considers either single or multiple vehicles in the fleet of vehicles, the use of a homogeneous fleet (vehicles with the same capacity) or a heterogeneous fleet (vehicles with different capacities), the consideration of time windows for visiting locations, and the formulation of the problem as deterministic, stochastic or dynamic. As for the second criterion, the proposed solving methods are categorized into exact methods, approximate methods, heuristics, and metaheuristics.

7. Electric Arc Routing Problem

UAVs can directly travel from a location to any other location, without the limitations of existing roads, whose characteristics are the foundations of ARP applications. Nevertheless, a major problem preventing the adoption of UAVs is the absence of airspace management to avoid collisions between UAVs themselves, with static objects such as buildings, dynamic flying objects such as birds and human-controlled flying objects such as planes or helicopters. Different studies have been made in this aspect, to develop systems where the UAVs avoid possible colliding objects with different solution approaches [62,63,64].

Campbell et al. [65] examined different aspects of ARPs involving a single UAV. They explored scenarios where the UAV would serve various edges sequentially, with the possibility of stopping service to one edge and serve another before returning to complete the service to the first edge. This turns the problem into a continuous optimization problem. To solve it, they approximated edges as polygonal chains, transforming it into a discrete optimization problem. They created random instances where a single UAV with unlimited range was used. Later, in Campbell et al. [66], they tackled a more realistic scenario by considering limited UAV range, necessitating a fleet of UAVs. They devised a mixed-integer linear model and solved it using a branch-and-cut algorithm. They also proposed a matheuristic approach based on edge splitting to tackle the problem. Chow [67] introduced a deterministic arc-inventory routing problem, particularly useful in scenarios with uncertainty like city monitoring during major events. They formulated a policy aimed at maximizing value under such uncertainty, treating it as a selective vehicle routing problem. To approximate this policy, they developed an approximate dynamic programming algorithm based on least squares Monte Carlo simulation. They tested the algorithm on real-time trajectory instances spanning five time periods to assess its effectiveness. Results indicated that, depending on the design parameters, the algorithm generally outperformed the myopic policy.

Real-world scenarios involving UAV EARPs have been extensively explored in research. For example, Li et al. [68] delved into the UAV scheduling problem with uncertain demands to enhance real-time monitoring of road traffic across multiple time periods. They devised a mixed-integer programming model by merging a capacitated ARP with an inventory routing problem and developed a local branching-based solution method for it. They applied this model to study road traffic in Shanghai, China, conducting numerical experiments to validate its effectiveness and the efficiency of the solution method. However, to overcome UAVs’ limited endurance, cooperation with vehicles can be beneficial. Liu et al. [69] investigated a new system for inspecting high-voltage power lines, involving a UAV and a ground vehicle. The ground vehicle served as a mobile platform for launching and retrieving the UAV, which inspected the power lines. They optimized both the ground vehicle and UAV routes to improve inspection efficiency, creating a two-layer point ARP. They designed constructive heuristics and local search strategies to enhance solution quality, testing their algorithms on practical cases based on Ji’an, China’s road and power line networks, and conducting sensitivity analysis on UAV-related parameters. A similar challenge is addressed by Luo et al. [70], who proposed and studied the traffic patrolling routing problem with UAVs in urban road systems. They modeled the problem as a double-layer ARP considering road network equations and task heterogeneity. They presented a mixed-integer linear programming formulation and two-stage heuristic solution approaches for practical-sized problems. Through numerical experiments, they demonstrated that their solution method could quickly provide optimal path planning for various test sets. They also analyzed relevant parameters of the patrol process and tested the algorithm’s performance on benchmark instances and a real-world case in Hefei, China.

Most literature concerning EARP typically focuses on the utilization of UAVs across various applications. However, Yurtseven and Gökçe [71] took a different approach by examining a waste collection scenario employing a heterogeneous fleet of electric street sweepers. Their aim was to execute a predetermined service within realistic operational constraints while minimizing energy consumption for service provision, travel, and disposal operations. They solved multiple small instances based on a real case in Izmir, Turkey, achieving optimality under different demand levels and time windows. Similarly, Moazzeni et al. [72] proposed a dynamic location-arc routing optimization model for waste collection utilizing EVs. Their model determined optimal routing plans and the best locations for charging stations, dynamic charging arcs, and waste collection centers. They utilized a GA and a Grey Wolf Optimizer (GWO) to tackle large-scale randomly generated location-arc routing problems. They presented a case study for Edmonton, Canada, demonstrating that the GWO outperformed the GA. Moreover, they showcased the necessary infrastructure—waste collection centers, charging stations, and dynamic charging arcs—to ensure a minimum required service for EVs throughout Edmonton’s waste collection system. Furthermore, Fernández et al. [73] explored the integration of EVs into waste collection operations, addressing practical aspects like dynamic charging while driving, speed-dependent energy consumption, and nonlinear charging functions based on battery state and charging time. They introduced the concept of an energy-indexed graph to handle these aspects, formulating an integer linear programming model and a solution framework using a branch-and-cut algorithm. They proposed efficient construction heuristics and a local search approach for approximately solving large-scale instances. Computational analysis on realistic problem instances not only evaluated the performance of their methods but also provided insights into strategic decisions regarding battery size and charging facility deployment.

Table 3. Summary and classification of revised EARP references.

Reference	Problem Characteristics	Solution Approach
Campbell et al. [65]	SP, HoF, DP	EM, MH
Campbell et al. [66]	SP, HoF, DP	H
Chow [67]	MP, HoF, SP	EM
Li et al. [68]	MP, HeF, SP	EM, H
Liu et al. [69]	SP, HoF, DP	H
Luo et al. [70]	SP, HoF, DP	H
Yurtseven and Gökçe [71]	SP, HeF, DP, TW	EM
Moazzeni et al. [72]	SP, HoF, DP	MH
Fernández et al. [73]	SP, HoF, DyP	EM, H

Note: SP = single period, MP = multi period, HoF = homogeneous fleet, HeF = heterogeneous fleet, DP = deterministic problem, SP = stochastic problem, DyP = dynamic problem, TW = time windows, EM = exact method, H = heuristic, MH = metaheuristic.

summarizes recent EARP articles and categorizes them according to the following dimensions: (i) the characteristics of the addressed problem and (ii) the employed solving approach. Regarding the first dimension, the analyzed papers can consider either routes with a single period or multiple periods, a homogeneous fleet where all vehicles have the same capacity or a heterogeneous fleet where vehicles have different capacities, and the problem variables and constraints can either be deterministic, stochastic or dynamic. As for the second dimension, exact methods, heuristic or metaheuristic approaches are the considered methods to solve the different EARP articles.

8. E-Routing under Uncertainty

Routing problems are frequently classified as NP-hard and large-scale, therefore exact methods require huge computing times in order to find optimal solutions. Consequently, approximate optimization methods, such as metaheuristics and heuristics are employed to solve these problems within reasonable times. In order to solve large-scale stochastic optimization problems, a combination of simulation and optimization is used. One of these hybrid methodologies is simheuristics, which integrates simulation and metaheuristics [74]. This method provides near-optimal solutions to stochastic optimization problems in short computing times and therefore has been vastly studied in recent years. Electric routing problems are often modeled as an extension of conventional routing problems. Therefore most changes regarding uncertainty made in deterministic routing problems can be applied to their electric counterparts. As highlighted in previous sections, when addressing vehicle routing problems, uncertainty can be taken into account in customer demands, charging station waiting times or travel costs, among others. When dealing with team orienteering problems, we can consider both stochastic or fuzzy reward quantity or travel times. In the context of the electric arc routing problem, edge demands and especially node rewards are often related to uncertainty. Moreover, the use of electric vehicles entails other considerations, such as energy consumption and charging stations which can be also considered as either stochastic or fuzzy variables. Multiple approaches have been made in order to address EVRP with uncertainty. Reyes-Rubiano et al. [75] developed a simheuristic to tackle the EVRP with stochastic travel times. The simulation-optimization method developed integrates a Monte Carlo simulation into a biased-randomized multi-start framework, allowing for fast generation of high-quality solutions. Computational experiments were conducted, illustrating that using deterministic solutions in stochastic scenarios could result in sub-optimal solutions, which can be easily improved with the use of a simulation-optimization technique.

Zhang et al. [76] discussed a location-routing problem with electric vehicles and stochastic demands, considering battery swapping stations (BSS) in addition to electric vehicle constraints – such as vehicle load capacity or battery capacity. The study proposed a hybrid algorithm called HVNS, which combines binary particle swarm optimization and variable neighborhood search. The former addressed the BSS location plan, being later improved with local search strategies, while the latter provided the routing plan. Computational experiments comparing the developed method and other algorithms and hybrid algorithms showcased the effectiveness of the HVNS. Regarding electric arc routing problems, most articles refer to the employment of UAVs. Chow [67] studied a dynamic stochastic arc-inventory routing problem. An approximate dynamic programming algorithm based on least squares Monte Carlo simulation was presented and computational tests verified its effectiveness while compared to the myopic policy. Similarly, the unmanned aerial vehicle scheduling problem with uncertain demands was addressed by Li et al. [68]. A mixed integer programming model was designed by combining the ARP with the inventory routing problem. To tackle this hybridized problem, a local branching-based solution method was proposed, achieving near-optimal solutions in much lower times than the ones obtained by CPLEX. In a similar context, Panadero et al. [77] tackled the challenge of UAV surveillance routing with stochastic travel times and reliability concerns. The problem involved a constrained fleet of UAVs with limited driving ranges tasked with visiting multiple target zones to carry out a monitoring mission. To face this problem, a simheuristic was developed, integrating Monte Carlo simulation and a multi-start biased-randomized metaheuristic. Computational results highlighted the importance of considering simulation when facing a stochastic scenario, as the deterministic solution offers a worse performance both in terms of expected cycle time and level of reliability. Previous articles added uncertainty to classical deterministic routing problems by acknowledging the stochastic behavior of some variables, such as travel times, customer demands, service times or battery durability. Nevertheless, some aspects cannot be represented with stochastic uncertainty. In these occasions, fuzzy techniques might be useful [78]. Following this logic, Oliva et al. [79] introduced the concept of fuzzy simheuristics, which extended the simheuristic approach by incorporating fuzzy techniques, allowing them to tackle optimization problems that included stochastic and non-stochastic elements. A TOP under an uncertainty scenario was proposed. In this problem, both stochastic and fuzzy rewards were contemplated. Computational experiments were conducted, demonstrating the effectiveness of the method to find solutions to the TOP with different degrees of uncertainty. Ghobadi et al. [80] examined a multi-depot electric vehicle routing problem with recharging stations and fuzzy time windows in pickup/delivery. Three metaheuristics were developed, made up of simulated annealing (SA), VNS, and a hybrid of SA and VNS. By analyzing numerical results, the authors concluded that the hybrid method outperforms the individual ones in all instances regardless of their size.

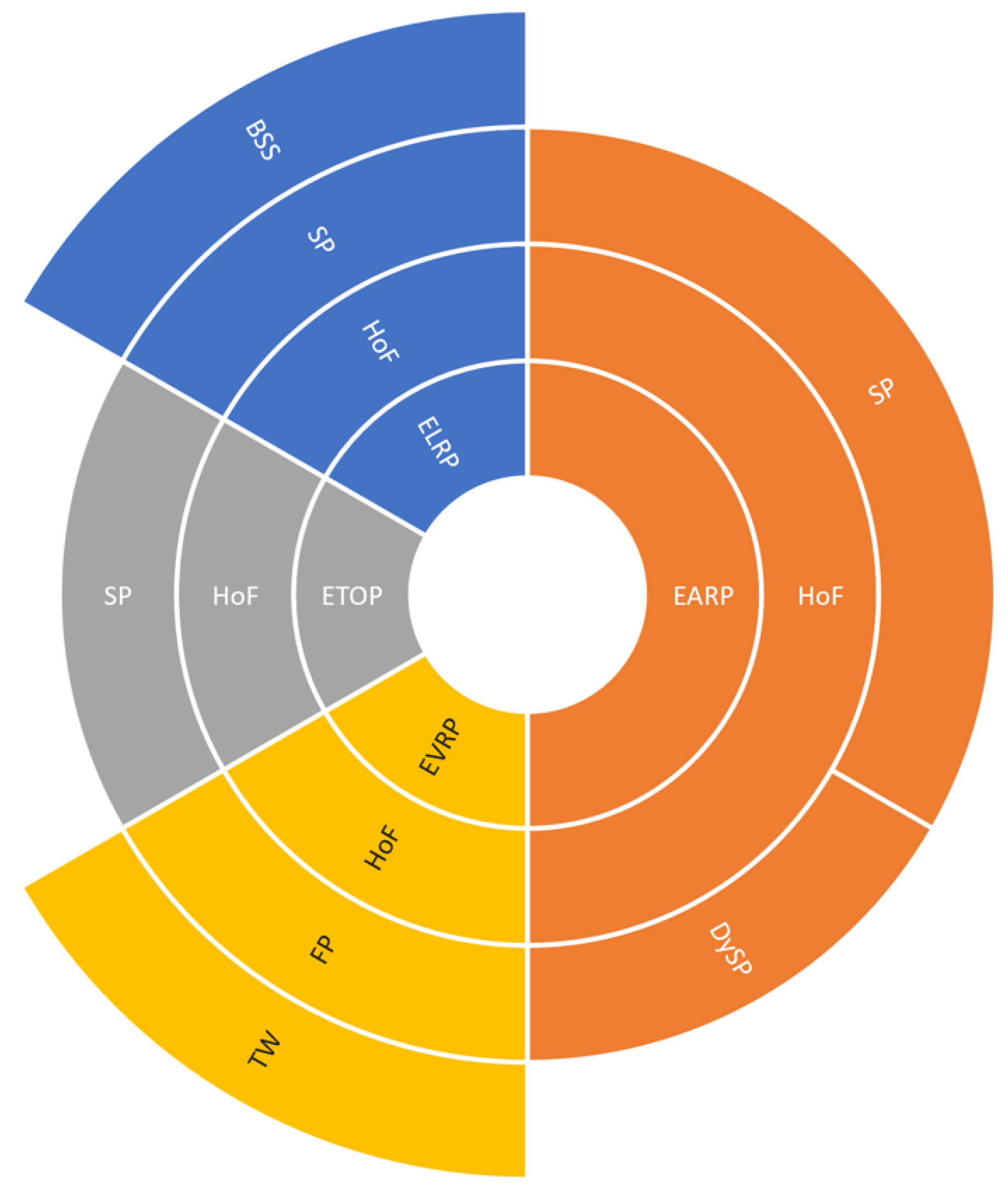
Figure 6 depicts a sunburst chart that summarizes and classifies the revised e-routing articles and categorizes them according to their problem characteristics. The problem characteristics consider the problem family (EVRP, ELRP, EARP or ETOP), either homogeneous or heterogeneous vehicles in the fleet (HoF or HeF), the uncertainty of the problem as stochastic, fuzzy, or dynamic-stochastic (SP, FP, or DySP), and the consideration of time windows (TW) or battery swapping solutions (BSS).

9. E-Routing under Dynamic Conditions

With the incorporation of EVs into the transport industry, the need to efficiently solve routing problems arises as the risk of draining the vehicle’s battery before reaching the destination becomes a reality. In order to avoid or at least minimize inaccuracies when modeling real-life problems, it is mandatory to consider traffic and weather conditions, as urban areas are subject to constant change and dynamism. For this reason, real-time data-driven problems need to be addressed. Machine learning techniques can take advantage of the real-time data, and with their incorporation into metaheuristics, the concept of learnheuristics comes to life, providing fast high-quality solutions to dynamic routing problems [81]. Different approaches have been made in order to include dynamism in routing problems. Bayliss et al. [82] addressed an aerial-drone team orienteering problem, where the goal was to maximize the reward from information gathering within a limited time lapse. The drone’s flight path can affect greatly its speed due to multiple conditions, therefore a learnheuristic consisting of the integration of a machine learning mechanism to a metaheuristic was developed. This algorithm was also improved by using biased-randomization techniques and different local search processes. Computational experiments were made, where the developed learnheurisic was compared to different metaheuristics. Results showed that the proposed algorithm obtained the second highest average reward while obtaining solutions in much lower computational times than all other algorithms. Regarding the EVRP, several studies have been made including dynamic conditions. Basso et al. [83] studied a dynamic stochastic EVRP. This problem was modeled as a Markov decision problem, and the goal was to find a route for a single EV to service deterministic or stochastic customer requests. They developed a safe reinforcement learning method and a re-optimization method, both combined with a roll-out heuristic based on a tabu search, obtaining good results with different levels of dynamism. The study concluded that the reinforcement learning algorithm could save, on average, $4.8\%$ of energy compared with the deterministic online re-optimization approach. In a similar way, Dong et al. [84] proposed an improved memetic algorithm with incorporated local search and economical random immigrant strategy to solve a dynamic EVRP with mid-route recharging and new demand arrival. After computational tests, the developed algorithm showed good performance time-wise and excellent performance under different dynamic environments regarding solution quality. Similarly, Bi and Tang [85] developed a hybrid roll-out algorithm (HRA) to address a dynamic EVRP in which traffic conditions and energy consumption were time-dependent and stochastic. Its aim was to minimize the overall service duration while not violating any EV-related constraints. The algorithm’s performance was evaluated by performing computational experiments and results showcased its effectiveness and robustness in finding near-optimal solutions in the studied instances. Another path was taken by Lu and Wang [86], who proposed a bi-strategy-based optimization algorithm to solve a dynamic capacitated EVRP. A partition between possible customers was made, dividing them into static and dynamic groups and extensive comparisons showcased the algorithm’s effectiveness in dealing with this dynamic problem. Other approaches were made to find greener solutions regarding vehicle routing problems. Xiao and Konak [87] addressed a time-dependent vehicle routing and scheduling problem with CO₂ emissions optimization. In order to tackle this problem, a hybrid solution approach was taken, combining a genetic algorithm with a dynamic programming procedure. A heterogeneous fleet and dynamic traffic environment were considered. For larger size instances, the problem was divided into two parts, the routing part and the scheduling part. Computational tests showcased the effectiveness and efficiency of the proposed methodology.

Figure 7 depicts a sunburst chart that summarizes and classifies the revised e-routing articles and categorizes them according to their problem characteristics. Regarding the characteristics, reviewed papers are categorized depending on the problem family (EVRP or ETOP), the use of homogeneous fleet or heterogeneous fleet of vehicles (HoF or HeF), and the uncertainty type involved which is dynamic, or dynamic-stochastic (DyP or DySP).

10. Agile E-Routing

Real-time decision-making is necessary for many practical applications of EVRPs. Urban areas are constantly exposed to a variety of dynamic conditions, particularly in the transportation sector, which emphasizes the necessity for intelligent and quick decision-making. These scenarios can arise when one of these systems fails, such as battery failure, unavailability of charging stations, or unexpected traffic congestion. In addition, the inherent characteristics of many routing problems are often NP-hard, large-scale, and dynamic, so traditional approaches of using exact methods or even metaheuristics are insufficient as decision-making must occur within constrained time frames. In this case, intelligent systems need to be able to respond fast and offer users high-quality solutions every few seconds to adapt to the dynamic changes in data related to these systems. Thus, there is an urgent need for approaches that can quickly produce near-optimal solutions to routing problems, particularly those tailored to the unique requirements of EVs. Obtaining high-quality solutions in real-time for large-scale optimization problems is a major challenge. It occasionally presupposes that the model will need to be re-optimized because inputs and constraints are subject to dynamic modification as a result of new data being incorporated or conditions changing. Heuristics are extremely fast algorithms designed to solve a specific problem, which construct feasible solutions but are not guaranteed to be optimal. However, this deterministic procedure can be expanded into a probabilistic algorithm by employing biased-randomization techniques [88]. These techniques make use of skewed (non-symmetric) probability distributions such as triangular or geometric ones to produce multiple different solutions, some of which will outperform the solutions given by the heuristics alone. Hence, the biased-randomized algorithms (BRAs) are still extremely fast procedures, which produce multiple high-quality solutions and require a reduced number of parameters.

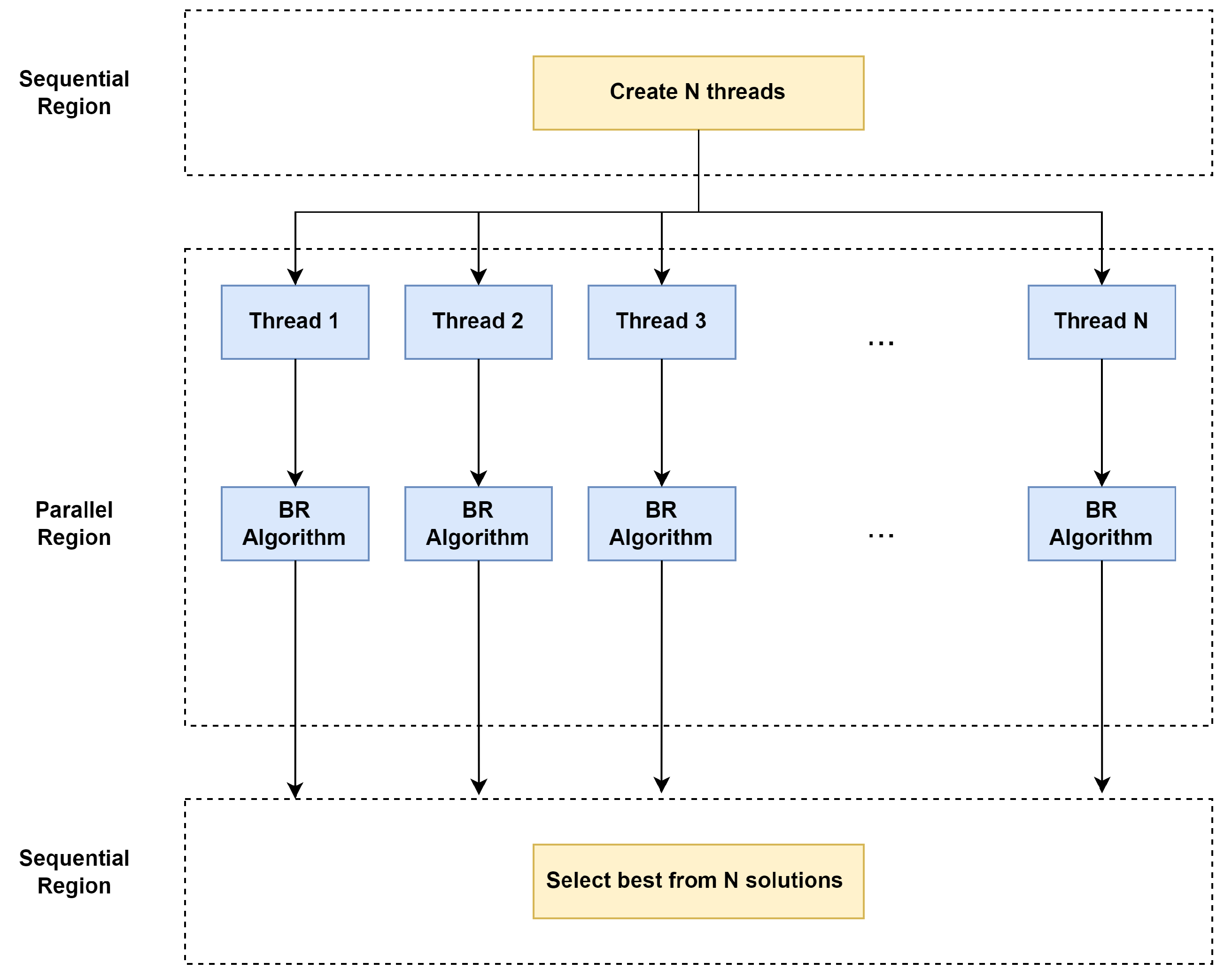
Naturally, BRAs can be extended to be executed in parallel, which is the foundational idea behind agile optimization (AO) algorithms. AO algorithms rely on employing massive parallelization techniques to concurrently execute a large number of BRAs, each one in a different thread. Consequently, multiple solutions are generated at virtually the same time as the one required by a single execution of the original heuristic, so thousands of solutions could be generated from the BRAs execution if thousands of threads are run in parallel. As a result, a pool of multiple alternative solutions is generated, from which the solution that outperforms the others will be selected to be returned by this AO procedure. Figure 8 depicts the main structure of the AO methodology. This combination of biased-randomized approaches with massive parallelization is really adaptable to many high-performance architectures, such as general-purpose computer processing units (CPUs), graphical processing units (GPUs), clustered and distributed computing environments or even cloud computing services. AO strategies leverage the strengths of both parallel computing and optimization algorithms to enable: (i) real-time, efficient solutions to large-scale, NP-hard optimization problems; and (ii) periodically re-optimize the model when inputs and constraints change dynamically as a result of new data arriving or conditions changing.

In their work, Panadero et al. [89] explored the increasing use of UAVs across various fields like smart cities, logistics in urban areas, humanitarian aid, response to natural disasters, and military operations. They focused on one particular challenge: optimizing UAV operations in scenarios where travel times are unpredictable. To tackle this challenge, they introduced a simheuristic algorithm that blends a biased-random approach with simulation methods. Additionally, they proposed an AO methodology to adapt to the ever-changing environment, stressing the urgency of providing real-time solutions to potentially save lives. Similarly, Panadero et al. [90] studied the growing concern of UAVs and self-driving vehicles in smart cities to serve customers by a specified due date efficiently. An AO algorithm combining an extremely fast biased-randomized heuristic with a parallel computing approach was proposed to solve the problem. The algorithm was able to generate high-quality solutions in a matter of seconds given the importance of providing real-time solutions. In the context of EVs, Almouhanna et al. [44] examined the shift towards greener road transportation practices with the introduction of EVs for routing operations. The study discussed the location routing problem with a maximum travel distance, which is a natural extension when EVs are utilized. An AO heuristic was proposed to solve the proposed problem using the well-known Tillman’s heuristic for the multi-depot VRP. A series of computational experiments showed that the AO heuristic was able to generate good-quality solutions in just a few seconds of computational time.

11. Synchronized E-Routing

Several real-world combinatorial optimization problems exhibit a high degree of dynamic nature. This requires a certain level of synchronization among agents and events. For instance, in order to reduce waiting times, it is crucial for EV routing operations to coordinate the arrival of vehicles to charging stations. Considering charging stations have a limited service capacity, this is achieved by giving priority to EVs in need of immediate charging to manage the charging station queues effectively. Similarly, in warehouse logistics, the routing of AGVs needs to be synchronized with the arrival of new products to maximize their battery usage. In both examples, a number of interconnected events are scheduled for the future, as operational decisions are made. Conventional optimization techniques find the synchronization of events challenging, while discrete-event simulation naturally processes the scheduling of events without an optimization component. Discrete-event heuristics (DEH) presents a solution-construction procedure combined with discrete-event simulation to solve optimization problems with synchronization issues. Fikar et al. [91] introduced the DEH methodology to manage synchronization issues and time dependencies in a ride-sharing problem. It was later extended to a biased-randomized DEH to generate multiple feasible and high-quality solutions. Figure 9 outlines the main characteristics of the DEH methodology. This allows us to solve practical large-scale optimization problems that cannot be solved with exact methods alone, or with other metaheuristic algorithms that do not take into account the synchronization of events. The main disadvantage of the methodology is likely the difficulty in evaluating the quality of its solutions in large-scale scenarios, where exact methods are not able to yield optimal solutions and where alternative metaheuristics may also be severely limited by the time-dependent events that characterize these highly dynamic environments.

Peyman et al. [92] developed a methodology based on DEH for solving a dynamic ride-sharing problem in the context of EVs sharing strategies. This algorithm facilitated the real-time processing of data collected from IoT systems to optimize automated decisions in the city transportation system. These decisions included the optimization of vehicle routing, the recommendation of personalized modes of transportation to citizens, the creation of effective ride-sharing and car-sharing schemes, and the location of ideal charging stations for EVs.

12. Future Trends

After a systematic review of a large variety of articles regarding routing problems, a great amount of options arise for future work. Future trends should focus on improving results obtained when dealing with a realistic problem, given the increasing necessity of providing agile and very good solutions to real-world transportation problems. In this sense, a vast amount of different options have been considered in order to turn a problem into a more realistic one. Regarding routing problems by themselves, different approaches have been made, including the consideration of uncertainty, including stochastic and fuzzy scenarios, dynamic conditions, the need for agile computations and synchronization issues. In the context of uncertainty, much more attention has been given to the study of stochastic scenarios than to fuzzy scenarios. Therefore, future trends might include focusing on developing fuzzy optimization methods for solving realistic problems, given that many uncertain conditions cannot be associated with a stochastic nature. In this regard, richer versions of the VRP and the TOP could employ and adapt fuzzy-simheuristic approaches.

Concerning dynamic conditions, studies can be found on EVRP and ETOP. However, very few articles addressing the electric arc routing problem under dynamic conditions are found, indicating the need for further research in this area. Additionally, the exploration of supervised learning methods, such as support vector machines, random forests, multiple regression, or neural networks, can make a difference. As previously mentioned, quick decision-making is becoming ever more needed as the transport sector is exposed to dynamic conditions. With parallel computing becoming more affordable and accessible, research into effectively parallelizing optimization methods would provide a valuable asset in supporting agile optimization methods. When taking into account constraints associated with the use of EVs, multiple ways have been explored. The energy consumption of an EV is influenced by various factors like road conditions, weather, driver behavior, and speed. To achieve more accurate results, these factors must be taken into account. Additionally, factors such as energy usage for heating or air conditioning and battery replenishment while driving downhill should also be considered. Some routes may lead to EVs arriving at charging stations or depots with near-zero battery levels. Ignoring or oversimplifying energy consumption aspects could lead to impractical routes. While modeling energy usage precisely in large-scale applications is challenging, it’s crucial to investigate when such impracticalities arise due to simplification. In energy consumption computations, charging amounts or times at charging stations are often assumed to follow a constant rate. However, the charging amount is not linearly proportional to the charged battery level, necessitating the adoption of non-linear formulations for charging operations to better reflect reality. While many routing problem studies use homogeneous fleets for simplicity, real-world scenarios often require heterogeneous fleets, comprising both pure EVs and a mix of conventional and pure EVs. Moreover, with several European cities implementing low-emission zones, there is a growing need for benchmark instances where specific customers can only be served by electric vehicles. Although some of these aspects have been addressed in prior research, studies typically focus on one or a few concepts, necessitating the consideration of various aspects to model problems realistically. Developing more efficient and powerful methods is crucial to address these challenges, as enhancing realism significantly increases problem complexity and computational time needed to find optimal solutions.

13. Conclusions

This paper has provided a comprehensive exploration of electric routing problems, including EVRPs, ETOPs, and EARPs. Specifically, 39% of the papers are dedicated to EVRPs, 34% contribute to ETOPs, and 27% discuss EARPs. In addition, the paper has analyzed diverse methodologies and scenarios, drawing from an extensive review of the literature. One of the main topics that appeared throughout the study is the need to address uncertainties. Simheuristic methodologies emphasize the significance of incorporating uncertainties in travel times, customer demands, and node rewards. In parallel, dynamic conditions in urban environments demand adaptive solutions. The exploration of dynamic scenarios is linked to the increasing need for real-time decision-making. The incorporation of machine learning techniques and the emergence of learnheuristics arise as innovative methodologies for considering the dynamic scenarios of urban logistics. Yet another concept is derived from the agile optimization algorithms. These algorithms combine biased-randomized techniques with massive parallelization in order to provide high-quality solutions, in real-time, to large-scale and NP-hard optimization problems. Factors influencing energy consumption in EVs are also discussed, with such factors ranging from road and weather conditions to driver behavior and auxiliary battery systems. Concretely, 25% have been solved by exact methods, another 25% with heuristic methods, and 36% with metaheuristic methods. The remaining 14% have been addressed using methods such as simheuristics, learnheuristics, agile optimization, or discrete-event heuristics. Thus, the study provides a thorough examination of electric routing problems and their associated solving methodologies.

Some research lines to be explored in future work are described next: (i) to explore and develop advanced fuzzy optimization methods for EVRPs, considering uncertainties beyond stochastic scenarios; (ii) to investigate the application of supervised learning methods to enhance decision-making in EVRPs; (iii) to further explore parallel computing techniques for solving large-scale optimization problems in real-time; (iv) to enhance models for energy consumption in EVs by considering additional factors, such as road and weather conditions, driver behavior, and the impact of heating or air conditioning systems; (v) to address routing problems involving heterogeneous fleets, including both conventional and electric vehicles; (vi) to extend the focus to last-mile delivery and urban logistics, addressing specific challenges related to EV routing in densely populated areas; and (vii) to explore multi-objective optimization techniques to simultaneously consider conflicting objectives in EVRPs, such as minimizing travel costs, reducing emissions, and optimizing delivery times.