Reaction Curve-Assisted Rule-Based PID Control Design for Islanded Microgrid

Abstract

In a renewable energy-based islanded microgrid system, frequency control is one of the major challenges. In general, frequency oscillations occur in islanded microgrids due to the stochastic nature of load and variable output power of distributed generating units (DGUs). In the presented research proposal, frequency oscillations are suppressed by implementing the proportional integral derivative (PID) controller-based control design strategy for an islanded microgrid. The modeling of the islanded microgrid is firstly presented in the form of a linearized transfer function. Further, the derived transfer function is approximated into its equivalent first-order plus dead time (FOPDT) form. The approximated FOPDT transfer function is obtained by employing the reaction curve method to calculate the parameters of the FOPDT transfer function. Furthermore, the desired frequency regulation is achieved for the manifested FOPDT transfer function by incorporating PID control design. For PID controller tuning, different rule-based methods are implemented. Additionally, comparative analysis is also performed to ensure the applicability of the comparatively better rule-based tuning method. The Wang–Chan–Juang (WCJ) method is found effective over other rule-based tuning methods. The efficacy of the WCJ method is proved in terms of transient response and frequency deviation. The tabulated data of tuning parameters, time domain specifications, and error indices along with responses are provided in support of the presented control strategy.

1. Introduction

The microgrid is a small electrical power distribution system that delivers electricity to autonomous locations [1]. Microgrids may consist of conventional and non-conventional energy sources to provide electric power to a load of specific geographical regions [2]. In general, microgrids can be classified into two modes based on grid connections, namely grid-connected mode and islanded mode. An islanded microgrid is a small-scale, localized, and self-sustained energy system that can generate, store, and distribute electricity, independently [3]. The term islanded refers to a microgrid that can operate as an autonomous entity. An islanded microgrid is often designed to serve a specific geographical area, group of customers, industry, etc. The major advantages of an islanded microgrid are as follows: (1) enhancement of energy security, (2) reduction in greenhouse gas emissions, (3) improvement in resilience of local energy infrastructure, etc.

In a microgrid, various sources deliver electric power to meet continuously varying load demands. In general, non-conventional sources are preferred over conventional ones, due to environmental and economic reasons [4]. Non-conventional sources such as a biodiesel engine generator (BDEG), biogas turbine generator (BGTG), wind turbine generator (WTG) plant, solar photovoltaic (SPV) power plant, aqua-electrolyzer (AE)-based fuel-cell (FC), etc. are preferred to meet load demand [5,6,7,8,9,10,11,12]. Among these sources, SPV plants and WTG plants are highly stochastic in nature and weather-dependent. To make a system reliable, conventional sources such as a diesel engine generator (DEG) are incorporated into the system as a backup generation source [13]. Moreover, energy storage devices (ESDs) are incorporated into the model to store the excess power and to deliver the stored power during switching or emergencies. In [2,5,6,9], the authors considered a flywheel energy storage system (FESS), battery energy storage system (BESS), and ultra-capacitor as main storage units. In addition to this, superconducting magnetic energy storage (SMES) is also incorporated in the microgrid model due to its fast dynamic response [10]. Recently, electric vehicles (EVs) gained attention in frequency control due to their high energy density and bidirectional charging-discharging ability [14]. In addition to this, eco-friendly sources such as BGTG and BDEG are utilized with DGUs and ESD units to supply the load [7,8].

Generally, frequency oscillations occur in the system due to sudden changes in load demand, which causes a mismatch in generated output power and load power [14,15]. Similarly, uncertainty occurs in the system, caused by variations in load, wind power output, and solar power output leading to frequency oscillations. These oscillations are compensated by decreasing or increasing the active power of controllable sources [6,11,16,17,18,19,20,21]. In [11], a micro-turbine generator (MTG) is utilized as a controllable source to compensate for power variations of solar and wind sources. Further, some control mechanisms like proportional integral-proportional derivative (PI-PD) [5], PD-PI [2,7], type-2 fuzzy proportional integral derivative (PID) [1,6], PID [11], and $H_{\infty }$ [3,14] controllers are employed to mitigate frequency deviation in the microgrid.

The primary objective of designing a PID controller is to maintain the frequency within a predefined limit. There are several advanced versions of PID controllers such as adaptive PID, auto-tuned PID, and intelligent PID controller [11,16,17,18,19] available in the literature for different applications [22,23]. Among these, the conventional PID controller is widely employed in frequency regulation due to simplicity in design and well-accepted performance [24]. A PID controller must be tuned properly to obtain the desired performance. The performance of the PID controller depends on three tuning parameters, i.e., a proportional constant, an integral constant, and a derivative constant. The manual tuning of the PID controller is time-consuming and needs an expert [6]. So, controller tuning with the help of rule-based methods is a preferred solution over manual tuning. Rule-based tuning methods require an accurate process model, which is generally challenging to obtain [25]. Moreover, a mathematical model of the power system is of higher order due to interconnection, which is less appropriate and comparatively complex for control design. Due to this, a higher-order transfer function (HOTF) may be converted into a lower-order transfer function (LOTF) using approximation methods.

In this article, the linearized transfer function of an islanded microgrid and its approximated first-order model are derived. The validation of the approximated model is carried out through step, impulse, and Bode diagrams. Further, a PID controller is designed to regulate the frequency of the islanded microgrid within acceptable bounds. To obtain PID controller gains, tuning is processed with rule-based methods. To implement rule-based methods, a first-order plus dead time (FOPDT) model of the system is needed. To achieve this, various approximation methods have appeared in the literature [26,27,28]. In this article, a step response-based reaction curve is utilized to obtain the FOPDT model. Based on this FOPDT model, rule-based PID tuning is proposed. The PID controller’s applicability in mitigating frequency deviation is illustrated by different plots. Additionally, a comparative study is conducted for frequency regulation for rule-based PID control design. The highlights of the presented article are as follows:

• To represent the islanded microgrid model mathematically, an equivalent transfer function is derived with the help of the first-order transfer function of all DGUs and ESDs.
• The derived transfer function is approximated into FOPDT form for ascertainment of suitable controller gain parameters.
• PID controller tuning is processed with rule-based tuning methods such as Ziegler–Nichols (ZN) step response method [29], Chien–Hrones–Reswick (CHR) method [30], approximate m-constrained integral gain optimization (AMIGO) method [31], Wang and Cluett (WC) method [32], Wang–Chan–Juang (WCJ) method [24], and Cohen–Coon (CC) method [33].
• Frequency regulation analysis for all rule-based controllers is conducted.
• The utility of the PID control design and employed rule-based controller tuning methods used to mitigate frequency deviation is analyzed by presenting step response, impulse response, Bode plot, and frequency deviation plot.

A brief outline of this contribution is summarized as follows. Generalized architecture and a brief description of DGUs and ESDs with equivalent transfer functions are discussed in Section 2. Section 3 demonstrates PID controller design with rule-based tuning methods. The overall transfer function and approximated transfer function of the islanded microgrid are derived in Section 4. The implementation of rule-based methods and comparative study with controller and without controller are also provided in this section. This discussion follows conclusions that are provided in Section 5.

2. Islanded-Microgrid: Architecture and Description

In general, an islanded microgrid includes DGUs, ESDs, loads, controllers, and power converters [34]. DGUs are of small ratings and may be conventional and non-conventional. It is important to understand that the output power of non-conventional sources like solar and wind is variable and uncertain due to variable weather conditions, geographic conditions, etc. To improve overall system reliability, DGUs and ESDs are interconnected through converters.

The schematic block diagram of the islanded microgrid considered in this work is shown in Figure 1. This model consists of different DGUs such as WTG, SPV panel, DEG, BDEG, BGTG, and MT units. Further, ESDs such as BESS, FESS, AE, FC, and EV units are incorporated. Power produced by DGUs is used to meet load demand, while excess power is stored in ESDs. Converters convert the electric power of DGUs and ESDs into the desired form. A brief overview of the mathematical modeling of DGUs and ESDs with their generalized representation in transfer function form is discussed as follows.

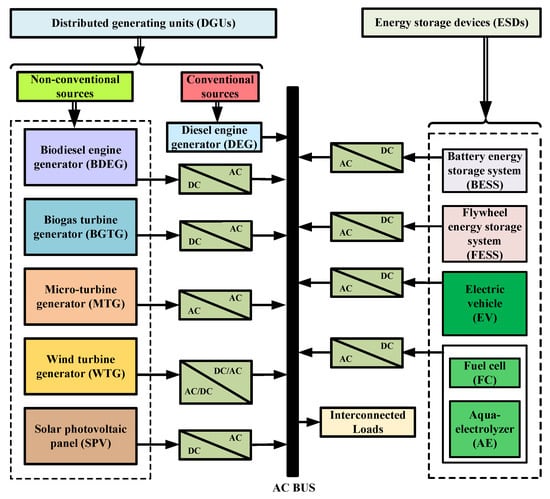
Figure 1. Schematic diagram of islanded microgrid.

2.1. Mathematical Models of Microgrid Components

2.1.1. Diesel Engine Generator

A DEG is a conventional source utilized as a backup power source to produce electrical power through fuel combustion [35]. DEG can be modeled as a first-order transfer function $\left(T{F}_{deg}\left(s\right)\right)$, which is expressed in (1).

$$T{F}_{deg}\left(s\right)=\frac{K_{deg}}{1+s{T}_{deg}}$$

(1)

In (1), $K_{deg}$ and $T_{deg}$ stand for gain and time constant of the DEG.

2.1.2. Solar Photovoltaic Panel

The SPV panel converts solar power into electrical power. Produced output power depends on the surface temperature and the amount of radiation that falls on the panel [36]. Overall the SPV system can be represented by first-order transfer function $\left(T{F}_{spv}\left(s\right)\right)$, which is expressed as

$$T{F}_{spv}\left(s\right)=\frac{K_{spv}}{1+s{T}_{spv}}$$

(2)

where $K_{spv}$ and $T_{spv}$ are the gain and time constant of the SPV system, respectively.

2.1.3. Wind Turbine Generator

The WTG produces electrical power utilizing the wind speed [35,36]. The first-order transfer function $\left(T{F}_{wt}\left(s\right)\right)$ of the WTG can be expressed as given in (3).

$$T{F}_{wt}\left(s\right)=\frac{K_{wt}}{1+s{T}_{wt}}$$

(3)

The time constant and gain of the WTG model are represented by the variables $T_{wt}$ and $K_{wt}$, respectively.

2.1.4. Biogas Turbine Generator

Animal waste and biodegradable garbage are used to produce biogas. Produced biogas is used to generate electricity [8]. The transfer function $\left(T{F}_{bgtg}\left(s\right)\right)$ of a BGTG can be shown as written in (4).

$$T{F}_{bgtg}\left(s\right)=\frac{1+s{X}_d}{(1+s{Y}_d)(1+s{d}_v)}·\frac{1+s{T}_{cri}}{1+s{T}_{bgd}}·\frac{1}{1+s{T}_{btt}}$$

(4)

In (4), $X_d$, $Y_d$, $d_v$, $T_{cri}$, $T_{bgd}$, and $T_{btt}$ refer to lead time, lag time, actuator-valve delay, combustion reaction delay, bio-gas delay, and discharge time constant of the BGTG, respectively. Further, the approximated first-order model of (4) can be represented as

$$T{F}_{bgtg}\left(s\right)\approx \frac{K_{bgtg}}{1+s{T}_{bgtg}}$$

(5)

where $K_{bgtg}$ and $T_{bgtg}$ refer to the gain and time constant of the approximated model of BGTG, respectively.

2.1.5. Biodiesel Engine Generator

Biodiesel is extracted from plants utilizing chemical methods. This biodiesel is used to generate electrical power [7,8]. The linearized transfer function $\left(T{F}_{bdeg}\left(s\right)\right)$ of BDEG model is given as follows:

$$T{F}_{bdeg}\left(s\right)=\frac{K_{va}}{1+s{T}_{va}}·\frac{K_{be}}{1+s{T}_{be}}\approx \frac{K_{bdeg}}{1+s{T}_{bdeg}}$$

(6)

where $K_{va}$, $T_{va}$, $K_{be}$, and $T_{be}$, respectively, represent valve gain, valve actuator delay, engine gain, and engine time constant of BDEG, respectively. Further, $K_{bdeg}$ and $T_{bdeg}$ represent the gain and time constant of the approximated first-order model of the BDEG.

2.1.6. Micro-Turbine Generator

The MTG is a small-sized turbine generator set used to produce electricity with the help of liquid or gaseous fuel [14]. The first-order transfer function $\left(T{F}_{mt}\left(s\right)\right)$ of MTG is given in (7).

$$T{F}_{mt}\left(s\right)=\frac{K_{mt}}{1+s{T}_{mt}}$$

(7)

In (7), $K_{mt}$ and $T_{mt}$ represent the gain and time constant of the MTG, respectively.

2.1.7. Aqua-Electrolyzer Fuel Cell

The AE transforms the excess power into hydrogen during off-peak hours and releases it during peak loads. FC uses stored hydrogen as a fuel to produce electrical energy [6,7,37]. The equivalent transfer function $\left(T{F}_{ae-fc}\left(s\right)\right)$ of the AE-based FC unit can be modeled as

$$T{F}_{ae-fc}\left(s\right)=\frac{K_{ae-fc}}{1+s{T}_{ae-fc}}$$

(8)

where $K_{ae-fc}$ and $T_{ae-fc}$ refer to the gain and time constant of AE-based FC unit, respectively.

2.1.8. Battery Energy Storage

The BESS is used to maintain dynamic stability by providing instantaneous power to load for a short time [36]. The first-order transfer function $\left(T{F}_{bess}\left(s\right)\right)$ of BESS can be written as

$$T{F}_{bess}\left(s\right)=\frac{K_{bess}}{1+s{T}_{bess}}$$

(9)

where $K_{bess}$ and $T_{bess}$ are termed as the gain and time constant of BESS, respectively.

2.1.9. Flywheel Energy Storage

The FESS stores excess energy in the form of kinetic energy during off-peak hours and releases it during peak load conditions [36]. The transfer function $\left(T{F}_{fess}\left(s\right)\right)$ of FESS can be given as

$$T{F}_{fess}\left(s\right)=\frac{K_{fess}}{1+s{T}_{fess}}$$

(10)

where $K_{fess}$ and $T_{fess}$ represent gain and time constant of FESS, respectively.

2.1.10. Electric Vehicle

An EV can be used as a storage system that can provide power during an emergency to maintain system stability [35]. The first-order transfer function $\left(T{F}_{ev}\left(s\right)\right)$ of EV can be given as shown in (11).

$$T{F}_{ev}\left(s\right)=\frac{K_{ev}}{1+s{T}_{ev}}$$

(11)

In (11), $K_{ev}$ and $T_{ev}$ represent the gain and time constant of EV, respectively.

2.1.11. Generator Dynamics

The transfer function $\left(T{F}_{gd}\left(s\right)\right)$ of the equivalent dynamic microgrid model can be represented as

$$T{F}_{gd}\left(s\right)=\frac{1}{D+sM}$$

(12)

where M is the equivalent inertia constant and D is the damping constant.

2.2. Block Diagram of Islanded Microgrid

The block diagram representation of the islanded microgrid given in Figure 1 is depicted in Figure 2. It consists of two loops namely primary control loop and secondary control loop. The primary control loop consists of ESDs whereas the secondary control loop consists of controllable DGUs. Additionally, uncontrollable DGUs like solar and wind are considered disturbances due to their variable power generation. Mathematical models of DGUs and ESDs are expressed in (1)–(12).

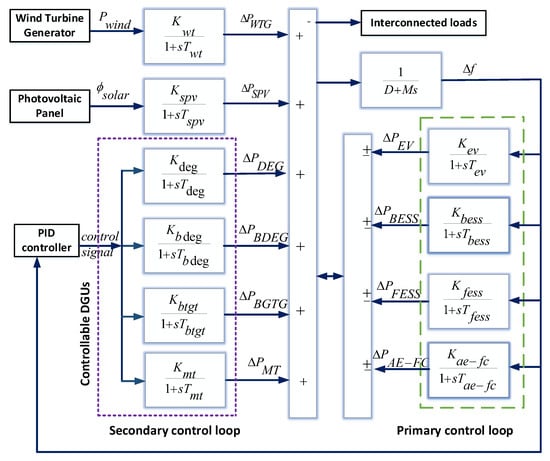
Figure 2. Block diagram of islanded microgrid.

The nominal values and equivalent first-order transfer functions of all DGUs and ESDs utilized in this model are depicted in Table 1. The sources like solar and wind are highly stochastic in nature and weather-dependent. Due to this, the generated output power of such sources is variable. To maintain the balance of generated power and load power, controllable DGUs such as BGDG, BGTG, MT, and DEG, are regulated. Additionally, ESDs act as backup power sources and provide sufficient power to load for a short time in emergency conditions. Power adjustments through ESDs act as primary control whereas power management by controllable sources represents secondary control.

Table 1. Equivalent first-order transfer functions of DGUs and ESDs [3,8,14,36,38].

DGUs/ESDs	Transfer Function and Parameters of DGUs and ESDs
	Equation Number	Parameters	Nominal Transfer Function
DEG	(1)	$T_{deg}=2$,	$T{F}_{deg}\left(s\right)=\frac{0.003}{1 + 2s}$
		$K_{deg}=0.003$
SPV	(2)	$T_{spv}=1.8$,	$T{F}_{spv}\left(s\right)=\frac{1}{1 + 1.8s}$
		$K_{spv}=1$
WTG	(3)	$T_{wt}=1.5$,	$T{F}_{wt}\left(s\right)=\frac{1}{1 + 1.5s}$
		$K_{wt}=1$
BGTG	(4)	$T_{bgtg}=0.55$,	$T{F}_{bdeg}\left(s\right)=\frac{1}{1 + 0.550s}$
		$K_{bgtg}=1$
BDEG	(6)	$T_{bdeg}=0.148$,	$T{F}_{bgtg}\left(s\right)=\frac{1}{1 + 0.148s}$
		$K_{bdeg}=1$
MT	(7)	$T_{mt}=1.5$,	$T{F}_{mt}\left(s\right)=\frac{1}{1 + 1.5s}$
		$K_{mt}=1$
AE-FC	(8)	$T_{ae}=0.5$,	$T{F}_{ae-fc}\left(s\right)=\frac{0.002}{1 + 0.5s}$
		$K_{ae}=0.002$
BESS	(9)	$T_{bess}=0.1$,	$T{F}_{bess}\left(s\right)=\frac{-0.003}{1 + 0.1s}$
		$K_{bess}=-0.003$
FESS	(10)	$T_{fess}=0.1$,	$T{F}_{fess}\left(s\right)=\frac{-0.01}{1 + 0.1s}$
		$K_{fess}=-0.01$
EV	(11)	$T_{ev}=0.9$,	$T{F}_{ev}\left(s\right)=\frac{-0.7}{1 + 0.9s}$
		$K_{ev}=-0.7$
Generator dynamics	(12)	$D=0.3$,	$T{F}_{gd}\left(s\right)=\frac{1}{0.3 + 0.4s}$
		$M=0.4$

The equivalent model of Figure 2 is demonstrated in Figure 3 by highlighting DGUs, ESDs, and equivalent system dynamics with their control signals, i.e., $P_{DGUs}$, $P_{ESDs}$, $P_{TOTAL}$, $\mathsf{\Delta }f$ and disturbance signal $D\left(s\right)$.

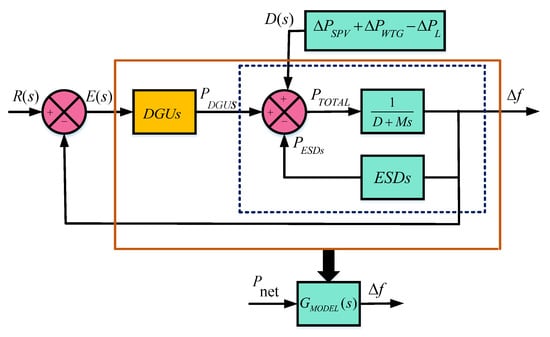
Figure 3. Equivalent block diagram of islanded microgrid depicted in Figure 2.

The equivalent forward path transfer function can be represented as $G_{MODEL}\left(s\right)$. The mathematical representation of $G_{MODEL}\left(s\right)$ in transfer function form can be written as

$$G_{MODEL}\left(s\right)=\frac{\mathsf{\Delta }f\left(s\right)}{\mathsf{\Delta }{P}_{net}\left(s\right)}$$

(13)

where

$$\mathsf{\Delta }f\left(s\right)=\sum _{i=0}^{n-1}{N}_i{s}^i$$

(14)

$$\mathsf{\Delta }{P}_{net}\left(s\right)=\sum _{i=0}^n{D}_i{s}^i$$

(15)

In (14) and (15), numerator coefficients are denoted as $N_i$ for $i=0,1,2,3,\dots ,(n-1)$, while denominator coefficients are denoted as $D_i$ for $i=0,1,2,3,\dots ,n$, respectively. This model is utilized to analyze the dynamic behavior of frequency deviations in the islanded microgrid.

2.3. Relation between Frequency Deviation and Net Generated Power

To maintain frequency within an acceptable range, variations in the interconnected load and output power of wind and solar are compensated by decreasing or increasing output powers of controllable DGUs. The power produced through DGUs and ESDs is the total generated power ($P_{TOTAL}$) that is available to meet load power ($P_L$). The total power comprises the output powers of WTG, SPV, DEG, MT, BGDG, and BGTG, and exchangeable powers of FESS, BESS, AE-FC, and EV, which is shown as

$$P_{TOTAL}=P_{WTG}+P_{SPV}+P_{DEG}+P_{BDEG}+P_{BGTG}+P_{MT}\pm P_{BESS}\pm P_{FESS}\pm P_{AE-FC}\pm P_{EV}$$

(16)

The power balance equation of the model at any moment is depicted by net power $\left(P_{\mathrm{net}}\right)$ which is depicted as

$$P_{\mathrm{net}}=\mathsf{\Delta }{P}_{WTG}+\mathsf{\Delta }{P}_{SPV}+\mathsf{\Delta }{P}_{DEG}+\mathsf{\Delta }{P}_{BDEG}+\mathsf{\Delta }{P}_{BGTG}+\mathsf{\Delta }{P}_{MT}\pm \mathsf{\Delta }{P}_{BESS}\pm \mathsf{\Delta }{P}_{FESS}\pm \mathsf{\Delta }{P}_{AE-FC}\pm \mathsf{\Delta }{P}_{EV}-\mathsf{\Delta }{P}_L$$

(17)

The net power $\left(P_{\mathrm{net}}\right)$ is the difference between total generated power and load power. A mismatch between total power and load power creates a difference that leads to frequency deviations ($\mathsf{\Delta }f$). A relation between $\mathsf{\Delta }f$ and $P_{\mathrm{net}}$ is expressed as

$$\mathsf{\Delta }f=\frac{1}{Ms+D}{P}_{\mathrm{net}}$$

(18)

Frequency deviation ($\mathsf{\Delta }f$) can be mitigated by maintaining the balance between ($P_{TOTAL}$) and $P_L$. To keep $\mathsf{\Delta }f$ within set bounds, the active power of ESDs and controllable DGUs is adjusted through some control mechanism. In this article, a PID controller is implemented to eliminate frequency deviation in the islanded microgrid.

2.4. Proportional Integral Derivative Controller

The major concern regarding the islanded microgrid containing RESs is ensuring frequency stability. To keep the frequency variation within set bounds, the active power of ESDs and DGUs is adjusted as per load variation. Proper coordination among DGUs and ESDs is required to regulate power flow and maintain the desired frequency. To achieve this purpose, a PID controller is designed and implemented. Closed loop control of islanded microgrid for frequency regulation is depicted in Figure 4.

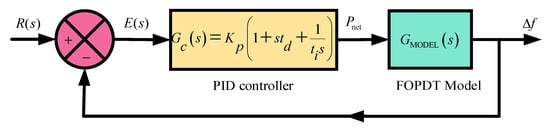
Figure 4. PID controller with islanded microgrid.

The PID controller is a widely used feedback controller in industry and provides excellent control performance under varying dynamics of the system [6]. The block diagram of the PID controller is shown in Figure 5. The mathematical representation of the PID controller in the time domain is given in (19).

$$u\left(t\right)=k_{p}e\left(t\right)+\frac{1}{t_i}{\int }_0^{t}e\left(t\right)dt+t_d\frac{de\left(t\right)}{dt}$$

(19)

In (19), $u\left(t\right)$ is controller output, $e\left(t\right)$ is the error between the desired and measured values. The constants $t_i$ and $t_d$ are the integral and derivative time constants. The PID controller [39] operates in three modes such as proportional, integral, and derivative. The working of each mode is briefly discussed as follows:

• Proportional term reduces the rise time. However, it does not eliminate steady-state error. A large proportional gain value can cause system instability. While, a small gain results in a smaller output response.
• Integral term eliminates steady-state errors. But it may have large values of transient response. Overshoot may be caused by a high integral gain. While sluggishness may be caused by a low integral gain.
• Derivative term increases the system’s stability, reduces overshoot, and improves transient response. A large derivative gain may make the system unstable.

The performance of the PID controller depends on the tuning of controller parameters. To tune PID parameters, rule-based approaches are utilized in this article.

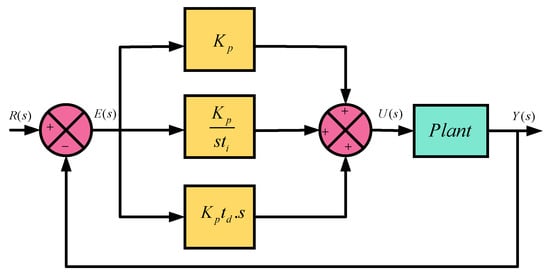
Figure 5. Block diagram of PID controller.

3. Controller Tuning: Rule-Based Methods

The designing of the PID controller means obtaining values of tuning parameters, i.e., $K_p$, $K_i$, and $K_d$, satisfying closed-loop system performance. Rule-based methods such as ZN step method [29], CHR method [30], WC method [32], WCJ method [40], AMIGO method [31], and CC method [33] are utilized to obtain the values of controller parameters. Rule-based methods are simple to use and have fixed formulae for the calculation of controller parameters [31,41]. To design a rule-based PID controller, the FOPDT model is essential, as these rules apply to the FOPDT model [31].

To achieve the FOPDT model, an approximation of a higher-order transfer function is carried out. Approximation methods such as Skogestad half rule method [27], Taylor series method [28], and reaction curve method [26], etc., are available in the literature [26,27,28]. In this article, the reaction curve method is utilized to obtain the FOPDT model. The generalized FOPTD model can be expressed as given in (20).

$$G_{FOPTD}=\frac{K}{1+s{T}_m}{e}^{-T_{d}s}$$

(20)

In (20), K, $T_m$, and $T_d$ represent the gain, time constant, and delay time of the FOPDT model. Based on these parameters ($K,T_m,T_d$), parameters $a,\tau ,\alpha$ are framed, which are depicted in (21).

$$a=\frac{k{T}_d}{T_m}, \tau =\frac{T_d}{T_d+T_m},\alpha =\frac{T_m}{T_a}$$

(21)

The parameters given in (20) and (21) are utilized in rule-based tuning to obtain PID controller gains. The formulation of controller gains using the parameters of (20) and (21) is explained as follows.

3.1. Ziegler–Nichols Method

This method was first proposed by Ziegler and Nichols (ZN) for tuning PID parameters [29]. This method applies to S-shaped step response and is widely used in industries. This method is applicable for the FOPDT model, which is depicted in (20). The ZN tuning rule for PID controller is shown in Table 2.

Table 2. Tuning parameters for ZN method.

Method	${\mathit{K}}_{\mathit{p}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{t}}_{\mathit{d}}$
ZN	$1.2T_m/T_d$	$2T_d$	$T_d/2$

3.2. Cohen–Coon Method

The ZN method exhibits a sluggish steady-state response when there is a substantial process delay as compared to the open-loop time constant [33]. The Cohen–Coon (CC) method provides a solution to overcome the limitations of the ZN method by modifying tuning rules with the help of parameter a. Table 3 provides the CC tuning rule for PID gains utilizing FOPDT parameters.

Table 3. Tuning parameters for CC method.

Method	${\mathit{K}}_{\mathit{p}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{t}}_{\mathit{d}}$
CC	$\frac{1.35}{a}\left(1+\frac{0.18T_m}{1 - T_m}\right)$	$\frac{2.5 - 2T_m}{1 - 0.39T_m}{T}_d$	$\frac{0.37 - 0.37T_m}{1 - 0.81T_m}{T}_d$

3.3. Wang–Cluett Method

Wang and Cluett [42] considered the FOPDT model and conducted an experimental study to derive a tuning rule for the PID controller. The tuning rule utilizes parameters ($T_m,K,T_d$) of reaction curve response and parameter $\alpha$. Utilizing $\alpha$, the tuning rule is framed and is depicted in Table 4.

Table 4. Tuning parameters for WC method.

Method	${\mathit{K}}_{\mathit{p}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{t}}_{\mathit{d}}$
WC	$\frac{0.13 + 0.51T_d}{K}$	$\frac{\alpha (0.25 + 0.96T_d)}{0.93 + 0.03T_d}$	$\frac{\alpha (-0.03 + 0.28T_d)}{0.25 + T_d}$

3.4. Wang–Chan–Juang Method

The Wang–Chan–Juang (WCJ) tuning method provides good performance for many processes and can achieve a desired trade-off between stability and performance [40]. The tuning rule for PID parameters is tabulated in Table 5.

Table 5. Tuning parameters for WCJ method.

Method	${\mathit{K}}_{\mathit{p}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{t}}_{\mathit{d}}$
WCJ	$\frac{\left(0.7303 + \frac{0.5307T_m}{T_d}\right)\left(T_m + 0.5T_d\right)}{K\left(T_m + T_d\right)}$	$T_m+0.5T_d$	$\frac{0.5T_m{T}_d}{T_m + 0.5T_d}$

3.5. Chien–Hrones–Reswick Method

The Chien–Hrones–Reswick (CHR) method evolved from the Ziegler–Nichols step response method. The CHR method possesses the flexibility of fine-tuning for both set point (SP) tracking and load rejection (LR) [30]. The CHR method provides tuning rules for no overshoot, i.e., 0% and a 20% overshoot. Table 6 outlines tuning rules for the PID controller for set point tracking and load rejection based on $T_m$ and $T_d$.

Table 6. Tuning parameters for CHR method.

Method	With 0% Overshoot			With 20% Overshoot
	${\mathit{K}}_{\mathit{p}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{t}}_{\mathit{d}}$	${\mathit{K}}_{\mathit{p}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{t}}_{\mathit{d}}$
$CH{R}_{SP}$	$\frac{0.6}{a}$	$T_m$	$0.5T_d$	$\frac{0.95}{a}$	$1.4T_m$	$0.47T_d$
$CH{R}_{LR}$	$\frac{0.95}{a}$	$2.4T_m$	$0.42\ast T_d$	$\frac{1.2}{a}$	$2T_m$	$0.42T_d$

3.6. Approximate M-Constrained Integral Gain Optimization Method

Approximate m-constrained integral gain optimization (AMIGO) is a design method obtained using simple parameter fitting [41]. The parameters of the model are determined by the 63% rule. This method utilizes parameters of the reaction curve to frame a rule for the calculation of controller parameters. The tuning rule for PID parameters is tabulated in Table 7.

Table 7. Tuning parameters for AMIGO method.

Method	${\mathit{K}}_{\mathit{p}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{t}}_{\mathit{d}}$
AMIGO	$\frac{1}{K}\left(0.2+0.4(T_m/T_d)\right)$	$\frac{\left(0.4T_d + 0.8T_m\right)}{T_d + 0.1T_m}$	$\frac{0.5T_d{T}_m}{0.3T_d + T_m}$

4. Results and Discussion

This section first presents the transfer function for an islanded microgrid and its approximated first-order model that is validated using step, impulse, and Bode diagrams. Further, rule-based methods, namely ZN, AMIGO, CC, CHR, WC, and WCJ are utilized to design a PID controller for frequency regulation of the islanded microgrid. A comparative study of these rule-based methods and tuned PID controllers is performed for frequency regulation.

4.1. Overall Model of Islanded Microgrid

The transfer function of the islanded microgrid is obtained considering deviation in frequency $\mathsf{\Delta }f$ as an output variable and deviation in net power $\mathsf{\Delta }{P}_{\mathrm{net}}$ as input variable using (13) and Figure 2. The equivalent transfer function of the islanded microgrid is expressed in (22).

$$G_{MODEL}=\frac{\mathsf{\Delta }f}{\mathsf{\Delta }{P}_{net}}=\frac{{\sum }_{i=0}^7{N}_i{s}^i}{{\sum }_{i=0}^9{D}_i{s}^i}$$

(22)

The numerator and denominator coefficients of the islanded microgrid represented by $G_{MODEL}$, are provided in Table 8.

Table 8. Coefficients of equivalent transfer function of islanded microgrid.

Numerator’s Coefficients		Denominator’s Coefficients
$N_0$	3.003	$D_0$	0.587
$N_1$	16.67	$D_1$	4.882
$N_2$	34.58	$D_2$	16.19
$N_3$	33.32	$D_3$	27.32
$N_4$	15.03	$D_4$	24.86
$N_5$	2.832	$D_5$	12.13
$N_6$	0.2324	$D_6$	3.147
$N_7$	0.00694	$D_7$	0.44
-	-	$D_8$	0.0312
-	-	$D_9$	0.00087

The transfer function of the proposed model, as depicted in (22), is of the ninth order. This ninth-order transfer function is approximated into the first-order model using the reaction curve method. The reaction curve for (22) is depicted in Figure 6. The corresponding parameters are tabulated in Table 9. The desired approximated FOPTD model for the islanded microgrid, as demonstrated in (22), is expressed in (23), obtained with the help of Table 9.

$$G_{FOPDT}=\frac{5.1877}{1+3.1265s}{e}^{-0.1471s}$$

(23)

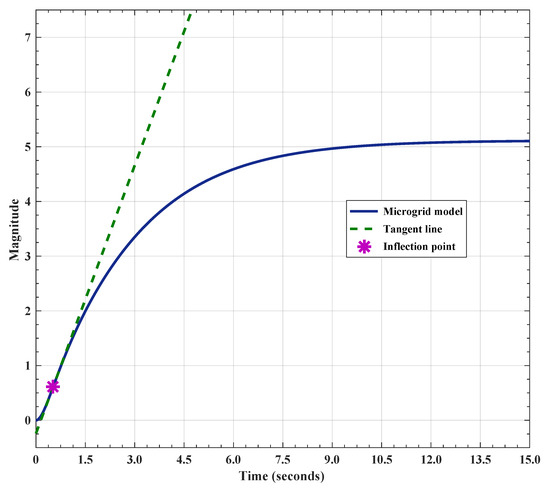
Figure 6. Reaction curve.

Table 9. Parameters of step response-based reaction curve.

Steady-State Gain (K)	Time Constant (${\mathit{T}}_{\mathit{m}}$)	Time Delay (${\mathit{T}}_{\mathit{d}}$)
5.1877	3.1265	0.1471

4.2. Validation of Approximated Model

To verify the response of the FOPDT model, step response analysis is performed, and is depicted in Figure 7. From Figure 7, it can be clearly observed that the approximated model response is stable and is similar to the response of the islanded microgrid system. Moreover, the approximated model also settles down at almost similar steady-state values. The approximated model’s peak value is acquired as $5.1877$ with no overshoot and no undershoot, which is similar to the respective time domain specifications of the microgrid system. Similar observations are identified in the case of the rise time and the peak time of the approximated model with respect to the microgrid system. The rise time of $5.6099$ s, and the peak time of $17.7748$ s are attained by the microgrid system, whereas the approximated model’s rise time and peak time are $6.8690$ s and $24.3327$ s, respectively. The settling time of the approximated model and microgrid system are also close to each other. To further verify the FOPDT model, impulse and Bode responses are plotted in Figure 8 and Figure 9, respectively. In the case of impulse and Bode responses, it is visible that the FOPDT model follows the microgrid system responses. The time domain specifications, i.e., rise time, peak time, settling time, and peak value for islanded microgrid and approximated model are tabulated in Table 10. Additionally, Table 11 is also provided to show the errors of the approximated microgrid model with respect to the islanded microgrid in terms of error indices. These error indices include integral absolute error (IAE), integral time absolute error (ITAE), integral squared error (ISE), and integral time squared error (ITSE). In Table 11, all error indices are in an acceptable range, which confirms the better manifestation of the approximated model for the microgrid system. Based on Figure 8 and Figure 9 and Table 10 and Table 11, it can be concluded that the FOPDT model replicates the islanded microgrid.

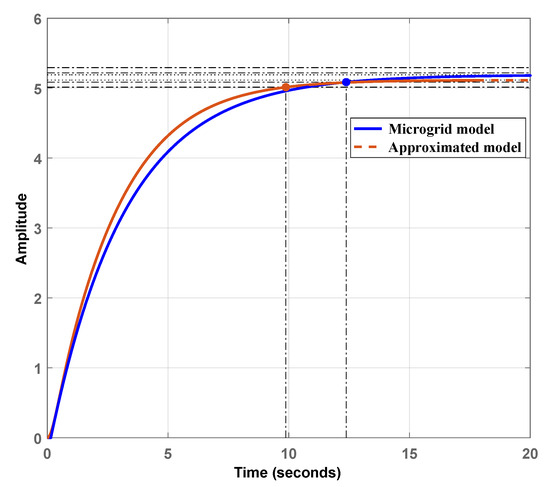
Figure 7. Step response of islanded microgrid model and its approximated model.

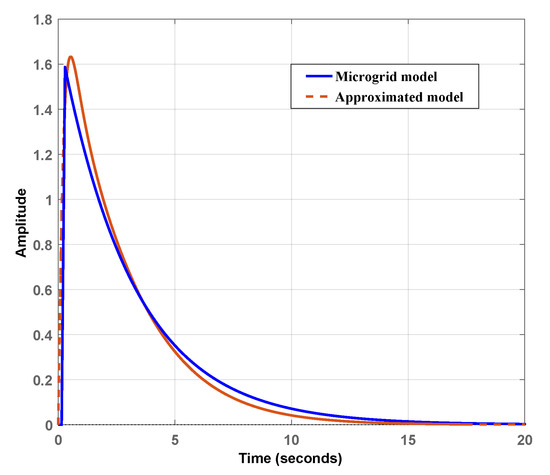
Figure 8. Impulse response of islanded microgrid model and its approximated model.

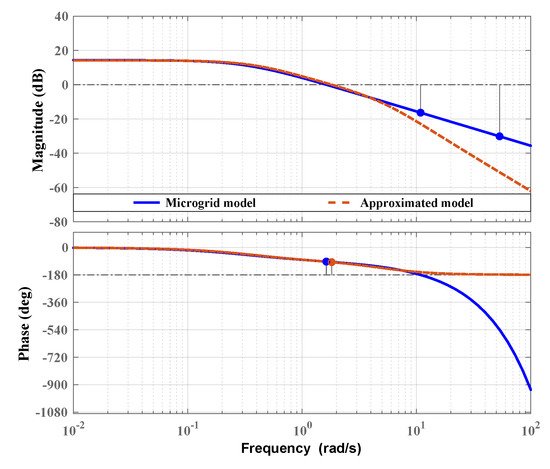
Figure 9. Bode plot of islanded microgrid model and its approximated model.

Table 10. Time domain specifications.

	Time Domain Specifications
	Rise Time (s)	Settling Time (s)	Peak	Peak Time (s)	Overshoot	Undershoot
Islanded microgrid	5.6099	9.8795	5.1123	17.7748	0	0
Approximated model	6.8690	12.3781	5.1877	24.3327	0	0

Table 11. Error indices of approximated microgrid model with respect to islanded microgrid.

Error Indices	IAE	ITAE	ISE	ITSE
Values	2.03053	14.12585	0.33672	1.72525

4.3. Frequency Regulation of Islanded Microgrid

The frequency response of the islanded microgrid without a controller is shown in Figure 10. It is observed that the presented response possesses a frequency deviation, and has an under-damped nature with a maximum overshoot ($M_P$) of 0.4 p.u. However, it shows good step-tracking performances with ±5.8% deviation. To mitigate the frequency deviation of the islanded microgrid, the PID controller is incorporated by employing rule-based tuning methods. These rule-based tuning methods are the ZN method, AMIGO method, CC method, CHR method, WC method, and WCJ method. The tuning parameters obtained using the aforementioned rule-based tuning methods for PID control design are tabulated in Table 12. With the help of tabulated tuning parameters, rule-based controller transfer functions are formulated. These formulated transfer functions are depicted in (24)–(29).

$$G_{ZN}=25.5129+\frac{86.7452}{s}+1.8759s$$

(24)

$$G_{CC}=5.5795+\frac{15.4666}{s}+0.3009s$$

(25)

$$G_{WC}=0.0395+\frac{0.1888}{s}+0.0005s$$

(26)

$$G_{CHR}=4.9180+\frac{16.7213}{s}+0.3616s$$

(27)

$$G_{AMIGO}=1.6779+\frac{0.3013}{s}+0.1217s$$

(28)

$$G_{WCJ}=24.2589+\frac{7.5808}{s}+1.7427s$$

(29)

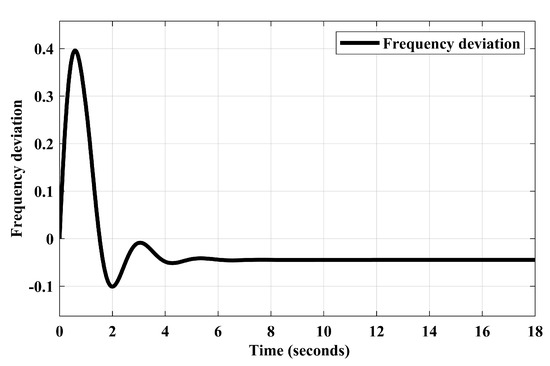
Figure 10. Frequency deviations of islanded microgrid without PID controller.

Table 12. Tuning parameters of various tuning methods.

Tuning Method	${\mathit{K}}_{\mathit{p}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{t}}_{\mathit{d}}$
ZN	25.5129	0.2941	0.0735
AMIGO	1.6779	5.5688	0.0725
CC	5.5795	0.3607	0.0539
CHR	4.9180	6.2531	0.0618
WC	0.0395	0.2093	0.0141
WCJ	24.2589	3.2001	0.0718

The impact of rule-based PID controllers on frequency deviation is depicted in Figure 11. From Figure 11, it can be easily recognized that the WCJ-tuned PID control design mitigates the frequency control in a better manner with the least deviation in comparison with other control design approaches. Additionally, Figure 12 is also provided to depict the control effort required for suppressing the frequency deviation. From Figure 12, it is clearly visible that the control effort required is minimal in the case of the WCJ-tuned PID controller.

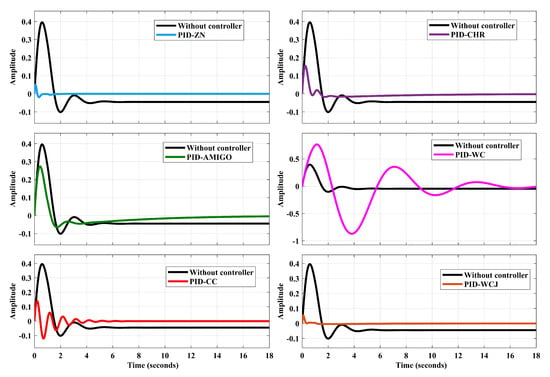
Figure 11. Frequency deviations for PID controller.

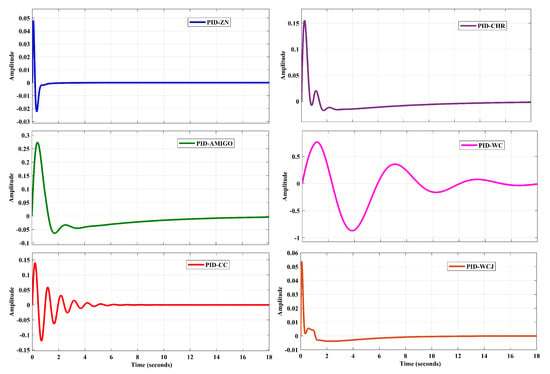
Figure 12. Comparative analysis of control signal of PID controller.

In the support of WCJ-tuned PID control design, time domain specifications of (24)–(29) are presented in Table 13. In Table 13, the settling time and peak time are found comparatively better for PID-WCJ (29), since the values, $0.4844$ s and $0.1733$ s, respectively, depict better values over other PID control design approaches provided in (24)–(28). Hence, time domain values presented in Table 13 also prove the efficacy of PID-WCJ control design over other approaches. Thus, from the findings and discussion, it is concluded that the WCJ method is found superior in comparison to other control design approaches in terms of frequency deviation and transient response.

Table 13. Time domain specifications corresponding to tuning rules.

Method	Time Domain Specifications
	Rise Time (s)	Settling Time (s)	Peak	Peak Time (s)	Overshoot	Undershoot
PID-ZN	0.0698	0.5369	1.2544	0.1786	25.4408	0
PID-AMIGO	0.5883	6.8357	0.9984	21.7943	0	0
PID-CC	0.1758	2.0267	1.4594	0.4385	45.9374	0
PID-CHR	0.2261	1.2370	1.1276	0.4558	12.7572	0
PID-WC	2.2228	18.5825	1.3544	5.590	35.4425	0
PID-WCJ	0.0760	0.4844	1.1710	0.1733	17.0960	0

5. Conclusions

The presented research article addresses the significant outcomes achieved in the frequency regulation of an islanded microgrid by employing a reaction curve-assisted Wang–Chan–Juaang (WCJ) tuning method for effective control design. The PID-based control design strategy is implemented on a linearized transfer function model of the islanded microgrid. The linearized islanded microgrid transfer function model is then approximated into an FOPDT form. One of the main contributions of this presented work is the successful utilization and implementation of the reaction curve method in the ascertainment of the FOPDT form of the linearized islanded microgrid transfer function model. Further, other rule-based methods, namely the ZN method, AMIGO method, CC method, CHR method, and WC method are involved in tuning the PID controller. A comparative analysis is conducted to identify the most effective tuning method to achieve better frequency regulation of the islanded microgrid. Among all rule-based tuning methods, the WCJ method performed better than other exploited tuning methods such as ZN, CHR, WC, AMIGO, and CC methods. To prove the effectiveness of the WCJ method, responses are presented to demonstrate its impact on transient response and frequency deviation. In support of the presented control design approach for frequency regulation of islanded microgrid system, tabulated data of tuning parameters and time domain specifications are also presented to validate the efficacy and applicability of the proposed control design strategy.

In the future, PID controller tuning can be accomplished by incorporating learning-based optimization approaches as an integration of advanced control techniques with experimental validation. Additionally, the fractional-order form of control design can be employed as an extended form of PID controller for frequency control. Another promising area for a possible extension of the presented work is the cyber-physical security of microgrids by addressing the cyber-physical security challenges associated with the implementation of advanced control strategies and resilience of microgrids.