Experimental Study on Gas-Liquid Two-Phase Stratified Flow at High Pressure in a Horizontal Pipe
Abstract
1. Introduction
2. Theoretical Basis of Experiments
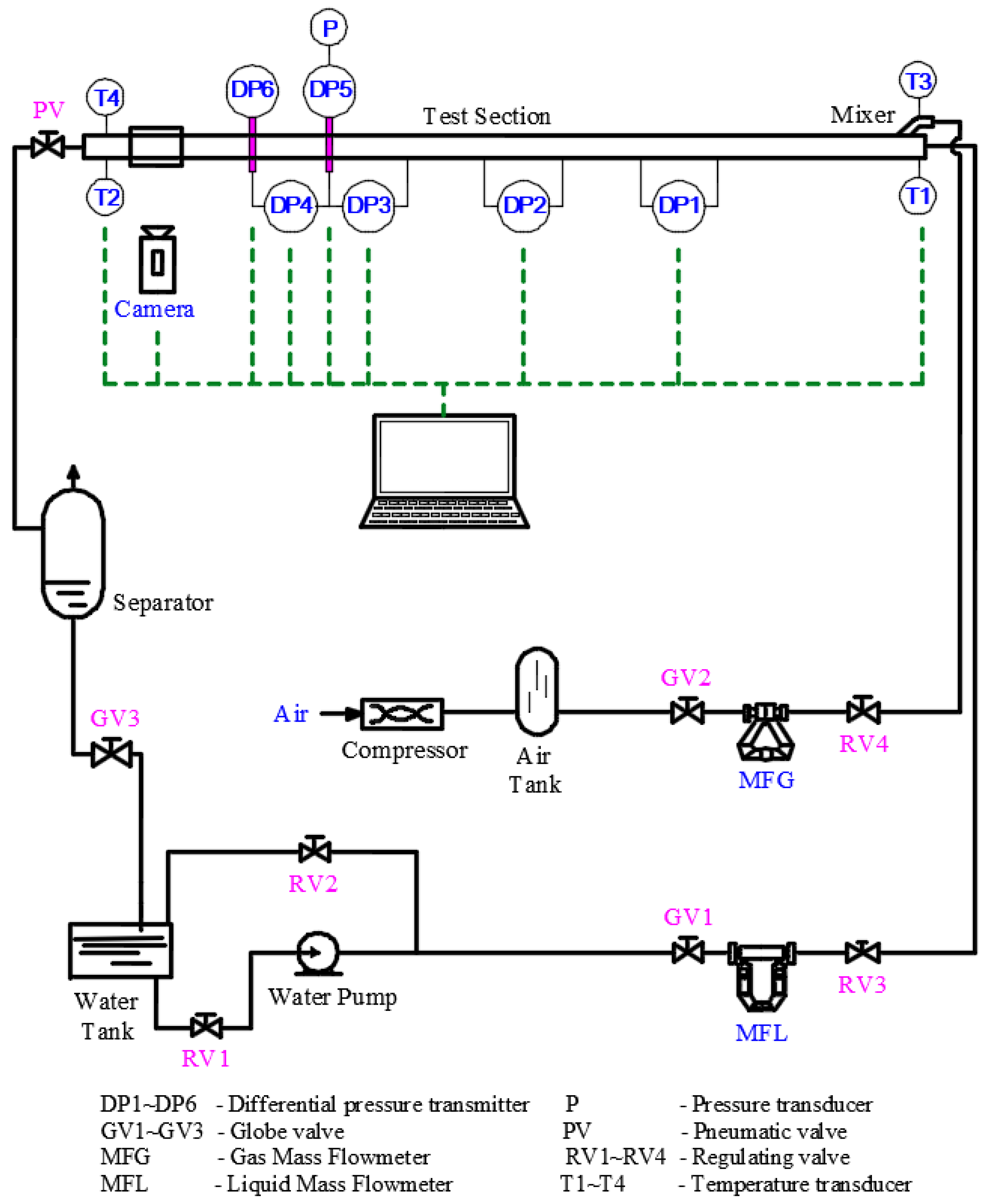
3. Experimental Facility
4. Results
4.1. Flow Pattern Map
4.2. Pressure Influence on Interface Profile
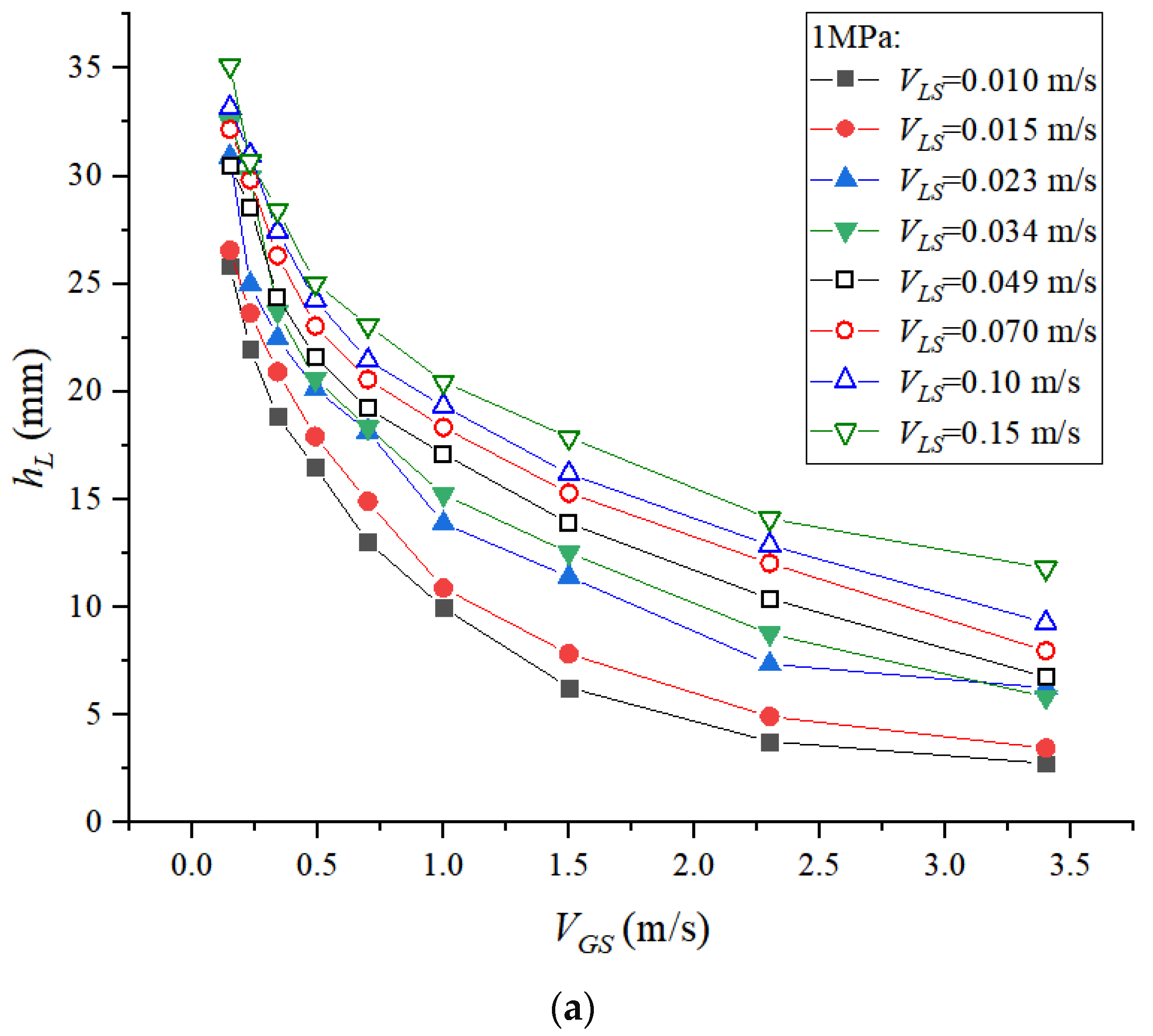
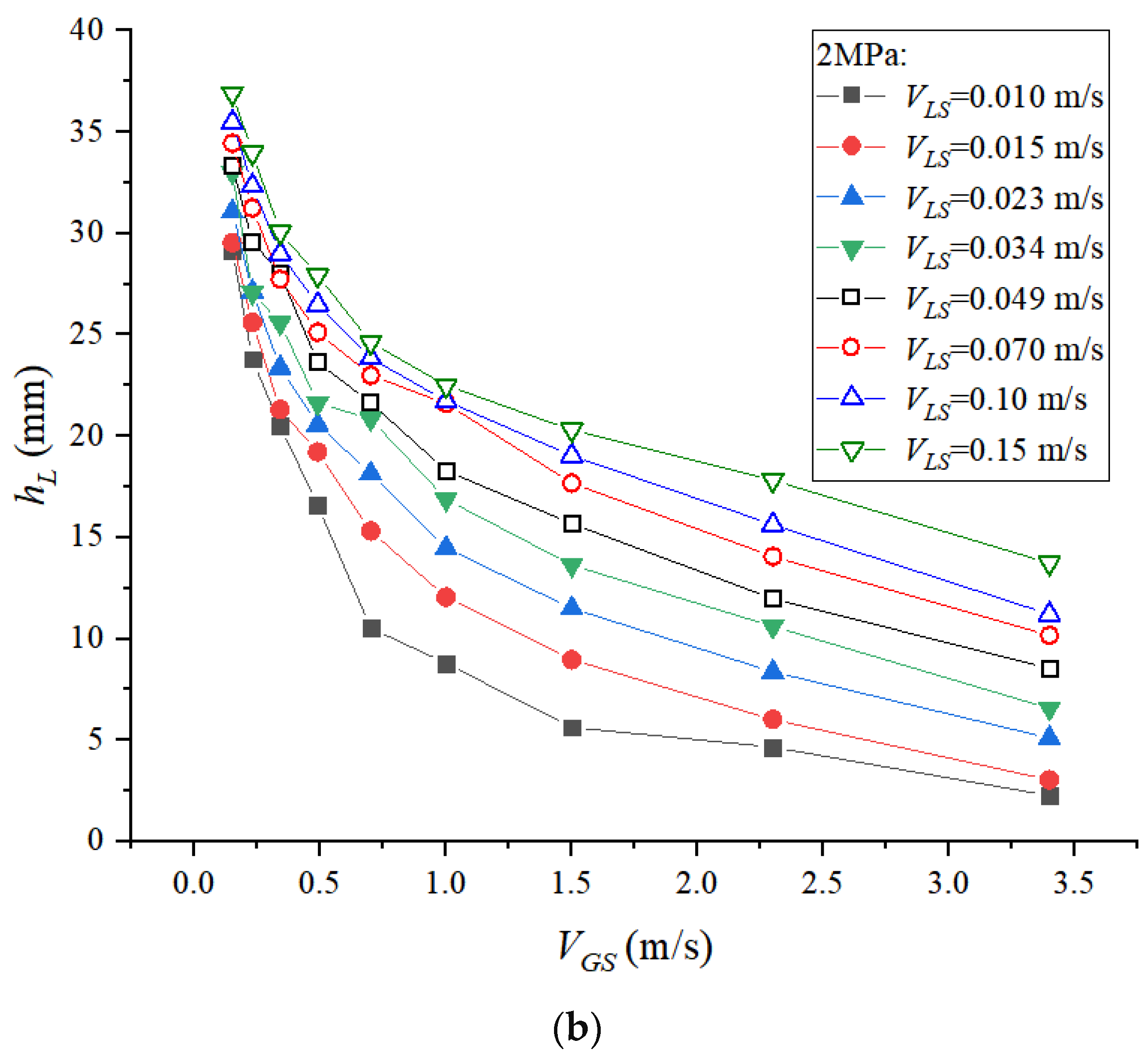
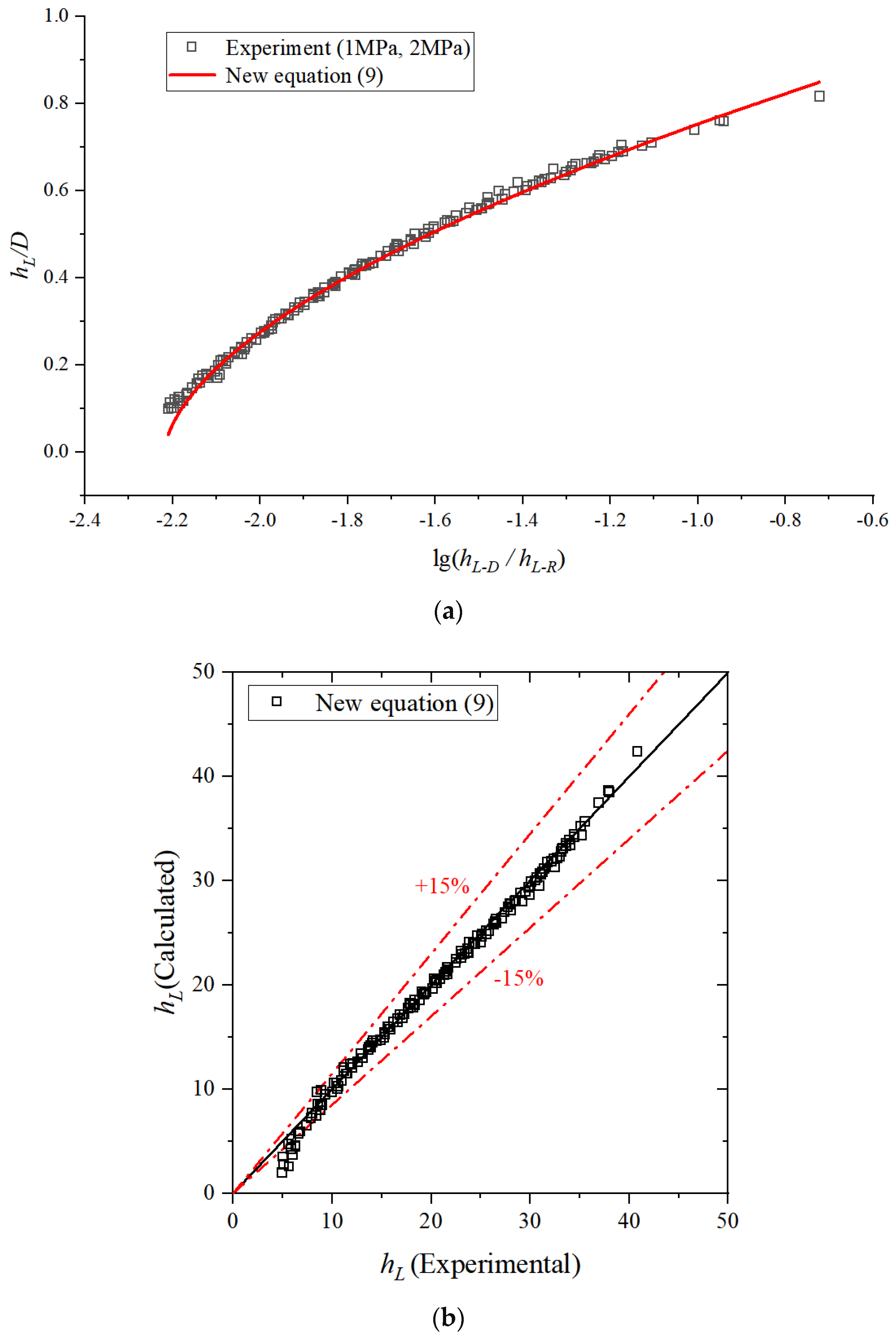
4.3. Liquid Film Thickness
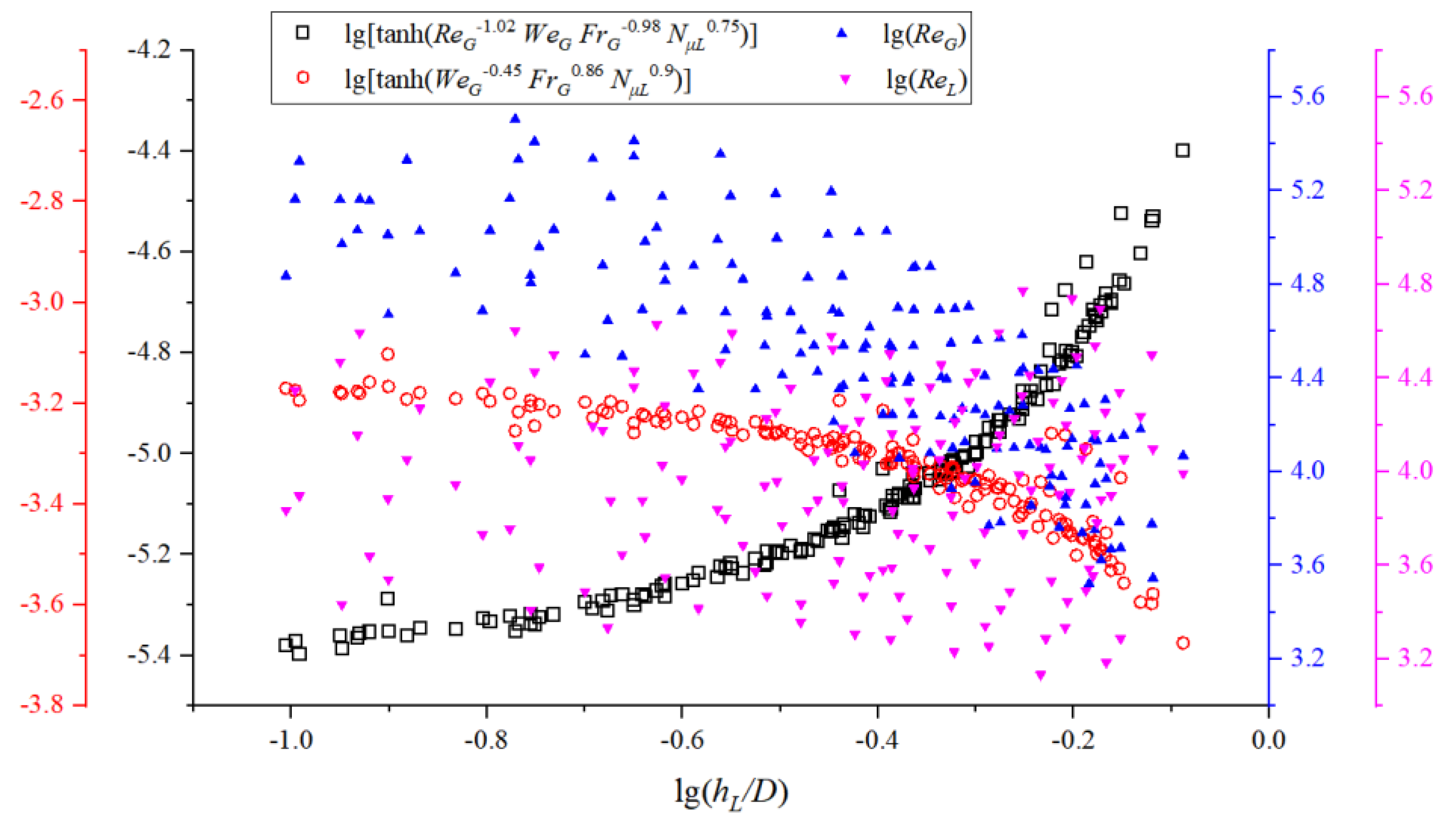
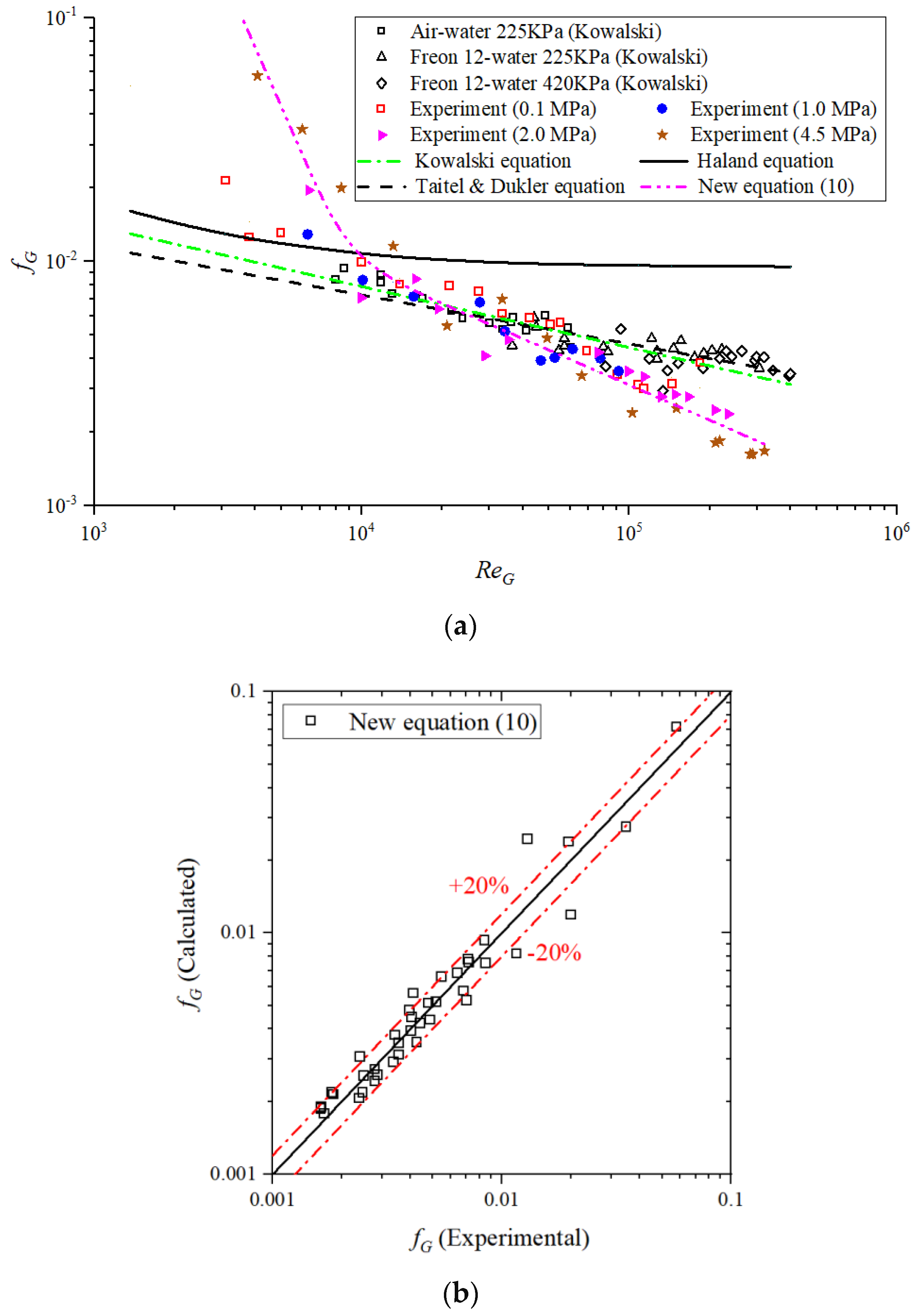
4.4. Gas-Wall Friction Factor
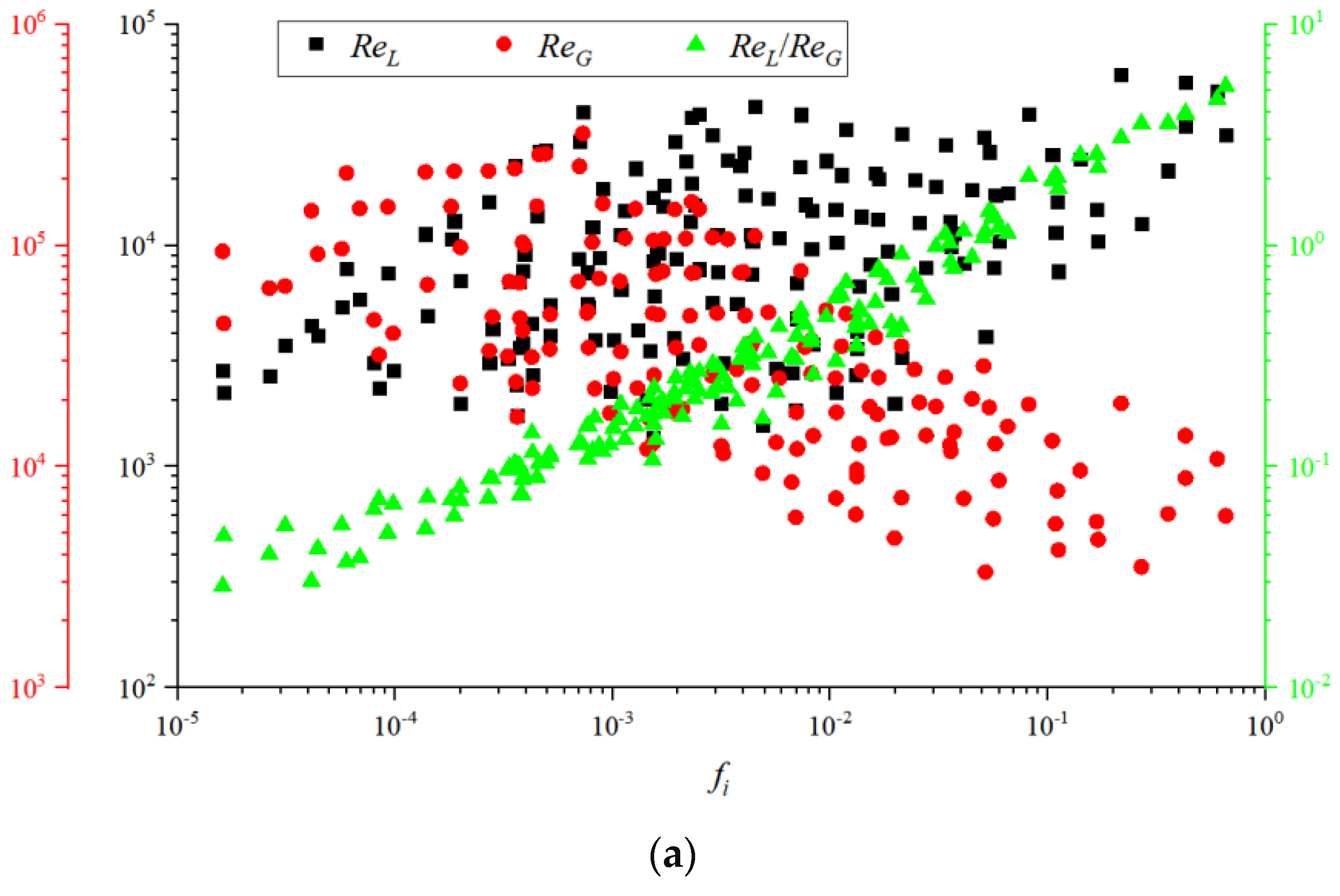
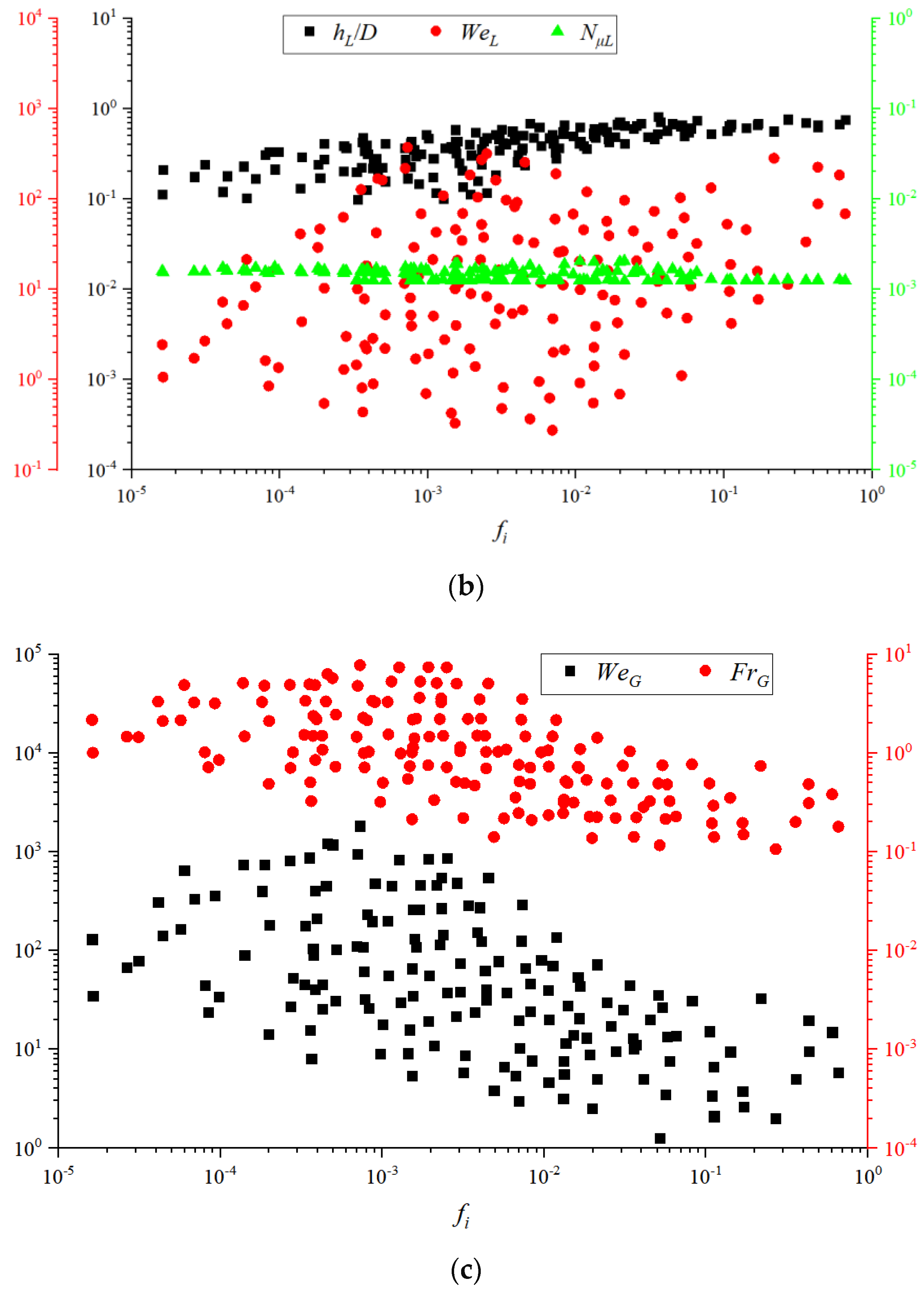
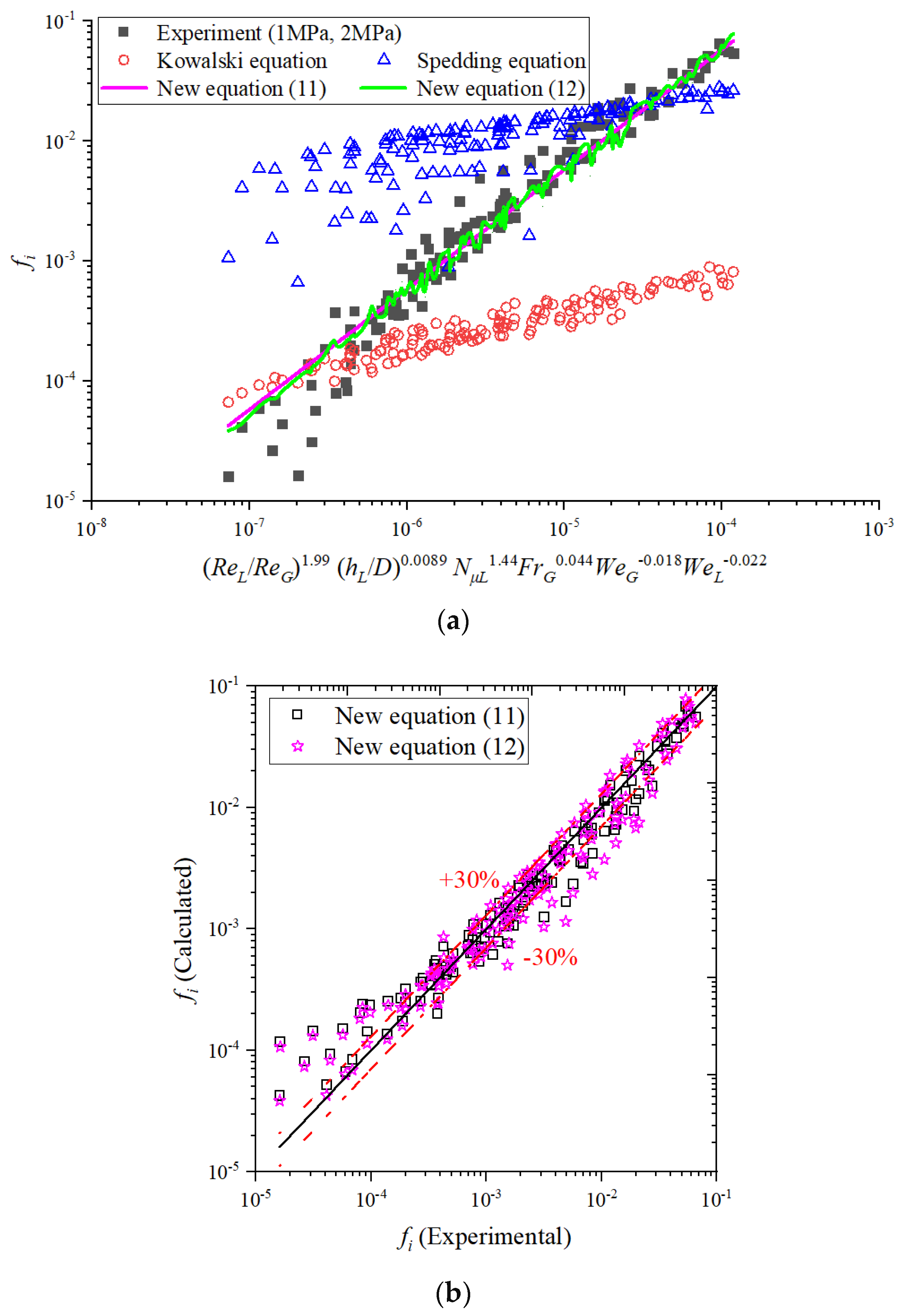
4.5. Interfacial Friction Factor
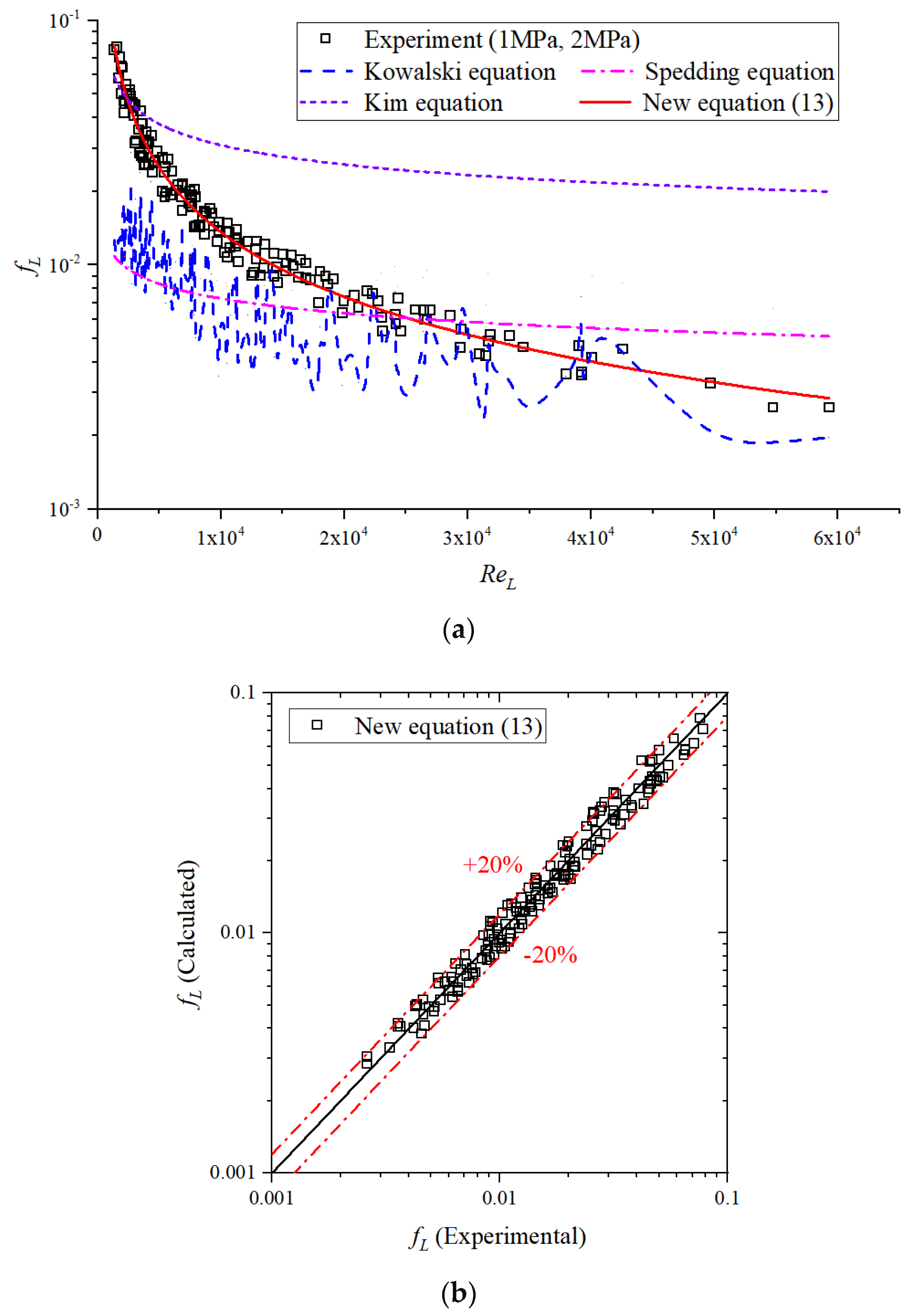
4.6. Liquid-Wall Friction Factor
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | VGS | Gas superficial velocity | |
| A | Cross-sectional area | VLS | Liquid superficial velocity |
| D | Pipe inner diameter | ||
| f | Friction factor | Greek symbols | |
| P | Pressure | ρ | Density |
| S | Perimeter | α | Void fraction |
| t | Time | μ | Viscosity |
| U | Average velocity in x direction | σ | Surface tension |
| x | X-axis of Cartesian coordinate system | τ | Shear stress |
| hL | Liquid film thickness | ||
| Fr | Froude number | Subscripts | |
| Nμ | Viscosity number | G | Gas phase |
| Re | Reynolds number | i | Interface |
| We | Weber number | L | Liquid phase |
References
- Mandhane, J.M.; Gregory, G.A.; Aziz, K. A flow pattern map for gas-liquid flow in horizontal pipes. Int. J. Multiph. Flow 1974, 1, 537–553. [Google Scholar] [CrossRef]
- Zou, S.; Guo, L.; Yao, T. Upstream-flow-based mechanisms for global flow regime transition of gas/liquid two-phase flow in pipeline-riser systems. Chem. Eng. Sci. 2021, 240, 116542. [Google Scholar] [CrossRef]
- Zou, S.; Guo, L.; Yao, T.; Li, W.; Wu, Q.; Zhou, H.; Xie, C.; Liu, W.; Kuang, S. NonUniformity of Gas/Liquid Flow in a Riser and Impacts of Pipe Configuration and Operation on Slugging Characteristics. Exp. Therm. Fluid Sci. 2018, 96, 329–346. [Google Scholar] [CrossRef]
- Taitel, Y.; Dukler, A.E. A model for predicting flow regime transitions in horizontal and near horizontal gas liquid flow. AIChE J. 1976, 22, 47–55. [Google Scholar] [CrossRef]
- Agrawal, S.S.; Gregory, G.A.; Govier, G.W. An analysis of horizontal stratified two-phase flow in pipes. Can. J. Chem. Eng. 1973, 51, 280–287. [Google Scholar] [CrossRef]
- Johnson, G.W.; Bertelsen, A.F.; Nossen, J. A Mechanistic Model for Roll Waves for Two-Phase Pipe Flow. AIChE J. 2009, 55, 2788–2795. [Google Scholar] [CrossRef]
- Shi, S.; Wu, X.; Han, G.; Zhong, Z.; Li, Z.; Sun, K. Numerical slug flow model of curved pipes with experimental validation. ACS Omega 2019, 4, 14831–14840. [Google Scholar] [CrossRef]
- Rodrigues, H.T.; Pereyra, E.; Saricai, C. Pressure Effects on Low-Liquid-Loading Oil/Gas Flow in Slightly Upward Inclined Pipes: Flow Pattern, Pressure Gradient, and Liquid Holdup. SPE J. 2019, 24, 191543. [Google Scholar] [CrossRef]
- Rodrigues, H.T.; Pereyra, E.; Sarica, C. A model for the thin film friction factor in near-horizontal stratified-annular. Int. J. Multiph. Flow 2018, 102, 29–37. [Google Scholar] [CrossRef]
- Fan, Y.; Sarica, C. Onset of Liquid-Film Reversal in Upward-Inclined Pipes. SPE J. 2018, 23, 1630–1647. [Google Scholar] [CrossRef]
- Wu, X.; Moin, P. A direct numerical simulation study on the mean velocity characteristics in turbulent pipe flow. J. Fluid Mech. 2008, 608, 81–112. [Google Scholar] [CrossRef]
- Baea, B.; Kima, H.; Kimb, K.; Jeong, J.J.; Yun, B. Force balance droplet entrainment model for the horizontal stratified flow condition. Int. J. Heat Mass Transf. 2021, 165, 120726. [Google Scholar] [CrossRef]
- Vollestad, P.; Angheluta, L.; Jensena, A. Experimental study of secondary flows above rough and flat interfaces in horizontal gas-liquid pipe flow. Int. J. Multiph. Flow 2020, 125, 103235. [Google Scholar] [CrossRef]
- Taitel, Y.; Dukler, A.E. A theoretical approach to the Lockhart Martinelli correlation for stratified flow. Int. J. Multiph. Flow 1976, 2, 477–485. [Google Scholar] [CrossRef]
- Kowalski, J.E. Wall and interfacial shear stress in stratified flow in a horizontal pipe. AIChE J. 1987, 33, 274–281. [Google Scholar] [CrossRef]
- Spedding, P.L.; Hand, N.P. Prediction in stratified gas-liquid co-current flow in horizontal pipelines. Int. J. Heat Mass Transf. 1997, 40, 1923–1935. [Google Scholar] [CrossRef]
- Haland, S.E. Simple and explicit formulas for the friction factor in turbulent pipe flow. J. Fluids Eng. 1983, 105, 89–90. [Google Scholar] [CrossRef]
- Kim, H.G.; Kim, S.M. Experimental investigation of flow and pressure drop characteristics of air-oil slug flow in a horizontal tube. Int. J. Heat Mass Transf. 2022, 183, 122063. [Google Scholar] [CrossRef]
- Ayati, A.A.; Kolaas, J.; Jensen, A.; Johnson, G.W. A PIV investigation of stratified gas-liquid flow in a horizontal pipe. Int. J. Multiph. Flow 2014, 55, 129–143. [Google Scholar] [CrossRef]
- Mascarenhas, N.; Lee, H.; Mudawar, I. Experimental and computational investigation of interfacial shear along a wavy two-phase interface. Int. J. Heat Mass Transf. 2015, 85, 265–280. [Google Scholar] [CrossRef]
- Belt, R.J.; Van’tWestende, J.M.C.; Portela, L.M. Prediction of the interfacial shear stress in vertical annular flow. Int. J. Multiph. Flow 2009, 35, 689–697. [Google Scholar] [CrossRef]
- Ju, P.; Brooks, C.S.; Ishii, M.; Liu, Y.; Hibiki, T. Film Thickness of vertical upward cocurrent adiabatic flow in pipes. Int. J. Heat Mass Transf. 2015, 85, 985–995. [Google Scholar] [CrossRef]
- Ju, P.; Liu, Y.; Brooks, C.S.; Ishii, M. Prediction of interfacial shear stress of vertical upward adiabatic annular flow in pipes. Int. J. Heat Mass Transf. 2019, 133, 500–509. [Google Scholar] [CrossRef]
- Ju, P.; Liu, Y.; Yang, X.; Ishii, M. Wave characteristics of vertical upward adiabatic annular flow in pipes. Int. J. Heat Mass Transf. 2019, 145, 118701. [Google Scholar] [CrossRef]
- Aliyu, A.M.; Baba, Y.D.; Lao, L.; Yeung, H.; Kim, K.C. Interfacial friction in upward annular gas-liquid two-phase flow in pipes. Exp. Therm. Fluid Sci. 2017, 84, 90–109. [Google Scholar] [CrossRef]
- Sawant, P.; Ishii, M.; Mori, M. Droplet entrainment correlation in vertical upward co-current annular two-phase flow. Nucl. Eng. Des. 2008, 238, 1342–1352. [Google Scholar] [CrossRef]






| Author(s) | Equation |
|---|---|
| Agrawal et al. [5] | , |
| Taitel & Dukler [14] | , , = G, L , , = G, L |
| Haland [17] | , = G, L |
| Kowalski [15] | |
| Spedding & Hand [16] | , |
| Aliyu et al. [25] | |
| Ju et al. [24] | |
| Kim & Kim [18] | , , |
| Measurement | Operating Range | Measurement Device | Relative Uncertainty |
|---|---|---|---|
| Liquid mass flow | 1.18–17.74 kg/min | RHEONIK RHE 08 | 0.68% |
| Gas mass flow | 0.41–9.26 kg/min | RHEONIK RHE 08 | 1.02% |
| Pressure | 0–2 MPa | Rosemount 3051TG Transmitter | 1.02% |
| Temperature | 0–50 °C | T-type armored thermocouple | 3.22% |
| Pressure drop | −200–200 Pa | Honeywell STD 820 Transmitter | 0.31% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yu, Y.; Liu, Z.; Chang, Y.; Zhao, X.; Wang, Q. Experimental Study on Gas-Liquid Two-Phase Stratified Flow at High Pressure in a Horizontal Pipe. Energies 2024, 17, 1056. https://doi.org/10.3390/en17051056
Wang Y, Yu Y, Liu Z, Chang Y, Zhao X, Wang Q. Experimental Study on Gas-Liquid Two-Phase Stratified Flow at High Pressure in a Horizontal Pipe. Energies. 2024; 17(5):1056. https://doi.org/10.3390/en17051056
Chicago/Turabian StyleWang, Yubo, Yanan Yu, Zhigang Liu, Yingjie Chang, Xiangyuan Zhao, and Qiming Wang. 2024. "Experimental Study on Gas-Liquid Two-Phase Stratified Flow at High Pressure in a Horizontal Pipe" Energies 17, no. 5: 1056. https://doi.org/10.3390/en17051056
APA StyleWang, Y., Yu, Y., Liu, Z., Chang, Y., Zhao, X., & Wang, Q. (2024). Experimental Study on Gas-Liquid Two-Phase Stratified Flow at High Pressure in a Horizontal Pipe. Energies, 17(5), 1056. https://doi.org/10.3390/en17051056






