Probabilistic Design Method for Aircraft Thermal Protective Layers Based on Surrogate Models
Abstract
1. Introduction
2. Model and Methods
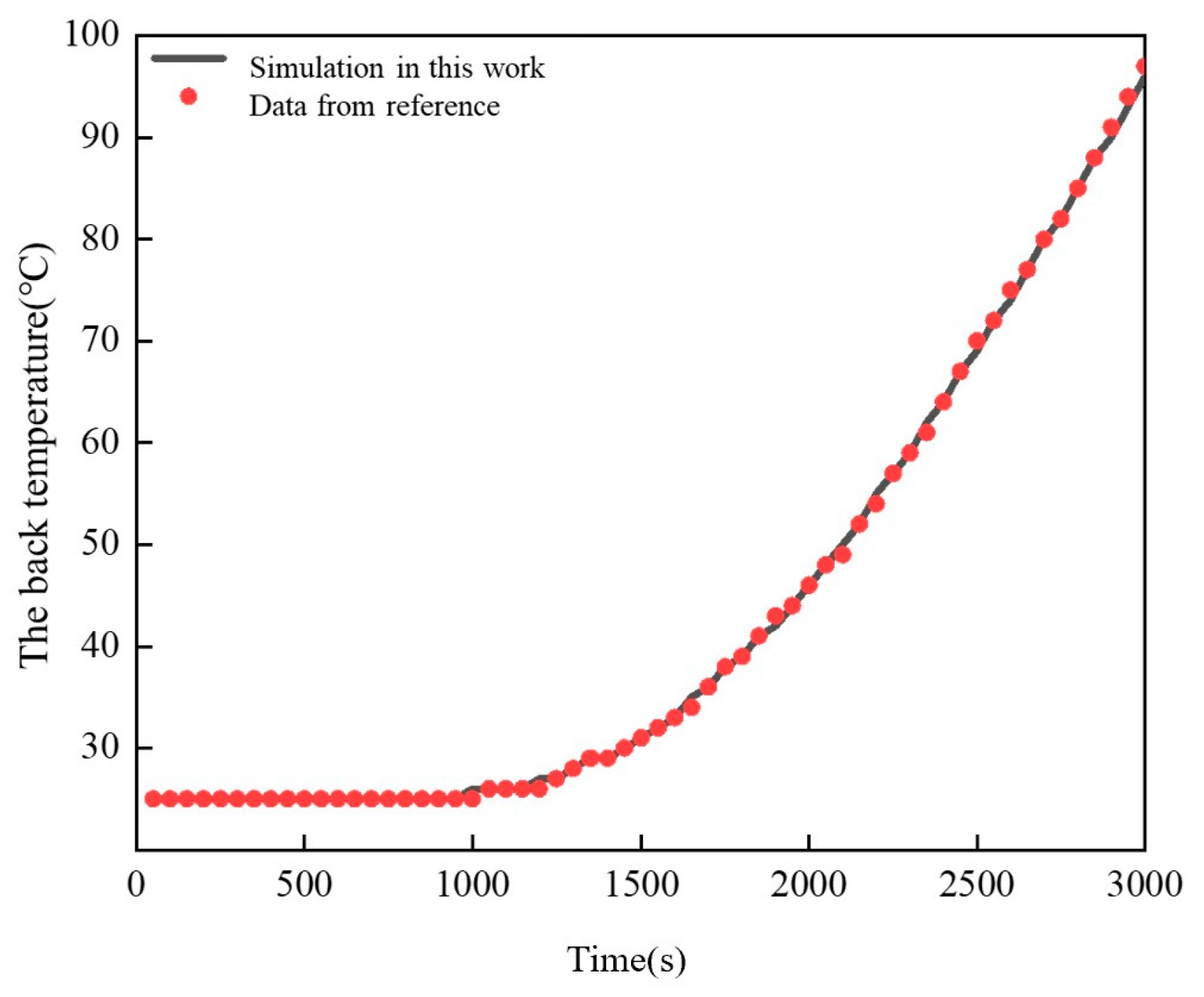
2.1. Finite Element Model Verification
2.2. Deterministic Simulation Modeling
- (a)
- The surface thermal loads on the aircraft, based on flight altitude, speed, atmospheric environment, navigation parameters, etc., were determined.
- (b)
- The structural forms and material types were determined based on the external surface heat flux distribution and internal surface temperature limits used in various parts of the thermal protection system for the aircraft.
- (c)
- With the determined basic structures and materials of the thermal protection system, the dimensions (mainly thickness) of the thermal protective layers were determined by heat transfer analysis as follows:
- (d)
- Considering the impact of uncertainties on the thermal protection performance, a reasonable safety margin was necessarily set on the nominal thickness to obtain the final dimensions and weight of the thermal protection layer. The design should meet the back temperature and weight limits.
- (e)
- After the preliminary design of the thermal protection system, an assessment and verification was conducted.
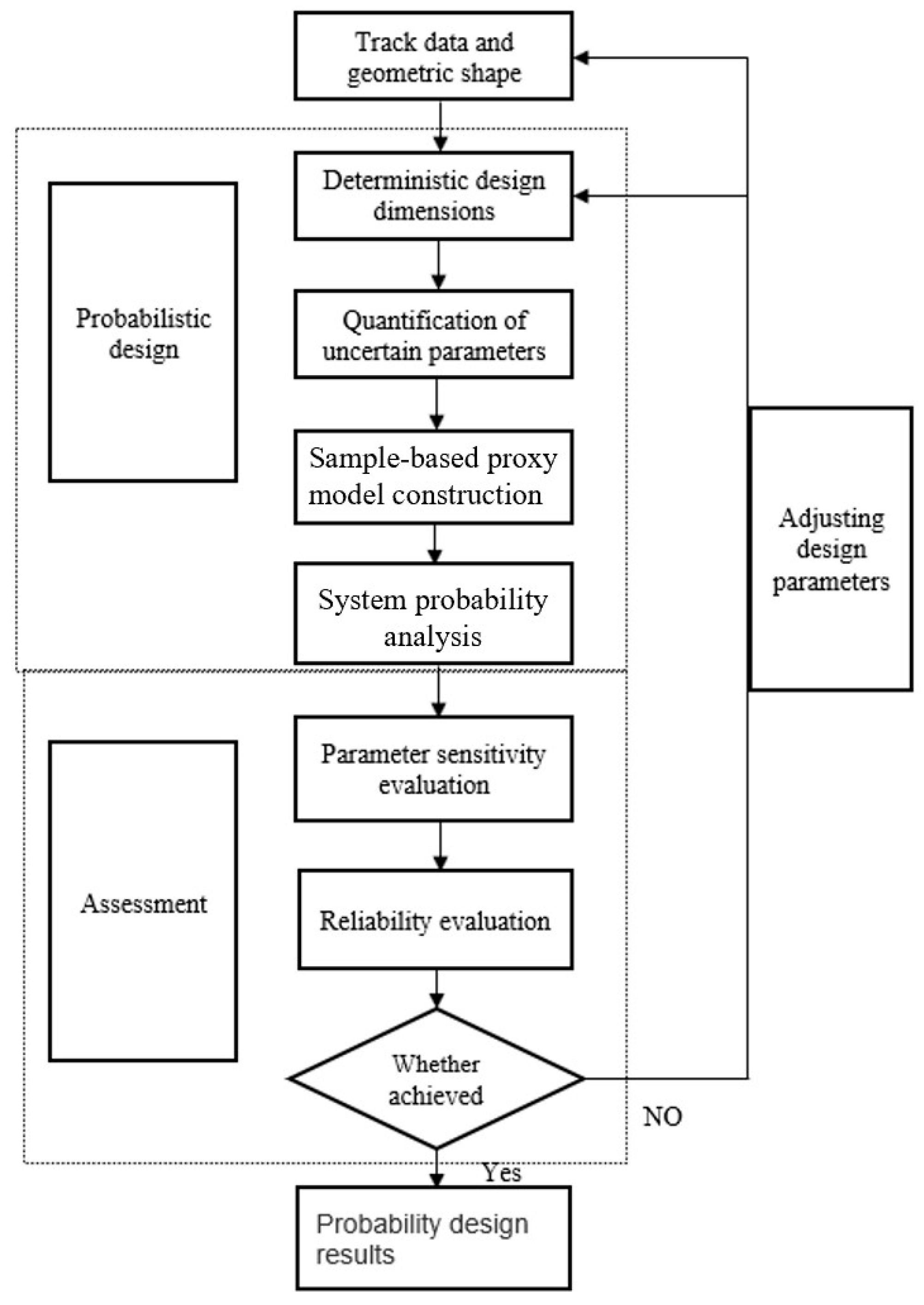
2.3. Probabilistic Simulation Modeling
3. Results and Discussion
3.1. Deterministic Determination
3.2. Probabilistic Designation
3.3. Comparison
4. Conclusions
- The developed engineering algorithm, combined with computational fluid dynamic (CFD) simulation methods, exhibits high accuracy.
- The weight of the coating layer of the TPS obtained through the deterministic method is 271.74 kg with the extreme deviation design method, while the weight derived from the probabilistic method is 229.31 kg. Compared to the deterministic method with the extreme deviation design, the probabilistic design yields a weight reduction of 15.61%. This indicates that probabilistic design is an efficient approach to enhance the performance of aircraft and reduce the overall weight of the aircraft.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wright, M.J.; Bose, D.; Chen, Y.K. Probabilistic Modeling of Aerothermal and Thermal Protection Material Response Uncertainties. AIAA J. 2007, 45, 399–410. [Google Scholar] [CrossRef]
- Zhao, S.Y.; Zhang, B.M.; Du, S.Y. Probabilistic Modeling of Transient Heat Transfer and Assessment of Thermal Reliability of Fibrous Insulation under Aerodynamic Heating Conditions. Int. J. Therm. Sci. 2009, 48, 1302–1310. [Google Scholar] [CrossRef]
- Green, L.L. The Challenges of Credible Thermal Protection System Reliability Quantification. In Proceedings of the International Planetary Probe Workshop (IPPW-10), San Jose, CA, USA, 17–21 June 2013. NF1676L-16765. [Google Scholar]
- Dec, J.; Mitcheltree, R. Probabilistic design of a Mars Sample Return Earth entry vehicle thermal protection system. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002; p. 910. [Google Scholar]
- Kumar, S.; Mahulikar, S.P. Selection of materials and design of multilayer lightweight passive thermal protection system. J. Therm. Sci. Eng. Appl. 2016, 8, 021003. [Google Scholar] [CrossRef]
- Li, W.; Huang, H.; Ai, B.; Zhang, Z. On the novel designs of charring composites for thermal protection application in reentry vehicles. Appl. Therm. Eng. 2016, 93, 849–855. [Google Scholar] [CrossRef]
- Villanueva, D.; Haftka, R.; Sankar, B. Including future tests in the design and optimization of an integrated thermal protection system. In Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 18th AIAA/ASME/AHS Adaptive Structures Conference 12th, Orlando, FL, USA, 12–15 April 2010; p. 2597. [Google Scholar]
- Zhao, S.; Zhang, W.; Lin, X.; Song, D.; Li, J. Effect of Parameters Correlation on Uncertainty and Sensitivity in Dynamic Thermal Analysis of Thermal Protection Blanket in Service. Int. J. Therm. Sci. 2015, 87, 158–168. [Google Scholar] [CrossRef]
- Howell, J.R. Monte Carlo Treatment of Data Uncertainties in Thermal Analysis. J. Spacecr. Rocket. 1973, 10, 411–414. [Google Scholar] [CrossRef]
- Mazzaracchio, A.; Marchetti, M. A probabilistic sizing tool and Monte Carlo analysis for entry vehicle ablative thermal protection systems. Acta Astronaut. 2010, 66, 821–835. [Google Scholar] [CrossRef]
- Chen, Y.K.; Squire, T.; Laub, B.; Wright, M. Monte Carlo analysis for spacecraft thermal protection system design. In Proceedings of the 9th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, San Francisco, CA, USA, 5–8 June 2006; p. 2951. [Google Scholar]
- Weaver, D.S.; Mišković, S. CFD-DEM validation and simulation of gas-liquid-solid three phase high-speed jet flow. Chem. Eng. Res. Des. 2023, 201, 561–578. [Google Scholar] [CrossRef]
- Sepka, S.; Wright, M. A Monte Carlo Approach to Fiat Uncertainties-Improvements and Results for MSL. In Proceedings of the 41st AIAA Thermophysics Conference, San Antonio, TX, USA, 22–25 June 2009; p. 4234. [Google Scholar]
- Wright, M.; Cozmuta, I.; Laub, B.; Chen, Y.K.; Wilcoxson, W.H. Defining ablative thermal protection system margins for planetary entry vehicles. In Proceedings of the 42nd AIAA Thermophysics Conference, Honolulu, HI, USA, 27–30 June 2011; p. 3757. [Google Scholar]
- Turchi, A.; Congedo, P.M.; Magin, T.E. Thermochemical ablation modeling forward uncertainty analysis—Part I: Numerical methods and effect of model parameters. Int. J. Therm. Sci. 2017, 118, 497–509. [Google Scholar] [CrossRef]
- Rivier, M.; Lachaud, J. Congedo P M. Ablative thermal protection system under uncertainties including pyrolysis gas composition. Aerosp. Sci. Technol. 2019, 84, 1059–1069. [Google Scholar] [CrossRef]
- Deng, S.; Xin, J.; Zhang, K.; Cheng, G. Thermal reliability evaluation method of Thermal protection system based on importance sampling method. J. Chongqing Univ. 2019, 42, 62–70. [Google Scholar]
- Zhang, K.; Yao, J.; He, Z.; Xin, J.; Fun, J. Probabilistic transient heat conduction analysis considering uncertainties in thermal loads using surrogate model. J. Spacecr. Rocket. 2021, 58, 1030–1042. [Google Scholar] [CrossRef]
- Havey, K.A., Jr. Entry vehicle performance in low-heat-load trajectories. J. Spacecr. Rocket. 1982, 19, 506–512. [Google Scholar] [CrossRef]
- Bose, D.; Wright, M.; Gokcen, T. Uncertainty and sensitivity analysis of thermochemical modeling for titan atmospheric entry. In Proceedings of the 37th AIAA Thermophysics Conference, Portland, OR, USA, 28 June–1 July 2004; p. 2455. [Google Scholar]
- Hollis, B.; Liechty, D. Boundary Layer Transition Correlations and Aeroheating Predictions for Mars Smart Lander. In Proceedings of the 32nd AIAA Fluid Dynamics Conference and Exhibit, St. Louis, MI, USA, 24–26 June 2002; p. 745. [Google Scholar]
- Villanueva, D.C.; Le Riche, R.; Picard, G.; Haftka, R. Dynamic design space partitioning for optimization of an integrated thermal protection system. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013; p. 1534. [Google Scholar]
- Guo, Q.; Wang, S.; Hui, W.; Li, Y.; Xie, Z. Thermo-mechanical optimization of metallic thermal protection system under aerodynamic heating. Struct. Multidiscip. Optim. 2020, 61, 819–836. [Google Scholar] [CrossRef]
- Kim, J.J.; Baek, S.T.; Song, D.G.; Myong, R.S. Computational simulation of lightning strike on aircraft and design of lightning protection system. J. Korean Soc. Aeronaut. Space Sci. 2016, 44, 1071–1086. [Google Scholar]
- Reeve, H.; Finney, A. Probabilistic analysis for aircraft thermal management system design and evaluation. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Qingdao, China, 24–27 May 2015; p. 148. [Google Scholar]
- Kciuk, M.; Bijok, T.; Lo Sciuto, G. Design and modeling of intelligent building office and thermal comfort based on probabilistic neural network. SN Comput. Sci. 2022, 3, 485. [Google Scholar] [CrossRef]
- Cao, D.; Bai, G.C. DNN-based surrogate modeling-based feasible performance reliability design methodology for aircraft engine. IEEE Access 2020, 8, 229201–229218. [Google Scholar] [CrossRef]
- Xin, J.Q.; Chen, J.M.; Dong, Y.P. Probabilistic Transient Thermal Analysis of a Multi-layer Thermal Protection System for Hypersonic Vehicle. Tactical Missile Technol. 2017, 1, 47–54. [Google Scholar]

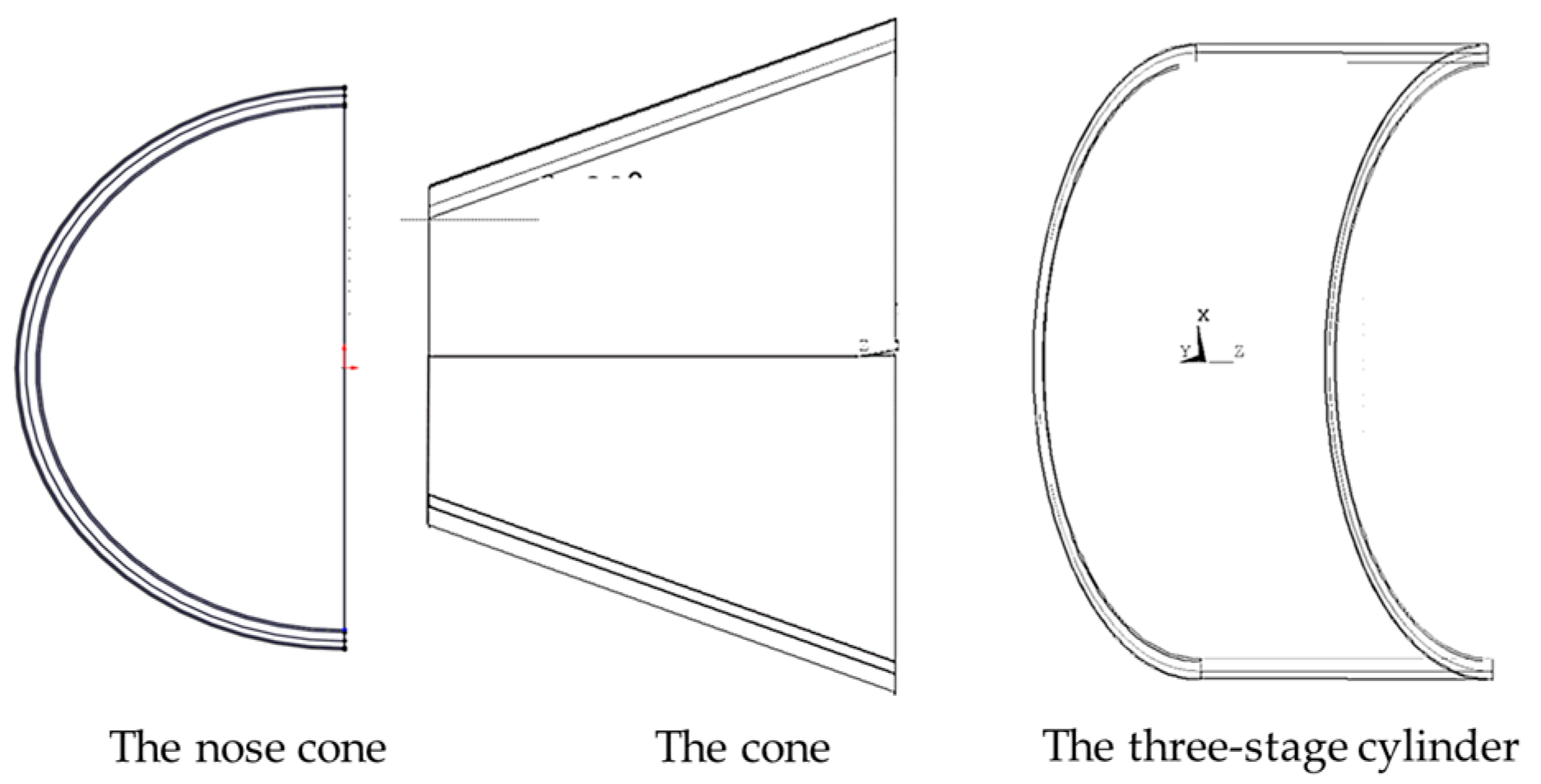


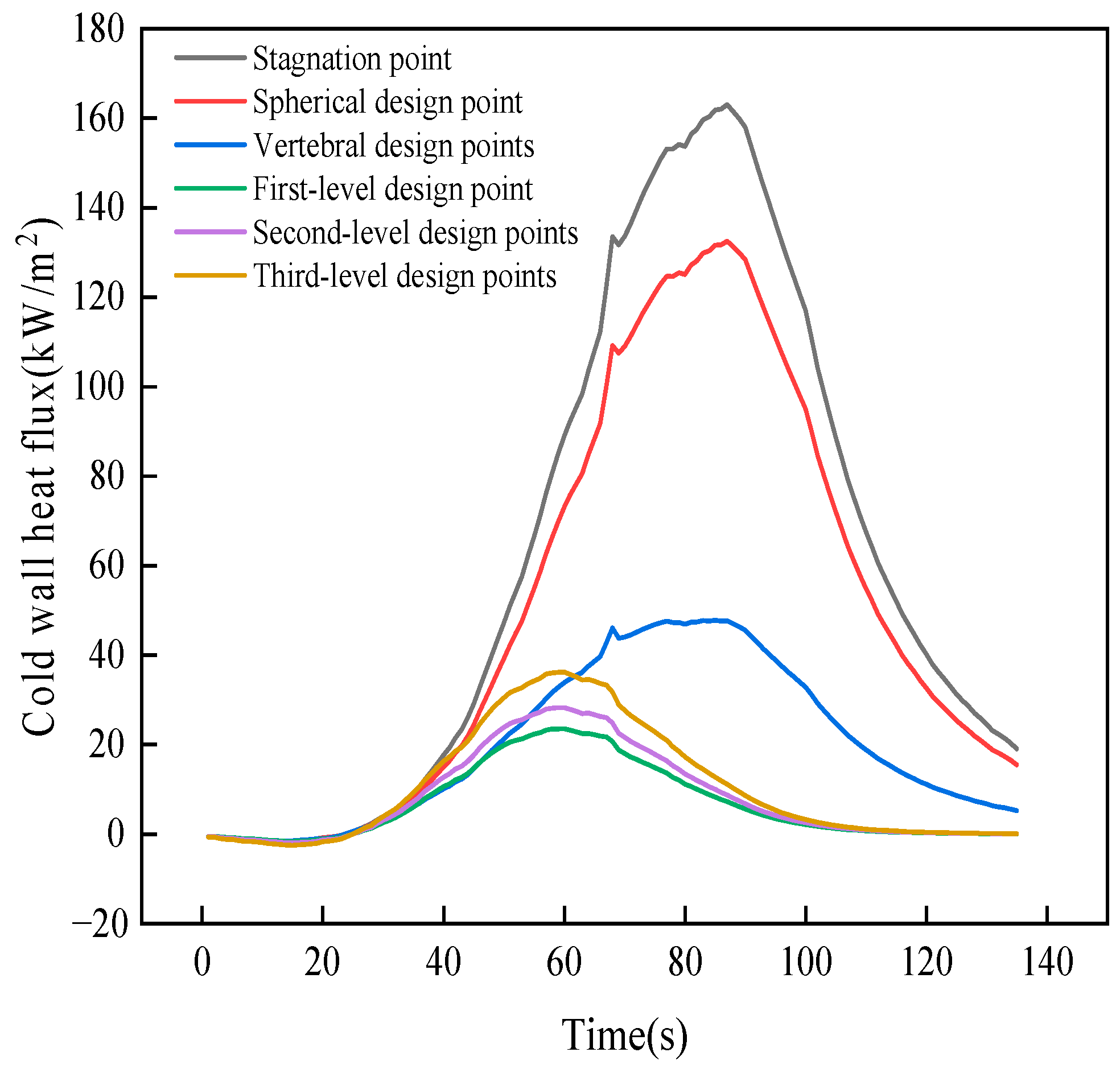

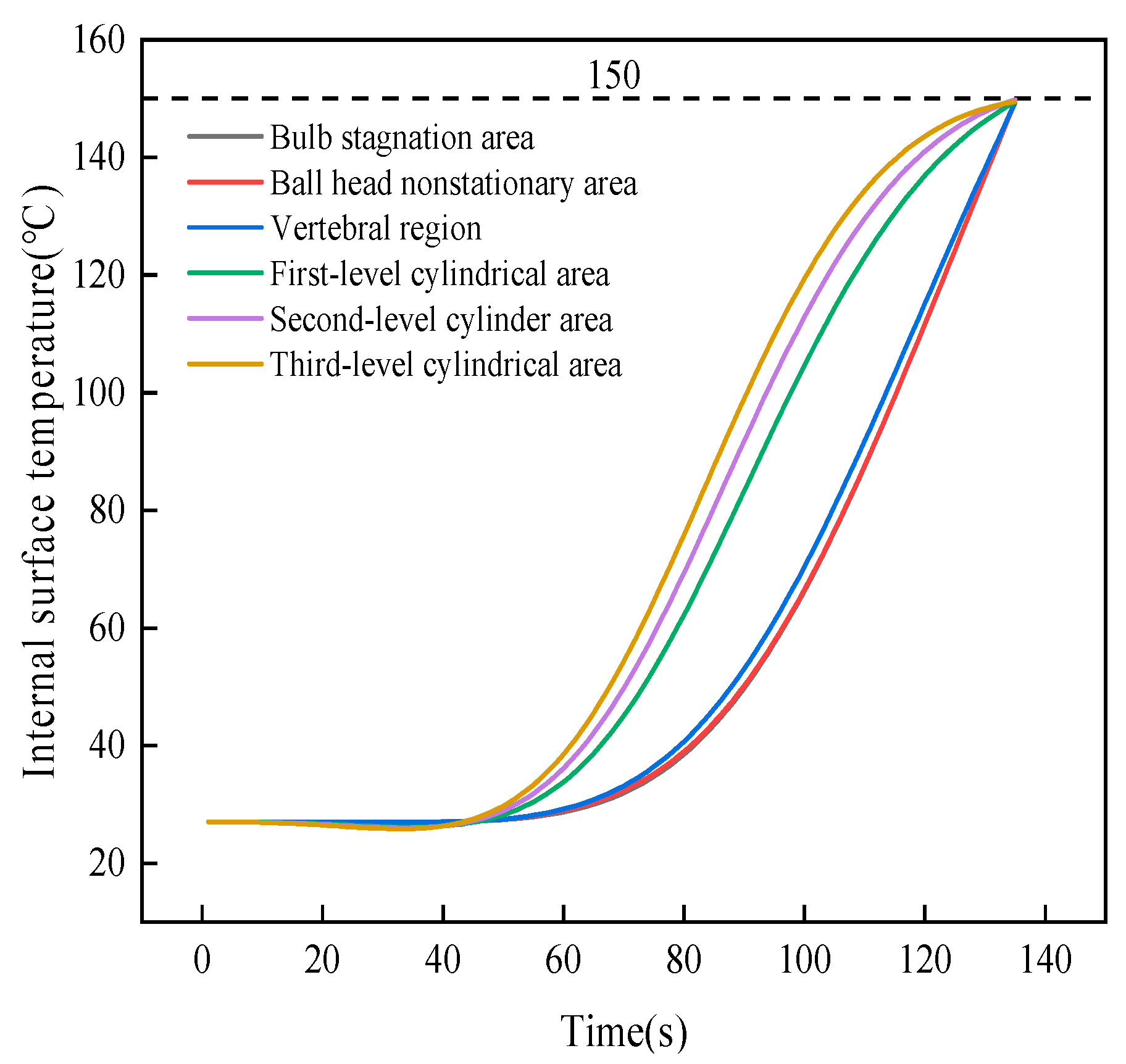
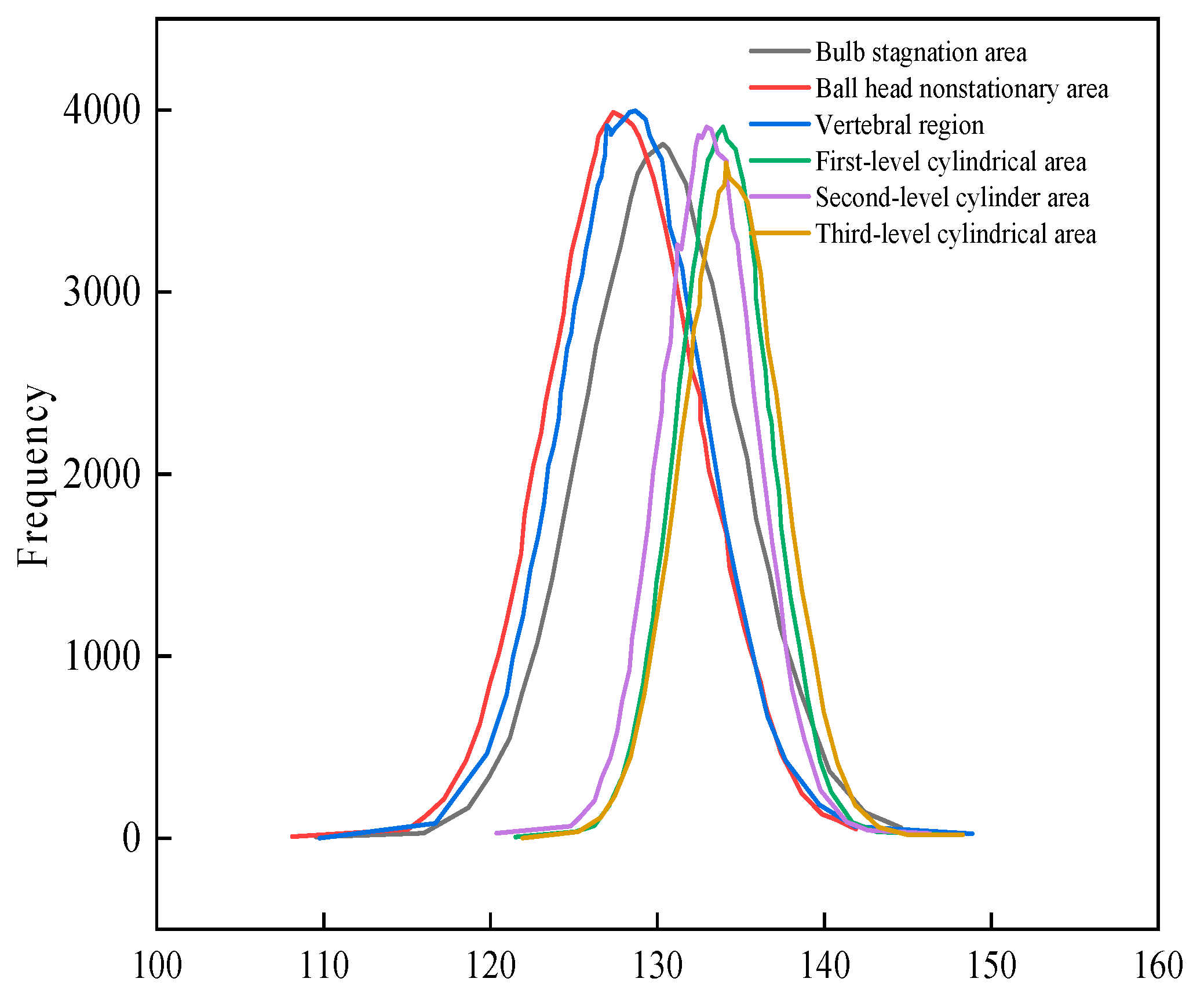
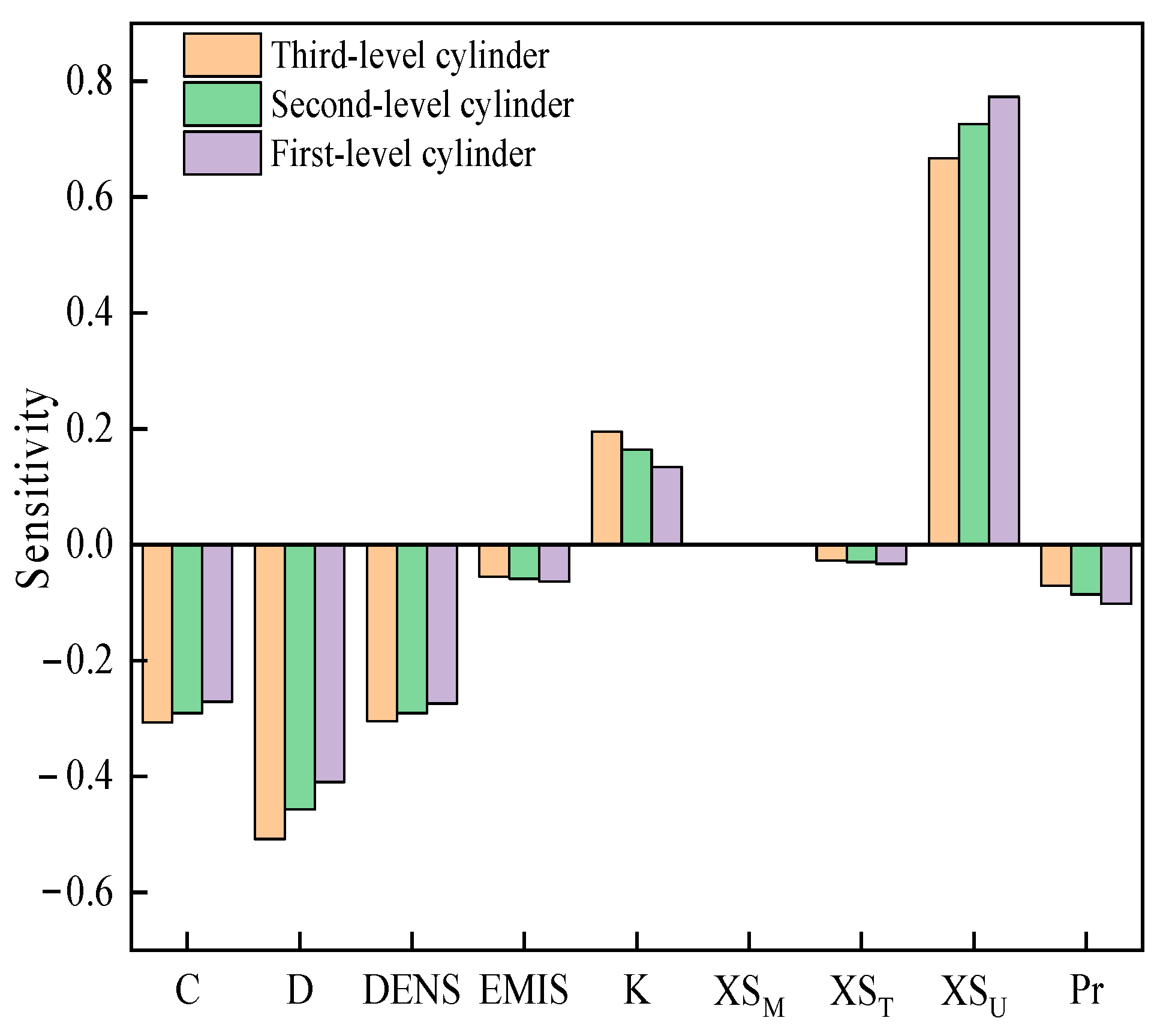
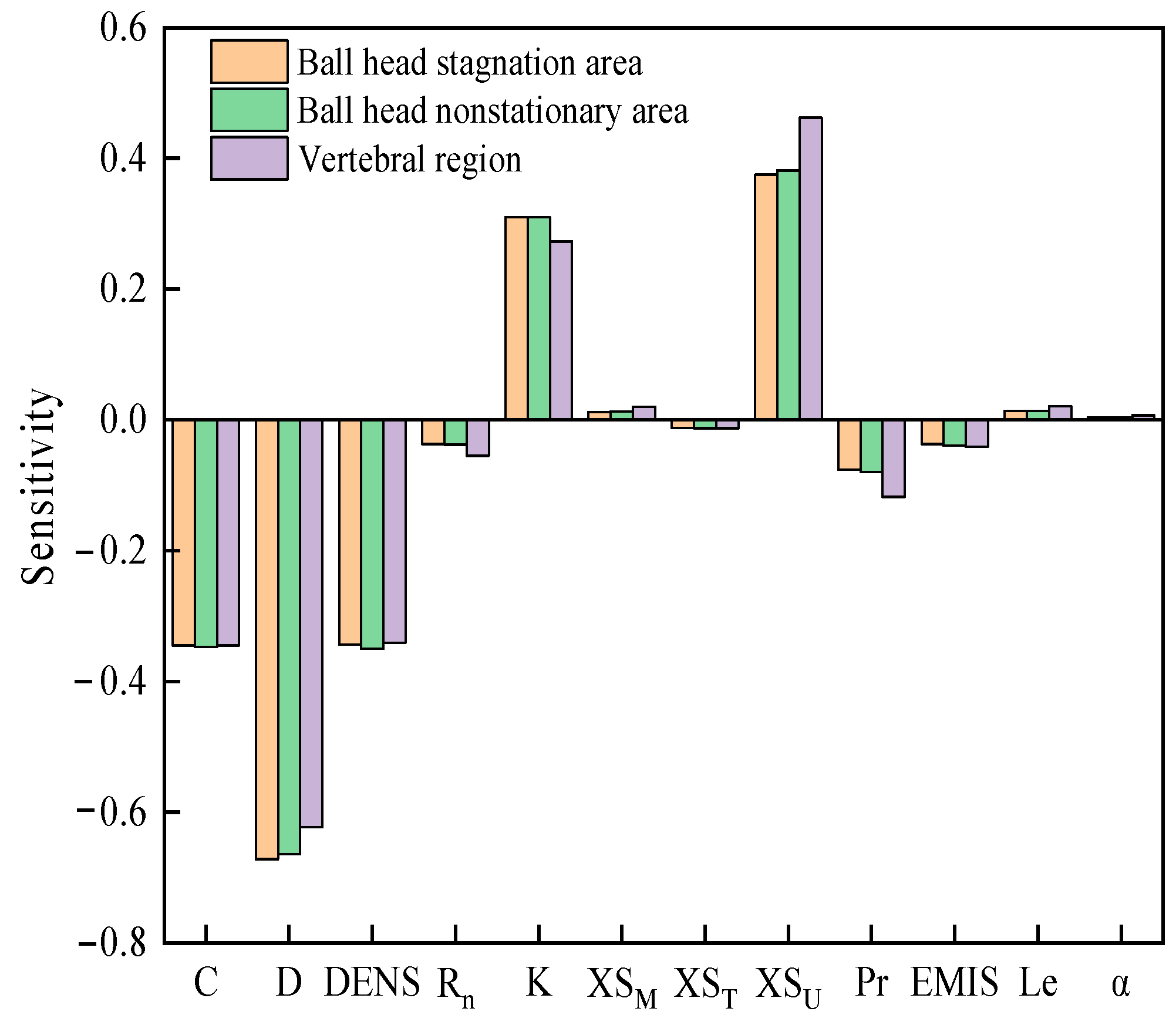
| Region | Calculated Value | Experimental Value | Error |
|---|---|---|---|
| Stagnation heat flux (kW/m2) | 693.8 | 670 | 3.55% |
| 227.08 | 215.7 | 5.2% | |
| Blunt cone heat flux ratio | 0.1302 | 0.122 | 6.7% |
| 0.063287 | 0.0664 | 4.68% | |
| 0.058 | 0.0636 | 8.86% | |
| 0.0537 | 0.0581 | 7.54% |
| Input Parameter | Variable Name | Unit | Mean Value |
|---|---|---|---|
| Thickness of ball head stagnation region | D1 | mm | 8 |
| Thickness of nonstationary area of ball head | D2 | mm | 8 |
| Cone area thickness | D3 | mm | 7 |
| Thickness of the third-level cylindrical region | D4 | mm | 5 |
| Thickness of the second-level cylindrical region | D5 | mm | 5 |
| Thickness of the first-level cylindrical region | D6 | mm | 5 |
| Input Parameter | Variable Name | Unit | Mean Value |
|---|---|---|---|
| Thickness of ball head stagnation region | D1 | mm | 9.3 |
| Thickness of nonstationary area of ball head | D2 | mm | 8.97 |
| Cone area thickness | D3 | mm | 8.83 |
| Thickness of the third-level cylindrical region | D4 | mm | 6.05 |
| Thickness of the second-level cylindrical region | D5 | mm | 5.55 |
| Thickness of the first-level cylindrical region | D6 | mm | 5.15 |
| Input Parameter | Variable Name | Distribution Type | Mean Value | Standard Deviation, % |
|---|---|---|---|---|
| Thickness of ball head stagnation region | D1, mm | Gaussian distribution | 8 | 1 |
| Thickness of nonstationary area of ball head | D2, mm | 8 | 1 | |
| Cone thickness | D3, mm | 7 | 1 | |
| First-level cylinder thickness | D4, mm | 5 | 1 | |
| Secondary cylinder thickness | D5, mm | 5 | 1 | |
| Third-level cylinder thickness | D6, mm | 5 | 1 | |
| Coating density | DENS, kg m−3 | 560 | 1 | |
| Coating specific heat capacity | C, J kg−1 K−1 | 1510 | 1 | |
| Coating thermal conductivity | k, W m−1 K−1 | 0.1 | 1 | |
| Coating emissivity | EMIS | 0.8 | 1 | |
| Flight speed coefficient | XSU | 1 | 1 | |
| Incoming flow density coefficient | XSM | 1 | 1 | |
| Incoming temperature coefficient | XST | 1 | 1 | |
| Ball head radius | Rn, m | 1 | 1 | |
| Planck number | Pr | Uniform distribution | 0.721 | 0.679 |
| Lewis number | Le | 1.442 | 1.358 | |
| Lewis number weight | α | 0.5356 | 0.5044 |
| Parameters | Linear Polynomial Response Surfaces | Nonlinear Polynomial Response Surfaces | ||
|---|---|---|---|---|
| N = 10 | N = 15 | N = 10 | N = 15 | |
| R2Adj | 0.991800 | 0.993251 | 0.999713 | 0.999966 |
| L2 | 0.011842 | 0.011021 | 0.002216 | 0.000787 |
| The Designed Parameter of Coating Layers | Variable Name | Unit | Mean Value |
|---|---|---|---|
| Thickness of ball head stagnation region | D1 | mm | 8 |
| Thickness of nonstationary area of ball head region | D2 | mm | 7.75 |
| Cone area thickness | D3 | mm | 7.55 |
| Thickness of the third-level cylindrical region | D4 | mm | 5.1 |
| Thickness of the second-level cylindrical region | D5 | mm | 4.7 |
| Thickness of the first-level cylindrical region | D6 | mm | 4.3 |
| Region | Standard Deviation of Uncertainty,% | Mean Back Temperature, °C | Standard Deviation of Back Temperature, °C | Reliability |
|---|---|---|---|---|
| Third-level circular plate region | 1 | 134.04 | 3.2599 | 99.9999% |
| 2.5 | 135.8 | 8.1811 | 95.5589% | |
| 5 | 136.05 | 16.33 | 80.6177% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Zhang, K.; Zhao, S.; Li, F.; Xu, F.; Chen, M. Probabilistic Design Method for Aircraft Thermal Protective Layers Based on Surrogate Models. Energies 2024, 17, 1051. https://doi.org/10.3390/en17051051
Chen Z, Zhang K, Zhao S, Li F, Xu F, Chen M. Probabilistic Design Method for Aircraft Thermal Protective Layers Based on Surrogate Models. Energies. 2024; 17(5):1051. https://doi.org/10.3390/en17051051
Chicago/Turabian StyleChen, Zhongcan, Kai Zhang, Shanshan Zhao, Feng Li, Fengtao Xu, and Min Chen. 2024. "Probabilistic Design Method for Aircraft Thermal Protective Layers Based on Surrogate Models" Energies 17, no. 5: 1051. https://doi.org/10.3390/en17051051
APA StyleChen, Z., Zhang, K., Zhao, S., Li, F., Xu, F., & Chen, M. (2024). Probabilistic Design Method for Aircraft Thermal Protective Layers Based on Surrogate Models. Energies, 17(5), 1051. https://doi.org/10.3390/en17051051





