Multifaceted Functionalities of Bridge-Type DC Reactor Fault Current Limiters: An Experimentally Validated Investigation
Abstract
1. Introduction
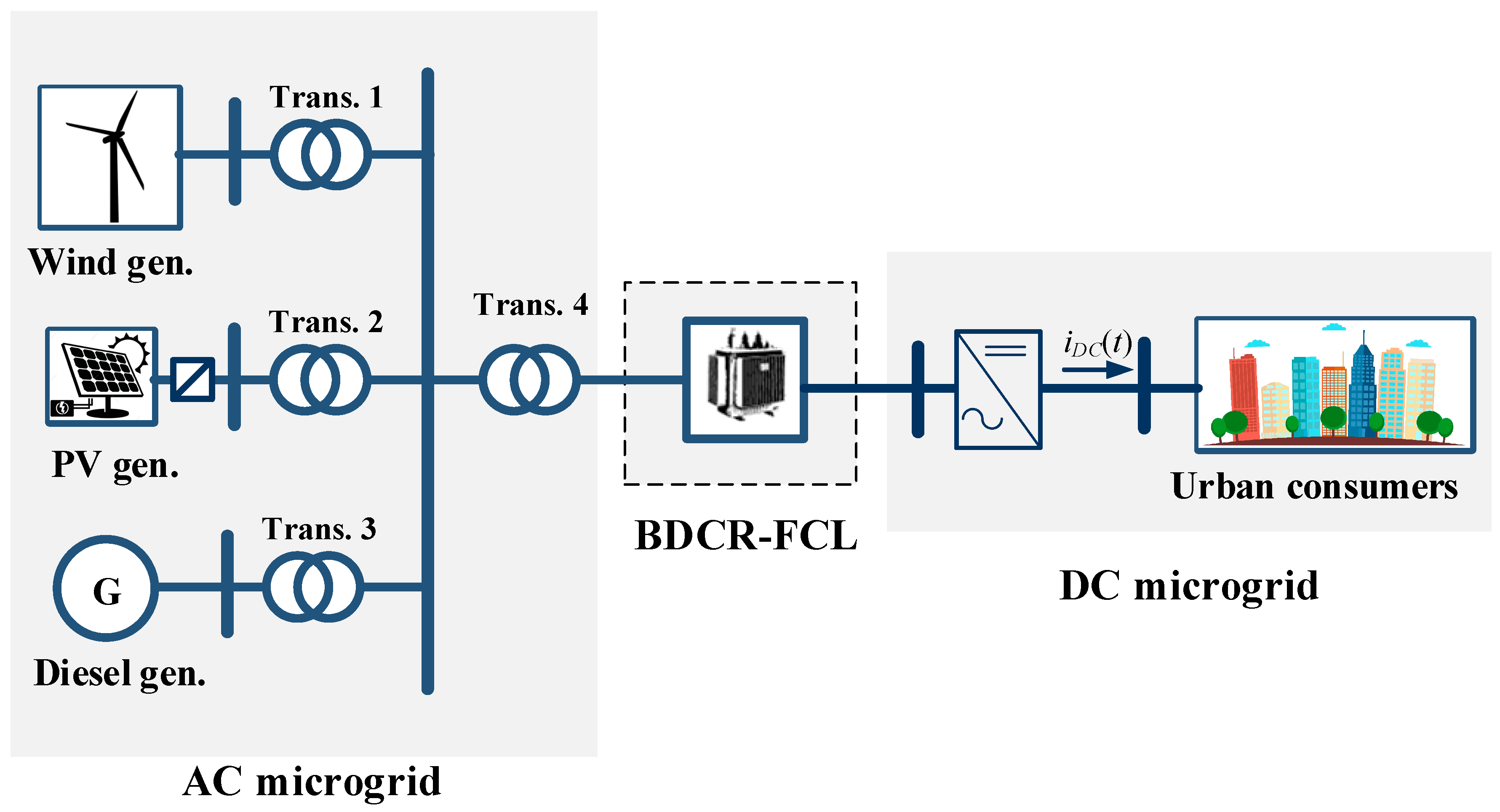
2. Analysis of BDCR-FCL Configurations in Microgrids
- Case 1: An AC microgrid connected to a DC line without the implementation of BDCR-FCL.
- Case 2: A linear load connected to an AC microgrid with a BDCR-FCL installed in series.
- Case 3: An AC microgrid connected to a DC line with the integration of BDCR-FCL.
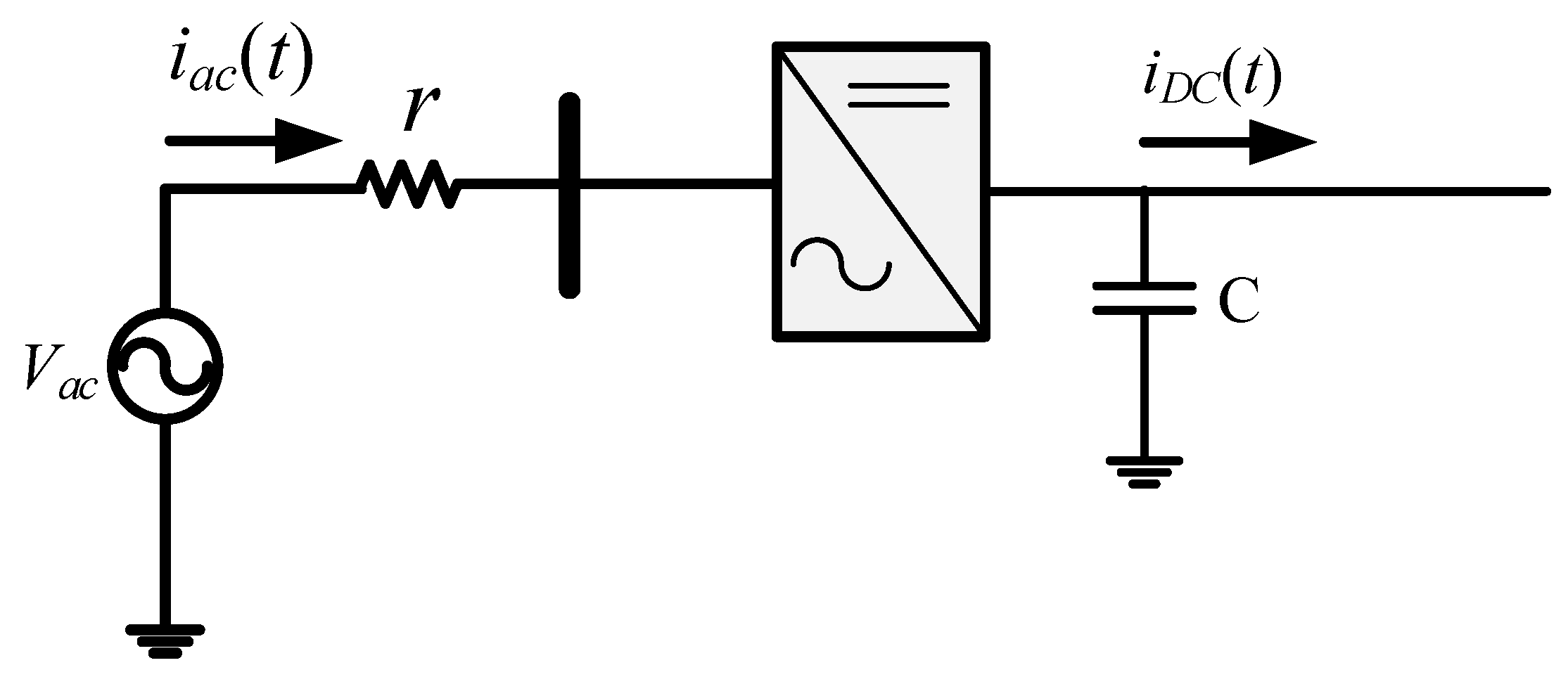
2.1. Case 1: AC Microgrid Connected to a DC Line without BDCR-FCL
2.2. Case 2: BDCR-FCL Connected in Series to an AC Load in an AC Microgrid
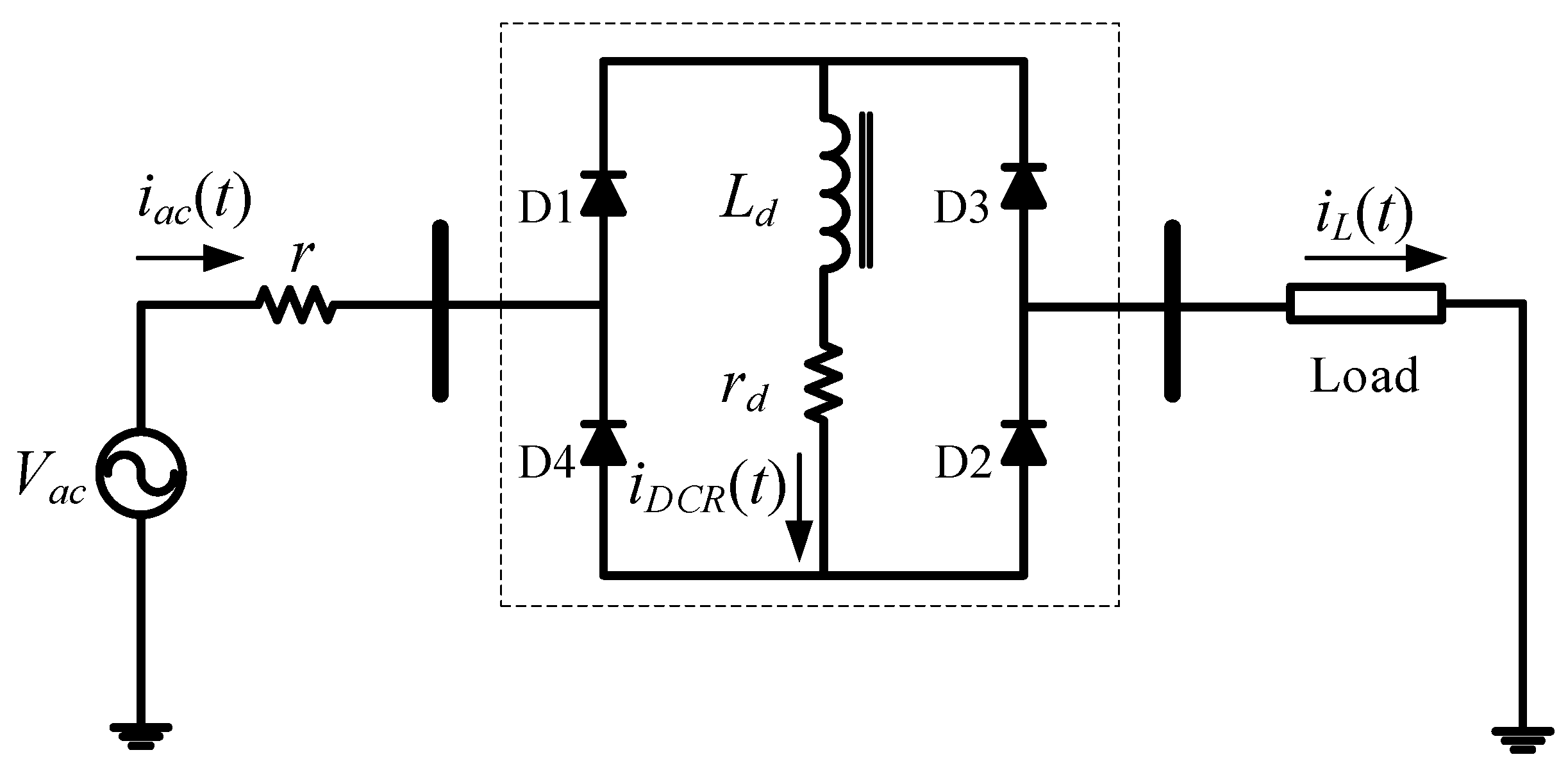
2.3. Case 3: BDCR-FCL Incorporated with an AC Microgrid Connected to a DC Line
3. Analytical Study on Functionalities of BDCR-FCL
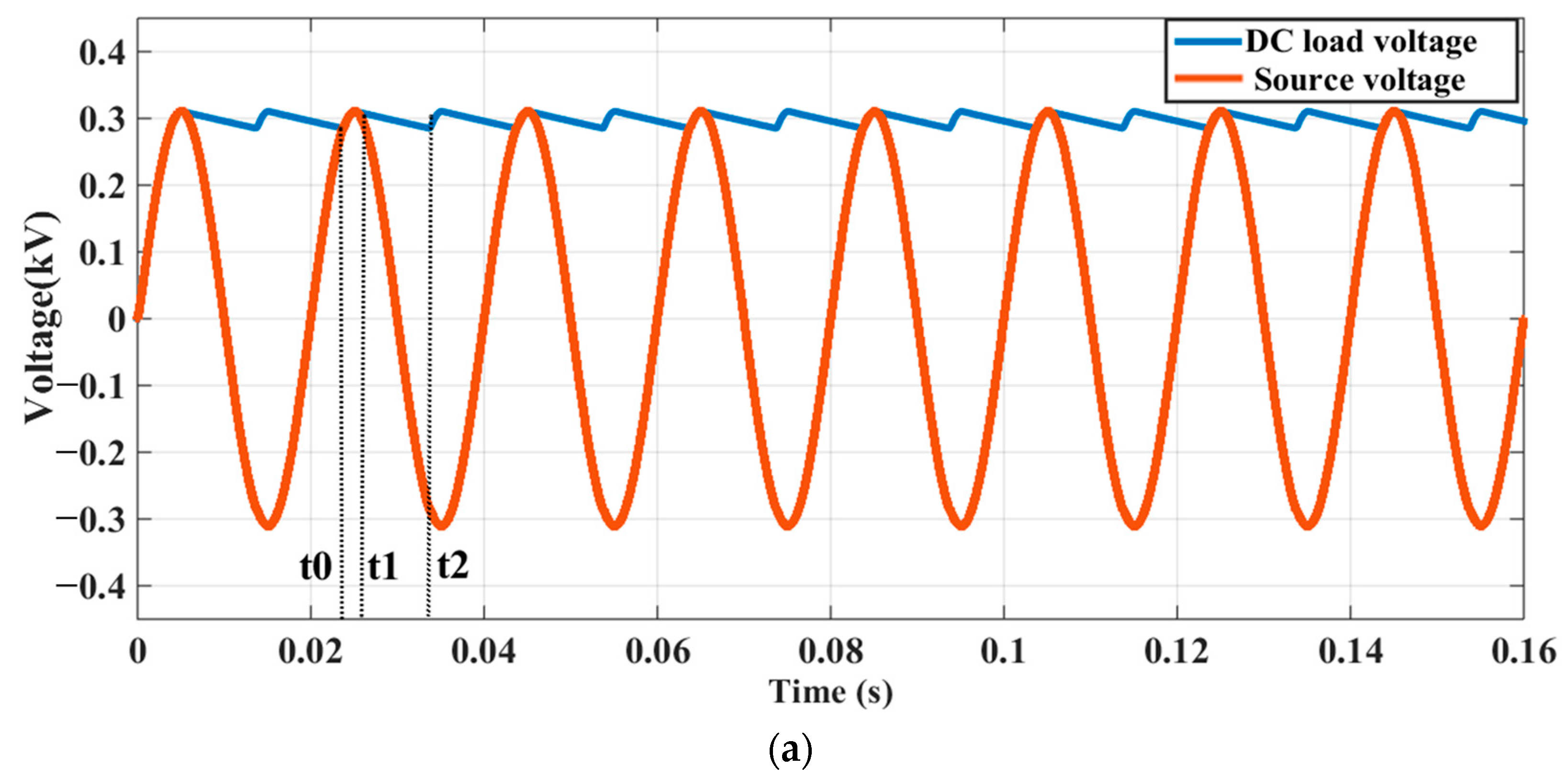
3.1. Analysis of an AC/DC Microgrid Interconnect without BDCR-SFCL (Case 1)
3.1.1. Operational Part 1: t0 ≤ t ≤ t1
3.1.2. Operational Part 2: t1 ≤ t ≤ t2
3.2. Analysis of BDCR-FCL Effect in AC Microgrid Feeding an AC Load (Case 2)
3.3. Analysis of BDCR-FCL Effect on AC Microgrid Connected to DC Line (Case 3)
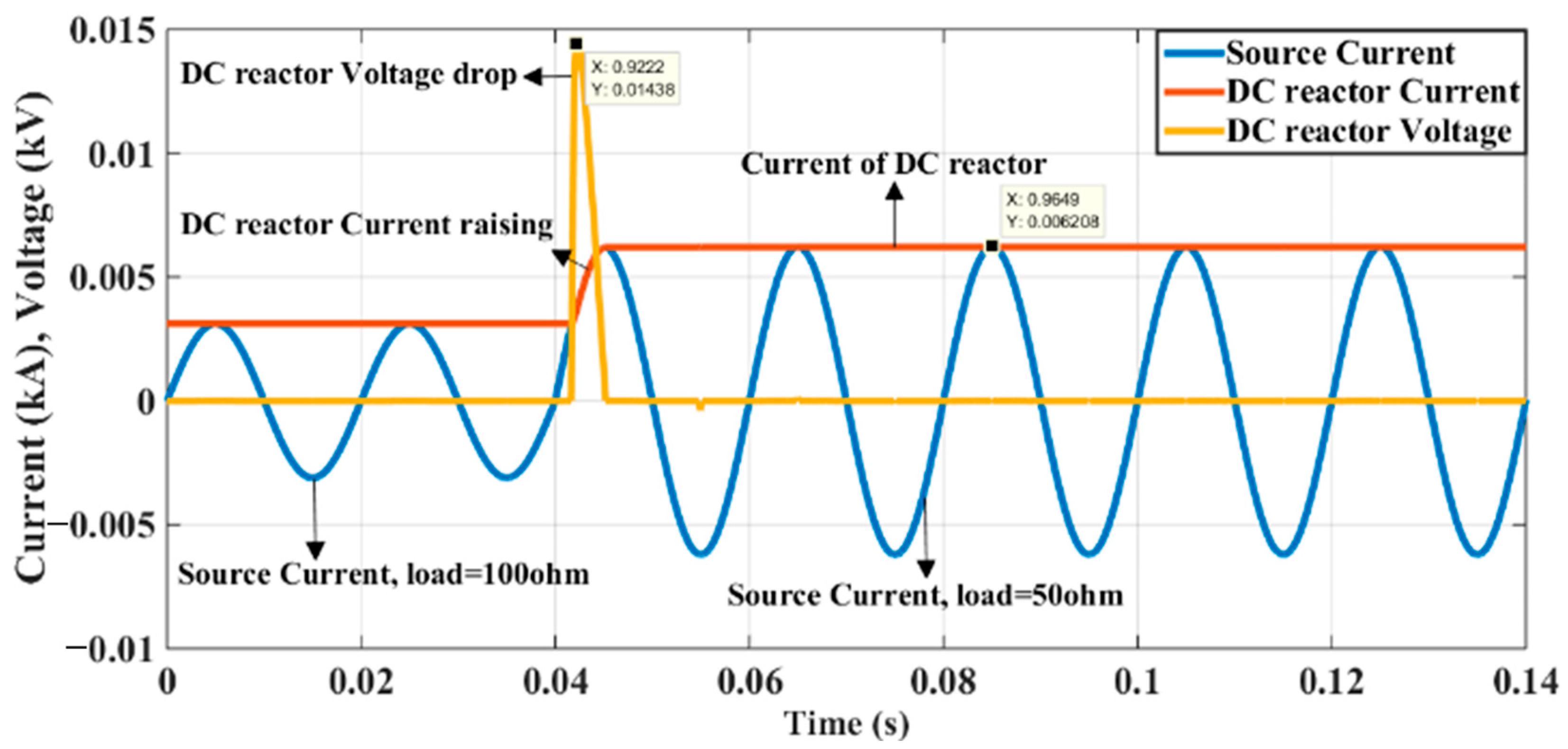
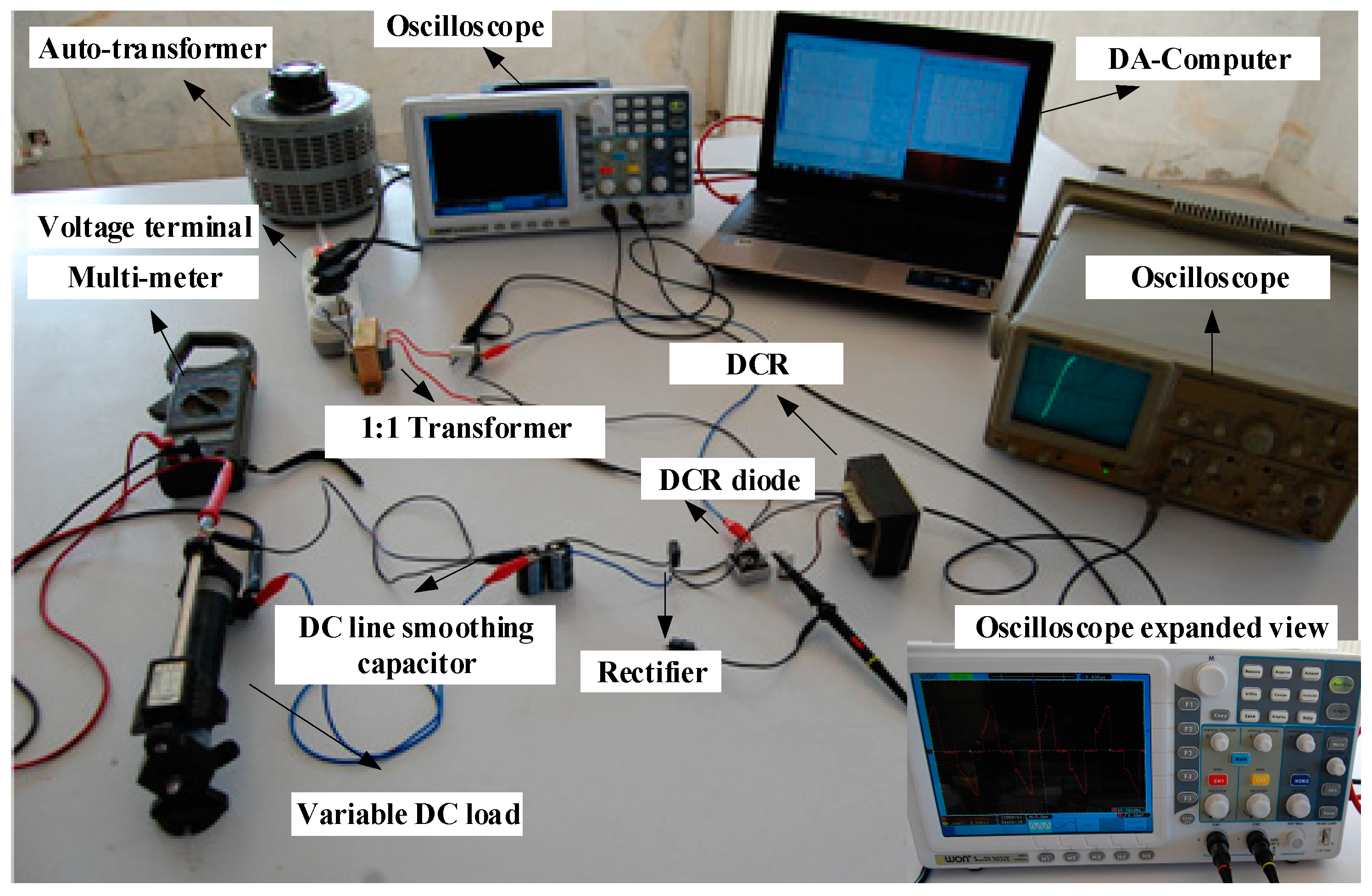
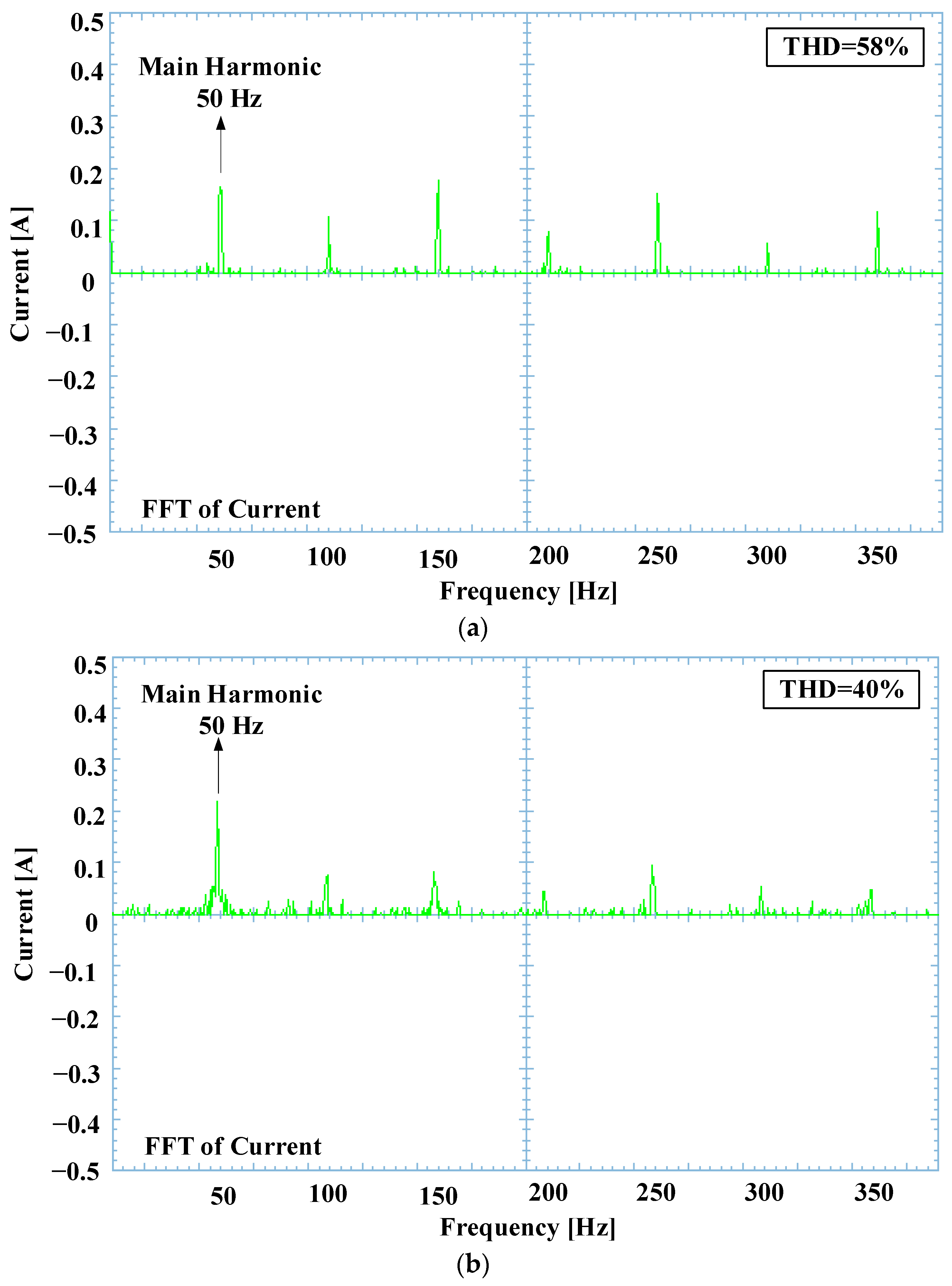
4. Experimental Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Safaei, A.; Zolfaghari, M.; Gilvanejad, M.; Gharehpetian, G.B. A survey on fault current limiters: Development and technical aspects. Int. J. Electr. Power Energy Syst. 2020, 118, 105729. [Google Scholar] [CrossRef]
- Behdani, B.; Shariatinasab, R.; Afrasiabi, M.; Aghaei, J. Analysis of Power Transformer Inrush Current in the Presence of Quasi-Direct Currents. In Proceedings of the 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I & CPS Europe), Prague, Czech Republic, 28 June–1 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- El-Ela, A.A.A.; El-Sehiemy, R.A.; Shaheen, A.M.; Ellien, A.R. Review on active distribution networks with fault current limiters and renewable energy resources. Energies 2022, 15, 7648. [Google Scholar] [CrossRef]
- Pulido, E.; Morán, L.; Villarroel, F.; Silva, J. Active reduction of short-circuit current in power distribution systems. Energies 2020, 13, 334. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Zakzouk, N.E. Bi-functional non-superconducting saturated-core inductor for single-stage grid-tied PV systems: Filter and fault current limiter. Energies 2023, 16, 4206. [Google Scholar] [CrossRef]
- Kartijkolaie, H.S.; Hsia, K.-H.; Mobayen, S.; Firouzi, M.; Shafiee, M. Controllable-dual bridge fault current limiter for interconnection micro-grids. Energies 2021, 14, 1026. [Google Scholar] [CrossRef]
- Afrasiabi, S.; Behdani, B.; Afrasiabi, M.; Mohammadi, M.; Asheralieva, A.; Gheisari, M. Differential Protection of Power Transformers based on RSLVQ-Gradient Approach Considering SFCL. In Proceedings of the 2021 IEEE Madrid PowerTech, Madrid, Spain, 28 June–2 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Heidary, A.; Yazdani-Asrami, M.; Hesami, M.; Sood, V. The TRV Improvement of Fast Circuit Breakers Using Solid-State Series Superconducting Reactor. IEEE Trans. Power Deliv. 2023, 38, 1259–1266. [Google Scholar] [CrossRef]
- You, H.; Jin, J. Characteristic analysis of a fully controlled bridge type superconducting fault current limiter. IEEE Trans. Appl. Supercond. 2016, 26, 5603706. [Google Scholar] [CrossRef]
- Heidary, A.; Popov, M.; Moghim, A.; Niasar, M.G.; Lekić, A. The Principles of Controlled DC-Reactor Fault Current Limiter for Battery Energy Storage Protection. IEEE Trans. Ind. Electron. 2024, 71, 1525–1534. [Google Scholar] [CrossRef]
- Heidary, A.; Radmanesh, H.; Rouzbehi, K.; Pou, J. A DC-Reactor-Based Solid-State Fault Current Limiter for HVdc Applications. IEEE Trans. Power Deliv. 2019, 34, 720–728. [Google Scholar] [CrossRef]
- Heidary, A.; Radmanesh, H.; Moghim, A.; Ghorbanyan, K.; Rouzbehi, K.; MGRodrigues, E.; Pouresmaeil, E. A multi-inductor H bridge fault current limiter. Electronics 2019, 8, 795. [Google Scholar] [CrossRef]
- Heidary, A.; Radmanesh, H.; Bakhshi, A.; Samandarpour, S.; Rouzbehi, K.; Shariati, N. Compound ferroresonance overvoltage and fault current limiter for power system protection. IET Energy Syst. Integr. 2020, 2, 325–330. [Google Scholar] [CrossRef]
- IEEE Std 519-2022 (Revision of IEEE Std 519-2014); IEEE Standard for Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2022; pp. 1–31. [CrossRef]
- IEEE Std 1547-2003; IEEE Standard for Interconnecting Distributed Resources with Electric Power Systems. IEEE: Piscataway, NJ, USA, 2003; pp. 1–28. [CrossRef]
- Heidary, A.; Radmanesh, H.; Rouzbehi, K.; Mehrizi-Sani, A.; Gharehpetian, G.B. Inductive fault current limiters: A review. Electr. Power Syst. Res. 2020, 187, 106499. [Google Scholar] [CrossRef]
- Heidary, A.; Rouzbehi, K.; Mehrizi-Sani, A.; Sood, V.K. A Self-Activated Fault Current Limiter for Distribution Network Protection. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 4626–4633. [Google Scholar] [CrossRef]
- Carbone, R.; Scappatura, A. A high efficiency passive power factor corrector for single-phase bridge diode rectifiers. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; Volume 2, pp. 1627–1630. [Google Scholar] [CrossRef]
- Sainz, L.; Pedra, J.; Mesas, J.J. Single-phase full-wave rectifier study with experimental measurements. Electr. Power Syst. Res. 2007, 77, 339–351. [Google Scholar] [CrossRef]
- Beres, R.N.; Wang, X.; Liserre, M.; Blaabjerg, F.; Bak, C.L. A Review of Passive Power Filters for Three-Phase Grid-Connected Voltage-Source Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 54–69. [Google Scholar] [CrossRef]
- Rockhill, A.A.; Liserre, M.; Teodorescu, R.; Rodriguez, P. Grid-Filter Design for a Multimegawatt Medium-Voltage Voltage-Source Inverter. IEEE Trans. Ind. Electron. 2011, 58, 1205–1217. [Google Scholar] [CrossRef]
- Beres, R.N.; Wang, X.; Blaabjerg, F.; Bak, C.L.; Liserre, M. Comparative analysis of the selective resonant LCL and LCL plus trap filters. In Proceedings of the 2014 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Bran, Romania, 22–24 May 2014; pp. 740–747. [Google Scholar] [CrossRef]
- Beres, R.N.; Wang, X.; Blaabjerg, F.; Liserre, M.; Bak, C.L. Optimal Design of High-Order Passive-Damped Filters for Grid-Connected Applications. IEEE Trans. Power Electron. 2016, 31, 2083–2098. [Google Scholar] [CrossRef]
- Xie, X.; Huang, Z.; Fan, X.; Tang, T. Adaptive single-phase auto-reclosing scheme based on the moving average filter-quadrature signal generator for transmission lines with shunt reactors. Electr. Power Syst. Res. 2023, 223, 109545. [Google Scholar] [CrossRef]
- Muhlethaler, J.; Schweizer, M.; Blattmann, R.; Kolar, J.W.; Ecklebe, A. Optimal Design of LCL Harmonic Filters for Three-Phase PFC Rectifiers. IEEE Trans. Power Electron. 2013, 28, 3114–3125. [Google Scholar] [CrossRef]
- Jennings, G.; de Villiers, L. Transient Stability improvement using series reactors: A case study. In Proceedings of the 2015 IEEE Electrical Power and Energy Conference (EPEC), London, ON, Canada, 26–28 October 2015; pp. 296–302. [Google Scholar] [CrossRef]
- Meral, M.E.; Çelik, D. Mitigation of DC-link voltage oscillations to reduce size of DC-side capacitor and improve lifetime of power converter. Electr. Power Syst. Res. 2021, 194, 107048. [Google Scholar] [CrossRef]
- Dommel, H.W. EMTP Theory Book; Microtran Power System Analysis Corporation: Vancouver, BC, Canada, 1992. [Google Scholar]
- Das, J.C. Power System Harmonics and Passive Filter Designs; John Wiley & Sons: Nashville, TN, USA, 2015. [Google Scholar]





| Symbol | Quantity | Value |
|---|---|---|
| Vac | AC microgrid Thevenin voltage | 220 VRMS |
| r | AC microgrid Thevenin resistance | 0.1 Ω |
| R | DC system load | 100 Ω |
| C | DC line shunt capacitor | 1 mF |
| Symbol | Quantity | Value |
|---|---|---|
| Vac | AC microgrid Thevenin voltage | 220 VRMS |
| r | AC microgrid Thevenin resistance | 0.1 Ω |
| R1 | System load branch 1 | 100 Ω |
| R2 | System load branch 2 | 100 Ω |
| Ld | BDCR-FCL inductance | 100 mH |
| rd | BDCR-FCL resistance | 0.05 Ω |
| VFB | Rectifier bridge voltage drop | 0.7 V |
| Symbol | Quantity | Value |
|---|---|---|
| Vac | AC microgrid Thevenin voltage | 220 VRMS |
| r | AC microgrid Thevenin resistance | 0.1 Ω |
| R | DC system load | 100 Ω |
| Ld | BDCR-FCL inductance | 100 mH |
| rd | BDCR-FCL resistance | 0.05 Ω |
| VFB | Rectifier bridge voltage drop | 0.7 V |
| Symbol | Quantity | Value |
|---|---|---|
| Vac | Source voltage | 220 VRMS |
| R | DC load | 100 Ω |
| Ld | BDCR-FCL inductance | 100 mH |
| rd | BDCR-FCL resistance | 0.1 Ω |
| C | DC line shunt capacitor | 1 mF |
| D | Rectifier bridge diode | 1N5819 |
| VFB | Rectifier bridge voltage drop | 0.7 V |
| Technology | Fault Current Limiting | Waveform Smoothing | PF Enhancement | THD Reduction |
|---|---|---|---|---|
| Reactor type [5] | Yes | No | No | No |
| Superconductor type [7] | Yes | No | No | No |
| BDCR | Yes | Yes | Yes | Yes |
| Issue | BDCR-FCL Effect |
|---|---|
| Nonlinear load peak current | Limits the nonlinear load peak |
| Nonlinear load conduction duration | Increases nonlinear load conduction duration |
| THD | Reduces the current THD |
| PF | Improves the PF |
| Load current variations | Smooths the load current variations |
| Rate of rise of current | Reduced rate of rise of current |
| Reactive power loss | No notable reactive power as a DC inductor |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behdani, B.; Moghim, A.; Mousavi, S.; Soltanfar, M.; Hojabri, M. Multifaceted Functionalities of Bridge-Type DC Reactor Fault Current Limiters: An Experimentally Validated Investigation. Energies 2024, 17, 975. https://doi.org/10.3390/en17040975
Behdani B, Moghim A, Mousavi S, Soltanfar M, Hojabri M. Multifaceted Functionalities of Bridge-Type DC Reactor Fault Current Limiters: An Experimentally Validated Investigation. Energies. 2024; 17(4):975. https://doi.org/10.3390/en17040975
Chicago/Turabian StyleBehdani, Behzad, Ali Moghim, Sheyda Mousavi, Mostafa Soltanfar, and Mojgan Hojabri. 2024. "Multifaceted Functionalities of Bridge-Type DC Reactor Fault Current Limiters: An Experimentally Validated Investigation" Energies 17, no. 4: 975. https://doi.org/10.3390/en17040975
APA StyleBehdani, B., Moghim, A., Mousavi, S., Soltanfar, M., & Hojabri, M. (2024). Multifaceted Functionalities of Bridge-Type DC Reactor Fault Current Limiters: An Experimentally Validated Investigation. Energies, 17(4), 975. https://doi.org/10.3390/en17040975






