Improving the Methodology for Determining the Biomass/Coal Co-Combustion Ratio: Predictive Modeling of the 14C Activity of Pure Biomass
Abstract
1. Introduction
2. Materials and Methods
2.1. Biomass Classification
2.2. Sampling and Processing
2.2.1. Tree Ring Samples
2.2.2. C3 Plants Samples
2.2.3. 14C Sample Preparation and Detection
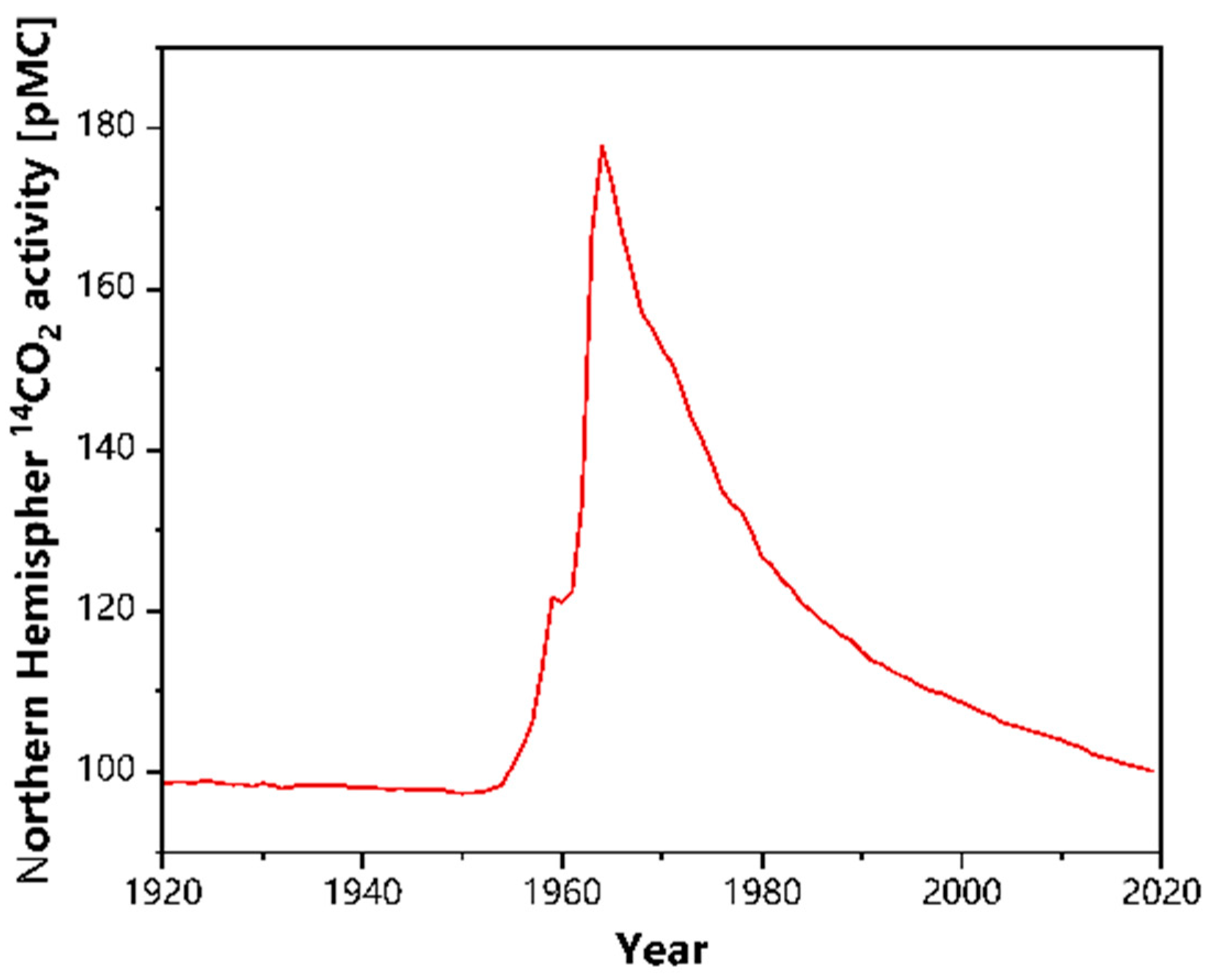
2.3. Data Acquisition
2.4. Prediction Method
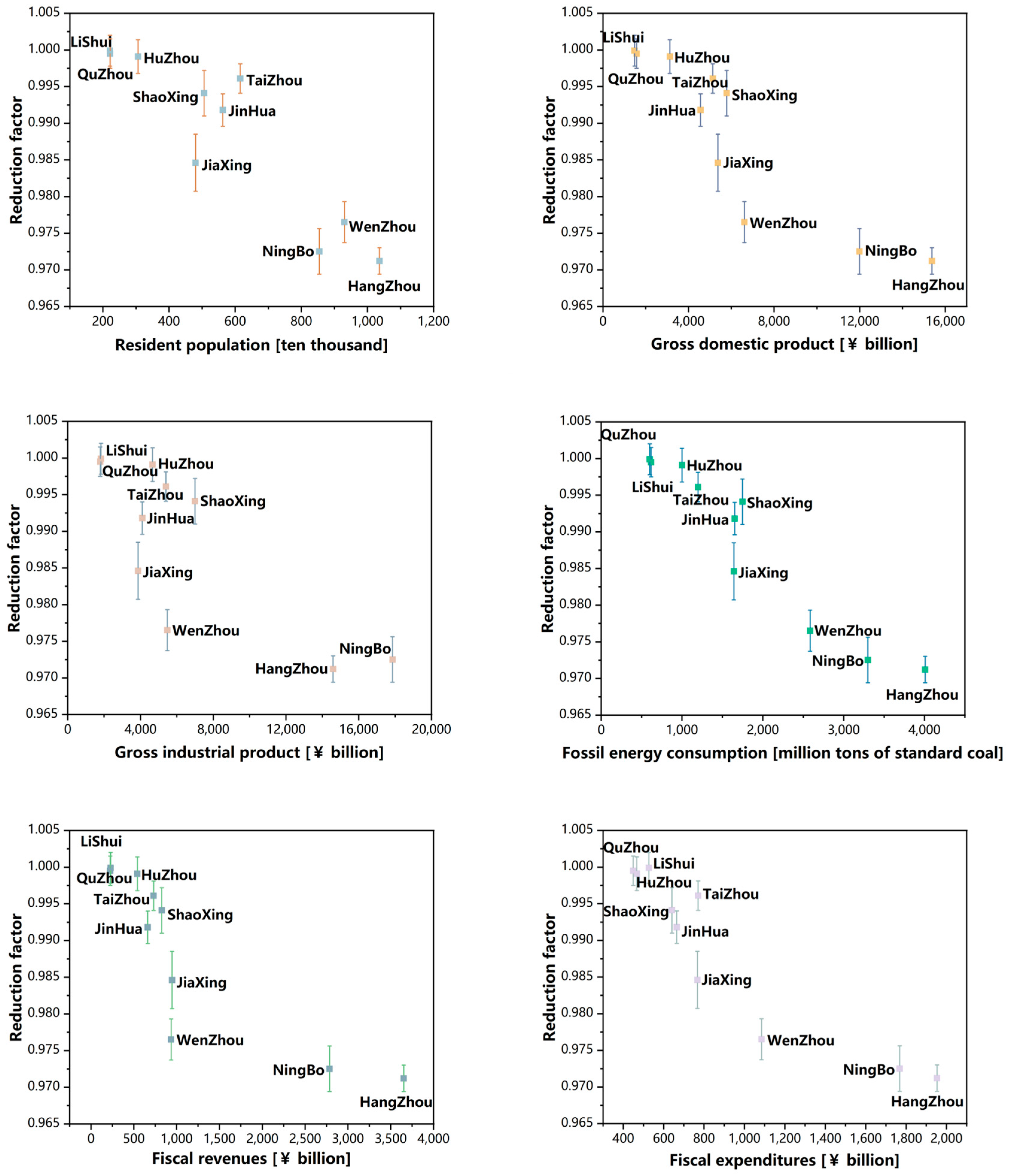
2.4.1. Regional Influencing Factors
2.4.2. Annual Biomass
2.4.3. Perennial Biomass
2.5. Improved Methodology
3. Results and Discussion
3.1. Regional Influencing Factors
3.1.1. Fitting Results at the City Level
3.1.2. Fitting Results at the District Level
3.2. 14C Content Bias of C3 Biomass
3.3. Perennial Biomass
3.3.1. Growth Function
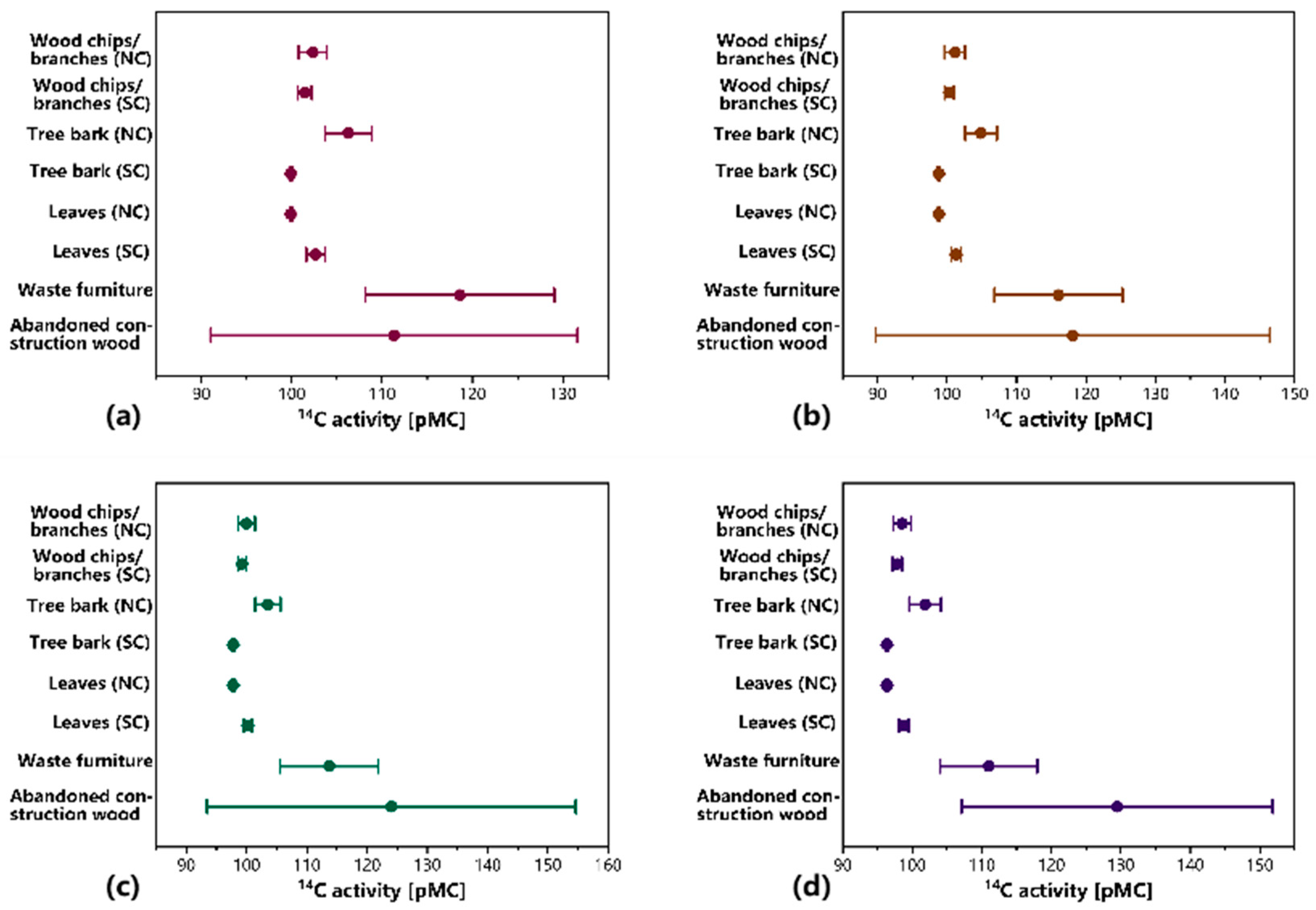
3.3.2. Prediction of Different Types of Perennial Biomass
Wood Chips and Branches
Tree Bark
Leaves
Waste Furniture
Abandoned Construction Wood
3.3.3. Summary of Values
3.4. Prediction Formula
3.5. Improved Methodology for Determining Biomass Blending Ratios
3.6. Error Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviations/Symbols | Description |
| The carbon-based blending ratio | |
| The 14C activity of CO2 in flue gas | |
| The 14C activity of the CO2 absorbed by NaOH | |
| The 14C activity of biomass | |
| The carbon-based fraction of CO2 absorbed by NaOH | |
| Reduction factor | |
| The local atmospheric 14CO2 reduction factor | |
| The isotope fractionation effect reduction factor | |
| The fitting coefficients in front of each variable of the linear equation | |
| Resident population | |
| Gross domestic product | |
| Gross industrial product | |
| Fossil energy consumption | |
| Fiscal revenues | |
| Fiscal expenditures | |
| The cost function for fitting the equation (the average value of the residuals of each array in the training set) | |
| The fitting value of under some values of | |
| The actual values of | |
| The matrix composed of each city’s economic indicators () | |
| The matrix composed of | |
| The 14C activity of biomass | |
| The corrected value of the 14C activity of biomass, that is, the 14C activity of C3 biomass | |
| The corrected value of the 13C activity of biomass, that is, the 13C activity of C3 biomass | |
| The 13C activity of air CO2 | |
| The thousandth difference of the 13C content of C3 biomass | |
| The thousandth difference of the 13C content of air CO2 | |
| Correction parameter | |
| RS | Rice straw |
| WS | Wheat straw |
| The growth function model of the plant | |
| The atmospheric 14C activity of every year | |
| The 14C activity of air CO2 | |
| The carbon-based fraction of air CO2 in flue gas | |
| The prediction value of the 14C activity of different types of biomass fuel | |
| The carbon-based percentage of the biomass fuel | |
| The original 14C activity of the fuel | |
| The atmospheric background 14CO2 value after 2019 | |
| The error in the measured blending ratio | |
| The uncertainty of the prediction value of the 14C activity of biomass |
References
- Li, Y.; Yang, L.; Luo, T. Energy System Low-Carbon Transition under Dual-Carbon Goals: The Case of Guangxi, China Using the EnergyPLAN Tool. Energies 2023, 16, 3416. [Google Scholar] [CrossRef]
- Xie, S.; Yang, Q.; Wang, Q.; Zhou, H.; Bartocci, P.; Fantozzi, F. Coal Power Decarbonization via Biomass Co-Firing with Carbon Capture and Storage: Tradeoff between Exergy Loss and GHG Reduction. Energy Convers. Manag. 2023, 288, 117155. [Google Scholar] [CrossRef]
- Król, K.; Nowak-Woźny, D.; Moroń, W. Study of Ash Sintering Temperature and Ash Deposition Behavior during Co-Firing of Polish Bituminous Coal with Barley Straw Using Non-Standard Tests. Energies 2023, 16, 4424. [Google Scholar] [CrossRef]
- Unyay, H.; Piersa, P.; Zabochnicka, M.; Romanowska-Duda, Z.; Kuryło, P.; Kuligowski, K.; Kazimierski, P.; Hutsol, T.; Dyjakon, A.; Wrzesińska-Jędrusiak, E.; et al. Torrefaction of Willow in Batch Reactor and Co-Firing of Torrefied Willow with Coal. Energies 2023, 16, 8083. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Z.; Tang, Y.; Wang, Q.; Yu, C.; Yang, X.; Chen, Q. Establishment and Verification of a Metering Scheme for Biomass-Coal Blending Ratios Based on 14C Determination. Fuel 2022, 327, 125198. [Google Scholar] [CrossRef]
- Palstra, S.W.L.; Meijer, H.A.J. Carbon-14 Based Determination of the Biogenic Fraction of Industrial CO2 Emissions—Application and Validation. Bioresour. Technol. 2010, 101, 3702–3710. [Google Scholar] [CrossRef]
- Tang, Y.; Luo, Z.; Yu, C.; Cen, J.; Chen, Q.; Zhang, W. Determination of Biomass-Coal Blending Ratio by 14C Measurement in Co-Firing Flue Gas. J. Zhejiang Univ.-Sci. A 2019, 20, 475–486. [Google Scholar] [CrossRef]
- Lee, Y.-J.; Go, Y.-J.; Yoo, H.-N.; Choi, G.-G.; Park, H.-Y.; Kang, J.-G.; Lee, W.-S.; Shin, S.-K. Measurement and Analysis of Biomass Content Using Gas Emissions from Solid Refuse Fuel Incineration. Waste Manag. 2021, 120, 392–399. [Google Scholar] [CrossRef]
- Ariyaratne, W.K.H.; Melaaen, M.C.; Tokheim, L.-A. Determination of Biomass Fraction for Partly Renewable Solid Fuels. Energy 2014, 70, 465–472. [Google Scholar] [CrossRef][Green Version]
- Muir, G.K.P.; Hayward, S.; Tripney, B.G.; Cook, G.T.; Naysmith, P.; Herbert, B.M.J.; Garnett, M.H.; Wilkinson, M. Determining the Biomass Fraction of Mixed Waste Fuels: A Comparison of Existing Industry and 14C-Based Methodologies. Waste Manag. 2015, 35, 293–300. [Google Scholar] [CrossRef]
- Tang, Y.; Luo, Z.; Yu, C. Accuracy Improvement of the 14C Method Applied in Biomass and Coal Co-Firing Power Stations. Processes 2021, 9, 994. [Google Scholar] [CrossRef]
- Fellner, J.; Rechberger, H. Abundance of 14C in Biomass Fractions of Wastes and Solid Recovered Fuels. Waste Manag. 2009, 29, 1495–1503. [Google Scholar] [CrossRef] [PubMed]
- Stuiver, M.; Reimer, P.J.; Braziunas, T.F. High-Precision Radiocarbon Age Calibration for Terrestrial and Marine Samples. Radiocarbon 1998, 40, 1127–1151. [Google Scholar] [CrossRef]
- Levin, I.; Kromer, B. The Tropospheric 14 CO2 Level in Mid-Latitudes of the Northern Hemisphere (1959–2003). Radiocarbon 2004, 46, 1261–1272. [Google Scholar] [CrossRef]
- Xi, X.; Ding, X.; Fu, D.; Zhou, L.; Liu, K. Regional Δ14C Patterns and Fossil Fuel Derived CO2 Distribution in the Beijing Area Using Annual Plants. Chin. Sci. Bull. 2011, 56, 1721–1726. [Google Scholar] [CrossRef]
- Xiong, X.; Zhou, W.; Wu, S.; Cheng, P.; Du, H.; Hou, Y.; Niu, Z.; Wang, P.; Lu, X.; Fu, Y. Two-Year Observation of Fossil Fuel Carbon Dioxide Spatial Distribution in Xi’an City. Adv. Atmos Sci. 2020, 37, 569–575. [Google Scholar] [CrossRef]
- Lewis, C.W.; Klouda, G.A.; Ellenson, W.D. Radiocarbon Measurement of the Biogenic Contribution to Summertime PM-2.5 Ambient Aerosol in Nashville, TN. Atmos. Environ. 2004, 38, 6053–6061. [Google Scholar] [CrossRef]
- Mohn, J.; Szidat, S.; Fellner, J.; Rechberger, H.; Quartier, R.; Buchmann, B.; Emmenegger, L. Determination of Biogenic and Fossil CO2 Emitted by Waste Incineration Based on 14CO2 and Mass Balances. Bioresour. Technol. 2008, 99, 6471–6479. [Google Scholar] [CrossRef]
- Li, Z.-H.; Magrini-Bair, K.; Wang, H.; Maltsev, O.V.; Geeza, T.J.; Mora, C.I.; Lee, J.E. Tracking Renewable Carbon in Bio-Oil/Crude Co-Processing with VGO through 13C/12C Ratio Analysis. Fuel 2020, 275, 117770. [Google Scholar] [CrossRef]
- Hou, Y.; Zhou, W.; Cheng, P.; Xiong, X.; Du, H.; Niu, Z.; Yu, X.; Fu, Y.; Lu, X. 14C-AMS Measurements in Modern Tree Rings to Trace Local Fossil Fuel-Derived CO2 in the Greater Xi’an Area, China. Sci. Total Environ. 2020, 715, 136669. [Google Scholar] [CrossRef]
- Niu, Z.; Zhou, W.; Feng, X.; Feng, T.; Wu, S.; Cheng, P.; Lu, X.; Du, H.; Xiong, X.; Fu, Y. Atmospheric Fossil Fuel CO2 Traced by 14CO2 and Air Quality Index Pollutant Observations in Beijing and Xiamen, China. Environ. Sci. Pollut. Res. 2018, 25, 17109–17117. [Google Scholar] [CrossRef] [PubMed]
- Hua, Q.; Turnbull, J.C.; Santos, G.M.; Rakowski, A.Z.; Ancapichún, S.; De Pol-Holz, R.; Hammer, S.; Lehman, S.J.; Levin, I.; Miller, J.B.; et al. Atmospheric radiocarbon for the period 1950–2019. Radiocarbon 2022, 64, 723–745. [Google Scholar] [CrossRef]
- Paula, J.; Thomas, A.; Ron, W. Discussion: Reporting and Calibration of Post-Bomb 14 C Data. Radiocarbon 2004, 46, 1299–1304. [Google Scholar] [CrossRef]
- Duan, B. Beijing Yearbook; Office of Beijing Local Chronicles Compilation Committee: Beijing, China, 2010.
- Duan, B. Beijing Yearbook; Office of Beijing Local Chronicles Compilation Committee: Beijing, China, 2011.
- Guo, Y. Guang Zhou Yearbook; Guangzhou Yearbook Society: Guangzhou, China, 2011. [Google Scholar]
- Feng, J.; An, P. Tian Jin Statistical Yearbook; China Statistics Press: Beijing, China, 2011.
- Zhang, Q. Zheng Zhou Yearbook; Zhongzhou Ancient Books Publishing House: Zhengzhou, China, 2011. [Google Scholar]
- Qu, B. Lin Fen Yearbook; Fangzhi Publishing House: Beijing, China, 2011. [Google Scholar]
- Zhang, M.; Han, G. Xi’an Statistical Yearbook; China Statistics Press: Beijing, China, 2011.
- Hou, F. Lasa Yearbook; China Literature and History Press: Beijing, China, 2011. [Google Scholar]
- Wang, X. Jiuquan Yearbook; Gansu Ethnic Publishing House: Jiuquan, China, 2011. [Google Scholar]
- Li, Z. Ordos Statistical Yearbook; China Statistics Press: Beijing, China, 2011.
- Yuan, H. Yi Bin Yearbook; Beijing Kehai Electronic Press: Beijing, China, 2011. [Google Scholar]
- Yang, Y. Haidong Yearbook; Guizhou Publishing Group Guizhou People’s Publishing House: Guiyang, China, 2011. [Google Scholar]
- Wang, J. Jin Cheng Statistical Yearbook; China Statistics Press: Beijing, China, 2011.
- Zheng, L. Yan’an Statistical Yearbook; China Statistics Press: Beijing, China, 2011.
- Yantai Bureau of Statistics. Statistical Yearbook of Yantai; China Statistics Press: Beijing, China, 2011.
- Wu, J.; Chen, Y. Zun Yi Statistical Yearbook; China Statistics Press: Beijing, China, 2011.
- Lin, R.; Chen, Z. Sanya Statistical Yearbook; China Statistics Press: Beijing, China, 2015.
- Tong, Y.; Li, Z. Harbin Statistical Yearbook; China Statistics Press: Beijing, China, 2015.
- Zhang, M.; Han, G. Xi’an Statistical Yearbook; China Statistics Press: Beijing, China, 2015.
- Huan, J.; Wu, H.; Yin, B. Hang Zhou Statistical Yearbook; China Statistics Press: Beijing, China, 2015.
- Xia, Q. Beijing Statistical Yearbook; China Statistics Press: Beijing, China, 2015.
- Lan, S. Qu Zhou Yearbook; Fangzhi Publishing House: Beijing, China, 2020. [Google Scholar]
- Xiang, S.; Ling, H. Jin Hua Statistical Yearbook; China Statistics Press: Beijing, China, 2020.
- Li, J.; Zhang, C. Li Shui Statistical Yearbook; China Statistics Press: Beijing, China, 2020.
- Chen, S.; Cheng, Z. Wen Zhou Statistical Yearbook; China Statistics Press: Beijing, China, 2020.
- Ningbo Bureau of Statistics. Ning Bo Statistical Yearbook; China Statistics Press: Beijing, China, 2020.
- Zheng, Z.; Hong, C. Tai Zhou Statistical Yearbook; China Statistics Press: Beijing, China, 2020.
- Shaoxing Bureau of Statistics. Shao Xing Statistical Yearbook; China Statistics Press: Beijing, China, 2020.
- Chen, W. Jia Xing Statistical Yearbook; China Statistics Press: Beijing, China, 2020.
- Huan, J.; Wu, H.; Yin, B. Hang Zhou Statistical Yearbook; China Statistics Press: Beijing, China, 2020.
- Fei, X.; Jin, X. Hu Zhou Statistical Yearbook; China Statistics Press: Beijing, China, 2020.
- Xi, X.T.; Ding, X.F.; Fu, D.P.; Zhou, L.P.; Liu, K.X. Δ14C Level of Annual Plants and Fossil Fuel Derived CO2 Distribution across Different Regions of China. Nucl. Instrum. Methods Phys. Res. B 2013, 294, 515–519. [Google Scholar] [CrossRef]
- Cheng, P.; Zhou, W.; Burr, G.S.; Fu, Y.; Fan, Y.; Wu, S. Authentication of Chinese Vintage Liquors Using Bomb-Pulse 14C. Sci. Rep. 2016, 6, 38381. [Google Scholar] [CrossRef] [PubMed]
- Ding, P.; Shen, C.D.; Yi, W.X.; Wang, N.; Ding, X.F.; Fu, D.P.; Liu, K.X. Fossil-Fuel-Derived CO2 Contribution to the Urban Atmosphere in Guangzhou, South China, Estimated by 14 CO2 Observation, 2010–2011. Radiocarbon 2013, 55, 791–803. [Google Scholar] [CrossRef]
- Niu, Z.; Zhou, W.; Cheng, P.; Wu, S.; Lu, X.; Xiong, X.; Du, H.; Fu, Y. Observations of Atmospheric Δ 14 CO2 at the Global and Regional Background Sites in China: Implication for Fossil Fuel CO2 Inputs. Environ. Sci. Technol. 2016, 50, 12122–12128. [Google Scholar] [CrossRef]
- Mook, W.G.; van der Plicht, J. Reporting 14C Activities and Concentrations. Radiocarbon 1999, 41, 227–239. [Google Scholar] [CrossRef]


| Tree Types | Growth Function | Harvesting Age |
|---|---|---|
| Eucalyptus | 6~10 | |
| Cypress | 40~50 | |
| Sassafras | 20~50 | |
| Birch | 15~50 | |
| Oak | 50~100 | |
| Willow | 15~20 | |
| Cedar | 20~40 | |
| Pinus Massoniana | 25~40 | |
| Chinese Red Pine | 30~60 | |
| Larch | 30~40 | |
| Camphor | 30~80 | |
| Poplar | 10~20 | |
| Beech | 50~100 | |
| Locust | 10~60 |
| Fitting Methods | Relative Error (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| Full factor | 1.0 × 100 | −1.4 × 10−5 | −5.4 × 10−7 | −8.6 × 10−8 | −3.4 × 10−6 | −3.3 × 10−6 | 7.6 × 10−6 | −0.21 |
| Single factor | 1.0 × 100 | - | - | - | −6.0 × 10−6 | - | - | −0.15 |
| Two factor | 1.0 × 100 | −9.4 × 10−6 | - | - | −4.0 × 10−6 | - | - | −0.07 |
| Three factor | 1.0 × 100 | −7.6 × 10−6 | - | −4.2 × 10−7 | −3.6 × 10−6 | - | - | −0.18 |
| Fitting Methods | Relative Error (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| Full factor | −9.5 × 10−1 | −3.2 × 10−5 | −2.2 × 10−5 | 1.8 × 10−5 | −6.3 × 10−5 | −4.2 × 10−4 | 7.0 × 10−4 | 0.89 |
| Single factor | 9.7 × 10−1 | - | - | - | −3.3 × 10−5 | - | - | −0.04 |
| Site | Sample | (pMC) | (‰) | (%) | |||
|---|---|---|---|---|---|---|---|
| LinJiang | RS | 96.31 | −25.02 | 97.50 | 0.9836 | 0.9877 | 1.3345 |
| Air | 97.91 | −12.89 | 98.71 | ||||
| HongTong | RS | 96.01 | −28.43 | 97.16 | 0.9795 | 0.9848 | 1.3527 |
| Air | 98.02 | −13.45 | 98.66 | ||||
| WangPing | WS | 96.19 | −30.05 | 97.00 | 0.9725 | 0.9808 | 1.4341 |
| Air | 98.90 | −11.02 | 98.90 | ||||
| GuangTian | WS | 97.13 | −31.12 | 96.89 | 0.9738 | 0.9815 | 1.4228 |
| Air | 99.75 | −12.85 | 98.72 |
| Year | Eucalyptus | Cypress | Sassafras | Birch | Oak | Willow | Cedar | Pinus Massoniana | Chinese Red Pine | Larch Pine | Camphor | Poplar | Beech | Locust |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2030 | 97.84 ± 0.67 | 105.30 ± 2.15 | 101.26 ± 4.43 | 99.87 ± 4.33 | 110.27 ± 9.64 | 102.15 ± 1.21 | 99.80 ± 1.41 | 99.38 ± 1.23 | 102.33 ± 5.76 | 102.93 ± 2.17 | 105.81 ± 11.2 | 98.54 ± 1.28 | 112.97 ± 8.97 | 103.97 ± 11.1 |
| 2029 | 98.19 ± 0.67 | 105.79 ± 2.22 | 101.67 ± 4.53 | 100.25 ± 4.41 | 110.83 ± 9.32 | 102.60 ± 1.21 | 100.18 ± 1.43 | 99.75 ± 1.25 | 102.76 ± 5.93 | 103.36 ± 2.20 | 106.34 ± 11.2 | 98.91 ± 1.30 | 113.45 ± 8.97 | 104.49 ± 11.7 |
| 2028 | 98.55 ± 0.67 | 106.30 ± 2.30 | 102.08 ± 4.64 | 100.64 ± 4.50 | 111.39 ± 8.96 | 103.07 ± 1.14 | 100.57 ± 1.46 | 100.13 ± 1.27 | 103.21 ± 6.11 | 103.80 ± 2.22 | 106.88 ± 11.3 | 99.26 ± 1.33 | 113.92 ± 8.95 | 105.02 ± 12.3 |
| 2027 | 98.90 ± 0.67 | 106.83 ± 2.39 | 102.50 ± 4.76 | 101.04 ± 4.60 | 111.95 ± 9.11 | 103.54 ± 1.05 | 100.96 ± 1.49 | 100.51 ± 1.29 | 103.67 ± 6.31 | 104.24 ± 2.26 | 107.43 ± 11.5 | 99.63 ± 1.36 | 114.39 ± 8.91 | 105.57 ± 12.9 |
| 2026 | 99.26 ± 0.67 | 107.37 ± 2.50 | 102.93 ± 4.90 | 101.44 ± 4.70 | 112.51 ± 9.23 | 103.98 ± 0.99 | 101.36 ± 1.52 | 100.90 ± 1.31 | 104.14 ± 6.53 | 104.69 ± 2.31 | 107.99 ± 11.6 | 99.99 ± 1.37 | 114.85 ± 8.84 | 106.15 ± 13.5 |
| 2025 | 99.61 ± 0.67 | 107.93 ± 2.61 | 103.37 ± 5.05 | 101.85 ± 4.82 | 113.07 ± 9.34 | 104.38 ± 0.97 | 101.76 ± 1.56 | 101.29 ± 1.33 | 104.62 ± 6.77 | 105.15 ± 2.36 | 108.56 ± 11.7 | 100.37 ± 1.43 | 115.30 ± 8.74 | 106.74 ± 14.3 |
| 2024 | 99.96 ± 0.66 | 103.82 ± 2.74 | 103.82 ± 5.21 | 102.26 ± 4.94 | 113.62 ± 9.43 | 104.78 ± 0.94 | 102.17 ± 1.59 | 101.69 ± 1.36 | 105.12 ± 7.04 | 105.62 ± 2.42 | 109.13 ± 11.7 | 100.75 ± 1.47 | 115.74 ± 8.62 | 107.36 ± 15.1 |
| 2023 | 100.32 ± 0.66 | 109.13 ± 2.88 | 104.28 ± 5.40 | 102.68 ± 5.08 | 114.17 ± 9.51 | 105.18 ± 1.06 | 102.58 ± 1.64 | 102.09 ± 1.39 | 105.63 ± 7.32 | 106.10 ± 2.49 | 109.72 ± 11.8 | 101.14 ± 1.50 | 116.17 ± 8.46 | 108.01 ± 15.9 |
| 2022 | 100.68 ± 0.68 | 109.77 ± 3.04 | 104.75 ± 5.60 | 103.11 ± 5.22 | 114.71 ± 9.57 | 105.62 ± 1.21 | 103.00 ± 1.68 | 102.50 ± 1.42 | 106.16 ± 7.61 | 106.59 ± 2.56 | 110.31 ± 11.8 | 101.53 ± 1.52 | 116.59 ± 8.26 | 108.68 ± 16.6 |
| 2021 | 101.04 ± 0.72 | 110.45 ± 3.22 | 105.24 ± 5.82 | 103.55 ± 5.39 | 115.25 ± 9.61 | 106.08 ± 1.28 | 103.44 ± 1.73 | 102.92 ± 1.45 | 106.71 ± 7.90 | 107.09 ± 2.63 | 110.91 ± 11.8 | 101.93 ± 1.54 | 117.01 ± 8.03 | 109.37 ± 17.0 |
| 2020 | 101.43 ± 0.78 | 111.15 ± 3.41 | 105.74 ± 6.07 | 104.00 ± 5.57 | 115.78 ± 9.62 | 106.58 ± 1.37 | 103.88 ± 1.79 | 103.35 ± 1.49 | 107.27 ± 8.21 | 107.60 ± 2.70 | 111.52 ± 11.8 | 102.34 ± 1.55 | 117.41 ± 7.74 | 110.07 ± 17.1 |
| Year | Eucalyptus | Cypress | Sassafras | Birch | Oak | Willow | Cedar | Pinus Massoniana | Chinese Red Pine | Larch Pine | Camphor | Poplar | Beech | Locust |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2030 | 96.35 ± 0.15 | 121.08 ± 7.07 | 113.1 ± 15.1 | 96.35 ± 0.15 | 118.56 ± 56.9 | 102.89 ± 1.24 | 109.04 ± 6.56 | 110.34 ± 5.26 | 124.61 ± 29.2 | 111.79 ± 3.81 | 125.55 ± 49.9 | 101.85 ± 2.28 | 118.56 ± 56.9 | 116.46 ± 37.4 |
| 2029 | 96.7 ± 0.15 | 122.48 ± 8.49 | 113.97 ± 17.0 | 96.7 ± 0.15 | 117.98 ± 57.5 | 103.36 ± 1.15 | 109.63 ± 6.97 | 111 ± 5.6 | 126.13 ± 29.9 | 112.49 ± 4.11 | 125.33 ± 50.1 | 102.27 ± 2.24 | 117.98 ± 57.5 | 117.56 ± 38.5 |
| 2028 | 97.06 ± 0.15 | 123.95 ± 8.81 | 114.88 ± 17.9 | 97.06 ± 0.15 | 117.34 ± 58.1 | 103.84 ± 1.04 | 110.25 ± 7.19 | 111.68 ± 5.76 | 127.75 ± 31.8 | 113.22 ± 4.22 | 125.1 ± 50.3 | 102.69 ± 2.19 | 117.34 ± 58.1 | 118.72 ± 40.8 |
| 2027 | 97.41 ± 0.15 | 125.46 ± 8.64 | 115.82 ± 18.3 | 97.41 ± 0.15 | 116.67 ± 58.8 | 104.28 ± 0.98 | 110.89 ± 7.45 | 112.38 ± 5.96 | 129.51 ± 35.0 | 113.99 ± 4.35 | 124.87 ± 50.6 | 103.11 ± 2.15 | 116.67 ± 58.8 | 119.97 ± 44.5 |
| 2026 | 97.77 ± 0.15 | 127.13 ± 9.53 | 116.83 ± 19.8 | 97.77 ± 0.15 | 115.97 ± 59.5 | 104.68 ± 0.95 | 111.56 ± 7.79 | 113.11 ± 6.24 | 131.44 ± 38.6 | 114.81 ± 4.53 | 124.62 ± 50.8 | 103.54 ± 2.09 | 115.97 ± 59.5 | 121.33 ± 48.7 |
| 2025 | 98.12 ± 0.15 | 128.99 ± 10.8 | 117.94 ± 21.9 | 98.12 ± 0.15 | 115.23 ± 60.2 | 105.07 ± 0.93 | 112.26 ± 8.17 | 113.86 ± 6.57 | 133.52 ± 41.9 | 115.67 ± 4.76 | 124.36 ± 51.1 | 103.97 ± 2.03 | 115.23 ± 60.2 | 122.78 ± 52.7 |
| 2024 | 98.48 ± 0.15 | 131 ± 11.48 | 119.11 ± 23.4 | 98.48 ± 0.15 | 114.43 ± 61.0 | 105.47 ± 1.08 | 113.02 ± 8.8 | 114.67 ± 7.15 | 135.48 ± 39.9 | 116.6 ± 5.22 | 124.1 ± 51.3 | 104.41 ± 2.14 | 114.43 ± 61.0 | 124.17 ± 51.3 |
| 2023 | 98.83 ± 0.15 | 133.15 ± 12.4 | 120.37 ± 25.2 | 98.83 ± 0.15 | 113.57 ± 61.9 | 105.91 ± 1.25 | 113.81 ± 9.49 | 115.54 ± 7.76 | 136.71 ± 38.7 | 117.61 ± 5.69 | 123.82 ± 51.6 | 104.88 ± 2.29 | 113.57 ± 61.9 | 125.12 ± 50.3 |
| 2022 | 99.19 ± 0.15 | 135.5 ± 13.6 | 121.72 ± 27.4 | 99.19 ± 0.15 | 112.65 ± 62.8 | 106.38 ± 1.31 | 114.65 ± 10.1 | 116.47 ± 8.28 | 137.2 ± 38.2 | 118.69 ± 6.06 | 123.52 ± 51.9 | 105.34 ± 2.35 | 112.65 ± 62.8 | 125.62 ± 46.9 |
| 2021 | 99.54 ± 0.15 | 137.95 ± 13.7 | 123.14 ± 28.5 | 99.54 ± 0.15 | 111.66 ± 63.8 | 106.89 ± 1.41 | 115.53 ± 10.6 | 117.46 ± 8.68 | 137.46 ± 38.0 | 119.83 ± 6.31 | 123.22 ± 52.2 | 105.8 ± 2.51 | 111.66 ± 63.8 | 125.98 ± 49.5 |
| 2020 | 99.89 ± 0.12 | 140.47 ± 13.4 | 124.61 ± 29.2 | 99.89 ± 0.12 | 110.62 ± 64.8 | 107.43 ± 1.44 | 116.47 ± 11.7 | 118.54 ± 9.61 | 137.69 ± 37.7 | 121.08 ± 7.07 | 122.9 ± 52.5 | 106.27 ± 2.6 | 110.62 ± 64.8 | 126.33 ± 49.1 |
| Year | Eucalyptus | Cypress | Sassafras | Birch | Oak | Willow | Cedar | Pinus Massoniana | Chinese Red Pine | Larch Pine | Camphor | Poplar | Beech | Locust |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2030 | 98.83 ± 0.71 | 121.08 ± 7.07 | 96.35 ± 0.15 | 96.35 ± 0.15 | 96.35 ± 0.15 | 96.35 ± 0.15 | 109.04 ± 6.56 | 110.34 ± 5.26 | 124.61 ± 29.2 | 96.35 ± 0.15 | 125.55 ± 49.9 | 96.35 ± 0.15 | 96.35 ± 0.15 | 96.35 ± 0.15 |
| 2029 | 99.19 ± 0.7 | 122.48 ± 8.49 | 96.7 ± 0.15 | 96.7 ± 0.15 | 96.7 ± 0.15 | 96.7 ± 0.15 | 109.63 ± 6.97 | 111.00 ± 5.6 | 126.13 ± 29.9 | 96.7 ± 0.15 | 125.33 ± 50.1 | 96.7 ± 0.15 | 96.7 ± 0.15 | 96.7 ± 0.15 |
| 2028 | 99.55 ± 0.73 | 123.95 ± 8.81 | 97.06 ± 0.15 | 97.06 ± 0.15 | 97.06 ± 0.15 | 97.06 ± 0.15 | 110.25 ± 7.19 | 111.68 ± 5.76 | 127.75 ± 31.8 | 97.06 ± 0.15 | 125.1 ± 50.3 | 97.06 ± 0.15 | 97.06 ± 0.15 | 97.06 ± 0.15 |
| 2027 | 99.9 ± 0.71 | 125.46 ± 8.64 | 97.41 ± 0.15 | 97.41 ± 0.15 | 97.41 ± 0.15 | 97.41 ± 0.15 | 110.89 ± 7.45 | 112.38 ± 5.96 | 129.51 ± 34.9 | 97.41 ± 0.15 | 124.87 ± 50.6 | 97.41 ± 0.15 | 97.41 ± 0.15 | 97.41 ± 0.15 |
| 2026 | 100.25 ± 0.67 | 127.13 ± 9.53 | 97.77 ± 0.15 | 97.77 ± 0.15 | 97.77 ± 0.15 | 97.77 ± 0.15 | 111.56 ± 7.79 | 113.11 ± 6.24 | 131.44 ± 38.6 | 97.77 ± 0.15 | 124.62 ± 50.8 | 97.77 ± 0.15 | 97.77 ± 0.15 | 97.77 ± 0.15 |
| 2025 | 100.6 ± 0.71 | 128.99 ± 10.8 | 98.12 ± 0.15 | 98.12 ± 0.15 | 98.12 ± 0.15 | 98.12 ± 0.15 | 112.26 ± 8.17 | 113.86 ± 6.57 | 133.52 ± 41.9 | 98.12 ± 0.15 | 124.36 ± 51.1 | 98.12 ± 0.15 | 98.12 ± 0.15 | 98.12 ± 0.15 |
| 2024 | 100.96 ± 0.72 | 131 ± 11.48 | 98.48 ± 0.15 | 98.48 ± 0.15 | 98.48 ± 0.15 | 98.48 ± 0.15 | 113.02 ± 8.8 | 114.67 ± 7.15 | 135.48 ± 39.9 | 98.48 ± 0.15 | 124.1 ± 51.3 | 98.48 ± 0.15 | 98.48 ± 0.15 | 98.48 ± 0.15 |
| 2023 | 101.31 ± 0.71 | 133.15 ± 12.4 | 98.83 ± 0.15 | 98.83 ± 0.15 | 98.83 ± 0.15 | 98.83 ± 0.15 | 113.81 ± 9.49 | 115.54 ± 7.76 | 136.71 ± 38.7 | 98.83 ± 0.15 | 123.82 ± 51.6 | 98.83 ± 0.15 | 98.83 ± 0.15 | 98.83 ± 0.15 |
| 2022 | 101.71 ± 0.91 | 135.5 ± 13.6 | 99.19 ± 0.15 | 99.19 ± 0.15 | 99.19 ± 0.15 | 99.19 ± 0.15 | 114.65 ± 10.1 | 116.47 ± 8.28 | 137.2 ± 38.2 | 99.19 ± 0.15 | 123.52 ± 51.9 | 99.19 ± 0.15 | 99.19 ± 0.15 | 99.19 ± 0.15 |
| 2021 | 102.17 ± 1.04 | 137.95 ± 13.7 | 99.54 ± 0.15 | 99.54 ± 0.15 | 99.54 ± 0.15 | 99.54 ± 0.15 | 115.53 ± 10.6 | 117.46 ± 8.68 | 137.46 ± 37.9 | 99.54 ± 0.15 | 123.22 ± 52.2 | 99.54 ± 0.15 | 99.54 ± 0.15 | 99.54 ± 0.15 |
| 2020 | 102.64 ± 1.03 | 140.47 ± 13.4 | 99.89 ± 0.12 | 99.89 ± 0.12 | 99.89 ± 0.12 | 99.89 ± 0.12 | 116.47 ± 11.7 | 118.54 ± 9.61 | 137.69 ± 37.7 | 99.89 ± 0.12 | 122.9 ± 52.5 | 99.89 ± 0.12 | 99.89 ± 0.12 | 99.89 ± 0.12 |
| Year | Eucalyptus | Birch | Willow | Pinus Massoniana | Chinese Red Pine | Camphor | Poplar |
|---|---|---|---|---|---|---|---|
| 2030 | 106.03 ± 5.12 | 109.76 ± 7.24 | 113.00 ± 8.87 | 108.62 ± 6.67 | 114.62 ± 8.93 | 117.84 ± 6.32 | 107.11 ± 5.65 |
| 2029 | 106.52 ± 5.25 | 110.42 ± 7.52 | 113.80 ± 9.47 | 109.24 ± 6.98 | 115.45 ± 9.13 | 118.46 ± 6.32 | 107.65 ± 5.86 |
| 2028 | 107.02 ± 5.42 | 111.11 ± 7.82 | 114.65 ± 10.28 | 109.87 ± 7.32 | 116.29 ± 9.31 | 119.07 ± 6.30 | 108.19 ± 6.10 |
| 2027 | 107.54 ± 5.64 | 111.83 ± 8.13 | 115.55 ± 11.12 | 110.54 ± 7.71 | 117.16 ± 9.45 | 119.67 ± 6.27 | 108.76 ± 6.34 |
| 2026 | 108.08 ± 5.90 | 112.57 ± 8.47 | 116.52 ± 11.90 | 111.24 ± 8.15 | 118.04 ± 9.57 | 120.26 ± 6.22 | 109.36 ± 6.70 |
| 2025 | 108.63 ± 6.21 | 113.34 ± 8.82 | 117.54 ± 12.77 | 111.98 ± 8.61 | 118.93 ± 9.64 | 120.83 ± 6.15 | 109.97 ± 7.06 |
| 2024 | 109.21 ± 6.53 | 114.15 ± 9.18 | 118.65 ± 12.83 | 112.75 ± 9.11 | 119.84 ± 9.65 | 121.40 ± 6.07 | 110.62 ± 7.46 |
| 2023 | 109.80 ± 6.88 | 114.98 ± 9.54 | 119.84 ± 14.94 | 113.56 ± 9.65 | 120.76 ± 9.61 | 121.95 ± 5.96 | 111.29 ± 7.90 |
| 2022 | 110.43 ± 7.24 | 115.84 ± 9.89 | 121.11 ± 16.02 | 114.42 ± 10.20 | 121.68 ± 9.50 | 122.47 ± 5.85 | 112.00 ± 8.39 |
| 2021 | 111.08 ± 7.63 | 116.74 ± 10.25 | 122.49 ± 17.25 | 115.32 ± 10.78 | 122.60 ± 9.33 | 122.98 ± 5.71 | 112.76 ± 8.95 |
| 2020 | 111.77 ± 8.05 | 117.67 ± 10.59 | 123.96 ± 18.58 | 116.26 ± 11.37 | 123.52 ± 9.38 | 123.47 ± 5.56 | 113.55 ± 9.55 |
| Year | Eucalyptus | Cypress | Sassafras | Birch | Oak | Willow | Cedar | Pinus Massoniana | Chinese Red Pine | Larch Pine | Camphor | Poplar | Beech | Locust |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2030 | 151.83 ± 13.9 | 112.99 ± 6.96 | 132.55 ± 7.36 | 139.16 ± 4.12 | 115.27 ± 4.69 | 121.63 ± 32.4 | 139.67 ± 5.14 | 142.47 ± 5.28 | 128.16 ± 7.50 | 118.63 ± 19.1 | 122.27 ± 5.55 | 149.86 ± 3.48 | 112.20 ± 3.17 | 125.88 ± 3.19 |
| 2029 | 153.87 ± 13.3 | 111.68 ± 6.75 | 131.30 ± 8.41 | 138.59 ± 5.62 | 114.39 ± 4.93 | 116.71 ± 30.2 | 138.92 ± 6.71 | 141.75 ± 7.16 | 126.82 ± 8.20 | 115.38 ± 18.4 | 121.26 ± 6.08 | 149.80 ± 6.78 | 111.49 ± 3.35 | 124.91 ± 3.93 |
| 2028 | 155.13 ± 11.8 | 110.43 ± 6.53 | 129.84 ± 9.42 | 137.73 ± 7.19 | 113.45 ± 5.16 | 112.36 ± 26.1 | 137.87 ± 8.32 | 140.68 ± 9.05 | 125.33 ± 8.85 | 112.37 ± 17.2 | 120.15 ± 6.60 | 149.10 ± 10.5 | 110.74 ± 3.53 | 123.78 ± 4.69 |
| 2027 | 155.42 ± 9.28 | 109.21 ± 6.30 | 128.18 ± 10.4 | 136.58 ± 8.93 | 112.47 ± 5.39 | 108.74 ± 20.2 | 136.52 ± 10.0 | 139.25 ± 11.0 | 123.71 ± 9.50 | 109.67 ± 15.7 | 118.94 ± 7.15 | 147.75 ± 14.1 | 109.96 ± 3.71 | 122.49 ± 5.50 |
| 2026 | 154.65 ± 17.0 | 108.05 ± 6.07 | 126.32 ± 11.4 | 135.08 ± 10.9 | 111.44 ± 5.65 | 105.96 ± 15.6 | 134.82 ± 11.95 | 137.43 ± 13.1 | 121.95 ± 10.2 | 107.30 ± 13.8 | 117.62 ± 7.75 | 145.73 ± 17.6 | 109.14 ± 3.92 | 121.04 ± 6.39 |
| 2025 | 152.83 ± 23.9 | 106.92 ± 5.85 | 124.24 ± 12.4 | 133.20 ± 13.3 | 110.36 ± 5.94 | 103.83 ± 13.1 | 132.75 ± 14.1 | 135.18 ± 15.4 | 120.05 ± 10.8 | 105.26 ± 11.9 | 116.17 ± 8.41 | 143.03 ± 20.7 | 108.27 ± 4.13 | 119.41 ± 7.31 |
| 2024 | 150.05 ± 28.7 | 105.83 ± 5.63 | 121.95 ± 13.5 | 130.87 ± 15.9 | 109.21 ± 6.25 | 102.12 ± 10.9 | 130.27 ± 16.4 | 132.49 ± 17.8 | 118.01 ± 11.5 | 103.56 ± 10.0 | 114.60 ± 9.12 | 139.71 ± 23.3 | 107.35 ± 4.34 | 117.59 ± 8.22 |
| 2023 | 146.41 ± 31.3 | 104.79 ± 5.41 | 119.48 ± 14.2 | 128.12 ± 18.3 | 108.03 ± 6.45 | 100.75 ± 8.22 | 127.42 ± 18.3 | 129.40 ± 19.8 | 115.86 ± 11.9 | 102.17 ± 8.18 | 112.91 ± 9.64 | 135.85 ± 24.9 | 106.39 ± 4.57 | 115.62 ± 9.11 |
| 2022 | 142.05 ± 31.8 | 103.81 ± 5.17 | 116.94 ± 13.9 | 125.11 ± 18.9 | 106.83 ± 6.23 | 99.75 ± 5.58 | 124.34 ± 18.6 | 126.07 ± 19.9 | 113.69 ± 11.6 | 101.06 ± 6.54 | 111.19 ± 9.46 | 131.66 ± 24.7 | 105.43 ± 4.73 | 113.58 ± 9.86 |
| 2021 | 137.06 ± 30.5 | 102.91 ± 4.89 | 114.44 ± 12.9 | 122.02 ± 17.8 | 105.68 ± 5.99 | 99.08 ± 3.70 | 121.21 ± 17.4 | 122.69 ± 18.6 | 111.56 ± 11.1 | 100.19 ± 5.10 | 109.49 ± 8.68 | 127.37 ± 22.8 | 104.50 ± 4.58 | 111.56 ± 10.3 |
| 2020 | 131.62 ± 31.6 | 102.10 ± 4.58 | 112.03 ± 13.2 | 118.92 ± 16.2 | 104.59 ± 5.99 | 98.64 ± 2.42 | 118.10 ± 16.4 | 119.33 ± 17.9 | 109.53 ± 11.1 | 99.53 ± 3.87 | 107.85 ± 8.86 | 123.08 ± 23.7 | 103.61 ± 4.04 | 109.61 ± 9.20 |
| Year | Wood Chips, Branches | Tree Bark | Leaves | Waste Furniture | Abandoned Construction Wood |
|---|---|---|---|---|---|
| 2030 | 98.54 ± 1.28 97.84 ± 0.67 | 101.85 ± 2.28 96.35 ± 0.15 | 96.35 ± 0.15 98.83 ± 0.71 | 111.00 ± 6.97 | 129.47 ± 22.36 |
| 2029 | 98.90 ± 1.30 98.19 ± 0.67 | 102.27 ± 2.24 96.70 ± 0.15 | 96.70 ± 0.15 99.19 ± 0.70 | 111.65 ± 7.22 | 128.35 ± 25.52 |
| 2028 | 99.26 ± 1.33 98.55 ± 0.67 | 102.69 ± 2.19 97.06 ± 0.15 | 97.06 ± 0.15 99.55 ± 0.73 | 112.32 ± 7.51 | 127.07 ± 28.06 |
| 2027 | 99.63 ± 1.36 98.90 ± 0.67 | 103.11 ± 2.15 97.41 ± 0.15 | 97.41 ± 0.15 99.90 ± 0.71 | 113.01 ± 7.81 | 125.64 ± 29.78 |
| 2026 | 99.99 ± 1.39 99.26 ± 0.67 | 103.54 ± 2.09 97.77 ± 0.15 | 97.76 ± 0.15 100.25 ± 0.67 | 113.72 ± 8.13 | 124.04 ± 30.61 |
| 2025 | 100.37 ± 1.43 99.61 ± 0.67 | 103.97 ± 2.03 98.12 ± 0.15 | 98.12 ± 0.15 100.60 ± 0.71 | 114.46 ± 8.47 | 122.25 ± 30.58 |
| 2024 | 100.75 ± 1.47 99.96 ± 0.66 | 104.41 ± 2.14 98.48 ± 0.15 | 98.48 ± 0.15 100.96 ± 0.72 | 115.23 ± 8.83 | 120.26 ± 29.79 |
| 2023 | 101.14 ± 1.50 100.32 ± 0.66 | 104.88 ± 2.29 98.83 ± 0.15 | 98.83 ± 0.15 101.31 ± 0.71 | 116.03 ± 9.21 | 118.09 ± 28.33 |
| 2022 | 101.53 ± 1.52 100.68 ± 0.68 | 105.34 ± 2.35 99.19 ± 0.15 | 99.19 ± 0.15 101.71 ± 0.91 | 116.85 ± 9.59 | 115.82 ± 26.22 |
| 2021 | 101.93 ± 1.54 101.04 ± 0.72 | 105.80 ± 2.51 99.54 ± 0.15 | 99.54 ± 0.15 102.17 ± 1.04 | 117.71 ± 9.99 | 113.56 ± 23.51 |
| 2020 | 102.34 ± 1.55 101.43 ± 0.78 | 106.27 ± 2.60 99.89 ± 0.15 | 99.89 ± 0.12 102.64 ± 1.03 | 118.60 ± 10.44 | 111.32 ± 20.30 |
| Year | Wood Chips, Branches | Tree Bark | Leaves | Waste Furniture | Abandoned Construction Wood |
|---|---|---|---|---|---|
| 2030 | ±1.29 ±0.68 | ±2.19 ±0.16 | ±0.16 ±0.71 | ±6.11 | ±14.73 |
| 2029 | ±1.30 ±0.67 | ±2.15 ±0.15 | ±0.15 ±0.70 | ±6.29 | ±16.59 |
| 2028 | ±1.32 ±0.67 | ±2.09 ±0.15 | ±0.15 ±0.73 | ±6.49 | ±18.09 |
| 2027 | ±1.34 ±0.67 | ±2.04 ±0.15 | ±0.15 ±0.71 | ±6.70 | ±19.16 |
| 2026 | ±1.38 ±0.67 | ±1.98 ±0.15 | ±0.15 ±0.66 | ±6.90 | ±19.79 |
| 2025 | ±1.41 ±0.66 | ±1.91 ±0.15 | ±0.15 ±0.70 | ±7.12 | ±20.07 |
| 2024 | ±1.44 ±0.66 | ±2.01 ±0.15 | ±0.15 ±0.71 | ±7.35 | ±19.85 |
| 2023 | ±1.46 ±0.66 | ±2.14 ±0.15 | ±0.15 ±0.70 | ±7.58 | ±19.35 |
| 2022 | ±1.47 ±0.67 | ±2.19 ±0.15 | ±0.15 ±0.89 | ±7.80 | ±18.46 |
| 2021 | ±1.49 ±0.71 | ±2.31 ±0.15 | ±0.15 ±1.01 | ±8.03 | ±17.15 |
| 2020 | ±1.50 ±0.77 | ±2.39 ±0.12 | ±0.12 ±1.00 | ±8.30 | ±15.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Luo, Z.; Yu, C.; Wang, S.; Wang, X.; Zhu, P. Improving the Methodology for Determining the Biomass/Coal Co-Combustion Ratio: Predictive Modeling of the 14C Activity of Pure Biomass. Energies 2024, 17, 942. https://doi.org/10.3390/en17040942
Wang Y, Luo Z, Yu C, Wang S, Wang X, Zhu P. Improving the Methodology for Determining the Biomass/Coal Co-Combustion Ratio: Predictive Modeling of the 14C Activity of Pure Biomass. Energies. 2024; 17(4):942. https://doi.org/10.3390/en17040942
Chicago/Turabian StyleWang, Yinchen, Zhongyang Luo, Chunjiang Yu, Sheng Wang, Xiaohuan Wang, and Peiliang Zhu. 2024. "Improving the Methodology for Determining the Biomass/Coal Co-Combustion Ratio: Predictive Modeling of the 14C Activity of Pure Biomass" Energies 17, no. 4: 942. https://doi.org/10.3390/en17040942
APA StyleWang, Y., Luo, Z., Yu, C., Wang, S., Wang, X., & Zhu, P. (2024). Improving the Methodology for Determining the Biomass/Coal Co-Combustion Ratio: Predictive Modeling of the 14C Activity of Pure Biomass. Energies, 17(4), 942. https://doi.org/10.3390/en17040942






