Measurement of High-Frequency Voltage Harmonics above 2 kHz in High-Voltage Networks

Abstract

Large-scale renewable energy plants, flexible AC (alternating current) and high voltage DC (direct current) transmission systems, and modern consumer devices utilize power electronics that tend to increase harmonic emissions. Furthermore, such emissions are nowadays known to exceed the traditional 2 kHz range typically considered for harmonic analysis. However, the accuracy of such harmonic measurements in medium and high voltage networks is questionable due to the lack of accuracy specifications for the respective instrument transformers that are being used in the measurement chain. Therefore, the motivation of this study is to review the existing techniques for measuring high-frequency voltage harmonics, i.e., those in the range 2–9 kHz, in medium-, high-, and extra high-voltage electricity networks, where most large-scale power electronic converters are being connected. Different transducer types are compared in terms of measurement accuracy. The reviewed literature indicates that some transducers can introduce errors due to their nonlinearities. The study also identifies the limitations of calibrating these transducers at frequencies above 2 kHz due to the unavailability of suitable sources capable of generating the required test waveforms. Furthermore, the study emphasizes the necessity for establishing accuracy limits for harmonic measurements above 2 kHz.

1. Introduction

1.1. Recent Trends in Electricity Supply Networks

The world is transitioning rapidly towards the use of renewable energy resources to minimize the adverse impacts of greenhouse gas emissions from conventional energy sources. The global grid connected capacity of renewable energy sources has increased from 1567 GW in 2013 to 3381 GW in 2022 [1]. Due to this accelerating shift in generation technology, the volume of power electronic converters, which provide the interface between the electricity grid and renewable energy sources, is known to be increasing rapidly. These converters are connected at all voltage levels in electricity supply networks, ranging from rooftop solar PV systems in low-voltage (LV) networks to large-scale renewable energy plants connected to medium-voltage (MV), high-voltage (HV) and extra high-voltage (EHV) networks (refer to voltage level classifications in

Table 1. Classification of AC voltage levels according to voltage (U_n) range [11].

Voltage Level	Voltage Range
Low voltage (LV)	Un ≤ 1000 V
Medium voltage (MV)	1000 V < Un ≤ 35 kV
High voltage (HV)	35 kV < Un ≤ 230 kV
Extra high voltage (EHV)	230 kV < Un

). Electric vehicles (EV), smart household and office appliances, air conditioners, and heating and cooking appliances are also reshaping how the electricity is consumed in modern homes [2,3]. In addition, emerging grid infrastructure technologies, such as microgrids, smart grids, high-voltage direct current transmission (HVDC) systems, flexible alternating current transmission systems (FACTS), and a variety of power electronic controlled equipment are steadily expanding both in capacity and their range of applications [4,5,6,7,8,9,10].

1.2. Harmonics in Electric Power Systems

Depending on the frequency range of emissions, the harmonics of the power system can be classified as shown in

Table 2. Classification of harmonic emissions according to the frequency (f) range [12].

Harmonic Emission Type	Frequency Range
Low frequency	100 Hz ≤ f ≤ 2 kHz
High frequency	2 kHz < f ≤ 9 kHz
Low-frequency conducted	9 kHz < f ≤ 150 kHz
High-frequency conducted	150 kHz < f ≤ 30 MHz
Radiated	30 MHz < f

.

Conventionally, magnetic transformers [13,14], rotating machines [15], electric arc furnaces [16,17], and traditional power electronic converters, such as line-commutated rectifiers and thyristor-based inverters [18,19], were identified as main contributors to harmonic emissions. These harmonic emissions were mostly limited to lower order harmonics with frequencies below 2 kHz. In addition, the number of harmonic sources was generally not significant enough to cause series power quality issues, beyond their own local installations, when their cumulative effects were considered. In contrast, modern harmonic emissions are mostly due to force-commutated power electronic converters. The switching frequency range of these power converters generally tends to exceed 2 kHz [12,20,21,22]. With the use of higher switching frequencies, an increasing number of high-frequency harmonics are injected into power systems [23]. Even though filtering techniques are used to reduce the level of harmonics, a small portion of the harmonics can still inevitably escape into power systems [12]. As an example of higher switching frequencies, switch-mode power supplies (SMPSs) contribute to the emission of higher order harmonics in the range of 10 kHz to 100 kHz [19]. Even though the individual emission levels of these devices are almost negligible, the rapid increase in the number of such devices can result in significant cumulative effects.

Table 3. High-frequency harmonic sources in modern power systems [2].

Equipment	Harmonic Emission Range
Industrial scale converters	9 kHz to 150 kHz
Streetlamps	up to 20 kHz
Electric vehicle (EV) chargers	15 kHz to 100 kHz
Photovoltaic (PV) inverters	4 kHz to 20 kHz
Household electronics	2 kHz to 150 kHz
Programmable logic controllers (PLC) in meter reading	9 kHz to 95 kHz

shows a summary of the different types of non-linear devices that generate high-frequency harmonics.

1.3. Importance of MV/HV/EHV Harmonic Measurements

Measurement of harmonic emissions is essential for maintaining the quality of electricity at the points of connections of consumer appliances to avoid life-time reduction and equipment failure [24]. Even though LV harmonic measurement methods and techniques are well established, harmonic measurements in MV/HV/EHV networks always require the use of additional external transducers, leading to inaccuracies compared to those measurements carried out at LV [25].

Large scale renewable energy generation plants are typically connected to the electricity grid at MV/HV. These plants are sources of harmonic emissions that could contribute to the increase in the total harmonic distortion at the point of connection [26,27,28]. Accurate harmonic measurement at the point of connection on the MV/HV side of the connection transformer is required to verify the fact that the harmonic emissions of connected plants remain within the specified emission limits. Furthermore, harmonic distortion level and the harmonic impedance at the point of connection of renewable generating plants directly impact the harmonic current emissions from the plant [29]. The harmonic impedance of the network and the generating plant can create resonance circuits, which may amplify or attenuate the harmonic emissions of the renewable power plant. The location of dominant harmonic sources has to be identified in order to design harmonic filters and to avoid the propagation of harmonics further into other parts of the power system.

Harmonic power flow studies are essentially based on either forward harmonic analysis or reverse harmonic analysis. In forward harmonic analysis, the location of the harmonic source is usually known [30]. In most cases, reverse analysis is utilized to identify the source of harmonics when the harmonic levels at a certain point in the power system exceed the stipulated limits or when a possible equipment failure due to high level of harmonic has been identified. When a significant source of harmonics has been identified, a harmonic filter should be used to minimize the harmonic propagation. By measuring the harmonic magnitudes that prevail, it is possible to determine the optimum harmonic filter parameters. After the installation of a suitable filter, it is necessary to verify whether the installation has achieved the desired performance. This can be achieved by performing a post-installation harmonic measurement.

Harmonic power flow studies require the measurement of harmonic phase angles [31]. In addition, harmonic phase angle measurements are required to evaluate the possibility of harmonic cancellation in power systems and for the design of active harmonic filters [32]. Furthermore, several studies have shown that the application of harmonic summation law according to [11,33] fails to provide an accurate harmonic emission estimation for frequencies above 2 kHz due to the variations in harmonic phase angles [34,35]. Therefore, incorporating harmonic phase angle measurements in high-frequency harmonic studies is essential.

1.4. Objectives of the Review and Research Gaps in the Existing Literature on MV/HV/EHV Harmonic Measurements

The previously published literature on harmonic measurement characteristics of instrument transformers is limited in scope and mostly focuses on covering specific types of instrument transducers. It fails to provide a comparative overview of all transducer types, covering both conventional and non-conventional types. This review addresses such limitations by providing a comprehensive comparison of all types of transducers in terms of their accuracy, frequency bandwidth, and the impact of external influences. Furthermore, previous research fails to provide a comparative study of different MV/HV calibration systems and methods used for the characterization of instrument transformers for harmonic measurements. This study compares different novel calibration systems that utilize different test signal conditions and reference transducer types used in the calibration process. This research also draws attention to the accuracy of harmonic phase angle measurements of each transducer type for frequencies that extend beyond the 2 kHz frequency range. In summary, this review consolidates novel and conventional knowledge on MV/HV/EHV harmonic measurement transducers.

The review study presented in this paper primarily focus on harmonic measurements in MV/HV/EHV electricity networks and in the frequency range from 2 kHz to 9 kHz due to several important reasons. The main reason is the rapid integration of large-scale renewable power plants, such as wind and solar farms, at MV/HV/EHV transmission network voltage levels. These large-scale plants utilize power electronic converters that use techniques, such as pulse width modulation (PWM) with switching frequencies, in the frequency range up to 10 kHz. This type of converter contributes directly to the emission of harmonics in the frequency range from 2 kHz to 9 kHz [36]. Even though the individual plant emissions may appear to be insignificant, the aggregate emissions and their cumulative impact may become significant with the continuous increase in the renewable penetration levels. In comparison, the harmonic sources that generate high-frequency harmonics in the range from 9 kHz to 150 kHz are present mostly in low-voltage networks and their presence in MV/HV/EHV electricity networks are often limited. Therefore, it is expected that the proportional levels of 2 kHz to 9 kHz MV/HV/EHV networks would gain further attention in the future [37].

However, the accuracy of instrument transformers utilized in MV/HV/EHV electricity networks in the frequency range from 2 kHz to 9 kHz are often unknown. Hence, the overall accuracy of harmonic measurements performed using such instrument transformers may lead to inaccurate interpretations regarding the harmonic levels in the MV/HV/EHV networks. Hence, a review of the accuracy of instrument transducers would enable the interested parties to gain an understanding regarding the respective measurements performed using such transducers.

Furthermore, in terms of the standards governing the harmonic measurements in electricity networks, the frequency range from 50 Hz to 2 kHz is covered by standards, such as the IEC 61000-4-30 [38] and IEEE 519 [39] standards. On the other hand, the emissions from 9 kHz and above are partially covered by CISPR standards. There is a requirement of standards governing the harmonic emissions from 2 kHz to 9 kHz. In developing such standards to cover the harmonic measurements in MV/HV/EHV networks, it is essential for the relevant working committees to identify the accuracy requirements instrument transducers that are being used for the measurements. In summary, the main objective of this review study is to provide an enhanced overview regarding the accuracy of different types of instrument transformers in the frequency range from 2 kHz to 9 kHz for MV/HV/EHV harmonic measurements.

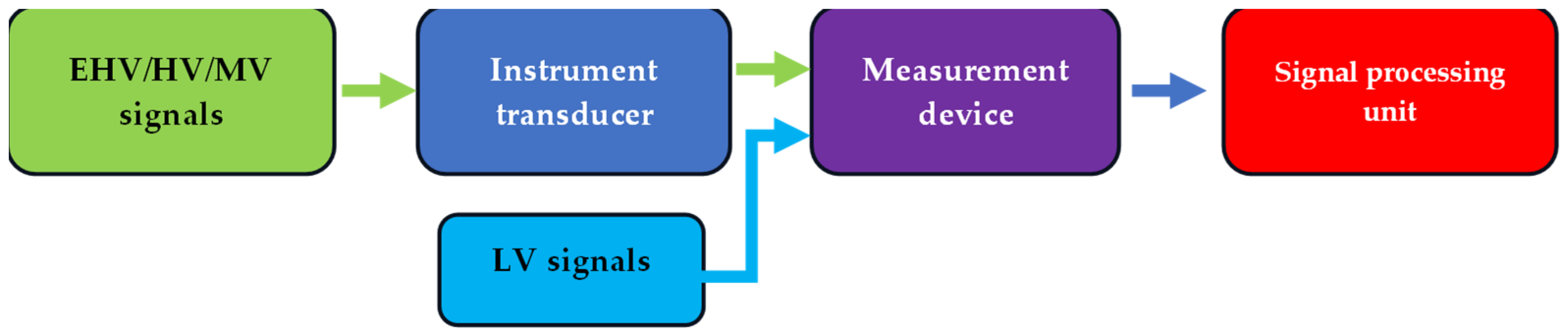
2. MV/HV/EHV Harmonic Measurement Process

The voltage rating of built-in input circuitry of existing power quality measurement instruments is generally 600 V or 1000 V. When the magnitude of the measured voltage exceeds these levels, an external transducer is required to reduce the voltage to a magnitude that is suitable to be connected to the instrument. Figure 1 shows the voltage measurement process used in electricity networks. The instrument transformer scales down the MV/HV/EHV signals to a level that is compatible with the LV measurement instrument. The measurement instrument samples and digitizes the analogue voltage signals at a high sampling frequency and uses fast Fourier transform (FFT) algorithms to calculate the harmonic amplitudes according to the procedure defined in IEC 61000-4-7 [40,41]. Most of the existing power quality analyzers combine the measurement device and signal processing into a single unit to provide solutions for field harmonic measurements.

2.1. Accuracy of LV Measurement Devices

State-of-the-art LV measurement devices available on the market can accurately measure harmonics in a frequency range up to tens of kilohertz.

Table 4. Commercially available power quality instruments and their specifications [42,43,44].

Instrument	Maximum Input Voltage	Harmonic Measurement Bandwidth
Fluke 1770 3-phase power quality analyzer (Manufactured by Fluke, Everett, WA, USA)	1 kV	30 kHz
Elspec G4500 3-phase power quality analyzer (Manufactured by Elspec, Caesarea, Israel)	1 kV	25.55 kHz
Hioki PQ3198 3-phase power quality analyzer (Manufactured by Hioki, Nagano, Japan)	600 V	80 kHz

shows a sample of such power quality analyzers developed in accordance with IEC 61000-4-7 [40] and their respective measurement voltage range and harmonic measurement bandwidths.

In the IEC 61000-4-7 standard [40], two accuracy classes are defined for LV harmonic measuring instruments. The defined error limits of each class are dependent on the amplitude of the measured voltage signal. It should be highlighted that IEC 61000-4-7 states that the maximum allowable error limits, as shown in

Table 5. Accuracy requirements for harmonic voltage instruments according to IEC 61000-4-7 [40].

Instrument Accuracy Class	Measurement Voltage Range	Maximum Error *
Class I	Um ≥ 1% Unom	±5% Um
	Um < 1% Unom	±0.05% Unom
Class II	Um ≥ 3% Unom	±5% Um
	Um < 3% Unom	±0.15% Unom

* U_m denotes the measured voltage amplitude/U_nom denotes the nominal input voltage range of the instrument.

, refer to only single-frequency steady state signals. However, real power system voltage signals are quasi-sinusoidal and consist of a strong fundamental frequency component and a spectrum of smaller amplitude harmonic components [45,46].

The IEC 61000-4-7 standard states that the above measurement accuracy classes and their respective errors are applicable up to the 50th harmonic order (i.e., up to 2.5 kHz for 50 Hz systems). A tentative definition for harmonic measurements from 2 kHz to 9 kHz is provided as an annex to IEC 61000-4-7 for informative purposes. This annex identifies that high-frequency emissions above 2 kHz are significantly smaller in magnitude in comparison to the low-frequency harmonics. Furthermore, these emissions can be of either a single frequency or broadband type. For these reasons, the output spectral components centered around each harmonic order are combined to form a group of harmonic bands with a width of 200 Hz. as given by the following equation:

$${\mathrm{Y}}_{\mathrm{B},\mathrm{n}}=\sqrt{\sum _{\mathrm{f}=\mathrm{n}-95\mathrm{H}\mathrm{z}}^{\mathrm{n}+100\mathrm{H}\mathrm{z}}{\mathrm{Y}}_{\mathrm{C}\mathrm{f}}^2}$$

(1)

where:

• ${\mathrm{Y}}_{\mathrm{B},\mathrm{n}}$ is the root-mean-square magnitude of 200 Hz band around the harmonic frequency (n).
• ${\mathrm{Y}}_{\mathrm{C}\mathrm{f}}$ is the root-mean-square magnitude of spectral bin at frequency (f) calculated by the FFT algorithm.

This type of harmonic grouping for emissions in the range from 2 kHz to 9 kHz has been selected to match the measurement bandwidth that is applied in the CISPR 16-1-2 standard which governs emissions between 9 kHz and 1 GHz [47].

2.2. Accuracy of Instrument Voltage Transformers

Instrument voltage transformers are an essential component in the MV/HV/EHV harmonic measurement chain where the following transducer types are used:

• Inductive voltage transformers (IVT);
• Capacitive voltage transformers (CVT);
• Resistive voltage dividers (RVD);
• Capacitive voltage dividers (CVD);
• Resistive–capacitive voltage dividers (RCVD);
• Optical voltage transducers (OVT);
• Non-conventional instrument transformer (NCIT).

The features relevant to harmonic measurement associated with each of the above instrument transformer type are given in subsections below.

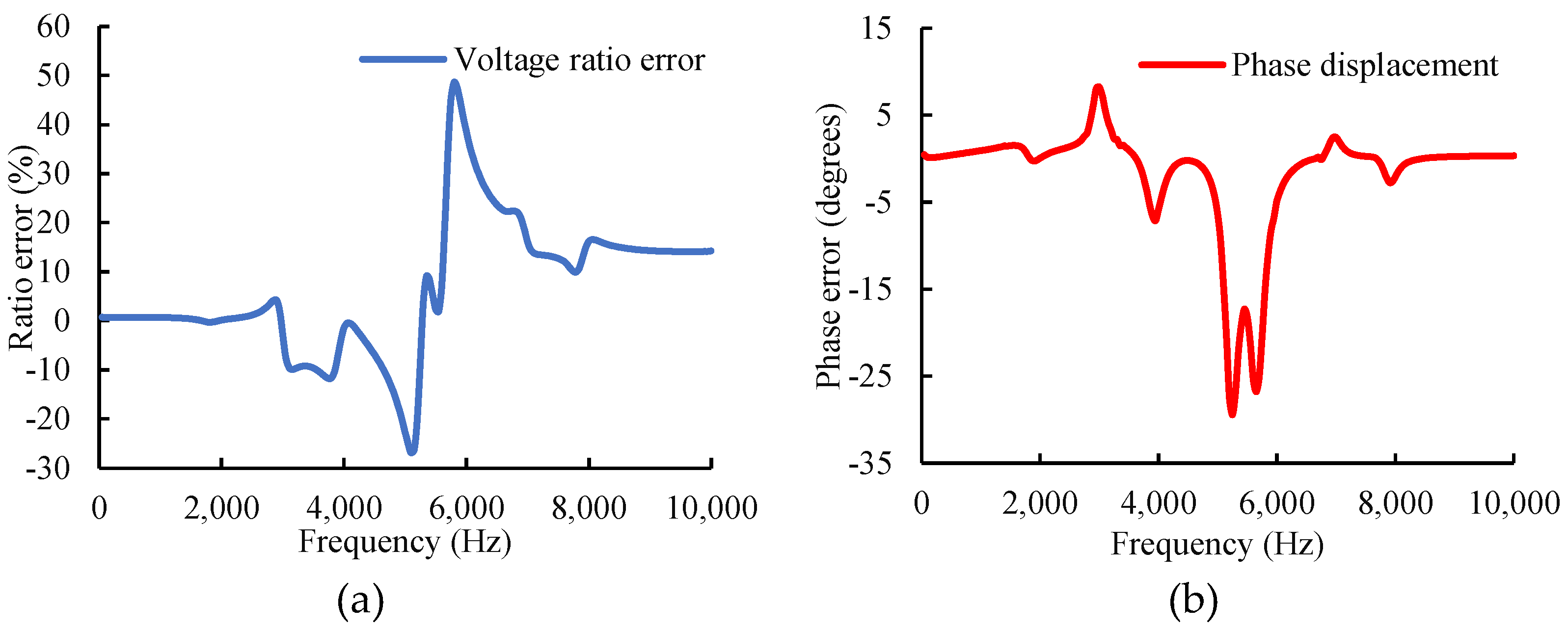
2.2.1. Inductive Voltage Transformers

IVTs use the principle of electromagnetic induction to scale high voltages down to low voltages based on the turns ratio of the primary to secondary winding. IVTs are widely used for voltage measurement in MV/HV power systems where the accuracy is specified only at the fundamental frequency [48]. Figure 2a,b show the voltage ratio error and phase displacement response of a 50 kV IVT with oil and paper insulation for frequencies from 50 Hz to 10 kHz.

It is apparent that there are wide variations in the ratio and phase errors across the frequency range which arise as a result of resonance. High magnitudes of deviation in both ratio and phase angle appear at their resonant frequencies. The peaks in the normalized ratio curves are due to the parallel resonance effect and the troughs are due to the series resonance effect [48]. In [49], the ratio correction factor (RCF) of the voltage transformers in the frequency range from 50 Hz to 10 kHz has been explained using the equivalent circuit model of an IVT. It is shown that the lowest resonant frequency can be due to the parallel resonant effect created by the core inductance and the primary winding capacitance of the transformer. This explanation was based on the measured parameters of the open-circuit input impedance of the IVTs. The capacitance of the primary winding relies on several factors, including the insulation materials and construction specific characteristics [20]. Therefore, the resonant frequency points are specific to each IVT, depending on the design type, voltage level, and manufacturing tolerances. The work of [31] also claims that the resonant frequencies are determined by the design of the IVT, manufacturing tolerances, rated primary voltage, secondary burden value, and operating temperature. In [46], it further states that characterizing IVTs for harmonic voltage measurement and developing comprehensive models or calculating the resonant frequencies is difficult as IVT frequency response could be contingent on a complex system of influence factors that is unique to each IVT [31]. Therefore, before using an IVT for harmonic measurement, its frequency response needs to be established to specify the suitable working frequency range, within which the desired accuracy can be achieved. This range should lie well below the lowest resonant frequency of the IVT [48]. Furthermore, it has been shown that the critical frequencies, up to which the IVT ratio error is less than 10%, are below 1 kHz for all types of VTs tested. It has also been found that the bandwidth of the IVT decreased with the increasing voltage rating. A reasonable argument for this was found in [31], where the authors evaluated the frequency response of the same type of IVTs with different rated primary voltages. The results showed that the lowest resonant frequency reduced with increasing rated primary voltage of the transformer. In [31], it was suggested that the reason for such a shift in resonant frequency was the voltage dependency of the winding inductance and inter-winding capacitance of the primary winding. As the voltage rating increases, the inductance and capacitance values increase, resulting in a lower resonant frequency. In addition, the design of the transformer can also affect the measurement frequency range [48]. Factors, such as the type of insulation used, the type of installation (outdoor or indoor), and the type of design (inductive or capacitive), can also result in variations in the inherent capacitive and inductive reactance of IVT, which lead to different resonant frequencies that limit the usable bandwidth of IVTs. Due to the aforementioned reasons, it can be concluded that IVTs are not suitable for measuring high-frequency harmonics in high-voltage power systems. The non-linear behavior of the IVT ferro-magnetic core can also have a direct impact on the harmonic measurement accuracies [50].

For MV network applications, inductive transformers with wideband accuracy up to 9 kHz have been recently developed [51]. However, the rated voltage level of these transformers is limited to $20/\sqrt{3}$ kV. According to the provided data, the frequency sweep test of the transformer, performed at 1% of its rated voltage (i.e., $200/\sqrt{3}$ V), resulted in a voltage ratio error below $\pm 3\%$ up to 9 kHz. This relatively low error is achieved because the first resonance frequency of the transformer lies above 9 kHz.

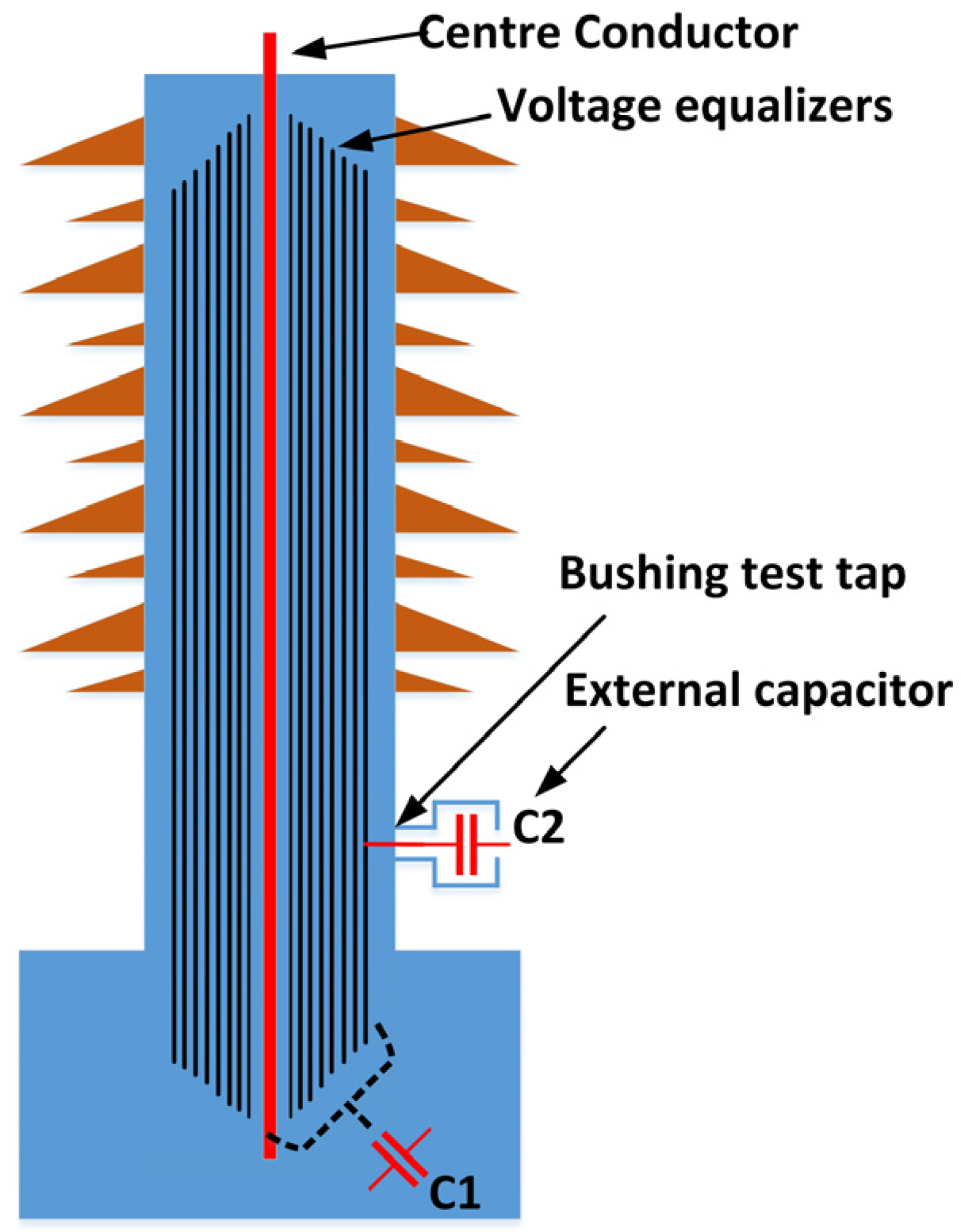
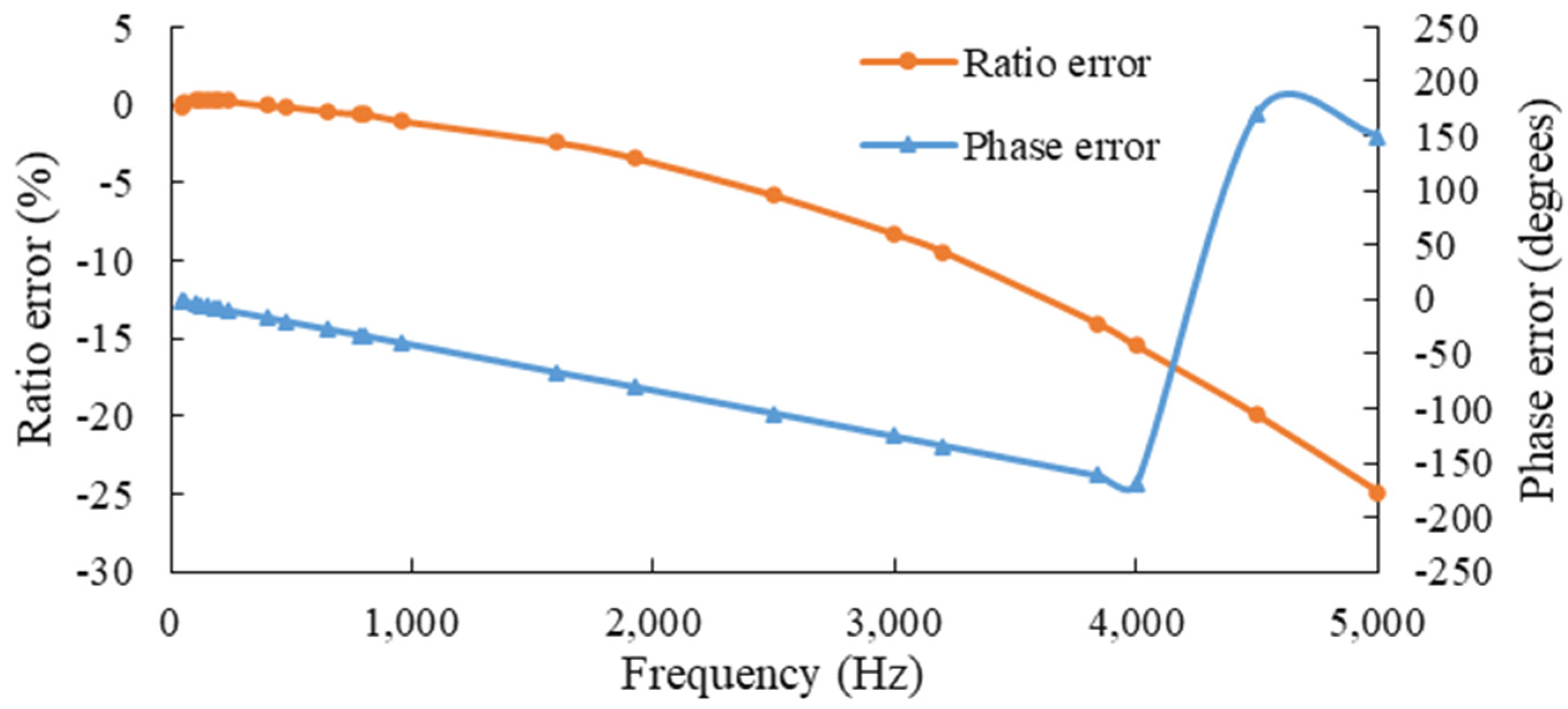
2.2.2. Capacitive Voltage Transformers

CVTs are widely used in HV/EHV systems to provide accurate voltage signals at rated fundamental frequencies for metering and protection purposes [52,53,54]. For HV/EHV networks, the size and insulation requirements for IVTs increase significantly, thus making them unsuitable. CVTs address these limitations by incorporating a capacitive divider to reduce the high voltage level to an intermediate level and then using an IVT at a lower rated voltage to reduce the voltage further to a level appropriate for the measurement instruments [55]. The capacitive impedance of the capacitive divider section and inductive reactance component of the IVT are tuned to create a resonant circuit at a rated frequency in order to achieve the required accuracy of voltage transformation ratio [25]. Due to this tuning, CVTs can have significant transformation ratio errors at harmonic frequencies starting from 100 Hz. Figure 3 shows the measured frequency responses of a 275 kV CVT up to 5 kHz for three burden levels.

As shown in Figure 3, the tested CVT shows a significant resonance point at frequencies below 1 kHz. Furthermore, the variation in the burden has a significant impact on the CVT frequency response especially close to the resonance points. For harmonic frequencies above 2 kHz, the CVT ratio is significantly reduced. This would further degrade the accuracy of small magnitude high-frequency harmonic measurements of a CVT.

It has also been shown that CVT frequency response changes significantly between those produced by different manufacturers, resulting from the dependency of CVT design factors [57]. CVT frequency response calculations based on secondary side impedance measurement and parameter estimation has been carried out in [55,58,59,60]. However, these models fail to take into account the variations in CVT response due to burden changes and the effect of magnetic core non-linearities, specifically at the resonance frequency points.

The following subsection presents the techniques that have been implemented to improve the harmonic measurement capabilities of CVTs.

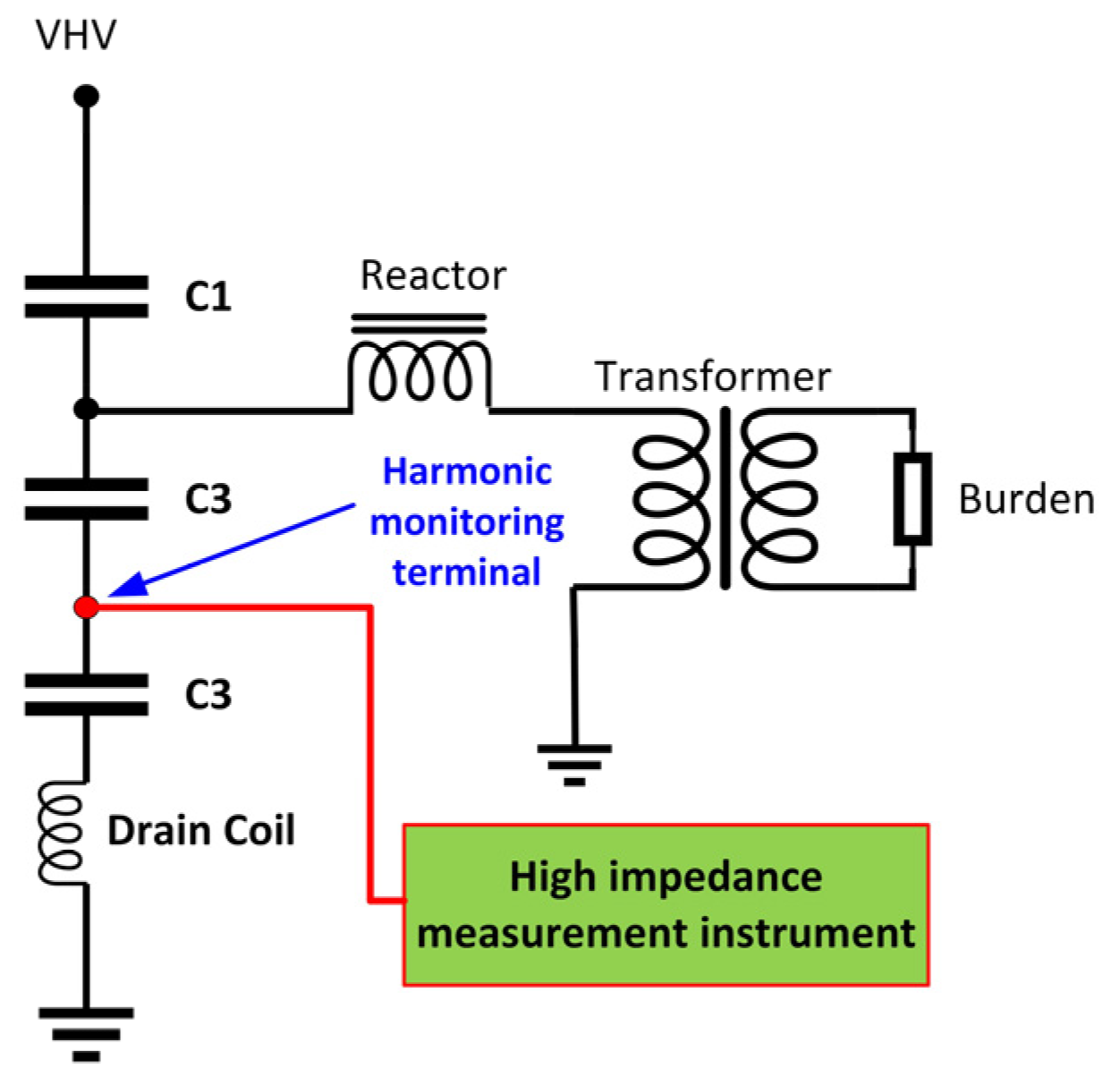
• CVT with dedicated harmonic monitoring terminals

Due to the fact that the inductive components of the CVT causes large errors in harmonics measurements, manufacturers have developed modified CVTs with harmonic monitoring terminals which utilize only the capacitive divider section [61]. By connecting a measurement instrument with an input impedance greater than 1 MΩ, the error in harmonic measurements performed using CVTs can be minimized. However, [25] states that this method is not suitable for harmonic phase angle measurements. Figure 4 shows the schematic diagram of such harmonic measurement terminals used in a 275 kV CVT.

Table 6. Ratio error of harmonic voltage measurements performed by using CVT harmonic monitoring terminals with different VA burdens [62].

Frequency (Hz)	Ratio Error at 0 VA (%)	Ratio Error at 200 VA (%)
180	−0.2	2.9
300	3.1	2.8
420	−1.5	3.7
560	−3.4	3.5
660	−2.9	4.8
780	7.5	4.6
900	−0.2	6.3
1020	−0.7	3.0
1140	13.2	7.2
1260	−3.1	4.9
1500	4.6	5.2
1620	1.2	8.9
1740	−3.9	9.0
2000	3.2	9.0
3000	1.5	7.8

shows the ratio error variation in CVT harmonic measurement terminals provided in [62]. The results show that ratio error of the harmonic monitoring terminal method depends on the CVT burden.

A modification technique to the existing CVTs by adding a capacitor between the CVT grounding terminal and ground is described in [63]. Even though the modelled results show that this method would provide accurate harmonic measurements, practical implementation is essential to gain more insight into the accuracy of the method.

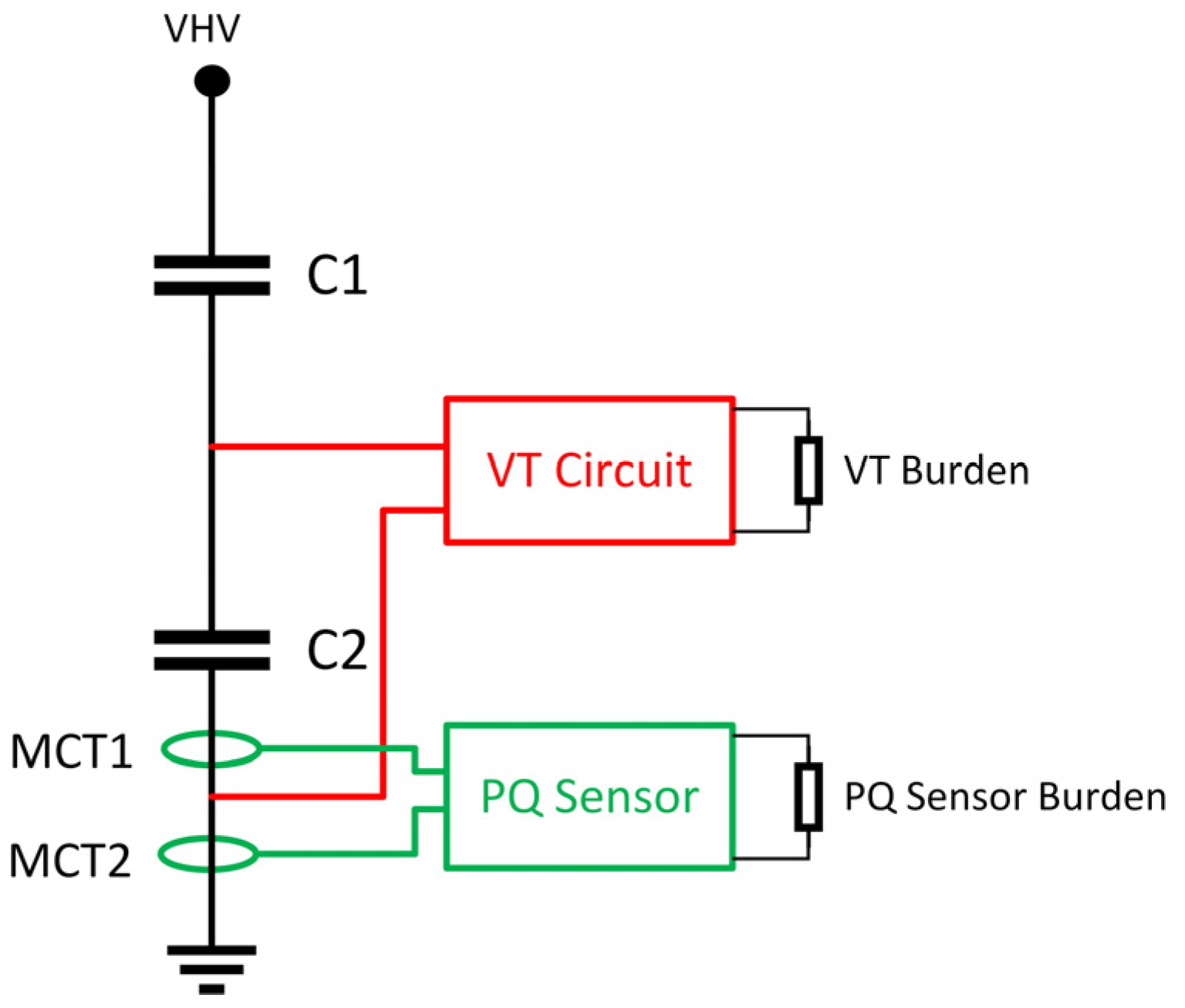
• PQ Sensor^TM (Manufactured by BVM systems, Gilford, United Kingdom) for capacitive voltage transformers

The PQ sensor shown in Figure 5 is a unique patented module that can be integrated into existing CVTs in order to measure harmonics at higher voltages; it is accurate up to several kilohertz. In addition to the capability of measuring harmonics, low-frequency phenomena, such as ferroresonance and subsynchronous resonance, can also be measured by using this type of sensor. The working principle of the PQ sensor is based on measuring the current flowing through the capacitive divider in a CVT, where two measurement current transformers (MCT1 and MCT2) are used for calculating the voltage drops across the HV and LV capacitor arms by using the two current measurements. The calculated high voltage magnitude is expressed according to Equations (2)–(4) [64].

$${\mathrm{V}}_{\mathrm{H}\mathrm{V}}\left(\mathrm{s}\right)={\mathrm{V}}_{\mathrm{C}1}\left(\mathrm{s}\right)+{\mathrm{V}}_{\mathrm{C}2}\left(\mathrm{s}\right)$$

(2)

$${\mathrm{V}}_{\mathrm{H}\mathrm{V}}\left(\mathrm{s}\right)=\frac{1}{{\mathrm{C}}_1\mathrm{s}}.{\mathrm{I}}_{\mathrm{C}1}\left(\mathrm{s}\right)+\frac{1}{{\mathrm{C}}_2\mathrm{s}}.{\mathrm{I}}_{\mathrm{C}2}\left(\mathrm{s}\right)$$

(3)

where:

• s = jω
• I_C1(s) and I_C2(s) are the currents flowing through the HV capacitor (C₁) and LV capacitor (C₂), respectively.
• I_C1 and I_C2 can be calculated from current measurements I_MCT1 and I_MCT2 that are taken from MCT₁ and MCT₂, respectively, according to the following Equation (4):

$${\mathrm{I}}_{\mathrm{C}2}={\mathrm{I}}_{\mathrm{M}\mathrm{C}\mathrm{T}1} {\mathrm{I}}_{\mathrm{C}1}={\mathrm{I}}_{\mathrm{M}\mathrm{C}\mathrm{T}1}+{\mathrm{I}}_{\mathrm{M}\mathrm{C}\mathrm{T}2}$$

(4)

For Equation (3), capacitance values are required to calculate the value of V_HV. These capacitance values can be obtained from the CVT datasheets or through field measurements. Field tests have verified that the PQ sensor has a linear response up to 5 kHz with a ratio error below 5% and a phase angle measurement error below $6°$ [65]. One important feature of the PQ sensor is that it does not affect the normal operation of the CVT, and the harmonic measurement accuracy is not significantly affected by the variation in the CVT burden. However, to date there is no scientific literature that investigates the influence on PQ sensor accuracy due to external factors, such as proximity effect, stray capacitances effects, ambient temperature effect, and long-term drift. The measured frequency response of CVT PQ sensor output is reported in [66]. However, this type of frequency response evaluation is carried out using a low-voltage sinusoidal frequency sweep with a magnitude of 0.5% relative to the rated voltage of the CVT. This type of evaluation does not consider the voltage dependence of the capacitances of the CVT when they are subjected to actual high-voltage waveforms. According to suggestions provided in the IEC 61869-103 technical report [25], PQ sensor frequency response should be evaluated by using composite high-voltage signals that consist of the rated fundamental high-voltage component that is superimposed with a harmonic sweep signal at 0.5% relative to the fundamental voltage to verify its accuracy under actual operating conditions.

Research on harmonic measurement based on the capacitive currents of the CVT similar to the PQ sensor technique is covered in [67]. The test results show that this method allows harmonic magnitude measurements up to 2.5 kHz with a ratio error below $\pm 2\%$.

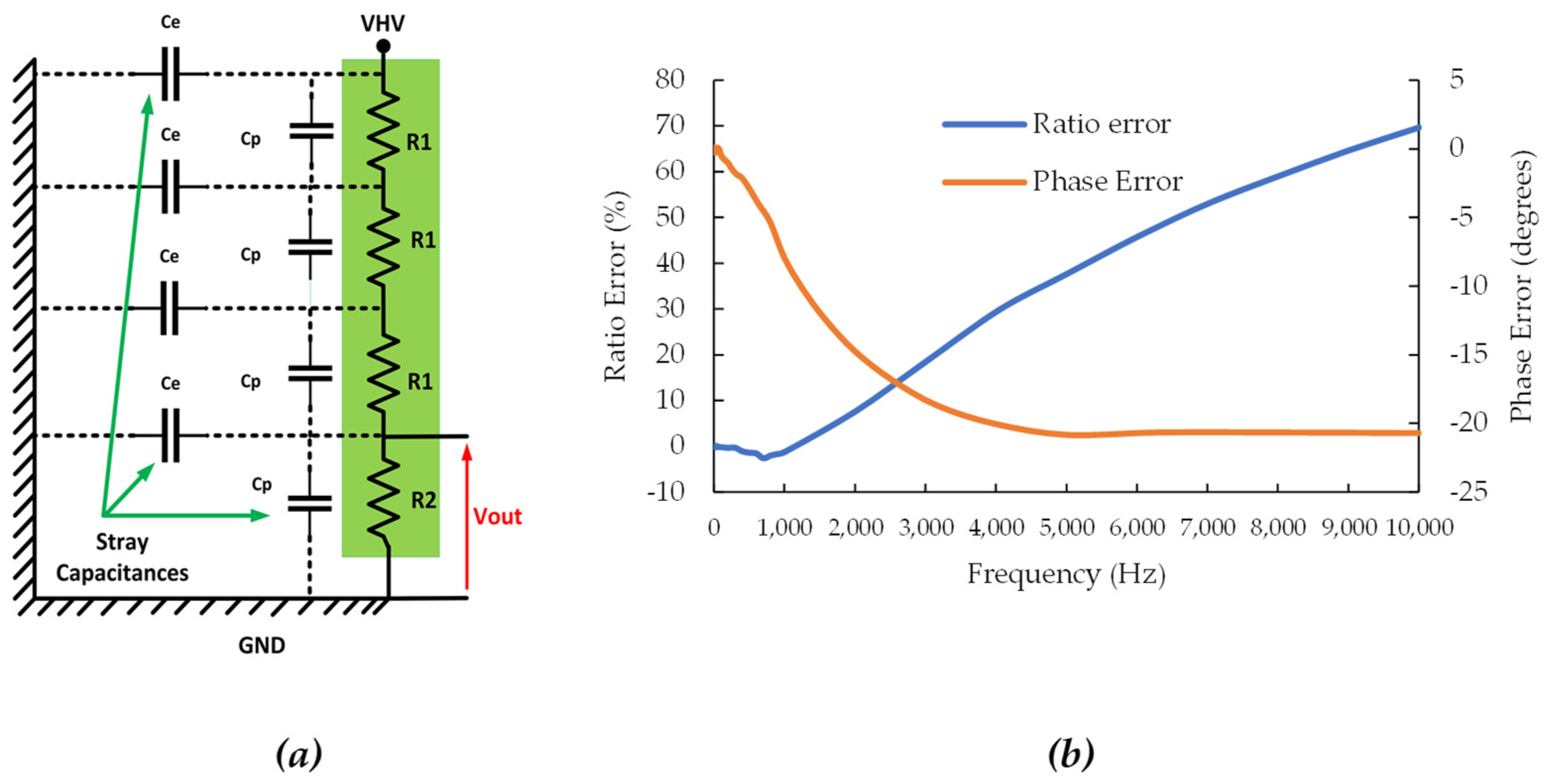
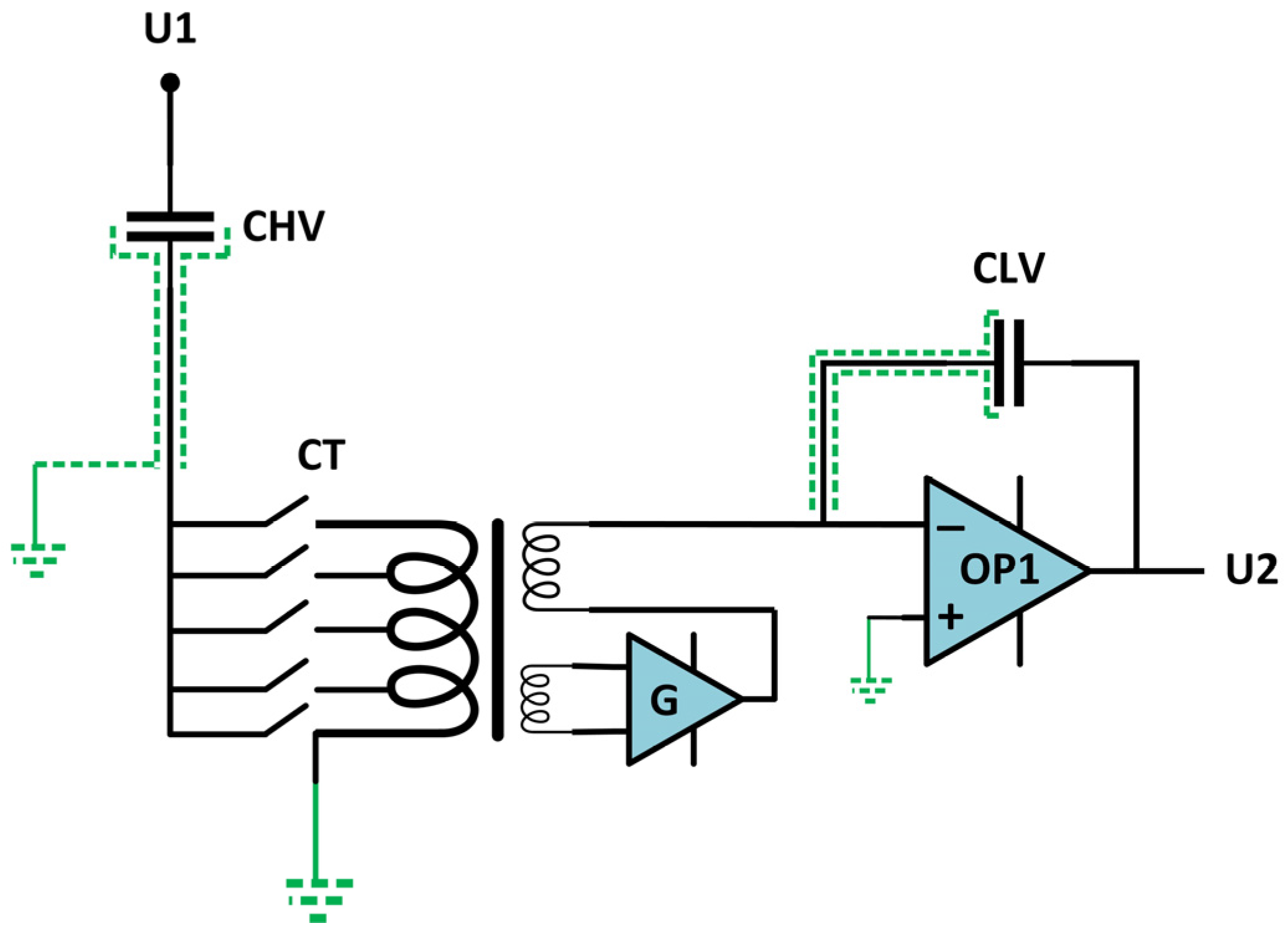
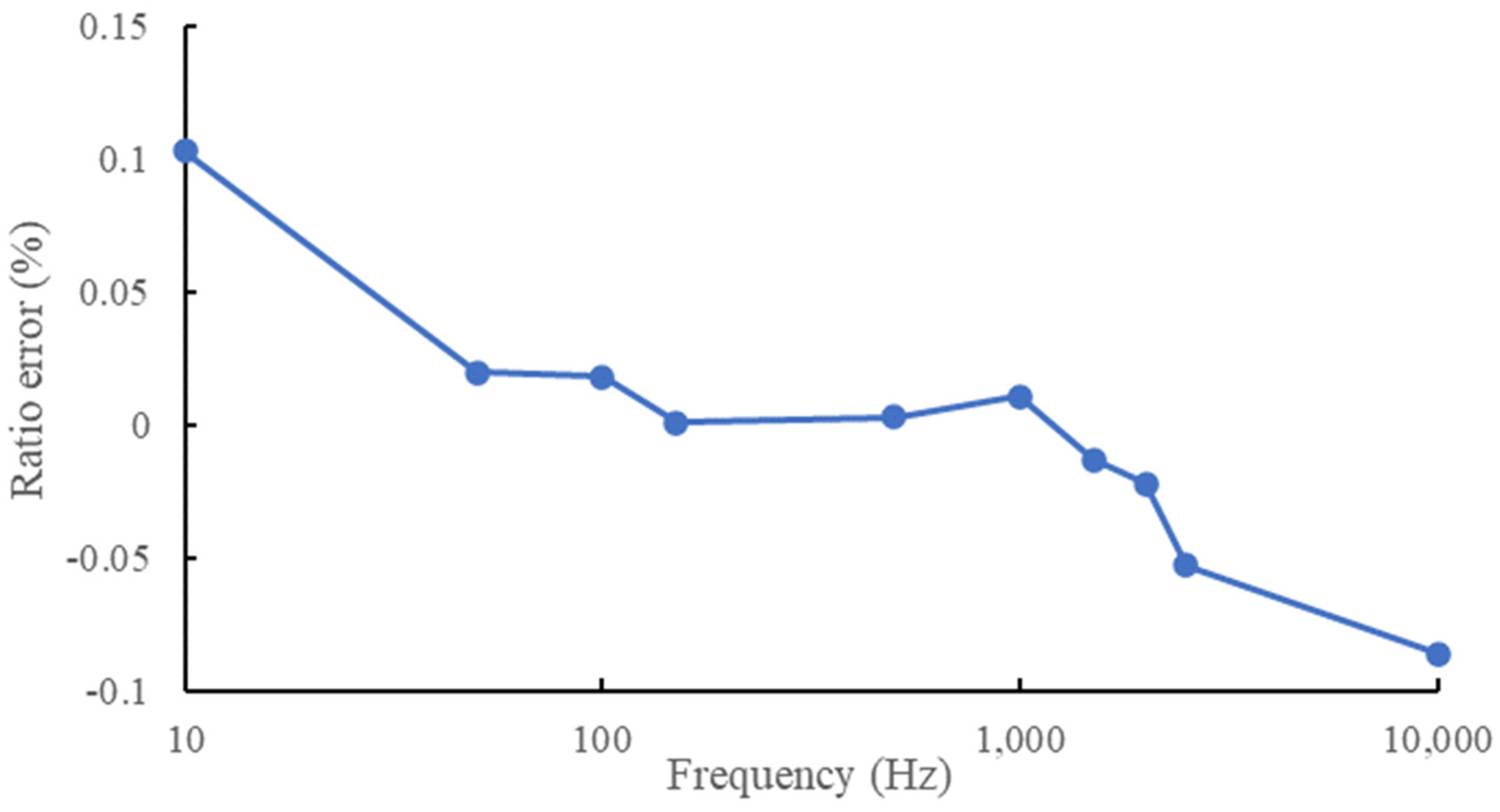
2.2.3. Resistive Voltage Dividers

Theoretically, RVDs can provide a linear frequency response for voltage measurement. However, the design of an RVD for HV applications requires high ohmic resistances and larger dimensions that limit their frequency bandwidth [68]. In [69], the main problems associated with the HV resistive dividers have been identified. The stray capacitance between the divider and ground can introduce phase errors in the measured signal as well as limiting the RVD measurement bandwidth. Figure 6a shows the representation of distributed stray capacitances of a multi-stage resistive divider. Furthermore, the temperature increase in the resistors can also contribute to errors in the ratio [70]. Due to these issues, resistive dividers are limited to DC and low-frequency measurements at high voltage levels.

Figure 6b shows the frequency response of a medium-voltage RVD without capacitive compensation. It can be seen that the ratio error increases significantly beyond 1 kHz and reaches 70% ratio error at 10 kHz. Due to this fact, it is essential to provide capacitive compensation for RVDs to obtain a linear frequency response.

The application of a resistive divider with capacitive compensation for harmonic measurements in 400 kV transmission networks can be found in [71,72]. To increase the measurement bandwidth of the resistive divider, each resistor branch includes a control capacitor in parallel with it. The experiments have shown that the divider was capable of measuring voltage harmonics in the frequency range from 50 Hz to 10 kHz with a ratio accuracy of ±3% over the frequency range.

In MV networks, accurate harmonic measurement can be provided by using compensated resistive voltage dividers. RVDs that allow harmonic measurements covering a frequency bandwidth up to 150 kHz in MV networks with rated voltages up to 45/$\sqrt{3}$ kV are manufactured by RITZ [73]. A schematic diagram for the RITZ RVD is shown in Figure 7. The accuracy achieved by these transducers is $\pm 5\%$ up to 150 kHz based on accuracy limits provided in IEC 61869-6 [74].

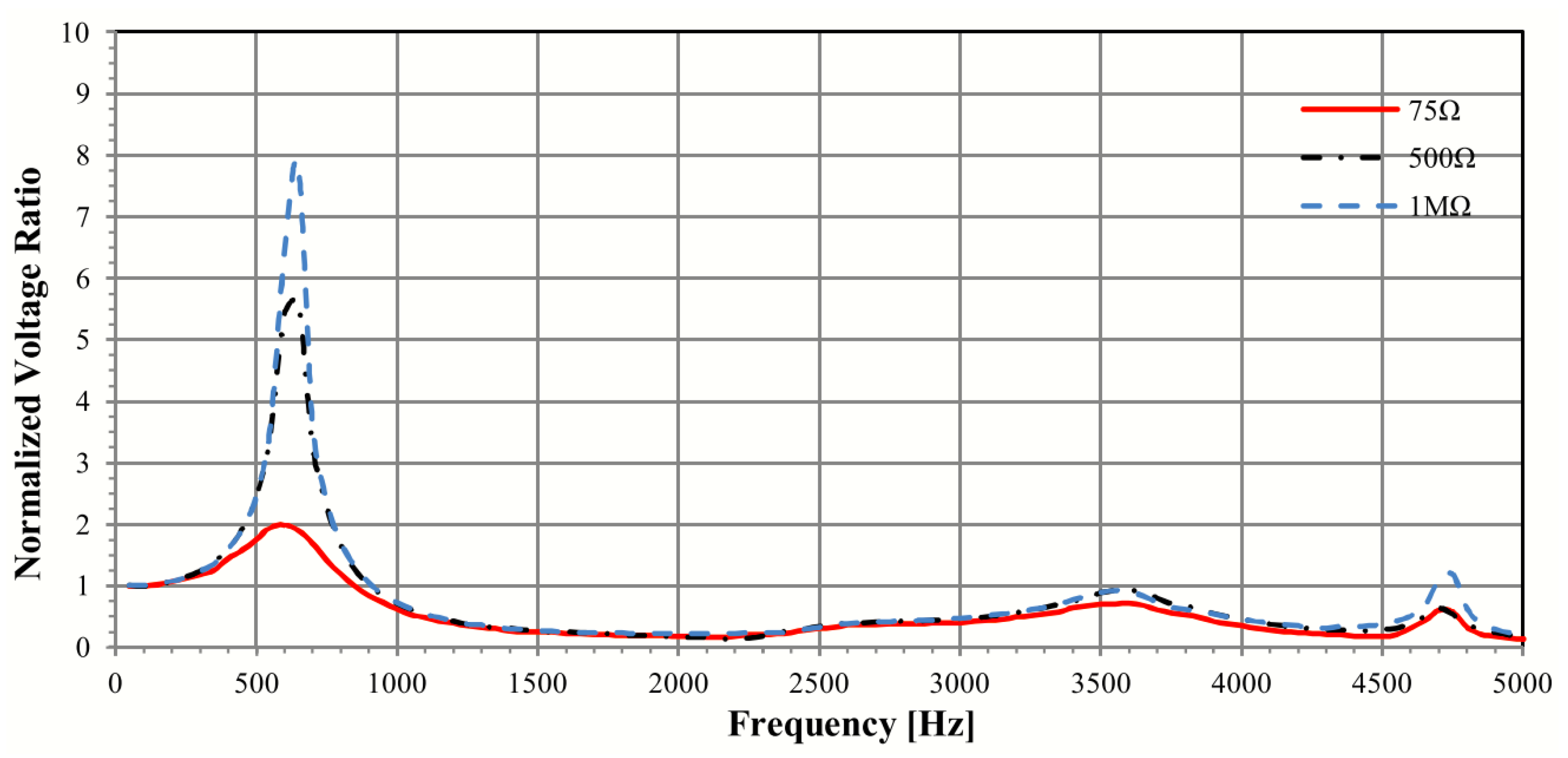
2.2.4. Capacitive Voltage Dividers

Capacitive dividers are considered to be a viable solution for harmonic measurements in high-voltage networks due to their linear frequency response compared to magnetic voltage transformers [75,76]. Capacitive dividers, which use compressed gas capacitors in the high-voltage arms, can be used as reference dividers in testing the frequency response of the VTs [77]. Capacitive dividers offer advantages, such as good frequency responses, low dielectric losses, low-voltage dependence, and a simpler structure [76].

It has been shown that the ratio error of a CVD developed by using a 200 kV SF₆ compressed gas capacitor was below ±1% for frequencies from 50 Hz to 3 kHz [75]. The divider ratio across the frequency range was calculated using the capacitances measured by an LCR meter. Such results indicate that capacitive voltage dividers have wider frequency bandwidths than other voltage transformers. However, it is worth nothing that the measurement of capacitors in this study were carried out at low voltages (<15 V). Thus, the influence of voltage dependence of the high-voltage arm capacitor has not been taken into consideration. Moreover, an evaluation of the impact of connection cables from the divider to the measurement instrument and the effect of other parasitic effects has not been performed.

Another study on a CVD developed by using a compressed gas capacitor in the high-voltage arm and ceramic capacitors in the low-voltage arm has shown a ratio error below ±1.2% for frequencies from 50 Hz to 20 kHz. The ratio of the divider has been evaluated by performing a 500 V sinusoidal voltage sweep across the frequency range and measuring the input and output voltage signals of the CVD by using digital multi-meters [78]. Once again, evaluation at 500 V means that the influence of the voltage dependence of the high-voltage arm capacitor has not been considered.

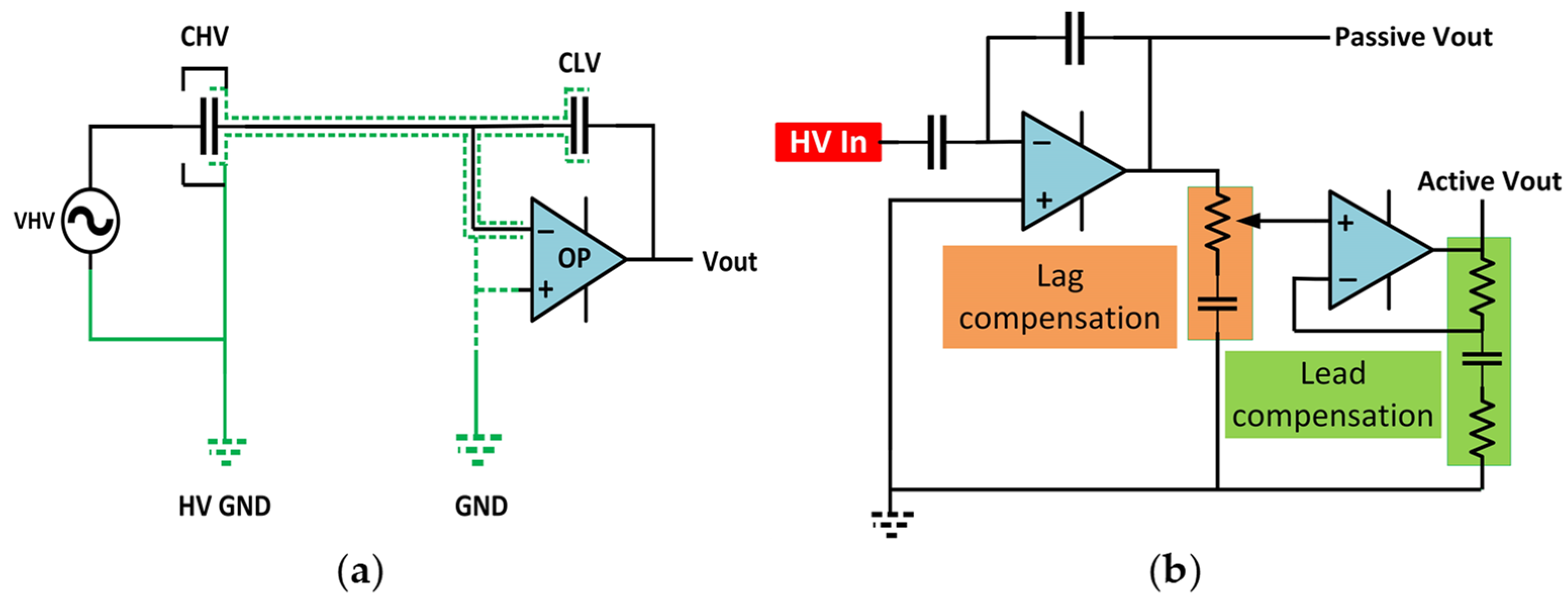
• CVDs with active low-voltage arms

The transfer function of an ideal CVD is independent of frequency. However, the actual transfer function of the CVD may be influenced by the loading effect of the measuring cables and low-voltage measurement equipment [77,79] as illustrated in Figure 8.

The actual transfer function of the CVD is given by Equation (5), considering the above loading effect. Equation (5) is as follows:

$$\frac{{\mathrm{V}}_{\mathrm{O}\mathrm{u}\mathrm{t}}\left(\mathrm{s}\right)}{{\mathrm{V}}_{\mathrm{I}\mathrm{n}}\left(\mathrm{s}\right)}=\frac{{\mathrm{R}}_{\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}}{\mathrm{C}}_{\mathrm{H}\mathrm{V}}\mathrm{s}}{{\mathrm{R}}_{\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}}\left({\mathrm{C}}_{\mathrm{e}\mathrm{q}}+{\mathrm{C}}_{\mathrm{H}\mathrm{V}}\right)\mathrm{s}+1}$$

(5)

where:

• s = jω;
• ${\mathrm{C}}_{\mathrm{e}\mathrm{q}}$ is the parallel equivalent capacitance of the low-voltage arm consisting of a low-voltage capacitor (${\mathrm{C}}_{\mathrm{L}\mathrm{V}}$), cable capacitance (${\mathrm{C}}_{\mathrm{c}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}}$), and the measurement instrument capacitance (${\mathrm{C}}_{\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}}$). The cable impedance mainly consists of its capacitance to the ground and the instrument impedance consists of input resistance in parallel with the input capacitance.

The use of an active low-voltage arm is suggested in [81] to avoid the loading errors on the CVD voltage ratio and phase error, where an inverting amplifier is used. The interconnection point of the high-voltage capacitor and low-voltage capacitor is virtually grounded. Figure 9 illustrates the active low-voltage arm techniques in CVDs.

However, careful attention must be given to the design of the amplifier circuit for the following reasons:

• DC voltage feedback for the operational amplifier (op-amp) should be provided to avoid saturation of its output.
• The operational amplifier finite open loop gain can cause distortion of the divider output waveform, especially at higher frequencies. Sufficient loop gain is required to make the operation of a practical op-amp as close to its ideal behavior as possible. Otherwise, the transfer function of the amplifier depends on amplifier internal components rather than on the external passive components.

The authors of [81] have developed a 50 kV/5 V (100 pF/1 µF) CVD with an active low-voltage arm. The accuracy of the active low-voltage arm of the CVD at 50 kV, 50 Hz is $\pm 1.5\%$for voltage ratio and $9.9\mathsf{\mu }$rad for phase error. The authors have further investigated the variation in the ratio error of the divider in the voltage range from 10% to 120% of the rated primary voltage 50 kV at 50 Hz. This variation was measured by comparing the output voltage of the capacitor divider against the output of a standard VT using a sampling ratio bridge [83]. The variation in ratio error over the entire voltage range was within 0.001% and within 3.5 µrad for phase displacement, indicating excellent voltage linearity. However, the frequency characteristics of the active low-voltage arm capacitive divider have not been measured.

Similar developments to improve CVD phase error, as shown in Figure 9b, have been undertaken to measure power frequency phase angles with a phase uncertainty below $25\mathsf{\mu }$rad [82]. In [84,85], a compressed gas standard capacitive voltage divider with an active inverter amplifier circuit to provide an input impedance greater than 5 GΩ is presented. The divider frequency response tests show that the ratio error of this device is below 0.5% for frequencies from 50 Hz to 2.5 kHz.

An active capacitor divider with current transformer compensation is covered in [77]. It is stated that the ratio and phase errors of a standard capacitor divider due to the loading effects of low-voltage instruments can be mitigated using this compensation method. The divider can be used for measuring the harmonic voltages up to 2.5 kHz at 10 kV voltage level. The schematic of the proposed voltage divider is shown in Figure 10. According to the reported results, the ratio error of the developed CVD is below 20 parts per million (ppm) and phase shift is below 200 $\mathsf{\mu }$rad for frequencies from 50 Hz to 2.5 kHz. However, it can be seen that the ratio error and phase shift of the proposed CVD shows an increasing behavior above 1 kHz.

• Active capacitive voltage divider with integrated optical power supplies

In comparison to the magnetic VTs, CVDs do not provide galvanic isolation between the HV side and the LV measurement equipment [86]. To address this issue, in [87], a capacitor divider-based high-voltage measurement system using an optical power supply unit is presented. As shown in Figure 11, the operational amplifier connected to the low-voltage arm of the capacitive divider is powered by optical power generated by a laser source. It is claimed that the laser power source is a reliable alternative to the use of a battery power supply for powering the active low-voltage arm of the divider.

The frequency response of the complete measurement system, evaluated by applying an LV signal to the divider, showed that the deviation of the voltage ratio was below ±0.5% for frequencies from 50 Hz to 5 kHz. It stated that the time delay of the output from input signal at 50 Hz was around 15 µs, corresponding to a phase error of 0.47 crad, i.e., 0.5 accuracy class according to IEC 61000-4-7 [40]. However, the accuracy of the system has not been verified at high voltage.

• High-voltage bushing-based capacitive divider

In the work presented in [70], a capacitive divider has been implemented using the capacitance-graded bushing of a power transformer as the high-voltage arm and a secondary capacitor connected to the bushing tap as the low-voltage capacitor. This arrangement is shown in Figure 12. The bandwidth measurements of the divider evaluated using a vector network analyzer (VNA) at low voltage have shown that the variation in the voltage ratio was below 1% of the measured ratio at 50 Hz up to a frequency of 100 kHz.

In [70], it is demonstrated that the temperature dependency of the divider due to the variation in capacitance of the graded bushing in the range from −20 °C to 60 °C results in a voltage ratio error below $\pm 2$% for all frequencies up to 100 kHz. However, no investigations have been undertaken to evaluate the voltage linearity of the divider capacitance at high voltage levels.

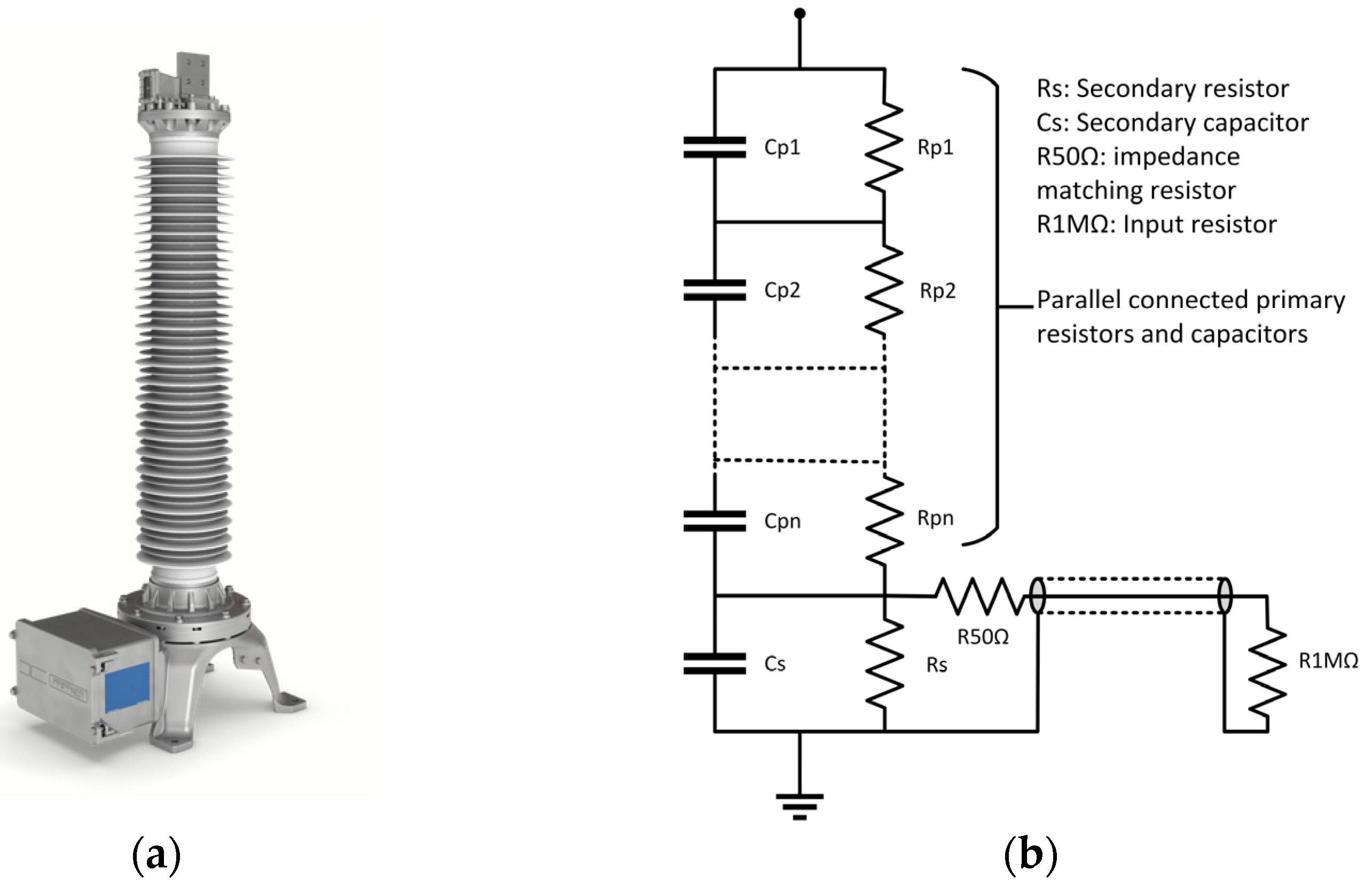
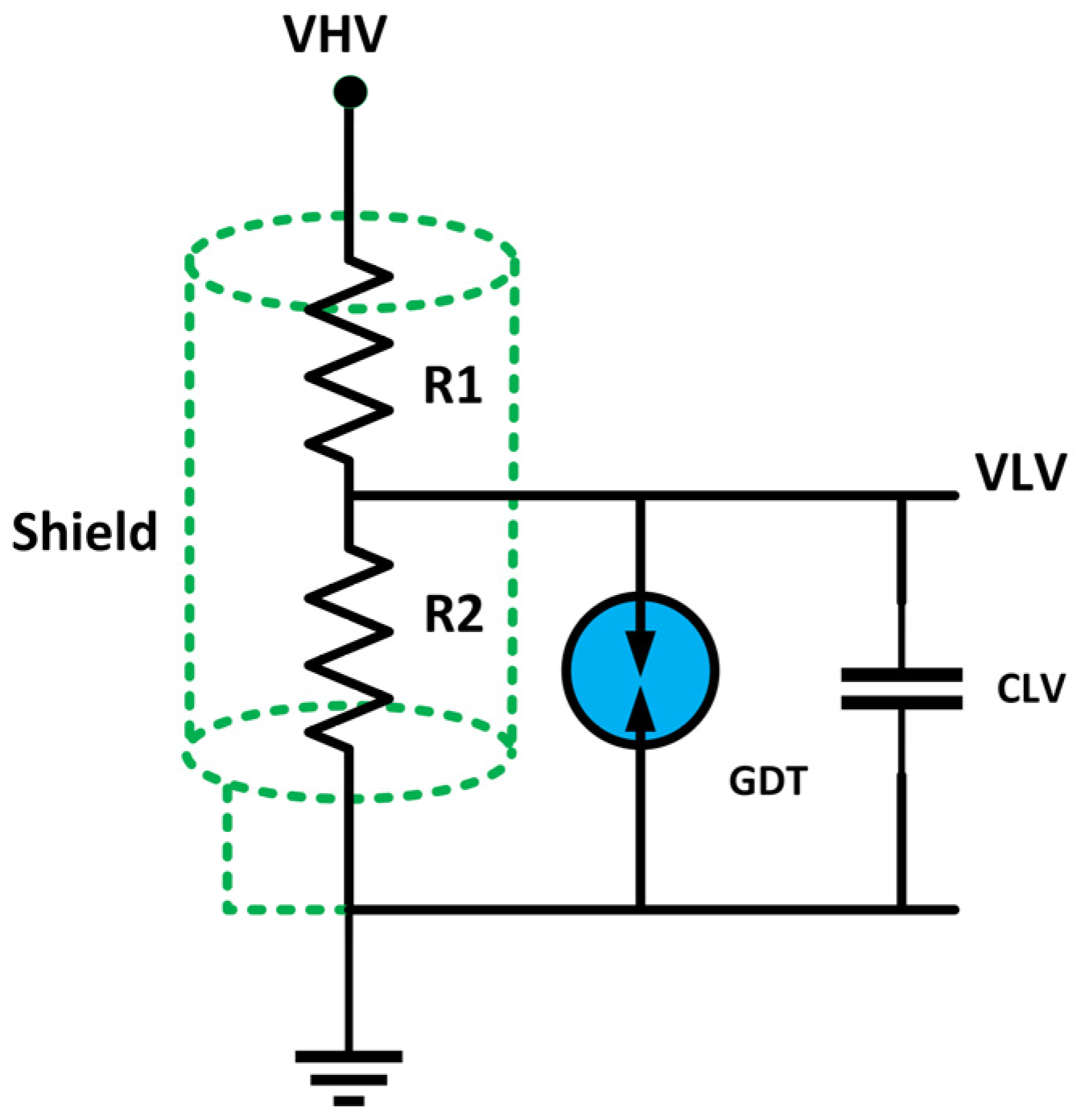
2.2.5. Resistive–Capacitive Voltage Dividers

An RCVD contains a resistive branch and a capacitive branch in parallel. The resistive branch consists of a primary resistor (R₁) and a secondary resistor (R₂). The capacitive branch consists of a primary capacitor (C₁) and a secondary capacitor (C₂). The voltage and phase transfer functions are given in the following Equations (6) and (7) [88]:

$$\frac{{\mathrm{V}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{j}\mathsf{\omega }\right)}{{\mathrm{V}}_{\mathrm{i}\mathrm{n}}\left(\mathrm{j}\mathsf{\omega }\right)}=\frac{{\mathrm{C}}_1}{{\mathrm{C}}_1+{\mathrm{C}}_2\left[\frac{1+\frac{1}{\mathrm{j}\mathsf{\omega }{\mathrm{R}}_2{\mathrm{C}}_2}}{1+\frac{1}{\mathrm{j}\mathsf{\omega }{\mathrm{R}}_1{\mathrm{C}}_1}}\right]}$$

(6)

where:

• V_out is the secondary voltage;
• V_in is the measured high voltage;
• ω is the angular frequency of the voltage.

$$∆\mathsf{\phi }=\arctan \left(\mathsf{\omega }{\mathrm{R}}_2{\mathrm{C}}_2\right)-\arctan \left(\mathsf{\omega }{\mathrm{R}}_1{\mathrm{C}}_1\right)$$

(7)

According to Equation (6), the voltage ratio is frequency dependent. In order to minimize the frequency dependency, the resistors and capacitors need to be selected using the following Equation (8):

$${\mathrm{R}}_1{\mathrm{C}}_1={\mathrm{R}}_2{\mathrm{C}}_2$$

(8)

However, in reality the voltage ratio can be non-linear as the frequency increases due to the non-ideal behavior of the capacitors. A practical capacitor consists of a parasitic inductive component, which creates an internal resonance point. It has been shown that a good frequency linearity can be obtained from DC to 1 MHz by selecting low inductance capacitors [88,89]. Commercial RCVDs have been developed by PFIFFNNER (Manufactured by PFIFFNNER Group, Maharashtra, India) and TRENCH (Manufactured by TRENCH Group, Bamberg, Germany) [90,91]. These dividers are capable of harmonic voltage measurements for network voltages ranging from 72 kV to 550 kV. The results in [88], shows that a 420 kV RCVD manufactured by PFINNER has a voltage ratio accuracy of ±0.2% in the frequency range from 15 Hz to 10 kHz. The maximum measured phase error has been noted to be 2.6 crad at 10 kHz. Compared with existing harmonic voltage measurement systems, such an accuracy is seen to be considerably higher and well within the accuracy limits for Class I instruments, as defined by IEC 61000-4-7 [40]. Figure 13a shows the RCVD manufactured by PFIFFNNER, while Figure 13b shows the circuit schematic of the TRENCH RCVD.

In further work [92], an RCVD rated at 420 kV with a nominal ratio of 3800 manufactured by TRENCH Switzerland was used as the reference divider in a harmonic voltage transformer calibration system. The manufacturer claims that the RCVD can be used for harmonic measurements up to 1 MHz. Figure 14 shows the frequency response of the TRENCH RCVD, as presented in [92]. The results show that the RCVD ratio error remains below $\pm 0.1$% up to 10 kHz.

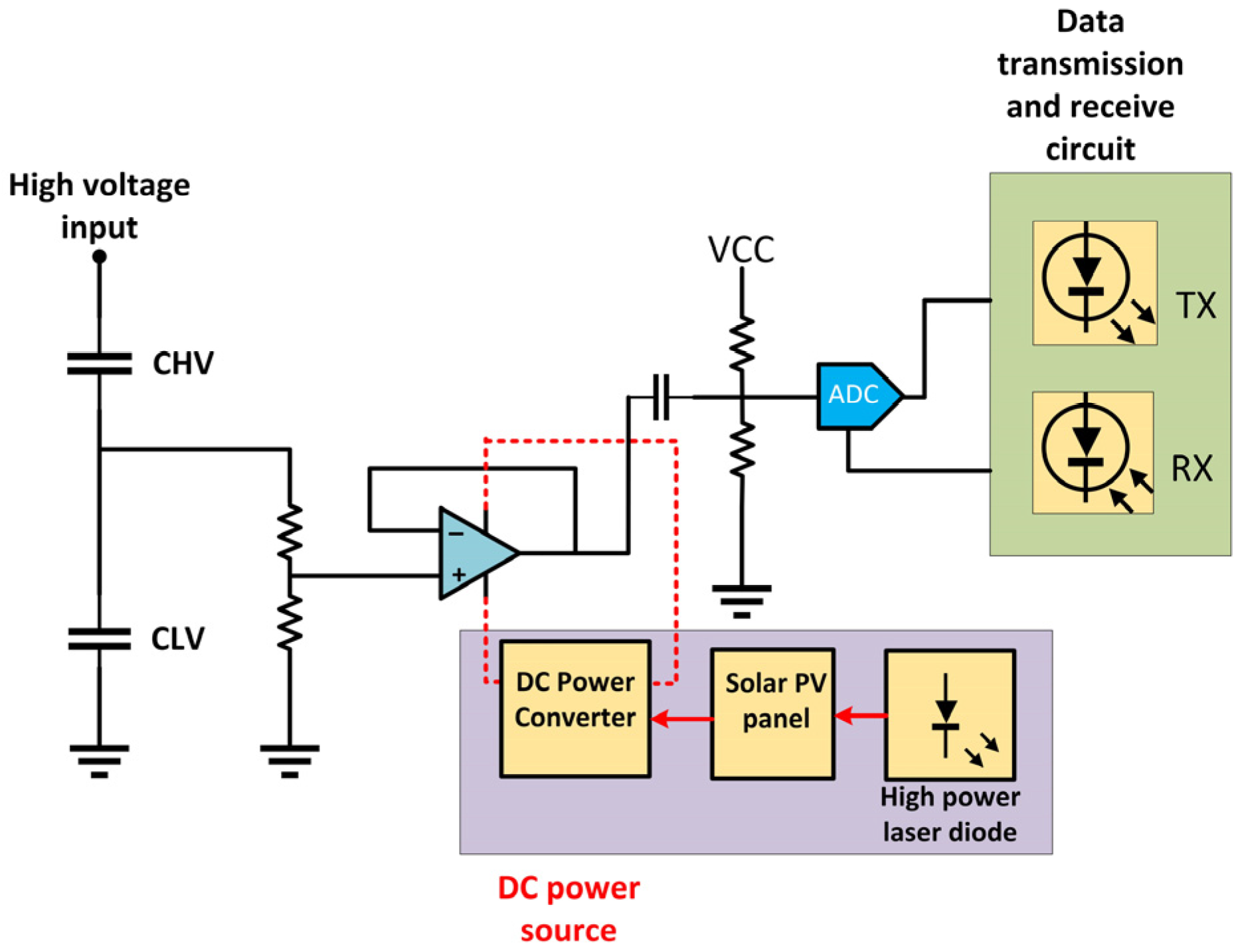
2.2.6. Optical Voltage Transducers

In contrast to traditional magnetic transformers, which are bulky due to their insulation requirements and the size of the magnetic cores and windings, optical voltage transducers (OVTs) offer many advantages, such as compact designs, inherent insulation capability, light weight, wide bandwidth, high accuracy, and immunity to electromagnetic interference [93]. In addition, they also mitigate catastrophic failures due to effects, such as magnetic saturation and ferroresonance, that could take place in conventional transformers [94]. OVTs can be categorized into two subgroups depending on the type of electro-optic modulation that is used for voltage measurement, as follows [95]:

• External electro-optic modulation-based OVTs, where the measured external voltage modulates the light wave carrier of the OVT sensor.
• Internal electro-optic modulation-based OVTs, where the measured voltage directly modulates the electroluminescent material of the sensor.

Each of the above is described in detail below.

• Optical voltage transducers based on the Pockels effect

In high-voltage measurement, the external electro-optical modulation type OVTs are more suitable due to their high-voltage withstanding capability [95]. These sensors are based on either the Pockels effect or Kerr effect [96] and they induce external electric field birefringence [97] in some types of crystalline materials. An OVT based on the quadrature method of the electro-optic voltage measurement principle is covered in [98]. It used three optical electric field sensors placed inside a resistive shield, which are used for reducing the effects of the stray electric field on the voltage measurements accuracy. The combined electric field measured by these three sensors is used for calculating the applied high voltage using a quadrature method [99,100]. The test showed that this OVT met the 0.2 accuracy class requirements of IEC 60044-2 [101]. Specifically, the ratio error relative to the nominal ratio at 50 Hz was below 5% up to 2 kHz. The phase angle errors were considerably higher for lower order harmonics.

A commercially available 230 kV phase to neutral rated OVT manufactured by NXTPhase T&D cooperation is used for high-voltage harmonic measurement in the study presented in [92]. Figure 15 shows the OVT frequency response characteristics plotted by employing the data provided in [92].

According to Figure 15, significant phase angle errors can be observed as the frequency increases. However, these results should not be generalized for all types of OVTs for their performance in harmonics measurements.

• Optical voltage transducers based on the electro-gyration effect

Electro-gyration is also an optical phenomenon in a material that is induced by the presence of an external electric field. Electro-gyration is a phenomenon that describes the circular birefringence in an optical material [102]. In the case of the linear electro-gyration effect, the linearly polarized incident light will be subjected to a polarization rotation by an angle which is proportional to the external electric field strength that is applied on the material [95]. The linear electro-gyration effect takes place in centrosymmetric crystals due to spatial dispersion which is different to the Faraday effect that occurs due to magnetic field vector reversal symmetry with time [103].

In [104], a voltage sensor based on the electro-gyration effect has been developed using a lead tungstate (PbWO₄) crystal. The linear dependency of the electro-gyration up to 10 kV has been experimentally verified, although no evaluation has been performed with different frequencies in this experiment.

A 35 kV optical voltage transducer has been developed recently by MarsEnergo™ (Manufactured by MarsEnergo, St. Petersburg, Russia) based on the linear electro-gyration effect [105]. This optical transducer shown in Figure 16 has a rated transformation ratio of 35 kV:110 V with a ratio error below 0.5% from 1 Hz to 10 kHz. The phase angle measurement error of the transducers is claimed to be below 2 min at a rated voltage. However, no information is provided regarding the harmonic phase angle measurement accuracy.

2.2.7. Non-Conventional Instrument Transformers

Two types of non-conventional instrument transformers are included below.

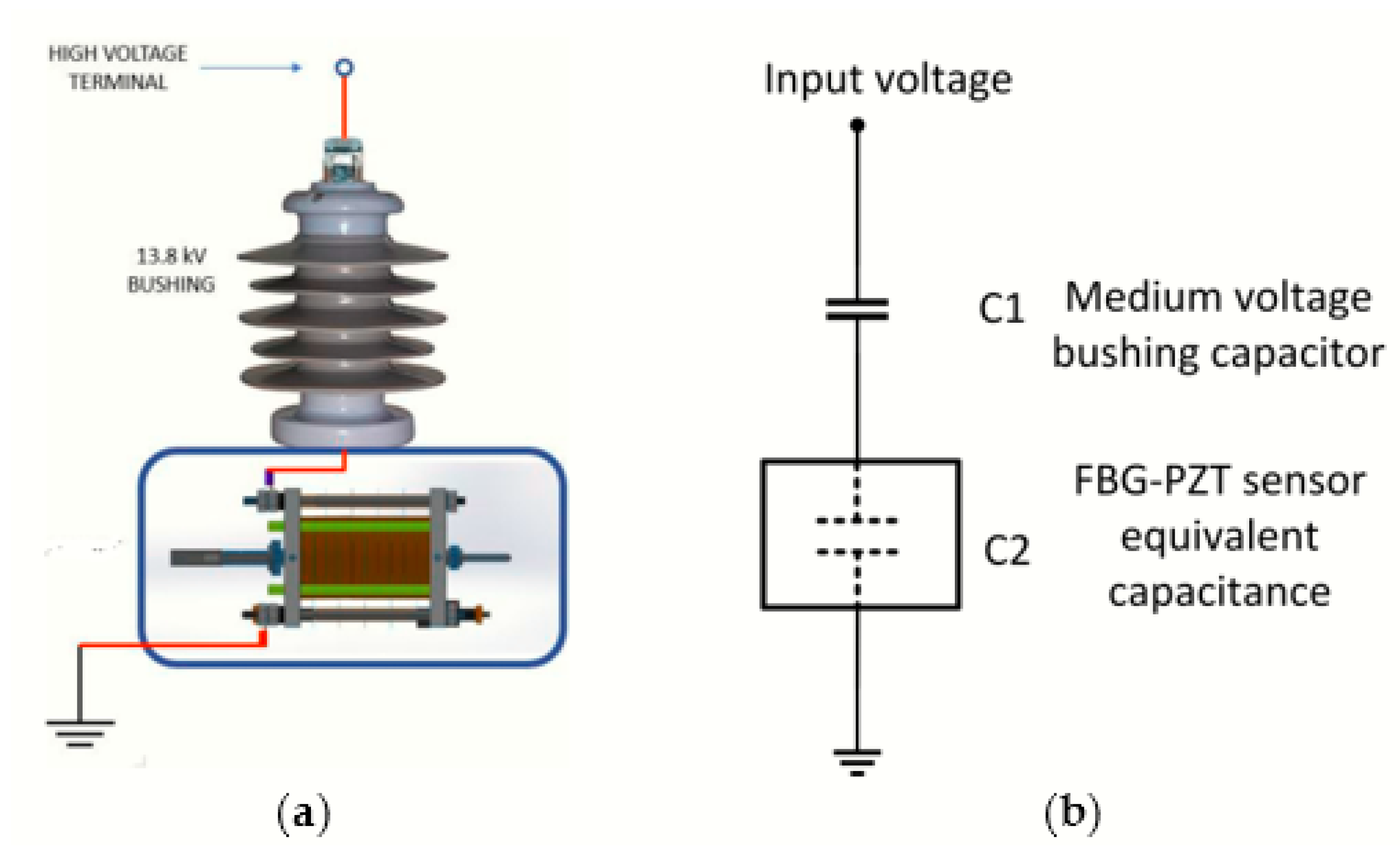
• Optical voltage transformers based on fiber Bragg grating (FBG) and piezoelectric ceramic (PZT) materials

An OVT based on a combination of piezoelectric material and a fiber-Bragg grating reflector is proposed for power quality measurements in MV networks, with a rated voltage of 4 kV [106]. To overcome this voltage limitation, a capacitive divider based on an insulator bushing, as shown in Figure 17a, has also been used to extend the application voltage to 13.8 kV. The tests of the developed sensor up to 2.5 kHz reveal that the frequency response of the combined sensor remains below $\pm 3$ dB relative to the voltage ratio at 50 Hz. However, at some frequencies, the error reaches $\pm$1 dB, implying percentage ratio errors of approximately $\pm 12\%$. Another combined transducer based on a capacitive divider and an FBG-PZT sensor is presented in [107]. However, no information is available on its harmonic measurement accuracy.

• Dry type insulation combined electronic voltage and current transformer

This type of transducer has the capability of simultaneous current and voltage measurement in MV/HV networks. The commercially available transducer presented in [108] is based on a capacitive voltage divider and a Rogowski coil to provide measurement and protection signals for digital substations according to the IEC 61850 communication protocol [109]. Figure 18 shows the internal circuit diagram of the combined transducer.

These types of transducers are relatively novel in their application in electrical power networks. Similar combined transducers have been developed by RITZ for applications in MV networks up to 30/$\sqrt{3}$ kV [110]. According to the low-voltage frequency sweep response, the transducer can measure harmonic voltages and current up to 3.15 kHz with a ratio accuracy of $\pm 3\%$.

2.3. Impact of External Factors on Instrument Transformer Frequency Response

The impact of external factors on instrument voltage transformer frequency response behavior is covered in [111,112,113]. These factors do not include certain issues, such as transducer design aspects and inherent errors due to manufacturing processes, since they are considered as internal factors. A detailed evaluation of the influence of internal factors on inductive transformer frequency response up to 10 kHz is given in [31]. The following main influential factors are identified and investigated:

(a)

Operating temperature;

(b)

Variation in instrument transformer burden;

(c)

Effect of vibration;

(d)

Proximity effects due to metallic objects;

(e)

Electric and magnetic fields created by nearby energized conductors;

(f)

Magnitude of the fundamental voltage component.

The above influencing factors are discussed in detail within the subsections below.

2.3.1. Operating Temperature

In [111], four resin cast insulated inductive voltage transformers with voltage ratings up to 35 kV were tested at zero burden for their frequency response up to 9 kHz at different temperatures in the range from $-25℃$ to 55 $℃$. Figure 19a shows the variation in frequency response for a 35 kV unit at different temperatures and Figure 19b shows the variation in the voltage ratio at the first resonance point at approximately 3.2 kHz. Each curve in Figure 19a,b shows the percentage difference in the voltage ratio of the transformer at different temperatures ($\vartheta$) relative to the voltage ratio evaluation at $20℃$. The results show that the resonance points of the IVT frequency response shift towards lower frequencies as the temperature increases. It is stated that this shift in resonance point is caused by the reduction in winding stray capacitances due to winding expansion at increased temperatures. Even though the voltage ratio error at the fundamental frequency and low order harmonics up to 2.5 kHz remains below $\pm 3\%$, the ratio error change near resonance frequencies is seen to be greater than 100%. This implies that IVTs cannot be utilized for reliable harmonic measurements above the first resonant frequency. Experimental results in [112,113] also report similar results for IVTs.

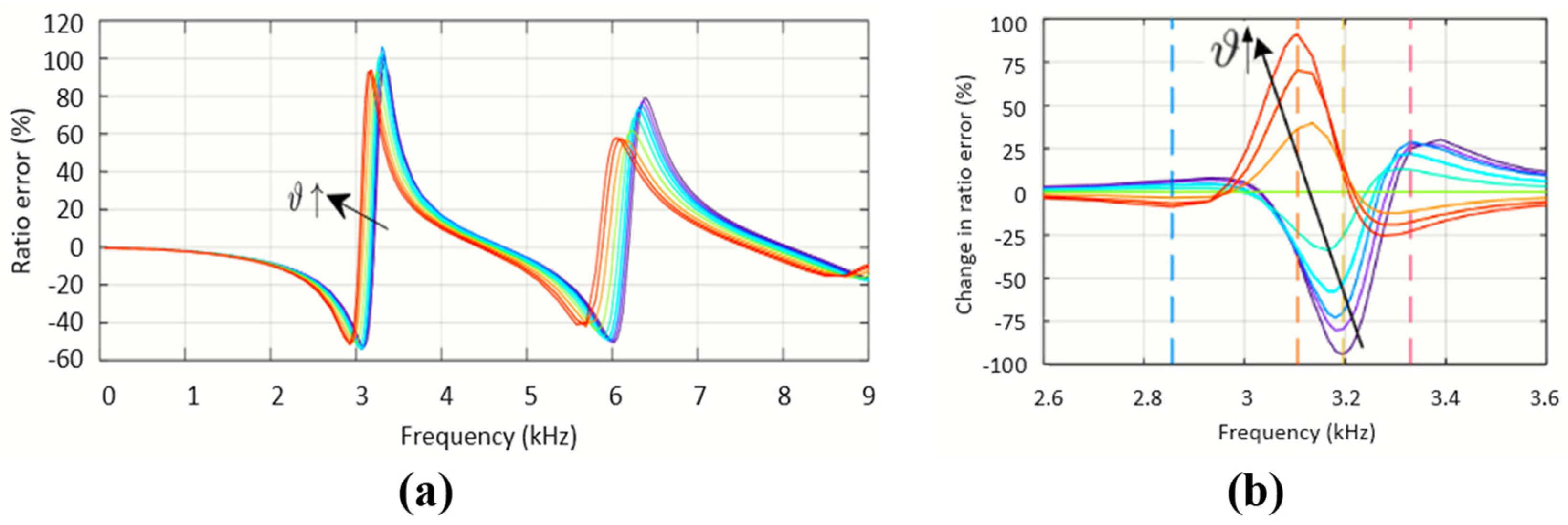
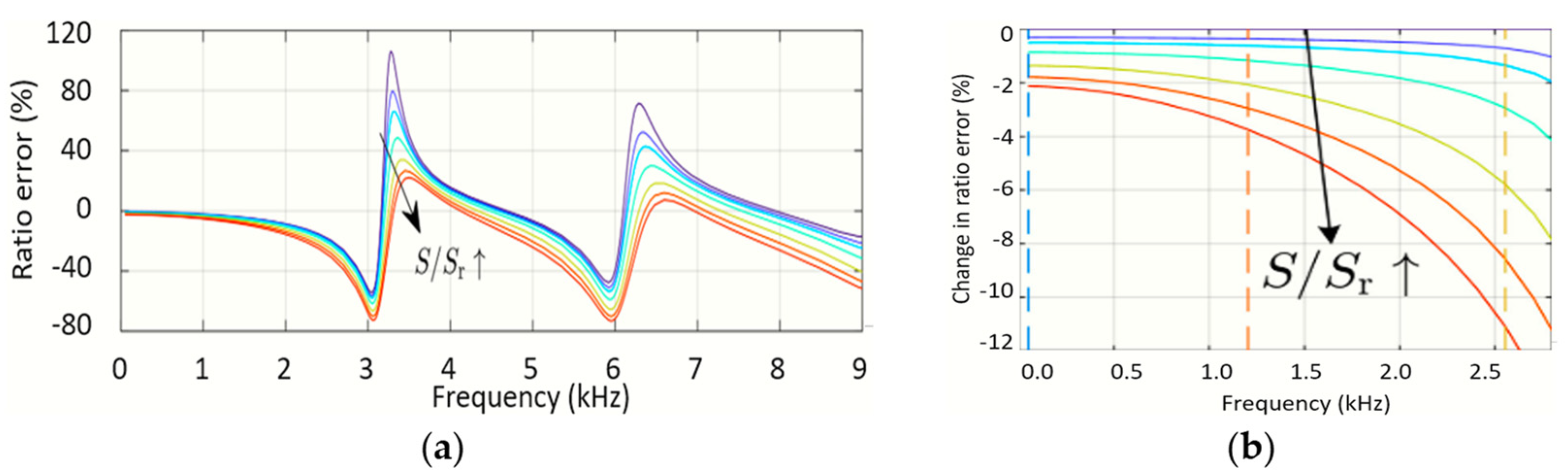
2.3.2. Impact of Burden

Impact of resistive burden on IVT voltage ratio error can be seen across a range of frequencies in Figure 20. Similar to the effect of temperature, the impact is highest at the resonant frequencies. However, no significant shift in the resonant frequency can be observed.

2.3.3. Impact of Proximity, Field Effects, and Vibration

In terms of proximity, field effects, and vibration, the changes in frequency response of the IVT are stated to be minimal and of no impact according to the results presented in [112].

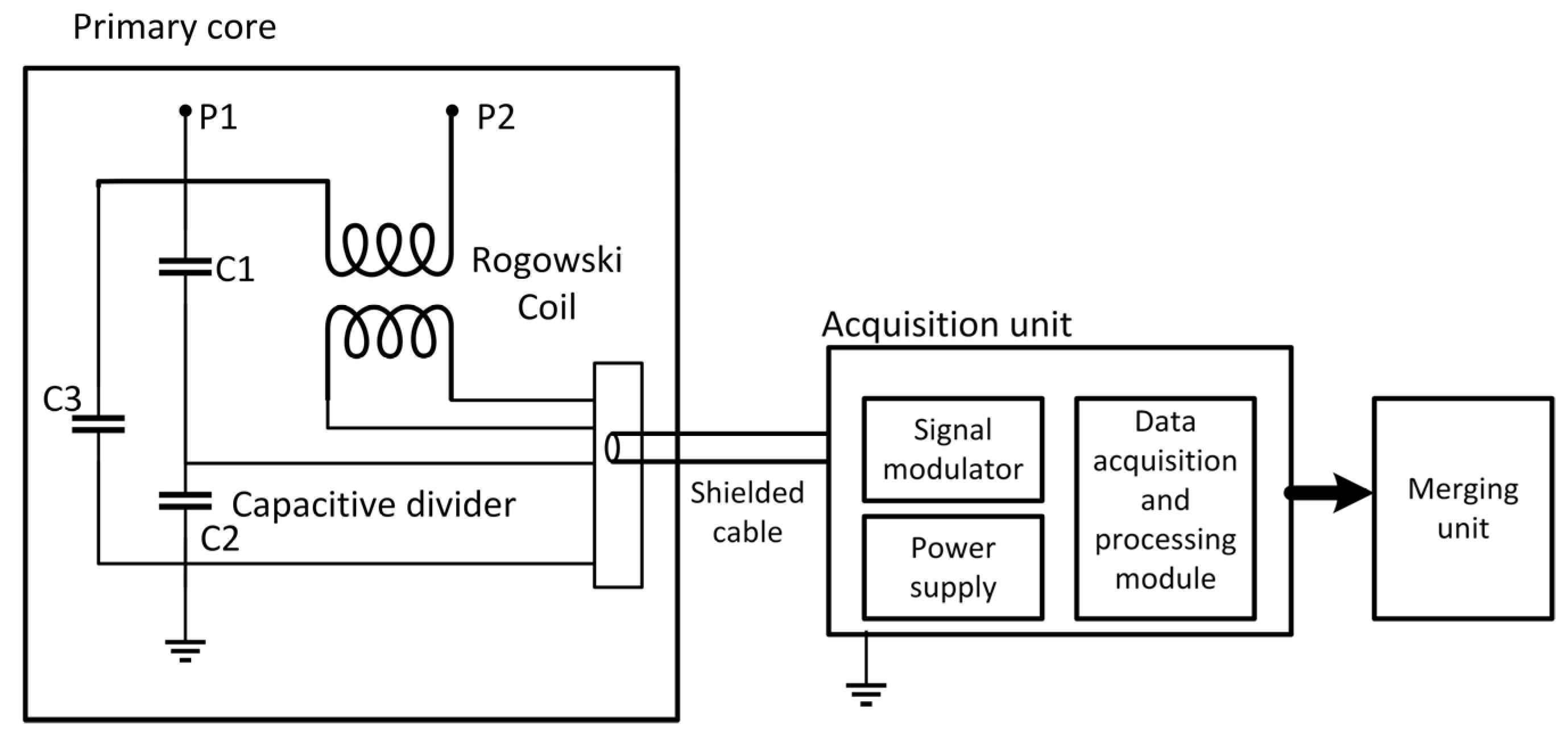
2.3.4. Impact of External Influencing Factors on Low-Power Instrument Transformers (LPITs)

Results of investigations into external influencing factors on LPITs do not yet exist in a consolidated manner. However, one study shows the impact of electric and magnetic fields by energized conductors and proximity effects on LPIT frequency response [112].

Table 7. Comparison of different types of LPITs against external influencing factors.

Transducer Type	E-Field and M-Field Effects	Proximity Effects	Combined Impact of Proximity and Field Effects
RVD	Medium impact	Medium impact	High impact
CVD	Low impact	No impact	No impact due to proximity
RVCD	Medium impact	High impact	High impact

shows the summary of the presented results.

2.4. Overall Comparison between the Accuracy of Instrument Transducers in the Frequency Range from 2 kHz to 9 kHz

Based on the details presented in the previous sections, an overall comparison between different transducer types is provided in

Table 8. Overview comparison of different types of instrument transducers based on their characteristics.

Transducer Type	Accuracy of Amplitude Measurement	Accuracy of Phase Angle Measurement	Ability to Measure 2 kHz–9 kHz Harmonics	Cost of Implementation	Impact of External Factors	Type of Calibration Required for Error Correction
IVT	Low (possibility of correction by calibration)	Low (possibility of correction by calibration)	Acceptable after calibration	Low	Low impact with possibility of correction by calibration	HV multi-tone signal calibration preferred (LV sinusoidal calibration acceptable with increased error)
CVT	Very low	Very low	Unacceptable	Low	Severe impact	Not applicable
CVT with harmonic terminals	Acceptable	Acceptable	Acceptable with increased margin of error	Low	Unknown	LV sinusoidal acceptable
CVT with PQ sensor	Good	Good	Acceptable	Medium	No significant impact	LV sinusoidal acceptable
RVD	Depends on provision of shielding	Depends on shielding	Depends on provision of shielding	Low to medium	Medium impact (avoidable by shielding)	LV sinusoidal acceptable for shielded RVDs
CVD	Good	Poor	Acceptable	Medium to high	No significant impact	LV sinusoidal acceptable
CVD with active LV arm	Better	Good	Acceptable	Medium to high	No significant impact	LV sinusoidal acceptable
RCVD	Excellent	Excellent	Acceptable	High	No impact	LV sinusoidal acceptable
OVT	Good	Depends on the type	Acceptable	High	No impact	LV sinusoidal acceptable
NCIT	To be decided after calibration	To be decided after calibration	To be decided after calibration	Depends on the type	To be decided after calibration	To be decided after calibration

. This comparison considers the accuracy, bandwidth of measurement, cost of implementation, impact of external factors, and the required calibration method for error correction.

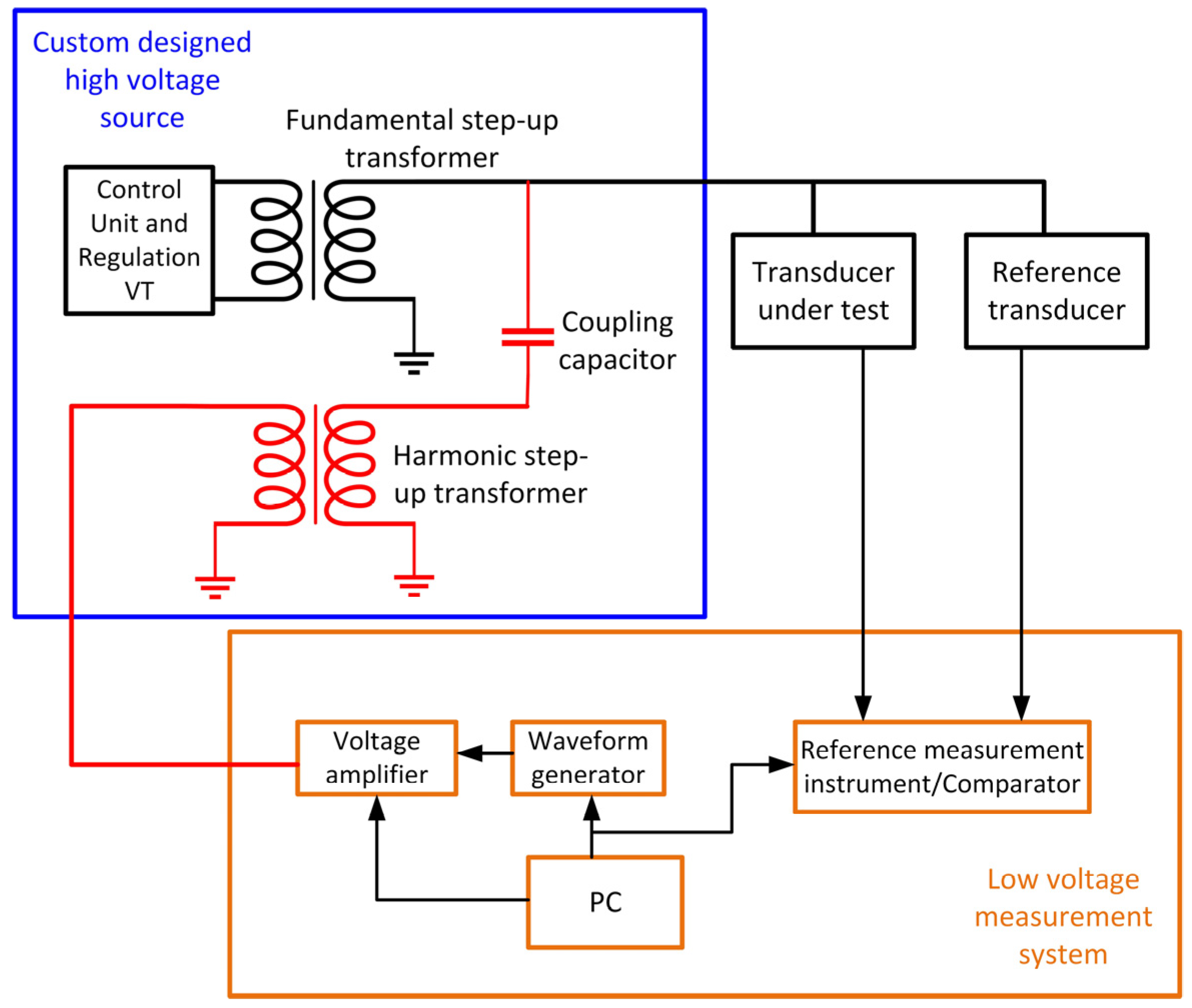
3. High-Voltage Calibration Systems to Evaluate Instrument Transformer Frequency Response

3.1. Instrument Voltage Transformer Calibration Process

Preceding sections have demonstrated that each type of voltage transformer demonstrates different frequency response behavior when they are used for harmonic measurements. Even though traditional inductive and capacitive transformers provide accurate measurements at the rated fundamental frequency, their voltage ratio and phase displacement at harmonic frequencies can vary significantly. CVDs and RCVDs can be identified as the transducers that have the fewest voltage ratio errors for harmonic measurements above 2 kHz. Even though OVTs are considered to be linear devices, their working voltage limitations enforce the use of voltage division technique to scale down the MV/HV/EHV voltages to compatible levels. For this reason, the combined voltage transducers based on an optical sensor and a voltage divider can also show increased voltage ratio and phase errors at harmonic frequencies. However, if the frequency response of a transducer does not drift with time, calibration against a reference voltage transducer can be performed to obtain the ratio and phase correction factors at each harmonic order to correct the measurement errors. The following section presents the existing MV/HV/EHV transducer calibration systems that have been utilized in the literature. The IEC 61869-103 technical report [25], provides detailed information on the test procedure and test apparatus set up for the accuracy evaluation of high-voltage transducers. According to these guidelines, two test methods are established based on the linearity characteristics and burden dependency of the test transducer, as shown in Figure 21.

According to the suggested procedure, two main calibration setups for MV/HV/EHV transducers can be identified as follows:

• The high-voltage composite signal calibration setup;
• Low-voltage frequency sweep calibration setup.

The selection of each type of test setup should be based on the voltage linearity of each transducer depending on whether its frequency response is affected by the presence of fundamental high-voltage amplitude.

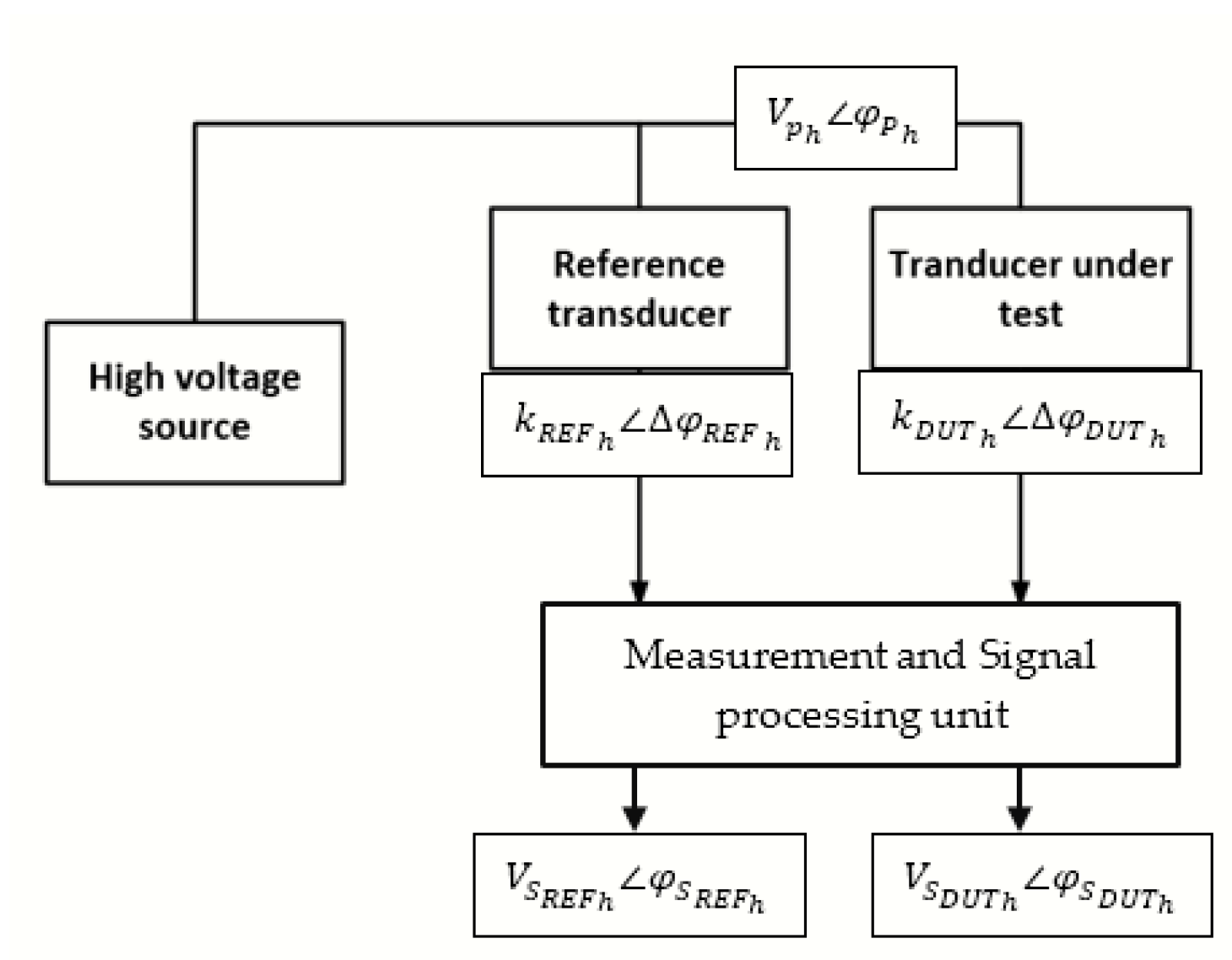
3.1.1. High-Voltage Calibration by Comparison against Reference Standard Transducer

The high-voltage transducer calibration process requires simultaneous measurement of the input high voltage and the output voltage signal of the transducer. The measurement of the output low voltage can be performed by direct connection of an appropriate measurement device. However, measurement of the input high voltage requires a reference transducer with a known frequency response denoted by $\left[{{\mathrm{k}}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}\mathrm{\angle }{{∆\mathsf{\phi }}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}\right]$. The setup for calibrating the transducer (device under test (DUT)) is shown in Figure 22.

The voltage ratio $\left({{\mathrm{k}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}\right)$ and phase displacement $(∆{{\mathsf{\phi }}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}})$ of the DUT at harmonic order (h) can be defined as follows:

$${{\mathrm{k}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}=\frac{{\mathrm{V}}_{{{\mathrm{S}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}}}{{\mathrm{V}}_{{\mathrm{p}}_{\mathrm{h}}}}$$

(9)

$${∆\mathsf{\phi }}_{\mathrm{D}\mathrm{U}\mathrm{T}\mathrm{h}}=\left[{\mathsf{\phi }}_{{{\mathrm{S}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}}-{\mathsf{\phi }}_{{\mathrm{p}}_{\mathrm{h}}}\right]$$

(10)

where:

• ${\mathrm{V}}_{{{\mathrm{S}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}}$ is the magnitude of the DUT secondary voltage signal at harmonic order (h);
• ${\mathrm{V}}_{{\mathrm{p}}_{\mathrm{h}}}$ is the magnitude of the primary high-voltage signal at harmonic order (h);
• ${\mathsf{\phi }}_{{{\mathrm{S}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}}$ is the phase angle of the DUT secondary voltage signal at harmonic order (h);
• ${\mathsf{\phi }}_{{\mathrm{p}}_{\mathrm{h}}}$ is the phase angle of the primary voltage signal at harmonic order (h).

In Equations (9) and (10), the magnitude and phase angle of the input high-voltage signal is calculated by using pre-existing voltage ratio and phase angle data of the reference transducer (i.e., ${{\mathrm{k}}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}\mathrm{\angle }{{∆\mathsf{\phi }}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}$) and by using the reference transducer output voltage measurement that is denoted by (${\mathrm{V}}_{{{\mathrm{S}}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}}\mathrm{\angle }{{\mathsf{\phi }}_{\mathrm{S}}}_{{\mathrm{R}\mathrm{E}\mathrm{F}}_{\mathrm{h}}}$), as follows:

$${\mathrm{V}}_{{\mathrm{p}}_{\mathrm{h}}}=\frac{{\mathrm{V}}_{{{\mathrm{S}}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}}}{{{\mathrm{k}}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}}$$

(11)

$${\mathsf{\phi }}_{{\mathrm{p}}_{\mathrm{h}}}={{\mathsf{\phi }}_{\mathrm{S}}}_{{\mathrm{R}\mathrm{E}\mathrm{F}}_{\mathrm{h}}}-{{∆\mathsf{\phi }}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}$$

(12)

where:

• ${\mathrm{V}}_{{{\mathrm{S}}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}}$ is the reference transducer output signal magnitude at harmonic order (h);
• ${{\mathrm{k}}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}$ is the voltage ratio of the reference transducer at harmonic order (h);
• ${{∆\mathsf{\phi }}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}$ is the phase error of the reference transducer at harmonic order (h);
• ${{\mathsf{\phi }}_{\mathrm{S}}}_{{\mathrm{R}\mathrm{E}\mathrm{F}}_{\mathrm{h}}}$ is the phase angle of the reference transducer output voltage signal at harmonic order (h).

Finally, the voltage ratio and phase displacement of the DUT can be expressed as follows:

$${{\mathrm{k}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}={{\mathrm{k}}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}.\frac{{\mathrm{V}}_{{{\mathrm{S}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}}}{{\mathrm{V}}_{{{\mathrm{S}}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}}}$$

(13)

$${∆\mathsf{\phi }}_{\mathrm{D}\mathrm{U}\mathrm{T}\mathrm{h}}={\mathsf{\phi }}_{{{\mathrm{S}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}}-{{\mathsf{\phi }}_{\mathrm{S}}}_{{\mathrm{R}\mathrm{E}\mathrm{F}}_{\mathrm{h}}}+{{∆\mathsf{\phi }}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}$$

(14)

For IVTs, the voltage ratio error ($\mathsf{\epsilon }$) and phase displacement ($\mathsf{\theta }$) are used to specify their accuracy at the rated fundamental frequency using the rated transformation ratio (${\mathrm{k}}_{\mathrm{r}}$) according to the definition provided in [114]. The same equations can be adopted to define IVT voltage ratio error (${\mathsf{\epsilon }}_{\mathrm{h}}$) and phase displacement error (${\mathsf{\theta }}_{\mathrm{h}}$) at a specific harmonic order (h), as follows:

$${\mathsf{\epsilon }}_{\mathrm{h}}=\left[\frac{{\mathrm{k}}_{\mathrm{r}}{\mathrm{V}}_{{\mathrm{s}}_{\mathrm{h}}}}{{\mathrm{V}}_{{\mathrm{p}}_{\mathrm{h}}}}-1\right]\times 100\mathrm{\%}=\left[\frac{{{\mathrm{k}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}}{{\mathrm{k}}_{\mathrm{r}}}-1\right]\times 100\mathrm{\%}=\left[\frac{{{\mathrm{k}}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}}{{\mathrm{k}}_{\mathrm{r}}}.\frac{{\mathrm{V}}_{{{\mathrm{S}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}}}{{\mathrm{V}}_{{{\mathrm{S}}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}}}-1\right]\times 100\mathrm{\%}$$

(15)

$${\mathsf{\theta }}_{\mathrm{h}}={\mathsf{\phi }}_{{{\mathrm{S}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}}-{{\mathsf{\phi }}_{\mathrm{S}}}_{{\mathrm{R}\mathrm{E}\mathrm{F}}_{\mathrm{h}}}+{{∆\mathsf{\phi }}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}$$

(16)

where:

• ${\mathrm{V}}_{{\mathrm{s}}_{\mathrm{h}}}$ is the secondary output voltage signal of the IVT at harmonic order (h);
• ${\mathrm{V}}_{{\mathrm{p}}_{\mathrm{h}}}$ is the primary input voltage signal applied to the IVT at harmonic order (h).

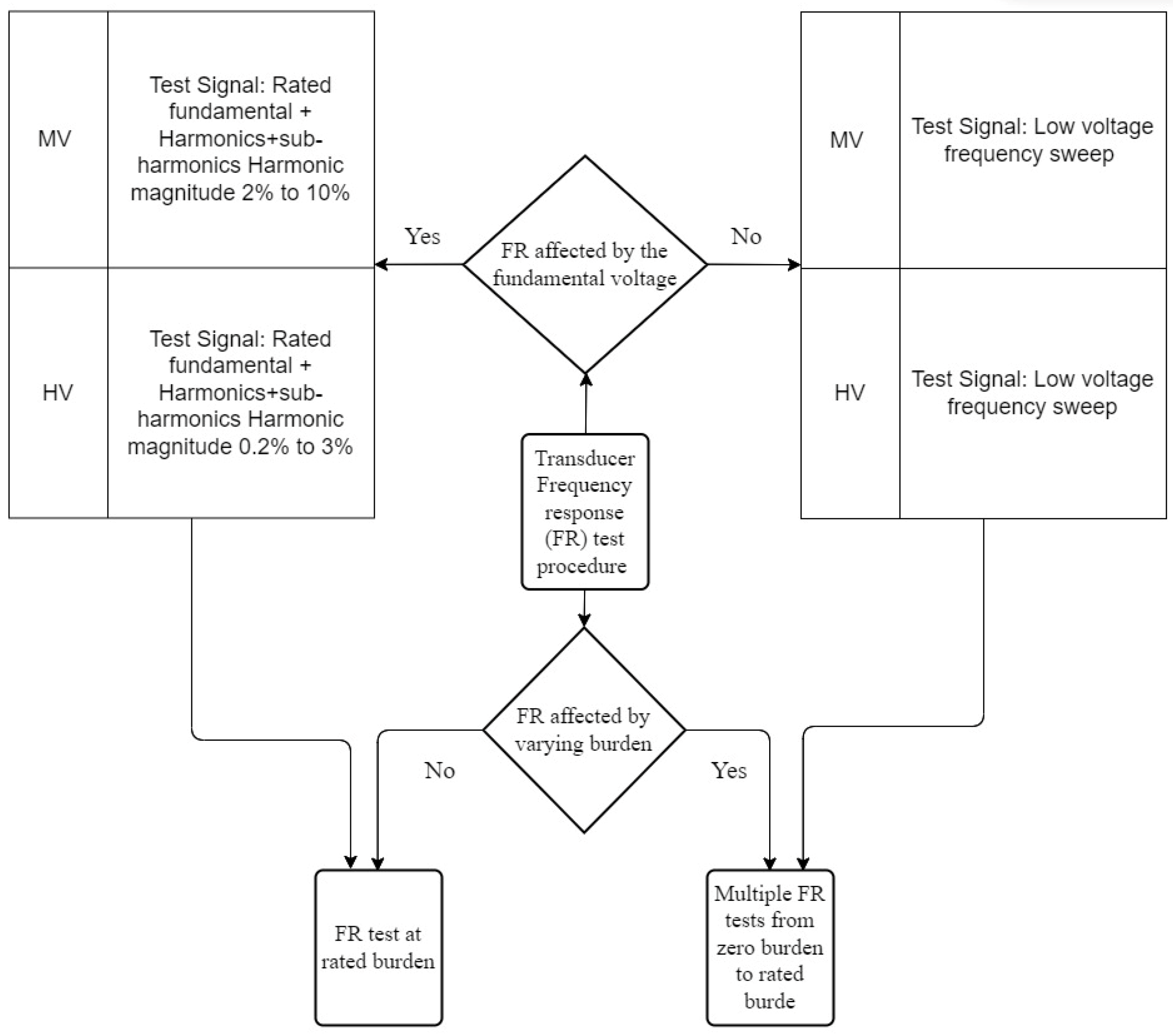
3.1.2. Low-Voltage Frequency Sweep Response Calibration Method

In cases where the DUT frequency response is not affected by the fundamental high-voltage component, LV frequency sweep calibration can be used. In addition, the lack of suitable voltage sources that can generate high-voltage composite signals and lack of accurate reference transducers mean that it can also be considered rational to use LV frequency sweep tests to evaluate DUT frequency response. In this method, the input signal to the transducer under test (i.e., ${\mathrm{V}}_{{\mathrm{p}}_{\mathrm{h}}}$) will be directly measured by the measurement device. In such cases, the voltage ratio error and phase error of the DUT can be directly calculated using the measurement results as follows.

$${\mathsf{\epsilon }}_{\mathrm{h}}=\left[\frac{{\mathrm{k}}_{\mathrm{r}}{\mathrm{V}}_{{\mathrm{s}}_{\mathrm{h}}}}{{\mathrm{V}}_{{\mathrm{p}}_{\mathrm{h}}}}-1\right]\times 100\mathrm{\%}=\left[\frac{{{\mathrm{k}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}}{{\mathrm{k}}_{\mathrm{r}}}-1\right]\times 100\mathrm{\%}=\left[\frac{1}{{\mathrm{k}}_{\mathrm{r}}}.\frac{{\mathrm{V}}_{{{\mathrm{S}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}}}{{\mathrm{V}}_{{{\mathrm{S}}_{\mathrm{R}\mathrm{E}\mathrm{F}}}_{\mathrm{h}}}}-1\right]\times 100\mathrm{\%}$$

(17)

$${\mathsf{\theta }}_{\mathrm{h}}={\mathsf{\phi }}_{{{\mathrm{S}}_{\mathrm{D}\mathrm{U}\mathrm{T}}}_{\mathrm{h}}}-{{\mathsf{\phi }}_{\mathrm{S}}}_{{\mathrm{R}\mathrm{E}\mathrm{F}}_{\mathrm{h}}}$$

(18)

It should be noted that for HV instrument transducers with very large voltage ratios, the input voltage signal used for an LV frequency sweep must be sufficiently large to generate measurable secondary output voltages. Otherwise, small output signals can cause measurement errors due to insufficient signal to noise ratio.

3.2. Application of Composite MV/HV/EHV Signals for Instrument Transformer Calibration

Based on the frequency response test procedure suggested in IEC 61869-103 [25], several studies have utilized composite MV/HV/EHV signals consisting of a fundamental frequency component and superimposed harmonics in the process of calibrating an instrument transducer.

Table 9. MV/HV/EHV instrument transformer calibration systems employing composite voltage signals.

Reference	Test Signal Type	Reference Transducer (If Any)	Tested Harmonic Bandwidth (Max 50 Hz/Max Harmonic Amplitude)
[112,113,115,116]	Composite signal (50 Hz + single harmonic)	RCVD	30 kV at 50 Hz/2% at 9 kHz
[117]	Composite signal (50 Hz + multiple harmonics)	CVD	92.5 kV at 50 Hz/10% at 10 kHz
[118]	Composite signal (50 Hz + single harmonic)	RCVD	20/$\sqrt{3}$ kV at 50 Hz/10% at 5 kHz
[119,120]	Composite signal (50 Hz + multiple harmonics)	RCVD	20/$\sqrt{3}$ kV at 50 Hz/3% at 1.25 kHz
[56,121]	Composite signal (50 Hz + single harmonic)	RCVD	230 kV at 50 Hz/1% at 1 kHz or 0.2% at 5 kHz

summarizes results of several studies related to calibration systems that use composite voltage signals consisting of fundamental and superimposed harmonics.

An automated frequency response test system has been developed by MARSENERGO for the certification of instrument voltage transformers [122]. This system allows the calibration of instrument voltage transformers that are rated for voltages from 6 kV to 200 kV. The test system allows the measurement of subharmonics and harmonics in the frequency range from 15 Hz to 2.5 kHz. The manufacturers claim that the test system complies with the accuracy requirements provided in the IEC 61869-103 technical report. Figure 23 shows the functional block diagram of the system.

According to Figure 23, the high-voltage composite source has a similar architecture to the composite voltage source presented in [56]. The fundamental component and the harmonic components are generated by two independent sources and stepped up through two voltage transformers. The harmonics generated from the broadband transformer are modulated into the HV side of the fundamental step-up transformer through a coupling capacitor. This allows a low impedance path for higher order harmonics while blocking the effect of fundamental component high voltage on the harmonic voltage amplifier due to higher capacitive impedance at the fundamental frequency. As per the view of the authors, this type of test setup is highly desirable for the evaluation of instrument transformer frequency response under actual high-voltage waveform conditions.

3.3. Standards Governing MV/HV Instrument Transformer Accuracy Requirements

The IEC 61869 series of standards can be considered as the main set of international standards that govern the accuracy requirements for both voltage and current instrument transformers. Previously, IEC 61869-1:2007 [123] and IEC 61869-6:2016 [74] were provided to specify general requirements for instrument transformers and low-power instrument transformers (LPITs) separately. In the 2023 revision, these two standards were combined into a single standard, namely IEC 61869-1:2023 [124]. In terms of IVT requirements, IEC 61869-3 [115] provides additional requirements that are not provided under the general requirements in IEC 61869-1 [123]. The requirements for CVTs are provided in IEC 61869-5 [125]. Furthermore, IEC 61869-11 provides additional requirements for low-power passive voltage transformers [126]. Each subset of this series of standards provides the test procedures and practices to evaluate the instrument transformer performance and the specified accuracy limits for various measurement parameters. In addition to these standards, the IEC 61869-103 technical report provides a comprehensive evaluation of the existing instrument transformer types and their power quality parameter measurement performance [25].

The IEC 61869-103 technical report provides suggestions for classifying all types of instrument transformers into power quality measurement accuracy classes, as shown in

Table 10. Voltage ratio and phase accuracy limits for power quality measurement transducers according to IEC 61869-103 [25].

Instrument Transformer Class	Ratio Error Harmonic Frequencies		Phase Error at Harmonic Frequencies
	100 Hz ≤ f ≤ 2.5 kHz	2.5 kHz < f < 250 kHz	100 Hz ≤ f ≤ 2.5 kHz	2.5 kHz < f < 250 kHz
PQ1	±5%	±10%	$\pm 5°$	N/D
PQ2	±10%	±20%	$\pm 10°$	N/D
PQ3	N/D	N/D	N/D	N/D
PQ4	N/D	N/D	N/D	N/D

N/D: Not defined.

. The four accuracy classes are defined as PQ1, PQ2, PQ3, and PQ4. The first accuracy class (PQ1) is identified with the highest accuracy and the fourth accuracy class (PQ4) is identified with the lowest accuracy performance. However, the accuracy requirements of the PQ3 and PQ4 classes are yet to be defined.

According to the above table, the accuracy requirements for the PQ3 and PQ3 instrument transformer classes are yet to be defined.

In terms of power quality measurements, IEC 61869-3 [115] and IEC 61869-5 [125] do not provide accuracy limits or relevant test procedures to evaluate the harmonic performance of IVTs or CVTs. However, IEC 61869-6 [74] provides comprehensive details on the accuracy of LPITs for harmonic measurement for all metering transformer classes. The provided accuracy limits are categorized in three sections, as follows:

• Accuracy limits for low-frequency harmonics (shown in

  Table 11. Voltage ratio and phase accuracy limits for lower order harmonic measurements of low-power instrument transformers according to IEC 61869-6 [74].

  Accuracy Class at Rated Frequency	Ratio Error (%) Harmonic Orders					Phase Error (°) Harmonic Orders
  	2–4	5–6	7–9	10–13	13 < h	2–4	5–6	7–9	10–13
  0.1	±1%	±2%	±4%	±8%	+8% > ${\epsilon }_h$ > −100%	$\pm 1°$	$\pm 2°$	$\pm 4°$	$\pm 8°$
  0.2	±2%	±4%	±8%	±16%	+16% >${\epsilon }_h$ > −100%	$\pm 2°$	$\pm 4°$	$\pm 8°$	$\pm 16°$
  0.5	±5%	±10%	±20%	±20%	+20% >${\epsilon }_h$ > −100%	$\pm 5°$	$\pm 10°$	$\pm 20°$	$\pm 20°$
  1.0	±10%	±20%	±20%	±20%	+20% >${\epsilon }_h$ > −100%	$\pm 10°$	$\pm 20°$	$\pm 20°$	$\pm 20°$

  );

2.

Accuracy limits for low bandwidth measurements (shown in

Table 12. Voltage ratio and phase accuracy limits for low bandwidth measurements of low-power instrument transformers according to IEC 61869-6 [74].

Accuracy Class at Rated Frequency	Ratio Error (%) Harmonic Frequency Range			Phase Error (°)
	(0.1 ≤ f < 1) kHz	(1 ≤ f < 1.5) kHz	(1.5 ≤ f < 3) kHz	(0.1 ≤ f < 1) kHz	(1 ≤ f < 1.5) kHz	(1.5 ≤ f < 3) kHz
0.1	±1%	±2%	±5%	$\pm 1°$	$\pm 2°$	$\pm 5°$
0.2	±2%	±4%	±5%	$\pm 2°$	$\pm 4°$	$\pm 5°$
0.5	±5%	±10%	±10%	$\pm 5°$	$\pm 10°$	$\pm 20°$
1.0	±10%	±20%	±20%	$\pm 10°$	$\pm 20°$	$\pm 20°$

)

3.

Accuracy limits for high bandwidth measurements (shown in

Table 13. Voltage ratio and phase accuracy limits for high bandwidth measurements of low-power instrument transformers according to IEC 61869-6 [74].

Accuracy Class at Rated Frequency	Ratio Error (%) Harmonic Frequency Range			Phase Error (°)
	(0.1 ≤ f < 5) kHz	(5 ≤ f < 10) kHz	(10 ≤ f < 20) kHz	(0.1 ≤ f < 5) kHz	(5 ≤ f < 10) kHz	(10 ≤ f < 20) kHz
0.1	±1%	±2%	±5%	$\pm 1°$	$\pm 2°$	$\pm 5°$
0.2	±2%	±4%	±5%	$\pm 2°$	$\pm 4°$	$\pm 5°$
0.5	±5%	±10%	±10%	$\pm 5°$	$\pm 10°$	$\pm 20°$
1.0	±10%	±20%	±20%	$\pm 10°$	$\pm 20°$	$\pm 20°$

)

It should be noted that the above accuracy limits covering the harmonic frequency range up to 20 kHz relate only to LPITs. IEC 61000-4-30, which deals with power quality measurement techniques, does not include the accuracy of instrument transducers as a normative requirement [38].

4. Discussion

This paper provides an extensive review of the conventional and novel MV/HV/EHV instrument transducers that are used for harmonic voltage measurements, focusing on their accuracy of transformation ratio at high frequencies above 2 kHz. Furthermore, calibration systems available in the literature for characterizing instrument transformer frequency response under low-voltage signals and composite high-voltage signals representing the actual grid waveforms are investigated. Standards and techniques governing the MV/HV/EHV harmonic measurement transducers are reviewed.

Based on the surveyed literature, the findings for each transducer type can be summarized as follows:

• MV/HV/EHV IVTs, known for their cost-effectiveness, exhibit significant voltage ratio errors in the 2 kHz to 9 kHz frequency range due to internal resonances. However, proper calibration can correct these errors, enabling IVTs to be used for both harmonic amplitude and phase angle measurements.
• Generally, CVTs cannot be utilized for harmonic measurements unless special adaptation techniques, such as harmonic monitoring terminals and PQ sensors^TM (Manufactured by BVM systems, Gilford, UK), are employed. These techniques offer cost-effective solutions for employing conventional CVTs for harmonic measurement in the 2 kHz to 9 kHz frequency range.
• RVDs without internal shielding may be severely affected by stray capacitances and should not be used for harmonic measurements. However, shielded RVDs can be employed in the considered frequency range. The accuracy of RVD harmonic measurement may decrease significantly with increasing frequency and voltage rating. Hence, the voltage ratio error and phase error of the RVD should be characterized within its entire operating range.
• CVDs are suitable for harmonic amplitude measurements in the 2 kHz to 9 kHz frequency range in MV/HV/EHV networks. However, phase angle measurements of CVDs are affected by loading effects from measuring cables and instruments. These limitations are mitigated by novel techniques, such as the use of active low-voltage arms. The cost of implementation may vary depending on the specific characteristics of CVD construction.
• RCVDs are considered to be the most accurate type of instrument transformer for both harmonic amplitude and phase angle measurements in the 2 kHz to 9 kHz frequency range. However, the significant cost of implementation limits the widespread application of these devices.
• OVTs are considered as a novel instrument transducer type which provides accurate harmonic amplitude measurements in the frequency range from 2 kHz to 9 kHz, However, the working voltage of such OVTs is limited to a range of several kilovolts. This requires the use of additional voltage dividers to be combined with OVTs in order to adapt these transducers for the measurement of harmonics in MV/HV/EHV electricity networks. In such cases, it is essential to characterize these transducer frequency responses using an accurate calibration system. Similar to the RCVDs, the cost of OVT implementation is considerably higher than the conventional IVTs and CVTs, which limits their widespread application for harmonic voltage measurements.
• The accuracy characteristics of NCITs could vary significantly due to the differences in their construction principles. Therefore, it is difficult to provide generalized conclusions regarding their accuracy of harmonic measurements in the frequency range from 2 kHz to 9 kHz. Hence, it is advisable to calibrate each NCIT for their frequency response using accurate calibration systems.

In summary, details presented in this paper can be considered as a guide in the development of further studies on the harmonic measurement performance of instrument transformers and develop more accurate methods and systems. Based on the reviewed literature, the following recommendations are provided:

• A suitable standard test procedure should be developed to evaluate the high-voltage instrument transformer harmonic measurement accuracy. Manufacturers use different types of instrument transformer frequency response characterization procedures. The establishment of a standard test procedure would facilitate comparability among different manufacturers.
• There is a wide variety of test waveforms used for instrument transformer calibration. A proper specification regarding the waveform characteristics should be defined by standardization authorities similar to the test signal requirements specified at the rated fundamental frequency.
• There is a lack of suitable high-voltage sources that can generate the required composite test waveforms for the calibration of instrument transformers under realistic conditions. Further research should focus on developing new high-voltage sources that would provide wideband high-voltage waveforms.
• Investigation of external influencing factors on instrument transformer frequency response has not been consolidated properly. The investigation of these parameters should be combined into a standard test procedure which should be defined in agreement with the equipment manufacturers, national metrological laboratories, and standardization authorities.
• National metrological laboratories should focus on the development of suitable reference transducers that could provide traceable calibrations for high-voltage harmonic measurements under realistic distorted test waveforms.
• The international standards covering the harmonic measurements in the frequency range from 2 kHz to 150 kHz are not properly consolidated. Most of the requirements are provided on an informative basis. However, with the increasing use of power electronic converters which contribute to high-frequency harmonic emissions, proper definitions of measurement techniques will be required for inclusion as essential requirements.