Achievements and Prospects of Molecular Dynamics Simulations in Thermofluid Sciences
Abstract
1. Introduction
2. Physical Modelling of Heat Transfer Phenomena in MD Simulations
2.1. Fundamentals of MD Approach
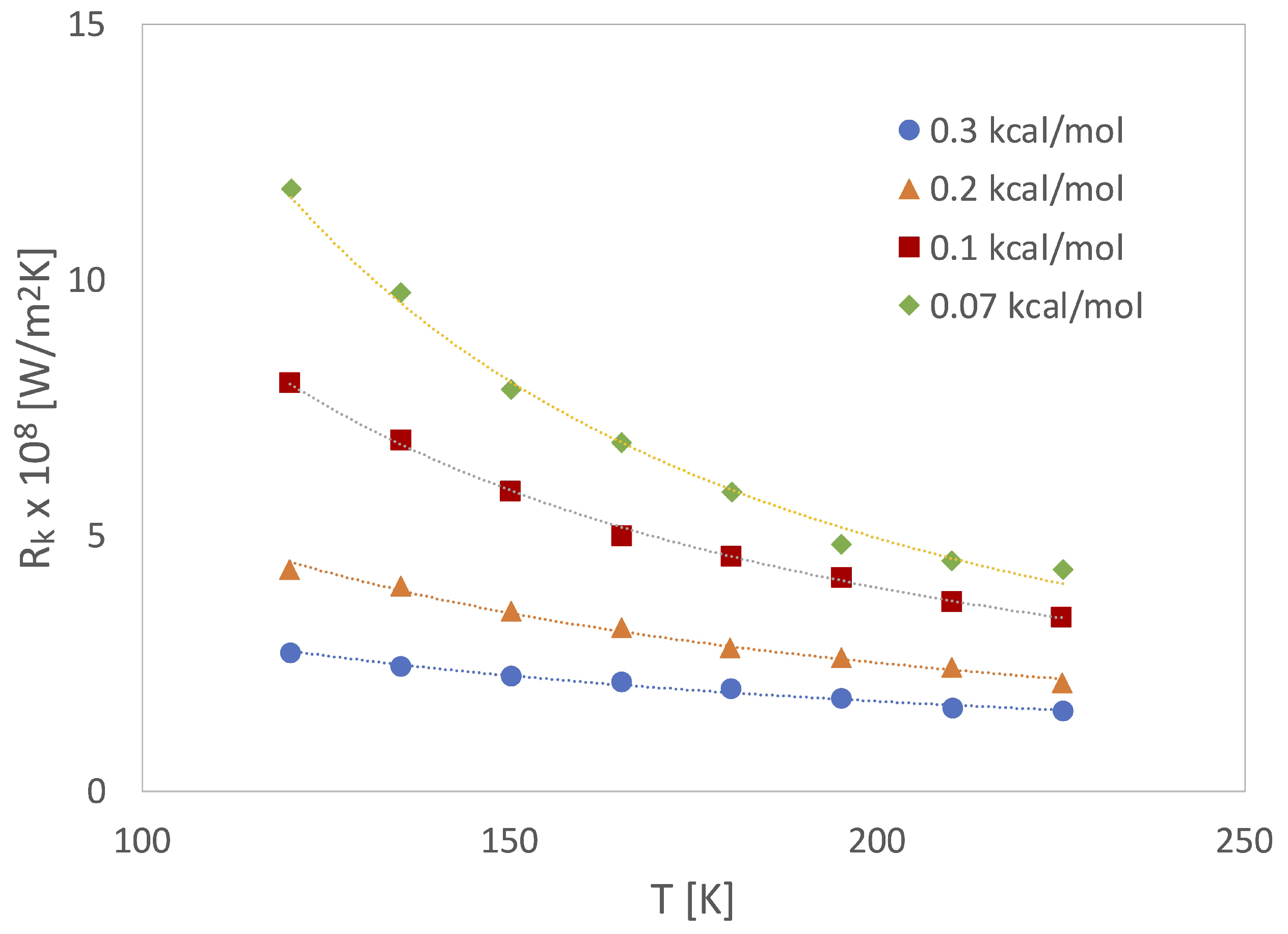
2.2. Heat Flux and Thermal Conductivity
2.3. Interface Behaviours in MD Simulations
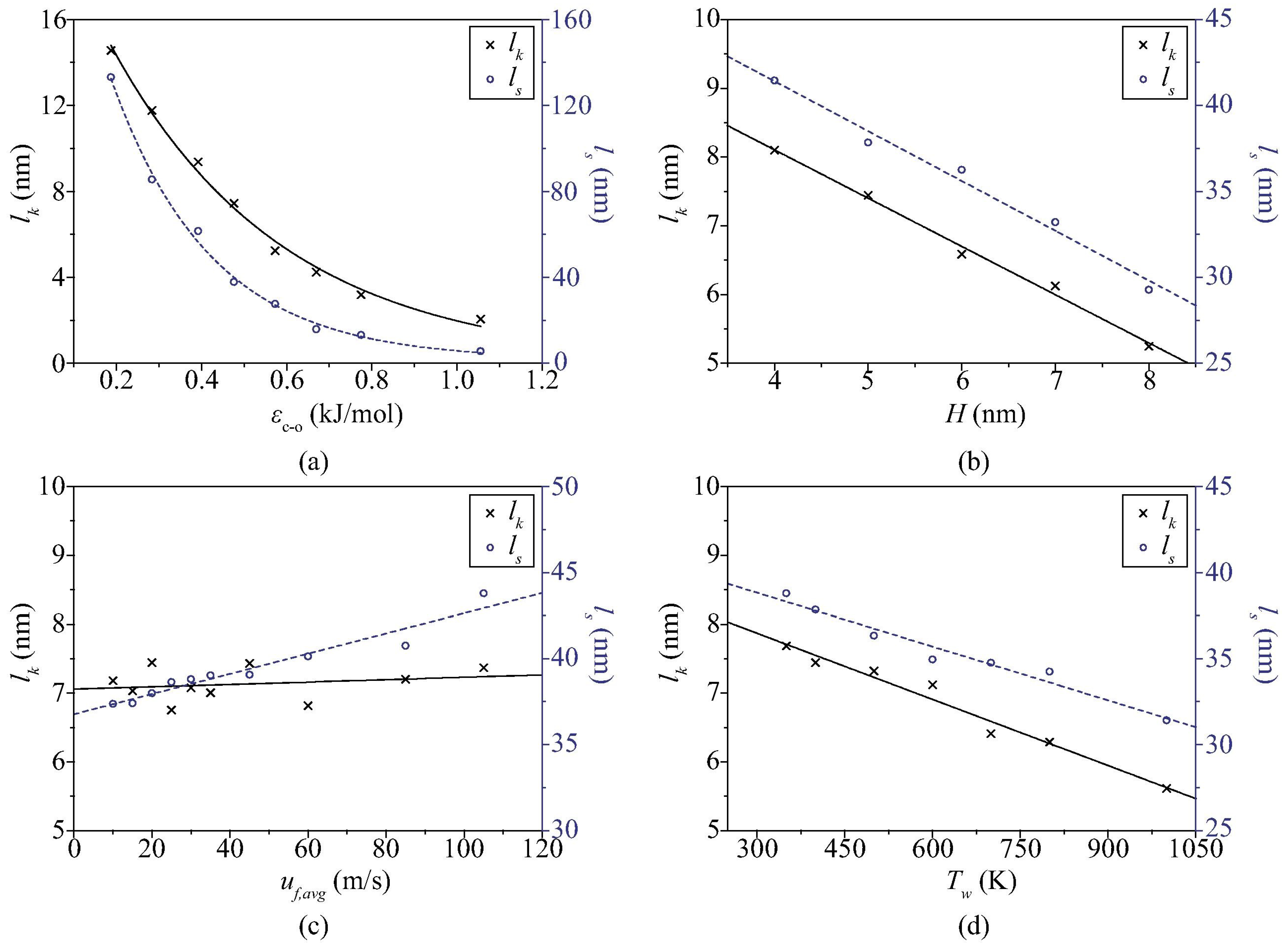
2.3.1. Hydrodynamic and Thermal Wall Slip
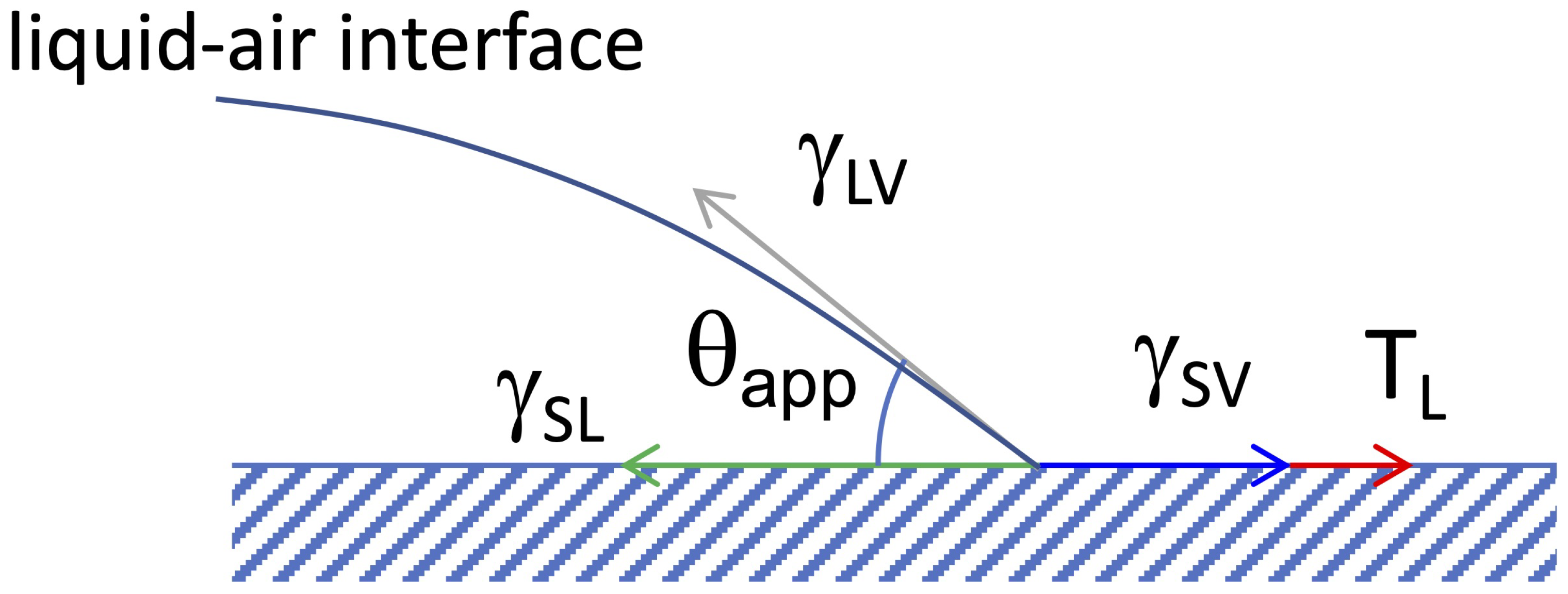
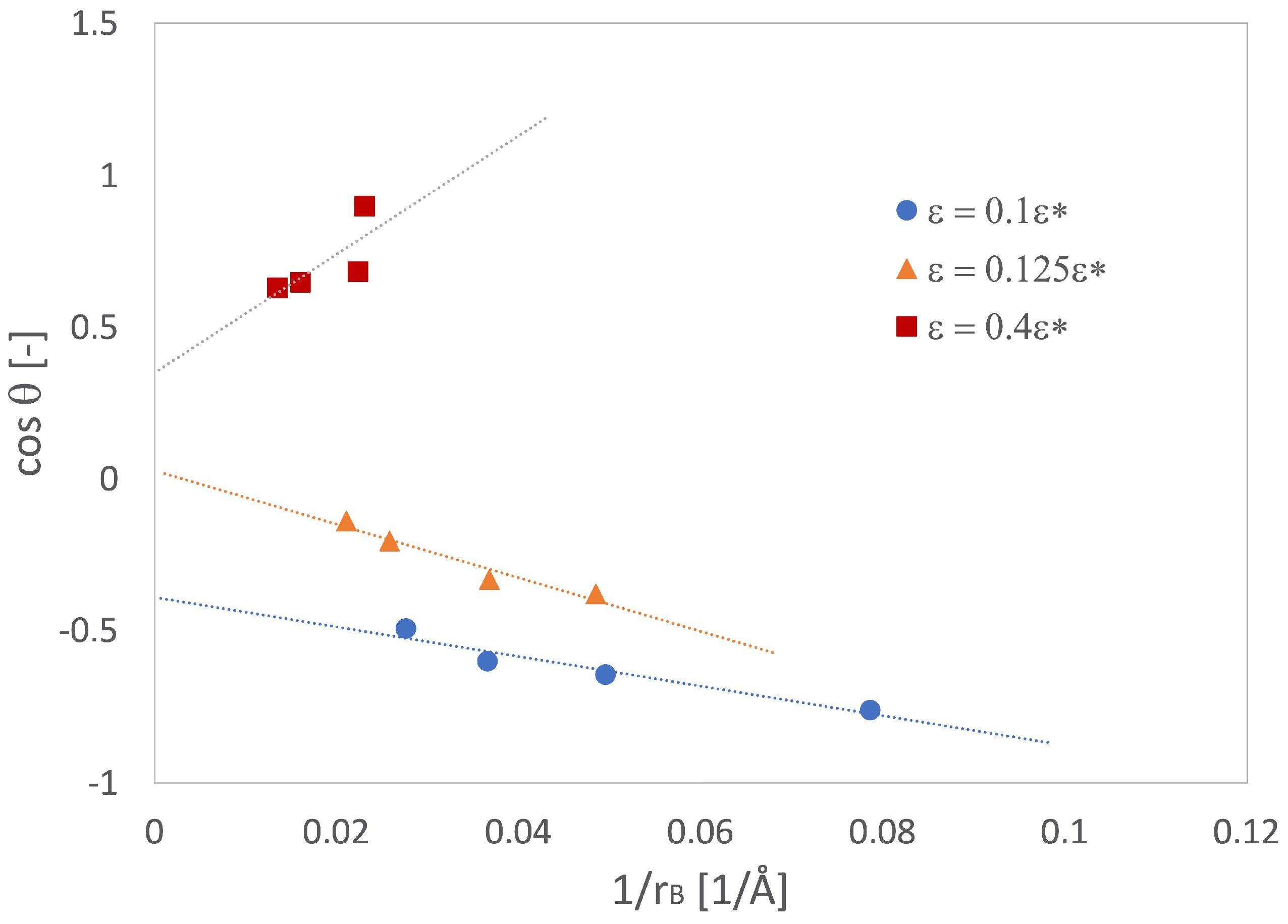
2.3.2. Wetting on Solid-Liquid Interfaces
2.4. Phase Change Phenomena in MD Simulations
2.4.1. Bubble Nucleation and Boiling
2.4.2. Evaporation
2.4.3. Effects of Surface Roughness
2.4.4. Condensation
3. Fluid Flow and Heat Transfer in Nanochannels by MD Simulations
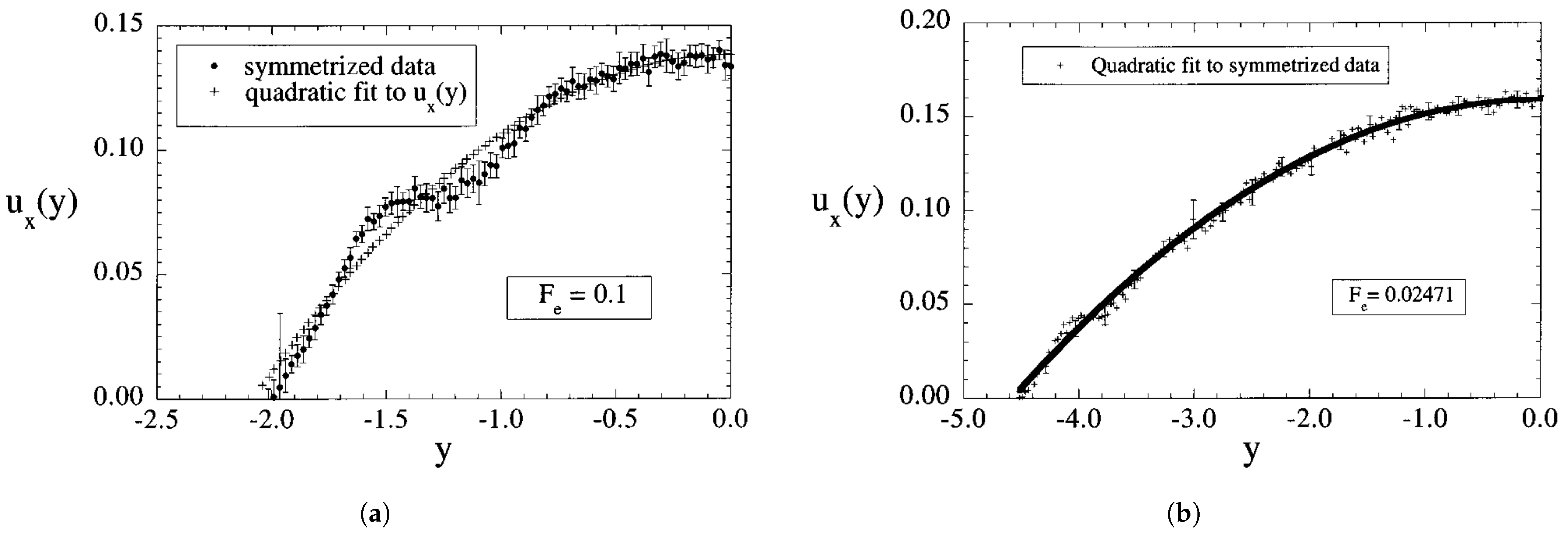
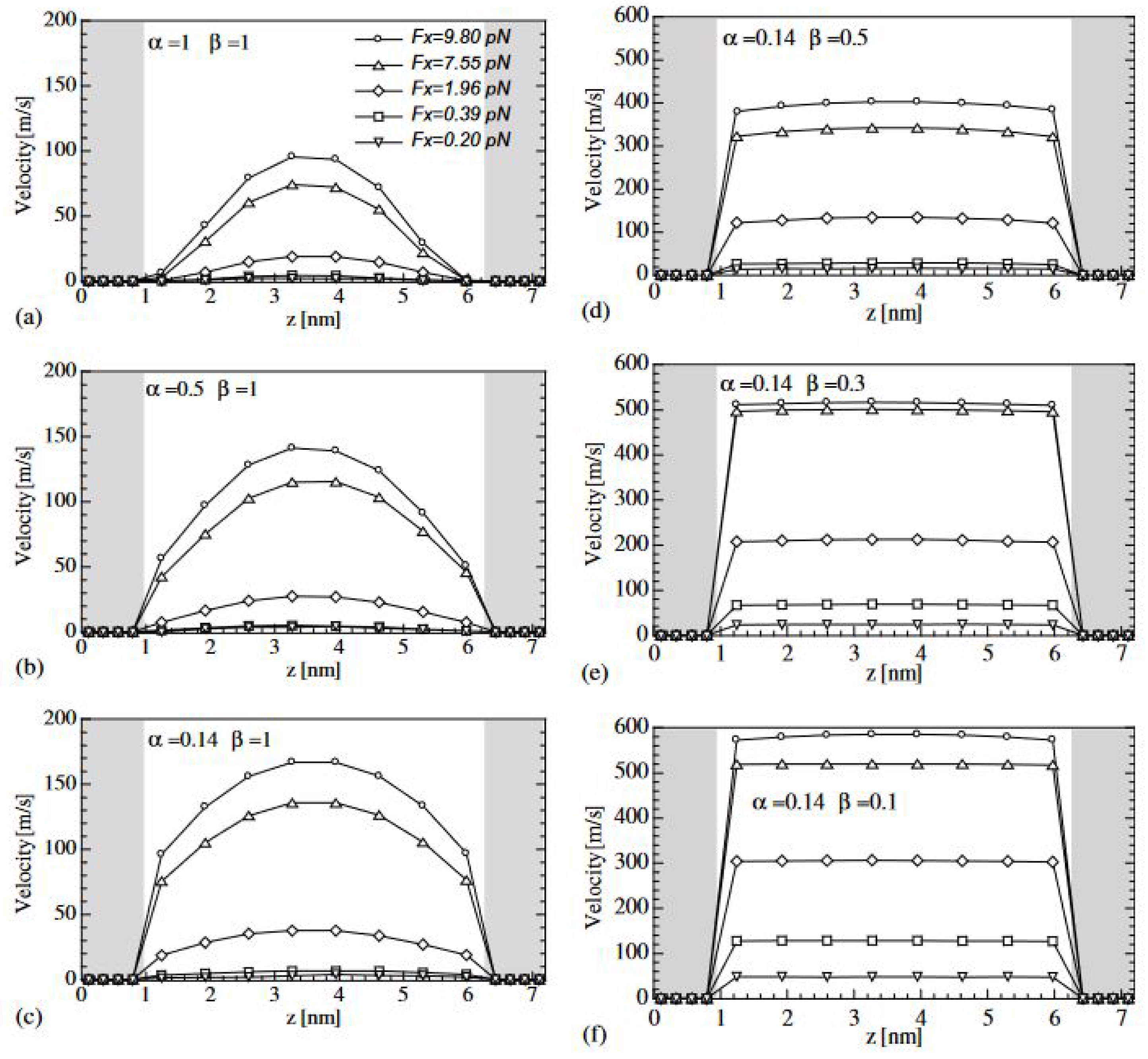
3.1. Adiabatic Flow in Nanochannels
3.2. Convective Heat Transfer in Nanochannels
3.3. Two Phase Flow in Nanochannels
4. Challenges and Scope for Future Studies
- Bridging the gap between molecular-level insights and macroscopic behavior through the integration of MD simulations with other computational techniques;
- The design of nanoscale heat exchangers, lab-on-a-chip devices, and the development of advanced thermal materials;
- Meeting the demand for increased computational resources to simulate larger and more complex systems;
- Improving intermolecular potentials for specific substances and conditions, especially in the area of life sciences, will enhance the accuracy of simulations.
- Developing suitable potentials to model the interactions between fluids and walls with complex molecular structure (e.g., polymer materials).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abgrall, P.; Nguyen, N.T. Nanofluidic devices and their applications. Anal. Chem. 2008, 80, 2326–2341. [Google Scholar] [CrossRef] [PubMed]
- Duan, C.; Wang, W.; Xie, Q. Fabrication of nanofluidic devices. Biomicrofluidics 2013, 7, 26501. [Google Scholar] [CrossRef] [PubMed]
- Gad-el Hak, M. MEMS: Introduction and Fundamentals; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Goh, P.; Ismail, A.; Ng, B. Carbon nanotubes for desalination: Performance evaluation and current hurdles. Desalination 2013, 308, 2–14. [Google Scholar] [CrossRef]
- Bhirde, A.A.; Patel, V.; Gavard, J.; Zhang, G.; Sousa, A.A.; Masedunskas, A.; Leapman, R.D.; Weigert, R.; Gutkind, J.S.; Rusling, J.F. Targeted killing of cancer cells in vivo and in vitro with EGF-directed carbon nanotube-based drug delivery. ACS Nano 2009, 3, 307–316. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Lee, I.; Jeon, T.J.; Kim, S.M. Micro-/nanofluidic device for tunable generation of a concentration gradient: Application to Caenorhabditis elegans chemotaxis. Anal. Bioanal. Chem. 2014, 406, 2679–2686. [Google Scholar] [CrossRef] [PubMed]
- Dror, R.O.; Dirks, R.M.; Grossman, J.; Xu, H.; Shaw, D.E. Biomolecular simulation: A computational microscope for molecular biology. Annu. Rev. Biophys. 2012, 41, 429–452. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Leach, A.R. Molecular Modelling: Principles and Applications; Pearson Education: London, UK, 2001. [Google Scholar]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Hockney, R.W.; Eastwood, J.W. Computer Simulation Using Particles; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Alder, B.J.; Wainwright, T.E. Phase transition for a hard sphere system. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef]
- Gibson, J.; Goland, A.N.; Milgram, M.; Vineyard, G. Dynamics of radiation damage. Phys. Rev. 1960, 120, 1229. [Google Scholar] [CrossRef]
- Rahman, A. Correlations in the motion of atoms in liquid argon. Phys. Rev. 1964, 136, A405. [Google Scholar] [CrossRef]
- Steinfeld, J.I.; Francisco, J.S.; Hase, W.L. Chemical Kinetics and Dynamics; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Andersen, M.; Panosetti, C.; Reuter, R. A Practical Guide to Surface Kinetic Monte Carlo Simulations. Front. Chem. 2019, 7, 202. [Google Scholar] [CrossRef]
- Bagayoko, D. Understanding density functional theory (DFT) and completing it in practice. AIP Adv. 2014, 4, 127104. [Google Scholar] [CrossRef]
- Casida, M.E.; Huix-Rotllant, M. Many-Body Perturbation Theory (MBPT) and Time-Dependent Density-Functional Theory (TD-DFT): MBPT Insights About What Is Missing In, and Corrections To, the TD-DFT Adiabatic Approximation. In Density-Functional Methods for Excited States; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–60. [Google Scholar] [CrossRef]
- Allen, M.P. Introduction to molecular dynamics simulation. Comput. Soft Matter Synth. Polym. Proteins 2004, 23, 1–28. [Google Scholar]
- Haile, J.M. Molecular Dynamics Simulation: Elementary Methods; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1992. [Google Scholar]
- Maruyama, S. Molecular dynamics method for microscale heat transfer. In Advances in Numerical Heat Transfer, Volume 2; CRC Press: Boca Raton, FL, USA, 2018; pp. 189–226. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms To Applications; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Kalweit, M.; Drikakis, D. Coupling strategies for hybrid molecular—Continuum simulation methods. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2008, 222, 797–806. [Google Scholar] [CrossRef]
- Semiromi, D.T.; Azimian, A. Molecular dynamics simulation of annular flow boiling with the modified Lennard-Jones potential function. Heat Mass Transf. 2012, 48, 141–152. [Google Scholar] [CrossRef]
- Dong, T.; Yang, Z.; Wu, H. Molecular simulations of R141b boiling flow in micro/nano channel: Interfacial phenomena. Energy Convers. Manag. 2006, 47, 2178–2191. [Google Scholar] [CrossRef]
- Long, L.N.; Micci, M.M.; Wong, B.C. Molecular dynamics simulations of droplet evaporation. Comput. Phys. Commun. 1996, 96, 167–172. [Google Scholar] [CrossRef]
- Lukes, J.R.; Li, D.; Liang, X.G.; Tien, C.L. Molecular dynamics study of solid thin-film thermal conductivity. J. Heat Transf. 2000, 122, 536–543. [Google Scholar] [CrossRef][Green Version]
- Matsumoto, M.; Wakabayashi, H.; Makino, T. Thermal resistance of crystal interface: Molecular dynamics simulation. Heat-Transf. Asian Res. Spons. Soc. Chem. Eng. Jpn. Heat Transf. Div. ASME 2005, 34, 135–146. [Google Scholar] [CrossRef]
- Maroo, S.C.; Chung, J. A novel fluid–wall heat transfer model for molecular dynamics simulations. J. Nanoparticle Res. 2010, 12, 1913–1924. [Google Scholar] [CrossRef]
- Ji, C.; Yan, Y. A molecular dynamics simulation of liquid–vapour–solid system near triple-phase contact line of flow boiling in a microchannel. Appl. Therm. Eng. 2008, 28, 195–202. [Google Scholar] [CrossRef][Green Version]
- Consolini, L.; Aggarwal, S.K.; Murad, S. A molecular dynamics simulation of droplet evaporation. Int. J. Heat Mass Transf. 2003, 46, 3179–3188. [Google Scholar] [CrossRef]
- Røsjorde, A.; Fossmo, D.; Bedeaux, D.; Kjelstrup, S.; Hafskjold, B. Nonequilibrium molecular dynamics simulations of steady-state heat and mass transport in condensation: I. Local equilibrium. J. Colloid Interface Sci. 2000, 232, 178–185. [Google Scholar] [CrossRef]
- Røsjorde, A.; Kjelstrup, S.; Bedeaux, D.; Hafskjold, B. Nonequilibrium molecular dynamics simulations of steady-state heat and mass transport in condensation. II. Transfer coefficients. J. Colloid Interface Sci. 2001, 240, 355–364. [Google Scholar] [CrossRef]
- Maroo, S.C.; Chung, J. Molecular dynamic simulation of platinum heater and associated nano-scale liquid argon film evaporation and colloidal adsorption characteristics. J. Colloid Interface Sci. 2008, 328, 134–146. [Google Scholar] [CrossRef]
- Nagayama, G.; Tsuruta, T.; Cheng, P. Molecular dynamics simulation on bubble formation in a nanochannel. Int. J. Heat Mass Transf. 2006, 49, 4437–4443. [Google Scholar] [CrossRef]
- Fu, T.; Mao, Y.; Tang, Y.; Zhang, Y.; Yuan, W. Effect of nanostructure on rapid boiling of water on a hot copper plate: A molecular dynamics study. Heat Mass Transf. 2016, 52, 1469–1478. [Google Scholar] [CrossRef]
- Xue, L.; Keblinski, P.; Phillpot, S.; Choi, S.S.; Eastman, J. Two regimes of thermal resistance at a liquid–solid interface. J. Chem. Phys. 2003, 118, 337–339. [Google Scholar] [CrossRef]
- Wang, Y.H.; Wang, S.Y.; Lu, G.; Wang, X.D. Explosive boiling of nano-liquid argon films on high temperature platinum walls: Effects of surface wettability and film thickness. Int. J. Therm. Sci. 2018, 132, 610–617. [Google Scholar] [CrossRef]
- Barrat, J.L.; Bocquet, L. Influence of wetting properties on hydrodynamic boundary conditions at a fluid/solid interface. Faraday Discuss. 1999, 112, 119–128. [Google Scholar] [CrossRef]
- Markvoort, A.J.; Hilbers, P.; Nedea, S. Molecular dynamics study of the influence of wall-gas interactions on heat flow in nanochannels. Phys. Rev. E 2005, 71, 066702. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.C. Effects of surface roughness and interface wettability on nanoscale flow in a nanochannel. Microfluid. Nanofluid. 2006, 2, 501–511. [Google Scholar] [CrossRef]
- Inaoka, H.; Ito, N. Numerical simulation of pool boiling of a Lennard-Jones liquid. Phys. A Stat. Mech. Its Appl. 2013, 392, 3863–3868. [Google Scholar] [CrossRef]
- Wu. A molecular dynamics simulation of bubble nucleation in homogeneous liquid under heating with constant mean negative pressure. Microscale Thermophys. Eng. 2003, 7, 137–151. [Google Scholar] [CrossRef]
- Kinjo, T.; Matsumoto, M. Cavitation processes and negative pressure. Fluid Phase Equilibria 1998, 144, 343–350. [Google Scholar] [CrossRef]
- Yamamoto, T.; Matsumoto, M. Initial stage of nucleate boiling: Molecular dynamics investigation. J. Therm. Sci. Technol. 2012, 7, 334–349. [Google Scholar] [CrossRef]
- Hens, A.; Agarwal, R.; Biswas, G. Nanoscale study of boiling and evaporation in a liquid Ar film on a Pt heater using molecular dynamics simulation. Int. J. Heat Mass Transf. 2014, 71, 303–312. [Google Scholar] [CrossRef]
- Sumardiono, S.; Fischer, J. Molecular simulations of droplet evaporation processes: Adiabatic pressure jump evaporation. Int. J. Heat Mass Transf. 2006, 49, 1148–1161. [Google Scholar] [CrossRef][Green Version]
- Niu, D.; Tang, G. The effect of surface wettability on water vapor condensation in nanoscale. Sci. Rep. 2016, 6, 19192. [Google Scholar] [CrossRef]
- Sheng, Q.; Sun, J.; Wang, Q.; Wang, W.; Wang, H.S. On the onset of surface condensation: Formation and transition mechanisms of condensation mode. Sci. Rep. 2016, 6, 30764. [Google Scholar] [CrossRef] [PubMed]
- Gu, K.; Watkins, C.B.; Koplik, J. Molecular dynamics simulation of the equilibrium liquid–vapor interphase with solidification. Fluid Phase Equilibria 2010, 297, 77–89. [Google Scholar] [CrossRef]
- Fujinaga, T.; Shibuta, Y. Molecular dynamics simulation of athermal heterogeneous nucleation of solidification. Comput. Mater. Sci. 2019, 164, 74–81. [Google Scholar] [CrossRef]
- Cui, S.; Cummings, P.; Cochran, H. Molecular simulation of the transition from liquidlike to solidlike behavior in complex fluids confined to nanoscale gaps. J. Chem. Phys. 2001, 114, 7189–7195. [Google Scholar] [CrossRef]
- Geiser, J. Coupled Navier–Stokes molecular dynamics simulation: Theory and applications based on iterative operator-splitting methods. Comput. Fluids 2013, 77, 97–111. [Google Scholar] [CrossRef]
- Asproulis, N.; Drikakis, D. An artificial neural network-based multiscale method for hybrid atomistic-continuum simulations. Microfluid. Nanofluid. 2013, 15, 559–574. [Google Scholar] [CrossRef]
- Werder, T.; Walther, J.H.; Koumoutsakos, P. Hybrid atomistic–continuum method for the simulation of dense fluid flows. J. Comput. Phys. 2005, 205, 373–390. [Google Scholar] [CrossRef]
- Stephenson, D.; Lockerby, D.A.; Borg, M.K.; Reese, J.M. Multiscale simulation of nanofluidic networks of arbitrary complexity. Microfluid. Nanofluid. 2015, 18, 841–858. [Google Scholar] [CrossRef]
- Borg, M.K.; Lockerby, D.A.; Reese, J.M. A hybrid molecular–continuum method for unsteady compressible multiscale flows. J. Fluid Mech. 2015, 768, 388–414. [Google Scholar] [CrossRef]
- Holland, D.M.; Lockerby, D.A.; Borg, M.K.; Nicholls, W.D.; Reese, J.M. Molecular dynamics pre-simulations for nanoscale computational fluid dynamics. Microfluid. Nanofluid. 2015, 18, 461–474. [Google Scholar] [CrossRef]
- Bertola, V.; Cafaro, E. On the speed of heat. Phys. Lett. Sect. Gen. At. Solid State Phys. 2007, 372, 1–4. [Google Scholar] [CrossRef]
- Lu, W.Q.; Fan, Q.M. Study for the particle’s scale effect on some thermophysical properties of nanofluids by a simplified molecular dynamics method. Eng. Anal. Bound. Elem. 2008, 32, 282–289. [Google Scholar] [CrossRef]
- Tuckerman, M.E. Statistical Mechanics: Theory and Molecular Simulation; Oxford University Press: Oxford, UK, 2023. [Google Scholar]
- Müller-Plathe, F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity. J. Chem. Phys. 1997, 106, 6082–6085. [Google Scholar] [CrossRef]
- Schneider, T.; Stoll, E. Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions. Phys. Rev. B 1978, 17, 1302. [Google Scholar] [CrossRef]
- Schelling, P.; Phillpot, S.; Keblinski, P. Phonon wave-packet dynamics at semiconductor interfaces by molecular-dynamics simulation. Appl. Phys. Lett. 2002, 80, 2484–2486. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Yezdimer, E.M.; Chialvo, A.A.; Cummings, P.T. Examination of chain length effects on the solubility of alkanes in near-critical and supercritical aqueous solutions. J. Phys. Chem. B 2001, 105, 841–847. [Google Scholar] [CrossRef]
- Delhommelle, J.; Millié, P. Inadequacy of the Lorentz-Berthelot combining rules for accurate predictions of equilibrium properties by molecular simulation. Mol. Phys. 2001, 99, 619–625. [Google Scholar] [CrossRef]
- Wang, C.; Chen, J.; Shiomi, J.; Maruyama, S. A study on the thermal resistance over solid–liquid–vapor interfaces in a finite-space by a molecular dynamics method. Int. J. Therm. Sci. 2007, 46, 1203–1210. [Google Scholar] [CrossRef]
- Ohara, T. Contribution of intermolecular energy transfer to heat conduction in a simple liquid. J. Chem. Phys. 1999, 111, 9667–9672. [Google Scholar] [CrossRef]
- Chen, Y.; Zou, Y.; Sun, D.; Wang, Y.; Yu, B. Molecular dynamics simulation of bubble nucleation on nanostructure surface. Int. J. Heat Mass Transf. 2018, 118, 1143–1151. [Google Scholar] [CrossRef]
- Reza Seyf, H.; Zhang, Y. Molecular dynamics simulation of normal and explosive boiling on nanostructured surface. J. Heat Transf. 2013, 135, 121503. [Google Scholar] [CrossRef]
- Sun, C.; Lu, W.Q.; Liu, J.; Bai, B. Molecular dynamics simulation of nanofluid’s effective thermal conductivity in high-shear-rate Couette flow. Int. J. Heat Mass Transf. 2011, 54, 2560–2567. [Google Scholar] [CrossRef]
- Toghraie, D.; Mokhtari, M.; Afrand, M. Molecular dynamic simulation of copper and platinum nanoparticles Poiseuille flow in a nanochannels. Phys. E -Low-Dimens. Syst. Nanostruct. 2016, 84, 152–161. [Google Scholar] [CrossRef]
- Jónsson, E.Ö.; Rasti, S.; Galynska, M.; Meyer, J.; Jónsson, H. Transferable Potential Function for Flexible H2O Molecules Based on the Single-Center Multipole Expansion. J. Chem. Theory Comput. 2022, 18, 7528–7543. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.; Liakopoulos, A. Transport properties of liquid argon in krypton nanochannels: Anisotropy and non-homogeneity introduced by the solid walls. Int. J. Heat Mass Transf. 2009, 52, 735–743. [Google Scholar] [CrossRef]
- Hu, H.; Sun, Y. Effect of nanopatterns on Kapitza resistance at a water-gold interface during boiling: A molecular dynamics study. J. Appl. Phys. 2012, 112. [Google Scholar] [CrossRef]
- Ghorbanian, J.; Beskok, A. Scale effects in nano-channel liquid flows. Microfluid. Nanofluid. 2016, 20, 1–11. [Google Scholar] [CrossRef]
- Al-Matar, A.K.; Rockstraw, D.A. A generating equation for mixing rules and two new mixing rules for interatomic potential energy parameters. J. Comput. Chem. 2004, 25, 660–668. [Google Scholar] [CrossRef]
- Thomas, J.A.; McGaughey, A.J.; Kuter-Arnebeck, O. Pressure-driven water flow through carbon nanotubes: Insights from molecular dynamics simulation. Int. J. Therm. Sci. 2010, 49, 281–289. [Google Scholar] [CrossRef]
- Thomas, J.A.; McGaughey, A.J. Reassessing fast water transport through carbon nanotubes. Nano Lett. 2008, 8, 2788–2793. [Google Scholar] [CrossRef]
- Alosious, S.; Kannam, S.K.; Sathian, S.P.; Todd, B. Nanoconfinement effects on the kapitza resistance at water–cnt interfaces. Langmuir 2021, 37, 2355–2361. [Google Scholar] [CrossRef]
- Hafskjold, B.; Ikeshoji, T.; Ratkje, S.K. On the molecular mechanism of thermal diffusion in liquids. Mol. Phys. 1993, 80, 1389–1412. [Google Scholar] [CrossRef]
- Ikeshoji, T.; Hafskjold, B. Non-equilibrium molecular dynamics calculation of heat conduction in liquid and through liquid-gas interface. Mol. Phys. 1994, 81, 251–261. [Google Scholar] [CrossRef]
- Irving, J.; Kirkwood, J.G. The statistical mechanical theory of transport processes. IV. The equations of hydrodynamics. J. Chem. Phys. 1950, 18, 817–829. [Google Scholar] [CrossRef]
- Tokumasu, T.; Ohara, T.; Kamijo, K. Effect of molecular elongation on the thermal conductivity of diatomic liquids. J. Chem. Phys. 2003, 118, 3677–3685. [Google Scholar] [CrossRef]
- Kim, B.H.; Beskok, A.; Cagin, T. Thermal interactions in nanoscale fluid flow: Molecular dynamics simulations with solid–liquid interfaces. Microfluid. Nanofluid. 2008, 5, 551–559. [Google Scholar] [CrossRef]
- Barrat, J.L.; Chiaruttini, F. Kapitza resistance at the liquid–solid interface. Mol. Phys. 2003, 101, 1605–1610. [Google Scholar] [CrossRef]
- Sarode, A.; Ahmed, Z.; Basarkar, P.; Bhargav, A.; Banerjee, D. Role of carbon nanotube on the interfacial thermal resistance: A molecular dynamics approach. In Proceedings of the 2017 16th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Orlando, FL, USA, 30 May–2 June 2017; pp. 352–356. [Google Scholar]
- Lautenschlaeger, M.P.; Hasse, H. Thermal, caloric and transport properties of the Lennard–Jones truncated and shifted fluid in the adsorbed layers at dispersive solid walls. Mol. Phys. 2020, 118, e1669838. [Google Scholar] [CrossRef]
- de Gennes, P.G. On fluid/wall slippage. Langmuir 2002, 18, 3413–3414. [Google Scholar] [CrossRef]
- Bonaccurso, E.; Kappl, M.; Butt, H.J. Hydrodynamic force measurements: Boundary slip of water on hydrophilic surfaces and electrokinetic effects. Phys. Rev. Lett. 2002, 88, 076103. [Google Scholar] [CrossRef] [PubMed]
- Bonaccurso, E.; Butt, H.J.; Craig, V.S. Surface roughness and hydrodynamic boundary slip of a Newtonian fluid in a completely wetting system. Phys. Rev. Lett. 2003, 90, 144501. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Granick, S. Limits of the hydrodynamic no-slip boundary condition. Phys. Rev. Lett. 2002, 88, 106102. [Google Scholar] [CrossRef] [PubMed]
- Craig, V.S.; Neto, C.; Williams, D.R. Shear-dependent boundary slip in an aqueous Newtonian liquid. Phys. Rev. Lett. 2001, 87, 054504. [Google Scholar] [CrossRef] [PubMed]
- Thompson, P.A.; Troian, S.M. A general boundary condition for liquid flow at solid surfaces. Nature 1997, 389, 360–362. [Google Scholar] [CrossRef]
- Sendner, C.; Horinek, D.; Bocquet, L.; Netz, R.R. Interfacial water at hydrophobic and hydrophilic surfaces: Slip, viscosity, and diffusion. Langmuir 2009, 25, 10768–10781. [Google Scholar] [CrossRef]
- Vinogradova, O.I.; Belyaev, A.V. Wetting, roughness and flow boundary conditions. J. Phys. Condens. Matter 2011, 23, 184104. [Google Scholar] [CrossRef]
- Cieplak, M.; Koplik, J.; Banavar, J.R. Boundary conditions at a fluid-solid interface. Phys. Rev. Lett. 2001, 86, 803. [Google Scholar] [CrossRef]
- Ohara, T.; Torii, D. Molecular dynamics study of thermal phenomena in an ultrathin liquid film sheared between solid surfaces: The influence of the crystal plane on energy and momentum transfer at solid-liquid interfaces. J. Chem. Phys. 2005, 122, 214717. [Google Scholar] [CrossRef]
- Torii, D.; Ohara, T.; Ishida, K. Molecular-scale mechanism of thermal resistance at the solid-liquid interfaces: Influence of interaction parameters between solid and liquid molecules. J. Heat Transf. 2010, 132, 1–9. [Google Scholar] [CrossRef]
- Dinh, Q.V.; Vo, T.Q.; Kim, B. Viscous heating and temperature profiles of liquid water flows in copper nanochannel. J. Mech. Sci. Technol. 2019, 33, 3257–3263. [Google Scholar] [CrossRef]
- Koplik, J.; Banavar, J.R.; Willemsen, J.F. Molecular dynamics of fluid flow at solid surfaces. Phys. Fluids A Fluid Dyn. 1989, 1, 781–794. [Google Scholar] [CrossRef]
- Bitsanis, I.; Somers, S.A.; Davis, H.T.; Tirrell, M. Microscopic dynamics of flow in molecularly narrow pores. J. Chem. Phys. 1990, 93, 3427–3431. [Google Scholar] [CrossRef]
- Thompson, P.A.; Robbins, M.O. Simulations of contact-line motion: Slip and the dynamic contact angle. Phys. Rev. Lett. 1989, 63, 766. [Google Scholar] [CrossRef] [PubMed]
- Thompson, P.A.; Robbins, M.O. Shear flow near solids: Epitaxial order and flow boundary conditions. Phys. Rev. A 1990, 41, 6830. [Google Scholar] [CrossRef] [PubMed]
- Thompson, P.A.; Grest, G.S.; Robbins, M.O. Phase transitions and universal dynamics in confined films. Phys. Rev. Lett. 1992, 68, 3448. [Google Scholar] [CrossRef] [PubMed]
- Somers, S.A.; Davis, H.T. Microscopic dynamics of fluids confined between smooth and atomically structured solid surfaces. J. Chem. Phys. 1992, 96, 5389–5407. [Google Scholar] [CrossRef]
- Gupta, S.; Cochran, H.; Cummings, P. Shear behavior of squalane and tetracosane under extreme confinement. I. Model, simulation method, and interfacial slip. J. Chem. Phys. 1997, 107, 10316–10326. [Google Scholar] [CrossRef][Green Version]
- Gupta, S.; Cochran, H.; Cummings, P. Shear behavior of squalane and tetracosane under extreme confinement. II. Confined film structure. J. Chem. Phys. 1997, 107, 10327–10334. [Google Scholar] [CrossRef][Green Version]
- Gupta, S.; Cochran, H.; Cummings, P. Shear behavior of squalane and tetracosane under extreme confinement. III. Effect of confinement on viscosity. J. Chem. Phys. 1997, 107, 10335–10343. [Google Scholar] [CrossRef][Green Version]
- Jabbarzadeh, A.; Atkinson, J.; Tanner, R. Rheological properties of thin liquid films by molecular dynamics simulations. J. Non-Newton. Fluid Mech. 1997, 69, 169–193. [Google Scholar] [CrossRef]
- Jabbarzadeh, A.; Atkinson, J.; Tanner, R. Effect of the wall roughness on slip and rheological properties of hexadecane in molecular dynamics simulation of Couette shear flow between two sinusoidal walls. Phys. Rev. E 2000, 61, 690. [Google Scholar] [CrossRef]
- Khare, R.; De Pablo, J.; Yethiraj, A. Molecular simulation and continuum mechanics study of simple fluids in non-isothermal planar couette flows. J. Chem. Phys. 1997, 107, 2589–2596. [Google Scholar] [CrossRef]
- Heinbuch, U.; Fischer, J. Liquid flow in pores: Slip, no-slip, or multilayer sticking. Phys. Rev. A 1989, 40, 1144. [Google Scholar] [CrossRef]
- Todd, B.; Evans, D.J. The heat flux vector for highly inhomogeneous nonequilibrium fluids in very narrow pores. J. Chem. Phys. 1995, 103, 9804–9809. [Google Scholar] [CrossRef]
- Ziarani, A.; Mohamad, A. A molecular dynamics study of perturbed Poiseuille flow in a nanochannel. Microfluid. Nanofluid. 2006, 2, 12–20. [Google Scholar] [CrossRef]
- Gao, J.; Luedtke, W.; Landman, U. Structures, solvation forces and shear of molecular films in a rough nano-confinement. Tribol. Lett. 2000, 9, 3–13. [Google Scholar] [CrossRef]
- Churaev, N.; Sobolev, V.; Somov, A. Slippage of liquids over lyophobic solid surfaces. J. Colloid Interface Sci. 1984, 97, 574–581. [Google Scholar] [CrossRef]
- Zhu, Y.; Granick, S. Rate-dependent slip of Newtonian liquid at smooth surfaces. Phys. Rev. Lett. 2001, 87, 096105. [Google Scholar] [CrossRef]
- Robbins, M.O.; Müser, M.H. Computer Simulations of Friction, Lubrication, and Wear. In Modern Tribology Handbook, Two Volume Set; CRC Press: Boca Raton, FL, USA, 2000; pp. 747–796. [Google Scholar]
- Barrat, J.L.; Bocquet, L. Large slip effect at a nonwetting fluid-solid interface. Phys. Rev. Lett. 1999, 82, 4671. [Google Scholar] [CrossRef]
- Heslot, F.; Fraysse, N.; Cazabat, A. Molecular layering in the spreading of wetting liquid drops. Nature 1989, 338, 640–642. [Google Scholar] [CrossRef]
- Cheng, L.; Fenter, P.; Nagy, K.; Schlegel, M.; Sturchio, N. Molecular-scale density oscillations in water adjacent to a mica surface. Phys. Rev. Lett. 2001, 87, 156103. [Google Scholar] [CrossRef] [PubMed]
- Heier, M.; Diewald, F.; Horsch, M.T.; Langenbach, K.; Müller, R.; Hasse, H. Molecular dynamics study of adsorption of the Lennard-Jones truncated and shifted fluid on planar walls. J. Chem. Eng. Data 2018, 64, 386–394. [Google Scholar] [CrossRef]
- Heier, M.; Stephan, S.; Diewald, F.; Müller, R.; Langenbach, K.; Hasse, H. Molecular dynamics study of wetting and adsorption of binary mixtures of the Lennard-Jones truncated and shifted fluid on a planar wall. Langmuir 2021, 37, 7405–7419. [Google Scholar] [CrossRef] [PubMed]
- Akkus, Y.; Nguyen, C.T.; Celebi, A.T.; Beskok, A. A first look at the performance of nano-grooved heat pipes. Int. J. Heat Mass Transf. 2019, 132, 280–287. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Barisik, M.; Kim, B. Wetting of chemically heterogeneous striped surfaces: Molecular dynamics simulations. AIP Adv. 2018, 8, 65003. [Google Scholar] [CrossRef]
- Noh, Y.; Vo, T.; Kim, B. Subatomic-Level Solid/Fluid Boundary of Lennard-Jones Atoms: A Molecular Dynamics Study of Metal-Inert Fluid Interface. Appl. Sci. 2019, 9, 2439. [Google Scholar] [CrossRef]
- Hubbard, A.T. The Handbook of Surface Imaging and Visualization; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Cahill, D.G.; Braun, P.V.; Chen, G.; Clarke, D.R.; Fan, S.; Goodson, K.E.; Keblinski, P.; King, W.P.; Mahan, G.D.; Majumdar, A.; et al. Nanoscale thermal transport. II. 2003–2012. Appl. Phys. Rev. 2014, 1, 11305. [Google Scholar] [CrossRef]
- Razavi, S.; Koplik, J.; Kretzschmar, I. Molecular dynamics simulations: Insight into molecular phenomena at interfaces. Langmuir 2014, 30, 11272–11283. [Google Scholar] [CrossRef]
- Bjornehohn, E.; Hansen, M.; Hodgson, A.; Liu, L.; Limmer, D.; Michaelides, A.; Pedevilla, P.; Rossmeisl, J.; Shen, H.; Tocci, G.; et al. Water at Interfaces. Chem. Rev. 2016, 116, 7698–7726. [Google Scholar] [CrossRef]
- Magda, J.; Tirrell, M.; Davis, H. Molecular dynamics of narrow, liquid-filled pores. J. Chem. Phys. 1985, 83, 1888–1901. [Google Scholar] [CrossRef]
- Pozhar, L.A. Structure and dynamics of nanofluids: Theory and simulations to calculate viscosity. Phys. Rev. E 2000, 61, 1432. [Google Scholar] [CrossRef] [PubMed]
- Bock, H.; Gubbins, K.E.; Schoen, M. Anisotropic self-diffusion in nanofluidic structures. J. Phys. Chem. C 2007, 111, 15493–15504. [Google Scholar] [CrossRef]
- Horn, R.G.; Israelachvili, J.N. Direct measurement of structural forces between two surfaces in a nonpolar liquid. J. Chem. Phys. 1981, 75, 1400–1411. [Google Scholar] [CrossRef]
- Schmitt, S.; Vo, T.; Lautenschlaeger, M.P.; Stephan, S.; Hasse, H. Molecular dynamics simulation study of heat transfer across solid–fluid interfaces in a simple model system. Mol. Phys. 2022, 120, e2057364. [Google Scholar] [CrossRef]
- Akkus, Y.; Beskok, A. Molecular diffusion replaces capillary pumping in phase-change-driven nanopumps. Microfluid. Nanofluid. 2019, 23, 14. [Google Scholar] [CrossRef]
- Hasan, M.R.; Vo, T.Q.; Kim, B. Manipulating thermal resistance at the solid–fluid interface through monolayer deposition. RSC Adv. 2019, 9, 4948–4956. [Google Scholar] [CrossRef]
- Maruyama, S.; Kimura, T. A study on thermal resistance over a solid-liquid interface by the molecular dynamics method. Therm. Sci. Eng 1999, 7, 63–68. [Google Scholar]
- Kim, B.H.; Beskok, A.; Cagin, T. Molecular dynamics simulations of thermal resistance at the liquid-solid interface. J. Chem. Phys. 2008, 129, 174701. [Google Scholar] [CrossRef] [PubMed]
- Barisik, M.; Beskok, A. Temperature dependence of thermal resistance at the water/silicon interface. Int. J. Therm. Sci. 2014, 77, 47–54. [Google Scholar] [CrossRef]
- Song, G.; Min, C. Temperature dependence of thermal resistance at a solid/liquid interface. Mol. Phys. 2013, 111, 903–908. [Google Scholar] [CrossRef]
- Pham, A.T.; Barisik, M.; Kim, B. Interfacial thermal resistance between the graphene-coated copper and liquid water. Int. J. Heat Mass Transf. 2016, 97, 422–431. [Google Scholar] [CrossRef]
- Murad, S.; Puri, I.K. Molecular simulation of thermal transport across hydrophilic interfaces. Chem. Phys. Lett. 2008, 467, 110–113. [Google Scholar] [CrossRef]
- Jabbari, F.; Rajabpour, A.; Saedodin, S.; Wongwises, S. Effect of water/carbon interaction strength on interfacial thermal resistance and the surrounding molecular nanolayer of CNT and graphene flake. J. Mol. Liq. 2019, 282, 197–204. [Google Scholar] [CrossRef]
- Alosious, S.; Kannam, S.K.; Sathian, S.P.; Todd, B. Kapitza resistance at water–graphene interfaces. J. Chem. Phys. 2020, 152, 224703. [Google Scholar] [CrossRef]
- Alexeev, D.; Chen, J.; Walther, J.H.; Giapis, K.P.; Angelikopoulos, P.; Koumoutsakos, P. Kapitza resistance between few-layer graphene and water: Liquid layering effects. Nano Lett. 2015, 15, 5744–5749. [Google Scholar] [CrossRef]
- Liang, Z.; Sasikumar, K.; Keblinski, P. Thermal transport across a substrate–thin-film interface: Effects of film thickness and surface roughness. Phys. Rev. Lett. 2014, 113, 65901. [Google Scholar] [CrossRef]
- Vera, J.; Bayazitoglu, Y. Temperature and heat flux dependence of thermal resistance of water/metal nanoparticle interfaces at sub-boiling temperatures. Int. J. Heat Mass Transf. 2015, 86, 433–442. [Google Scholar] [CrossRef]
- Pham, A.T.; Barisik, M.; Kim, B. Molecular dynamics simulations of Kapitza length for argon-silicon and water-silicon interfaces. Int. J. Precis. Eng. Manuf. 2014, 15, 323–329. [Google Scholar] [CrossRef]
- Ong, Z.Y. Thickness-dependent Kapitza resistance in multilayered graphene and other two-dimensional crystals. Phys. Rev. B 2017, 95, 155309. [Google Scholar] [CrossRef]
- Ghatage, D.; Tomar, G.; Shukla, R.K. Thermostat-induced spurious interfacial resistance in non-equilibrium molecular dynamics simulations of solid–liquid and solid–solid systems. J. Chem. Phys. 2020, 153, 164110. [Google Scholar] [CrossRef] [PubMed]
- Pham, A.; Barisik, M.; Kim, B. Pressure dependence of Kapitza resistance at gold/water and silicon/water interfaces. J. Chem. Phys. 2013, 139, 244702. [Google Scholar] [CrossRef] [PubMed]
- Amani, A.; Karimian, S.; Seyednia, M. A molecular dynamics simulation on the effect of different parameters on thermal resistance of graphene-argon interface. Mol. Simul. 2017, 43, 276–283. [Google Scholar] [CrossRef]
- Vo, T.Q.; Kim, B. Interface thermal resistance between liquid water and various metallic surfaces. Int. J. Precis. Eng. Manuf. 2015, 16, 1341–1346. [Google Scholar] [CrossRef]
- France-Lanord, A.; Soukiassian, P.; Glattli, C.; Wimmer, E. Ab initio parameterization of a charge optimized many-body forcefield for Si–SiO2: Validation and thermal transport in nanostructures. J. Chem. Phys. 2016, 144, 104705. [Google Scholar] [CrossRef] [PubMed]
- Ge, S.; Chen, M. Vibrational coupling and Kapitza resistance at a solid–liquid interface. Int. J. Thermophys. 2013, 34, 64–77. [Google Scholar] [CrossRef]
- Murad, S.; Puri, I.K. Thermal transport across nanoscale solid-fluid interfaces. Appl. Phys. Lett. 2008, 92, 133105. [Google Scholar] [CrossRef]
- Biolè, D.; Bertola, V. A goniometric mask to measure contact angles from digital images of liquid drops. Colloids Surfaces Physicochem. Eng. Asp. 2015, 467, 149–156. [Google Scholar] [CrossRef]
- Biolè, D.; Wang, M.; Bertola, V. Assessment of direct image processing methods to measure the apparent contact angle of liquid drops. Exp. Therm. Fluid Sci. 2016, 76, 296–305. [Google Scholar] [CrossRef]
- Wang, J.; Betelu, S.; Law, B. Line tension approaching a first-order wetting transition: Experimental results from contact angle measurements. Phys. Rev. E 2001, 63, 031601. [Google Scholar] [CrossRef]
- Brinkmann, M.; Kierfeld, J.; Lipowsky, R. A general stability criterion for droplets on structured substrates. J. Phys. Math. Gen. 2004, 37, 11547. [Google Scholar] [CrossRef][Green Version]
- Barisik, M.; Beskok, A. Wetting characterisation of silicon (1, 0, 0) surface. Mol. Simul. 2013, 39, 700–709. [Google Scholar] [CrossRef]
- Shi, Z.; Barisik, M.; Beskok, A. Molecular dynamics modeling of thermal resistance at argon-graphite and argon-silver interfaces. Int. J. Therm. Sci. 2012, 59, 29–37. [Google Scholar] [CrossRef]
- Pompe, T.; Herminghaus, S. Three-phase contact line energetics from nanoscale liquid surface topographies. Phys. Rev. Lett. 2000, 85, 1930. [Google Scholar] [CrossRef] [PubMed]
- Goicochea, J.V.; Hu, M.; Michel, B.; Poulikakos, D. Surface Functionalization Mechanisms of Enhancing Heat Transfer at Solid-Liquid Interfaces. J. Heat Transf. 2011, 133, ARTN-082401. [Google Scholar] [CrossRef]
- Acharya, H.; Mozdzierz, N.; Keblinski, P.; Garde, S. How Chemistry, Nanoscale Roughness, and the Direction of Heat Flow Affect Thermal Conductance of Solid-Water Interfaces. Ind. Eng. Chem. Res. 2012, 51, 1767–1773. [Google Scholar] [CrossRef]
- Lundgren, M.; Allan, N.L.; Cosgrove, T. Modeling of wetting: A study of nanowetting at rough and heterogeneous surfaces. Langmuir 2007, 23, 1187–1194. [Google Scholar] [CrossRef]
- Halverson, J.D.; Maldarelli, C.; Couzis, A.; Koplik, J. Atomistic simulations of the wetting behavior of nanodroplets of water on homogeneous and phase separated self-assembled monolayers. Soft Matter 2010, 6, 1297–1307. [Google Scholar] [CrossRef]
- Israelachvili, J.N.; Gee, M.L. Contact angles on chemically heterogeneous surfaces. Langmuir 1989, 5, 288–289. [Google Scholar] [CrossRef]
- Wang, J.; Bratko, D.; Luzar, A. Probing surface tension additivity on chemically heterogeneous surfaces by a molecular approach. Proc. Natl. Acad. Sci. USA 2011, 108, 6374–6379. [Google Scholar] [CrossRef] [PubMed]
- Blander, M.; Katz, J.L. Bubble nucleation in liquids. AIChE J. 1975, 21, 833–848. [Google Scholar] [CrossRef]
- Kelton, K.; Greer, A.L. Nucleation in Condensed Matter: Applications in Materials And Biology; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Zeng, X.; Oxtoby, D.W. Gas–liquid nucleation in Lennard-Jones fluids. J. Chem. Phys. 1991, 94, 4472–4478. [Google Scholar] [CrossRef]
- Shen, V.K.; Debenedetti, P.G. Density-functional study of homogeneous bubble nucleation in the stretched Lennard-Jones fluid. J. Chem. Phys. 2001, 114, 4149–4159. [Google Scholar] [CrossRef]
- Wilhelmsen, Ø.; Bedeaux, D.; Kjelstrup, S.; Reguera, D. Thermodynamic stability of nanosized multicomponent bubbles/droplets: The square gradient theory and the capillary approach. J. Chem. Phys. 2014, 140, 24704. [Google Scholar] [CrossRef] [PubMed]
- Delale, C.F.; Hruby, J.; Marsik, F. Homogeneous bubble nucleation in liquids: The classical theory revisited. J. Chem. Phys. 2003, 118, 792–806. [Google Scholar] [CrossRef]
- Shen, V.K.; Debenedetti, P.G. A kinetic theory of homogeneous bubble nucleation. J. Chem. Phys. 2003, 118, 768–783. [Google Scholar] [CrossRef]
- Zhukhovitskii, D. Molecular dynamics study of cluster evolution in supersaturated vapor. J. Chem. Phys. 1995, 103, 9401–9407. [Google Scholar] [CrossRef]
- Yasuoka, K.; Matsumoto, M. Molecular dynamics of homogeneous nucleation in the vapor phase. I. Lennard-Jones fluid. J. Chem. Phys. 1998, 109, 8451–8462. [Google Scholar] [CrossRef]
- Yasuoka, K.; Matsumoto, M. Molecular dynamics of homogeneous nucleation in the vapor phase. II. Water. J. Chem. Phys. 1998, 109, 8463–8470. [Google Scholar] [CrossRef]
- Maruyama, S.; Kimura, T.; Yamaguchi, Y. A molecular dynamics simulation of a bubble nucleation on solid surface. In Proceedings of the National Heat Transfer Symposium of Japan; Heat Transfer Society of Japan: Tokyo, Japan, 1997; Volume 34, pp. 675–676. [Google Scholar]
- Kimura, T.; Maruyama, S. Molecular dynamics simulation of heterogeneous nucleation of a liquid droplet on a solid surface. Microscale Thermophys. Eng. 2002, 6, 3–13. [Google Scholar] [CrossRef]
- Nagayama, G.; Cheng, P. Effects of interface wettability on microscale flow by molecular dynamics simulation. Int. J. Heat Mass Transf. 2004, 47, 501–513. [Google Scholar] [CrossRef]
- She, X.; Shedd, T.A.; Lindeman, B.; Yin, Y.; Zhang, X. Bubble formation on solid surface with a cavity based on molecular dynamics simulation. Int. J. Heat Mass Transf. 2016, 95, 278–287. [Google Scholar] [CrossRef]
- Davis, E.J.; Ray, A.K. Submicron droplet evaporation in the continuum and non-continuum regimes. J. Aerosol Sci. 1978, 9, 411–422. [Google Scholar] [CrossRef]
- Little, J.K. Simulation of Droplet Evaporation in Supercritical Environments Using Parallel Molecular Dynamics; The Pennsylvania State University: State College, PA, USA, 1996. [Google Scholar]
- Kuo, K.K. Principles of Combustion; Wiley: State College, PA, USA, 2005. [Google Scholar]
- Walther, J.H.; Koumoutsakos, P. Molecular dynamics simulation of nanodroplet evaporation. J. Heat Transf. 2001, 123, 741–748. [Google Scholar] [CrossRef]
- Gong, Y.; Xiao, G.; Ma, X.; Luo, K.H.; Shuai, S.; Xu, H. Phase transitions of multi-component fuel droplets under sub-and supercritical conditions. Fuel 2021, 287, 119516. [Google Scholar] [CrossRef]
- Ju, D.; Huang, L.; Zhang, K.; Ye, M.; Huang, Z.; Yi, G. Comparison of evaporation rate constants of a single fuel droplet entering subcritical and supercritical environments. J. Mol. Liq. 2022, 347, 118346. [Google Scholar] [CrossRef]
- Wu, Y.; Pan, C. Molecular dynamics simulation of thin film evaporation of Lennard-Jones liquid. Nanoscale Microscale Thermophys. Eng. 2006, 10, 157–170. [Google Scholar] [CrossRef]
- Yi, P.; Poulikakos, D.; Walther, J.; Yadigaroglu, G. Molecular dynamics simulation of vaporization of an ultra-thin liquid argon layer on a surface. Int. J. Heat Mass Transf. 2002, 45, 2087–2100. [Google Scholar] [CrossRef]
- Dou, Y.; Zhigilei, L.V.; Winograd, N.; Garrison, B.J. Explosive boiling of water films adjacent to heated surfaces: A microscopic description. J. Phys. Chem. A 2001, 105, 2748–2755. [Google Scholar] [CrossRef]
- Li, C.; Wang, Z.; Wang, P.I.; Peles, Y.; Koratkar, N.; Peterson, G. Nanostructured copper interfaces for enhanced boiling. Small 2008, 4, 1084–1088. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Lu, M.C.; Srinivasan, V.; Wang, Z.; Cho, H.H.; Majumdar, A. Nanowires for enhanced boiling heat transfer. Nano Lett. 2009, 9, 548–553. [Google Scholar] [CrossRef]
- Betz, A.R.; Xu, J.; Qiu, H.; Attinger, D. Do surfaces with mixed hydrophilic and hydrophobic areas enhance pool boiling? Appl. Phys. Lett. 2010, 97, 141909. [Google Scholar] [CrossRef]
- Yao, Z.; Lu, Y.W.; Kandlikar, S. Effects of nanowire height on pool boiling performance of water on silicon chips. Int. J. Therm. Sci. 2011, 50, 2084–2090. [Google Scholar] [CrossRef]
- Weibel, J.A.; Kim, S.; Fisher, T.S.; Garimella, S.V. Carbon nanotube coatings for enhanced capillary-fed boiling from porous microstructures. Nanoscale Microscale Thermophys. Eng. 2012, 16, 1–17. [Google Scholar] [CrossRef]
- Kim, D.E.; Yu, D.I.; Jerng, D.W.; Kim, M.H.; Ahn, H.S. Review of boiling heat transfer enhancement on micro/nanostructured surfaces. Exp. Therm. Fluid Sci. 2015, 66, 173–196. [Google Scholar] [CrossRef]
- Nagayama, G.; Tsuruta, T. A general expression for the condensation coefficient based on transition state theory and molecular dynamics simulation. J. Chem. Phys. 2003, 118, 1392–1399. [Google Scholar] [CrossRef]
- Kesälä, E.; Kuronen, A.; Nordlund, K. Molecular dynamics simulation of pressure dependence of cluster growth in inert gas condensation. Phys. Rev. B 2007, 75, 174121. [Google Scholar] [CrossRef]
- Ranathunga, D.T.; Shamir, A.; Dai, X.; Nielsen, S.O. Molecular dynamics simulations of water condensation on surfaces with tunable wettability. Langmuir 2020, 36, 7383–7391. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Liu, X.; He, M.; Zhang, Y. Molecular dynamics simulation of thermophysical properties and condensation process of R1233zd (E). Int. J. Refrig. 2020, 112, 341–347. [Google Scholar] [CrossRef]
- Hinds, B.J.; Chopra, N.; Rantell, T.; Andrews, R.; Gavalas, V.; Bachas, L.G. Aligned multiwalled carbon nanotube membranes. Science 2004, 303, 62–65. [Google Scholar] [CrossRef] [PubMed]
- Bernard, S.; Wirth, R.; Schreiber, A.; Schulz, H.M.; Horsfield, B. Formation of nanoporous pyrobitumen residues during maturation of the Barnett Shale (Fort Worth Basin). Int. J. Coal Geol. 2012, 103, 3–11. [Google Scholar] [CrossRef]
- Park, S.; Kim, Y.S.; Kim, W.B.; Jon, S. Carbon nanosyringe array as a platform for intracellular delivery. Nano Lett. 2009, 9, 1325–1329. [Google Scholar] [CrossRef]
- Travis, K.P.; Todd, B.; Evans, D.J. Departure from Navier-Stokes hydrodynamics in confined liquids. Phys. Rev. E 1997, 55, 4288. [Google Scholar] [CrossRef]
- Travis, K.P.; Gubbins, K.E. Poiseuille flow of Lennard-Jones fluids in narrow slit pores. J. Chem. Phys. 2000, 112, 1984–1994. [Google Scholar] [CrossRef]
- Koplik, J.; Banavar, J.R. Continuum deductions from molecular hydrodynamics. Annu. Rev. Fluid Mech. 1995, 27, 257–292. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Y.; Yang, L.; Shi, M. Self-diffusion for Lennard-Jones fluid confined in a nanoscale space. Int. J. Heat Mass Transf. 2011, 54, 4770–4773. [Google Scholar] [CrossRef]
- Sokhan, V.P.; Nicholson, D.; Quirke, N. Fluid flow in nanopores: Accurate boundary conditions for carbon nanotubes. J. Chem. Phys. 2002, 117, 8531–8539. [Google Scholar] [CrossRef]
- Stokes, G. On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Philos. Soc. 1850, 3, 1880–1905. [Google Scholar]
- Cao, B.Y.; Sun, J.; Chen, M.; Guo, Z.Y. Molecular momentum transport at fluid-solid interfaces in MEMS/NEMS: A review. Int. J. Mol. Sci. 2009, 10, 4638–4706. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Cheng, P. Friction factors in smooth trapezoidal silicon microchannels with different aspect ratios. Int. J. Heat Mass Transf. 2003, 46, 2519–2525. [Google Scholar] [CrossRef]
- Soong, C.; Yen, T.; Tzeng, P. Molecular dynamics simulation of nanochannel flows with effects of wall lattice-fluid interactions. Phys. Rev. E 2007, 76, 036303. [Google Scholar] [CrossRef]
- Gandomi, Y.A.; Edmundson, M.; Busby, F.; Mench, M.M. Water management in polymer electrolyte fuel cells through asymmetric thermal and mass transport engineering of the micro-porous layers. J. Electrochem. Soc. 2016, 163, F933. [Google Scholar] [CrossRef]
- Ge, S.; Gu, Y.; Chen, M. A molecular dynamics simulation on the convective heat transfer in nanochannels. Mol. Phys. 2015, 113, 703–710. [Google Scholar] [CrossRef]
- Shkarah, A.J.; Sulaiman, M.Y.B.; Ayob, M.R.B.H.; Togun, H. A 3D numerical study of heat transfer in a single-phase micro-channel heat sink using graphene, aluminum and silicon as substrates. Int. Commun. Heat Mass Transf. 2013, 48, 108–115. [Google Scholar] [CrossRef]
- Thekkethala, J.F.; Sathian, S.P. The effect of graphene layers on interfacial thermal resistance in composite nanochannels with flow. Microfluid. Nanofluid. 2015, 18, 637–648. [Google Scholar] [CrossRef]
- Ghasemi, H.; Ward, C. Mechanism of sessile water droplet evaporation: Kapitza resistance at the solid–liquid interface. J. Phys. Chem. C 2011, 115, 21311–21319. [Google Scholar] [CrossRef]
- Marable, D.C.; Shin, S.; Nobakht, A.Y. Investigation into the microscopic mechanisms influencing convective heat transfer of water flow in graphene nanochannels. Int. J. Heat Mass Transf. 2017, 109, 28–39. [Google Scholar] [CrossRef]
- Motlagh, M.B.; Kalteh, M. Molecular dynamics simulation of nanofluid convective heat transfer in a nanochannel: Effect of nanoparticles shape, aggregation and wall roughness. J. Mol. Liq. 2020, 318, 114028. [Google Scholar] [CrossRef]
- Motlagh, M.B.; Kalteh, M. Simulating the convective heat transfer of nanofluid Poiseuille flow in a nanochannel by molecular dynamics method. Int. Commun. Heat Mass Transf. 2020, 111, 104478. [Google Scholar] [CrossRef]
- Chakraborty, P.; Ma, T.; Cao, L.; Wang, Y. Significantly enhanced convective heat transfer through surface modification in nanochannels. Int. J. Heat Mass Transf. 2019, 136, 702–708. [Google Scholar] [CrossRef]
- Toghraie, D.; Hekmatifar, M.; Salehipour, Y.; Afrand, M. Molecular dynamics simulation of Couette and Poiseuille Water-Copper nanofluid flows in rough and smooth nanochannels with different roughness configurations. Chem. Phys. 2019, 527, 110505. [Google Scholar] [CrossRef]
- Jiang, L.; Wong, M.; Zohar, Y. Forced convection boiling in a microchannel heat sink. J. Microelectromech. Syst. 2001, 10, 80–87. [Google Scholar] [CrossRef]
- Qu, W.; Mudawar, I. Flow boiling heat transfer in two-phase micro-channel heat sinks—II. Annular two-phase flow model. Int. J. Heat Mass Transf. 2003, 46, 2773–2784. [Google Scholar] [CrossRef]
- Maruyama, S. Molecular dynamics method for microscale heat transfer. Adv. Numer. Heat Transf. 2000, 2, 189–226. [Google Scholar]
- Qu, W.; Mudawar, I. Flow boiling heat transfer in two-phase micro-channel heat sinks—I. Experimental investigation and assessment of correlation methods. Int. J. Heat Mass Transf. 2003, 46, 2755–2771. [Google Scholar] [CrossRef]
- Zarringhalam, M.; Ahmadi-Danesh-Ashtiani, H.; Toghraie, D.; Fazaeli, R. The effects of suspending Copper nanoparticles into Argon base fluid inside a microchannel under boiling flow condition by using of molecular dynamic simulation. J. Mol. Liq. 2019, 293, 111474. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, Y.; Bertola, V. Achievements and Prospects of Molecular Dynamics Simulations in Thermofluid Sciences. Energies 2024, 17, 888. https://doi.org/10.3390/en17040888
Ran Y, Bertola V. Achievements and Prospects of Molecular Dynamics Simulations in Thermofluid Sciences. Energies. 2024; 17(4):888. https://doi.org/10.3390/en17040888
Chicago/Turabian StyleRan, Yunmin, and Volfango Bertola. 2024. "Achievements and Prospects of Molecular Dynamics Simulations in Thermofluid Sciences" Energies 17, no. 4: 888. https://doi.org/10.3390/en17040888
APA StyleRan, Y., & Bertola, V. (2024). Achievements and Prospects of Molecular Dynamics Simulations in Thermofluid Sciences. Energies, 17(4), 888. https://doi.org/10.3390/en17040888






