An Inductive Method for Comprehensive Estimation of Temperature-Dependent Electrical and Thermal Properties of Conductive Ferromagnetic Materials

Abstract

Reliable information about the properties of the processed materials has a significant impact on the effects of their processing. In induction heating processes, this also applies to information about the influence of temperature T on these properties. These are both thermal and electro-magnetic properties. Based on previous studies, a comprehensive experimental method is presented for estimating the temperature characteristics of thermal diffusivity, volumetric heat capacity and resistivity on one measurement station, with particular attention to ferromagnetic materials. The estimation process is carried out on an induction heating stand using forcing signals from an inverter generator. In a computer-controlled cycle that changes the base temperature level, basic measurements of thermal and electrical properties are carried out on a material sample in the form of a cylindrical disk. They are the results of the analysis of the temperature and electromagnetic responses of a material sample to short- and long-term step pulses of a sinusoidal excitation signal with a frequency of approximately 40 kHz. The presented estimation method can be treated as a final method or a preliminary procedure for radically narrowing the variability in decision variables inthe optimization process of simultaneous determination of the sought material characteristics.

1. Introduction

Material properties are an important element in the design and implementation of many technological processes. This obviously also applies to thermal processes, in which we often deal with large temperature changes that can significantly affect these properties. For this reason, knowledge of the temperature characteristics of material properties is usually required for these processes. Different technological processes require knowledge of different material properties. The induction heating process involves transferring the energy of the electromagnetic field generated by the alternating current I flowing in the inductor to the electrically conductive heated object (charge). This is performed using the phenomenon of electromagnetic induction, described by Faraday’s law, which generates an electromotive force E through the time-varying magnetic flux Φ. For sinusoidal waveforms, this can be written in the form [1]:

$$E=\mathrm{j}·\omega ·\Phi$$

(1)

where ω = 2⋅π⋅f—current pulsation at frequency f.

In the case of conductive objects (charges), the induced electromotive force E leads to the flow of current I_ch in the charge, which, according to Joule’s law, becomes a source of thermal power in them [1]:

$$p_{\mathrm{V}}=\rho ·J_{\mathrm{c}\mathrm{h}}^2$$

(2)

where p_v—volume density of the generated power, ρ—resistivity of the charge material and J_ch—effective value of the current density in the charge.

The distribution of current density J_ch in a massive charge depends on the intensity of electromagnetic field attenuation, which can be expressed using the so-called penetration depth δ [1], that is, the length of the path along which the intensity H of the magnetic field (and the density J_ch of the induced current) decreases by an e-fold:

$$\delta =\sqrt{\frac{2·\rho }{\omega ·\mu }}$$

(3)

where µ—magnetic permeability of the charge material.

Given the conditions of heat exchange with the environment, the heating effect, that is, the temperature value and its distribution in the charge, depends on both the value and distribution of the volume power density p_v and the specific heat c (or volumetric heat capacity χ = ρ_m^.c, where ρ_m—mass density) and specific thermal conductivity λ of the charge material. With a known value of volumetric heat capacity, thermal conductivity can be easily determined from the thermal diffusivity a = λ/χ.

In the case of the induction heating process, the four above-mentioned properties of the charge material have a basic impact on the heating effect:

• Specific thermal conductivity;
• Volumetric heat capacity;
• Resistivity,
• Magnetic permeability—especially important for ferromagnetic materials.

Correct information about the temperature characteristics of the above material properties is important both at the design stage and during the implementation of the induction heating process. The measurement and determination of these parameters, especially in the form of temperature characteristics, requires the use of various techniques and measuring devices as well as qualified personnel. Consequently, such measurements are expensive and time-consuming. On the other hand, growing technological requirements increasingly lead to the need for precise, reliable information about the properties of the processed material, which leads to the need to verify them in situ. The importance of the problem raised is confirmed by numerous publications [2,3,4,5,6,7,8,9,10,11], in which the issue of the possibly simplest and quickest way to determine material properties is considered, preferably several at once using one measurement station. The cited literature examples mainly concern attempts to determine thermal properties, that is, thermal diffusivity and volumetric heat capacity. Unfortunately, some of the presented techniques [2,3] either do not take into account the influence of temperature on thermal properties, cannot be used to test metals [3] or take into account temperature changes to a very small extent [4]. In the frequently used contact methods of providing thermal forcing, there are also significant problems with eliminating the influence of thermal resistances on connections [5]. In recent years, there has been promising information [6,7] about measurement techniques, allowing for the simultaneous determination of the temperature characteristics of specific heat and the specific thermal conductivity of metal samples with an accuracy of several percent. However, these techniques are based on the use of a resistive contact heat source, which makes them less useful in the case of higher temperatures encountered in metal processing thermal processes. The above-mentioned methods for simultaneous determination of more than one thermal material property are based on solving the problem of reverse heat conduction. A similar approach to determining the thermal material properties of metals, but using the induction heating method, is presented in the studies [8,9]. Also here, based on optimization techniques and measurement of temperature distribution in the tested sample, the possibility of indirectly determining the thermal properties of materials was indicated. The conclusions drawn from the above studies indicate that solving the inverse problem based on optimization techniques in order to simultaneously determine more than one material property is burdened with a significant risk of the so-called local minimum traps. This is an error resulting from the possibility of a similar effect of various properties sought on the measured temperature distribution. The risk of this error increases if we are dealing with a large range of temperature changes, which is typical for induction heating. In the case of induction heating, we also have to determine not only thermal but also electrical and magnetic properties, which further increases the risk of this error. In [10], an initial attempt was made to solve this problem by extending the scope of measurements performed. This extension involves performing measurement experiments on a test stand that will enable, with the highest possible accuracy, the estimation of the value of each of the sought material parameters separately. This allows for a very significant reduction in the range of variability of these parameters, the exact value of which can then be determined in the procedure of solving the inverse heat conduction problem (for example, in [8,9]), where a comprehensive multi-factor analysis is performed. A full development of this approach using the induction method as a source of excitation was presented for conductive, non-magnetic materials in [11]. Due to the significant influence of magnetic permeability on the effect of inducing eddy currents in the tested material, the method presented there cannot be directly transferred to ferromagnetic materials. The issue of isotropic ferromagnetic materials was taken up in this study.

The rest of the article initially presents brief information about the measurement station and the simulation analysis methods used. The method of using the modified Flash method [12,13,14,15,16,17] for the measurement of thermal diffusivity at an induction heating measurement station was presented, and the possibilities of measuring the volumetric heat capacity of ferromagnetic materials using the same measurement station were analysed. The influence of resistivity and magnetic permeability on the tested electrical parameters of the measurement system is discussed, and the possibilities of distinguishing the influence of each of these properties individually are indicated. In the final part, a comprehensive algorithm for estimating the temperature characteristics of thermal and electrical properties of conductive magnetic materials was analysed using the induction heating method.

2. Measuring the Stand of an Inductive Method of Comprehensive Estimation of the Properties of Conductive Materials

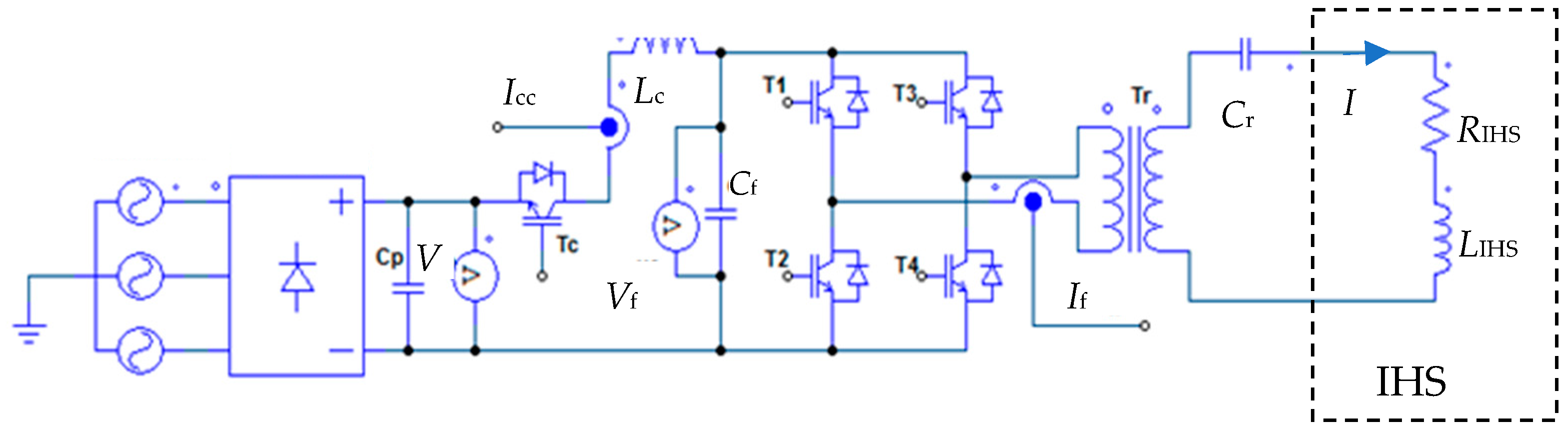
It was assumed that the measurement estimation of the sought material properties would be carried out on a stand based on the use of a GE generator for medium-frequency induction heating in the bridge version of IGBT transistors with series resonance, as shown in Figure 1.

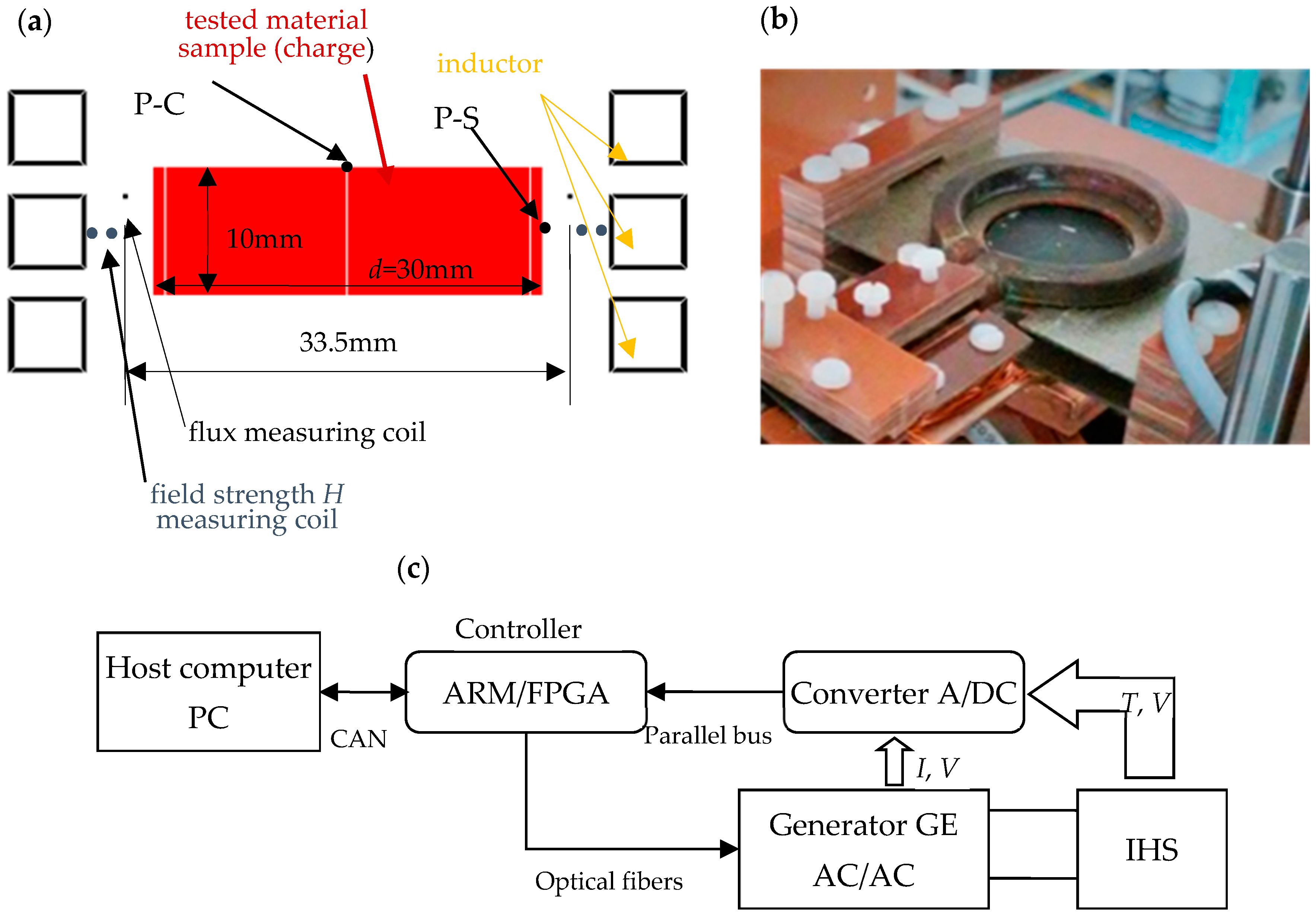
These types of sources, which are relatively easy to control, are quite commonly used for induction heating. A set of basic measurements will be carried out on a test stand containing an IHS induction heating system (inductor-charge), which constitutes the equivalent R_IHS resistance and L_IHS inductance for the generator powering it. After the analyses [11], the use of a cylindrical inductor-charge system was adopted, in which the tested material sample constituting the charge has the shape of a cylindrical disc, as shown in Figure 2a. A view of the actual IHS is shown in Figure 2b.

The operation of the entire measurement station is supervised by a central PC computer, cooperating via a CAN bus with a controller based on an ARM architecture microcontroller and a programmable FPGA gate system. The controller is used, among others, to control the operation of the GE generator and is used to measure, through the A/DC converter, analogue measurement signals from the GE generator and IHS, as shown in Figure 2c.

The basic analysis of the possibility of using IHS from Figure 2 to estimate the temperature characteristics of the sought thermal and electrical properties of conductive materials, including ferromagnetic ones, was based on simulation calculations based on the FEM finite element method.

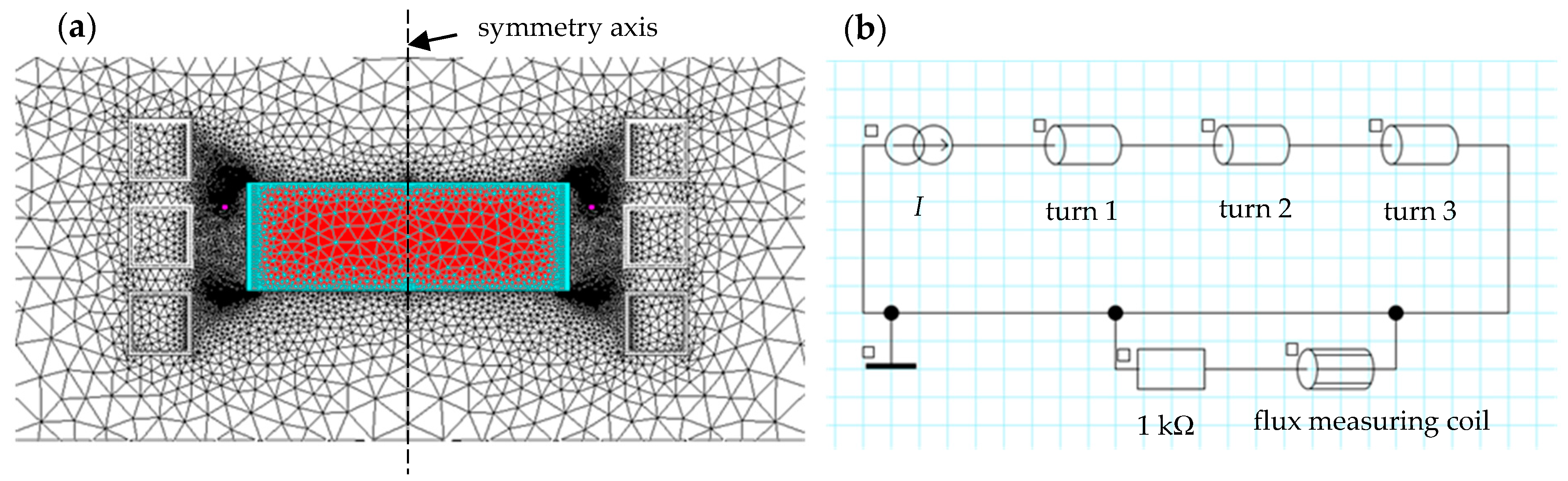
Simulation calculations of the coupled electromagnetic fields and temperature in the system from Figure 3a were carried out using the commercial Flux^® program.

The main part of the calculations was made assuming the sinusoidality of current and voltage waveforms, which allows the analysis of the electromagnetic field to be reduced to solving Maxwell’s equation in the form [1]:

$$\mathrm{j}\omega \gamma \mathit{A}+\mathbf{r}\mathbf{o}\mathbf{t}\left(\frac{1}{\mathsf{\mu }}\mathbf{r}\mathbf{o}\mathbf{t}\mathit{A}\right)=\mathit{J}$$

(4)

where A—magnetic vector potential defined as B = rotA, B—magnetic induction, J—current density, ω = 2⋅π⋅f—pulsation, f—frequency, μ—magnetic permeability and γ = 1/ρ—conductivity.

It should be noted here that the assumption of the sinusoidality of the electromagnetic field applies to both the electric and magnetic fields, which can only occur in magnetically linear environments. The analyses carried out in this study also apply to ferromagnetic materials, that is, magnetically nonlinear materials, which may give the impression of a collision with the adopted assumption. This inconsistency was significantly alleviated by using the methods described in [18,19,20], that is, the use of modified, substitute relationships between the magnetic induction B and the magnetic field intensity H.

Thermal calculations of the heating of the tested samples induced by eddy currents were computationally carried out by coupling the solution of Equation (4) with the Fourier–Kirchhoff equation [21]:

$$\mathrm{d}\mathrm{i}\mathrm{v}\left(-\lambda ·\mathbf{g}\mathbf{r}\mathbf{a}\mathbf{d}T\right)+{\rho }_{\mathrm{m}}·c\frac{\partial T}{\partial t}=p_{\mathrm{v}}$$

(5)

where λ—thermal conductivity, ρ_m—mass density, c—specific heat, p_v—volumetric density of heat source power and t—time, taking into account the appropriate boundary conditions and initial condition.

3. Using the Impulse Method to Estimate the Thermal Diffusivity of Conductive Magnetic Materials on an Induction Heating Measuring Stand

By analysing conductive non-magnetic materials [11], it was found that in the system in Figure 2a, it is possible to use the modified Flash method [12,13,14,15,16,17] to estimate the thermal diffusivity of a cylindrical sample of the tested material. The application of the Flash method in the considered inductor-charge system consisted of implementing, using the system from Figure 2c, excitation in the form of short 20 or 10 millisecond pulses of the inductor current with a frequency of f = 40 kHz and RSM values of I = 1100 and 1550A, respectively. The analysed response of the sample of the tested material was the temperature course at point P_C (Figure 2a). Due to the method of generating energy excitation with the power of the eddy current induced in the sample and the cylindrical shape of the sample with radius R, it was necessary to modify the literature [12] computational relationship (classic Flash method) for determining the diffusivity value based on the so-called half-response time t_1/2, that is, the time after which the temperature response reaches half the maximum temperature. In [11], after an analysis focused on testing the estimation accuracy for a wide range of variability in thermal diffusivity of samples of non-magnetic materials, a new relationship for calculating thermal diffusivity is provided:

$$a=0.11\frac{{RR}^2}{t_{1/2}-\frac{3}{4}\Delta t}$$

(6)

where RR = R − δ/2 and δ—the value of the penetration depth of the electromagnetic wave into the tested material at the applied frequency of the excitation current.

For non-magnetic materials, relation (6) allows, for times t_1/2 measured in the system from Figure 2a, to estimate the thermal diffusivity a_cal of the material of the tested sample with an error below 5%.

In this study, for magnetic materials, it was analysed whether the magnetic parameters, that is, magnetic permeability, and the related electrical parameters, that is, resistivity, can significantly affect the accuracy of the estimation of the thermal diffusivity by dependence (6) in the system from Figure 2a. The study was carried out in accordance with the classic one-factor-at-a-time (OFAT) approach, that is, examining the impact of each parameter separately. With a small (two) number of parameters, this also allows for easy orientation and graphical representation of multi-factorial influence. 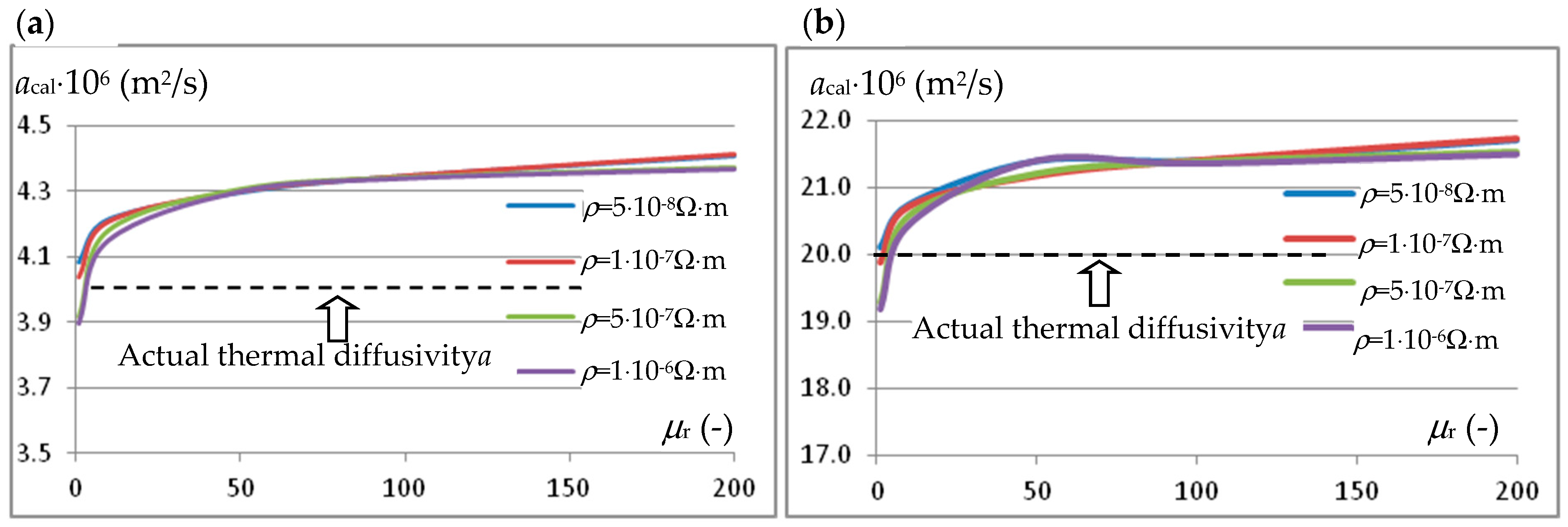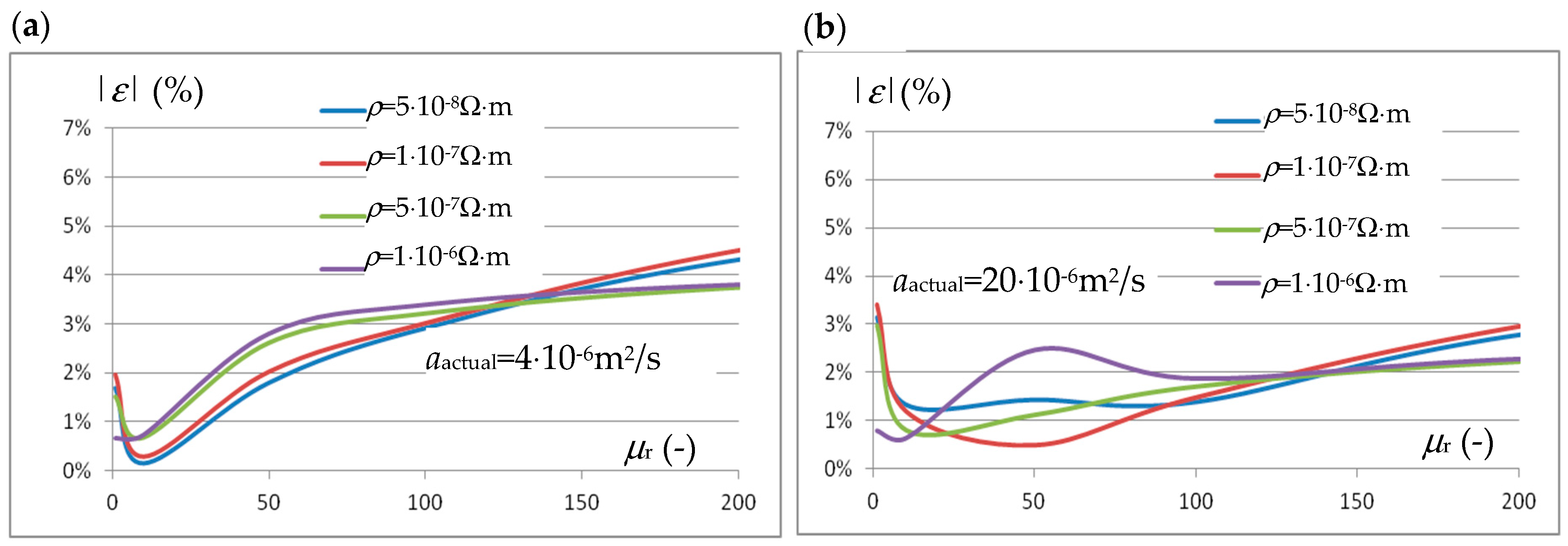Figure 4, for step excitation Δt = 10 ms with a current of frequency f = 40 kHz and intensity I = 1550 A, shows an example of the influence of the value of the relative magnetic permeability μ_r of the magnetic materials in the sample on the value of thermal diffusivity a_cal. calculated using Equation (6). In Figure 4a, with a change in relative magnetic permeability in the range μ_r = 1 ÷ 200, this effect is presented for a material with thermal diffusivity a = λ/χ = 20/(5 × 10⁶) = 4 × 10⁻⁶ m²/s for four significantly different material resistivity values, that is, ρ = 5 × 10⁻⁸, ρ = 1 × 10⁻⁷, ρ = 5 × 10⁻⁷ and ρ = 1 × 10⁻⁶ Ω⋅m. In Figure 4b, this effect is presented for materials with thermal diffusivity a = λ/χ = 100/(5 × 10⁶) = 20 × 10⁻⁶ m²/s. When determining the parameters of the forcing signal, the main consideration was the value of the energy supplied to the charge, so that the temperature increases obtained were several degrees. On the one hand, this allows us to talk about measurement at a specific base temperature (a specific point of the temperature characteristic), and on the other hand, it allows us to maintain high accuracy in measuring temperature changes.

The graphs in Figure 4 indicate that an increase in the value of the relative magnetic permeability of the tested material increases the error in estimating the thermal diffusivity dependency (6) in the system from Figure 2. The scale of this influence additionally depends on the resistivity value of the sample material. At permeability values, μ_r, of the order of 200, the error in estimating thermal diffusivity may exceed 10%.

It should be noted that μ_r = 200 is a relatively high value taking into account the excitation current values used in this method, which translates into magnetic field strengths on the surface of the charge significantly exceeding 50 kA/m. On the other hand, however, it should be borne in mind that this error is determined by simulation, assuming a constant value of the magnetic permeability of the entire sample, which may lower the determined error value. Taking this into account, it was concluded that the scale of the increase in the diffusivity estimation error observed with the increase in the magnetic permeability value is much too large. Reducing the scale of this error was sought by modifying the relationship (6) used to estimate diffusivity based on the half-response time t_1/2. A relationship was sought that would, on the one hand, not reduce the accuracy of diffusivity estimation for non-magnetic materials and, on the other hand, reduce the impact of the magnetic permeability value on the accuracy of this estimation. It was found that these requirements can be met by the following relationship:

$$a=0.104\frac{{RR}_{\mathrm{n}}^2}{t_{1/2}-\frac{3}{4}\Delta t}$$

(7)

where RR_n = R − δ/4 and δ—the value of the penetration depth of the electromagnetic wave into the tested material at the applied frequency of the excitation current.

Figure 5, for forcing the inductor current as above, shows the influence of the magnetic permeability value on the thermal diffusivity a_cal value calculated by the new relationship (7) for the magnetic materials of the sample.

The absolute values of the error $\epsilon =(a-a_{cal})/a$ in the estimation of thermal diffusivity in the system from Figure 2a, obtained for the impulse method using Equation (7), are shown in Figure 6. The dependencies in Figure 5 and Figure 6 show that using Equation (7), it is possible to reduce the error of estimating diffusivity below 5%, even with relatively high values of relative magnetic permeability and a wide range of changes in the resistivity of the material of the tested sample.

Relations (6) and (7), used for computational estimation of thermal diffusivity based on the half-response time, require knowledge of the electrical and magnetic properties of the tested material when determining the value of the equivalent radius RR of the sample. This concerns knowledge of the penetration depth value for the tested material. In the case of relation (6) used for non-magnetic charges, it comes down only to knowing the resistivity value, which is also estimated at the same test stand. With a known value of the frequency of the excitation current, the value of the penetration depth can then be easily determined from Equation (3), assuming a constant value of resistivity determined for a given base temperature of the sample. During the impulse estimation of thermal diffusivity, there is only a several-degree radial temperature difference, which has no practical impact on the change in the resistivity value with temperature. In the case of extending the research to magnetic materials, as analysed in this study, the use of the proposed relationship (7) is more difficult, especially since it was established by assuming a constant value of magnetic permeability for the entire tested material sample. For ferromagnetic materials, however, in practice, we are dealing with a magnetically nonlinear inductor-charge system with spatially different values of magnetic permeability (magnetic induction B) of the sample material depending on the magnetic field strength H. In such a case, even the determination of the penetration depth value using the relationship (3) is debatable.

The study attempts to determine the scale of the error in estimating thermal diffusivity using Equation (7) in the case of magnetically nonlinear materials and attempts to limit this error. Assuming, as before, the time Δt = 10 ms of the duration of the impulse excitation of the inductor current with a frequency of f = 40 kHz and an intensity of I = I_D = 1550 A, the temperature responses T_ch(t) at point P_C of the sample were analysed for a material with nonlinear magnetization characteristics B(H). Figure 7a shows, for example, the responses T_ch(t) at point P_C for a material with thermal diffusivity a = λ/χ = 20/(5 × 10⁶) = 4 × 10⁻⁶ m²/s and with the magnetization characteristics B(H) shown in Figure 7b correspond to the characteristics of steel 1.3207 (SK10V), assuming three different resistivity values, that is, ρ = 1 × 10⁻⁷, ρ = 5 × 10⁻⁷ and ρ = 1 × 10⁻⁶ Ω⋅m.

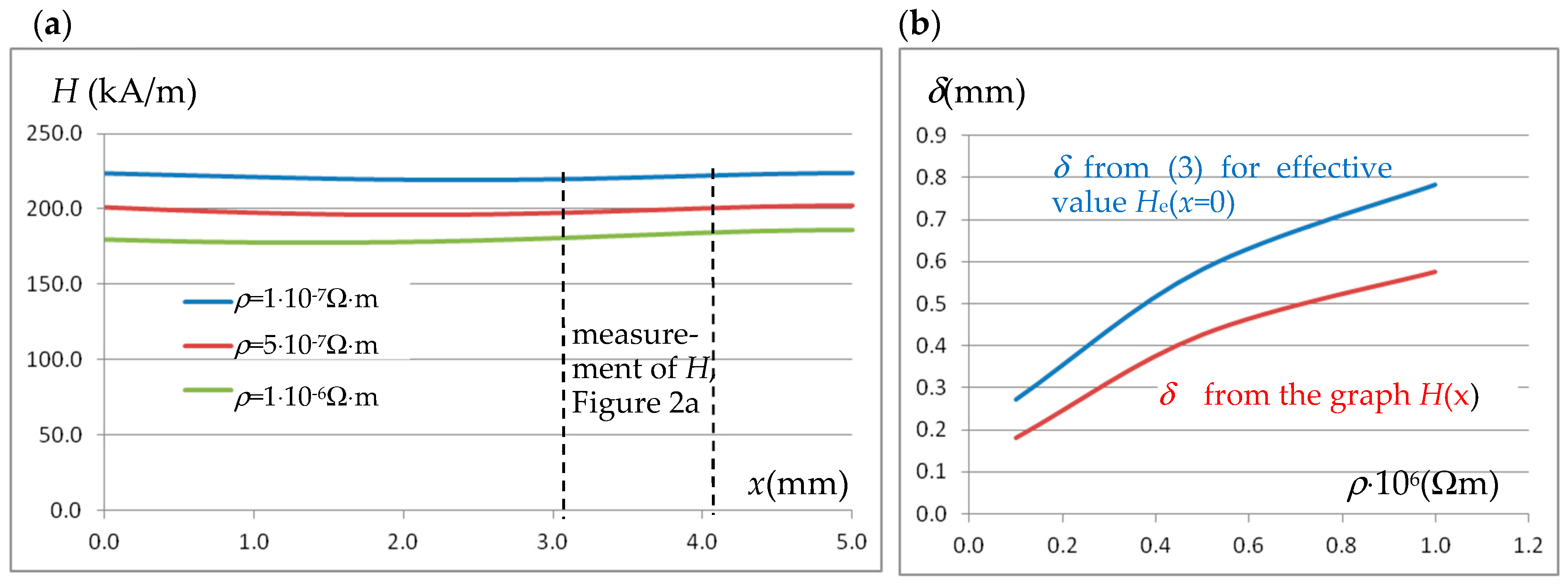
The distribution of the amplitude of the magnetic field intensity H in the near-surface layer at half the thickness of the cylindrical sample (from point P_S into the sample, Figure 2a) and the values of the penetration depth δ at different resistivities ρ of the sample material are given in Figure 8a.

For the magnetic permeability that changes with the magnetic field intensity H, the value of the penetration depth was determined graphically from the H(x) distribution, as the distance over which the intensity H₀ decreases e times. Figure 8a also shows the values of relative magnetic permeability at the surface point P_S of the charge (corresponding to the value of the H₀ amplitude at this point). Using the graphically determined values of the penetration depth and a_cal calculated from (7), Figure 8b shows the absolute values of the error $\epsilon =(a-a_{cal})/a$ in the estimation of thermal diffusivity.

The obtained errors are relatively small, which on the one hand indicates that the relationship (7) determined in linear simulation analyses can be used for real nonlinear magnetic materials and, on the other hand, is an obvious result of the high magnetic saturation of the sample material during impulse excitation. As shown in Figure 8a, with the inductor current amplitudes used in the method of estimating thermal diffusivity, the values of relative magnetic permeability on the surface of the charge (corresponding to the amplitude of the magnetic field intensity) are usually below the level of μ_r = 10.

The error results presented in Figure 8b (for graphical determination of δ) are satisfactory, but they cannot be compared to actual measurements on the test stand, where it is not possible to determine the penetration depth graphically, and it must be calculated computationally from (3), which requires the use of a certain equivalent magnetic permeability μ_re. Taking into account that the corresponding magnetic permeability increases deeper into the charge with decreasing H intensity, the value of μ_re should be higher than that occurring on the surface. The value of the permeability resulting from the magnetization characteristics for the effective value of the magnetic field intensity H_0e on the sample surface near the P_S point (in the middle of the sample thickness) was assumed to be the value of the equivalent permeability μ_re.

Figure 9a shows, for the considered cases of magnetically nonlinear charges, the radial distribution of the tangential component of the magnetic field intensity H in the inductor-load gap, halfway through the thickness of the tested sample.

The presented waveforms indicate that (in the vicinity of the P_S point) there is only a slight change in the magnetic field strength across the width of the inductor-load air gap. This area can therefore be used to measure the H₀ field intensity, taken as the intensity on the surface of the charge (the tested material sample). For this purpose, a single-turn measuring coil with a measuring field width of 1 mm was placed at a distance of 3 mm from the surface of the charge (see Figure 2a and Figure 9a), in which the measured induced voltage V_{H_coil} depends on the field intensity H_{H_coil}

$$V_{H\_coil}=\omega {\mu }_0{H}_{{H\_}_{coil}}{F}_{H_{\_coil}}$$

(8)

where F_{H_coil} = π⋅37 × 10⁻⁶ (m)—surface of the coil for measuring the magnetic field intensity and μ₀—magnetic permeability of air.

Figure 9b compares the penetration depth values obtained graphically from the H(x) distribution presented in Figure 8a and those calculated from (3), assuming the relative magnetic permeability μ_re corresponding to the effective value H_e(x = 0) = H_0e of the magnetic field intensity on the sample surface (at point P_S). The presented relationships show that the value of μ_re determined in this way is still too small, which results in an overestimated value of the penetration depth. However, when using formula (7) to estimate thermal diffusivity, the impact of the accuracy of determining the penetration depth on the accuracy of determining the diffusivity is intentionally significantly limited. For this reason, as shown in Figure 8b, differences in the penetration depth values do not result in a significant increase in the thermal diffusivity estimation error.

4. Using Eddy Current Forcing to Estimate Volumetric Heat Capacity

For isothermal systems, the volumetric heat capacity χ can be easily determined by measuring the derivative of temperature changes of the system subjected to step forcing by P_ch power:

$$\chi =\frac{P_{\mathrm{c}\mathrm{h}}}{V_{\mathrm{c}\mathrm{h}}·\frac{\mathrm{d}{T}_{\mathrm{c}\mathrm{h}}}{\mathrm{d}t}}$$

(9)

where P_ch—power dissipated in the charge (tested material sample), V_ch—sample volume and dT_ch/dt—time derivative of sample temperature changes.

In the system of Figure 2a and samples made of non-magnetic materials, this relationship [11] can also be used if the maximum value of the temperature derivative at the control point P_C is used. As shown, the time Δ_Ct to reach this maximum does not exceed five times the half-response time Δ_Ct < 5⋅t_1/2 determined in the thermal diffusivity test. The expected errors in determining the volumetric heat capacity for the considered non-magnetic materials can be estimated at only a few percent. However, using (9) requires not only information about the maximum value of the derivative but also about the value of power dissipated in the sample. For the considered eddy current forcing in the sample, this power can only be determined indirectly as follows:

$$P_{\mathrm{c}\mathrm{h}}=P_{\mathrm{I}\mathrm{H}\mathrm{S}}-P_{\mathrm{i}\mathrm{n}\mathrm{d}}$$

(10)

where P_IHS—power delivered to the inductor-charge system and P_ind—power losses in the inductor.

The P_IHS power in the considered power supply system (Figure 1) can be measured as the active power supplied to the IHS, while measuring the power losses in the inductor is technically difficult to implement in real-world conditions for estimating the volumetric heat capacity of the sample material. It can be performed during system calibration (maintaining the operating frequency value) and transferred to the value of the equivalent resistance of the inductor, which, with a known current value, gives information about the P_ind loss power in the inductor. However, such an approach is only possible when the material parameters of the charge, that is, resistivity and magnetic permeability, do not affect the value of the equivalent resistance of the inductor (that is, the P_ind value at a given current intensity and frequency). For non-magnetic samples [11], this effect is negligible and can be neglected.

Assuming the magnetic linearity of the charge, the influence of the resistivity and relative magnetic permeability of the sample material on the losses in the inductor was analysed. Figure 10a shows the relationship P_ind(μ_r,ρ) at the inductor current I = I_C = 300 A and f = 40 kHz. The graphs in Figure 10a confirm that there is a slight influence of the resistivity ρ of the sample material on P_ind when its magnetic permeability μ_r ≈ 1. With increasing permeability values, especially with higher resistivity values ρ, this influence increases significantly, although it is usually much smaller than 10%. It should be emphasized here that, unlike the impulse estimation of thermal diffusivity described above, carried out with short-term Δt but large I_D values of the inductor current (which leads to strong magnetic saturation of the sample), volumetric heat capacity measurements are carried out with many times longer Δ_At but significantly weaker I_C excitations inductor current so that the sample temperature increases by only a few degrees. For magnetic charges, this leads to weak magnetic saturation and much higher magnetic permeability values at the surface, and thus the possibility of a greater impact on the P_ind value.

For this reason, for magnetic materials, in order to minimize the error in estimating thermal accumulation, it is advisable to correct the inductor resistance value (P_ind loss value) as a function of the resistivity and magnetic permeability of the material of the tested sample. Such corrections as a function of the resistivity and magnetic permeability of the material of the tested sample were also carried out in the thermal diffusivity estimation procedure described above by entering the penetration depth values into formula (7).

Taking into account the power-law shape of the curves presented in Figure 10a, correcting the P_ind value for μ_r > 1 can be based on the relationship:

$$P_{\mathrm{i}\mathrm{n}\mathrm{d}}=P_{\mathrm{i}\mathrm{n}\mathrm{d}}\left({\mu }_r=1\right){\mu }_r^{[0.06+0.0035·\ln \left(\rho \right)]}$$

(11)

Using (11), Figure 10b shows exemplary waveforms of functions approximating P_ind(μ_r) for several different values of resistivity ρ of the sample material. The magnetic permeability value necessary when using (11) should be determined on the basis of the magnetization characteristics B(H) of the sample material and the effective value of the magnetic field intensity H_{H_coil} measured with the probe described above. Measurements should be performed during the volumetric heat capacity estimation procedure. The necessary resistivity value of the sample material will be determined in the resistivity determination procedure described below. The procedures for determining thermal diffusivity, accumulation and resistivity are carried out in a sequential cycle. The first of these procedures requires a short, strong current pulse, and the second requires a much weaker but much longer excitation, while the third can be performed with both long and short excitation. Estimating resistivity does not require knowledge of thermal parameters (diffusivity and accumulation), so there is no implicit function of the material dependencies sought.

Apart from the correction of the P_ind loss power value presented above, the procedure for estimating volumetric heat capacity, including during the temperature characteristic estimation cycle, can be performed in a manner analogous to that presented in [11] for non-magnetic materials.

5. Procedure for Estimating the Resistivity of a Sample’s Magnetic Material by Eddy Current Forcing

Knowledge about the resistivity value of the processed material is a very important technical parameter, especially in processes such as induction heating, where the heating effect is strongly dependent on this parameter. For magnetic materials and a wide range of potential resistivity variability ρ = (5 × 10⁻⁸ ÷ 4 × 10⁻⁶) Ωm, the possibility of estimating the resistivity value at the station in Figure 2a was examined. 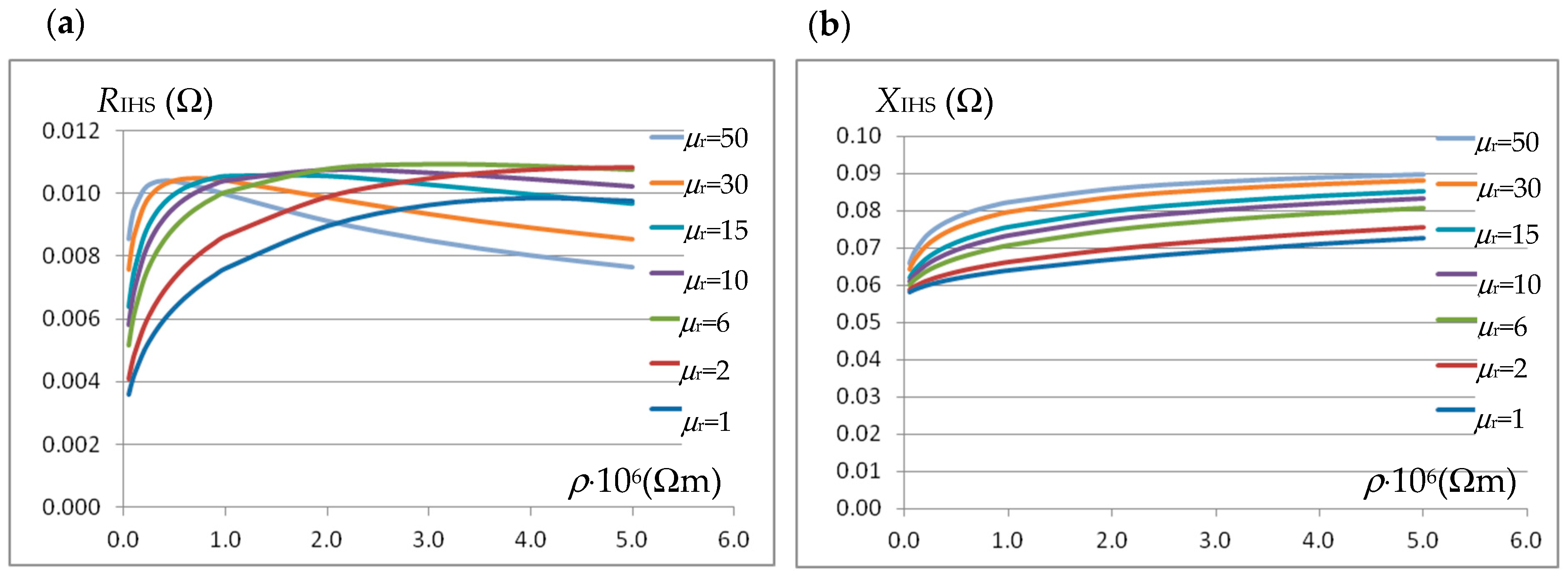In a measurement system such as in Figure 2, based on eddy currents, the resistivity of the test sample material affects both the resistance R_IHS and the reactance X_IHS of the induction heating system. For the above-mentioned resistivity variability, Figure 11 shows the simulation-calculated changes in R_IHS(ρ) and X_IHS(ρ) for different values of the magnetic permeability of the linear material of charge. As shown in Figure 11a, the resistance change function R_IHS(ρ) is not monotonic, and with the increase in magnetic permeability, the beginning of the resistance decrease occurs for increasingly lower resistivity values. The R_IHS resistance measurement cannot therefore be used to estimate resistivity, even with a known magnetic permeability value. Although the reactance change function X_IHS(ρ) is monotonic, the derivative of the changes is small, which also makes it of little use for estimating resistivity.

For this reason, an additional single-turn coil was introduced in the system in Figure 2a to measure the magnetic flux. To ensure the greatest possible impact of the charge material on the V_coil voltage induced in the coil, its diameter should be as close as possible to the diameter of the charge. Taking into account the thermal aspect (heating of the sample when estimating the temperature characteristics of material parameters), the coil diameter was set at D_coil = 33.5 mm. For samples with different resistivities and magnetic permeabilities, the voltage response of the coil to the excitation current of the inductor I = 300 A and f = 40 kHz was calculated. To better illustrate the nature of the obtained waveforms, both the V_coil(ρ) dependence (Figure 12a) for different values of μ_r and the V_coil(μ_r) dependence (Figure 12b) for various ρ values are presented.

Comparing the graphs from Figure 11b and Figure 12a, it can be easily seen that, as assumed, the V_coil(ρ) voltage signal is more sensitive to changes in the resistivity of the sample material than the X_IHS(ρ) signal. It is also visible that the value of the V_coil voltage is similarly influenced by both the resistance and the relative magnetic permeability of the material. This is in line with expectations because, for a "long" inductor-charge system, the magnetic flux penetrating the load is proportional to the square root of the product of resistivity and magnetic permeability. In the considered "short" inductor-charge system, with the diameter D_coil significantly larger than the diameter d of the sample, it can be seen that for the upper range of the considered variability of ρ and μ_r, there are very small sensitivities of the induced voltage V_coil to changes in ρ and μ_r. So, as the values of ρ and μ_r increase, the accuracy of their estimation based on the value of the induced voltage V_coil decreases.

The value of magnetic permeability affects V_coil, but in real nonlinear systems (as presented above when discussing the estimation of thermal diffusivity), this value varies deeper into the charge. For the considered dimensions of the sample, with a diameter of d = 30 mm and a frequency of f = 40 kHz, it is not possible to determine the magnetization characteristics B(H) based on the V_coil test. One can only conclude about the magnetic permeability μ_r of the surface layer. However, such information may be completely sufficient to estimate the resistivity of magnetic samples based on V_coil. The measurement of the V_coil voltage is therefore intended to determine the resistivity of the sample material with a known value of μ_r on its surface, which in turn, with the known B(H) characteristic, can be estimated (as discussed above) by measuring the effective value of the magnetic field strength H_{H_coil} with the probe described above. Determination of the B(H) characteristic itself can also be carried out using the same generator for induction heating, but in a different measurement system and with a different shape (triangle) and frequency of the forcing current (which is not described in detail in this article).

Taking into account that for large values of μ_r, the steepness of the V_coil(ρ) characteristic decreases, it is advisable to estimate the resistivity at high magnetic saturation of the sample (high inductor current), which leads to small values of μ_r. Such conditions occur during the thermal diffusivity estimation described above. When estimating the volumetric heat capacity, low inductor currents are used in order to obtain only a few-degree increase in the sample temperature. For magnetic materials, the resistivity estimation procedure must be performed together with the diffusivity estimation procedure (for non-magnetic materials, it may as well be combined with the volumetric heat capacity estimation procedure [11]). Further considerations will be made assuming that the relative magnetic permittivity of the tested material is μ_r < 40.

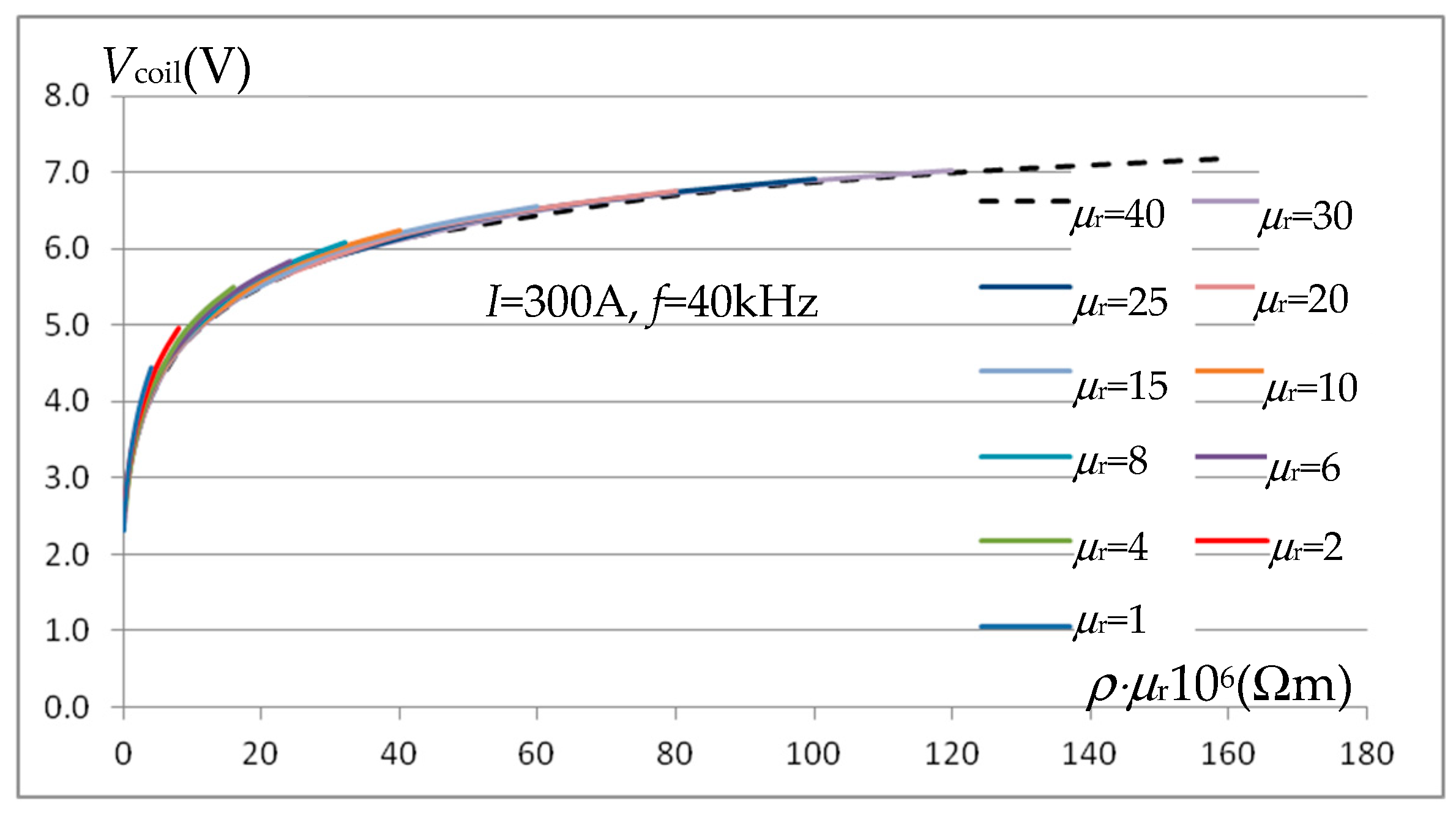
Taking into account the similar influence of ρ and μ_r on the V_coil voltage, it was examined whether, in the considered system (as in the "long" system), it is also possible to talk about the unambiguity dependence of V_coil(ρ⋅μ_r) on the product of these parameters. Figure 13 shows the family of characteristics V_coil(ρ⋅μ_r) obtained from the characteristics presented in Figure 12, that is, determined while maintaining constant values of μ_r. The obtained waveforms indicate that with an error not exceeding 4%, one V_coil(ρ⋅μ_r) characteristic can be used, which significantly facilitates the resistivity estimation procedure.

With the assumed magnetic linearity and maintaining the frequency, the value of the voltage V_coil(ρ⋅μ_r) is proportional to the value I of the exciter current. The approximation of the curve in Figure 13 using the function can therefore be performed for any current value.

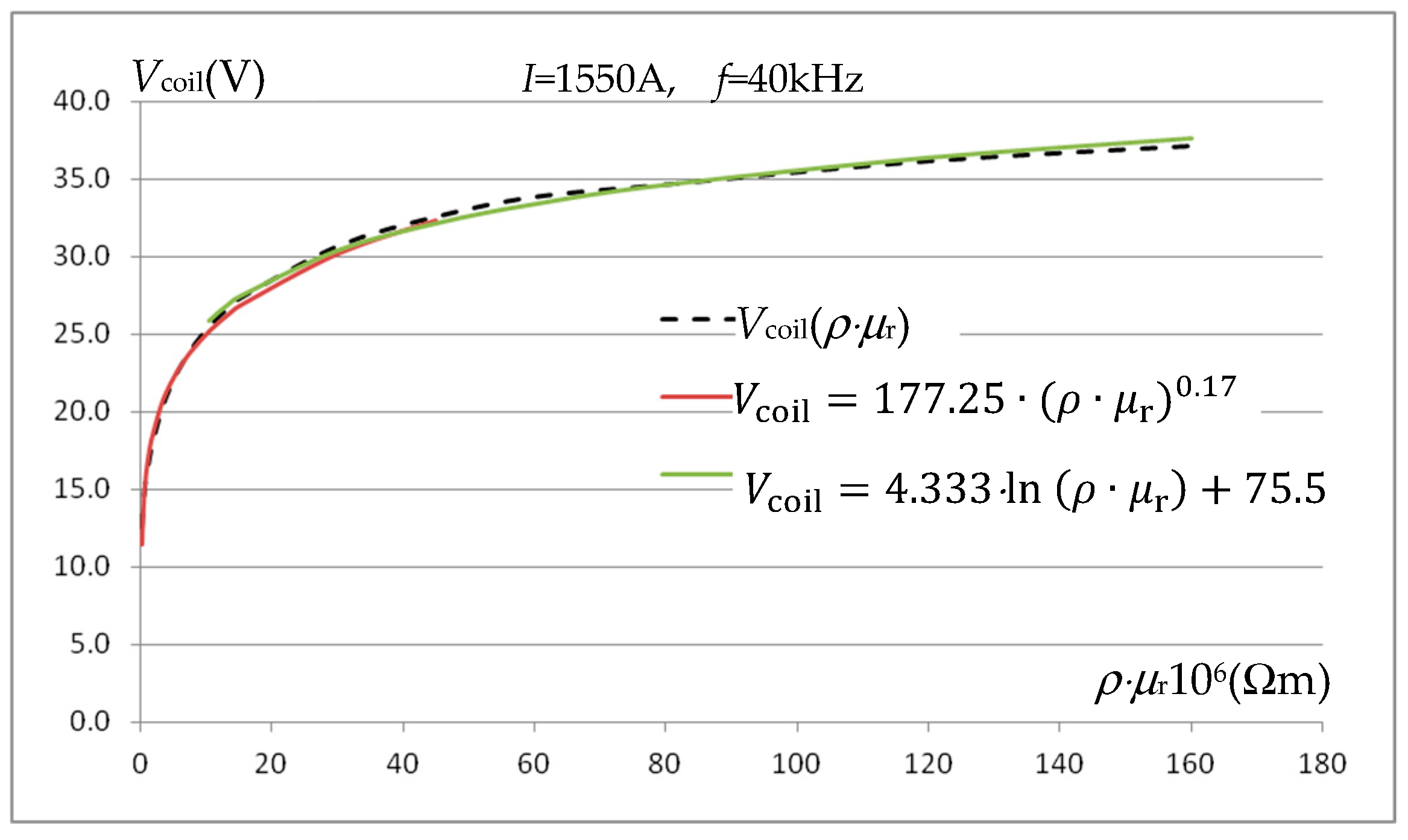
As stated above, the estimation of the resistivity of magnetic materials should be performed at high inductor currents, preferably when estimating thermal diffusivity implemented in the system from Figure 2 (with a current of I = 1550 A). For excitation with an inductor current of I = 1550 A at a frequency of f = 40 kHz, the relationship V_coil(ρ⋅μ_r) can be approximated with an error of less than 3% by the following dependencies:

$$\begin{array}{l}-\mathrm{for}{V}_{\mathrm{coil}}<(25÷30)\mathrm{V}{V}_{\mathrm{c}\mathrm{o}\mathrm{i}\mathrm{l}}=177.25{·(\rho ·{\mu }_{\mathrm{r}})}^{0.17}\\ -\mathrm{for}{V}_{\mathrm{coil}}>(25÷30)\mathrm{V}{V}_{\mathrm{c}\mathrm{o}\mathrm{i}\mathrm{l}}=4.333·\mathrm{l}\mathrm{n}\left(\rho ·{\mu }_{\mathrm{r}}\right)+75.5\end{array}$$

(12)

Figure 14, for I = 1550 A and frequency f = 40 kHz, presents a graphical approximation of the V_coil(ρ⋅μ_r) relationship with functions (12).

6. Algorithm for Comprehensive Estimation of Temperature Characteristics of Thermal and Electrical Properties of Conductive Ferromagnetic Materials

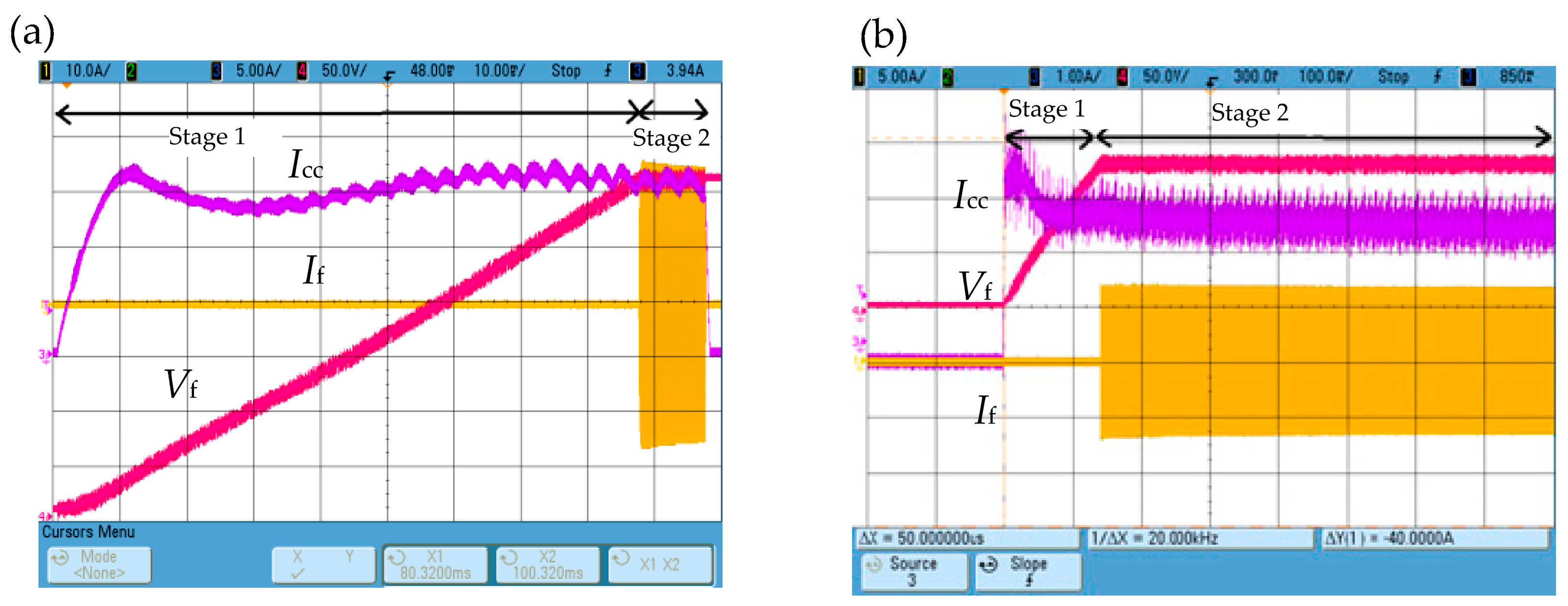
During the implementation of the procedures for estimating thermal and electrical material properties discussed above, a 10 kW generator with IGBT transistors was used as the power source, as shown in Figure 1. An important part of the power supply system is the control system, which is based on an ARM microcontroller and an FPGA-programmable system. It allows you to control the operation of the generator itself, enables cooperation with the host in managing the entire cycle of estimating the temperature characteristics of material properties and also enables cooperation with measurement systems of electrical signals and temperature, as shown schematically in Figure 2c. The control system is equipped with algorithms [11] enabling the implementation of a step-increasing and then constant amplitude of the inverter current. This applies to both short millisecond high-current pulses (similar to Dirac pulses) and long waveforms lasting several dozen seconds, but with a much smaller amplitude. Examples of oscillograms showing the possibility of performing such step excitations of the current amplitude of the inverter I_f (of inductor current I) in the research system Figure 1 are shown in Figure 15.

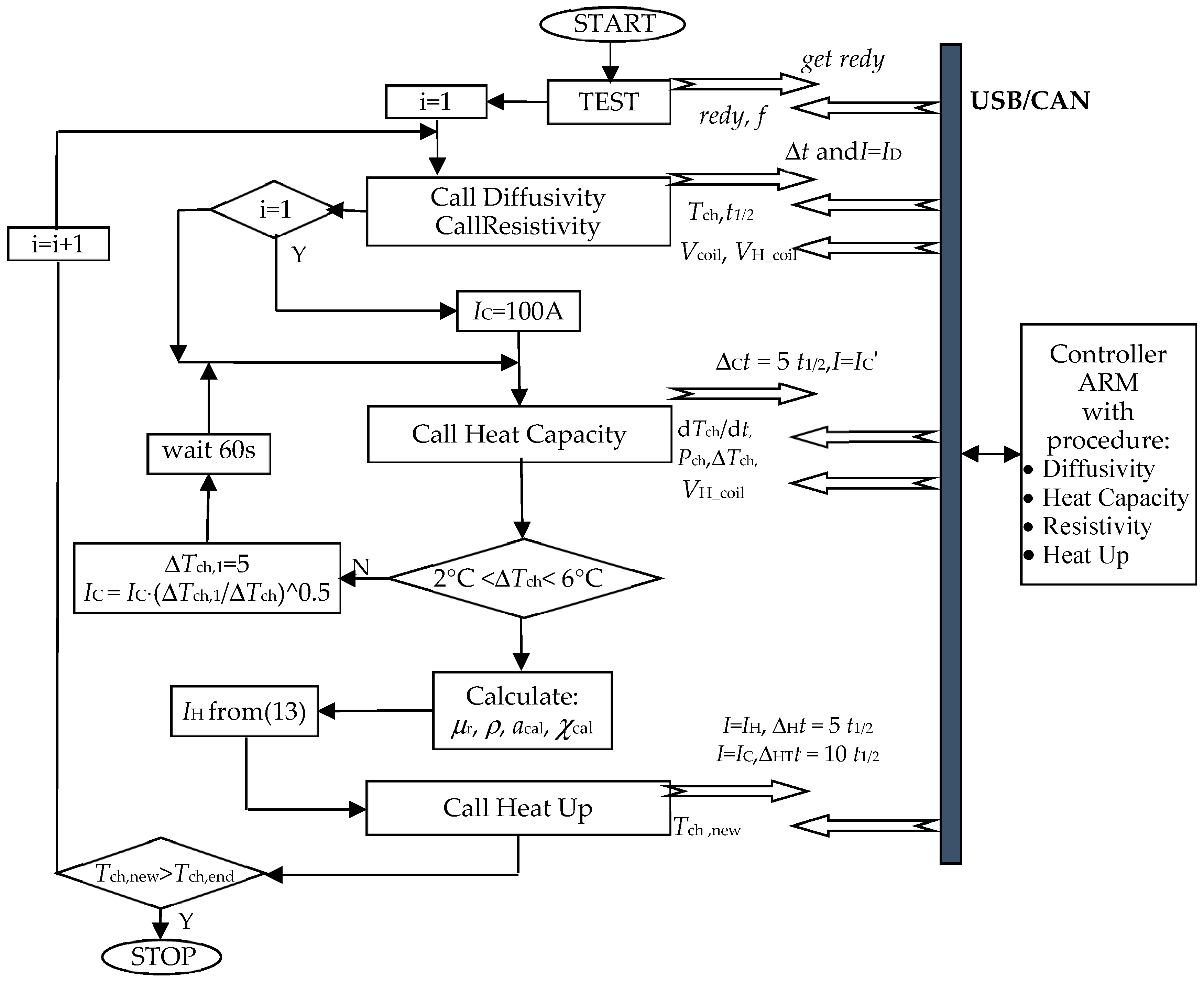
Both the thermal and electrical properties of materials are more or less dependent on temperature. For this reason, industrial practice usually requires knowledge about not only material properties at ambient temperature but also the temperature characteristics of these properties. At the discussed station, as shown in Figure 2, it is possible to comprehensively estimate the temperature characteristics of the conductive properties of the magnetic materials discussed above by sequentially implementing the diffusivity, resistivity and heat capacity procedures. This is a very important functionality of the discussed method. Using eddy current heating, it is possible to successively increase by step Δ_stepT_ch the base temperature of the tested sample (Heat Up procedure) and to sequentially estimate the parameters at different temperatures of the tested material. For magnetic materials, knowledge of the previously determined magnetization characteristic B(H) is required. A simplified algorithm for the comprehensive estimation of the temperature characteristics of thermal diffusivity, resistivity and volumetric heat capacity for conductive magnetic materials is shown in Figure 16.

The Heat Up procedure should enable the sample of the tested material to achieve (and in the shortest possible time) a thermally steady state at a new base temperature level. This requires providing the control system with information about the approximate values of power and its delivery time for this state to be achieved. The knowledge obtained in the first measurements about the volumetric heat capacity χ_cal at the ambient temperature (or in the previous measurement step of the characteristic) makes it possible to approximately determine the energy E_H needed to increase the enthalpy of the tested sample by the desired step of temperature Δ_stepT_ch. The value of thermal diffusivity a_cal measured on the basis of time t_1/2 (it affects the intensity of sample temperature equalization) may be helpful in determining the time Δ_Ht and the P_H power (and the value of the inductor current I_H allowing to obtain P_H) to provide energy E_H. As presented in [11], it can be assumed that the time Δ_Ht should be Δ_Ht = 5⋅t_1/2. The value of the I_H current (as well as the value of the I_C current for estimating volumetric heat capacity) can be approximately determined using a trial test impulse of the inductor current when starting the volumetric heat capacity estimation procedure. In the absence of preliminary information about both the volumetric heat capacity and the resistivity of the sample, it is difficult to determine the value of the inductor current, which, when estimating the volumetric heat capacity, will lead to an appropriate (that is, by several degrees) increase in the sample temperature.

For the sample volume V_ch considered in the system in Figure 2a and the assumed possible range of variability ρ and μ_r, the test effective value of the inductor current was set at I_C = 100 A. By measuring the power value P_ch,100 supplied to the tested sample, the value of the inductor current can be corrected in the next test to obtain the required power in the charge (sample). In the case of determining the value of the current I_H appropriate to increase the enthalpy of the sample by E_H in time Δ_Ht, the following relationship can be used:

$$\begin{array}{c}{I}_{\mathrm{H}}=\sqrt{\frac{E_{\mathrm{H}}/{∆}_{H}t}{P_{\mathrm{c}\mathrm{h},100}}}·100\\ \mathrm{for}:\\ E_{\mathrm{H}}={\chi }_{\mathrm{c}\mathrm{a}\mathrm{l}}{V}_{\mathrm{c}\mathrm{h}}{∆}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}{T}_{\mathrm{c}\mathrm{h}}\end{array}$$

(13)

After the time Δ_Ht of supplying P_H power, the current value should be reduced to a level that covers heat losses from the sample to the environment, that is, no change in temperature at the measurement point P_C (thermal steady state). To improve the speed of operation of the temperature stabilizing control system, after the time Δ_Ht, the value of the exciter current can be rapidly reduced to the level corresponding to the last used I_C value of the volumetric heat capacity estimation procedure. The state of thermal stabilization at the new temperature level should be maintained for at least Δ_HTt = 10·t_1/2.

7. Conclusions

The accuracy of both simulation calculations and the real induction heating process is largely dependent on the knowledge of the actual values of material properties. In induction heating processes, where we usually deal with significant changes in the temperature of the heated charges, knowledge of the temperature characteristics of these material properties is required. This applies to both electrical and magnetic parameters influencing the process of power transfer from the power source to the charge, as well as thermal parameters influencing the value and distribution of temperature in the heated object. These parameters include, in particular, thermal conductivity and specific heat, as well as resistivity and magnetic permeability in the case of magnetic charges. For various types of conductive materials, especially alloys, the values of these parameters vary significantly, and often, even during the heating process, their values change by several hundred percent. With such great diversity and variability, there is often a lack of information about the temperature characteristics of the processed material, and their measurements are, unfortunately, troublesome and expensive. Therefore, it seems reasonable to develop a method allowing for as accurate as possible estimation of these characteristics, preferably on one research stand. Attempts [2,3,4,5,6,7,8,9] to simultaneously determine more than one parameter are usually based on the use of optimization techniques, but especially with a wide range of permissible changes in parameter values, they are burdened with a high risk of error. The solution can be sought [10,11] in the measurement estimation of parameters at one stand, which then, depending on the obtained and required accuracy, can be treated as final results or as an introduction to the optimization process of simultaneous determination of characteristics but with a strongly narrowed range of permissible changes in decision variables (parameter values).

The study shows that even in the case of ferromagnetic materials, it is possible to estimate the temperature characteristics of thermal diffusivity, volumetric heat capacityand resistivity with only a few percent error. All these characteristics can be estimated on the same IHS, that is, for one sample shape and the same power source. It has been shown that by appropriately controlling the transistor power source, it is possible to obtain the required shapes of the inductor currents in the real IHS, that is, to implement the excitations required in the developed measurement procedures. As shown in the study, the estimation of the above characteristics can also apply to ferromagnetic materials with high accuracy. In this case, however, the estimation of these characteristics requires knowledge of the magnetization characteristics B(H), which cannot be determined with the same massive shape of the sample. A preliminary study shows that for a changed shape, it also seems possible to estimate this characteristic using the same, appropriately controlled power source controlled by the same host managing the station’s operation.