Linear Matrix Inequality-Based Robust Model Predictive Speed Control for a Permanent Magnetic Synchronous Motor with a Disturbance Observer
Abstract
1. Introduction
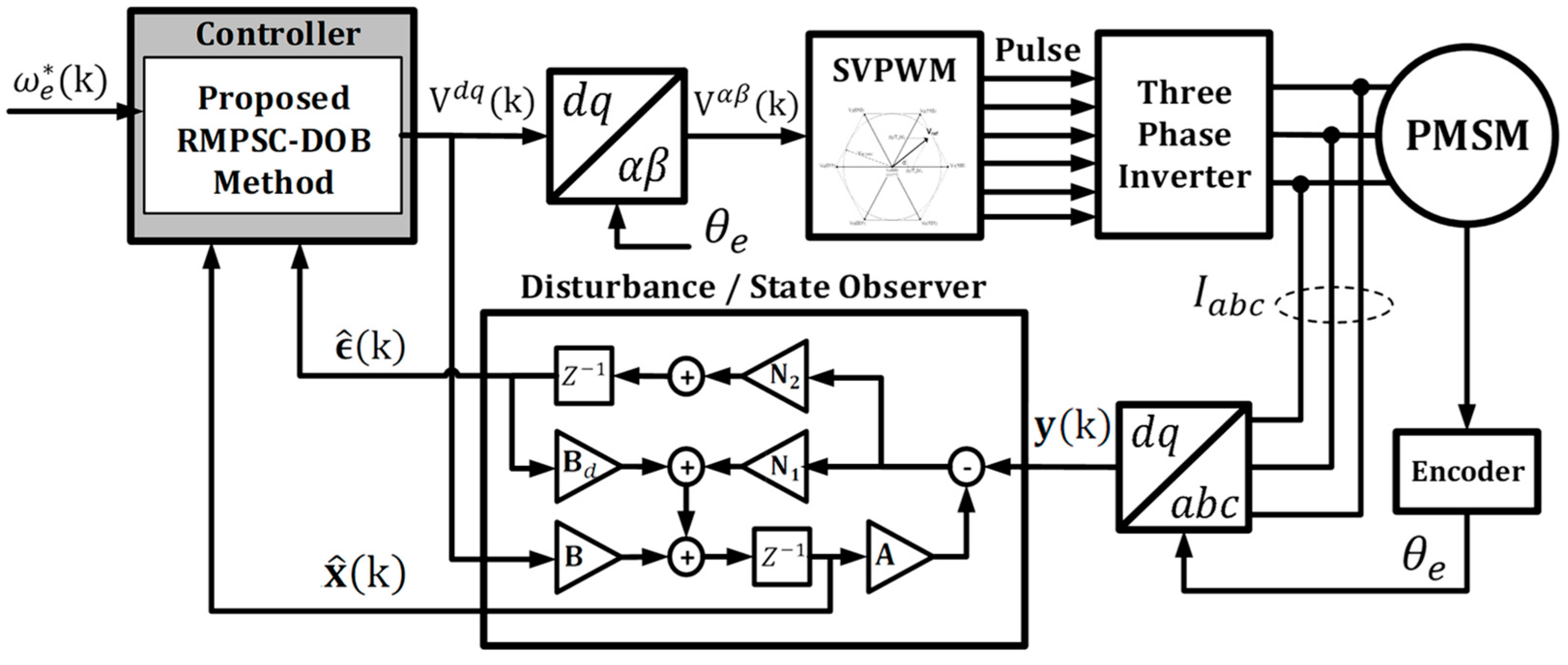
2. System Description
3. Disturbance and State Observer Design
4. Robust Model Predictive Speed Controller (RMPSC) Design
4.1. Steady-State Condition
4.2. Cost Function of the RMPSC
5. Simulation Result
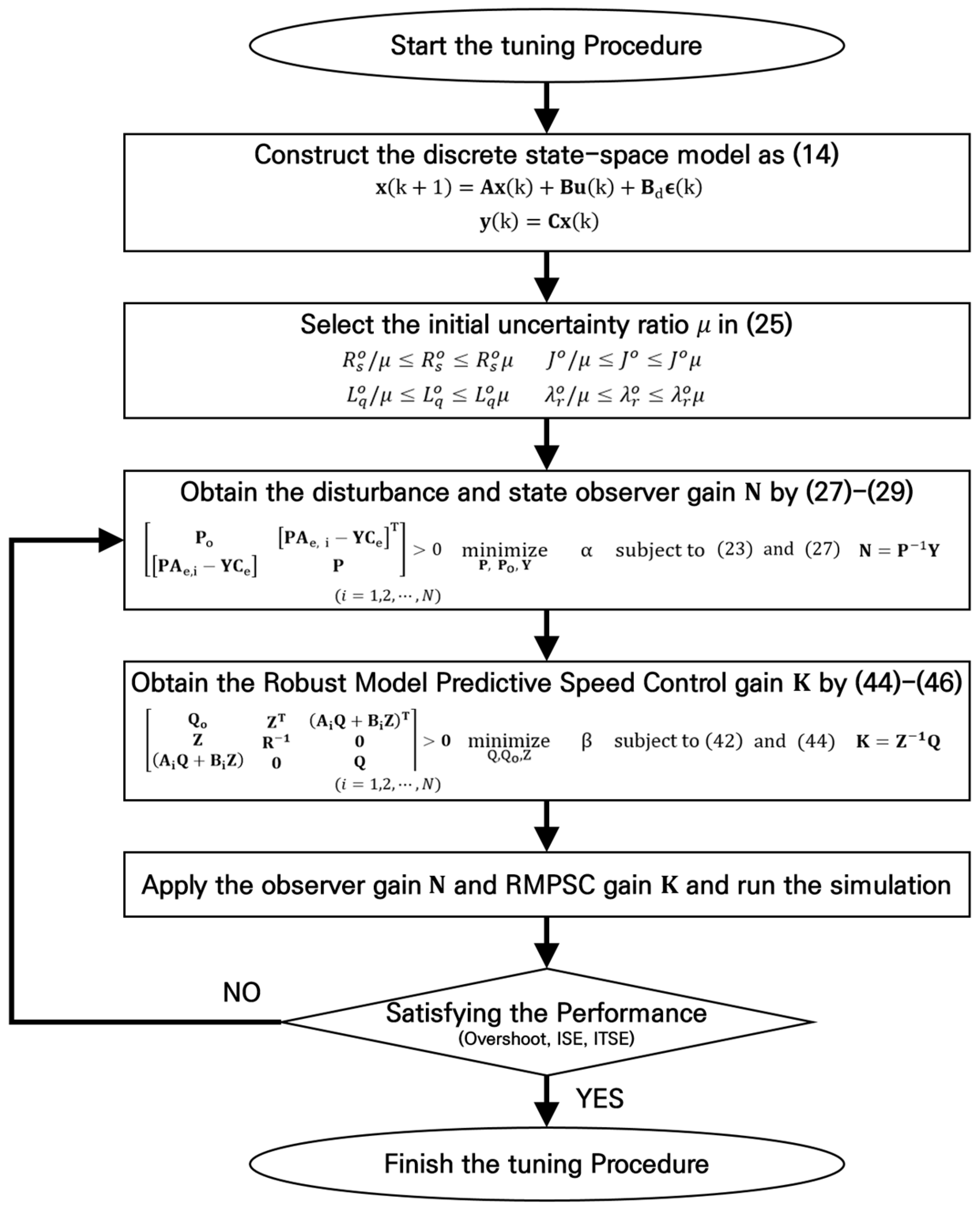
5.1. Tuning Procedure for RMPSC
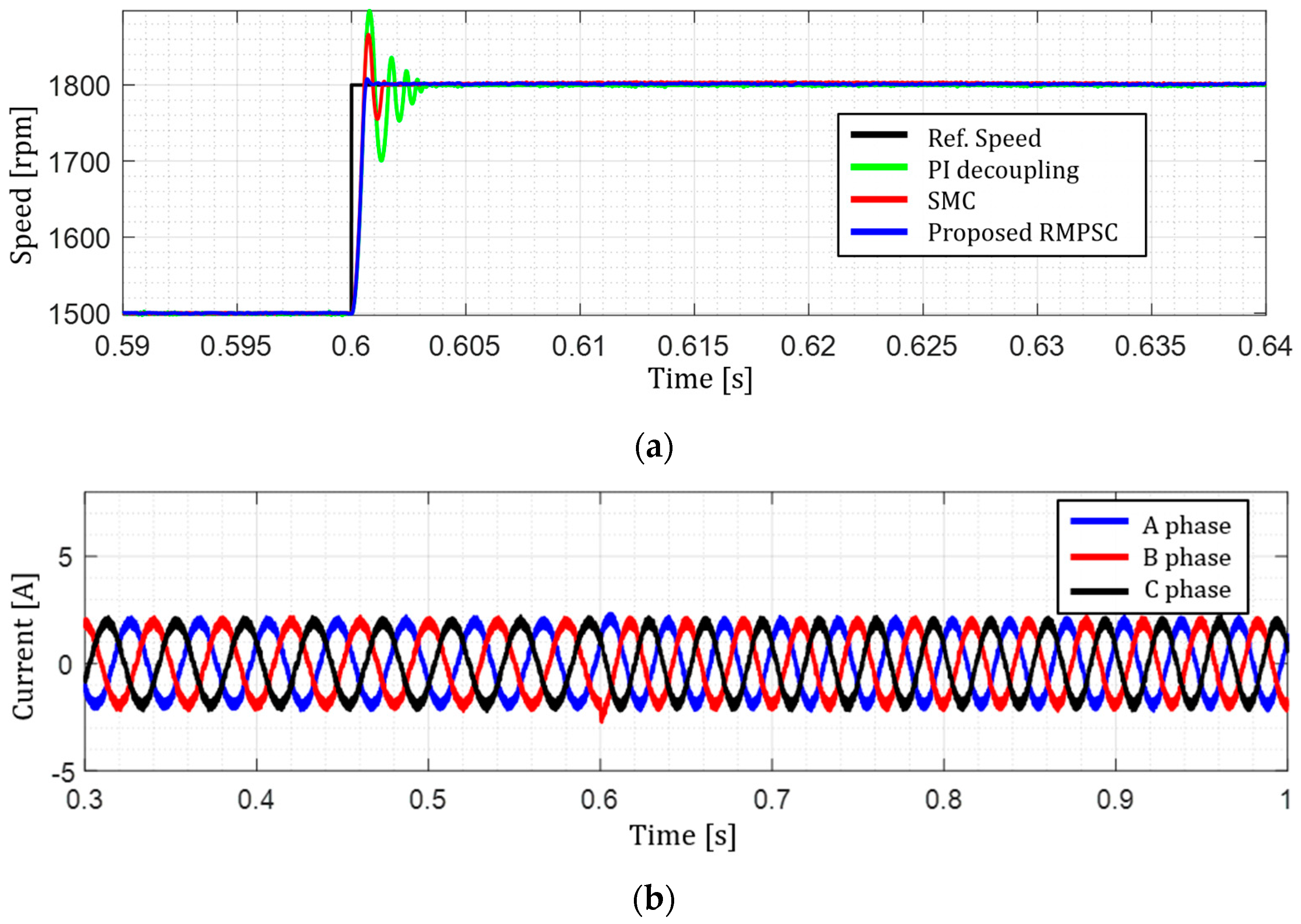
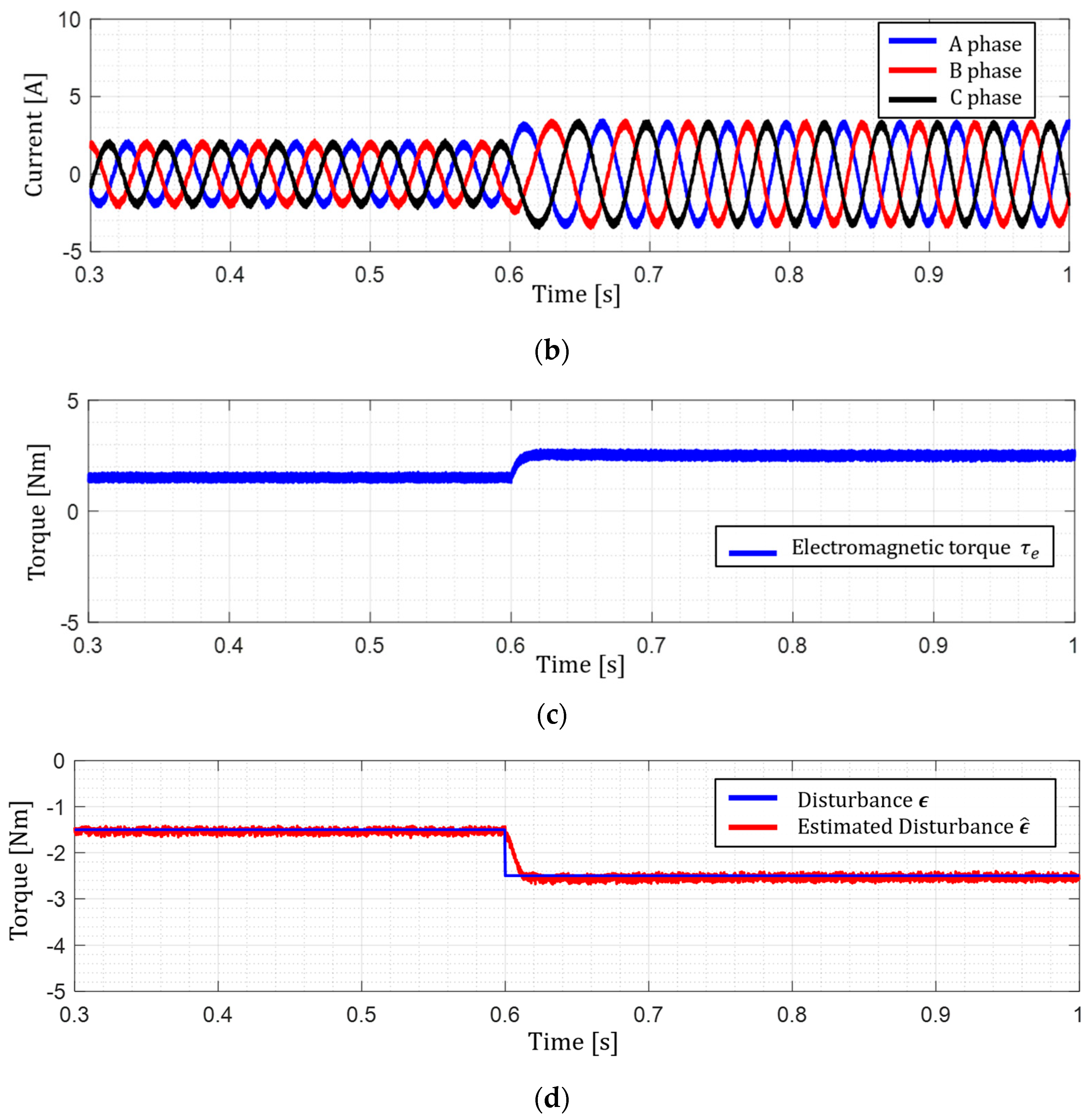
5.2. Simulation Result
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohanraj, D.; Gopalakrishnan, J.; Chokkalingam, B.; Mihet-Popa, L. Critical Aspects of Electric Motor Drive Controllers and Mitigation of Torque Ripple—Review. IEEE Access 2022, 10, 73635–73674. [Google Scholar] [CrossRef]
- Yang, J.; Chen, W.-H.; Li, S.; Guo, L.; Yan, Y. Disturbance/Uncertainty Estimation and Attenuation Techniques in PMSM Drives—A Survey. IEEE Trans. Ind. Electron. 2017, 64, 3273–3285. [Google Scholar] [CrossRef]
- Hasoun, M.; Afia, A.E.; Khafallah, M. Performance Comparison of Two-SVPWM-Strategies Based Vector Space Decomposition Controlled Dual Three-Phase PMSM for Electric Ship Propulsion. In Proceedings of the 2019 7th International Renewable and Sustainable Energy Conference (IRSEC), Agadir, Morocco, 27–30 November 2019; pp. 1–8. [Google Scholar]
- Hori, S.; Doki, S. Examination of Current Sensor Fail-Safe of PMSM current control system which using current and position state estimation techniques. In Proceedings of the 2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 24–27 November 2020; pp. 694–698. [Google Scholar]
- Yuan, T.; Wang, D.; Wang, X.; Wang, X.; Sun, Z. High-Precision Servo Control of Industrial Robot Driven by PMSM-DTC Utilizing Composite Active Vectors. IEEE Access 2019, 7, 7577–7587. [Google Scholar] [CrossRef]
- Gong, C.; Hu, Y.; Gao, J.; Wu, Z.; Liu, J.; Wen, H.; Wang, Z. Winding-Based DC-Bus Capacitor Discharge Technique Selection Principles Based on Parametric Analysis for EV-PMSM Drives in Post-Crash Conditions. IEEE Trans. Power Electron. 2021, 36, 3551–3562. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; Depernet, D.; Djerdir, A.; Cirrincione, M. Disturbance-Observer-Based Complementary Sliding-Mode Speed Control for PMSM Drives: A Super-Twisting Sliding-Mode Observer-Based Approach. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5416–5428. [Google Scholar] [CrossRef]
- Novak, Z.; Novak, M. Adaptive PLL-Based Sensorless Control for Improved Dynamics of High-Speed PMSM. IEEE Trans. Power Electron. 2022, 37, 10154–10165. [Google Scholar] [CrossRef]
- Apte, A.; Joshi, V.A.; Mehta, H.; Walambe, R. Disturbance-Observer-Based Sensorless Control of PMSM Using Integral State Feedback Controller. IEEE Trans. Power Electron. 2020, 35, 6082–6090. [Google Scholar] [CrossRef]
- Zhu, H.; Xiao, X.; Li, Y. PI type dynamic decoupling control scheme for PMSM high speed operation. In Proceedings of the 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010; pp. 1736–1739. [Google Scholar]
- Sant, A.V.; Rajagopal, K.R. PM Synchronous Motor Speed Control Using Hybrid Fuzzy-PI with Novel Switching Functions. IEEE Trans. Magn. 2009, 45, 4672–4675. [Google Scholar] [CrossRef]
- Li, H.; Song, B.; Chen, T.; Xie, Y.; Zhou, X. Adaptive fuzzy PI controller for permanent magnet synchronous motor drive based on predictive functional control. J. Frankl. Inst. 2021, 358, 7333–7364. [Google Scholar] [CrossRef]
- Guo, J.; Fan, T.; Li, Q.; Wen, X. An Angle-Compensating, Complex-Coefficient PI Controller Used for Decoupling Control of a Permanent-Magnet Synchronous Motor. Symmetry 2022, 14, 101. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, W.; Wang, H. Adaptive PI and RBFNN PID Current Decoupling Controller for Permanent Magnet Synchronous Motor Drives: Hardware-Validated Results. Energies 2022, 15, 6353. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Y.; Zhang, X.; Liang, J. A New Reaching Law for Antidisturbance Sliding-Mode Control of PMSM Speed Regulation System. IEEE Trans. Power Electron. 2020, 35, 4117–4126. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, W.; Mu, C.; Liu, Y. Improved Deadbeat Predictive Current Control Combined Sliding Mode Strategy for PMSM Drive System. IEEE Trans. Veh. Technol. 2018, 67, 251–263. [Google Scholar] [CrossRef]
- Liao, Z.; Hao, Y.; Guo, T.; Lv, B.; Wang, Q. Second-Order Sliding Mode Control of Permanent Magnet Synchronous Motor Based on Singular Perturbation. Energies 2022, 15, 8028. [Google Scholar] [CrossRef]
- Leu, V.Q.; Choi, H.H.; Jung, J.W. Fuzzy sliding mode speed controller for PM synchronous motors with a load torque observer. IEEE Trans. Power Electron. 2012, 27, 1530–1539. [Google Scholar] [CrossRef]
- Bao, G.; Qi, W.; He, T. Direct Torque Control of PMSM with Modified Finite Set Model Predictive Control. Energies 2020, 13, 234. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, D.; Huang, L. Generalized multiple-vector-based model predictive control for pmsm drives. IEEE Trans. Ind. Electron. 2018, 65, 9356–9366. [Google Scholar] [CrossRef]
- Xie, W.; Wang, X.; Wang, F.; Xu, W.; Kennel, R.M.; Gerling, D.; Lorenz, R.D. Finite-Control-Set Model Predictive Torque Control With a Deadbeat Solution for PMSM Drives. IEEE Trans. Ind. Electron. 2015, 62, 5402–5410. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, S.; Hu, J.; Huang, D. A Novel Active Disturbance Rejection Control of PMSM Based on Deep Reinforcement Learning for More Electric Aircraft. IEEE Trans. Energy Convers. 2023, 38, 1461–1470. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, S.; Hu, J.; Huang, D. Multiscenarios Parameter Optimization Method for Active Disturbance Rejection Control of PMSM Based on Deep Reinforcement Learning. IEEE Trans. Ind. Electron. 2023, 70, 10957–10968. [Google Scholar] [CrossRef]
- Abu-Ali, M.; Berkel, F.; Manderla, M.; Reimann, S.; Kennel, R.; Abdelrahem, M. Deep Learning-Based Long-Horizon MPC: Robust, High Performing, and Computationally Efficient Control for PMSM Drives. IEEE Trans. Power Electron. 2022, 37, 12486–12501. [Google Scholar] [CrossRef]
- Apte, A.; Joshi, A.; Walambe, R.A.; Godbole, A. Speed Control of PMSM Using Disturbance Observer. IFAC-PapersOnLine 2016, 49, 308–313. [Google Scholar] [CrossRef]
- Singh, S.; Singh, S.; Tiwari, A. PMSM drives and its application: An overview. Recent Adv. Elect. Electron. Eng. Former. Recent Pat. Elect. Electron. Eng. 2023, 16, 4–16. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Huynh, V.K.; Senanyaka, J.S.L.; Robbersmyr, K.G. Robust Multiple-Fault Diagnosis of PMSM Drives Under Variant Operations and Noisy Conditions. IEEE Open J. Ind. Electron. Soc. 2023, 4, 762–772. [Google Scholar] [CrossRef]
- Sun, X.; Yi, Y.; Cao, S.; Liu, H.; Zhang, T. Robust PI-type position controller design for permanent magnet synchronous motor using LMI techniques. In Proceedings of the 2015 Chinese Intelligent Automation Conference: Intelligent Automation, Fuzhou, China, 8–10 May 2015; Lecture Notes in Electrical Engineering. Springer: Berlin/Heidelberg, Germany, 2015; Volume 337, pp. 405–412. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Workman, M. Digital Control of Dynamic Systems; Addison Wesley Longman: Reading, MA, USA, 1997. [Google Scholar]
- Boyd, S.P.; Ghaoui, L.E.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]




| Symbol | Description | Value | Unit |
|---|---|---|---|
| Rated Power | 0.4 | kW | |
| Stator Inductance | 6.71 | mH | |
| Stator Resistance | 1.55 | ohm | |
| Flux Linkage of Permanent Magnets | 0.175 | Wb | |
| Viscous Friction Coefficient | 0.0003 | Nms | |
| Rotational Inertia | 0.0002 | ||
| Pole Pairs | 3 | - | |
| Sampling Time | 100 | μs |
| Overshoot [rpm] | Undershoot [rpm] | ISE | ITSE | |
|---|---|---|---|---|
| 1.0 | 1570 | 1496 | 26.905 | 2.690 × 10−4 |
| 1.3 | 1510 | 1495 | 25.905 | 2.590 × 10−4 |
| 1.5 | 1505 | 1493 | 26.446 | 2.644 × 10−4 |
| 1.7 | 1502 | 1491 | 32.045 | 3.204 × 10−4 |
| 2.0 | 1501 | 1486 | 45.451 | 4.545 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.-J.; Kim, B. Linear Matrix Inequality-Based Robust Model Predictive Speed Control for a Permanent Magnetic Synchronous Motor with a Disturbance Observer. Energies 2024, 17, 869. https://doi.org/10.3390/en17040869
Kim D-J, Kim B. Linear Matrix Inequality-Based Robust Model Predictive Speed Control for a Permanent Magnetic Synchronous Motor with a Disturbance Observer. Energies. 2024; 17(4):869. https://doi.org/10.3390/en17040869
Chicago/Turabian StyleKim, Dae-Jin, and Byungki Kim. 2024. "Linear Matrix Inequality-Based Robust Model Predictive Speed Control for a Permanent Magnetic Synchronous Motor with a Disturbance Observer" Energies 17, no. 4: 869. https://doi.org/10.3390/en17040869
APA StyleKim, D.-J., & Kim, B. (2024). Linear Matrix Inequality-Based Robust Model Predictive Speed Control for a Permanent Magnetic Synchronous Motor with a Disturbance Observer. Energies, 17(4), 869. https://doi.org/10.3390/en17040869







