Design, Detection, and Countermeasure of Frequency Spectrum Attack and Its Impact on Long Short-Term Memory Load Forecasting and Microgrid Energy Management †
Abstract
1. Introduction
- 1-
- The proposed FSA is extended that transforms the load data into the frequency domain and manipulates the amplitudes of dominant frequencies while keeping them in the statistical range of healthy amplitudes to not only cause a huge prediction error but also enhance stealth of the proposed FSA.
- 2-
- FSA is tested on a deep LSTM model to investigate the effectiveness of FSA on the state-of-the-art deep learning model for time-series forecasting. The impact of the attacked LSTM on the EMS’s output of a microgrid is studied as well.
- 3-
- A detection method is proposed, which integrates statistical analysis of the crafted attack and a machine-learning-based classification model to effectively detect the FSA and distinguish it from healthy and noisy signals.
- 4-
- A countermeasure is introduced, based on statistical analysis of the frequency spectrum of healthy signals, to mitigate the impact of FSA on load forecasting.
2. Frequency Spectrum Attack
2.1. FSA Principles
2.2. LSTM-Based Load Forecasting
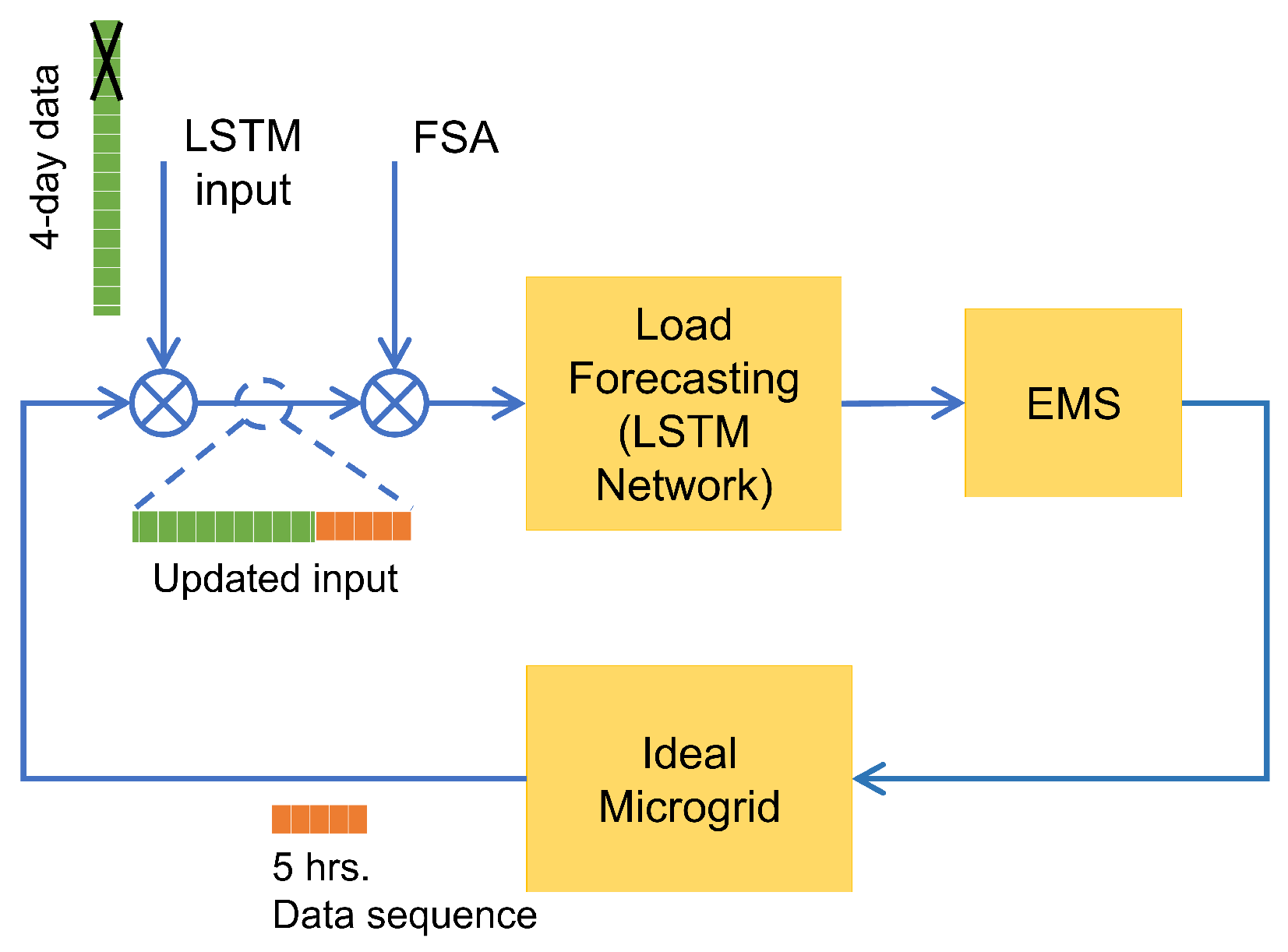
3. FSA Implementation
| Algorithm 1 FSA Implementation |
|
3.1. FSA Results on Load Prediction
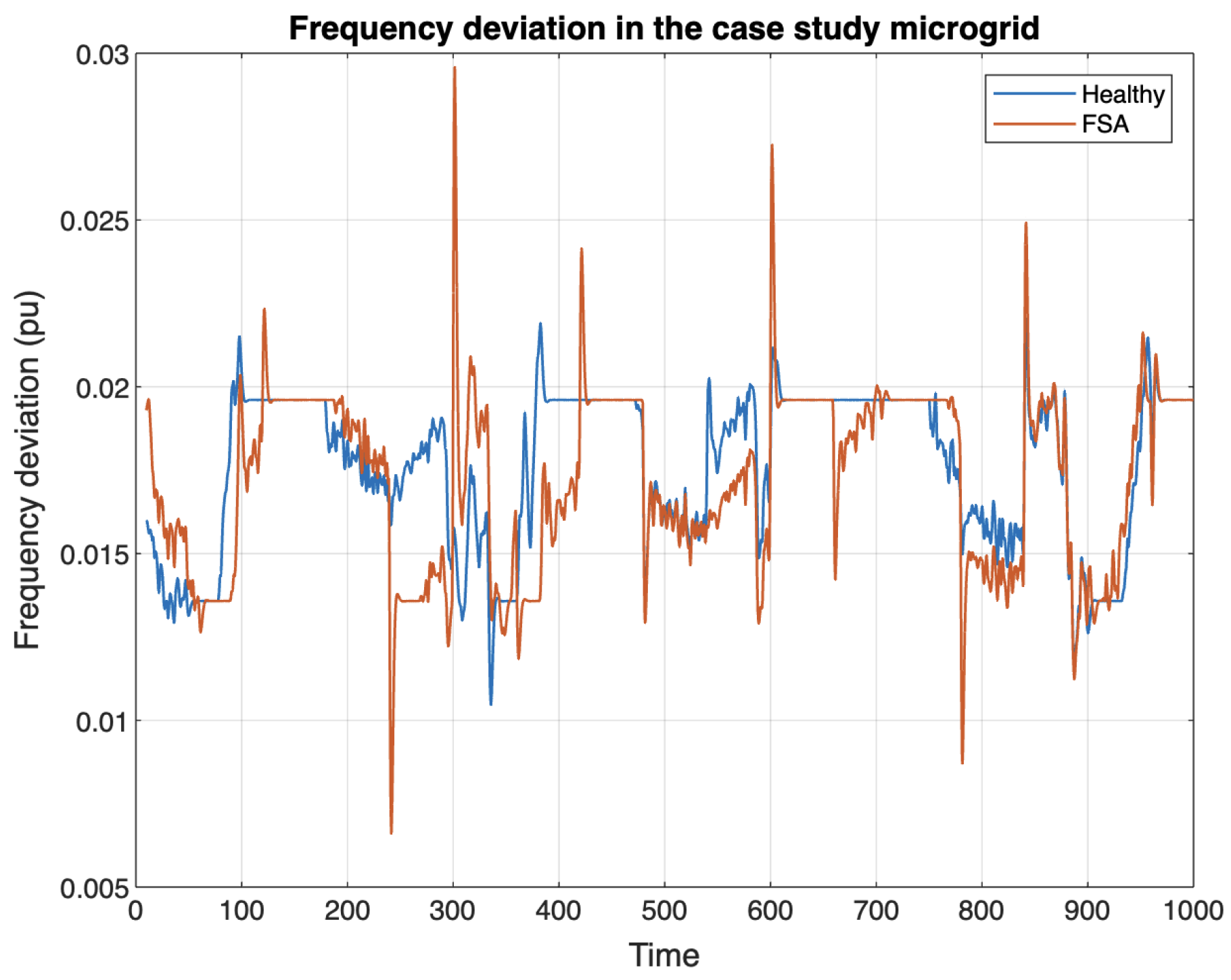
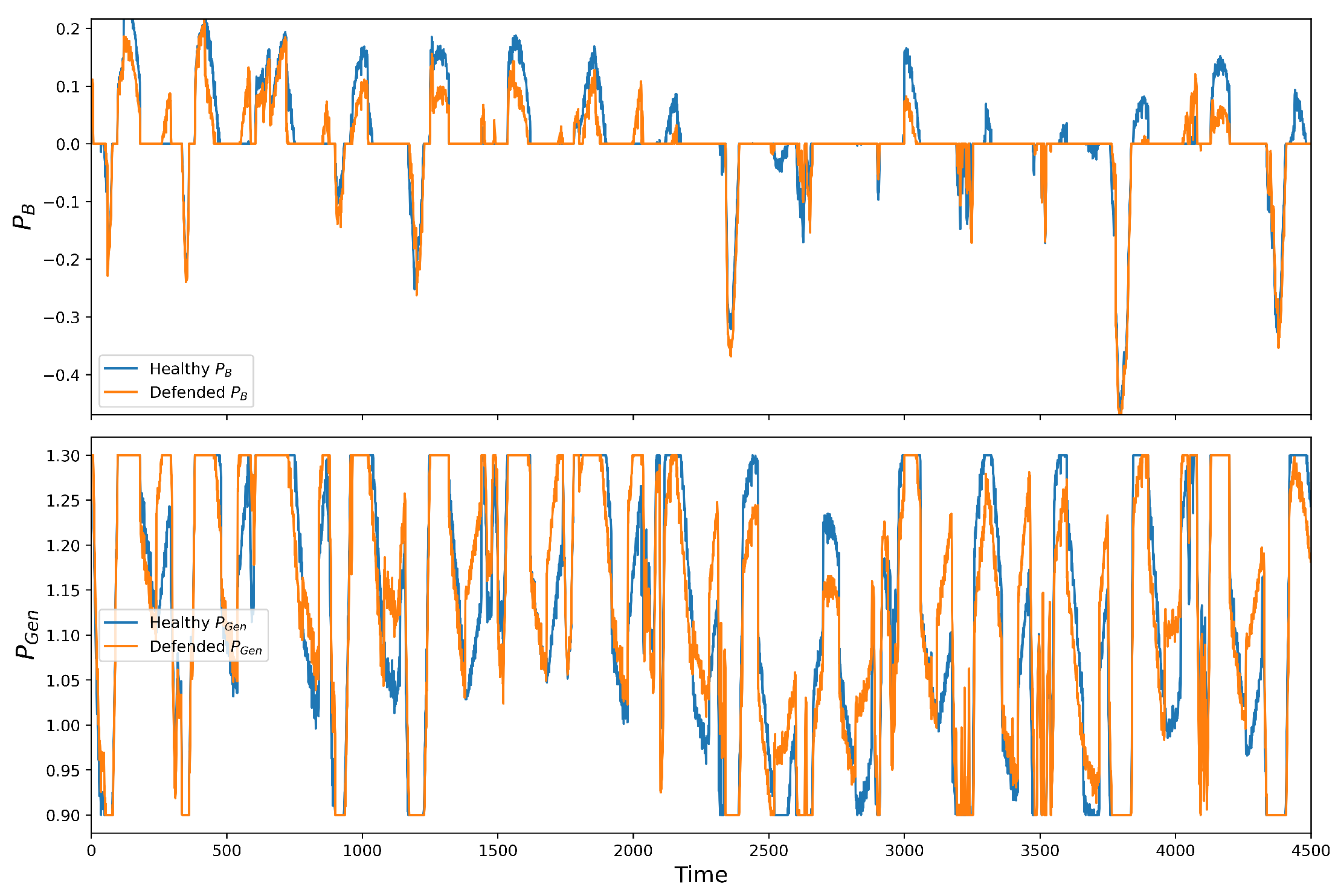
3.2. FSA Results on EMS and Microgrid
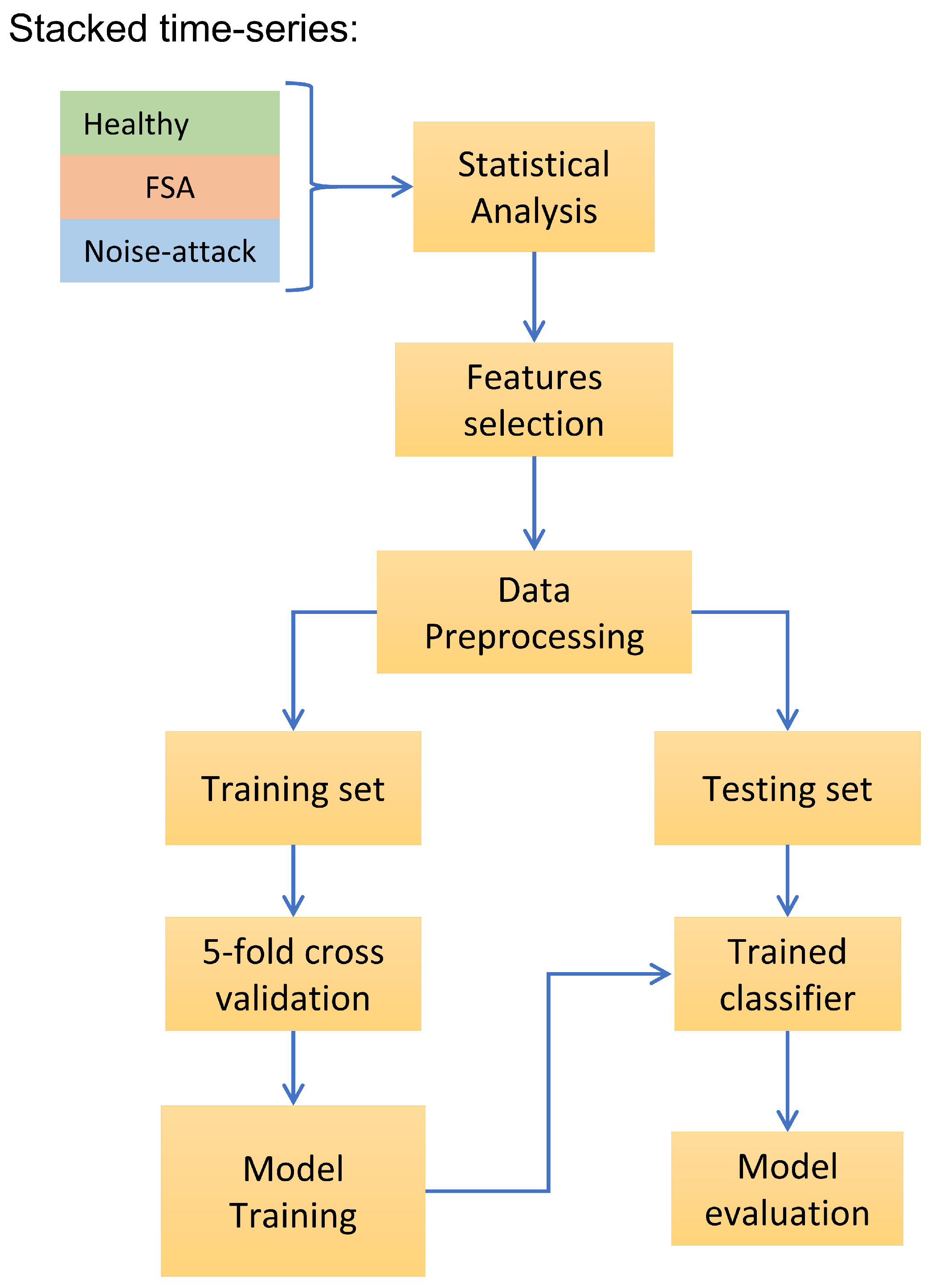
4. FSA Detection
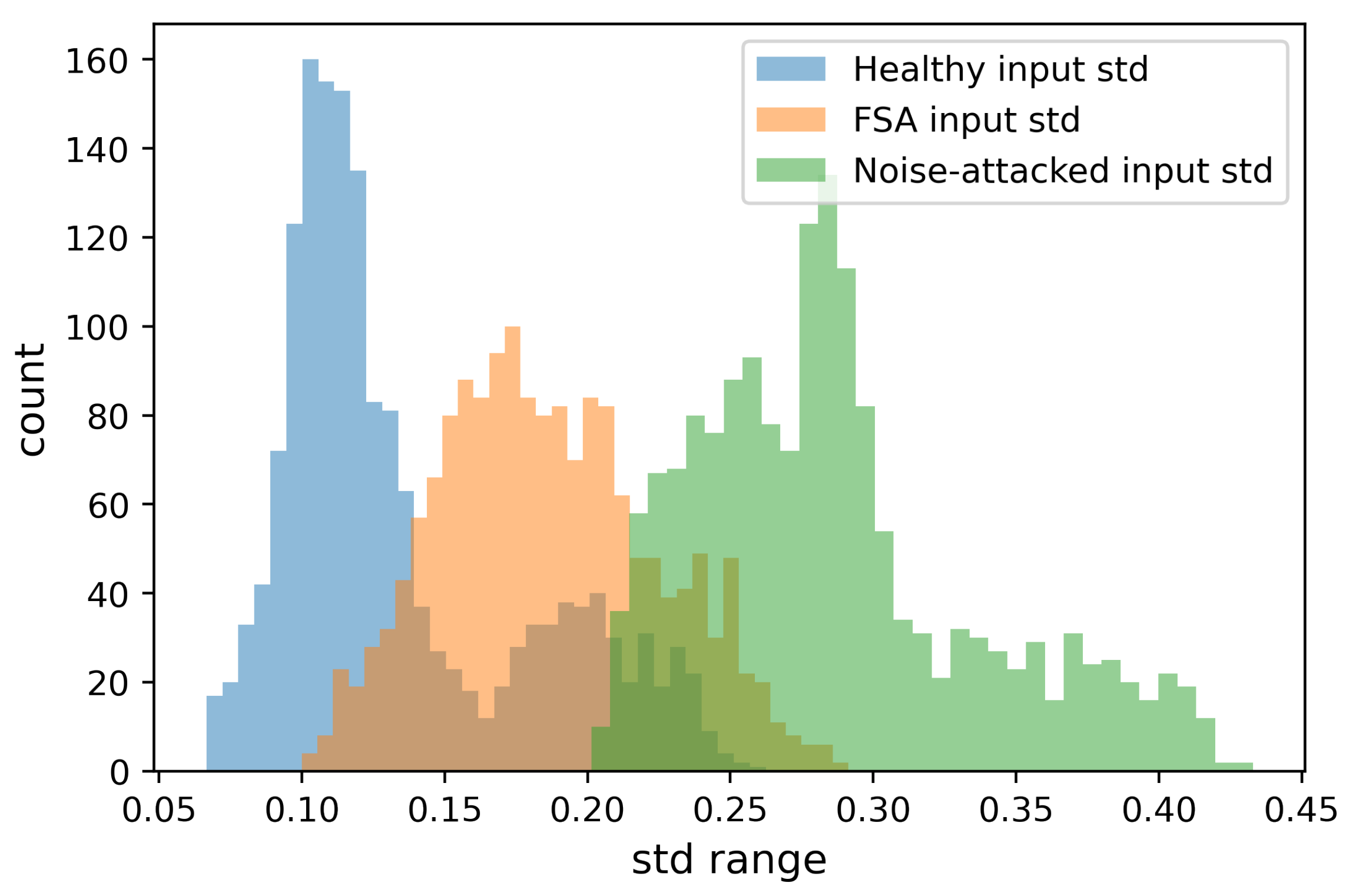
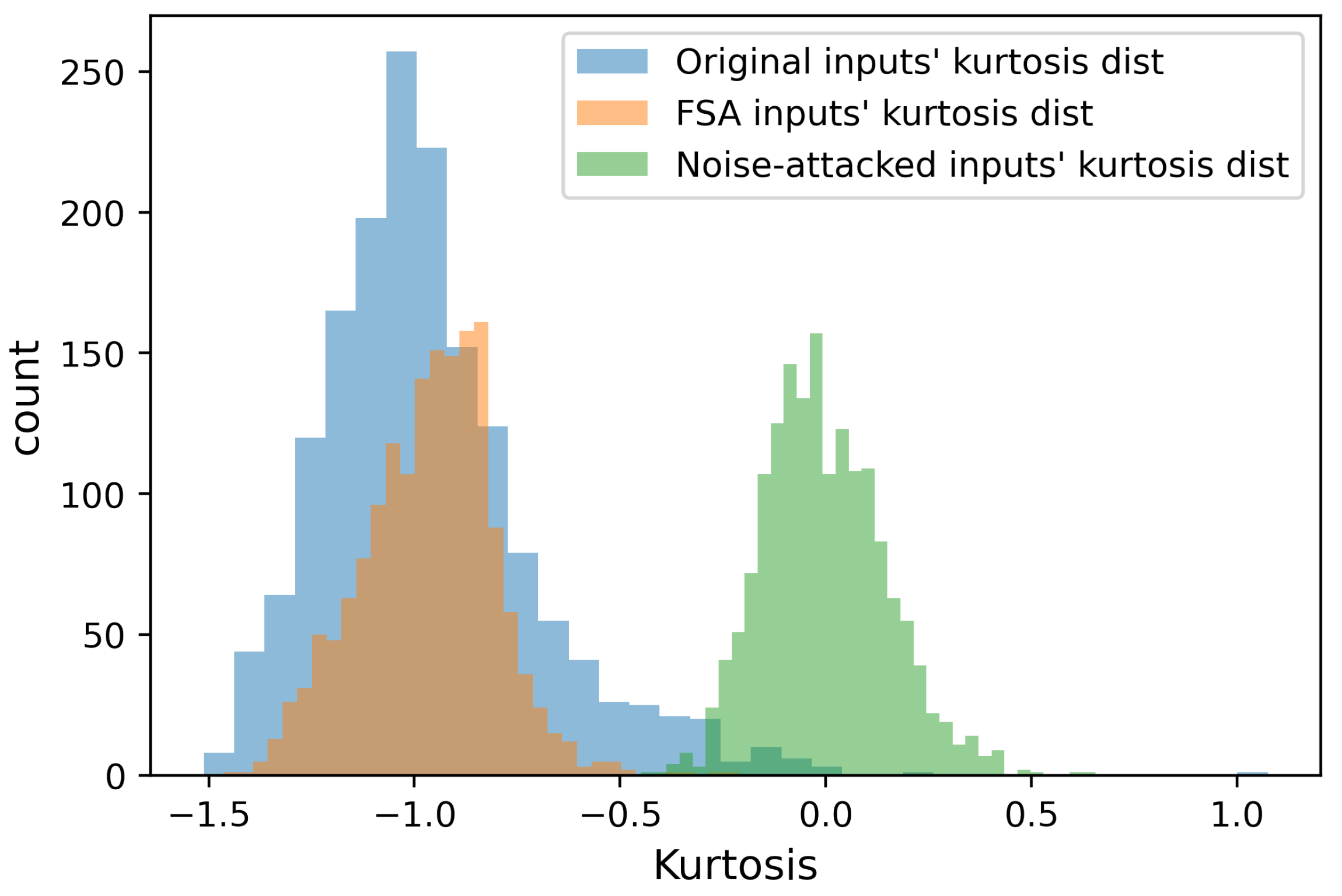
4.1. Explanatory Data Analysis of FSA and Statistical Modeling
4.2. ML-Based Attack Detection
5. FSA Defense
| Algorithm 2 Defense Algorithm |
|
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FSA | Frequency Spectrum Attack |
| FFT | Fast Fourier Transformation |
| IFFT | Inverse Fast Fourier Transformation |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| EMS | Energy management system |
| RNN | Recurrent Neural Network |
| DNN | Deep Neural Network |
| CNN | Convolutional Neural Network |
| MTS | Multiple time series |
| FGSM | Fast Gradient Sign Method |
| PGD | Projected Gradient Descent |
| FDIA | False data injection attack |
| ACE | Area Control Error |
| EDA | Exploratory Data Analysis |
| GA | Genetic Algorithm |
| SNR | Signal-to-noise ratio |
| NREL | National Renewable Energy Laboratory |
| STD | Standard deviation |
| IQR | Interquartile range |
| GLM | Generalized Linear Model |
| CI | confidence interval |
| NT | Number of Trees |
| MD | Maximum Depth of each tree |
| CLT | Central Limit Theory |
References
- Hirsch, A.; Parag, Y.; Guerrero, J. Microgrids: A review of technologies, key drivers, and outstanding issues. Renew. Sustain. Energy Rev. 2018, 90, 402–411. [Google Scholar] [CrossRef]
- Wang, P.; Liu, B.; Hong, T. Electric load forecasting with recency effect: A big data approach. Int. J. Forecast. 2016, 32, 585–597. [Google Scholar] [CrossRef]
- Dong, X.; Qian, L.; Huang, L. Short-term load forecasting in smart grid: A combined CNN and K-means clustering approach. In Proceedings of the 2017 IEEE International Conference on Big Data and Smart Computing (BigComp), Jeju Island, South Korea, 13–16 February 2017; pp. 119–125. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, J.L.; Chang, P.C. A multiple time series-based recurrent neural network for short-term load forecasting. Soft Comput. 2018, 22, 4099–4112. [Google Scholar] [CrossRef]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Li, B.; Liao, M.; Xu, C.; Chen, H.; Li, W. Stability and Hopf Bifurcation of a Class of Six-Neuron Fractional BAM Neural Networks with Multiple Delays. Fractal Fract. 2023, 7, 142. [Google Scholar] [CrossRef]
- Chen, Y.; Tan, Y.; Zhang, B. Exploiting Vulnerabilities of Load Forecasting through Adversarial Attacks. In Proceedings of the Tenth ACM International Conference on Future Energy Systems, New York, NY, USA, 25–28 June 2019; pp. 1–11. [Google Scholar] [CrossRef]
- Akhtar, N.; Mian, A. Threat of adversarial attacks on deep learning in computer vision: A survey. IEEE Access 2018, 6, 14410–14430. [Google Scholar] [CrossRef]
- Huang, S.; Papernot, N.; Goodfellow, I.; Duan, Y.; Abbeel, P. Adversarial attacks on neural network policies. arXiv 2017, arXiv:1702.02284. [Google Scholar]
- An, D.; Yang, Q.; Liu, W.; Zhang, Y. Defending against data integrity attacks in smart grid: A deep reinforcement learning-based approach. IEEE Access 2019, 7, 110835–110845. [Google Scholar] [CrossRef]
- Lin, J.; Yu, W.; Yang, X. On false data injection attack against multistep electricity price in electricity market in smart grid. In Proceedings of the 2013 IEEE Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013; pp. 760–765. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards deep learning models resistant to adversarial attacks. arXiv 2017, arXiv:1706.06083. [Google Scholar]
- Zhang, J.; Li, C. Adversarial examples: Opportunities and challenges. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 2578–2593. [Google Scholar] [CrossRef]
- Nowroozi, E.; Mekdad, Y.; Berenjestanaki, M.H.; Conti, M.; El Fergougui, A. Demystifying the transferability of adversarial attacks in computer networks. IEEE Trans. Netw. Serv. Manag. 2022, 19, 3387–3400. [Google Scholar] [CrossRef]
- Sridhar, S.; Govindarasu, M. Model-based attack detection and mitigation for automatic generation control. IEEE Trans. Smart Grid 2014, 5, 580–591. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Mohammadpourfard, M.; Konstantinou, C.; Genc, I.; Kim, T.; Mohammadi-Ivatloo, B. Electric load forecasting under False Data Injection Attacks using deep learning. Energy Rep. 2022, 8, 9933–9945. [Google Scholar] [CrossRef]
- Tan, R.; Badrinath Krishna, V.; Yau, D.K.; Kalbarczyk, Z. Impact of integrity attacks on real-time pricing in smart grids. In Proceedings of the 2013 ACM SIGSAC Conference on COMPUTER & Communications Security, Berlin, Germany, 4–8 November 2013; pp. 439–450. [Google Scholar]
- Giraldo, J.; Cárdenas, A.; Quijano, N. Integrity Attacks on Real-Time Pricing in Smart Grids: Impact and Countermeasures. IEEE Trans. Smart Grid 2017, 8, 2249–2257. [Google Scholar] [CrossRef]
- Ntalampiras, S. Detection of Integrity Attacks in Cyber-Physical Critical Infrastructures Using Ensemble Modeling. IEEE Trans. Ind. Inform. 2015, 11, 104–111. [Google Scholar] [CrossRef]
- Yan, W.; Mestha, L.K.; Abbaszadeh, M. Attack detection for securing cyber physical systems. IEEE Internet Things J. 2019, 6, 8471–8481. [Google Scholar] [CrossRef]
- Nazeri, A.; Biroon, R.A.; Pisu, P. Black-Box Stealthy Frequency Spectrum Attack on LSTM-based Power Load Forecasting in an Energy Management System with Islanded Microgrid. In Proceedings of the 2023 North American Power Symposium (NAPS), Asheville, NC, USA, 15–17 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Nazeri, A.; Biroon, R.A.; Westman, J.K.; Pisu, P.; Hadidi, R. Machine Learning-assisted Energy Management System for an Islanded Microgrid and Investigation of Data Integrity Attack on Power Generation. In Proceedings of the 2022 North American Power Symposium (NAPS), Salt Lake City, UT, USA, 9–11 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- In Proceedings of the The New York Independent System Operator—NYISO. Available online: http://mis.nyiso.com/public/ (accessed on 1 January 2020).
- Nazeri, A.; Pisu, P. LSTM-based Load Forecasting Robustness Against Noise Injection Attack in Microgrid. arXiv 2023, arXiv:2304.13104. Available online: http://arxiv.org/abs/2304.13104 (accessed on 25 April 2023).
- Dinkhah, S.; Cuellar, J.S.; Khanbaghi, M. Optimal Power and Frequency Control of Microgrid Cluster with Mixed Loads. IEEE Open Access J. Power Energy 2022, 9, 143–150. [Google Scholar] [CrossRef]
- In Proceedings of the National Renewable Energy Laboratory. Available online: https://www.nrel.gov/gis/solar.html (accessed on 1 January 2020).
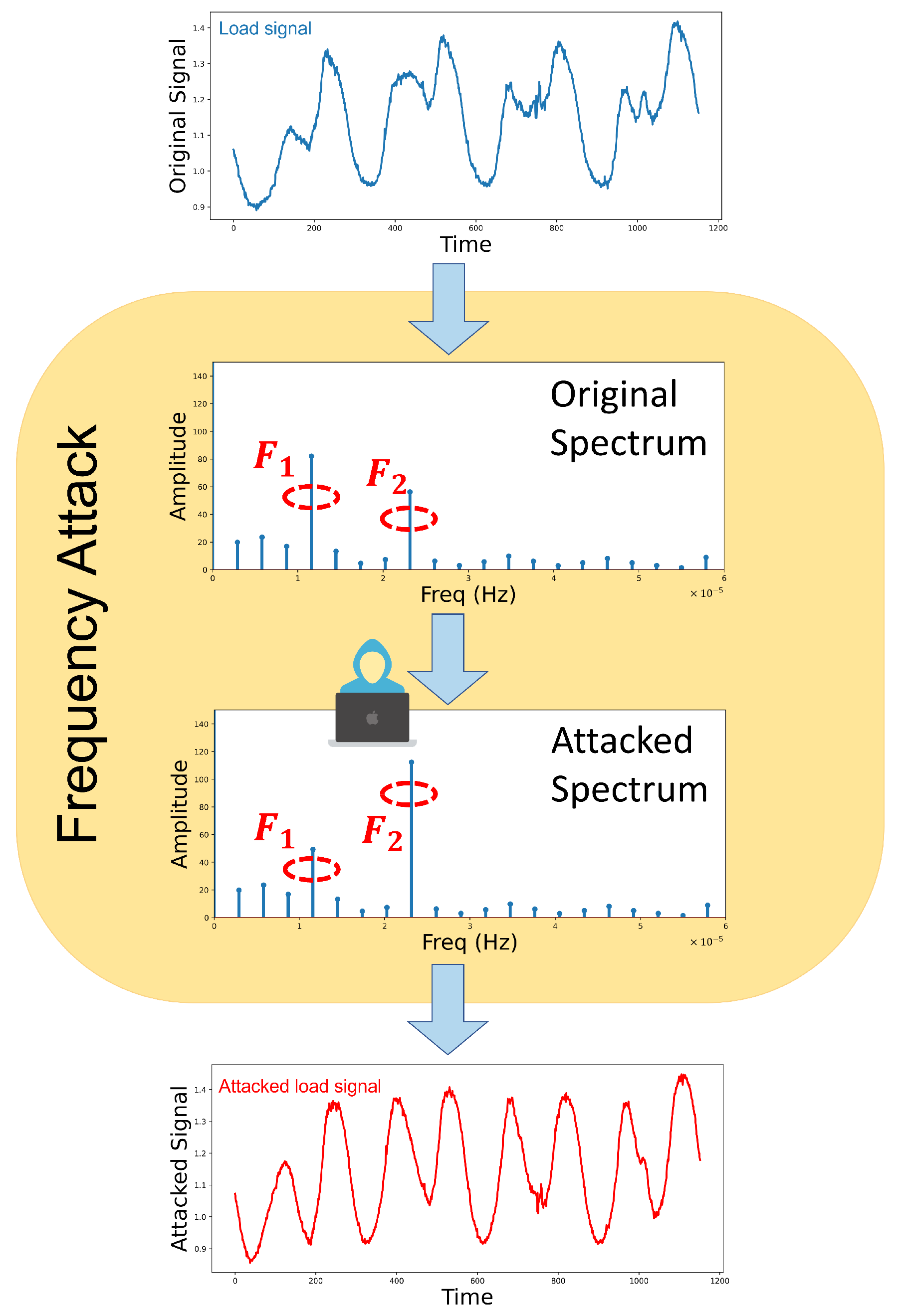

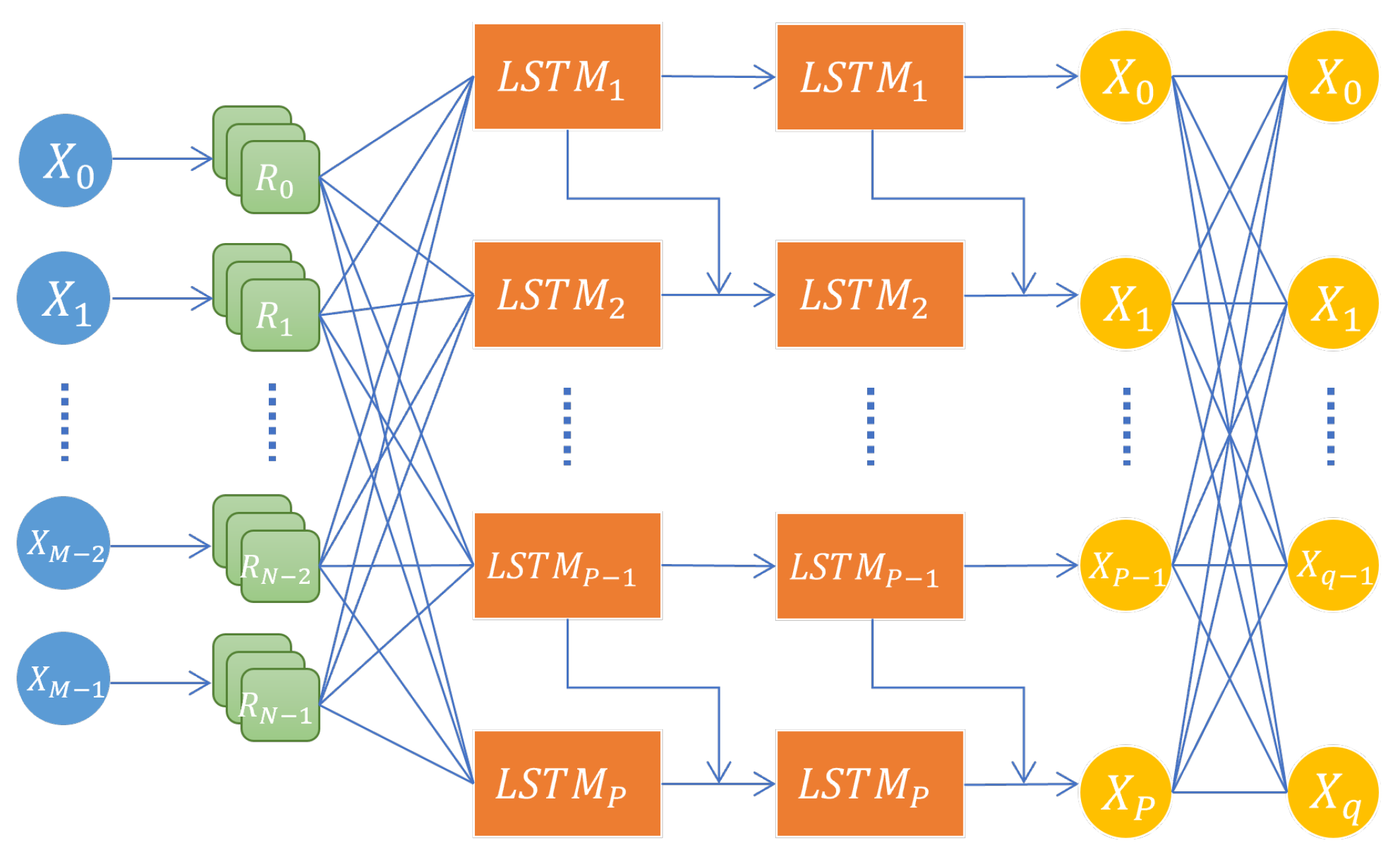
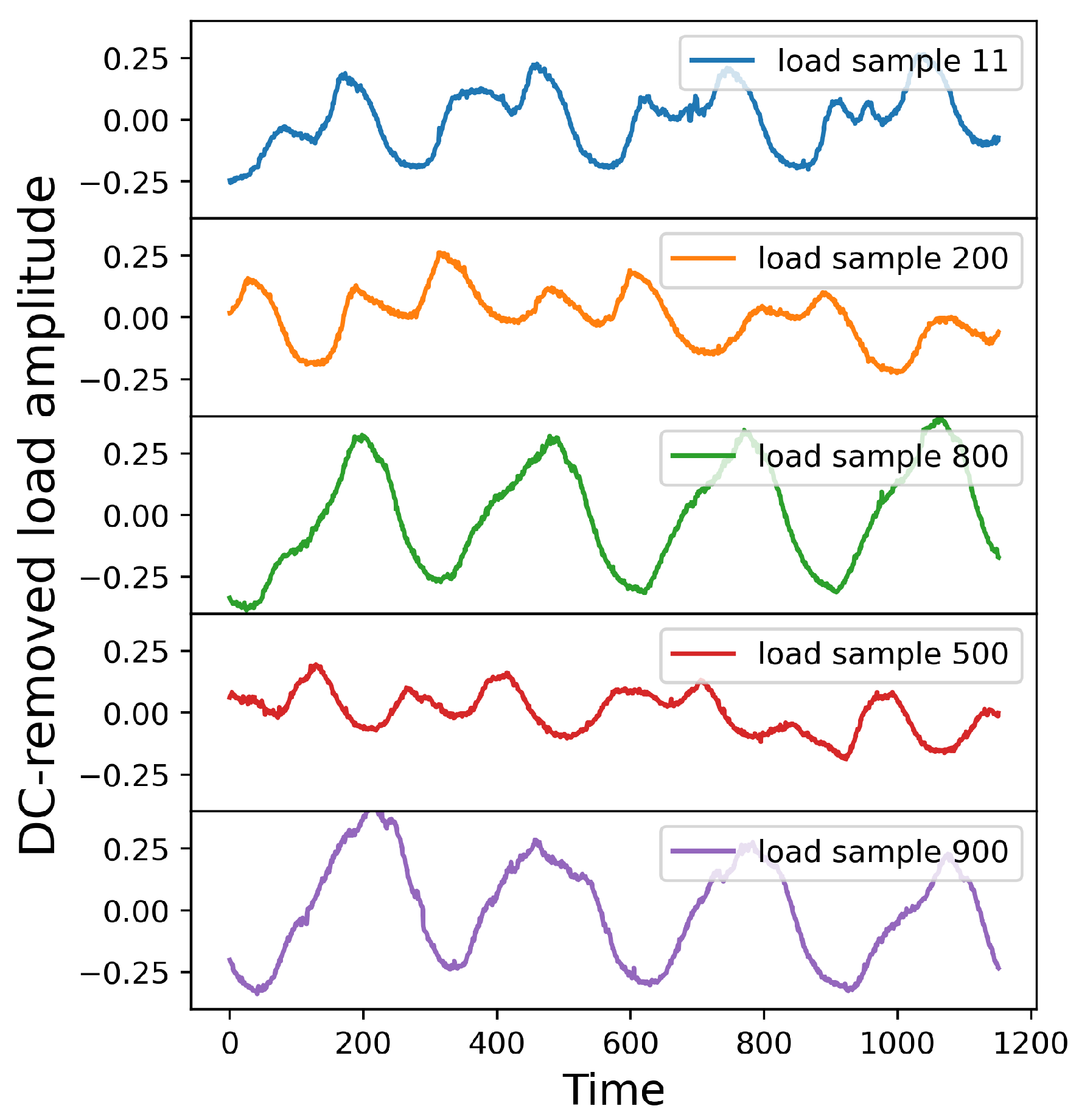
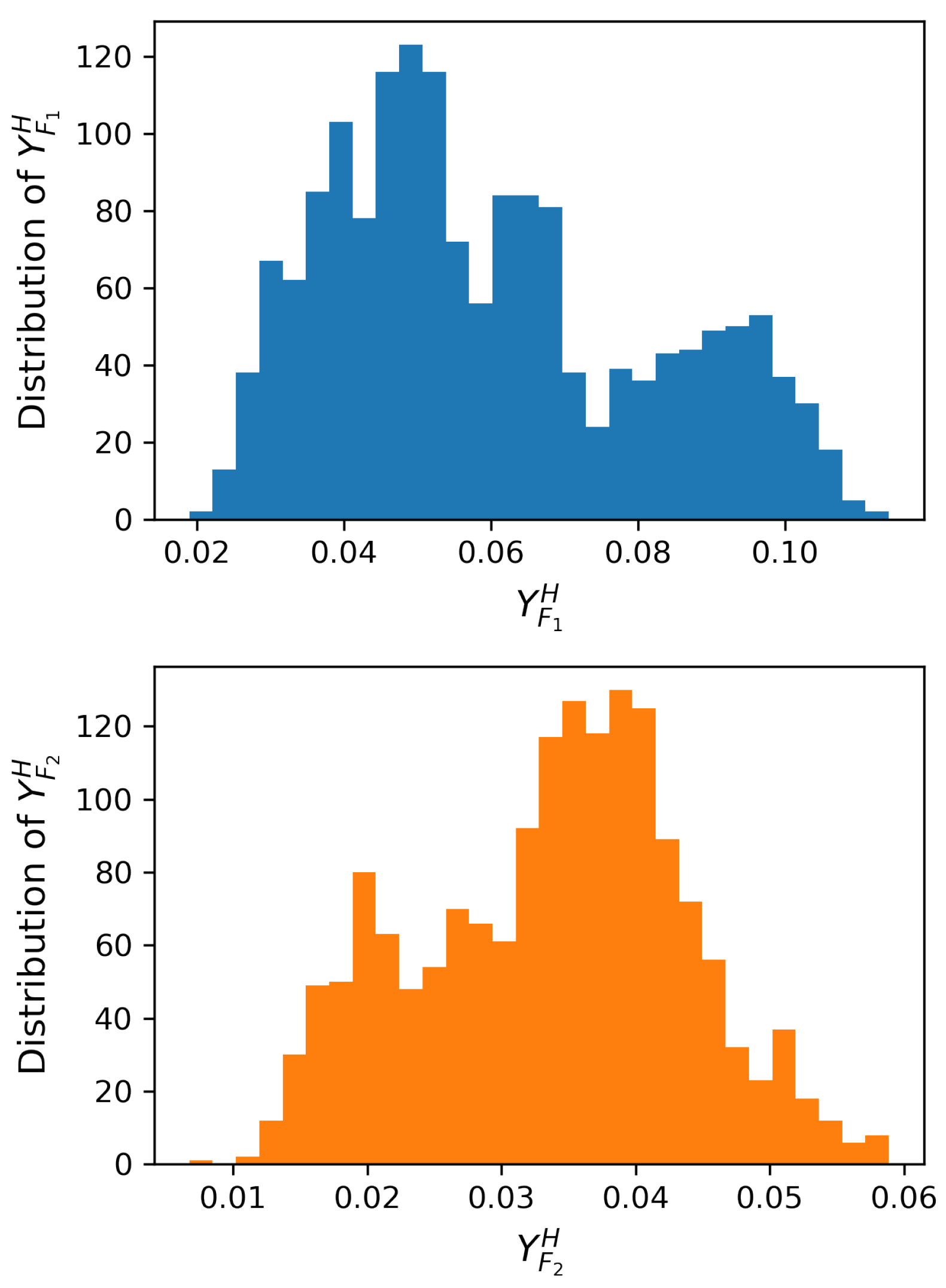




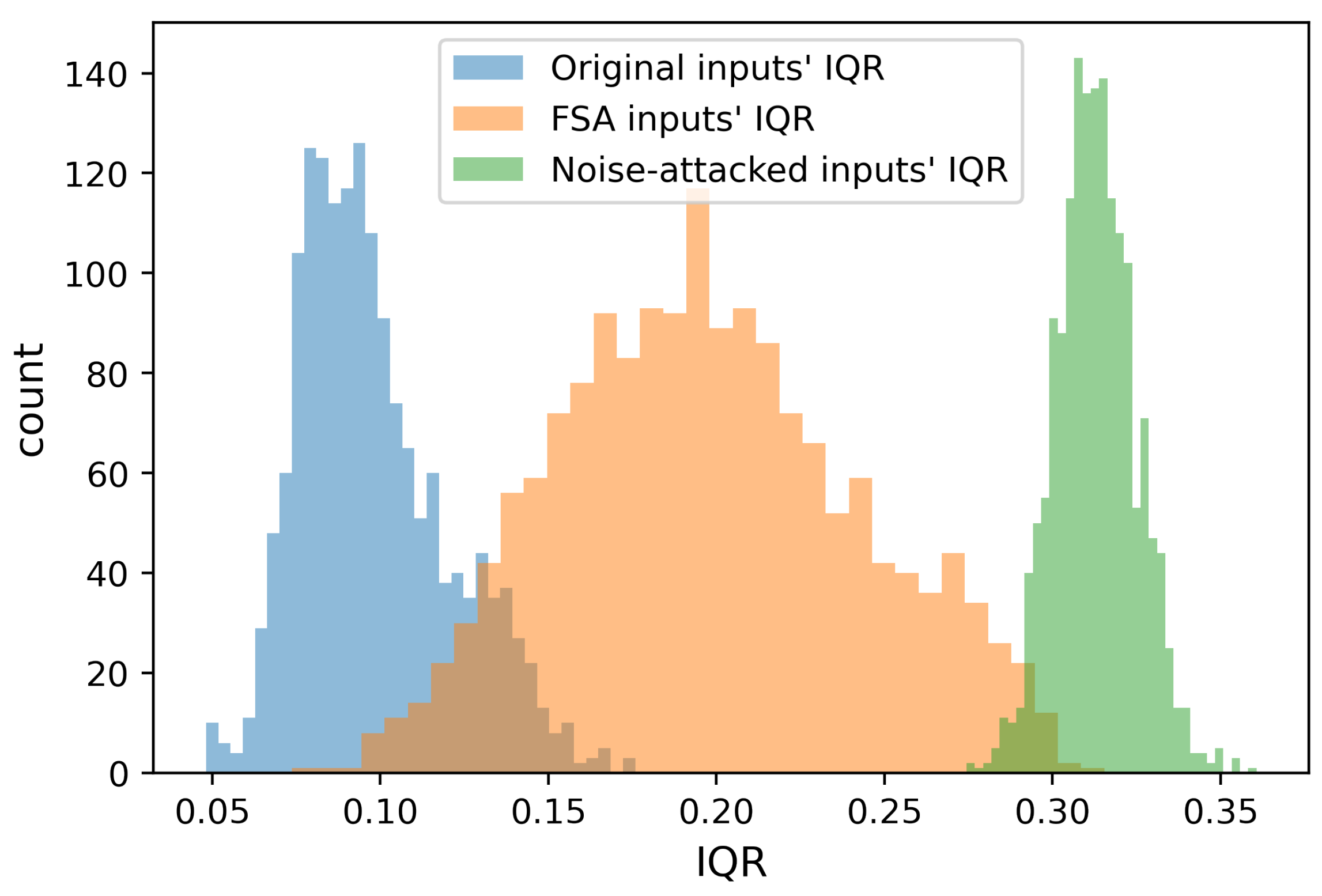
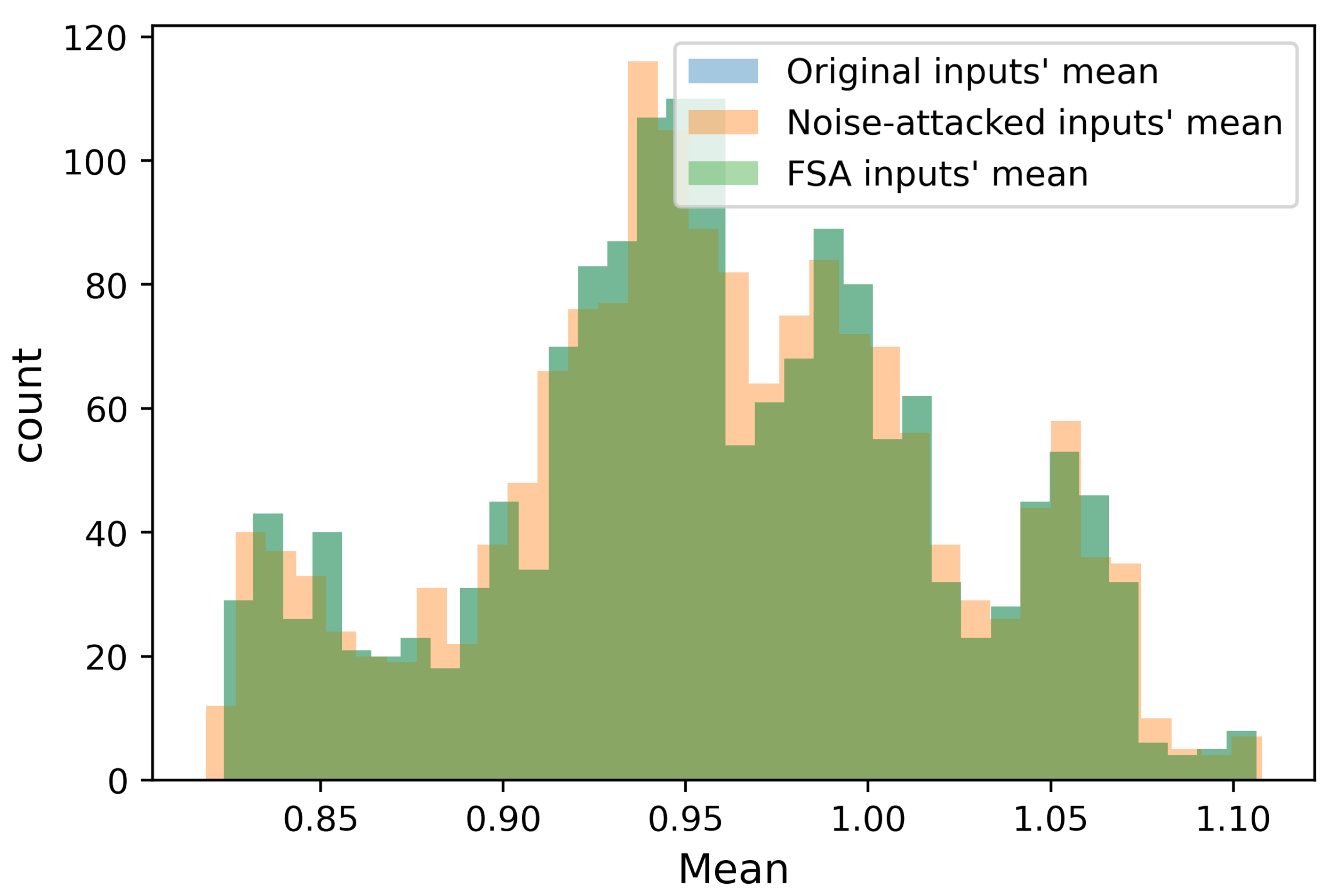
| Scenario | Mean Absolute Error (MAE) Per Recording [MWatt] |
|---|---|
| No attack | 0.046 |
| Noise injection attack [25] | 0.079 |
| Our proposed FSA | 0.135 |
| STD | Kurtosis | IQR | Mean | Input Label | |
|---|---|---|---|---|---|
| STD | 1 | 0.825 | 0.931 | 0.049 | 0.961 |
| Kurtosis | 0.825 | 1 | 0.756 | −0.009 | 0.795 |
| IQR | 0.931 | 0.756 | 1 | −0.098 | 0.945 |
| Mean | 0.049 | −0.009 | −0.098 | 1 | −0.001 |
| Input label | 0.961 | 0.795 | 0.945 | −0.001 | 1 |
| Coefficient | Standard Error | z | [0.025–0.975] @%95 CI | ||
|---|---|---|---|---|---|
| Intercept | −0.6620 | 0.048 | −13.750 | 0.000 | (−0.756, −0.568) |
| STD | 6.5243 | 0.139 | 46.902 | 0.000 | (6.252, 6.797) |
| Kurtosis | 0.0592 | 0.010 | 5.847 | 0.000 | (0.039, 0.079) |
| IQR | 3.5019 | 0.090 | 38.933 | 0.000 | (3.326, 3.678) |
| Mean | 0.1290 | 0.049 | 2.656 | 0.008 | (0.034, 0.224) |
| ML Model | Features Set | F1-Score | Acc |
|---|---|---|---|
| Logistic Regression | F1 | 0.95 | 0.9676 |
| Logistic Regression | F2 | 0.97 | 0.98 |
| Logistic Regression | F3 | 0.954 | 0.968 |
| Logistic Regression | F4 | 0.97 | 0.98 |
| Logistic Regression | F5 | 0.972 | 0.981 |
| Naive Bayes | F1 | 0.96 | 0.973 |
| Naive Bayes | F2 | 0.973 | 0.982 |
| Naive Bayes | F3 | 0.961 | 0.974 |
| Naive Bayes | F4 | 0.973 | 0.982 |
| Naive Bayes | F5 | 0.975 | 0.983 |
| Random Forest (50, 10) | F1 | 0.957 | 0.97 |
| Random Forest (50, 5) | F2 | 0.973 | 0.982 |
| Random Forest (50, 20) | F3 | 0.963 | 0.975 |
| Random Forest (50, 20) | F4 | 0.981 | 0.987 |
| Random Forest (50, 10) | F5 | 0.978 | 0.985 |
| Defense Model | Sampling Range | MAEPR |
|---|---|---|
| Defense 1 | 0.058 | |
| Defense 2 | 0.054 | |
| Defense 3 | 0.053 | |
| Defense 4 | 0.054 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazeri, A.; Biroon, R.; Pisu, P.; Schoenwald, D. Design, Detection, and Countermeasure of Frequency Spectrum Attack and Its Impact on Long Short-Term Memory Load Forecasting and Microgrid Energy Management. Energies 2024, 17, 868. https://doi.org/10.3390/en17040868
Nazeri A, Biroon R, Pisu P, Schoenwald D. Design, Detection, and Countermeasure of Frequency Spectrum Attack and Its Impact on Long Short-Term Memory Load Forecasting and Microgrid Energy Management. Energies. 2024; 17(4):868. https://doi.org/10.3390/en17040868
Chicago/Turabian StyleNazeri, Amirhossein, Roghieh Biroon, Pierluigi Pisu, and David Schoenwald. 2024. "Design, Detection, and Countermeasure of Frequency Spectrum Attack and Its Impact on Long Short-Term Memory Load Forecasting and Microgrid Energy Management" Energies 17, no. 4: 868. https://doi.org/10.3390/en17040868
APA StyleNazeri, A., Biroon, R., Pisu, P., & Schoenwald, D. (2024). Design, Detection, and Countermeasure of Frequency Spectrum Attack and Its Impact on Long Short-Term Memory Load Forecasting and Microgrid Energy Management. Energies, 17(4), 868. https://doi.org/10.3390/en17040868








