Rapid Design Method of Heavy-Loaded Propeller for Distributed Electric Propulsion Aircraft
Abstract
1. Introduction
2. Materials and Methods
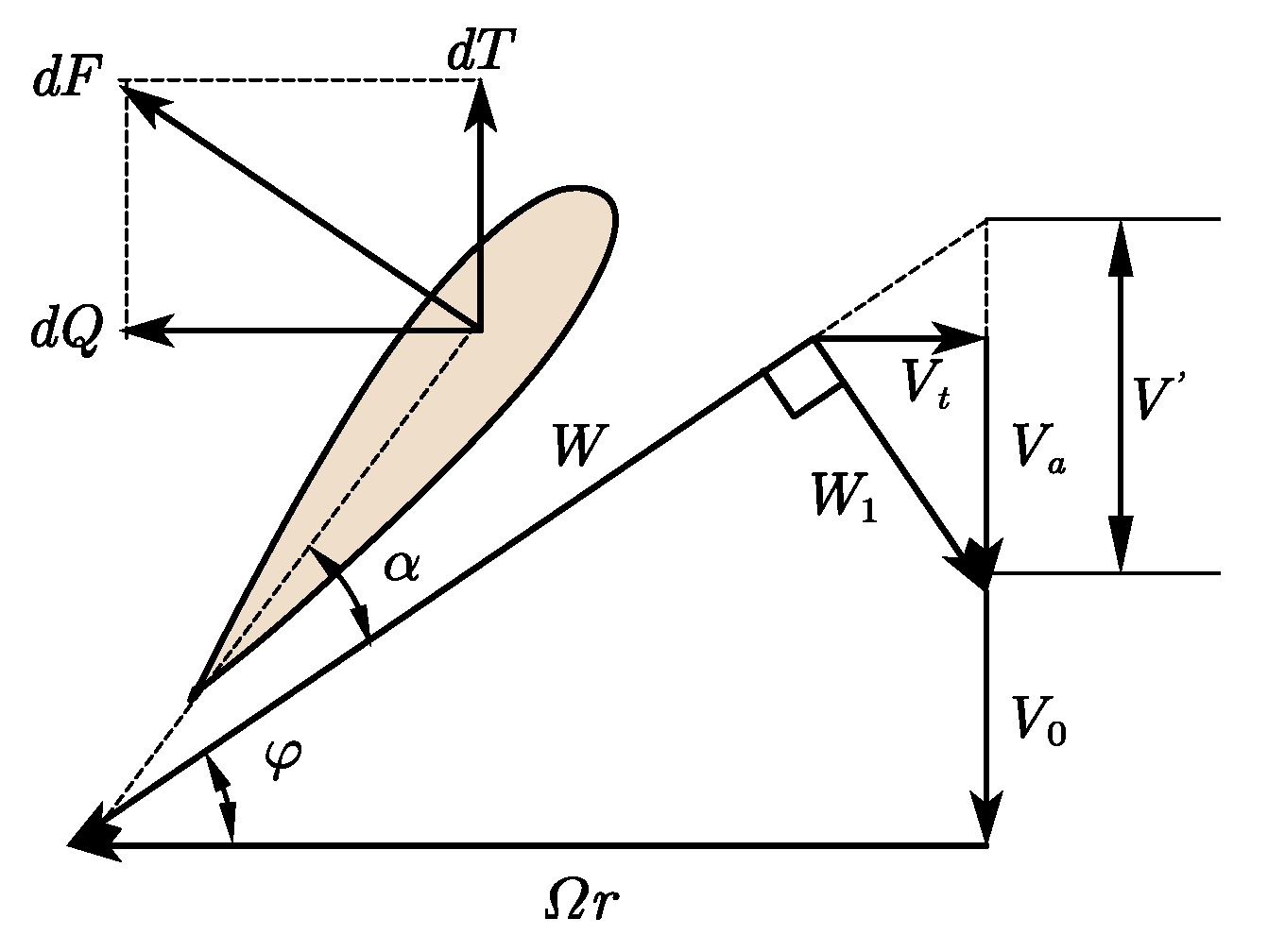
2.1. Design Method of Light Loaded Propeller Based on Betz Condition
2.2. Rapid Design Method for Heavy Loaded Propellers
- Give the design requirements, including specified thrust requirement T, flight speed , number of blades , rotational velocity , tip radius , hub radius and the atmospheric density .
- Solve for the axial velocity displacement according to Equation (22).
- Determine the optimal circulation distribution at each section according to Equation (13).
- Perform cubic spline interpolation on the circulation of sections other than the blade tip, and then perform extrapolation based on the obtained interpolation functions to obtain the circulation at the blade tip to avoid this circulation being zero.
- Determine the actual inflow angle at each section according to Equation (23).
- Obtain the tangential-induced velocity at each section according to Equation (20).
- Calculate the total velocity W at each section according to Equation (24)
- Assume a certain value for the lift coefficient at each section (selected based on the airfoil) and calculate the initial chord length b at each section according to Equation (28).
- Compute the aerodynamic characteristics of the given airfoil at a specified Reynolds number and Mach number using aerodynamic tools such as XFOIL [25] according to the chord length calculated in the previous step. Identify the optimum angle of attack and its corresponding lift coefficient .
- Substitute the obtained in step 9 into Equation (28) to update the chord length b.
- Calculate the blade pitch angle at each section based on the optimum angle of attack and inflow angle using Equation (29).
- Determine the airfoil, chord length b, and pitch angle at each section of the propeller by following the above steps, and then determine the geometry of the propeller with a specified number of blades.
3. Results and Discussion
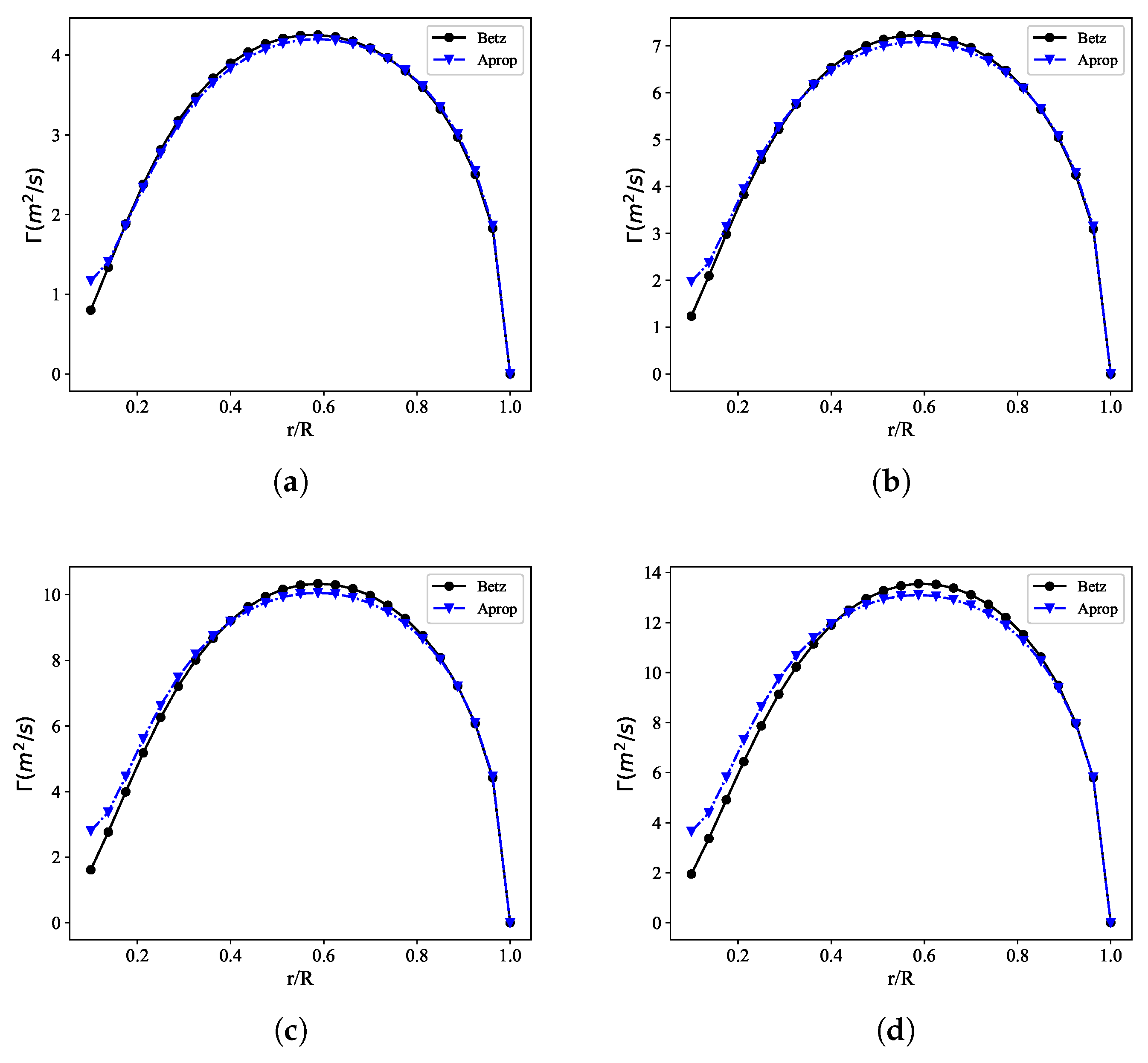
3.1. Blade Geometry
3.2. Aerodynamic Performance
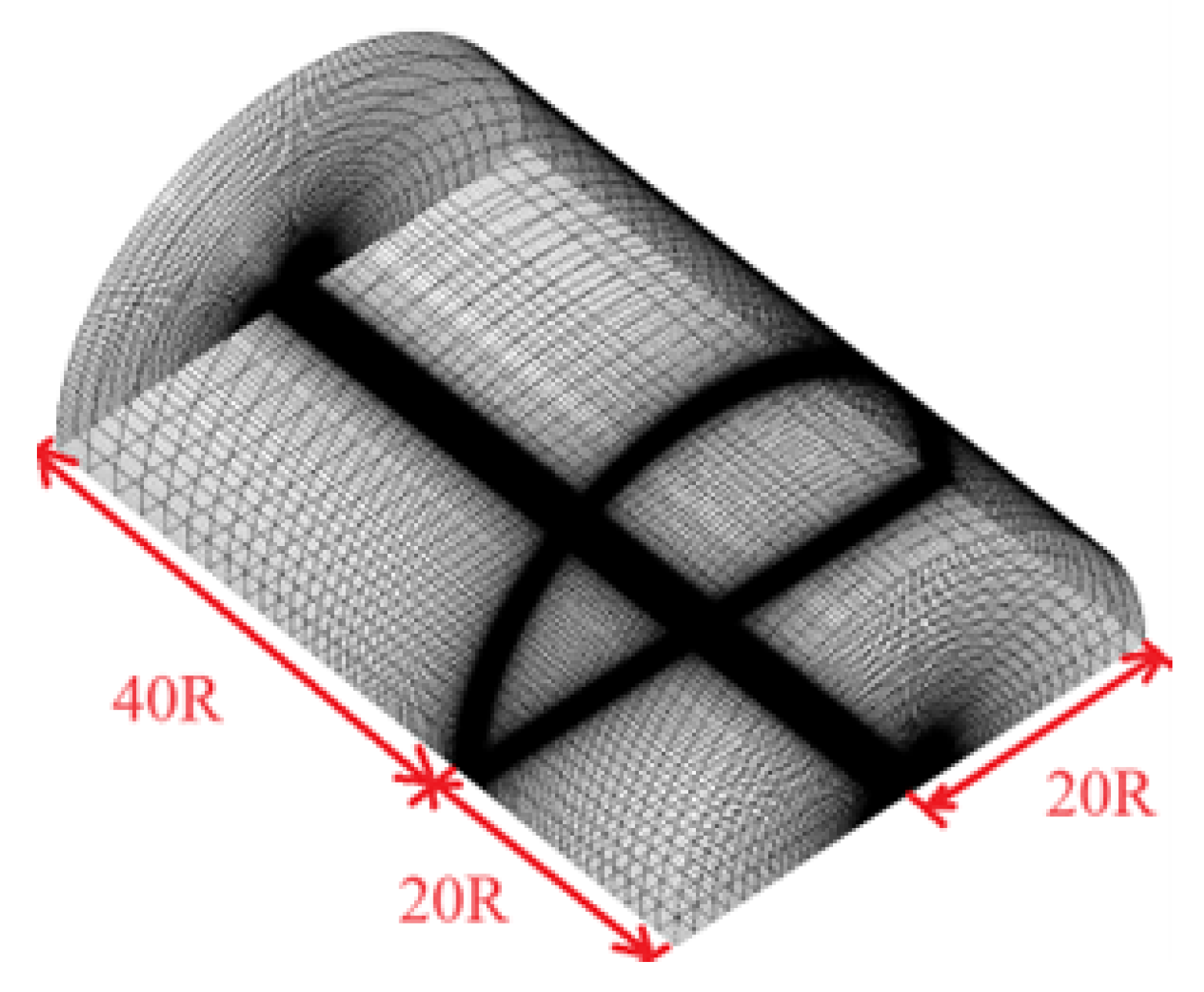
Mesh and CFD Setup
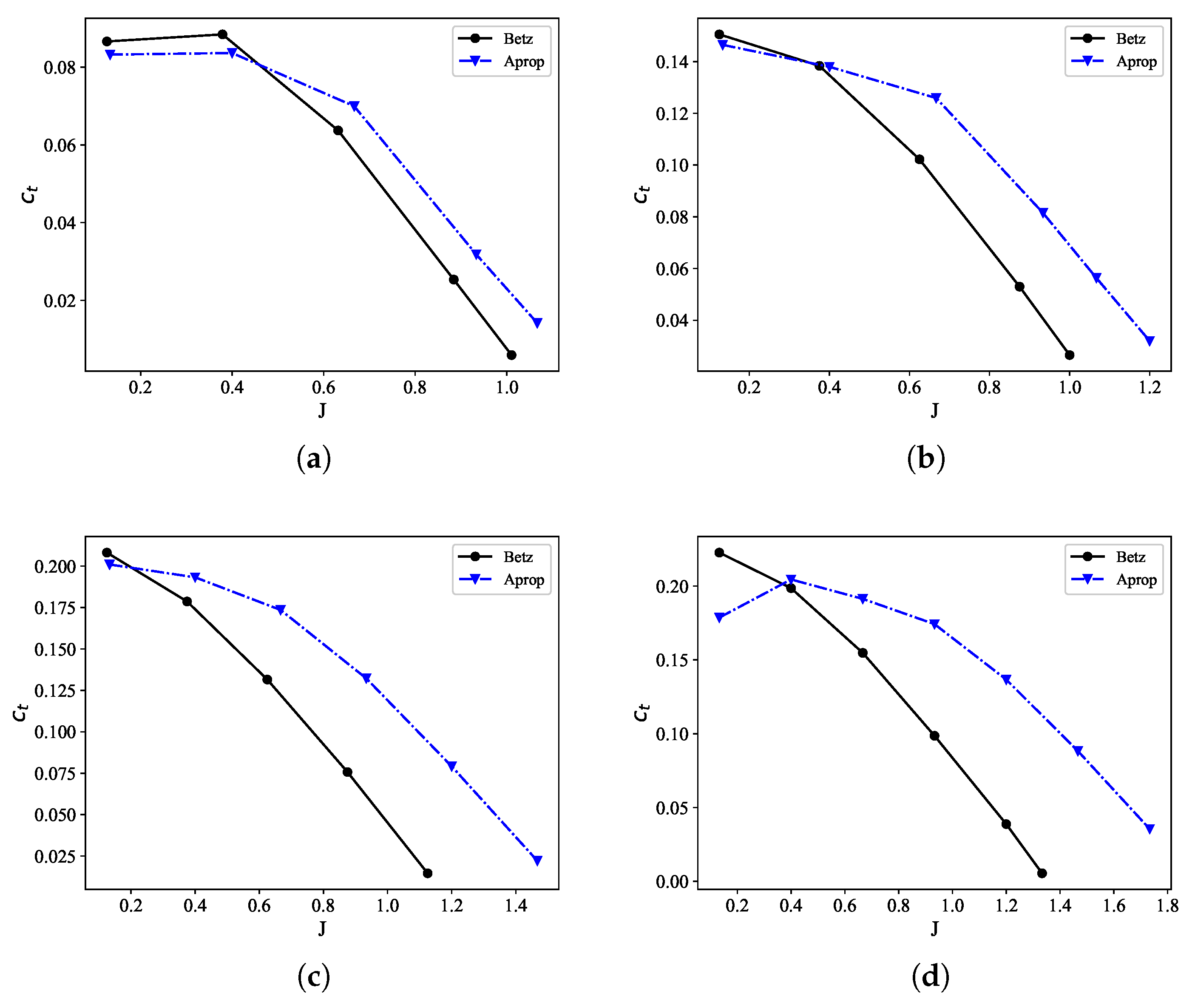
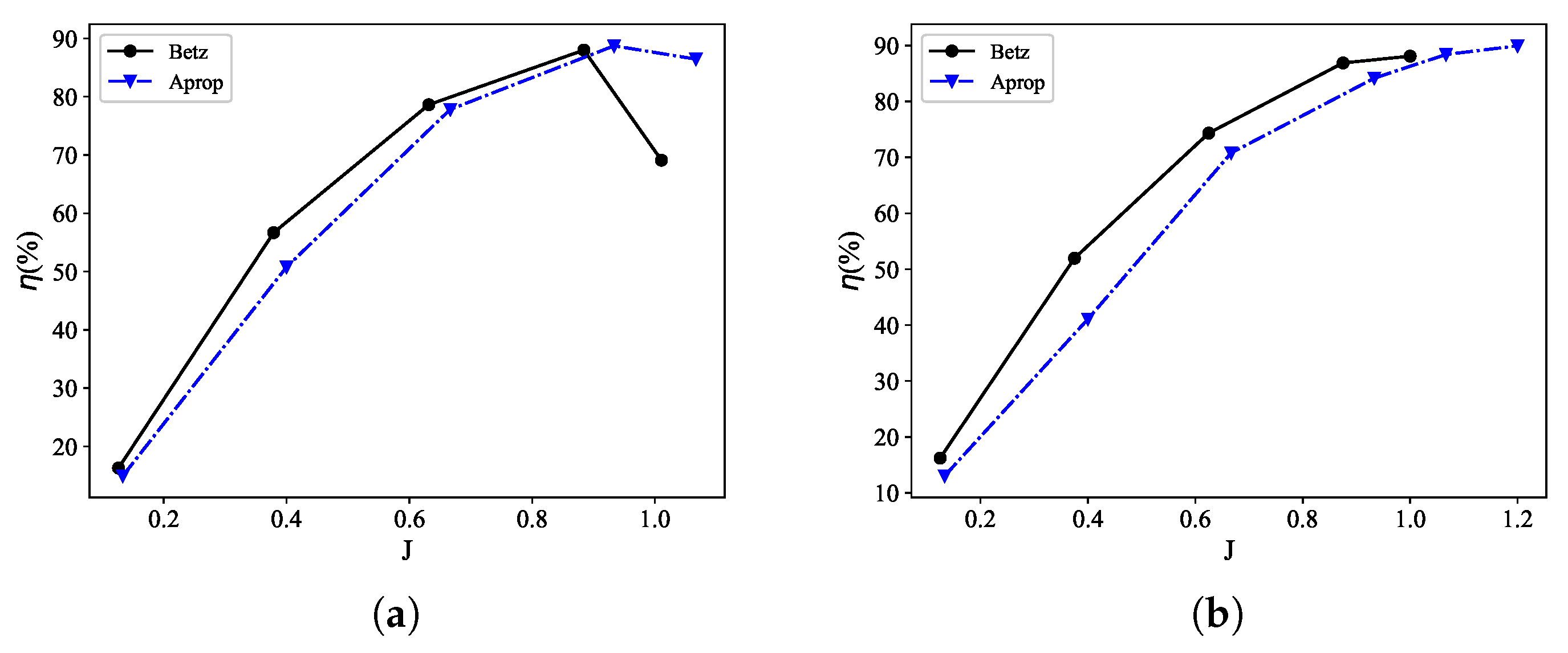
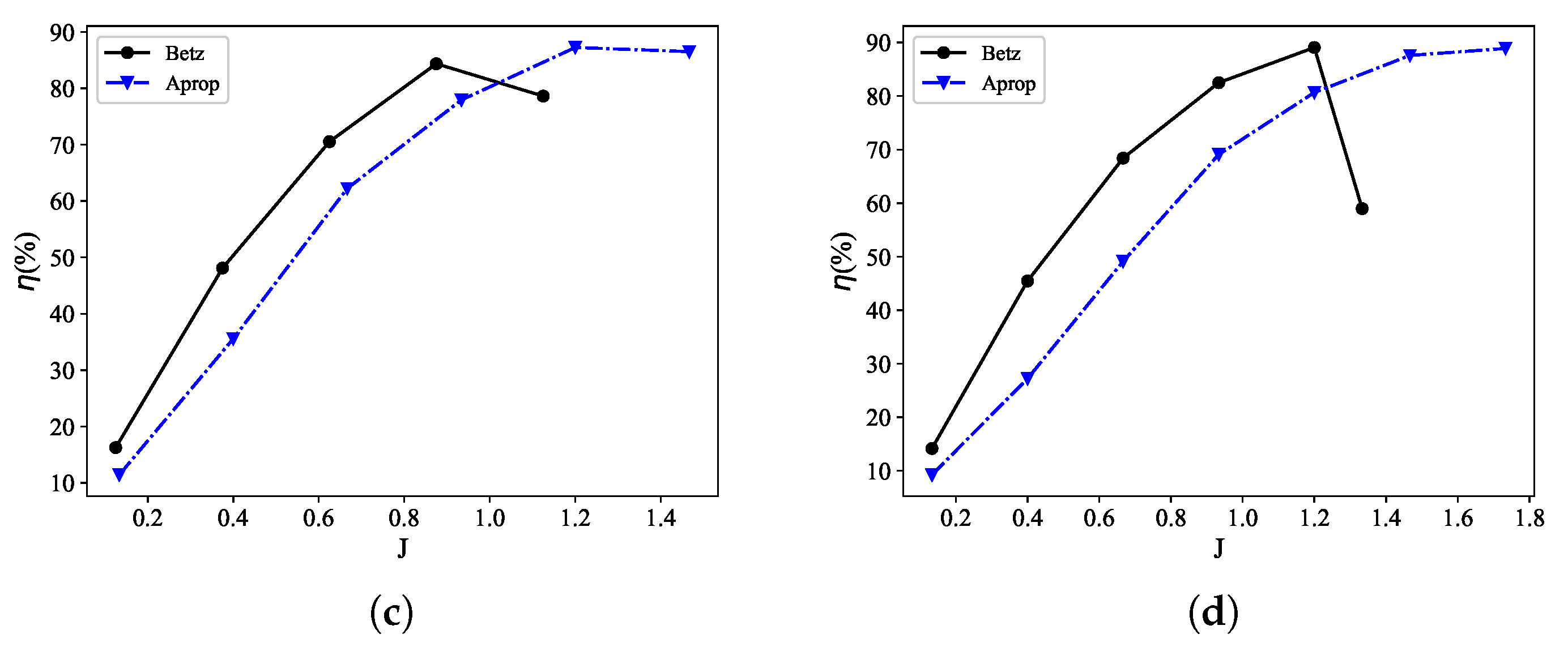
3.3. Comparison of Aerodynamic Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Abbreviations
| DEP | Distributed Electric Propulsion |
| BEMT | Blade Element Momentum Theory |
| CFD | Computational Fluid Dynamics |
| MRF | Multiple Reference Frame |
| ISA | International Standard Atmosphere |
References
- Sinnige, T.; van Arnhem, N.; Stokkermans, T.C.A.; Eitelberg, G.; Veldhuis, L.L.M. Wingtip-Mounted Propellers: Aerodynamic Analysis of Interaction Effects and Comparison with Conventional Layout. J. Aircr. 2018, 56, 295–312. [Google Scholar] [CrossRef]
- Stoll, A.M.; Bevirt, J.B.; Moore, M.D.; Fredericks, W.J.; Borer, N.K. Drag Reduction Through Distributed Electric Propulsion. In Proceedings of the 14th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Firnhaber Beckers, M.; Schollenberger, M.; Lutz, T.; Bongen, D.; Radespiel, R.; Florenciano, J.L.; Funes-Sebastian, D.E. CFD Investigation of High-Lift Propeller Positions for a Distributed Propulsion System. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022. [Google Scholar] [CrossRef]
- Wu, J.; Gao, F.; Li, S.; Yang, F. Conceptual Design and Optimization of Distributed Electric Propulsion General Aviation Aircraft. Aerospace 2023, 10, 387. [Google Scholar] [CrossRef]
- Moore, M.D.; Goodrich, K.H. High Speed Mobility through On-Demand Aviation. In Proceedings of the 2013 Aviation Technology, Integration, and Operations Conference, Los Angeles, CA, USA, 12–14 August 2013. [Google Scholar] [CrossRef]
- Litherland, B.L.; Borer, N.K.; Zawodny, N.S. X-57 Maxwell High-Lift Propeller Testing and Model Development. In Proceedings of the AIAA Aviation 2021 Forum, Virtual Event, 2–6 August 2021. [Google Scholar] [CrossRef]
- Yoo, S.; Duensing, J.C.; Deere, K.A.; Viken, J.K.; Frederick, M. Computational Analysis on the Effects of High-lift Propellers and Wing-tip Cruise Propellers on X-57. In Proceedings of the AIAA Aviation 2023 Forum, San Diego, CA, USA, 12–16 June 2023; p. 3382. [Google Scholar]
- Borer, N.K.; Patterson, M.D. X-57 high-lift propeller control schedule development. In Proceedings of the AIAA Aviation 2020 Forum, Online, 15–19 June 2020; p. 3091. [Google Scholar]
- Huang, Z.; Yao, H.; Lundbladh, A.; Davidson, L. Low-Noise Propeller Design for Quiet Electric Aircraft. In Proceedings of the AIAA Aviation 2020 Forum, Virtual Event, 15–19 June 2020. [Google Scholar] [CrossRef]
- Keller, D. Towards higher aerodynamic efficiency of propeller-driven aircraft with distributed propulsion. CEAS Aeronaut. J. 2021, 12, 777–791. [Google Scholar] [CrossRef]
- Rankine, W. On the mechanical principles of the action of propellers. Trans. Inst. Nav. Archit. 1865, 13, 13–30. [Google Scholar]
- Betz, A. Schraubenpropeller mit geringstem Energieverlust. Mit einem Zusatz von l. Prandtl. Nachrichten Ges. Wiss. Gott. Math.-Phys. Kl. 1919, 1919, 193–217. [Google Scholar]
- Goldstein, S. On the vortex theory of screw propellers. Proc. R. Soc. London Ser. A Contain. Pap. A Math. Phys. Character 1929, 123, 440–465. [Google Scholar]
- Theodore, T. Theory of Propellers. Aeronaut. J. 1948, 52, 574. [Google Scholar] [CrossRef]
- Larrabee, E.E. Practical Design of Minimum Induced Loss Propellers. SAE Trans. 1979, 88, 2053–2062. [Google Scholar]
- Adkins, C.; Liebeck, R. Design of optimum propellers. In Proceedings of the 21st Aerospace Sciences Meeting, Reno, NV, USA, 10–13 January 1983; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1983. [Google Scholar] [CrossRef]
- Traub, L.W. Simplified propeller analysis and design including effects of stall. Aeronaut. J. 2016, 120, 796–818. [Google Scholar] [CrossRef]
- Patterson, M.D.; Borer, N.K.; German, B. A simple method for high-lift propeller conceptual design. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 0770. [Google Scholar]
- Patterson, M.D. Conceptual Design of High-Lift Propeller Systems for Small Electric Aircraft. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2016. [Google Scholar]
- Fan, Z.; Zhou, Z.; Zhu, X. A design method for propeller with arbitrary circulation distribution. J. Aerosp. Power 2019, 34, 434–441. [Google Scholar]
- Wang, K.; Zhou, Z.; Fan, Z.; Guo, J. Aerodynamic design of tractor propeller for high-performance distributed electric propulsion aircraft. Chin. J. Aeronaut. 2021, 34, 20–35. [Google Scholar] [CrossRef]
- Xue, C.; Zhou, Z. Inverse aerodynamic design for DEP propeller based on desired propeller slipstream. Aerosp. Sci. Technol. 2020, 102, 105820. [Google Scholar] [CrossRef]
- Young, T.M. International Standard Atmosphere (ISA) Table. In Performance of the Jet Transport Airplane: Analysis Methods, Flight Operations and Regulations; John Wiley & Sons, Ltd.: Chichester, UK, 2017; pp. 583–590. [Google Scholar] [CrossRef]
- Peng, P.; Yao, L.j. Prediction of Propeller Slipstream Influence Based on Optimal Circulation Distribution. J. Propuls. Technol. 2019, 40, 2692–2699. [Google Scholar] [CrossRef]
- Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils. In Low Reynolds Number Aerodynamics; Mueller, T.J., Ed.; Springer: Berlin, Heidelberg, 1989; pp. 1–12. [Google Scholar]
- Cadence. Unstructured Viscous Boundary Layer Meshing: T-Rex. 2023. Available online: https://www.pointwise.com/doc/user-manual/grid/solve/unstructured-blocks/t-rex.html (accessed on 8 October 2023).
- Bergmann, O.; Götten, F.; Braun, C.; Janser, F. Comparison and evaluation of blade element methods against RANS simulations and test data. CEAS Aeronaut. J. 2022, 13, 535–557. [Google Scholar] [CrossRef]
- Siddiqi, Z.; Lee, J.W. Experimental and numerical study of novel Coanda-based unmanned aerial vehicle. J. Eng. Appl. Sci. 2022, 69, 1–19. [Google Scholar] [CrossRef]
- Lopez, O.D.; Escobar, J.A.; Pérez, A.M. Computational Study of the Wake of a Quadcopter Propeller in Hover. In Proceedings of the 23rd AIAA Computational Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Kutty, H.A.; Rajendran, P. 3D CFD Simulation and Experimental Validation of Small APC Slow Flyer Propeller Blade. Aerospace 2017, 4, 10. [Google Scholar] [CrossRef]
- Stajuda, M.; Karczewski, M.; Obidowski, D.; Jóźwik, K. Development of a CFD model for propeller simulation. Mech. Mech. Eng. 2016, 20, 579–593. [Google Scholar]



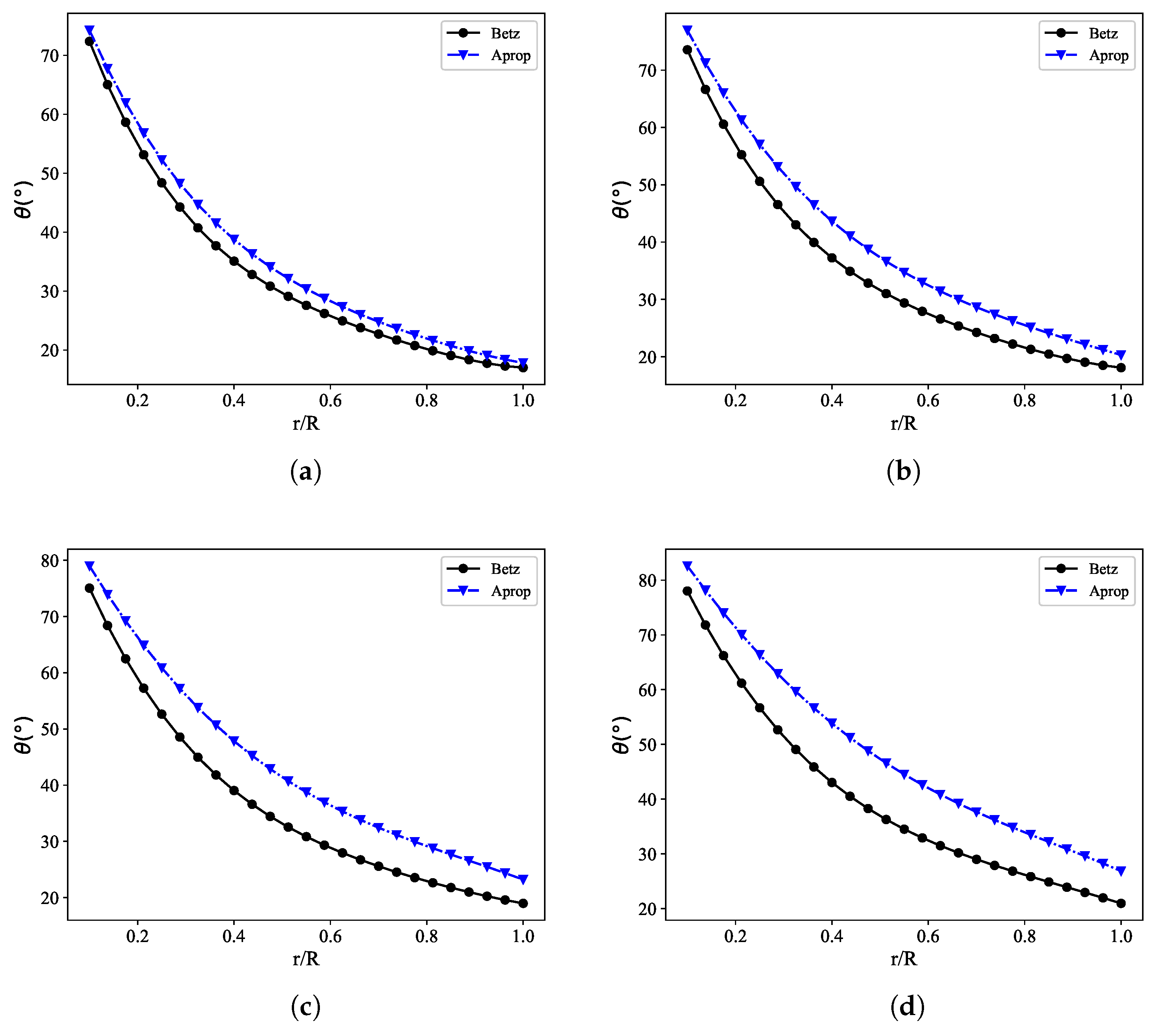




| Airfoil | J | ||||
|---|---|---|---|---|---|
| 50 m/s | 4500 RPM | 0.5 m | 2 | S9000 | 0.67 |
| Disc Load (Pa) | Betz (m/s) | Aprop (m/s) |
|---|---|---|
| 600 | 7.38 | 19.47 |
| 1000 | 12.11 | 32.85 |
| 1400 | 16.83 | 46.63 |
| 1800 | 21.57 | 60.74 |
| Mesh | Mesh Size | Thrust (N) | Efficiency (%) |
|---|---|---|---|
| Mesh1 | 2,115,711 | 382.08 | 79.62 |
| Mesh2 | 3,082,141 | 381.31 | 79.63 |
| Mesh3 | 5,609,432 | 380.60 | 79.71 |
| Mesh4 | 6,025,615 | 380.23 | 79.49 |
| Disc Load (Pa) | Design Thrust (N) | Design Method | Thrust (N) | Efficiency (%) | Relative Thrust Error (%) |
|---|---|---|---|---|---|
| 600 | 471.24 | Betz | 397.18 | 78.95 | −15.67 |
| Adkins | 408.33 | 81.19 | −13.35 | ||
| Aprop | 459.63 | 75.59 | −2.42 | ||
| 1000 | 785.40 | Betz | 648.94 | 75.46 | −17.33 |
| Adkins | 655.57 | 77.55 | −16.53 | ||
| Aprop | 797.49 | 67.97 | 1.59 | ||
| 1400 | 1099.56 | Betz | 875.99 | 71.97 | −20.36 |
| Adkins | 857.34 | 73.59 | −22.03 | ||
| Aprop | 1069.46 | 58.39 | −2.78 | ||
| 1800 | 1413.72 | Betz | 1066.36 | 68.41 | −24.57 |
| Adkins | 1053.84 | 69.74 | −25.46 | ||
| Aprop | 1318.43 | 49.12 | −6.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, S.; Huo, J.; Liu, Z.; Zou, A. Rapid Design Method of Heavy-Loaded Propeller for Distributed Electric Propulsion Aircraft. Energies 2024, 17, 786. https://doi.org/10.3390/en17040786
Shi S, Huo J, Liu Z, Zou A. Rapid Design Method of Heavy-Loaded Propeller for Distributed Electric Propulsion Aircraft. Energies. 2024; 17(4):786. https://doi.org/10.3390/en17040786
Chicago/Turabian StyleShi, Shijie, Jiabo Huo, Zhongbao Liu, and Aicheng Zou. 2024. "Rapid Design Method of Heavy-Loaded Propeller for Distributed Electric Propulsion Aircraft" Energies 17, no. 4: 786. https://doi.org/10.3390/en17040786
APA StyleShi, S., Huo, J., Liu, Z., & Zou, A. (2024). Rapid Design Method of Heavy-Loaded Propeller for Distributed Electric Propulsion Aircraft. Energies, 17(4), 786. https://doi.org/10.3390/en17040786






