Consideration of Multi-Objective Stochastic Optimization in Inter-Annual Optimization Scheduling of Cascade Hydropower Stations

Abstract

There exists a temporal and spatial coupling effect among the hydropower units in cascade hydropower stations which constitutes a complex planning problem. Researching the multi-objective optimization scheduling of cascade hydropower stations under various spatiotemporal inflow impacts is of significant importance. Previous studies have typically only focused on the economic dispatch issues of cascade hydropower stations, with little attention given to their coupling mechanism models and the uncertainty impacts of inflows. Firstly, this paper establishes a coupled optimization scheduling model for cascade hydropower stations and elaborates on the operational mechanism of cascade hydropower stations. Secondly, according to the needs of actual scenarios, two types of optimization objectives are set, considering both the supply adequacy and peak-shaving capacity as indicators, with the total residual load and the peak-valley difference of the residual load as comprehensive optimization objectives. Subsequently, considering the uncertainty impact of the inflow side, a stochastic optimization model for inflow is established based on a normal distribution probability. Finally, case study analyses demonstrate that the proposed model not only effectively achieves supply stability but also reduces the peak-valley difference in load, and can achieve optimized scheduling under the uncertain environment of inflow.

1. Introduction

China is actively addressing the goals of peaking carbon emissions and achieving carbon neutrality [1]. To achieve this, it is crucial to develop an electricity system that adapts to the increasing share of new energy sources, which is also an intrinsic requirement for ensuring the national energy security. However, new energy sources such as wind and solar power exhibit seasonal, stochastic, and intermittent fluctuations, imposing multi-level flexibility requirements on the electricity system across different time scales, including daily, monthly, seasonal, and yearly fluctuations. Energy storage technology is a crucial means of addressing the mismatch between new energy sources and load demand [2]. China has formulated plans for the development of energy storage, with an expected capacity of over 30 GW for new types of energy storage by 2025 and a total pumped storage capacity of around 120 GW by 2030. However, other new energy storage technologies such as electrochemical energy storage, compressed air energy storage, and flywheel energy storage are still in the development stage and require further maturity in technology, improved economic reliability, scalability, and enhanced long-duration discharge capabilities. Furthermore, pumped storage and new energy storage are primarily utilized for short-term peak shaving and frequency regulation, making it challenging to meet the mid-to-long-term adjustment needs of the grid on weekly, monthly, seasonal, and yearly scales. In this context, academia and industry propose the concept of “reshaping the role and function of hydropower”, aiming to fully leverage the vast and broad-scale regulation potential of China’s hydropower resources to address the challenges faced by the electricity system [3].

In the field of electrical power systems, hydroelectric power stations have always been regarded as a crucial component of renewable energy. However, the traditional independent operation mode of individual hydroelectric power stations has a series of drawbacks. These hydroelectric power stations typically adopt a fixed scheduling mode, where their electricity generation and water release remain relatively stable within certain time periods, making it challenging for the power system to cope with the increasingly complex and diverse operational requirements, thereby reducing the overall flexibility of the power system. Furthermore, as noted in references [4,5,6], variations in seasonal weather conditions, such as rainy and dry seasons, significantly impact the electricity generation capacity of hydroelectric power stations, making it challenging for individual stations to meet the power system’s requirements during different seasons, especially over the course of a year. However, according to reference [7], it has been discovered that cascading hydroelectric power stations possess multi-level reservoir energy storage capacity, typically consisting of multiple reservoirs, which enables them to better cope with seasonal fluctuations and efficiently allocate water resources to meet various seasonal demands. Furthermore, as indicated in references [8,9,10], cascading hydroelectric power stations can achieve more flexible electricity generation scheduling by adjusting the water discharge and electricity generation levels of each reservoir, meeting the power system’s demands across various time scales, including those spanning years. Most importantly, reference [11] points out that collaborative interactions can take place between different reservoirs, leading to energy balance, the optimal utilization of water resources, and improved electricity generation efficiency. Therefore, compared to the independent operation of individual hydroelectric power stations, cascading hydroelectric power stations exhibit greater flexibility, schedulability, and synergy, enabling them to better address multi-objective stochastic optimization problems and provide a more reliable power supply. As a result, the adoption of cascading hydroelectric power stations holds significant potential for widespread application in power systems and is crucial for enhancing the stability and efficiency of the electrical grid.

The optimal scheduling of cascading hydroelectric power stations has always been a topic of great interest in power system management. In recent years, multi-objective optimization methods have demonstrated significant advantages in addressing the optimization problems of cascading hydroelectric power stations. Research in references [12,13,14,15] indicates that these methods employ multiple objective functions to comprehensively consider performance indicators from various aspects, providing a more comprehensive perspective for decision making. This comprehensive performance assessment helps decision makers gain a comprehensive understanding of the trade-offs and compromises between various factors, enabling the formulation of more effective optimization strategies.

Furthermore, reference [16] points out that multi-objective optimization methods exhibit flexibility and adaptability, allowing for balancing and flexibility adjustments when considering different objectives. This implies that objective weights can be adjusted according to specific needs and conditions to meet different optimization requirements. Research results from references [17,18,19] indicate that these methods enhance problem diversity by generating multiple potential solutions, facilitating the discovery of diversified optimization strategies and providing more choices for decision making. Reference [20] notes that multi-objective optimization methods can provide decision makers with a series of optimized solutions, enabling them to better understand the trade-offs and consequences between different decision options, thus supporting the decision-making process and making it more transparent. Reference [21] explores the application of multi-objective optimization methods in addressing uncertainty factors in power systems, such as weather changes and demand fluctuations. These methods can provide robust optimization strategies to cope with changes in system operation. Therefore, multi-objective optimization methods have significant advantages in the field of cascading hydroelectric power station optimization, offering comprehensive performance assessments, flexibility, diversity, and decision-making support. These methods contribute to improving the operational efficiency, reliability, and sustainability of cascading hydroelectric power stations, providing powerful tools for power system management.

Random optimization methods have significant advantages in the field of cascading hydroelectric power station optimization. Reference [22] effectively considers various uncertainty factors in the power system, such as weather changes and demand fluctuations, to generate robust optimization solutions. Reference [23] provides probability distribution information, enabling decision makers to have a more comprehensive understanding of multiple possible outcomes, thereby enhancing risk management and decision making. Reference [24] demonstrates that the flexibility of random optimization methods allows them to adapt to various problem settings and objectives, providing optimal operational strategies to address various factors such as seasonal variations, demand fluctuations, and water resource changes. Furthermore, reference [25] effectively reduces computational complexity, especially in large-scale hydroelectric power station systems, by employing techniques such as Monte Carlo simulations. Therefore, random optimization methods provide powerful tools for addressing the challenges in the complex and dynamic environment of cascading hydroelectric power station optimization.

Above all, to provide more effective solutions in power system management, the complex scheduling issues of hydroelectric power stations must be addressed. This paper establishes a coupled optimization scheduling model for cascading hydroelectric power stations, elucidating the operational principles of cascading hydroelectric power stations. Secondly, based on practical scenarios, two types of optimization objectives are set, considering the adequacy of supply and peak load capability as indicators, with the total remaining load and peak-valley difference of remaining load as comprehensive optimization objectives. Furthermore, the uncertainty impact on the water supply side is considered, and a stochastic optimization model for water inflow is established with a normal distribution as the probability distribution.

2. Basic System Framework

The joint dispatching framework of cascade hydropower stations established in this paper is shown in Figure 1. Under the considered framework, multiple hydropower stations have a coupling effect in time and space, where spatial coupling is manifested by multiple hydropower stations being coupled during the same period through inflow, outflow, and incoming water. Temporal coupling is reflected by the fact that different hydropower stations have reservoirs at different times, with a certain water storage effect, and each hydropower station needs to consider the latency of water flow. Compared to the individual operation of each hydropower station, cascading them together can reduce water wastage and fully enhance the utilization of water resources. Within the cascade hydropower system, each hydropower station has a certain capacity of reservoir, which can temporarily store or release water, alleviating the delay in water delivery between different hydropower stations.

In this system structure: Hydropower Station No. 1 is the main source of inflow; Hydropower Station No. 7 is the main outflow side; Hydropower Stations No. 1–No. 7 form the mainline group; while Hydropower Stations No. 8–No. 10 form the branch group. There is a coupled relationship between the inflow and outflow of each hydropower station, and there is a delay effect over time. Each hydropower station needs to flexibly allocate its own water discharge and storage, and joint optimization operation ensures that the overall supply of water is optimized, minimizing the system’s water wastage and fully utilizing the system’s water resources.

3. The Objective Function and Its Subsidiarization

3.1. Objective Function

For the problem of cascade hydropower stations, two factors are usually considered: (1) maximizing the utilization of water resources as much as possible; (2) Utilizing water resources to achieve peak shaving and valley filling, i.e., fully exerting the peak-shaving capacity to reduce the burden on the larger power grid. Therefore, the objective functions considered in this paper include two categories: one category focuses on the overall utilization of water resources, and the other category is from the perspective of peak shaving.

Considering the full utilization of water resources, the objective function is as follows.

$$\mathit{min}{F}_1=\sum _{t=1}^T(P_{L,t}-\sum _{i=1}^I{P}_{i,t})$$

(1)

The above formula represents the minimization of the total residual load of the system. $T$ is the total time scale of the optimization dispatch, which in this paper is one day; $I$ is the total number of hydropower stations; $P_{L,t}$ is the load demand in $t$ period within a day; $P_{i,t}$ is the net water discharge power generation (output) of hydropower station $i$ in $t$ period.

Considering the full exertion of the peak-shaving capability of cascade hydropower stations, the objective function is as follows:

$$\mathit{min}{F}_2=\mathit{max}\sum _{t=1}^T(P_{L,t}-\sum _{i=1}^I{P}_{i,t})-\mathit{min}\sum _{t=1}^T(P_{L,t}-\sum _{i=1}^I{P}_{i,t})$$

(2)

The above formula represents the minimization of the peak-valley difference of the residual load of the system.

3.2. Affinity Function

Due to the different magnitudes of Objective 1 and Objective 2, obviously, the magnitude of Objective 1 is higher than that of Objective 2. To better balance the optimization relationship between Objective 1 and Objective 2, the method of a membership function is used to normalize the magnitudes of the two objectives to the same range, i.e., within the range of 0–1. This makes the optimization process effective, allowing both objective functions to be fully considered. The membership boundaries of the two objective functions are set:

$$K_1^{max}=k_1^{max}max{F}_1,K_1^{min}=k_1^{min}min{F}_1$$

(3)

$$K_2^{max}=k_2^{max}max{F}_2,K_2^{min}=k_2^{min}min{F}_2$$

(4)

where $K_1^{max}$, $K_1^{min}$, respectively, denote the boundary maximum and minimum values after membership degree transformation of Objective 1; $K_2^{max}$, $K_2^{min}$, respectively, denote the boundary maximum and minimum values after membership degree transformation of Objective 2; $k_1^{max}$, $k_1^{min}$, respectively, denote the adjustment coefficient for the maximum and minimum values of Objective 1. In this paper, they are taken as 0.9 and 1.2, respectively. The adjustment coefficients for Objective 2 are similar, which is not elaborated upon here.

Based on the above membership boundaries, the membership functions of the two objective functions are as follows.

$$u\left(F_1\right)=\left\{\begin{array}{cc}1& F_1\ge K_1^{max}\\ \frac{K_1^{max}-min{F}_1}{K_1^{max}}& K_1^{min}\le F_1<K_1^{max}\\ 0& F_1<K_1^{min}\end{array}\right.$$

(5)

$$u\left(F_2\right)=\left\{\begin{array}{cc}1& F_2\ge K_2^{max}\\ \frac{K_2^{max}-min{F}_2}{K_2^{max}}& K_2^{min}\le F_2<K_2^{max}\\ 0& F_2<K_2^{min}\end{array}\right.$$

(6)

Based on the above membership function model, the values of the two optimization objective functions can be limited within the range of 0–1, effectively balancing the relationship between the two.

Establish a multi-objective optimization model

$$\mathit{min}F={\lambda }_{1}u\left(F_1\right)+{\lambda }_{2}u\left(F_2\right)$$

(7)

where ${\lambda }_1,{\lambda }_2$ represent the weight factors for Objective 1 and Objective 2, respectively, where a larger the weight indicates a more important objective function.

4. Optimization Model for Stepped Hydroelectric Power Plants

Cascade hydropower stations play an important role in the power system and are crucial in power dispatching. Due to the seasonal and periodic variations of water flow, cascade hydropower stations have certain capabilities in peak shaving and load adjustment. By reasonably planning and managing reservoir water levels, they can provide more electricity during peak demand periods and moderately reduce generation during low demand periods, which helps balance the supply and demand of the power system, thereby improving the flexibility and stability of system operation.

4.1. Mathematical Modeling of Step Hydro Power Plants

Establishing a mathematical model can provide a research basis for assessing the performance of power stations under different working conditions. By simulating different water levels, flow rates, and load conditions, we can better understand the response characteristics of cascade hydropower stations, thereby formulating more reasonable operation strategies. This helps improve the stability and reliability of the power stations, ensuring their efficient operation under different environmental conditions. The significance of the mathematical modeling of cascade hydropower stations lies in improving energy production efficiency, optimizing the operation strategies, reducing the impact on the ecological environment, and promoting the sustainable development of clean energy.

In the process of establishing the optimization model for cascade hydropower stations in this paper, it is necessary to consider factors such as the output limits of the hydropower units, the coupling relationship of reservoir capacity, the limitation of reservoir capacity, the delay of water flow, and the generation flow limits of the units. The specific establishment process is as follows.

Since the role of hydropower units in the entire power system is that of auxiliary adjustment, the system still mainly relies on thermal power generation. Therefore, the total output of the hydropower unit group at any moment should not exceed the system load, and this is specifically represented as follows.

$$P_{L,t}-\sum _{i=1}^I{P}_{i,t}\ge 0,\forall t,i$$

(8)

For each hydropower station, internally, there are upper and lower limits to the output of each hydropower unit, similarly to thermal power units. Unlike thermal power units, hydropower units have almost no constraints on ramp rate during operation, which is specifically represented as follows.

$$P_i^{min}\le P_{i,t}\le P_i^{max},\forall t,i$$

(9)

In the formula, $P_i^{max}$ and $P_i^{min}$, respectively, represent the upper and lower limits of the output of hydropower unit $i$.

Additionally, each hydropower unit not only needs to consider the limitation of output power during the generation process, but also the flow constraints of water resources involved in the generation process, hence the constraint is expressed as follows:

$$q_i^{min}\le q_i\le q_i^{max},\forall i$$

(10)

In the formula, $q_i^{max}$ and $q_i^{min}$, respectively, represent the upper and lower limits of the generation flow of hydropower unit $i$.

Besides considering the internal constraints of each hydropower unit, the overall output constraints of each hydropower station also need to be considered, which are specifically expressed as follows:

$$P_Y^{min}\le \sum _{i\in Y}{P}_{i,t}\le P_Y^{max},\forall t,Y$$

(11)

In the formula, $P_Y^{max}$ and $P_Y^{min}$, respectively, represent the upper and lower limits of the output of hydropower station $Y$.

In addition to the operational hydropower units within each hydropower station, the constraints of the reservoir also need to be considered, including the coupling constraints of the reservoir at different times, the upper and lower limits of reservoir capacity, and the constraints on the initial and final capacities of the reservoir, which are specifically expressed as follows.

$$V_{Y,t}=V_{Y,t-1}+(R_{Y,t}-Q_{Y,t})\Delta t$$

(12)

$$V_{Y,t}^{min}\le V_{Y,t}\le V_{Y,t}^{max}$$

(13)

$$V_{Y,0}=V_{Y,in}$$

(14)

$$V_{Y,T}=V_{Y,out}$$

(15)

In the formula, $V_{Y,t}$ represents the capacity of the reservoir of hydropower station $Y$; $R_{Y,t}$ represents the inlet flow of hydropower station $Y$; $V_{Y,t}^{max}$ and $V_{Y,t}^{min},$ respectively, represent the upper and lower limits of the capacity of the reservoir of hydropower station $Y$; $V_{Y,0}$ and $V_{Y,T},$ respectively, represent the capacity of the reservoir of hydropower station $Y$ at the initial and final moments; $V_{Y,in}$ and $V_{Y,out}$, respectively, represent the set values of the capacity of the reservoir of hydropower station $Y$ at the initial and final moments.

Additionally, constraints on the spillway flow also need to be considered, which are specifically expressed as follows.

$$Q_{Y,t}=\sum _{i\in Y}{q}_{i,t}+s_{Y,t}$$

(16)

$$Q_{Y,t}^{min}\le Q_{Y,t}\le Q_{Y,t}^{max}$$

(17)

In the formula, $Q_{Y,t}$ represents the turbinated flow of hydropower station $Y$; $Q_{Y,t}^{max}$ and $Q_{Y,t}^{min}$, respectively, represent the upper and lower limits of the turbinated flow of hydropower station $Y$; and $s_{Y,t}$ represents the wasted water flow of hydropower station $Y$.

4.2. Stochastic Optimization Model with Incoming Water Uncertainty

In this study, we employ mixed-integer programming (MIP) methodology to address the optimization scheduling problem of multi-year cascade hydropower stations. This problem involves multi-objective decision making, where some decision variables are discrete (such as the on/off states of generators), while others are continuous (like the water level of the reservoir and the amount of electricity generated). Mixed-integer programming allows us to handle these discrete and continuous variables simultaneously within a single mathematical model, providing a comprehensive and precise framework for optimization scheduling.

In our model, integer variables are typically used to represent operational decisions, such as the scheduling and start-stop status of the units. These decisions are discrete, as units cannot be in a partially on or off state. Continuous variables are employed to represent the physical and operational parameters of the hydropower station, for instance, reservoir water levels, flow rates, and electricity output.

Our MIP model is designed to maximize the overall performance of the hydropower station, taking into account operational constraints, water resource management, and electricity demand. The multi-objective function reflects a comprehensive consideration of electricity production efficiency, the sustainable use of water resources, and system operational costs. Through this approach, we are able to find the best trade-off point among different objectives.

The application of mixed-integer programming lends flexibility and adaptability to the optimization process, especially in dealing with complex systems and variable operational environments. This method not only enhances the accuracy of problem-solving but also boosts the practical applicability of the model in real-world scenarios, particularly when facing uncertain factors and fluctuating market demands.

In summary, the application of mixed-integer programming in this study provides a powerful and flexible tool for solving the optimization scheduling problem of multi-year cascade hydropower stations. It effectively manages and balances the complex and diverse decisions inherent in multi-objective optimization problems.

The variability of inflow poses challenges to the energy output and economic benefits of hydropower stations. Stochastic optimization models have significant advantages in addressing these uncertainties. They can better consider the probability distribution of inflow, rather than relying on deterministic values. By introducing randomness to simulate various meteorological and hydrological conditions, the robustness of the model is enhanced. Stochastic optimization models show obvious advantages in handling the uncertainty of inflow in cascade hydropower stations by comprehensively considering probability distributions, improving model robustness, integrating multiple factors, and assessing risks, offering more scientific and flexible decision support for the operation and planning of hydropower stations. This paper considers the inflow volume as an uncertain variable, following a normal distribution, and applies the scenario analysis method in stochastic optimization models for simulation.

5. Example Analysis

5.1. Description of Scenarios

In this study, we propose a novel multi-objective stochastic optimization approach for the operational scheduling of multi-year cascade hydropower stations. This method specifically addresses multiple operational objectives inherent in hydropower station management, such as maximizing hydropower production and effectively managing water resources. A key challenge lies in the potential conflicts among these objectives: optimizing one goal (such as minimizing the total residual load) might lead to the relative weakening of another (like minimizing the peak-valley difference of the residual load). Our approach utilizes a membership function to balance these multi-objective relationships. Here, the membership function acts as a regulator, enabling us to adjust the optimization process based on the relative importance of different objectives. The essence of this method is the transformation of traditional single-objective optimization problems into a multi-objective optimization framework, allowing for the simultaneous consideration and optimization of multiple goals.

During the optimization process, we observed that the relationships between objectives exhibit nonlinear characteristics, indicating the absence of a single optimal solution and the presence of an optimal solution set. By adjusting the weight factors in the membership function, we can effectively control the trade-off relationships between these optimization objectives. This adjustment not only demonstrates the flexibility of the model under the different priority settings of objectives but also verifies the robustness of our proposed method.

Overall, the multi-objective stochastic optimization method presented in this study offers an innovative and effective solution for the scheduling problems of multi-year cascade hydropower stations. This method achieves a balance among several conflicting optimization objectives and flexibly responds to different operational scenarios and priority levels of objectives, thereby facilitating the more efficient and sustainable management of hydropower stations.

To analyze the feasibility of the model proposed in this paper, four operational scenarios were established, namely: Scenario 1—optimization of Objective 1, where the objective function is set to minimize the total residual load; Scenario 2—optimization of Objective 2, where the objective function is set to minimize the peak-valley difference of the residual load; Scenario 3—multi-objective optimization considering both Objective 1 and Objective 2, that is, a comprehensive optimization mode that balances both objectives; and Scenario 4—stochastic optimization considering the uncertainty of inflow within the multi-objective optimization framework of Scenario 3, which means random optimization. 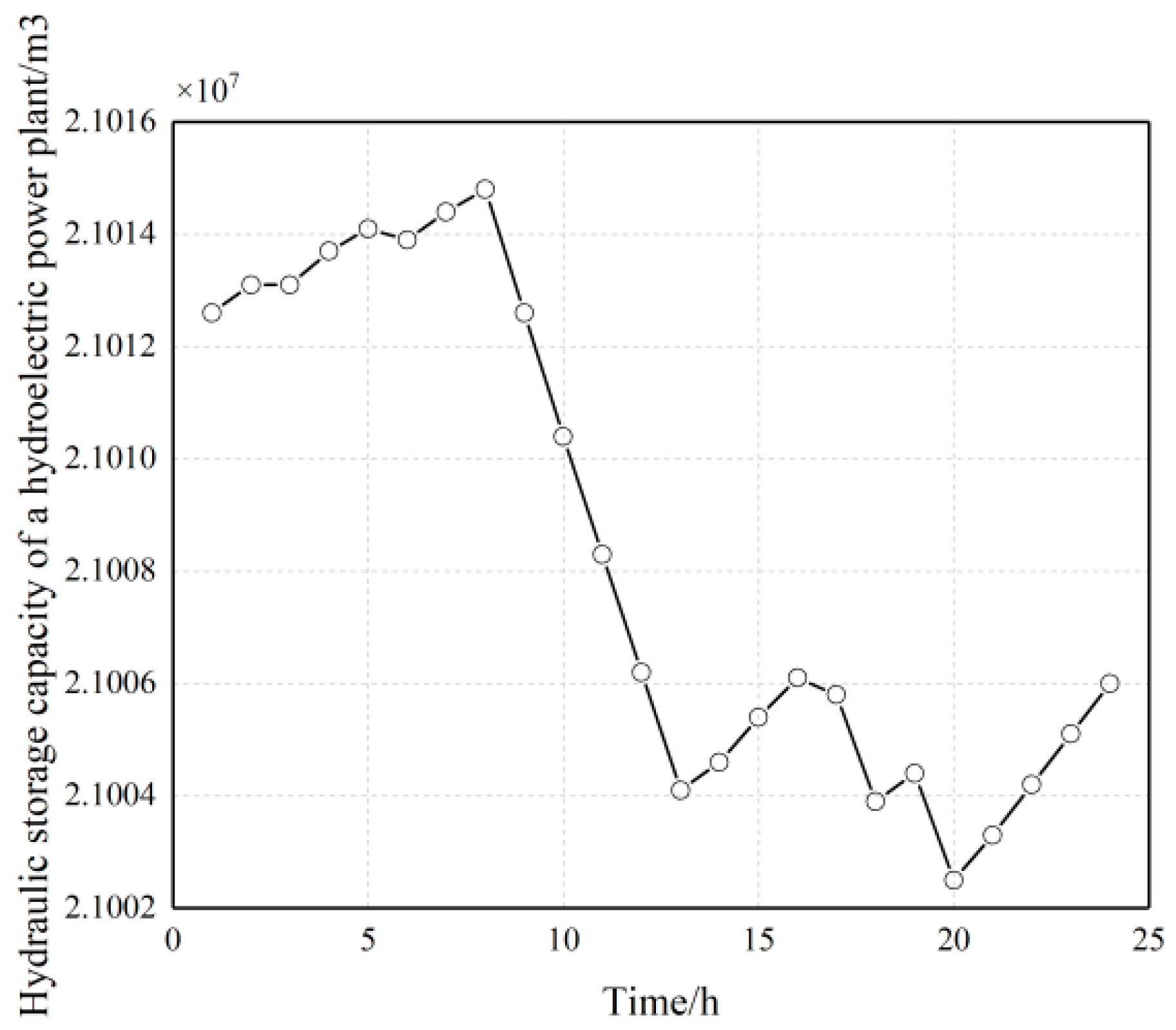The internal coupling relationships of the cascade hydropower stations are shown in Figure 1, consisting of 10 hydropower stations. The upper and lower limits of the hydropower unit output per time period are 15 MW and 0 MW, respectively. The initial reservoir capacity is 21.01 Mm³, and the final reservoir capacity is 21.01 Mm³, with the minimum and maximum reservoir capacities being 3.85 and 25.22 Mm³, respectively. The minimum and maximum turbinated flow rates are 200 and 3000 m³/s, respectively. The number of hydropower units in each station is as follows: 3, 3, 4, 3, 5, 5, 4, 3, 2, 2.

5.2. Analysis of Results

The total residual load and the peak-valley difference of the residual load in the system under the four scenarios are as presented in

Table 1. Total residual load on the system with peak-to-valley differential.

Scenario	Total Remaining Load (MW)	Residual Load Peak-Valley Difference (MW)
Scenario 1	15,781.86	643.65
Scenario 2	16,088.15	255.65
Scenario 3	15,781.86	350.00
Scenario 4	15,788.06	259.45

.

According to the above table, under Scenario 1, the system’s total residual load is optimized to the smallest, at 15,781.86 MW, but the peak-valley difference of the residual load remains large, at 643.65 MW. In this scenario, the system’s water supply stability is fully guaranteed, but its peak-shaving ability is not utilized. Similarly, in the optimization of Scenario 2, the optimized results for the system’s total residual load and the peak-valley difference of the residual load are 16,088.15 MW and 255.65 MW, respectively, indicating that, in this scenario, the system’s peak-shaving ability is fully utilized, but the optimization of water supply is neglected. Under Scenario 3, the optimized results for the total residual load and the peak-valley difference of the residual load are 15,781.86 MW and 350.00 MW, respectively, indicating that this scenario can balance both objectives, considering both the system’s water supply capacity and peak-shaving ability. In Scenario 4, the optimized results for the total residual load and the peak-valley difference of the residual load are 15,788.06 MW and 259.45 MW, respectively; compared to Scenario 3, it indicates that the uncertainty of inflow considered in Scenario 4 poses a challenge to the water supply capacity of the cascade hydropower stations, causing an increase in fluctuations in the system’s total residual load. In this scenario, the cascade hydropower stations in the region need to focus on ensuring the water supply capacity.

The comparison of the system’s original load and optimized residual load, total output of hydropower units, turbinated flow, reservoir capacity optimization curve, etc., under the four scenarios are as follows.

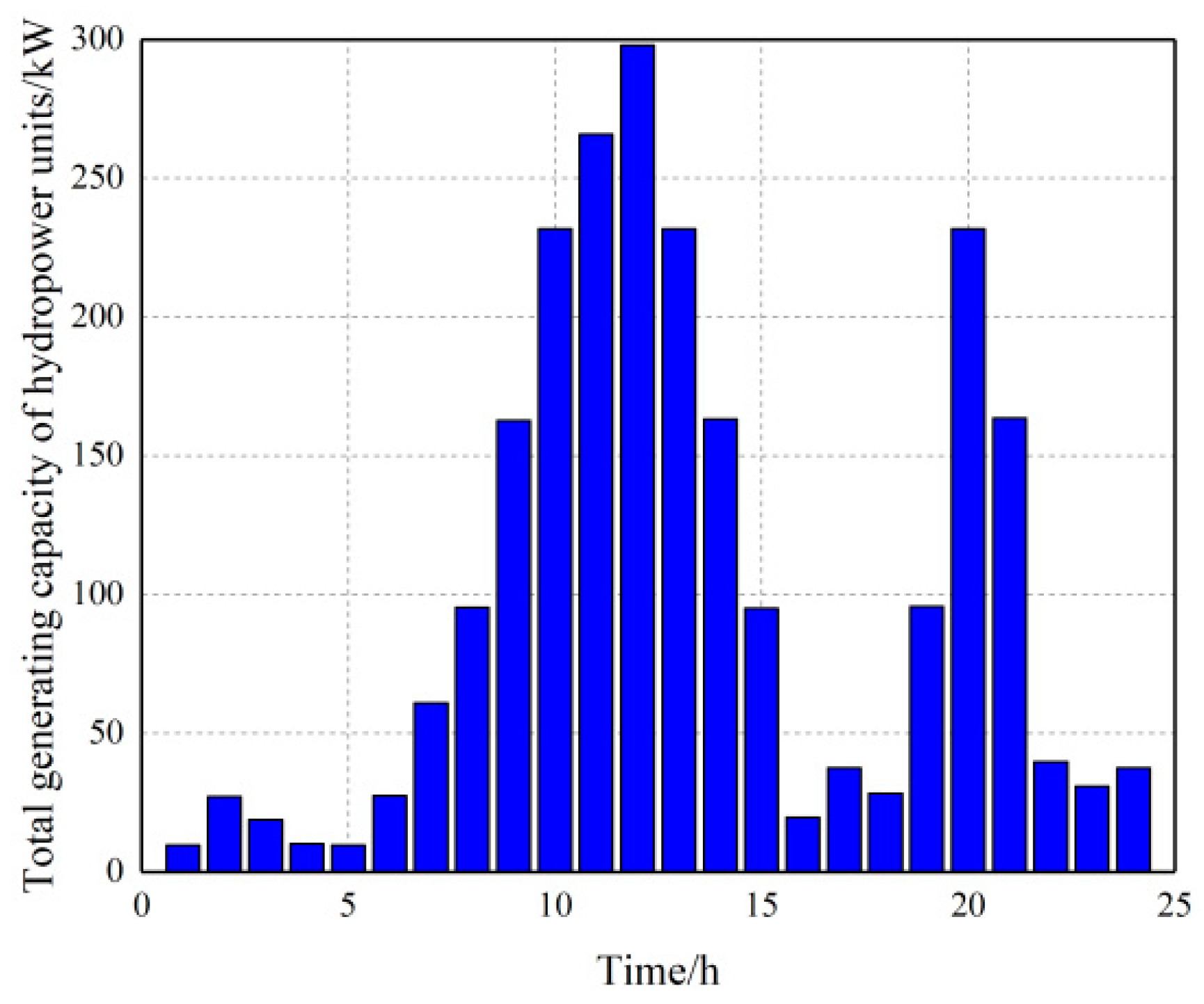
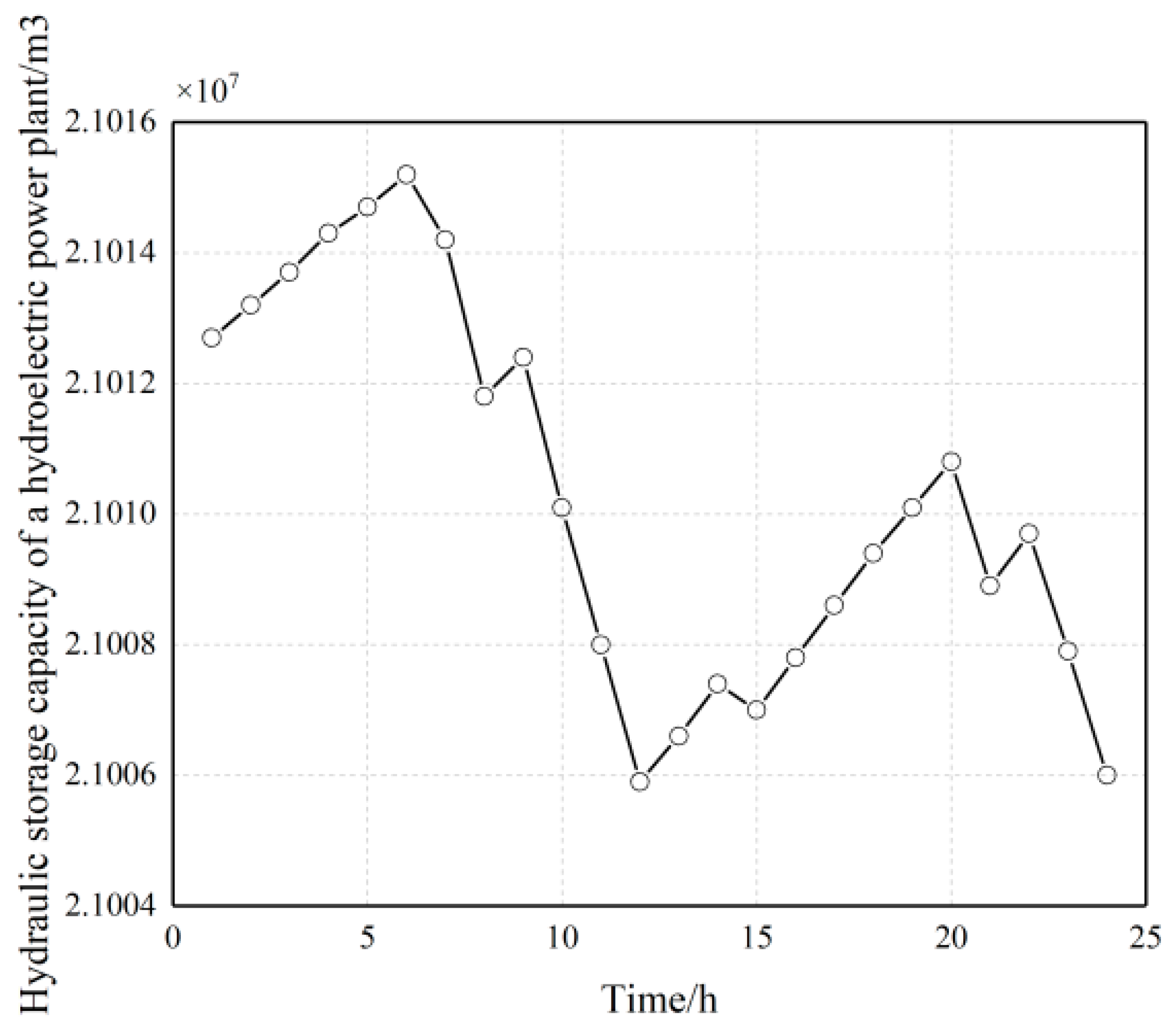
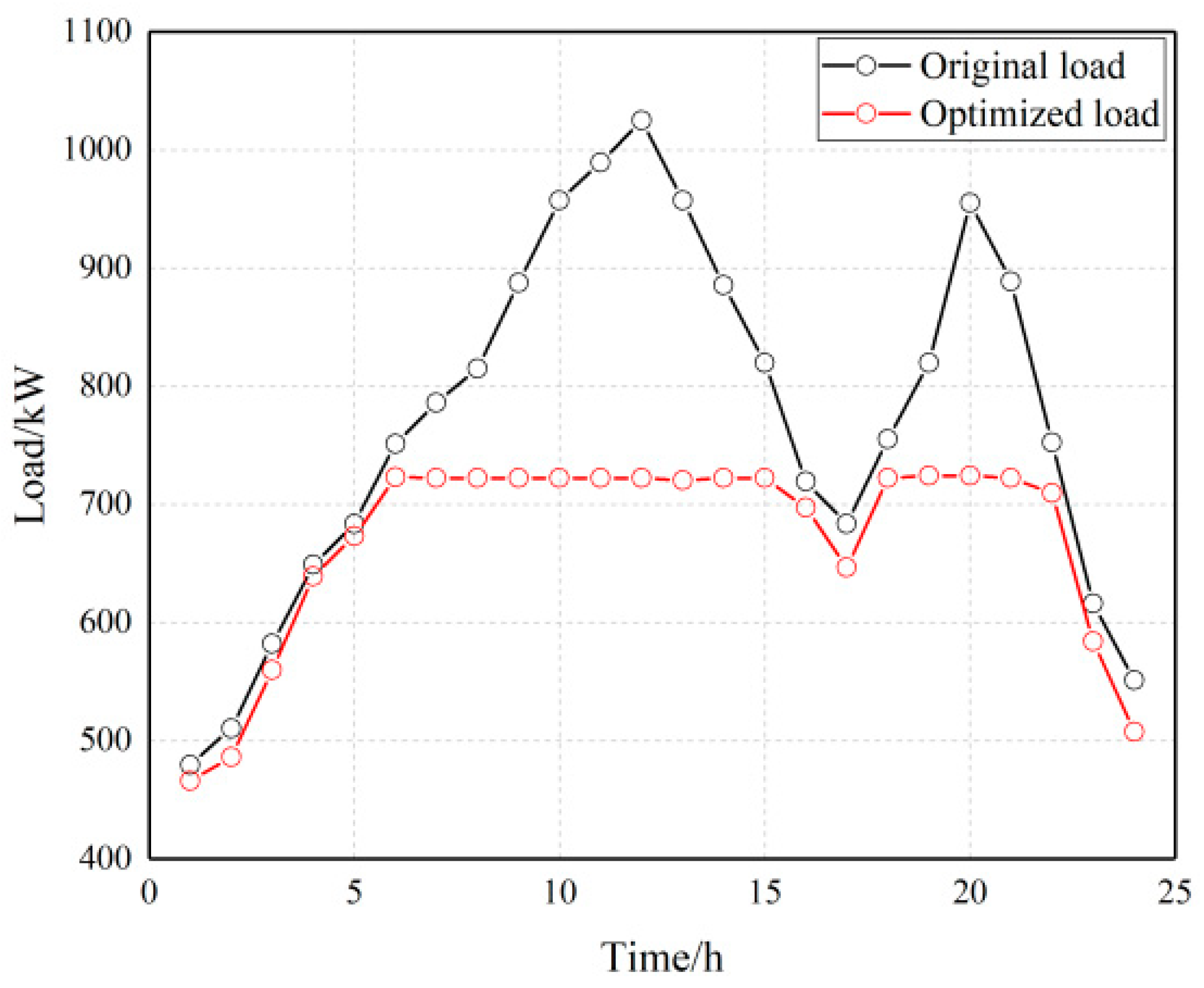
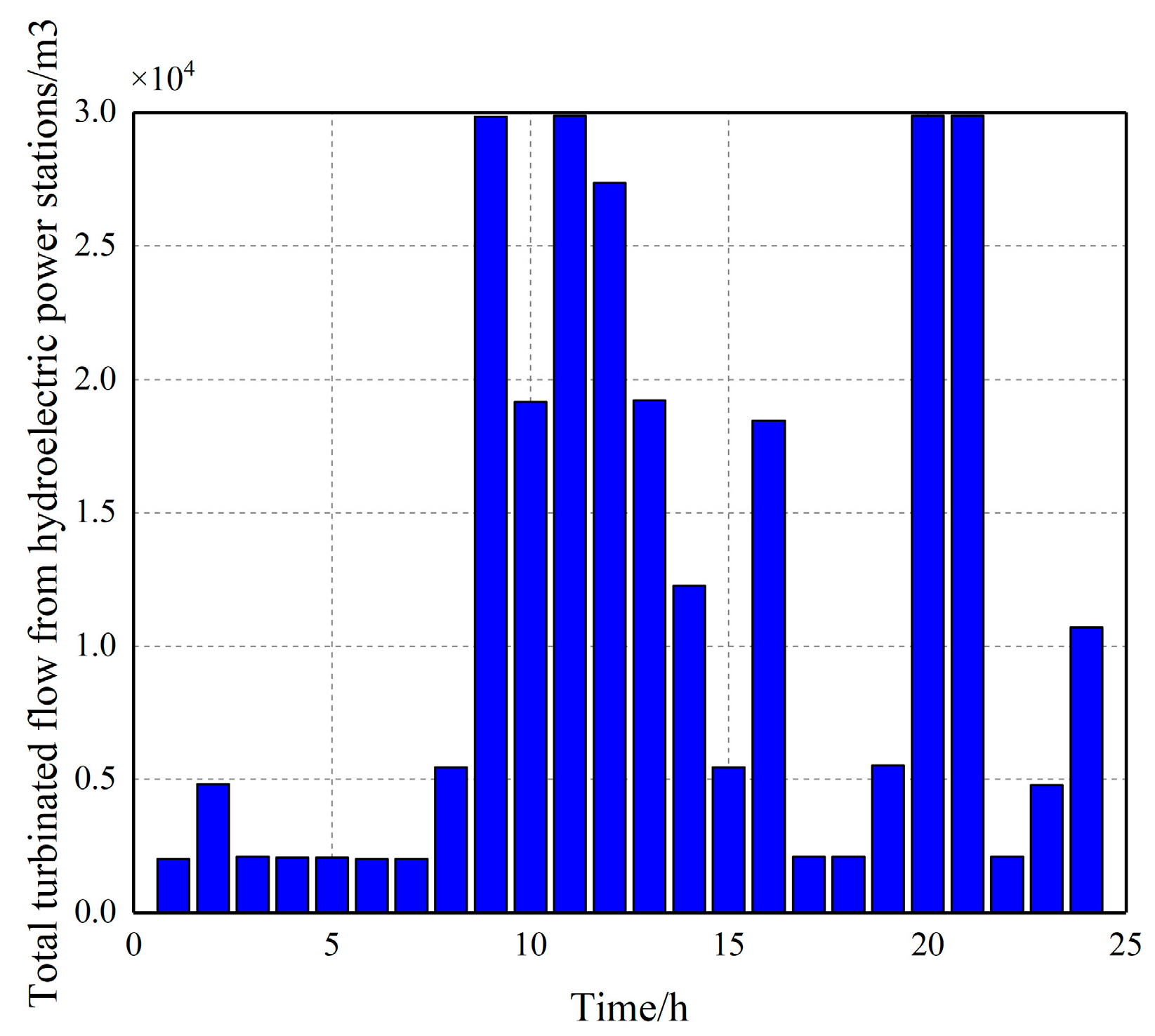
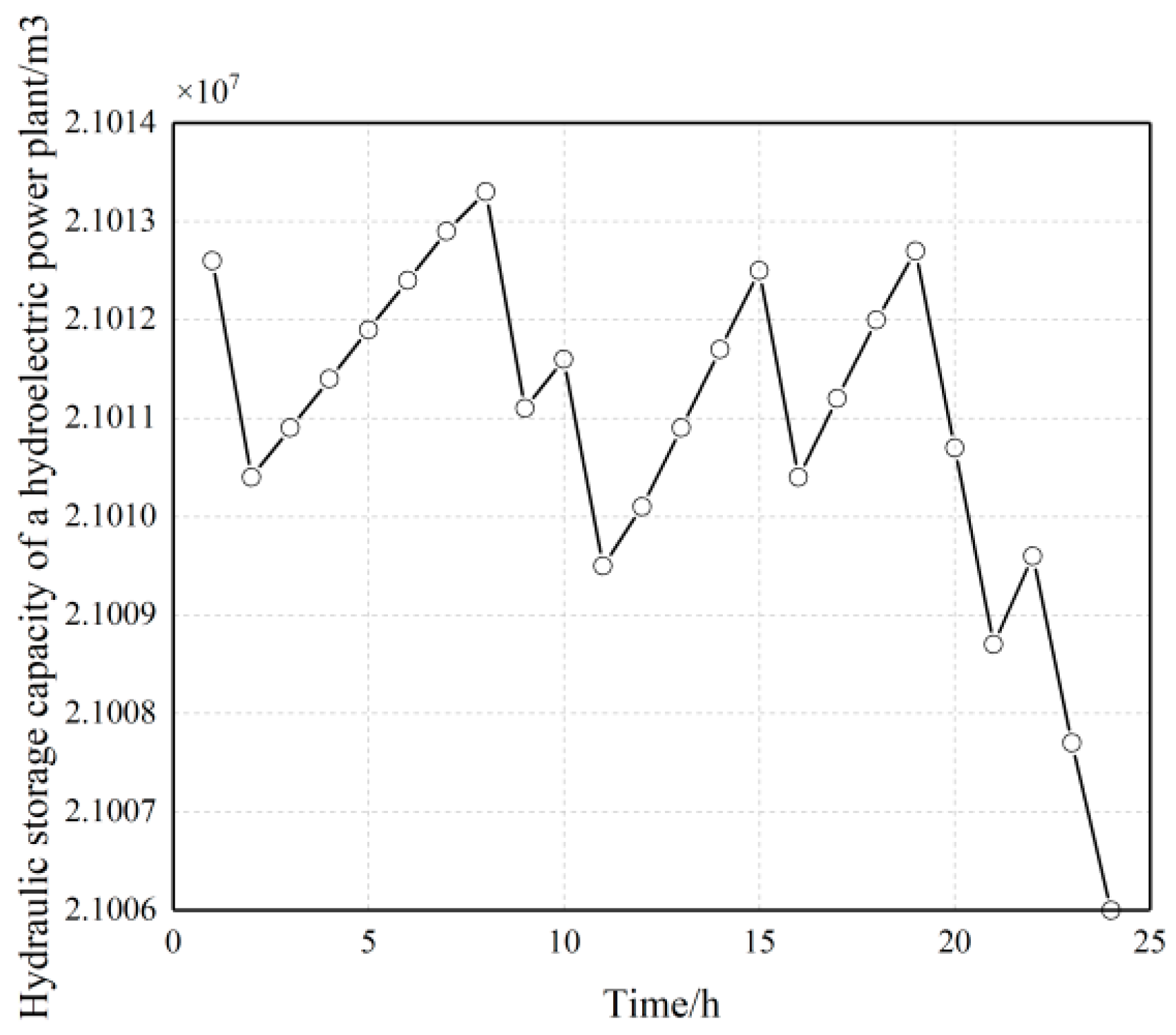
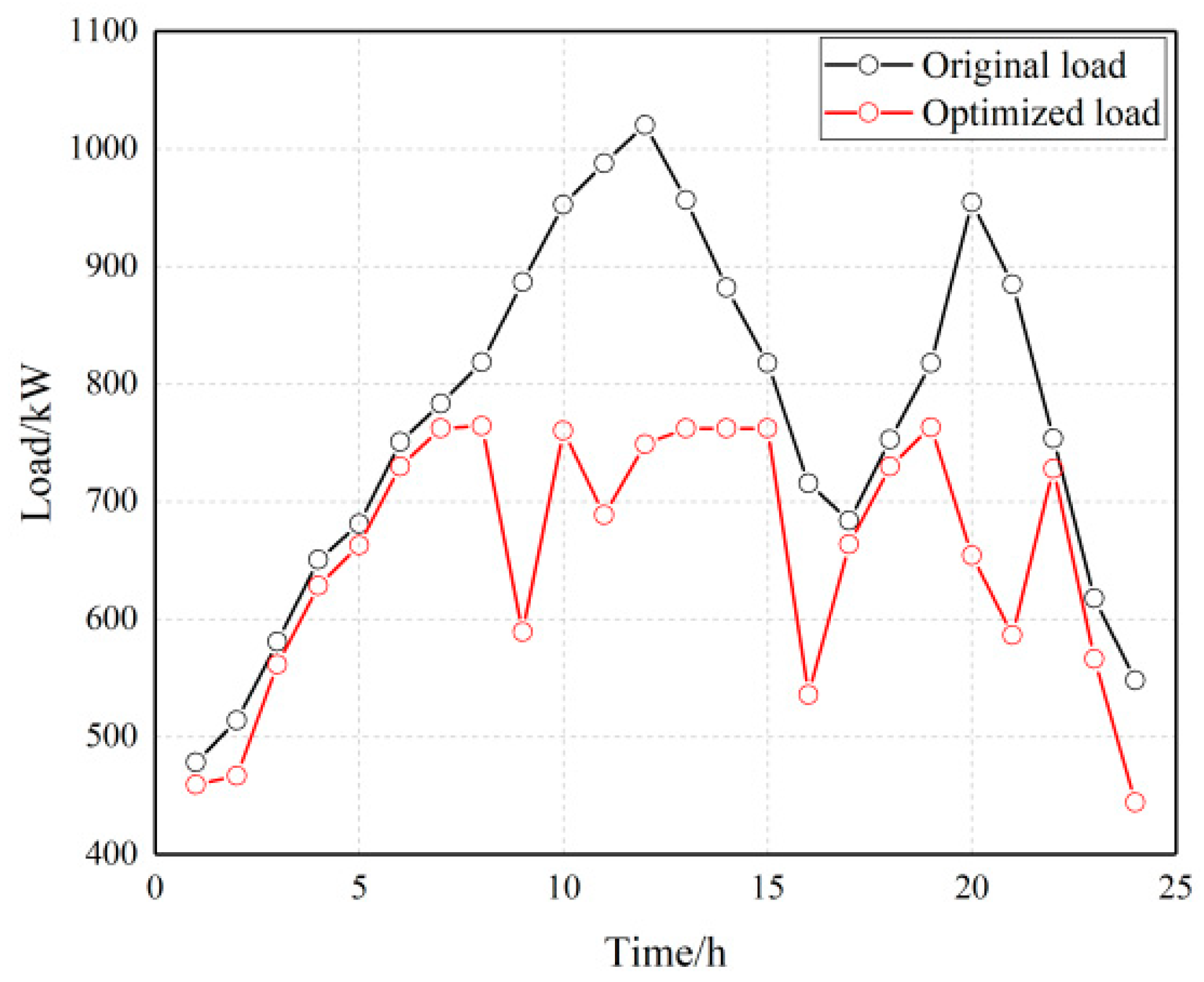
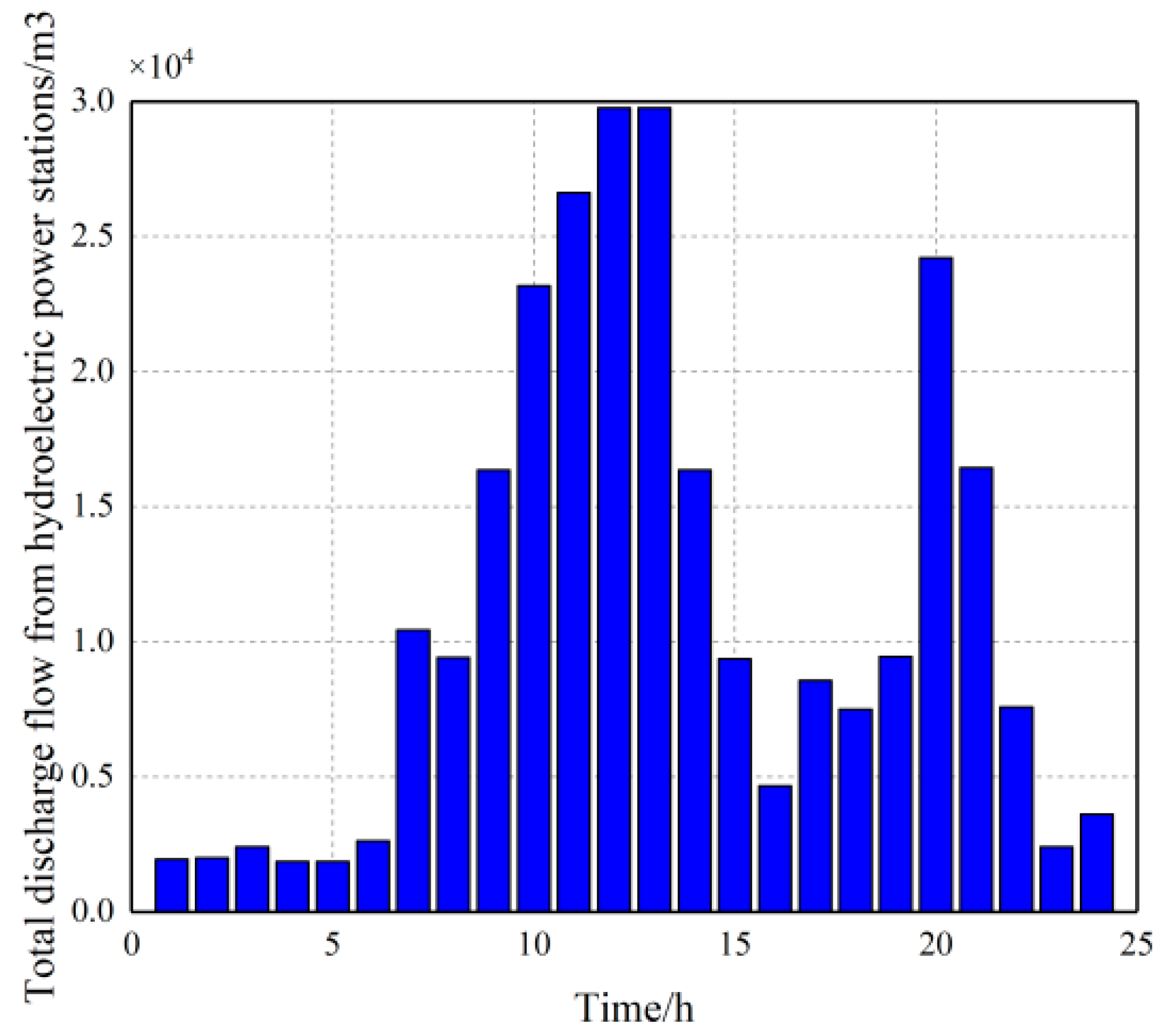
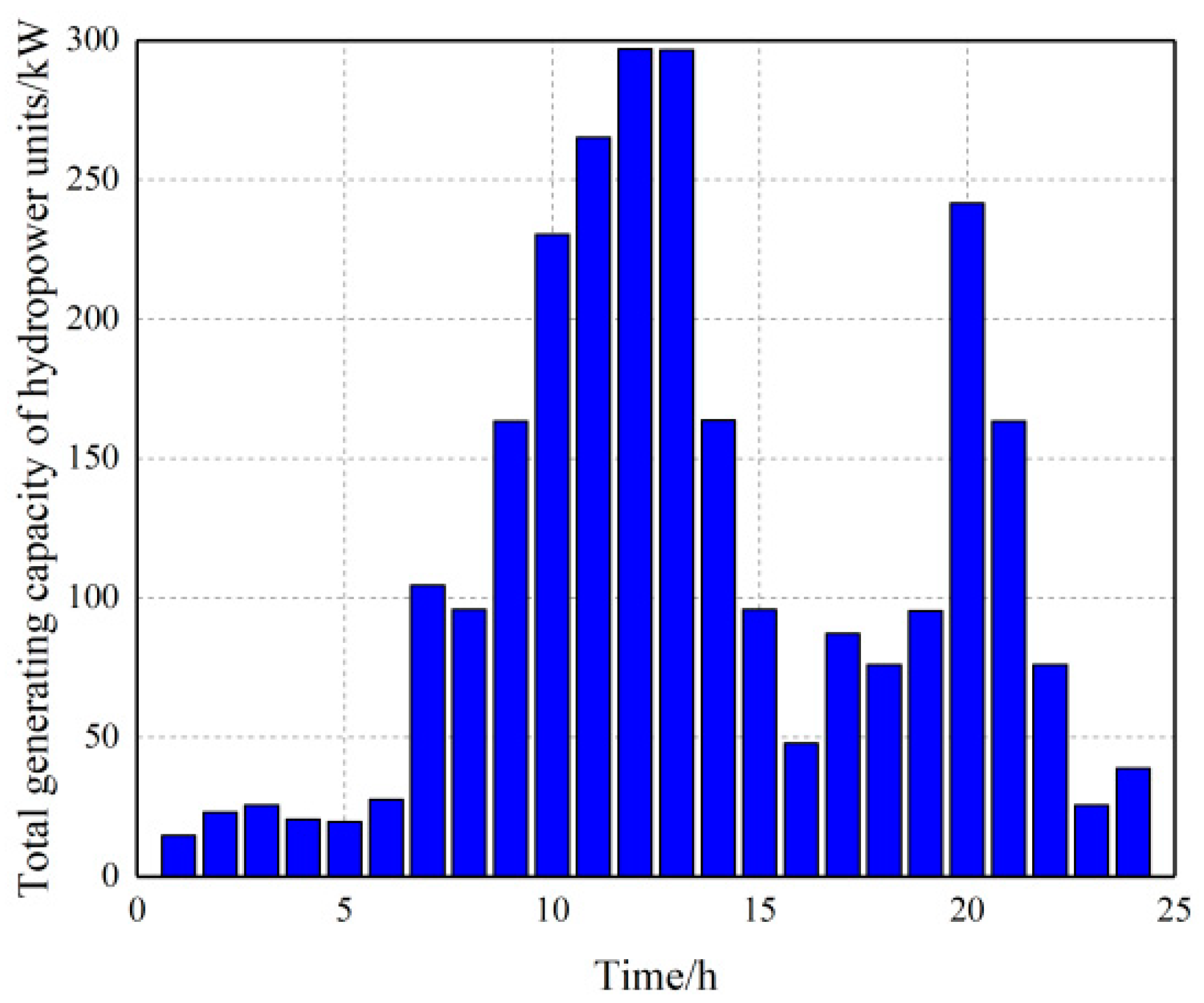
From the Figure 2, Figure 3, Figure 4 and Figure 5, it can be analyzed that the comparison of the original load and the optimized residual load in Scenario 1 indicates that there are differences in the water supply optimization volume of each period in the cascade hydropower stations. The reason is that, in this scenario, the system optimization goal is to minimize the total residual load of the system, which requires the cascade hydropower stations to optimize the water discharge in each period, and the water discharge of each period is related to the interactive water volume and inflow of the coupled hydropower stations, resulting in different optimization values for the load reduction of each period. The total power output of the hydropower stations and the optimization curve of the load reduction correspond to each period, indicating the effectiveness of the results. From the reservoir capacity optimization curve of the hydropower station, it can be analyzed that there is an initial and end capacity requirement for the reservoir capacity of the hydropower station. The change in capacity indicates the phenomenon of water storage and discharge in the hydropower station’s reservoir. The optimization trend is generally a significant increase from 7:00 to 13:00, and a significant decrease from 13:00 to 17:00, with minor fluctuations in other periods due to the coupling of the hydropower unit groups within the cascade hydropower station.

Similarly to the analysis of Scenario 1, from the analysis of the Figure 6, Figure 7, Figure 8 and Figure 9, it can be determined that, based on the curve of the original load and the optimized residual load, the peak-valley difference of the residual load curve is optimized to the minimum. The optimization process can be roughly analyzed based on the characteristics of the original load curve, which involves supplying the load of the two peak periods as much as possible, thereby reducing the peak-valley difference and utilizing the peak-shaving ability of the cascade hydropower stations. According to the total output of the hydropower units, there is a large output from 6:00 to 15:00 and 19:00 to 21:00, consistently with the above analysis. According to the reservoir capacity optimization curve, the system reservoir is storing water from 0:00 to 6:00 and discharging water from 6:00 to 12:00. The reason is that from 6:00, the system faces the first peak load period, and the reservoir needs to coordinate with the hydropower units for discharging water.

From the analysis of the Figure 10, Figure 11, Figure 12 and Figure 13, it can be deduced that, by comparing the curve of the original load and the optimized residual load, the peak-valley difference of the residual load curve is larger than in Scenario 2, and the peak baseline is higher. However, there are periods of “deep reduction” in the load during several middle periods. The reason is that, in this scenario, the cascade hydropower stations need to balance the optimization of the two objective functions. During the “deep reduction” periods, although the peak-shaving ability is sacrificed, it demonstrates certain water supply capabilities. Comparing the total output of the hydropower units and the reservoir capacity optimization curve, the frequency of fluctuations in these curves is higher compared to Scenario 1 and Scenario 2. This is due to the optimization results of the cascade hydropower stations when searching for deep water supply periods.

As shown in Figure 14, Figure 15, Figure 16 and Figure 17. The analysis of Scenario 4 is similar to that of Scenario 3, as both belong to the category of multi-objective optimization. The difference is that Scenario 4 involves the uncertainty factor of inflow, which will not be elaborated upon here. To illustrate the robustness of the multi-objective membership degree optimization model established in this paper, the weight factors in the multi-objective optimization model are varied to obtain the optimization solution sets for the two objectives, as shown in the following figure.

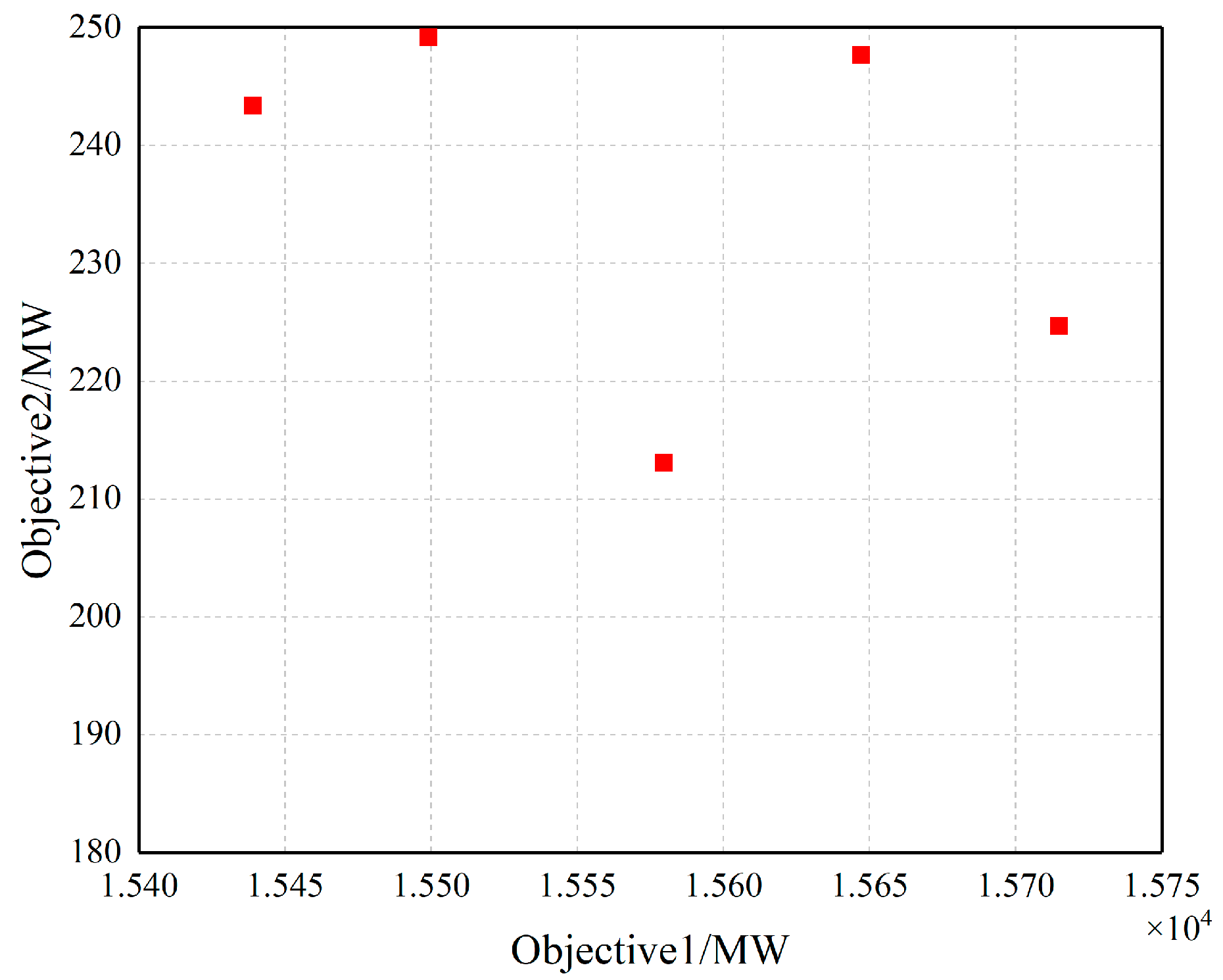
To analyze the performance of the model in the absence of weighting factors, a set of control experiments was conducted. In these experiments, both optimization objectives were treated equally, meaning that no additional priority was given to any one objective. As demonstrated in Figure 18, the optimization paths and final solution sets of the two objectives are presented without the influence of weight preferences. In the absence of constraints from weighting factors, the model exhibited a different set of optimization solutions, characterized by a more dispersed distribution of objective values. This further confirms the pivotal role that weighting factors play in the optimization process and reveals the different dynamics involved in balancing between optimization objectives.

According to the analysis of the Figure 19, when the optimization objective 1 decreases, the optimization objective 2 increases, and this process is nonlinear, indicating that this model does not have an optimal solution but an optimal solution set. At the same time, the magnitudes of the two objective optimization values are different. Changing the weight factors can effectively change their variations, verifying the robustness of the proposed membership degree function multi-objective optimization.

6. Conclusions

This paper considers the uncertainty of inflow, the diversity of optimization objectives, and the complex coupling mechanism within cascade hydropower stations, and proposes a multi-objective stochastic optimization model for the inter-annual optimization scheduling of cascade hydropower stations. The conclusions are as follows:

(1)

This paper establishes a multi-objective stochastic optimization model for the inter-annual optimization scheduling of cascade hydropower stations. It effectively balances the optimization among multiple objectives by setting a membership function, not only satisfying the supply stability of the entire system but also achieving peak shaving and valley filling on the load side.

(2)

In the proposed model, the uncertainty of inflow volume on the inflow side is comprehensively considered, transforming the traditional deterministic model into a stochastic optimization model. This endows the proposed model with better robustness in uncertain environments.

(3)

In the proposed model, different hydropower stations can enhance their energy efficiency utilization through temporal and spatial coupling, increasing the energy efficiency utilization among each other, breaking the independence of individual supply in traditional models, and significantly improving the overall energy utilization of the system.