Optimal Reactive Power Flow of AC-DC Power System with Shunt Capacitors Using Backtracking Search Algorithm
Abstract
1. Introduction
2. Materials and Methods
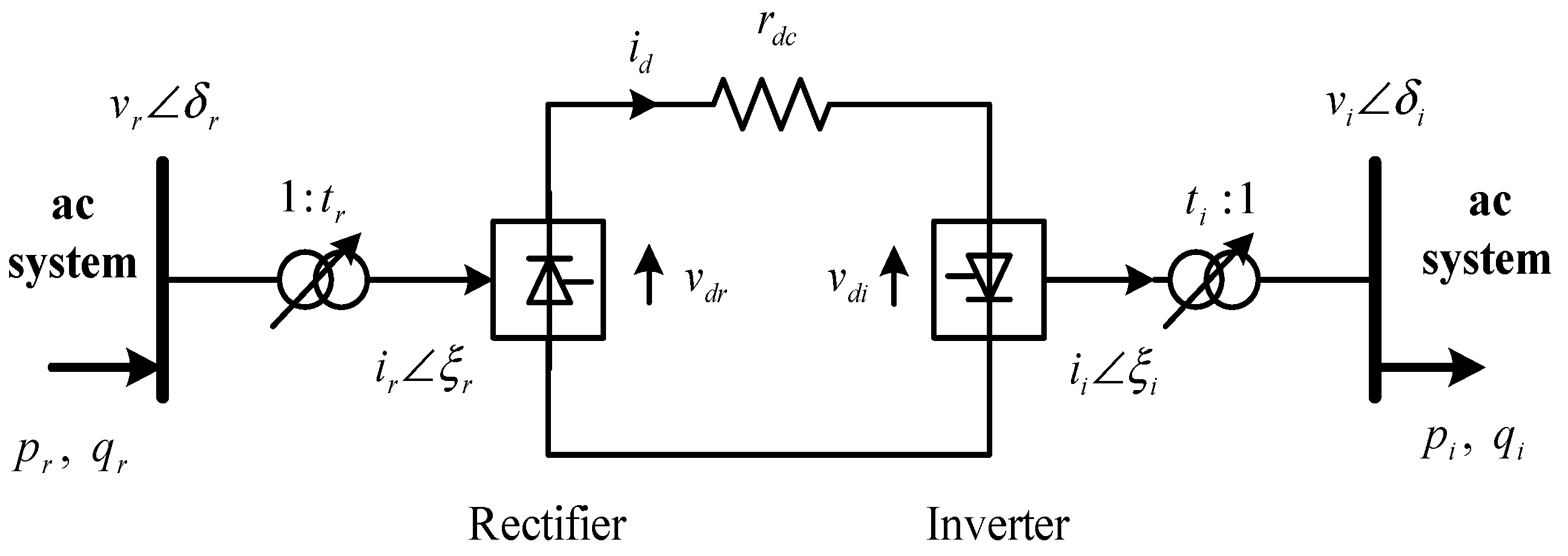
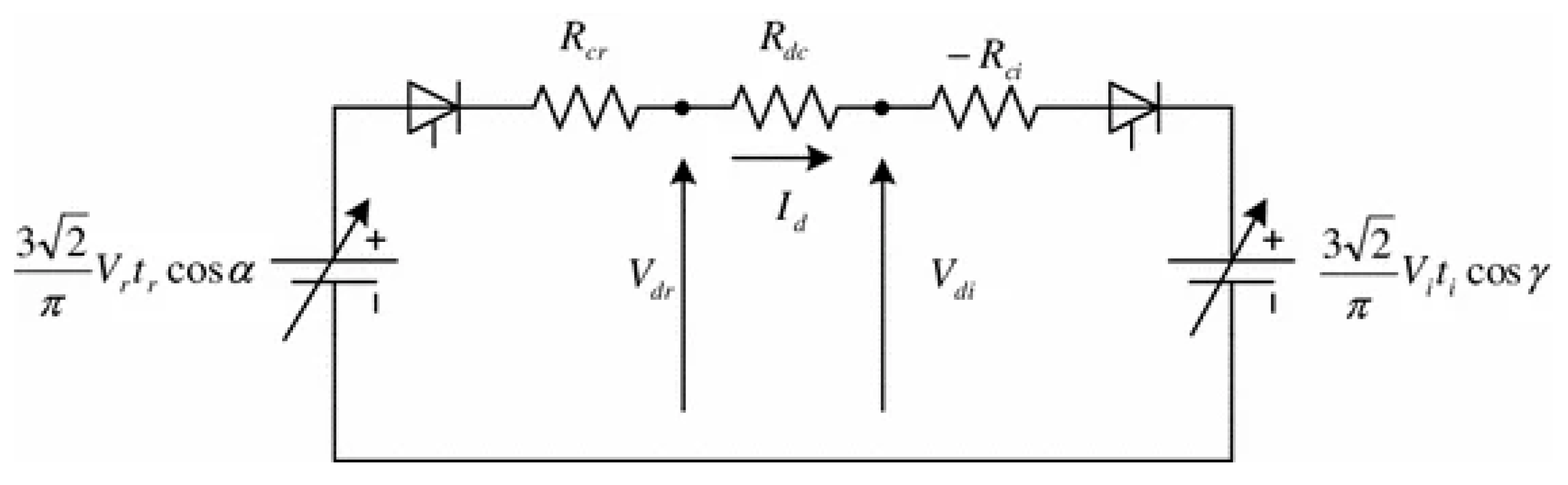
2.1. The State and Control Variables of DC and AC System
2.2. Power Loss
2.3. Fitness Function
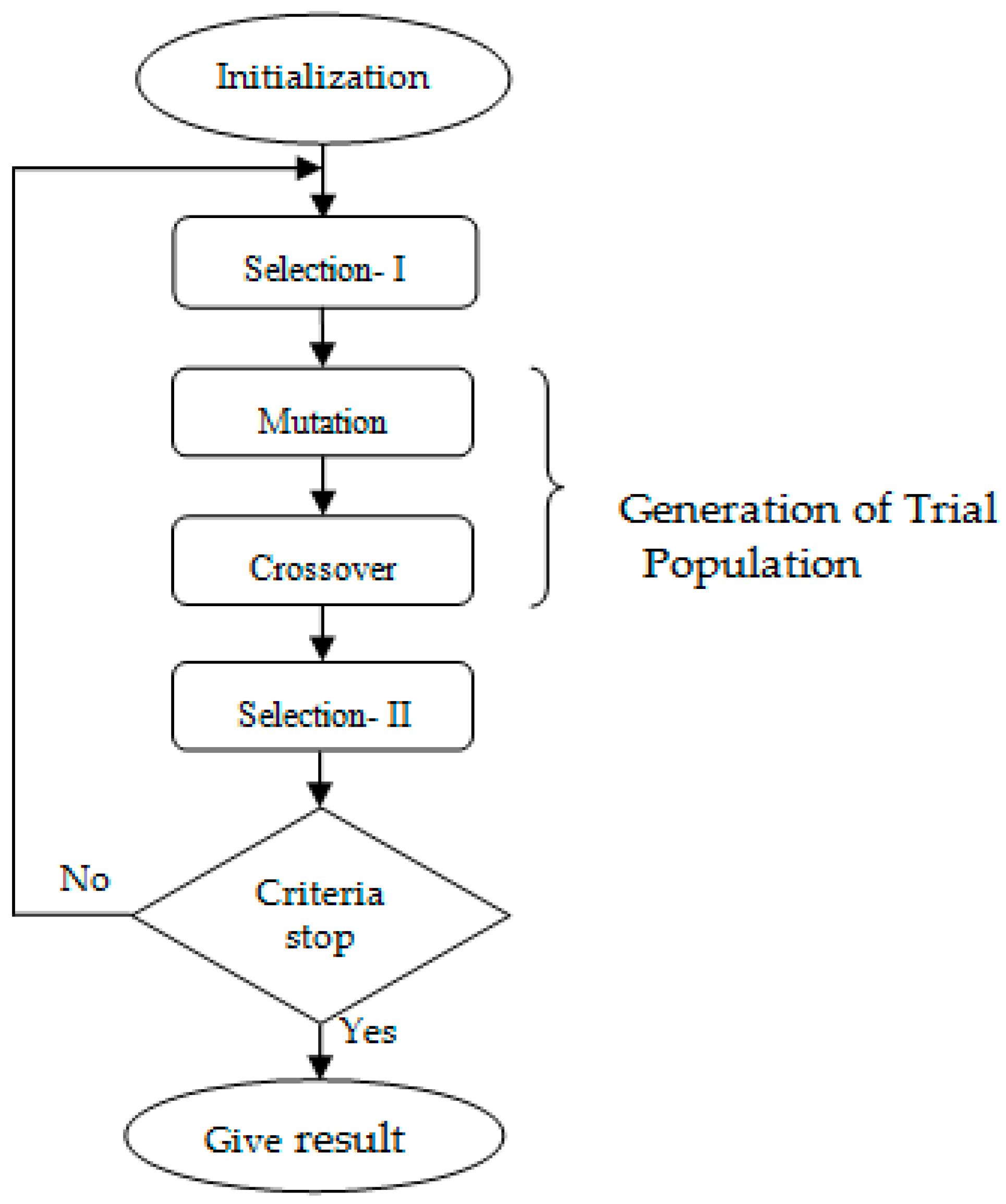
3. Backtracking Search Algorithm
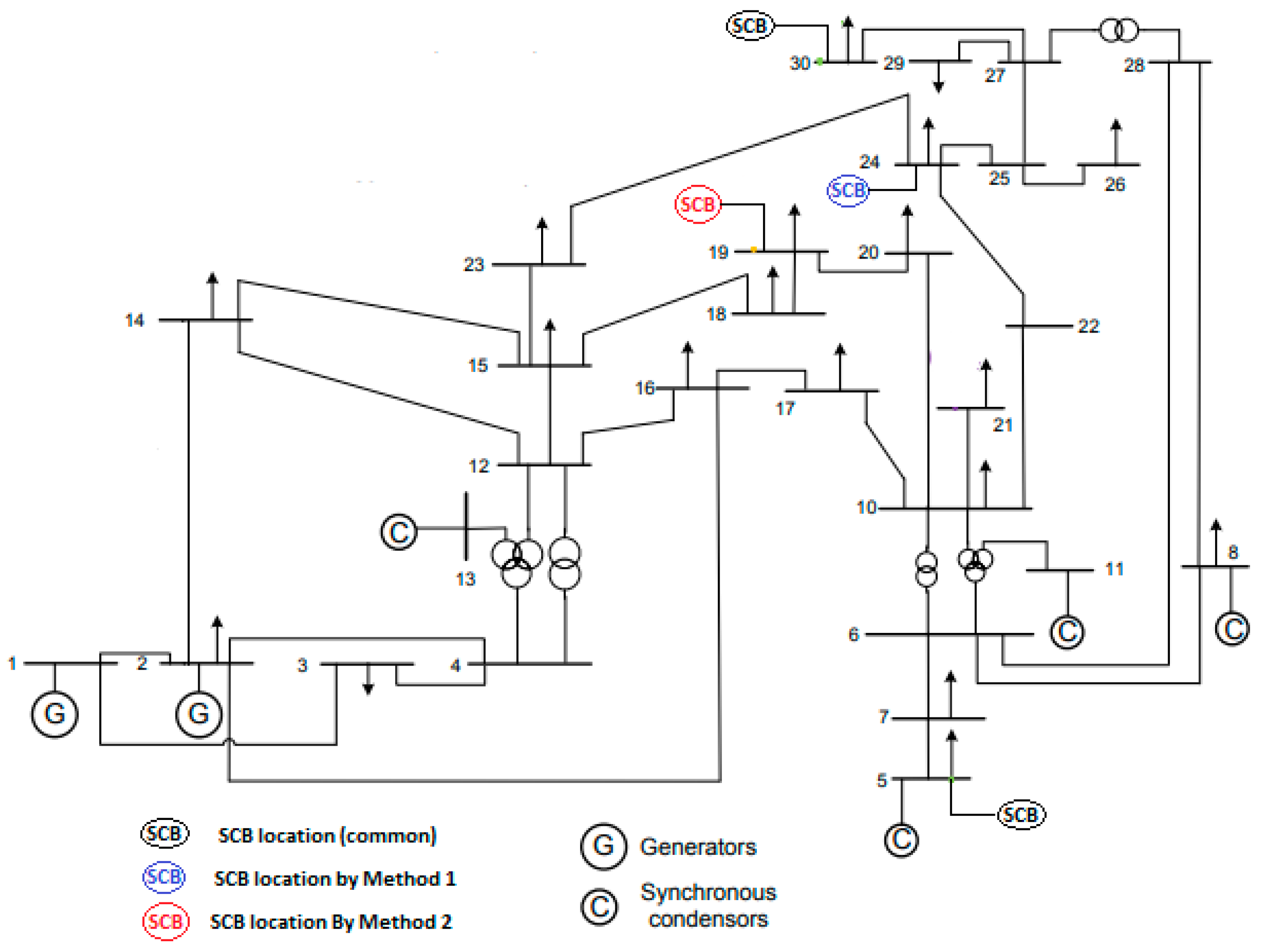
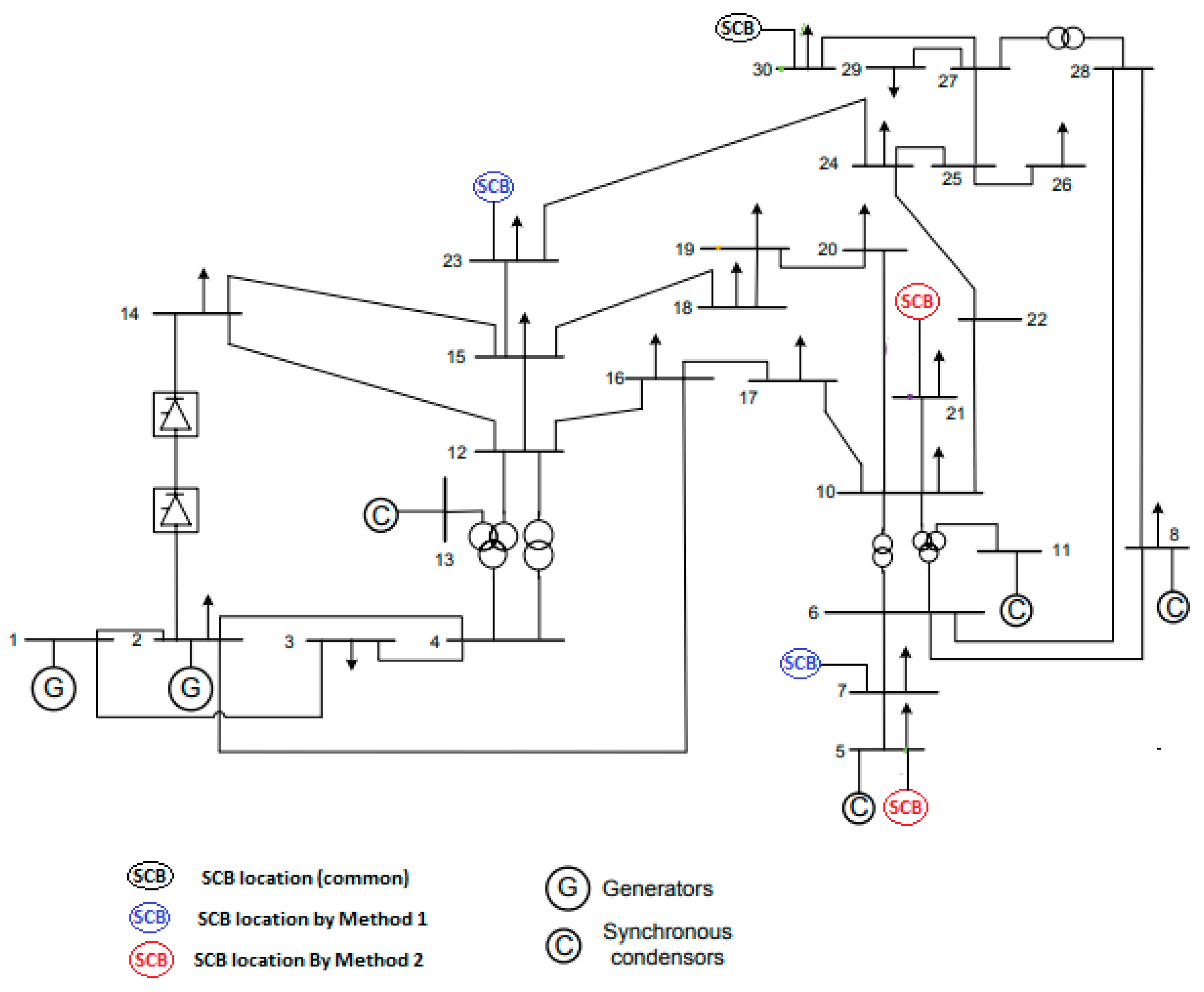
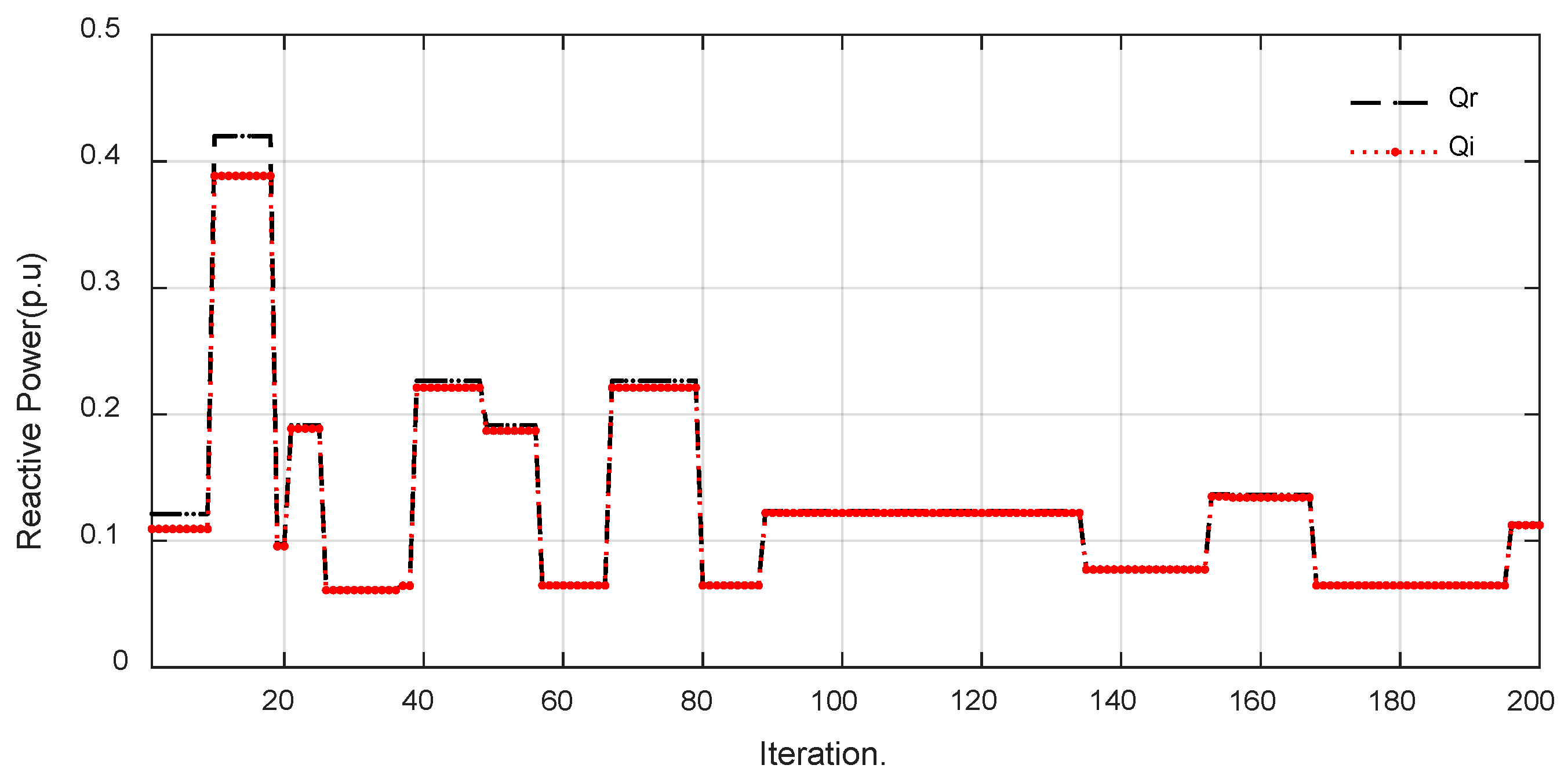
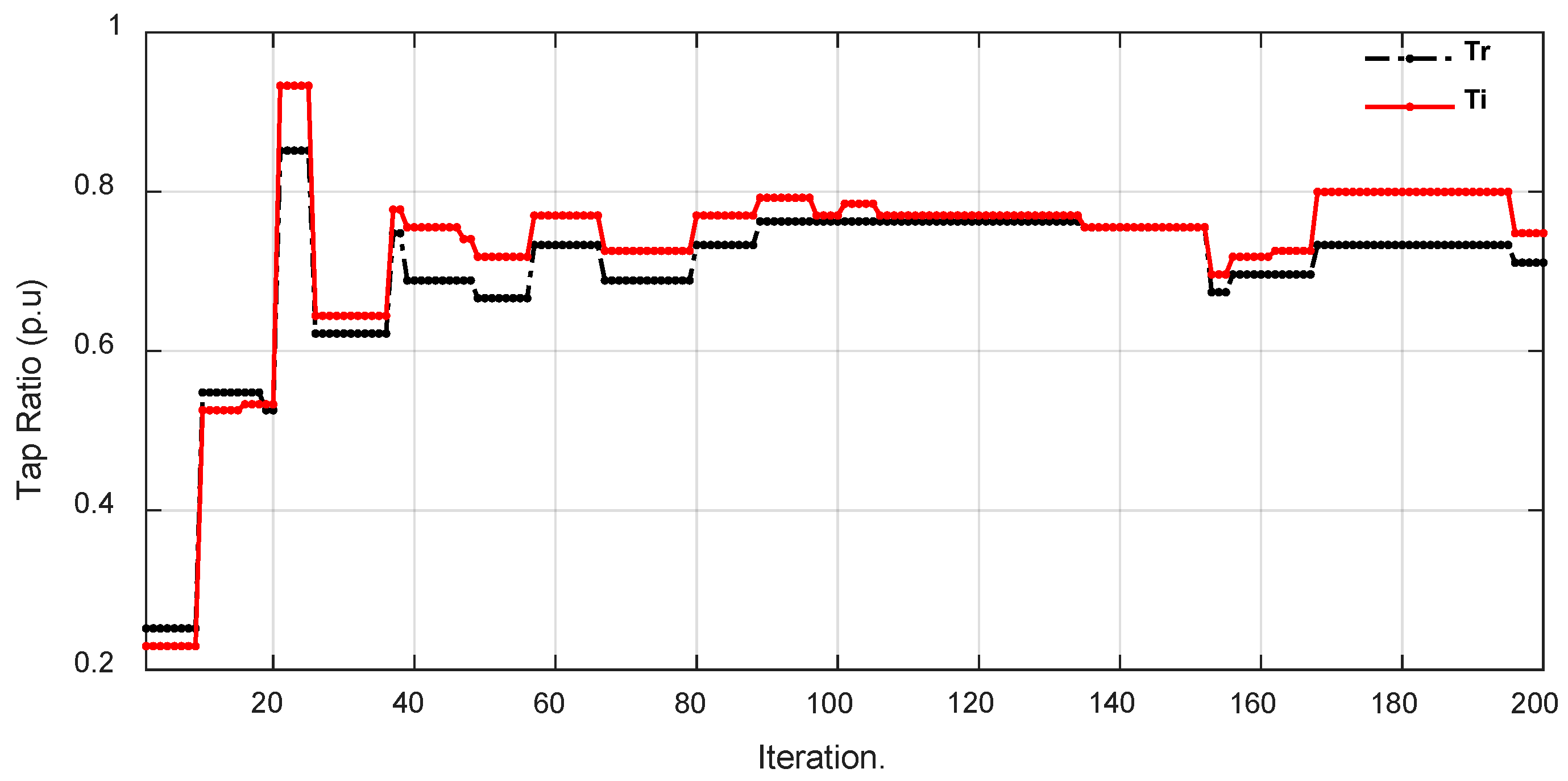
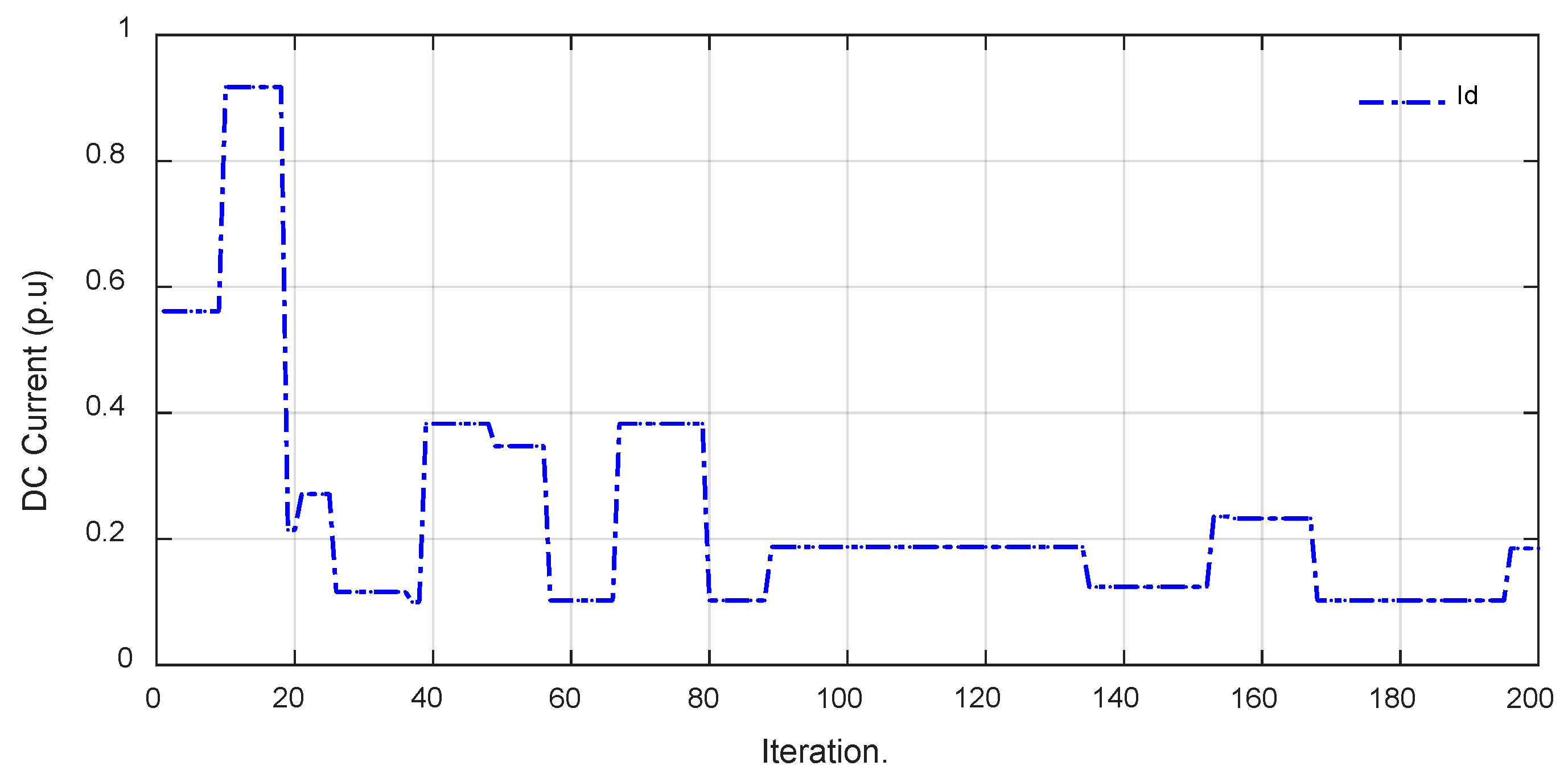
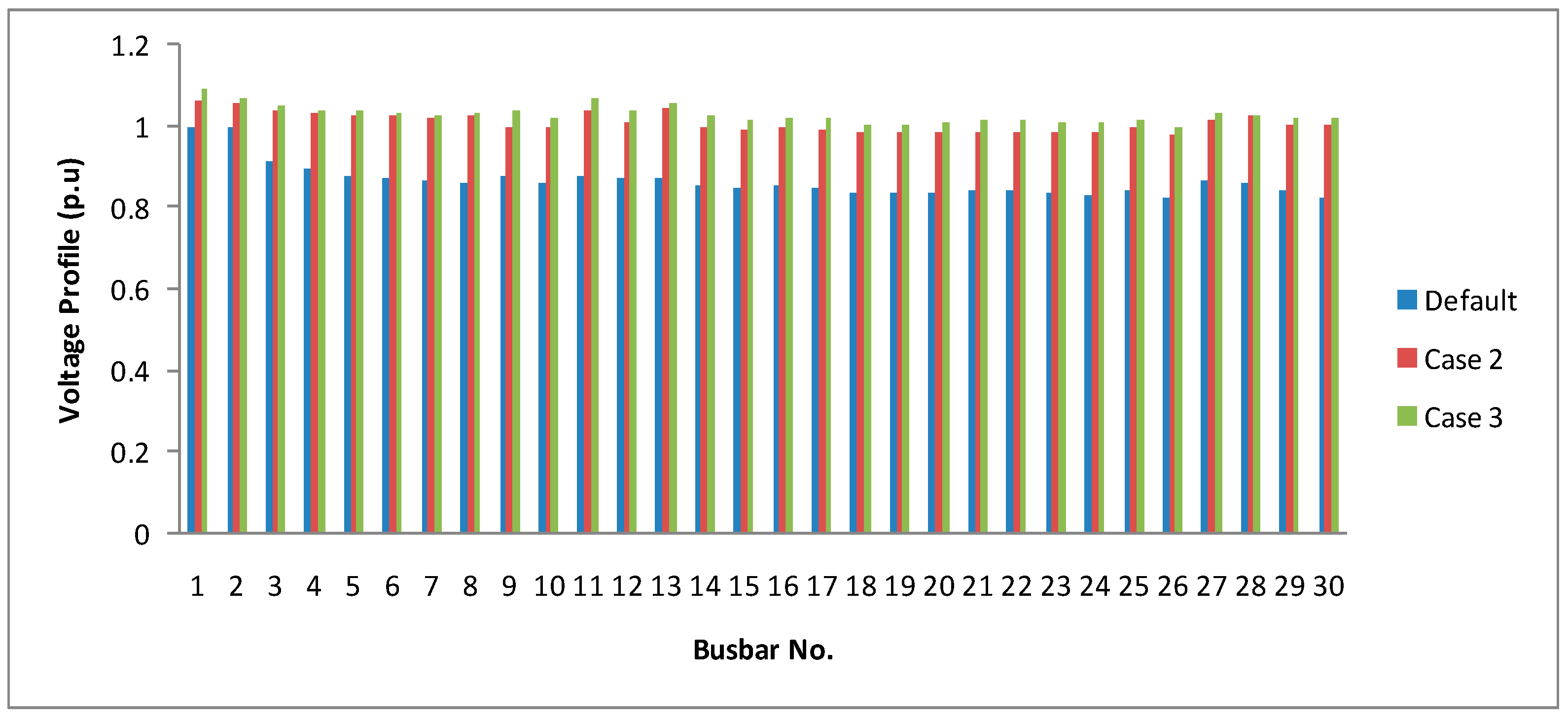
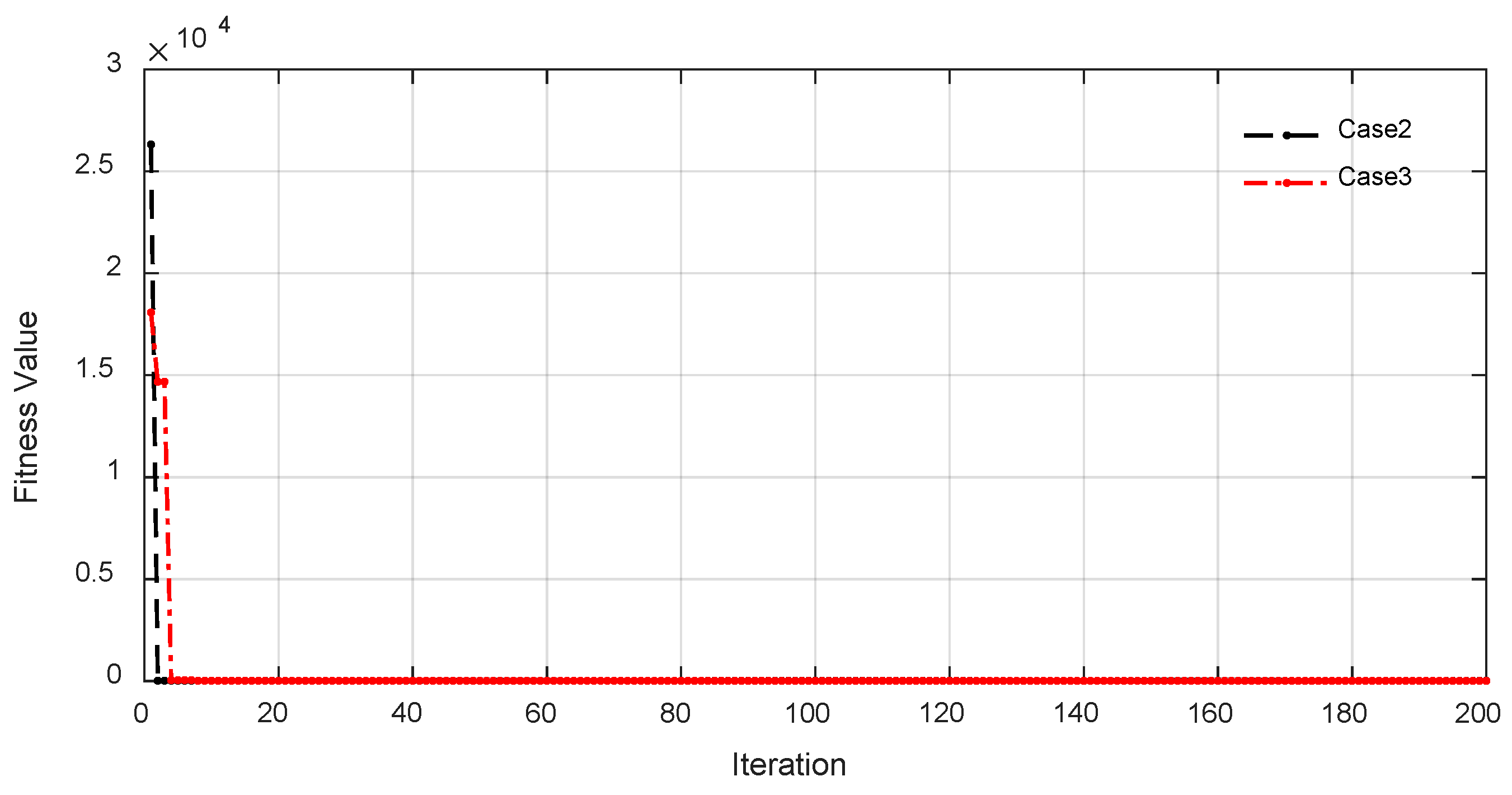
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| N | Total number of buses in the system | Active power given to dc link at kth bus, | |
| Number of generator buses | Reactive power of shunt compensator | ||
| Number of load buses | Reactive power consumed by converter at kth bus, | ||
| Number of transformers | Reactive power of shunt compensator at kth bus, | ||
| Number of shunt compensators | PV active power outputs | ||
| Number of SCB | Location of SCB | ||
| Reference bus active power output | Per unit voltage of ith load bus | ||
| , | The generator’s active and reactive powers when linked to the kth bus | , | DC voltages at rectifier—inverter terminals |
| , | Active and reactive power of ith generator per unit | Per unit voltage of ith generator | |
| , | Active power at rectifier and inverter terminals | , | Rectifier-inverter effective transformer tap ratio |
| , | Converter reactive power absorbed at rectifier and inverter terminals | Effective tap ratio of ith transformer | |
| Power system per unit power loss | , | Excitation angle for rectifier and inverter | |
| , | Active—reactive loads of kth bus | DC current | |
| , | Active-reactive power given to ac line at kth bus | DC link resistance | |
| Reactive power injected by SCB | Location of SCB |
References
- Diahovchenko; Kolcun, M.; Čonka, Z.; Savkiv, V.; Mykhailyshyn, R. Progress and challenges in smart grids: Distributed generation, smart metering, energy storage and smart loads. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 1319–1333. [Google Scholar] [CrossRef]
- Jabir, H.J.; Teh, J.; Isha, D.; Abunima, H. Impacts of demand-side management on electrical power systems: A review. Energies 2018, 11, 1050. [Google Scholar] [CrossRef]
- Al-Ammar, E.A.; Ghazi, G.A.; Ko, W. Impact of ambient temperature on shunt capacitor placement in a distorted radial distribution system. Energies 2018, 11, 1585. [Google Scholar] [CrossRef]
- Luo, S. A review of distributed power systems part I: DC distributed power system. IEEE Aerosp. Electron. Syst. Mag. 2005, 20, 5–16. [Google Scholar] [CrossRef]
- Muthukumar, K.; Jayalalitha, S. Optimal placement and sizing of distributed generators and shunt capacitors for power loss minimization in radial distribution networks using hybrid heuristic search optimization technique. Int. J. Electr. Power Energy Syst. 2016, 78, 299–319. [Google Scholar] [CrossRef]
- Amin, K.; Andishgar, M.H. Simultaneous placement and sizing of DGs and shunt capacitors in distribution systems by using IMDE algorithm. Int. J. Electr. Power Energy Syst. 2016, 82, 599–607. [Google Scholar]
- Zeinalzadeh, A.; Mohammadi, Y.; Moradi, M.H. Optimal multi objective placement and sizing of multiple DGs and shunt capacitor banks simultaneously considering load uncertainty via MOPSO approach. Int. J. Electr. Power Energy Syst. 2015, 67, 336–349. [Google Scholar] [CrossRef]
- Kowsalya, M.I.A.M. Optimal distributed generation and capacitor placement in power distribution networks for power loss minimization. In Proceedings of the 2014 International Conference on Advances in Electrical Engineering (ICAEE), Vellore, India, 9–11 January 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Chandrashekhar, S.R.; Prasad, P.V.N.; Laxmi, A.J. Placement of distributed generator, capacitor and DG and capacitor in distribution system for loss reduction and reliability improvement. Ed. Chief 2013, 101, 198–212. [Google Scholar]
- Aman, M.M.; Jasmon, G.B.; Solangi, K.H.; Bakar, A.H.A.; Mokhlis, H. Optimum simultaneous DG and capacitor placement on the basis of minimization of power losses. Int. J. Comput. Electr. Eng. 2013, 5, 516. [Google Scholar] [CrossRef]
- Gopiya, N.S.; Khatod, D.K.; Sharma, M.P. Optimal allocation of combined DG and capacitor for real power loss minimization in distribution networks. Int. J. Electr. Power Energy Syst. 2013, 53, 967–973. [Google Scholar] [CrossRef]
- Mohssen, S.S.; Haghifam, M.; Salehi, J. Simultaneous placement of distributed generation and capacitors in distribution networks considering voltage stability index. Int. J. Electr. Power Energy Syst. 2013, 46, 366–375. [Google Scholar]
- Esmaeilian, H.R.; Darijany, O.; Mohammadian, M. Optimal placement and sizing of DG units and capacitors simultaneously in radial distribution networks based on the voltage stability security margin. Turk. J. Elec. Eng. Comp. Sci. 2014, 10, 1–14. [Google Scholar]
- Yuancheng, L.; Wang, Y.; Bin, L. A hybrid artificial bee colony assisted differential evolution algorithm for optimal reactive power flow. Int. J. Electr. Power Energy Syst. 2013, 52, 25–33. [Google Scholar]
- Fadel, W.; Kilic, U.; Taskin, S. Placement of Dg, Cb, and Tcsc in radial distribution system for power loss minimization using back-tracking search algorithm. Electr. Eng. 2017, 99, 791–802. [Google Scholar] [CrossRef]
- Mquqwana, M.A.; Krishnamurthy, S. System-Based Testing of Protection for Center-Tapped Shunt Capacitor Banks. Energies 2022, 15, 3791. [Google Scholar] [CrossRef]
- Soma, G.G. Optimal sizing and placement of capacitor banks in distribution networks using a genetic algorithm. Electricity 2021, 2, 187–204. [Google Scholar] [CrossRef]
- Ivanov, O.; Neagu, B.C.; Grigoras, G.; Gavrilas, M. Optimal capacitor bank allocation in electricity distribution networks using metaheuristic algorithms. Energies 2019, 12, 4239. [Google Scholar] [CrossRef]
- Abedin, T.; Lipu, M.S.H.; Hannan, M.A.; Ker, P.J.; Rahman, S.A.; Yaw, C.T.; Tiong, S.K.; Muttaqi, K.M. Dynamic modeling of hvdc for power system stability assessment: A review, issues, and recommendations. Energies 2021, 14, 4829. [Google Scholar] [CrossRef]
- Bakır, H.; Guvenc, U.; Duman, S.; Kahraman, H.T. Optimal power flow for hybrid AC/DC electrical networks configured with VSC-MTDC transmission lines and renewable energy sources. IEEE Syst. J. 2023, 17, 3938–3949. [Google Scholar] [CrossRef]
- Salih, K.; Mohammed, T.; Zozan, S.H.; Firas, S.A. Voltage Profile Enhancing Using HVDC for 132KV Power System: Kurdistan Case Study. J. Eng. 2022, 28, 52–64. [Google Scholar] [CrossRef]
- Kılıç, U.; Ayan, K.; Arifoğlu, U. Optimizing reactive power flow of HVDC systems using genetic algorithm. Int. J. Electr. Power Energy Syst. 2014, 55, 1–12. [Google Scholar] [CrossRef]
- Sayah, S.; Hamouda, A. Optimal power flow solution of integrated AC-DC power system using enhanced differential evolution algorithm. Int. Trans. Electr. Energy Syst. 2019, 29, e2737. [Google Scholar] [CrossRef]
- Samir, S. Modified differential evolution approach for practical optimal reactive power dispatch of hybrid AC–DC power systems. Appl. Soft Comput. 2018, 73, 591–606. [Google Scholar]
- Fazel, M.; Nazri, G.; Saif, M. An improved mixed AC/DC power flow algorithm in hybrid AC/DC grids with MT-HVDC systems. Appl. Sci. 2019, 10, 297. [Google Scholar]
- KILIÇ, U.; Ayan, K. Artificial bee colony algorithm based optimal reactive power flow of two-terminal HVDC systems. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 1075–1090. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Etemadi, A.H.; Dehghanian, P. Adaptive harmonic power flow algorithm for hybrid AC/DC transmission systems. In Proceedings of the 2022 IEEE Industry Applications Society Annual Meeting (IAS), Detroit, MI, USA, 9–14 October 2022. [Google Scholar]
- Mostafa, E. A New Hybrid Method to Assess Available Transfer Capability in AC–DC Networks Using the Wind Power Plant Interconnection. IEEE Syst. J. 2022, 17, 1375–1382. [Google Scholar]
- Khaled, A.; Alrajhi, H.; El-Shatshat, R. Optimal power flow for hybrid AC/MTDC systems. Arab. J. Sci. Eng. 2021, 47, 2977–2986. [Google Scholar]
- Chen, F.; Liu, Z.; Sun, H.; Dong, X. Optimal Power Flow Under Renewable Enery Integrated For AC/DC Grids With VSC-HVDC. In Proceedings of the 2022 IEEE 6th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 4–6 March 2022. [Google Scholar]
- Fadel, W.; Kilic, U.; Ayan, K. Optimal reactive power flow of power systems with two-terminal HVDC and multi distributed generations using backtracking search algorithm. Int. J. Electr. Power Energy Syst. 2021, 127, 106667. [Google Scholar] [CrossRef]
- Babu, B.S. TLBO based Power System Optimization for AC/DC Hybrid Systems. J. Phys. Conf. Ser. IOP Publ. 2021, 1916, 012023. [Google Scholar] [CrossRef]
- Saadeh, O.; Sba, B.A.; Dalala, Z.; Bashaireh, A. Comparative performance analysis of HVDC and HVAC transmission systems in the presence of PV generation: A case study using the IEEE-5-bus network. In Proceedings of the 2023 AEIT HVDC International Conference (AEIT HVDC), Rome, Italy, 25–26 May 2023; pp. 1–5. [Google Scholar]
- Ndlela, N.W.; Davidson, I.E. Network Coordination between High-Voltage DC and High-Voltage AC Transmission Systems Using Flexible AC Transmission System Controllers. Energies 2022, 15, 7402. [Google Scholar] [CrossRef]
- Sarhan, S.; Shaheen, A.M.; El-Sehiemy, R.A.; Gafar, M. Enhanced Teaching Learning-Based Algorithm for Fuel Costs and Losses Minimization in AC-DC Systems. Mathematics 2022, 10, 2337. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw Hill: New York, NY, USA, 1994. [Google Scholar]
- Kılıç, U.; Ayan, K. Optimal power flow solution of two-terminal HVDC systems using genetic algorithm. Electr. Eng. 2014, 96, 65–77. [Google Scholar] [CrossRef]
- Civicioglu, P. Backtracking search optimization algorithm for numerical optimization problems. Appl. Math. Comput. 2013, 219, 8121–8144. [Google Scholar] [CrossRef]
- Chaib, A.E.; Bouchekara, H.R.E.H.; Mehasni, R.; Abido, M.A. Optimal power flow with emission and non-smooth cost functions using backtracking search optimization algorithm. Int. J. Electr. Power Energy Syst. 2016, 81, 64–77. [Google Scholar] [CrossRef]
- Daqaq, F.; Ellaia, R.; Ouassaid, M. Multiobjective backtracking search algorithm for solving optimal power flow. In Proceedings of the 2017 International Conference on Electrical and Information Technologies (ICEIT), Rabat, Morocco, 15–18 November 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Delshad, M.M. Backtracking Search Algorithm For Optimal Power Dispatch in Power System. Ph.D. Thesis, Faculty of Engineering Unıversity of Malaya Kuala Lumpur, Kuala Lumpur, Malaysia, 2016; 187p. [Google Scholar]
- Power Systems Test Case Archive. Available online: http://www.pinarcivicioglu.com/bsa.html (accessed on 3 June 2014).
- Systems Archive. Available online: http://www.ee.washington.edu/research/pstca/ (accessed on 30 December 2023).
| Method | Objective Function | Test System | Year | |
|---|---|---|---|---|
| [20] | Fitness-distance Balance-based Stochastic Fractal Search (SFS), (FDB-SFS) | Power Loss Voltage Deviation, Cost | IEEE 30 bus system | 2023 |
| [21] | ETAP | Voltage Profile | 36 bus (real system) | 2022 |
| [22] | Genetic Algorithm | Power Loss | IEEE 14 and 30-bus system The modified New England 39 | 2014 |
| [23] | Differential evolution algorithm | Cost | IEEE 5, 9, 118-bus The modified New England 39 | 2018 |
| [24] | Differential evolution with neighborhood mutation (DENM) | Power Loss | The modified New England 39, 114 bus (real system) | 2018 |
| [25] | Power Flow (PF) algorithm | Power Loss | IEEE 5 bus and Modified England IEEE 39 bus system | 2019 |
| [26] | Artificia Bee Colony (ABC) | Power Loss Voltage Deviation Cost | IEEE 30 bus system | 2016 |
| [27] | Harmonic Power Flow | Harmonic | IEEE 30 bus system | 2022 |
| [28] | Fast Differential Equation Power Flow (DEPF) | relative speed of computations (RSC) | IEEE 39, 118, 145, 300-bus system, 1153 bus (real system), and 4438 bus(real system) | 2023 |
| [29] | Semidefinite programming (SDP) | Power Loss | Modified CIGRE, IEEE 33 bus system | 2022 |
| [30] | OPF model | Cost | IEEE 39 bus system | 2022 |
| [31] | BSA | Power Loss | IEEE 30 bus system | 2021 |
| [32] | Teaching Learning-based Optimization (TLBO) | Cost | IEEE14, 30 and 57 | 2021 |
| Control Variables | Limit | Method 1 (Case 2) | Method 2 (Case 2) | Default (Case 1) | |
|---|---|---|---|---|---|
| Low | High | ||||
| pg1 | 0 | 3.602 | 1.22745 | 1.27188 | 2.57549 |
| pg2 | 0 | 1.4 | 1.40000 | 1.36250 | 0.51450 |
| qg1 | −1 | 1 | −0.11026 | 0.03135 | −0.18687 |
| qg2 | −0.4 | 0.5 | 0.27830 | 0.08594 | 2.17192 |
| qc5 | −0.4 | 0.4 | 0.400000 | 0.366644 | -- |
| qc8 | −0.1 | 0.4 | 0.400000 | 0.400000 | -- |
| qc11 | −0.06 | 0.24 | 0.240000 | 0.194316 | -- |
| qc13 | −0.06 | 0.24 | 0.090000 | 0.240000 | -- |
| v1 | 1 | 1.15 | 1.078 | 1.071 | 1.000 |
| v2 | 1 | 1.15 | 1.073 | 1.058 | 1.000 |
| v5 | 1 | 1.15 | 1.046 | 1.029 | 0.875 |
| v8 | 1 | 1.15 | 1.038 | 1.027 | 0.857 |
| v11 | 1 | 1.15 | 1.089 | 1.078 | 0.877 |
| v13 | 1 | 1.15 | 1.022 | 1.054 | 0.872 |
| t(6–9) | 0.9 | 1.1 | 0.9896 | 0.9878 | 0.9500 |
| t(6–10) | 0.9 | 1.1 | 0.9716 | 0.9315 | 0.9500 |
| t(4–12) | 0.9 | 1.1 | 1.0180 | 1.0236 | 0.9500 |
| t(28–27) | 0.9 | 1.1 | 0.9753 | 0.9864 | 0.9500 |
| CB1(MVAR) | 0 | 10 | 10.0(5) | 9.5(5) | -- |
| CB2(MVAR) | 0 | 10 | 10.0(24) | 10.0(30) | -- |
| CB3(MVAR) | 0 | 10 | 10.0(30) | 10.0(19) | -- |
| Power loss(p.u) | 9.3450 | 9.5373 | 25.599 | ||
| Control Variables | Limit | Method 1 | Method 2 | |
|---|---|---|---|---|
| Low | High | |||
| pg1 | 0 | 3.602 | 1.23817 | 1.29303 |
| pg2 | 0 | 1.4 | 1.40000 | 1.37267 |
| qg1 | −1 | 1 | −0.02148 | 0.09383 |
| qg2 | −0.4 | 0.5 | 0.25030 | 0.33611 |
| qc5 | −0.4 | 0.4 | 0.40 | 0.39 |
| qc8 | −0.1 | 0.4 | 0.40 | 0.40 |
| qc11 | −0.06 | 0.24 | 0.24 | 0.13 |
| qc13 | −0.06 | 0.24 | 0.23 | 0.24 |
| v1 | 1 | 1.15 | 1.066 | 1.079 |
| v2 | 1 | 1.15 | 1.055 | 1.064 |
| v5 | 1 | 1.15 | 1.028 | 1.036 |
| v8 | 1 | 1.15 | 1.027 | 1.030 |
| v11 | 1 | 1.15 | 1.083 | 1.070 |
| v13 | 1 | 1.15 | 1.036 | 1.081 |
| t(6–9) | 0.9 | 1.1 | 0.97 | 0.99 |
| t(6–10) | 0.9 | 1.1 | 1.00 | 0.90 |
| t(4–12) | 0.9 | 1.1 | 1.02 | 0.96 |
| t(28–27) | 0.9 | 1.1 | 1.01 | 0.98 |
| CB1(MVAR) | 0 | 10 | 10.0 (7) | 8.75(5) |
| CB2(MVAR) | 0 | 10 | 10.0 (23) | 8.50(30) |
| CB3(MVAR) | 0 | 10 | 9.0(30) | 9.50(21) |
| Ploss(p.u) | 9.1607 | 9.272 | ||
| Control Variables | pdr | pdi | qdr | qdi | tr | ti | alfa(o) | theta | vdr | vdi | id |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Minimum limit | 0.1 | 0.1 | 0.05 | 0.05 | 0.9 | 0.9 | 9.74 | 8.59 | 1 | 1 | 0.1 |
| Maximum limit | 1.5 | 1.5 | 0.75 | 0.75 | 1.1 | 1.1 | 26 | 30 | 1.5 | 1.5 | 1 |
| Method 1 | 0.2271 | 0.2246 | 0.1136 | 0.1123 | 0.96 | 1.01 | 25.6539 | 26.1374 | 1.2278 | 1.2139 | 0.1850 |
| Method 2 | 0.3400 | 0.3336 | 0.1700 | 0.1668 | 0.90 | 0.90 | 25.8333 | 25.2593 | 1.1564 | 1.1343 | 0.2941 |
| Line | Case1 | Case2 | Case3 |
|---|---|---|---|
| 1–2 | 6.1530 | 0.6980 | 0.8340 |
| 1–3 | 3.7630 | 1.3470 | 1.1520 |
| 2–4 | 2.4390 | 1.0670 | 0.7420 |
| 2–5 | 4.5240 | 2.4080 | 2.4550 |
| 2–6 | 4.0250 | 1.7700 | 1.3600 |
| 3–4 | 1.0440 | 0.3610 | 0.3070 |
| 4–6 | 0.8780 | 0.3550 | 0.3650 |
| 4–12 | 0 | 0 | 0 |
| 5–7 | 0.2240 | 0.1460 | 0.2850 |
| 6–7 | 0.4920 | 0.2820 | 0.2990 |
| 6–8 | 0.2540 | 0.0990 | 0.1000 |
| 6–9 | 0 | 0 | 0 |
| 6–10 | 0 | 0 | 0 |
| 2–28 | 0.1200 | 0.0270 | 0.0220 |
| 8–28 | 0.0040 | 0.0070 | 0.0060 |
| 9–11 | 0 | 0 | 0 |
| 9–10 | 0 | 0 | 0 |
| 10–20 | 0.1280 | 0.1190 | 0.0710 |
| 10–17 | 0.0230 | 0.0390 | 0.0220 |
| 10–21 | 0.1610 | 0.0840 | 0.1070 |
| 10–22 | 0.0750 | 0.0360 | 0.0490 |
| 12–13 | 0 | 0 | 0 |
| 12–14 | 0.1070 | 0.0540 | 0.1220 |
| 12–15 | 0.3030 | 0.1150 | 0.1040 |
| 12–16 | 0.0710 | 0.0210 | 0.0800 |
| 14–15 | 0.0080 | 0 | 0.2660 |
| 15–18 | 0.0540 | 0.0270 | 0.0930 |
| 15–23 | 0.0390 | 0.0020 | 0.0020 |
| 16–17 | 0.0090 | 0.0030 | 0.0180 |
| 18–19 | 0.0060 | 0.0030 | 0.0260 |
| 19–20 | 0.0270 | 0.0280 | 0.0160 |
| 20–22 | 0.0010 | 0.0050 | 0.0030 |
| 22–24 | 0.0550 | 0.0340 | 0.0620 |
| 23–24 | 0.0060 | 0.0170 | 0.0660 |
| 24–25 | 0.0350 | 0.0400 | 0.0060 |
| 25–26 | 0.0660 | 0.0450 | 0.0480 |
| 25–27 | 0.0960 | 0.0840 | 0.0380 |
| 27–28 | 0 | 0 | 0 |
| 27–29 | 0.1240 | 0.0120 | 0.0180 |
| 27–30 | 0.2340 | 0.0090 | 0.0150 |
| 29–30 | 0.0480 | 0.0010 | 0.0010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arab, M.; Fadel, W. Optimal Reactive Power Flow of AC-DC Power System with Shunt Capacitors Using Backtracking Search Algorithm. Energies 2024, 17, 749. https://doi.org/10.3390/en17030749
Arab M, Fadel W. Optimal Reactive Power Flow of AC-DC Power System with Shunt Capacitors Using Backtracking Search Algorithm. Energies. 2024; 17(3):749. https://doi.org/10.3390/en17030749
Chicago/Turabian StyleArab, Meraa, and Waleed Fadel. 2024. "Optimal Reactive Power Flow of AC-DC Power System with Shunt Capacitors Using Backtracking Search Algorithm" Energies 17, no. 3: 749. https://doi.org/10.3390/en17030749
APA StyleArab, M., & Fadel, W. (2024). Optimal Reactive Power Flow of AC-DC Power System with Shunt Capacitors Using Backtracking Search Algorithm. Energies, 17(3), 749. https://doi.org/10.3390/en17030749






