Locational Role Analysis of Energy Storage Systems Based on Optimal Capacity Needs and Operations under High Penetration of Renewable Energy
Abstract
1. Introduction
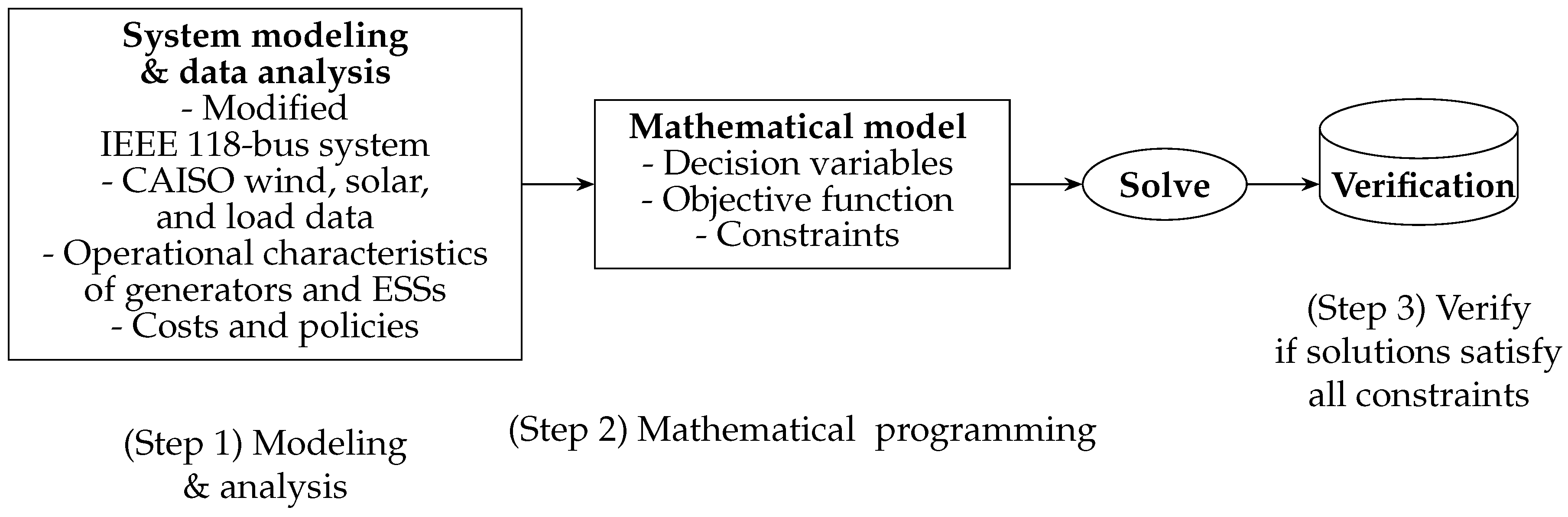
2. Simulation Model
3. Case Study
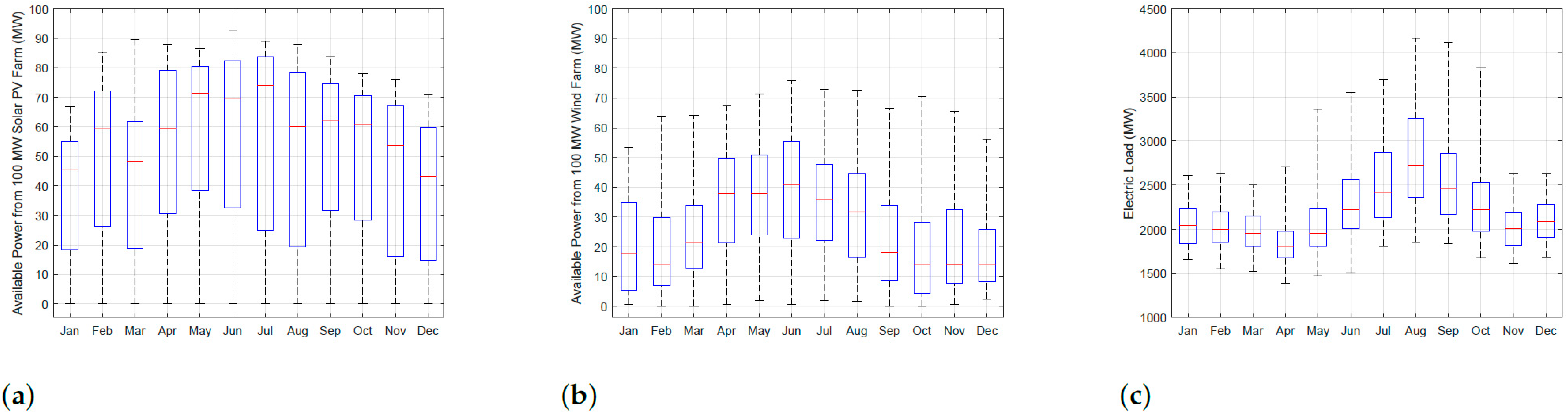
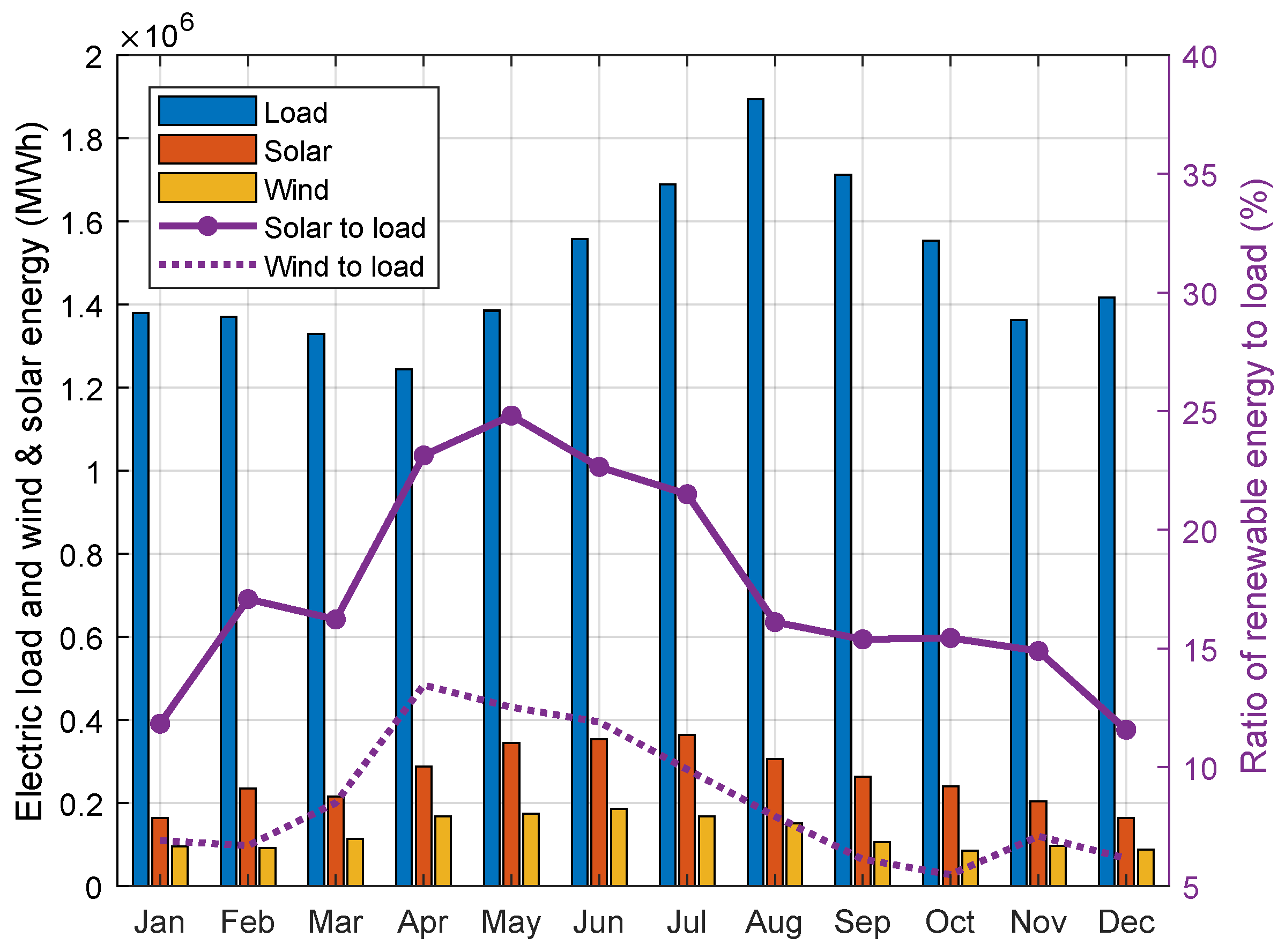
3.1. Available Renewable Power and Electric Load
3.2. Test System and Simulation Conditions
4. Simulation Results
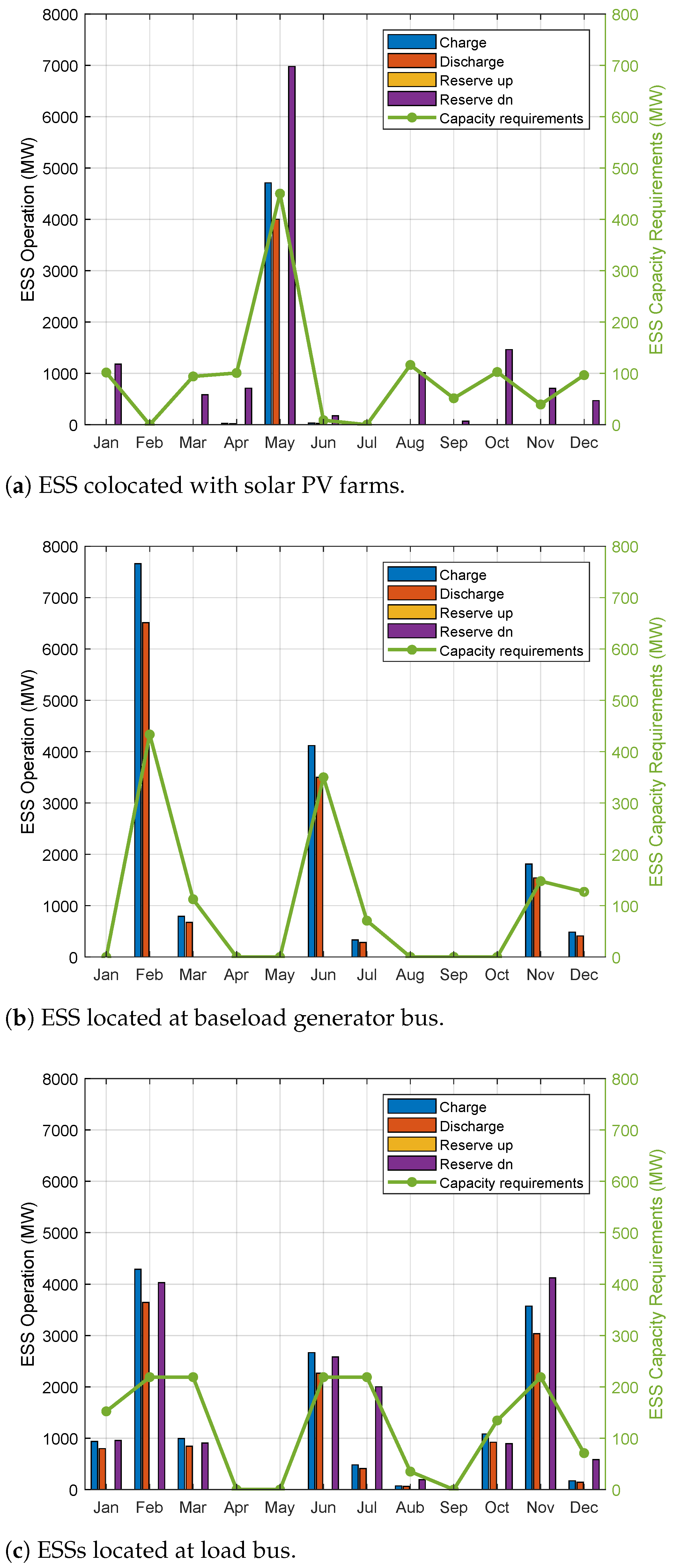
4.1. Optimal ESS Capacity Needs and Operations
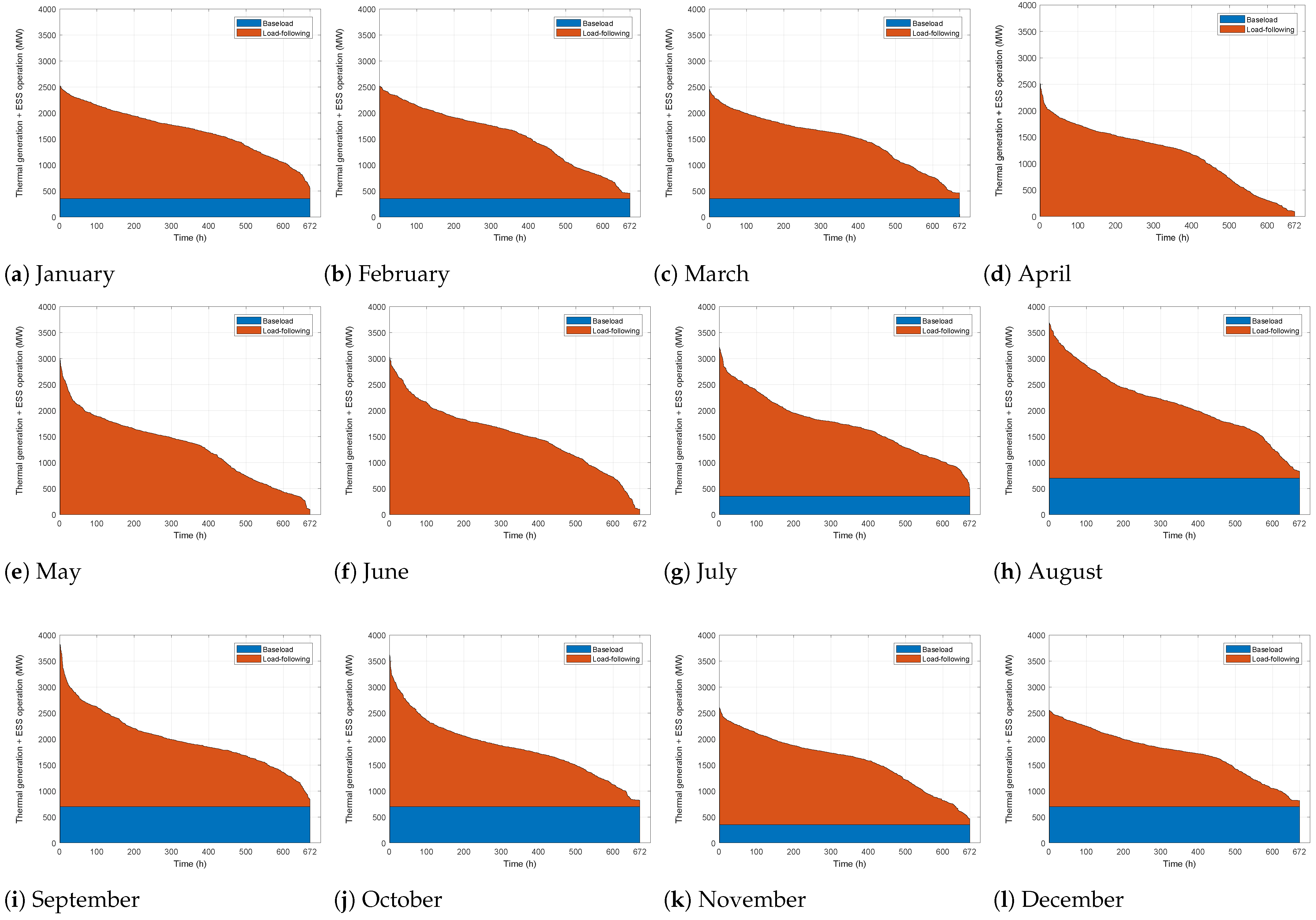
4.2. Impact of ESS Operations on Flexible Generation Capacity
4.3. Renewable Energy Generation and Curtailment
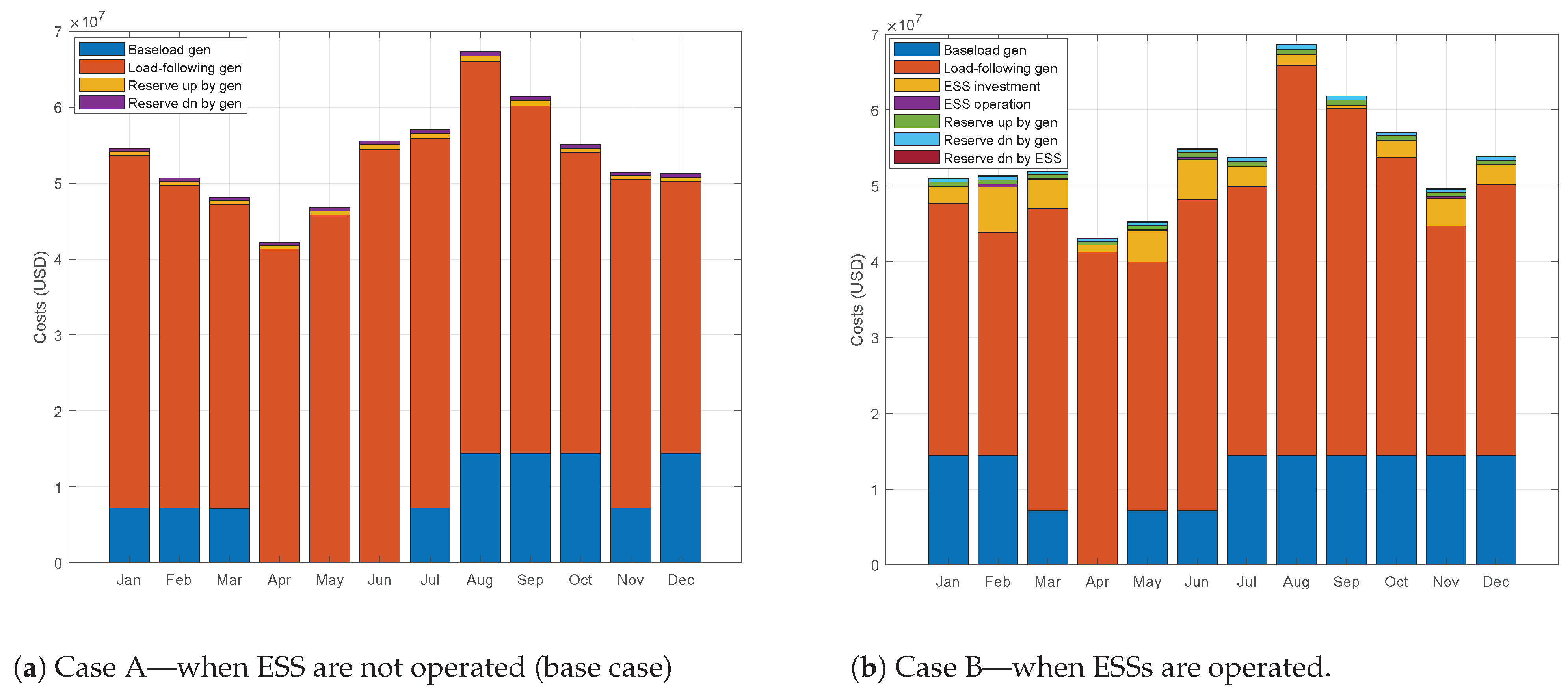
4.4. Cost Analysis
4.5. Analysis of the Roles in a Grid System
5. Conclusions and Discussion
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Sets/Indices | |
| Time intervals, | |
| All generators | |
| , | Conventional and baseload generators |
| Renewable energy generators | |
| , | Wind generators and solar PV systems |
| Energy storage systems (ESSs) | |
| ESSs on baseload generation side, | |
| ESSs on load side, | |
| Electric buses | |
| Electric load | |
| Transmission lines | |
| Data/Parameters | |
| ESS investment cost ($/MWh) | |
| Reserve costs for thermal generators (USD/MW) | |
| Reserve costs for ESSs (USD/MW) | |
| Generation cost (USD/MWh) | |
| Penalty cost for unserved demand (USD/MWh) | |
| ESS charging and discharging cost (USD/MWh) | |
| Penalty cost for excess of carbon emissions (USD/metric ton) | |
| Penalty cost for shortage of RPS requirement (USD/MWh) | |
| RPS requirements rate to the demand | |
| h | Operating hour for time interval (h) |
| Duration of ESS (h) | |
| , | Conventional generator-node, renewable farm-node incidence matrix |
| Transmission line-node incidence matrix | |
| Demand-node incidence matrix | |
| , , | Storage-baseload generator, storage-wind farm, and storage-solar PVs incidence matrices |
| , | Storage at load-node, storage at generator bus-node incidence matrices |
| Load distribution factor for demand, d | |
| Solar power distribution factor for solar PV farm, w | |
| Wind power distribution factor for wind farm, w | |
| Upward and down reserve requirements at time t (MW) | |
| Ramp up and down rates for generator c (MW/h) | |
| , | Maximum generation and minimum generation level for c and b (MW) |
| , | Available solar and wind power at time t (MW) |
| Maximum capacity of ESS, e (MW) | |
| emissions rate for generator c (metric ton/MWh) | |
| Maximum power flow on line l (MW) | |
| Reactance of line l (p.u.) | |
| CO2 emission cap (metric ton) | |
| Stored energy in ESS, e, at time (MWh) | |
| Round-trip efficiency of ESS | |
| Binary decision variables | |
| Unit commitment for baseload generators | |
| Continuous decision variables | |
| Capacity needs of ESS, e (MW) | |
| , , | Power generation from g, c, and r at time t (MW) |
| , , | Renewable power injection from r, s, and w at time t (MW) |
| , | Upward and downward reserves of generator c at time t (MW) |
| , | Upward and downward reserves of ESS, e, at time t (MW) |
| Stored energy in ESS, e [MWh] | |
| Charging and discharging power of ESS, e, at time t (MW) | |
| Power flow on transmission line l (MW) | |
| Bus voltage angle at bus i (radian) | |
| Unserved electricity demand (MW) | |
| Excess of CO2 emissions (metric ton) | |
| Shortage of renewable generation (MWh) | |
Appendix A
| Month | Without ESS Operation (Thousand USD) | With ESS Operation (Thousand USD) | Cost Change (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Baseload Gen | Load- Following Gen | Res. Up by Gen | Res. dn by Gen | Baseload Gen | Load- Following Gen | ESS Invest | ESS Oper. | Res. Up by Gen | Res. dn by Gen | Res. dn by ESSs | ||
| Jan | 7195 | 46,407 | 533 | 438 | 14,390 | 33,261 | 2314 | 35 | 521 | 429 | 43 | −6.56 |
| Feb | 7195 | 42,515 | 523 | 436 | 14,390 | 29,498 | 5944 | 442 | 513 | 396 | 175 | 1.36 |
| Mar | 7184 | 40,003 | 507 | 423 | 7184 | 39,835 | 3877 | 66 | 507 | 415 | 34 | 7.90 |
| Apr | 0 | 41,311 | 473 | 395 | 0 | 41,276 | 918 | 1 | 473 | 392 | 14 | 2.12 |
| May | 0 | 45,775 | 535 | 440 | 7195 | 32,786 | 4102 | 174 | 521 | 408 | 140 | −3.05 |
| Jun | 0 | 54,436 | 619 | 495 | 7195 | 41,027 | 5264 | 252 | 598 | 475 | 85 | −1.18 |
| Jul | 7195 | 48,682 | 663 | 537 | 14,390 | 35,536 | 2640 | 30 | 643 | 526 | 49 | −5.72 |
| Aug | 14,390 | 51,573 | 758 | 602 | 14,390 | 51,512 | 1380 | 3 | 757 | 597 | 24 | 1.99 |
| Sep | 14,390 | 45,786 | 672 | 544 | 14,390 | 45,783 | 469 | 0 | 672 | 544 | 1 | 0.76 |
| Oct | 14,390 | 39,575 | 600 | 494 | 14,390 | 39,406 | 2161 | 40 | 600 | 483 | 47 | 3.76 |
| Nov | 7205 | 43,275 | 522 | 433 | 14,411 | 30,271 | 3700 | 199 | 511 | 403 | 133 | −3.51 |
| Dec | 14,390 | 35,861 | 539 | 451 | 14,390 | 35,747 | 2684 | 24 | 539 | 442 | 35 | 5.11 |
| Total | 93,532 | 535,200 | 6944 | 5688 | 136,711 | 455,936 | 35,453 | 1267 | 6854 | 5510 | 780 | 0.18 |
References
- Sandia National Laboratories. Energy Storage for the Electricity Grid: Benefits and Market Potential Assessment Guide; Sandia National Laboratories: Albuquerque, NM, USA; Livermore, CA, USA, 2010. [CrossRef]
- Evans, A.; Strezov, V.; Evans, T.J. Assessment of utility energy storage options for increased renewable energy penetration. Renew. Sustain. Energy Rev. 2012, 16, 4141–4147. [Google Scholar] [CrossRef]
- Zayed, M.E.; Kabeel, A.; Shboul, B.; Ashraf, W.M.; Ghazy, M.; Irshad, K.; Rehman, S.; Zayed, A.A. Performance augmentation and machine learning-based modeling of wavy corrugated solar air collector embedded with thermal energy storage: Support vector machine combined with Monte Carlo simulation. J. Energy Storage 2023, 74, 109533. [Google Scholar] [CrossRef]
- Yao, L.; Yang, B.; Cui, H.; Zhuang, J.; Ye, J.; Xue, J. Challenges and progresses of energy storage technology and its application in power systems. J. Mod. Power Syst. Clean Energy 2016, 4, 519–528. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energ. 2015, 137, 511–536. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory. The Role of Energy Storage with Renewable Electricity Generation. Available online: https://www.nrel.gov/docs/fy10osti/47187.pdf (accessed on 12 January 2024).
- Roberts, B.P.; Sandberg, C. The Role of Energy Storage in Development of Smart Grids. Proc. IEEE 2011, 99, 1139–1144. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory. The Value of Energy Storage for Grid Applications. Available online: https://www.nrel.gov/docs/fy13osti/58465.pdf (accessed on 12 January 2024).
- Oudalov, A.; Chartouni, D.; Ohler, C.; Linhofer, G. Value Analysis of Battery Energy Storage Applications in Power Systems. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006. [Google Scholar] [CrossRef]
- Bitaraf, H.; Rahman, S. Reducing Curtailed Wind Energy Through Energy Storage and Demand Response. IEEE Trans. Sustain. Energy 2018, 9, 228–236. [Google Scholar] [CrossRef]
- Cleary, B.; Duffy, A.; O’Connor, A.; Conlon, M.; Fthenakis, V. Assessing the Economic Benefits of Compressed Air Energy Storage for Mitigating Wind Curtailment. IEEE Trans. Sustain. Energy 2015, 6, 1021–1028. [Google Scholar] [CrossRef]
- Jafari, M.; Botterud, A.; Sakti, A. Decarbonizing power systems: A critical review of the role of energy storage. Renew. Sust. Energ. Rev. 2022, 158, 112077. [Google Scholar] [CrossRef]
- Levin, T.; Bistline, J.; Sioshansi, R.; Cole, W.J.; Kwon, J.; Burger, S.P.; Crabtree, G.W.; Jenkins, J.D.; O’Neil, R.; Korpøas, M.; et al. Energy storage solutions to decarbonize electricity through enhanced capacity expansion modelling. Nat. Energy 2023, 8, 1199–1208. [Google Scholar] [CrossRef]
- Xu, B.; Wang, Y.; Dvorkin, Y.; Fernández-Blanco, R.; Silva-Monroy, C.A.; Watson, J.P.; Kirschen, D.S. Scalable Planning for Energy Storage in Energy and Reserve Markets. IEEE Trans. Power Syst. 2017, 32, 4515–4527. [Google Scholar] [CrossRef]
- Tang, Z.; Liu, Y.; Wu, L.; Liu, J.; Gao, H. Reserve Model of Energy Storage in Day-Ahead Joint Energy and Reserve Markets: A Stochastic UC Solution. IEEE Trans. on Smart Grid 2021, 12, 372–382. [Google Scholar] [CrossRef]
- Byrne, R.H.; Silva-Monroy, C.A. Potential revenue from electrical energy storage in the Electricity Reliability Council of Texas (ERCOT). In Proceedings of the 2014 IEEE PES General Meeting, National Harbor, MD, USA, 27–31 July 2014. [Google Scholar] [CrossRef]
- Denholm, P.; Hand, M. Grid flexibility and storage required to achieve very high penetration of variable renewable electricity. Energy Policy 2011, 39, 1817–1830. [Google Scholar] [CrossRef]
- Nikoobakht, A.; Aghaei, J.; Shafie-Khah, M.; Cataláo, J.P.S. Assessing Increased Flexibility of Energy Storage and Demand Response to Accommodate a High Penetration of Renewable Energy Sources. IEEE Trans. Sustain. Energy 2019, 10, 659–669. [Google Scholar] [CrossRef]
- Troy, N.; Denny, E.; O’Malley, M. Base-Load Cycling on a System With Significant Wind Penetration. IEEE Trans. Power Syst. 2010, 25, 1088–1097. [Google Scholar] [CrossRef]
- Bertsimas, D.; Tsitsiklis, J.N. Introduction to Linear Optimization; Athena Scientific: Belmont, MA, USA, 1997. [Google Scholar]
- Wolsey, L. Integer Programming; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1998. [Google Scholar]
- California Independent System Operator. Available online: www.caiso.com (accessed on 12 January 2024).
- IEEE 118-Bus. Available online: http://motor.ece.iit.edu/data/JEAS_IEEE118.doc (accessed on 12 January 2024).
- Illinois Center for a Smarter Electric Grid (ICSEG). IEEE 118-Bus System. Available online: https://icseg.iti.illinois.edu/ieee-118-bus-system/ (accessed on 12 January 2024).
- National Renewable Energy Laboratory. Cost Projections for Utility-Scale Battery Storage: 2021 Update. Available online: https://www.nrel.gov/docs/fy21osti/79236.pdf (accessed on 12 January 2024).
- GAMS Documentation 33. Available online: https://www.gams.com/latest/docs/S_CPLEX.html (accessed on 12 January 2024).


| Gen. Type | Number of Units | Capacity (MW) | Share (%) |
|---|---|---|---|
| Coal | 2 | 650 | 8.99 |
| Natural gas | 31 | 3730 | 51.59 |
| Nuclear | 2 | 700 | 9.68 |
| Wind | 4 | 700 | 9.68 |
| Solar | 10 | 1450 | 20.06 |
| Total | 49 | 7230 | 100 |
| ESS Types | Number of Units | Capacity (MW) |
|---|---|---|
| ESS colocated with wind | 4 | 700 |
| ESS colocated with solar | 10 | 1450 |
| ESS at baseload gen bus | 4 | 1350 |
| ESS at load bus | 3 | 219 |
| Total | 21 | 3719 |
| Month | Consumed Energy (GWh) | Solar Energy (GWh) | Wind Energy (GWh) | Solar Curtail without ESSs (GWh) | Wind Curtail without ESSs (GWh) | Penetration Level with ESSs (%) | Penetration Level without ESSs (%) |
|---|---|---|---|---|---|---|---|
| Jan | 1379.35 | 163.21 | 95.32 | 0.00 | 0 | 18.74 | 18.74 |
| Feb | 1369.56 | 233.98 | 91.71 | 3.05 | 0 | 23.78 | 23.56 |
| Mar | 1329.03 | 215.67 | 112.94 | 3.47 | 0 | 24.73 | 24.46 |
| Apr | 1243.75 | 287.72 | 167.39 | 0.74 | 0 | 36.59 | 36.53 |
| May | 1384.85 | 343.66 | 173.44 | 0.55 | 0 | 37.34 | 37.30 |
| Jun | 1556.54 | 352.55 | 185.31 | 0.91 | 0 | 34.55 | 34.50 |
| Jul | 1689.21 | 363.23 | 167.33 | 0.00 | 0 | 31.41 | 31.41 |
| Aug | 1893.87 | 305.17 | 150.34 | 1.28 | 0 | 24.05 | 23.98 |
| Sep | 1711.49 | 263.35 | 104.82 | 0.07 | 0 | 21.51 | 21.51 |
| Oct | 1553.79 | 239.95 | 85.05 | 3.44 | 0 | 20.92 | 20.70 |
| Nov | 1362.11 | 202.90 | 96.62 | 0.41 | 0 | 21.99 | 21.96 |
| Dec | 1416.00 | 163.94 | 87.20 | 2.39 | 0 | 17.74 | 17.57 |
| Total | 17,889.55 | 3135.31 | 1517.47 | 16.30 | 0 | 26.01 | 25.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, H. Locational Role Analysis of Energy Storage Systems Based on Optimal Capacity Needs and Operations under High Penetration of Renewable Energy. Energies 2024, 17, 743. https://doi.org/10.3390/en17030743
Park H. Locational Role Analysis of Energy Storage Systems Based on Optimal Capacity Needs and Operations under High Penetration of Renewable Energy. Energies. 2024; 17(3):743. https://doi.org/10.3390/en17030743
Chicago/Turabian StylePark, Heejung. 2024. "Locational Role Analysis of Energy Storage Systems Based on Optimal Capacity Needs and Operations under High Penetration of Renewable Energy" Energies 17, no. 3: 743. https://doi.org/10.3390/en17030743
APA StylePark, H. (2024). Locational Role Analysis of Energy Storage Systems Based on Optimal Capacity Needs and Operations under High Penetration of Renewable Energy. Energies, 17(3), 743. https://doi.org/10.3390/en17030743





