A Fault Location Algorithm for Multi-Section Combined Transmission Lines Considering Unsynchronized Sampling
Abstract
1. Introduction
1.1. Literature Review
1.2. Our Motivation and Contributions
- Fault locations on combined transmission lines can be accurately estimated even when the fault record sampling data are not synchronized,
- The performance of the proposed algorithm remains accurate under various types of faults, fault resistances, fault inception angles, and sources of impedance variation,
- Faults are accurately located even if they lie very close to interconnection points,
- The proposed algorithm can be modified to accommodate different numbers of sections according to real-world applications.
2. The Fault Location Algorithm
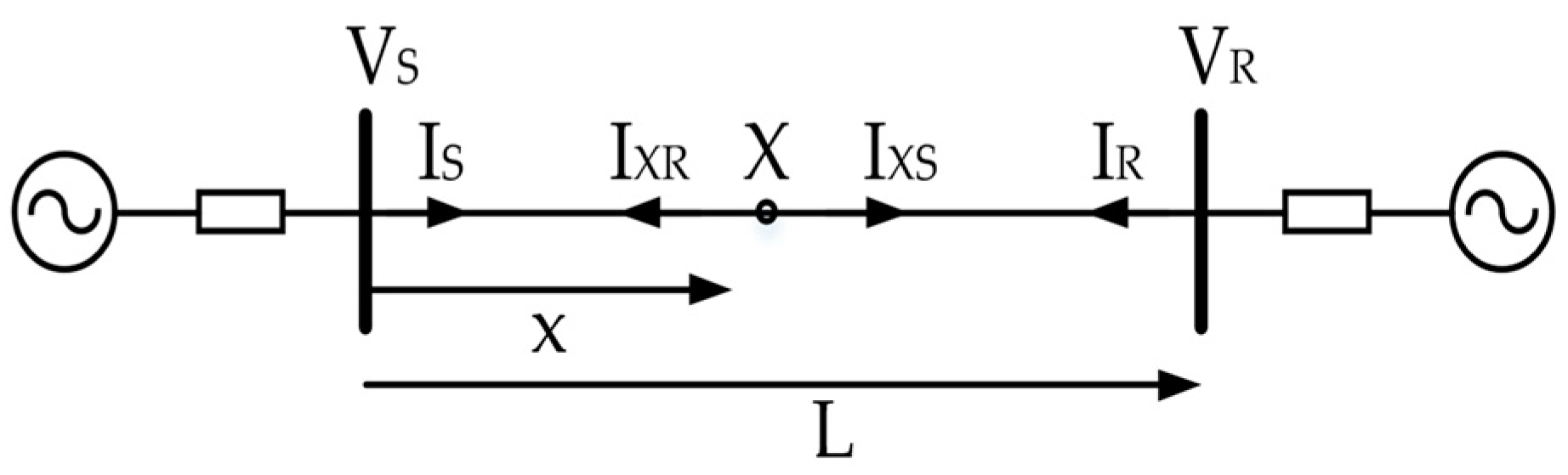
2.1. Voltages and Currents along the Homogenous Transmission Line
2.2. Voltages and Currents along the Three-Section Combined Transmission Line
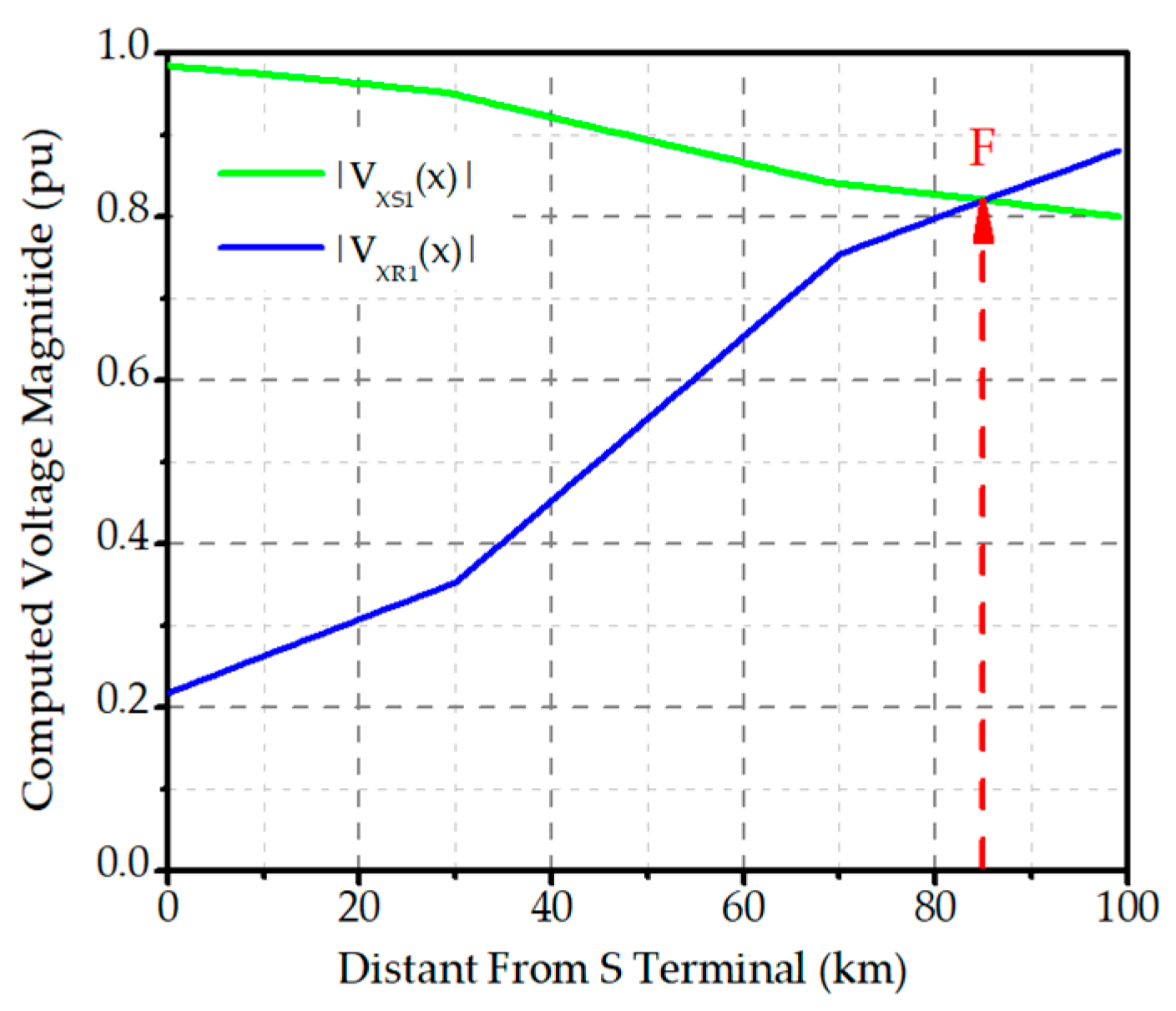
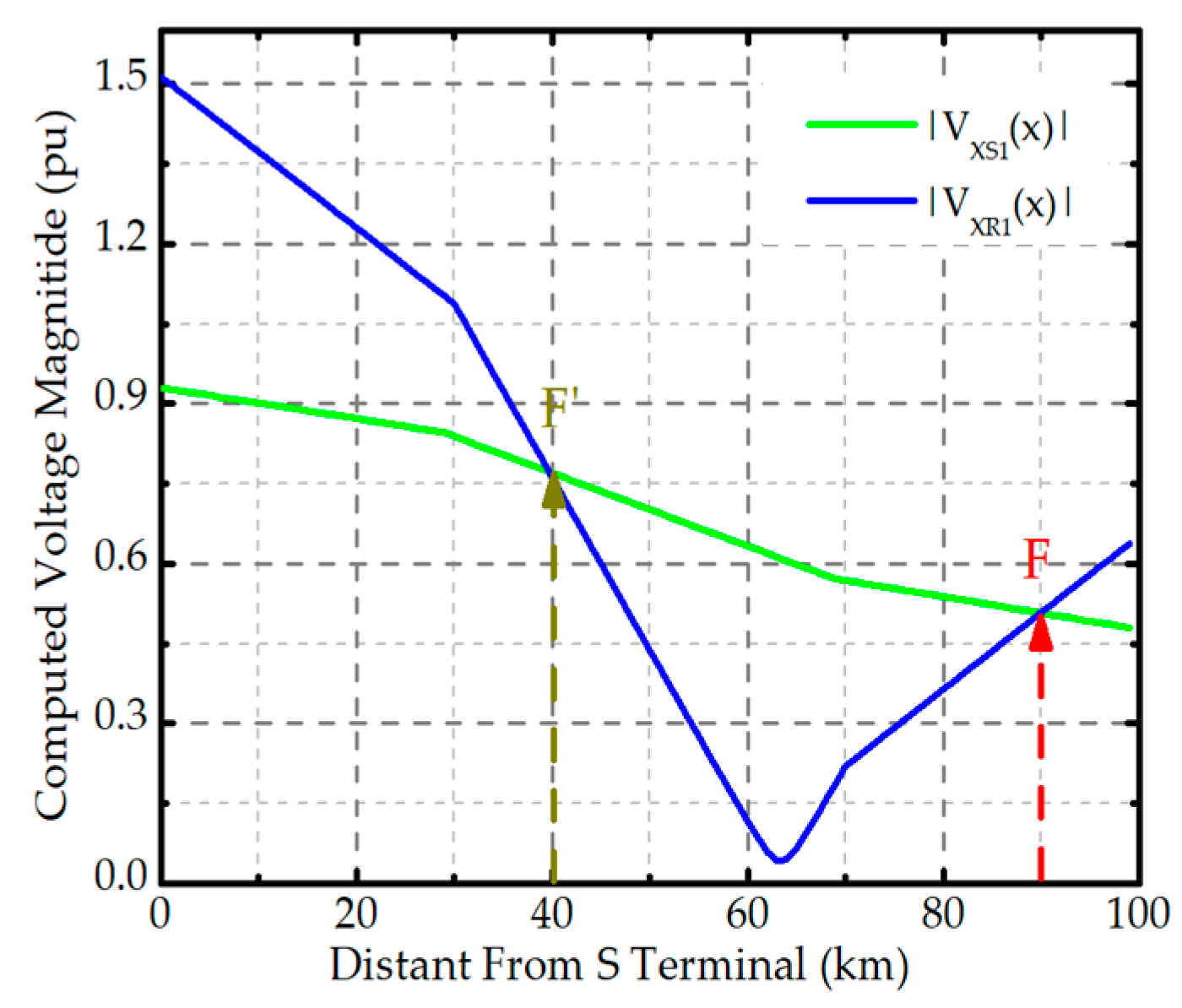
2.3. The Voltage Magnitude Intersection Points
2.4. Real Fault Localization
3. Simulation Results and Performance Evaluation
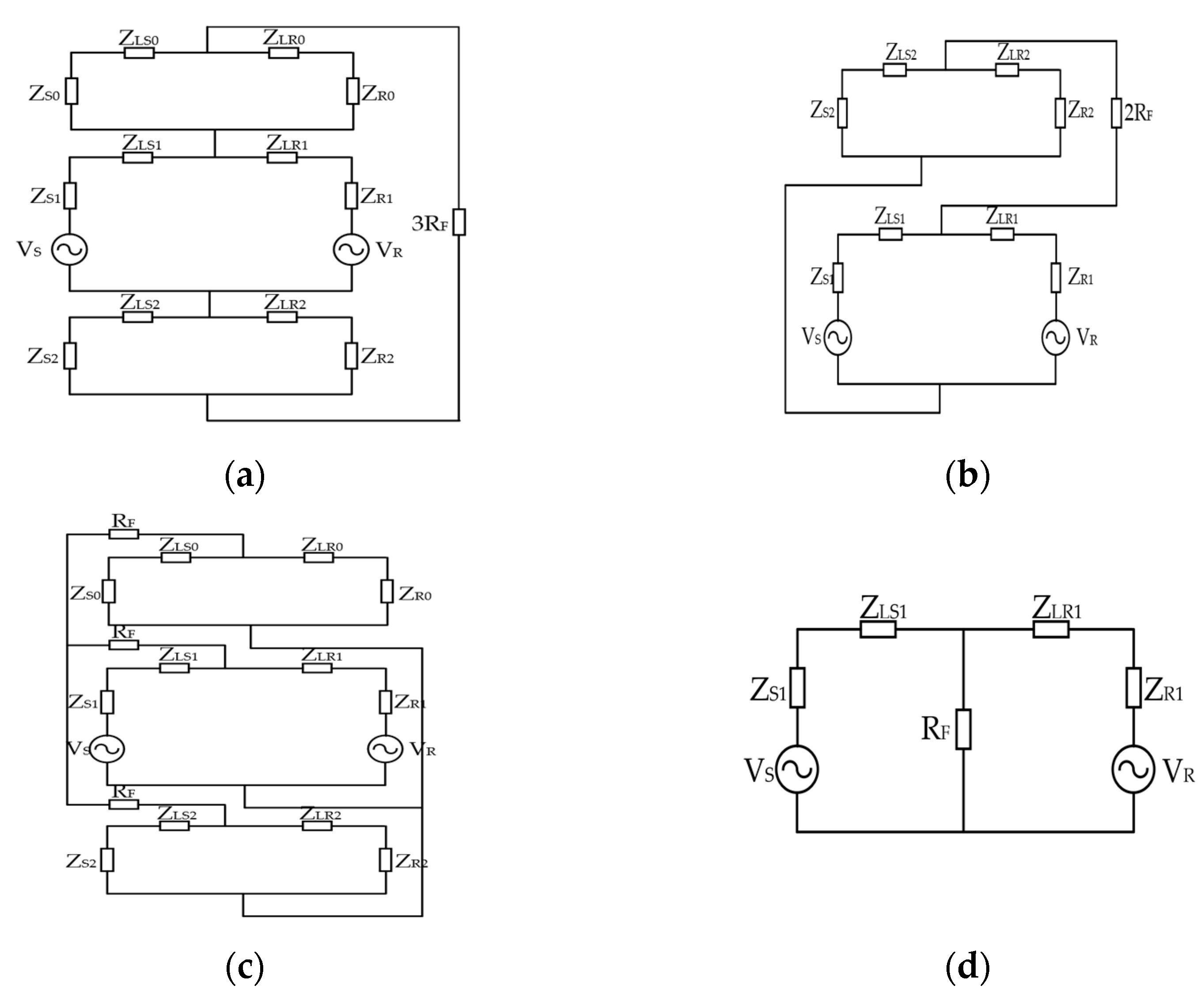
3.1. The Test Environment
3.2. Case Studies
3.2.1. Influence of the Phasor Synchronization Error and Fault Types
3.2.2. Influence of Fault Inception Angles
3.2.3. Influence of Source Impedance Variation
3.2.4. Comparison of the Proposed Algorithm with the Algorithm in [31]
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Name | Symbols | Values |
|---|---|---|
| Increasing Rate | α | 5 × 10−2 |
| Margin for Phasor Estimation Error | 1 × 10−3 | |
| Perturbation Value | 1 × 10−8 | |
| Maximum Iteration Number | cnt_max | 1 × 105 |
Appendix B

| Cable Usage | Stranding | |||||
|---|---|---|---|---|---|---|
| Conductor Size | No. of Wires | Wire Diameter | DC Resistance | |||
| TAL | Steel | TAL | Steel | |||
| (mm2) | (No.) | (No.) | (mm) | (mm) | (Ω/km) | |
| Conductor | 410 | 26 | 7 | 4.5 | 4.5 | 0.0665 |
| Ground Wire | 120 | 1 | 0 | 12.36 | - | 0.2352 |

| Layers | Iner Radius | Outer Radius | Resistivity | Relative Permittivity | Relative Permeability |
|---|---|---|---|---|---|
| (m) | (m) | (Ω × m) | - | - | |
| Conductor | 0.00000 | 0.02690 | 1.700 × 10−8 | - | 1.0 |
| 1st insulating | 0.02690 | 0.05190 | - | 2.5 | 1.0 |
| Sheath | 0.05190 | 0.06395 | 2.826 × 10−8 | - | 1.0 |
| 2nd insulating | 0.06395 | 0.06990 | - | 8.0 | 1.0 |
| Transmission Line | Impedance (pu) | Admittance (pu) | ||
|---|---|---|---|---|
| Real | Image | Real | Image | |
| Overhead | 2.01 × 10−7 | 3.45 × 10−6 | 8.89 × 10−10 | 4.68 × 10−7 |
| Underground | 1.93 × 10−7 | 1.52 × 10−6 | 1.12 × 10−10 | 7.09 × 10−6 |
References
- IEEE Std C37.114-2004; IEEE Guide for Determining Fault Location on AC Transmission and Distribution Lines. IEEE Power Engineering Society: Piscataway, NJ, USA, 2005; pp. 1–44.
- Mazon, A.J.; Zamora, I.; Miñambres, J.F.; Zorrozua, M.A.; Barandiaran, J.J.; Sagastabeitia, K. A new approach to fault location in two-terminal transmission lines using artificial neural networks. Electr. Power Syst. Res. 2000, 56, 261–266. [Google Scholar] [CrossRef]
- Rocha, S.A.; Mattos, T.G.; Cardoso, R.T.N.; Silveira, E.G. Applying Artificial Neural Networks and Nonlinear Optimization Techniques to Fault Location in Transmission Lines—Statistical Analysis. Energies 2022, 15, 4095. [Google Scholar] [CrossRef]
- Stanojević, V.A.; Preston, G.; Terzija, V. Synchronised Measurements Based Algorithm for Long Transmission Line Fault Analysis. IEEE Trans. Smart Grid 2018, 9, 4448–4457. [Google Scholar] [CrossRef]
- Kalita, K.; Anand, S.; Parida, S.K. A Novel Non-Iterative Fault Location Algorithm for Transmission Line With Unsynchronized Terminal. IEEE Trans. Power Deliv. 2021, 36, 1917–1920. [Google Scholar] [CrossRef]
- Naidu, O.; Pradhan, A.K. A Traveling Wave-Based Fault Location Method Using Unsynchronized Current Measurements. IEEE Trans. Power Deliv. 2019, 34, 505–513. [Google Scholar] [CrossRef]
- Carrión, D.; González, J.W.; Issac, I.A.; López, G.J. Optimal fault location in transmission lines using hybrid method. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference—Latin America (ISGT Latin America), Quito, Ecuador, 20–22 September 2017. [Google Scholar]
- Elnozahy, A.; Sayed, K.; Bahyeldin, M. Artificial Neural Network Based Fault Classification and Location for Transmission Lines. In Proceedings of the 2019 IEEE Conference on Power Electronics and Renewable Energy (CPERE), Aswan, Egypt, 23–25 October 2019. [Google Scholar]
- Fahim, S.R.; Sarker, Y.; Islam, O.K.; Sarker, S.K.; Ishraque, M.F.; Das, S.K. An Intelligent Approach of Fault Classification and Localization of a Power Transmission Line. In Proceedings of the 2019 IEEE International Conference on Power, Electrical, and Electronics and Industrial Applications (PEEIACON), Dhaka, Bangladesh, 29 November–1 December 2019. [Google Scholar]
- Livani, H.; Evrenosoglu, C.Y. A Machine Learning and Wavelet-Based Fault Location Method for Hybrid Transmission Lines. IEEE Trans. Smart Grid 2014, 5, 51–59. [Google Scholar] [CrossRef]
- Sadeh, J.; Afradi, H. A new and accurate fault location algorithm for combined transmission lines using Adaptive Network-Based Fuzzy Inference System. Electr. Power Syst. Res. 2009, 79, 1538–1545. [Google Scholar] [CrossRef]
- Patel, B. A new FDOST entropy based intelligent digital relaying for detection, classification and localization of faults on the hybrid transmission line. Electr. Power Syst. Res. 2018, 157, 39–47. [Google Scholar] [CrossRef]
- Abur, A.; Magnago, F.H. Use of time delays between modal components in wavelet based fault location. Int. J. Electr. Power Energy Syst. 2000, 22, 397–403. [Google Scholar] [CrossRef]
- Faybisovich, V.; Khoroshev, M.I. A Frequency domain double-ended method of fault location for transmission lines. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008. [Google Scholar]
- Styvaktakis, E.; Bollen, M.H.J.; Gu, I.Y.H. A fault location technique using high frequency fault clearing transients. IEEE Power Eng. Rev. 1999, 19, 58–60. [Google Scholar] [CrossRef]
- Gilany, M.I.; Tag Eldin, E.S.M.; Abdel Aziz, M.M.; Ibrahim, D.K. Travelling Wave-Based Fault Location Scheme for Aged Underground Cable Combined with Overhead Line. Int. J. Emerg. Electr. 2005, 2. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Ma, Z. Fault location method based on the periodicity of the transient voltage traveling wave. In Proceedings of the 2004 IEEE Region 10 Conference TENCON 2004, Chiang Mai, Thailand, 24 November 2004. [Google Scholar]
- Jung, C.K.; Lee, J.B. Fault Location Using Wavelet Transform in Combined Transmission Systems. IFAC Proc. Vol. 2003, 36, 617–622. [Google Scholar] [CrossRef]
- Niazy, I.; Sadeh, J. A new single ended fault location algorithm for combined transmission line considering fault clearing transients without using line parameters. Int. J. Electr. Power Energy Syst. 2013, 44, 816–823. [Google Scholar] [CrossRef]
- Takagi, T.; Yamakoshi, Y.; Baba, J.; Uemura, K.; Sakaguchi, T. A New Algorithm of an Accurate Fault Location for EHV/UHV Transmission Lines: Part II—Laplace Transform Method. IEEE Trans. Power App. Syst. 1982, PAS-101, 564–573. [Google Scholar] [CrossRef]
- Takagi, T.; Yamakoshi, Y.; Yamaura, M.; Kondow, R.; Matsushima, T. Development of a New Type Fault Locator Using the One-Terminal Voltage and Current Data. IEEE Trans. Power App. Syst. 1982, PER-2, 59–60. [Google Scholar]
- Zahran, A.D.; Elkalashy, N.I.; Elsadd, M.A.; Kawady, T.A.; Taalab, A.-M.I. Improved ground distance protection for cascaded overhead-submarine cable transmission system. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017. [Google Scholar]
- Bukvisova, Z.; Orsagova, J.; Topolanek, D.; Toman, P. Two-Terminal Algorithm Analysis for Unsymmetrical Fault Location on 110 kV Lines. Energies 2019, 12, 1193. [Google Scholar] [CrossRef]
- Kezunović, M.; Mrkić, J.; Peruničić, B. An accurate fault location algorithm using synchronized sampling. Electr. Power Syst. Res. 1994, 29, 161–169. [Google Scholar] [CrossRef]
- Kezunovic, M.; Perunicic, B. Automated transmission line fault analysis using synchronized sampling at two ends. IEEE Trans. Power Syst. 1996, 11, 441–447. [Google Scholar] [CrossRef]
- Dalcastagne, A.L.; Filho, S.N.; Zurn, H.H.; Seara, R. An Iterative Two-Terminal Fault-Location Method Based on Unsynchronized Phasors. IEEE Trans. Power Deliv. 2008, 23, 2318–2329. [Google Scholar] [CrossRef]
- Yu, C.-S. An Unsynchronized Measurements Correction Method for Two-Terminal Fault-Location Problems. IEEE Trans. Power Deliv. 2010, 25, 1325–1333. [Google Scholar] [CrossRef]
- Elsadd, M.A.; Abdelaziz, A.Y. Unsynchronized fault-location technique for two- and three-terminal transmission lines. Electr. Power Syst. Res. 2018, 158, 228–239. [Google Scholar] [CrossRef]
- Lin, T.C.; Xu, Z.R.; Ouedraogo, F.B.; Lee, Y.J. A new fault location technique for three-terminal transmission grids using unsynchronized sampling. Int. J. Electr. Power Energy Syst. 2020, 123, 106229. [Google Scholar] [CrossRef]
- Aziz, M.M.A.; Khalil Ibrahim, D.; Gilany, M. Fault location scheme for combined overhead line with underground power cable. Electr. Power Syst. Res. 2006, 76, 928–935. [Google Scholar]
- Liu, C.-W.; Lin, T.-C.; Yu, C.-S.; Yang, J.-Z. A Fault Location Technique for Two-Terminal Multisection Compound Transmission Lines Using Synchronized Phasor Measurements. IEEE Trans. Smart Grid 2012, 3, 113–121. [Google Scholar] [CrossRef]
- Elsadd, M.A.; Omar, H.A.; Adly, A.R.; Zobaa, A.F. Fault-Locator Scheme for Combined Taba-Aqaba Transmission System Based on New Faulted Segment Identification Method. IEEE Access 2023, 11, 104270–104284. [Google Scholar] [CrossRef]
- Hashemian, S.M.; Hashemian, S.N.; Gholipour, M. Unsynchronized parameter free fault location scheme for hybrid transmission line. Electr. Power Syst. Res. 2021, 192, 106982. [Google Scholar] [CrossRef]
- Jiang, J.A.; Yang, J.Z.; Lin, Y.H.; Liu, C.W.; Ma, J.C. An adaptive PMU based fault detection/location technique for transmission lines. I. IEEE Trans. Power Deliv. 2000, 15, 486–493. [Google Scholar] [CrossRef]
- Guo, Y.; Kezunovic, M.; Chen, D. Simplified algorithms for removal of the effect of exponentially decaying DC-offset on the Fourier algorithm. IEEE Trans. Power Deliv. 2003, 18, 711–717. [Google Scholar]



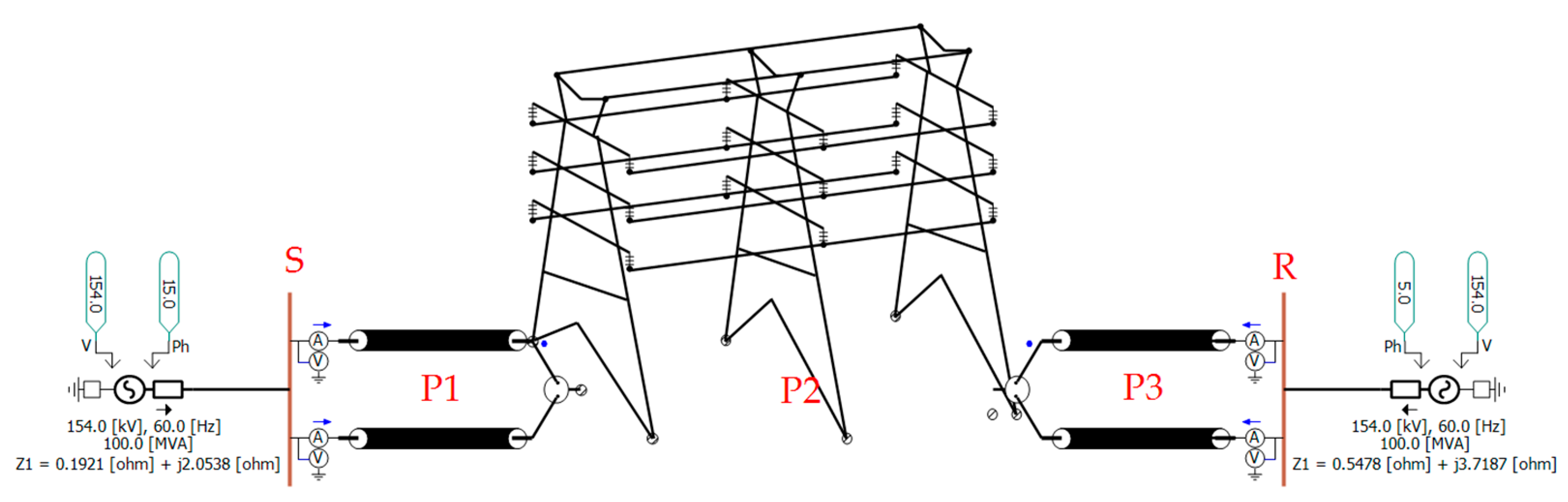
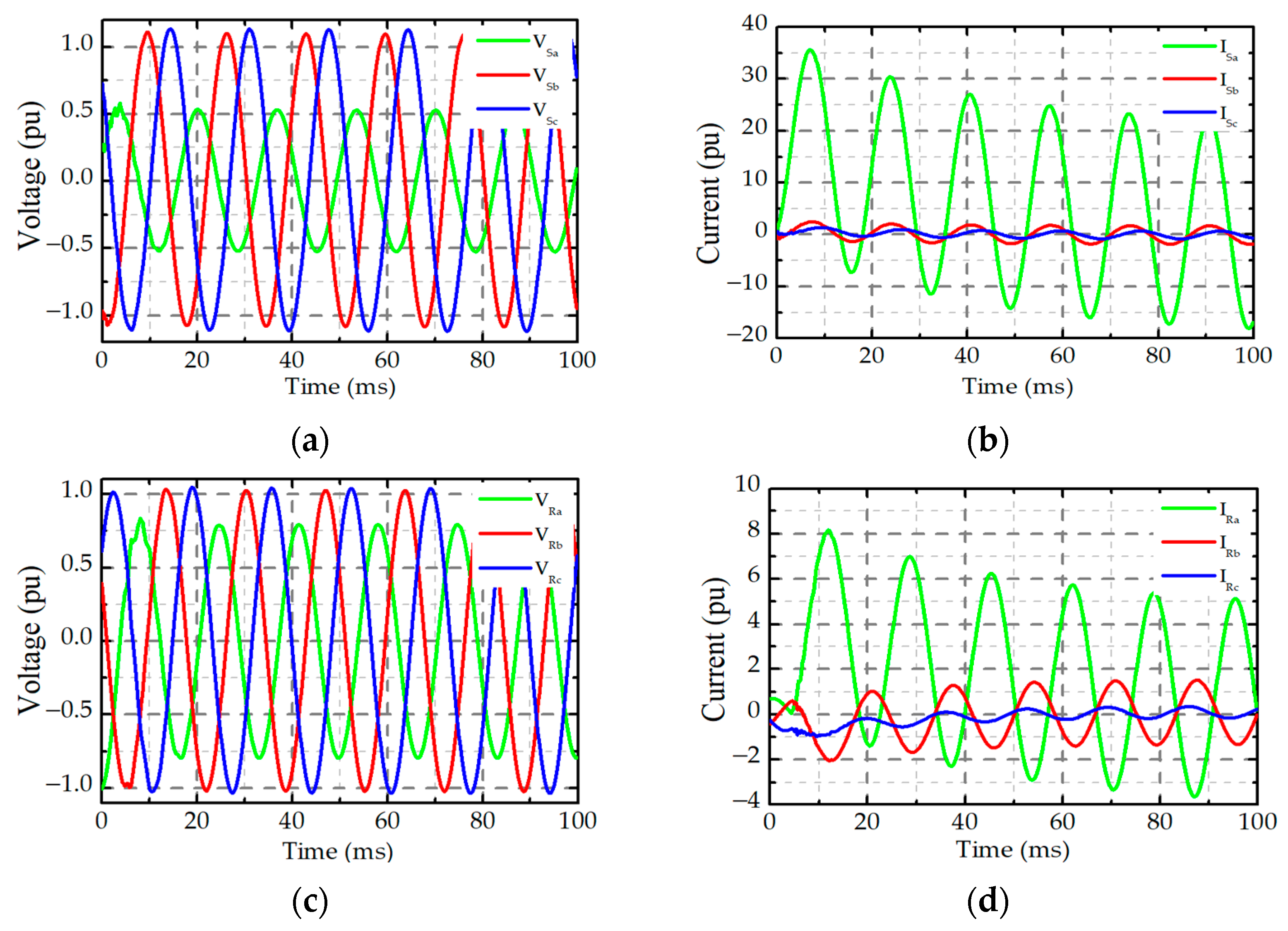
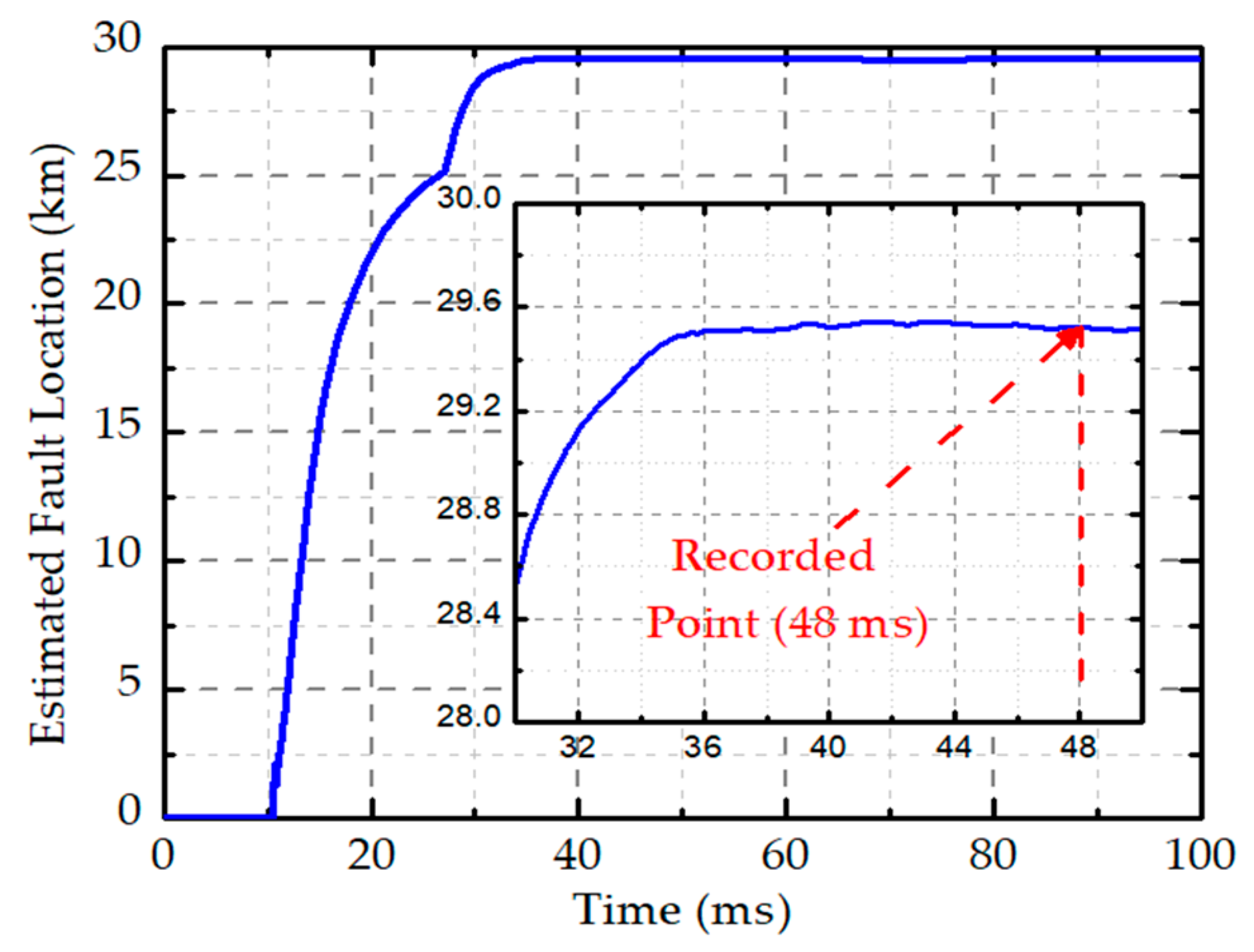
| Acronym | Units | Definition |
|---|---|---|
| cnt_max | Maximum iteration number | |
| d | pu | Different voltage magnitude |
| F | km | Fault location |
| FDOST | Fast-discrete orthogonal S-transform | |
| FPrev | km | Estimated fault location of the previous sample |
| F’ | km | Voltage magnitude intersection point but not a real fault |
| LP1, LP2, L | km | Distance from the S terminal to points M and N and total length |
| M, N | Interconnection points on the combined transmission line | |
| P1, P2, P3 | Sections on the combined transmission line | |
| VF, IF | Fault voltage and current | |
| VMR1, IMR1, VNR1, INR1 | pu | Positive-sequence voltage and current at the points of interconnection M and N computed based on R terminal data |
| VMS1, IMS1, VNS1, INS1 | pu | Positive-sequence voltage and current at points M and N computed based on S terminal data |
| VS, IS, VR, IR | pu | Three-phase voltage and current at the S and R terminals |
| VS1, IS1, VR1, IR1 | pu | Positive-sequence voltage and current at the S and R terminals |
| VXR, IXR | pu | Three-phase voltage and current at point X computed based on R terminal data |
| VXR1, IXR1 | pu | Positive-sequence voltage and current at a specific point along the transmission line computed based on R terminal data |
| VXS, IXS | pu | Three-phase voltage and current at point X computed based on the S terminal data |
| VXS1, IXS1 | pu | Positive-sequence voltage and current at a specific point along the transmission line computed based on S terminal data |
| X | Voltage magnitude computation point | |
| x | pu | Distance from S terminal to point X |
| Y1, Y1_P1, Y1_P2, Y1_P3 | pu | Positive-sequence admittance of the homogenous transmission line and sections P1, P2, and P3 of the combined transmission line |
| ZC1, Z C1_P1, Z C1_P2, Z C1_P3 | Positive-sequence characteristic impedance of the homogenous transmission line and sections P1, P2, and P3 of the combined transmission line | |
| Zeq | Equivalent impedance | |
| Z1, Z1_P1, Z1_P2, Z1_P3 | pu | Positive-sequence impedance of the homogenous transmission line and sections P1, P2, and P3 of the combined transmission line |
| , , , | Positive-sequence propagation constant of the homogenous transmission line and sections P1, P2, and P3 of the combined transmission line | |
| α | Increasing rate | |
| δ | Perturbation value | |
| ε | Margin for phasor estimation error | |
| Inverse angle of the equivalent impedance |
| Fault Resistance | Phase Error | 10 km (P1) | 50 km (P2) | 80 km (P3) | |||
|---|---|---|---|---|---|---|---|
| (Ω) | (°) | Location (km) | Error (%) | Location (km) | Error (%) | Location (km) | Error (%) |
| 0 | 0 | 9.992 | 0.008 | 49.995 | 0.005 | 79.976 | 0.024 |
| 30 | 9.994 | 0.006 | 49.996 | 0.004 | 79.980 | 0.020 | |
| 60 | 9.995 | 0.005 | 49.995 | 0.005 | 79.984 | 0.016 | |
| 90 | 10.002 | 0.002 | 49.995 | 0.005 | 79.972 | 0.028 | |
| 180 | 10.023 | 0.023 | 50.012 | 0.012 | 79.996 | 0.004 | |
| 30 | 0 | 9.656 | 0.344 | 49.859 | 0.141 | 79.668 | 0.332 |
| 30 | 9.788 | 0.212 | 49.904 | 0.096 | 79.783 | 0.217 | |
| 60 | 9.930 | 0.070 | 49.891 | 0.109 | 79.886 | 0.114 | |
| 90 | 10.031 | 0.031 | 49.984 | 0.016 | 80.282 | 0.282 | |
| 180 | 10.468 | 0.468 | 50.135 | 0.135 | 79.902 | 0.098 | |
| 50 | 0 | 9.310 | 0.690 | 49.686 | 0.314 | 79.401 | 0.599 |
| 30 | 9.553 | 0.447 | 49.787 | 0.213 | 79.601 | 0.399 | |
| 60 | 9.836 | 0.164 | 49.892 | 0.108 | 79.813 | 0.187 | |
| 90 | 10.034 | 0.034 | 50.019 | 0.019 | 79.992 | 0.008 | |
| 180 | 9.378 | 0.623 | 50.381 | 0.381 | 79.683 | 0.317 | |
| Fault Resistance | Phase Error | 10 km (P1) | 50 km (P2) | 80 km (P3) | |||
|---|---|---|---|---|---|---|---|
| (Ω) | (°) | Location (km) | Error (%) | Location (km) | Error (%) | Location (km) | Error (%) |
| 0 | 0 | 9.995 | 0.005 | 50.018 | 0.018 | 79.992 | 0.008 |
| 30 | 10.009 | 0.009 | 50.018 | 0.018 | 79.991 | 0.009 | |
| 60 | 10.013 | 0.013 | 50.019 | 0.019 | 79.990 | 0.010 | |
| 90 | 10.019 | 0.019 | 50.020 | 0.020 | 79.994 | 0.006 | |
| 180 | 10.043 | 0.043 | 50.024 | 0.024 | 80.003 | 0.003 | |
| 30 | 0 | 9.703 | 0.297 | 50.060 | 0.060 | 79.953 | 0.047 |
| 30 | 9.775 | 0.225 | 50.096 | 0.096 | 80.017 | 0.017 | |
| 60 | 9.877 | 0.123 | 50.129 | 0.129 | 80.085 | 0.085 | |
| 90 | 9.919 | 0.081 | 50.144 | 0.144 | 80.139 | 0.139 | |
| 180 | 10.194 | 0.194 | 50.276 | 0.276 | 80.363 | 0.363 | |
| 50 | 0 | 9.605 | 0.395 | 49.981 | 0.019 | 79.939 | 0.061 |
| 30 | 9.771 | 0.229 | 50.050 | 0.050 | 80.064 | 0.064 | |
| 60 | 9.955 | 0.045 | 50.137 | 0.137 | 80.202 | 0.202 | |
| 90 | 10.020 | 0.020 | 50.171 | 0.171 | 80.315 | 0.315 | |
| 180 | 10.495 | 0.495 | 50.458 | 0.458 | 80.757 | 0.757 | |
| Fault Resistance | Phase Error | 10 km (P1) | 50 km (P2) | 80 km (P3) | |||
|---|---|---|---|---|---|---|---|
| (Ω) | (°) | Location (km) | Error (%) | Location (km) | Error (%) | Location (km) | Error (%) |
| 0 | 0 | 10.001 | 0.001 | 50.013 | 0.013 | 79.994 | 0.006 |
| 30 | 10.020 | 0.020 | 50.014 | 0.014 | 79.998 | 0.002 | |
| 60 | 10.014 | 0.014 | 50.015 | 0.015 | 79.998 | 0.002 | |
| 90 | 10.016 | 0.016 | 50.016 | 0.016 | 79.998 | 0.002 | |
| 180 | 9.984 | 0.016 | 50.013 | 0.013 | 79.996 | 0.004 | |
| 30 | 0 | 10.004 | 0.004 | 50.062 | 0.062 | 79.857 | 0.143 |
| 30 | 10.052 | 0.052 | 50.077 | 0.077 | 79.890 | 0.110 | |
| 60 | 10.094 | 0.094 | 50.092 | 0.092 | 79.924 | 0.076 | |
| 90 | 10.125 | 0.125 | 50.105 | 0.105 | 79.955 | 0.045 | |
| 180 | 10.243 | 0.243 | 50.177 | 0.177 | 80.047 | 0.047 | |
| 50 | 0 | 10.005 | 0.005 | 50.028 | 0.028 | 79.765 | 0.235 |
| 30 | 10.086 | 0.086 | 50.061 | 0.061 | 79.832 | 0.168 | |
| 60 | 10.197 | 0.197 | 50.095 | 0.095 | 79.902 | 0.098 | |
| 90 | 10.233 | 0.233 | 50.124 | 0.124 | 79.963 | 0.037 | |
| 180 | 10.477 | 0.477 | 50.246 | 0.246 | 80.176 | 0.176 | |
| Fault Resistance | Phase Error | 10 km (P1) | 50 km (P2) | 80 km (P3) | |||
|---|---|---|---|---|---|---|---|
| (Ω) | (°) | Location (km) | Error (%) | Location (km) | Error (%) | Location (km) | Error (%) |
| 0 | 0 | 9.816 | 0.184 | 49.697 | 0.303 | 80.112 | 0.112 |
| 30 | 9.801 | 0.199 | 49.750 | 0.250 | 80.114 | 0.114 | |
| 60 | 9.791 | 0.209 | 49.753 | 0.247 | 80.113 | 0.113 | |
| 90 | 9.777 | 0.223 | 49.626 | 0.374 | 80.118 | 0.118 | |
| 180 | 9.721 | 0.279 | 49.458 | 0.542 | 80.118 | 0.118 | |
| 30 | 0 | 9.845 | 0.155 | 49.846 | 0.154 | 79.731 | 0.269 |
| 30 | 9.915 | 0.085 | 49.900 | 0.100 | 79.801 | 0.199 | |
| 60 | 9.989 | 0.011 | 49.961 | 0.039 | 79.869 | 0.131 | |
| 90 | 10.039 | 0.039 | 49.965 | 0.035 | 79.931 | 0.069 | |
| 180 | 10.235 | 0.235 | 50.207 | 0.207 | 80.188 | 0.188 | |
| 50 | 0 | 9.710 | 0.290 | 49.705 | 0.295 | 79.610 | 0.390 |
| 30 | 9.810 | 0.190 | 49.820 | 0.180 | 79.726 | 0.274 | |
| 60 | 9.958 | 0.042 | 49.943 | 0.057 | 79.847 | 0.153 | |
| 90 | 10.028 | 0.028 | 50.016 | 0.016 | 79.953 | 0.047 | |
| 180 | 10.334 | 0.334 | 50.372 | 0.372 | 80.362 | 0.362 | |
| Fault Resistance | Fault Inception Angle | 10 km (P1) | 50 km (P2) | 80 km (P3) | |||
|---|---|---|---|---|---|---|---|
| (Ω) | (°) | Location (km) | Error (%) | Location (km) | Error (%) | Location (km) | Error (%) |
| 0 | 0 | 10.012 | 0.012 | 49.984 | 0.016 | 79.958 | 0.042 |
| 30 | 9.970 | 0.030 | 49.991 | 0.009 | 79.958 | 0.042 | |
| 60 | 9.951 | 0.049 | 49.885 | 0.115 | 79.993 | 0.007 | |
| 90 | 9.938 | 0.062 | 49.974 | 0.026 | 79.862 | 0.138 | |
| 180 | 9.988 | 0.012 | 50.008 | 0.008 | 80.032 | 0.032 | |
| 30 | 0 | 9.668 | 0.332 | 49.860 | 0.140 | 79.677 | 0.323 |
| 30 | 9.419 | 0.581 | 49.946 | 0.054 | 79.411 | 0.589 | |
| 60 | 9.901 | 0.099 | 49.970 | 0.030 | 79.483 | 0.517 | |
| 90 | 10.027 | 0.027 | 49.906 | 0.094 | 79.803 | 0.197 | |
| 180 | 9.627 | 0.373 | 49.618 | 0.382 | 79.763 | 0.237 | |
| 50 | 0 | 9.351 | 0.649 | 49.711 | 0.289 | 79.396 | 0.604 |
| 30 | 9.171 | 0.829 | 49.753 | 0.247 | 79.533 | 0.467 | |
| 60 | 9.417 | 0.583 | 49.532 | 0.468 | 79.582 | 0.418 | |
| 90 | 9.417 | 0.583 | 49.596 | 0.404 | 79.495 | 0.505 | |
| 180 | 9.179 | 0.821 | 49.685 | 0.315 | 80.362 | 0.362 | |
| Source S | Source R | 10 km | 50 km | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Positive | Zero | Positive | Zero | ||||||||
| R1 | X1 | R0 | X0 | R1 | X1 | R0 | X0 | Location (km) | Error (%) | Location (km) | Error (%) |
| (Ω) | (Ω) | (Ω) | (Ω) | ||||||||
| 0.1729 | 1.8484 | 0.8196 | 4.1749 | 0.4930 | 3.3468 | 2.0042 | 9.7779 | 10.135 | 0.135 | 49.983 | 0.017 |
| 0.2113 | 2.2592 | 1.0018 | 5.1027 | 0.6026 | 4.0906 | 2.4496 | 11.9507 | 10.105 | 0.105 | 50.001 | 0.001 |
| Fault Types | Fault Location | Proposed Algorithm | Algorithm in [31] | ||
|---|---|---|---|---|---|
| (km) | Location (km) | Error (%) | Location (km) | Error (%) | |
| Single-phase-to-ground | 10 | 9.931 | 0.069 | 10.124 | 0.124 |
| 50 | 49.991 | 0.009 | 49.992 | 0.008 | |
| 80 | 79.947 | 0.053 | 80.005 | 0.005 | |
| Phase-to-phase | 10 | 9.845 | 0.155 | 10.253 | 0.253 |
| 50 | 49.860 | 0.140 | 50.092 | 0.092 | |
| 80 | 79.783 | 0.217 | 79.857 | 0.143 | |
| Phase-to-phase-to ground | 10 | 9.982 | 0.018 | 09.832 | 0.168 |
| 50 | 49.970 | 0.030 | 50.020 | 0.020 | |
| 80 | 79.936 | 0.064 | 79.927 | 0.073 | |
| Three-phase | 10 | 9.489 | 0.511 | 10.006 | 0.006 |
| 50 | 49.499 | 0.501 | 49.987 | 0.013 | |
| 80 | 80.294 | 0.294 | 80.154 | 0.154 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lak, P.Y.; Ha, K.-M.; Nam, S.-R. A Fault Location Algorithm for Multi-Section Combined Transmission Lines Considering Unsynchronized Sampling. Energies 2024, 17, 703. https://doi.org/10.3390/en17030703
Lak PY, Ha K-M, Nam S-R. A Fault Location Algorithm for Multi-Section Combined Transmission Lines Considering Unsynchronized Sampling. Energies. 2024; 17(3):703. https://doi.org/10.3390/en17030703
Chicago/Turabian StyleLak, Peng Y., Kwang-Min Ha, and Soon-Ryul Nam. 2024. "A Fault Location Algorithm for Multi-Section Combined Transmission Lines Considering Unsynchronized Sampling" Energies 17, no. 3: 703. https://doi.org/10.3390/en17030703
APA StyleLak, P. Y., Ha, K.-M., & Nam, S.-R. (2024). A Fault Location Algorithm for Multi-Section Combined Transmission Lines Considering Unsynchronized Sampling. Energies, 17(3), 703. https://doi.org/10.3390/en17030703






