Bayesian Entropy Methodology: A Novel Approach to Setting Anti-Islanding Protections with Enhanced Stability and Sensibility

Abstract

The risk of unintentional islanding creation in distributed energy systems poses a significant security concern since unintentional islanding formation could lead to a supply of energy outside of the optimal quality limits. This constitutes a risk for users, maintenance personnel, infrastructure, and devices. To mitigate this problem, anti-islanding protections are widely used to prevent the distributed generator from feeding a portion of the radial distribution grid when a protection device trips upstream. However, the effectiveness of these protections heavily relies on properly tuning protection setting thresholds (such as time delay and pickup). This work proposes a novel approach that utilizes entropy as a model and metric of the uncertainty associated with a particular protection setting. By minimizing entropy, the proposed method aims to improve stability and sensitivity, consequently improving the overall performance of anti-islanding protection. Simulation results demonstrate that the Bayesian entropy methodology (BEM) approach achieves enhanced stability in various scenarios, including frequency transients, and demonstrates a notable reduction in the size of the dataset and computational burden, ranging between 91% and 98%, when compared to related works, with an improvement of the uncertainty achieved. The findings of this study contribute to the development of more robust and reliable anti-islanding protections.

1. Introduction

1.1. Background and Motivation

Integrating distributed energy resources (DERs) poses several technical challenges that must be addressed for effective deployment [1,2]. The bidirectional power flow in distribution systems with DERs requires robust protection schemes and grid interconnection standards to ensure safe and reliable operation. In this context, one of the most significant issues is associated with the possibility of unintended islanding formation. In many cases, the electric system is designed to intentionally form islands. For instance, an electrical microgrid could be designed to continue operating in island mode in the event of a power supply failure from the main grid [3,4]. Accidentally formed, or unintended, islands are not planned as such and therefore are not prepared to operate independently of the main electrical system. One of the mechanisms that can cause unintended islanding is when automatic reclosing devices act in an attempt to clear temporary faults in radial distribution systems [5]. Hazardous situations for equipment and individuals in the event of an unwanted islanding formation imply that the frequency and voltage may become uncontrolled, which opens up the possibility of supplying energy outside of optimal quality parameters [6]. Additionally, arc flash incident energy increases monotonically as the time taken to detect islanding and cease islanding operation increases, posing a risk to users and maintenance personnel [7]. For the reasons presented above, anti-islanding protection is mandatory in many regulations and grid codes [8,9,10,11]. The anti-islanding protection in power systems needs to be both sensitive and stable [12]. Sensitivity refers to the ability of the protection system to detect the occurrence of an islanding condition accurately. Stability refers to the ability of the protection system to discriminate between islanding conditions and other transient, adjacent faults [13].

Several of the anti-islanding protections based on threshold definition pose serious difficulties in appropriately defining the correct calibration thresholds to ensure proper operation [14,15]. Improper setting of anti-islanding protection increases the likelihood of false tripping of the DERs. False tripping can disrupt the distribution system operation and cause unnecessary outages [16]. Furthermore, the stability of anti-islanding protection is crucial for the secure operation of electric power systems (EPS) with a significant penetration of DERs [17]. This importance was highlighted, for example, by the events of 9 August 2019 in the United Kingdom EPS. During this incident, the unstable functioning of anti-islanding (also known as loss of main protection) resulted in the widespread disconnection of DERs, which aggravated the original disturbance. Consequently, the load shedding in the UK EPS, known as low-frequency demand disconnection (LFDD), was triggered, leading to a significant disconnection of the demand [18,19,20].

Some countries have undertaken expensive retrofit programs to reconfigure DER protection thresholds and thus mitigate their impact when disturbances occur in the power system [21,22]. It is evidently crucial to have a methodology that enables the identification of an optimal configuration for anti-islanding protection to ensure that the anti-islanding protection will operate correctly in the majority of possible cases, including EPS disturbances [23,24]. This work introduces a novel methodology for finding the optimal settings of anti-islanding protection. The overall objective of this approach is to configure anti-islanding protection in such a way that it can make the best possible decisions. The aim is to achieve the highest possible certainty about decisions.

1.2. Literature Review of Islanding Detection Methods

Numerous islanding detection methods (IDMs) are described in the literature to implement anti-islanding protections [25,26]. IDMs can be classified into two main categories, i.e., local and remote. Remote methods utilize a communication link, such as power line communication (PLC), to transmit information to the protected distributed generator (DG) from protective devices located upstream or from substation. Some of the challenges associated with these methods include signal attenuation, noise immunity, and the maximum signaling distance [27]. However, the primary disadvantage of remote methods is their high cost, which renders them impractical for small-generation units [28]. Furthermore, they require the use of a local method for backup in the event of a communication link failure. These drawbacks highlight the greater relevance of local IDMs over remote ones. Local methods, conversely, employ information from electric variables measured at the point of common coupling (PCC) and use this information to make a sound decision. These can be subdivided into passive or active, depending on the operating hypothesis they employ [29]. Active IDMs continuously introduce perturbations at the PCC and assess the effect of these perturbations on the electric variables [30,31]. The central hypothesis behind active IDMs is that the introduced perturbation can be negligible when a DG is connected to the main grid but significantly affects sensed variables when an unintentional island is formed. General issues associated with these methodologies include the effect of introduced disturbances on product quality, electromagnetic compatibility due to potential interference among different DGs, and the limitation of these techniques to converter-based generation technologies [32].

Passive IDMs measure different electric variables at the PCC such as voltage, current, frequency, phase angle, total harmonic distortion (THD), active power, reactive power, and others [33], without introducing any perturbation. These IDMs operate under the assumption that when an island forms, there will be an imbalance between demand and generation that affects the sensed variables. Although these techniques offer advantages over others, such as low cost, simplicity, no harmonic injection, and applicability to various generation technologies of DERs, they have a significant issue with large non-detection zones (NDZs), which are specific operational ranges or conditions under which the IDM fails to identify to the occurrence of islanding [34]. An NDZ represents a scenario where the electric quantities, such as frequency and voltage, remain within acceptable limits despite the formation of an island; then, the performance of these techniques is strongly associated with the defined trip thresholds.

Passive IDMs are typically categorized into classic and advanced methods. Classic methods, such as the frequency and voltage threshold method (FVT) ANSI 81U/O and ANSI 27/59, rate of change of frequency (RoCoF) method ANSI 81R, and voltage vector shift (VVS) detection method [35,36,37]. They are the methods most commonly used currently in many distribution systems with high penetration of DERs [10,38,39]. Advanced passive methods, on the other hand, integrate sophisticated signal processing, machine learning, and classifier techniques to improve performance, prevent false tripping, and reduce the NDZ of classic techniques [40]. While they offer performance enhancements compared to classic methods, their complexity necessitates devices capable of the required signal processing, and substantial computational efforts are required for implementation due to the large number of cases of training that need to be analyzed [41,42,43]. Ultimately, these methods, like classic methods, still rely on the definition of thresholds for their operation. For the existing passive methods in the literature, defining the correct thresholds is a complex task [44].

In [45], the authors have presented a new passive method based on combining the decision-making of five conventional passive methods: under/over current, voltage, frequency, RoCoF, and DC-link voltage-based IDM. While this approach could avoid the need for complex processing techniques, in this work the thresholds were arbitrarily chosen with no certainty of their optimality. Moreover, the method was only tested for protecting photovoltaic systems, and the selected thresholds may not be suitable when synchronous or asynchronous machines are present in the formed island, as they can change the dynamics of the electrical variables and the NDZ [46].

In [47], the automatic setting map methodology (ASMM) is presented. It proposes calculating optimal settings through an algorithm that maximizes a weighted objective function, where weights can be arbitrarily chosen based on a preference for higher sensitivity or stability. Significant computational effort is required due to the number of cases employed to maximize the objective function. Moreover, the methodology has not been evaluated for frequency transients caused by disturbances in the EPS, whose duration can be longer than the times involved in islanding detection, complicating the application of this method, which is based on the superposition of the variables’ dynamics in a temporal framework. Additionally, as it is based on a dynamic analysis of the variables, applying this method for the threshold adjustment of other protections necessitates modifications to the original algorithm, further increasing the computational effort, as is presented in [48], where the ASMM is used to find the best under-voltage block setting to improve the performance of commonly used passive IDM.

In [49,50], the thresholds for an IDM based on the slip angle and acceleration angle are presented. The thresholds provided have only been calculated for very few scenarios, and only two fault cases have been evaluated for which the protection should be stable. Moreover, no validation instances have been presented for a set of scenarios different from those used to calculate the presented adjustments, and therefore, the confusion matrix of the adjustments achieved with this technique, with which they could be evaluated and compared, has not been studied.

In [51], a methodology based on dynamic security regions is presented to identify the minimum requirements for RoCoF-based (ANSI 81R) anti-islanding protections for DERs that ensure the safe operation of the Brazilian Interconnected Power System. While this methodology successfully identified minimal safety conditions for setting the lowest RoCoF thresholds, it did not provide an analysis of the performance of these settings in terms of sensitivity across various islanding scenarios, relegating the contribution of this work solely to the analysis of security in the EPS.

1.3. Contributios of Bayesian Entropy Methodology

After reviewing the literature on island IDMs, it is evident that there is a clear need for a methodology to properly set anti-islanding protections. This methodology should address limitations commonly found in the preceding literature, such as computational effort, insufficient abstraction of the signal involved in island detection, and the capability to analyze disturbances of various natures across different temporal frameworks, among others. This work presents an innovative approach using entropy to model decision-making uncertainty and Bayesian inference. Under this new approach, if a protection system were configured to have minimal entropy, the uncertainty of its decisions (i.e., disconnecting a DER or not when a disturbance occurs) would also be minimized. This combination of powerful theories (Bayesian inference and entropy) gives rise to the Bayesian entropy methodology (BEM). The main contributions of this work include:

• Modeling the protection uncertainty: The entropy model is not only an objective function; entropy also is the model of the uncertainty of the protection system. This allows for the search of optimal settings but furthermore, this also enables the comparison of different IDMs in terms of their minimum achievable entropy.
• Abstracting the signal and its dynamics involved in island detection: By defining a statistical experiment, BEM simply counts successes or failures. This allows treating the protection system as a ‘black box’ and identifying which setting minimizes entropy. It also makes the methodology independent of the time duration of each of the cases used, not needing them to be equal in the time framework.
• Reduction of the computational burden: This is possible thanks to the employed Bayesian inference, which is computationally efficient compared to frequentist alternatives, reducing the size of datasets.
• Ability to measure the experiment’s uncertainty: BEM not only allows for the protection uncertainty but also enables the measurement of the uncertainty of the defined statistical experiment. This feature clearly determines the number of cases needed for evaluation in search of the optimal adjustment for the protection.

To validate the proposed BEM, simulations were performed on a test system using DIgSILENT Power Factory 2018 SP3. Datasets for both the calculation and validation of settings for RoCoF and frequency-based anti-islanding protections were obtained. Subsequently, a MATLAB-based BEM algorithm was employed to derive the optimal settings. These settings were then rigorously tested and validated on a separate validation dataset. The remainder of this work has been organized as follows. In Section 2, entropy is introduced as a model for the protection uncertainty. In Section 3, the employed Bayesian inference model and BEM are presented. Section 4 introduces the test system and the generated datasets of different islanding and cases of no islanding. Section 5 presents the obtained results and validation instances. In Section 6, these results are compared with those of other published works, and finally, in Section 7, the conclusions are presented.

2. Entropy Mathematic Model of Anti-Islanding Protection

The uncertainty associated with each decision made by the protection is directly linked to the probability of that decision being incorrect. Engaging in a priori, frequentist statistical modeling of the problem is essential to determine the probabilities associated with these decisions. Within this modeling framework, the first step involves defining a universe of potential events. This universe comprises a set of events categorized into subsets, such as islanding events and events of no islanding. Each subset represents a distinct outcome or scenario:

$$\{e_i\}=\left\{\begin{array}{c}I:island events\\ NI: events of no islanding\end{array}\right.$$

(1)

Depending on the composition of this set, there will be a priori probability associated with each of the defined events. These probabilities do not depend on the protection but on its environment. Thus, there will be a pair of probabilities for islanding events and events of no islanding, respectively, as determined by Equation (2):

$$p_I+p_{NI}=1$$

(2)

Suppose the behavior of the protection system is statistically evaluated, considering it as a closed black box with a defined universe of events. In that case, it becomes possible to determine a set of probabilities for success and failure for each subset of events. For specific anti-islanding protection with an arbitrarily defined configuration, within the subset of islanding events, there will exist the following probabilities:

$$p_{D/I}+p_{ND/I}=1$$

(3)

In Equation (3), the first term represents the probability of detecting an island when it has actually occurred (success), while the second term represents the probability of not detecting an island when it has occurred (failure). The set of probabilities, ($p_{D/I}$ and $p_{ND/I}$), is associated with the sensitivity of the protection. Similarly, within the subset of events of no islanding, the probabilities are as follows:

$$p_{D/NI}+p_{ND/NI}=1$$

(4)

In Equation (4), the first term corresponds to the probability of detecting an island when it has not occurred (failure), and the second term corresponds to the probability of not detecting an island when it has not happened (success). The set of probabilities, ($p_{D/NI}$ and $p_{ND/NI}$) is associated with the stability of the protection.

Figure 1 shows a forward probability diagram depicting the possible paths in the occurrence of an event, whether it is an island or not, and the associated probabilities of detecting the island (triggering the protection) either correctly or mistakenly.

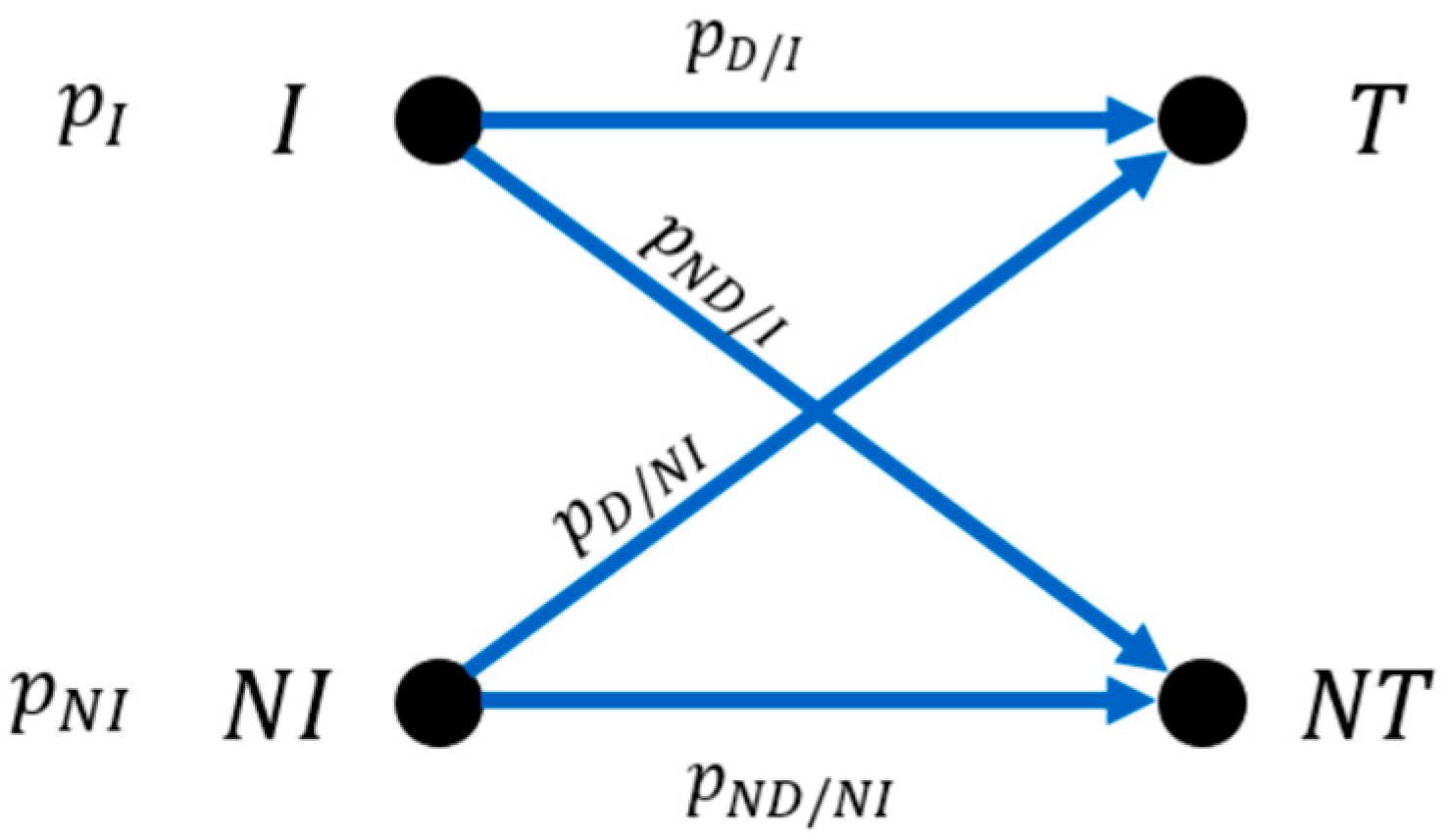
Under this probabilistic model, an ideal anti-islanding protection (with no uncertainty about its decisions) should have a probability of success for detecting islands of one ($p_{D/I}=1$) and a probability of success of one for not detecting false islands ($p_{ND/NI}=1$).

According to Shannon’s mathematical theory of communication [52], the uncertainty of the forward probability set {$p_{D/I}$; $p_{ND/I}; p_{D/NI}$; $p_{ND/NI}$} is determined by the entropy as expressed by Equations (5) and (6):

$$H=\sum _{i=1}^{i=N}{p}_i\mathit{log}\frac{1}{p_i}$$

(5)

$$H_f=p_{D/I}\mathit{log}\frac{1}{p_{D/I}}+p_{ND/I}\mathit{log}\frac{1}{p_{ND/I}}+p_{ND/NI}\mathit{log}\frac{1}{p_{ND/NI}}+p_{D/NI}\mathit{log}\frac{1}{p_{D/NI}}$$

(6)

In the case of the mentioned ideal protection, Equation (6) results in zero when the probabilities $p_{D/I}$ and $p_{ND/NI}$ are equal to one. Moreover, entropy will be maximum when the probabilities are equal, thus generating the highest uncertainty regarding the protection behavior when it evaluates an event. On the other hand, a ‘worst’ ideal protection system, in terms of its sensitivity and stability, will have a probability of success of zero for detecting islands when it actually occurs (corresponding to non-sensible protection) or a probability of success of zero for not detecting false islands when other events occur (corresponding to non-stable protection). In these two new ideal situations, there is no uncertainty, similar to the first ideal protection, as there is no doubt about the protection behavior when the protection evaluates a known event (islanding or not). However, the latter is not entirely true, as from the protection’s perspective, when it has operated, it is not known what event triggered it (islanding or not).

To determine the uncertainty over the point of view of the anti-islanding protection, it is necessary to analyze the backward probability scheme depicted in Figure 2. Two new events related to the first are defined. The first event involves triggering the protection (T), while the second involves not triggering it (NT).

The probabilities associated with these events are known as posterior probabilities, and they can be determined using Equation (7):

$$\left[\begin{array}{c}{p}_T\\ p_{NT}\end{array}\right]=\left[\begin{array}{cc}{p}_{D/I}& p_{D/NI}\\ p_{ND/I}& p_{ND/NI}\end{array}\right]\left[\begin{array}{c}{p}_I\\ p_{NI}\end{array}\right]$$

(7)

The matrix equation (Equation (7)) calculates the probabilities of the events, triggering the protection and not triggering it, based on the confusion matrix. It is to be noted that this matrix is made up of the set of forward probabilities described above: {$p_{D/I}$; $p_{ND/I};p_{D/NI}$; $p_{ND/NI}$}. In this way, to calculate the backward entropy, it is necessary to determine the set of backward probabilities illustrated in Figure 2. The backward probabilities can be determined as follows:

$$p_{I/T}=\frac{p_I·p_{D/I}}{p_T}=\frac{p_I·p_{D/I}}{p_I·p_{D/I}+p_{NI}·p_{D/NI}}$$

(8)

$$p_{NI/T}=\frac{p_{NI}·p_{D/NI}}{p_T}=\frac{p_{NI}·p_{D/NI}}{p_I·p_{D/I}+p_{NI}·p_{D/NI}}$$

(9)

In Equations (8) and (9), the probability that an islanding event and an event of no islanding have triggered the protection, i.e., $p_{I/T}$ and $p_{NI/T}$, are calculated respectively. Each of these probabilities is calculated as the forward probability of triggering the protection by an islanding event and an event of no islanding, respectively, divided by the total probability of triggering it. Similarly, when the protection does not trigger:

$$p_{I/NT}=\frac{p_I·p_{ND/I}}{p_{NT}}=\frac{p_I·p_{ND/I}}{p_I·p_{ND/I}+p_{NI}·p_{ND/NI}}$$

(10)

$$p_{NI/NT}=\frac{p_{NI}·p_{D/NI}}{p_{NT}}=\frac{p_{NI}·p_{D/NI}}{p_I·p_{ND/I}+p_{NI}·p_{ND/NI}}$$

(11)

In Equations (10) and (11), the probabilities of an islanding event and an event of no islanding not triggering the protection are calculated, respectively.

$$H_b=p_{I/T}\mathit{log}\frac{1}{p_{I/T}}+p_{NI/T}\mathit{log}\frac{1}{p_{NI/T}}+p_{I/NT}\mathit{log}\frac{1}{p_{I/NT}}+p_{NI/NT}\mathit{log}\frac{1}{p_{NI/NT}}$$

(12)

In Equation (12), the backward entropy is determined similarly to forward entropy.

$$H_{protection}=H_f+H_b$$

(13)

Finally, in Equation (13), the total entropy (entropy of the protection) is obtained by adding the backward entropy and the forward entropy. The forward entropy depends on a set of probabilities where only two are independent variables. On the other hand, the backward probabilities rely solely on the forward probabilities, as stated in Equation (7). It is possible to express the entropy of the protection in terms of the forward success probabilities, $p_{D/I}$ and $p_{ND/NI}$. This allows defining an uncertainty surface based on these probabilities, as shown in Figure 3.

Once the uncertainty of the protection has been modeled using entropy, it is possible to determine its minimums. In Figure 3, it is observed that the entropy has two local minimums when both forward success probabilities ($p_{D/I}$ and $p_{ND/NI}$) tend to be one or zero. When both success probabilities tend to zero there is no uncertainty about the performance of the protection, since this protection never would act and this constitutes a particular mathematical case. Furthermore, it has two additional local minimums when one probability tends to zero and the other to one. The reaching of the referred local minimums means that the protection has low stability or low sensitivity.

Ideal Anti-Islanding Protection Model

The commonly employed electrical quantities in passive anti-islanding protection include frequency, RoCoF, voltage vector shift (also called vector surge or vector jump), and voltage magnitude. However, it is also possible to utilize other magnitudes measured at the PCC, as suggested in the existing literature on anti-islanding protections. To achieve generalization, the selected signal for island detection will be treated as a ‘feature’ signal, i.e., a general mathematical signal without necessary correspondence to a physical quantity. Figure 4b evaluates a generic feature signal over time. The protection would trip if a disturbance caused this signal to deviate outside the defined pickup ($pk$) calibration during the time-delay ($td$) settings. In this work, a mathematical idealization of the anti-islanding protection is employed. Thus, anti-islanding protection is treated as an idealized element that extracts a feature based on phase voltages at the PCC and assesses whether this characteristic complies with the trip criteria defined by the time-delay ($td$) and pickup ($pk$). A block diagram of the proposed model is presented in Figure 4a.

The protection setting defines a region that can be interpreted as the minimum detection energy $e_d$ that the signal must exceed to trigger the anti-islanding protection, as presented in Figure 4b. Suppose the calibration is adjusted very close to the normal operating values of the feature signal. In that case, the probability of the anti-islanding protection detecting islanding events $p_{D/I}$ will inevitably increase. Nevertheless, as a trade-off, the probability of not detecting false islands $p_{ND/NI}$ would decrease; thus reducing the protection entropy.

According to the simplification proposed in the anti-islanding protection model, the probability of detecting islands will depend only on the setting made for the protection. Unfortunately, there is no deterministic relationship between the calibration of the protection time-delay $td$ and pickup $pk$ setting and its probability of detecting events, and therefore the protection entropy defined by Equation (13). However, it is possible to establish an incremental relationship with the concept of detection energy presented in Figure 4b. When the detection energy increases, it becomes less likely to detect islands because more significant disturbances in the selected feature will be required for detection. Conversely, if the detection energy decreases, there is a higher probability of triggering incorrect protection responses to other disturbances. Finally, if the pickup and time-delay were made to vary, it would be possible to explore the entropy surface presented in Figure 3, but depending on the protection settings.

3. Bayesian Methodology for Forward Success Probability Calculation

To calculate the protection entropy, it is initially necessary to know the forward success probabilities $p_{D/I}$ and $p_{ND/NI}$. If a frequentist estimation approach were employed, it would be essential to conduct a substantial number of simulations over a wide range of scenarios by the central limit theorem. Using high sampling rates in this context often results in a significant computational burden. Bayesian inference is more efficient in terms of the amount of data required than the frequentist estimation. This allows estimation of the probabilities without iterating through many simulated cases. To perform a Bayesian inference calculation, defining the statistical experiment employed to estimate the forward probabilities is necessary.

3.1. Definition of the Statistical Experiment for Probabilities Estimation

To define the statistical experiment, islanding detection will be treated as a Bernoulli trial, where the probability of success ‘p’ represents successful detection and the probability of failure ‘q = 1 − p’ denotes unsuccessful detection. These probabilities are intricately linked to the feature selected to detect islands and protection settings. Furthermore, the following key considerations must be taken into account:

• There are an infinite quantity of possible cases of islanding and events of no islanding. A random sample of cases is taken with a uniform probability distribution, and the sample size is $n_i$ and $n_{ni}$ cases, respectively.
• The experiment will consist of testing the protection performance for each case with a particular fixed setting for time delay ($td$) and pickup $(pk$). Each case will be considered a one-off trial, like throwing a dice, resulting in success or failure. The probability of success will remain constant from one trial to another, as the parameters of the protection setting will not be modified after each trial.
• The experiment will be conducted in two distinct populations: firstly, for the subset of islanding formation cases, and secondly, for the subset of events of no islanding cases, ensuring independence. For the set of islanding events, the population probability of success will be the probability $p_{D/I}$. In the same way, for the set of events of no islanding cases, the population probability of success will be the probability $p_{ND/NI}$.
• Based on the previous considerations, the probability of achieving ‘x’ successes for specific anti-islanding protection with a success population probability on a sample of $n_i$ and $n_{ni}$ island events can be calculated as follows:

  $$f\left(x_1,n_i,p_{D/I}\right)=\left(\genfrac{}{}{0pt}{}{n_i}{x_1}\right)·{\left(p_{D/I}\right)}^{x_1}·{\left(1-p_{D/I }\right)}^{n_i-x_1}$$

  (14)

  $$f\left(x_2,n_{ni},p_{ND/NI}\right)=\left(\genfrac{}{}{0pt}{}{n_{Ni}}{x_2}\right)·{\left(p_{ND/NI}\right)}^{x_2}·{\left(1-p_{ND/NI }\right)}^{n_{ni}-x_2}$$

  (15)

Equation (14) represents the binomial model used to calculate the probability of obtaining $x_1$ success in a sample of $n_i$ trials with a success population probability $p_{D/I}$. Similarly, Equation (15) is used for obtaining $x_2$ success on a sample of $n_{ni}$ trials with a success population probability $p_{ND/NI}$. These statistical probability models will be used to estimate the population success probabilities mentioned above.

3.2. Bayesian Inference for Forward Success Probabilities

Bayesian inference [53,54] represents a compelling alternative in scenarios where limitations arise regarding data availability or required computational time. This approach offers valuable prospects for addressing such constraints, allowing for robust statistical inference even under restricted data conditions or when computational resources are limited. The parameter to be estimated is denoted as ${\theta }_j$ and represents, on the statistical experiment defined above, the probability $p_{D/I}$ and $p_{ND/NI}$ of success in both populations (island events and no-island events). To estimate this parameter, a non-informative prior probability distribution of ${\theta }_j$ will be used:

$$\pi \left({\theta }_j\right)=1=\frac{\Gamma ({\alpha }_0+{\beta }_0)}{\Gamma \left({\alpha }_0\right)\Gamma \left({\beta }_0\right)} {\theta }_j^{{\alpha }_0-1}·{\left(1-{\theta }_j\right)}^{{\beta }_0-1}$$

(16)

Equation (16) is the uniform distribution for $0<{\theta }_j<1$, but it actually has a beta distribution with parameters ${\alpha }_0=1$ and ${\beta }_0=1$. If the previously described experiment is repeated $m$ times, after observing the successful cases, the probability of their occurrence according to the binomial model presented in Equations (14) and (15) is given as follows:

$$f\left(x_{j1,},x_{j2},\cdots ,x_{jm}/{\theta }_j\right)\propto {\theta }_j^{m\overline{x}}·{\left(1-{\theta }_j\right)}^{m(n_j-\overline{x})}$$

(17)

Equation (17) denotes that the distribution for obtaining a successful set of $X=\left\{x_{j1,},x_{j2},\cdots ,x_{jm}\right\}$ in $m{·n}_j$ trials, where $n_j$ represents the size of the sample obtained from the population $j$ of islands or no-island events, is proportional to a beta distribution with parameters ${\alpha }_1+1=m\overline{x}$ and ${\beta }_1+1=m(n-\overline{x})$. With the previously defined uniform prior distribution, the posterior distribution will be:

$$\pi \left({\theta }_j/x_{j1,},x_{j2},\cdots ,x_{jm}\right)\propto {\theta }_j^{m\overline{x}}·{\left(1-{\theta }_j\right)}^{m\left(n_j-\overline{x}\right)}· {\theta }_j^{{\alpha }_0-1}·{\left(1-{\theta }_j\right)}^{{\beta }_0-1}$$

(18)

Equation (18) is the posterior distribution of ${\theta }_j$ and it is a beta distribution with parameters ${\alpha }_2=m\overline{x}+{\alpha }_0$ and ${\beta }_2=m\left(n-\overline{x}\right)+{\beta }_0$. Considering this posterior distribution, the mean is given for:

$${\theta }_j^{*}=E\left({\theta }_j/X\right)=\frac{{\alpha }_2}{{\alpha }_2+{\beta }_2}=\frac{m\overline{x}+1}{m·n_j+2}$$

(19)

Equation (19) is the Bayes estimate of ${\theta }_j$ under the squared-error loss function. This result allows for point estimation of forward population success probabilities based on a fixed anti-islanding setting.

The methodology for estimating success probabilities and entropy calculation can be summarized using the flowchart in Figure 5. Datasets of islanding and events of no islanding of size $n_i$ and $n_{ni}$ are respectively formed, and simulations are conducted using DIgSILENT Power Factory 2018 SP3. Then, with each simulation, the experiment is performed to verify whether the tested anti-islanding protection model detects the event, counting the successful cases using MATLAB R2021a. This process is repeated until all events in the obtained dataset are verified. Once these results are obtained, Equation (19) can be used to find point estimators for the success probabilities. Finally, it is possible to calculate the entropy of the protection using Equation (13).

3.3. Entropy of the Experiment

The methodology presented for estimating probabilities involves associated uncertainty. It is possible to employ the uncertainty model, as presented in Equation (13), to measure the uncertainty associated with the experiment used to estimate the probabilities. If the tested protection were a perfect ideal protection, it would always be tripping when testing an islanding formation case and never tripping erroneously when testing a no islanding formation case.

$${{\theta }_j^{*}}_{MAX}=\frac{m\overline{x}+1}{m·n_j+2}=\frac{m·n_j+1}{m·n_j+2}$$

(20)

Equation (20) represents the maximum achievable probability estimate if the tested protection were perfect. Under this consideration, the average of success $\overline{x}$ matches the number of trials (sample size resulting: $\overline{x}=n_j$. When the experiment is performed only once ($m=1$), the point estimates of forward success probabilities can be obtained as follows:

$$\left\{\begin{array}{c}{p_{D/I}^{*}}_{MAX} =\frac{n_i+1}{n_i+2}\\ {p_{ND/NI}^{*}}_{MAX}=\frac{n_{ni}+1}{n_{ni}+2}\end{array}\right.$$

(21)

Equation (21) presents a set of maximum probabilities that only depend on the sample size, depending on how the statistical experiment is defined. By utilizing the set of probabilities from Equation (21), it becomes possible to determine the minimum achievable entropy through a specific experiment using Equation (13). This conclusion holds tremendous significance when aiming to minimize the uncertainty of the protection, as it represents the lowest conceivable level of uncertainty that can be calculated for a given experiment.

4. Power System and Datasets of Events

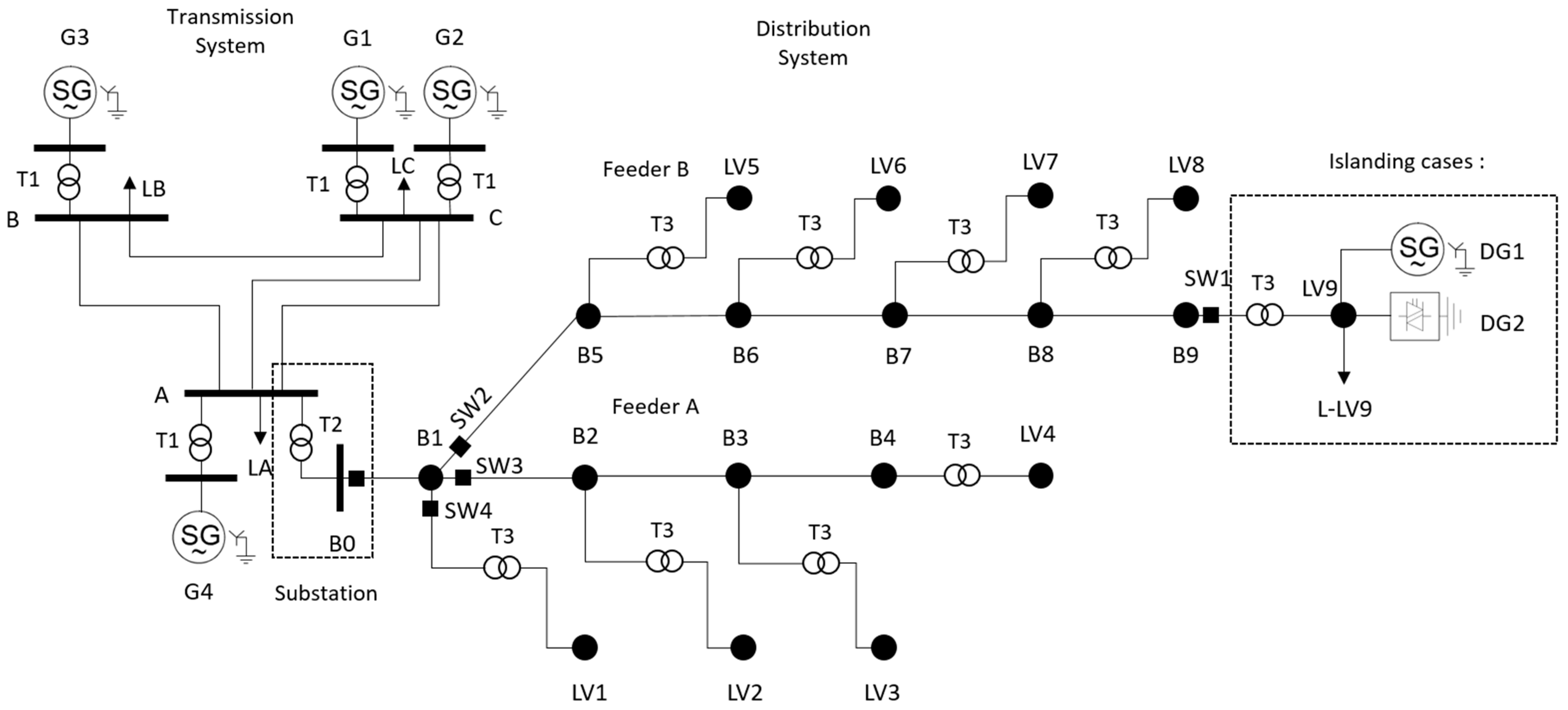
4.1. Test System

The test system used in this work is shown in Figure 6 as a single-line diagram. The transmission system is designed to replicate the essential characteristics of a larger-scale power network, allowing for accurate simulations of various system disturbances. It consists of a three-bus configuration, representing the interconnected nature of power grids, and operates at a voltage level of 132 kV. Each generator was modeled as a steam turbine-governor model IEEE G1, while the automatic voltage regulator (AVR) was modeled using the IEEE T1 model available in the DIgSILENT Power Factory SP3 libraries. Finally, given the simulations conducted, no power system stabilizer (PSS) was considered for the generator models. On the other hand, the distribution system included in the test system incorporates two feeders operating at 13.2 kV. It represents the radial distribution network typically found in real-world distribution systems. In Appendix A,

Table A1. 132 KV transmission power lines.

Line	Type	Length	${\mathit{R}}_{\mathrm{1,2}}$	${\mathit{X}}_{\mathrm{1,2}}$
A-B	OHL-Δ	90 Km	0.2533 Ω/Km	0.436 Ω/Km
B-C	OHL-Δ	220 Km	0.2533 Ω/Km	0.436 Ω/Km
A-C (1)	OHL-Δ	1 Km	0.2533 Ω/Km	0.436 Ω/Km
A-C (2)	OHL-Δ	1 Km	0.2533 Ω/Km	0.436 Ω/Km

,

Table A2. Synchronous generators.

Generator	${\mathit{S}}_{\mathit{N}}$ [MVA]	Voltage [kV]	Connection	${\mathit{H}}_{\mathit{S}\mathit{g}\mathit{n}}$ [s]
G1 (Ref.)	210	15.75	YN	7.34
G2	46.55	10.5	YN	6.92
G3	210	15.75	YN	7.34
G4	46.55	10.5	YN	6.92

,

Table A3. 13.2 KV feeder A distribution lines.

Line	Type	Length	${\mathit{R}}_{\mathrm{1,2}}$	${\mathit{X}}_{\mathrm{1,2}}$
B0-B1	Cable-Δ	2 Km	0.1281 Ω/Km	0.09424 Ω/Km
B1-B2	Cable-Δ	3 Km	0.1281 Ω/Km	0.09424 Ω/Km
B2-B3	Cable-Δ	5 Km	0.1281 Ω/Km	0.09424 Ω/Km
B3-B4	Cable-Δ	2 Km	0.1281 Ω/Km	0.09424 Ω/Km

,

Table A4. 13.2 KV feeder B distribution lines.

Line	Type	Length	${\mathit{R}}_{\mathrm{1,2}}$	${\mathit{X}}_{\mathrm{1,2}}$
B1-B5	Cable-Δ	10 Km	0.1281 Ω/Km	0.09424 Ω/Km
B5-B6	Cable-Δ	2 Km	0.1281 Ω/Km	0.09424 Ω/Km
B6-B7	Cable-Δ	10 Km	0.1281 Ω/Km	0.09424 Ω/Km
B7-B8	Cable-Δ	8 Km	0.1281 Ω/Km	0.09424 Ω/Km
B8-B9	Cable-Δ	12 Km	0.1281 Ω/Km	0.09424 Ω/Km

and

Table A5. DERs at bus LV9.

DER	${\mathit{S}}_{\mathit{N}}$ [MVA]	Voltage [kV]	Connection	${\mathit{H}}_{\mathit{S}\mathit{g}\mathit{n}}$
DG1	0.2	0.22	YN	4
DG2	0.5	0.22	YN	0

, the parameters of the power system are presented.

4.2. Islanding Samples Dataset

The set of islanding scenarios was generated through electromagnetic transient (EMT) simulations in DIgSILENT Power Factory 2018 SP3 by opening SW1 at 0.25 s in the diagram presented in Figure 6. According to these considerations, the island must be detected at the latest by time t = 2.25 to comply with the 2-s requirement established in the IEEE 1547 Standard [8]; for this reason, the simulations of islanding cases were conducted for a total duration of 2.5 s. Three datasets of distinct cases were considered, each constraining the demand and generation imbalance of the cases within different thresholds, as detailed in

Table 1. Islanding scenarios datasets.

Name	${\mathit{n}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{D}\mathit{G}\mathbf{1}} \mathbf{\left[}\mathbf{M}\mathbf{W}\mathbf{\right]}$	${\mathit{Q}}_{\mathit{D}\mathit{G}\mathbf{1}} \mathbf{\left[}\mathbf{M}\mathbf{V}\mathbf{a}\mathbf{r}\mathbf{\right]}$	${\mathit{P}}_{\mathit{D}\mathit{G}\mathbf{2}} \mathbf{\left[}\mathbf{M}\mathbf{W}\mathbf{\right]}$	${\mathit{Q}}_{\mathit{D}\mathit{G}2} \mathbf{\left[}\mathbf{M}\mathbf{V}\mathbf{a}\mathbf{r}\mathbf{\right]}$	${\mathit{P}}_{\mathit{l}\mathit{o}\mathit{a}\mathit{d}} \mathbf{\left[}\mathbf{\%}\mathbf{\right]}$	$\mathit{P}\mathit{F}$
Islanding 30%	30	0.15	0.1	[0;0.15]	[0;0.15]	[70%;130%]	0.85
Islanding 50%	30	0.15	0.1	[0;0.15]	[0;0.15]	[50%;150%]	0.85
Islanding 150%	30	0.15	0.1	[0;0.15]	[0;0.15]	[0;150%]	0.85
Validation: (Islanding 150%)	100	0.15	0.1	[0;0.15]	[0;0.15]	[0;150%]	0.85

. Additionally, a distinct validation dataset of 100 cases was calculated. Each case in the datasets outlined in Table 1 was generated using a specifically programmed DIgSILENT Power Factory 2018 SP3 Programming Language (DPL) script. The aim was to generate each case as randomly as possible to ensure statistical robustness to validate BEM. To achieve this, synchronous generation power values ($P_{DG1}$ and $Q_{DG1}$) were fixed for each simulated case, as detailed in Table 1. Conversely, renewable generation powers ($P_{DG2}$ and $Q_{DG2}$) were randomly determined within the specified range in Table 1, and using uniform probability, distribution demand powers were also randomly assigned within a percentage range relative to the island’s total generation. This approach guarantees randomness in the analyzed scenarios but confines cases to a specific percentage range. For instance, in the Islanding 150% dataset, island cases can only have a $∆P_{island}$ imbalance ranging from −50% to 100%, meaning the demand can randomly be 50% higher or 100% lower than the total generation in the island.

4.3. Disturbances Samples Dataset (Events of No Islanding)

The set of events of no islanding cases was divided into two scenarios. The first scenario focused on random adjacent faults at the LV9 node within the distribution system. The location of these faults, especially their proximity to LV9, and the likelihood of their occurrence play a crucial role in determining the optimal thresholds to set anti-islanding protections. Faults occurring further away result in less severe disturbances, which in turn allows for setting thresholds closer to the nominal values with minimal entropy. To simulate a realistic scenario, a DPL script was employed to randomly select both the type of fault and its location. Each fault simulation was set to occur at t = 0.25 s, with a random clearing time between 30 ms and 45 ms. Additionally, the demand and generation parameters of the DG connected to the LV9 bus were generated using the same random logic as for the islanding cases. This comprehensive approach ensures a realistic representation of fault scenarios in the network. In the second scenario, synchronous generators from the three-bus transmission system, presented in Figure 6, were randomly disconnected as detailed in

Table 2. Disturbance scenarios datasets.

Name	${\mathit{n}}_{\mathit{n}\mathit{i}}$	Simulation Time	Events	Location	EPS Generation
Distribution Faults	30	2.5 s	1/2/3-Ph.ShortCircuit	B1;B2;B3;LV4 LV5;LV6;LV7;LV8	-
Validation Distribution Faults	100	2.5 s	1/2/3-Ph.ShortCircuit	B1;B2;B3;LV4 LV5;LV6;LV7;LV8	-
EPS Disturbances	30	10.5 s	G2;G3;G4 trips	-	[1; 5]%
Validation EPS Disturbances	100	10.5 s	G2;G3;G4 trips	-	[1; 5]%

. The demands at each bus of the transmission system were randomly assigned between 50 and 90 MW of active power and between 10 and 50 MVar of reactive power using DPL scripts. In each generator tripping case, a frequency response occurred in the test system. Since anti-islanding protections must exhibit stable behavior throughout the frequency response, the simulation time was set at 10.5 s, considering it a success if the anti-islanding protection did not trip during the entire frequency transient.

4.4. Minimum Achievable Entropy for the Defined Datasets

In this section, we discuss the attainable minimum entropy as a function of the defined experiment. According to the diagram presented in Figure 5 and the dataset sizes defined in the previous section, to calculate the entropy for a particular set of calibrations $t{d}_0$ and $k_0$, the number of successes must be counted when testing the protection in both the island dataset and events of no islanding datasets. This results in a total of 60 tests (30 + 30). However, since distribution systems are typically unbalanced, as in the distribution faults dataset, with asymmetric faults considered detection in each electric phase at PCC is considered a new repetition of the experiment. This means for each of the 60 cases, the experiment is repeated three times, once for each phase, leading to the consideration of $m=3$ in the expression of Equation (20). Thus, the following maximum probabilities can be obtained:

$$\left\{\begin{array}{c}{p_{D/I}^{*}}_{MAX} =\frac{3\times 30+1}{3\times 30+2}=0.9891\\ {p_{ND/NI}^{*}}_{MAX}=\frac{3\times 30+1}{3\times 30+2}=0.9891\end{array}\right.$$

(22)

In Equation (22), the calculated probabilities represent the maximum visible success probability for the experiment. This implies that even if an ideally perfect protection system with unitary probabilities were tested, it could not be measured accurately due to the inherent uncertainty of the experiment. For the experiment defined according to the datasets and previous considerations, the following minimum entropy is given by:

$$H_{min}(n_i=30,n_{ni}=30,m=3)=0.34602$$

(23)

The minimum entropy value indicated in Equation (23) represents the maximum uncertainty that a particular calibration generating this value might have. It is possible that a configuration with $t{d}_i$ and $p{k}_i$ could have even less uncertainty. However, to quantify it, the experiment would need to be redefined by adding more cases randomly taken from the test system, i.e., expanding the size of the datasets. Regardless, achieving minimum uncertainty ensures that the success probabilities will be between one and those indicated in Equation (22).

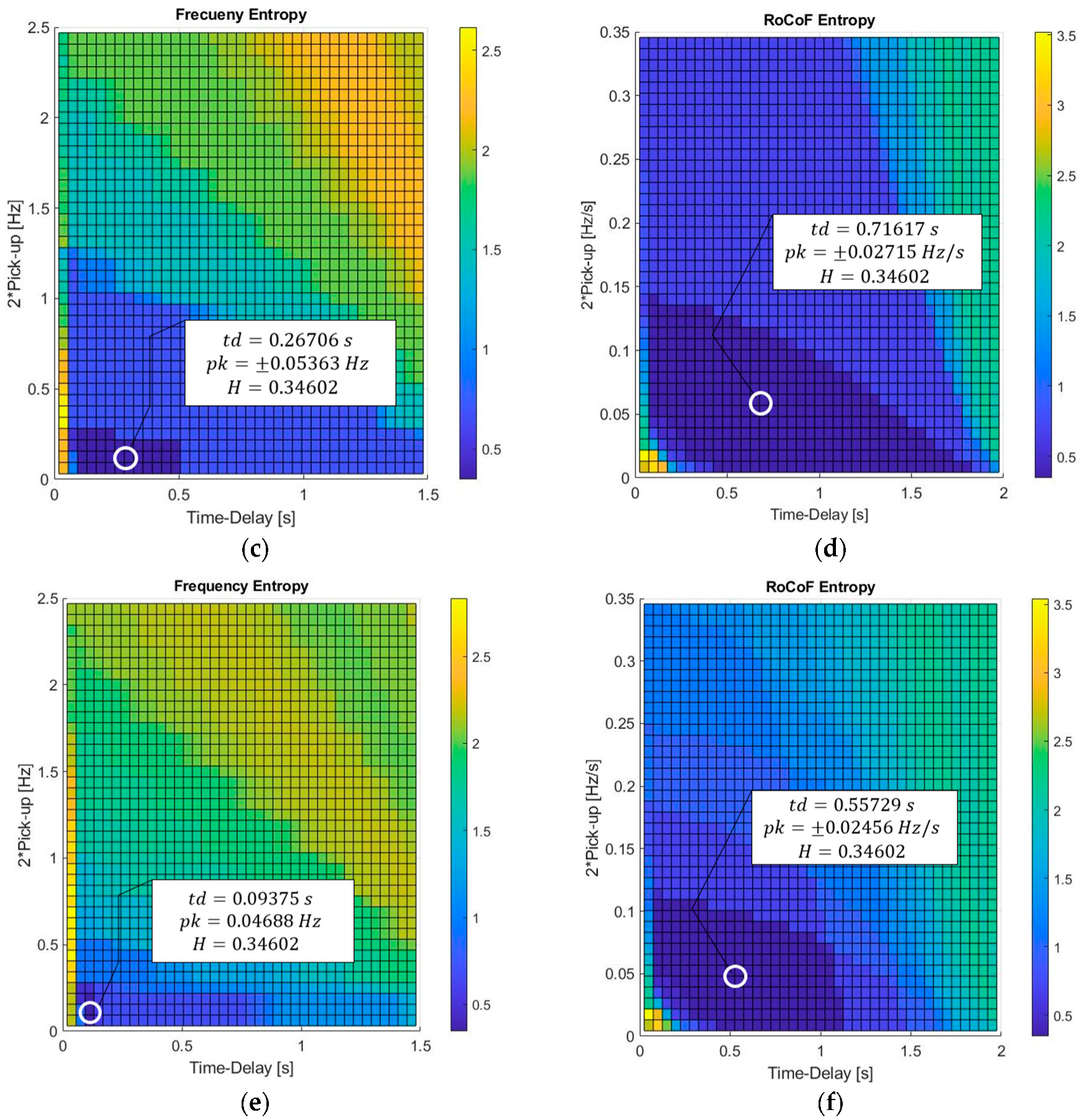
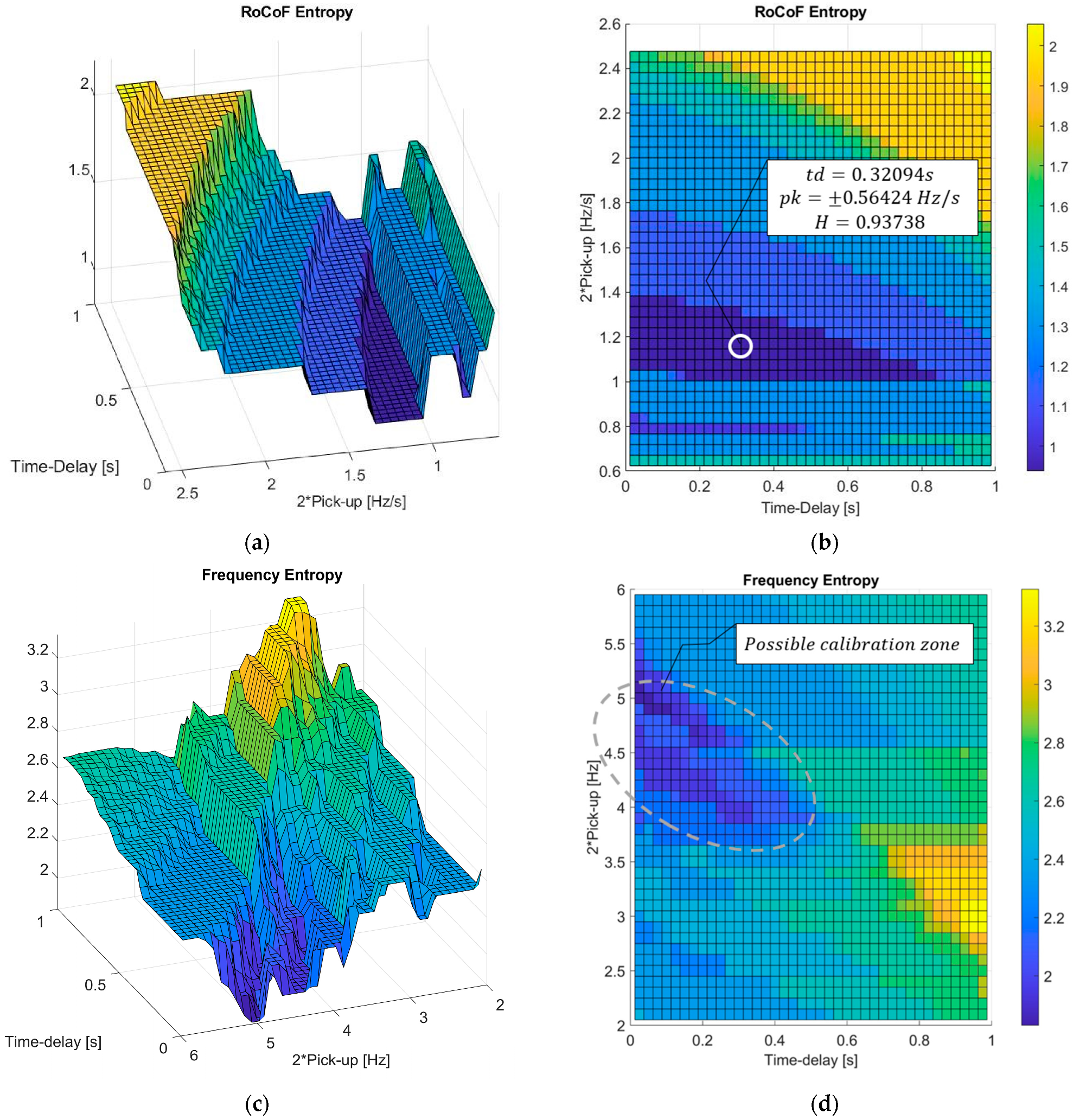
5. Results

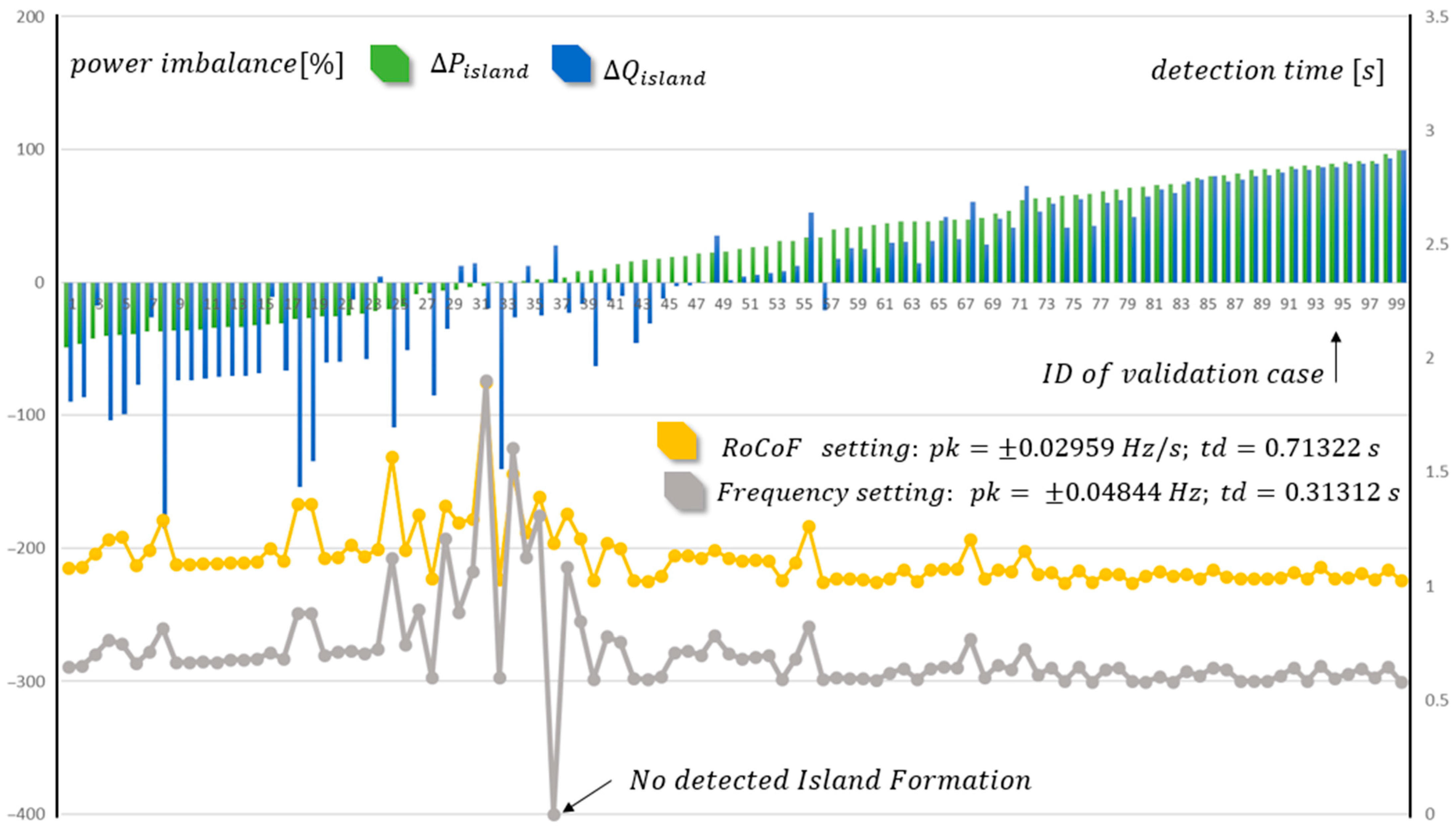
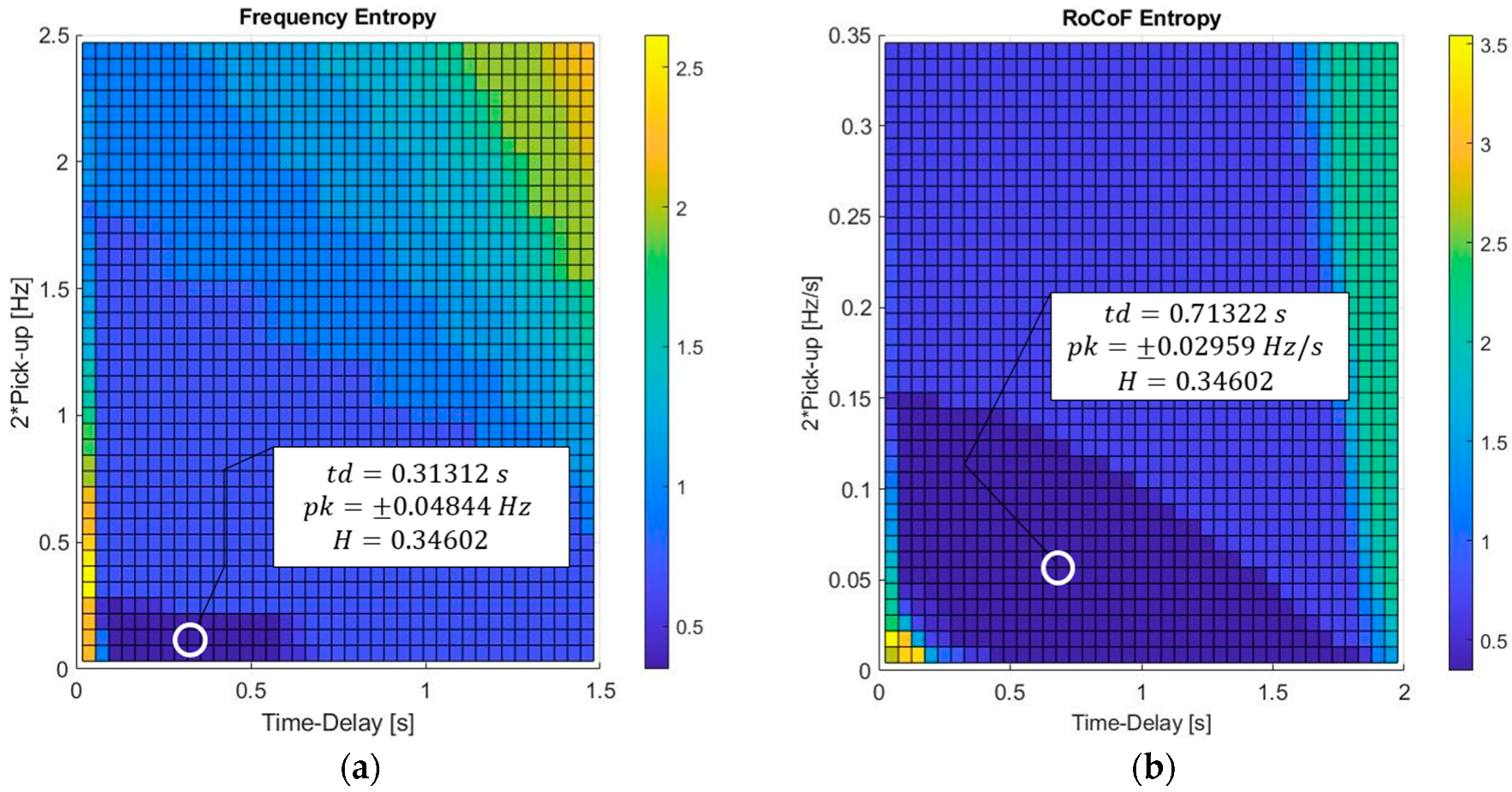
5.1. Entropy Surface Exploration, Minimal Entropy Settings and Validation Instances

To explore the probability surface depicted in Figure 3, a MATLAB-based algorithm was implemented following the flowchart shown in Figure 5. This algorithm enabled the calculation of point-wise entropy. It was executed multiple times for an array of time delay and pickup configurations, aiming to investigate the entropy surface concerning the protection calibration variables, $td$ and $pk$. The features selected to conduct simulations and test the proposed BEM were RoCoF and frequency at PCC. Figure 7a,b present the entropy surfaces calculated using the islanding 150% dataset versus the distribution faults dataset.

For both entropy surfaces presented in Figure 7, it is notable that entropy (uncertainty) reaches a minimum floor, thus establishing regions of minimum entropy (the minimum entropy visible in the experiment). The surfaces presented in the preceding figure differ in shape from the surface shown in Figure 3, but not in coherence. In Figure 3, the entropy surface is presented as a function of the probabilities $p_{D/I}$ and $p_{ND/NI}$. This surface is based on a deterministic relationship given by Equation (13). The entropy surfaces in Figure 7a,b are functions of the variables $td$ and $pk$; this relationship is non-deterministic, unlike the former. Moreover, the relationship between entropy and the variables $td$ and $pk$ could be different for different features used to detect islanding. In the case of the frequency entropy surface, Figure 7a, it is observed that the region of minimum entropy is smaller than the minimum entropy region calculated for the RoCoF relay. Within each of these regions, it is possible to define any calibration point and ensure that the entropy over that calibration is, at most, the minimum entropy value of the experiment. Figure 3 provides the necessary theoretical support for interpreting the obtained results. Based on the analysis conducted for Figure 3, it can be inferred that since the minimum regions found in Figure 7a,b are less than two, the presence of local minima associated with low stability or sensitivity, as mentioned earlier, can be ruled out. Attaining entropy equal to two implies that with the selected feature for island detection, achieving an optimal calibration threshold that maximizes stability and sensitivity is not feasible.

It remains to be deduced which of the remaining two local minima analyzed in Figure 3 corresponds to the regions of minimum entropy found; this can be achieved by examining the probability surfaces associated with the entropy surface. The estimated probability surfaces $p_{D/I}^{\mathrm{*}}(pk,td)$ and $p_{ND/NI}^{\mathrm{*}}(pk,td)$ were plotted as a function of $td$ and $pk$, as shown in Figure 8. These probability surfaces correspond to the frequency feature, i.e., they are associated with Figure 7a. It can be observed that where the entropy becomes minimal, the estimated probability surfaces tend towards one, allowing us to rule out the association of the region of minimum uncertainty with the local minimum presented in Figure 3 associated with probabilities tending towards zero.

Finally, since the found minima entropy region is associated with the adequate local minima presented in Figure 3, and there is a logical relationship between the calibration value and the probability of detecting events, the centroid of the geometric region defined on the entropy surfaces was chosen as the optimal compromise point for calibrating the protection. The setting results for these centroids and the achieved entropy obtained considering the islanding 150% dataset are also presented in Figure 7.

A validation instance was conducted to assess the time delay and pickup configuration of the minimum entropy obtained. Figure 9 shows the results of evaluating the sensitivity of the RoCoF and frequency-based protection models on the validation dataset presented in Table 1. The islanding cases were arranged based on the level of active power imbalance. For the RoCoF-based IDM, island creation was successfully detected in all 100 evaluated cases. In contrast, for the frequency-based IDM, the island was detected in 99 out of 100 cases. It is noteworthy that despite failing in one case, the probability of detecting islands still fell between one and the maximum probability as indicated in Equation (22). A notable increase in detection time was observed as the active and reactive power imbalances in the island approached zero. This is where it is expected to be found for RoCoF and FVT NDZ [15,35]. Furthermore, the stability of the minimal entropy settings, presented in Figure 7, was assessed using the validation distribution faults dataset detailed in Table 2. For both feature-based IDMs analyzed, none of the 100 cases in the set were erroneously detected. This confirms the proper stability against such disturbances for the calculated setting employing BEM.

In Figure 10, the records of the calculated frequency and RoCoF features in phase ‘a’ are presented for one of the worst-case scenarios encountered in the islanding validation dataset. Furthermore, the threshold detection result is shown; the trip signal is activated, indicating the detection time. Similarly, in Figure 11, the three-phase records of the calculated frequency and RoCoF features are presented for one of the worst cases encountered in the distribution faults validation dataset. The fault corresponds to an adjacent fault to node LV9. In the records presented in Figure 11, it can be observed how the disturbance repeatedly violates the thresholds but fails to trip the protection. Additionally, this figure illustrates how different magnitudes of disturbances are observed in the various phases, due to the asymmetric nature of the analyzed fault.

5.2. Sensitivity Analysis: Islanding Datasets Comparison

This section compares the different island datasets presented in Table 1 to analyze the effect of restricting the maximum and minimum possible power imbalances in the scenario on the entropy of the settings. For this purpose, the entropy surface results for RoCoF and frequency relays are presented. Figure 12a,b display the entropy surfaces for the Islanding 150% dataset and the Distribution Faults dataset. These surfaces are compared to those presented in Figure 12c,d, depicting the entropy surfaces for the Islanding 50% datasets, and in Figure 10e,f, corresponding to the Islanding 30% scenarios. Additionally, in each of these figures, the minimal entropy settings considering the centroid of the minimum entropy region are indicated in the figure and the associated entropy.

The comparative analysis of the regions of minimum entropy shown in Figure 12 reveals that reducing the maximum and minimum thresholds for possible power imbalance cases in each dataset, within the islanding scenario samples as presented in Table 1, results in a decrease in the minimal region of the entropy surface. This outcome aligns with the anticipated behavior of relays based on RoCoF and frequency. Specifically, as the probability increases that the cases align with the NDZ, the likelihood of detecting the island diminishes for the various settings (time-delay and pickup) tested in the statistical experiment. Consequently, this outcome contributes to an increase in entropy. Based on this result, in Figure 12, it can be observed that as the percentage of imbalance between demand and maximum generation is constrained within the dataset, the minimum entropy adjustments tend to decrease both in their time-delay and pickup adjustment values.

5.3. Stability against Tranmission System Disturbances Analysis

As presented in the introduction of the work, anti-islanding protections must avoid false trips when disturbances occur in the transmission system. Unstable behavior of anti-islanding protection can worsen disturbances from EPS. Figure 13 displays the test results for the calculated calibrations in Section 5.1 when a disturbance was simulated on the three-bus transmission system presented in Figure 6. The results specifically focus on the frequency and RoCoF recorded in phase ‘a’, as the recordings from the other phases are almost identical.

The graphs in Figure 13 illustrate the characteristic frequency response of the system when frequency regulation is active. The detection test presented in Figure 13 was conducted over a time interval longer than the duration recommended by the IEEE 1547-2018 standard [8]. This extended duration aims to thoroughly assess the stability of the protection throughout the entire disturbance (the frequency response of the transmission system). However, the activation of the trip signal for the tested settings can be verified, indicating a lack of stability in the face of such disturbances.

To determine a new minimum entropy setting for the described type of disturbances, the entropy surface was recalculated considering the EPS disturbances dataset vs the Islanding 150% dataset. The results for the RoCoF and frequency features are presented in Figure 14. Achieving a region of minimum entropy of less than two proved impossible for the frequency-based detection relay. However, in Figure 14d a possible calibration region is distinguished, even though the entropy is not low enough to ensure a good adjustment.

When considering disturbances in the power system, compared to the region of minimum uncertainty, two crucial differences were noted concerning the surfaces presented in Figure 12. Firstly, the center of the region of minimum entropy shifted; this indicates a higher pickup calibration. Secondly, although acceptable, the entropy value obtained was not the minimum in previous cases. Indeed, it was a higher value, as shown in Figure 14b.

If the surface of forward success probabilities were analyzed, similar to what was calculated in Figure 8, it can be observed that the reduction in entropy would be due to a decrease in the probability of detecting islands. In other words, while the minimum entropy setting in relation to the EPS disturbances dataset reduces the probability of island detection, the minimal entropy settings calculated using BEM are optimal in terms of uncertainty.

To assess the effectiveness of the minimal entropy setting shown in Figure 14b, a comparison was made between the minimal entropy adjustment found using the BEM and the setting indicated in the Engineering Recommendation G83 (ER G83), currently employed in the UK grid code [55]. This setting for RoCoF-based anti-islanding protection (also known as loss of main protection) is $pk=\pm 1 \mathrm{H}\mathrm{z}/\mathrm{s}, td=0.5 \mathrm{s}$. These adjustments were compared with those obtained using BEM: $pk=\pm 0.56424 \mathrm{H}\mathrm{z}/\mathrm{s}, td=0.32094 \mathrm{s}$. Figure 15 presents a comparative graph of detection times in the validation dataset of 100 island cases (in the same order as in Figure 9).

As can be observed in Figure 15, the ER G83 setting failed to detect 32 out of 100 cases in less than 2 s whereas the adjustment calculated using BEM only failed to detect 15 out of 100 cases. These cases correspond to scenarios with $∆P_{island}\approx \pm 10\%,$ falling within the well-known NDZ for this type of IDM [15,35,56]. Furthermore, the detection time in all cases was shorter for the adjustment achieved using BEM compared to ER G83. This evidences an enhanced sensitivity with respect to the setting of ER G83.

In addition, in Figure 16, a detection stability test is presented for RoCoF with the same disturbance as in Figure 13, but with the recalculated settings provided in Figure 14b. The absence of trip signal activation throughout the disturbance can be observed. The same was verified in 100 out of 100 cases of the Validation EPS Disturbances dataset, meaning that the adjustment achieved through the BEM improved sensitivity while maintaining stability.

6. Discussion

This section compares the results obtained with other works published in the literature. The effectiveness of the BEM in enhancing performance and reducing computational burden was evaluated and compared to the most essential works in the field. The comparison was based on the size of the simulation dataset and the minimum entropy achieved. The results are presented in

Table 3. Comparison of simulation dataset size and minimum entropy achieved with that of other islanding detection works.

Work	IDM	Dataset Size	${{\mathit{p}}_{\mathit{D}/\mathit{I}}^{\mathbf{*}}}_{\mathit{M}\mathit{A}\mathit{X}}$	${{\mathit{p}}_{\mathit{N}\mathit{D}/\mathit{N}\mathit{I}}^{\mathbf{*}}}_{\mathit{M}\mathit{A}\mathit{X}}$	Equivalent Achievable Entropy
Current Work: (BEM)	RoCoF	60	0.9891	0.9891	0.34602
Setting Map Methodology (SMM) [47,48]	RoCoF	4606	0.9781	0.9902	0.4568
Pattern Recognition Approach [41]	Wavelet Decision Tree classifier	2091	0.9765	0.9520	0.8752
Wavelets and Deep Learning Methodology (WDLM) [42]	Wavelet Deep Learning	2046	0.9891	0.9855	0.3915
Reliable Islanding Detection Scheme (RIDS) [43]	Modified Intrinsic Mode Functions (MIMF)	720	0.9740	0.9859	0.5672

.

The BEM approach achieved a minimum entropy of 0.34602, signifying a notably low level of uncertainty. This outcome is particularly significant when compared to existing studies. As demonstrated in Table 3, the BEM approach effectively reduces the uncertainty in anti-islanding protection, and it achieves this using much smaller datasets than those used in other works.

7. Conclusions

This work introduces the Bayesian entropy methodology (BEM) for setting anti-islanding protection with improved stability and sensitivity. This methodology enables the optimization of protection systems to make the best decisions possible, ultimately reducing uncertainty and improving the performance of the protection device. Furthermore, BEM effectively overcomes previous limitations such as computational effort, inadequate signal abstraction, and the challenge of analyzing various disturbances in different temporal frameworks. Key achievements of this work include:

• Innovative uncertainty modeling: The use of entropy as a model for protection uncertainty has proved to be a significant advancement. It not only serves as an objective function but also provides a comparative measure for different IDMs based on their minimum achievable entropy.
• Computational efficiency: The employment of Bayesian inference in BEM has considerably reduced computational burdens. This efficiency is evident in the reduced size of datasets required compared to other methods, significantly, ranging between 91% and 98%.
• Signal abstraction: The process of abstracting the signal and its dynamics in island detection involves treating the protection system as a ‘black box’, defining a statistical experiment, and simply counting successes and failures when evaluating a protection system. This level of abstraction has facilitated the computation of minimal settings by comparing islanding cases lasting 2.5 s with disturbances of 10.5 s duration.
• Precise dataset sizing: A novel aspect of BEM is its ability to measure the uncertainty of the statistical experiment itself, allowing for an accurate sizing of the datasets based on success probabilities using the concept of entropy. It has been verified that defining the dataset size with a total of 60 cases enables the achievement of a minimum entropy value of H = 0.34602. This is associated with forward success probabilities ranging between unity and 0.9891. These findings have been appropriately confirmed through validation instances.

Future research efforts may extend the BEM to a broader range of protection systems, including the potential application to any characteristic obtainable at the PCC, encompassing DC systems. Such studies would entail examining how minimal entropy settings could enhance the optimization of various protection systems beyond anti-islanding. Additionally, further research should be conducted to explore additional aspects of the BEM approach and its potential for implementation in real-world power systems, potentially leading to significant advancements in the field of power system protection and reliability.