Abstract
Gas turbines play a key role in generating power. It is really important that they work efficiently, safely, and reliably. However, their performance can be adversely affected by factors such as component wear, vibrations, and temperature fluctuations, often leading to abnormal patterns indicative of potential failures. As a result, anomaly detection has become an area of active research. Matrix Profile (MP) methods have emerged as a promising solution for identifying significant deviations in time series data from normal operational patterns. While most existing MP methods focus on vibration analysis of gas turbines, this paper introduces a novel approach using the outlet power signal. This modified approach, termed Cluster-based Matrix Profile (CMP) analysis, facilitates the identification of abnormal patterns and subsequent anomaly detection within the gas turbine engine system. Significantly, CMP analysis not only accelerates processing speed, but also provides user-friendly support information for operators. The experimental results on real-world gas turbines demonstrate the effectiveness of our approach in the early detection of anomalies and potential system failures.
1. Introduction
One of the main features of Industry [1] is its capacity of gathering real-time operational data. These data can be mined to extract normal or abnormal operation patterns, which can be used to undertake condition monitoring of any industrial process. Therefore, maintenance is a basic task deeply related to the machines’ status, which can be determined by a continuous condition-monitoring process [2]. Predictive maintenance tries to prevent machine failures in advance, usually through the diagnostic analysis of operational data. The diagnosis process commonly involves anomaly detection, which leads to the performance optimization of the machine operation.
Industrial gas turbines are used in several industrial sectors as mechanical power engines, such as in power plants, aerospace, transportation, or off-shore platforms [3]. In this context, gas turbines’ maintenance and performance improvement are key components in industries.
In real-world pattern-recognition applications, the ability to detect and report novel or abnormal events in data are of paramount importance. Due to the broad nature of this task, several other terms with similar meanings have been employed across a range of disciplines, including anomaly detection, intrusion detection, fault detection, condition monitoring, and outlier detection [4,5]. While the specific terminology may vary, the underlying goal remains consistent: to identify and isolate patterns that deviate from the norm and that may indicate a potential threat, fault, or anomaly. Diagnostic process can be performed by a data-driven approach or a model-based approach. In this article, we follow a data-driven approach.
Data-mining techniques have been widely employed across a range of domains to extract relevant knowledge from large datasets, in order to support informed decision-making processes [6]. In particular, increasing attention has been directed towards the application of data-mining techniques for knowledge extraction from time series data—i.e., an ordered set of observations recorded over time pertaining to a particular phenomenon and measured across a defined time span [7,8].
Machine learning is a rapidly evolving research area that provides a suite of algorithms and methods for use in data mining. However, many of these algorithms struggle to effectively analyze temporal and sequential data. In contrast to the natural ordering of time series data, where the likelihood of an observation occurring at a given point in time is influenced by past observations, machine learning algorithms often assume independent and identically distributed data [9]. This can limit their ability to effectively model and interpret time series data. Furthermore, data labeling represents a significant challenge in real-world time series projects, which often require extensive retroactive analysis. In many cases, these tasks are unsupervised, meaning that the data are unlabeled, and the algorithm must identify meaningful patterns and relationships on its own.
The Matrix Profile (MP) technique is a powerful tool for identifying patterns and anomalies in large, complex datasets, particularly in time series data. Compared to other techniques, MP methods offer several unique advantages. For example, the MP is highly scalable, making it ideal for analyzing massive datasets. It is also domain-agnostic, with the length of a subsequence being the only parameter specified by the application programmer. Furthermore, the MP procedure allows for parallel computing and gradual updating, among other advantages [9,10].
In addition to its remarkable efficiency and scalability, the MP possesses numerous other outstanding qualities, making it an extremely versatile technique. One of its most-important features is its extraordinary generality. It is also robust, scalable, simple, and parameter-free [11,12,13,14,15]. Additionally, the MP is space-efficient, an anytime algorithm, and incrementally maintainable [16,17]. The MP algorithm eliminates the need for a similarity threshold or distance to be set by the user, as it achieves constant time complexity in the subsequence distance [18,19]. Moreover, the MP is deterministic in its execution and can be efficiently executed on hardware.
Usually, the MP technique is applied to vibration data gathered from gas turbines [20,21,22,23]. In our proposed approach, we used only the outlet energy signal for the anomaly detection, aiming to simplify the interpretation of the possible discords, i.e., a possible anomalous subsequence or pattern, by the end-user. On the other side, we introduce a Cluster-based Matrix Profile (CMP) algorithm to improve the computational time of MP execution. The use of just one prototype for each cluster of points instead of all the points, at each possible discord, substantially reduces the computational cost spent by the algorithm.
This study aims to discover motifs and discords in time series data collected from a gas turbine [24] using the proposed CMP technique. The remainder of this article is structured in the following manner: Section 2 will outline the definition of the MP method for time series, and specifically for anomaly detection, both mathematically and conceptually, to provide the basis for the new proposed CMP method. Furthermore, other time series discord detection methods are reviewed. In Section 3, a detailed description of our proposed CMP is presented. Section 4 comprises the experimental setup of our gas turbine case study and the results of the work, while Section 5 summarizes the key findings of the study and highlights their significance.
2. Background
In this section, the use of the MP technique in time series, and especially for times series anomaly detection, will be analyzed. Furthermore, the MP method will be detailed and its algorithmic formulation will be introduced. Finally, other time series discord-detection methods will be reviewed, as those techniques have become the most-used methods in time anomaly detection.
2.1. Matrix Profile
In this subsection, we will explore how the MP is applied to time series. We will first discuss its use within time series, followed by a deeper examination of its significance for detecting anomalies within them. In addition, the intricacies of the MP method and its algorithmic underpinnings will be analyzed, providing a comprehensive understanding before moving on to other commonly used time series discord-detection methods.
2.1.1. Matrix Profile in Time Series
A time series motif refers to a repeated pattern within an unlabeled time series and is critical in many data-mining tasks [24]. Conversely, a discord is a subsequence in a time series that differs significantly from other subsequences and is often an indicator of anomalous behavior [25]. The MP is a recently developed data-driven time series pattern-discovery method that records and annotates the location (index) and distance to the nearest neighbor of each subsequence of a time series [26]. This information can be used to identify time series motifs and anomalies, or time series discords, which are frequently used in time series data mining [27,28,29,30].
While the Fourier transform, wavelet transform, and ARIMA models are also used for time series analysis, these techniques may not be as effective or versatile as MP methods when handling complex, large-scale datasets.
The versatility and scalability of the MP technique make it a valuable tool for a wide range of time series data-mining tasks [14,15,27,31,32]. Its applications span diverse domains, such as website user data analysis [33], medical diagnostics [34], music analysis [35,36], and critical business applications [37,38]. In particular, the technique has found extensive use in domains such as finance, healthcare, weather, and sensor data analysis. Thanks to their scalability and efficiency, MP algorithms are well-suited for analyzing large-scale datasets, including streaming data and big data.
2.1.2. Matrix Profile for Time Series Anomaly Detection
Time series discord detection aims to identify anomalies over time. The MP technique can detect unusual patterns in time series, enabling the identification of unexpected events or deviations from the norm in diverse applications such as sensor data analysis, network intrusion detection, and financial time series analysis [26,27].
Moreover, motif discovery is an important task that provides valuable insight into the underlying structure and behavior of time series. This approach has been successfully applied to many problems in various domains, including medicine, motion-capture, robotics, and video surveillance. MP methods are highly effective at analyzing more-complex time series primitives, such as semantic segmentation [39], time series chain discovery [40], and snippet extraction [41], and finding predictive patterns in weakly labeled data [42]. This area of research is active and continues to evolve.
While there are alternative methods for discovering these primitives, the MP is highly efficient regardless of subsequence length or dimensionality, making it a valuable attribute in comparison to other algorithms, which often suffer from the curse of dimensionality [28,29,43].
In time series analysis, the tasks of discord detection and motif discovery are crucial, and the MP is a highly effective technique, which has been extensively reviewed and demonstrated to be effective in identifying anomalies (discords) and recurring patterns (motifs) in time series data. It offers an efficient and effective means of identifying unusual patterns and behaviors in time series data [30,42,44].
2.1.3. Matrix Profile Method
Throughout this section, the terminology and definitions for the MP technique are introduced [26,42].
Definition 1
(Time series). A sequence of real-valued numbers called a time series is defined as the equation , where n is the length of the time series T.
In our research, focus is put on similarities between local regions of a time series. A local region of a time series is called a subsequence.
Definition 2
(Subsequence). The term refers to a subsequence of length m in time series T, which is a sequence of m contiguous elements beginning at position i and ending at position in time series T.
Sliding a window of size m across a time series allows us to extract all its subsequences. It is called the all-subsequence set.
Definition 3
(All-subsequence set). The all-subsequence set of a time series T consists of the subsequences of T ordered in the following way:
where is represented by .
In this definition, the all-subsequence set is just notational. Since this would require a significant amount of time and memory, we do not extract subsequences in this form in our implementation. It is possible to compute the distance between any subsequence from a time series and the rest of the sequences in an all-subsequence set. These distance data are stored in a vector called a distance profile (see Figure 1):

Figure 1.
An extraction of a subsequence Q is used for querying each subsequence in T, and a distance profile is generated from the vector of all distances.
Definition 4
(Distance profile). A distance profile is a vector that represents the distances between a given query and every other subsequence in the all-subsequence set:
where denotes the Euclidean distance between the z-scores of two subsequences.
It is important to note that the query sequence and all-subsequence set are not required to come from the same time series. By definition, when both the query subsequence and the all-subsequence set belong to the same time series T, their distance profiles must be zero at the query location and near zero before and after. The literature refers to these matches as trivial matches [29], which are avoided by ignoring an exclusion zone (shown as a grey region in Figure 1) of length before and after the query location. As a general rule, the distance values in the exclusion zone are set to infinity. A time series distance profile aims to identify a subsequence’s nearest neighbor, except for trivial neighbors.
As a result, a subsequence is the nearest neighbor of a subsequence if and a subsequence is a trivial nearest neighbor of if and . Now, it is possible to formalize the Matrix Profile as follows.
Definition 5
(Matrix Profile). A Matrix Profile of a time series T is composed of a vector of distances between each subsequence and its nearest nontrivial neighbors:
where represents the minimal distance between and its nontrivial neighbors.
Time series analysis uses the term nontrivial neighbors to refer to subsequences in the Matrix Profile that are not identical to the target subsequence. The concept of nontrivial neighbors refers to identifying patterns in a time series that are similar, but not identical, as they have some minor variations.
Definition 6
(Matrix Profile index). A Matrix Profile index is a vector that stores the index of the nearest nontrivial neighbors of each subsequence of a time series T:
In the same way as distance profiles, Matrix Profiles can also be considered as metadata for annotating time series. Several interesting and exploitable properties exist in the profile. For example, the maximum value or the highest point of the profile corresponds to a possible anomalous subsequence (a discord) [31,45], whereas the minimal values or the lowest point correspond to the best motif subsequence pair in the series [29], and the variance can be viewed as a measure of T’s complexity. Additionally, the time series density is exactly estimated by the histogram of the values in the Matrix Profile [46]. If the query subsequence and the all-subsequence set come from different time series, the Matrix Profile and Matrix Profile index can be generalized to two time series. In this case, we refer to and as the joint Matrix Profile and Matrix Profile Index, respectively. Typically, , and . Figure 2 shows the Matrix Profile of time series T.

Figure 2.
Matrix Profile of time series T. A color box indicates the location of embedded motif pairs (bottom two points on ).
Summarizing, the MP method can be described algorithmically as follows (Algorithm 1).
| Algorithm 1 Matrix Profile. |
Input: T, a time series of length n m, the length of the subsequence/pattern Output: , the Matrix Profile begin
end |
Based on the Matrix Profile algorithm, the usual K discord computation is as follows (Algorithm 2).
| Algorithm 2 K discords’ computation. |
Input: T, a time series of length n m, the length of the subsequence/pattern K, the number of discords Output: in the time series T for a given subsequence of length m begin
end |
2.2. Other Time Series Discord Methods
In the area of anomaly detection, time series discords have become some of the most-effective and -competitive methods. Discords in time series are the most-unusual time series subsequences that are maximally different from any other subsequence in the same series. This term was introduced by [25]. The primary purpose of time series discords is to detect anomalies over time. Time series discords can be identified using several algorithms, each of which uses different techniques for measuring the distance or dissimilarity between subsequences and for identifying the most-anomalous subsequences [47,48]. In addition to the MP method, here are a few examples:
- HotSAX is an algorithm that detects discords in time series data. By using Symbolic Aggregate Approximation (SAX), each subsequence is converted into a sequence of symbols, which are then compared to determine where the discord lies [25,49,50,51].
- iSAX uses a hierarchical approach to symbolization, allowing for faster and more-efficient detection of discords than HotSAX [51,52].
- Data discords can also be detected using deep learning techniques such as Convolutional Neural Networks (CNNs) and Long Short-Term Memory (LSTM) networks [53]. An anomalous pattern can be flagged as a discord by these models, which are trained to detect patterns in the data [54,55,56].
- Weighted Anomaly Thresholding (WAT) is another algorithm that uses weighted moving averages to detect anomalies in time series data. Data points that fall outside of a certain threshold are identified by computing a moving average of the time series [57,58,59,60].
Time series discords can be detected using MP and iSAX, but their approaches and performances differ. As for time complexity, iSAX has an complexity, whereas MP has an complexity. Additionally, MP is more robust to noise compared to iSAX because it uses a sliding window approach, while iSAX relies on a symbolization technique, which can be sensitive to small fluctuations in the data. The MP is also scalable, as it can handle datasets of varying lengths and resolutions, versus iSAX’s fixed-length subsequence requirements. Furthermore, the MP has fewer parameters and a simpler output format than iSAX, making it generally easier to use. Due to its symbolization technique, iSAX can be difficult to interpret, whereas the MP provides a clear and understandable output. The MP algorithm has a time complexity of and is suitable for larger datasets, whereas the HotSAX algorithm has a time complexity of , where n is the length of the time series and w is the length of the subsequences being compared. The iSAX algorithm has a time complexity of .
Concerning the approach, the MP is a statistical and mathematical approach to detecting discords in time series data. To accomplish this, it uses a sliding window and distance measures. While Artificial Neural Networks (ANNs) employ a model-driven approach, using a trained model to predict discords, WAT is a statistical approach that uses a weighted moving average to discover anomalies. When compared to WAT and ANNs, the MP emphasizes data-driven discord identification and makes use of a sliding window and distance measures.
Furthermore, the MP algorithm is more robust to noise than other algorithms like HotSAX, iSAX, and WAT. This is because the MP utilizes a sliding window approach to compute distance measures that are less influenced by noise. On the other hand, HotSAX and iSAX both rely on symbolization techniques, which can be sensitive to small fluctuations in the data, making them more prone to noise. WAT uses a weighted moving average, which is easily affected by outliers and fluctuations in the data, making it more sensitive to noise than MP.
As far as scalability is concerned, the MP algorithm can be applied to datasets with various lengths and resolutions, making it more appropriate for data that may be irregular or sparse in real-world applications. In terms of scalability, the MP algorithm is a scalable approach that can be applied to datasets with varying lengths and resolutions, making it more suitable for real-world applications where the data may be irregular or sparse. However, HotSAX and iSAX require fixed-length subsequences and may not be so scalable in these cases. Additionally, ANNs are computationally expensive and require many data to train, even though they can detect anomalies accurately. Meanwhile, WAT is applicable to datasets of varying lengths and resolutions, but requires several parameters to be tuned for optimal results. As a result, the MP is more scalable and requires fewer parameters to be tuned, making it an effective approach for detecting discords in time series.
As for interpretability, the MP algorithm is known for providing an interpretable output, which can be used to understand the structures and patterns in data. By using an MP plot, the discords and their locations are clearly displayed. In contrast, iSAX is based on a symbolization technique, which can be difficult to interpret. Moreover, Neural Networks are black box models, so understanding their predictions can be challenging. Nevertheless, WAT provides clear and interpretable output in the form of anomalies, but MP’s plot is highly useful for identifying discords and locating them in time series data.
Given the advantages mentioned above, the present study employed the MP approach as a basis for our new proposed method to detect discordance in time series data as a result of simplicity, robustness to noise, scalability, and interpretability.
3. Cluster-Based Matrix Profile Methodology
The Matrix Profile has two primary components: a distance profile and a Matrix Profile index . The distance profile is a vector that represents the minimum z-normalized Euclidean distances between any subsequence within a time series and its nearest neighbors. In practice, the Matrix Profile will only store the smallest non-trivial distance from each distance profile, thereby significantly reducing the spatial complexity to . Its first nearest neighbor index appears in the profile index where the most-similar subsequence resides. Matrix Profiles are calculated with sliding windows. With m as the window size, the algorithm is as follows: A windowed subsequence is compared with the entire time series to calculate its distance. The distance profile is updated with minimal values, and the first nearest neighbor index is set. A distance calculation occurs times, where n shows the length of the time series and m shows the window size [26].
In real-world datasets, not all anomalies are of equal importance. Despite some anomalies being indicative of critical issues or deviations from expected behavior, others might be relatively benign minor fluctuations. By focusing on identifying the most-relevant and -impactful anomalies, instead of overwhelming analysts with hundreds, it is possible to improve the quality of the analysis.
Detecting anomalies in various domains is an essential task, and one critical variant of the problem is the top K discord detection. An algorithm aims to identify those anomalies within datasets that are most significant or impactful. The parameter K denotes this, where K is a user-defined parameter. These anomalies are often those that deviate the most from the expected or normal patterns within the dataset. The challenge lies in efficiently selecting and presenting these K anomalies to provide actionable insights to users. In this paper, we introduce an innovative approach to Optimal Discord Detection, which diverges from the conventional pursuit of simply identifying the top K discords. Our method revolves around a refined emphasis on optimizing the selection and presentation of these paramount anomalies. Our method employs clustering techniques to identify closely related anomalies, reducing redundancy, and subsequently, employs nearest neighbor methods to pinpoint the exact data points within the Matrix Profile that correspond to these highly impactful anomalies. The core objective of our approach is to provide more-meaningful and -interpretable results.
At the heart of our methodology lies a crucial insight: as the user-defined parameter, denoted as K, is increased, the Matrix Profile often yields a growing number of closely located index points. These points exhibit remarkably similar patterns, occasionally differing by only a single data point within the original dataset sub-series. The conventional Matrix Profile approach typically treats each of these closely related points as individual discord candidates, potentially overwhelming users with a multitude of closely related anomalies.
To overcome this challenge, we introduce a systematic process that commences by grouping these closely located points in Matrix Profile into clusters. This clustering step effectively consolidates related anomalies, resulting in a more-coherent representation of the underlying data characteristics. Subsequently, we deploy a center-based clustering algorithm to identify representative cluster centers, which serve as proxies for the remaining Matrix Profile’s index points within each cluster.
What distinguishes our innovation is the utilization of these cluster centers as foundational elements for discord detection. Leveraging nearest neighbor methods, we precisely pinpoint the exact data points within the Matrix Profile that correspond to these centers, introducing them as our discerning discord index points. Significantly, our approach grants users the flexibility to choose K by their preference, as the clustering process inherently determines the optimal number of discord candidates. This alleviates the need for users to specify K in advance.
This novel approach empowers users to efficiently detect anomalies in time series data, providing them with a refined, intuitive, and efficient tool. Notably, our “optimal discord detection” method not only delivers the option to choose K, but also ensures that the selected K represents the most-representative discord points within the Matrix Profile.
Our proposed approach can be described by the following algorithm (Algorithm 3).
| Algorithm 3 Optimal Discord Detection method. |
Input: T, a time series of length n m, the length of the subsequence/pattern Output: , the Matrix Profile , The Matrix Profile top K discords begin
end |
4. Experimentation and Results
This section covers our experiments and their outcomes. First, we describe the dataset we used and the tools we employed in Section 4.1 “Experimental Setup”. Then, in Section 4.2 “Results”, we present our findings.
4.1. Experimental Setup
In this section, we will go over the specifics of our experimental setup. We will detail the datasets we used and the software and hardware configurations we set up. This provides clarity for our results.
4.1.1. Dataset
The proposed methodology was tested on a dataset acquired from a medium-sized power gas turbine owned by Siemens Industrial Turbomachinery (SIT). Due to confidentiality constraints, this dataset is not available for disclosure. To monitor the gas turbine’s behavior, sensors were strategically placed at various locations to gather the data. Given the importance of detecting transient effects in operational modes, it is essential that datasets have a minimum duration of one minute. In the context of an industrial gas turbine, numerous valuable signals are present. In this study, a dataset with a one-minute sample time, denoted as , was examined. This dataset comprises n = 23,000 data points, equivalent to nearly 16 days, and includes the Turbine Outlet Energy (TOE) signal—the energy emitted from the turbine, with . These data were incorporated into the system as a time series T.
A gas turbine generates mechanical power by initially compressing air (or another fluid) in a compressor, followed by fuel combustion in the combustor. This process elevates the temperature, facilitating the expansion of the fluid through a turbine, which, in turn, produces energy. The respective components are illustrated in Figure 3. Toward the conclusion of the process, both temperature and pressure are concurrently diminished, culminating in the transfer of mechanical power to the intended application [61].

Figure 3.
A gas As one of our co-authors is from Siemens turbine (Siemens Industrial Turbomachinery AB, 2015) [62].
4.1.2. Software and Hardware
In order to implement this method, Python 3 [63] was used along with libraries like numpy [64], pandas [65], scikit-learn [66], matplotlib [67], seaborn [68], and scipy [69] for data analysis. Additional libraries called stumpy [70] and matrixprofile [71] were used for motif discovery and anomaly recording. The hardware used to run the software was the SageMaker by Amazon Web Services (AWS), version , (Frankfurt, Germany), with 16 CPUs and 64 GiB.
4.2. Results
In addition to finding the motif in the TOE’s time series data, the MP construction also helps with finding the anomaly present in the TOE. Operation patterns that are similar and have low values in the MP are termed motifs, whereas those exhibiting high values and being dissimilar are termed anomalies. We will, therefore, be able to detect anomalies accurately and efficiently using the proposed method. The proposed method is simple and easy to implement. Below, the procedure for detecting anomalies in the proposed method is described.
On the above-mentioned dataset, which is also displayed in Figure 4, experiments with different motif lengths (m) were conducted. As shown in Figure 5, Figure 6, Figure 7 and Figure 8, firstly, we have a sample dataset with red and green shades showing the motifs detected for the indicated window size, and then, we have an MP in which the dots indicate where the patterns started. The third plot illustrates the zoomed-in patterns detected, and the fourth plot illustrates the density of the data at that point by a violin plot. For instance, Figure 5 and Figure 6 both depict processes transitioning from high to low values during operation. The detailed view in the zoomed-in plot, along with the violin plot, clearly shows how these two patterns align. In contrast, the operational mode in Figure 7 shifts from a low to a high value. Furthermore, the mode of operation in Figure 8 progresses beyond the patterns observed in Figure 5 and Figure 6, eventually reaching higher values. Additionally, Table 1 displays the motif discoveries for different window sizes and the corresponding indexes of similar patterns, as well as their behavior according to the operation mode.

Figure 4.
The one-minute sample time dataset with 23,000 data points (almost 16 days) and Turbine Outlet Energy/Power (TOE) signal values.
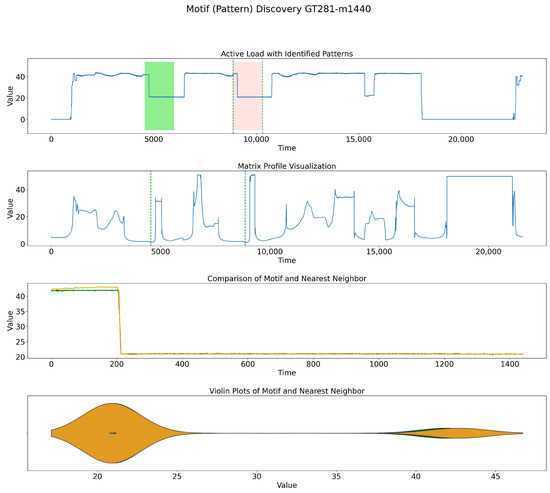
Figure 5.
MP method discovering motifs’ patterns for a window size of 1440.
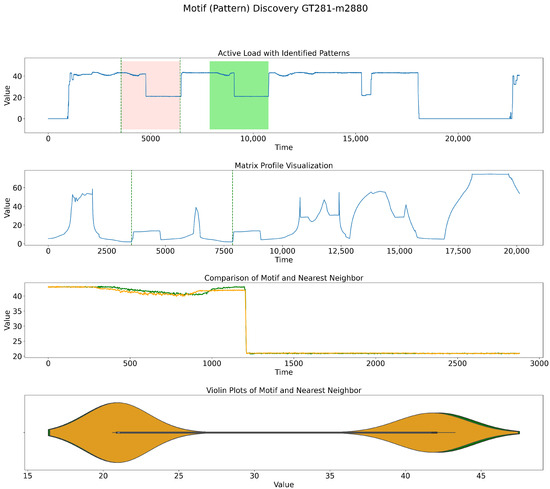
Figure 6.
MP method discovering motifs’ patterns for a window size of 2880.
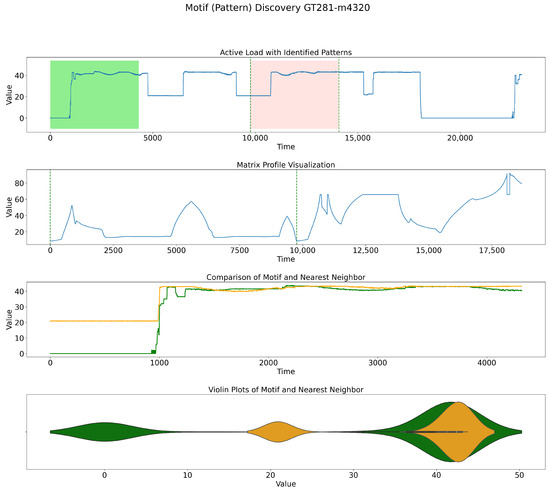
Figure 7.
MP method discovering motifs’ patterns for a window size of 4320.

Figure 8.
MP method discovering motifs’ patterns for a window size of 5760.

Table 1.
Summary of using motif discovery for different time window sizes.
In order to obtain a better idea of what we are dealing with, the raw data is provided in Figure 4. It may be possible to see some patterns in the data visually, but let us imagine what would happen if there were more than 16 days’ worth of data or if we looked at the values for the whole year. Without some type of transformation, it would be pretty difficult to visualize what is happening. The MP method will be calculated over different window sizes in order to discover any interesting pattern.
Now, we will focus on the CMP within the 24 to 96 h windows, as there are some evident discords (peaks on the plots). First, to find discords, we utilized our CMP algorithm. In the CMP, the top K discords refer to the K most-anomalous or unusual sub-series within a time series. Thus, the top K discords represent the sub-series with the lowest similarity scores, indicating their distinct dissimilarity. These are particularly useful in time series analysis and anomaly detection, as they assist in identifying patterns and events that differ from the usual.
The plots in Figure 9, Figure 10, Figure 11 and Figure 12 show the top optimal discords through the Matrix Profile with red stars and the red pattern in the corresponding time series. Our analysis indicates that they are optimal because, as the parameter K is increased, the number of close index points in the Matrix Profile increases, but they are so close together that they show the patterns being so similar and perhaps just a one-point difference between their original points in the dataset sub-series. Figure 13 is provided for better understanding.
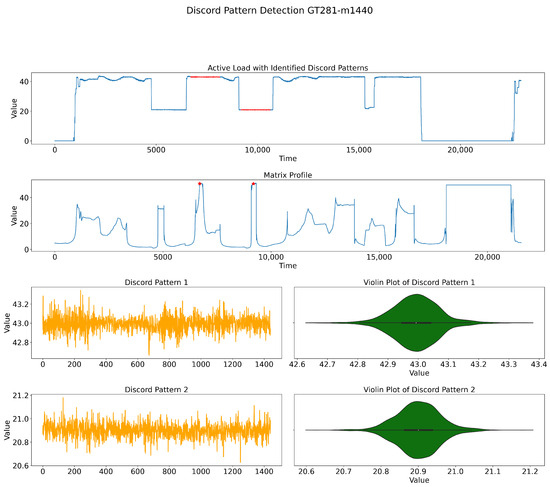
Figure 9.
CMP method discovering discords’ patterns for a window size of 1440.
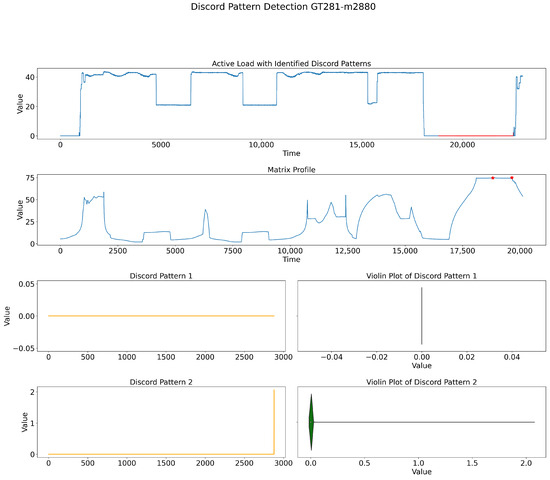
Figure 10.
CMP method discovering discords’ patterns for a window size of 2880.

Figure 11.
CMP method discovering discords’ patterns for a window size of 4320.

Figure 12.
CMP method discovering discords’ patterns for a window size of 5760.

Figure 13.
Close-up view of Matrix Profile method discovering discords’ patterns for a window size of 1440.
To avoid unnecessary discord index points in the Matrix Profiles, we propose a new algorithm, namely the CMP. This algorithm initially groups close points together and, then, separates unrelated points using a center-based clustering algorithm. Subsequently, the center of each cluster is used as a representative for the other points within that cluster. After identifying the cluster centers, we employed the nearest neighbor methods to precisely locate the exact points in the Matrix Profile, introducing them as discord index points. The number of clusters was also used to determine an optimal discord number. Consequently, regardless of the chosen value of K for detecting discords, the system will automatically select the optimal number. In our analysis, various values of K were evaluated, but we ultimately selected 101 for the system. This choice ensured a sufficiently large K to prevent potential discords in the dataset from being missed.
Table 2 presents the results of an analysis conducted on the aforementioned time series data, employing various window sizes to identify discords. The table details the number of discords, their indexes, and their associated operational patterns for each window size. The columns represent the “window size” in minutes, the “number of discords” identified, the “discord index”, and the “operation pattern”. The latter describes the behavior of the time series data at each discord’s location. These operation patterns, or discords, were readily identifiable as anomalies due to their stark contrast to the operational mode labels of their vicinity. These operational modes represent the states of the gas turbine process. The operational mode labels were derived through an automatic data-driven approach based on an ensemble of clustering methods [72], further validated by gas turbine process experts. The results indicate that the number and characteristics of the detected discords are influenced by the window size used in the analysis. For instance, smaller window sizes (1440 to 4320 min) identified two discords each, exhibiting simpler operational patterns like “High”, “Middle”, “Low”, and variations of “Low”. In contrast, the largest window size (5760 min) detected only one discord, but with a more-complex pattern (“High_Middle_High_Low”). Smaller window sizes tend to identify more-discrete and less-complex anomalies, while a larger window size may consolidate multiple anomalies into a single, more-complex detection or indicate fewer anomalies. While the window size certainly affects the number and complexity of detected discords, each result can be meaningful and useful for different aspects of discord analysis. For example, a smaller window size may be useful in identifying more, short-term anomalous patterns, while a larger window size may be more appropriate for identifying longer-term trends and patterns. The choice of the window size ultimately depends on the goals and requirements of the specific analysis, and it is important to choose an appropriate window size to obtain meaningful results that meet the needs of the analysis. This information is crucial for understanding the operational dynamics of the system under study such as gas turbines.

Table 2.
Discord detection results for different window sizes.
5. Conclusions
This study introduced a novel methodology for anomaly detection in gas turbines, specifically targeting the Turbine Outlet Energy (TOE) signal. Our study utilized a one-minute sample time dataset from a medium-sized power gas turbine, demonstrating the proficiency of the Cluster-based Matrix Profile (CMP) method in detecting anomalies in the TOE’s time series data. The CMP approach demonstrated its ability to distinguish between normal operational patterns and anomalies, showcasing its effectiveness in accurate and efficient anomaly detection. By using Matrix Profile construction, the methodology can identify both motifs and anomalies, based on their similarities and value patterns in the time series data. This ability is important for the early detection of potential issues in turbine operation and operational settings, allowing for more-accurate predictions and maintenance scheduling, thereby enhancing the overall efficiency and safety of gas turbine operations. The method’s simplicity and straightforward implementation further contribute to its practical applicability in real-world settings. Moreover, the study’s exploration of discord detection using the CMP method and the top K discords algorithm illuminates the ability of the system to identify the most-significant anomalous sub-series within a dataset by optimizing detection through center-based clustering and nearest neighbor methods. Our experiments validated the CMP method’s efficacy in identifying anomalous patterns across various window sizes. These findings underline the method’s versatility and adaptability to different operational contexts and data scales. The anomaly detection results were corroborated by gas turbine process experts, further attesting to the practical applicability and reliability of the CMP method in real-world scenarios. The proposed CMP method stands out for its simplicity and ease of implementation, making it an accessible tool for practitioners in the field. This creates new opportunities for exploring more-complex datasets and operational scenarios, potentially extending its application beyond gas turbines to other industrial processes.
Author Contributions
Conceptualization, M.B.G., M.S.-M. and C.A.; methodology, M.B.G., D.N., M.S.-M. and C.A.; software, M.B.G.; validation, M.B.G.; formal analysis, M.B.G., M.S.-M. and C.A.; investigation, M.B.G. and M.S.-M.; resources, M.B.G. and D.N.; data curation, M.B.G.; writing—original draft preparation, M.B.G., M.S.-M. and C.A.; writing—review and editing, M.B.G., M.S.-M. and C.A.; visualization, M.B.G.; supervision, M.S.-M. and C.A.; project administration, D.N.; funding acquisition, C.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by Siemens Energy under agreement Siemens-UPC (C-11193), by the Ministry of State for Digitalization and Artificial Intelligence, and by the European Union—Next Generation EU funds.
Data Availability Statement
Restrictions apply to the availability of these data. The data were obtained from Siemens Energy and are available from the authors with the permission of Siemens Energy.
Acknowledgments
The authors would like to express their appreciation to Siemens Energy Service Oil & Gas in Sweden and Barcelona for their support and assistance in the elaboration of the study.
Conflicts of Interest
Author Davood Naderi was employed by the company Siemens Energy. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Kagermann, H.; Wahlster, W.; Helbig, J. Recommendations for Implementing the Strategic Initiative INDUSTRIE 4.0: Securing the Future of German Manufacturing Industry; Final Report of the Industrie 4.0 Working Group; National Academy of Science and Engineering: Munich, Germany, 2013. [Google Scholar]
- Osmani, A.; Hamidi, M.; Bouhouche, S. Monitoring of a Dynamic System Based on Autoencoders. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI-19, Macao, China, 10–16 August 2019; pp. 1836–1843. [Google Scholar] [CrossRef]
- Liu, Y.; Banerjee, A.; Ravichandran, T.; Kumar, A.; Heppler, G. Data Analytics for Performance Monitoring of Gas Turbine Engine. In Proceedings of the Annual Conference of the PHM Society, Philadelphia, PA, USA, 24–27 September 2018; Volume 10. [Google Scholar] [CrossRef]
- Pimentel, M.A.; Clifton, D.A.; Clifton, L.; Tarassenko, L. A review of novelty detection. Signal Process. 2014, 99, 215–249. [Google Scholar] [CrossRef]
- Panza, M.A.; Pota, M.; Esposito, M. Anomaly Detection Methods for Industrial Applications: A Comparative Study. Electronics 2023, 12, 3971. [Google Scholar] [CrossRef]
- Kang, H.S.; Choi, Y.S.; Yu, J.S.; Jin, S.W.; Lee, J.M.; Kim, Y.J. Hyperparameter Tuning of OC-SVM for Industrial Gas Turbine Anomaly Detection. Energies 2022, 15, 8757. [Google Scholar] [CrossRef]
- Agung, I.G.N. Advanced Time Series Data Analysis; John Wiley & Sons, Ltd.: Bridgewater, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Li, F.; Wang, H.; Zhou, G.; Yu, D.; Li, J.; Gao, H. Anomaly detection in gas turbine fuel systems using a sequential symbolic method. Energies 2017, 10, 724. [Google Scholar] [CrossRef]
- Zhu, Y.; Gharghabi, S.; Silva, D.F.; Dau, H.A.; Yeh, C.C.M.; Shakibay Senobari, N.; Almaslukh, A.; Kamgar, K.; Zimmerman, Z.; Funning, G.; et al. The Swiss army knife of time series data mining: Ten useful things you can do with the Matrix Profile and ten lines of code. Data Min. Knowl. Discov. 2020, 34, 949–979. [Google Scholar] [CrossRef]
- Zhu, Y.; Zimmerman, Z.; Senobari, N.S.; Yeh, C.C.M.; Funning, G.; Mueen, A.; Brisk, P.; Keogh, E. Matrix Profile II: Exploiting a novel algorithm and GPUs to break the one hundred million barrier for time series motifs and joins. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016; pp. 739–748. [Google Scholar] [CrossRef]
- Kamgar, K.; Gharghabi, S.; Keogh, E. Matrix Profile XV: Exploiting time series consensus motifs to find structure in time series sets. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 1156–1161. [Google Scholar] [CrossRef]
- Luo, W.; Tan, H.; Mao, H.; Ni, L.M. Efficient similarity joins on massive high-dimensional datasets using MapReduce. In Proceedings of the 2012 IEEE 13th International Conference on Mobile Data Management, Bengaluru, India, 23–26 July 2012; pp. 1–10. [Google Scholar] [CrossRef]
- Ma, Y.; Meng, X.; Wang, S. Parallel similarity joins on massive high-dimensional data using MapReduce. Concurr. Comput. Pract. Exp. 2016, 28, 166–183. [Google Scholar] [CrossRef]
- Yoon, C.E.; O’Reilly, O.; Bergen, K.J.; Beroza, G.C. Earthquake detection through computationally efficient similarity search. Sci. Adv. 2015, 1, e1501057. [Google Scholar] [CrossRef]
- Hehir, C.; Smeaton, A.F. Calculating the Matrix Profile from noisy data. PLoS ONE 2023, 18, e0286763. [Google Scholar] [CrossRef]
- Assent, I.; Kranen, P.; Baldauf, C.; Seidl, T. AnyOut: Anytime outlier detection on streaming data. In Proceedings of the International Conference on Database Systems for Advanced Applications, Busan, Republic of Korea, 15–19 April 2012; Lee, S., Peng, Z., Zhou, X., Moon, Y.S., Unland, R., Yoo, J., Eds.; pp. 228–242. [Google Scholar] [CrossRef]
- Ueno, K.; Xi, X.; Keogh, E.; Lee, D. Anytime classification using the nearest neighbor algorithm with applications to stream mining. In Proceedings of the Sixth International Conference on Data Mining (ICDM’06), Hong Kong, China, 18–22 December 2006; pp. 623–632. [Google Scholar] [CrossRef]
- Ding, H.; Trajcevski, G.; Scheuermann, P.; Wang, X.; Keogh, E. Querying and mining of time series data: Experimental comparison of representations and distance measures. Proc. VLDB Endow. 2008, 1, 1542–1552. [Google Scholar] [CrossRef]
- Mueen, A. Time series motif discovery: Dimensions and applications. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2014, 4, 152–159. [Google Scholar] [CrossRef]
- Takahashi, Y. Anomaly Detection using Vibration Analysis with Machine Learning Technology for Industrial IoT System. OKI Tech. Rev. 2017, 84, 30–33. Available online: https://www.oki.com/en/otr/2017/n230/pdf/otr-230-R09.pdf (accessed on 24 January 2024).
- Lee, Y.Q.; Beh, W.L.; Ooi, B.Y. Tracking Operation Status of Machines through Vibration Analysis using Motif Discovery. J. Phys. Conf. Ser. 2020, 1529, 052005. [Google Scholar] [CrossRef]
- Durgam, S.; Bawankule, L.N.; Khindkar, P.S. Prediction of Fault Detection Based on Vibration Analysis for Motor Applications. In Proceedings of the 2021 4th Biennial International Conference on Nascent Technologies in Engineering (ICNTE), NaviMumbai, India, 15–16 January 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Do, J.S.; Kareem, A.B.; Hur, J.W. LSTM-autoencoder for vibration anomaly detection in vertical carousel storage and retrieval system (VCSRS). Sensors 2023, 23, 1009. [Google Scholar] [CrossRef]
- Al Aghbari, Z.; Al-Hamadi, A. Finding k most significant motifs in big time series data. Procedia Comput. Sci. 2020, 170, 595–601. [Google Scholar] [CrossRef]
- Keogh, E.; Lin, J.; Fu, A. HOT SAX: Finding the most unusual time series subsequence: Algorithms and applications. In Proceedings of the Fifth IEEE International Conference on Data Mining (ICDM’05), Houston, TX, USA, 27–30 November 2005; pp. 440–449. [Google Scholar] [CrossRef]
- Yeh, C.C.M.; Zhu, Y.; Ulanova, L.; Begum, N.; Ding, Y.; Dau, H.A.; Silva, D.F.; Mueen, A.; Keogh, E. Matrix Profile I: All pairs similarity joins for time series: A unifying view that includes motifs, discords and shapelets. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016; pp. 1317–1322. [Google Scholar] [CrossRef]
- Gerazov, B.; Hadjieva, E.; Krivošei, A.; Sanchez, F.I.S.; Rostovski, J.; Kuusik, A.; Alam, M. Matrix Profile based Anomaly Detection in Streaming Gait Data for Fall Prevention. In Proceedings of the 2023 30th International Conference on Systems, Signals and Image Processing (IWSSIP), Ohrid, North Macedonia, 27–29 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Li, Y.; Leong, H.U.; Yiu, M.L.; Gong, Z. Quick-motif: An efficient and scalable framework for exact motif discovery. In Proceedings of the 2015 IEEE 31st International Conference on Data Engineering, Seoul, Republic of Korea, 13–17 April 2015; pp. 579–590. [Google Scholar] [CrossRef]
- Mueen, A.; Keogh, E.; Zhu, Q.; Cash, S.; Westover, B. Exact discovery of time series motifs. In Proceedings of the 2009 SIAM International Conference on Data Mining, Sparks, NV, USA, 30 April–2 May 2009; pp. 473–484. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, R.; Mueen, A.; Zuluaga, M.A.; Keogh, E. Matrix Profile XXIV: Scaling time series anomaly detection to trillions of datapoints and ultra-fast arriving data streams. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 1173–1182. [Google Scholar] [CrossRef]
- Chandola, V.; Cheboli, D.; Kumar, V. Detecting Anomalies in a Time Series Database; Technical Report 09-004; University of Minnesota Twin Cities: Minneapolis, MN, USA, 2009; Available online: https://hdl.handle.net/11299/215791 (accessed on 24 January 2024).
- Hills, J.; Lines, J.; Baranauskas, E.; Mapp, J.; Bagnall, A. Classification of time series by shapelet transformation. Data Min. Knowl. Discov. 2014, 28, 851–881. [Google Scholar] [CrossRef]
- De Francisci Morales, G.; Gionis, A. Streaming Similarity Self-Join. Proc. VLDB Endow. 2016, 9, 792–803. [Google Scholar] [CrossRef]
- Lainscsek, C.; Hernandez, M.E.; Weyhenmeyer, J.; Sejnowski, T.J.; Poizner, H. Non-linear dynamical analysis of EEG time series distinguishes patients with Parkinson’s disease from healthy individuals. Front. Neurol. 2013, 4, 200. [Google Scholar] [CrossRef] [PubMed]
- Serrà, J.; Müller, M.; Grosche, P.; Arcos, J.L. Unsupervised music structure annotation by time series structure features and segment similarity. IEEE Trans. Multimed. 2014, 16, 1229–1240. [Google Scholar] [CrossRef]
- Silva, D.F.; Yeh, C.C.M.; Zhu, Y.; Batista, G.E.A.P.A.; Keogh, E. Fast similarity Matrix Profile for music analysis and exploration. IEEE Trans. Multimed. 2018, 21, 29–38. [Google Scholar] [CrossRef]
- Reinhardt, A.; Christin, D.; Kanhere, S.S. Predicting the power consumption of electric appliances through time series pattern matching. In Proceedings of the 5th ACM Workshop on Embedded Systems For Energy-Efficient Buildings, Roma, Italy, 13–14 November 2013; pp. 1–2. [Google Scholar] [CrossRef]
- Zymbler, M.; Ivanova, E. Matrix Profile-based approach to industrial sensor data analysis inside RDBMS. Mathematics 2021, 9, 2146. [Google Scholar] [CrossRef]
- Gharghabi, S.; Ding, Y.; Yeh, C.C.M.; Kamgar, K.; Ulanova, L.; Keogh, E. Matrix Profile VIII: Domain agnostic online semantic segmentation at superhuman performance levels. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 117–126. [Google Scholar] [CrossRef]
- Zhu, Y.; Imamura, M.; Nikovski, D.; Keogh, E. Matrix Profile VII: Time series chains: A new primitive for time series data mining (best student paper award). In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 695–704. [Google Scholar] [CrossRef]
- Imani, S.; Madrid, F.; Ding, W.; Crouter, S.; Keogh, E. Matrix Profile XIII: Time series snippets: A new primitive for time series data mining. In Proceedings of the 2018 IEEE International Conference on Big Knowledge (ICBK), Singapore, 17–18 November 2018; pp. 382–389. [Google Scholar] [CrossRef]
- Yeh, C.C.M.; Kavantzas, N.; Keogh, E. Matrix Profile VI: Meaningful multidimensional motif discovery. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 565–574. [Google Scholar] [CrossRef]
- Yankov, D.; Keogh, E.; Medina, J.; Chiu, B.; Zordan, V. Detecting time series motifs under uniform scaling. In Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Jose, CA, USA, 13–15 August 2007; pp. 844–853. [Google Scholar] [CrossRef]
- Tafazoli, S.; Keogh, E. Matrix Profile XXVIII: Discovering Multi-Dimensional Time Series Anomalies with K of N Anomaly Detection. In Proceedings of the 2023 SIAM International Conference on Data Mining (SDM), Minnesota, MN, USA, 27–29 April 2023; pp. 685–693. [Google Scholar] [CrossRef]
- Yankov, D.; Keogh, E.; Rebbapragada, U. Disk aware discord discovery: Finding unusual time series in terabyte sized datasets. Knowl. Inf. Syst. 2008, 17, 241–262. [Google Scholar] [CrossRef]
- Bouezmarni, T.; Rombouts, J.V. Nonparametric density estimation for positive time series. Comput. Stat. Data Anal. 2010, 54, 245–261. [Google Scholar] [CrossRef]
- Blázquez-García, A.; Conde, A.; Mori, U.; Lozano, J.A. A review on outlier/anomaly detection in time series data. ACM Comput. Surv. (CSUR) 2021, 54, 56. [Google Scholar] [CrossRef]
- DeMedeiros, K.; Hendawi, A.; Alvarez, M. A survey of AI-based anomaly detection in IoT and sensor networks. Sensors 2023, 23, 1352. [Google Scholar] [CrossRef]
- Wang, X.; Lin, J.; Patel, N.; Braun, M. Exact variable-length anomaly detection algorithm for univariate and multivariate time series. Data Min. Knowl. Discov. 2018, 32, 1806–1844. [Google Scholar] [CrossRef]
- Schmidl, S.; Wenig, P.; Papenbrock, T. Anomaly detection in time series: A comprehensive evaluation. Proc. VLDB Endow. 2022, 15, 1779–1797. [Google Scholar] [CrossRef]
- Liu, J.; Huang, W.; Li, H.; Ji, S.; Du, Y.; Li, T. SLAFusion: Attention fusion based on SAX and LSTM for dangerous driving behavior detection. Inf. Sci. 2023, 640, 119063. [Google Scholar] [CrossRef]
- Buu, H.T.Q.; Anh, D.T. Time series discord discovery based on iSAX symbolic representation. In Proceedings of the 2011 Third International Conference on Knowledge and Systems Engineering, Hanoi, Vietnam, 14–17 October 2011; pp. 11–18. [Google Scholar] [CrossRef]
- Bai, M.; Liu, J.; Ma, Y.; Zhao, X.; Long, Z.; Yu, D. Long short-term memory network-based normal pattern group for fault detection of three-shaft marine gas turbine. Energies 2020, 14, 13. [Google Scholar] [CrossRef]
- Choi, H.; Kim, S.; Kang, P. Recurrent auto-encoder with multi-resolution ensemble and predictive coding for multivariate time series anomaly detection. Appl. Intell. 2023, 53, 25330–25342. [Google Scholar] [CrossRef]
- Bhoomika, A.; Chitta, S.N.S.; Laxmisetti, K.; Sirisha, B. Time Series Forecasting and Point Anomaly Detection of Sensor Signals Using LSTM Neural Network Architectures. In Proceedings of the 2023 10th International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 15–17 March 2023; pp. 1257–1262. [Google Scholar]
- Nor, A.K.M.; Pedapati, S.R.; Muhammad, M.; Leiva, V. Abnormality detection and failure prediction using explainable Bayesian deep learning: Methodology and case study with industrial data. Mathematics 2022, 10, 554. [Google Scholar] [CrossRef]
- Bu, Y.; Leung, T.W.; Fu, A.W.C.; Keogh, E.; Pei, J.; Meshkin, S. WAT: Finding top-K discords in time series database. In Proceedings of the 2007 SIAM International Conference on Data Mining, Minneapolis, MN, USA, 26–28 April 2007; pp. 449–454. [Google Scholar] [CrossRef]
- Khanh, N.D.K.; Anh, D.T. Time series discord discovery using WAT algorithm and iSAX representation. In Proceedings of the 3rd Symposium on Information and Communication Technology, Ha Long, Vietnam, 23–14 August 2012; pp. 207–213. [Google Scholar] [CrossRef]
- van Leeuwen, R.; Koole, G. Anomaly detection in univariate time series incorporating active learning. J. Comput. Math. Data Sci. 2023, 6, 100072. [Google Scholar] [CrossRef]
- Liu, H.; Li, L. Anomaly detection of high-frequency sensing data in transportation infrastructure monitoring system based on fine-tuned model. IEEE Sens. J. 2023, 23, 8630–8638. [Google Scholar] [CrossRef]
- Larsson, E. Model Based Diagnosis and Supervision of Industrial Gas Turbines; Linköping Studies in Science and Technology. Ph.D. Thesis, Department of Electrical Engineering, Linköping University, Linköping, Sweden, 2014. [Google Scholar]
- Sgt-800: Industrial Gas Turbine: Gas Turbines: Manufacturer: Siemens Energy Global. Available online: https://www.siemens-energy.com/global/en/offerings/power-generation/gas-turbines/sgt-800.html (accessed on 3 November 2021).
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- McKinney, W. Data structures for statistical computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; Volume 445, pp. 56–61. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Waskom, M.; Botvinnik, O.; O’Kane, D.; Hobson, P.; Lukauskas, S.; Gemperline, D.C.; Augspurger, T.; Halchenko, Y.; Cole, J.B.; Warmenhoven, J.; et al. mwaskom/seaborn: V0.8.1 (September 2017). 2017. Available online: https://zenodo.org/records/883859 (accessed on 26 January 2024).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Law, S.M. STUMPY: A Powerful and Scalable Python Library for Time Series Data Mining. J. Open Source Softw. 2019, 4, 1504. [Google Scholar] [CrossRef]
- Van Benschoten, A.H.; Ouyang, A.; Bischoff, F.; Marrs, T.W. MPA: A novel cross-language API for time series analysis. J. Open Source Softw. 2020, 5, 2179. [Google Scholar] [CrossRef]
- Bagherzade Ghazvini, M.; Sànchez-Marrè, M.; Bahilo, E.; Angulo, C. Operational Modes Detection in Industrial Gas Turbines Using an Ensemble of Clustering Methods. Sensors 2021, 21, 8047. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).