CO2 Emission Prediction for Coal-Fired Power Plants by Random Forest-Recursive Feature Elimination-Deep Forest-Optuna Framework
Abstract
1. Introduction
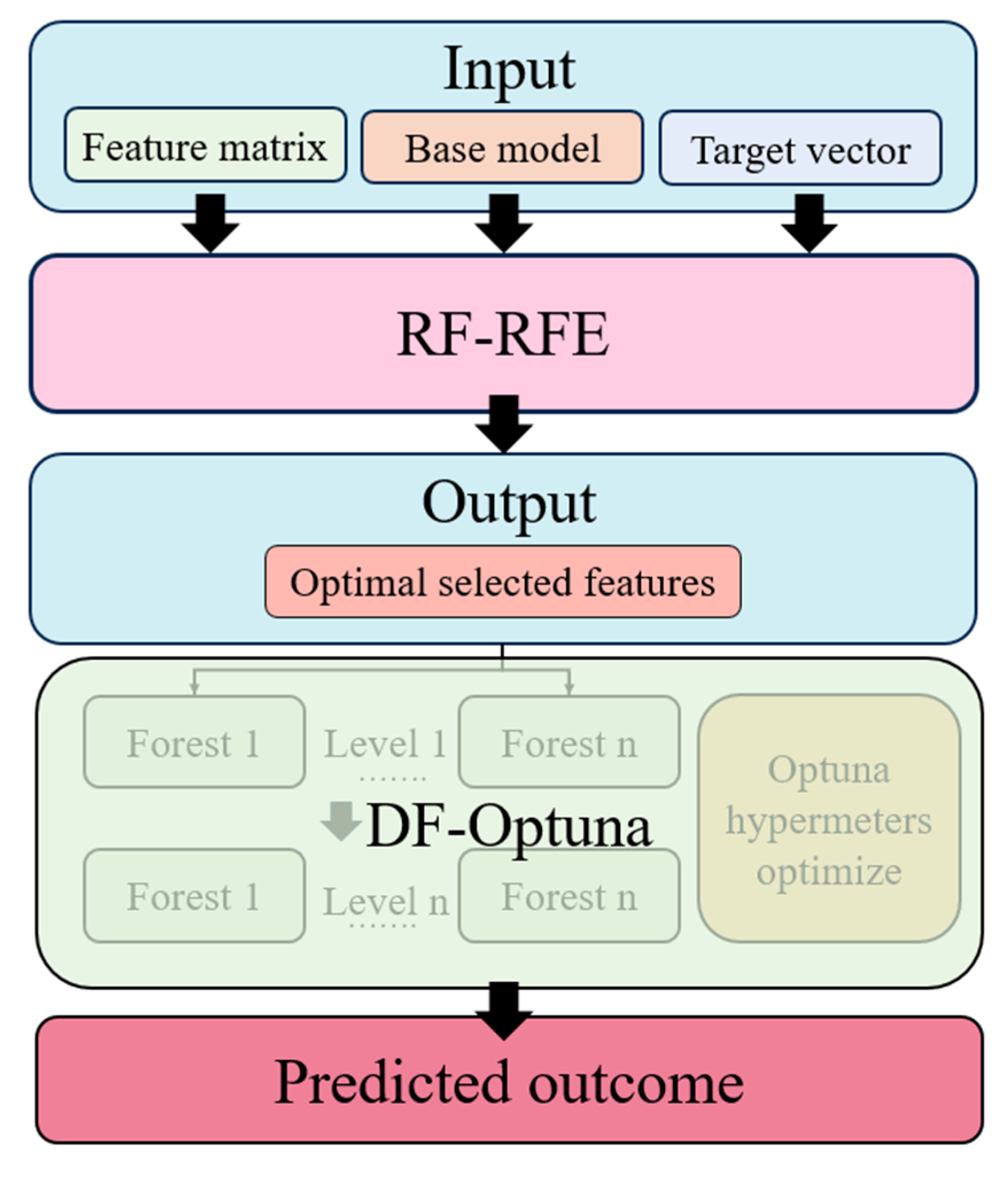
2. Methods
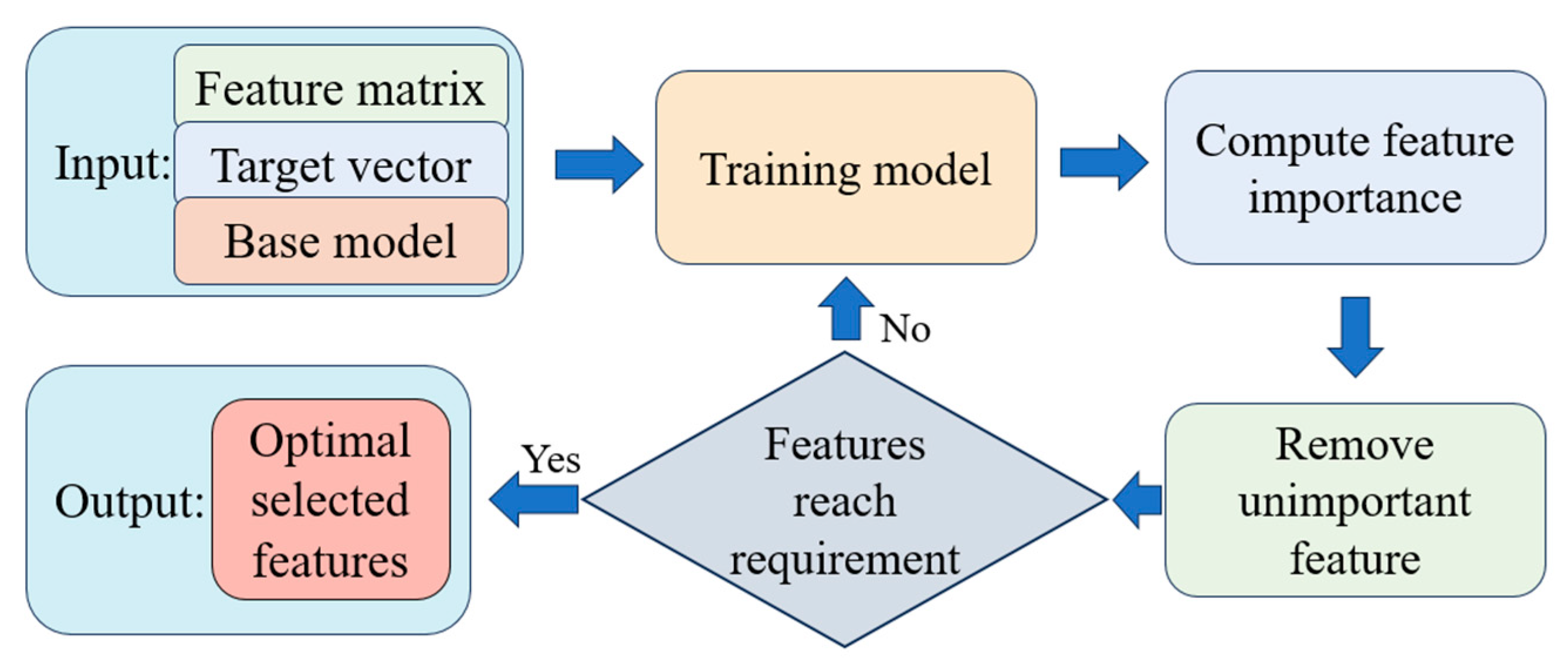
2.1. Recursive Feature Elimination
2.2. Deep Forest Model
2.3. Optuna Framework
2.4. Evaluation Metrics
3. Results and Discussion
3.1. Data Collection and Processing
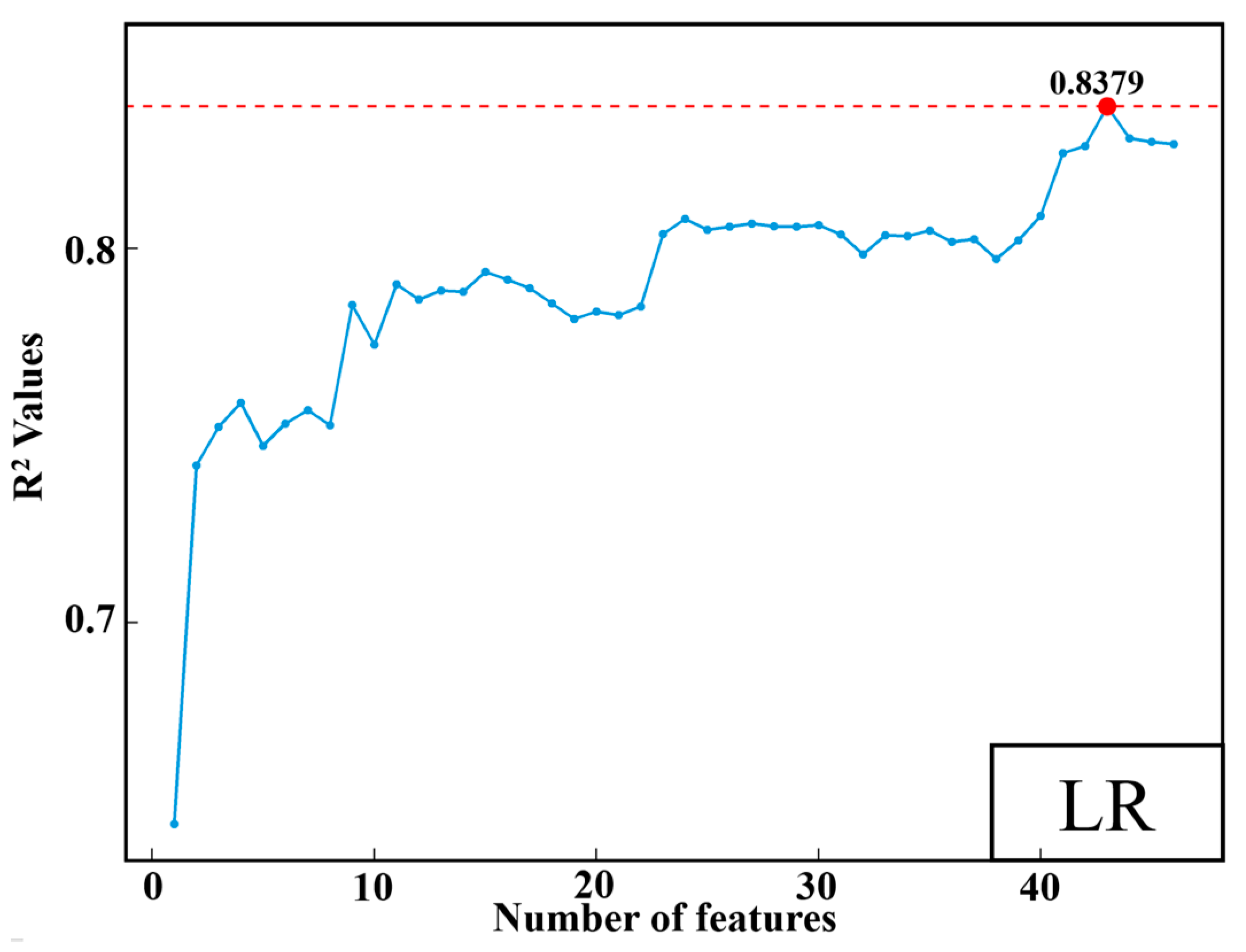
3.2. Features Selection
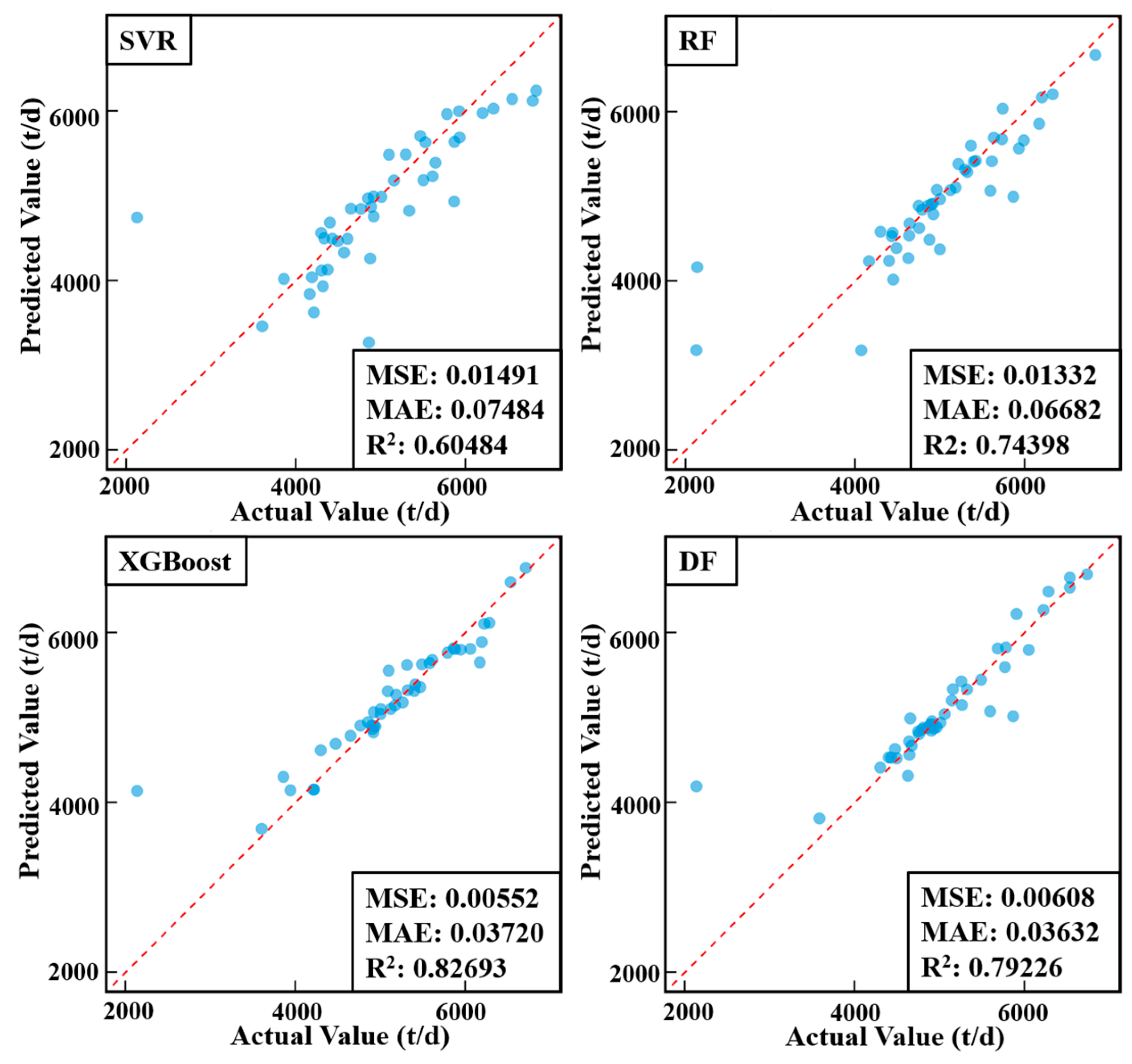
3.3. Prediction of CO2 Emission
3.3.1. Prediction Model Evaluation
3.3.2. Hyperparameters Optimization with OPTUNA
4. Conclusions
- The RF-RFE-DF-Optuna framework was produced to select critical features using the RF-RFE method systematically and then employed the DF model integrated with Optuna for enhanced prediction precision, significantly improving the accuracy of CO2 emission forecasting in coal-fired power plants.
- Establish RF-RFE model framework to effectively select five key features from 46 data points to predict CO2 emissions from coal-fired power plants, reducing computational resources without sacrificing accuracy.
- The construction of the DF-Optuna model has achieved precise predictions of CO2 emissions. Compared to traditional models, it has significantly increased R2 by 0.12706, with reductions in MSE and MAE by 81.70% and 36.88%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, X.; Ma, X.; Chen, B.; Shang, Y.; Song, M. Challenges toward carbon neutrality in China: Strategies and countermeasures. Resour. Conserv. Recycl. 2022, 176, 105959. [Google Scholar] [CrossRef]
- Davenport, J.W.N. Statistical Review of World Energy; Energy Institute: London, UK, 2024. [Google Scholar]
- Dong, L.; Wang, L.; Wen, H.; Lin, Z.; Yao, Z.; Zou, C.; Xu, H.; Hu, H.; Yao, H. Numerical investigation of the oxy-fuel combustion in the fluidized bed using macroscopic model supported by CFD-DDPM. J. Environ. Chem. Eng. 2024, 12, 113959. [Google Scholar] [CrossRef]
- Zhu, Z.; Huang, Y.; Dong, L.; Xu, W.; Yu, M.; Li, Z.; Xiao, Y.; Cheng, H. Dual effects of NaCl on the high temperature adsorption of heavy metals by montmorillonite. Chem. Eng. J. 2024, 494, 152661. [Google Scholar] [CrossRef]
- Zhu, Z.; Huang, Y.; Dong, L.; Yu, M.; Xu, W.; Li, Z.; Xiao, Y.; Cheng, H. Effect of aluminosilicates on the release and form transformation of semi-volatile heavy metals during the combustion of hyperaccumulator plants. J. Clean. Prod. 2024, 461, 142604. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, S.; Sha, Y.; Ding, Q.; Yuan, J.; Guo, X. Coal power overcapacity in China: Province-Level estimates and policy implications. Resour. Conserv. Recycl. 2018, 137, 89–100. [Google Scholar] [CrossRef]
- Ghadimi, P.; Wang, C.; Azadnia, A.H.; Lim, M.K.; Sutherland, J.W. Life cycle-based environmental performance indicator for the coal-to-energy supply chain: A Chinese case application. Resour. Conserv. Recycl. 2019, 147, 28–38. [Google Scholar] [CrossRef]
- IPCC. Guidelines for National Greenhouse Gas Inventories; Institute for Global Environmental Strategies: Hayama, Japan, 2006. [Google Scholar]
- AlKheder, S.; Almusalam, A. Forecasting of carbon dioxide emissions from power plants in Kuwait using United States Environmental Protection Agency, Intergovernmental Panel on Climate Change, and machine learning methods. Renew. Energy 2022, 191, 819–827. [Google Scholar] [CrossRef]
- Liu, Z.; Guan, D.; Wei, W.; Davis, S.J.; Ciais, P.; Bai, J.; Peng, S.; Zhang, Q.; Hubacek, K.; Marland, G.; et al. Reduced carbon emission estimates from fossil fuel combustion and cement production in China. Nature 2015, 524, 335–338. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, Y.; Zhang, J.; Xiong, Z. Research progress on carbon measurement methods for coal-fired power plants under the dual carbon targets. Clean Coal Technol. 2022, 28, 170–183. [Google Scholar] [CrossRef]
- Tang, L.; Jia, M.; Yang, J.; Li, L.; Bo, X.; Mi, Z. Chinese industrial air pollution emissions based on the continuous emission monitoring systems network. Sci. Data 2023, 10, 110–153. [Google Scholar] [CrossRef]
- Wu, N.; Geng, G.; Qin, X.; Tong, D.; Zheng, Y.; Lei, Y.; Zhang, Q. Daily emission patterns of coal-fired power plants in China based on multisource data fusion. ACS Environ. Au 2022, 2, 363–372. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Shi, Y. Estimating CO2 emissions from large-scale coal-fired power plants using OCO-2 observations and emission inventories. Atmosphere 2021, 12, 811. [Google Scholar] [CrossRef]
- Sun, J.; Kong, X.; Chen, Y. Review of carbon emission accounting methods for the whole process of power systems. Autom. Electr. Power Syst. 2024, 1–14. Available online: https://link.cnki.net/urlid/32.1180.TP.20240410.1325.002 (accessed on 19 December 2024).
- Hu, Z.; Yuan, Y.; Li, X.; Wang, Y.; Dacres, O.D.; Yi, L.; Liu, X.; Hu, H.; Liu, H.; Luo, G.; et al. “Thermal-dissolution based carbon enrichment” treatment of biomass: Modeling and kinetic study via combined lumped reaction model and machine learning algorithm. Fuel 2022, 324, 124701. [Google Scholar] [CrossRef]
- Tang, Q.; Chen, Y.; Yang, H.; Liu, M.; Xiao, H.; Wang, S.; Chen, H.; Naqvi, S.R. Machine learning prediction of pyrolytic gas yield and compositions with feature reduction methods: Effects of pyrolysis conditions and biomass characteristics. Bioresour. Technol. 2021, 339, 125581. [Google Scholar] [CrossRef]
- Gupta, A.; Gowda, S.; Tiwari, A.; Gupta, A.K. XGBoost-SHAP framework for asphalt pavement condition evaluation. Constr. Build. Mater. 2024, 426, 136182. [Google Scholar] [CrossRef]
- Zhu, C.; Shi, P.; Li, Z.; Li, M.; Zhang, H.; Ding, T. Carbon emission prediction of thermal power plants based on machine learning techniques. In Proceedings of the 5th International Conference on Energy, Electrical and Power Engineering (CEEPE), Chongqing, China, 22–24 April 2022. [Google Scholar] [CrossRef]
- Saleh, C.; Dzakiyullah, N.R.; Nugroho, J.B. Carbon dioxide emission prediction using support vector machine. IOP Conf. Ser. Mater. Sci. Eng. 2016, 114, 12148–12155. [Google Scholar] [CrossRef]
- Zhou, S.; He, H.; Zhang, L.; Zhao, W.; Wang, F. A data-driven method to monitor carbon dioxide emissions of coal-fired power plants. Energies 2023, 16, 1646. [Google Scholar] [CrossRef]
- Liao, Y.; Zhong, J.; Meng, X.; Sun, L.W.; Fan, J.H. Research on the prediction model of CO2 emission based on different operating conditions for 100MW boiler. In Proceedings of the New Energy and Sustainable Development Conference(NESD), Changsha, China, 19–20 March 2016; pp. 458–467. [Google Scholar] [CrossRef]
- Chen, J.; Zheng, L.; Che, W.; Liu, L.; Huang, H.; Liu, J.; Xing, C.; Qiu, P. A method for measuring carbon emissions from power plants using a CNN-LSTM-Attention model with Bayesian optimization. Case Stud. Therm. Eng. 2024, 63, 105334. [Google Scholar] [CrossRef]
- Cheng, D.; Xiao, J.; Sun, L.; Liu, Y.; Feng, Y.; Kang, Y.; Ma, L.; Lu, H. Research on CO2 emission prediction of coal-fired power plant based on RBF neural network. In Proceedings of the 2023 IEEE International Conference on Smart Electrical Grid and Renewable Energy, Changsha, China, 16–19 June 2023. [Google Scholar] [CrossRef]
- Chen, X.; Qian, X.; Song, W. Image Classification Algorithm Based on Lightweight Feature Fusion Convolutional Network. Comput. Eng. 2021, 47, 268–275. [Google Scholar] [CrossRef]
- Buyukkececi, M.; Okur, M.C. An Empirical Evaluation of Feature Selection Stability and Classification Accuracy. Gazi Univ. J. Sci. 2024, 37, 606–620. [Google Scholar] [CrossRef]
- Li, P.; Zhou, W.; Bai, X.; Chen, C.; Liu, S.; Sun, T. Carbon emission performance calculation and impact analysis of coal-fired power plants. Clean Coal Technol. 2024, 30, 66–74. [Google Scholar] [CrossRef]
- Lima, M.T.; do Nascimento, D.C.; Pimentel, B.A. Optimization on selecting XGBoost hyperparameters using meta-learning. Expert Syst. 2024, 41, e13611. [Google Scholar] [CrossRef]
- Wojciuk, M.; Swiderska-Chadaj, Z.; Siwek, K.; Gertych, A. Improving classification accuracy of fine-tuned CNN models: Impact of hyperparameter optimization. Heliyon 2024, 10, e26586. [Google Scholar] [CrossRef] [PubMed]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Li, Q.; Du, Z.; Chen, Z.; Huang, X.; Li, Q. Multiview Deep Forest for Overall Survival Prediction in Cancer. Comput. Math. Methods Med. 2023, 2023, 7931321. [Google Scholar] [CrossRef]
- Liu, B.; Sun, Y.; Gao, L. An improved container-based deep forest model for predicting groundwater recharge. J. Phys. Conf. Ser. 2024, 2816, 012033. [Google Scholar] [CrossRef]
- Ma, X.; Huo, Z.; Lu, J.; Wong, Y.D. Deep Forest with SHapley additive explanations on detailed risky driving behavior data for freeway crash risk prediction. Eng. Appl. Artif. Intell. 2024, 141, 109787. [Google Scholar] [CrossRef]
- Sharma, A.; Singh, M. Batch reinforcement learning approach using recursive feature elimination for network intrusion detection. Eng. Appl. Artif. Intell. 2024, 136, 109013. [Google Scholar] [CrossRef]
- Benjamin, K.J.M.; Katipalli, T.; Paquola, A.C.M. DRFEtools: Dynamic recursive feature elimination for omics. Bioinformatics 2023, 39, btad513. [Google Scholar] [CrossRef]
- Idris, N.F.; Ismail, M.A.; Jaya, M.I.M.; Ibrahim, A.O.; Abulfaraj, A.W.; Binzagr, F. Stacking with Recursive Feature Elimination-Isolation Forest for classification of diabetes mellitus. PLoS ONE 2024, 19, e0302595. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Feng, J. Deep Forest: Towards an Alternative to Deep Neural Networks. arXiv 2017. [Google Scholar] [CrossRef]
- Tan, Q.; Wen, Y.; Xu, Y.; Liu, K.; He, S.; Bo, X. Multi-view uncertainty deep forest: An innovative deep forest equipped with uncertainty estimation for drug-induced liver injury prediction. Inf. Sci. 2024, 667, 120342. [Google Scholar] [CrossRef]
- Zhou, T.; Sun, X.; Xia, X.; Li, B.; Chen, X. Improving defect prediction with deep forest. Inf. Softw. Technol. 2019, 114, 204–216. [Google Scholar] [CrossRef]
- Ma, C.; Liu, Z.; Cao, Z.; Song, W.; Zhang, J.; Zeng, W. Cost-sensitive deep forest for price prediction. Pattern Recognit. 2020, 107, 107499. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, New York, NY, USA, 4–8 August 2019. [Google Scholar] [CrossRef]
- Li, Y.; Hu, L.; Li, N.; Shen, W. A light attention-mixed-base deep learning architecture toward process multivariable modeling and knowledge discovery. Comput. Chem. Eng. 2023, 174, 108259. [Google Scholar] [CrossRef]
- Almarzooq, H.; Bin Waheed, U. Automating hyperparameter optimization in geophysics with Optuna: A comparative study. Geophys. Prospect. 2024, 72, 1778–1788. [Google Scholar] [CrossRef]
- Li, Y.; Cao, Y.; Yang, J.; Wu, M.; Yang, A.; Li, J. Optuna-DFNN: An Optuna framework-driven deep fuzzy neural network for predicting sintering performance in big data. Alex. Eng. J. 2024, 97, 100–113. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, L.; Wang, Q.; Chen, Y.; Yang, Q.; Xing, L.; Ba, S. A novel deep learning carbon price short-term prediction model with dual-stage attention mechanism. Appl. Energy 2023, 347, 121380. [Google Scholar] [CrossRef]




| Type of Features | Features Name | |||
|---|---|---|---|---|
| Boiler Operating Parameters | Load | Boiler Efficiency | Main Steam Flow | Total Coal Feed |
| Main Steam Pressure | Main Steam Temperature | |||
| Flue Gas Parameters | Standard Gas Flow | Flue Gas Oxygen at SCR Inlet | ||
| Oxygen Level at Air Preheater Outlet | ||||
| Temperature Parameters | Air Supply Temperature | Flue Gas Temperature | ||
| Air Preheater Outlet Primary Air Temperature | ||||
| Flue Gas Pollutant Parameters | SCR Inlet NOx Value | SCR Outlet NOx Value | ||
| Total Ammonia Injection Flow | Desulfurization Inlet SO2 Value | |||
| Coal Quality Parameters | SCR Inlet NOx Value | SCR Outlet NOx Value | ||
| Total Ammonia Injection Flow | Desulfurization Inlet SO2 Value | |||
| Key Features Name | Mean | Median | Standard Deviation |
|---|---|---|---|
| A-side air preheater differential pressure (kPa) | 0.77 | 0.78 | 0.12 |
| B-side air preheater differential pressure (kPa) | 0.79 | 0.79 | 0.17 |
| Main steam flow (t/h) | 696.26 | 694.48 | 97.47 |
| Total feed water flow (t/h) | 736.25 | 735.05 | 95.09 |
| Total ammonia injection flow (t/h) | 319.10 | 333.86 | 175.31 |
| Hyperparameters Name | Setting | Hyperparameters Name | Setting |
|---|---|---|---|
| DF_N_estimators | 2 | RF_N_estimators | 50 |
| DF_Max_layers | None | RF_Max_depth | 3 |
| DF_N_trees | 100 | RF_Min_samples_split | 4 |
| DF_Max_depth | None | RF_Min_samples_leaf | 5 |
| DF_Min_samples_split | 2 | RF_Max_Features | none |
| XGBoost_N_estimators | 100 | SVR_Kernel | rbf |
| XGBoost_Max_depth | 6 | SVR_C | 1.0 |
| XGBoost_Learning_rate | 0.3 | SVR_Epsilon | 0.1 |
| XGBoost_Colsample_bytree | 1 | XGBoost_Subsample | 1 |
| Hyperparameters Name | Searching Range | Best Hyperparameters |
|---|---|---|
| SVR_Kernel | [1, 100] | 29.72 |
| SVR_C | [0.01, 0.5] | 0.0549 |
| SVR_Epsilon | [rbf, poly] | poly |
| RF_N_estimators | [30, 100] | 89 |
| RF_Max_depth | [3, 8] | 7 |
| RF_Min_samples_split | [2, 10] | 4 |
| RF_Min_samples_leaf | [3, 10] | 3 |
| RF_Max_Features | [sqrt, log2, none] | sqrt |
| XGBoost_N_estimators | [50, 200] | 200 |
| XGBoost_Max_depth | [3, 10] | 6 |
| XGBoost_Learning_rate | [0.01, 0.3] | 0.0114 |
| XGBoost_Colsample_bytree | [0.5, 1] | 0.7899 |
| XGBoost_Subsample | [0.5, 1] | 0.8735 |
| DF_N_estimators | [30, 100] | 86 |
| DF_Max_layers | [2, 5] | 2 |
| DF_N_trees | [30, 100] | 34 |
| DF_Max_depth | [3, 8] | 4 |
| DF_Min_samples_split | [3, 10] | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, K.; Wang, Y.; Li, X.; Wang, X.; Hu, Z.; Luo, B.; Shi, L.; Li, M.; Luo, G.; Yao, H. CO2 Emission Prediction for Coal-Fired Power Plants by Random Forest-Recursive Feature Elimination-Deep Forest-Optuna Framework. Energies 2024, 17, 6449. https://doi.org/10.3390/en17246449
Tu K, Wang Y, Li X, Wang X, Hu Z, Luo B, Shi L, Li M, Luo G, Yao H. CO2 Emission Prediction for Coal-Fired Power Plants by Random Forest-Recursive Feature Elimination-Deep Forest-Optuna Framework. Energies. 2024; 17(24):6449. https://doi.org/10.3390/en17246449
Chicago/Turabian StyleTu, Kezhi, Yanfeng Wang, Xian Li, Xiangxi Wang, Zhenzhong Hu, Bo Luo, Liu Shi, Minghan Li, Guangqian Luo, and Hong Yao. 2024. "CO2 Emission Prediction for Coal-Fired Power Plants by Random Forest-Recursive Feature Elimination-Deep Forest-Optuna Framework" Energies 17, no. 24: 6449. https://doi.org/10.3390/en17246449
APA StyleTu, K., Wang, Y., Li, X., Wang, X., Hu, Z., Luo, B., Shi, L., Li, M., Luo, G., & Yao, H. (2024). CO2 Emission Prediction for Coal-Fired Power Plants by Random Forest-Recursive Feature Elimination-Deep Forest-Optuna Framework. Energies, 17(24), 6449. https://doi.org/10.3390/en17246449





