Research on the Economic Scheduling Problem of Cogeneration Based on the Improved Artificial Hummingbird Algorithm
Abstract
1. Introduction
2. Formulation of the CHPED Problem
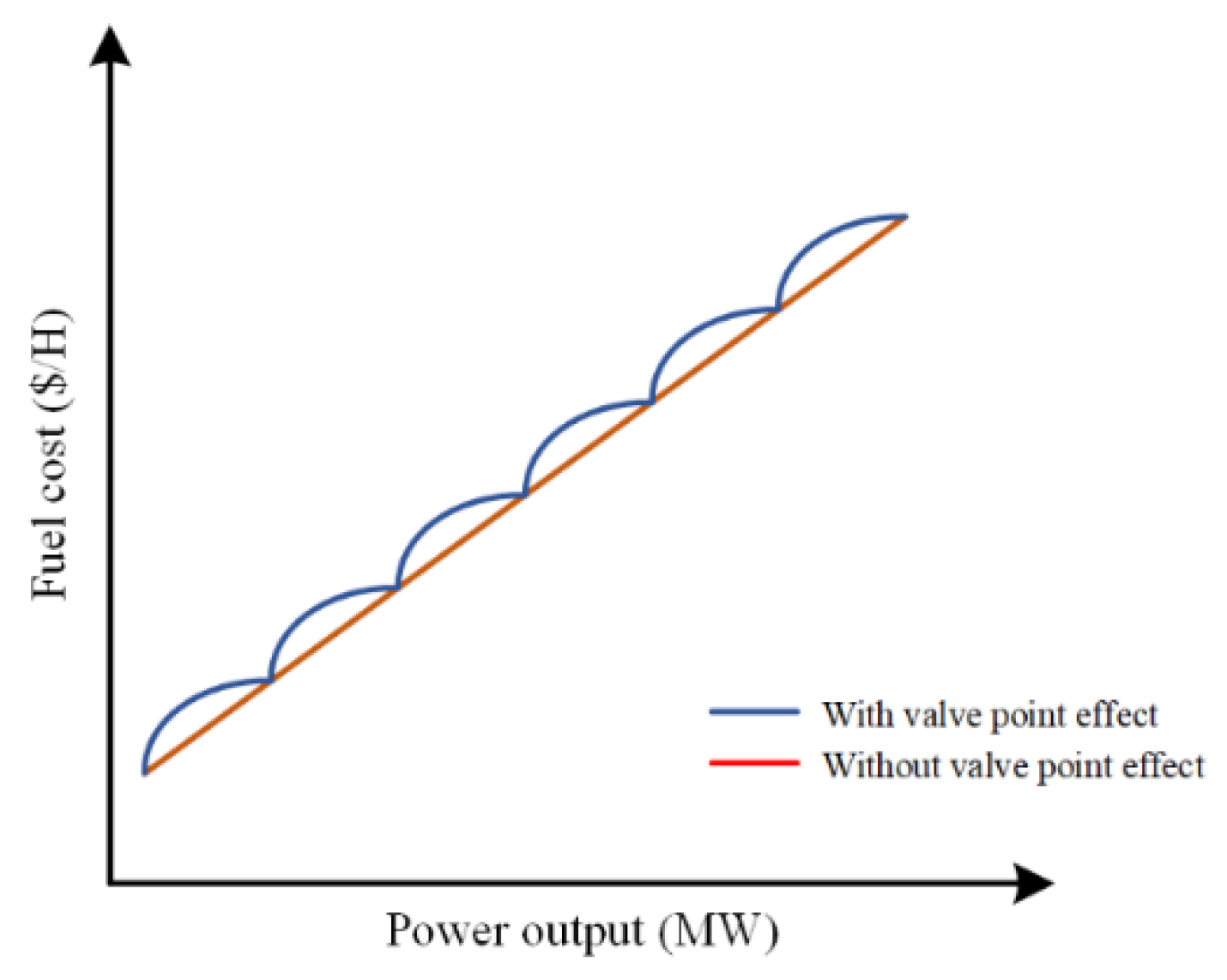
2.1. Objective Function
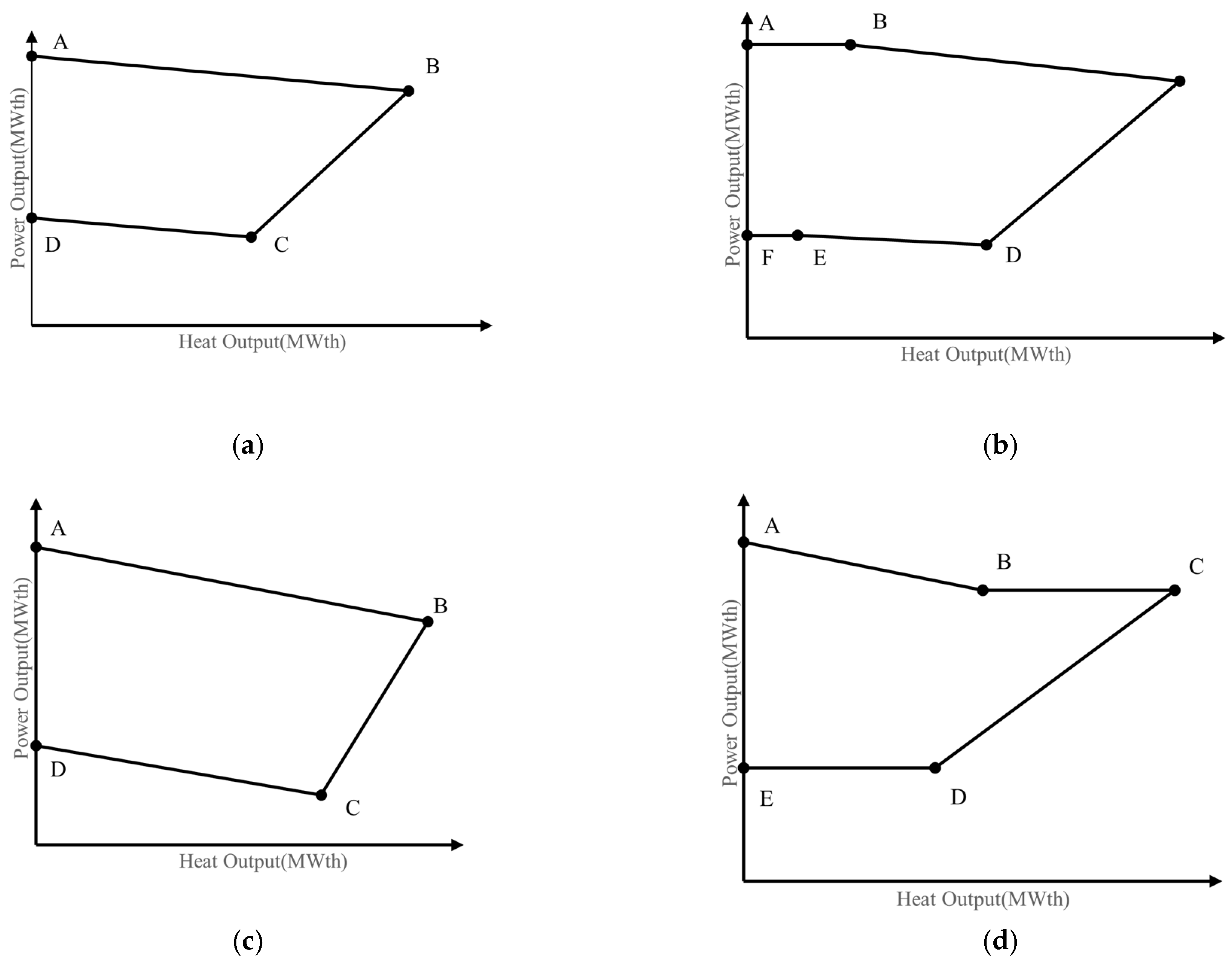
2.2. Optimization Constraints
2.3. Constraint Repair Technique
2.3.1. Equality Constraint Handling
- 1.
- For the power-only units, is repaired as in Equation (13):
- 2.
- For the heat-only units, is repaired as in Equation (14):
- 3.
- For the CHP units, the power and heat output are interrelated and mutually restricted. and are calculated based on . Then, is repaired as in Equation (15):
2.3.2. Handling of Equality Constraints
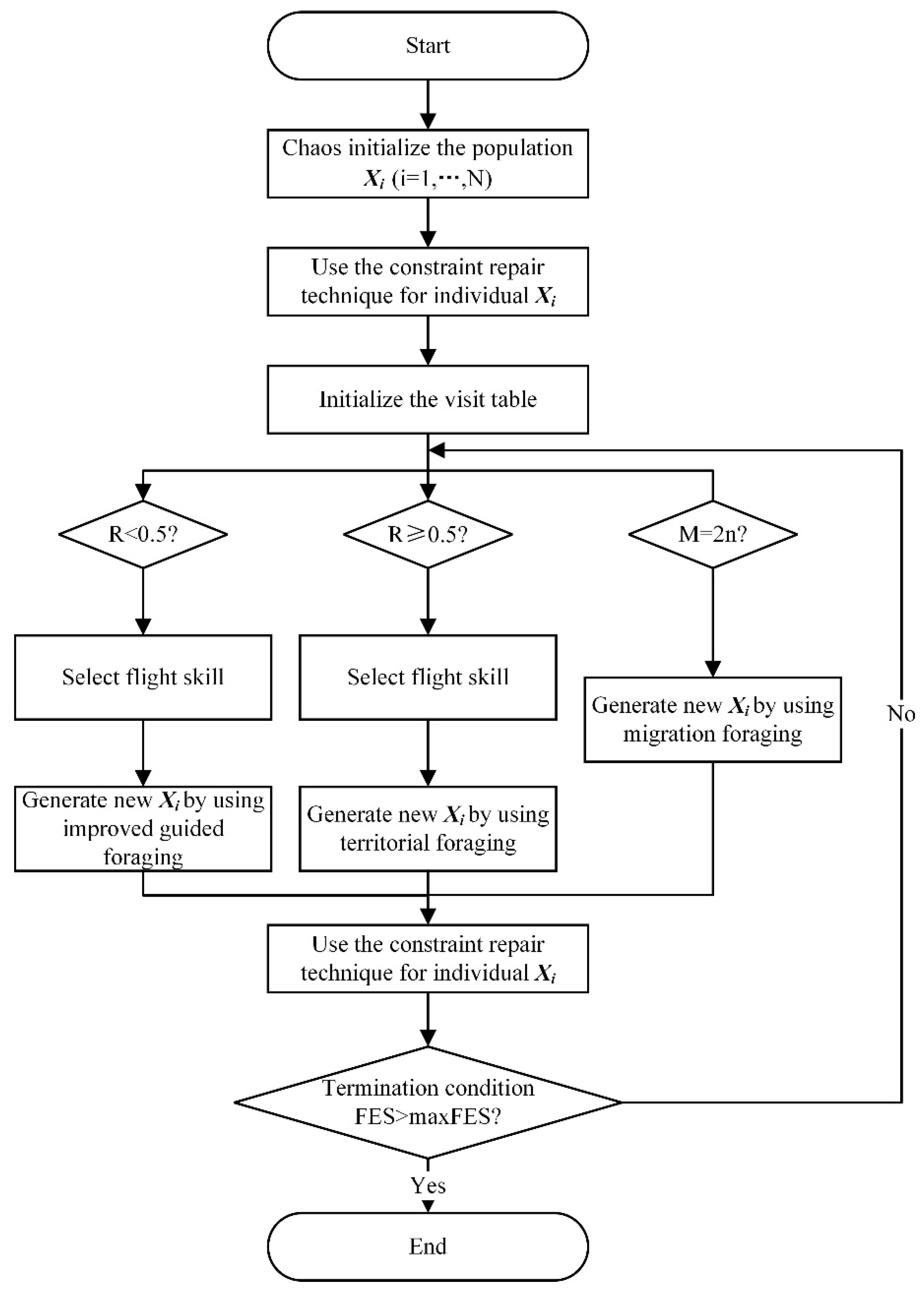
3. Improved Artificial Hummingbird Algorithm
3.1. Introduction of the Artificial Hummingbird Algorithm
3.1.1. Flight Patterns
3.1.2. Foraging Methods
3.2. Improving the Artificial Hummingbird Algorithm
3.2.1. Initial Solution
3.2.2. Modify Update Mechanism
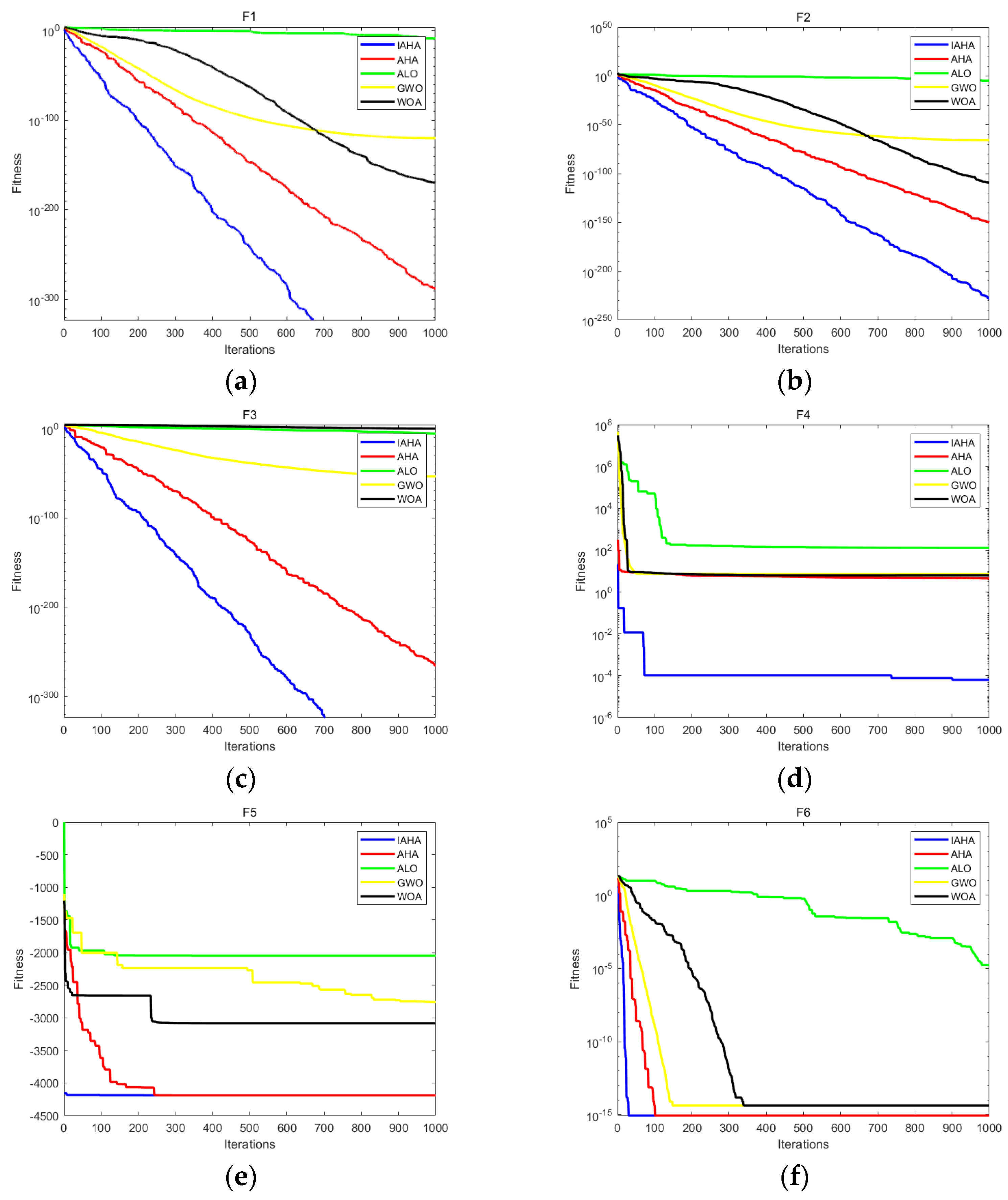
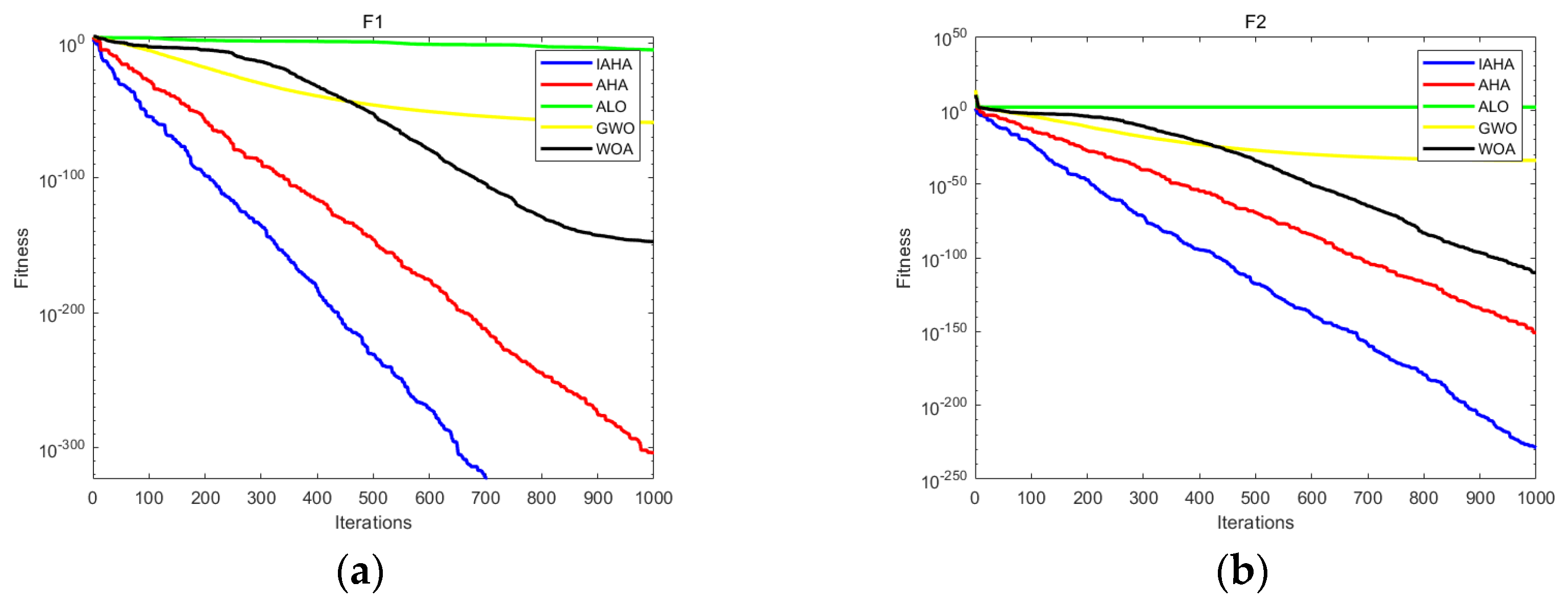
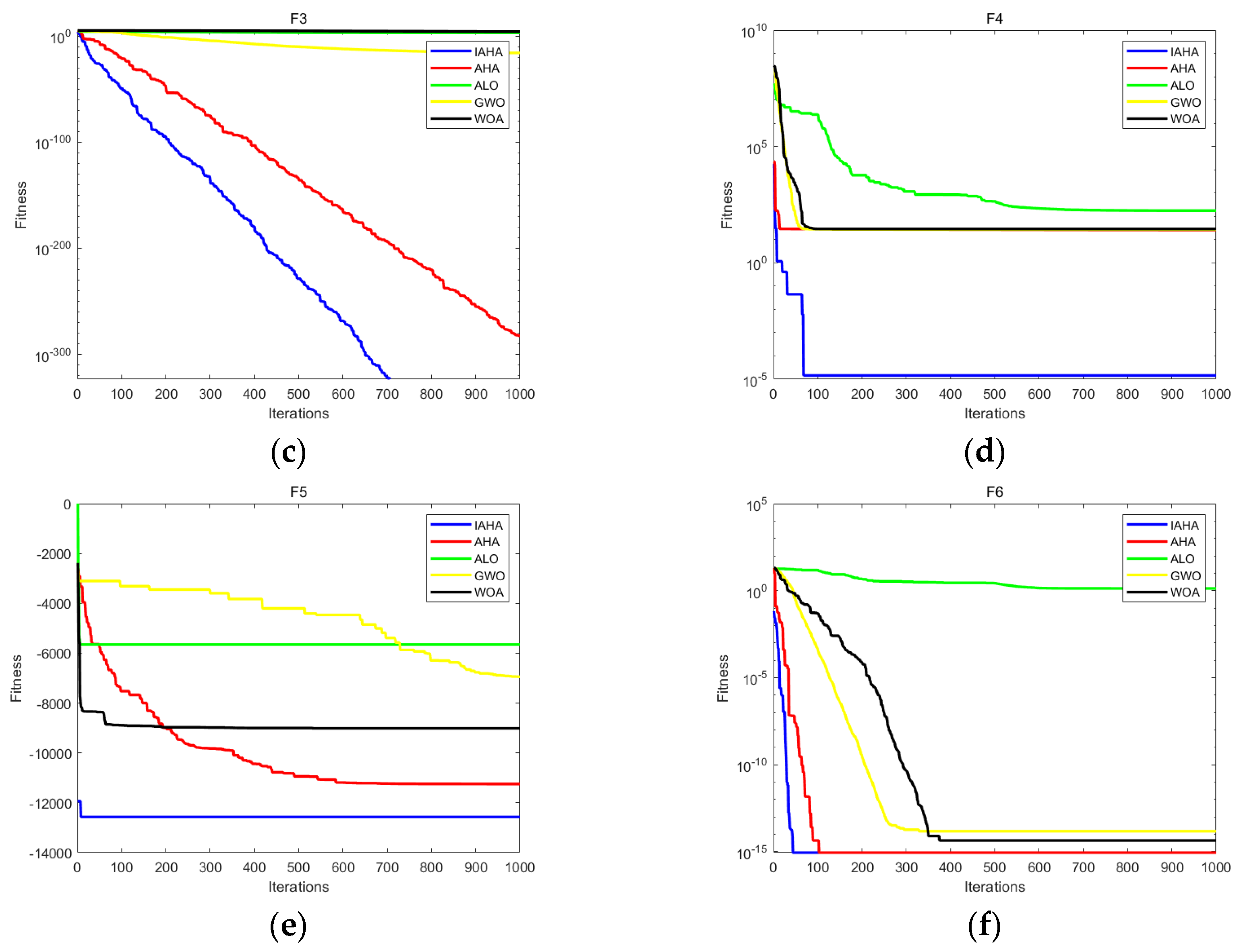
4. Performance Verification of the IAHA
5. Experimental Results
5.1. Population Coding
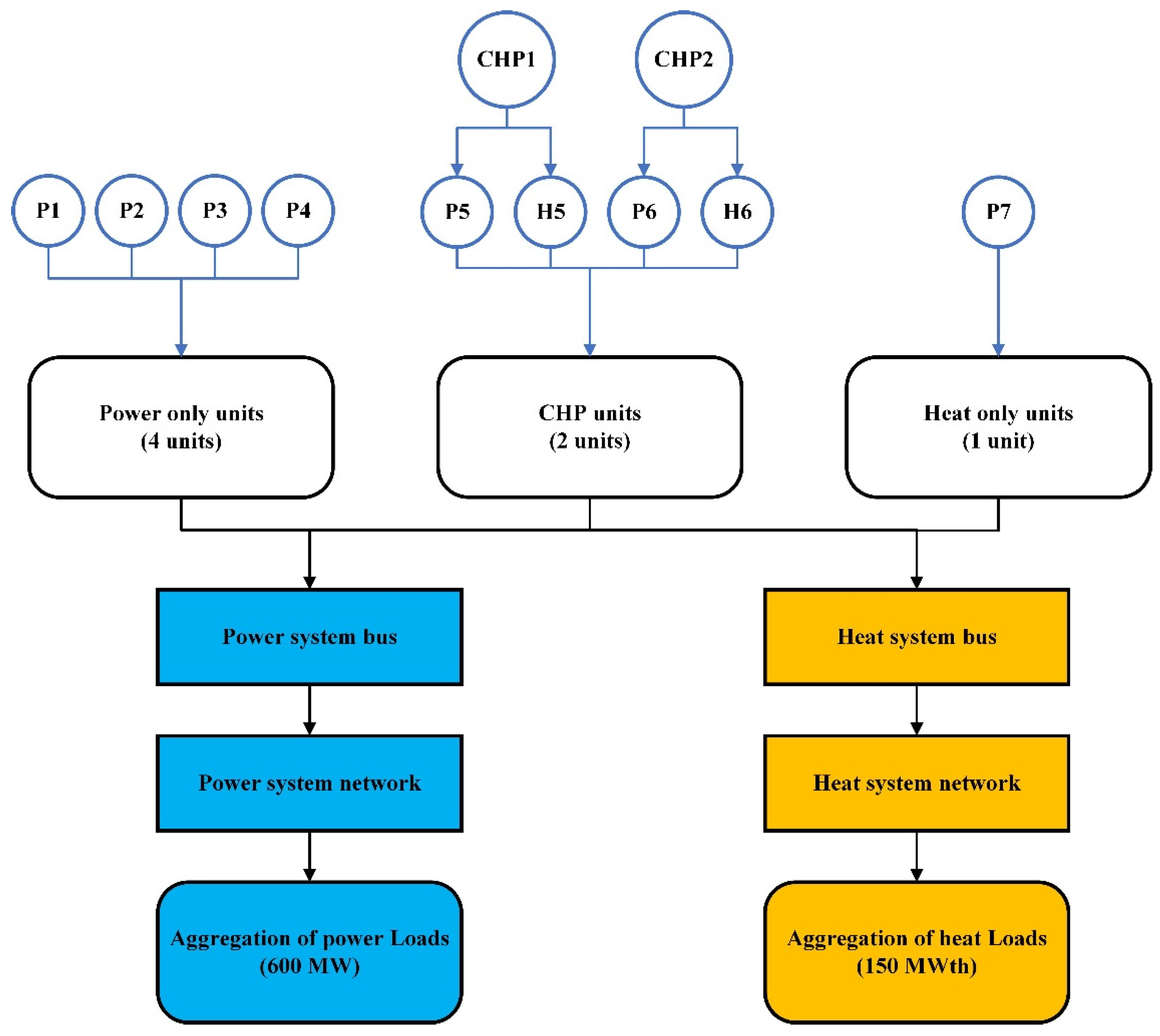
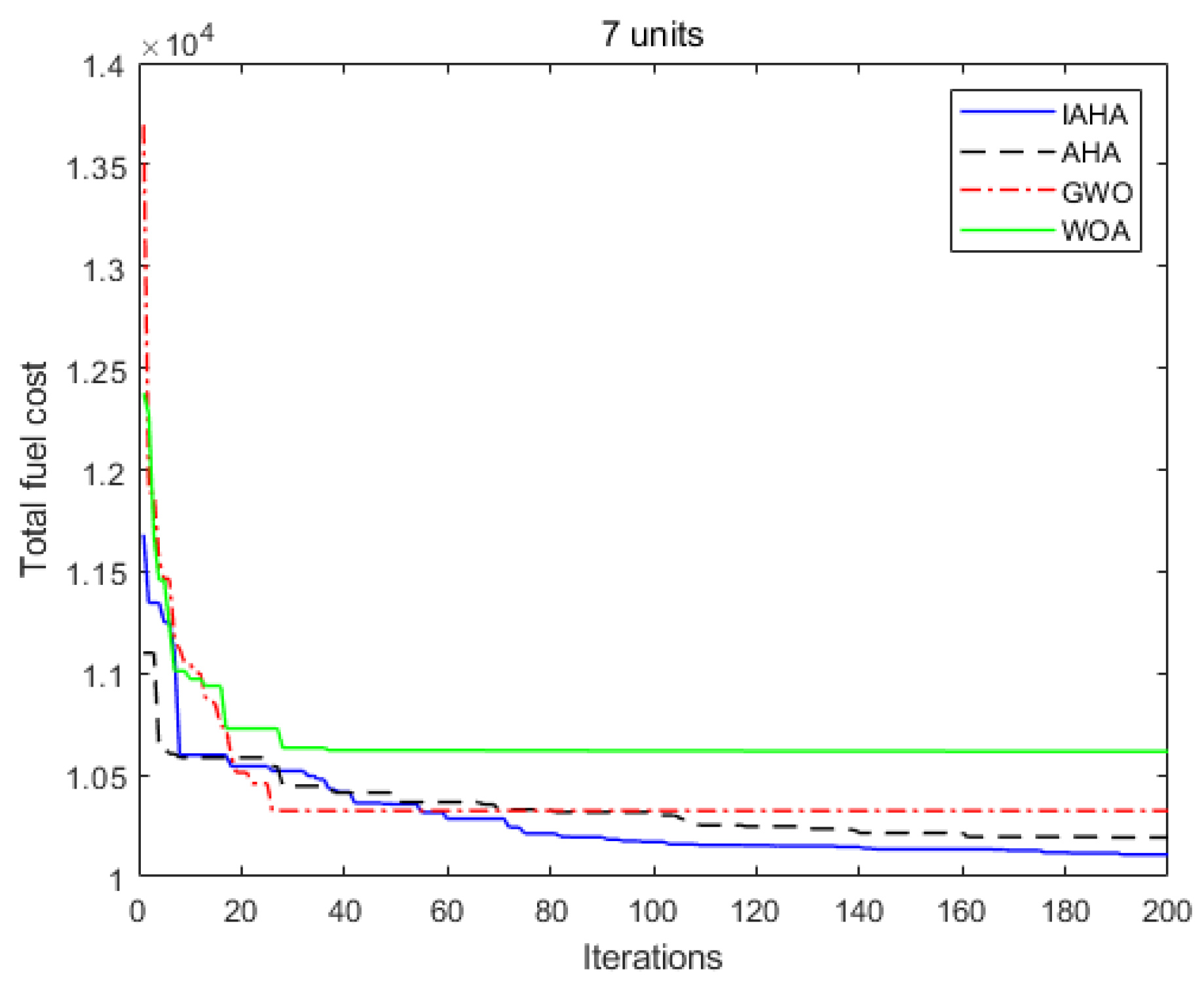
5.2. Test System 1: 7-Unit CHPED Problem
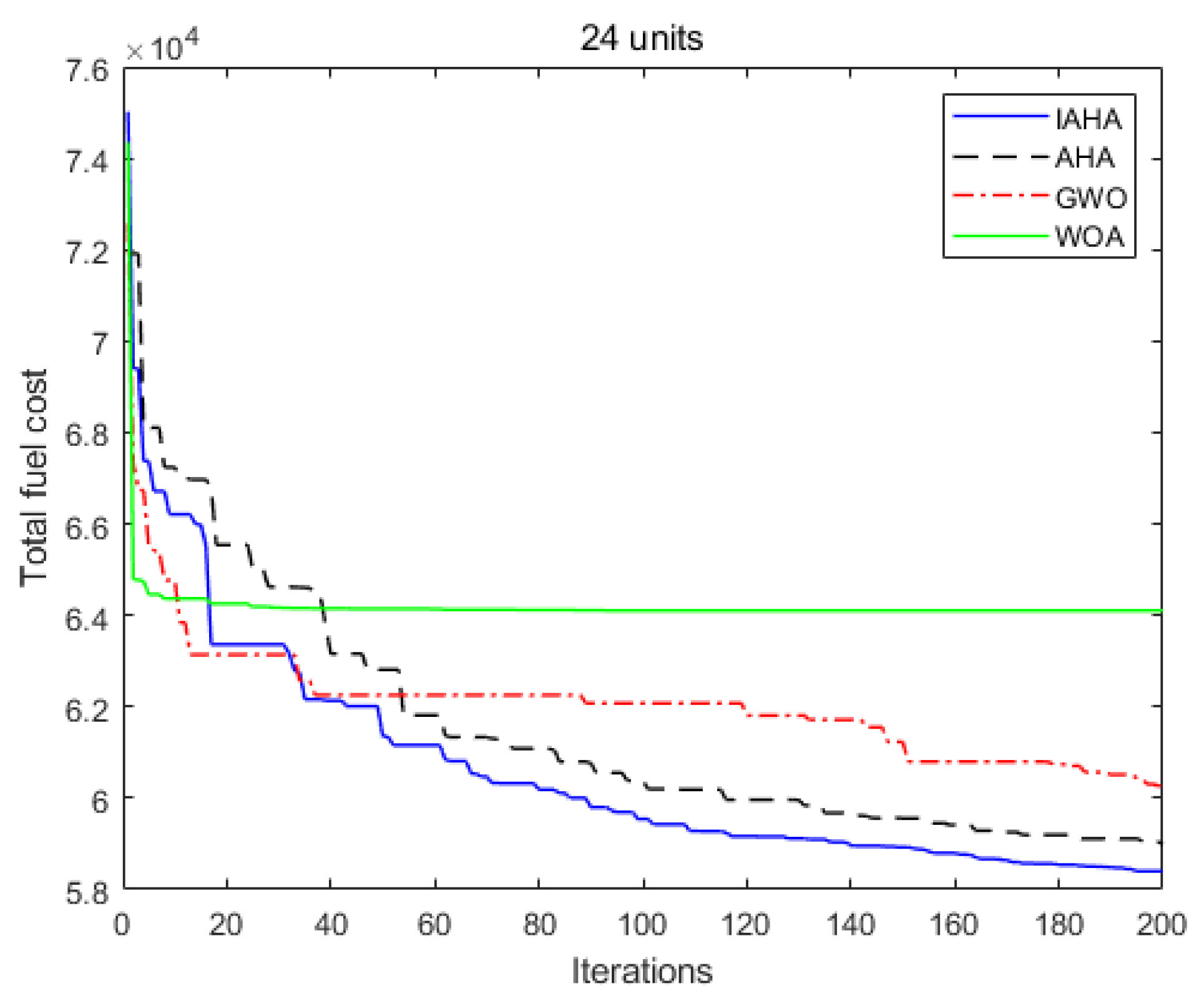
5.3. Test System 2: 24-Unit CHPED Problem
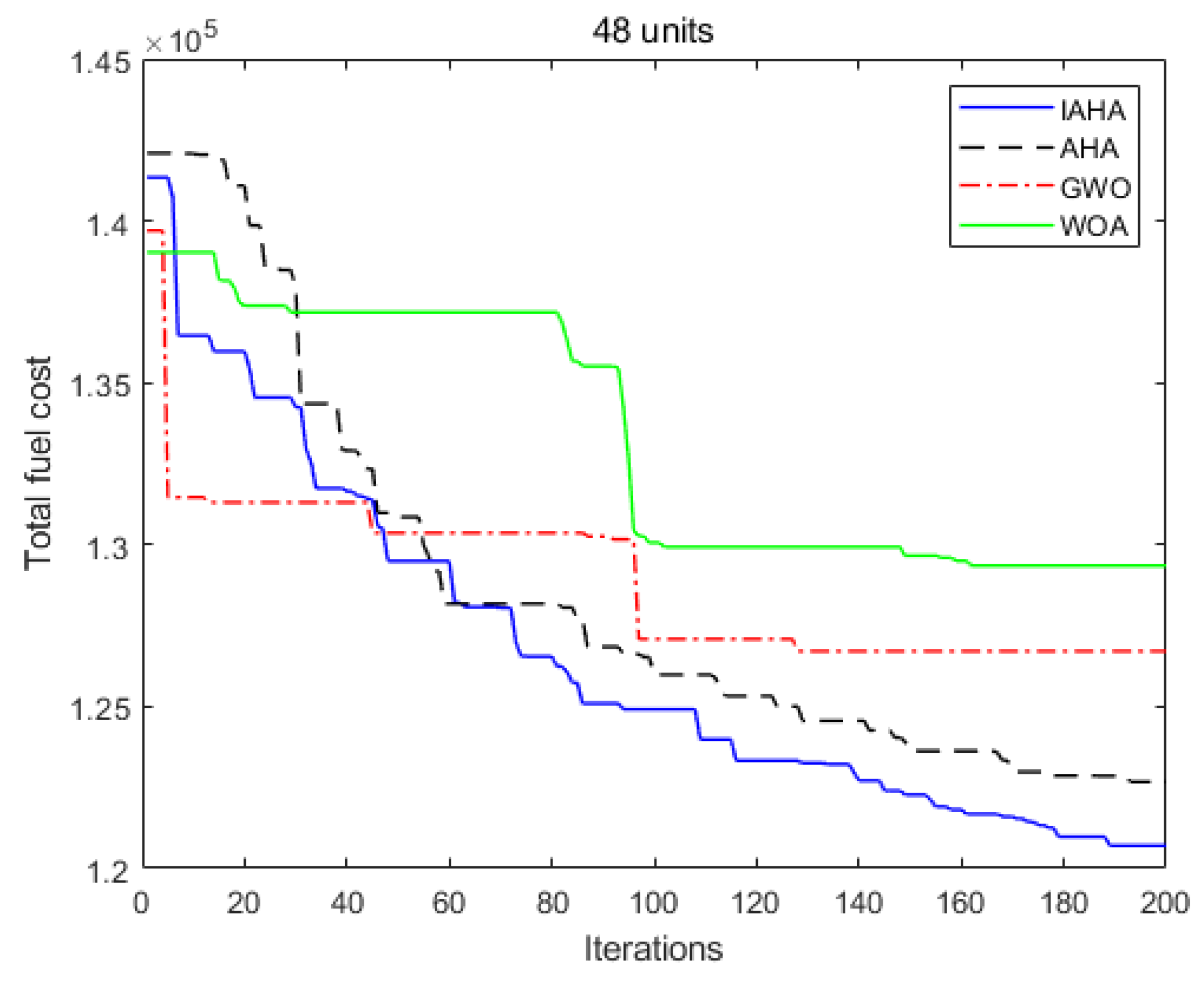
6. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, W.; Zhang, Y.; Zhu, X.; Li, K.; Yang, Z. Research on Dynamic Economic Dispatch Optimization Problem Based on Improved Grey Wolf Algorithm. Energies 2024, 17, 1491. [Google Scholar] [CrossRef]
- Li, D.; Yang, C. A Modified Genetic Algorithm for Combined Heat and Power Economic Dispatch. J. Bionic Eng. 2024, 21, 2569–2586. [Google Scholar] [CrossRef]
- Wang, S.K.; Zhang, L.; Liu, C.; Liu, Z.M.; Lan, S.; Li, Q.B.; Wang, X.N. Techno-economic-environmental evaluation of a combined cooling heating and power system for gas turbine waste heat recovery. Energy 2021, 231, 15. [Google Scholar] [CrossRef]
- Xiao, T.Y.; Liu, C.; Wang, X.R.; Wang, S.K.; Xu, X.X.; Li, Q.B.; Li, X.X. Life cycle assessment of the solar thermal power plant integrated with air-cooled supercritical CO2 Brayton cycle. Renew. Energy 2022, 182, 15. [Google Scholar] [CrossRef]
- Chen, X.; Shen, A. Self-adaptive differential evolution with Gaussian–Cauchy mutation for large-scale CHP economic dispatch problem. Neural Comput. Appl. 2022, 34, 11769–11787. [Google Scholar] [CrossRef]
- Kaur, P.; Chaturvedi, K.T.; Kolhe, M.L. Techno-Economic Power Dispatching of Combined Heat and Power Plant Considering Prohibited Operating Zones and Valve Point Loading. Processes 2022, 10, 817. [Google Scholar] [CrossRef]
- Miller, T.; Durlik, I.; Kostecka, E.; Kozlovska, P.; Jakubowski, A.; Łobodzińska, A. Waste Heat Utilization in Marine Energy Systems for Enhanced Efficiency. Energies 2024, 17, 5653. [Google Scholar] [CrossRef]
- Jadoun, V.K.; Prashanth, G.R.; Joshi, S.S.; Agarwal, A.; Almutairi, A. Optimal Scheduling of Non-Convex Cogeneration Units Using Exponentially Varying Whale Optimization Algorithm. Energies 2021, 14, 1008. [Google Scholar] [CrossRef]
- Zou, D.; Ma, L.; Li, C. An enhanced NSGA-II and a fast constraint repairing method for combined heat and power dynamic economic emission dispatch. Inf. Sci. 2024, 678, 120915. [Google Scholar] [CrossRef]
- Wong, K.P.; Algie, C. Evolutionary programming approach for combined heat and power dispatch. Electr. Power Syst. Res. 2002, 61, 227–232. [Google Scholar] [CrossRef]
- Rooijers, F.J.; Van Amerongen, R.A.M. Static economic dispatch for co-generation systems. Power Syst. IEEE Trans. 1994, 9, 1392–1398. [Google Scholar] [CrossRef]
- Haghrah, A.; Nekoui, M.; Nazari-Heris, M.; Mohammadi-Ivatloo, B. An improved real-coded genetic algorithm with random walk based mutation for solving combined heat and power economic dispatch. J. Ambient Intell. Humaniz. Comput. 2021, 12, 8561–8584. [Google Scholar] [CrossRef]
- Liu, D.; Hu, Z.; Su, Q.; Liu, M. A niching differential evolution algorithm for the large-scale combined heat and power economic dispatch problem. Appl. Soft Comput. 2021, 113, 108017. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Elsayed, A.M.; Ginidi, A.R.; El-Sehiemy, R.A.; Ghoneim, S.S.M. A novel improved marine predators algorithm for combined heat and power economic dispatch problem. AEJ-Alex. Eng. J. 2021, 61, 1834–1851. [Google Scholar] [CrossRef]
- Ramachandran, M.; Mirjalili, S.; Ramalingam, M.M.; Gnanakkan, C.A.R.C.; Parvathysankar, D.S.; Sundaram, A. A ranking-based fuzzy adaptive hybrid crow search algorithm for combined heat and power economic dispatch. Expert Syst. Appl. 2022, 197, 116625. [Google Scholar] [CrossRef]
- Sun, J.; Deng, J.; Li, Y. Indicator & crowding Distance-Based Evolutionary Algorithm for Combined Heat and Power Economic Emission Dispatch. arXiv 2020, arXiv:2002.11513. [Google Scholar]
- Zhou, T.; Chen, J.; Xu, X.; Ou, Z.; Yin, H.; Luo, J.; Meng, A. A novel multi-agent based crisscross algorithm with hybrid neighboring topology for combined heat and power economic dispatch. Appl. Energy 2023, 342, 121167. [Google Scholar] [CrossRef]
- Pattanaik, J.K.; Basu, M.; Dash, D.P. Heat transfer search algorithm for combined heat and power economic dispatch. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 963–978. [Google Scholar] [CrossRef]
- Ozkaya, B.; Duman, S.; Kahraman, H.T.; Guvenc, U. Optimal solution of the combined heat and power economic dispatch problem by adaptive fitness-distance balance based artificial rabbits optimization algorithm. Expert Syst. Appl. 2024, 238, 122272. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Asadi, S.; Geem, Z.W. Large-Scale Combined Heat and Power Economic Dispatch Using a Novel Multi-Player Harmony Search Method. Appl. Therm. Eng. 2019, 154, 493–504. [Google Scholar] [CrossRef]
- Huang, Z.; Gao, Z.; Qi, L.; Duan, H. A Heterogeneous Evolving Cuckoo Search Algorithm for Solving Large-scale Combined Heat and Power Economic Dispatch Problems. IEEE Access 2019, 7, 111287–111301. [Google Scholar] [CrossRef]
- Rabiee, A.; Jamadi, M.; Mohammadi-Ivatloo, B.; Ahmadian, A. Optimal Non-Convex Combined Heat and Power Economic Dispatch via Improved Artificial Bee Colony Algorithm. Processes 2020, 8, 1036. [Google Scholar] [CrossRef]
- Spea, S.R. Social network search algorithm for combined heat and power economic dispatch. Electr. Power Syst. Res. 2023, 221, 109400. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, X.B.; Yang, L.; Li, J.; Zhang, J.; Liu, Y.L.; Sun, Y.J.; Yan, F. Research on Load Optimal Dispatch for High-Temperature CHP Plants through Grey Wolf Optimization Algorithm with the Levy Flight. Processes 2022, 10, 1546. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Ramachandran, M.; Mirjalili, S.; Nazari-Heris, M.; Parvathysankar, D.S.; Sundaram, A.; Gnanakkan, C. A hybrid Grasshopper Optimization Algorithm and Harris Hawks Optimizer for Combined Heat and Power Economic Dispatch problem. Eng. Appl. Artif. Intell. 2022, 111, 39. [Google Scholar] [CrossRef]
- Zhao, W.G.; Wang, L.Y.; Mirjalili, S. Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications. Comput. Meth. Appl. Mech. Eng. 2022, 388, 45. [Google Scholar] [CrossRef]
- Kansal, V.; Dhillon, J.S.; Yan, J. Ameliorated artificial hummingbird algorithm for coordinated wind-solar-thermal generation scheduling problem in multiobjective framework. Appl. Energy 2022, 326, 120031. [Google Scholar] [CrossRef]
- Ozkaya, B.; Kahraman, H.T.; Duman, S.; Guvenc, U.; Akbel, M. Combined heat and power economic emission dispatch using dynamic switched crowding based multi-objective symbiotic organism search algorithm. Appl. Soft Comput. 2024, 151, 111106. [Google Scholar] [CrossRef]
- Chen, X.; Fang, S.; Li, K. Reinforcement-Learning-Based Multi-Objective Differential Evolution Algorithm for Large-Scale Combined Heat and Power Economic Emission Dispatch. Energies 2023, 16, 3753. [Google Scholar] [CrossRef]
- Mekhamer, S.; Abdelaziz, A.; Badr, M.; Kamh, M. Enhancing the performance of Hopfield neural network applied to the economic dispatch problem. In Proceedings of the 2006 Eleventh International Middle East Power Systems Conference, El-Minia, Egypt, 19–21 December 2006; pp. 347–352. [Google Scholar]
- Yin, L.; Sun, Z. Multi-layer distributed multi-objective consensus algorithm for multi-objective economic dispatch of large-scale multi-area interconnected power systems. Appl. Energy 2021, 300, 117391. [Google Scholar] [CrossRef]
- Yang, W.; Zhu, X.; Nie, F.; Jiao, H.; Xiao, Q.; Yang, Z. Chaos Moth Flame Algorithm for Multi-Objective Dynamic Economic Dispatch Integrating with Plug-In Electric Vehicles. Electronics 2023, 12, 2742. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Basu, M. Combined Heat and Power Economic Dispatch by Using Differential Evolution. Electr. Power Compon. Syst. 2010, 38, 996–1004. [Google Scholar] [CrossRef]
- Mohammadi-Ivatloo, B.; Moradi-Dalvand, M.; Rabiee, A. Combined heat and power economic dispatch problem solution using particle swarm optimization with time varying acceleration coefficients. Electr. Power Syst. Res. 2013, 95, 9–18. [Google Scholar] [CrossRef]
- Chen, X.; Li, K.; Xu, B.; Yang, Z. Biogeography-based learning particle swarm optimization for combined heat and power economic dispatch problem. Knowl.-Based Syst. 2020, 208, 106463. [Google Scholar] [CrossRef]
- Gafar, M.; Ginidi, A.; El-Sehiemy, R.; Sarhan, S. Improved SNS algorithm with high exploitative strategy for dynamic combined heat and power dispatch in co-generation systems. Energy Rep. 2022, 8, 8857–8873. [Google Scholar] [CrossRef]
- Zou, D.; Li, S.; Kong, X.; Ouyang, H.; Li, Z. Solving the combined heat and power economic dispatch problems by an improved genetic algorithm and a new constraint handling strategy. Appl. Energy 2019, 237, 646–670. [Google Scholar] [CrossRef]
- Ginidi, A.; Elsayed, A.; Shaheen, A.; Elattar, E.; El-Sehiemy, R. An Innovative Hybrid Heap-Based and Jellyfish Search Algorithm for Combined Heat and Power Economic Dispatch in Electrical Grids. Mathematics 2021, 9, 2053. [Google Scholar] [CrossRef]

| Table of Abbreviations | Abbreviations |
|---|---|
| 1. Artificial Hummingbird Algorithm | AHA [27] |
| 2. Ant Lion Optimizer | ALO [35] |
| 3. Grey Wolf Optimizer | GWO [34] |
| 4. Whale Optimization Algorithm | WOA [36] |
| 5. Improved Artificial Hummingbird Algorithm | IAHA |
| Algorithms | Parameter Settings | Iteration |
|---|---|---|
| Artificial Hummingbird Algorithm | NP = 30 | 1000 |
| Ant Lion Optimizer | NP = 30 | 1000 |
| Grey Wolf Optimizer | NP = 30 | 1000 |
| Whale Optimization Algorithm | NP = 30, b = 1 | 1000 |
| Improved Artificial Hummingbird Algorithm | NP = 30 | 1000 |
| Function Name | Dim | Range | Fmin |
|---|---|---|---|
| Sphere | 10/30/50 | [−100, 100] | 0 |
| Schwefel 2.22 | 10/30/50 | [−10, 10] | 0 |
| Schwefel 1.2 | 10/30/50 | [−100, 100] | 0 |
| Rosenbrock | 10/30/50 | [−30, 30] | 0 |
| Schwefel | 10/30/50 | [−500, 500] | −12,569.5 |
| Ackley | 10/30/50 | [−32, 32] | 0 |
| NO. | Statistics | ALO | GWO | WOA | AHA | IAHA |
|---|---|---|---|---|---|---|
| F1 | Mean | 2.67 × 10−9 | 4.07 × 10−117 | 1.02 × 10−157 | 2.12 × 10−277 | 0.00 |
| Sta | 1.16 × 10−9 | 1.99 × 10−116 | 4.69 × 10−157 | 0.00 | 0.00 | |
| Best | 1.09 × 10−9 | 1.08 × 10−123 | 8.64 × 10−174 | 1.02 × 10−310 | 0.00 | |
| Time (s) | 160.24 | 160.28 | 160.33 | 155.18 | 155.24 | |
| Winner | 1 | 1 | 1 | 1 | ||
| F2 | Mean | 2.69 × 10−1 | 2.98 × 10−67 | 1.49 × 10−106 | 4.24 × 10−144 | 3.25 × 10−226 |
| Sta | 7.77 × 10−1 | 4.99 × 10−67 | 6.20 × 10−106 | 1.56 × 10−143 | 0.00 | |
| Best | 6.57 × 10−6 | 1.78 × 10−69 | 9.19 × 10−106 | 1.13 × 10−154 | 1.74 × 10−242 | |
| Time (s) | 158.32 | 158.37 | 158.42 | 153.29 | 153.35 | |
| Winner | 1 | 1 | 1 | 1 | ||
| F3 | Mean | 9.38 × 10−6 | 5.46 × 10−52 | 2.35 × 101 | 1.73 × 10−244 | 0.00 |
| Sta | 1.05 × 10−5 | 2.03 × 10−51 | 8.07 × 101 | 0.00 | 0.00 | |
| Best | 1.09 × 10−7 | 1.10 × 10−64 | 3.56 × 10−10 | 1.70 × 10−278 | 0.00 | |
| Time (s) | 163.46 | 163.56 | 163.66 | 158.39 | 158.49 | |
| Winner | 1 | 1 | 1 | 1 | ||
| F4 | Mean | 5.21 × 10−1 | 0.65 × 101 | 0.62 × 101 | 0.45 × 101 | 1.87 × 10−4 |
| Sta | 1.04 × 102 | 0.09 × 101 | 0.04 × 101 | 0.04 × 101 | 6.58 × 10−4 | |
| Best | 5.15 × 10−4 | 0.47 × 101 | 0.55 × 101 | 0.34 × 101 | 4.4 × 10−7 | |
| Time (s) | 159.53 | 159.59 | 159.66 | 154.44 | 154.50 | |
| Winner | 1 | 1 | 1 | 1 | ||
| F5 | Mean | −2.47 × 103 | −2.71 × 103 | −3.37 × 103 | −4.19 × 103 | −4.19 × 103 |
| Sta | 6.42 × 10−2 | 2.96 × 10−2 | 6.06 × 10−2 | 2.80 × 10−7 | 3.13 × 10−3 | |
| Best | −4.19 × 103 | −3.23 × 103 | −4.19 × 103 | −4.19 × 103 | −4.19 × 103 | |
| Time (s) | 157.85 | 157.91 | 157.99 | 152.83 | 152.89 | |
| Winner | 1 | 1 | 1 | −1 | ||
| F6 | Mean | 1.60 × 10−1 | 4.67 × 10−15 | 4.09 × 10−15 | 8.88 × 10−16 | 8.88 × 10−16 |
| Sta | 5.03 × 10−1 | 9.01 × 10−16 | 2.16 × 10−15 | 0.00 | 0.00 | |
| Best | 1.50 × 10−5 | 4.44 × 10−15 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | |
| Time (s) | 344.87 | 344.92 | 344.98 | 339.82 | 339.87 | |
| Winner | 1 | 1 | 1 | −1 |
| NO. | Statistics | ALO | GWO | WOA | AHA | IAHA |
|---|---|---|---|---|---|---|
| F1 | Mean | 1.02 × 10−5 | 6.40 × 10−59 | 2.16 × 10−149 | 3.05 × 10−284 | 0.00 |
| Sta | 7.63 × 10−6 | 1.37 × 10−58 | 1.04 × 10−148 | 0.00 | 0.00 | |
| Best | 1.16 × 10−6 | 2.20 × 10−62 | 7.01 × 10−169 | 1.54 × 10−315 | 0.00 | |
| Time (s) | 663.6472 | 663.7312 | 663.7962 | 647.4758 | 649.5391 | |
| Winner | 1 | 1 | 1 | 1 | ||
| F2 | Mean | 4.34 × 101 | 7.84 × 10−35 | 8.90 × 10−104 | 5.01 × 10−148 | 1.05 × 10−224 |
| Sta | 5.26 × 101 | 4.84 × 10−35 | 4.51 × 10−103 | 1.71 × 10−147 | 0.00 | |
| Best | 1.99 × 10−2 | 4.96 × 10−36 | 1.06 × 10−112 | 1.06 × 10−162 | 3.71 × 10−245 | |
| Time (s) | 520.2035 | 520.2883 | 520.3485 | 506.1642 | 506.2296 | |
| Winner | 1 | 1 | 1 | 1 | ||
| F3 | Mean | 1.09 × 103 | 5.24 × 10−15 | 2.07 × 104 | 2.00 × 10−264 | 0.00 |
| Sta | 6.43 × 102 | 1.47 × 10−14 | 9.64 × 103 | 0.00 | 0.00 | |
| Best | 3.89 × 102 | 1.01 × 10−20 | 3.30 × 103 | 5.68 × 10−301 | 0.00 | |
| Time (s) | 456.5424 | 456.7693 | 456.9743 | 442.0417 | 442.2414 | |
| Winner | 1 | 1 | 1 | 1 | ||
| F4 | Mean | 2.84 × 102 | 2.70 × 101 | 2.71 × 101 | 2.57 × 101 | 1.20 × 10−3 |
| Sta | 4.02 × 102 | 5.49 × 10−1 | 4.71 × 10−1 | 3.81 × 10−1 | 3.90 × 10−3 | |
| Best | 2.12 × 101 | 2.52 × 101 | 2.66 × 101 | 2.51 × 101 | 1.71 × 10−7 | |
| Time (s) | 439.1047 | 439.2087 | 439.2835 | 424.8770 | 424.9433 | |
| Winner | 1 | 1 | 1 | 1 | ||
| F5 | Mean | −5.57 × 103 | −5.79 × 103 | −1.14 × 104 | −1.21 × 104 | −1.26 × 104 |
| Sta | 4.79 × 102 | 8.10 × 102 | 1.51 × 103 | 3.94 × 102 | 1.16 × 10−2 | |
| Best | −8.07 × 103 | −6.94 × 103 | −1.26 × 104 | −1.26 × 104 | −1.26 × 104 | |
| Time (s) | 438.1611 | 438.2655 | 438.3335 | 423.9423 | 424.0128 | |
| Winner | 1 | 1 | 1 | 0 | ||
| F6 | Mean | 0.21 × 101 | 1.55 × 10−14 | 4.44 × 10−15 | 8.88 × 10−16 | 8.88 × 10−16 |
| Sta | 7.53 × 10−1 | 1.71 × 10−15 | 1.87 × 10−15 | 0.00 | 0.00 | |
| Best | 9.13 × 10−4 | 1.15 × 10−14 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | |
| Time (s) | 436.6612 | 436.7514 | 436.8130 | 422.4533 | 422.5068 | |
| Winner | 1 | 1 | 1 | −1 |
| NO. | Statistics | ALO | GWO | WOA | AHA | IAHA |
|---|---|---|---|---|---|---|
| F1 | Mean | 7.41 × 10−4 | 2.16 × 10−43 | 9.72 × 10−151 | 1.58 × 10−287 | 0.00 |
| Sta | 2.94 × 10−4 | 6.42 × 10−43 | 5.27 × 10−150 | 0.00 | 0.00 | |
| Best | 3.09 × 10−4 | 4.78 × 10−45 | 6.77 × 10−168 | 0.00 | 0.00 | |
| Time (s) | 1144.81 | 1144.93 | 1144.99 | 1121.32 | 1121.38 | |
| Winner | 1 | 1 | 1 | 1 | ||
| F2 | Mean | 1.07 × 102 | 4.55 × 10−26 | 1.61 × 10−102 | 7.94 × 10−146 | 7.25 × 10−222 |
| Sta | 8.67 × 101 | 2.46 × 10−26 | 7.53 × 10−102 | 4.35 × 10−145 | 0.00 | |
| Best | 0.45 × 101 | 9.83 × 10−27 | 5.53 × 10−115 | 6.94 × 10−167 | 3.95 × 10−250 | |
| Time (s) | 727.8588 | 727.9880 | 728.0518 | 704.1420 | 704.2151 | |
| Winner | 1 | 1 | 1 | 1 | ||
| F3 | Mean | 9.17 × 103 | 5.97 × 10−6 | 1.23 × 105 | 5.91 × 10−261 | 0.00 |
| Sta | 2.77 × 103 | 2.03 × 10−5 | 3.57 × 104 | 0.00 | 0.00 | |
| Best | 3.54 × 103 | 2.03 × 10−11 | 5.96 × 104 | 5.55 × 10−302 | 0.00 | |
| Time (s) | 1277.53 | 1277.91 | 1278.24 | 1252.25 | 1252.57 | |
| Winner | 1 | 1 | 1 | 1 | ||
| F4 | Mean | 3.37e × 102 | 4.71 × 101 | 4.75 × 101 | 4.62 × 101 | 2.92 × 10−4 |
| Sta | 3.59e × 102 | 8.62 × 10−1 | 5.83 × 10−1 | 4.76 × 10−1 | 6.99 × 10−4 | |
| Best | 4.26 × 101 | 4.54 × 101 | 4.67 × 101 | 4.55 × 101 | 8.76 × 10−7 | |
| Time (s) | 1430.55 | 1430.71 | 1430.80 | 1405.94 | 1406.01 | |
| Winner | 1 | 1 | 1 | 1 | ||
| F5 | Mean | −9.57 × 103 | −8.86 × 103 | −1.75 × 104 | −1.92 × 104 | −2.09 × 104 |
| Sta | 1.58 × 103 | 1.55 × 103 | 3.17 × 103 | 5.59 × 102 | 1.85 × 10−2 | |
| Best | −1.49 × 104 | −1.11 × 104 | −2.09 × 104 | −2.02 × 104 | −2.09 × 104 | |
| Time (s) | 1390.45 | 1390.64 | 1390.77 | 1360.35 | 1360.68 | |
| Winner | 1 | 1 | 1 | 1 | ||
| F6 | Mean | 0.45 × 101 | 3.39 × 10−14 | 4.09 × 10−15 | 8.88 × 10−16 | 8.88 × 10−16 |
| Sta | 0.26 × 101 | 4.39 × 10−15 | 2.69 × 10−15 | 0.00 | 0.00 | |
| Best | 0.24 × 101 | 2.93 × 10−14 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | |
| Time (s) | 1126.10 | 1126.46 | 1126.64 | 1057.07 | 1057.31 | |
| Winner | 1 | 1 | 1 | −1 |
| Power-Only Units | αi | βi | γi | eei | ffi | Pimin | Pimax |
|---|---|---|---|---|---|---|---|
| 1 | 0.008 | 2 | 25 | 100 | 0.042 | 10 | 75 |
| 2 | 0.003 | 1.8 | 60 | 140 | 0.04 | 20 | 125 |
| 3 | 0.0012 | 2.1 | 100 | 160 | 0.038 | 30 | 175 |
| 4 | 0.001 | 2 | 120 | 180 | 0.037 | 40 | 250 |
| CHP Units | aj | bj | cj | dj | ej | fj | Feasible Region Coordinates |
|---|---|---|---|---|---|---|---|
| 5 | 0.0345 | 14.5 | 2650 | 0.03 | 4.2 | 0.031 | [98.8, 0], [81, 104.8], [215, 180], [247, 0] |
| 6 | 0.0435 | 36 | 1250 | 0.027 | 0.6 | 0.011 | [44, 0], [44, 15.9], [40, 75], [110.2, 135.6], [125.8, 32.4], [125.8, 0] |
| Heat-Only Units | φk | ηk | λk | Hmin | Hmax |
|---|---|---|---|---|---|
| 7 | 0.038 | 2.0109 | 950 | 0 | 2695.20 |
| Optimizer | OBC (USD) | Average | Worst | maxFES | Time (s) |
|---|---|---|---|---|---|
| IAHA | 10,093.75 | 10,093.76 | 10,093.78 | 1000 | 2.67 |
| AHA | 10,095.25 | 10,097.22 | 10,098.25 | 1000 | 2.23 |
| GWO | 10,117.52 | 10,123.10 | 10,126.94 | 1000 | 18.37 |
| WOA | 10,326.40 | 10,341.20 | 10,345.72 | 1000 | 18.41 |
| HTS [18] | 10,104.2707 | 10,104.4054 | 10,104.7031 | 100 | 2.4405 |
| BLPSO [39] | 10,101.3079 | 10,101.5626 | 10,102.1864 | 20,000 | 6.18 |
| ISNS [40] | 10,094.4196 | NA | NA | NA | NA |
| Levy-GWO [24] | 10,111.79 | NA | NA | NA | NA |
| Items | GWO | WOA | AHA | IAHA |
|---|---|---|---|---|
| P1 (MW) | 42.59 | 75 | 45.50 | 45.48 |
| P2 (MW) | 98.55 | 125 | 98.53 | 98.54 |
| P3 (MW) | 112.47 | 139.65 | 112.69 | 112.67 |
| P4 (MW) | 209.77 | 125.30 | 209.85 | 209.82 |
| P5 (MW) | 97.25 | 95.67 | 94.01 | 94.07 |
| P6 (MW) | 40.01 | 40.00 | 40.03 | 40.00 |
| H5 (MWth) | 9.12 | 18.41 | 28.25 | 27.84 |
| H6 (MWth) | 74.96 | 74.99 | 74.69 | 74.99 |
| H7 (MWth) | 65.92 | 56.59 | 47.06 | 47.16 |
| Best Cost (USD) | 10,117.52 | 10,326.40 | 10,095.25 | 10,093.75 |
| Average cost (USD) | 10,123.10 | 10,341.20 | 10,097.22 | 10,093.76 |
| Worst cost (USD) | 10,126.94 | 10,345.72 | 10,098.25 | 10,093.78 |
| Time (s) | 18.37 | 18.41 | 2.23 | 2.67 |
| Power-Only Units | αi | βi | γi | eei | ffi | Pimin | Pimax |
|---|---|---|---|---|---|---|---|
| 1 | 0.00028 | 8.10 | 550 | 300 | 0.035 | 0 | 680 |
| 2 | 0.00056 | 8.10 | 309 | 200 | 0.042 | 0 | 360 |
| 3 | 0.00056 | 8.10 | 309 | 200 | 0.042 | 0 | 360 |
| 4 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 5 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 6 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 7 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 8 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 9 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 10 | 0.00284 | 8.60 | 126 | 100 | 0.084 | 40 | 120 |
| 11 | 0.00284 | 8.60 | 126 | 100 | 0.084 | 40 | 120 |
| 12 | 0.00284 | 8.60 | 126 | 100 | 0.084 | 55 | 120 |
| 13 | 0.00284 | 8.60 | 126 | 100 | 0.084 | 55 | 120 |
| CHP Units | aj | bj | cj | dj | ej | fj | Feasible Region Coordinates |
|---|---|---|---|---|---|---|---|
| 14 | 0.0345 | 14.5 | 2650 | 0.030 | 4.2 | 0.031 | [98.8, 0], [81, 104.8], [215, 180], [247, 0] |
| 15 | 0.0435 | 36.0 | 1250 | 0.027 | 0.6 | 0.011 | [44, 0], [44, 15.9], [40, 75], [110.2, 135.6], [125.8, 32.4], [125.8, 0] |
| 16 | 0.0345 | 14.5 | 2650 | 0.030 | 4.2 | 0.031 | [98.8, 0], [81, 104.8], [215, 180], [247, 0] |
| 17 | 0.0435 | 36.0 | 1250 | 0.027 | 0.6 | 0.011 | [44, 0], [44, 15.9], [40, 75], [110.2, 135.6], [125.8, 32.4], [125.8, 0] |
| 18 | 0.1035 | 34.5 | 2650 | 0.025 | 2.203 | 0.051 | [20, 0], [10, 40], [45, 55], [60, 0] |
| 19 | 0.0720 | 20.0 | 1565 | 0.020 | 2.340 | 0.040 | [35, 0]. [35, 20], [90, 45], [90, 25], [105, 0] |
| Heat-Only Units | φk | ηk | λk | Hmin | Hmax |
|---|---|---|---|---|---|
| 20 | 0.038 | 2.0109 | 950 | 0 | 2695.20 |
| 21 | 0.038 | 2.0109 | 950 | 0 | 60 |
| 22 | 0.038 | 2.0109 | 950 | 0 | 60 |
| 23 | 0.052 | 3.0651 | 480 | 0 | 120 |
| 24 | 0.052 | 3.0651 | 480 | 0 | 120 |
| Optimizer | OBC ($) | Average | Worst | maxFES | Time (s) |
|---|---|---|---|---|---|
| IAHA | 57,876.5508 | 57,894.9375 | 57,915.0069 | 4000 | 26.4515 |
| AHA | 57,996.9548 | 57,998.8079 | 58,012.4878 | 4000 | 24.8515 |
| GWO | 59,521.2456 | 59,670.0777 | 59,781.7602 | 4000 | 565.0260 |
| WOA | 61,883.1815 | 62,242.9196 | 62,345.7564 | 4000 | 570.1440 |
| Proposed CHPED Algorithm [6] | 57,895.6050 | 57,896.7356 | 57,897.8129 | 1000 | 11.2710 |
| HTS [18] | 57,959.4100 | 57,959.9200 | 57,960.7300 | 200 | 6.6877 |
| ISNS [40] | 58,082.5371 | 58,302.4427 | 58,556.2406 | NA | NA |
| SNS [40] | 58,109.3402 | 58,362.8765 | 58,710.1045 | NA | NA |
| Items | GWO | WOA | AHA | IAHA |
|---|---|---|---|---|
| P1 (MW) | 538.4775 | 451.0720 | 538.5587 | 628.3185 |
| P2 (MW) | 299.3808 | 184.2383 | 149.5996 | 299.2009 |
| P3 (MW) | 55.4767 | 305.4657 | 299.1799 | 149.6151 |
| P4 (MW) | 110.9189 | 136.9736 | 159.7323 | 109.8666 |
| P5 (MW) | 98.0100 | 130.1374 | 109.8661 | 109.8666 |
| P6 (MW) | 159.6166 | 112.6991 | 109.8663 | 159.7331 |
| P7 (MW) | 112.2540 | 98.0116 | 109.8666 | 109.8666 |
| P8 (MW) | 79.3887 | 138.1284 | 109.8663 | 109.8666 |
| P9 (MW) | 159.9315 | 112.0139 | 109.8665 | 109.8666 |
| P10 (MW) | 77.2408 | 52.7221 | 76.8571 | 40.0000 |
| P11 (MW) | 42.0301 | 42.7646 | 76.3756 | 77.3999 |
| P12 (MW) | 91.9634 | 101.0753 | 92.0504 | 92.3999 |
| P13 (MW) | 92.0569 | 79.1348 | 92.1309 | 55.0000 |
| P14 (MW) | 141.3902 | 83.8794 | 94.0647 | 86.0327 |
| P15 (MW) | 43.5152 | 83.3590 | 40.0000 | 40.0012 |
| P16 (MW) | 141.4363 | 83.0794 | 95.9973 | 87.9656 |
| P17 (MW) | 45.2182 | 68.2452 | 40.0108 | 40.0000 |
| P18 (MW) | 23.8396 | 35.6075 | 11.1110 | 10.0000 |
| P19 (MW) | 37.8548 | 51.3427 | 35.0000 | 35.0003 |
| H14 (MWth) | 137.9082 | 87.8725 | 112.1328 | 107.6252 |
| H15 (MWth) | 78.0325 | 104.2315 | 74.9981 | 74.9992 |
| H16 (MWth) | 138.7176 | 105.9643 | 113.2173 | 108.7099 |
| H17 (MWth) | 79.5025 | 98.7734 | 75.0074 | 74.9981 |
| H18 (MWth) | 45.9133 | 35.6416 | 40.4767 | 40.0006 |
| H19 (MWth) | 20.9020 | 16.8535 | 19.9984 | 19.9985 |
| H20 (MWth) | 389.8931 | 449.8231 | 454.1693 | 463.6685 |
| H21 (MWth) | 59.7296 | 50.8744 | 60.0000 | 60.0000 |
| H22 (MWth) | 59.8629 | 59.9934 | 60.0000 | 60.0000 |
| H23 (MWth) | 119.9360 | 120.0000 | 120.0000 | 120.0000 |
| H24 (MWth) | 119.6025 | 119.9723 | 120.0000 | 120.0000 |
| Best cost ($) | 59,521.2456 | 61,883.1815 | 57,996.9548 | 57,876.5508 |
| Average cost ($) | 59,670.0777 | 62,242.9196 | 57,998.8079 | 57,894.9375 |
| Worst cost ($) | 59,781.7602 | 62,345.7564 | 58,012.4878 | 57,915.0069 |
| Time (s) | 565.0260 | 570.1440 | 24.8515 | 26.4515 |
| Power-Only Units | αi | βi | γi | eei | ffi | Pimin | Pimax |
|---|---|---|---|---|---|---|---|
| 1 | 0.00028 | 8.10 | 550 | 300 | 0.035 | 0 | 680 |
| 2 | 0.00056 | 8.10 | 309 | 200 | 0.042 | 0 | 360 |
| 3 | 0.00056 | 8.10 | 309 | 200 | 0.042 | 0 | 360 |
| 4 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 5 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 6 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 7 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 8 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 9 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 10 | 0.00284 | 8.60 | 126 | 100 | 0.084 | 40 | 120 |
| 11 | 0.00284 | 8.60 | 126 | 100 | 0.084 | 40 | 120 |
| 12 | 0.00284 | 8.60 | 126 | 100 | 0.084 | 55 | 120 |
| 13 | 0.00284 | 8.60 | 126 | 100 | 0.084 | 55 | 120 |
| 14 | 0.00028 | 8.10 | 550 | 300 | 0.035 | 0 | 680 |
| 15 | 0.00056 | 8.10 | 309 | 200 | 0.042 | 0 | 360 |
| 16 | 0.00056 | 8.10 | 309 | 200 | 0.042 | 0 | 360 |
| 17 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 18 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 19 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 20 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 21 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 22 | 0.00324 | 7.74 | 240 | 150 | 0.063 | 60 | 180 |
| 23 | 0.00284 | 8.60 | 126 | 100 | 0.084 | 40 | 120 |
| 24 | 0.00284 | 8.60 | 126 | 100 | 0.084 | 40 | 120 |
| 25 | 0.00284 | 8.60 | 126 | 100 | 0.084 | 55 | 120 |
| 26 | 0.00284 | 8.60 | 126 | 100 | 0.084 | 55 | 120 |
| CHP Units | aj | bj | cj | dj | ej | fj | Feasible Region Coordinates |
|---|---|---|---|---|---|---|---|
| 27 | 0.0345 | 14.5 | 2650 | 0.030 | 4.2 | 0.031 | [98.8, 0], [81, 104.8], [215, 180], [247, 0] |
| 28 | 0.0435 | 36.0 | 1250 | 0.027 | 0.6 | 0.011 | [44, 0], [44, 15.9], [40, 75], [110.2, 135.6], [125.8, 32.4], [125.8, 0] |
| 29 | 0.0345 | 14.5 | 2650 | 0.030 | 4.2 | 0.031 | [98.8, 0], [81, 104.8], [215, 180], [247, 0] |
| 30 | 0.0435 | 36.0 | 1250 | 0.027 | 0.6 | 0.011 | [44, 0], [44, 15.9], [40, 75], [110.2, 135.6], [125.8, 32.4], [125.8, 0] |
| 31 | 0.1035 | 34.5 | 2650 | 0.025 | 2.203 | 0.051 | [20, 0], [10, 40], [45, 55], [60, 0] |
| 32 | 0.0720 | 20.0 | 1565 | 0.020 | 2.340 | 0.040 | [35, 0]. [35, 20], [90. 45], [90, 25], [105, 0] |
| 33 | 0.0345 | 14.5 | 2650 | 0.030 | 4.2 | 0.031 | [98.8, 0], [81, 104.8], [215, 180], [247, 0] |
| 34 | 0.0435 | 36.0 | 1250 | 0.027 | 0.6 | 0.011 | [44, 0], [44, 15.9], [40, 75], [110.2, 135.6], [125.8, 32.4], [125.8, 0] |
| 35 | 0.0345 | 14.5 | 2650 | 0.030 | 4.2 | 0.031 | [98.8, 0], [81, 104.8], [215, 180], [247, 0] |
| 36 | 0.0435 | 36.0 | 1250 | 0.027 | 0.6 | 0.011 | [44, 0], [44, 15.9], [40, 75], [110.2, 135.6], [125.8, 32.4], [125.8, 0] |
| 37 | 0.1035 | 34.5 | 2650 | 0.025 | 2.203 | 0.051 | [20, 0], [10, 40], [45, 55], [60, 0] |
| 38 | 0.0720 | 20.0 | 1565 | 0.020 | 2.340 | 0.040 | [35, 0]. [35, 20], [90, 45], [90, 25], [105, 0] |
| Heat-Only Units | φk | ηk | λk | Hmin | Hmax |
|---|---|---|---|---|---|
| 39 | 0.038 | 2.0109 | 950 | 0 | 2695.20 |
| 40 | 0.038 | 2.0109 | 950 | 0 | 60 |
| 41 | 0.038 | 2.0109 | 950 | 0 | 60 |
| 42 | 0.052 | 3.0651 | 480 | 0 | 120 |
| 43 | 0.052 | 3.0651 | 480 | 0 | 120 |
| 44 | 0.038 | 2.0109 | 950 | 0 | 2695.20 |
| 45 | 0.038 | 2.0109 | 950 | 0 | 60 |
| 46 | 0.038 | 2.0109 | 950 | 0 | 60 |
| 47 | 0.052 | 3.0651 | 480 | 0 | 120 |
| 48 | 0.052 | 3.0651 | 480 | 0 | 120 |
| Optimizer | OBC ($) | Average | Worst | maxFES | Time (s) |
|---|---|---|---|---|---|
| IAHA | 116,048.1539 | 116,111.1857 | 116,149.3838 | 20,000 | 272.8630 |
| AHA | 116,125.5048 | 116,181.8785 | 116,241.6110 | 20,000 | 233.1710 |
| GWO | 125,338.4898 | 125,443.0591 | 125,665.7251 | 20,000 | 8866.4285 |
| WOA | 130,045.9012 | 130,747.9537 | 131,933.1849 | 20,000 | 9142.3150 |
| HTS [18] | 116,918.90 | 116,924.75 | 116,935.38 | 300 | 6.9056 |
| ISNS [40] | 116,582.0833 | 117,059.3330 | 117,512.2505 | NA | NA |
| SNS [40] | 116,710.7282 | 117,150.5584 | 117,658.2387 | NA | NA |
| HBJSA [42] | 1161,40.34 | NA | NA | 900 | NA |
| Items | GWO | WOA | AHA | IAHA |
|---|---|---|---|---|
| P1 (MW) | 621.8124 | 537.9541 | 628.4013 | 628.3187 |
| P2 (MW) | 331.0854 | 235.9879 | 299.1948 | 299.1993 |
| P3 (MW) | 322.0548 | 240.8566 | 299.1995 | 299.1993 |
| P4 (MW) | 114.9221 | 81.7905 | 159.7334 | 159.7331 |
| P5 (MW) | 123.8439 | 169.6766 | 159.7148 | 159.7331 |
| P6 (MW) | 116.7211 | 143.8568 | 159.7354 | 159.7332 |
| P7 (MW) | 178.0947 | 99.9090 | 159.7024 | 109.8666 |
| P8 (MW) | 140.5066 | 113.1946 | 159.7163 | 109.8666 |
| P9 (MW) | 132.9864 | 113.8379 | 109.8675 | 109.8666 |
| P10 (MW) | 54.7267 | 79.4349 | 77.3979 | 77.3999 |
| P11 (MW) | 91.9046 | 96.2005 | 77.3641 | 77.3999 |
| P12 (MW) | 91.3963 | 79.1883 | 92.0451 | 92.3999 |
| P13 (MW) | 96.1018 | 62.2822 | 92.3741 | 120.0000 |
| P14 (MW) | 152.3511 | 346.2562 | 179.5187 | 179.5196 |
| P15 (MW) | 27.3960 | 229.3590 | 149.5985 | 159.6051 |
| P16 (MW) | 225.0296 | 185.5076 | 149.5965 | 299.1993 |
| P17 (MW) | 149.4663 | 126.4464 | 109.8680 | 109.8666 |
| P18 (MW) | 98.2292 | 85.2319 | 159.7187 | 109.8666 |
| P19 (MW) | 122.1164 | 123.8847 | 109.8712 | 109.8666 |
| P20 (MW) | 115.9117 | 96.0316 | 159.7310 | 109.8665 |
| P21 (MW) | 83.0334 | 87.2576 | 109.8668 | 109.8666 |
| P22 (MW) | 70.2352 | 71.6450 | 109.8670 | 159.7331 |
| P23 (MW) | 57.6080 | 90.1981 | 77.3999 | 77.3999 |
| P24 (MW) | 60.6206 | 63.5091 | 77.4017 | 77.4000 |
| P25 (MW) | 77.9824 | 84.0430 | 92.4006 | 92.3999 |
| P26 (MW) | 85.3007 | 71.0718 | 92.3995 | 92.3999 |
| P27 (MW) | 119.4496 | 136.6224 | 117.6223 | 103.1602 |
| P28 (MW) | 41.6005 | 82.3386 | 40.0007 | 40.0001 |
| P29 (MW) | 152.1515 | 83.1478 | 85.3225 | 87.0991 |
| P30 (MW) | 68.5788 | 46.8083 | 40.0026 | 40.0000 |
| P31 (MW) | 27.4758 | 37.3482 | 10.0159 | 10.0000 |
| P32 (MW) | 49.1511 | 78.1141 | 35.0136 | 35.0000 |
| P33 (MW) | 136.6217 | 162.7575 | 101.7523 | 87.8648 |
| P34 (MW) | 50.5656 | 50.4175 | 40.0009 | 40.0000 |
| P35 (MW) | 178.9121 | 172.8019 | 93.5791 | 92.1699 |
| P36 (MW) | 44.4178 | 59.0721 | 40.0035 | 40.0000 |
| P37 (MW) | 43.4296 | 17.4293 | 10.0010 | 10.0000 |
| P38 (MW) | 36.2045 | 57.5305 | 35.0008 | 35.0000 |
| H27 (MWth) | 126.3787 | 105.1637 | 125.3533 | 117.2372 |
| H28 (MWth) | 76.3796 | 110.8909 | 74.9982 | 74.9982 |
| H29 (MWth) | 143.4418 | 92.1800 | 107.2264 | 108.2237 |
| H30 (MWth) | 58.6803 | 80.8750 | 74.9999 | 74.9981 |
| H31 (MWth) | 43.1512 | 50.1953 | 40.0074 | 40.0006 |
| H32 (MWth) | 16.7663 | 17.1735 | 20.0042 | 19.9984 |
| H33 (MWth) | 134.5339 | 125.9003 | 116.4470 | 108.6534 |
| H34 (MWth) | 84.1183 | 65.7802 | 74.9982 | 74.9981 |
| H35 (MWth) | 158.9286 | 139.0957 | 111.8603 | 111.0694 |
| H36 (MWth) | 78.8115 | 80.3278 | 75.0004 | 74.9981 |
| H37 (MWth) | 40.4266 | 10.2830 | 40.0000 | 40.0006 |
| H38 (MWth) | 20.5459 | 16.9296 | 19.9987 | 19.9984 |
| H39 (MWth) | 422.2681 | 406.9643 | 444.2832 | 457.2425 |
| H40 (MWth) | 45.8771 | 48.1419 | 59.9983 | 60.0000 |
| H41 (MWth) | 40.0031 | 43.5554 | 59.9986 | 60.0000 |
| H42 (MWth) | 101.5608 | 80.9111 | 119.9982 | 120.0000 |
| H43 (MWth) | 115.0466 | 69.9596 | 119.9999 | 120.0000 |
| H44 (MWth) | 433.0814 | 595.6730 | 454.8273 | 457.5834 |
| H45 (MWth) | 60.0000 | 60.0000 | 60.0000 | 60.0000 |
| H46 (MWth) | 60.0000 | 60.0000 | 60.0000 | 60.0000 |
| H47 (MWth) | 120.0000 | 120.0000 | 120.0000 | 120.0000 |
| H48 (MWth) | 120.0000 | 120.0000 | 120.0000 | 120.0000 |
| Best cost ($) | 125,338.4898 | 130,045.9012 | 116,125.5048 | 116,048.1539 |
| Average cost ($) | 125,443.0591 | 130,747.9537 | 116,181.8785 | 116,111.1857 |
| Worst cost ($) | 125,665.7251 | 131,933.1849 | 116,241.6110 | 116,149.3838 |
| Time (s) | 9142.3150 | 8866.4285 | 233.1710 | 272.8630 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, X.; Li, K.; Zhang, Y.; Tian, G.; Dong, N. Research on the Economic Scheduling Problem of Cogeneration Based on the Improved Artificial Hummingbird Algorithm. Energies 2024, 17, 6411. https://doi.org/10.3390/en17246411
Kong X, Li K, Zhang Y, Tian G, Dong N. Research on the Economic Scheduling Problem of Cogeneration Based on the Improved Artificial Hummingbird Algorithm. Energies. 2024; 17(24):6411. https://doi.org/10.3390/en17246411
Chicago/Turabian StyleKong, Xiaohong, Kunyan Li, Yihang Zhang, Guocai Tian, and Ning Dong. 2024. "Research on the Economic Scheduling Problem of Cogeneration Based on the Improved Artificial Hummingbird Algorithm" Energies 17, no. 24: 6411. https://doi.org/10.3390/en17246411
APA StyleKong, X., Li, K., Zhang, Y., Tian, G., & Dong, N. (2024). Research on the Economic Scheduling Problem of Cogeneration Based on the Improved Artificial Hummingbird Algorithm. Energies, 17(24), 6411. https://doi.org/10.3390/en17246411





