SOC Equalization Control Method Considering SOH in DC–DC Converter Cascaded Energy Storage Systems
Abstract
1. Introduction
- (1)
- The focus of this paper is on DC–DC converters in cascaded energy storage systems, where an analysis is conducted on both the structure of the P-I series droop closed-loop control system and the operational mechanism of the DC–DC converter in charge and discharge modes. Additionally, it explores the significance of considering SOH during SOC equalization and its impact on the process.
- (2)
- An SOC equalization control strategy considering SOH is proposed. In DC–DC converter cascaded energy storage systems, the power distribution is managed to allocate the voltage on the bus side of each DC–DC converter according to the specified power ratio. The ratio of to in relation to the reciprocal power droop coefficient is directly proportional to the ratio of the voltage on each DC–DC converter’s bus side to that of the total bus voltage. Based on this relationship, a larger is allocated to the smallest SOC during charging process to enhance equalization speed, while others are allocated proportionally based on their reciprocal SOC values. During the discharge process, a larger is assigned to the largest SOC and others are allocated according to their SOC ratios. Finally, is recalibrated based on relative SOH proportions, resulting in obtaining . Power adjustment for each DC–DC converter aims at achieving SOC equalization.
- (3)
- The effectiveness of the proposed method is verified through simulation and experimentation, providing a technical foundation for its application in energy storage system engineering. The number of DC–DC converters can be adjusted based on cost and equalization objectives to achieve more precise battery charge and discharge management, mitigate the decay rate of battery modules with low state of health (SOH), and prolong their service life.
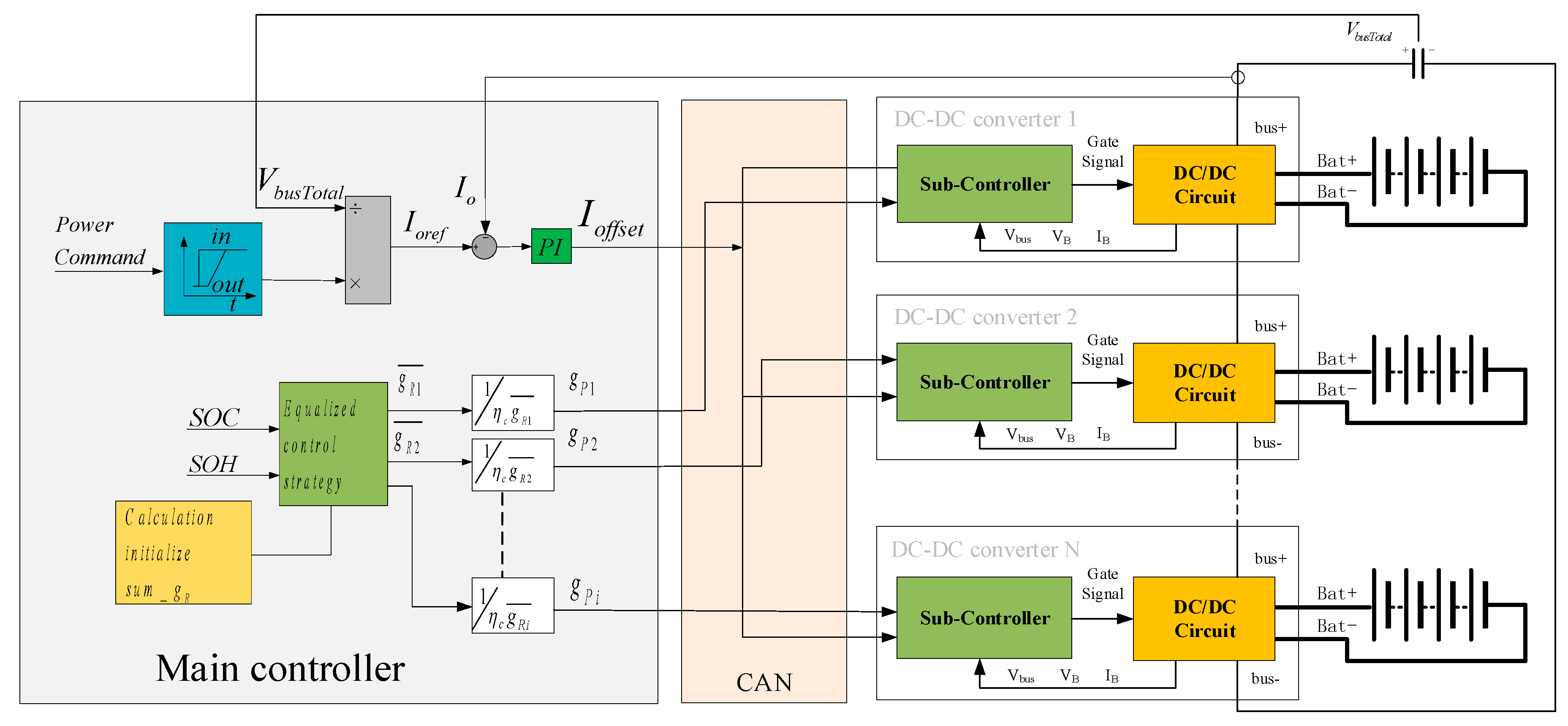
2. The Cascaded Energy Storage Systems with DC–DC Converters
2.1. The Architecture of a Cascading Energy Storage System for DC–DC Applications
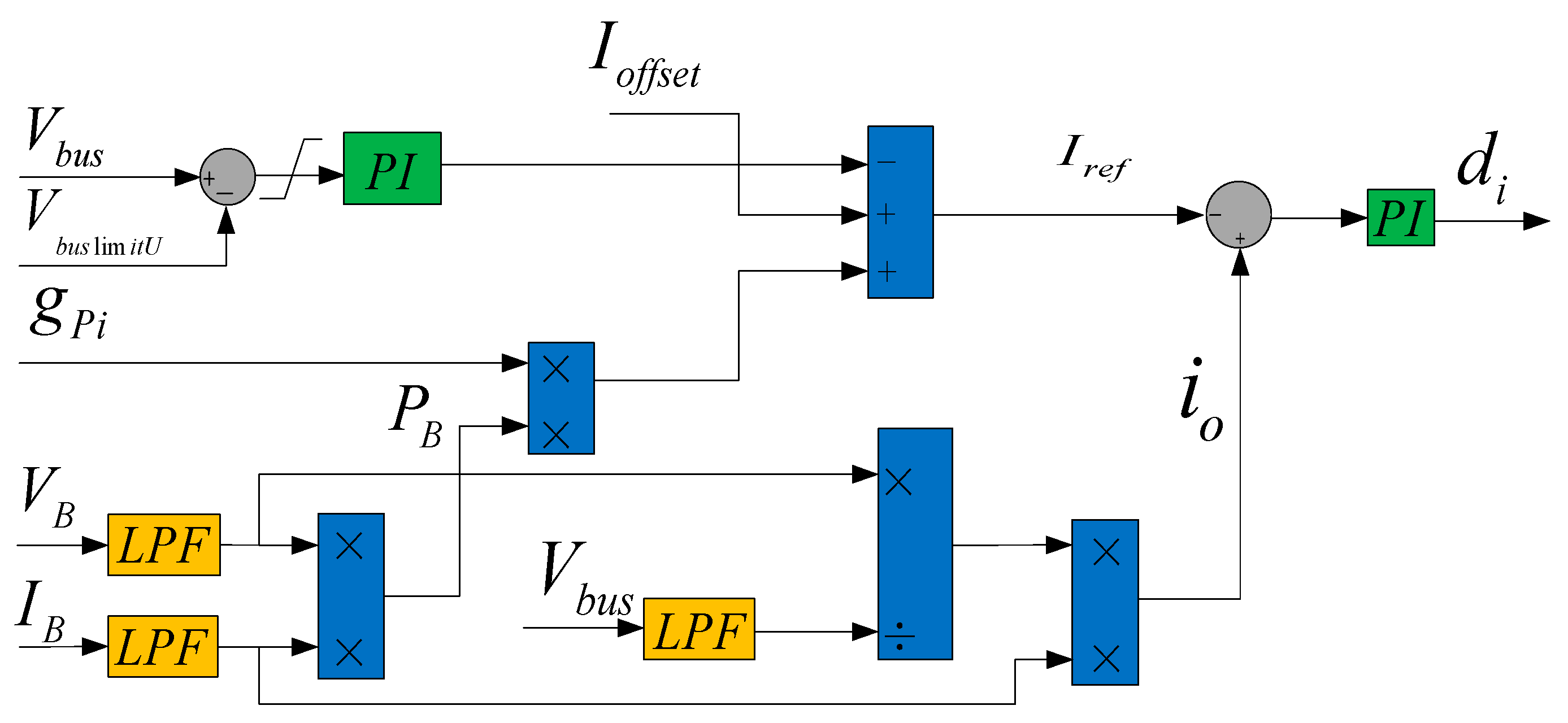
2.2. Closed-Loop Control of SOC Equalization in a DC–DC Cascaded Energy Storage System Based on Droop Control
3. SOC Equalization Control Strategies
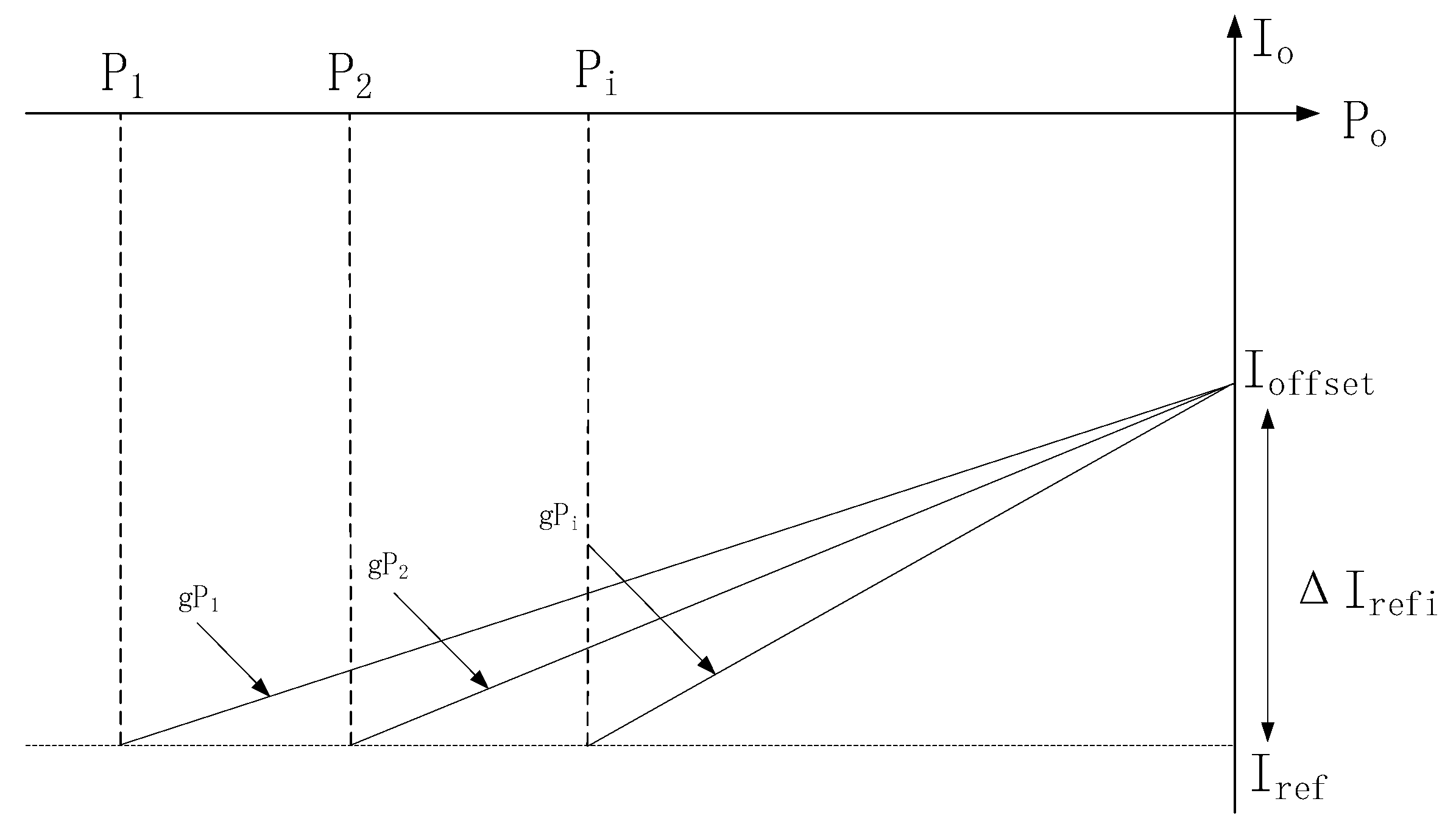
3.1. SOC Equalization Control
3.2. SOC Equalizing Control Method with Consideration of SOH
4. System Simulation and Experimental Analysis
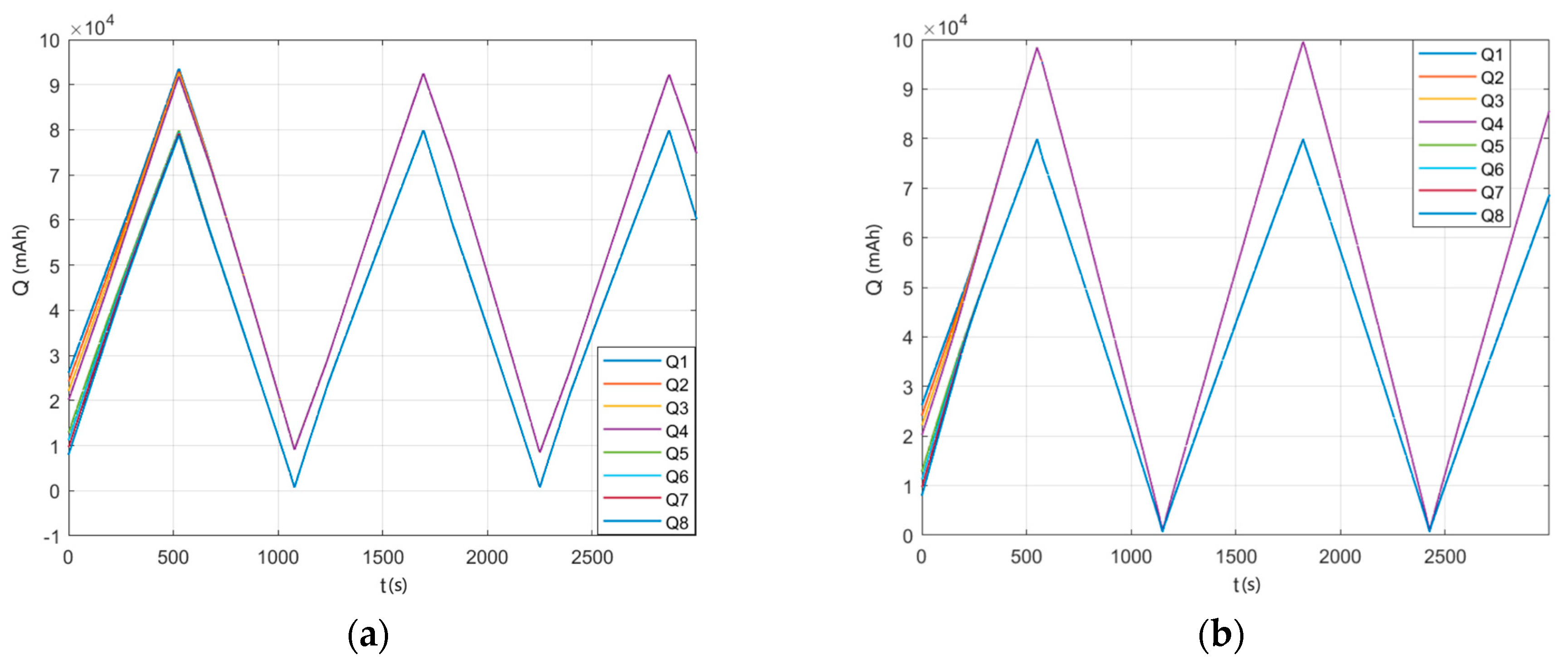
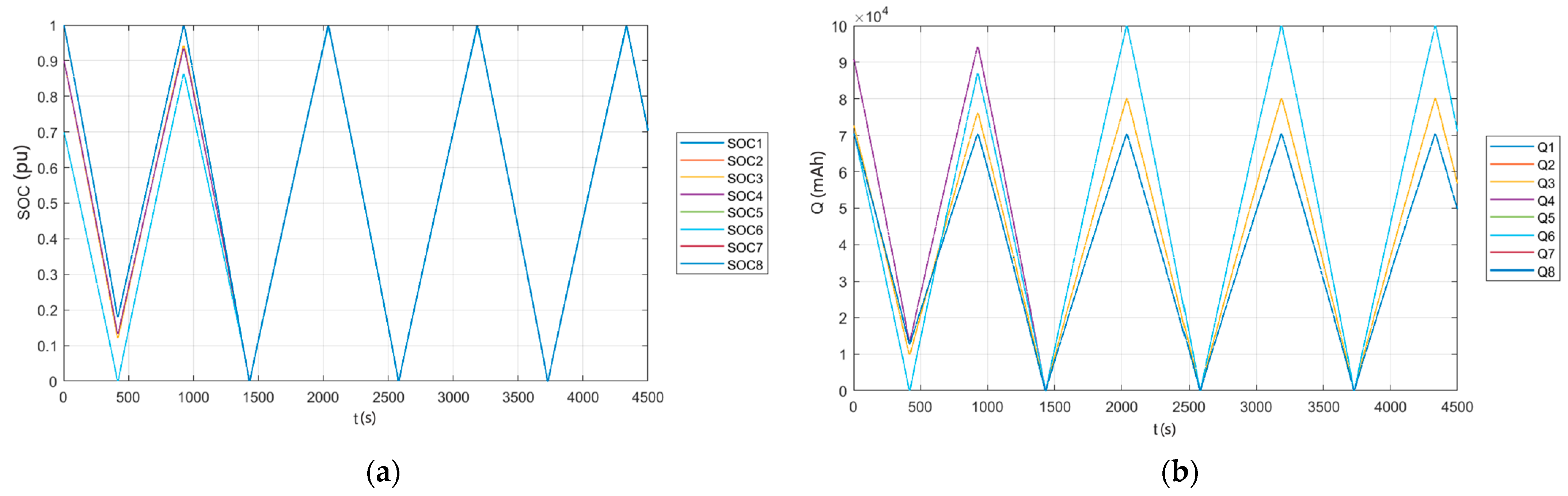
4.1. System Simulation
4.2. Experimental Analysis
4.2.1. Experimental System
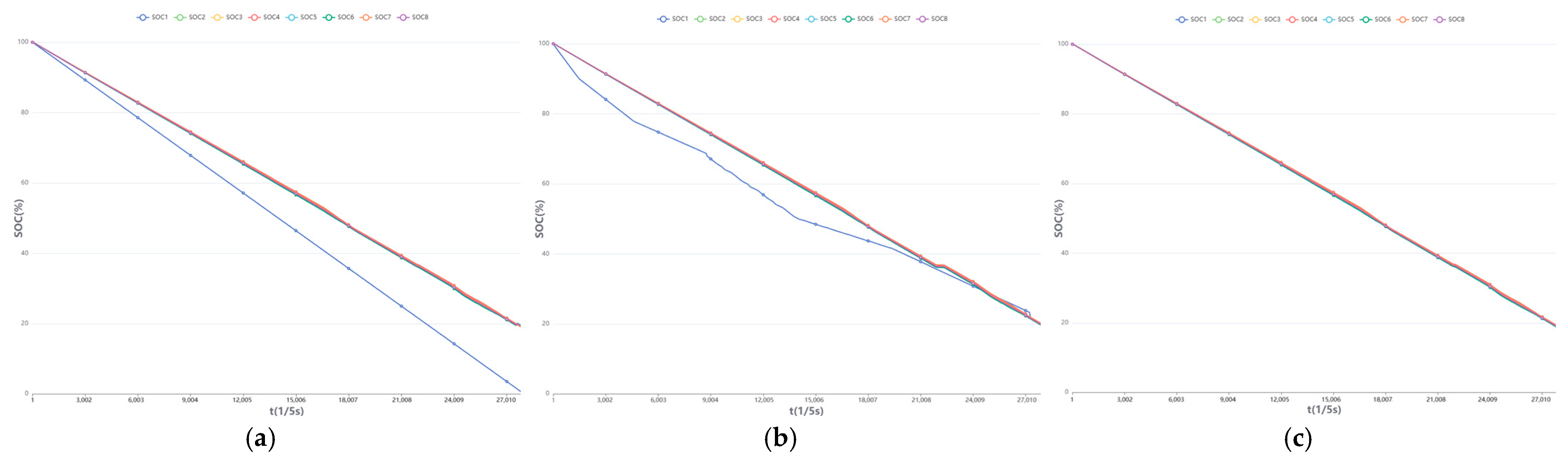
4.2.2. Charge Experiment
4.2.3. Discharge Experiment
5. Conclusions
- (1)
- The attenuation of energy storage batteries in industrial and commercial energy storage systems, as well as power station energy storage systems, varies due to factors such as temperature at the application site. To effectively enhance the recharge capacity, discharge capacity, and overall cost-effectiveness of energy storage equipment, considering only SOC is inadequate for the SOC equalization of battery modules; instead, one must also take into account the SOH, which has a significant equalization effect. By considering both SOH and SOC simultaneously, the efficiency of charging and discharging in an energy storage system can be improved. In this study’s experimental conditions, the charge and discharge capacity increased by 1.85%/10 min.
- (2)
- The essence of SOC equalization, taking into account the SOH, lies in achieving charge distribution equalization among battery modules. During the initial stages of battery usage, the SOH values across all battery modules are essentially identical. However, the discrepancies between batteries increase over long-term use. Therefore, relying solely on a single parameter such as SOC fails to achieve optimal balancing effects.
- (3)
- The number of cells utilized by each DC–DC converter in the DC–DC cascaded energy storage system is determined based on the cost of the system, considering the application of a high-capacity lithium-ion phosphate battery in industrial and commercial energy storage systems. Additionally, the number of matched cells can be adjusted according to specific requirements, thereby enhancing the precise management of battery charging and discharging within the system.
- (4)
- The cascaded energy storage system employing DC–DC converters mitigates the impact of cell degradation on the overall system performance. Despite employing a more refined decomposition and fewer batteries corresponding to each DC–DC converter, there remains an issue of varying degrees of battery attenuation within each battery module. In subsequent research, bypassing the battery modules will be employed as a solution to address this problem.
- (5)
- The DC–DC cascaded energy storage system with SOC equalization, considering the SOH, demonstrates an optimal equalization effect, thereby validating the effectiveness of the proposed methodology and providing technical solutions for large-scale electrochemical energy storage engineering applications. This approach enhances both the recharge and discharge capacities of the energy storage system while improving its overall efficiency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, L.; Zhang, J. A new model of jointed states of charge and health for lithium batteries. Proc. CSEE 2018, 38, 3613–3620. [Google Scholar]
- Li, C.; Xiao, F.; Fan, Y. An approach to state of charge estimation of lithium-ion batteries based on recurrent neural networks with gated recurrent unit. Energies 2019, 12, 1592. [Google Scholar] [CrossRef]
- Dai, H.; Zhao, G.; Lin, M.; Wu, J.; Zheng, G. A novel estimation method for the state of health of lithium-ion battery using prior knowledge-based neural network and Markov chain. IEEE Trans. Ind. Electron. 2018, 66, 7706–7716. [Google Scholar] [CrossRef]
- Liu, P.; Li, Z.; Cai, S.; Wang, W.; Xia, X. Based on the fusion of equivalent circuit model and data-driven model Joint SOC and SOH estimation method. Trans. China Electrotech. Soc. 2024, 39, 3232–3243. [Google Scholar]
- Zhao, J.; Hu, J.; Zhang, X.; Zhang, W. Joint SOC-SOH estimation based on lithium battery model and fractional order theory. Trans. China Electrotech. Soc. Electr. Mach. Control. 2023, 38, 4551–4560. [Google Scholar]
- Feng, F.; Song, K.; Lu, R.; Wei, G.; Zhu, C. Equalization Control Strategy and SOC Estimation for LiFePO4 Battery Pack. Trans. China Electrotech. Soc. 2015, 30, 186–193. [Google Scholar]
- Liu, J.; Yang, P.; Li, L. A Method to Estimate the Capacity of the Lithium-ion Battery Based on Energy Model. Power Syst. Prot. Control 2015, 30, 100–107. [Google Scholar]
- Vennam, G.; Sahoo, A. A Dynamic SOH-Coupled Lithium-Ion Cell Model for State and Parameter Estimation. IEEE Trans. Energy Convers. 2023, 38, 1186–1201. [Google Scholar] [CrossRef]
- Tan, B.; Du, J.; Ye, X.; Cao, X.; Qu, C. Overview of SOC estimation methods for lithium-ion batteries based on model. Energy Storage Sci. Technol. 2023, 12, 1995–2011. [Google Scholar]
- Miao, Q.; Wu, J.Y.; Ai, H.K.; Xiong, F.; Qi, D.W.; Hao, L.L. Study on coordinating control strategy of hybrid cascade energy storage and bi-directional power regulation device. Asia-Pac. Conf. Electr. Eng. Autom. 2014, 852, 655–659. [Google Scholar] [CrossRef]
- Xu, J. Research on DC-DC Cascaded Energy Storage Converter Based on Droop Control. Master’s Thesis, Beijing Jiao Tong University, Beijing, China, 2019. [Google Scholar]
- Vikhorev, N.; Kurkin, A.; Aleshin, D.; Ulyanov, D.; Konstantinov, M.; Shalukho, A. Battery Dynamic Balancing Method Based on Calculation of Cell Voltage Reference Value. Energies 2023, 16, 3733. [Google Scholar] [CrossRef]
- Koseoglou, M.; Tsioumas, E.; Jabbour, N.; Mademlis, C. Highly effective cell equalization in a lithium-ion battery management system. IEEE Trans. Power Electron. 2019, 35, 2088–2099. [Google Scholar] [CrossRef]
- Hemavathi, S. Overview of Cell Balancing Methods for Lion Battery Technology Energy Storage; Wiley Online Library: Hoboken, NJ, USA, 2020. [Google Scholar]
- Wu, T.; Qi, Y.; Liao, L.; Ji, F.; Chen, H. Research on equalization strategy of lithium-ion batteries based on fuzzy logic control. J. Energy Storage 2021, 40, 102722. [Google Scholar] [CrossRef]
- Khan, N.; Ooi, C.A.; Shreasth. A novel active cell balancing topology for serially connected Li-ion cells in the battery pack for electric vehicle applications. Sci. Rep. 2024, 14, 18600. [Google Scholar] [CrossRef]
- Uno, M.; Kukita, A. String-to-battery voltage equalizer based on a half-bridge converter with multistacked current doublers for series-connected batteries. IEEE Trans. Power Electron. 2019, 34, 1286–1298. [Google Scholar] [CrossRef]
- Samanta, A.; Chowdhuri, S. Active cell balancing of lithium-ion battery pack using dual DC-DC converter and auxiliary lead acid battery. Energy Storage 2021, 33, 102109. [Google Scholar] [CrossRef]
- Cao, Y.; Li, K.; Lu, M. Balancing method based on flyback converter for series-connected cells. IEEE Access 2021, 9, 52393–52403. [Google Scholar] [CrossRef]
- Cui, X.; Shen, W.; Zhang, Y.; Hu, C.; Zheng, J. Novel active LiFePO4 battery balancing method based on chargeable and dischargeable capacity. Comput. Chem. Eng. 2017, 97, 27. [Google Scholar] [CrossRef]
- Chowdhury, S.M.; Badawy, M.O.; Sozer, Y.; Garcia, J.A.D.A. A Novel Battery Management System Using a Duality of the Adaptive Droop Control Theory. IEEE Trans. Ind. Appl. 2019, 55, 5078–5088. [Google Scholar] [CrossRef]
- Xia, Z.; Qahouq, J.A.A. State-of-charge Balancing of Lithium-ion Batterieswith State-of-health Awareness Capability. IEEE Trans. Ind. Appl. 2020, 57, 673–684. [Google Scholar] [CrossRef]
- Mukherjee, N.; Strickland, D. Control of Second Life Hybrid Battery Energy Storage System Based on Modular Boost-Multilevel Buck nverter. IEEE Trans. Ind. Appl. 2014, 10, 0046–0058. [Google Scholar]
- Liu, H.; Zhang, Z. The Equalizer of Charging and Discharging and the Balancing Strategies for Lithium-Ion Battery Pack. Trans. China Electrotech. Soc. 2015, 30, 186–193. [Google Scholar]
- Xu, B.; Tu, H.; Du, Y.; Yu, H.; Liang, H.; Lukic, S. A Distributed Control Architecture for Cascaded H-Bridge Converter with Integrated Battery Energy Storage. IEEE Trans. Ind. Appl. 2020, 57, 845–856. [Google Scholar] [CrossRef]
- Shi, R.; Zhang, X.; Liu, S.; Huang, L.; Liao, S.; Hu, Z. Review on wind speed prediction based on spatial correlation. Acta Energiae Solaris Sin. 2023, 44, 546–552. [Google Scholar]
- Li, Y.; Han, Y. A Module-Integrated Distributed Battery Energy Storage and Management System. IEEE Trans. Power Electron. 2016, 31, 8260–8271. [Google Scholar] [CrossRef]
- Fares, A.; Klumpner, C.; Sumner, M. Investigating the Benefits and Limitations of Cascaded Converter Topologies Used in Modular Battery Systems. IEEE Trans. Power Syst. 2017, 29, 2123–2130. [Google Scholar]
- Kamel, M.; Zane, R.A.; Maksimović, D. Voltage Sharing with Series Output Connected Battery Modules in a Plug-and-Play DC Microgrid. IEEE Trans. Power Electron. 2021, 36, 13118–13127. [Google Scholar] [CrossRef]





| Parameter Variable | Definition Specification | Numerical Range |
|---|---|---|
| Battery module voltage | ||
| Battery module current (negative for charging, positive for discharging) | ||
| The power on the battery side of the DC–DC converter | ||
| DC–DC converter bus side voltage Upper voltage limit | ||
| Total power of the DC–DC cascading system | ||
| The reciprocal of the efficiency product for each DC–DC converter and the power droop factor parameters of the i-th DC–DC converter Maximum Minimum | ||
| The consideration of the in SOH should be taken into account Maximum Minimum | ||
| Droop coefficient | ||
| Efficiency of DC–DC converters | ||
| Cluster current reference value | ||
| Measurement of cluster current | ||
| The current reference on the DC–DC bus side | ||
| Cluster current reference | ||
| The total voltage on the bus side of the DC–DC converter | ||
| The maximum SOC in multiple battery modules | ||
| The minimum SOC in multiple battery modules | ||
| The maximum SOH in multiple battery modules | ||
| The minimum SOH in multiple battery modules | ||
| The duty cycle of the i-th DC–DC converter | ||
| Battery capacity | mAh |
| The Number of Battery Modules | Initial State of Charge (SoC) | SOH |
|---|---|---|
| 1 | 0.26 | 1.0 |
| 2 | 0.24 | 1.0 |
| 3 | 0.22 | 1.0 |
| 4 | 0.2 | 1.0 |
| 5 | 0.16 | 0.8 |
| 6 | 0.14 | 0.8 |
| 7 | 0.12 | 0.8 |
| 8 | 0.10 | 0.8 |
| The Number of Battery Modules | Initial State of Charge (SoC) | SOH |
|---|---|---|
| 1 | 0.9 | 0.8 |
| 2 | 0.9 | 0.8 |
| 3 | 0.9 | 0.8 |
| 4 | 0.7 | 1.0 |
| 5 | 0.7 | 1.0 |
| 6 | 0.7 | 1.0 |
| 7 | 1.0 | 0.7 |
| 8 | 1.0 | 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, S.; Tong, X.; Ma, X.; Zhou, J. SOC Equalization Control Method Considering SOH in DC–DC Converter Cascaded Energy Storage Systems. Energies 2024, 17, 6385. https://doi.org/10.3390/en17246385
Bai S, Tong X, Ma X, Zhou J. SOC Equalization Control Method Considering SOH in DC–DC Converter Cascaded Energy Storage Systems. Energies. 2024; 17(24):6385. https://doi.org/10.3390/en17246385
Chicago/Turabian StyleBai, Shixian, Xiangqian Tong, Xin Ma, and Jie Zhou. 2024. "SOC Equalization Control Method Considering SOH in DC–DC Converter Cascaded Energy Storage Systems" Energies 17, no. 24: 6385. https://doi.org/10.3390/en17246385
APA StyleBai, S., Tong, X., Ma, X., & Zhou, J. (2024). SOC Equalization Control Method Considering SOH in DC–DC Converter Cascaded Energy Storage Systems. Energies, 17(24), 6385. https://doi.org/10.3390/en17246385






