Multi-Time-Scale Layered Energy Management Strategy for Integrated Production, Storage, and Supply Hydrogen Refueling Stations Based on Flexible Hydrogen Load Characteristics of Ports
Abstract
1. Introduction
- The upper layer considers minimizing the HFS daily operating costs, including operation and maintenance costs, purchased electricity cost, and purchased hydrogen cost. A PSA-PSO algorithm is proposed to solve the upper-layer energy management, thus improving the solving efficiency;
- The objective function of the lower layer is to minimize the intra-day and day-ahead scheduling errors and the power fluctuations of the electrolyzer (Elz) and grid. The SMPC algorithm for solving the optimization problem is proposed to reduce the interference of stochastic variables and achieve better optimization results;
- An example analysis is conducted using measured data from southeastern China to verify the proposed energy management. The results show that the proposed energy management strategy has good control effects in different typical scenarios.
2. Guidelines for Manuscript Preparation
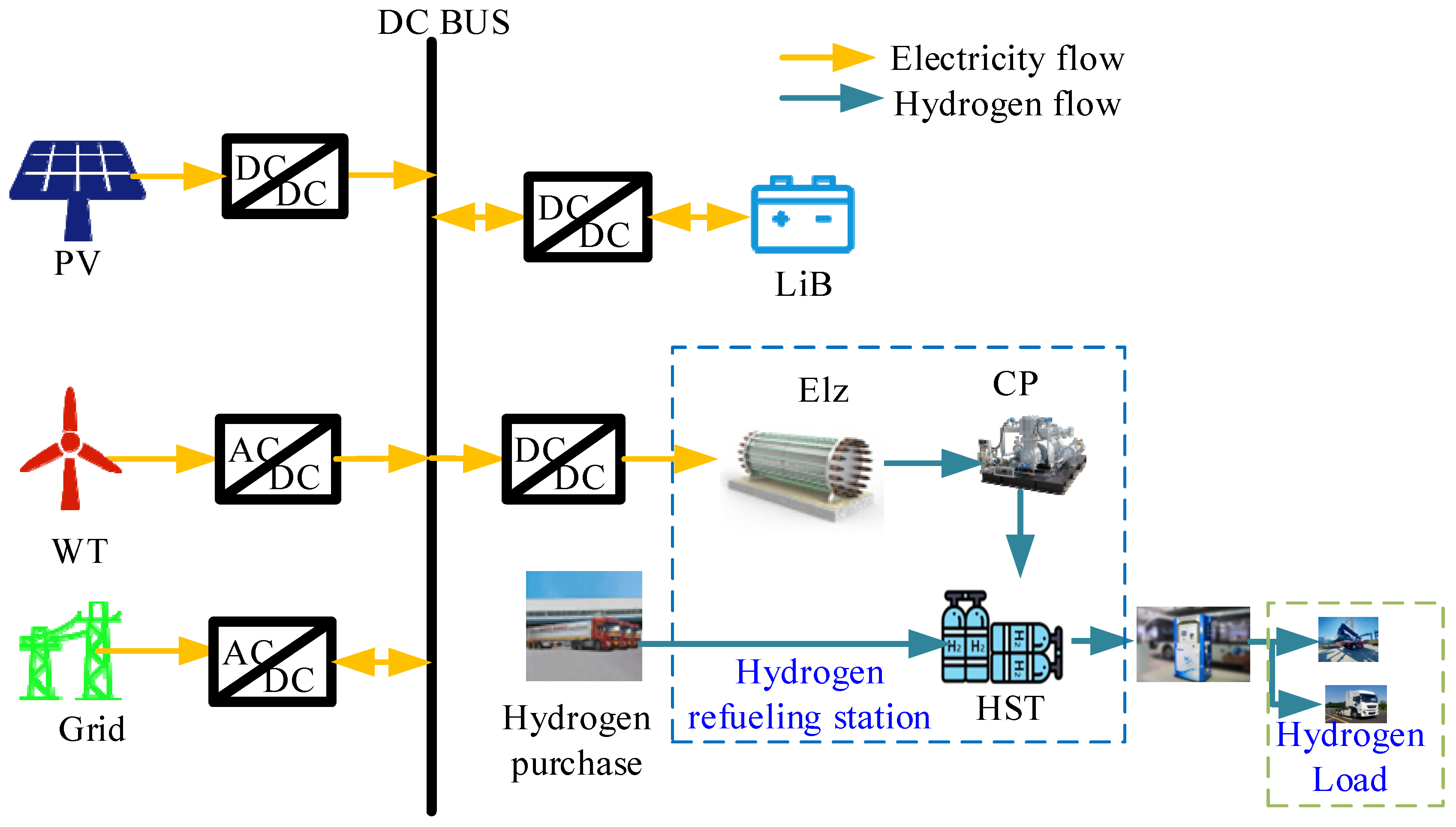
3. Multi-Time-Scale Energy Management Strategies
3.1. Upper-Layer Energy Management Strategy
- (1)
- LiB mainly includes charging and discharging power constraints and state of charge (SOC) constraints:where Pbatmin, Pbatmax, R, ηbat, SOCmin, SOCmax, Ebat, and ΔT represent the minimum operating power of the LiB, the maximum operating power of the LiB, self-discharge rate of LiB, charge/discharge rate of LiB, the minimum SOC value of the LiB, maximum SOC value of the LiB, capacity of the LiB, and time interval of the scheduling cycle. If Pbat is positive, the LiB is charging. Otherwise, the LiB is discharging.
- (2)
- The constraints of the Elz mainly include operating power constraints and hydrogen production constraints. The Elz operating power range is from minimum operation to rated power operation, and the minimum power of the Elz is usually 10% of its rated power [20,21]:where Pelemin, Pelemax, HHV, and ηele represent the minimum operating power of the Elz, the maximum operating power of the Elz, the high heat value of hydrogen, and the efficiency of the Elz.
- (3)
- The operation of the CP mainly considers its power consumption, and its value is directly related to the hydrogen production of the Elz [22]:where Cp is the calorific value of hydrogen, Tin is the temperature of hydrogen at the inlet (K), ηcomp denotes the compress efficiency, which is taken as 0.7 in this paper, Pin and Pout denote the inlet and outlet pressures of the CP, r denotes the isentropic exponent of the hydrogen, which is usually taken as 1.4, and nh2 denotes the flow rate of the hydrogen. The hydrogen flow rate of CP is directly from the Elz, which can be expressed as [23]:where nc is the number of cells connected in series in the Elz, Iel is the Elz current, Z is the number of charges transferred during the electrolysis of water, F denotes the Faraday constant, and ηF is the current efficiency of the Elz, which means the ratio of the charge required for the production of hydrogen to the total charge consumed by the Elz:
- (4)
- The level of hydrogen (LOH) is a key parameter to characterize the internal hydrogen storage amount of HST, which needs to meet the following constraints:where LOHmin, LOHmax, mstore, moff, mload, and mmax respectively represent the minimum LOH value, the maximum LOH value, the internal hydrogen mass of the HST, the mass of external hydrogen source supply, the hydrogen load demand, and maximum allowable hydrogen mass allowed to be stored in the HST.
- (5)
- At the end of each day, SOC and LOH are required to meet the operational requirements of the following day:where SOC0 and LOH0 denote the initial values of SOC and LOH, respectively. amin and amax denote the SOC constraint coefficients. Taking the coupling relationship between different constraints into account, amin and amax are taken as 0.7 and 1.2, respectively.
- (6)
- The power of the grid needs to meet certain constraint:where Pgridmin and Pgridmax respectively represent the minimum and maximum power of the grid.
- (7)
- The electricity of the system needs to be balanced:where Ppv and Pwt represent power of the PV and WT.
- (1)
- In the PSO algorithm, ω directly affects the global search ability [25]. A larger inertia weight has a stronger global search ability so the algorithm is more likely to obtain the optimal solution, while a smaller inertia weight will give particles a stronger local search ability and accelerate the convergence of the algorithm. Therefore, this paper adaptively adjusts the inertia weight. In the early stage, it can quickly obtain the optimal solution by achieving a larger ω. In the later stage of the iteration process, a lower ω is beneficial to algorithm convergence.where ωmax and ωmin represent the upper and lower limits of the weight coefficient. In this paper, 0.9 and 0.4 are taken, respectively. t1 represents the current number of iterations, and Maxit represents the maximum number of iterations, which is set to 100.
- (2)
- The learning factors C1 and C2 are also important parameters for regulating algorithm performance. At the beginning of the algorithm iteration, so that the particles can search in the whole space, larger C1 and smaller C2 can be set. As the number of iterations increases, to make the particle search results more inclined toward the global optimal solution, larger C2 and smaller C1 are set. Additionally, to enhance the adaptive adjustment capability of parameters, the sine function and tangent function are applied in the formula for parameter adjustment, namely:where C1max and C2min are taken as 2 and 0.5, respectively.
- (3)
- This paper introduces Gaussian disturbance after each particle updates position to enhance particle diversity and jumps out of the local optimal solution. At the same time, an adaptive disturbance step size is set. As the number of iterations increases, the disturbance component gradually increases, thereby enhancing the ability to quickly search for the optimal solution. Namely:where μ represents disturbance step size and Gauss represents the Gaussian disturbance term.
3.2. Lower-Layer Energy Management Strategy
- (1)
- Divide the sample into m equal probability distribution intervals;
- (2)
- Randomly select a point within the interval in (1);
- (3)
- Randomly combine the points obtained in (2) with other variables to obtain the sampling points xi, and obtain the sample values of the sampling points through the inverse transformation of the cumulative probability distribution function f (xi) = Pi.
- (1)
- Set two specific scenarios at a certain time step as ai and aj, then calculate the probability distance d (ai, aj) of pairwise scenarios in the scenario set:where Pi represents the probability of scenario I;
- (2)
- Delete the scenario with the smallest distance obtained in (1);
- (3)
- Modify the remaining number of scenarios P = P − 1 to ensure that the sum of probabilities for all scenarios is equal to 1, and add the probability of the deleted scenario to the nearest scenario;
- (4)
- Repeat the above steps at each time step until the number of scenarios reaches the set value M, and the probability of each scenario is εi.
- (1)
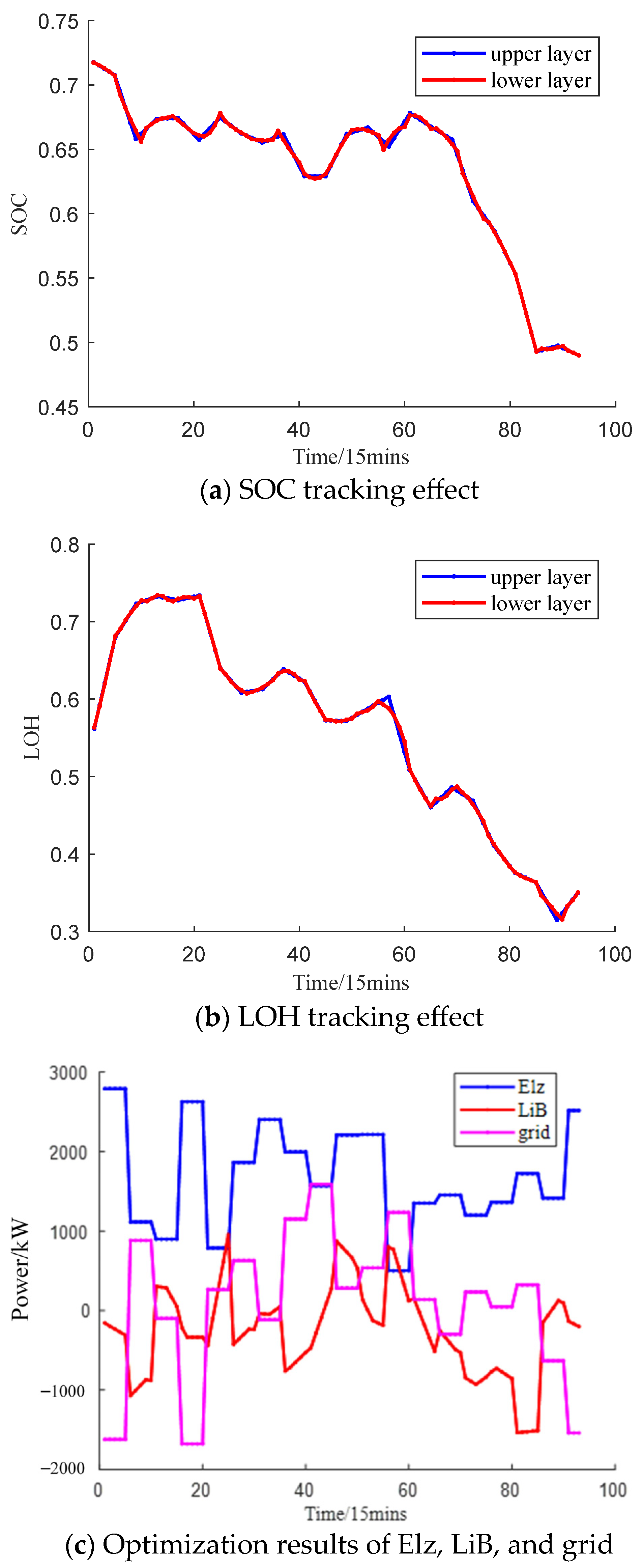
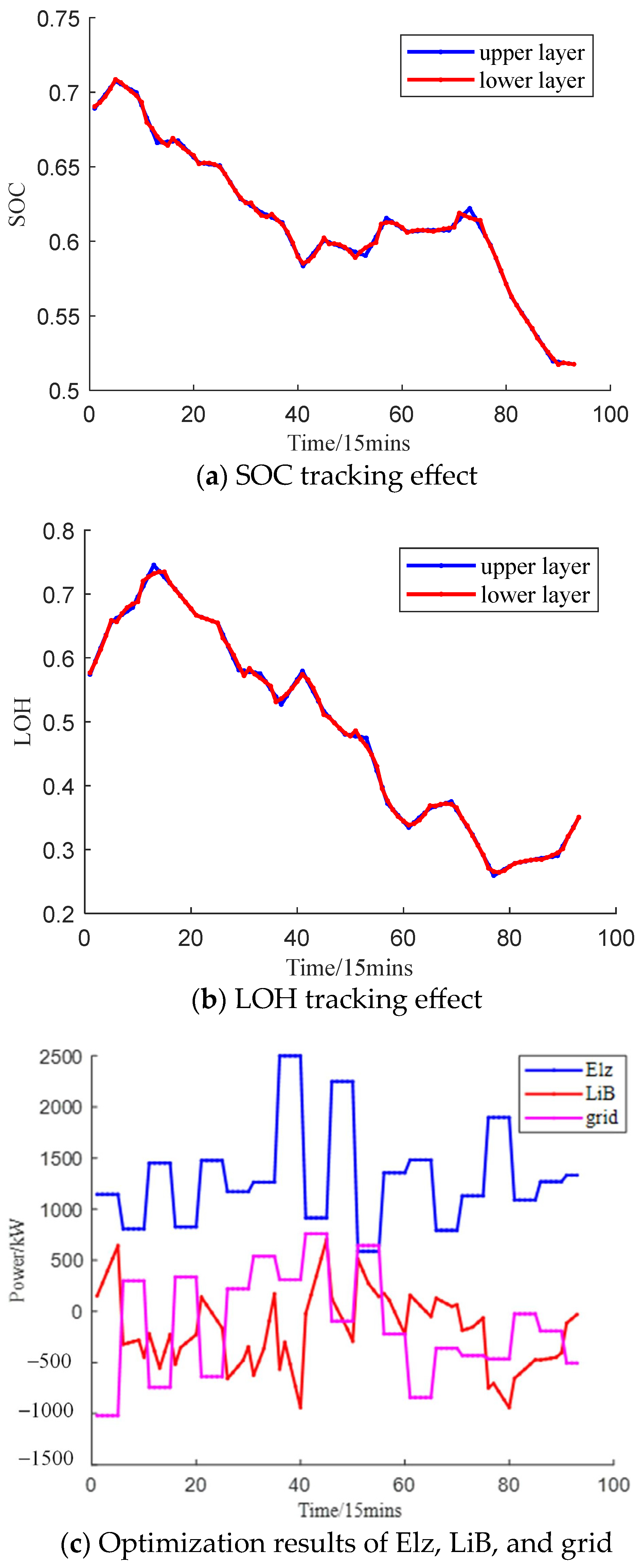
- State variables SOC and LOH should track the optimization results of the upper-layer energy management as much as possible;
- (2)
- Minimize power fluctuations of the Elz and grid during each control cycle;
- (3)
- Introduce penalty factors, which allow the value of the state variables to exceed the limit, but still aim to minimize the exceeding value of the lower layer state variables as much as possible.
- (1)
- In the process of tracking state variables, the values of lower-layer state variables are likely to exceed the limit. Therefore, this paper introduces slack variables ε1 and ε2, which allows for a small amount of overstepping of the lower layer state variables:
- (2)
- In addition, the fluctuations of power need to meet the constraints:
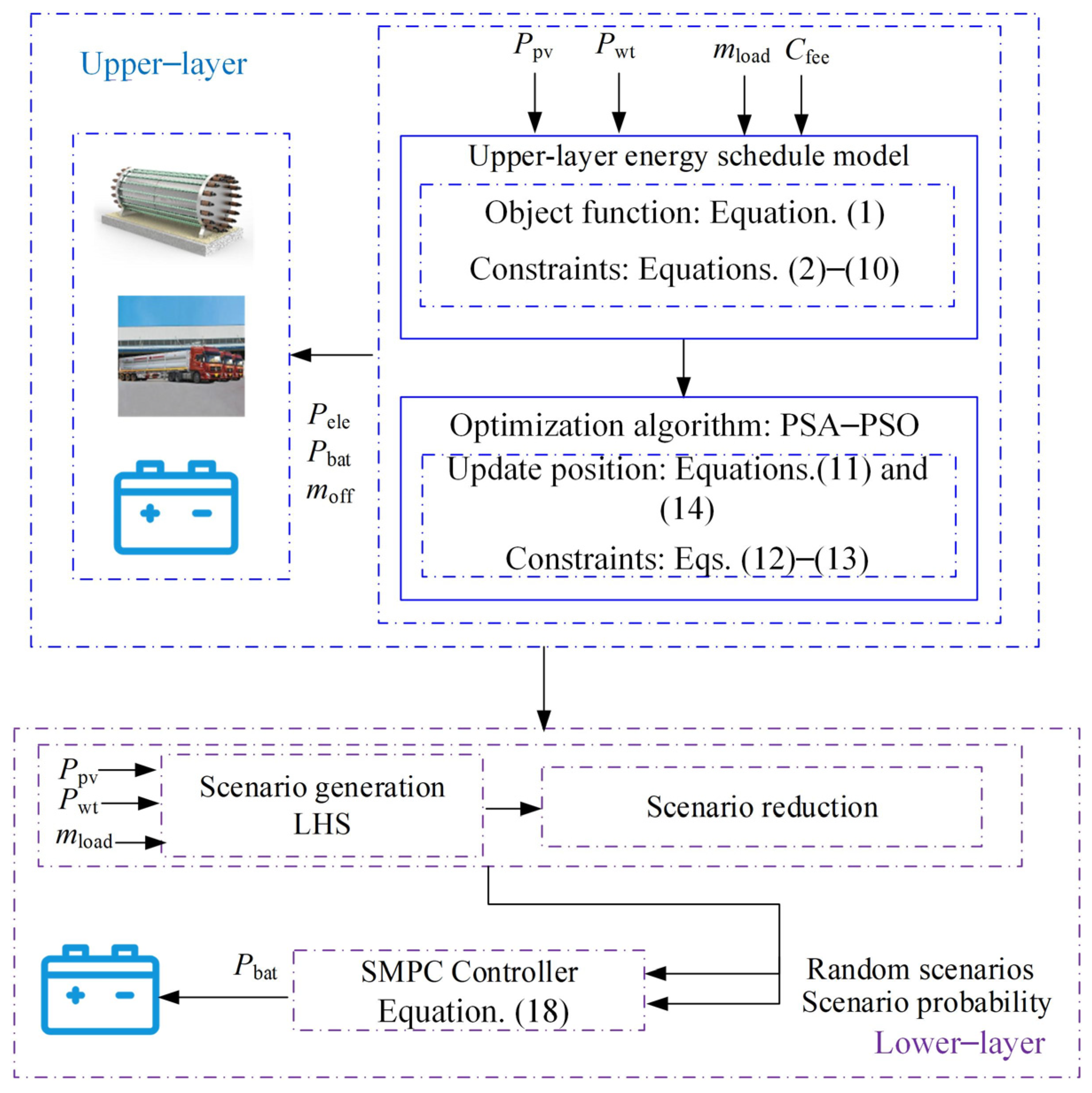
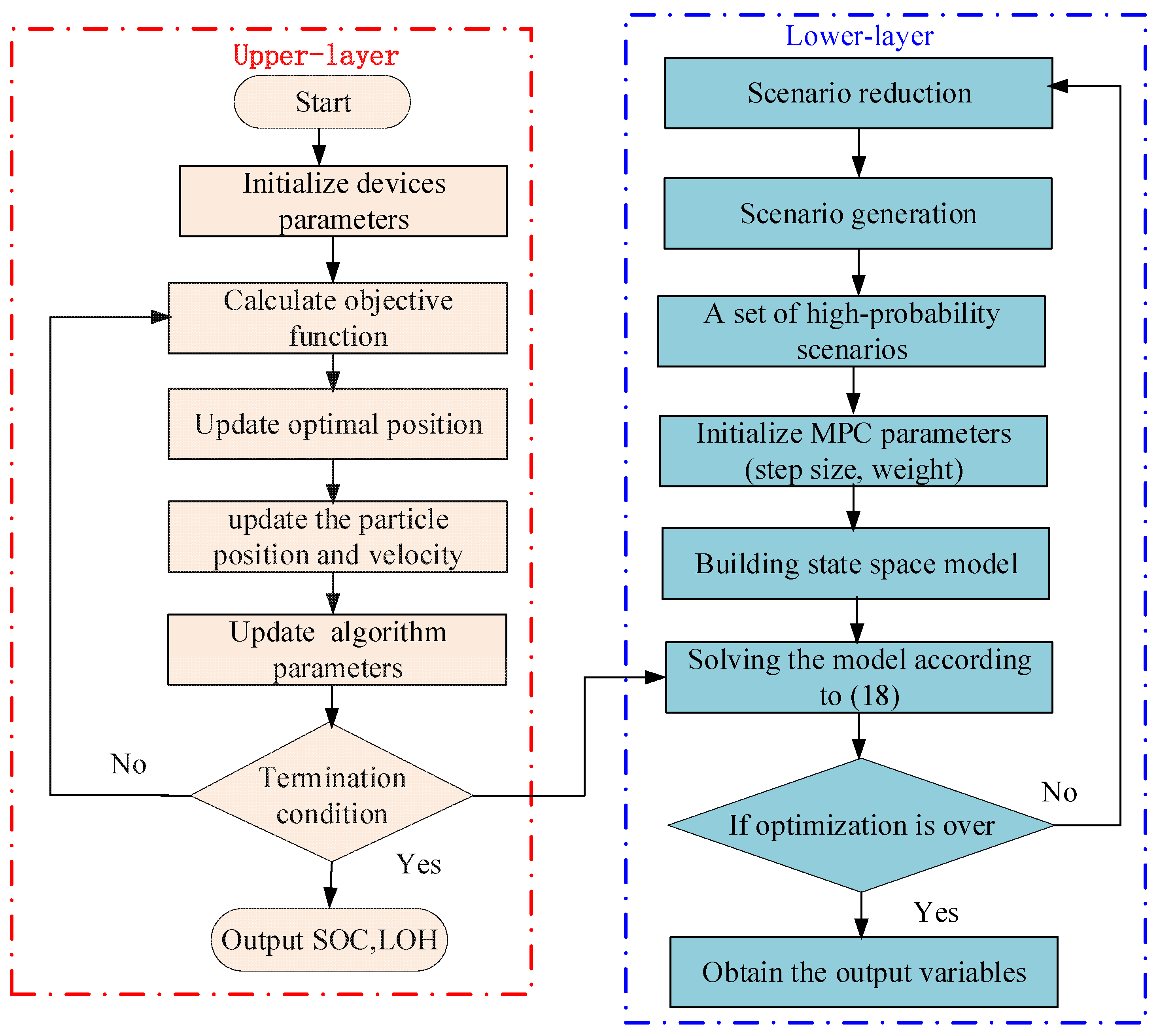
4. Multi-Time-Scale Energy Management Strategy Flow Chart
- (1)
- Initialize PSA-PSO algorithm parameters and device parameters;
- (2)
- Each iteration of the upper layer energy management updates the speed and position according to Equations (11) and (14), and updates the algorithm parameters according to Equations (12) and (13) at the end of the iteration;
- (3)
- If the termination condition is met (the current iteration number reaches the maximum iteration number), SOC and LOH are output to complete the upper layer energy management algorithm solution. Otherwise, continue searching from (2) until the termination condition is met;
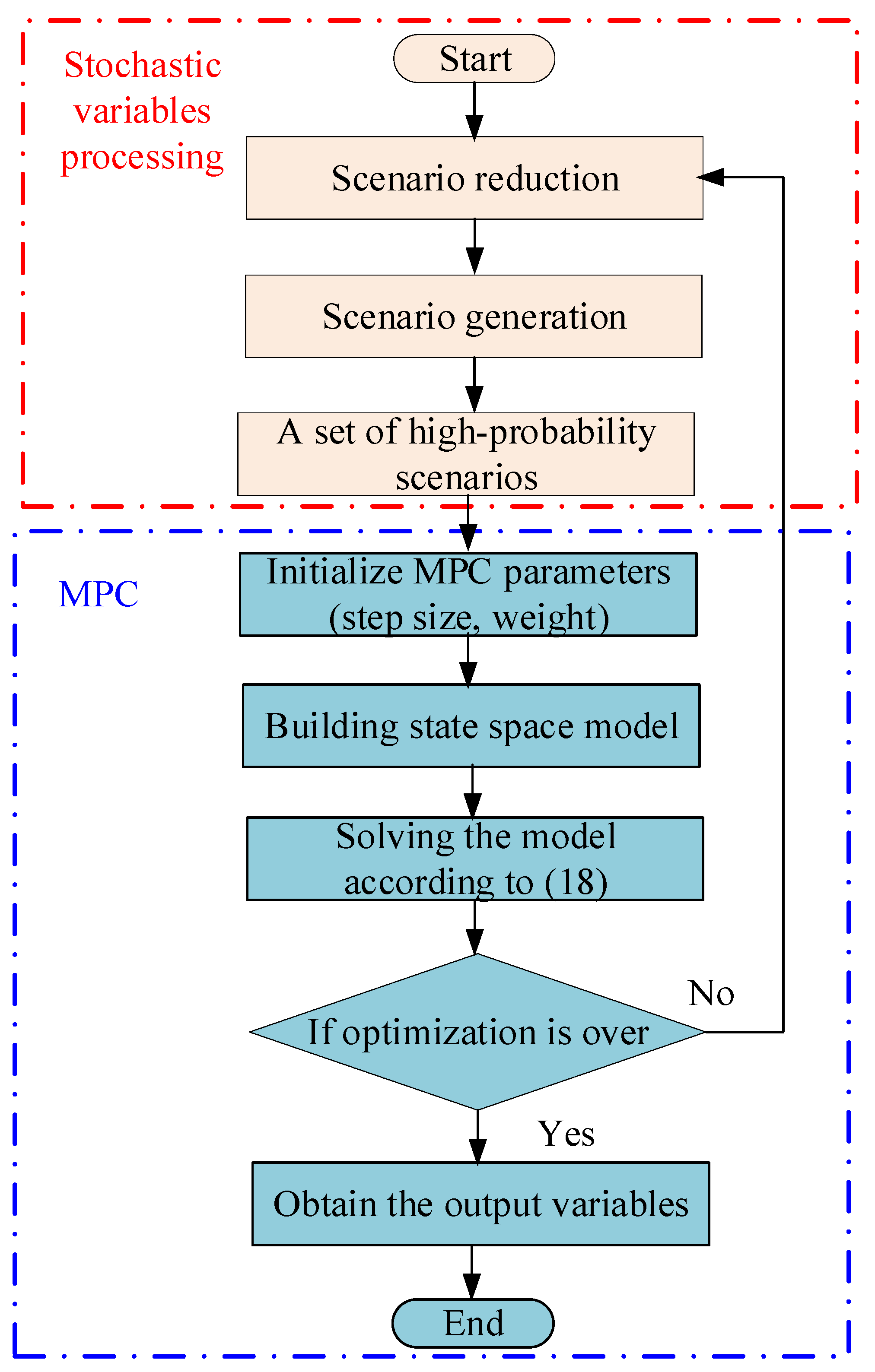
- (4)
- Stochastic variables (WT and PV power, and hydrogen load) are preprocessed by linear interpolation to meet the time scale requirements for lower-layer control;
- (5)
- A large amount of renewable energy power generation and hydrogen load consumption are obtained through LHS within the prediction step size;
- (6)
- Reduce scenarios at different time steps through the simultaneous backward reduction method and obtain the probability of the reduced scenarios;
- (7)
- Initialize the parameters of MPC, including prediction step size and weight coefficients;
- (8)
- Establish a state space model of HFS;
- (9)
- Combine the stochastic variable scenarios, corresponding probability values processed in (6) and the state variables input in (3), the MPC model is solved according to Equation (18);
- (10)
- When the optimization cycle ends, the solution is completed and Pbat is output. Otherwise, repeat (5)–(8) until the optimization cycle ends.
5. Guidelines for Graphics Preparation and Submission
6. Conclusions
- (1)
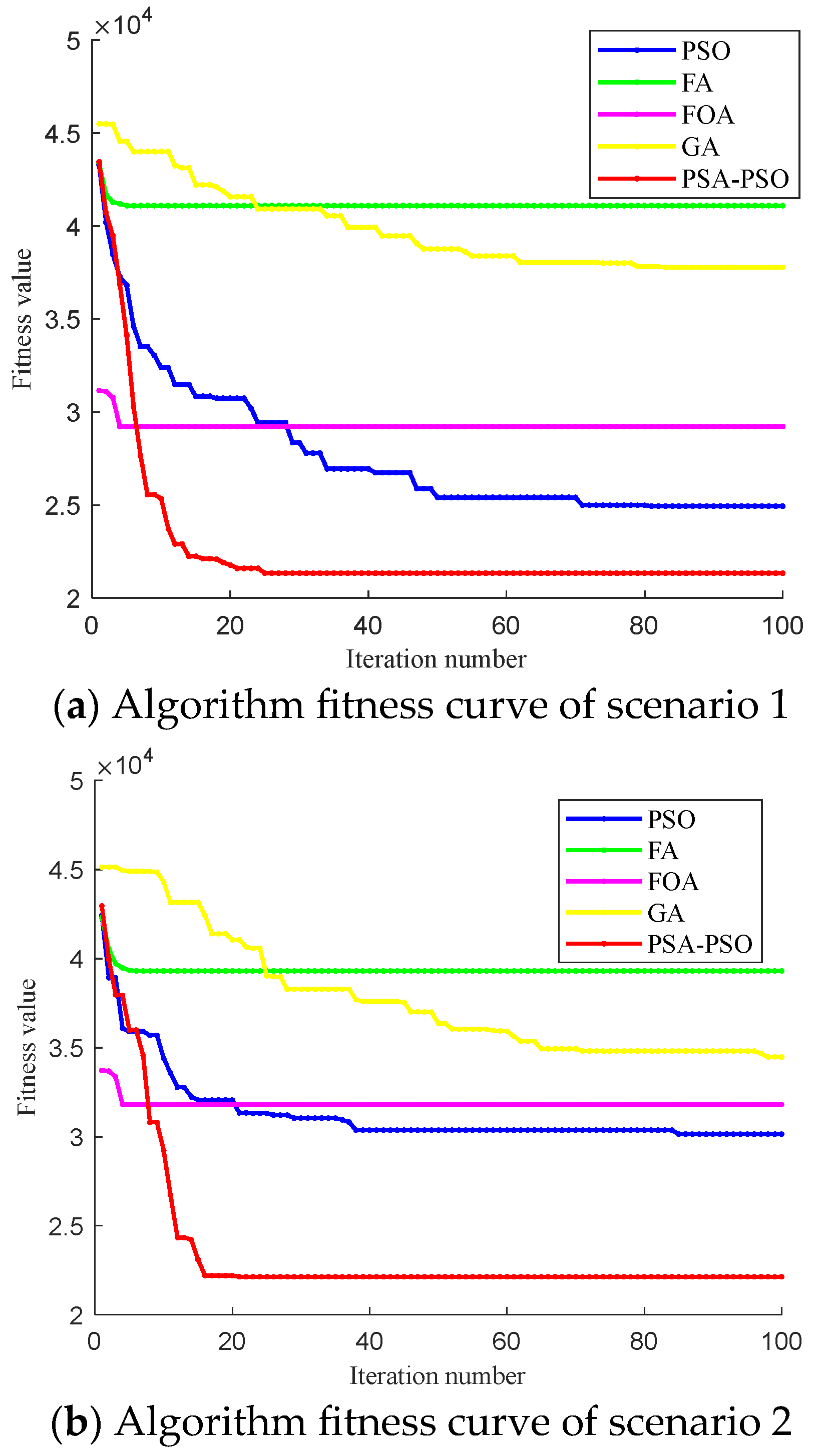
- Aiming at the economic issues of HFSs, the upper layer of the proposed strategy is on an hourly level, and the optimization goal is to minimize the sum of equipment operation and maintenance costs, electricity purchase cost, and hydrogen purchase cost. Aiming at the problems of the PSO algorithm, including being prone to local optimal value and slow convergence speed, a PSA-PSO algorithm is proposed to solve those problems. This algorithm introduced Gaussian disturbance with adaptive adjustment of the learning factor, inertia weight, and disturbance step size to improve solution accuracy and convergence speed.
- (2)
- Aiming at the randomness of renewable energy and hydrogen load, the lower layer is at the minute-level time scale. To address the disturbance caused by the randomness of the renewable energy and hydrogen load on the system, the SMPC algorithm is proposed. The LHS and simultaneous backward reduction method have been used to generate and reduce stochastic variables to obtain a set of high-probability scenarios, which have been brought into the MPC to suppress the interference of stochastic variables on the operation of HFS.
- (3)
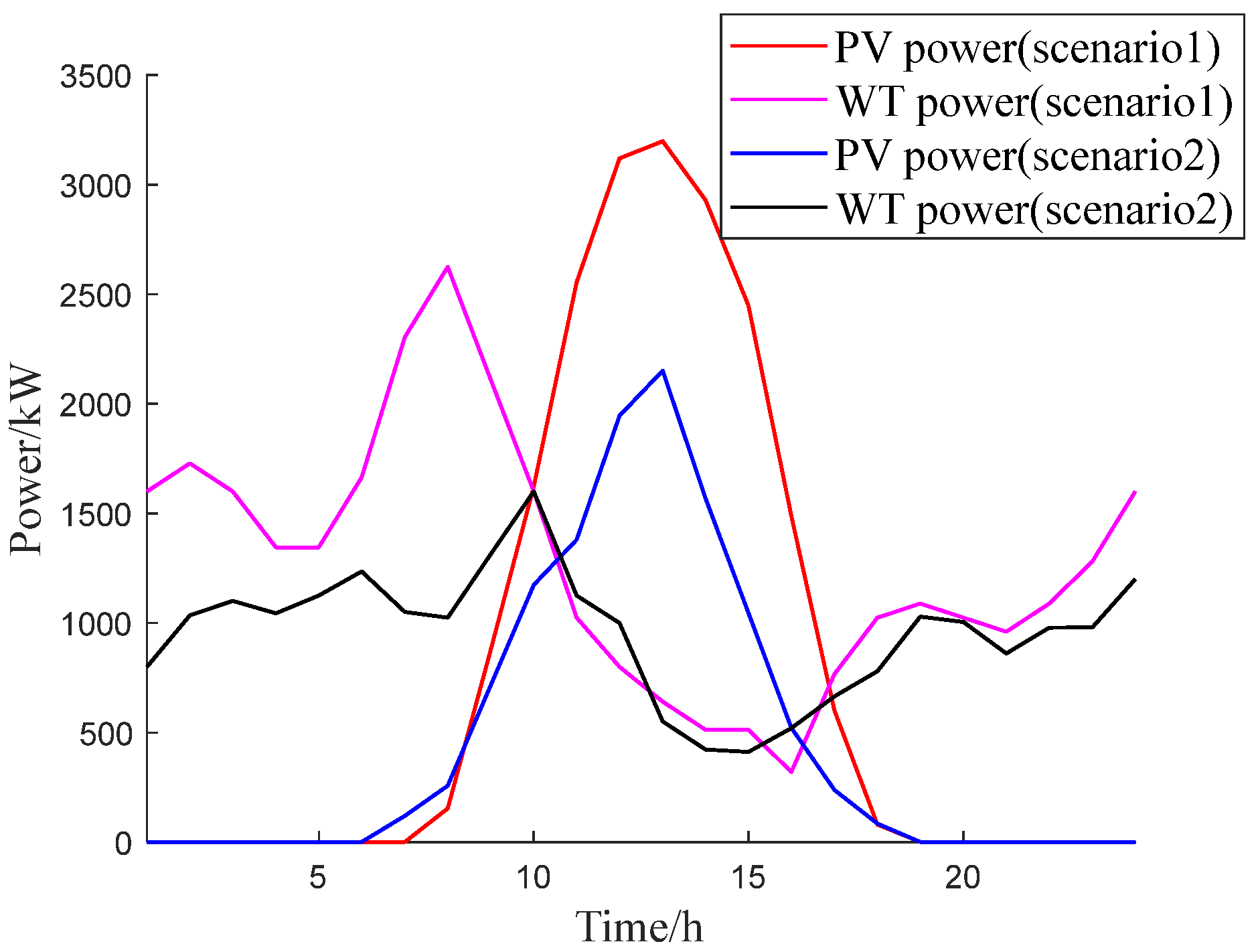
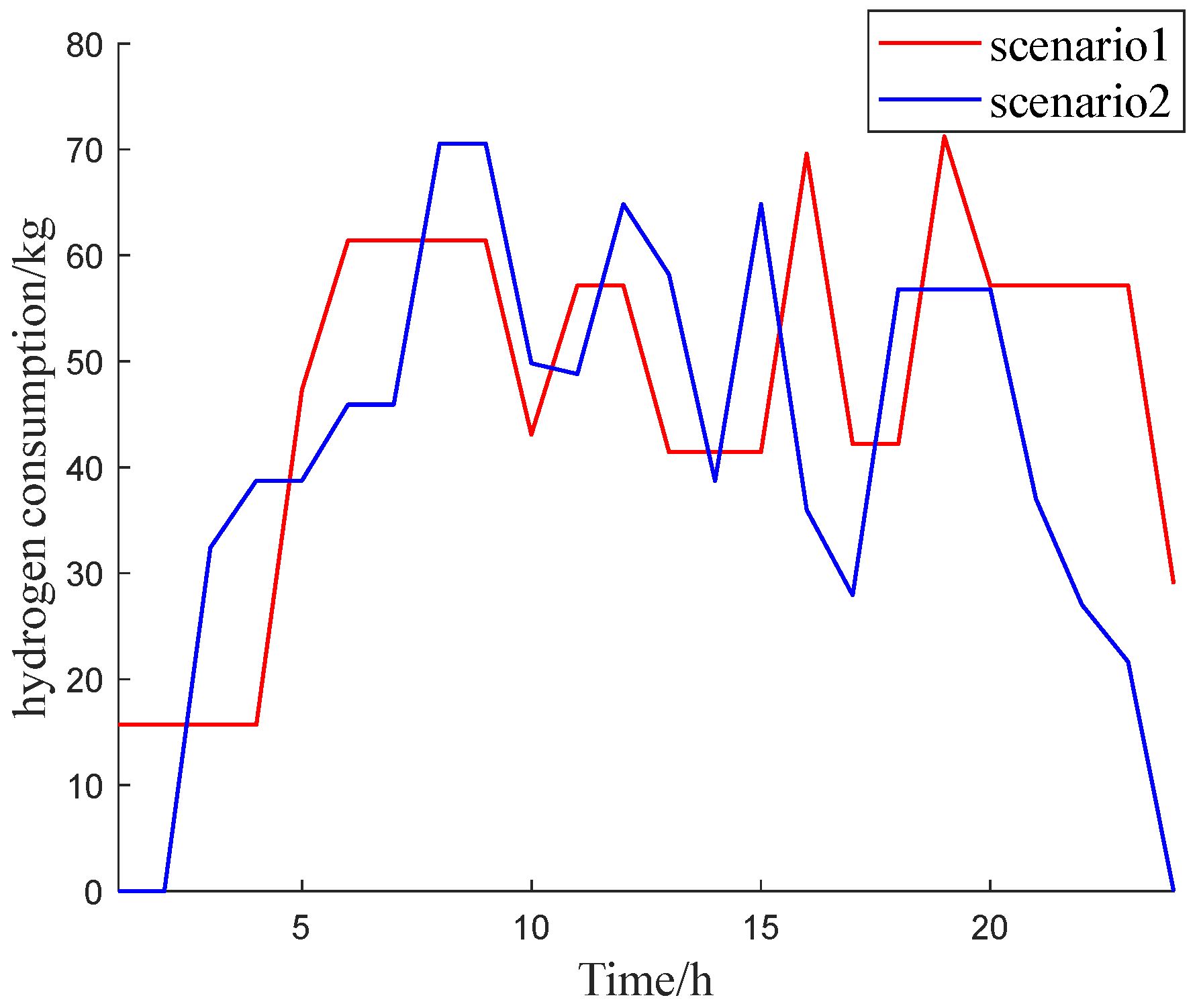
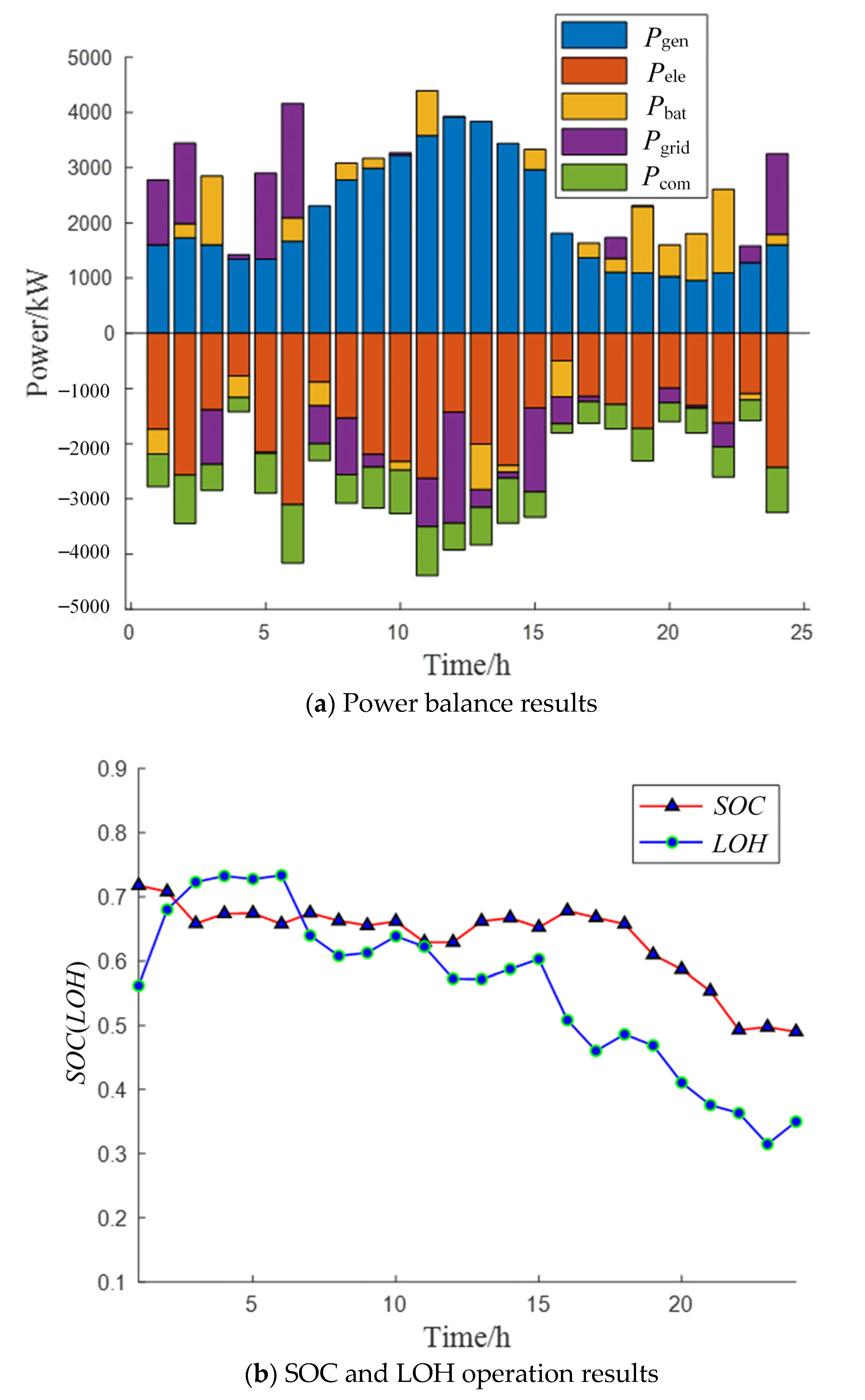
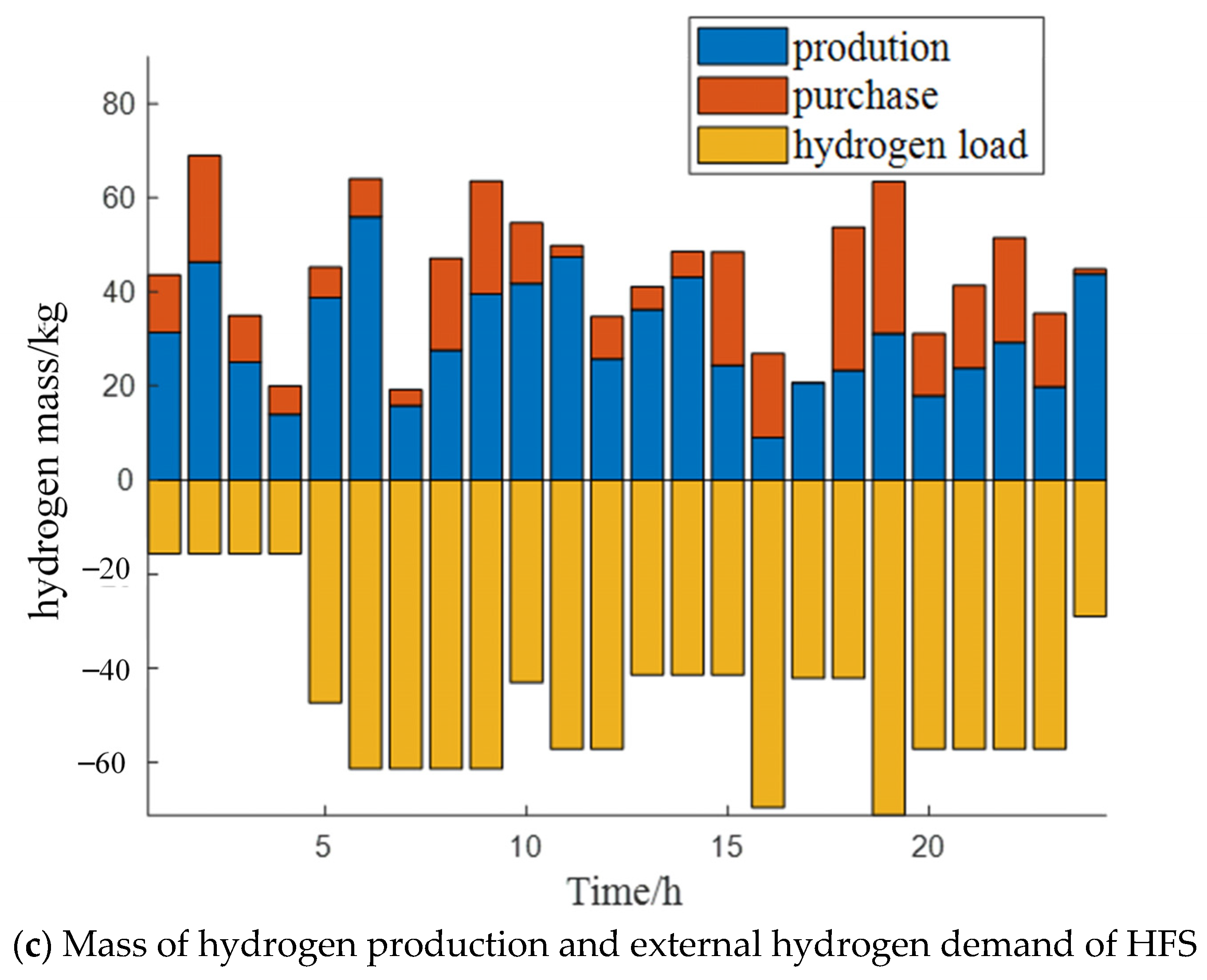
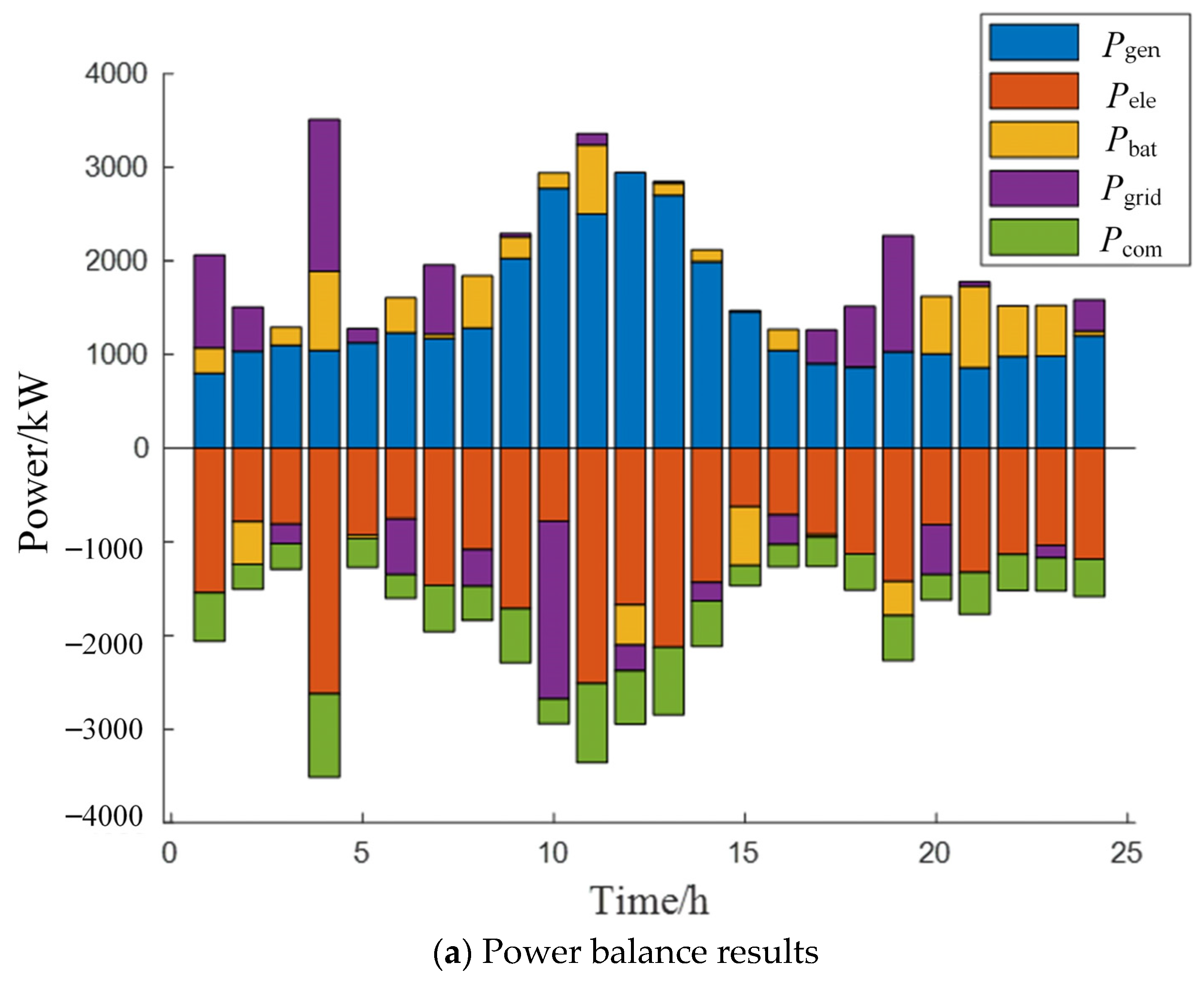
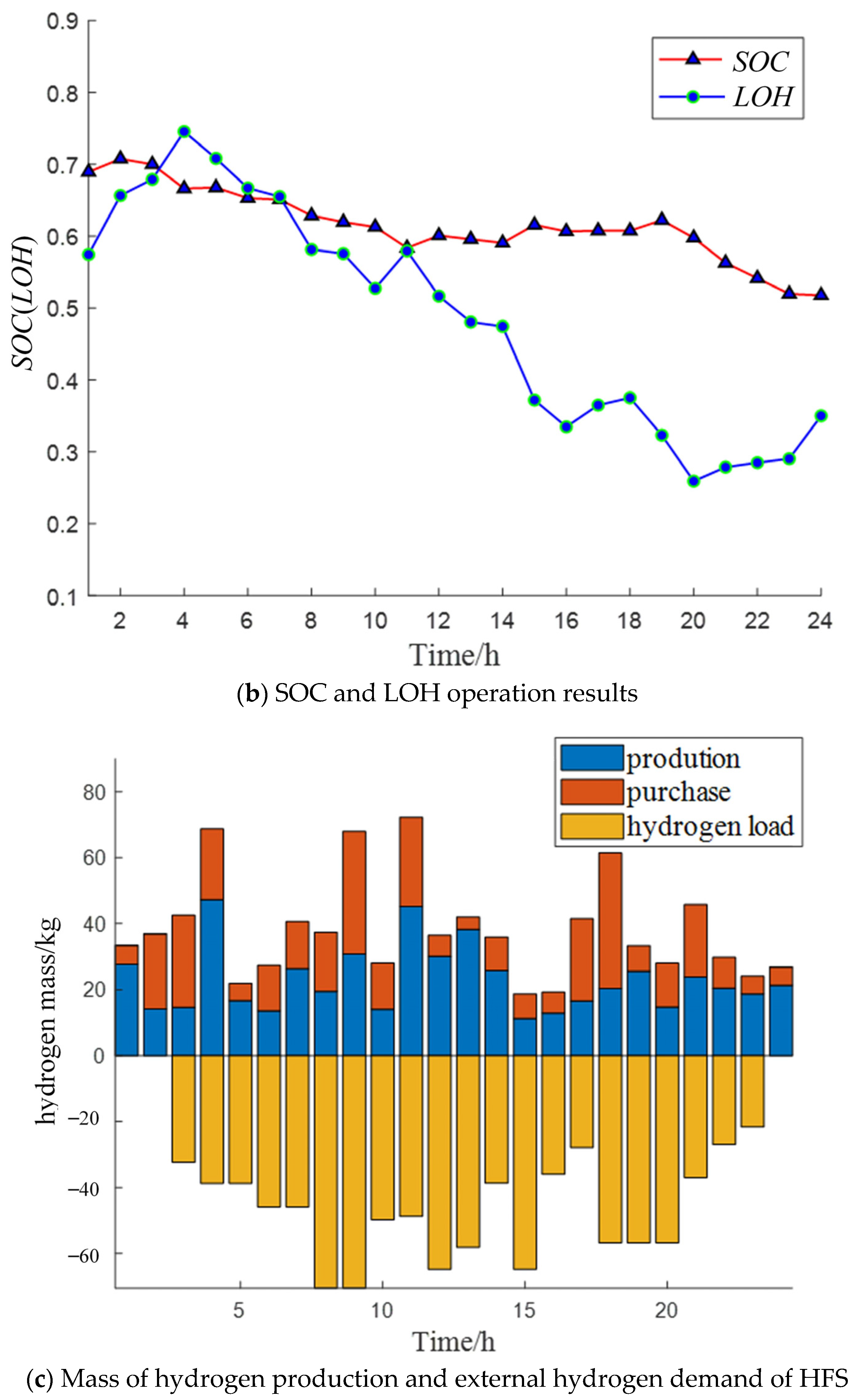
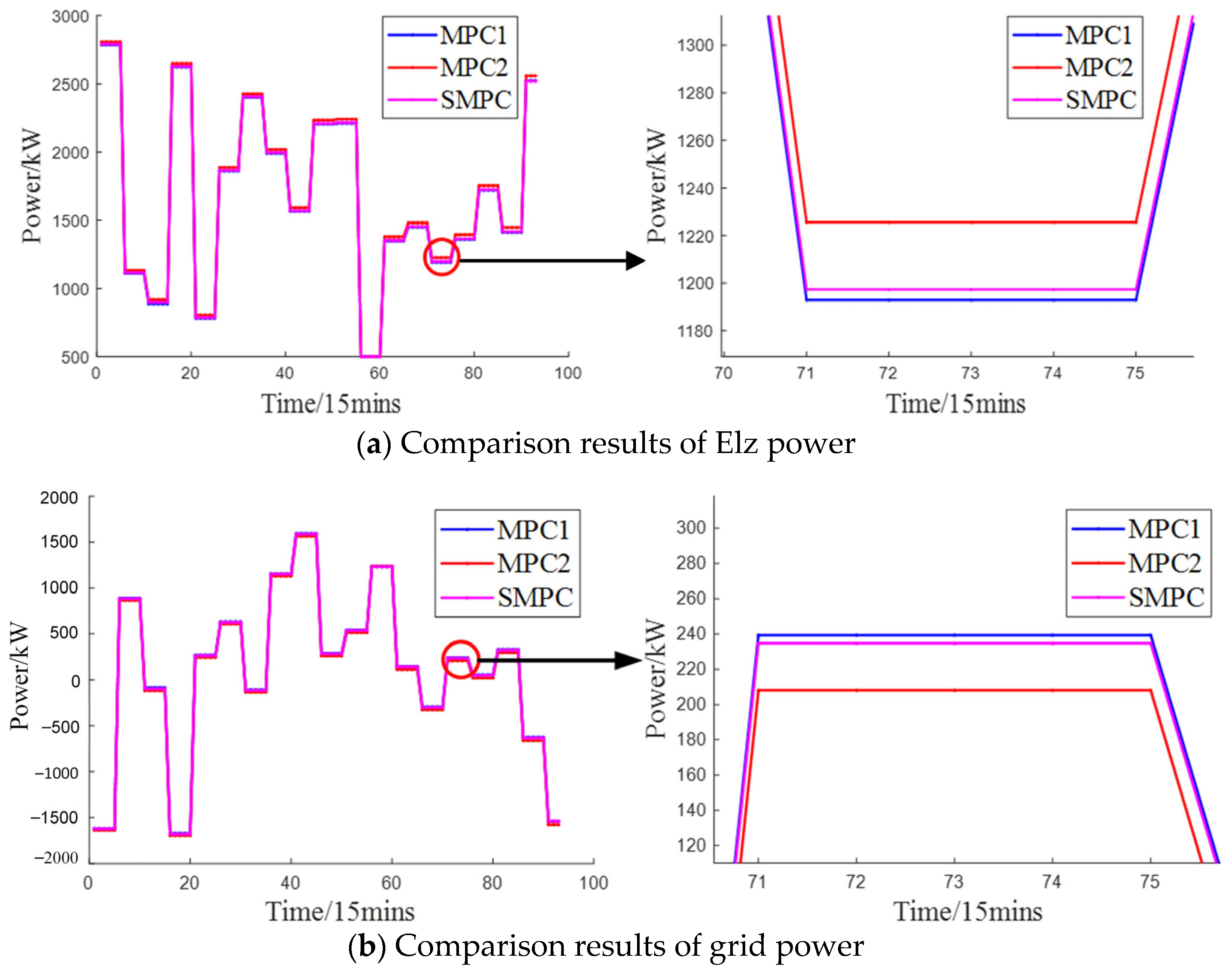
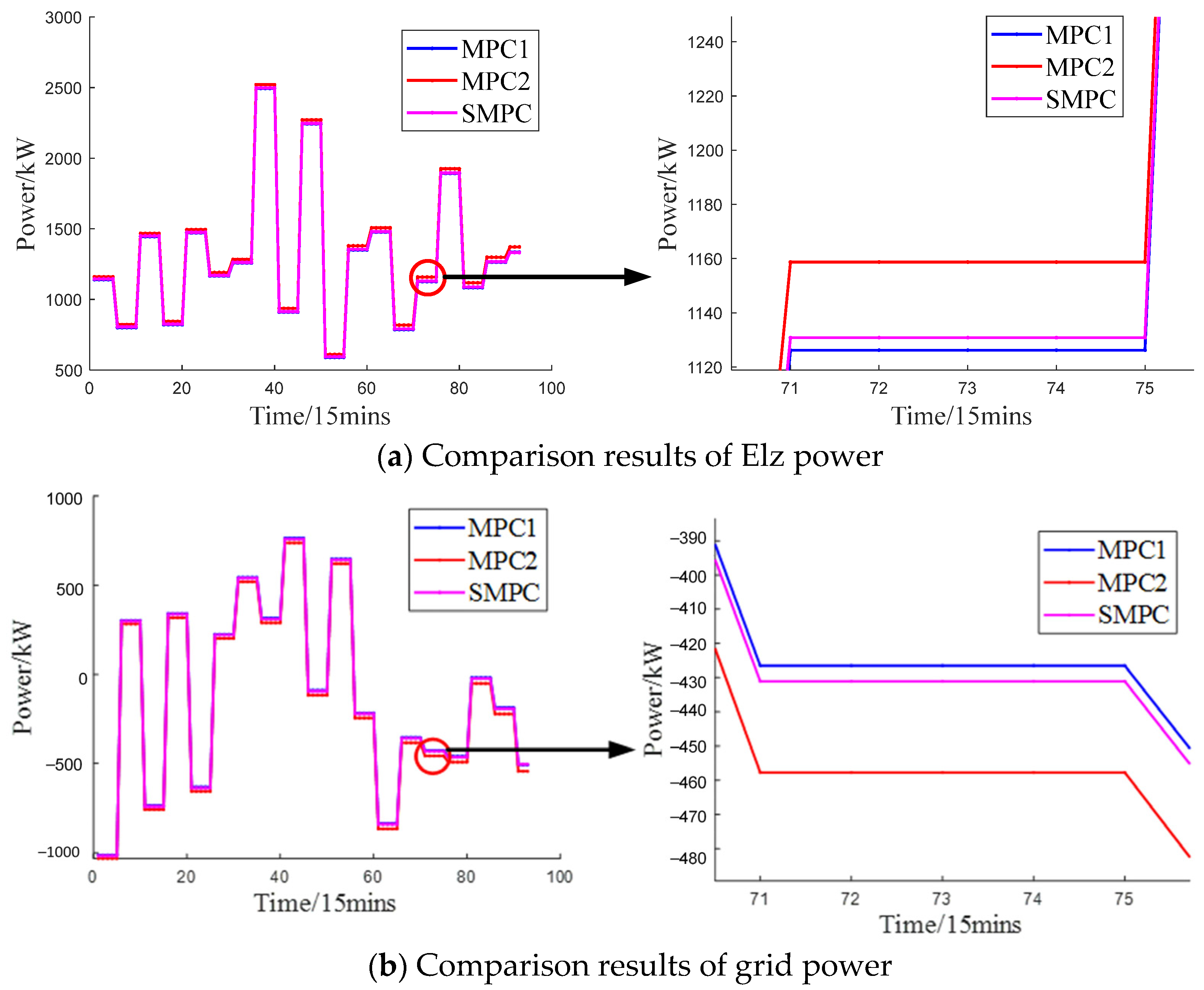
- Operation data from southeastern China were used for example analysis. The results show that the proposed PSA-PSO algorithm can better balance the characteristics of fast convergence speed and good optimization effect compared with traditional optimization algorithms, such as PSO, FA, FOA, and GA. The daily operation cost solved by PSA-PSO can be reduced by up to 16,460 ¥ and 17,170 ¥ in different scenarios. The proposed SMPC algorithm can significantly reduce with the inference of renewable energy and hydrogen load to Elz and grid compared with the traditional MPC algorithm. Compared with the traditional MPC algorithm, the Pflu of Elz in different scenarios was reduced by 16.2% and 14.9%, the Pflu of grid in different scenarios was reduced by 17.2% and 15.9%.
- (4)
- Regarding future work, the large-capacity electrolytic hydrogen production model is a simple electrochemical empirical model, and it is necessary to establish a large-capacity electrolytic cell model that considers the deep coupling of energy–material flow to comprehensively reflect the energy change and material transfer laws of electrolytic hydrogen production equipment under different working conditions. The refined energy management strategy is verified using equipment from an actual HFS in Zhoushan Port, Ningbo, Zhejiang Province, China.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, N.; Zhao, W.; Wang, W.; Li, X.; Zhou, H. Large scale of green hydrogen storage: Opportunities and challenges. Int. J. Hydrogen Energy 2024, 50, 379–396. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. A review of energy efficiency in ports: Operational strategies, technologies and energy management systems. Renew. Sustain. Energy Rev. 2019, 112, 170–182. [Google Scholar] [CrossRef]
- Apostolou, D.; Xydis, G. A literature review on hydrogen refuelling stations and infrastructure. Current status and future prospects. Renew. Sustain. Energy Rev. 2019, 113, 109292. [Google Scholar] [CrossRef]
- Hossain, A.; Islam, R.; Hossain, A.; Hossain, M. Control strategy review for hydrogen-renewable energy power system. J. Energy Storage 2023, 72, 108170. [Google Scholar] [CrossRef]
- Van, L.P.; Chi, K.D.; Duc, T.N. Review of hydrogen technologies based microgrid: Energy management systems, challenges and future recommendations. Int. J. Hydrogen Energy 2023, 48, 14127–14148. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Ghadimi, A.A.; Miveh, M.R.; Bayat, M.; Jurado, F. Uncertainty-aware energy management strategies for PV-assisted refuelling stations with onsite hydrogen generation. J. Clean. Prod. 2022, 365, 132869. [Google Scholar] [CrossRef]
- Shams, M.H.; Niaz, H.; Liu, J.J. Energy management of HFSs in a distribution system: A bilevel chance-constrained approach. J. Power Sources 2022, 533, 231400. [Google Scholar] [CrossRef]
- Abomazid, A.M.; El-Taweel, N.A.; Farag, H.E.Z. Optimal Energy Management of Hydrogen Energy Facility Using Integrated Battery Energy Storage and Solar Photovoltaic Systems. IEEE Trans. Sustain. Energy 2022, 13, 1457–1468. [Google Scholar] [CrossRef]
- Pang, Y.; Pan, L.; Zhang, J.; Chen, J.; Dong, Y.; Sun, H. Integrated sizing and scheduling of an off-grid integrated energy system for an isolated renewable energy HFS. Appl. Energy 2022, 323, 119573. [Google Scholar] [CrossRef]
- Dadkhah, A.; Bozalakov, D.; De Kooning, J.D.M.; Vandevelde, L. On the optimal planning of a hydrogen refuelling station participating in the electricity and balancing markets. Int. J. Hydrogen Energy 2021, 46, 1488–1500. [Google Scholar] [CrossRef]
- Zhang, W.; Maleki, A.; Nazari, M.A. Optimal operation of a hydrogen station using multi-source renewable energy (solar/wind) by a new approach. J. Energy Storage 2022, 53, 104983. [Google Scholar] [CrossRef]
- Erdinç, F.G.; Çiçek, A. Cost minimization oriented energy management of PV-assisted refueling and recharging stations for FC-ultracapacitor hybrid trams. Energy Convers. Manag. 2023, 287, 117103. [Google Scholar] [CrossRef]
- Liu, L.; Su, X.; Chen, L.; Wang, S.; Li, J.; Liu, S. Elite Genetic Algorithm Based Self-Sufficient Energy Management System for Integrated Energy Station. IEEE Trans. Ind. Applicat. 2024, 60, 1023–1033. [Google Scholar] [CrossRef]
- Jordehi, A.R.; Mansouri, S.A.; Tostado-Veliz, M.; Safaraliev, M.; Hakimi, S.M.; Nasir, M. A tri-level stochastic model for operational planning of microgrids with hydrogen refuelling station-integrated energy hubs. Int. J. Hydrogen Energy 2024, 96, 1131–1145. [Google Scholar] [CrossRef]
- Fang, X.; Wang, Y.; Dong, W.; Yang, Q.; Sun, S. Optimal energy management of multiple electricity-hydrogen integrated charging stations. Energy 2023, 262, 125624. [Google Scholar] [CrossRef]
- Rahbar, K.; Xu, J.; Zhang, R. Real-Time Energy Storage Management for Renewable Integration in Microgrid: An Off-Line Optimization Approach. IEEE Trans. Smart Grid 2015, 6, 124–134. [Google Scholar] [CrossRef]
- Velarde, P.; Valverde, L.; Maestre, J.; Ocampo-Martinez, C.; Bordons, C. On the comparison of stochastic model predictive control strategies applied to a hydrogen-based microgrid. J. Power Sources 2017, 343, 161–173. [Google Scholar] [CrossRef]
- Ahmad, S.; Shafiullah, M.; Ahmed, C.B.; Alowaifeer, M. A Review of Microgrid Energy Management and Control Strategies. IEEE Access 2023, 11, 21729–21757. [Google Scholar] [CrossRef]
- Vivas, F.J.; De Las Heras, A.; Segura, F.; Andújar, J.M. A review of energy management strategies for renewable hybrid energy systems with hydrogen backup. Renew. Sustain. Energy Rev. 2018, 82, 126–155. [Google Scholar] [CrossRef]
- Haider, S.A.; Sajid, M.; Iqbal, S. Forecasting hydrogen production potential in islamabad from solar energy using water electrolysis. Int. J. Hydrogen Energy 2021, 46, 1671–1681. [Google Scholar] [CrossRef]
- Eichman, J.; Harrison, K.; Peters, M. Novel Electrolyzer Applications: Providing More Than Just Hydrogen; No. NREL/TP-5400-61758; National Renewable Energy Lab.: Golden, CO, USA, 2014; Volume 61758, p. 1159377. [Google Scholar] [CrossRef]
- Zhang, Y.; Campana, P.E.; Lundblad, A.; Yan, J. Comparative study of hydrogen storage and battery storage in grid connected photovoltaic system: Storage sizing and rule-based operation. Appl. Energy 2017, 201, 397–411. [Google Scholar] [CrossRef]
- Hu, S.; Guo, B.; Ding, S.; Yang, F.; Dang, J.; Liu, B.; Gu, J.; Ma, J.; Ouyang, M. A comprehensive review of alkaline water electrolysis mathematical modeling. Appl. Energy 2022, 327, 120099. [Google Scholar] [CrossRef]
- Ahangar, H.G.; Yew, W.K.; Flynn, D. Smart Local Energy Systems: Optimal Planning of Stand-Alone Hybrid Green Power Systems for On-Line Charging of Electric Vehicles. IEEE Access 2023, 11, 7398–7409. [Google Scholar] [CrossRef]
- Li, S.-B.; Kang, Z.-T. Capacity Optimization of Clean Renewable Energy in Power Grid Considering Low Temperature Environment Constraint. IEEE Access 2022, 10, 2740–2752. [Google Scholar] [CrossRef]
- Wang, D.; Fu, C.; Zhao, Q.; Hu, T. A PSO-Based Optimization Design of W-Type Noncontact Transformer for Stable Power Transfer in DWPT System. IEEE Trans. Ind. Appl. 2022, 58, 1211–1221. [Google Scholar] [CrossRef]
- Growe-Kuska, N.; Heitsch, H.; Romisch, W. Scenario reduction and scenario tree construction for power management problems. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 3, p. 7. [Google Scholar] [CrossRef]
- He, J.; Shi, C.; Wei, T.; Jia, D. Stochastic Model Predictive Control of Hybrid Energy Storage for Improving AGC Performance of Thermal Generators. IEEE Trans. Smart Grid 2022, 13, 393–405. [Google Scholar] [CrossRef]
- Gennitsaris, S.G.; Kanellos, F.D. Emission-Aware and Cost-Effective Distributed Demand Response System for Extensively Electrified Large Ports. IEEE Trans. Power Syst. 2019, 34, 4341–4351. [Google Scholar] [CrossRef]
- Garcia-Torres, F.; Vilaplana, D.G.; Bordons, C.; Roncero-Sanchez, P.; Ridao, M.A. Optimal Management of Microgrids with External Agents Including Battery/Fuel Cell Electric Vehicles. IEEE Trans. Smart Grid 2019, 10, 4299–4308. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, B.; Ge, L.; He, J.; Liao, W.; Ma, P. Day-ahead optimal scheduling strategy for electrolytic water to hydrogen production in zero-carbon parks type microgrid for optimal utilization of electrolyzer. J. Energy Storage 2023, 68, 107653. [Google Scholar] [CrossRef]
- Wang, S.; Kong, L.; Liu, C.; Cai, G. MPC-based energy optimization and regulation for zero-carbon energy supply building. Int. J. Hydrogen Energy 2024, 82, 1196–1210. [Google Scholar] [CrossRef]
- He, J.; Shi, C.; Wei, T.; Peng, X.; Guan, Y. Hierarchical optimal energy management strategy of hybrid energy storage considering uncertainty for a 100% clean energy town. J. Energy Storage 2021, 41, 102917. [Google Scholar] [CrossRef]
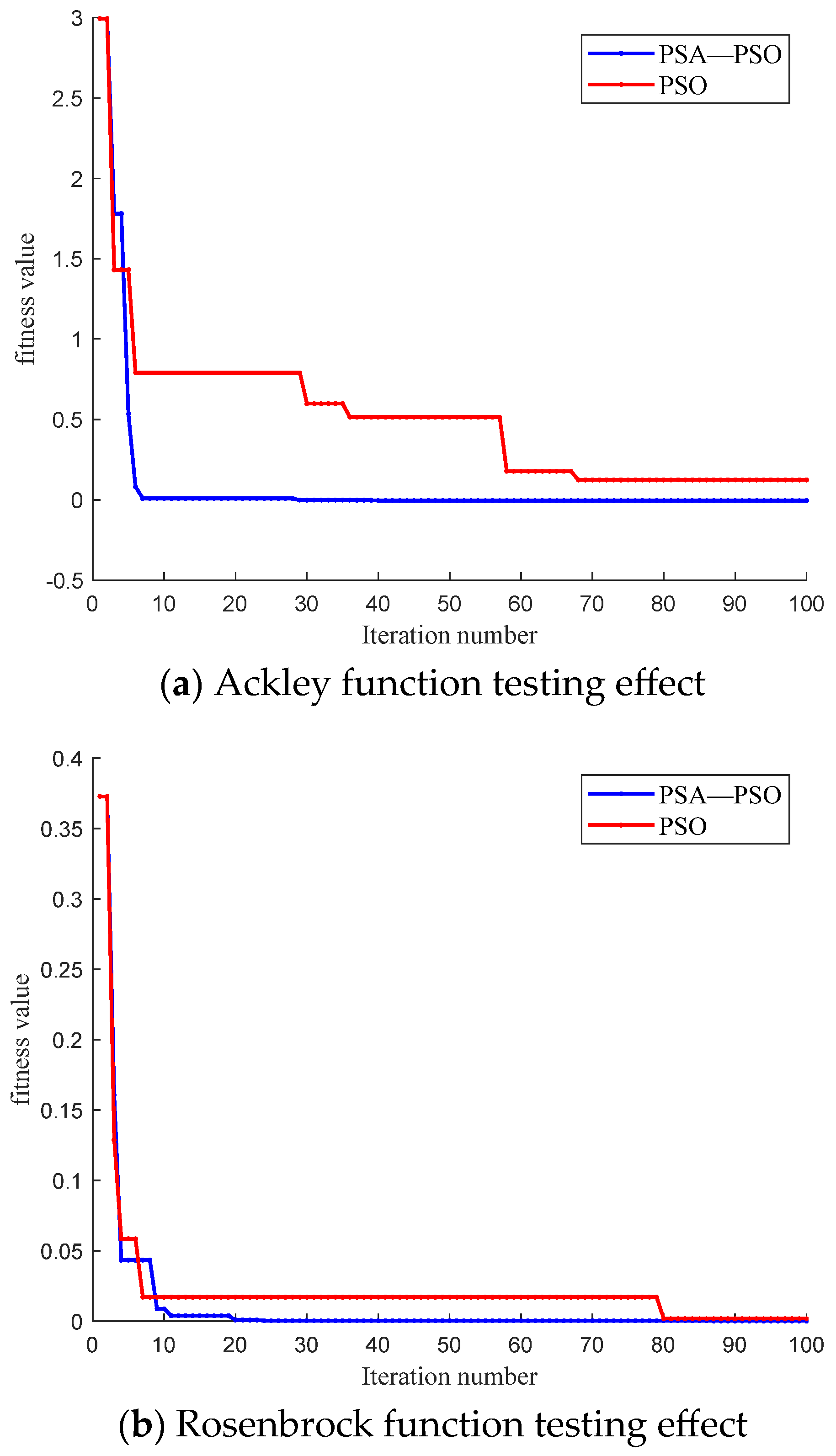

| Test Function | Algorithm | Optimal Result | Real Optimal Result |
|---|---|---|---|
| Ackley | PSO | 0.1238 | 0 |
| PSA-PSO | −0.0054 | 0 | |
| Rosenbrock | PSO | 0.0018 | 0 |
| PSA-PSO | 0.0004 | 0 |
| Parameters (Unit) | Value |
|---|---|
| HHV (kWh/Kg) | 39.7 |
| ηele | 0.7 |
| Upper and lower limits of SOC | 0.9, 0.1 |
| Upper and lower limits of LOH | 0.8, 0.2 |
| Upper and lower limits of Elz power (KW) | 5000, 500 |
| Upper and lower limits of LiB power (KW) | −2000, 2000 |
| LiB capacity (kWh) | 20,000 |
| Mass of hydrogen storage tank (Kg) | 450 |
| Operation and maintenance coefficients Elz and LiB (¥/KW) | 0.1, 0.1 |
| Hydrogen price (¥/Kg) | 40 |
| Upper and lower limits of grid power (KW) | 5000, −5000 |
| Upper and lower limits of Elz power fluctuation (KW) | −50, 50 |
| Upper and lower limits of grid power fluctuation (KW) | −50, 50 |
| Weight of state variables Q1, Q2 | 1, 10 |
| Weight of control variables R1, R2 | 10, 1 |
| Weight of penalty variables Q3, Q4 | 80,000, 10,000 |
| Algorithm | Cost (Scenario 1)/¥ | Cost (Scenario 2) /¥ | Convergence Speed (Scenario 1) | Convergence Speed (Scenario 2) |
|---|---|---|---|---|
| GA | 37,799 | 34,470 | 83 | 99 |
| FOA | 29,128 | 31,800 | 4 | 4 |
| FA | 41,095 | 39,308 | 5 | 6 |
| PSO | 24,939 | 30,137 | 82 | 85 |
| PSA-PSO | 21,339 | 22,138 | 25 | 21 |
| Scenario Name | Cost (Scenario 1)/¥ | Cost (Scenario 2)/¥ |
|---|---|---|
| F2 | 21,339 | 22,138 |
| F3 | 20,314 | 20,048 |
| F4 | 22,688 | 21,799 |
| F4 | 22,815 | 22,609 |
| F5 | 21,534 | 21,342 |
| Algorithm | Elz Power Pflu/KW | Grid Power Pflu/KW |
|---|---|---|
| MPC2 | 26.73 | 25.85 |
| SMPC | 22.39 | 21.40 |
| Algorithm | Elz Power Pflu/KW | Grid Power Pflu/KW |
|---|---|---|
| MPC2 | 27.86 | 26.85 |
| SMPC | 23.71 | 22.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Liu, R.; Guan, W.; Xiong, L.; Shi, C.; Yin, J. Multi-Time-Scale Layered Energy Management Strategy for Integrated Production, Storage, and Supply Hydrogen Refueling Stations Based on Flexible Hydrogen Load Characteristics of Ports. Energies 2025, 18, 1583. https://doi.org/10.3390/en18071583
Jiang Z, Liu R, Guan W, Xiong L, Shi C, Yin J. Multi-Time-Scale Layered Energy Management Strategy for Integrated Production, Storage, and Supply Hydrogen Refueling Stations Based on Flexible Hydrogen Load Characteristics of Ports. Energies. 2025; 18(7):1583. https://doi.org/10.3390/en18071583
Chicago/Turabian StyleJiang, Zhuoyu, Rujie Liu, Weiwei Guan, Lei Xiong, Changli Shi, and Jingyuan Yin. 2025. "Multi-Time-Scale Layered Energy Management Strategy for Integrated Production, Storage, and Supply Hydrogen Refueling Stations Based on Flexible Hydrogen Load Characteristics of Ports" Energies 18, no. 7: 1583. https://doi.org/10.3390/en18071583
APA StyleJiang, Z., Liu, R., Guan, W., Xiong, L., Shi, C., & Yin, J. (2025). Multi-Time-Scale Layered Energy Management Strategy for Integrated Production, Storage, and Supply Hydrogen Refueling Stations Based on Flexible Hydrogen Load Characteristics of Ports. Energies, 18(7), 1583. https://doi.org/10.3390/en18071583







