Short-Term Photovoltaic Power Forecasting Using PV Data and Sky Images in an Auto Cross Modal Correlation Attention Multimodal Framework
Abstract
1. Introduction
- An end-to-end multimodal prediction framework based on an attention mechanism for short-term PV power generation prediction is proposed. This framework can effectively fuse timing data and image data and substantially enhance the prediction accuracy.
- A novel auto cross modal correlation attention mechanism was designed to automatically capture the correlation between timing and image data, fully integrate multimodal features, and enhance the information complementarity between different modal data.
- The effectiveness of the proposed method was validated using real-world datasets, combining historical PV time-series data and sky images. Under consistent experimental conditions, the model outperformed other state-of-the-art methods in accuracy and efficiency across forecast horizons of 10 to 20 min.
2. Related Works
3. Data and Preprocessing
3.1. Data
3.1.1. Sky Image
3.1.2. PV Power
3.2. Data Processing
3.3. Data Partition and Cross Validation
4. Methodology
4.1. Short-Term Photovoltaic Power Forecasting Framework
- denotes the predicted PV power output for time steps ahead, where is adjustable depending on the experimental configuration;
- represents the historical PV power data over the past 10 min (containing 11 lagged terms);
- represents the historical sky image sequence over the same 10 min.
4.2. Auto Cross Modal Correlation Attention
4.2.1. PV Feature Autocorrelation Learning Stage
4.2.2. Cross-Modal Feature Fusion Stage
4.3. Feature Encoder for Learning Cloud Movement from Sky Images
5. Experimental Setup
5.1. Evaluation Metrics
5.2. Benchmark Models
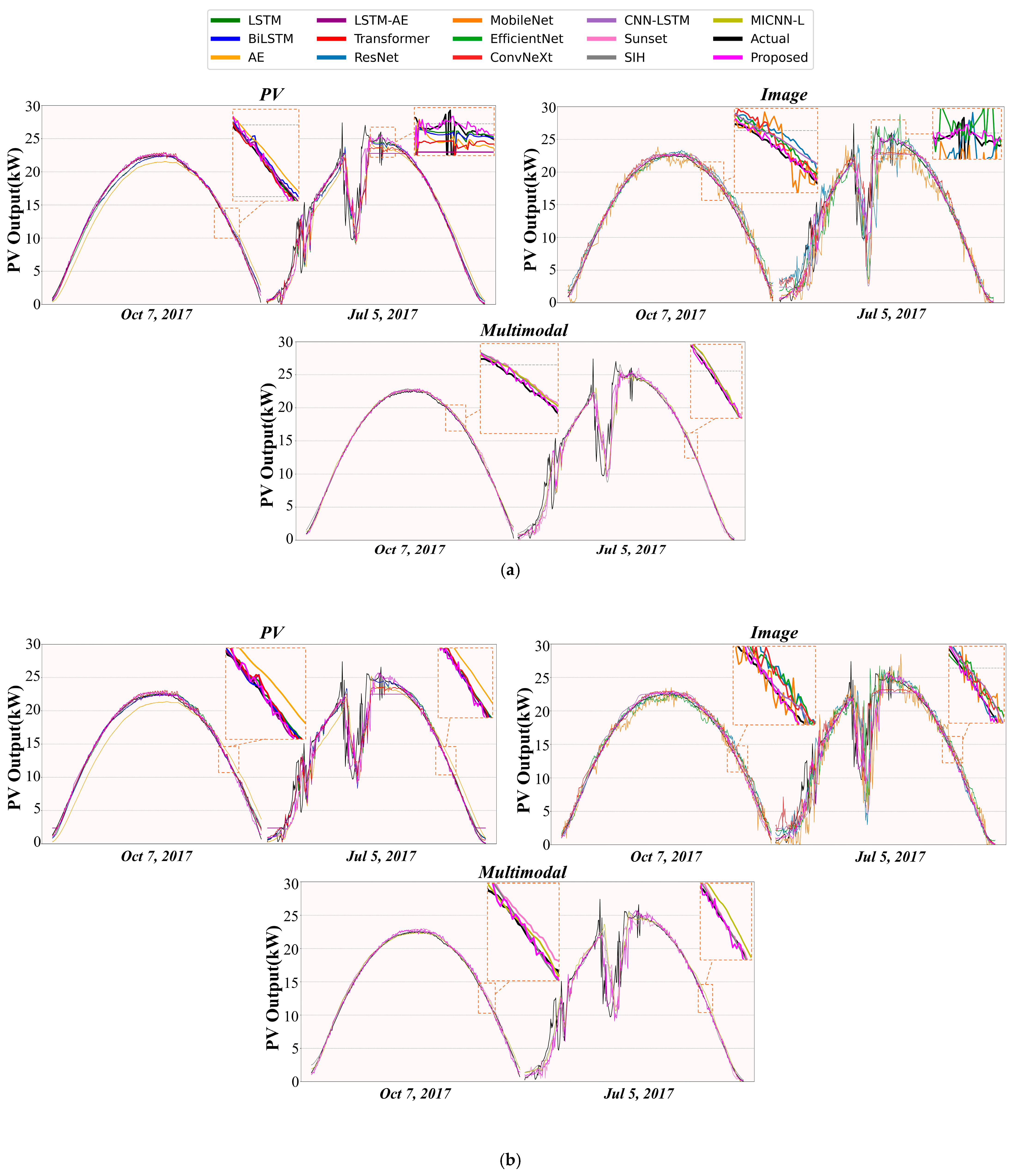
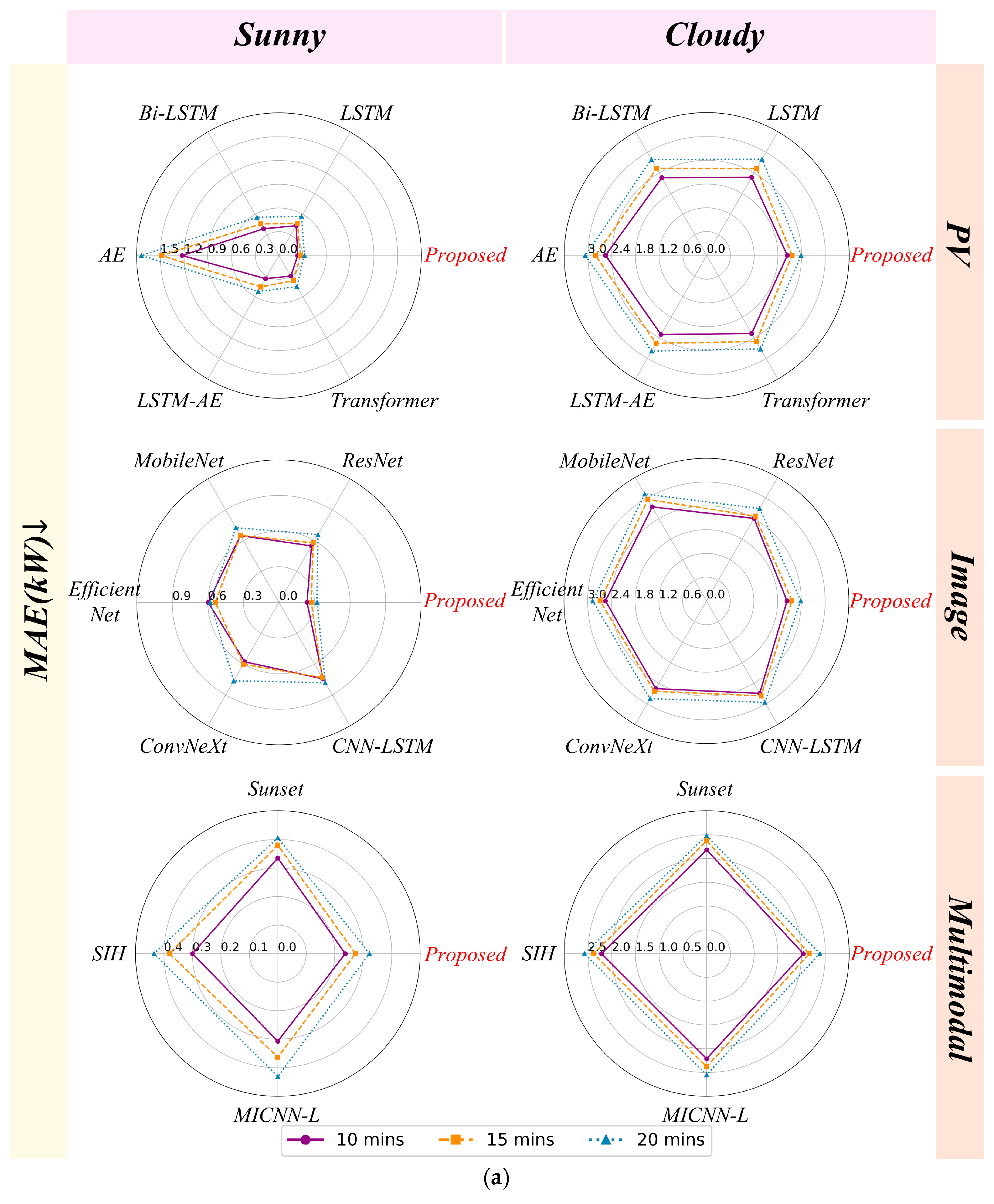
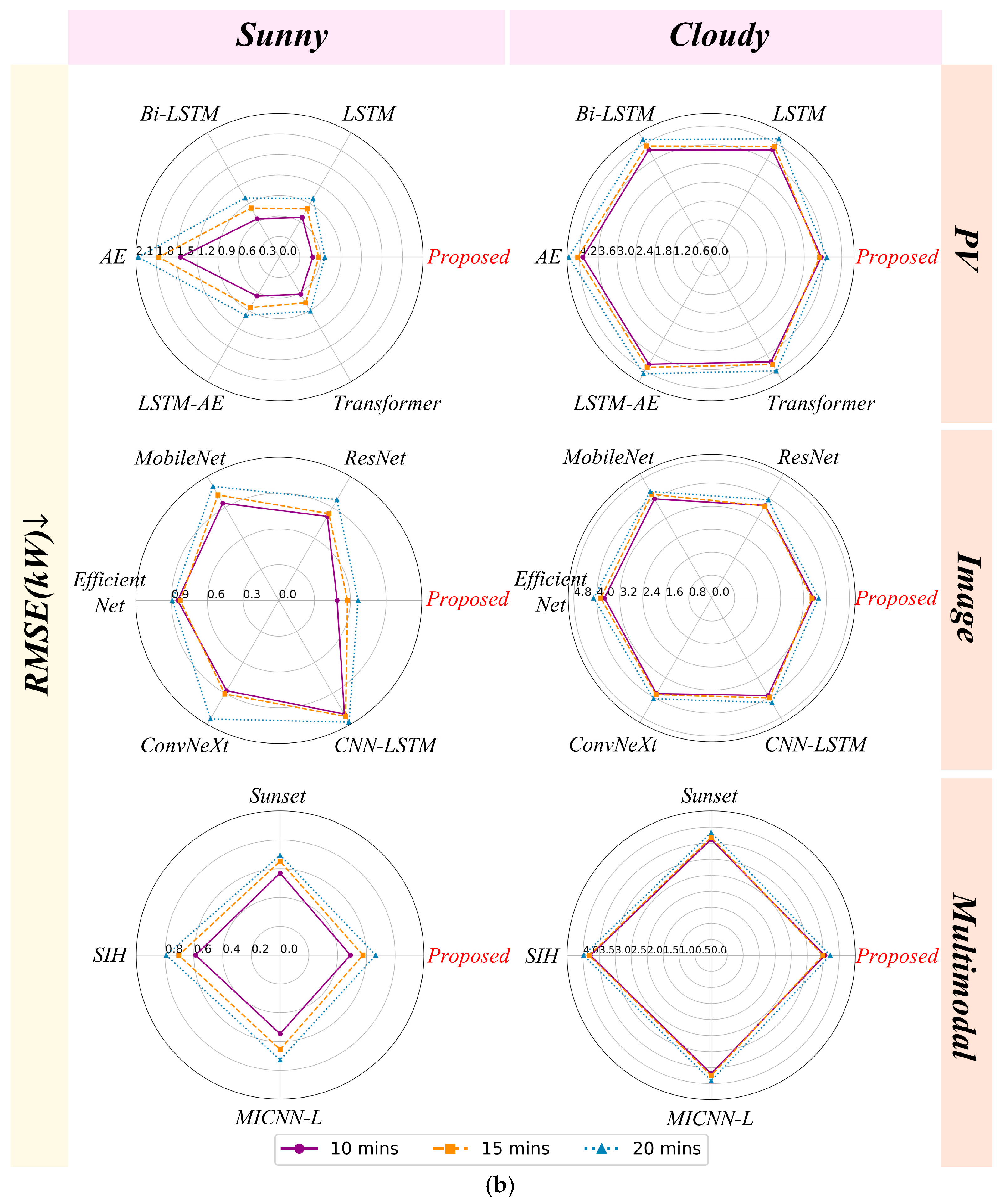
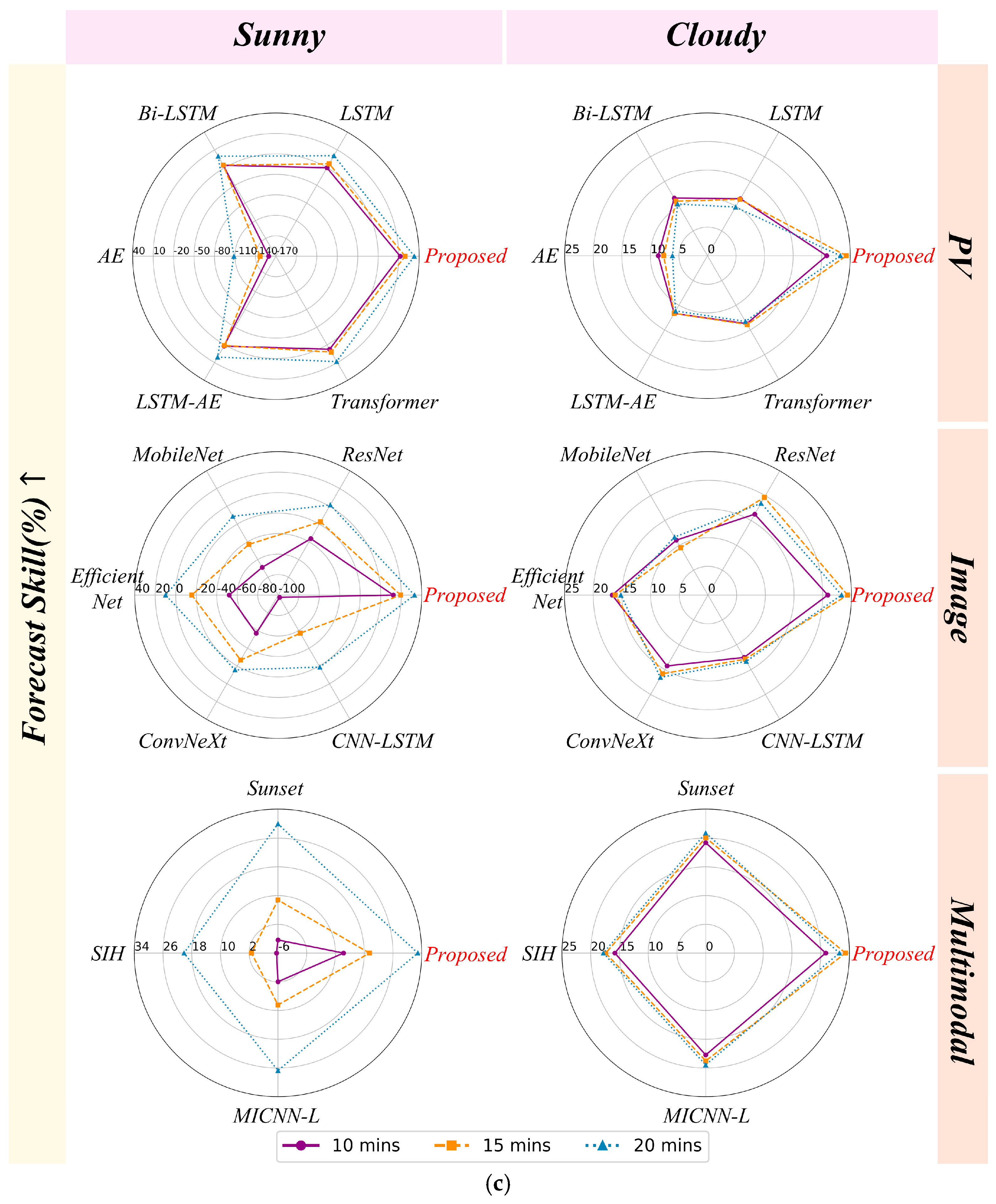
6. Result and Discussion
6.1. Comparison of the Proposed Model with the Benchmark Models
6.1.1. Overall Performance of the Proposed Model and Benchmark Models Comparisons
6.1.2. Comparison of Different Weather Conditions
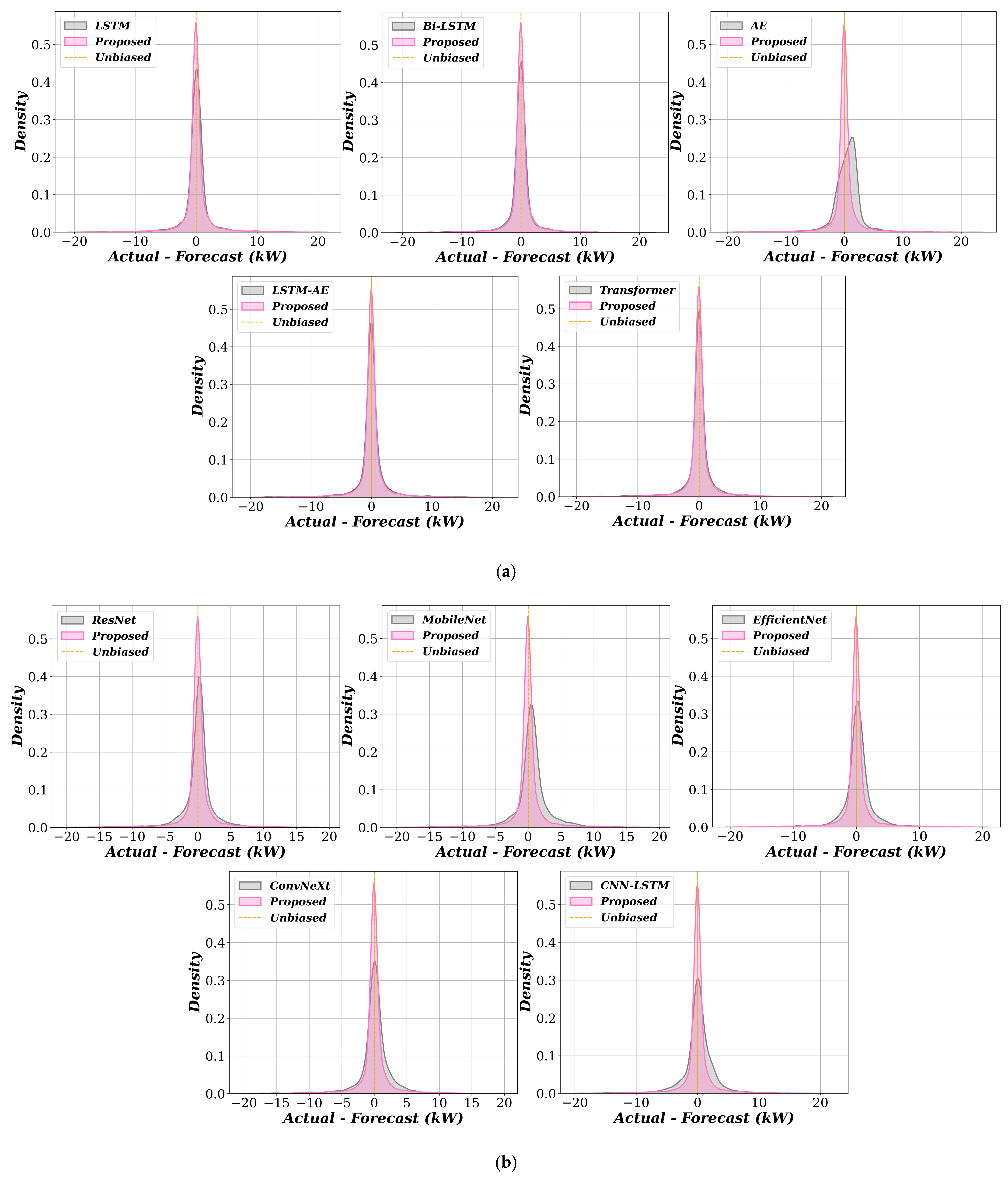
6.1.3. Uncertainty Analysis of the Proposed Model and the Benchmark Model
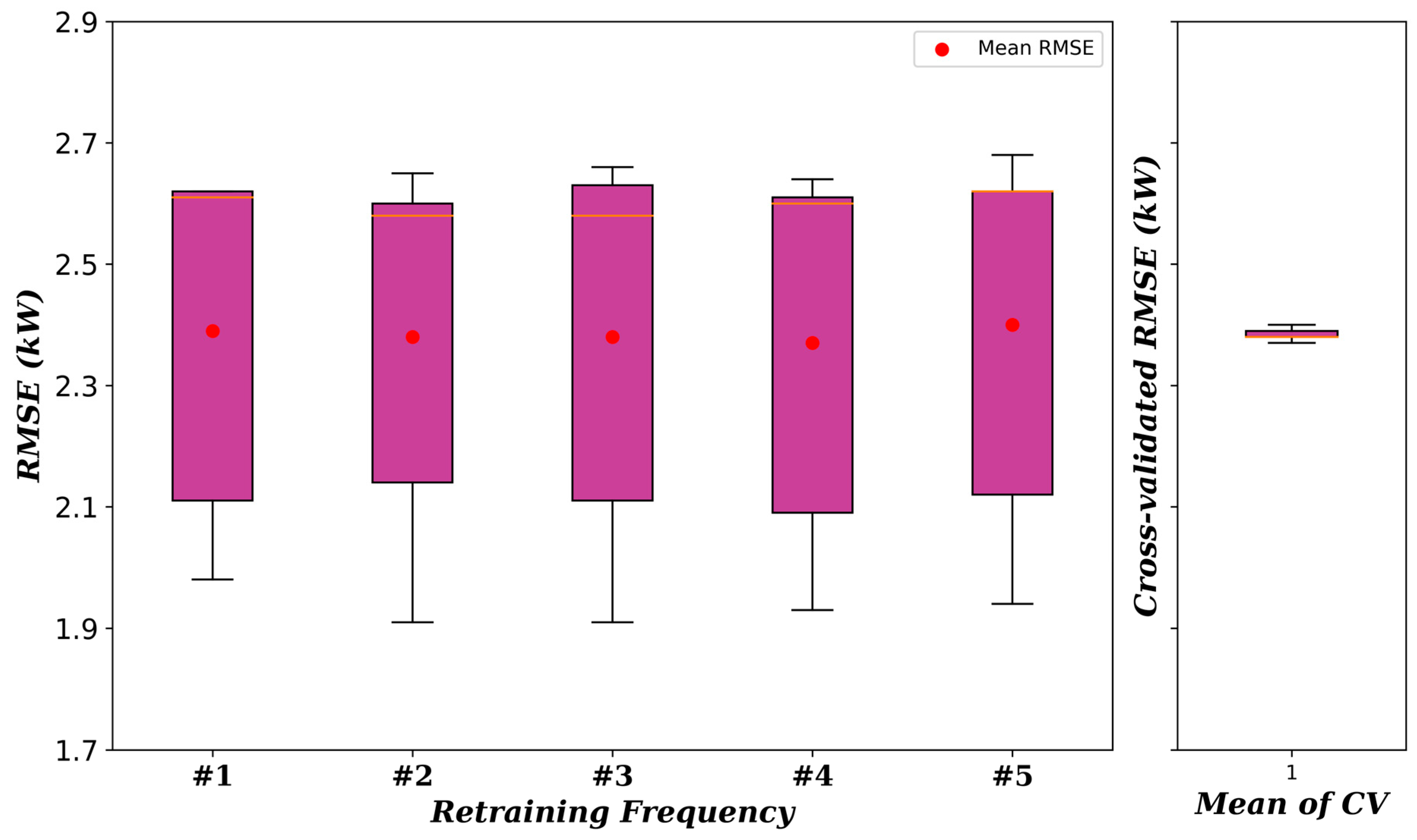
6.2. The Uncertainty in Mean RMSE of the Proposed Model
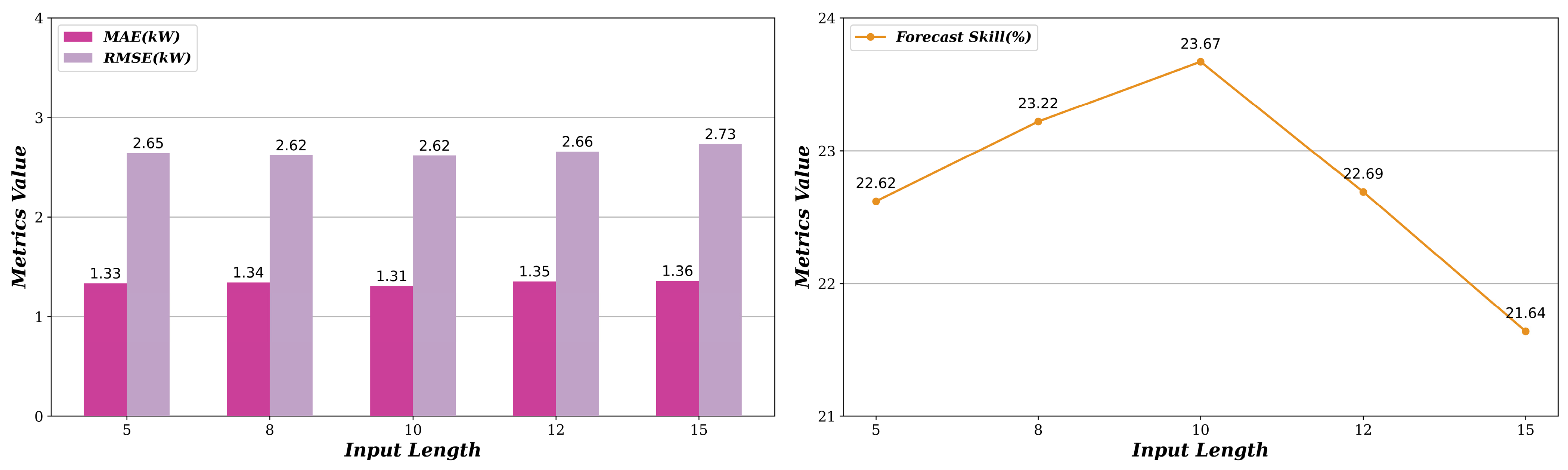
6.3. Sensitivity Analysis of Input Sequence Length
6.4. Ablation Experiments for the Proposed Model
6.5. Sensitivity Analysis of Input Degradation and Missingness
7. Conclusions
- The multimodal learning prediction framework proposed in this paper effectively captures dynamic changes in PV power generation by integrating time-series data and image data. Experimental results demonstrated strong prediction performance across various weather conditions, significantly enhancing the stability and accuracy of VPPs in short-term power forecasting.
- The designed ACMCA mechanism enables the deep fusion of multimodal features by adaptively learning correlations between temporal and image data, enhancing the complementarity of different modalities. Compared to traditional baseline models, ACMCA showed greater robustness in handling complex weather conditions (e.g., cloudy), offering a more reliable basis for PV power forecasting.
- Extensive experiments showed that the proposed method surpassed the existing unimodal and other multimodal approaches in prediction error, accuracy, and efficiency. Particularly in multimodal data applications, it consistently outperformed traditional baseline models across different time periods and complex weather conditions, validating its practical value for VPP management.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- REN21. Renewables 2018 Global Status Report; REN21 Secretariat: Paris, France, 2018; ISBN 978-3-9818911-3-3. Available online: https://www.ren21.net/gsr-2018/ (accessed on 12 December 2024).
- Cozzi, L.; Gould, T.; Bouckart, S.; Crow, D.; Kim, T.-Y.; McGlade, C.; Olejarnik, P.; Wanner, B.; Wetzel, D. World energy outlook 2020. Energy 2020, 2019, 30. [Google Scholar]
- Shahsavari, A.; Akbari, M. Potential of solar energy in developing countries for reducing energy-related emissions. Renew. Sustain. Energy Rev. 2018, 90, 275–291. [Google Scholar] [CrossRef]
- Ding, M.; Xu, Z.; Wang, W.; Wang, X.; Song, Y.; Chen, D. A review on China׳ s large-scale PV integration: Progress, challenges and recommendations. Renew. Sustain. Energy Rev. 2016, 53, 639–652. [Google Scholar] [CrossRef]
- Marquez, R.; Coimbra, C.F.M. Intra-hour DNI forecasting based on cloud tracking image analysis. Sol. Energy 2013, 91, 327–336. [Google Scholar] [CrossRef]
- Quesada-Ruiz, S.; Chu, Y.; Tovar-Pescador, J.; Pedro, H.T.; Coimbra, C.F. Cloud-tracking methodology for intra-hour DNI forecasting. Sol. Energy 2014, 102, 267–275. [Google Scholar] [CrossRef]
- Mahmud, K.; Khan, B.; Ravishankar, J.; Ahmadi, A.; Siano, P. An internet of energy framework with distributed energy resources, prosumers and small-scale virtual power plants: An overview. Renew. Sustain. Energy Rev. 2020, 127, 109840. [Google Scholar] [CrossRef]
- Jakoplić, A.; Franković, D.; Kirinčić, V.; Plavšić, T. Benefits of short-term photovoltaic power production forecasting to the power system. Optim. Eng. 2021, 22, 9–27. [Google Scholar] [CrossRef]
- Radzi, M.; Liyana, P.N.; Akhter, M.N.; Mekhilef, S.; Shah, N.M. Review on the application of photovoltaic forecasting using machine learning for very short-to long-term forecasting. Sustainability 2023, 15, 2942. [Google Scholar] [CrossRef]
- Chen, Y.; Bhutta, M.S.; Abubakar, M.; Xiao, D.; Almasoudi, F.M.; Naeem, H.; Faheem, M. Evaluation of machine learning models for smart grid parameters: Performance analysis of ARIMA and Bi-LSTM. Sustainability 2023, 15, 8555. [Google Scholar] [CrossRef]
- Kuo, W.-C.; Chen, C.-H.; Hua, S.-H.; Wang, C.-C. Assessment of different deep learning methods of power generation forecasting for solar PV system. Appl. Sci. 2022, 12, 7529. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S.; Cai, T.; Liu, B. Online 24-h solar power forecasting based on weather type classification using artificial neural network. Sol. Energy 2011, 85, 2856–2870. [Google Scholar] [CrossRef]
- Chu, Y.; Pedro, H.T.C.; Coimbra, C.F.M. Hybrid intra-hour DNI forecasts with sky image processing enhanced by stochastic learning. Sol. Energy 2013, 98, 592–603. [Google Scholar] [CrossRef]
- Nie, Y.; Sun, Y.; Chen, Y.; Orsini, R.; Brandt, A. PV power output prediction from sky images using convolutional neural network: The comparison of sky-condition-specific sub-models and an end-to-end model. J. Renew. Sustain. Energy 2020, 12, 046101. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M.D. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Shi, J.; Lee, W.-J.; Liu, Y.; Yang, Y.; Wang, P. Forecasting power output of photovoltaic systems based on weather classification and support vector machines. IEEE Trans. Ind. Appl. 2012, 48, 1064–1069. [Google Scholar] [CrossRef]
- Haputhanthri, D.; De Silva, D.; Sierla, S.; Alahakoon, D.; Nawaratne, R.; Jennings, R.; Vyatkin, V. Solar irradiance nowcasting for virtual power plants using multimodal long short-term memory networks. Front. Energy Res. 2021, 9, 722212. [Google Scholar] [CrossRef]
- Zuo, H.-M.; Qiu, J.; Li, F.-F. Ultra-short-term forecasting of global horizontal irradiance (GHI) integrating all-sky images and historical sequences. J. Renew. Sustain. Energy 2023, 15, 0163759. [Google Scholar] [CrossRef]
- Li, J.; Hong, D.; Gao, L.; Yao, J.; Zheng, K.; Zhang, B.; Chanussot, J. Deep learning in multimodal remote sensing data fusion: A comprehensive review. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102926. [Google Scholar] [CrossRef]
- Kong, W.; Jia, Y.; Dong, Z.Y.; Meng, K.; Chai, S. Hybrid approaches based on deep whole-sky-image learning to photovoltaic generation forecasting. Appl. Energy 2020, 280, 115875. [Google Scholar] [CrossRef]
- Wan, C.; Zhao, J.; Song, Y.; Xu, Z.; Lin, J.; Hu, Z. Photovoltaic and solar power forecasting for smart grid energy management. CSEE J. Power Energy Syst. 2015, 1, 38–46. [Google Scholar] [CrossRef]
- Lipperheide, M.; Bosch, J.L.; Kleissl, J. Embedded nowcasting method using cloud speed persistence for a photovoltaic power plant. Sol. Energy 2015, 112, 232–238. [Google Scholar] [CrossRef]
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- Sreekumar, S.; Bhakar, R. Solar power prediction models: Classification based on time horizon, input, output and application. In Proceedings of the 2018 International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 11–12 July 2018. [Google Scholar] [CrossRef]
- Dong, J.; Olama, M.M.; Kuruganti, T.; Melin, A.M.; Djouadi, S.M.; Zhang, Y.; Xue, Y. Novel stochastic methods to predict short-term solar radiation and photovoltaic power. Renew. Energy 2020, 145, 333–346. [Google Scholar] [CrossRef]
- Sheng, H.; Xiao, J.; Cheng, Y.; Ni, Q.; Wang, S. Short-term solar power forecasting based on weighted Gaussian process regression. IEEE Trans. Ind. Electron. 2017, 65, 300–308. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, J. Hourly-similarity based solar forecasting using multi-model machine learning blending. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.-Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Ren, S.; Hu, W.; Bradbury, K.; Harrison-Atlas, D.; Valeri, L.M.; Murray, B.; Malof, J.M. Automated extraction of energy systems information from remotely sensed data: A review and analysis. Appl. Energy 2022, 326, 119876. [Google Scholar] [CrossRef]
- Cheng, L.; Zang, H.; Wei, Z.; Ding, T.; Xu, R.; Sun, G. Short-term solar power prediction learning directly from satellite images with regions of interest. IEEE Trans. Sustain. Energy 2021, 13, 629–639. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, J. SolarNet: A sky image-based deep convolutional neural network for intra-hour solar forecasting. Sol. Energy 2020, 204, 71–78. [Google Scholar] [CrossRef]
- Niu, T.; Li, J.; Wei, W.; Yue, H. A hybrid deep learning framework integrating feature selection and transfer learning for multi-step global horizontal irradiation forecasting. Appl. Energy 2022, 326, 119964. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015. proceedings, part III 18. [Google Scholar] [CrossRef]
- Yao, T.; Wang, J.; Wu, H.; Zhang, P.; Li, S.; Xu, K.; Liu, X.; Chi, X. Intra-hour photovoltaic generation forecasting based on multi-source data and deep learning methods. IEEE Trans. Sustain. Energy 2021, 13, 607–618. [Google Scholar] [CrossRef]
- Lotter, W.; Kreiman, G.; Cox, D. Deep predictive coding networks for video prediction and unsupervised learning. arXiv 2016, arXiv:1605.08104. [Google Scholar]
- Lin, Z.; Li, M.; Zheng, Z.; Cheng, Y.; Yuan, C. Self-attention convlstm for spatiotemporal prediction. Proc. AAAI Conf. Artif. Intell. 2020, 34, 11531–11538. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, J.; Zhang, W.; Hodge, B.-M. Convolutional neural networks for intra-hour solar forecasting based on sky image sequences. Appl. Energy 2022, 310, 118438. [Google Scholar] [CrossRef]
- Baltrušaitis, T.; Ahuja, C.; Morency, L.-P. Multimodal machine learning: A survey and taxonomy. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 423–443. [Google Scholar] [CrossRef]
- Ngiam, J.; Khosla, A.; Kim, M.; Nam, J.; Lee, H.; Ng, A.Y. Multimodal deep learning. In Proceedings of the 28th international conference on machine learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Yu, G.; Lu, L.; Tang, B.; Wang, S.; Yang, X.; Chen, R.S. An improved hybrid neural network ultra-short-term photovoltaic power forecasting method based on cloud image feature extraction. Proc. CSEE 2021, 41, 6989–7002. [Google Scholar]
- Bay, H.; Ess, R.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Sun, Y.; Venugopal, V.; Brandt, A.R. Short-term solar power forecast with deep learning: Exploring optimal input and output configuration. Sol. Energy 2019, 188, 730–741. [Google Scholar] [CrossRef]
- Cheng, L.; Zang, H.; Wei, Z.; Ding, T.; Sun, G. Solar power prediction based on satellite measurements–a graphical learning method for tracking cloud motion. IEEE Trans. Power Syst. 2021, 37, 2335–2345. [Google Scholar] [CrossRef]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; de M Gonçalves, J.L.; Sparovek, G. Köppen’s climate classification map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef]
- Nie, Y.; Li, X.; Scott, E.; Sun, Y.; Venugopal, V.; Brandt, A. SKIPP’D: A SKy Images and Photovoltaic Power Generation Dataset for short-term solar forecasting. Sol. Energy 2023, 255, 171–179. [Google Scholar] [CrossRef]
- Sun, Y.; Szűcs, G.; Brandt, A.R. Solar PV output prediction from video streams using convolutional neural networks. Energy Environ. Sci. 2018, 11, 1811–1818. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar]
- Wiener, N. Generalized harmonic analysis. Acta Math. 1930, 55, 117–258. [Google Scholar] [CrossRef]
- Tsai, Y.-H.H.; Bai, S.; Liang, P.P.; Kolter, J.Z.; Morency, L.-P.; Salakhutdinov, R. Multimodal transformer for unaligned multimodal language sequences. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Association for Computational Linguistics, Florence, Italy, 28–31 July 2019; pp. 6558–6569. [Google Scholar] [CrossRef]
- Dosovitskiy, A. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016. Proceedings, Part IV 14. [Google Scholar] [CrossRef]
- Ramesh, G.; Logeshwaran, J.; Kiruthiga, T.; Lloret, J. Prediction of energy production level in large pv plants through auto-encoder based neural-network (auto-nn) with restricted boltzmann feature extraction. Future Internet 2023, 15, 46. [Google Scholar] [CrossRef]
- Sabri, M.; El Hassouni, M. Photovoltaic power forecasting with a long short-term memory autoencoder networks. Soft Comput. 2023, 27, 10533–10553. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Howard, R.G. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. arXiv 2019, arXiv:1905.11946. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.-Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A convnet for the 2020s. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar] [CrossRef]
- Agga, A.; Abbou, A.; Labbadi, M.; El Houm, Y. Short-term self consumption PV plant power production forecasts based on hybrid CNN-LSTM, ConvLSTM models. Renew. Energy 2021, 177, 101–112. [Google Scholar] [CrossRef]
- Ajith, M.; Martínez-Ramón, M. Deep learning based solar radiation micro forecast by fusion of infrared cloud images and radiation data. Appl. Energy 2021, 294, 117014. [Google Scholar] [CrossRef]





| Date | Index | Mean (kW) | Max (kW) | Std (kW) |
|---|---|---|---|---|
| 20 May 2017 | Sunny_1 | 14.93 | 24.56 | 8.34 |
| 4 June 2017 | Sunny_2 | 15.25 | 25.41 | 8.66 |
| 6 July 2017 | Sunny_3 | 14.16 | 23.93 | 8.16 |
| 19 August 2017 | Sunny_4 | 13.93 | 23.47 | 8.24 |
| 15 September 2017 | Sunny_5 | 15.67 | 24.35 | 7.52 |
| 7 October 2017 | Sunny_6 | 15.40 | 22.66 | 6.71 |
| 1 November 2017 | Sunny_7 | 14.40 | 21.35 | 6.17 |
| 26 December 2017 | Sunny_8 | 14.74 | 19.93 | 5.68 |
| 20 January 2018 | Sunny_9 | 14.71 | 21.73 | 6.39 |
| 16 February 2018 | Sunny_10 | 15.92 | 22.88 | 6.25 |
| 24 May 2018 | Cloudy_1 | 15.02 | 26.90 | 9.66 |
| 5 July 2018 | Cloudy_2 | 13.93 | 27.41 | 8.14 |
| 6 September 2018 | Cloudy_3 | 10.00 | 26.96 | 6.77 |
| 22 September 2017 | Cloudy_4 | 14.70 | 28.13 | 8.19 |
| 4 November 2017 | Cloudy_5 | 4.78 | 25.29 | 5.56 |
| 29 December 2017 | Cloudy_6 | 12.74 | 20.10 | 5.50 |
| 7 January 2018 | Cloudy_7 | 3.72 | 9.10 | 1.88 |
| 1 February 2018 | Cloudy_8 | 14.47 | 22.68 | 5.89 |
| 18 February 2018 | Cloudy_9 | 9.99 | 29.12 | 8.20 |
| 9 March 2018 | Cloudy_10 | 12.81 | 25.60 | 6.84 |
| Stage | Model | |||
|---|---|---|---|---|
| Only PV | LSTM [11] | 1.315 | 2.786 | 10.91 |
| Bi-LSTM [10] | 1.286 | 2.78 | 11.12 | |
| AE [52] | 1.861 | 3.02 | 3.44 | |
| LSTM-AE [53] | 1.281 | 2.781 | 11.09 | |
| Transformer [54] | 1.244 | 2.713 | 13.25 | |
| Only image | ResNet [55] | 1.438 | 2.641 | 15.14 |
| MobileNet [56] | 1.65 | 2.841 | 9.16 | |
| EfficientNet [57] | 1.533 | 2.656 | 15.09 | |
| ConvNeXt [58] | 1.526 | 2.733 | 12.62 | |
| CNN-LSTM [59] | 1.678 | 2.826 | 9.64 | |
| Multimodal | Sunset [42] | 1.219 | 2.539 | 18.81 |
| SIH [20] | 1.217 | 2.646 | 15.41 | |
| MICNN-L [60] | 1.218 | 2.582 | 17.45 | |
| Proposed | 1.099 | 2.48 | 20.72 |
| Stage | Model | |||
|---|---|---|---|---|
| Only PV | LSTM [11] | 1.451 | 2.887 | 10.66 |
| Bi-LSTM [10] | 1.45 | 2.9 | 10.25 | |
| AE [52] | 2.118 | 3.21 | 0.67 | |
| LSTM-AE [53] | 1.463 | 2.884 | 10.75 | |
| Transformer [54] | 1.391 | 2.802 | 13.28 | |
| Only image | ResNet [55] | 1.484 | 2.633 | 18.52 |
| MobileNet [56] | 1.754 | 2.978 | 7.83 | |
| EfficientNet [57] | 1.566 | 2.74 | 15.22 | |
| ConvNeXt [58] | 1.574 | 2.763 | 14.5 | |
| CNN-LSTM [59] | 1.705 | 2.894 | 10.44 | |
| Multimodal | Sunset [42] | 1.333 | 2.592 | 19.78 |
| SIH [20] | 1.339 | 2.684 | 16.94 | |
| MICNN-L [60] | 1.328 | 2.634 | 18.49 | |
| Proposed | 1.176 | 2.45 | 24.2 |
| Stage | Model | |||
|---|---|---|---|---|
| Only PV | LSTM [11] | 1.636 | 3.107 | 9.4 |
| Bi-LSTM [10] | 1.626 | 3.088 | 9.95 | |
| AE [52] | 2.373 | 3.484 | −1.59 | |
| LSTM-AE [53] | 1.605 | 3.062 | 10.7 | |
| Transformer [54] | 1.539 | 2.982 | 13.05 | |
| Only image | ResNet [55] | 1.63 | 2.823 | 17.68 |
| MobileNet [56] | 1.869 | 3.068 | 10.54 | |
| EfficientNet [57] | 1.676 | 2.917 | 14.95 | |
| ConvNeXt [58] | 1.76 | 2.918 | 14.92 | |
| CNN-LSTM [59] | 1.82 | 3.028 | 11.7 | |
| Multimodal | Sunset [42] | 1.4 | 2.7 | 21.27 |
| SIH [20] | 1.459 | 2.815 | 17.91 | |
| MICNN-L [60] | 1.443 | 2.752 | 19.76 | |
| Proposed | 1.308 | 2.618 | 23.67 |
| Model | |||
|---|---|---|---|
| Proposed without PV stage | 1.143 | 2.528 | 19.17 |
| Proposed without image stage | 1.251 | 2.572 | 17.77 |
| Proposed without fusion stage | 1.135 | 2.537 | 18.88 |
| Proposed | 1.099 | 2.48 | 20.72 |
| Model | |||
|---|---|---|---|
| Proposed without PV stage | 1.251 | 2.507 | 22.42 |
| Proposed without image stage | 1.371 | 2.625 | 18.78 |
| Proposed without fusion stage | 1.22 | 2.543 | 21.3 |
| Proposed | 1.176 | 2.45 | 24.2 |
| Model | |||
|---|---|---|---|
| Proposed without PV stage | 1.388 | 2.672 | 22.1 |
| Proposed without image stage | 1.476 | 2.769 | 19.25 |
| Proposed without fusion stage | 1.322 | 2.649 | 22.76 |
| Proposed | 1.308 | 2.618 | 23.67 |
| Experiment Type | Noise/Dropout Rate | |||
|---|---|---|---|---|
| Proposed | 0% | 1.099 | 2.480 | 20.72 |
| Degradation | 1% | 1.097 | 2.480 | 20.73 |
| 5% | 1.095 | 2.482 | 20.66 | |
| 10% | 1.100 | 2.481 | 20.70 | |
| Missingness | 1% | 1.110 | 2.482 | 20.64 |
| 3% | 1.137 | 2.493 | 20.30 | |
| 5% | 1.171 | 2.498 | 20.12 |
| Experiment Type | Noise/Dropout Rate | |||
|---|---|---|---|---|
| Proposed | 0% | 1.176 | 2.450 | 24.20 |
| Degradation | 1% | 1.179 | 2.453 | 24.09 |
| 5% | 1.181 | 2.456 | 24.00 | |
| 10% | 1.182 | 2.459 | 23.94 | |
| Missingness | 1% | 1.192 | 2.452 | 24.13 |
| 3% | 1.224 | 2.463 | 23.77 | |
| 5% | 1.270 | 2.494 | 22.81 |
| Experiment Type | Noise/Dropout Rate | |||
|---|---|---|---|---|
| Proposed | 0% | 1.308 | 2.618 | 23.67 |
| Degradation | 1% | 1.312 | 2.615 | 23.76 |
| 5% | 1.315 | 2.623 | 23.54 | |
| 10% | 1.308 | 2.611 | 23.89 | |
| Missingness | 1% | 1.318 | 2.613 | 23.80 |
| 3% | 1.360 | 2.618 | 23.66 | |
| 5% | 1.401 | 2.639 | 23.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, C.; Liu, Y.; Oh, Y.; Lim, C. Short-Term Photovoltaic Power Forecasting Using PV Data and Sky Images in an Auto Cross Modal Correlation Attention Multimodal Framework. Energies 2024, 17, 6378. https://doi.org/10.3390/en17246378
Pan C, Liu Y, Oh Y, Lim C. Short-Term Photovoltaic Power Forecasting Using PV Data and Sky Images in an Auto Cross Modal Correlation Attention Multimodal Framework. Energies. 2024; 17(24):6378. https://doi.org/10.3390/en17246378
Chicago/Turabian StylePan, Chen, Yuqiao Liu, Yeonjae Oh, and Changgyoon Lim. 2024. "Short-Term Photovoltaic Power Forecasting Using PV Data and Sky Images in an Auto Cross Modal Correlation Attention Multimodal Framework" Energies 17, no. 24: 6378. https://doi.org/10.3390/en17246378
APA StylePan, C., Liu, Y., Oh, Y., & Lim, C. (2024). Short-Term Photovoltaic Power Forecasting Using PV Data and Sky Images in an Auto Cross Modal Correlation Attention Multimodal Framework. Energies, 17(24), 6378. https://doi.org/10.3390/en17246378







