Analysis of an Axial Field Hybrid Excitation Synchronous Generator
Abstract
1. Introduction
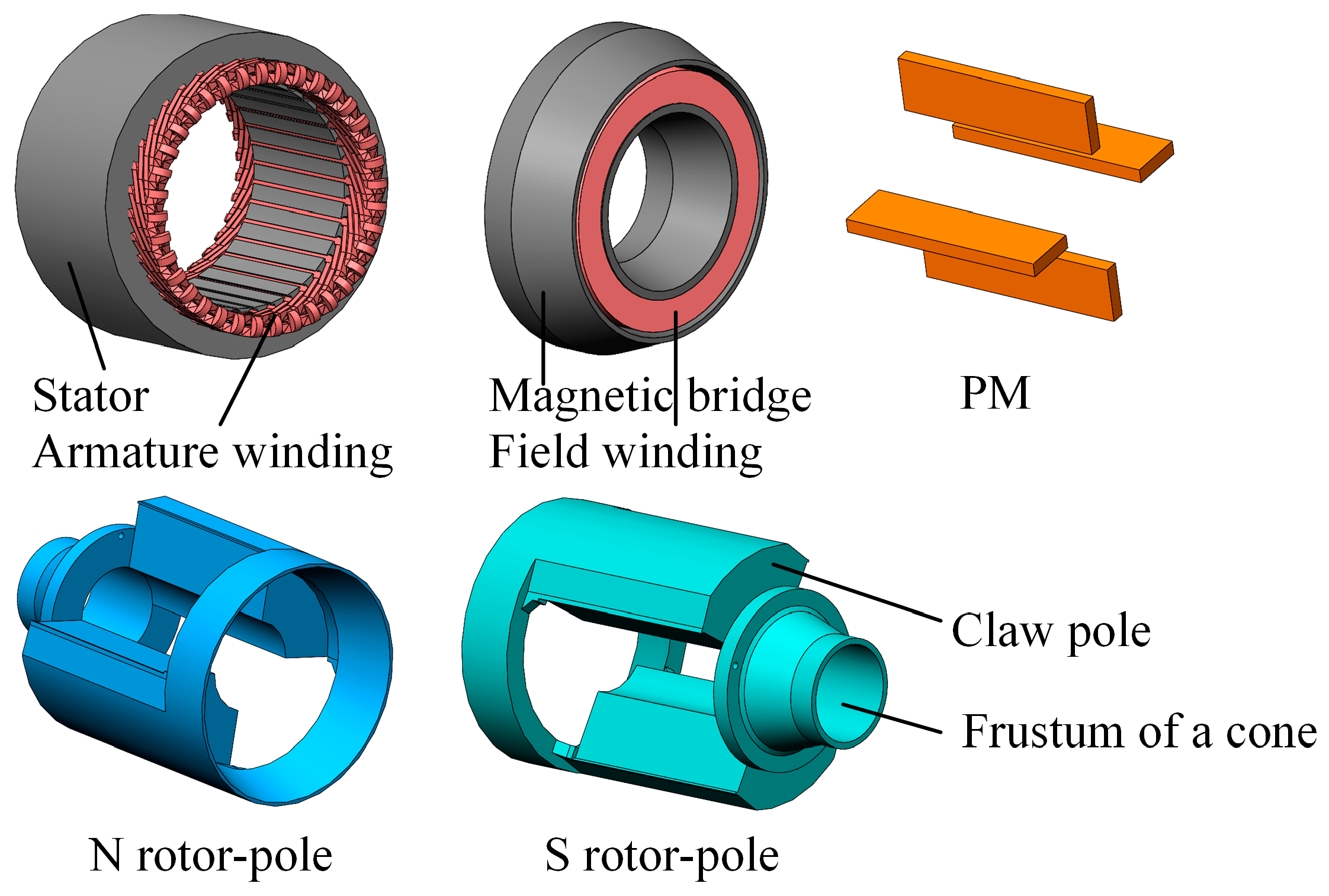
2. Machine Topology and Operating Principle
2.1. Topology
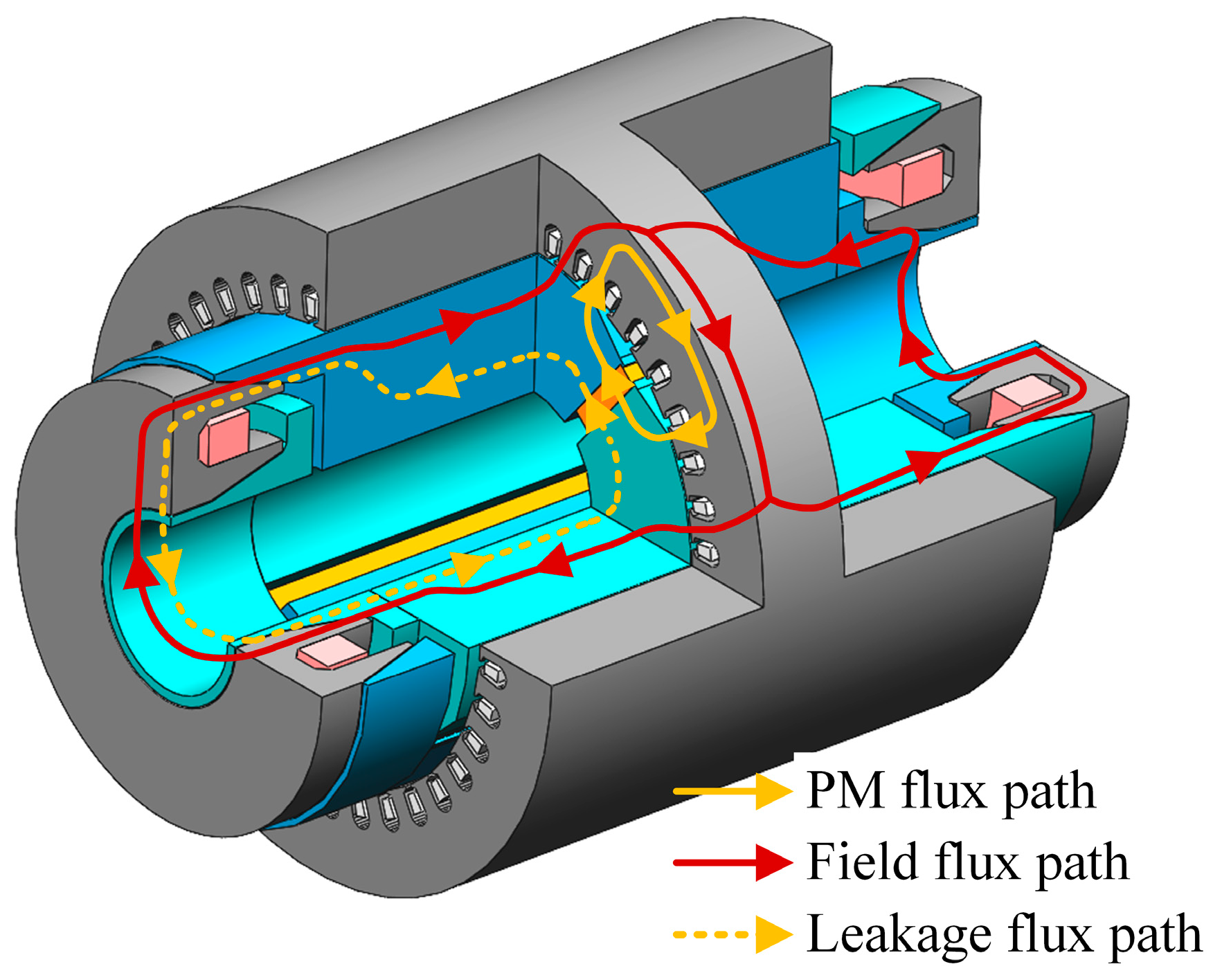
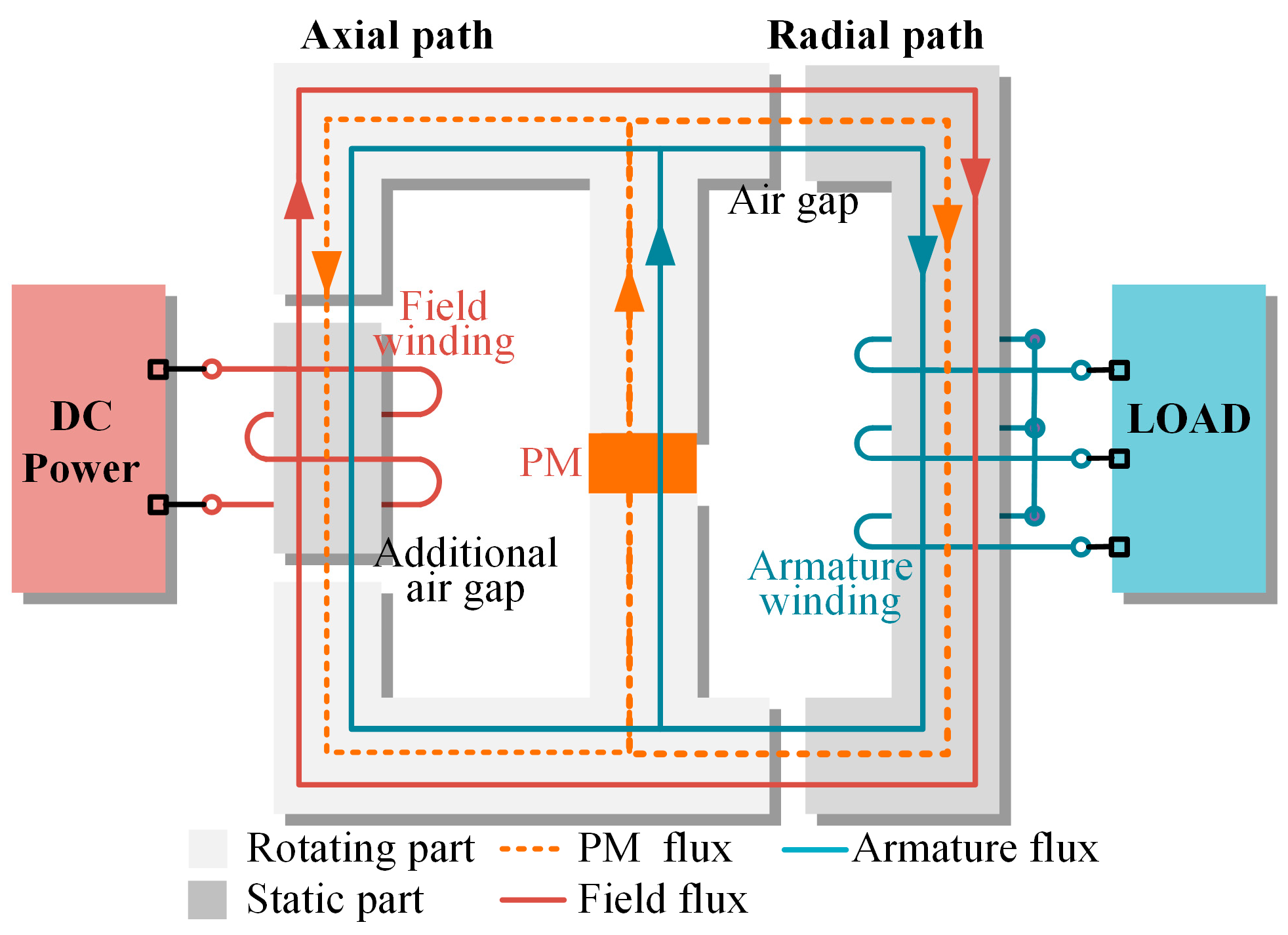
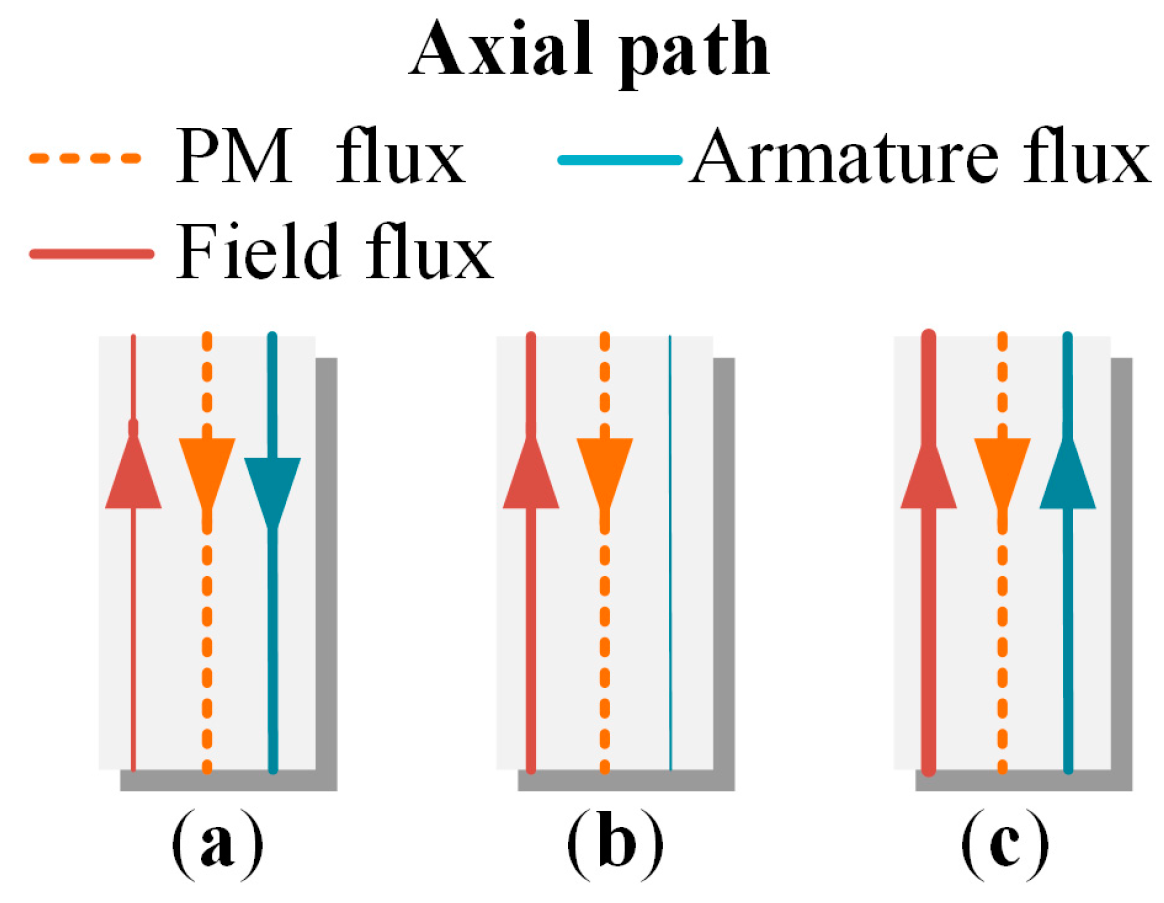
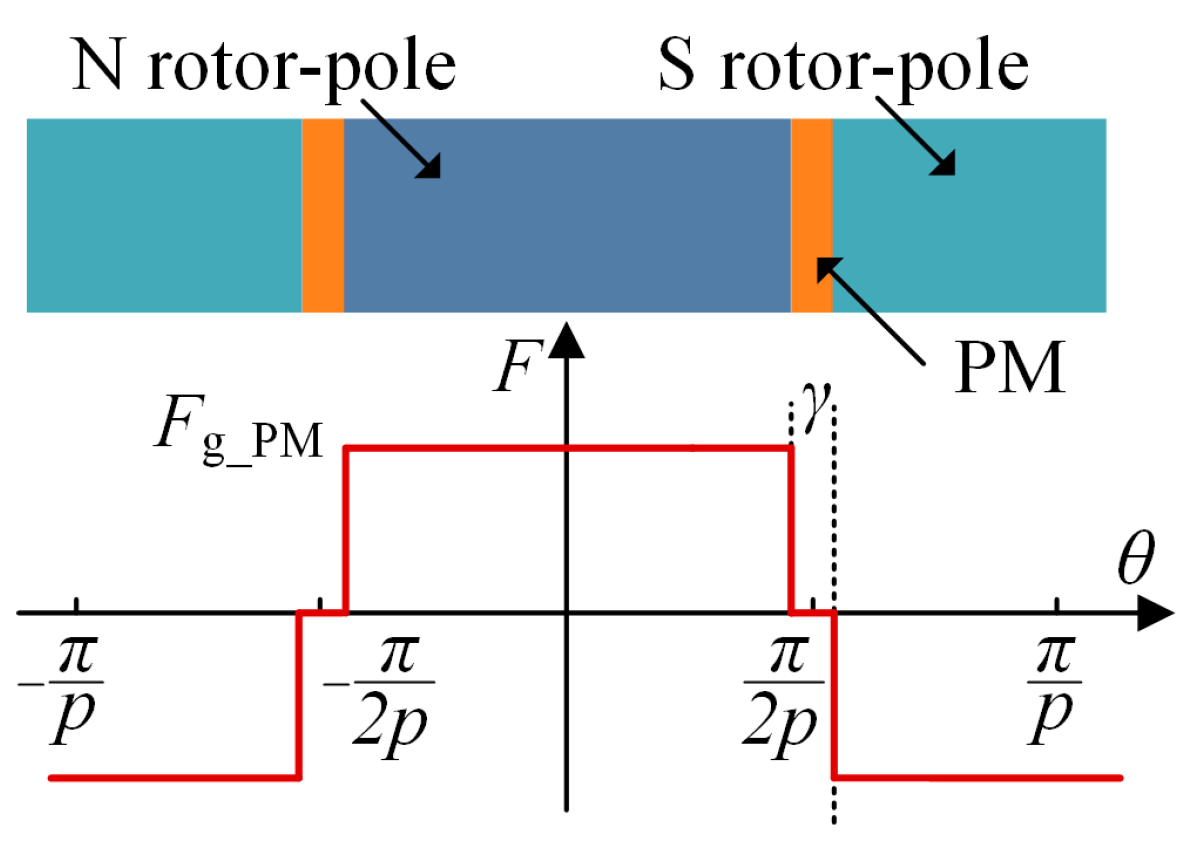
2.2. Operating Principle
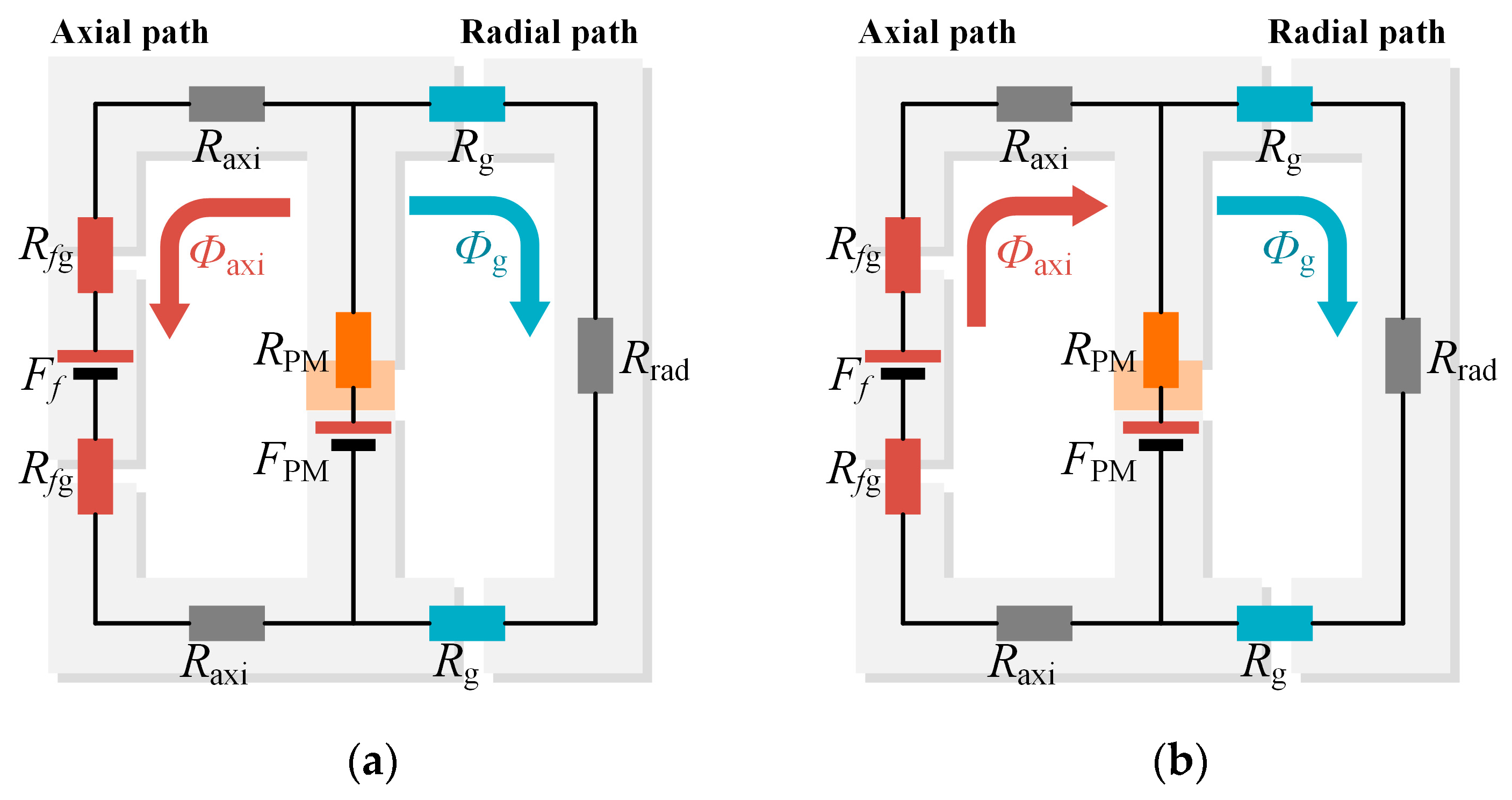
2.3. Equivalent Magnetic Circuit Model
3. Performance Analysis of AF-HESG
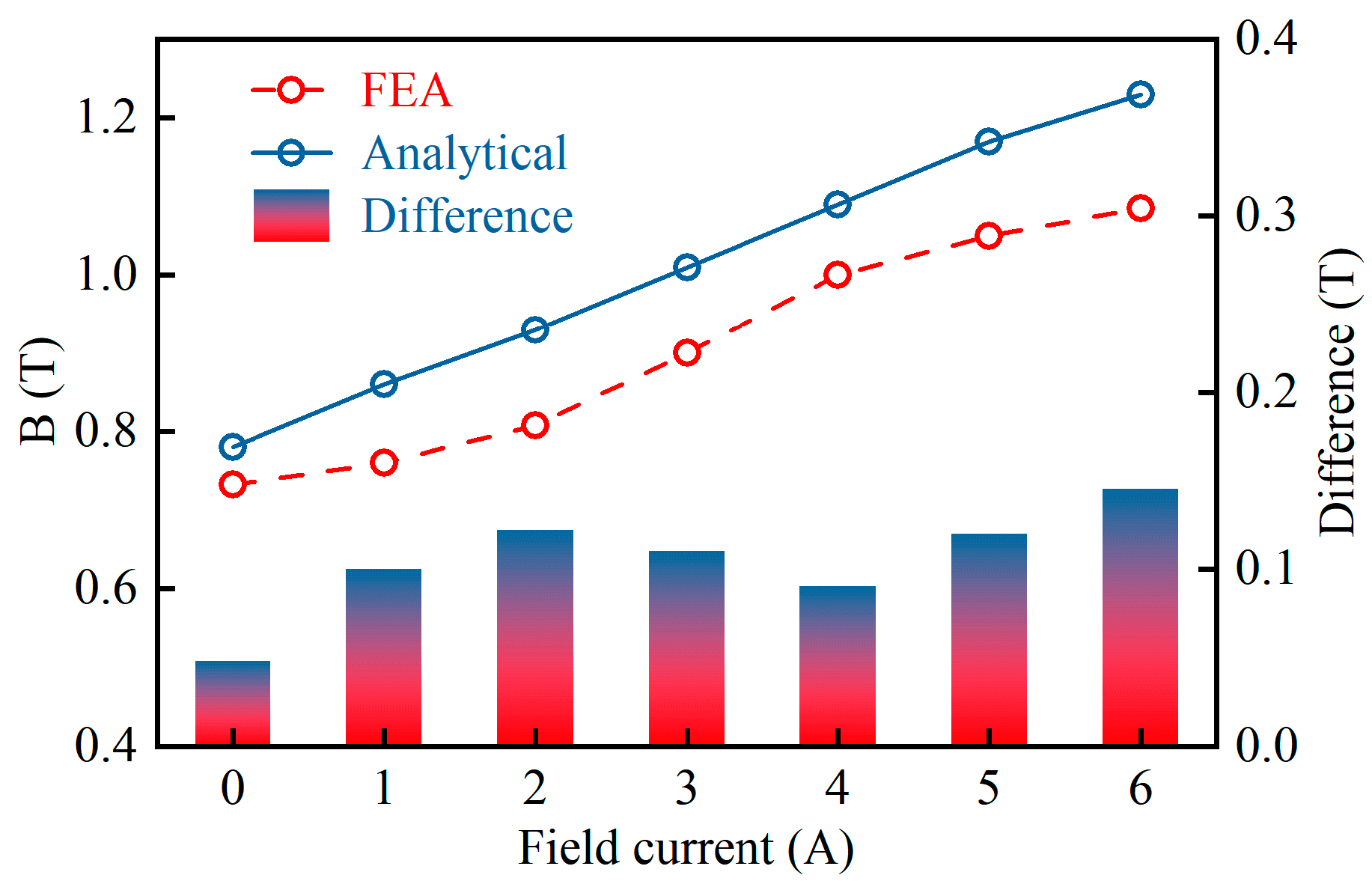
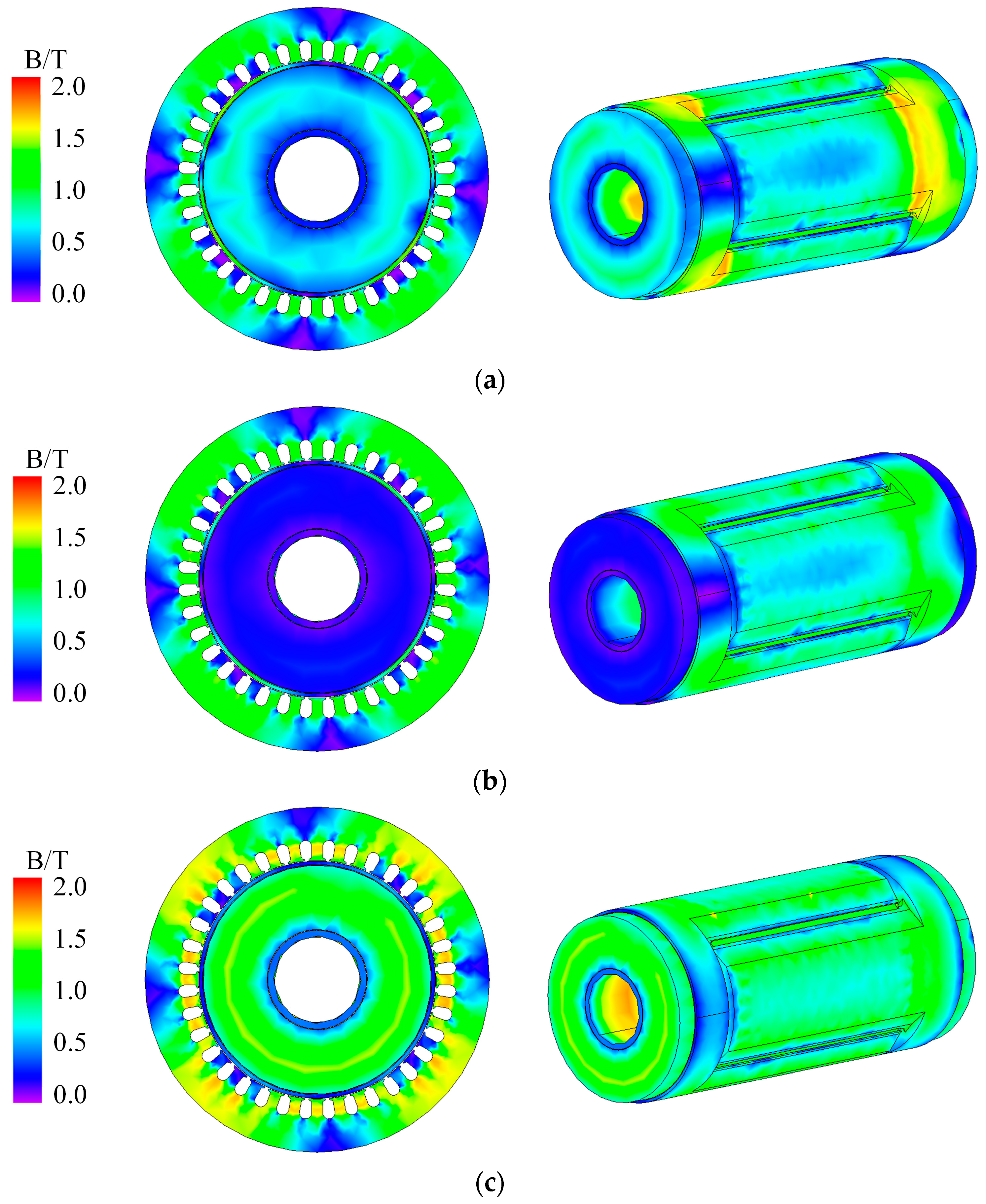
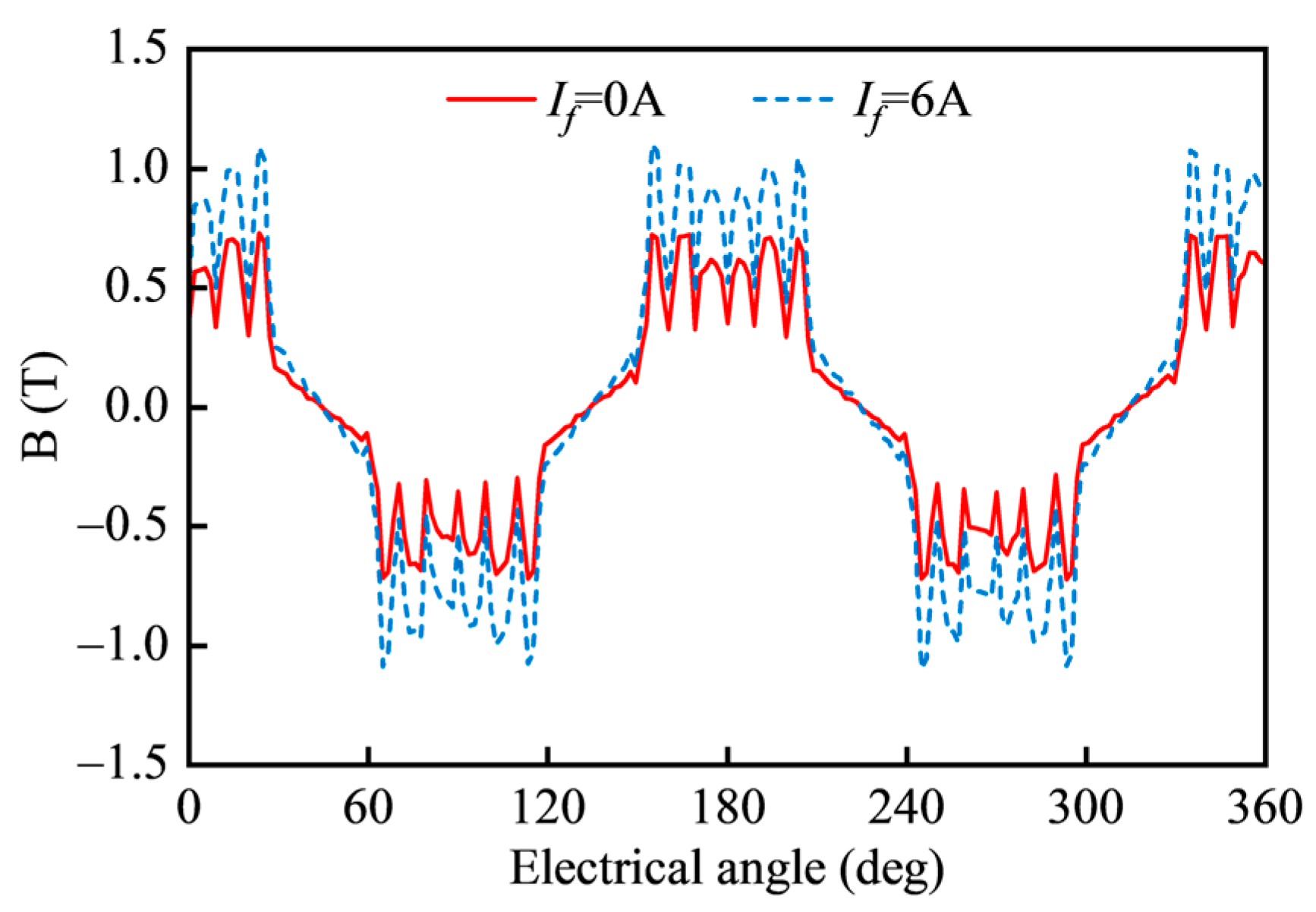
3.1. Magnetic Field Analysis
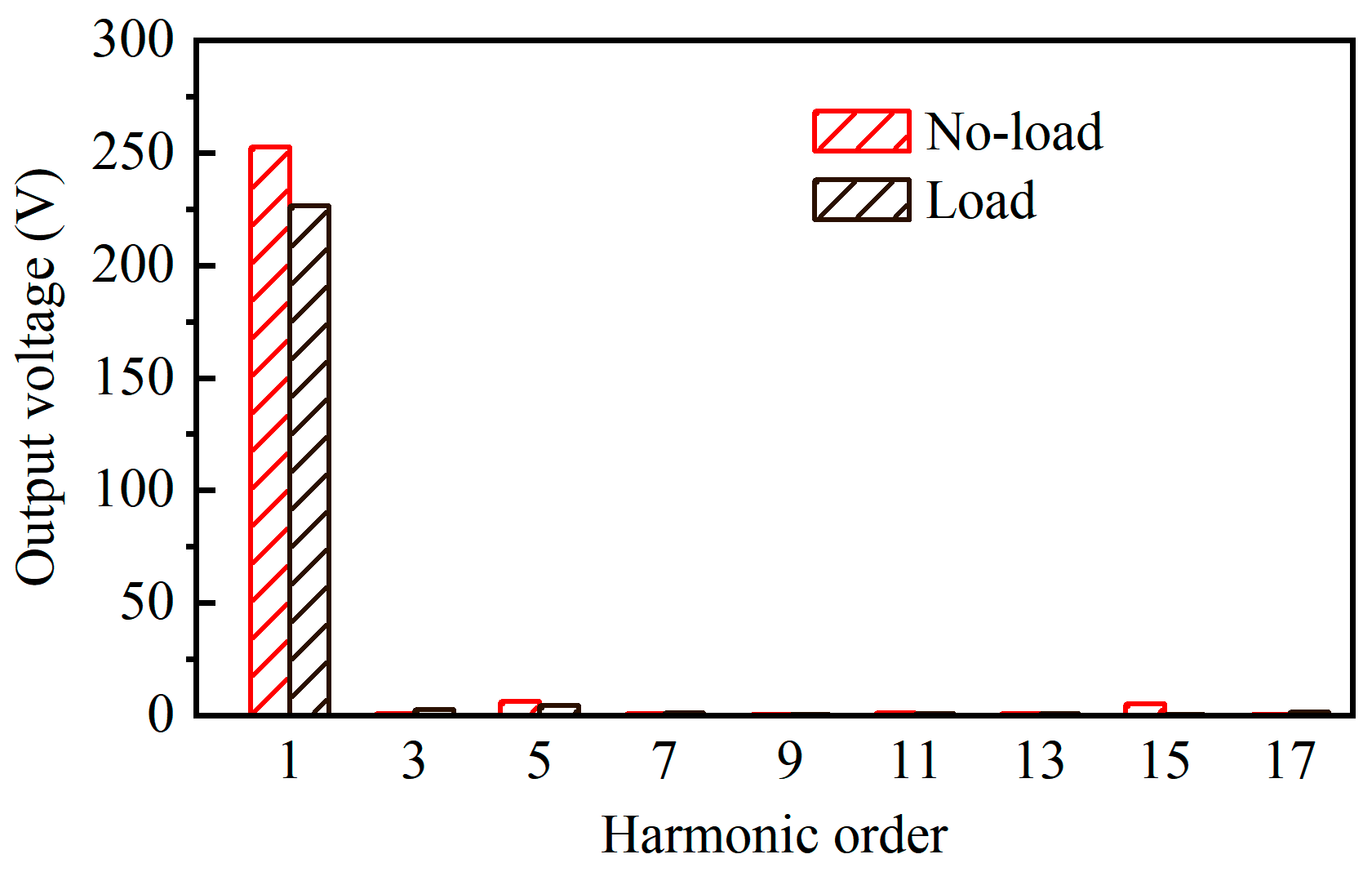
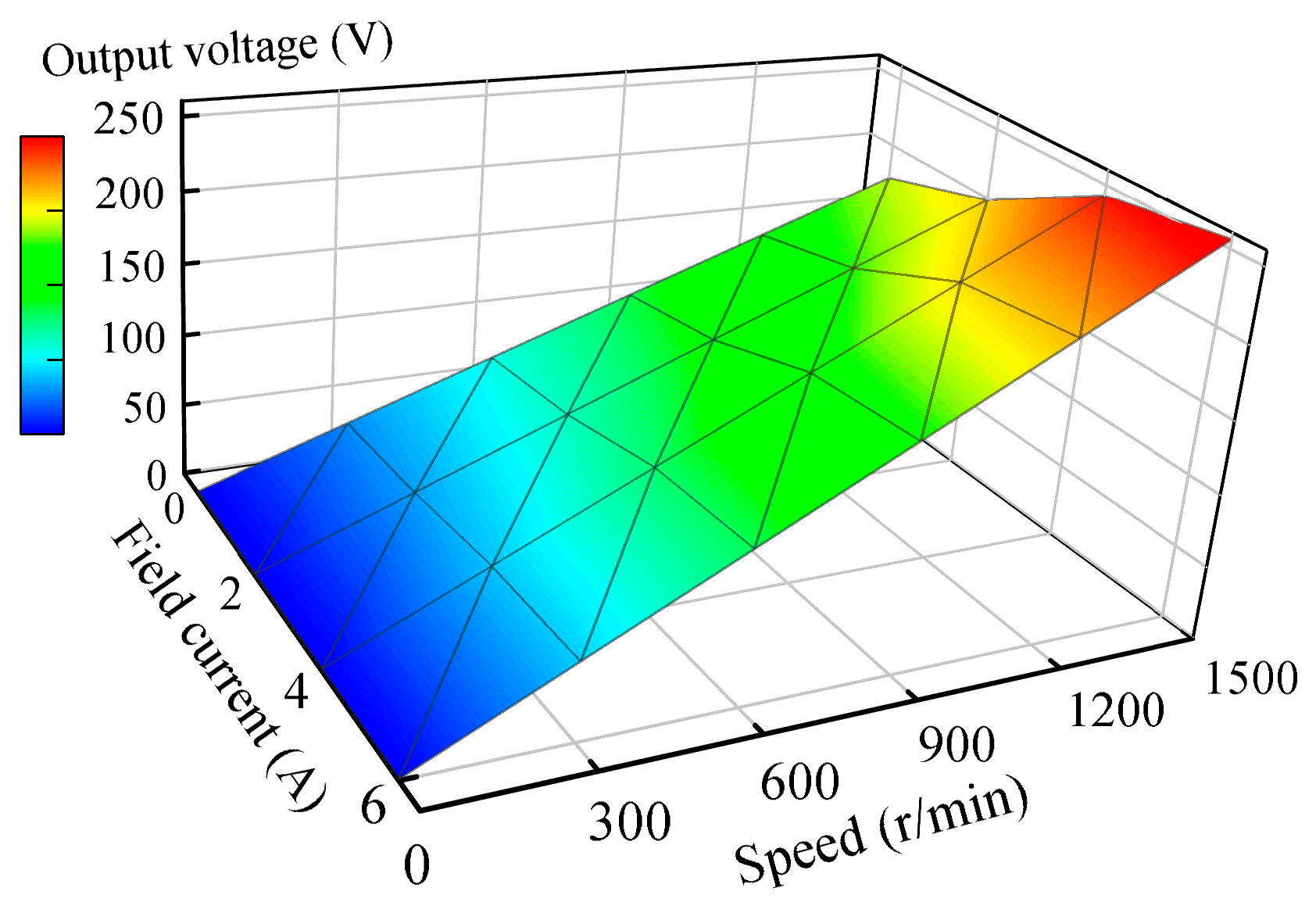
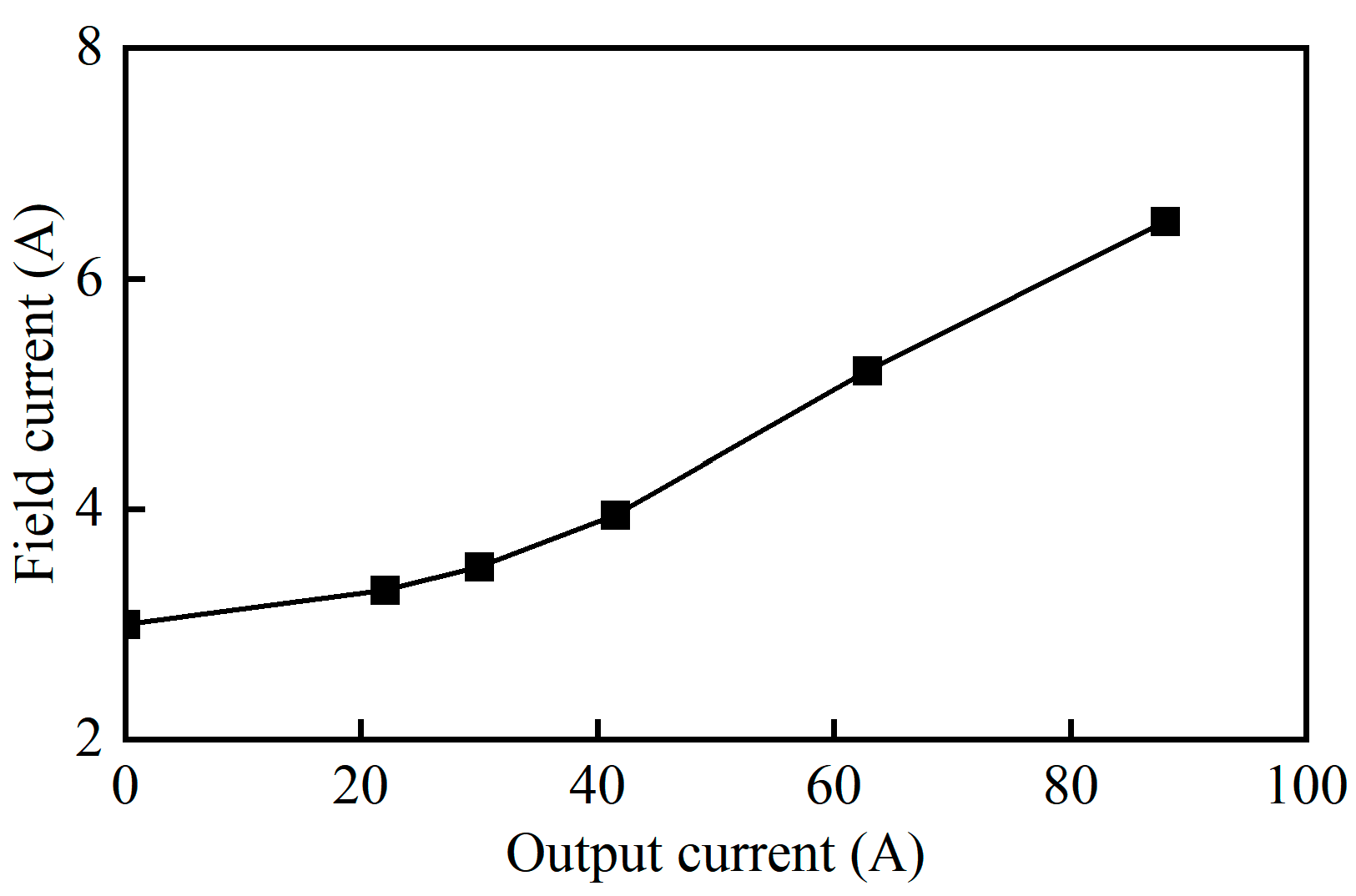
3.2. Operating Characteristics Analysis
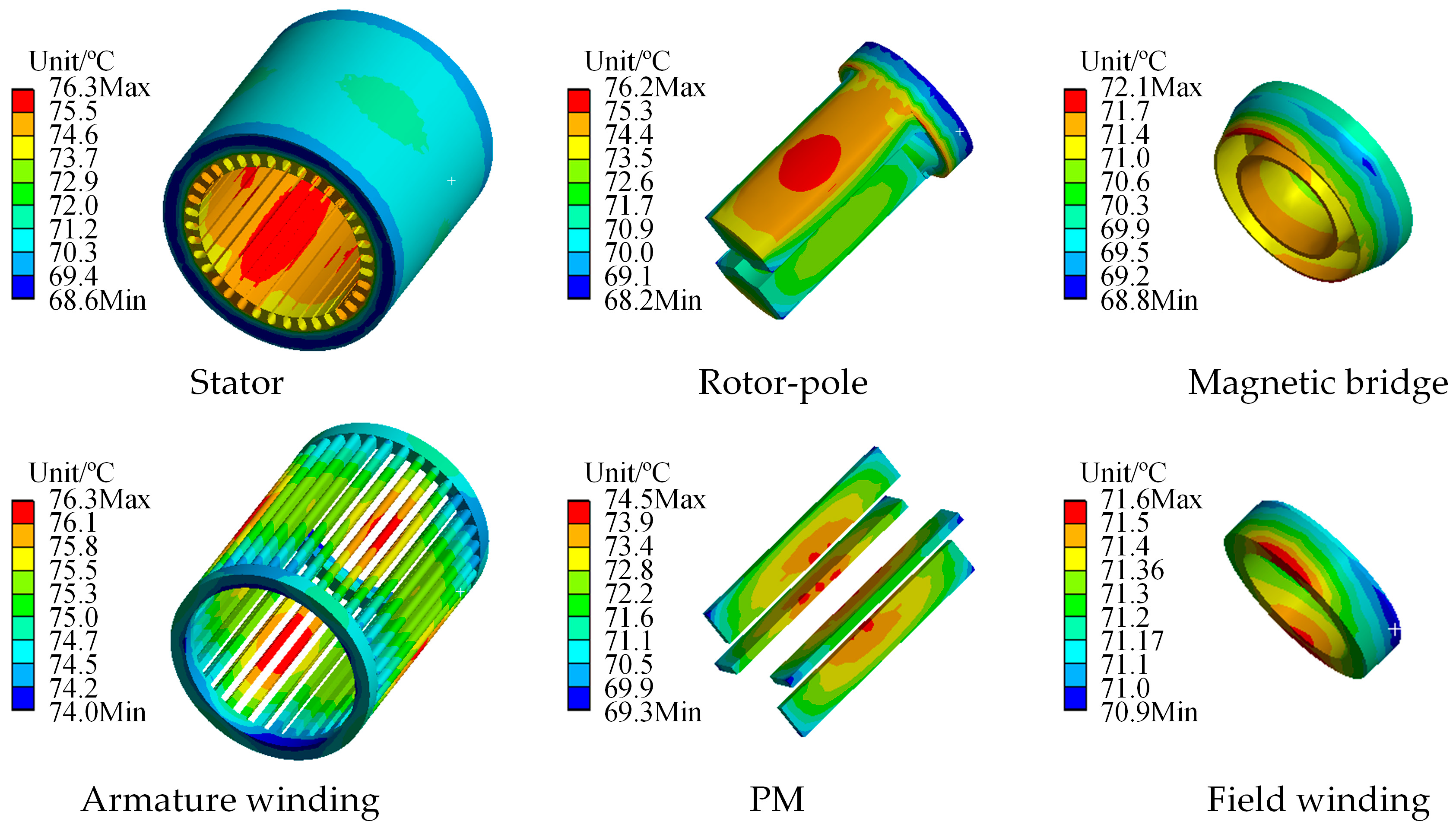
3.3. Loss and Temperature Field Analysis
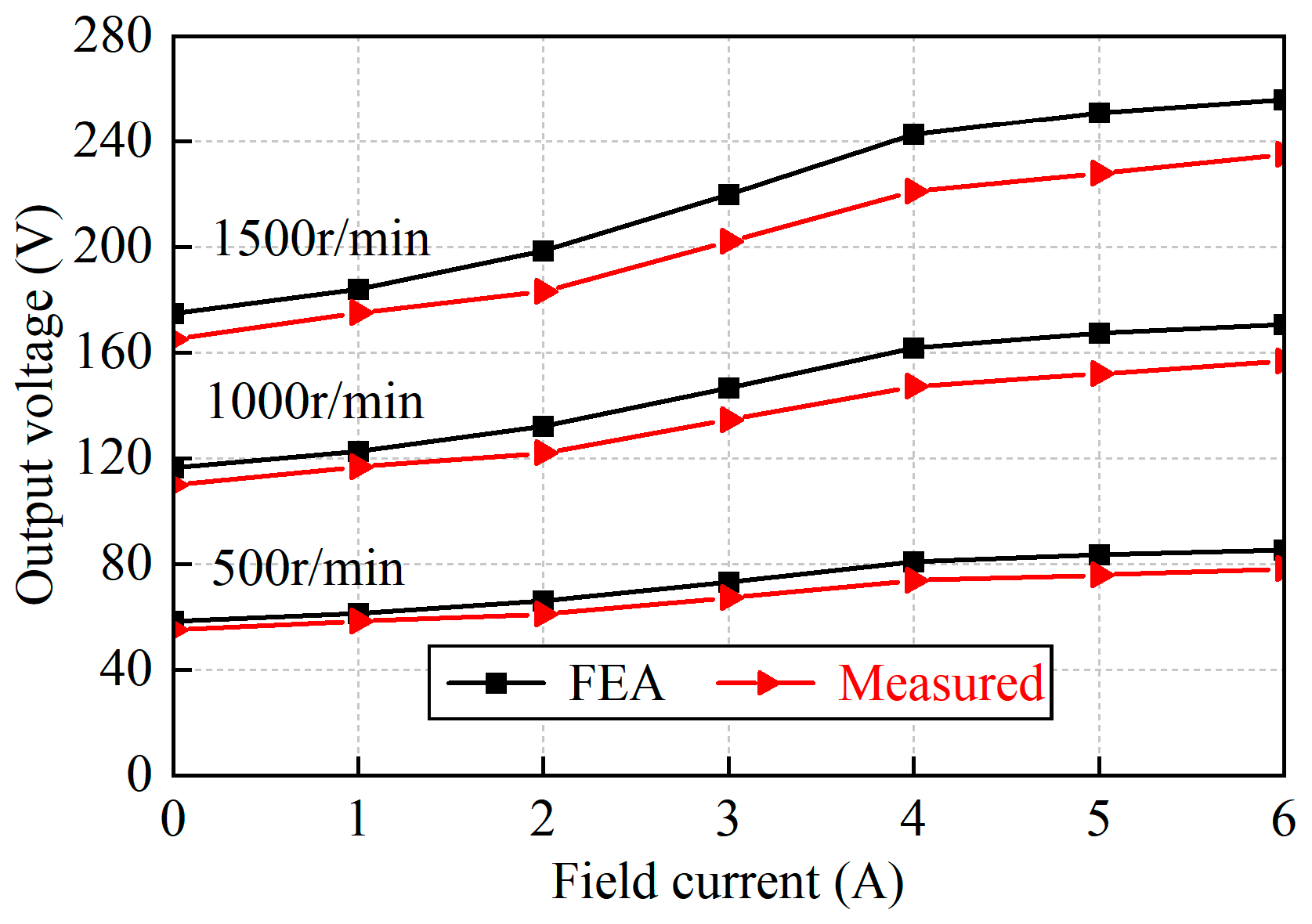
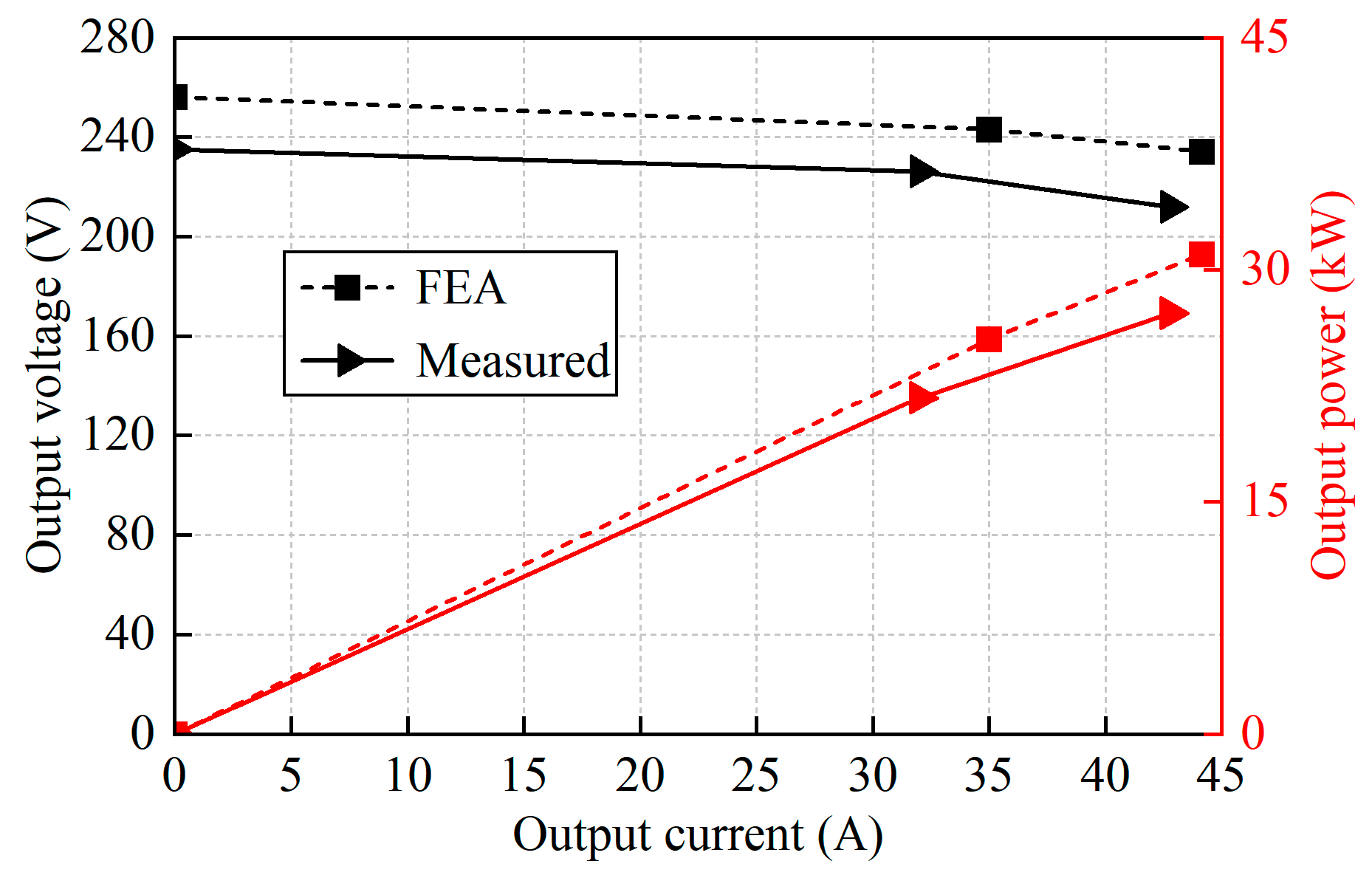
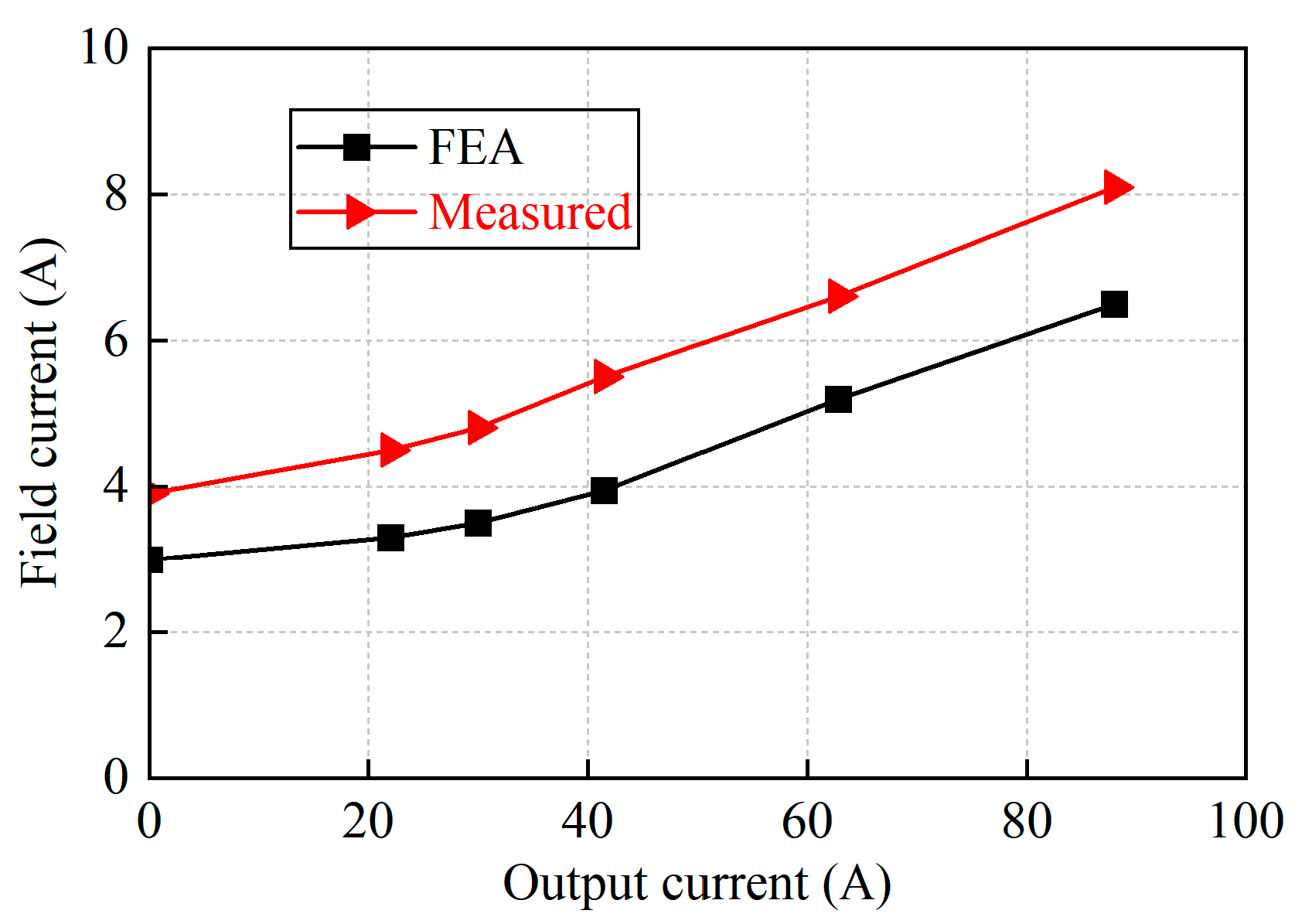
4. Experimental Verification
5. Conclusions
- (1)
- AF-HESG provides a field flux path without passing through permanent magnets by adding an axial magnetic circuit, achieving brushless excitation.
- (2)
- According to the analysis of the air-gap flux density, it can be concluded that AF-HESG can increase the flux-regulation range by changing the additional air-gap length and cross-sectional area, so the AF-HESG adopts an inclined additional air gap, which can effectively increase the flux-regulation capability.
- (3)
- Finite element simulations are conducted to validate the model and analyze the output characteristics of the generator. The load voltage regulation efficiency is 46.5%. The voltage adjustment rate is 9.36%. Due to the axial magnetic circuit of the generator, the rotor is made of solid materials. Therefore, the eddy current loss of the rotor is relatively large. And the temperature is relatively average under rated load conditions.
- (4)
- A prototype is manufactured. Due to the relatively complex structure of the generator, processing is difficult, and it is not easy to mass produce. The feasibility of the generator principle is verified through comparison between the measured results and simulations. And it reflects that AF-HESG has good magnetic field regulation ability and stable voltage output ability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, Z.Q.; Cai, S. Overview of Hybrid Excited Machines for Electric Vehicles. In Proceedings of the 2019 Fourteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 8–10 May 2019; pp. 1–14. [Google Scholar]
- Zhu, S.; Liu, C.; Wang, K.; Zhou, Z.; Yu, J. Structure and Operating Performance of a Double Electrical Excitation Synchronous Generator with Embedded Brushless Synchronous Exciter Utilizing DC-Field Excitation. IEEE Trans. Energy Convers. 2022, 37, 50–64. [Google Scholar] [CrossRef]
- Michieletto, D.; Cinti, L.; Bianchi, N. Hybrid Excitation PM Synchronous Motors: Part I—Per Unit Analysis. IEEE Trans. Energy Convers. 2022, 37, 487–494. [Google Scholar] [CrossRef]
- Shushu, Z.; Chuang, L.; Yinhang, N.; Jie, T. A Two-Stage Brushless Excitation Method for Hybrid Excitation Synchronous Generator. IEEE Trans. Magn. 2015, 51, 8105411. [Google Scholar] [CrossRef]
- Geng, H.; Zhang, X.; Tong, L.; Ma, Q.; Xu, M.; Zhang, Y.; Wang, L. Performance Optimization Analysis of Hybrid Excitation Generator with the Electromagnetic Rotor and Embedded Permanent Magnet Rotor for Vehicle. IEEE Access 2021, 9, 163640–163653. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, X.; Ren, J.; Yan, S.; Wang, L.; Pang, X.; Liu, W.; Kong, Z. Study of Electromagnetic Characteristics of Brushless Reverse Claw Pole Electromagnetic and Permanent Magnet Hybrid Excitation Generator for Automobiles. IEEE Trans. Energy Convers. 2024, 39, 1288–1300. [Google Scholar] [CrossRef]
- Li, J.; Wang, K.; Zhu, S.S.; Liu, C. Integrated-Induction-Based Hybrid Excitation Brushless DC Generator with Consequent-Pole Rotor. IEEE Trans. Transp. Electrific. 2022, 8, 2233–2248. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, Z.; Gu, X.; Yu, L. Analysis of a Hybrid Excitation Brushless DC Generator with an Integrated Shared-Flux-Path Exciter. IEEE Trans. Ind. Electron. 2021, 68, 6672–6681. [Google Scholar] [CrossRef]
- Ayub, M.; Jawad, G.; Kwon, B. Consequent-Pole Hybrid Excitation Brushless Wound Field Synchronous Machine with Fractional Slot Concentrated Winding. IEEE Trans. Magn. 2019, 55, 8203805. [Google Scholar] [CrossRef]
- Li, J.; Wang, K.; Liu, C. Improvement of Integrated-Induction-Based Hybrid Excitation Brushless DC Generator by Employing Novel Consequent-Pole Rotor. IEEE Trans. Ind. Electron. 2022, 69, 12042–12054. [Google Scholar] [CrossRef]
- Zhang, Z.; Han, J.; Wang, C. A Brushless Hybrid Excited Starter-Generator with Independent Excitation Flux Circuit for Aircraft AC Power Generation. IEEE Trans. Transp. Electrific. 2024, 10, 4689–4698. [Google Scholar] [CrossRef]
- Xu, L.; Zhu, X.; Jiang, T.; Niu, S. Design and Optimization of a Partitioned Stator Hybrid Excited Machine with Inset PM From Perspective of Airgap Field Harmonics. IEEE Trans. Energy Convers. 2023, 38, 2871–2883. [Google Scholar] [CrossRef]
- Zhao, X.; Niu, S.; Zhang, X.; Fu, W. Flux-Modulated Relieving-DC-Saturation Hybrid Reluctance Machine with Synthetic Slot-PM Excitation for Electric Vehicle In-Wheel Propulsion. IEEE Trans. Ind. Electron. 2021, 68, 6075–6086. [Google Scholar] [CrossRef]
- Li, X.; Shen, F.; Yu, S.; Xue, Z. Flux-Regulation Principle and Performance Analysis of a Novel Axial Partitioned Stator Hybrid-Excitation Flux-Switching Machine Using Parallel Magnetic Circuit. IEEE Trans. Ind. Electron. 2021, 68, 6560–6573. [Google Scholar] [CrossRef]
- Wei, F.; Zhu, Z.Q.; Yan, L.; Qi, J. Investigation of Stator/Rotor Pole Number Combinations and PM Numbers in Consequent-Pole Hybrid Excited Flux Reversal Machine. IEEE Trans. Energy Convers. 2022, 37, 2092–2106. [Google Scholar] [CrossRef]
- Zhao, X.; Jiang, J.; Niu, S.; Wang, Q. Slot-PM-Assisted Hybrid Reluctance Generator with Self-Excited DC Source for Stand-Alone Wind Power Generation. IEEE Trans. Magn. 2022, 58, 8700106. [Google Scholar] [CrossRef]
- Hou, J.; Geng, W.; Li, Q.; Zhang, Z. 3-D Equivalent Magnetic Network Modeling and FEA Verification of a Novel Axial-Flux Hybrid-Excitation In-Wheel Motor. IEEE Trans. Magn. 2021, 57, 8106912. [Google Scholar] [CrossRef]
- Wang, X.; Wan, Z.; Tang, L.; Xu, W.; Zhao, M. Electromagnetic Performance Analysis of an Axial Flux Hybrid Excitation Motor for HEV Drives. IEEE Trans. Appl. Supercond. 2021, 31, 5205605. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Z.; Liu, Y.; Gao, H. Mechanical Design and Analysis of a High-Torque Modular Hybrid Excitation Synchronous Machine for Electric Vehicle Propulsion Applications. IEEE Trans. Veh. Technol. 2020, 69, 9624–9633. [Google Scholar] [CrossRef]
- Ye, C.; Du, Y.; Yang, J.; Liang, X.; Xiong, F.; Xu, W. Research of an Axial Flux Stator Partition Hybrid Excitation Brushless Synchronous Generator. IEEE Trans. Magn. 2018, 54, 8204304. [Google Scholar] [CrossRef]
- Yu, J.; Cao, Y.; Zhu, S.; Liu, C. Comparison Research of Hybrid Excitation Synchronous Generator between Uniform and Nonuniform Rotor Structure. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 951–956. [Google Scholar]
- Xu, W.; Zhang, Y.; Du, G.; He, M.; Zhu, J. No-Load Performance Analysis of an Asymmetric-Pole Single-Phase Doubly Salient Permanent Magnet Machine. IEEE Trans. Ind. Electron. 2021, 68, 2907–2918. [Google Scholar] [CrossRef]
- Jiang, W.; Feng, S.; Zhang, Z.; Zhang, J.; Zhang, Z. Study of Efficiency Characteristics of Interior Permanent Magnet Synchronous Motors. IEEE Trans. Magn. 2018, 54, 8108005. [Google Scholar] [CrossRef]










| Parameters | Value |
|---|---|
| Rated power | 30 kW |
| Rated speed | 1500 r/min |
| Rated phase voltage | 220 V |
| Number of pole pairs | 2 |
| Width of PM | 40 mm |
| Thickness of PM | 10 mm |
| Length of stator core | 250 mm |
| Number of stator slots | 36 |
| The field current | 6 A |
| Parameters | Affected Parameters | Variation Range |
|---|---|---|
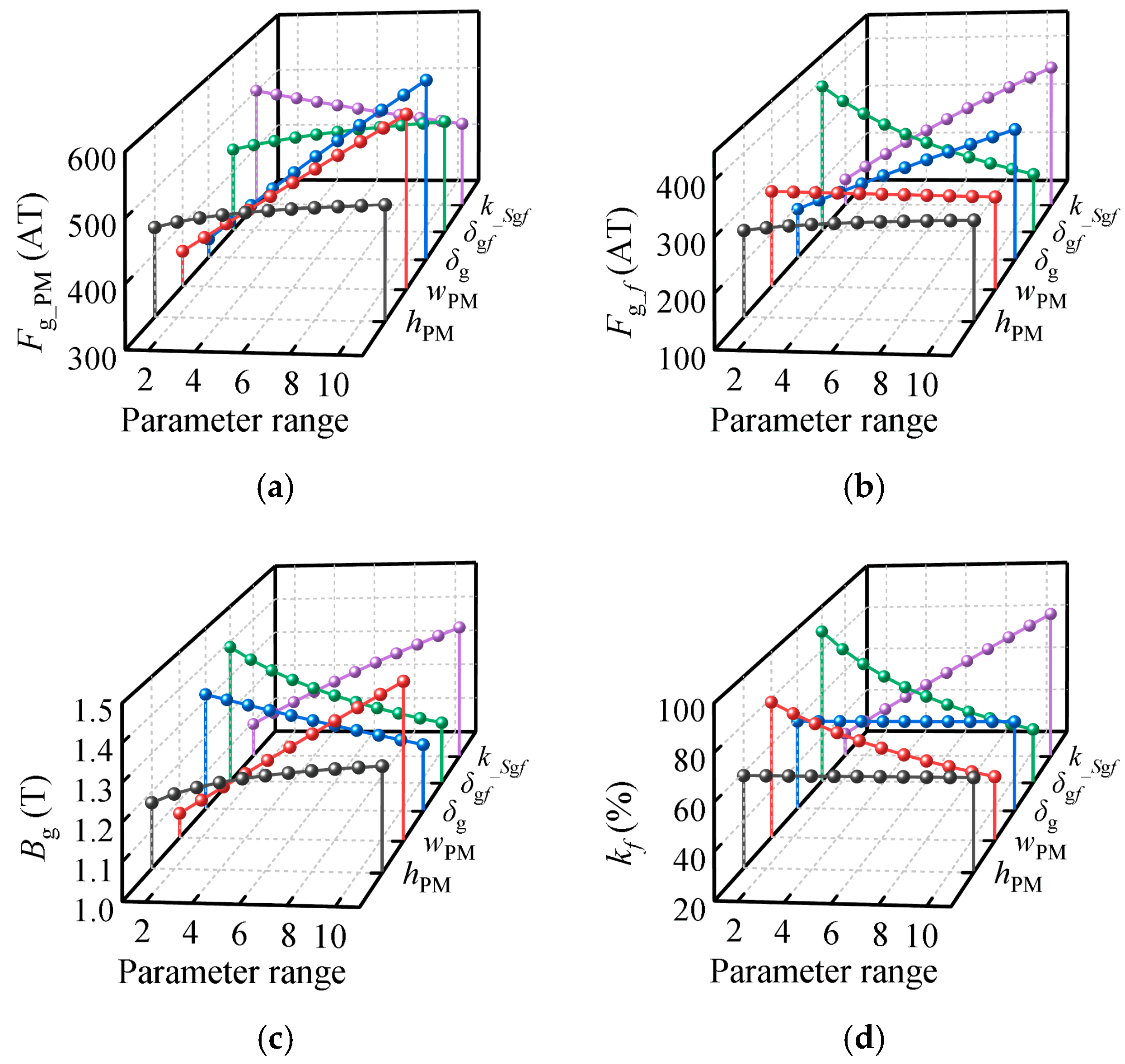
| PM height hPM | FPM, RPM | 5~15 mm |
| PM width wPM | RPM | 30~50 mm |
| Air-gap length δg | Rg, Λg | 0.5~1 mm |
| Additional air-gap length δfg | Rfg | 0.45~0.95 mm |
| Multiple of additional air-gap cross-sectional area k_sgf | Rfg | 0.5~1 |
| Components | Ploss (W) | V (m3) | Q (W/m3) |
|---|---|---|---|
| Stator | 319 | 6.58 × 10−3 | 48,443 |
| Rotor-pole | 1296 | 5.87 × 10−3 | 220,783 |
| Magnetic bridge | 48 | 1.28 × 10−3 | 37,500 |
| PM | 38 | 4 × 10−4 | 95,000 |
| Armature winding | 1452 | 1.52 × 10−3 | 954,007 |
| Field winding | 187 | 7.05 × 10−4 | 265,531 |
| Components | Material | λt (W/m·K) | αt (W/m2·K) |
|---|---|---|---|
| Stator | 50WW600 | 27.2 | / |
| Rotor/Magnetic bridge | Steel No. 10 | 45 | / |
| PM | N35UH | 7.6 | / |
| Winding | copper | 400 | / |
| Air-gap | Equivalent air | 0.098 | / |
| Shell/shaft | Aluminum | 237 | / |
| Surface of shell | / | / | 41.76 |
| Stator end | / | / | 69.2 |
| Rotor end | / | / | 100.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Zhu, S.; Liu, C. Analysis of an Axial Field Hybrid Excitation Synchronous Generator. Energies 2024, 17, 6329. https://doi.org/10.3390/en17246329
Yu J, Zhu S, Liu C. Analysis of an Axial Field Hybrid Excitation Synchronous Generator. Energies. 2024; 17(24):6329. https://doi.org/10.3390/en17246329
Chicago/Turabian StyleYu, Junyue, Shushu Zhu, and Chuang Liu. 2024. "Analysis of an Axial Field Hybrid Excitation Synchronous Generator" Energies 17, no. 24: 6329. https://doi.org/10.3390/en17246329
APA StyleYu, J., Zhu, S., & Liu, C. (2024). Analysis of an Axial Field Hybrid Excitation Synchronous Generator. Energies, 17(24), 6329. https://doi.org/10.3390/en17246329






