Oil Cooling Method for Internal Heat Sources in the Outer Rotor Hub Motor of ElectricVehicle and Thermal Characteristics Research
Abstract
1. Introduction
2. Oil Cooling Structure Model Inside the Outer Rotor Hub Motor
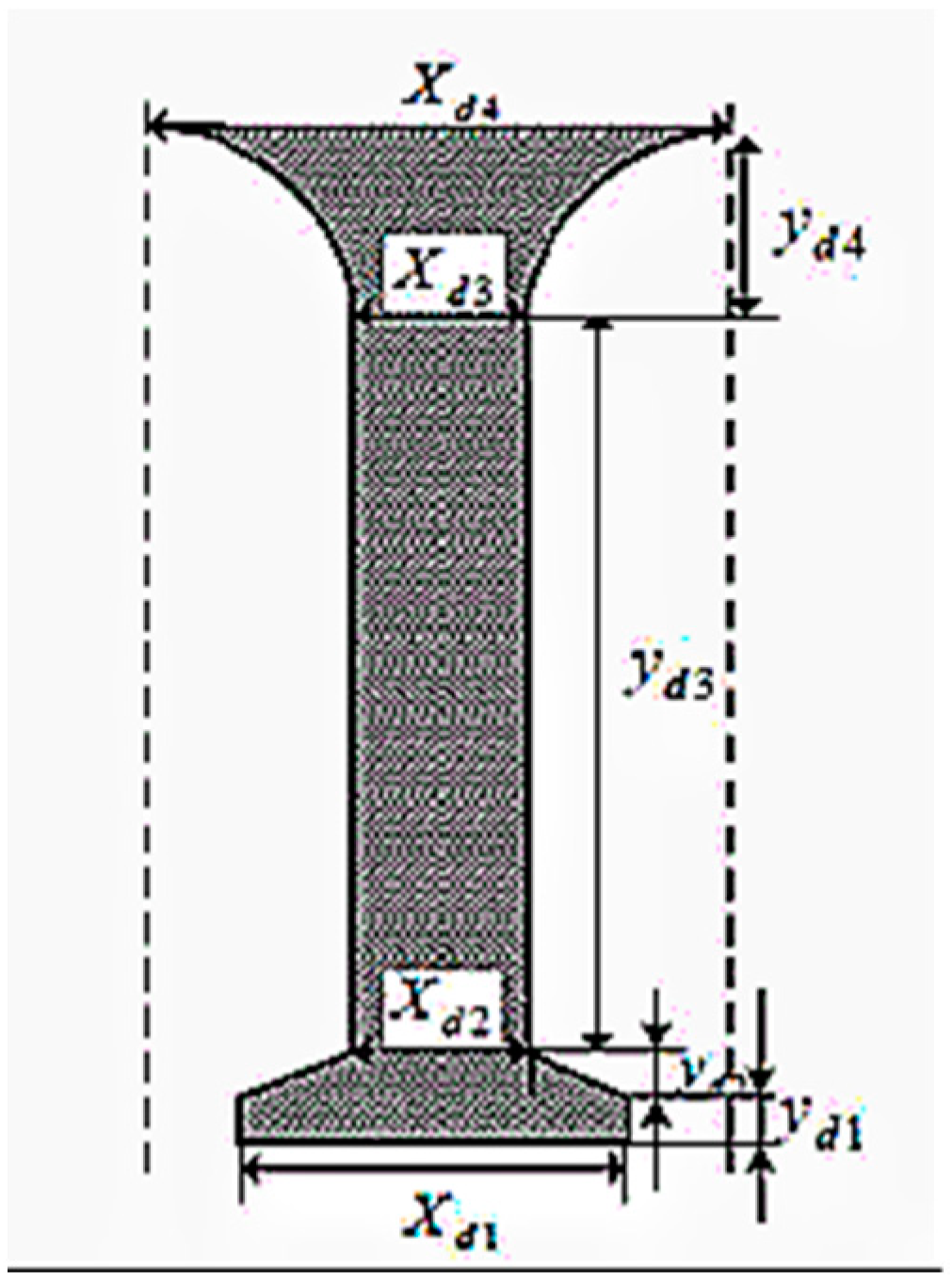
3. Calculation of the Cooling Oil Distribution
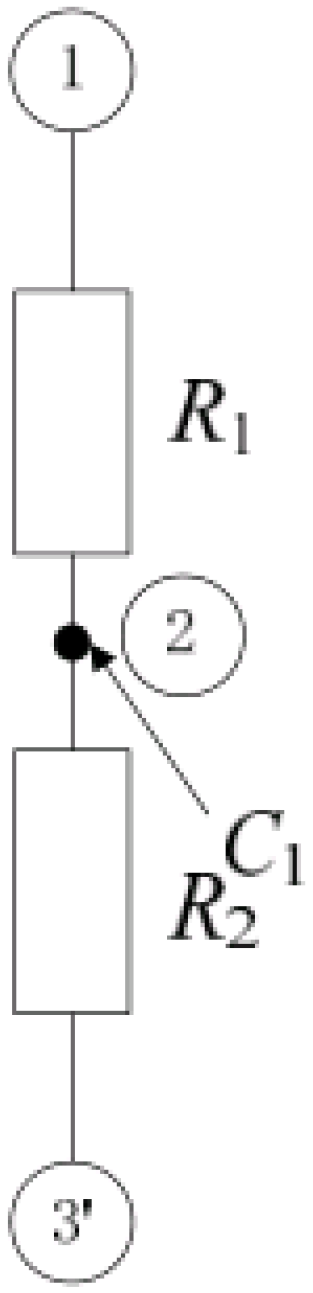
4. Motor Heat Distribution Model
5. Temperature Field Simulation
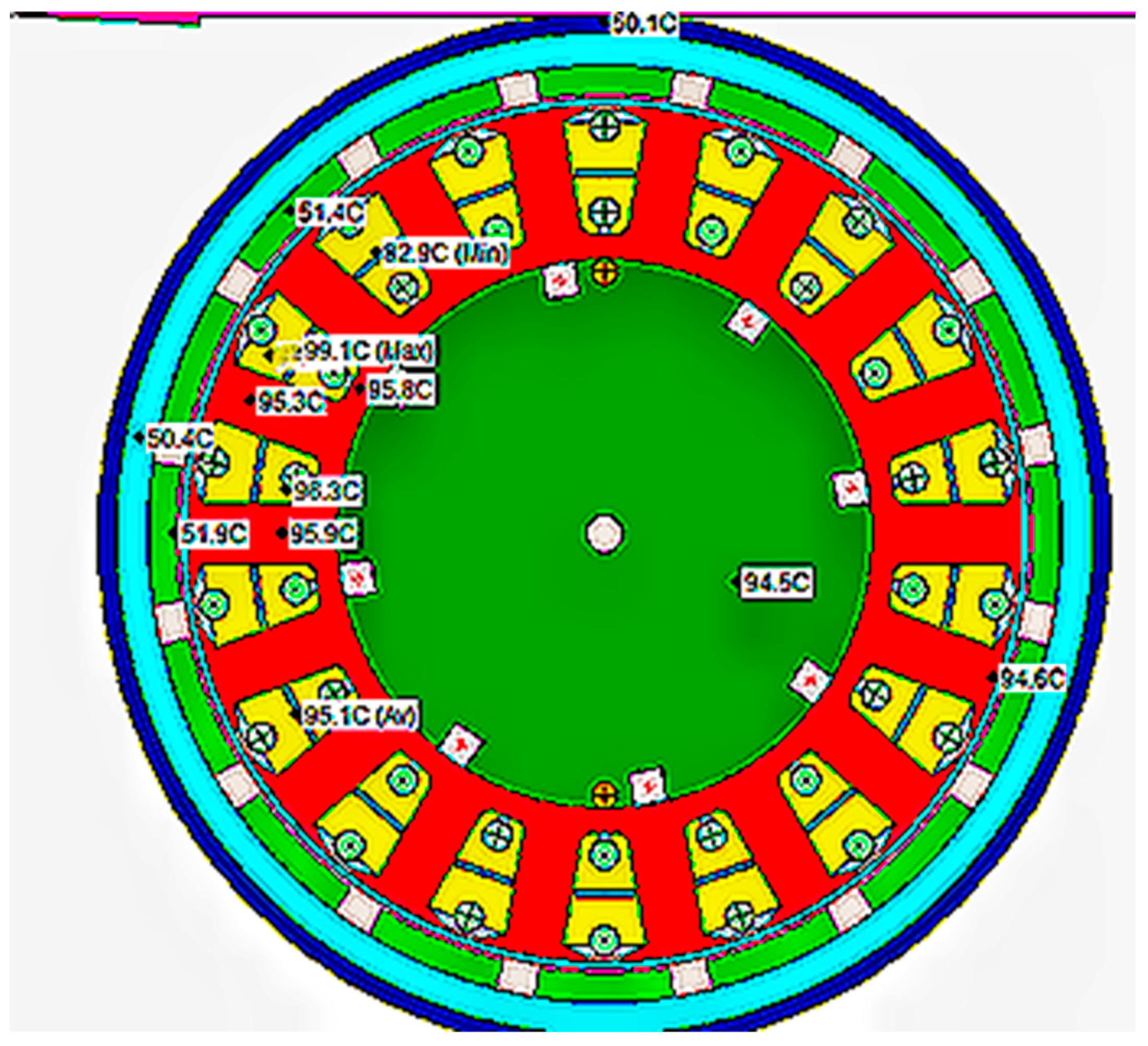
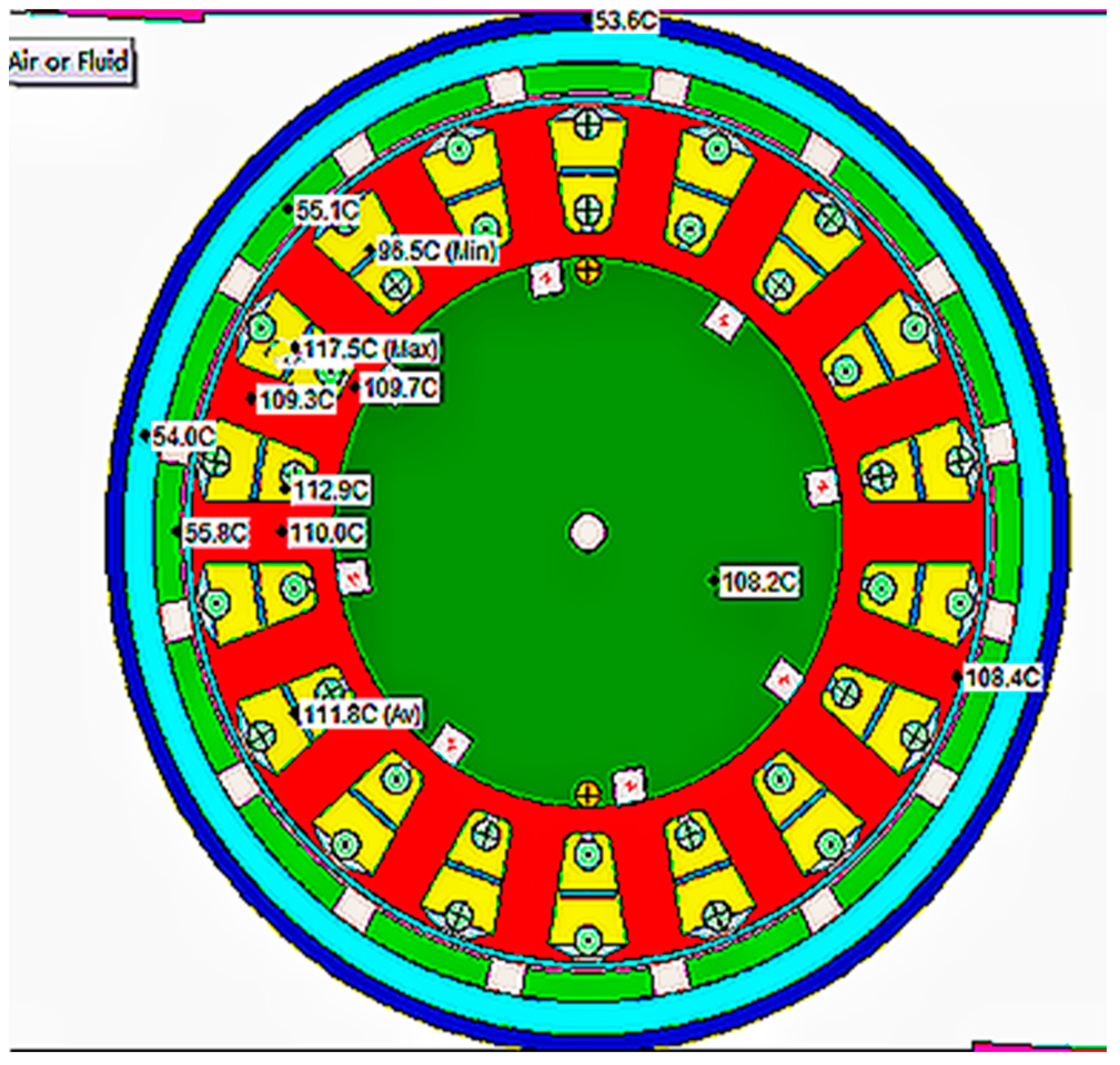
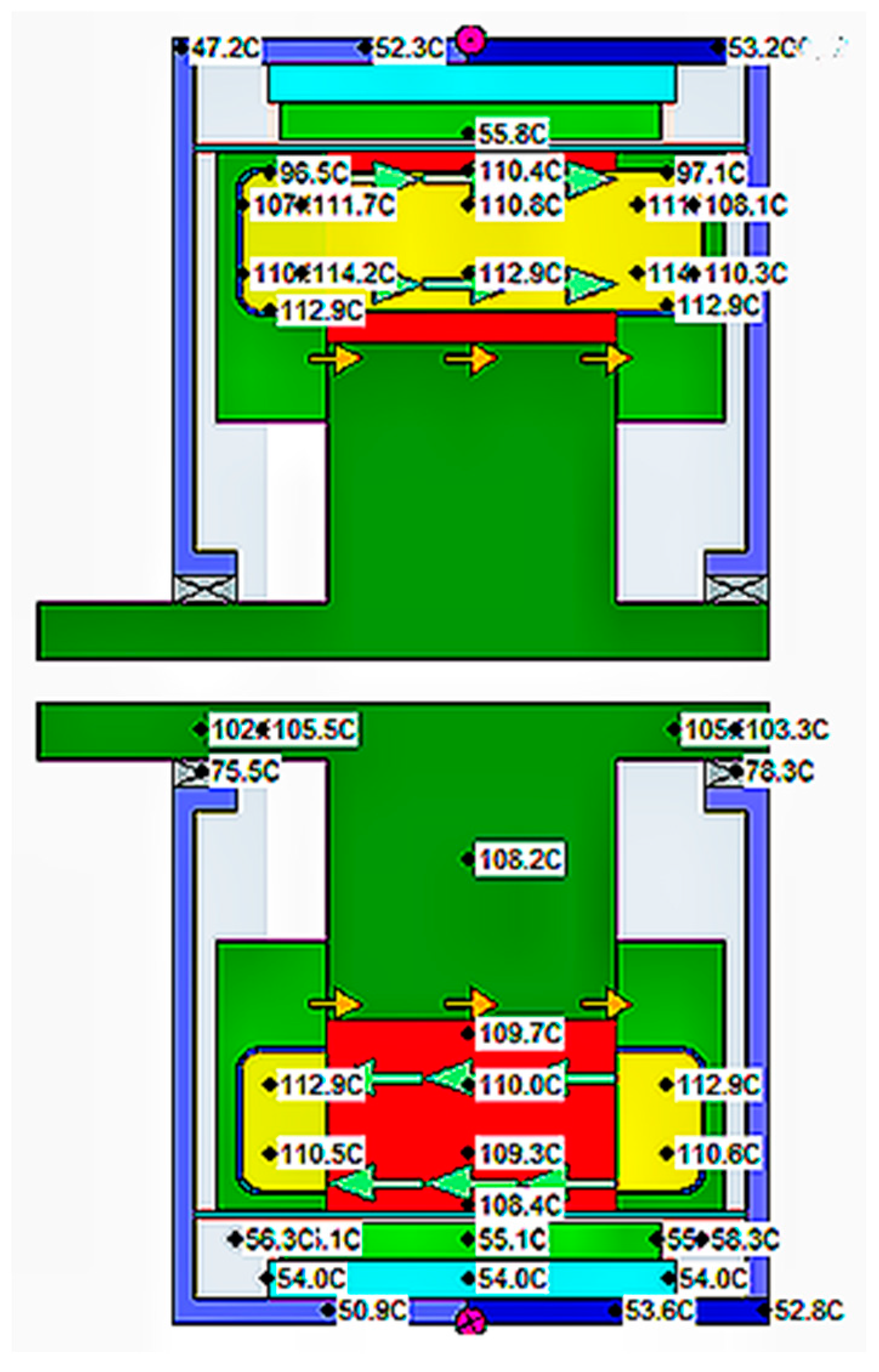
5.1. Simulation Results of the Rated Operating Conditions
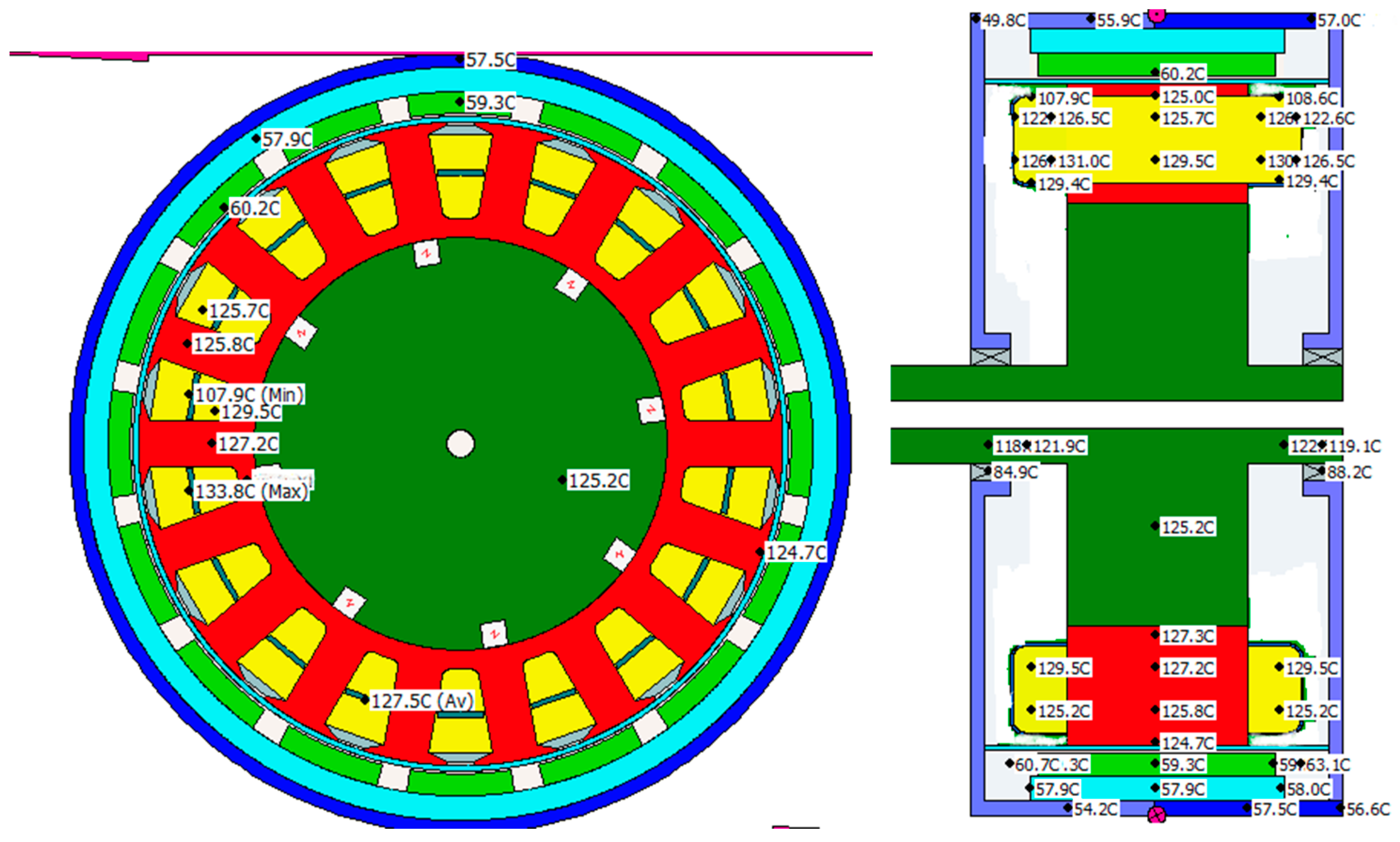
5.2. Simulation Results of Low Speed and High Torque Condition
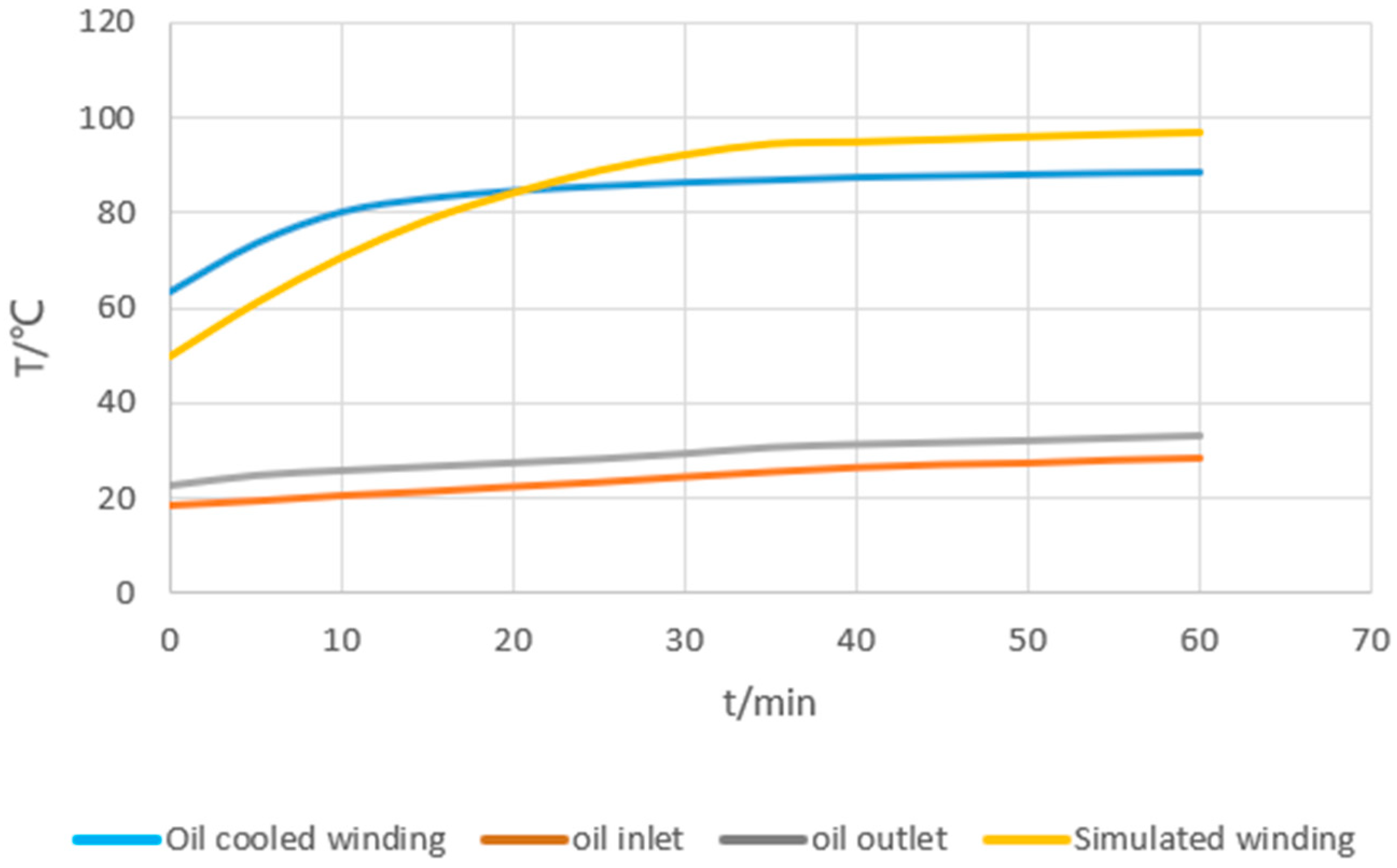
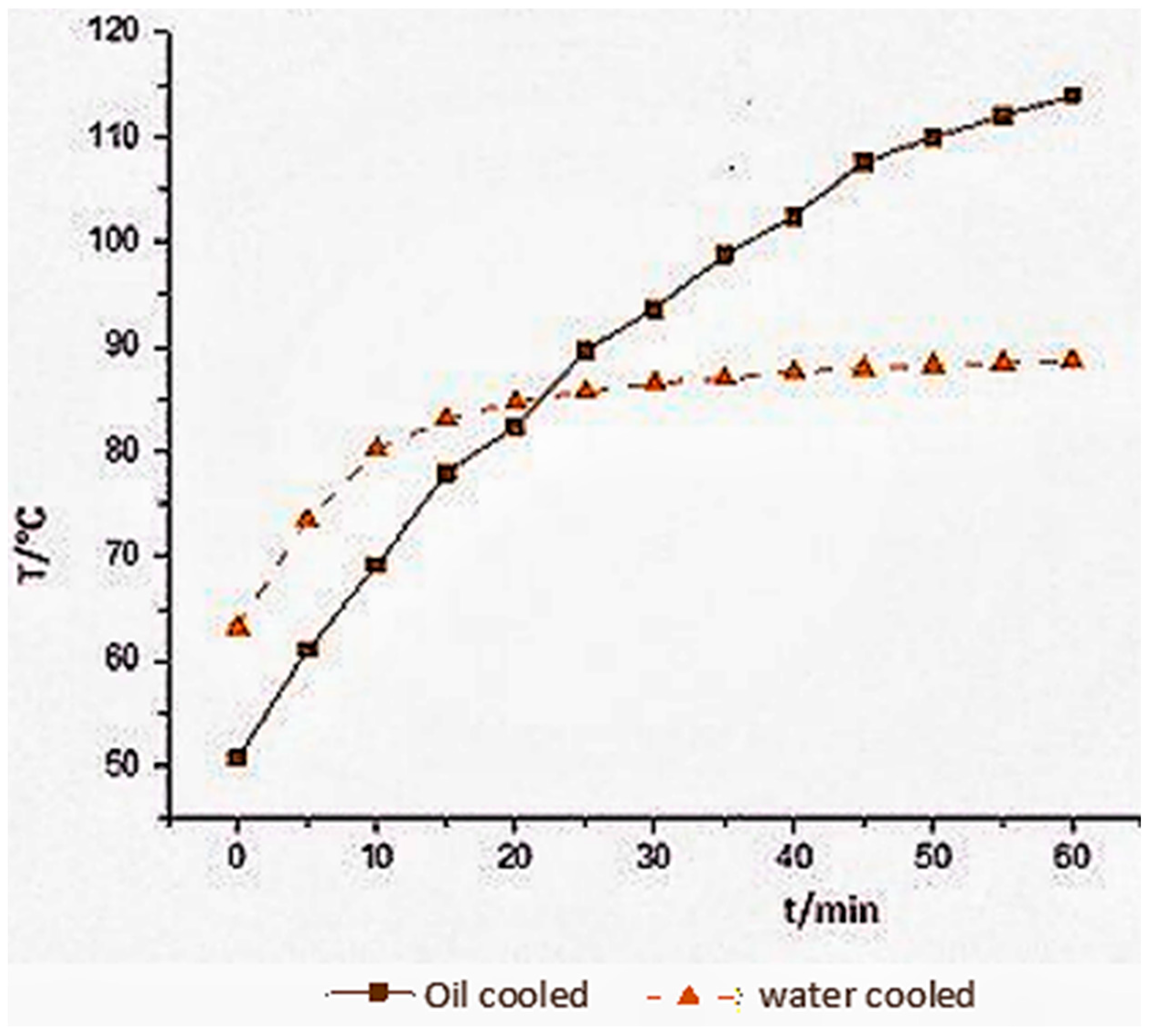
6. Motor Test Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Staton, D.A.; Cavagnino, A. Convection Heat Transfer and Flow Calculations Suitable for Electric Machines Thermal Models. IEEE Trans. Ind. Electron. 2008, 55, 3509–3516. [Google Scholar] [CrossRef]
- Márquez-Fernández, F.; Reinap, A.; Huang, Z.; Alaküla, M. Design, optimization and construction of an electric motor for an Electric Rear Wheel Drive Unit application for a Hybrid Passenger Car. In Proceedings of the XIX International Conference on Electrical Machines-ICEM 2010, Rome, Italy, 6–8 September 2010. [Google Scholar]
- Zhou, Z.; Yang, W.; Li, Z. Temperature Field and Thermal Stress of External Rotor In-Wheel Motor. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2022, 41, 142–150. [Google Scholar]
- Chai, X. Temperature Rise and Heat Dissipation Analysis of In-wheel Motor Angle Module System under the Action of Multi-physics Coupling. Automob. Appl. Technol. 2023, 48, 124–134. [Google Scholar]
- Liu, Z.; Yan, Y. Research on axial U-shaped water channel cooling structure of hub motor. J. Shanghai Univ. Eng. Sci. 2023, 37, 240–246. [Google Scholar]
- Li, Y.; Fan, T.; Wen, X.; Li, Y. Numerical research on hydraulic and thermal performance of the motor water jackets based on the orthogonal experiment. Int. Conf. Electr. Mach. Syst. 2013, 2013, 860–863. [Google Scholar]
- Jiao, B.F.; Li, D.S.; Du, X. Performance analysis and experimentation of a liquid-cooled eddy current retarder with a dual salient poles design. IEEE Trans. Energy Convers. 2014, 29, 84–90. [Google Scholar] [CrossRef]
- Lindh, P.M. Direct Liquid Cooling in Low-Power Electrical Machines: Proof-of-Concept. IEEE Trans. Energy Convers. 2016, 31, 1257–1266. [Google Scholar] [CrossRef]
- Liu, M.; Li, Y.; Ding, H.; Sarlioglu, B. Thermal management and cooling of windings in electrical machines for electric vehicle and traction application. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 22–24 June 2017; pp. 668–673. [Google Scholar]
- Wu, W.; Hu, C.; Hu, J.; Yuan, S. Cooling for rolling Bearings: Flow visualization and temperature distribution. Appl. Therm. Eng. 2016, 105, 217–224. [Google Scholar] [CrossRef]
- Liu, C.Y.; Jiang, K.J.; Zhang, Y. Study on temperature rise performance of eddy current retarder in automobile. In Proceedings of the 2010 International Conference on Future Information Technology and Management Engineering (FITME), Changzhou, China, 9–10 October 2010; pp. 550–553. [Google Scholar]
- Camilleri, R. Predicting the Temperature and Flow Distribution in a Direct Oil-Cooled Electrical Machine With Segmented Stator. IEEE Trans. Ind. Electron. 2016, 63, 82–87. [Google Scholar] [CrossRef]
- Jungreuthmayer, C.; Bauml, T.; Winter, O.; Ganchev, M.; Kapeller, H.; Haumer, A.; Kral, C. A detailed heat and fluid flow analysis of an internal permanent magnet synchronous machine by means of computational fluid dynamics. IEEE Trans. Ind. Electron. 2012, 59, 4568–4578. [Google Scholar] [CrossRef]
- Wang, R.J.; Heyns, G.C. Thermal analysis of a water-cooled interior permanent magnet traction machine. In Proceedings of the 2013 IEEE International Conference on Industrial Technology (ICIT), Cape Town, South Africa, 25–28 February 2013; pp. 416–421. [Google Scholar]
- Rashid, M.I.M.; Daniyal, H.; Mohamed, D. Comparison performance of split plug-in hybrid electric vehicle and hybrid electric vehicle using ADVISOR. In Proceedings of the 2nd International Conference on Automotive Innovation and Green Vehicle (AIGEV 2016), Cyberjaya, Malaysia, 2–3 August 2016. [Google Scholar]
- Qu, H.; Li, J.; Wang, Y.; Li, Z. Semi-Closed Type Oil Cooling System for Motor for Compressor. CN104467288, 31 December 2014. [Google Scholar]
- Wang, K.; Zhu, Z.Q.; Ombach, G. Synthesis of high performance fractional-slot permanent-magnet machines with coil-pitch of two slotpitches. IEEE Trans. Energy Convers. 2014, 29, 758–770. [Google Scholar] [CrossRef]
- Ping, Z.; Liu, R.; Thelin, P.; Nordlund, E.; Sadarangani, C. Research on the cooling system of a 4QT prototype machine used for HEV. IEEE Trans. Energy Convers. 2008, 23, 61–67. [Google Scholar]
- Polikarpova, M. Liquid Cooling Solutions for Rotating Permanent Magnet Synchronous Machines. Ph.D. Thesis, Lappeenranta University Technology, Lappeenranta, Finland, 2014. [Google Scholar]
- Li, Q.; Fan, T.; Wen, X.; Ning, P. An Analytical Approach to Magnet Eddy-Current Losses for Interior Permanent-Magnet Synchronous Machines During Flux Weakening. IEEE Trans. Magn. 2015, 51, 8107109. [Google Scholar]
- Caricchi, F.; Crescimbini, F.; Di Napoli, A. Prototype of innovative wheel direct drive with water-cooled axial-flux PM motor for electric vehicle applications. In Proceedings of the IEEE Applied Power Electronics Conference, San Jose, CA, USA, 3–7 March 1996; pp. 764–770. [Google Scholar]
- Ulbrich, S.; Kopte, J.; Proske, J. Cooling Fin Optimization on a TEFC Electrical Machine Housing Using a 2-D Conjugate Heat Transfer Model. IEEE Trans. Ind. Electron. 2018, 65, 1711–1718. [Google Scholar] [CrossRef]
- Ishak, D.; Zhu, Z.Q.; Howe, D. Eddy-current loss in the rotor magnets of permanent-magnet brushless machines having a fractional number of slots per pole. Magnetics. IEEE Trans. Magn. 2005, 41, 2462–2469. [Google Scholar] [CrossRef]
- JMAG Version 10 -User’s Manual Solver; JSOL Corporation: Tokyo, Japan, 2010.
- Eason, G.; Noble, B.; Sneddon, I.N. On certain integrals of Lipschitz-Hankel type involving products of Bessel functions. Phil. Trans. Roy. Soc. 1955, A247, 529–551. [Google Scholar]
- Liu, R.; Zheng, P.; Xie, D.; Wang, L. Research on the High Power Density Electromagnetic Propeller. IEEE Trans. Magn. 2007, 43, 355–358. [Google Scholar] [CrossRef]
- Janna, W.S. Engineering Heat Transfer; Van Nostrand: New York, NY, USA, 1988. [Google Scholar]
- Boglietti, A.; Cavagnino, A.; Lazzari, M. A simplified thermal model for variable-speed self-cooled industrial induction motor. IEEE Trans. Ind. Appl. 2003, 39, 945–952. [Google Scholar] [CrossRef]
- Staton, D.; Boglietti, A.; Cavagnino, A. Solving the More Difficult Aspects of Electric Motor Thermal Analysis in Small and Medium Size Industrial Induction Motors. IEEE Trans. Energy Convers. 2005, 20, 620–628. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A. Analysis of the Endwinding Cooling Effects in TEFC InductionMotors. In Proceedings of the IEEE Conference on Industry Applications Conference, Tampa, FL, USA, 8–12 October 2006; pp. 797–804. [Google Scholar]
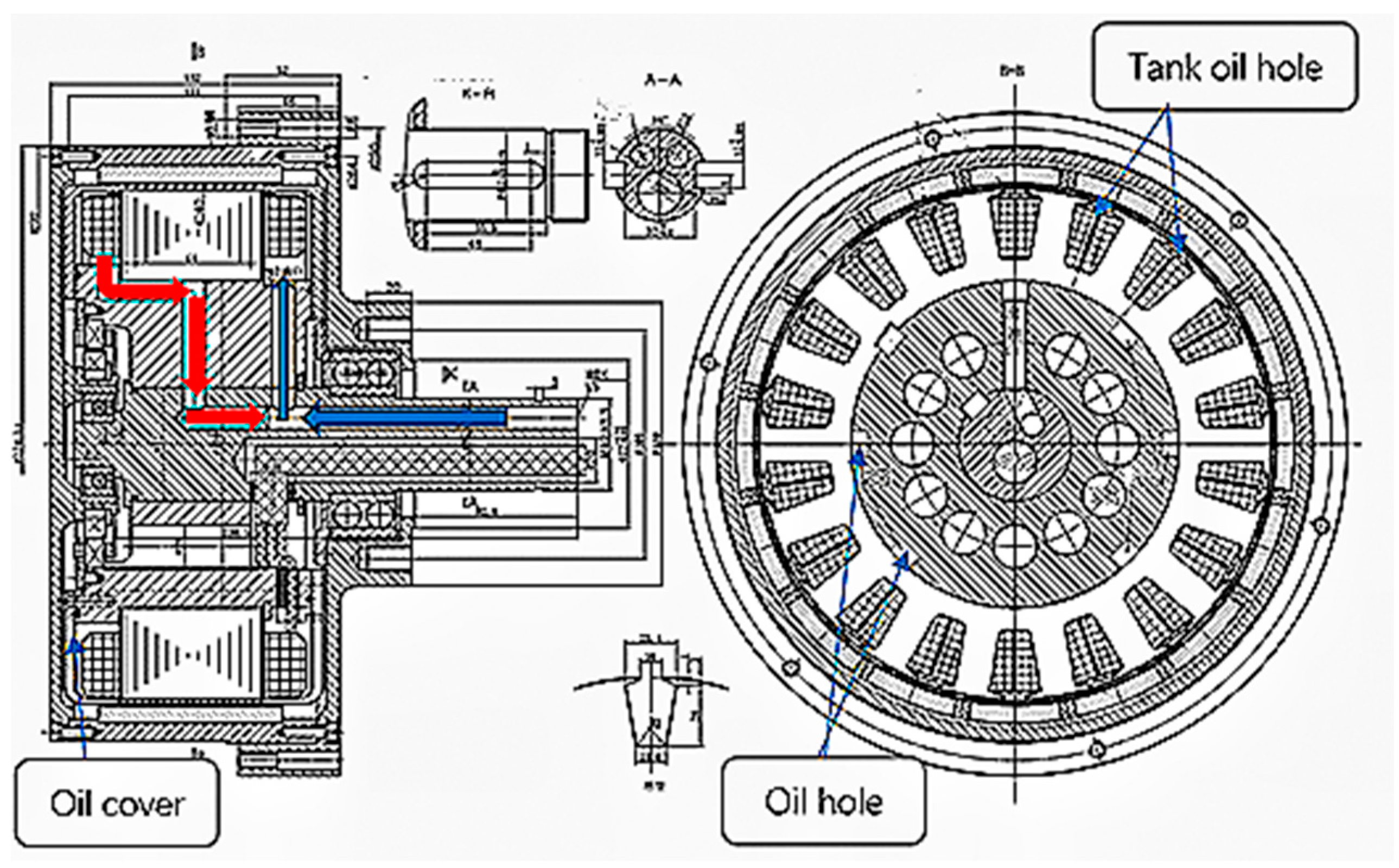
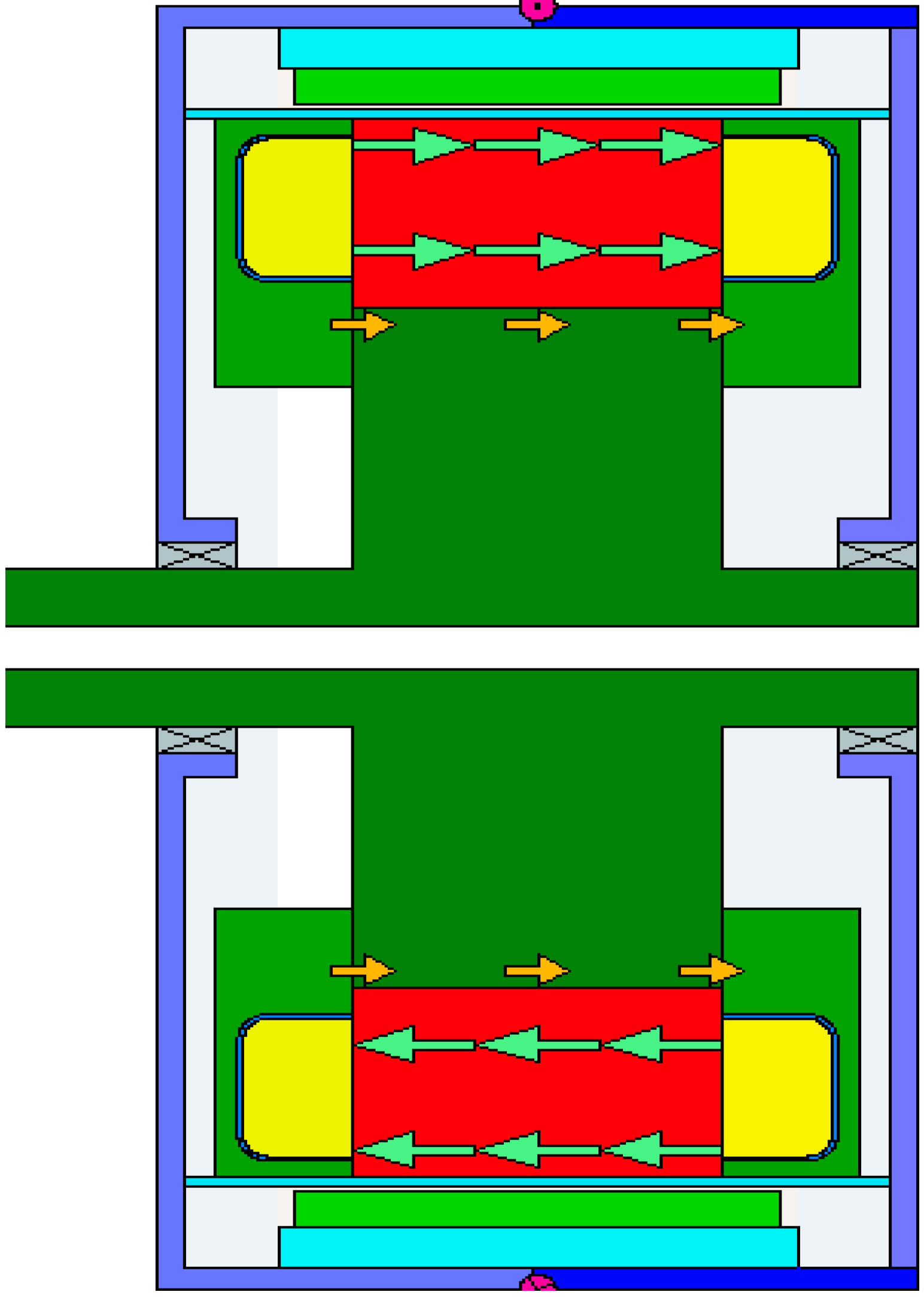
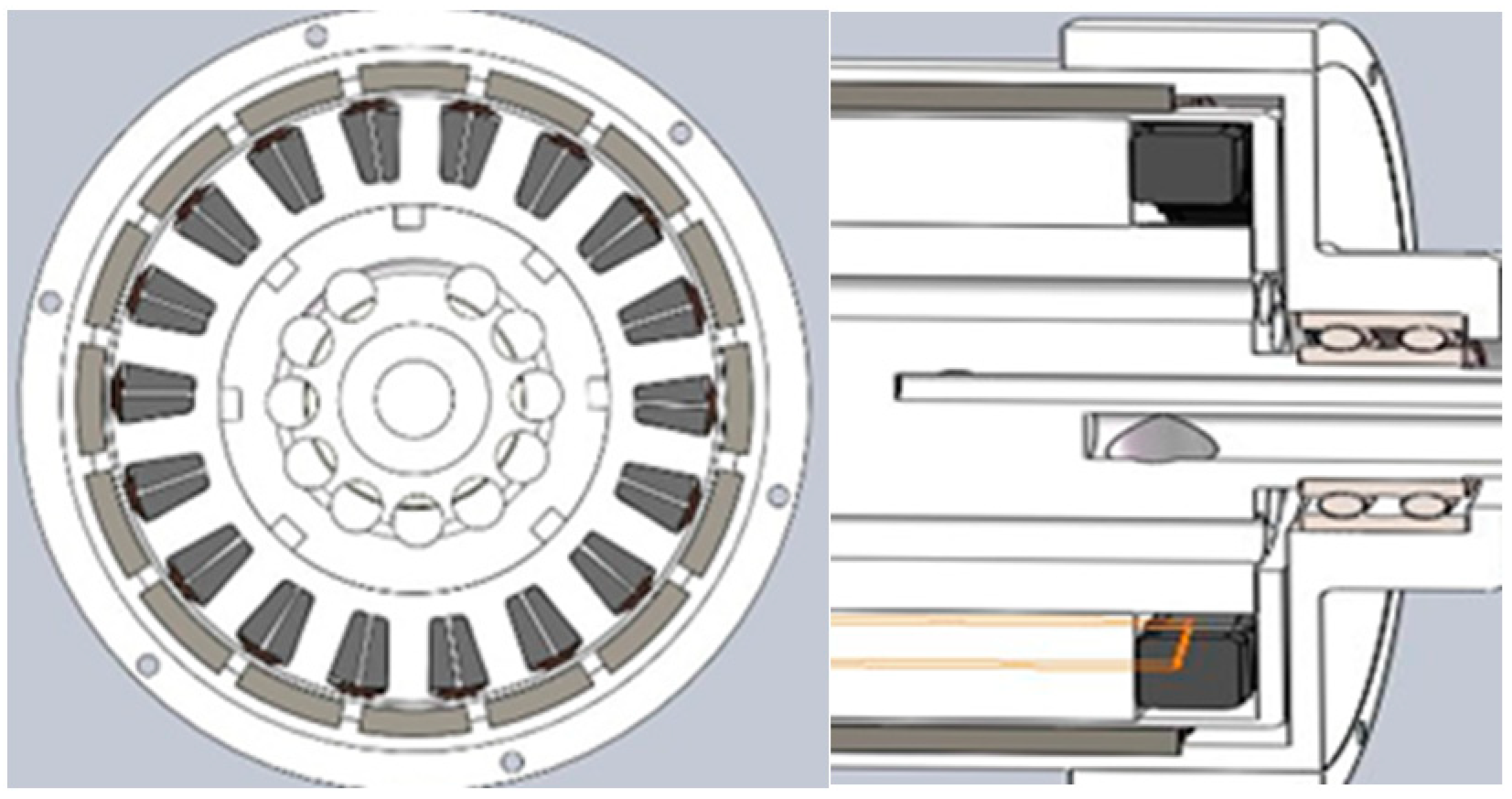
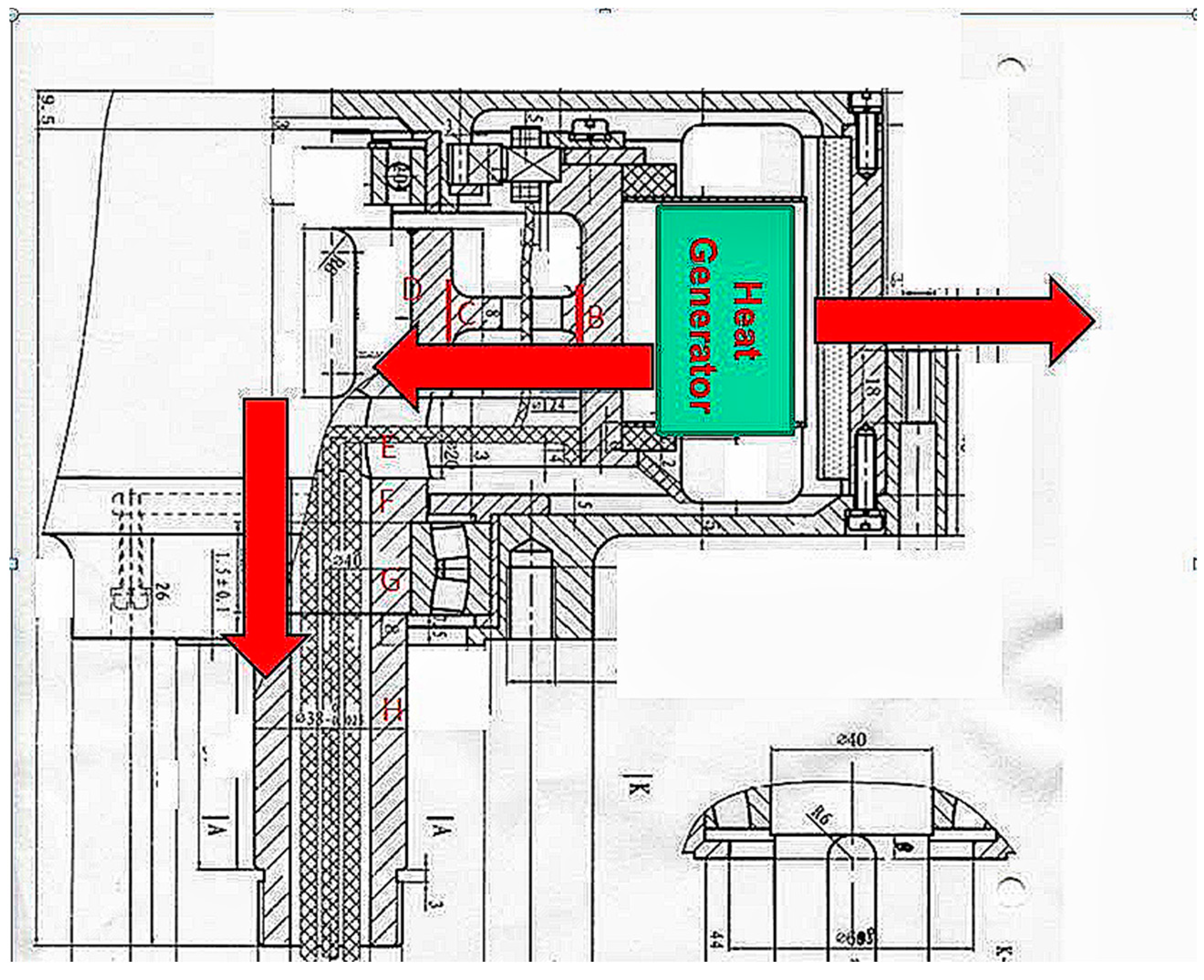





| Oil-Cooled Hub Motor Parameters | Parameters |
|---|---|
| Highest speed (r/min) | 1400 |
| Rated power (kw) | 10 |
| Peak power (30 s) | 20 |
| Rated torque (Nm) | 150 |
| Peak torque (30 s) | 335 |
| Motor quality (kg) | 35 |
| Motor Structure | Material | Thermal Conductivity (W/m·K) | Specific Heat Capacity (J/kg·°C) |
|---|---|---|---|
| stator core | DW-465 | 40 | 426 |
| conductor | copper | 386 | 383 |
| insulation in slots | insulation paint, slot insulation, air gap | 0.3 | 1340 |
| permanent magnet | NdFeB | 9 | 420 |
| air gap | air | 0.028 | 992 |
| cooling oil | lubricating oil | 0.147 | 1796 |
| Cooling Position | Convective Heat Transfer Coefficient (W/m2·K) |
|---|---|
| Oil in stator shaft and iron core | 23284.1 |
| Oil in slot wedge | 92401.1 |
| End cap oil | 185.1 |
| Air gap | 0.0262 |
| Motor Parts | Thermal Resistance (k/W) |
|---|---|
| slot insulation | 0.012 |
| air gap | 0.439314 |
| end winding | 0.52854 |
| stator tooth | 0.03217 |
| stator reactance | 0.0205 |
| stator B | 0.0054 |
| stator C | 0.176 |
| stator D | 0.176 |
| stator E + F | 0.2349 |
| stator G | 0.305 |
| stator H | 1.258 |
| permanent magnet | 0.0126 |
| rotor reactance | 0.002703 |
| right side shell | 0.000509 |
| left side shell | 0.0003685 |
| shell-convection resistance | 0.27087 |
| copper wire from stator | 16.375 |
| oil-convection resistance stator core | 0.37993 |
| oil-convection resistance groove wedge | 0.4399 |
| oil-convection resistance end cap | 0.2196 |
| core and oil shield contacts thermal resistance | 0.562 |
| Time (s) | Torque (Nm) | Motor Speed (r/min) | Initial Winding Temperature (°C) | Terminal Winding Temperature (°C) | Input DC Voltage (V) | Input DC Current (A) | System Efficiency |
|---|---|---|---|---|---|---|---|
| 30 | 335.9 | 189 | 56.3 | 118 | 355 | 46.3 | 40% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, F.; Zhang, C. Oil Cooling Method for Internal Heat Sources in the Outer Rotor Hub Motor of ElectricVehicle and Thermal Characteristics Research. Energies 2024, 17, 6312. https://doi.org/10.3390/en17246312
Guo F, Zhang C. Oil Cooling Method for Internal Heat Sources in the Outer Rotor Hub Motor of ElectricVehicle and Thermal Characteristics Research. Energies. 2024; 17(24):6312. https://doi.org/10.3390/en17246312
Chicago/Turabian StyleGuo, Fulai, and Chengning Zhang. 2024. "Oil Cooling Method for Internal Heat Sources in the Outer Rotor Hub Motor of ElectricVehicle and Thermal Characteristics Research" Energies 17, no. 24: 6312. https://doi.org/10.3390/en17246312
APA StyleGuo, F., & Zhang, C. (2024). Oil Cooling Method for Internal Heat Sources in the Outer Rotor Hub Motor of ElectricVehicle and Thermal Characteristics Research. Energies, 17(24), 6312. https://doi.org/10.3390/en17246312





