Abstract
Effective energy management techniques are essential for the full utilization of energy in the field of extended-range electric vehicle research, with the goals of lowering energy consumption and exhaust emissions, enhancing driving comfort, and extending battery life. To achieve optimal comprehensive usage costs, this article uses bargaining game theory to design an adaptive energy management strategy (EMSad-bg) that focuses on battery life. In the study, a power system model was first built based on AVL/Cruise software and MATLAB/Simulink software. The impact of discount factors on strategy results was analyzed through simulation experiments. The results showed that the discount factor for auxiliary power unit (APU) focused more on energy optimization, while the discount factor for battery focused more on optimizing the degradation of battery life. When the initial state of charge (SoC) is high, the specific value of the discount factor also has a significant impact on the battery SoC value at the end of the trip. To improve the strategy’s adaptability to various initial SoC values, a fuzzy controller was created that can adaptively modify the discount factor based on the battery SoC. The results of the simulation experiment demonstrate that the bargaining game strategy taking SoC into account has more pronounced advantages in terms of overall usage cost when compared to the strategy of the fixed discount factor. The creation of an EMSad-bg that takes battery life into account based on a bargaining game can serve as a helpful model for the creation of a clever EMS that lowers the total cost of operating a vehicle.
1. Introduction
Faced with global challenges such as resource scarcity, environmental degradation, and the intensified greenhouse effect, the environmental pollution caused by traditional fuel vehicles cannot be ignored, and promoting the transformation of the automotive industry towards green and low-carbon has become an inevitable trend [1,2]. Despite being an eco-friendly option, pure electric vehicles’ considerable drop in driving range in cold climates has turned into a serious drawback. Because of their benefits in reducing range anxiety, range-extended electric vehicles (R-EEV) have garnered a lot of attention in this context as a transitional solution for pure electric vehicles. R-EEV enhances the vehicle’s endurance by adding an auxiliary power unit (APU), which consists of a generator, engine, and controller [3]. R-EEV not only have a large battery capacity and a long pure electric range but also can flexibly switch driving modes according to the driving status, and the generator and engine are connected in series. Among them, energy management strategy (EMS), as a key research direction for optimizing the automotive economy, is crucial for the development of R-EEV [4]. Furthermore, a key objective of the control strategy is to reasonably control the battery SoC to maintain battery health and lower the overall operating cost of the R-EEV. To maximize economic efficiency, extend battery life, and lower vehicle emissions, an efficient EMS must be able to precisely distribute power from two energy sources. Therefore, the research on EMS not only has theoretical value but also has significant implications for promoting the practical application of R-EEV.
1.1. Literature Review
The energy management control methods for R-EEV can be mainly divided into two categories: one focuses on the start-stop control of the APU [5], while the other is to deal with the power allocation problem of dual energy sources [6]. Nowadays, the EMS can be roughly divided into two categories: rule-based and optimization-based. Deterministic rules and fuzzy rules are the two subtypes of rule-based energy management techniques. To meet energy efficiency management objectives, the determination rule incorporates a fixed-point strategy that keeps the engine running at a predetermined fixed operating point and decides when to start and stop the APU based on the battery SoC [7]. Another established rule is the power following strategy, derived from the management philosophy of traditional hybrid vehicles, which is aimed at stabilizing battery SoC, avoiding the impact of frequent charging and discharging and high current on battery life, and extending battery life by adjusting APU power to follow vehicle demand power [8]. Fuzzy rules, also known as fuzzy control strategies, utilize the principles of fuzzy logic for control [9]. Rule-based strategies, relying on long-term accumulated expert experience and good applicability and robustness, have been widely used in energy management of R-EEV. However, it is challenging to optimize its control effect because of the absence of accurate mathematical model support. Therefore, the research focus is gradually moving towards optimized EMS to investigate better control solutions [10]. The optimized EMS utilizes cutting-edge algorithms and theoretical frameworks, relying on precise mathematical models to finely optimize single or multiple objectives to achieve optimal control efficiency. According to different optimization execution methods, this type of strategy can be further divided into two categories: global optimization and real-time optimization [11]. The global optimization strategy, which includes techniques like Dynamic Programming (DP) [12], Pontryagin’s Minimum Principle (PMP) [13], Genetic Algorithm (GA) [14], and Particle Swarm Optimization (PSO) [15], focuses on integrating and using global information to solve the optimal solution. These techniques all seek to achieve the best system performance thorough analysis. The goal of the real-time optimization strategy is to find the best solution at every time point by optimizing the current state without the need for global information. This type of strategy mainly includes Model Predictive Control (MPC) [16] and Equivalent Fuel Consumption Minimization Strategy (ECMS) [17]. Although the optimization results might not reach global optimality, real-time optimization strategies are renowned for their quick computation speeds and good applicability. MPC is a typical real-time optimization method that predicts the behavior of the controlled object in advance and formulates control strategies based on these predicted results. Unlike pursuing global optimal control, MPC focuses on targeted optimization of predicted future scenarios, ensuring that the system can achieve good real-time control effects in constantly changing environments through a continuous rolling optimization process [18].
Energy consumption maintenance strategy, a representative method, determines engine state based on battery SoC. High battery capacity leads to pure electric mode priority; insufficient capacity triggers engine start for supplementation. Optimization-based EMS optimizes control rate to minimize vehicle energy consumption. It can achieve global optima but depends on known conditions. A variable equivalent factor strategy based on location was proposed for sub-optimal real-time control, yet its equivalent factor impacts control, making its determination difficult. With the development of machine learning, learning-based EMS has gained attention. It features interaction-based learning, strong adaptability, and deep reinforcement learning application. Notably, a method was proposed that used a deep deterministic policy gradient for engine power change rate, with a two-layer learning framework for online parameter update and energy-saving. The classification of electric vehicle EMS can be clearly divided into three categories: rule-based, optimization-based, and learning-based. Each type of strategy has its own characteristics and application scenarios, and the learning-based EMS is gradually becoming a research hotspot due to its powerful learning and adaptation ability. In future research, we can further explore how to combine the advantages of different strategies to achieve more efficient and intelligent electric vehicle EMS.
Game theory is a theoretical framework that explores how multiple agents make optimal decisions under different environmental and information constraints. After being widely used in economics, this theory swiftly spread to engineering [19]. The dynamic game theory optimization framework has been utilized to formulate the optimal charging problem [20], and the multi participant shared energy storage collaborative operation framework and energy interaction have been analyzed based on the dynamic game model equilibrium theory, resulting in a cooperative operation plan that balances the demand for shared energy storage regulation and economy [21]. Due to its efficiency and robustness, game theory has become an important tool in the field of energy management for hybrid electric vehicles. Researchers can more precisely simulate the energy allocation between the APU and battery by building a game model. This allows them to identify the best course of action for enhancing the system’s overall efficiency. To find the optimal EMS to improve the overall efficiency of the system, researchers constructed a bargaining game model to accurately simulate the interaction of multiple energy sources in the energy allocation process of hybrid electric vehicles. This approach brings the decision more in line with reality by fully accounting for information and environmental constraints in addition to the influence between agents. This provides a new perspective and method for solving the problem of benefit distribution in multi-agent systems and brings about innovative solutions for EMS. Zen uses game theory to simultaneously control cruise speed and energy management [22]. Ruan used bargaining games to optimize HEVs’ longitudinal driving and energy management [23]. The energy management problem is expressed as a differential game to improve computational efficiency and control performance, and a new neural network-based adaptive dynamic programming algorithm is proposed to approximate the Nash equilibrium and pareto solution of non-cooperative differential games in real-time applications [24]. In addition, the core concept and technical framework of the energy management method proposed in this paper are also applicable to the railway transportation system, where the optimization of energy efficiency is also an important goal [25]. By introducing an energy management system similar to that of EV, railway vehicles can more accurately control the distribution and use of energy, thereby reducing energy consumption and improving operational efficiency. Especially in scenarios such as high-speed railways and intercity trains that require extended journeys and high-speed operation, the optimization of the energy management system can significantly improve the overall energy efficiency of the train [26].
In summary, EMS has a direct impact on the range and performance of R-EEV. By scientifically allocating the power of batteries and APU, the energy efficiency of vehicles can be significantly improved, battery life can be extended, and sufficient power can be provided at critical moments. Therefore, it is especially crucial to carry out in-depth research and continuously optimize EMS to support the practical application and popularization of R-EEV. Current optimization strategies still have various problems, such as failing to consider battery life and the jumble of calculations. In addition, there is currently limited research on the application of bargaining games in EMS research. Therefore, this article investigates operation mode control and energy management power allocation during the motion process of R-EEV in an effort to further lower the overall cost of these vehicles.
1.2. Motivation and Innovation
This article takes R-EEV as the research object, aiming to construct and optimize EMS. The research uses bargaining game theory to design an adaptive energy management strategy that focuses on battery life. The research includes the construction of power and control models for R-EEV, the design of EMS based on bargaining games, and verification of adaptive EMS considering battery SoC. The innovative highlights of the research are as follows:
(1) A novel energy management model based on the bargaining games theory was developed, which effectively reduces the comprehensive energy cost and battery life degradation cost, providing a new perspective and method for the EMS of R-EEV.
(2) An online adaptive control module algorithm has been implemented, enabling the EMS to be dynamically adjusted according to the actual situation, after the impact of discount factors on the results of bargaining games was deeply explored and analyzed.
(3) Fuzzy control algorithms are combined in this strategy to accomplish an adaptive EMS that considers battery SoC. By solving the optimal combination of each SoC discount factor group, the energy of both the APU and the battery was reasonably allocated while ensuring good tracking of the theoretical SoC, thus achieving the optimization of the overall vehicle operating cost.
2. Design of EMS Based on Bargaining Game
This section comprehensively considers the energy consumption and battery life during operation, introduces bargaining game theory, and constructs an EMS based on a bargaining model on this basis. To accomplish more cost-effective and efficient energy management, this strategy seeks to maximize the vehicle’s overall usage cost.
2.1. Configuration of the Studied REEV Model
R-EEV have evolved from pure electric vehicles by adding an APU to their structure. The engine of this APU does not directly drive the vehicle but rather acts as a generator to charge the battery or indirectly provide power [27]. Figure 1 illustrates in detail the specific configuration of an R-EEV. This article selects an R-EEV as a research case. The vehicle’s APU combines a 1.5 L displacement engine with a rated power of 40 kW electric motor. The peak power of the driving motor is 120 kW, and the battery capacity is about 50 Ah. It can support pure electric driving of the vehicle for about 80 km. The main technical parameters are shown in Table 1.
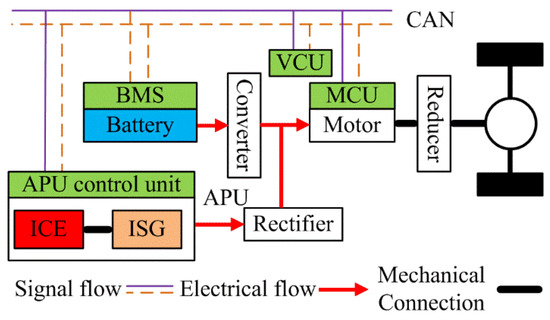
Figure 1.
Configuration of the studied R-EEV.

Table 1.
Fundamental parameters of the research object REEV model.
The fundamental parameters of the target vehicle researched are shown in Table 1.
2.2. EMS Based on Bargaining Game
As a 11 that takes into account the dynamic game between the two power sources, the bargaining model is especially well-suited for energy management issues. Based on the principle of this model, the energy management game model for R-EEV is constructed as follows: First, the APU and battery are regarded as two independent game participants, which need to allocate the required power of the entire vehicle at each moment reasonably. This improves the overall cost-effectiveness while meeting the power requirements of the entire vehicle. The vehicle total power in APU drive mode is equal to the sum of the power from the APU and the power battery. Therefore, the vehicle required power (Preq) can be seen as a common and necessary task faced by these two participants. The APU and battery can decide how much power is allocated to the task. Considering that the main objective of overall optimization is comprehensive energy cost, the APU is set as the first to move in this bargaining game. The energy management model based on the bargaining game is shown in Figure 2. Battery SoC is a key decision variable in formulating the EMS, directly affecting the system revenue. When the SoC is high, it tends to discharge to obtain revenue, and when the SoC is low, it needs to be charged for later use. Therefore, in the bargaining game, the EMS and revenue distribution need to be dynamically adjusted according to the dynamic change of the battery SoC.
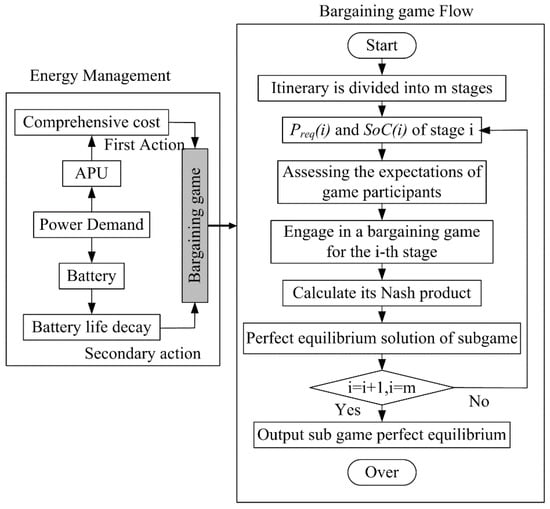
Figure 2.
Realization of energy management based on a bargaining game for R-EEV.
A key idea in game theory is the bargaining game, which describes how both players in a game negotiate a mutually agreeable distribution of interests to arrive at a state of equilibrium that is satisfactory to all. In this process, all possible allocation schemes can form a set. Specifically, in the i-th stage, participants in the game will propose an allocation scheme, which can be represented as an element in the set. This representation method enables a clear understanding and analysis of the strategic choices and benefit distribution of each party in different stages of bargaining games.
where, Mi represents the solution proposed by the i-th stage game participant; Ii represents the benefit of one participant; and 1 − Ii represents the benefit of the other participant.
During the game, time is considered to be a factor closely related to the return. As the game progresses, the gains of each participant will gradually decrease; in other words, the longer the game takes, the lower the final benefits obtained by the participants. A discount factor was introduced to account for this time effect and the participants’ patience level. Specifically, kAPU and kBatt represent the discount factors of the APU system and battery system, respectively, reflecting their respective levels of patience during the game. When the game reaches the T-stage and ends, the final profits of the APU system and the battery system can be calculated by considering their respective profits and corresponding discount factors in each stage of the game. These final return expressions will accurately capture the effects of participant patience, time passing, and return distribution at every phase of the game process:
where, MAPU and MBatt are the discount benefits of APU and battery, respectively, IAPU is the share obtained by APU system, and kAPU and kBatt are the discount factors of APU system and battery system, respectively.
The passage of time during a game stalemate can result in additional loss of profits for game participants, and there is no deadlock point in bargaining games. There will still be a break point in the game when the negotiation breaks down, and the benefits of the break point can be determined as follows:
where, Mbreak represents the overall negotiation breakdown benefit, and the negotiation breakdown benefits for the APU system and battery system are M*APU and M*Batt, respectively.
For general bargaining games, the Nash bargaining solution can be represented by the maximum Nash product of the allocation scheme in the Nash bargaining solution:
where, N0 is a general Nash equilibrium solution and P*T is the allocation share under the Nash equilibrium solution.
In the case where both parties in the game cannot achieve a better equilibrium by making changes on their own, the perfect equilibrium of the subgame in this game can be expressed as follows:
where, N* represents the perfect equilibrium of the sub game of the indefinite dynamic bargaining game in a state of complete information; kBatt ∈ [0, 1], kAPU ∈ [0, 1], if kAPU = kBatt.
In the game process, when the discount factors of both parties are the same and both are less than 1, the party that first proposes the allocation plan will occupy an advantageous position. This advantage is reflected in the fact that one party will ultimately receive a larger share than the other, which is called the first mover advantage. The result of the game tends to favor the posterior player, giving them a more advantageous share, if the posterior player’s discount factor is 1, which indicates infinite patience. This situation is called posterior advantage.
The game process is as follows: First, the battery decides whether to accept the power allocation scheme that the APU system proposes. If the battery rejects the plan, the game enters the next stage, where the battery proposes a new allocation plan and the APU decides whether to accept it. During this process, the APU and battery will take turns proposing solutions until one party’s proposal is accepted by the other party. It is worth noting that when the sum of the APU power and the battery power does not meet the required power of the entire vehicle, both parties have no profit. Therefore, the break point profit of the bargaining game between them is set to 0. Additionally, the battery SoC control value is set to 0.3 to prevent additional capacity degradation caused by excessive discharge. When the battery SoC is higher than 0.3, the battery does not need to be charged. At this time, the APU, as the first participant in the game to propose an allocation plan, aims to minimize energy consumption as much as possible. When the battery SoC approaches 0.3, the main consideration is fuel consumption, that is, pursuing a smaller fuel consumption rate. When the APU is not working, fuel consumption is zero. Based on these game expectations, the APU may propose the following solutions:
where, M represents the allocation scheme proposed by the APU; PAPU is the power borne by the range extender in this scheme; and PBatt is the power borne by the battery in this scheme.
The discount benefits for both parties in the game can be expressed by the following equation:
The Nash equilibrium solution of this game can be represented by the Nash product:
where, N0 is the Nash product of the game and PAPU and PBatt represent the power of the range extender and battery in the Nash equilibrium solution of this game, respectively.
According to the bargaining model, the sub game has a perfect equilibrium F′:
When the battery SoC is below 0.3, the APU faces a dual task: on the one hand, it needs to increase the battery SoC to at least 0.3 to protect the battery health. On the other hand, the APU also hopes to minimize fuel consumption as much as possible. To achieve these goals, the APU will choose to operate at its optimal operating power, which means it will take on as much power demand as possible. Correspondingly, the battery needs to bear the remaining power demand, which is the difference between the vehicle’s required power and the optimal operating power of the APU. However, to reduce capacity degradation, power batteries tend to lower their own burden by reducing the current. As a result, the battery may choose to reject the APU’s proposed power allocation scheme. This scheme can be formalized as follows:
Because the expectations for the battery have not changed, his proposed solution is the same as the one proposed by the battery in the previous game. The discount benefits for both parties are shown in the following formula:
The Nash equilibrium solution of this game can be represented by the Nash product:
According to the bargaining model, the sub game achieved in this bargaining game is perfectly balanced as follows:
2.3. Analysis of the Impact of Discount Factors on Game Results Based on Simulation Experiments
According to the bargaining model, different discount factors will influence the outcome of the game. To better understand the influence of discount factors on different control effects of each participant in the bargaining game, a simulation analysis was conducted on a R-EEV, and a WLTP trip was selected as the overall simulation condition. The vehicle dynamic model and the proposed EMS are established in AVL/Cruise 2017 software and MATLAB/Simulink 2022 software, respectively, and the co-simulation model is seen in Figure 3. The simulation is carried out using a high-performance computing server, which is equipped with a multi-core processor and large-capacity memory to ensure efficient processing of complex simulation models and algorithms. The Stateflow module in Simulink is used to simulate the development of complex control logic and algorithms.
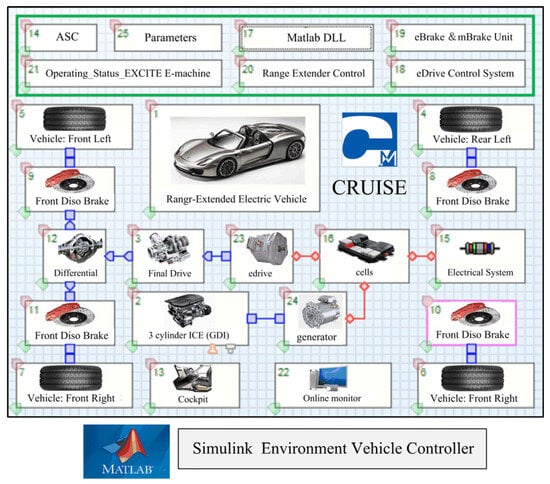
Figure 3.
Simulation platform of the R-EEV for the MOO problem.
To reasonably evaluate the energy consumption of the R-EEV, the energy consumption is converted into electricity cost, and the comprehensive energy cost is calculated to evaluate the overall energy economy [28]. First, define the comprehensive cost function Fc, which includes three sub-costs: fuel usage cost, electricity usage cost, and battery usage cost caused by battery capacity degradation. Battery manufacturing technology, daily charging and discharging frequency, and usage environment all play a role in the relatively complex battery capacity decay [29]. The battery life itself also includes calendar life and cycle life. The research on the battery body can be said to be an independent research direction. A fitted empirical formula is used to evaluate and utilize information on battery capacity degradation in terms of battery life, given that the research of EMS for R-EEV models is the main focus of this article. The cost of power loss is the total cost of replacing the battery pack after the battery capacity decays by more than 0.3, which is evenly distributed among the expenses incurred during this driving process [30]. The comprehensive cost function Fc, fuel usage cost function, and electricity usage cost function are calculated as follows:
where, cprioil, cpriele, and cpribatt_sub are the fuel price (CNY/L), electricity price (CNY/kW·h), and battery degradation price (CNY/kW·h), respectively; Qfuel, Qele, and Qbatt_loss represent the fuel consumption (L), electricity consumption (kW·h), and battery capacity degradation (kW·h) during this cycle of driving, respectively; m(t) represents the fuel consumption per unit time (g/s); tCD_Blend represents the operating time of the system in CD Blend mode; tCD_Blend represents the operating time of the system in CS Blend mode; and tCD_EV represents the operating time of the system in CD-EV mode. The working hours are as follows:
Set the initial battery SoCs to 0.3 and 0.4, respectively, and conduct simulation experiments by changing the discount factor between APU and battery. Analyze the impact of different discount factors on comprehensive energy costs, battery life degradation, and comprehensive usage costs based on the results data. After simulation experiments, the comprehensive cost function Fc was obtained as shown in Figure 4 and Figure 5.
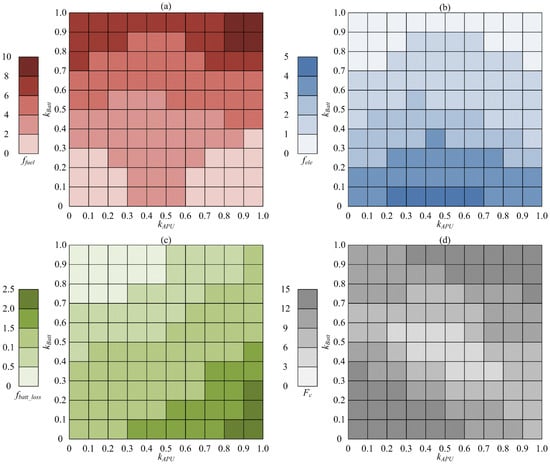
Figure 4.
The results of different discount factors on performance under the first mover advantage when the initial SoC is 0.3: (a) ffuel; (b) fele; (c) fbatt_loss; (d) Fc.
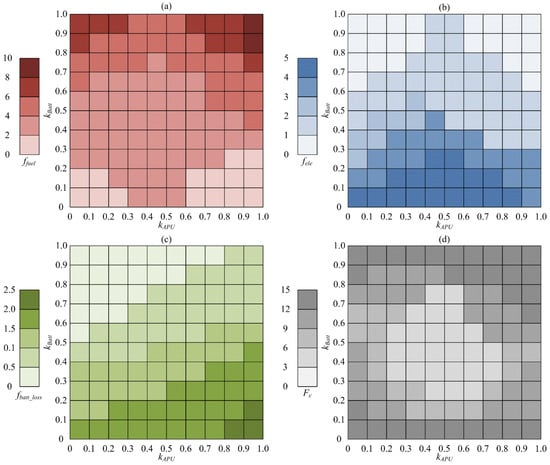
Figure 5.
The results of different discount factors on performance under the first mover advantage when the initial SoC is 0.4: (a) ffuel; (b) fele; (c) fbatt_loss; (d) Fc.
The control results of both parties in the game are deeply influenced by the specific values of their respective discount factors. Specifically, when the discount factor of APU remains constant, an increase in the battery discount factor will result in the power of the APU approaching the required power. On the contrary, if the battery discount factor is fixed, a decrease in the APU discount factor will also make the APU power closer to the required power. While the game’s final result tends to meet the APU’s expectations, the graphical information indicates that the strategy has a similar impact on the control results of APU power and overall energy costs in the case of first mover advantage. Further observation revealed that when the battery SoC is above 0.3, the APU power approaches zero. When the battery SoC is below 0.3, the APU power approaches its optimal operating power. The smaller the discount factor, the more significant the bias of the game results, and the lower the overall energy cost. In extreme cases of preemptive advantage, increasing the discount factor can reduce the fluctuation of battery SoC, and the difference in comprehensive energy costs also reaches its maximum; this is especially true when the discount factor is 1, as the comprehensive energy cost is the highest. If both discount factors are 0, the game result will be based on APU’s expectations. However, due to the constant fluctuation of battery SoC around 0.3, the expectation of the APU will change frequently. This may lead to certain deviations in the power control of the APU, as frequent start-stop of APU will have an impact on the power control of the APU. On the other hand, reducing the discount factor will cause the game results to deviate more and more from the expectations of the battery, increase the fluctuation of battery current, accelerate the decline of battery life, and increase the overall cost of vehicle use. There is a significant difference in the decline of battery life under different discount factors, which has a significant impact on the overall cost of use. In summary, the overall comprehensive usage cost will increase as the discount factor decreases because of differences in battery life decay, under similar comprehensive energy costs.
Posterior advantage refers to a phenomenon of advantage in a game where the discount factor of the latecomer is 1, while the discount factor of the first mover is not 1. This is especially true when the discount factor of the battery is set to 1, as the rear mover; regardless of how the discount factor of the APU changes, the result of the game will tilt towards the direction of the power battery. At this point, the discount factor of the APU has no effect on the bargaining strategy, and the formulation of the strategy depends entirely on the discount factor of the battery. The APU’s output power always approaches the vehicle’s required power in this situation because the bargaining strategy control results under different APU discount factors are the same and all close to the power following strategy. This leads to the APU operating more in non-efficient areas, which increases fuel consumption, and the battery power not being fully utilized at the end of the trip, which results in additional energy conversion consumption. When the bargaining game is neither a first mover advantage nor a second mover advantage, if the discount factor of the battery is large and the discount factor of the APU is small, the power performance of the APU will be close to that of the second mover advantage. The battery SoC may not be able to stabilize at 0.3 at the end of the trip if it is high at the start of the trip. This will maximize the overall usage cost and cause secondary energy conversion losses. Although the optimized value for battery life degradation has decreased in this situation, it cannot offset the increase in energy costs. On the contrary, when the discount factor of the battery is small and the discount factor of the APU is large, the power performance of the APU will be close to the first mover advantage. Especially when the initial SoC is high at 0.4 and the battery discount factor is large while the APU discount factor is small, the battery SoC may not be able to be controlled at 0.3 at the end of the trip, which will result in additional fuel consumption. In addition, an APU with a larger discount factor will have a lower overall energy cost even though the battery life will degrade more when the battery discount factor stays constant. On the contrary, when the APU discount factor remains constant, the larger the battery discount factor, the smaller the battery life decay, but the overall usage cost is higher. It is worth noting that the impact of both on battery life decay is similar. The greater the difference between the battery discount factor and the APU discount factor, the smaller the fluctuation of battery current. But, if the battery discount factor remains constant, an increase in the APU discount factor will lead to a faster decline in battery life, although this may reduce overall energy costs.
In conclusion, in the application of bargaining strategies, the discount factor of the APU mainly tends to achieve an optimized energy configuration, while the discount factor of the battery focuses more on extending the battery’s service life and reducing its lifespan decay. Neither the first mover advantage nor the second mover advantage is an optimal choice for discount factors in bargaining strategies when the vehicle’s initial SoC gets close to 0.3. In other cases, the larger the discount factor of the APU, the lower the overall energy cost, but this effect is relatively limited, so the impact of the APU discount factor on the overall comprehensive usage cost is not significant. Conversely, the larger the discount factor of the battery, the less the decline in battery life, which, to some extent, affects the overall cost of use by reducing the loss of battery life. Furthermore, when the initial SoC is high, the specific value of the discount factor will also have an impact on the battery SoC value at the end of the trip. Especially when the discount factor of the battery is high and significantly different from that of the APU, the battery SoC value at the end of the trip may be too high, which can lead to additional energy conversion consumption and affect the degradation of battery life throughout the trip. Therefore, the control effect of the bargaining strategy can be further optimized to achieve optimal energy allocation, extending battery life and reducing overall usage costs by reasonably adjusting the value of the discount factor.
3. EMS Based on Bargaining Game Considering Battery Life
The bargaining strategy’s control effect is affected by the discount factor. When using a fixed discount factor, this strategy is difficult to effectively deal with different initial battery SoC values and may lead to excessively high battery SoC at the end of the trip, resulting in additional energy conversion losses [28]. To improve the control performance of the strategy, the bargaining strategy has been improved by optimizing the performance indicator range to adjust the parameter k in real time and taking corresponding control measures to achieve optimal performance. In this section, a fuzzy controller is introduced as an adaptive adjustment tool. Maintaining a relatively stable battery SoC trajectory is crucial for extending battery life to more effectively utilize the energy between the battery and the engine.
The hybrid energy storage system provides an effective solution for extending battery life by integrating the functions of an APU and batteries. Figure 6 illustrates how a fuzzy logic controller is employed to determine the threshold adjustment factor ∆k in the optimal control process, which updates the kth-m value in real time according to the given equation.
where, ∆k is the threshold adjustment factor value of the kAPU and kBatt, and kAPU_0 and kBatt_0 are the initial threshold value after the optimization decision.
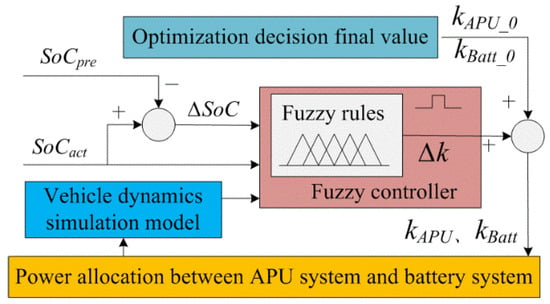
Figure 6.
Diagram of parameter adjustment based on fuzzy controller.
A fuzzy logic controller is a system that maps logical rules from input to output, aiming to achieve real-time parameter adjustment [31]. When the APU discount factor remains constant, the smaller the battery discount factor, the greater the fluctuation of battery current. Conversely, when the battery discount factor remains small and constant, the smaller the APU discount factor, the smaller the battery current fluctuation. However, when the battery discount factor is large and significantly different from the APU discount factor, although the battery current fluctuation is small, the battery SoC will be high after the end of the trip, and the bargaining strategy cannot meet the demand for controlling the battery SoC. When the battery discount factor is the same, the larger the APU discount factor, the more the battery life will decay. Conversely, when the APU discount factor is the same, the larger the battery discount factor, the smaller the decline in battery life. The impact of both on battery life decay is similar, but this rule does not apply when the battery discount factor is large and the APU discount factor is small. In addition, when the battery discount factor is the same, the larger the APU discount factor, the lower the overall usage cost. Conversely, when the APU discount factor is the same, the larger the battery discount factor, the higher the overall usage cost. It is particularly important to note that when the battery discount factor is large and the APU discount factor is small, due to the high remaining battery SoC after the trip, additional energy conversion consumption will occur, resulting in the highest overall usage cost at this time. In this instance, even though battery life degradation optimization has decreased, the increase in energy costs cannot be offset by this decrease. The following is a detailed explanation of the fuzzy controller:
(1) Fuzzy processing: The two inputs of the fuzzy logic controller are the difference ΔSoC between the actual SoC (SoCact) of the battery and the predefined SoC, as well as the battery SoC. The range of ΔSoC values is (−0.05, 0.05), while the range of SoC values is (0.0, 1.0). The output of the controller is the adjustment factor Δ kth-m, which ranges from (−0.5, 0.5). The membership function is divided into seven levels, including negative big (NB), negative medium (NM), negative small (NS), zero (ZO), positive small (PS), positive medium (PM), and positive big (PB).
(2) Rule library construction: Table 2 provides a detailed list of the rule library for the fuzzy logic controller. These rules follow the typical logical pattern of M + N → W (if M and N, then W), where M represents the fuzzy set of ΔSoC, N represents the fuzzy set of SoC, and W is the fuzzy set of Δk. In this study, the determination of condition W is based on the professional knowledge and practical experience of experts and research teams in the fields of transportation systems, energy management, and control engineering for design and determination.

Table 2.
The fuzzy control rules based of parameters adjustment.
(3) Fuzzy reasoning and deblurring process: The Mamdani method is used for fuzzy logic computation. To improve calculation speed while ensuring control accuracy, the fuzzy controller adopts the weighted average method in the deblurring stage, which has been widely used in the field of industrial control.
The membership functions and output surface of the fuzzy controller are shown in Figure 7.
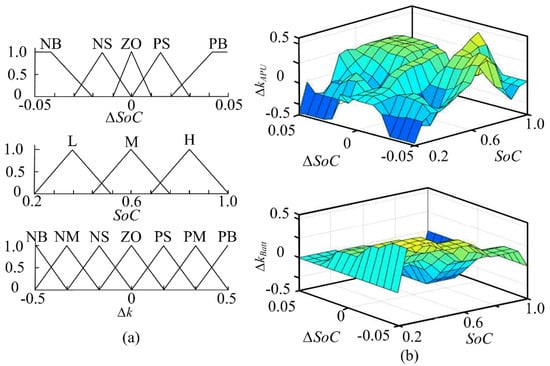
Figure 7.
Membership functions and output surface of the fuzzy controller: (a) membership functions; (b) output surface.
When exploring the comprehensive cost of use, it is necessary to consider the different effects of the APU discount factor and the battery discount factor. The former focuses on energy optimization, while the latter focuses on optimizing battery life decay. The impact of these two discount factors on the overall usage cost varies with the battery SoC. When the battery SoC value differs significantly from the control target, the discount factor has a significant impact on the overall energy cost, which in turn affects the overall usage cost. In order to control the SoC at the end of the trip and achieve the lowest comprehensive usage cost, a larger APU discount factor (kAPU_0 = 0.9) and a smaller battery discount factor (kBatt_0 = 0.2) will be selected to increase the proportion of battery usage and ensure that the battery SoC can be maintained at a level of about 0.3 at the end of the trip. At this stage, the specific numerical changes of the discount factor group are relatively small. However, as the battery SoC gradually decreases to near 0.3, the impact of discount factors on overall energy costs weakens and costs tend to stabilize. At this point, the impact of the APU discount factor on the overall energy cost decreases, while the impact of battery life decay on the overall usage cost gradually increases. As the initial SoC drops, the battery discount factor will rise to lessen battery life degradation. At the same time, the discount factor of the APU has been reduced from about 0.9 to about 0.3. By increasing the proportion of APU usage during driving and adopting a bargaining strategy to optimize battery life decay, lower comprehensive usage costs can be obtained.
4. Verification and Discussion
In this section, to verify the optimal performance of the proposed EMS based on the bargaining game strategy and the proposed adaptive energy management strategy (EMSad-bg) considering battery SoC in reducing the synthesis cost, the EMS described in this paper was validated on simulation and experimental platforms.
4.1. Verification of Bargaining Adaptive Strategy Considering SoC
To verify the superiority of the optimized bargaining strategy, two scenarios were set with an initial SoC of 0.3 and 0.4 for the battery, respectively. The battery SoC of the entire journey and the comprehensive cost are shown in Figure 8. As a comparison strategy with fixed parameters, this process is called energy management strategy-based game (EMSbg).
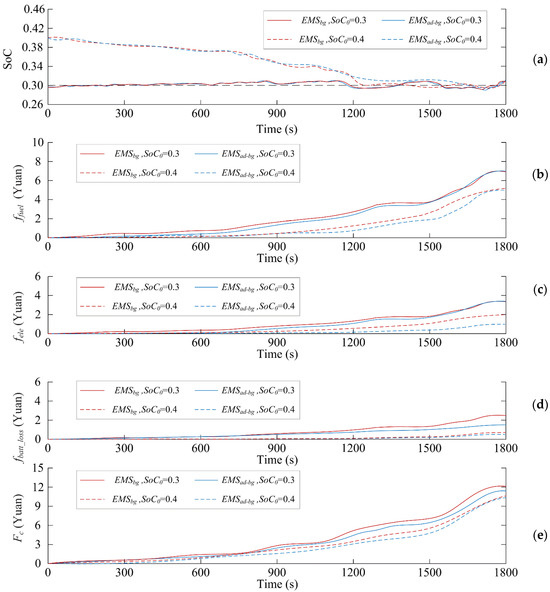
Figure 8.
The battery SoC of the entire journey and the comprehensive cost: (a) SoC; (b) ffuel; (c) fele; (d) fbatt_loss; (e) Fc.
In this case, the battery SoC remains at around 0.3 throughout the entire journey, with a fluctuation amplitude of less than 0.1. Thus, the control effects are comparable whether a fixed discount factor bargaining strategy or a SoC bargaining strategy is used. At the end of the trip, the battery SoC remained at 0.31, with a comprehensive energy cost of 7.23 CNY and a comprehensive usage cost of 12.11 CNY. The situation is different when the initial SoC is 0.4. To control the battery SoC, the bargaining strategy using a fixed discount factor can only choose a larger APU discount factor and a smaller battery discount factor. The bargaining strategy for considering SoC dynamically adjusts the discount factor group based on changes in battery SoC, slowing down the rate of SoC decline in the latter half of the journey. In the end, the battery SoC values of both strategies reached 0.32 at the end of the trip, meeting the control requirements. In the bargaining strategy with fixed discount factors, the main focus is on energy optimization. When the battery SoC decreases in the latter half of the trip, this strategy has a slight advantage in overall energy costs compared to bargaining strategies that consider SoC. However, when electricity consumption is the same, the overall energy cost difference between different discount factor groups is not significant because bargaining games have the same expectations. In the first half of the trip, the specific values of the discount factor groups for the two strategies are similar, so the comprehensive cost curve is also basically equal. However, in the latter half of the journey, as the battery SoC drops to around 0.3, the overall energy cost tends to stabilize. At this point, the overall cost of use is mainly affected by the decline in battery life. Considering the bargaining strategy of SoC, the focus of control has shifted from energy optimization to battery life optimization by adjusting the discount factor group. Therefore, at the end of the trip, this strategy achieved lower overall usage costs.
4.2. Comparison of Simulation Results for Different Control Strategies
To further evaluate the proposed strategy, a selection of the fixed-point strategy (EMS1p), the three-point strategy (EMS3p), and power-following strategy (EMSpf) has been made as references. By simulating different operating conditions and initial SoC values, the advantages of the bargaining strategy considering SoC in energy cost savings, battery life control, and control reliability under various driving conditions and SoC levels were verified. The results are shown in Figure 9.
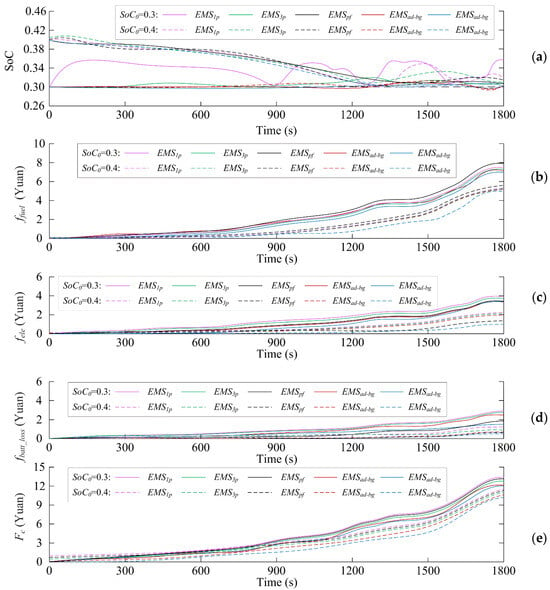
Figure 9.
The battery SoC of the entire journey and the comprehensive cost: (a) SoC; (b) ffuel; (c) fele; (d) fbatt_loss; (e) Fc.
Specifically, when the battery SoC is low, the bargaining strategy considering SoC tends to optimize battery life, resulting in relatively small SoC fluctuations. In contrast, EMS1p mainly focuses on energy optimization, significantly reducing fuel consumption by running the APU at several high-efficiency points, and SoC fluctuations are also relatively small. However, to reduce energy consumption during high-demand power periods, EMS3p will keep the APU running at slightly higher efficiency points than demand, resulting in an increase in SoC and increased SoC fluctuations. The fixed-point strategy control logic is simple, and the state of the APU is determined based on SoC, but its SoC fluctuates the most. EMSpf is implemented through multiple following points higher than the required power, resulting in a slow increase in SoC. At the end of the trip, only considering the bargaining strategy, EMSad-bg can meet the SoC control requirements. In terms of energy costs, EMSad-bg achieved the lowest comprehensive energy cost (9.73 CNY), followed by the EMSbg (10.21 CNY), as it optimizes both energy consumption and battery life decay. Due to their inability to effectively control SoC, the EMS3p and EMSpf have high comprehensive energy costs (11.89 CNY and 12.06 CNY, respectively). It is worth noting that the comprehensive energy cost growth considering SoC bargaining strategy is relatively flat, being close to the global optimal result. In terms of battery life, EMSad-bg has the lowest battery current fluctuation and the lowest battery life decay value. EMSpf does not take into account battery life, resulting in slightly larger fluctuations in battery current and a higher lifetime decay. When considering the bargaining strategy, the battery current fluctuation of the EMSad-bg is smaller than that of the EMSbg.
The bargaining strategy considering battery SoC EMSad-bg achieved the lowest comprehensive usage cost, followed by EMSbg. This is because of the significant advantage of the SoC bargaining strategy in battery life, and because it has a lower comprehensive usage cost. In contrast, both EMS1p and EMSpf have poor control effects and higher overall usage costs due to additional energy conversion consumption. Therefore, considering the bargaining strategy of SoC, it reduces the comprehensive usage cost, demonstrating a better control effect.
4.3. Experimental Test Implementation and Its Results
The experimental results reveal that different EMS have a significant impact on performance, which requires further validation. The verification process was carried out on the AVL test bench, and the specific structure of the experimental platform is shown in Figure 10. High-precision sensors and measuring equipment are installed on the bench to monitor and record the vehicle’s operating status and energy consumption data in real time. A high-performance embedded controller is used to execute the energy management strategy. Corresponding actuator mechanisms (such as motor drivers, battery management systems, etc.) are equipped to achieve precise control of the vehicle’s energy distribution. An embedded operating system is used to manage the scheduling and execution of control tasks. The standard CAN bus communication protocol is adopted between the controller, sensors, and actuators to ensure reliable data transmission and synchronization. Specialized data recording software is developed to record various data during the experiment in real time, including vehicle status, energy consumption, and the execution of control strategies.
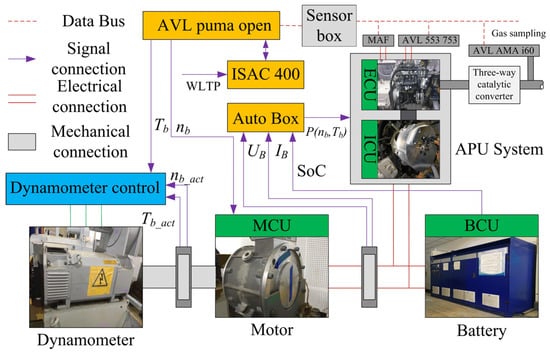
Figure 10.
Structure of the experimental platform.
The experimental process is summarized as follows: First, the vehicle parameters and preset WLTP driving cycle conditions are input into the road load simulation software. Next, the AVL system simulates actual road loads by closed-loop control of the speed and torque of the motor and electric dynamometer. Meanwhile, considering the DC bus voltage and current, the real-time electric power is calculated. Subsequently, the control system collects the battery SoC and executes EMS based on it, outputting the target speed and torque of the engine and generator. Finally, the APU coordinated control strategy determined the power output of the APU system. To verify the effectiveness of power trajectory tracking, the calculated APU power was set as the target power, and experiments were conducted on the five strategies proposed in Section 4.3. The test results are presented by comparing the fuel economy and final battery SoC of each control strategy under two repeated WLTP cycles.
After calculation, the data for the five strategies are presented in Table 3. The following conclusion can be drawn from the analysis of this table: when SoC0 = 0.3, the performance of single point strategy and power following strategy in SoC control is poor; EMSbg and EMSad bg were able to successfully achieve the SoC control target, with SoC approaching 0.3 at the end of the trip, specifically 0.304 and 0.315. From the perspective of fuel consumption cost, the cost of EMSad bg is 7.12 CNY, which saves 16.6% compared to MES1p and 1.9% compared to EMSbg. In the optimization of comprehensive energy costs, the bargaining strategy considering SoC performs better. EMSad bg has saved 11.0% in electricity consumption costs compared to MES1p and 0.3% compared to EMSbg. In addition, EMSad bg also performs well in optimizing battery capacity decay values, with decay values close to MESpf, saving 82.6% compared to MES1p and 43.2% compared to EMSbg. In terms of comprehensive usage cost, EMSad bg achieved the lowest value at 10.74 CNY. Compared with EMSbg, it decreased by 2.8%; compared with MES1p, it decreased by 14.6%; compared with MESpf, it decreased by 20.8%. Thus, in terms of overall performance, EMSad-bg is the best. When SoC0 = 0.4, the overall cost optimization results are similar to those when SoC0 = 0.3. Due to the increased battery capacity, this means an increase in electricity costs and a decrease in energy consumption costs, while the overall cost has reached a certain level of decrease. This may be the reason why the price of electricity is lower than the optimal price. It can be observed that EMSad-bg still demonstrates superior control performance in several indicators.

Table 3.
Test results five several strategies.
The final battery SoC can be brought closer to the target control value while the optimized system can significantly decrease fuel consumption. This suggests that R-EEV are more likely to use electricity to save more energy between fuel and electricity consumption. This performance is closely related to the selection of kAPU and kBatt mentioned in the research. Specifically, kAPU focuses mainly on optimizing energy configuration, while kBatt focuses more on extending battery life and reducing its lifespan decay. When the value of kAPU increases, it usually leads to a decrease in overall energy costs. Although increasing the value of kBatt can reduce the degradation of battery life, it will increase the cost of electricity usage and may mean that the energy allocation strategies are more inclined to increase the frequency of engine use. The EMSad bg system reduces battery life loss, which to some extent affects the overall cost of use. When the initial SoC is high, kAPU and kBatt will have an impact on the battery SoC value at the end of the trip (SoCfinal). The EMS lean towards pure electric propulsion and reducing engine usage, particularly when the value of kBatt is high and significantly different from kAPU. This could result in excessively high SoCfinal values, which would require more energy conversion and affect the degradation of battery life during the entire journey. Overall, there are significant differences in energy consumption and battery health among these strategies. The proposed EMSad bg system has a SoC-based adjustable parameter module that can provide balanced performance among multiple targets, achieving substantial overall improvement despite slight trade-offs in energy usage. This method provides a valuable reference for the design and optimization of EMS.
5. Conclusions
To achieve the optimal energy allocation of two energy sources, this paper proposes and solves an EMS based on a bargaining game for a R-EEV taking battery life into consideration. First, a complete vehicle model and control system model of R-EEV were established based on AVL/Cruise and MATLAB/Simulink platforms. On this basis, an adaptive energy management strategy was designed and implemented, and a bargaining model for R-EEV was constructed and applied to energy management problems. The effect of discount factors on the game’s outcome was then examined. The analysis results show that the discount factor of the APU mainly tends towards energy optimization, while the battery discount factor is more inclined towards optimizing battery life decay. In addition, the specific values of the discount factor group will also have an impact on the battery SoC value at the end of the trip when the initial SoC is high. To further optimize the bargaining strategy, a bargaining strategy considering SoC was designed, and a fuzzy adaptive parameter optimization module was introduced. This module can update key parameters of the strategy in real-time, thereby achieving dynamic energy allocation with optimal battery state adaptability. The results indicate that the parameter adaptive module based on a fuzzy algorithm can complete the predetermined control tasks and control logic. By comparing the results of parameter fixed and parameter adaptive optimization, we found that parameter adaptive optimization performs better in terms of SoC adaptability. Through simulation and bench-testing verification, the optimized bargaining strategy achieved lower comprehensive usage costs at initial SoC values of 0.3 and 0.4. Compared to the original strategy, the comprehensive usage costs have been reduced by 12.6% and 17.3%, respectively. Although the EMS designed in this article mainly optimizes economy, emissions, noise, and driving comfort are also important indicators for evaluating cars during operation. Therefore, future EMS can consider combining economics with emission issues to achieve comprehensive optimization of multiple performance aspects. The bargaining strategy designed in the research has achieved significant cost reduction effects under specific conditions, but there are still some limitations that need to be improved. In practical applications, the complexity of the strategy may lead to an increase in implementation costs or a decrease in real-time response speed. In addition, the bargaining strategy may need to be coordinated with multiple systems such as the battery management system, charging facilities, and power grid dispatching of electric vehicles. If the strategy is incompatible with other systems, it may lead to implementation difficulties or performance degradation. All of these should be considered in future research.
Author Contributions
H.L. managed the project and conceptualized scheme; H.L. and Z.G. conceived the control method; C.C. and Z.G. completed the modeling and performed the simulation experiments, and finished the manuscript; J.L., S.L., Z.S. and W.S. collected the data and reviewed the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Design of Key Mechanical Components and Development of Intelligent Control System for Customized Material Handling Equipment (No. 2023220103000068), and Research on Collaborative Optimization of Optimal Speed Control and Energy Management for Connected Automated Range-Extended Electric Vehicle (No. 232699HJ0103108631). Partly supported by the Key R&D and promotion projects in Henan Province (No. 232102241029).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
References
- Tarroja, B.; Shaffer, B.; Samuelsen, S. The importance of grid integration for achievable greenhouse gas emissions reductions from alternative vehicle technologies. Energy 2015, 87, 504–519. [Google Scholar] [CrossRef]
- Zhang, S.; Xiong, R. Adaptive energy management of a plug-in hybrid electric vehicle based on driving pattern recognition and dynamic programming. Appl. Energy 2015, 155, 68–78. [Google Scholar] [CrossRef]
- Chen, B.C.; Wu, Y.Y.; Tsai, H.C. Design and analysis of power management strategy for range extended electric vehicle using dynamic programming. Appl. Energy 2014, 113, 1764–1774. [Google Scholar] [CrossRef]
- Lan, S.; Stobart, R.; Chen, R. Performance comparison of a thermoelectric generator applied in conventional vehicles and extended-range electric vehicles. Energy Convers. Manag. 2022, 266, 115791. [Google Scholar] [CrossRef]
- Wu, X.; Gu, Y.; Xu, M. Adaptive energy management strategy for extended-range electric vehicle based on micro-trip identification. IEEE Access 2020, 8, 176555–176564. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Cheng, X.Q.; Xing, Z.Y.; Wang, Z.H. Energy management strategy optimization for hybrid energy storage system of tram based on competitive particle swarm algorithms. J. Energy Storage 2024, 75, 109698. [Google Scholar] [CrossRef]
- Li, J.; Wu, X.; Min, X.; Liu, Y. A real-time optimization energy management of range extended electric vehicles for battery lifetime and energy consumption. J. Power Sources 2021, 498, 229939. [Google Scholar] [CrossRef]
- Bai, Y.; Li, J.; He, H.; Dos Santos, R.C.; Yang, Q. Optimal design of a hybrid energy storage system in a plug-in hybrid electric vehicle for battery lifetime improvement. IEEE Access 2020, 8, 142148–142158. [Google Scholar] [CrossRef]
- Hwang, J.J.; Hu, J.S.; Lin, C.H. A Novel Range-Extended Strategy for Fuel Cell/Battery Electric Vehicles. Sci. World J. 2015, 2015, 363094. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J.; Du, S.; Ma, H.; Zhao, W.; Li, H. Energy management strategies for hybrid construction machinery: Evolution, classification, comparison and future trends. Energies 2019, 12, 2024. [Google Scholar] [CrossRef]
- Kong, Y.; Xu, N.; Zhang, Y.J. Acquisition of full-factor tripinformation for global optimization energy management in multi-energy source vehicles and the measure of the amount of information to be transmitted. Energy 2021, 236, 121423. [Google Scholar] [CrossRef]
- Peng, J.; He, H.; Xiong, R. Rule based energy management strategy for a series–parallel plug-in hybrid electric bus optimized by dynamic programming. Appl. Energy 2017, 185, 1633–1643. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, L.; Coskun, S.; Cui, Y.; Pang, H. Computationally Efficient Energy Management in Hybrid Electric Vehicles Based on Approximate Pontryagin’s Minimum Principle. World Electr. Veh. J. 2020, 11, 65. [Google Scholar] [CrossRef]
- Fernández, R.; Caraballo, S.; Cilleruelo, F. Fuel optimization strategy for hydrogen fuel cell range extender vehicles applying genetic algorithms. Renew. Sustain. Energy Rev. 2018, 81, 655–668. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Cao, J. Particle swarm optimization-based optimal power management of plug-in hybrid electric vehicles considering uncertain driving conditions. Energy 2016, 96, 197–208. [Google Scholar] [CrossRef]
- Li, H.; Ravey, A.; N’Diaye, A.; Djerdir, A. Online adaptive equivalent consumption minimization strategy for fuel cell hybrid electric vehicle considering power sources degradation. Energy Convers. Manag. 2019, 192, 133–149. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, Z.; Wang, Z.; Tian, Y.; Wang, J.; Tian, Z.; Xu, F.; Jiao, X.; Li, L.; Wen, G. Hierarchical eco-driving control strategy for connected automated fuel cell hybrid vehicles and scenario-/hardware-in-the loop validation. Energy 2024, 292, 130592.1–130592.18. [Google Scholar] [CrossRef]
- Wang, H.; Huang, Y.; Khajepour, A.; Song, Q. Model predictive control-based energy management strategy for a series hybrid electric tracked vehicle. Appl. Energy 2016, 182, 105–114. [Google Scholar] [CrossRef]
- Lin, K. Research on Energy Management Optimization of Micro Energy Network Based on Game Theory. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2020. [Google Scholar]
- Zhu, Z.; Lambotharan, S.; Chin, W.H.; Fan, Z. A mean field game theoretic approach to electric vehicles charging. IEEE Access 2016, 4, 3501–3510. [Google Scholar] [CrossRef]
- Wen, J.; Du, X.; Li, X.; Chen, L. A Dynamic game approach for multi-objectives regulating in shared energy storage scenarios. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 5321–5326. [Google Scholar]
- Zeng, X.; Gao, H.; Chen, Z.; Yang, D.; Song, D. Cooperative optimization of speed planning and energy management for hybrid electric vehicles based on Nash equilibrium. J. Power Sources 2023, 571, 233070. [Google Scholar] [CrossRef]
- Ruan, S.; Ma, Y.; Yang, N.; Yan, Q.; Xiang, C. Multiobjective optimization of longitudinal dynamics and energy management for HEVs based on nash bargaining game. Energy 2023, 262, 125422. [Google Scholar] [CrossRef]
- Ruan, S.; Ma, Y.; Wei, Z.; Zhang, C.; Xiang, C. Data-Driven Cooperative Differential Game Based Energy Management Strategy for Hybrid Electric Propulsion System of a Flying Car. IEEE Trans. Intell. Transp. Syst. 2024, 25, 14770–14784. [Google Scholar] [CrossRef]
- Khodaparastan, M.; Mohamed, A.A.; Brandauer, W. Recuperation of Regenerative Braking Energy in Electric Rail Transit Systems. IEEE Trans. Intell. Transp. Syst. 2018, 20, 2831–2847. [Google Scholar] [CrossRef]
- Chen, J.; Hu, H.; Wang, M.; Ge, Y.; Wang, K.; Huang, Y.; Yang, K.; He, Z.; Xu, Z.; Li, Y.R. Power Flow Control-Based Regenerative Braking Energy Utilization in AC Electrified Railways: Review and Future Trends. IEEE Trans. Intell. Transp. Syst. 2024, 25, 6345–6365. [Google Scholar] [CrossRef]
- Liu, H.; Lei, Y.; Fu, Y.; Li, X. Parameter matching and optimization for power system of range-extended electric vehicle based on requirements. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 095440702093678. [Google Scholar] [CrossRef]
- Li, J.; Jin, X.; Xiong, R. Multi-objective optimization study of energy management strategy and economic analysis for a range-extended electric bus. Appl. Energy 2017, 194, 798–807. [Google Scholar] [CrossRef]
- Song, D.; Yang, L.; Zeng, X.; Wang, X.; Liang, W.; Yang, N. Optimization of hybrid electric vehicle battery life based on driving cycle synthesis. J. Jilin Univ. Eng. Ed. 2021, 51, 781–791. [Google Scholar]
- Sun, F.; Xiong, R.; He, H. A systematic state-of-charge estimation framework for multi-cell battery pack in electric vehicles using bias correction technique. Appl. Energy 2016, 162, 1399–1409. [Google Scholar] [CrossRef]
- Vassilyev, S.N.; Kudinov, Y.I.; Pashchenko, F.F.; Durgaryan, I.S.; Kelina, A.Y.; Kudinov, I.Y.; Pashchenko, A.F. Intelligent Control Systems and Fuzzy Controllers. II. Trained Fuzzy Controllers, Fuzzy PID Controllers. Autom. Remote Control 2020, 81, 922–934. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).