Optimized Scheduling Model Considering the Demand Response and Sequential Requirements of Polysilicon Production
Abstract
:1. Introduction
- Psychological modeling, which considers the psychological reaction of users to electricity prices and its impact on their electricity demand. This assumes that the user response behavior to price changes has a dead zone and a saturation zone. Only when the price changes fall between the thresholds of the dead zone and the saturation zone will the user’s electricity demand change accordingly. Otherwise, the user either does not respond or their response does not change. However, this method does not clearly distinguish between the adjustments in electricity demand made at different times during the same period (peak, off-peak, and flat periods), and thus still has many shortcomings [13,14,15,16].
- The matrix modeling of demand price elasticity, which uses the ratio of the rate of change in the electricity demand to the rate of change in price (demand price elasticity coefficient) to represent the user’s response to price. This indicator intuitively reflects the degree of user response to price during different periods, providing a theoretical basis for formulating pricing policies. However, calculating the demand price elasticity coefficient requires a large amount of historical load data, and the quality of these data significantly impacts model accuracy [17,18,19,20].
- The detailed modeling of user and equipment electricity consumption characteristics is used by some scholars, considering the complex operational characteristics of user loads, to propose a model in which users respond rationally to prices with the goal of minimizing their electricity costs. This method, compared to the three previous black-box models, better reveals the mechanism by which price signals influence user electricity usage behavior, making it more suitable for analyzing the electricity response behavior of polysilicon companies, which have clear electricity plans and a strong desire to reduce costs, as industrial users of large amounts of energy [21,22,23,24,25].
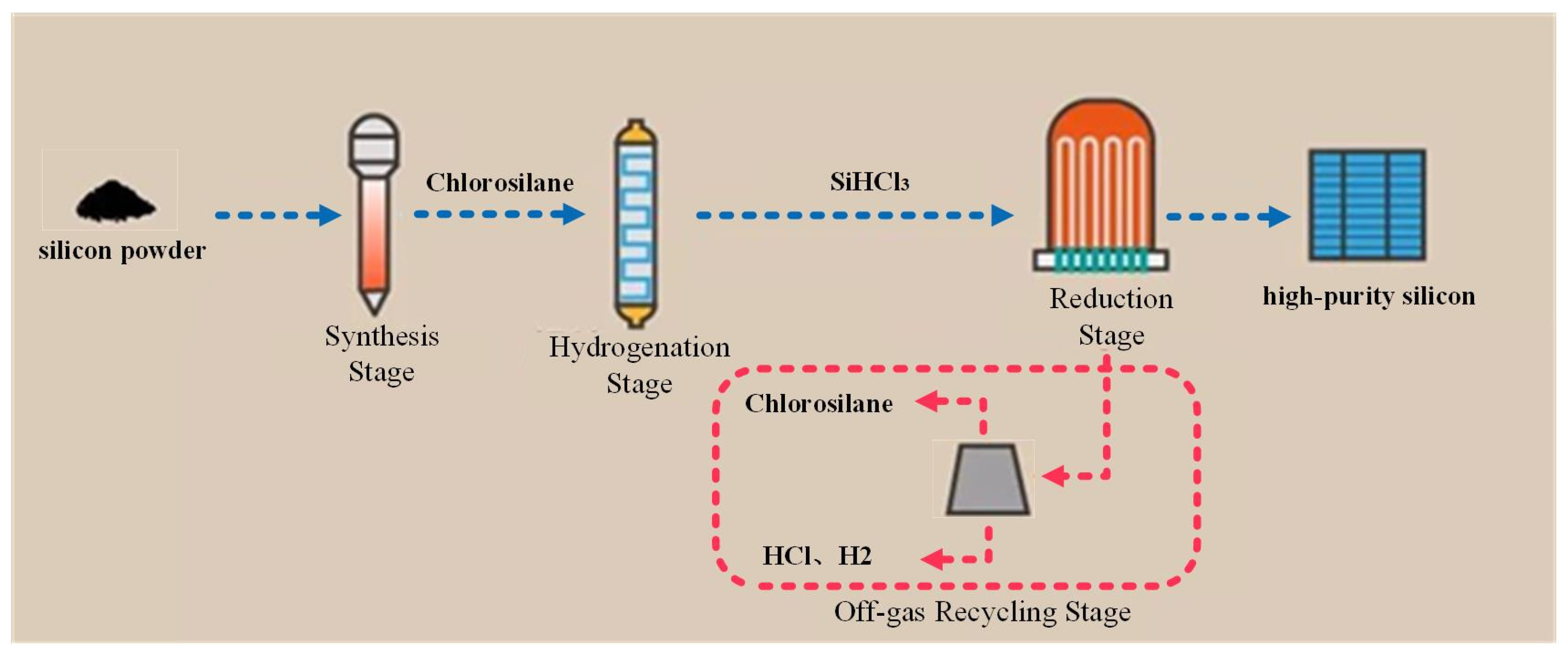
2. Analysis of the Sequential Requirements of Polysilicon Production
2.1. Synthesis Stage
2.2. Purification Stage
2.3. Reduction Stage
2.4. Off-Gas Recycling Stage
2.5. Hydrogenation Stage
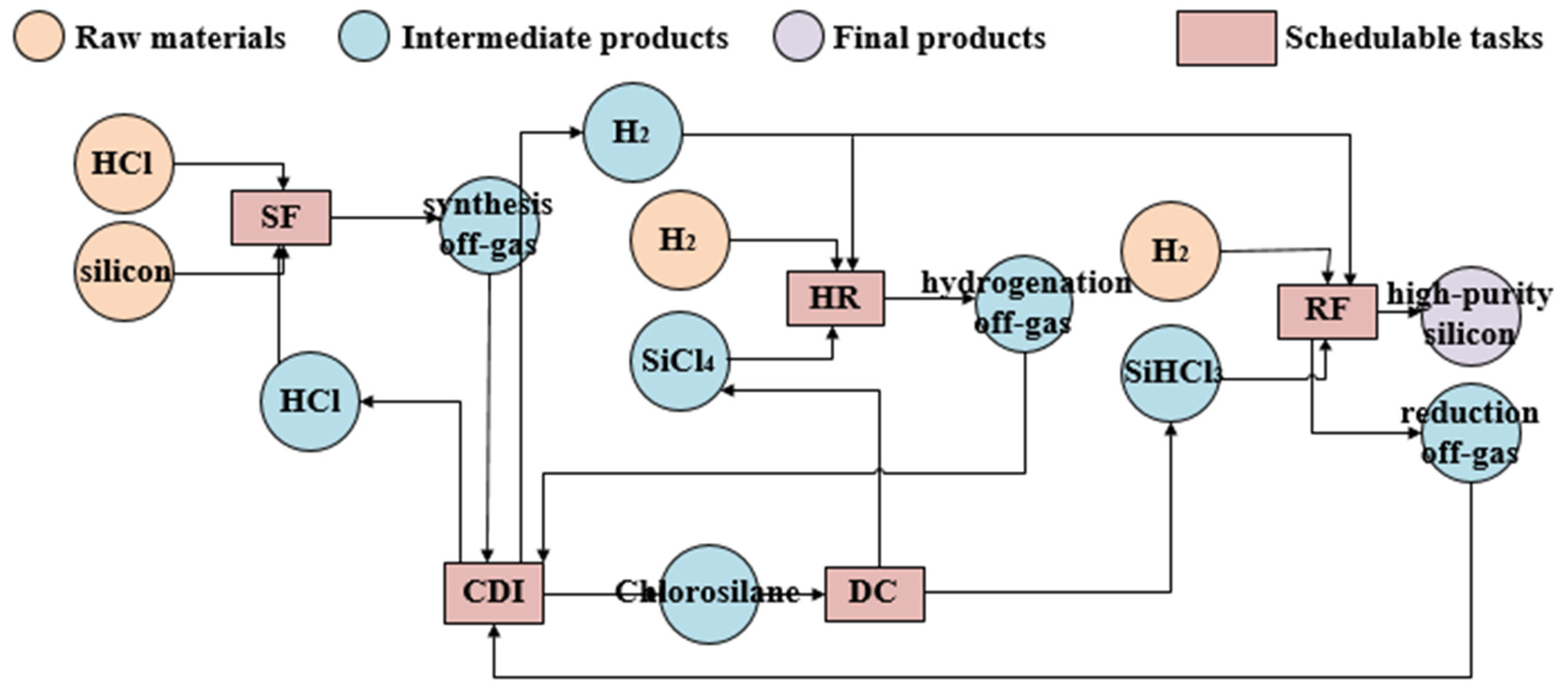
3. Polysilicon Scheduling Optimization Model
3.1. Sequential Constraints for Polysilicon Production
3.1.1. Material Balance Constraint
3.1.2. Power Balance Constraint
3.1.3. Storage Constraint
3.1.4. Production Output Constraint
3.1.5. Purification Task Constraint
3.1.6. Reduction Task Constraint
3.2. Objective Function of Polysilicon Scheduling Optimization Model
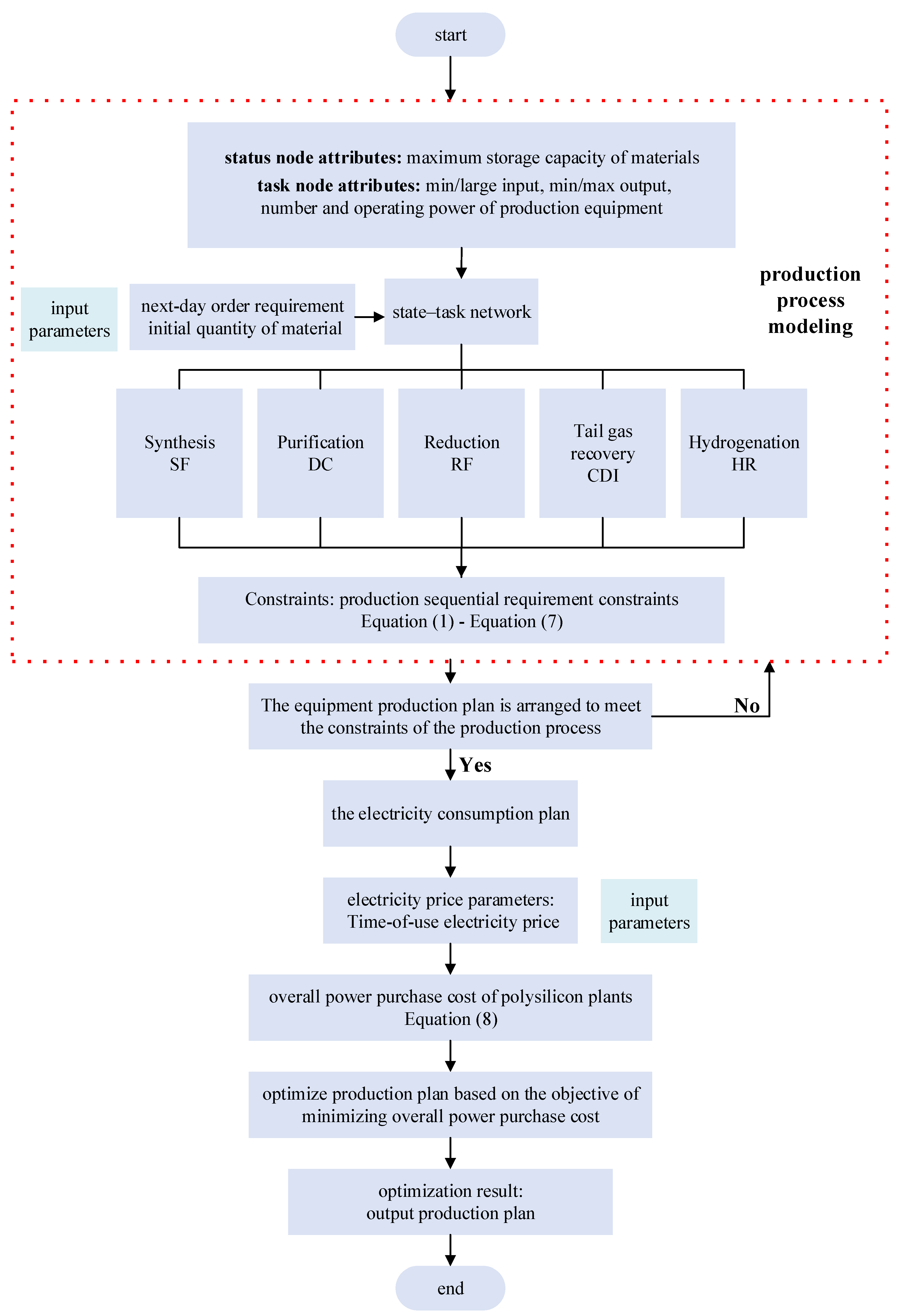
3.3. Solution Procedure for Polysilicon Scheduling Optimization Model
4. Case Study Analysis
4.1. Impact of Considering Production Processes on the Daily Production Schedule of the Polysilicon Plant
- Situation 1: Minimize total electricity costs; remove storage, purification and reduction task constraints; keep production quantity constraint.
- Situation 2: Minimize total electricity costs; remove storage constraint; keep other constraints.
- Situation 3: Minimize total electricity costs and keep all process constraints, i.e., the optimized scheduling model in this paper, which considers the sequential requirements of production.
4.2. Impact of Different Modeling Methods on the Daily Production Schedule of the Polysilicon Plant
- Modeling method 2: Based on Ref. [33], the task equipment considered in this paper belongs to the transferable load in this method. With the goal of minimizing the total electricity cost, the storage constraint and the purification and reduction task constraints are removed, and the production quantity constraint is kept, and the constraint of a minimum continuous operation time of 2 h is increased to ensure that all production tasks are completed within the scheduled cycle.
- Modeling method 3: Minimize total electricity costs and consider all process constraints, i.e., the optimized scheduling model in this paper, which considers the sequential requirements of production.
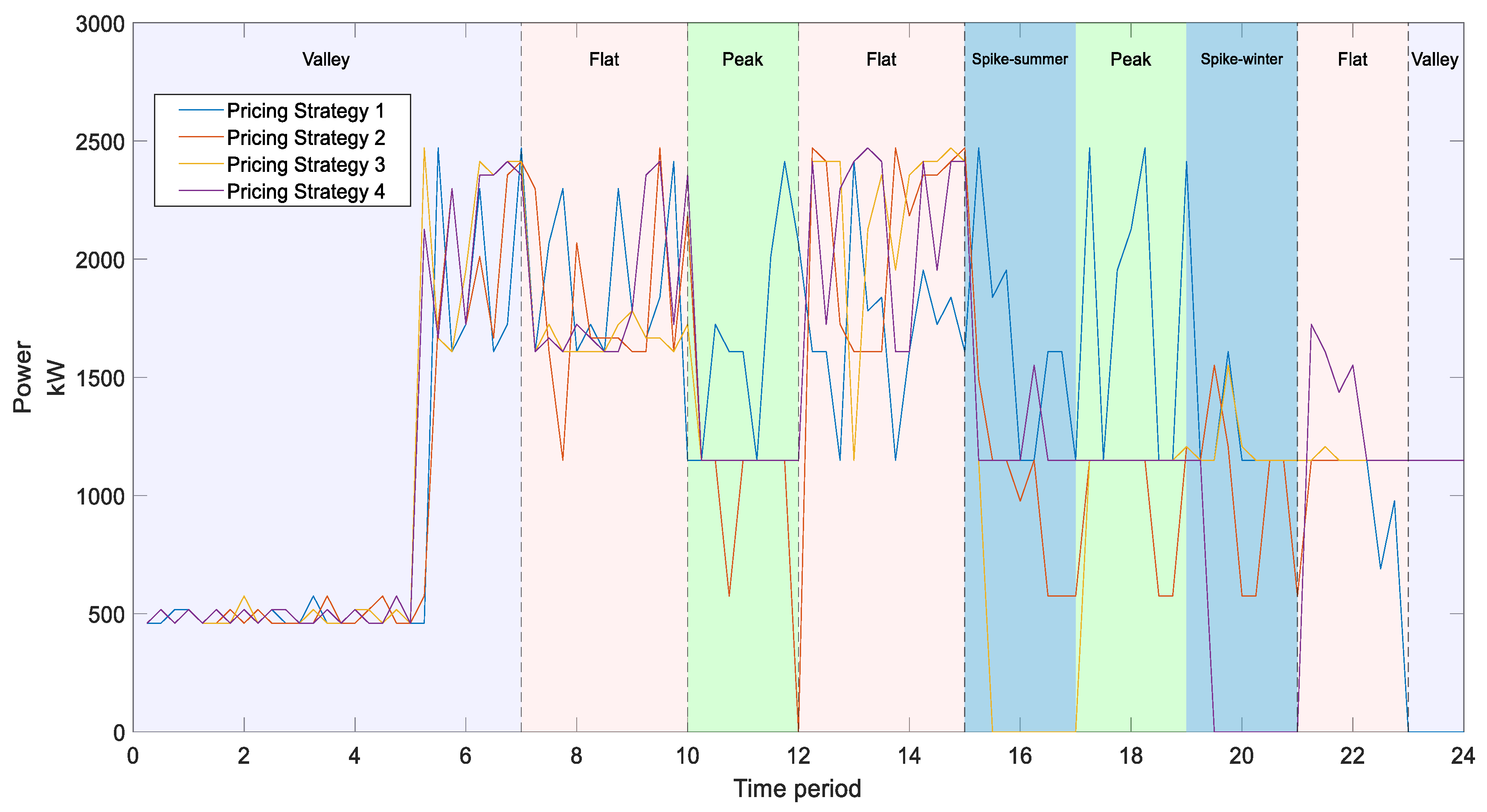
4.3. Impact of Different Time-of-Use Pricing Strategies on the Daily Production Schedule of the Polysilicon Plant
- Time-of-use Pricing Strategy 1: Implement a fixed electricity price, which is determined by the weighted average of the time-of-use electricity price, and then the polysilicon plant executes the power consumption plan with the shortest completion time;
- Time-of-use Pricing Strategy 2: Implement the time-of-use electricity prices of peak, flat and valley times, as in this paper;
- Time-of-use Pricing Strategy 3: Consider the electricity price to spike from 15:00 to 17:00 in July and August in summer, during which time the electricity price is 1.1313 CNY/kWh
- Time-of-use Pricing Strategy 4: Consider the electricity price to spike from 19:00 to 21:00 in January and December in winter, during which time the electricity price is 1.1313 CNY/kWh.
4.4. Impact of Different Product Order Quantities on the Adjustable Capacity of the Polysilicon Plant
- Order Quantity 1: 3200 kg;
- Order Quantity 2: 3600 kg;
- Order Quantity 3: 4000 kg.
5. Conclusions
- An Analysis of Polysilicon Production Sequential Requirements: Focusing on the most common polysilicon production method, the improved Siemens method, this study analyzes the production processes involved in its synthesis, purification, reduction, exhaust gas recovery, and hydrogenation stages. From this analysis, the production requirements, core electricity-consuming equipment, equipment adjustment methods, and material flow for each stage are extracted, providing a foundation for constructing a polysilicon production STN model and proposing constraints on the sequential requirements of production.
- The Development of Polysilicon Optimized Scheduling Model: Based on the polysilicon production STN model, an optimized day-ahead scheduling model that considers the sequential requirements of polysilicon production is established in the context of time-of-use electricity pricing. This model optimizes the operating status of the production equipment at each stage, with the objective of minimizing the overall electricity cost for the polysilicon plant. It provides an economically optimal and feasible production plan for polysilicon enterprises, encouraging them to actively adjust their production schedules to enable their off-peak and peak-avoidance operation without affecting normal production. The constraints considered include material balance, electricity balance, storage, production quantity, purification task, and reduction task constraints. At the same time, by comparing the equipment operation status and material reserves of polysilicon plants under different process constraints, the necessity of considering all production constraints within the model in this paper is illustrated.
- The Analysis of Polysilicon Adjustable Capacity: The optimized scheduling model is run under different order quantities to analyze how electricity consumption changes as the order volume increases. The results show that the adjustable capacity of polysilicon enterprises varies with different order volumes. Specifically, when the ordered output is small, the output requirements can be met while only running the plant during the valley periods of electricity prices; with an increase in the ordered output, only running the plant during the valley periods of electricity prices cannot meet the output requirements of the order, and the plant needs to be operated during flat sections or even during peak periods of the electricity price. At this time, in order to meet the requirements of the order, the space available for shifting electricity consumption is compressed to meet the order requirements, resulting in a decrease in its capacity for adjustments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gholian, A.; Mohsenian-Rad, H.; Hua, Y.; Qin, J. Optimal Industrial Load Control in Smart Grid: A Case Study for Oil Refineries. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]
- Tan, M. Analysis and Scheduling of Slab Hot Rolling Load Based on Power Demand Response. Ph.D. Thesis, Xiangtan University, Xiangtan, China, 2015. [Google Scholar]
- Liu, X.; Wang, Z.; Gao, F.; Wu, J.; Guan, X.; Zhou, D. Power Consumption Response of High Energy-Consuming Enterprises under Time-of-Use Pricing. Autom. Electr. Power Syst. 2014, 38, 41–49. [Google Scholar]
- Zhang, Q.; Wang, X.; Wang, J.; Feng, C.; Liu, L. A Review of Demand Response Research in Power Markets. Autom. Electr. Power Syst. 2008, 32, 97–106. [Google Scholar]
- Tian, S.; Wang, B.; Zhang, J. Key Technologies of Demand Response under Smart Grid Conditions. Proc. Chin. Soc. Electr. Eng. 2014, 34, 3576–3589. [Google Scholar]
- Tao, X.; Zhou, W. Research Progress and Literature Review on Power Demand Response. J. Beijing Inst. Technol. (Soc. Sci. Ed.) 2014, 16, 32–40. [Google Scholar]
- Lu, R.; Bai, R.; Huang, Y.; Li, Y.; Jiang, J.; Ding, Y. Data-Driven Real-Time Price-Based Demand Response for Industrial Facilities Energy Management. Appl. Energy 2021, 283, 116291. [Google Scholar] [CrossRef]
- Luo, Z.; Hong, S.H.; Kim, J.B. A Price-Based Demand Response Scheme for Discrete Manufacturing in Smart Grids. Energies 2016, 9, 650. [Google Scholar] [CrossRef]
- Zhang, H. Dynamic Economic Dispatch of Power Systems with Wind Farms Based on User-Side Interaction. Master’s Thesis, Shenyang Agricultural University, Shenyang, China, 2021. [Google Scholar]
- Huang, Y.; Kang, C.; Li, H.; Xia, Q.; Wang, G.; Hu, Z. Modeling and Application of Electricity Demand Curves. New Technol. Electr. Eng. Energy 2004, 2004, 29–33. [Google Scholar]
- Ding, W.; Yuan, J.; Hu, Z. Decision-Making Model for Time-of-Use Pricing Based on User Price Response and Satisfaction. Autom. Electr. Power Syst. 2005, 2005, 14–18. [Google Scholar]
- Liu, J. Benefit Assessment and Characteristic Analysis of Power Demand Side Response. Ph.D. Thesis, Shandong University, Jinan, China, 2014. [Google Scholar]
- De, J.C.; Hobbs, B.F.; Belmans, R. Optimal Generation Mix with Short-Term Demand Response and Wind Penetration. IEEE Trans. Power Syst. 2012, 27, 830–839. [Google Scholar]
- Li, G. Research on Time-of-Use Pricing Optimization Based on User Demand Response. Master’s Thesis, Nanjing University of Posts and Telecommunications, Nanjing, China, 2023. [Google Scholar]
- Zhao, N. Research on Demand Response Characteristics Modeling and Application for Energy Interconnection. Ph.D. Thesis, Southeast University, Nanjing, China, 2022. [Google Scholar]
- Ruan, W.; Wang, B.; Li, Y.; Yang, S. Research on User Response Behavior under Time-of-Use Pricing. Power Syst. Technol. 2012, 36, 86–93. [Google Scholar]
- Hu, Y.; Li, Y.; Chen, L. Multi-Objective Optimization of Time-of-Use Price for Tertiary Industry Based on Generalized Seasonal Multi-Model Structure. IEEE Access 2019, 7, 89234–89244. [Google Scholar] [CrossRef]
- Li, Z. Assessment of the Potential for Power Demand Response and Its Applications. Master’s Thesis, South China University of Technology, Guangzhou, China, 2018. [Google Scholar]
- Yang, H.; Shi, R.; Ma, Y. Scheduling Strategy for Power Storage Systems Considering Multiple Time-of-Use Prices and Benefit Potential. Power Autom. Equip. 2021, 41, 130–137. [Google Scholar]
- Sun, W.; Li, S. Research on Time-of-Use Pricing in Power Demand Side Management. Electr. Appl. 2008, 2008, 63–66. [Google Scholar]
- Hou, H.; Fan, H.; Xie, J.; Luo, J.; Ke, X. Optimal Charging Strategy for Rational Price Users under Time-of-Use Pricing. China Electr. Power 2018, 51, 171–178. [Google Scholar]
- Liao, S.; Xiao, Y.; Xu, J.; Li, L.; Xu, X.; Jia, H. Economic Dispatch Model Considering Production Process of the Energy-Intensive Industrial Load Under Demand Response. Autom. Electr. Power Syst. 2024, in press. [Google Scholar]
- Yang, M. Optimization Scheduling of Power Load Based on Demand Side Management. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2019. [Google Scholar]
- Liao, S.; Xie, H.; Xu, J.; Sun, Y.; Ke, D.; Jiang, Y. Demand Response Control Strategy for High-energy-consuming Loads Aligned with Demand-side Market Response Transaction Rules. Proc. Chin. Soc. Electr. Eng. 2024, in press. [Google Scholar]
- Liao, S.; Bian, S.; Xu, J.; Ke, D.; Sun, Y. Evaluation of Grid-load Interactive Adjustable Capacity of Electrolytic Aluminum Load Considering Optimization of Electrolytic Cell Energy Flow. Proc. Chin. Soc. Electr. Eng. 2024, in press. [Google Scholar]
- Hou, Y. Theoretical Analysis and Modeling of the Improved Siemens Method for Preparing Polycrystalline Silicon. Ph.D. Thesis, Kunming University of Science and Technology, Kunming, China, 2014. [Google Scholar]
- Xiao, Y. Energy Consumption Analysis and Prediction of the Reduction Process in Polycrystalline Silicon Reduction Furnaces. Master’s Thesis, Guangdong University of Technology, Guangzhou, China, 2019. [Google Scholar]
- Xiao, Y.; Liao, S.; Li, L.; Yang, J.; He, X.; Liang, J. Optimization Scheduling Strategy Considering Polycrystalline Silicon Production Process under Combined Demand Response. In Proceedings of the 2024 6th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 28–31 March 2024. [Google Scholar]
- Yao, M.; Han, X.; Zheng, Y.; Hu, Z. Thoughts on Promoting Participation of High Energy-Consuming Industries in the Power Auxiliary Service Market. China Energy 2018, 40, 22–26+47. [Google Scholar]
- Zhang, X.; Hug, G.; Harjunkoski, I. Cost-Effective Scheduling of Steel Plants with Flexible EAFs. IEEE Trans. Smart Grid 2017, 8, 239–249. [Google Scholar] [CrossRef]
- Chen, Y. Research on Frequency Control Strategy of Isolated Wind Power Grid with High Permeability Based on Polysilicon Load Control. Master’s Thesis, Wuhan University, Wuhan, China, 2018. [Google Scholar]
- Jiang, X.; Xu, J.; Liao, S.; Sun, Y. Cooperative control method for multi-type load coordination to stabilize wind power fluctuation in industrial parks considering the difference of industrial users’ response intentions. Geomat. Eng. Sci. Wuhan Univ. 2022, 55, 876–885. [Google Scholar]
- Lv, H.; Deng, B.; Zhang, P.; Han, G.; Zhang, K. Optimal Scheduling of Industrial Loads in Chemical Park in Low-Carbon. In Proceedings of the 2024 IEEE 2nd International Conference on Power Science and Technology (ICPST), Dali, China, 9–11 May 2024; pp. 2035–2041. [Google Scholar]
- Dai, X.; Che, H.; Xiao, D.; He, Q. A Review of the Application and Research of Industrial Demand Response Technologies in the Power Market Environment. Power Grid Technol. 2022, 46, 4169–4186. [Google Scholar]
- Ding, Y.M.; Hong, S.H.; Li, X.H. A Demand Response Energy Management Scheme for Industrial Facilities in Smart Grid. IEEE Trans. Ind. Inform. 2014, 10, 2257–2269. [Google Scholar] [CrossRef]
- Lin, J.; Shi, J.; Wen, F.; Li, L.; Qian, F.; Xiang, L. Coordinated Optimization Scheduling of Industrial Microgrids Considering Controllable Loads. Electr. Power Constr. 2018, 39, 1–9. [Google Scholar]





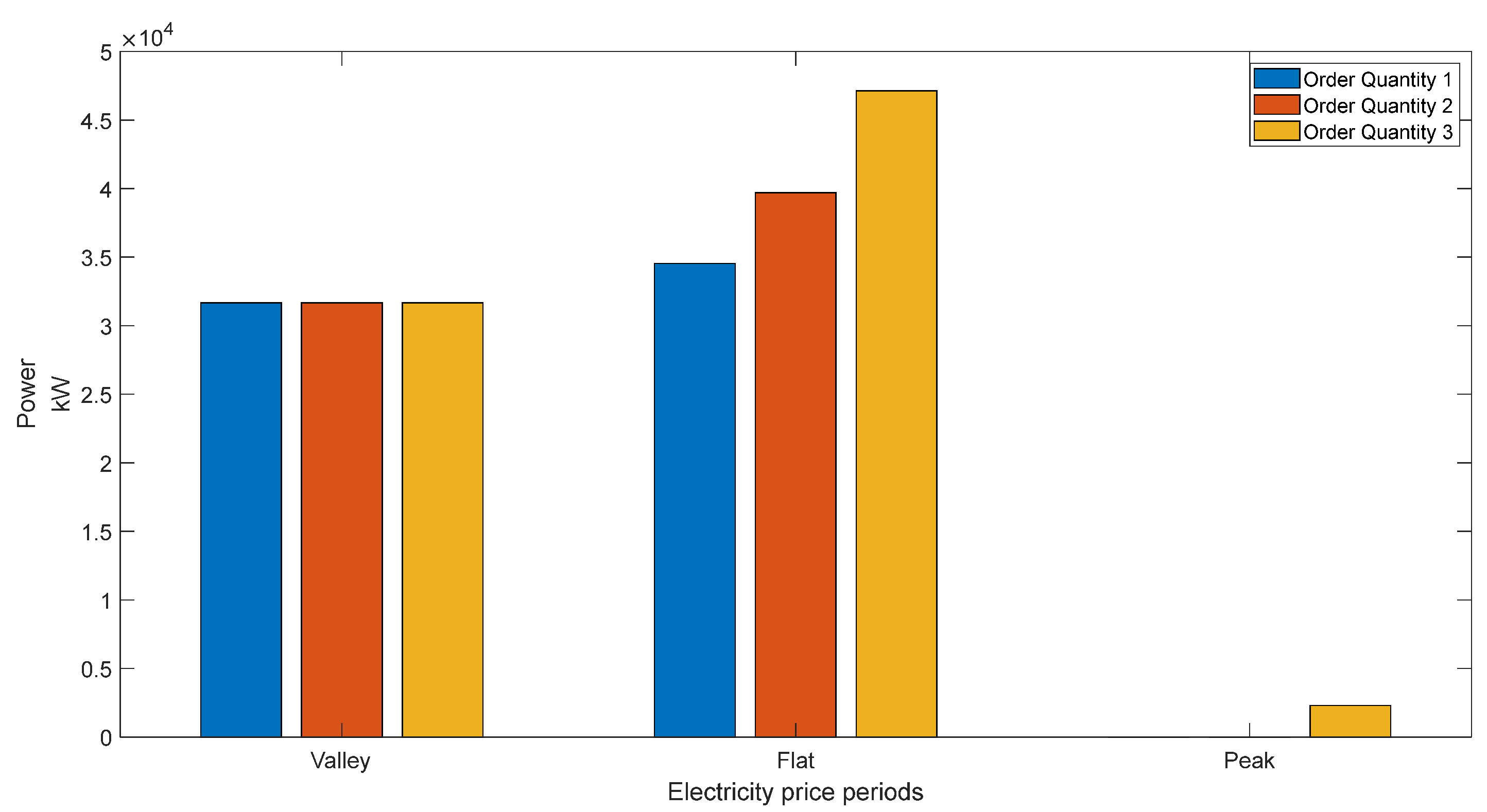
| Equipment | Synthesis Furnace | Distillation Column | Reduction Furnace | CDI Exhaust Gas Recovery System | Hydrogenation Furnace |
|---|---|---|---|---|---|
| Production Stage | Synthesis | Purification | Reduction | Gas Recovery | Hydrogenation |
| Rated Power (kW) | 230 | 58 | 575 | 50 | 345 |
| Number | 2 | 2 | 2 | 2 | 2 |
| Peak | Flat | Valley | |
|---|---|---|---|
| Time Period | 10:00–12:00 15:00–21:00 | 07:00–10:00 12:00–15:00 21:00–23:00 | 00:00–07:00 23:00–24:00 |
| Price (CNY/kWh) | 0.9427 | 0.5892 | 0.2357 |
| Situation | Situation 1 | Situation 2 | Situation 3 |
|---|---|---|---|
| Electricity Cost (CNY 10,000) | 1.5508 | 2.4853 | 3.0860 |
| Modeling Method | Modeling Method 1 | Modeling Method 2 | Modeling Method 3 |
|---|---|---|---|
| Total Electricity Cost (CNY 10,000) | / | 2.5300 | 3.0860 |
| Electricity Cost of the Reduction Task (CNY 10,000) | 1.5508 | 1.8420 | 2.3228 |
| Strategy | Strategy 1 | Strategy 2 | Strategy 3 | Strategy 4 |
|---|---|---|---|---|
| Electricity Cost (CNY 10,000) | 7.3713 | 6.8302 | 6.9500 | 7.0022 |
| Order Quantity | Order Quantity 1 | Order Quantity 2 | Order Quantity 3 |
|---|---|---|---|
| Electricity Cost (CNY 10,000) | 2.7812 | 3.0860 | 3.7395 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Chen, B.; Xiao, Y.; Liao, S.; Ye, X.; Bai, J. Optimized Scheduling Model Considering the Demand Response and Sequential Requirements of Polysilicon Production. Energies 2024, 17, 6048. https://doi.org/10.3390/en17236048
Wang X, Chen B, Xiao Y, Liao S, Ye X, Bai J. Optimized Scheduling Model Considering the Demand Response and Sequential Requirements of Polysilicon Production. Energies. 2024; 17(23):6048. https://doi.org/10.3390/en17236048
Chicago/Turabian StyleWang, Xi, Baorui Chen, Yuduo Xiao, Siyang Liao, Xi Ye, and Jiayu Bai. 2024. "Optimized Scheduling Model Considering the Demand Response and Sequential Requirements of Polysilicon Production" Energies 17, no. 23: 6048. https://doi.org/10.3390/en17236048
APA StyleWang, X., Chen, B., Xiao, Y., Liao, S., Ye, X., & Bai, J. (2024). Optimized Scheduling Model Considering the Demand Response and Sequential Requirements of Polysilicon Production. Energies, 17(23), 6048. https://doi.org/10.3390/en17236048







