Heat Transfer in Annular Channels with the Inner Rotating Cylinder and the Radial Array of Cylinders
Abstract
1. Introduction
2. Mathematical Formulation
3. Numerical Procedure
3.1. Computational Details
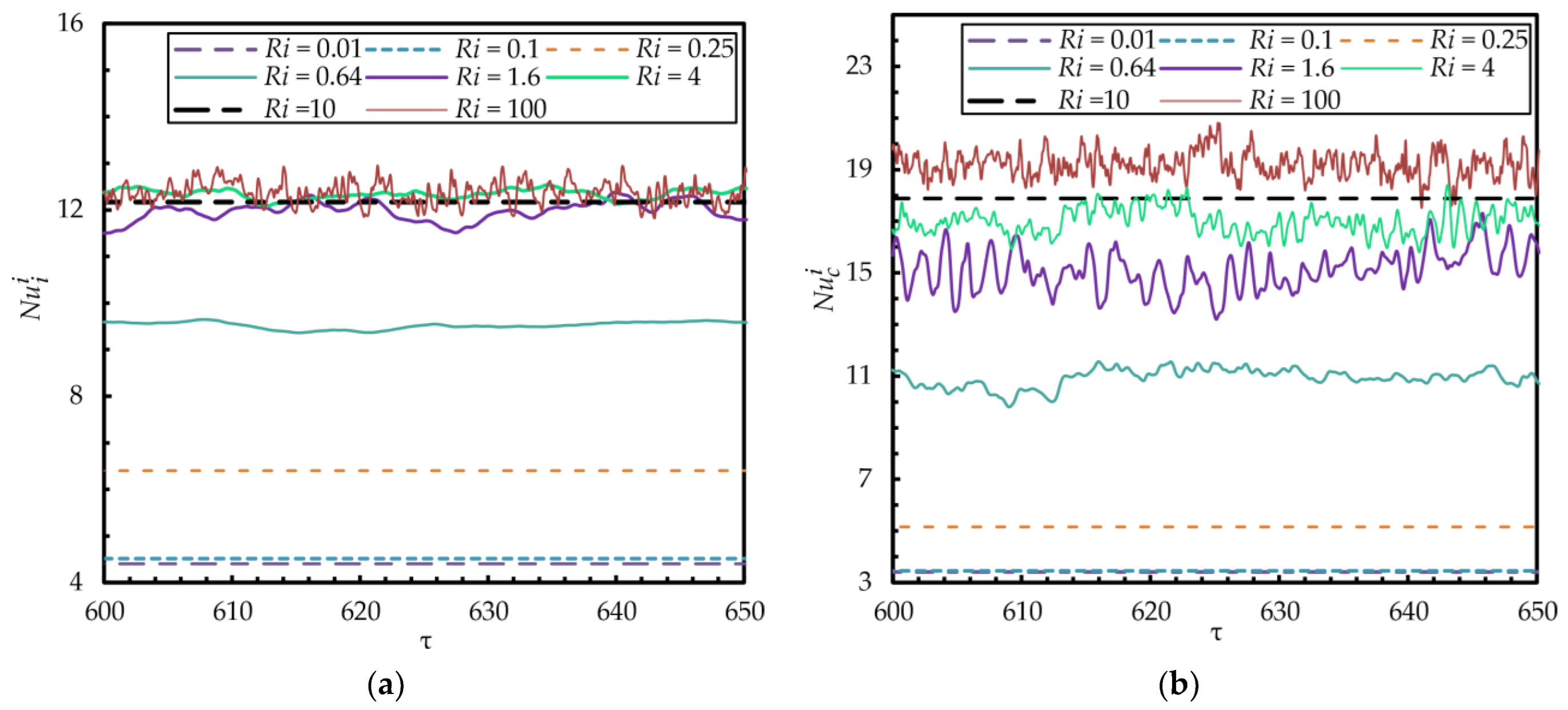
3.2. Grid Independency Test
3.3. Validation of the Model
4. Results and Discussion
4.1. The Aim and Constraints of the Parametric Research
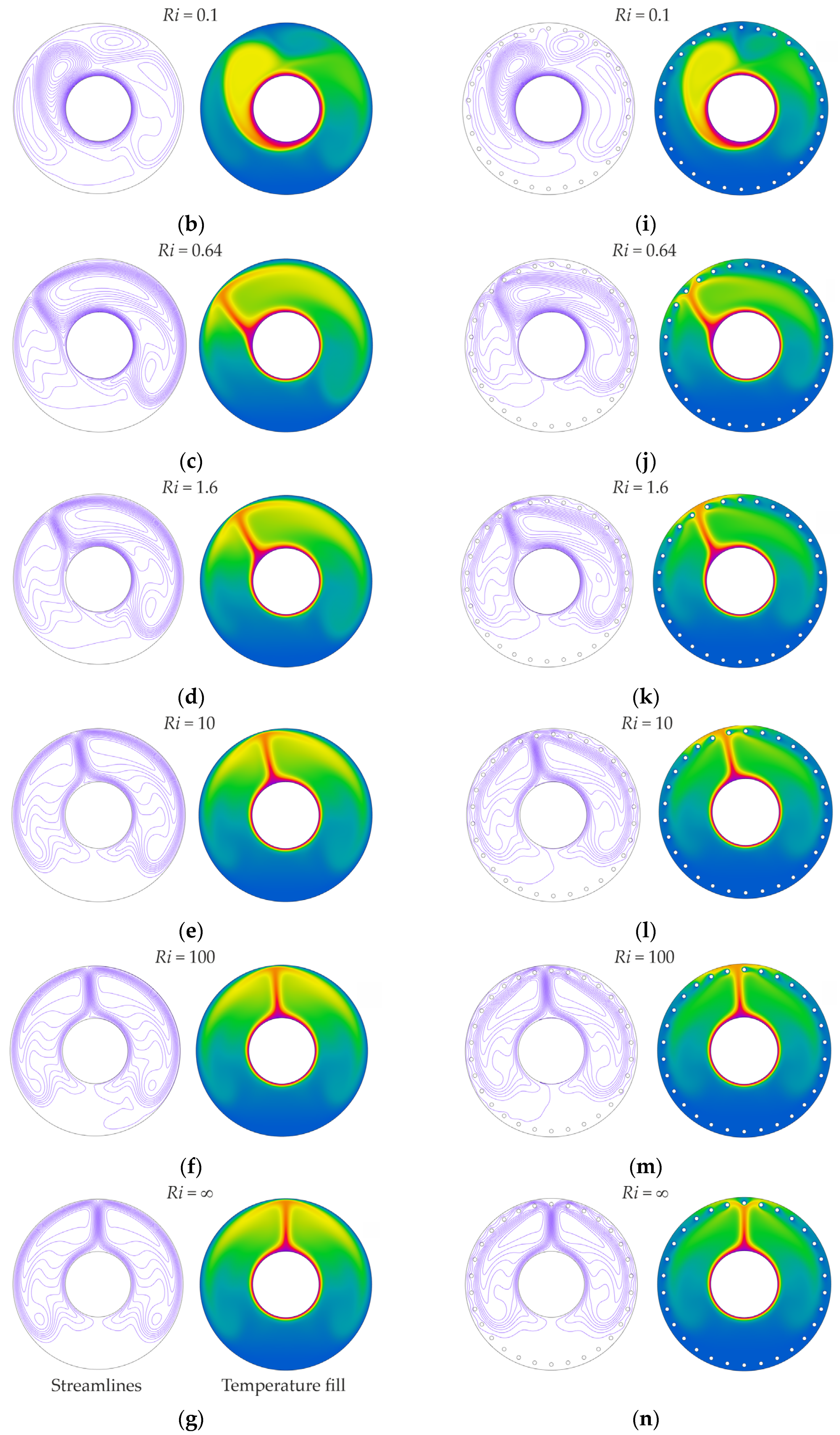
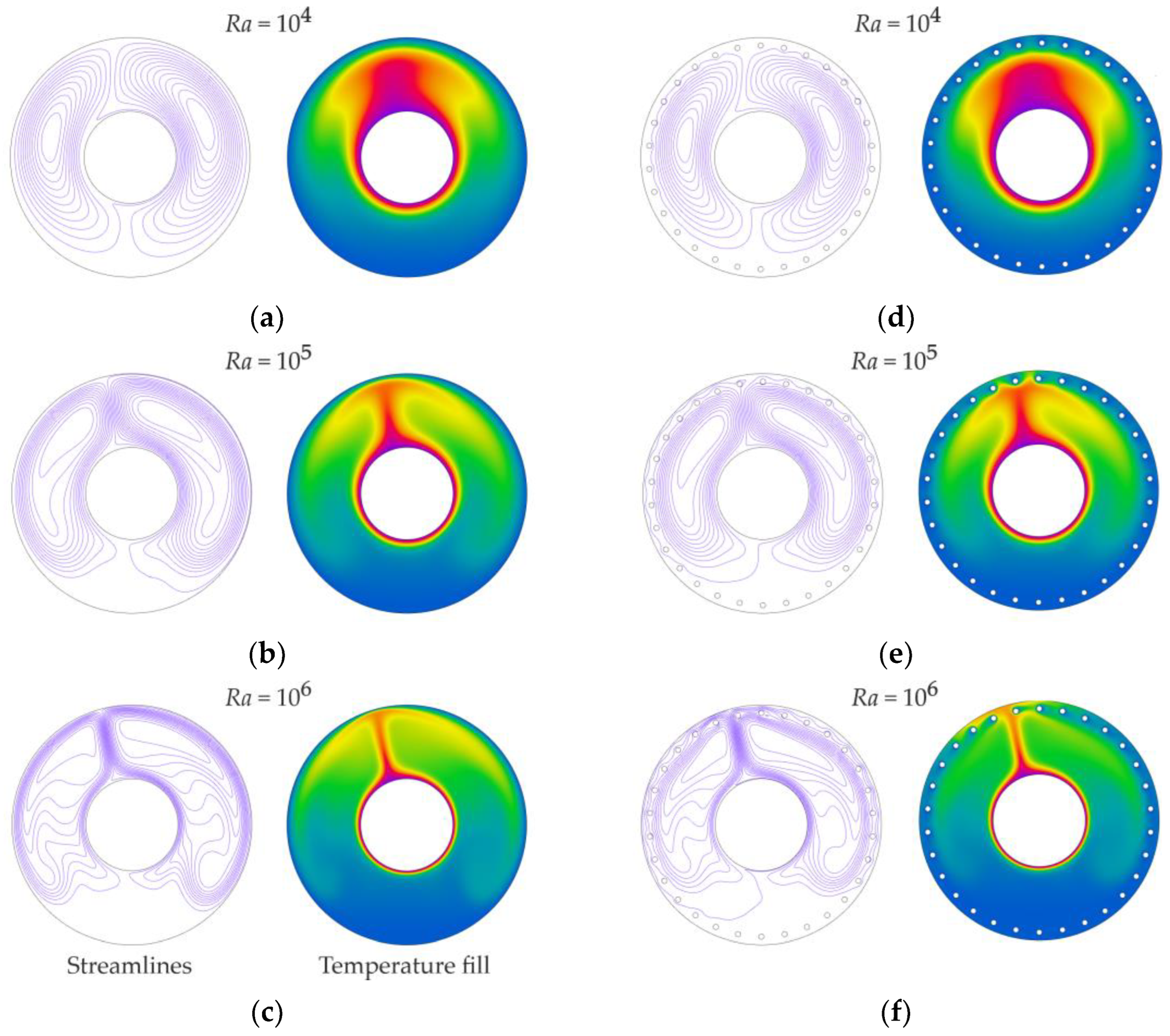
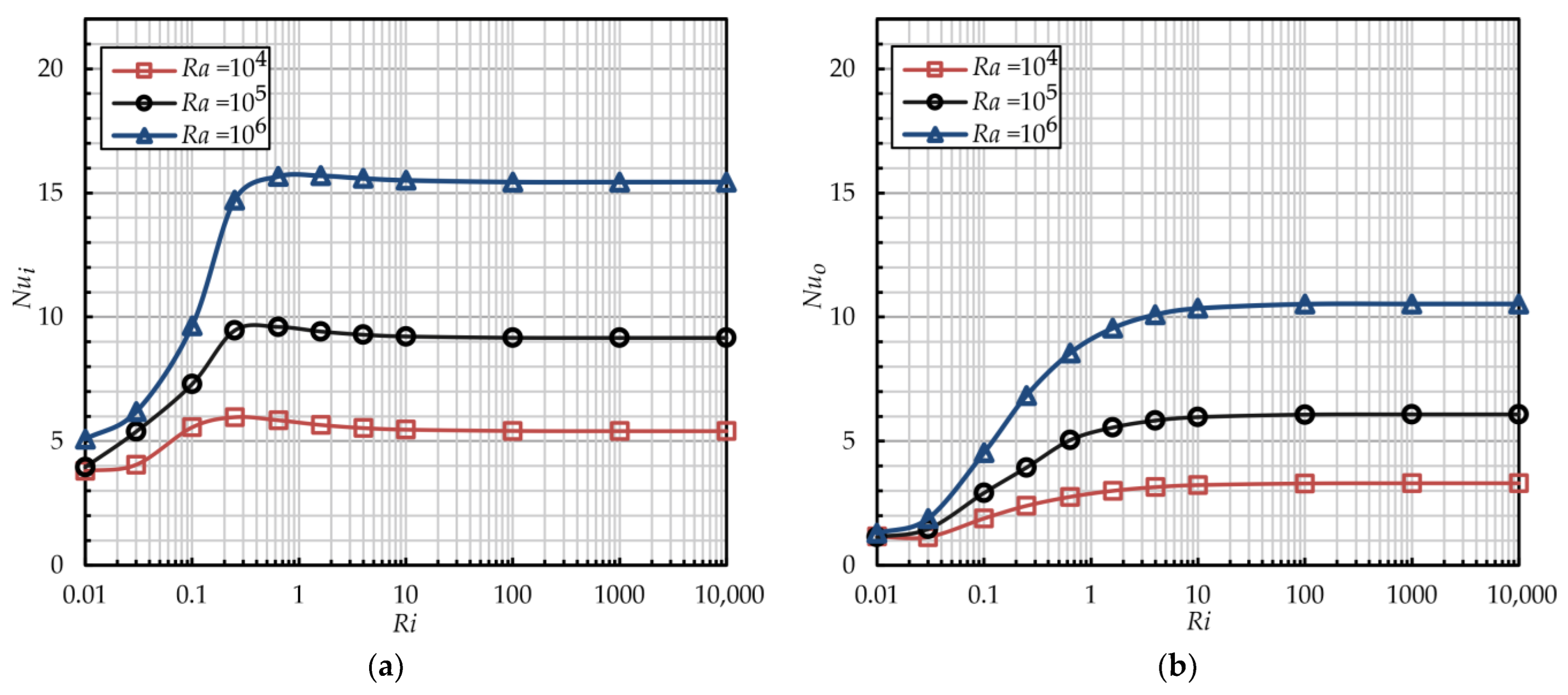
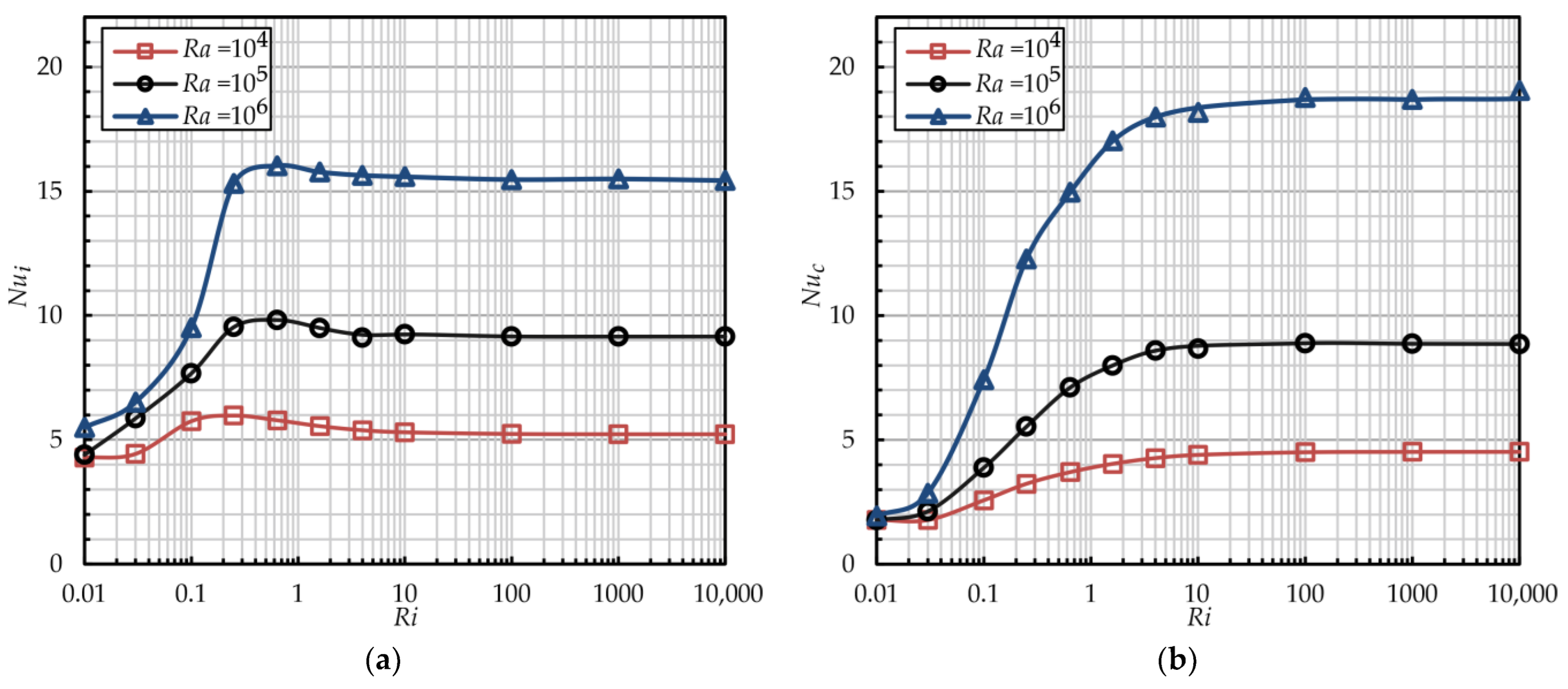
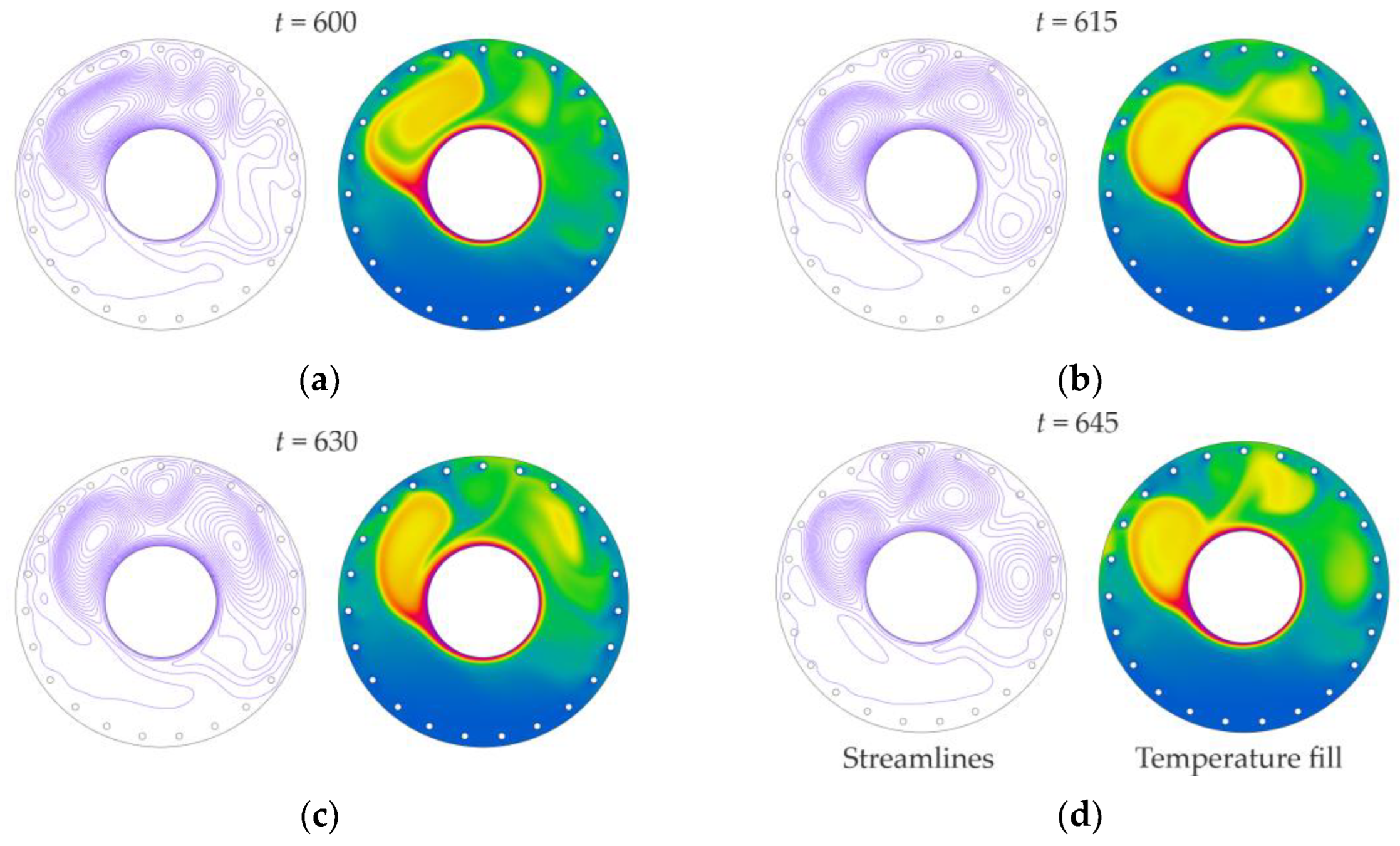
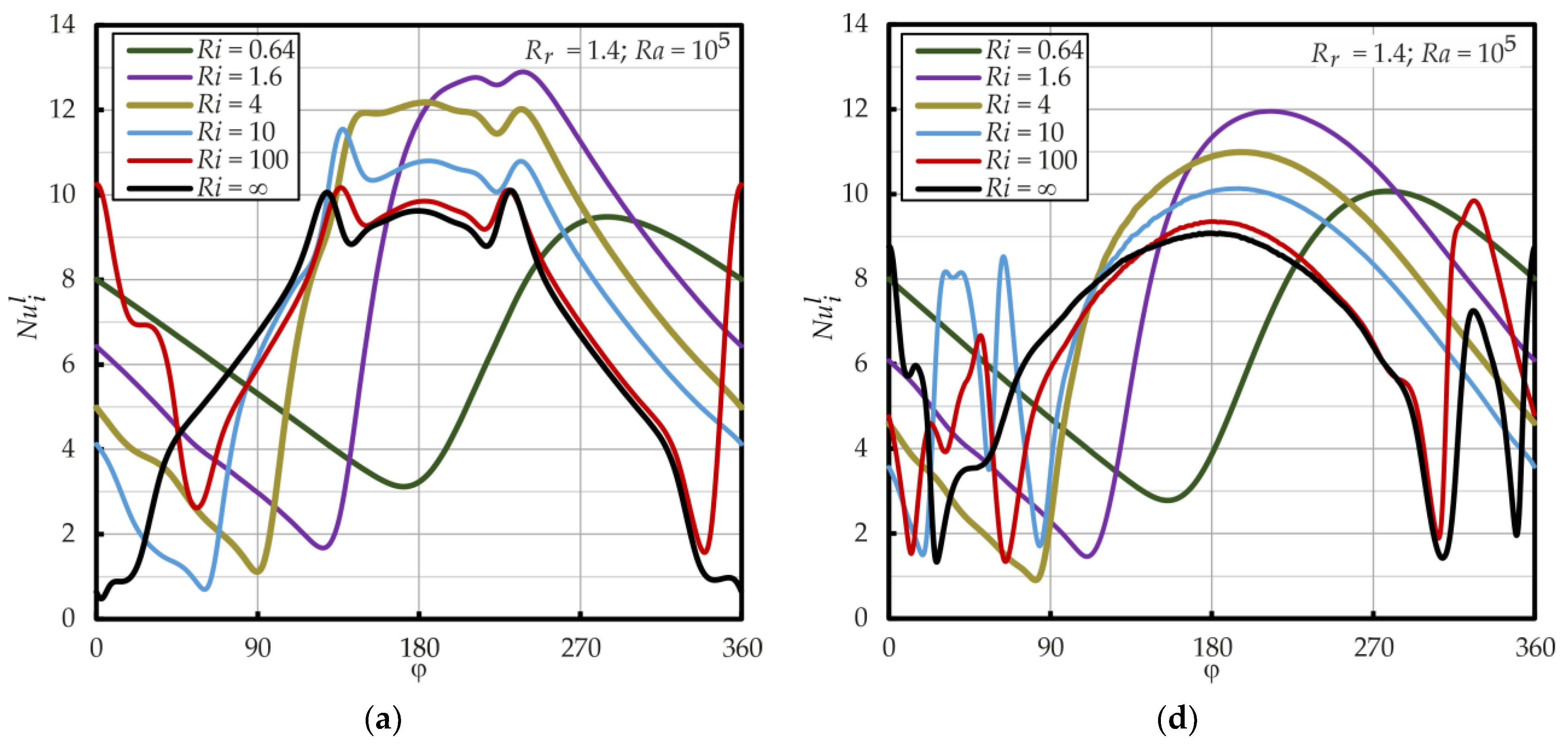
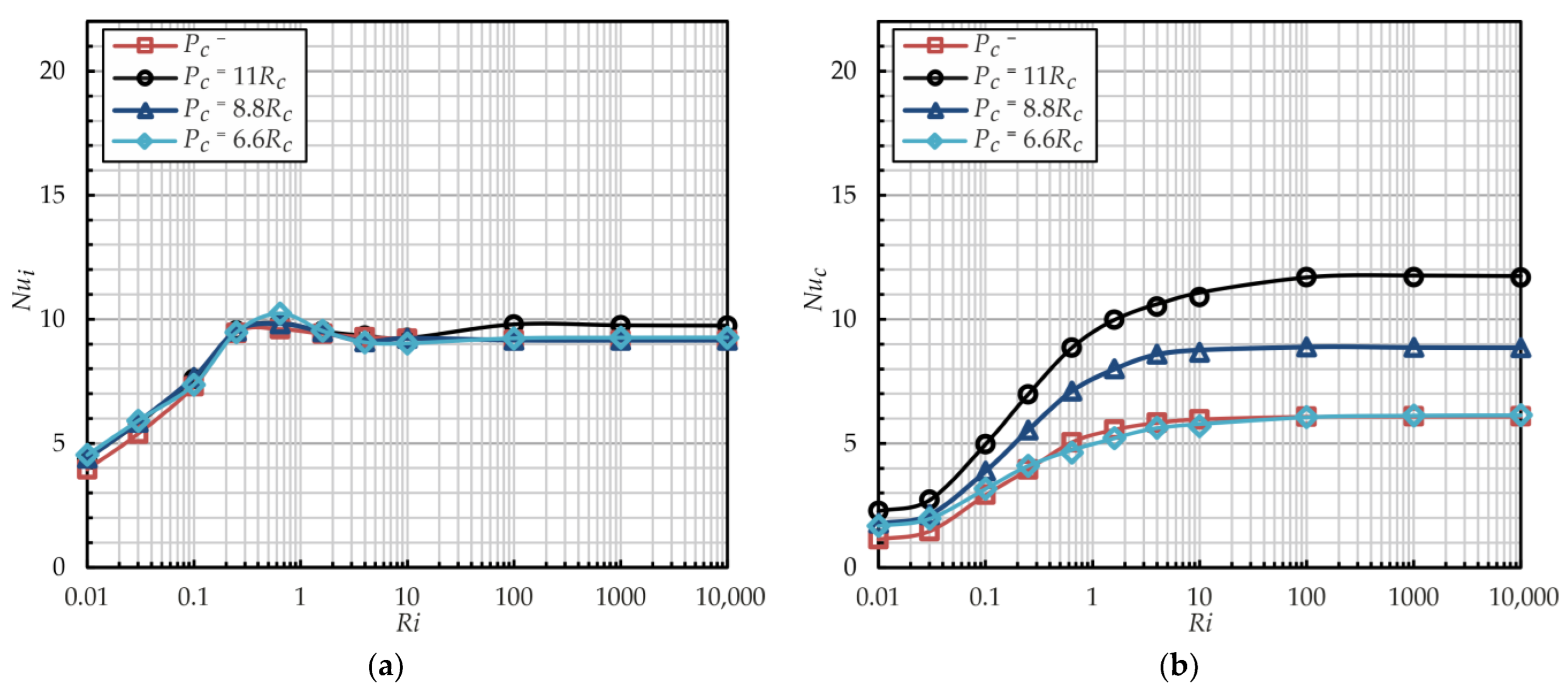
4.2. Influences of the Rayleigh and the Richardson Numbers
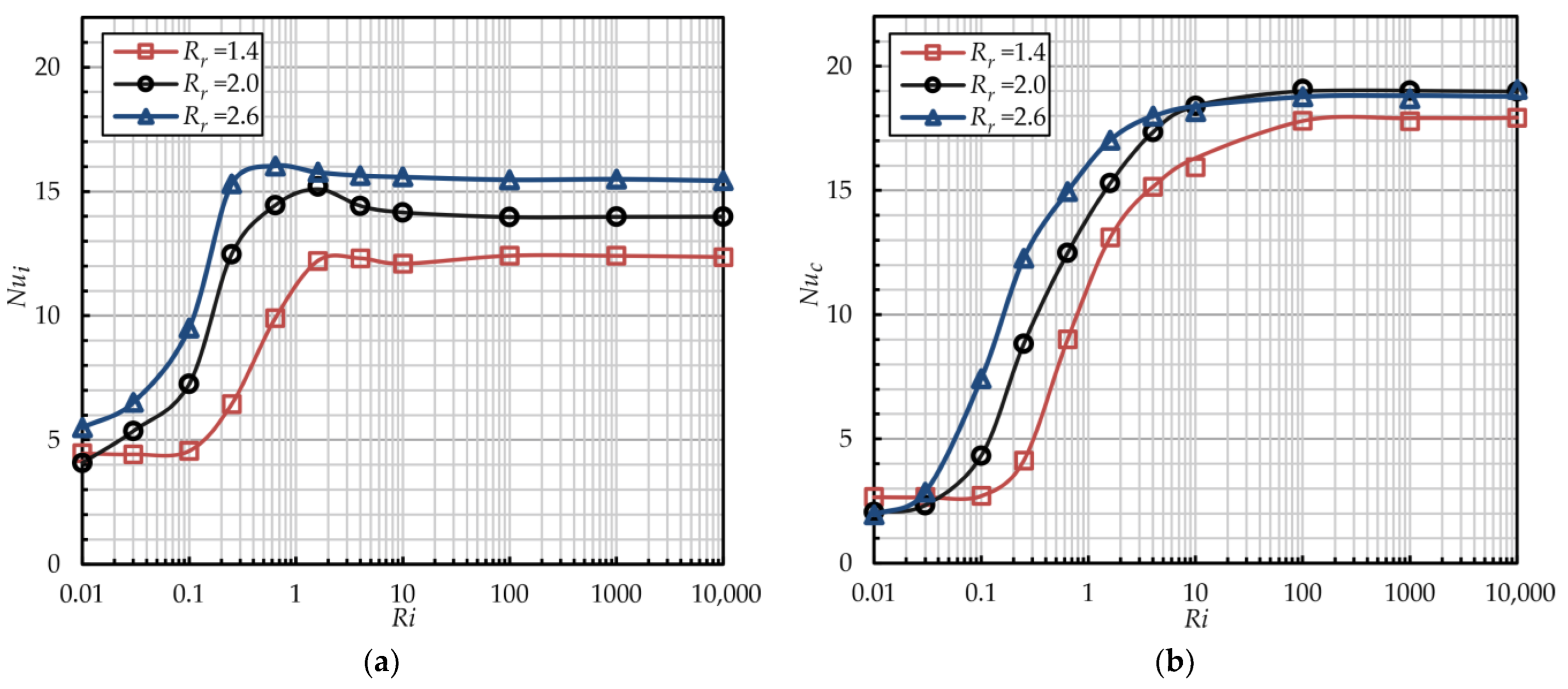
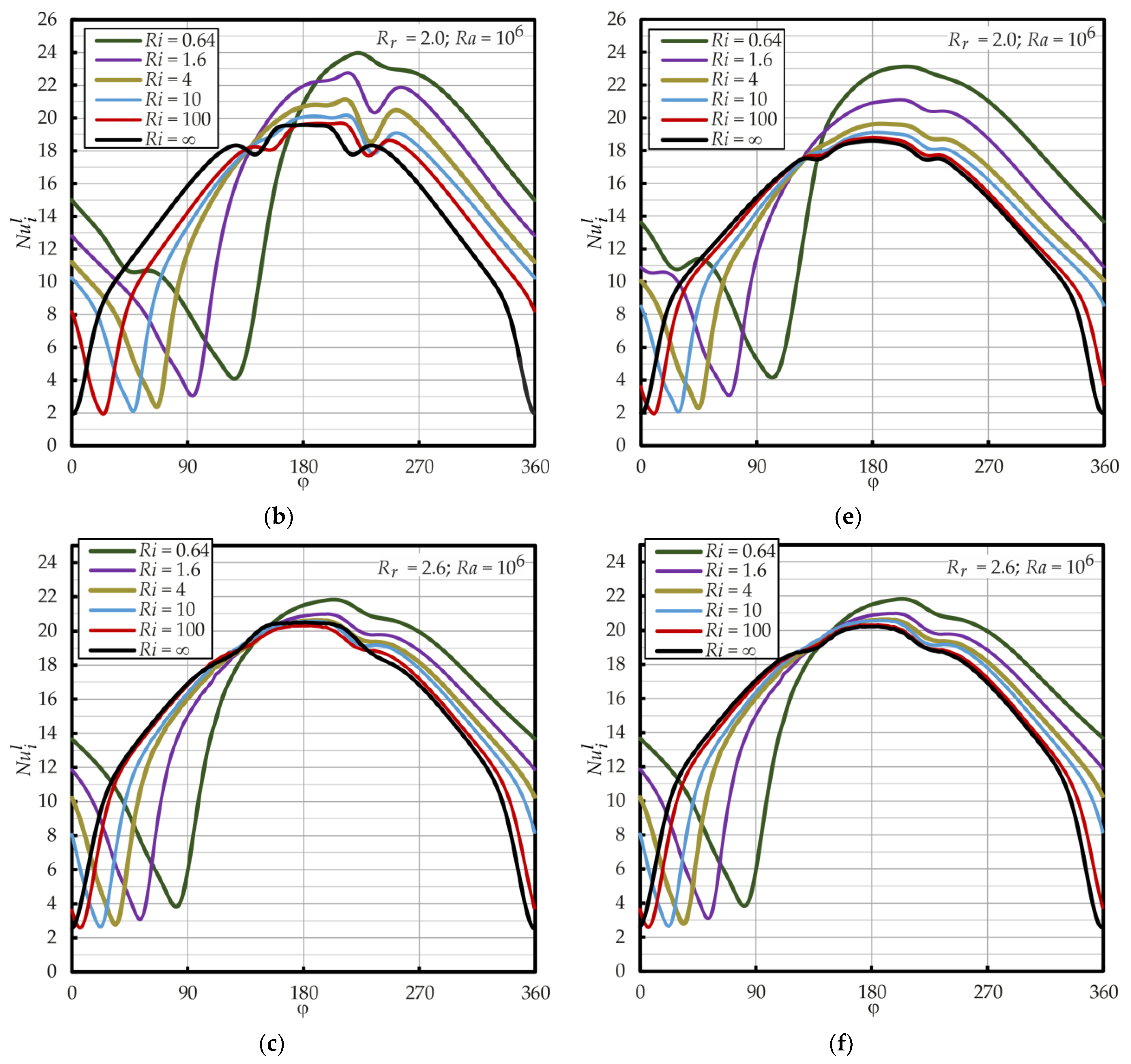
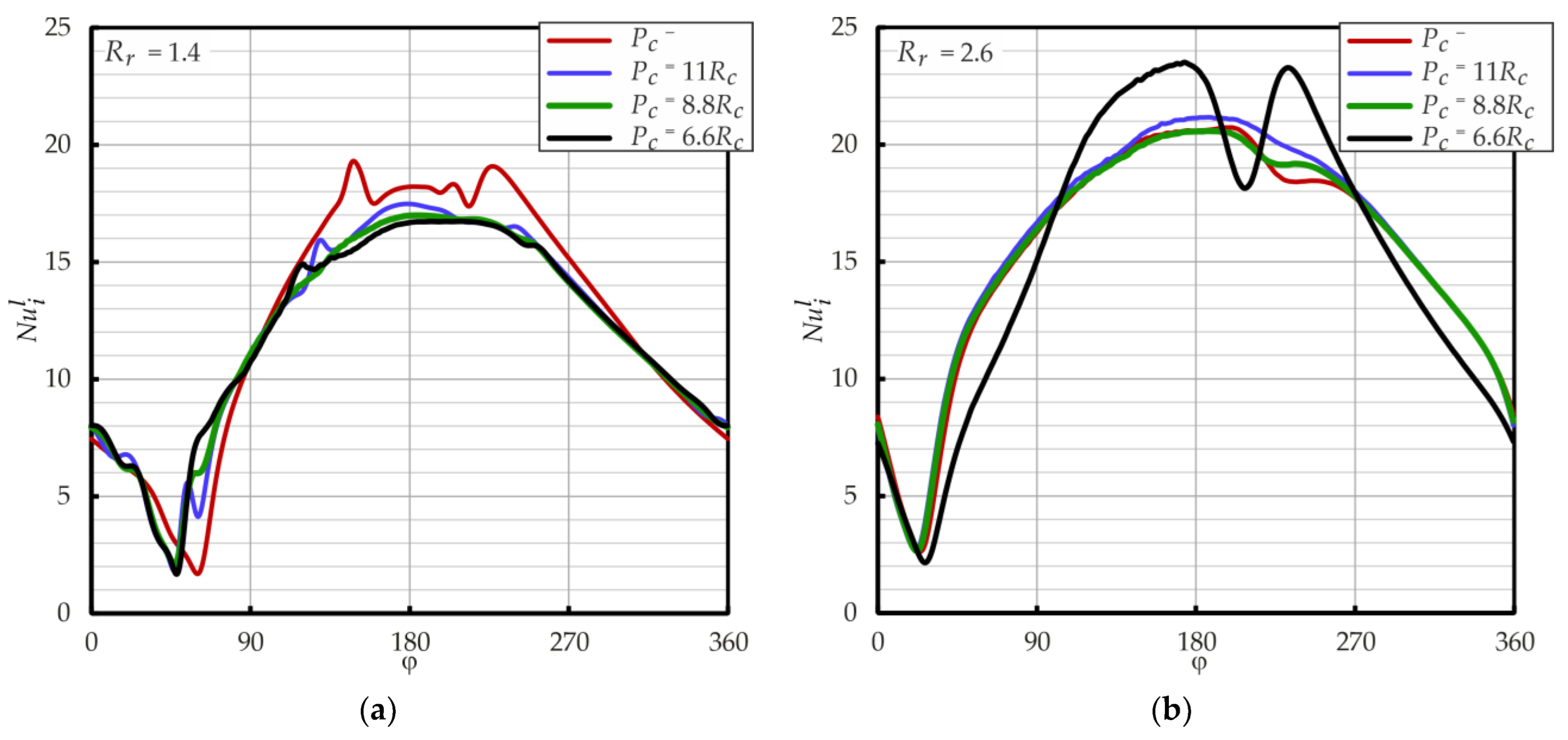
4.3. Influence of Radius Ratio Rr
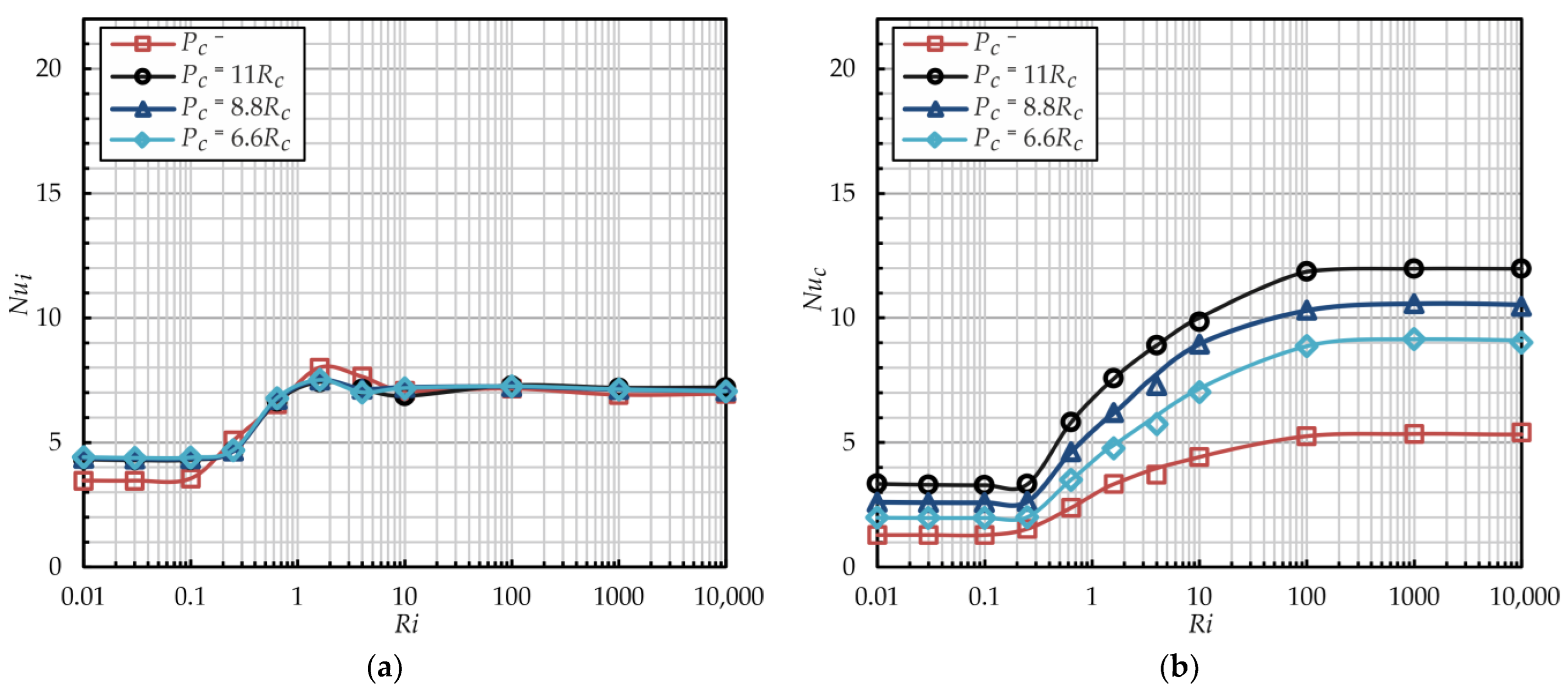
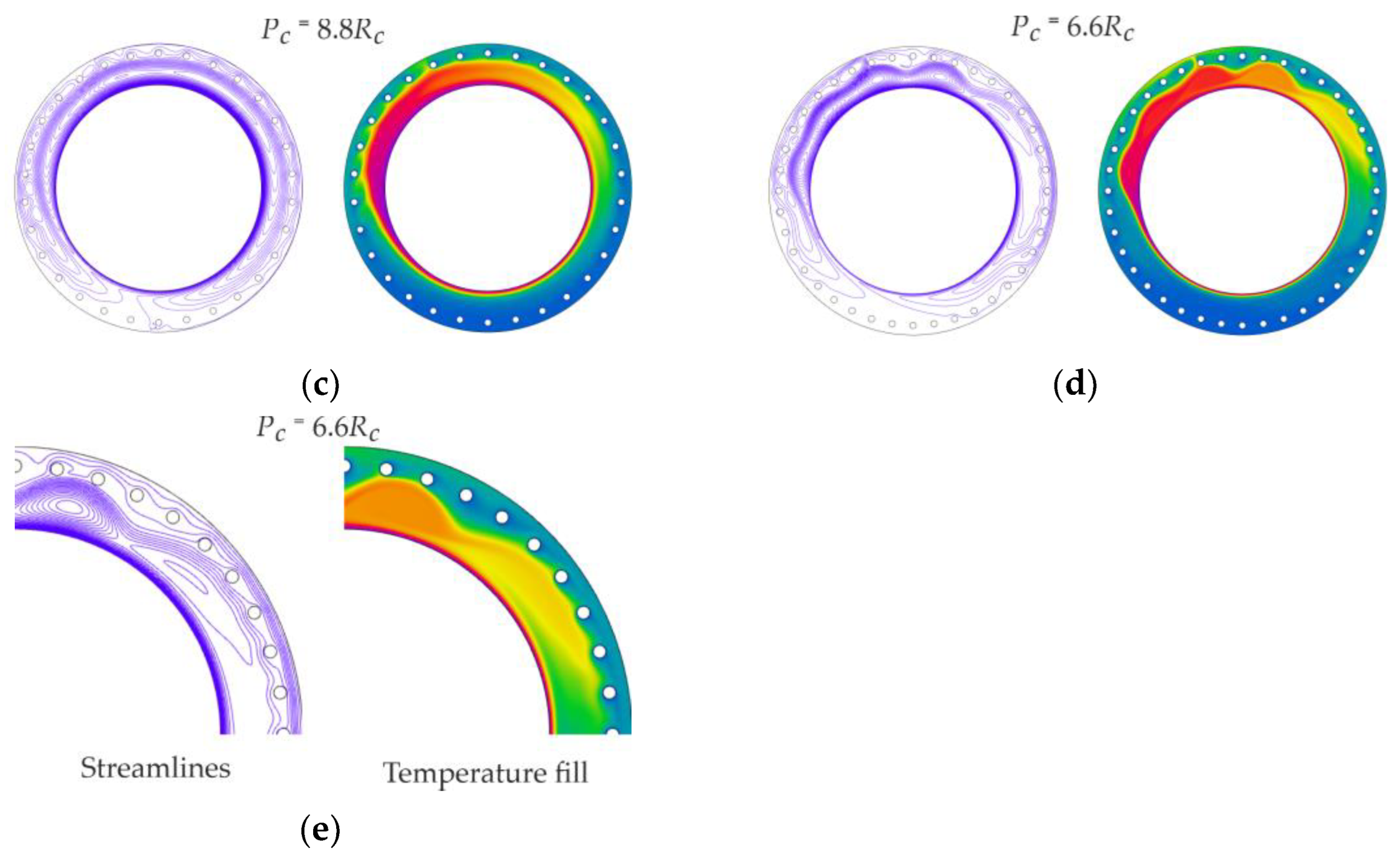
4.4. Effect of the Radial Cylinder Spacing
5. Conclusions
- The addition of radial cylinders does not result in significant changes in the critical Ri, nor does it alter the intensity or local distribution of the heat transfer on the inner rotating cylinder. The Nusselt number increases when the outer flat surface is replaced by the radial cylinder array: in the free convection regime, 1.4 times and 1.8 times with Ra = 104 and Ra > 105, respectively, and in the forced convection regime, two times. In the forced regime, the intensity of heat transfer on the inner and radial cylinders varies only minimally. With Ra = 106, the Nusselt number for the radial cylinders is 20% higher than that of the inner cylinder.
- For wide annuli gaps Rr > 2.0 with radial cylinders, the maximal values of the Nusselt number are observed with the maximal pitch (Pc = 11Rc), and with the minimal pitch (Pc = 3.3Rc), the heat transfer intensity falls to the same level as for annuli without radial cylinders (approximately 2 times lower). In narrow gaps Rr < 2.0, the maximal Nusselt number is also observed with the maximal pitch; however, with the minimal pitch, the heat transfer intensity is still approximately 1.8 times higher than for the flat outer wall.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nomenclature | |
| Cp | specific heat, J∙(kgK)−1 |
| g | gravitational acceleration, 9.81 m∙s−2 |
| Gr | Grashof number |
| L = ro − ri | characteristic length (annuli gap width), m |
| nc | number of radial cylinders |
| Nu | Nusselt number |
| p, P | pressure, Pa, dimensionless pressure |
| pc, Pc | radial spacing of radial cylinders (pitch), m, dimensionless spacing |
| Pr | Prandtl number |
| r, R | radius, m, dimensionless radius |
| Ra | Rayleigh number |
| rcc, Rcc | distance from radial cylinder centers to the annular channel center, m, dimensionless distance |
| Re | Reynolds number |
| Ri | Richardson number |
| Rr | radius ratio |
| S | area of surface, m2 |
| t, Θ | temperature, K, dimensionless temperature |
| T, τ | time, s, dimensionless time |
| Tp | averaging period |
| u,v; U,V | velocity components in x and y directions, m∙s−1; dimensionless velocity components |
| x, y; X,Y | Cartesian coordinates, m; dimensionless coordinates |
| Greek symbols | |
| β | thermal expansion factor, K−1 |
| φ | angle |
| λ | thermal conductivity, W∙(m∙K)−1 |
| ν | kinematic viscosity, m2∙s−1 |
| ρ | density, kg∙m−3 |
| ω | rotational rate, s−1 |
| Subscripts | |
| c | radial cylinders |
| i | inner cylinder |
| o | outer wall |
| b | bulk |
| Supersubscripts | |
| f | finest mesh |
| i | instantaneous |
| l | local |
References
- Yoo, J.-S. Mixed Convection of Air between Two Horizontal Concentric Cylinders with a Cooled Rotating Outer Cylinder. Int. J. Heat Mass Transf. 1998, 41, 293–302. [Google Scholar] [CrossRef]
- Chart, M. Numerical Prediction of Turbulent Mixed Convection in a Concentric Horizontal Rotating Annulus with Low-Re Two-Equation Models. Int. J. Heat Mass Transf. 1998, 41, 1633–1643. [Google Scholar] [CrossRef]
- Farouk, B.; Ball, K.S. Convective Flows around a Rotating Isothermal Cylinder. Int. J. Heat Mass Transf. 1985, 28, 1921–1935. [Google Scholar] [CrossRef]
- Ozerdem, B. Measurement of Convective Heat Transfer Coefficient for a Horizontal Cylinder Rotating in Quiescent Air. Int. Commun. Heat Mass Transf. 2000, 27, 389–395. [Google Scholar] [CrossRef]
- Ma, H.; Xia, W.; Zhou, W.; Liu, W.; Guo, Z.; Zhang, C.; Zhang, Y.; Deng, N. Experimental Investigation on the Steady, External Laminar Mixed Convection Heat Transfer Characteristics around a Large Diameter Horizontal Rotating Cylinder. Int. Commun. Heat Mass Transf. 2014, 57, 239–246. [Google Scholar] [CrossRef]
- Ma, H.; Lu, W.; Zhou, W.; Ding, Z.; Lü, X.; Cao, Y.; Zhang, Y.; Deng, N. Effects of Rotation on the Trailing Vortex and Heat Transfer from a Horizontal Rotating Cylinder at Higher Grashof Number. Int. Commun. Heat Mass Transf. 2015, 68, 20–26. [Google Scholar] [CrossRef]
- Ghaddar, N.K.; Thiele, F. Natural Convection over a Rotating Cylindrical Heat Source in a Rectangular Enclosure. Numer. Heat Transf. Part A Appl. 1994, 26, 701–719. [Google Scholar] [CrossRef]
- Costa, V.A.F.; Raimundo, A.M. Steady Mixed Convection in a Differentially Heated Square Enclosure with an Active Rotating Circular Cylinder. Int. J. Heat Mass Transf. 2010, 53, 1208–1219. [Google Scholar] [CrossRef]
- Hussain, S.H.; Hussein, A.K. Mixed Convection Heat Transfer in a Differentially Heated Square Enclosure with a Conductive Rotating Circular Cylinder at Different Vertical Locations. Int. Commun. Heat Mass Transf. 2011, 38, 263–274. [Google Scholar] [CrossRef]
- Khanafer, K.; Aithal, S.M. Mixed Convection Heat Transfer in a Lid-Driven Cavity with a Rotating Circular Cylinder. Int. Commun. Heat Mass Transf. 2017, 86, 131–142. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Alshukri, M.J.; Jabbar, N.A.; Eidan, A.A.; Hashim, I. Entropy Generation and Mixed Convection of a Nanofluid in a 3D Wave Tank with Rotating Inner Cylinder. Energies 2022, 16, 244. [Google Scholar] [CrossRef]
- Hassen, W.; Selimefendigil, F.; Ben Khedher, N.; Kolsi, L.; Borjini, M.N.; Alresheedi, F. Control of Magnetohydrodynamic Mixed Convection and Entropy Generation in a Porous Cavity by Using Double Rotating Cylinders and Curved Partition. ACS Omega 2021, 6, 35607–35618. [Google Scholar] [CrossRef] [PubMed]
- Fénot, M.; Bertin, Y.; Dorignac, E.; Lalizel, G. A Review of Heat Transfer between Concentric Rotating Cylinders with or without Axial Flow. Int. J. Therm. Sci. 2011, 50, 1138–1155. [Google Scholar] [CrossRef]
- Lee, T.S. Laminar Fluid Convection between Concentric and Eccentric Heated Horizontal Rotating Cylinders for Low-Prandtl-Number Fluids. Int. J. Numer. Methods Fluids 1992, 4, 1037–1062. [Google Scholar] [CrossRef]
- Lee, T.S. Numerical Study of Mixed Heat and Fluid Flow in Annuli of Heated Rotating Cylinders. Int. J. Comput. Fluid Dyn. 1998, 9, 151–163. [Google Scholar] [CrossRef]
- Prud’homme, M.; Robillard, L.; Hilal, M. Natural Convection in an Annular Fluid Layer Rotating at Weak Angular Velocity. Int. J. Heat Mass Transf. 1993, 36, 1529–1539. [Google Scholar] [CrossRef]
- Schneider, M.; Younis, B.A.; Weigand, B. Large-Eddy Simulations of Flow and Heat Transfer in Heated Concentric Annulus with Inner Cylinder Rotation. Int. J. Heat Mass Transf. 2017, 114, 1248–1262. [Google Scholar] [CrossRef][Green Version]
- Yang, H.Q.; Yang, K.T.; Lloyd, J.R. Natural Convection Suppression in Horizontal Annuli by Azimuthal Baffles. Int. J. Heat Mass Transf. 1988, 31, 2123–2135. [Google Scholar] [CrossRef]
- Kitamura, K.; Mitsuishi, A.; Suzuki, T. Natural Convection Heat Transfer from Horizontal Array of Heated Cylinders. Trans. JSME 2014, 80, TEP0201. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Kitamura, K.; Mitsuishi, A.; Suzuki, T.; Kimura, F. Fluid Flow and Heat Transfer of Natural Convection Induced around a Vertical Row of Heated Horizontal Cylinders. Int. J. Heat Mass Transf. 2016, 92, 414–429. [Google Scholar] [CrossRef]
- Ashjaee, M.; Yousefi, T. Experimental Study of Free Convection Heat Transfer from Horizontal Isothermal Cylinders Arranged in Vertical and Inclined Arrays. Heat Transf. Eng. 2007, 28, 460–471. [Google Scholar] [CrossRef]
- Mun, G.S.; Park, Y.G.; Yoon, H.S.; Kim, M.; Yeong Ha, M. Natural Convection in a Cold Enclosure with Four Hot Inner Cylinders Based on Diamond Arrays (Part-I: Effect of Horizontal and Vertical Equal Distance of Inner Cylinders). Int. J. Heat Mass Transf. 2017, 111, 755–770. [Google Scholar] [CrossRef]
- Mun, G.S.; Seo, Y.M.; Park, Y.G.; Ha, M.Y. Natural Convection in a Cold Enclosure with Four Hot Inner Cylinders in a Diamond Array (Part-II: Effect of Unequal Horizontal and Vertical Distances of Inner Cylinders). Int. J. Heat Mass Transf. 2018, 120, 1365–1373. [Google Scholar] [CrossRef]
- Abd Al-Hasan, A.Q.; Ismael, M.A.; Ghalambaz, M. Heat Transfer in a Vessel-Tubes Array with a Rotating Baffle: A Rotating Frame Modeling Approach. Int. J. Thermofluids 2024, 22, 100659. [Google Scholar] [CrossRef]
- Liao, C.C.; Lin, C.A. Mixed Convection of a Heated Rotating Cylinder in a Square Enclosure. Int. J. Heat Mass Transf. 2014, 72, 9–22. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Electro Skills Series; Hemisphere Publishing Corporation: London, UK, 1980; ISBN 978-0-07-048740-6. [Google Scholar]
- Yang, H.; Zhang, W.; Zhu, Z. Unsteady Mixed Convection in a Square Enclosure with an Inner Cylinder Rotating in a Bi-Directional and Time-Periodic Mode. Int. J. Heat Mass Transf. 2019, 136, 563–580. [Google Scholar] [CrossRef]
- Raithby, G.D.; Hollands, K.G.T. A General Method of Obtaining Approximate Solutions to Laminar and Turbulent Free Convection Problems. Adv. Heat Transf. 1975, 11, 265–315. [Google Scholar] [CrossRef]
- Kuehn, T.H.; Goldstein, R.J. An Experimental Study of Natural Convection Heat Transfer in Concentric and Eccentric Horizontal Cylindrical Annuli. J. Heat Transf. 1978, 100, 635–640. [Google Scholar] [CrossRef]
- Choi, J.Y.; Kimt, M.-U. Three-Dimensional Linear Stability of Mixed-Convective Flow between Rotating Horizontal Concentric Cylinders. Int. J. Heat Mass Transf. 1995, 38, 27–285. [Google Scholar] [CrossRef]

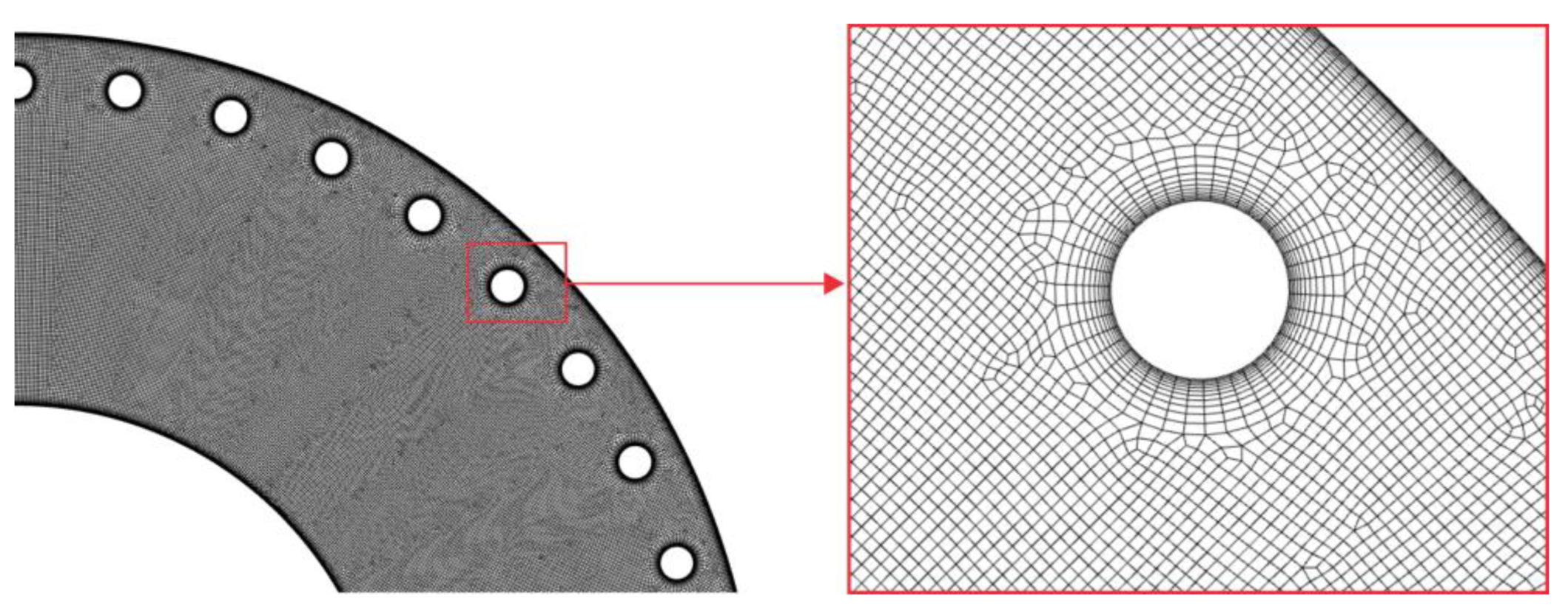








| Mesh | rc/Near-Wall Cell Height | Elements |
|---|---|---|
| Mesh#1 | 35 | 65,163 |
| Mesh#2 | 42 | 85,414 |
| Mesh#3 | 50 | 116,428 |
| Mesh#4 | 60 | 171,362 |
| Mesh#5 | 72 | 240,216 |
| Error, % | ||||||||
|---|---|---|---|---|---|---|---|---|
| Ri | 10−2 | 10−1 | 1.60 | 10 | 102 | 103 | 104 | |
| Mesh#1 | Nui | 1.17 | 2.07 | 1.19 | 1.12 | 0.90 | 1.02 | 1.05 |
| Nuc | 2.43 | 1.61 | 1.03 | 1.63 | 1.21 | 1.53 | 1.59 | |
| Mesh#2 | Nui | 3.97 | 0.51 | 0.61 | 0.62 | 0.61 | 0.59 | 0.57 |
| Nuc | 3.32 | 0.13 | 0.58 | 0.84 | 0.93 | 0.87 | 0.84 | |
| Mesh#3 | Nui | 4.38 | 0.51 | 0.40 | 0.43 | 0.44 | 0.48 | 0.49 |
| Nuc | 3.43 | 0.01 | 0.30 | 0.53 | 0.62 | 0.68 | 0.71 | |
| Mesh#4 | Nui | 0.69 | 0.09 | 0.02 | 0.08 | 0.04 | 0.08 | 0.07 |
| Nuc | 0.87 | 0.13 | 0.11 | 0.09 | 0.03 | 0.14 | 0.10 | |
| Ra | Rr | Present | Raithby and Hollands [27] | Error, % |
|---|---|---|---|---|
| 104 | 1.4 | 0.70 | 0.65 | 7.29 |
| 105 | 1.4 | 11.88 | 11.51 | 3.14 |
| 106 | 1.4 | 210.64 | 204.60 | 2.87 |
| 104 | 1.7 | 0.16 | 0.15 | 2.62 |
| 105 | 1.7 | 2.56 | 2.69 | 5.34 |
| 106 | 1.7 | 44.69 | 47.86 | 7.10 |
| 104 | 2.0 | 0.06 | 0.07 | 6.81 |
| 105 | 2.0 | 1.25 | 1.21 | 3.53 |
| 106 | 2.0 | 21.82 | 21.50 | 1.46 |
| 104 | 2.6 | 0.03 | 0.03 | 3.39 |
| 105 | 2.6 | 0.47 | 0.49 | 5.17 |
| 106 | 2.6 | 7.95 | 8.74 | 9.89 |
| Average | 4.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayrullin, A.; Sinyavin, A.; Haibullina, A.; Khusnutdinova, M.; Bronskaya, V.; Bashkirov, D.; Gilmutdinov, I.; Ignashina, T. Heat Transfer in Annular Channels with the Inner Rotating Cylinder and the Radial Array of Cylinders. Energies 2024, 17, 6047. https://doi.org/10.3390/en17236047
Hayrullin A, Sinyavin A, Haibullina A, Khusnutdinova M, Bronskaya V, Bashkirov D, Gilmutdinov I, Ignashina T. Heat Transfer in Annular Channels with the Inner Rotating Cylinder and the Radial Array of Cylinders. Energies. 2024; 17(23):6047. https://doi.org/10.3390/en17236047
Chicago/Turabian StyleHayrullin, Aidar, Alex Sinyavin, Aigul Haibullina, Margarita Khusnutdinova, Veronika Bronskaya, Dmitry Bashkirov, Ilnur Gilmutdinov, and Tatyana Ignashina. 2024. "Heat Transfer in Annular Channels with the Inner Rotating Cylinder and the Radial Array of Cylinders" Energies 17, no. 23: 6047. https://doi.org/10.3390/en17236047
APA StyleHayrullin, A., Sinyavin, A., Haibullina, A., Khusnutdinova, M., Bronskaya, V., Bashkirov, D., Gilmutdinov, I., & Ignashina, T. (2024). Heat Transfer in Annular Channels with the Inner Rotating Cylinder and the Radial Array of Cylinders. Energies, 17(23), 6047. https://doi.org/10.3390/en17236047






