Analysis of Factors Influencing Life Cycle Costs of Transformers Based on TOPSIS Method
Abstract
1. Introduction
2. Methodology
2.1. LCC Theory
2.1.1. The Initial Investment of the Transformer [31]
2.1.2. Operation and Repair Costs
2.1.3. Failure Costs
2.1.4. Disposal Costs
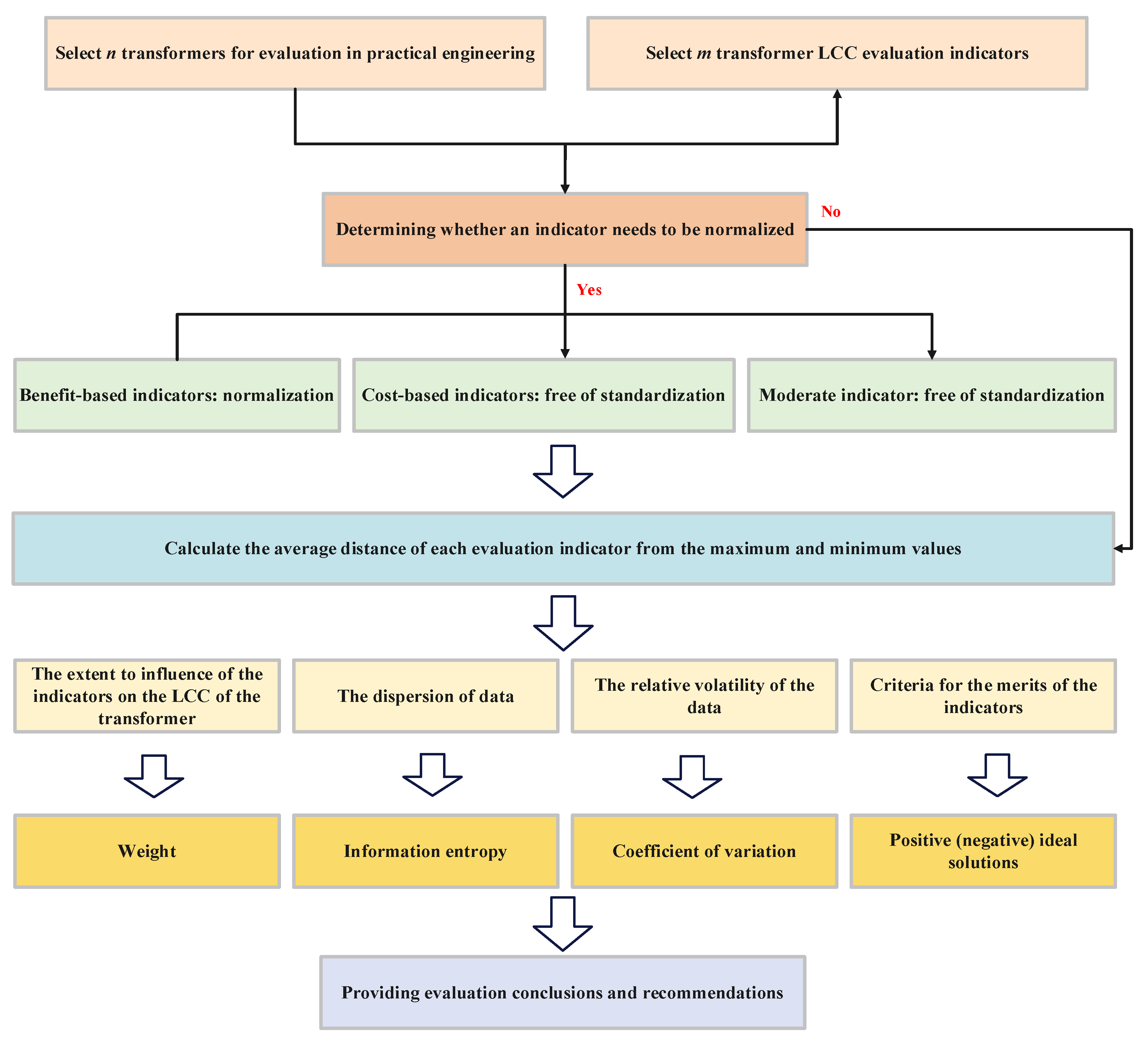
2.2. TOPSIS Method
2.2.1. Basic Data Matrix
2.2.2. Data Standardization
2.2.3. Information Entropy Weights for Indicators
2.2.4. Coefficient of Variation
2.2.5. Weights for Indicators
3. Results and Discussion
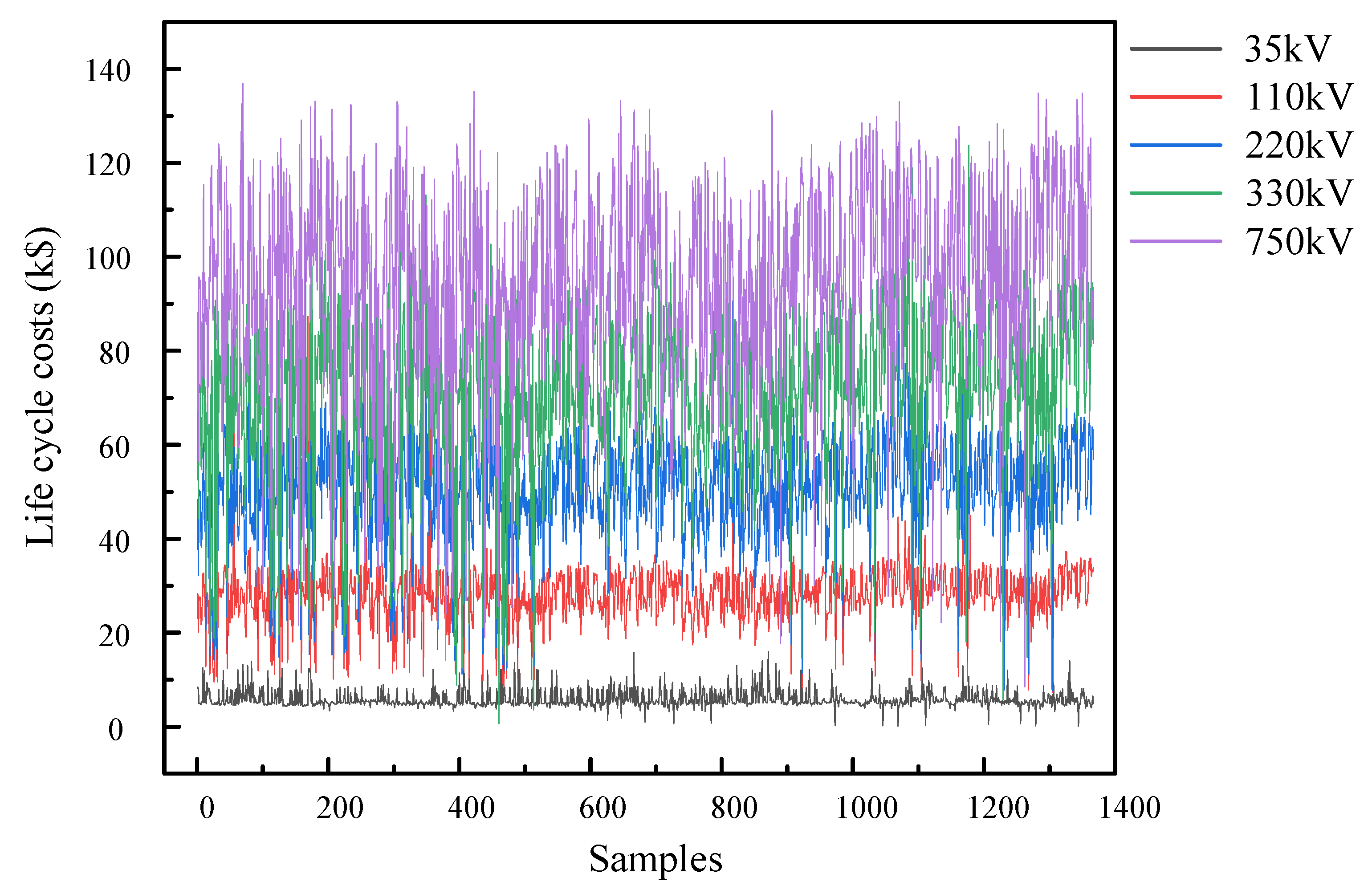
3.1. LCC Results
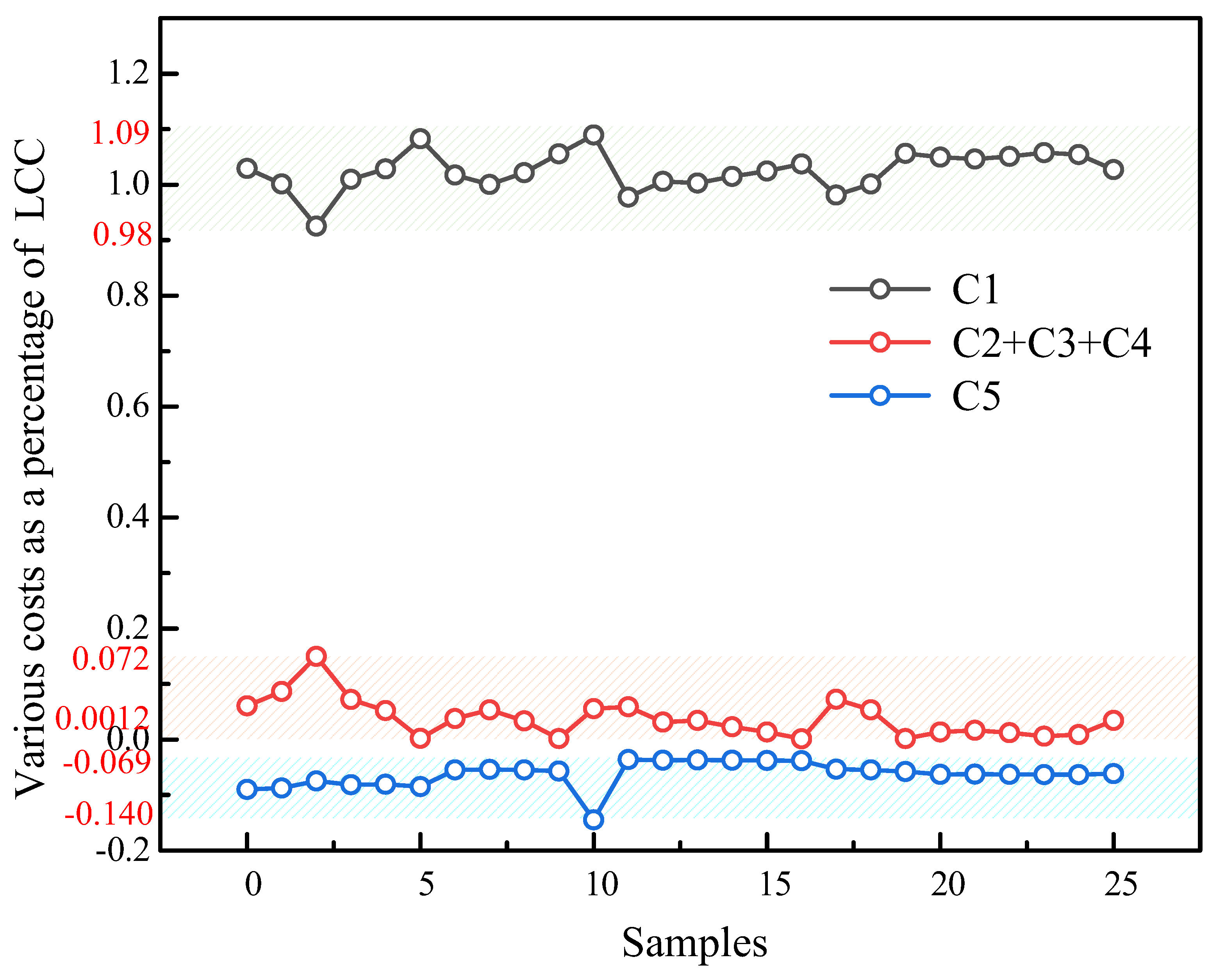
3.2. Weighted Assessment
3.3. Single-Factor Impacts
3.3.1. Voltage Level
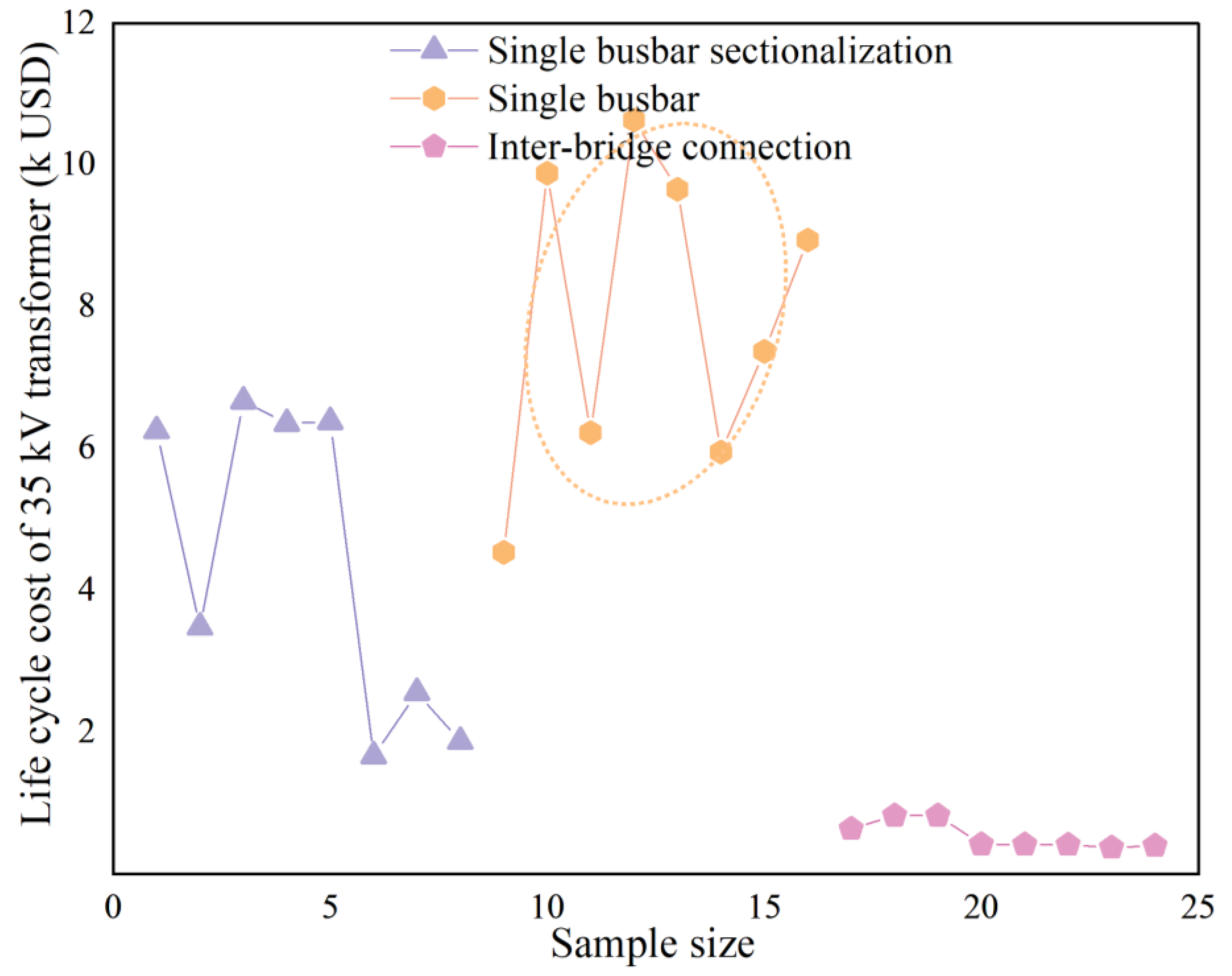
3.3.2. Wiring Methods
3.3.3. Transformer Types
3.3.4. Cooling Methods
3.4. Multifactor Coupling Impact
4. Discussion
4.1. Conclusions
4.2. Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | alternating current |
| LCC | life cycle cost |
| TOPSIS | Technique for Order Preference by Similarity to an Ideal Solution |
| ONAN | oil-immersed natural air-cooled |
| ONAF | oil-immersed forced air-cooled |
| OFAF | forced oil circulation air-cooled |
| ODAF | forced oil circulation directed air cooling |
| O&M costs | operation and maintenance costs |
| UHV | ultra-high voltage |
References
- Fan, L.; Chen, H.; Zhao, S.; Wang, Y. Comparative Economic Analysis of Transmission Lines Adopted for Energy-Saving Conductors Considering Life Cycle Cost. Inventions 2024, 9, 75. [Google Scholar] [CrossRef]
- Zhou, C.; Che, C.; Wang, P.; Zhang, Q. Diformer: A dynamic self-differential transformer for new energy power autoregressive prediction. Knowl. Based Syst. 2023, 281, 111061. [Google Scholar] [CrossRef]
- Marchi, B.; Zanoni, S.; Mazzoldi, L.; Reboldi, R. Energy Efficient EAF Transformer—A Holistic Life Cycle Cost Approach. Procedia CIRP 2016, 48, 319–324. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, B.; Li, Y.; Sun, Q.; Pedersen, T.B.; Gao, D.W. Pricing Game and Blockchain for Electricity Data Trading in Low-Carbon Smart Energy Systems. IEEE Trans. Ind. Inform. 2024, 20, 6446–6456. [Google Scholar] [CrossRef]
- Soni, R.; Mehta, B. Evaluation of power transformer health analysis by internal fault criticalities to prevent premature failure using statistical data analytics approach. Eng. Fail. Anal. 2022, 136, 106213. [Google Scholar] [CrossRef]
- Han, G.; Feng, G.; Tang, C.; Pan, C.; Zhou, W.; Zhu, J. Evaluation of the ventilation mode in an ISO class 6 electronic cleanroom by the AHP-entropy weight method. Energy 2023, 284, 128586. [Google Scholar] [CrossRef]
- Zhao, X.; Gui, F.; Chen, H.; Fan, L.; Pan, P. Life Cycle Cost Estimation and Analysis of Transformers Based on Failure Rate. Appl. Sci. 2024, 14, 1210. [Google Scholar] [CrossRef]
- Han, H.; Li, X.; Gu, X.; Li, G. Urban rivers health assessment based on the concept of resilience using improved FCM-EWM-MABAC model. Ecol. Indic. 2023, 154, 110833. [Google Scholar] [CrossRef]
- Fan, L.; Chen, H.; Zhao, S.; Pan, P.; Xin, C.; Jiang, X. Research on the Impact of Carbon Emission Reduction Technology on the Cost of Transmission and Transformation Project Based on Hierarchical Analysis Method. In Proceedings of the 2023 6th International Conference on Renewable Energy and Power Engineering (REPE), Beijing, China, 15–17 September 2023; pp. 346–351. [Google Scholar]
- Cervero, D.; Fotopoulou, M.; Muñoz-Cruzado, J.; Rakopoulos, D.; Stergiopoulos, F.; Nikolopoulos, N.; Voutetakis, S.; Sanz, J.F. Solid State Transformers: A Critical Review of Projects with Relevant Prototypes and Demonstrators. Electronics 2023, 12, 931. [Google Scholar] [CrossRef]
- Meyer, C.; De Doncker, R.W. LCC Analysis of Different Resonant Circuits and Solid-State Circuit Breakers for Medium-Voltage Grids. IEEE Trans. Power Deliv. 2006, 21, 1414–1420. [Google Scholar] [CrossRef]
- Gustavsen, B.; Portillo, A.; Ronchi, R.; Mjelve, A. Measurements for validation of manufacturer’s white-box transformer models. Procedia Eng. 2017, 202, 240–250. [Google Scholar] [CrossRef]
- Safaei, F.; Niasati, M. Calculation of UHV transformer insulation risk by extended Monte Carlo method. Electr. Power Syst. Res. 2023, 218, 109219. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Chen, J.; Wang, Q. Air pollution concentration forecasting based on wavelet transform and combined weighting forecasting model. Atmos. Pollut. Res. 2021, 12, 101144. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, H.; Zhao, S.; Fan, L.; Xin, C.; Jiang, X.; Yao, F. Benefit Evaluation of Carbon Reduction in Power Transmission and Transformation Projects Based on the Modified TOPSIS-RSR Method. Energies 2024, 17, 2988. [Google Scholar] [CrossRef]
- Xin, C.; Zhao, S.; Shi, W.; Huo, H.; Chen, H. Comprehensive Cost and Benefit Evaluation of Carbon Reduction Technologies for Power Transmission and Transformation Projects Based on Hierarchical Analysis and Entropy Power Method. In Proceedings of the 2023 8th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 22–25 September 2023; pp. 1541–1545. [Google Scholar]
- Wang, Y.; Liu, P.; Yao, Y. BMW-TOPSIS: A generalized TOPSIS model based on three-way decision. Inf. Sci. 2022, 607, 799–818. [Google Scholar] [CrossRef]
- Chen, X.; Ou, Y. Carbon emission accounting for power transmission and transformation equipment: An extended life cycle approach. Energy Rep. 2023, 10, 1369–1378. [Google Scholar] [CrossRef]
- Liu, S.; Dong, F.; Hao, J.; Qiao, L.; Guo, J.; Wang, S.; Luo, R.; Lv, Y.; Cui, J. Combination of hyperspectral imaging and entropy weight method for the comprehensive assessment of antioxidant enzyme activity in Tan mutton. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2023, 291, 122342. [Google Scholar] [CrossRef]
- Yu, X.; Qian, L.; Wang, W.; Hu, X.; Dong, J.; Pi, Y.; Fan, K. Comprehensive evaluation of terrestrial evapotranspiration from different models under extreme condition over conterminous United States. Agric. Water Manag. 2023, 289, 108555. [Google Scholar] [CrossRef]
- Xu, S.; Xu, D.; Liu, L. Construction of regional informatization ecological environment based on the entropy weight modified AHP hierarchy model. Sustain. Comput. Inform. Syst. 2019, 22, 26–31. [Google Scholar] [CrossRef]
- Cao, J.; Xu, F. Entropy-Based Fuzzy TOPSIS Method for Investment Decision Optimization of Large-Scale Projects. Comput. Intell. Neurosci. 2022, 2022, 4381293. [Google Scholar] [CrossRef]
- Santiago, L.; Bedregal, B. Multidimensional fuzzy sets: Negations and an algorithm for multi-attribute group decision making. Int. J. Approx. Reason. 2024, 169, 109171. [Google Scholar] [CrossRef]
- Ahmad, R.; Gabriel, H.F.; Alam, F.; Zarin, R.; Raziq, A.; Nouman, M.; Young, H.-W.V.; Liou, Y.-A. Remote sensing and GIS based multi-criteria analysis approach with application of AHP and FAHP for structures suitability of rainwater harvesting structures in Lai Nullah, Rawalpindi, Pakistan. Urban Clim. 2024, 53, 101817. [Google Scholar] [CrossRef]
- Jin, L.; Kim, D.; Abu-Siada, A. State-of-the-art review on asset management methodologies for oil-immersed power transformers. Electr. Power Syst. Res. 2023, 218, 109194. [Google Scholar] [CrossRef]
- Wątróbski, J.; Bączkiewicz, A.; Ziemba, E.; Sałabun, W. Sustainable cities and communities assessment using the DARIA-TOPSIS method. Sustain. Cities Soc. 2022, 83, 103926. [Google Scholar] [CrossRef]
- Lei, X.; Xin-gang, Z. The synergistic effect between Renewable Portfolio Standards and carbon emission trading system: A perspective of China. Renew. Energy 2023, 211, 1010–1023. [Google Scholar] [CrossRef]
- Guamán, W.; Pesántez, G.; Falcones, S.; Urquizo, J. Optimal dynamic reactive power compensation in power systems: Case study of Ecuador-Perú interconnection. Electr. Power Syst. Res. 2023, 218, 109191. [Google Scholar] [CrossRef]
- Awais, M.; Basit, A.; Adnan, R.; Khan, Z.A.; Qasim, U.; Shafique, T.; Javaid, N. Overload Management in Transmission System Using Particle Swarm Optimization. Procedia Comput. Sci. 2015, 52, 858–865. [Google Scholar] [CrossRef]
- Shilei, G.; Zhixin, B. The analysis of energy saving transformer with variable energy saving effect evaluation efficiency considering the typical load characteristic. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 3078–3083. [Google Scholar]
- Zhao, S.; Chen, H.; Fan, L.; Pan, P.; Xin, C.; Jiang, X. Comprehensive Evaluation and Optimal Selection of Carbon Reduction Technologies for Power Transmission and Transformation Projects. In Proceedings of the 2023 6th International Conference on Renewable Energy and Power Engineering (REPE), Beijing, China, 15–17 September 2023; pp. 381–385. [Google Scholar]
- Jia, C.; Chen, H.; Zhao, S.; Xin, C.; Jiang, X.; Chen, H. Performance Evaluation of Transformer Substations Based on EWM-GRA. In Proceedings of the 2023 6th International Conference on Renewable Energy and Power Engineering (REPE), Beijing, China, 15–17 September 2023; pp. 122–126. [Google Scholar]
- Li, C.; Zhang, H.; Zhou, H.; Sun, D.; Dong, Z.; Li, J. Double-layer optimized configuration of distributed energy storage and transformer capacity in distribution network. Int. J. Electr. Power Energy Syst. 2023, 147, 108834. [Google Scholar] [CrossRef]
- Oliyide, R.O.; Cipcigan, L.M. Adaptive thermal model for loading of transformers in low carbon electricity distribution networks. Sci. Afr. 2023, 20, e1683. [Google Scholar] [CrossRef]
- Guo, H.; Gao, Y.; Li, J. The greenhouse gas emissions of power transformers based on life cycle analysis. Energy Rep. 2022, 8, 413–419. [Google Scholar] [CrossRef]
- Li, Q.; Duan, H.; Xie, M.; Kang, P.; Ma, Y.; Zhong, R.; Gao, T.; Zhong, W.; Wen, B.; Bai, F.; et al. Life cycle assessment and life cycle cost analysis of a 40 MW wind farm with consideration of the infrastructure. Renew. Sustain. Energy Rev. 2021, 138, 110499. [Google Scholar] [CrossRef]
- Pei, Z.; Liu, J.; Hao, F.; Zhou, B. FLM-TOPSIS: The fuzzy linguistic multiset TOPSIS method and its application in linguistic decision making. Inf. Fusion 2019, 45, 266–281. [Google Scholar] [CrossRef]
- Liang, H.; Lin, D.S. Research on the Transformer Condition Assessment Based on the Entropy Weight Method. Adv. Mater. Res. 2013, 732, 930–935. [Google Scholar] [CrossRef]
- Zaharuddin, F.; Thayoob, Y.M.; Verayiah, R.; Ghazali, Y.Y. Life Cycle Cost Estimation of Distribution Transformer Failure from Life Data Exploration. Int. J. Eng. Adv. Technol. 2019, 9, 4025–4029. [Google Scholar] [CrossRef]
- Firis, F.A. Determining the optimum medium voltage level by analysis of different voltage levels. World J. Environ. Res. 2020, 10, 37–49. [Google Scholar] [CrossRef]
- Noran, M.N.; Shukri, Z. Adaptive breaker failure protection scheme for double busbar substation using IEC 61850 GOOSE message communication. In Proceedings of the 2015 International Symposium on Technology Management and Emerging Technologies (ISTMET), Langkawai Island, Malaysia, 25–27 August 2015. [Google Scholar]
- Ma, H.; Saha, T.K.; Ekanayake, C.; Martin, D. Smart Transformer for Smart Grid—Intelligent Framework and Techniques for Power Transformer Asset Management. IEEE Trans. Smart Grid 2015, 6, 1026–1034. [Google Scholar] [CrossRef]
- Taghikhani, M.A.; Afshar, M.R. Fans arrangement analysis in oil forced air natural cooling method of power transformer radiator. Proc. Inst. Mech. Eng. Part A: J. Power Energy 2020, 235, 904–913. [Google Scholar] [CrossRef]
- Zhan, W.; Goulart, A.E.; Falahi, M.; Rondla, P. Development of a Low-Cost Self-Diagnostic Module for Oil-Immerse Forced-Air Cooling Transformers. IEEE Trans. Power Deliv. 2015, 30, 129–137. [Google Scholar] [CrossRef]
- Garg, A.; Velandy, J. Thermal hydraulic network model for prediction of oil and temperature distribution in ester oil transformer under air natural and air forced cooling conditions. In Proceedings of the 2019 IEEE 4th International Conference on Condition Assessment Techniques in Electrical Systems (CATCON), Chennai, India, 21–23 November 2019. [Google Scholar]
- Dai, Y.; Zhang, M.; Zhang, F.; Chen, B.; Wang, H.; Li, W.; Dong, X. Practical Scheme of Optical Voltage Transformer in High Voltage Substations. In Proceedings of the 2022 IEEE 5th International Conference on Electronics Technology (ICET), Chengdu, China, 13–16 May 2022. [Google Scholar]


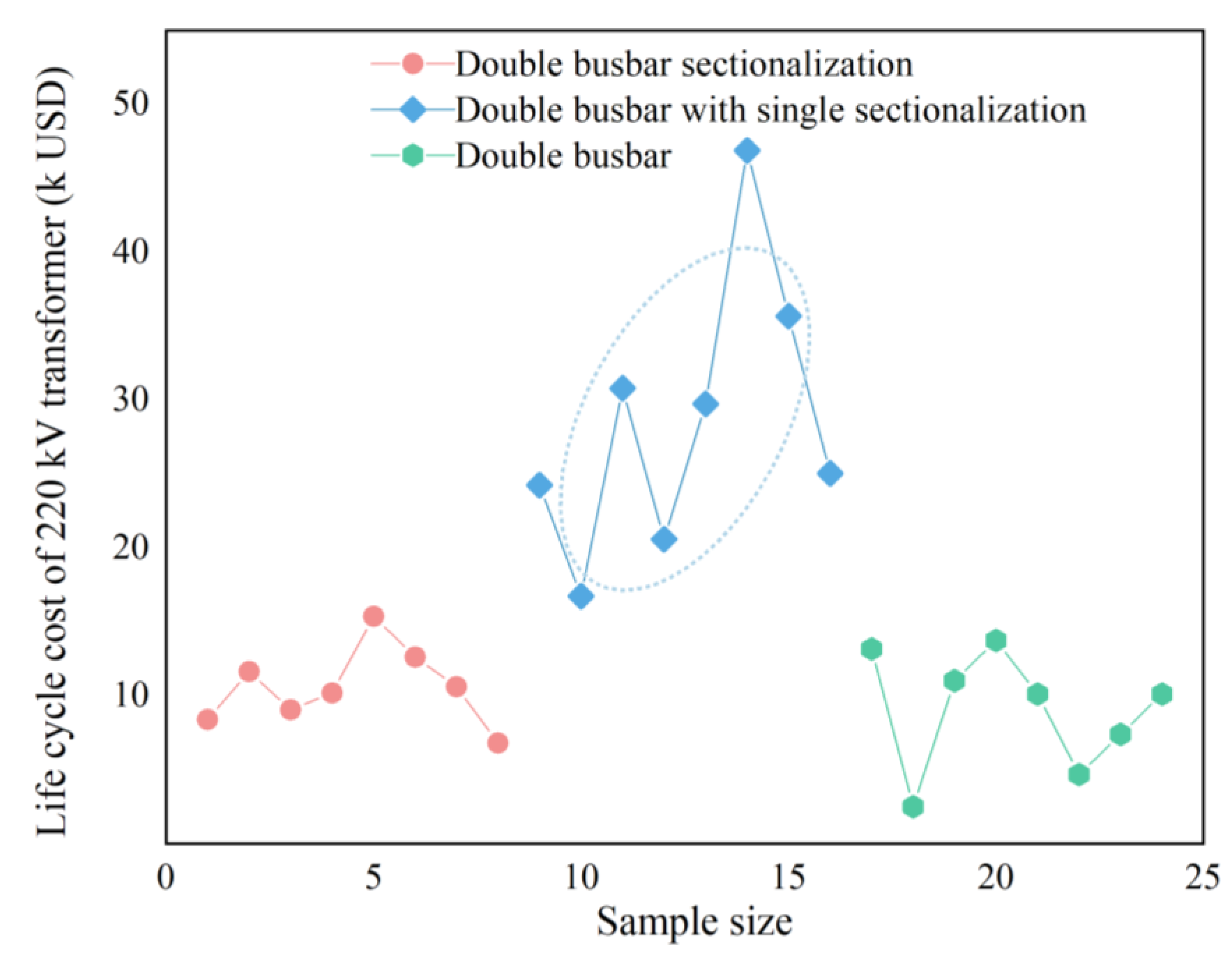


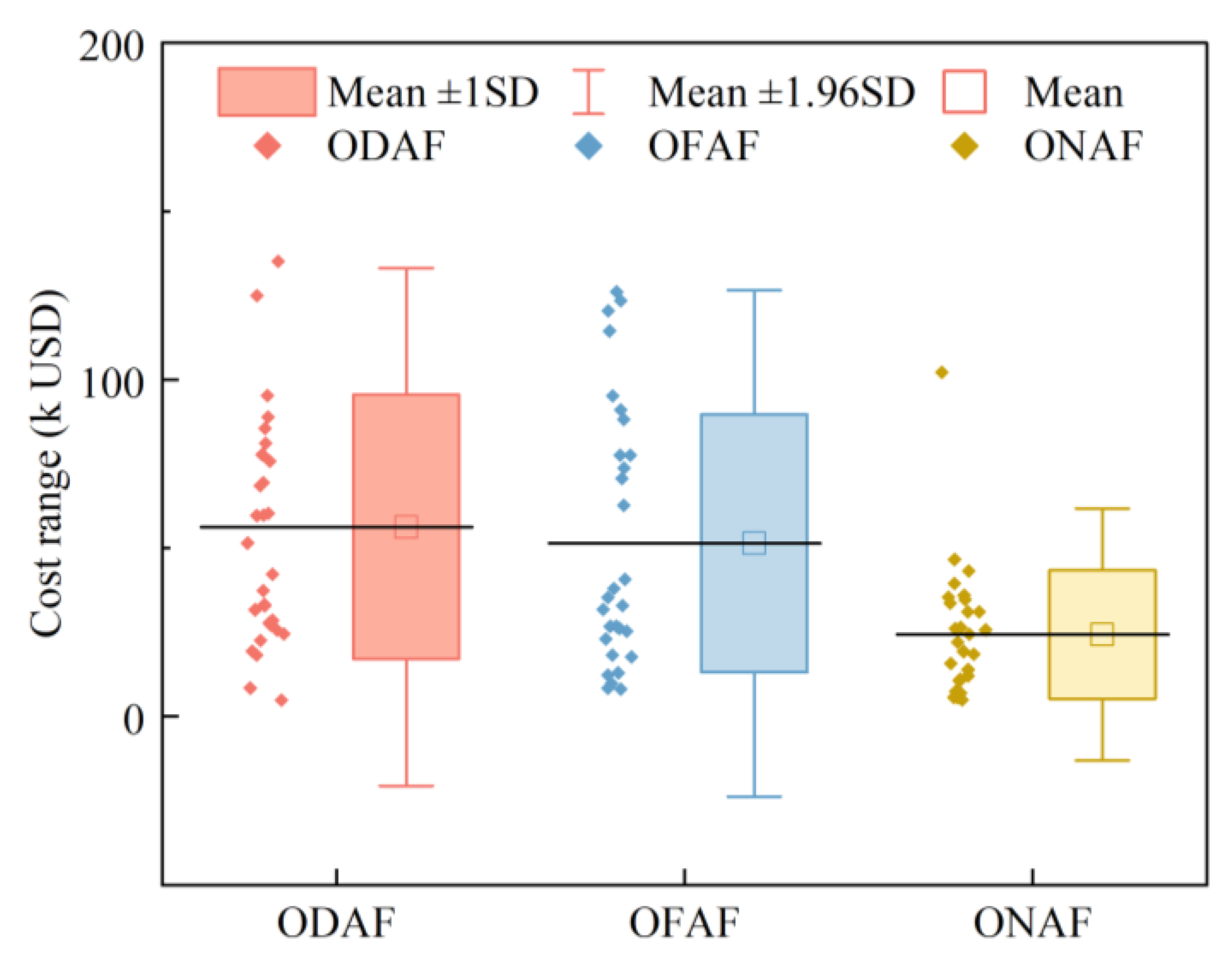

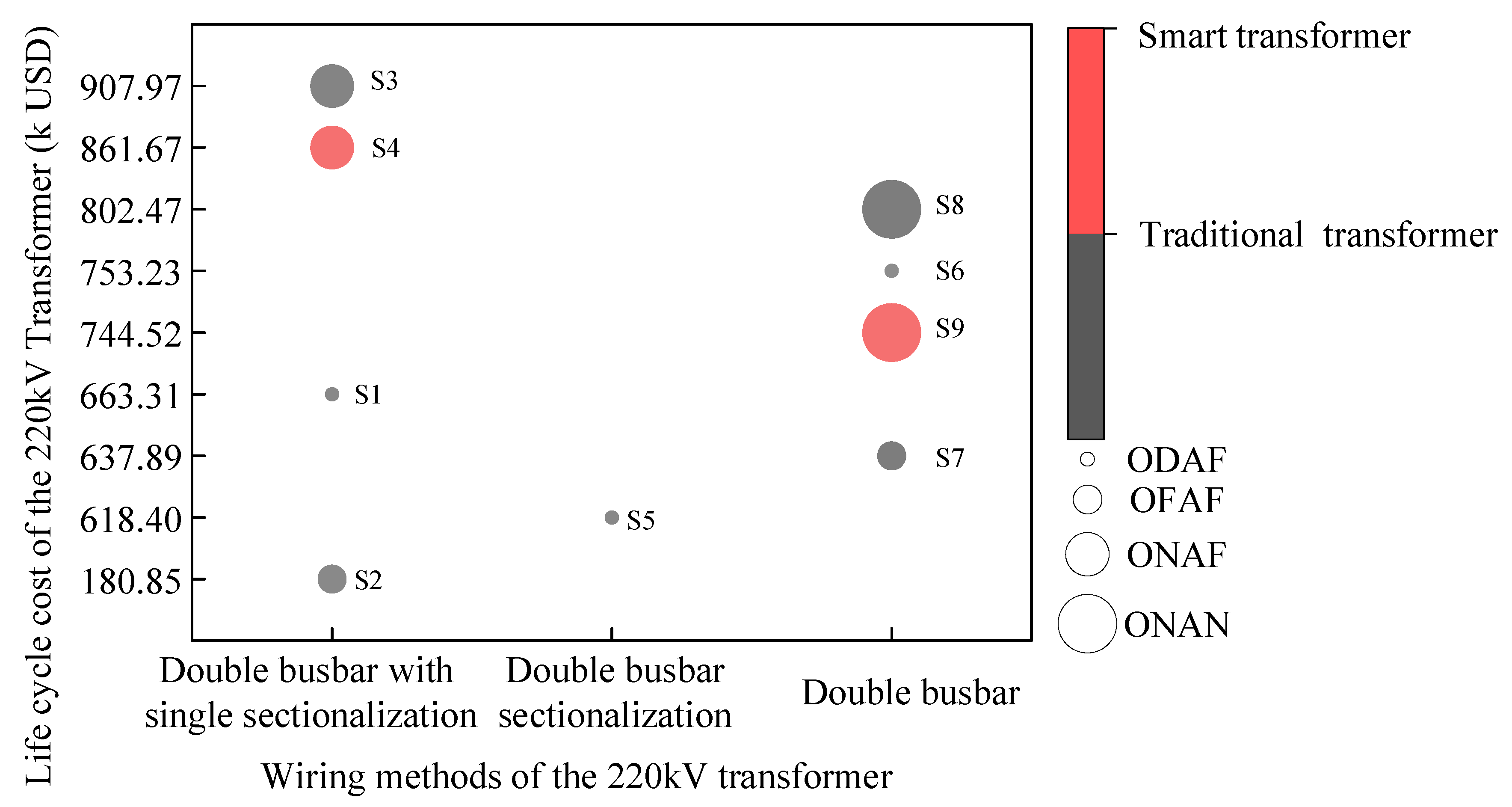

| Case | Substation | Wiring Scheme | Voltage Level | Switchgear | Is it a Smart Transformer? | Layout | Topographical Conditions | Cooling Method | RLA (Year) | LCC (USD) |
|---|---|---|---|---|---|---|---|---|---|---|
| Sample 1 | Qingshan substation | Single-busbar sectionalization | AC-35 kV | AIS | No | Indoor | Flatland | ONAN | 7 | 16,923.08 |
| Sample 2 | Yangming substation | Single busbar | AC-35 kV | AIS | No | Indoor | Mountain | ONAN | 6 | 15,600.77 |
| Sample 3 | Baimian substation | Single busbar | AC-35 kV | AIS | No | Indoor | Hills | ONAN | 6 | 17,443.89 |
| Sample 4 | Heping substation | Single busbar | AC-110 kV | AIS | No | Outdoor | Flatland | ONAN | 6 | 20,242.09 |
| Sample 5 | Binhe substation | Double-busbar sectionalization | AC-110 kV | AIS | No | Outdoor | Flatland | ONAN | 8.5 | 20,148.99 |
| Sample 6 | Zhonghe Substation | Single-busbar sectionalization | AC-110 kV | GIS | Yes | Outdoor | Mountain | ONAN | 6 | 19,011.31 |
| Sample 7 | Pingjibao Substation | Double busbar with single sectionalization | AC-220 kV | AIS | No | Outdoor | Flatland | ODAF | 6 | 32,582.86 |
| Sample 8 | Yuxiang Substation | Double busbar with single sectionalization | AC-220 kV | GIS | Yes | Outdoor | Flatland | ONAN | 6 | 22,209.88 |
| Sample 9 | Lanshan Substation | Double busbar | AC-220 kV | AIS | No | Outdoor | Flatland | ODAF | 6 | 34,098.58 |
| Sample 10 | Yingshuiqiao Substation | 3/2 wiring connection | AC-330 kV | GIS | No | Outdoor | Flatland | OFAF | 8 | 49,018.35 |
| Sample 11 | Muhe Substation | Double busbar with double sectionalization | AC-330 kV | AIS | Yes | Outdoor | Flatland | OFAF | 8 | 45,464.63 |
| Sample 12 | Yanzhou Substation | 3/2 wiring connection | AC-330 kV | AIS | No | Outdoor | Mountain | ODAF | 6 | 40,134.12 |
| Sample 13 | Yellow River Substation | 3/2 wiring connection | AC-750 kV | AIS | Yes | Indoor | Flatland | OFAF | 6 | 226,286.99 |
| Sample 14 | Helanshan Substation | Double busbar with double sectionalization | AC-750 kV | AIS | No | Outdoor | Mountain | OFAF | 6 | 61,318.65 |
| Sample 15 | Helanshan Substation Ⅱ | 3/2 wiring connection | AC-750 kV | GIS | No | Outdoor | Mountain | OFAF | 6 | 81,319.32 |
| Item | Wiring Scheme | Voltage Level | Switchgear | Is It a Smart Transformer? | Layout | Topographical Conditions | Cooling Method | RLA |
|---|---|---|---|---|---|---|---|---|
| Sample 1 | 0.3333 | 0 | 0 | 0 | 1 | 0 | 0 | 0.4 |
| Sample 2 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Sample 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Sample 4 | 0 | 0.25 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sample 5 | 0.1667 | 0.25 | 0 | 0 | 0 | 0 | 0 | 1 |
| Sample 6 | 0.3333 | 0.25 | 1 | 1 | 0 | 1 | 0 | 0 |
| Sample 7 | 0.6667 | 0.5 | 0 | 0 | 0 | 0 | 0.5 | 0 |
| Sample 8 | 0.6667 | 0.5 | 1 | 1 | 0 | 1 | 0 | 0 |
| Sample 9 | 0.5 | 0.5 | 0 | 0 | 0 | 0 | 0.5 | 0 |
| Sample 10 | 0 | 0.75 | 1 | 0 | 0 | 1 | 1 | 0.8 |
| Sample 11 | 1 | 0.75 | 0 | 1 | 0 | 0 | 1 | 0.8 |
| Sample 12 | 0.8333 | 0.75 | 0 | 0 | 0 | 0 | 0.5 | 0 |
| Sample 13 | 0.8333 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| Sample 14 | 0.8333 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| Sample 15 | 0.8333 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| … | … | … | … | … | … | … | … | … |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, L.; Chang, H.; Zhu, X.; Zhao, X.; Wei, G.; Cai, Z.; Xie, H.; Zhao, X.; Chen, H. Analysis of Factors Influencing Life Cycle Costs of Transformers Based on TOPSIS Method. Energies 2024, 17, 5912. https://doi.org/10.3390/en17235912
Zhan L, Chang H, Zhu X, Zhao X, Wei G, Cai Z, Xie H, Zhao X, Chen H. Analysis of Factors Influencing Life Cycle Costs of Transformers Based on TOPSIS Method. Energies. 2024; 17(23):5912. https://doi.org/10.3390/en17235912
Chicago/Turabian StyleZhan, Long, Hui Chang, Xiaolu Zhu, Xin Zhao, Gang Wei, Ziyu Cai, Haibin Xie, Xinyue Zhao, and Heng Chen. 2024. "Analysis of Factors Influencing Life Cycle Costs of Transformers Based on TOPSIS Method" Energies 17, no. 23: 5912. https://doi.org/10.3390/en17235912
APA StyleZhan, L., Chang, H., Zhu, X., Zhao, X., Wei, G., Cai, Z., Xie, H., Zhao, X., & Chen, H. (2024). Analysis of Factors Influencing Life Cycle Costs of Transformers Based on TOPSIS Method. Energies, 17(23), 5912. https://doi.org/10.3390/en17235912






