Proposal of Low-Speed Sensorless Control of IPMSM Using a Two-Interval Six-Segment High-Frequency Injection Method with DC-Link Current Sensing
Abstract
1. Introduction
2. Proposed Saliency-Based Sensorless Control Method
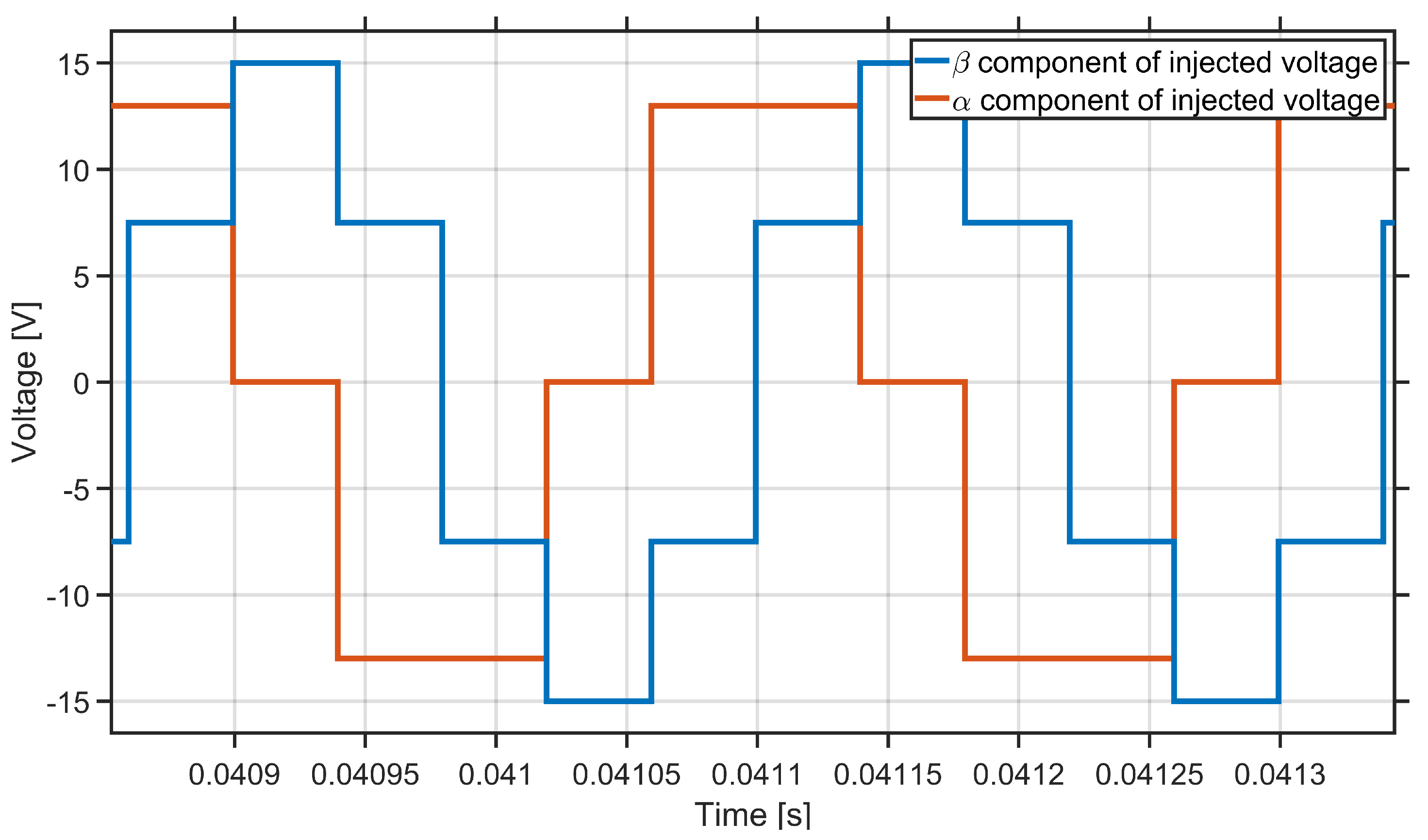
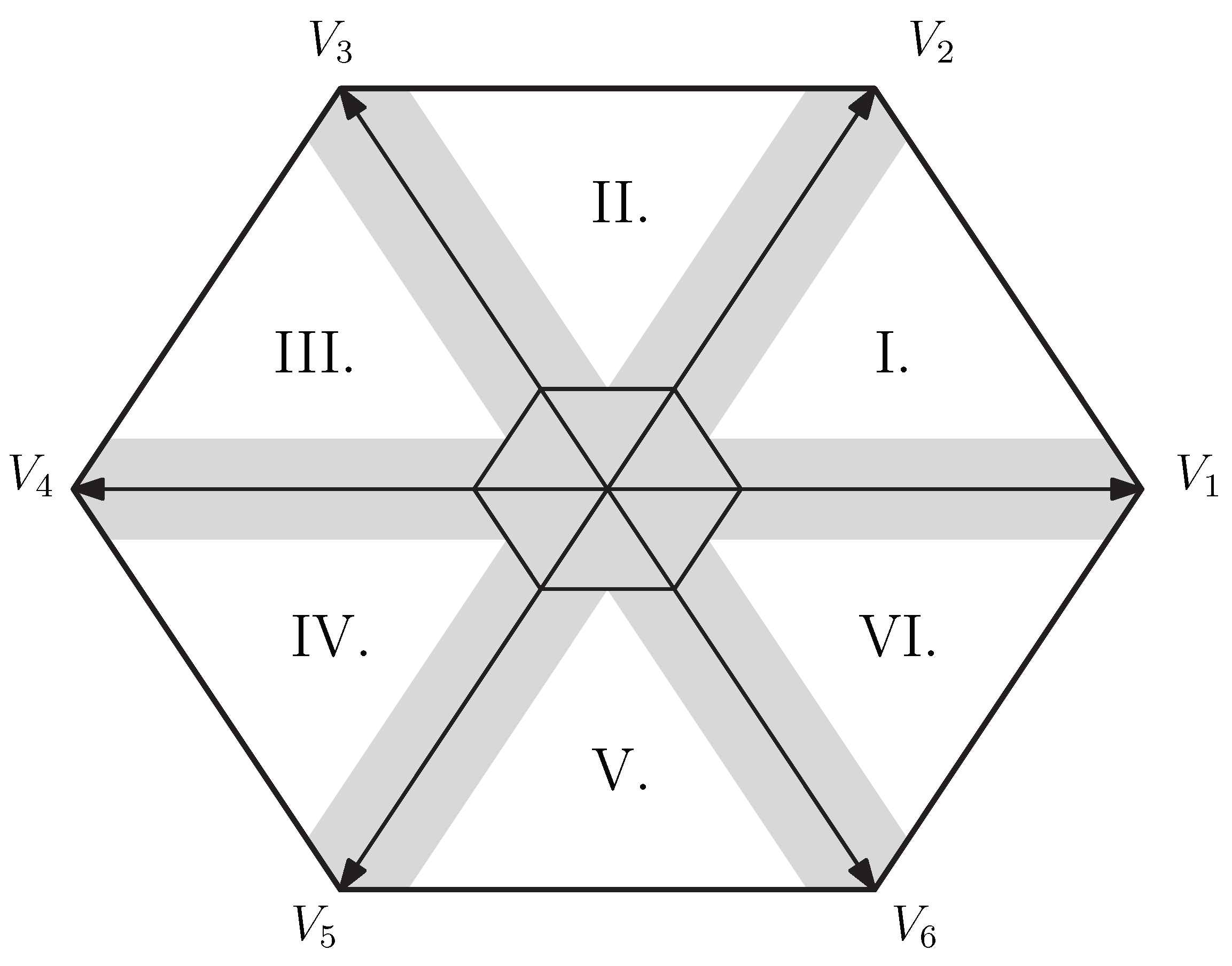
2.1. Six-Segment High-Frequency Injection Method
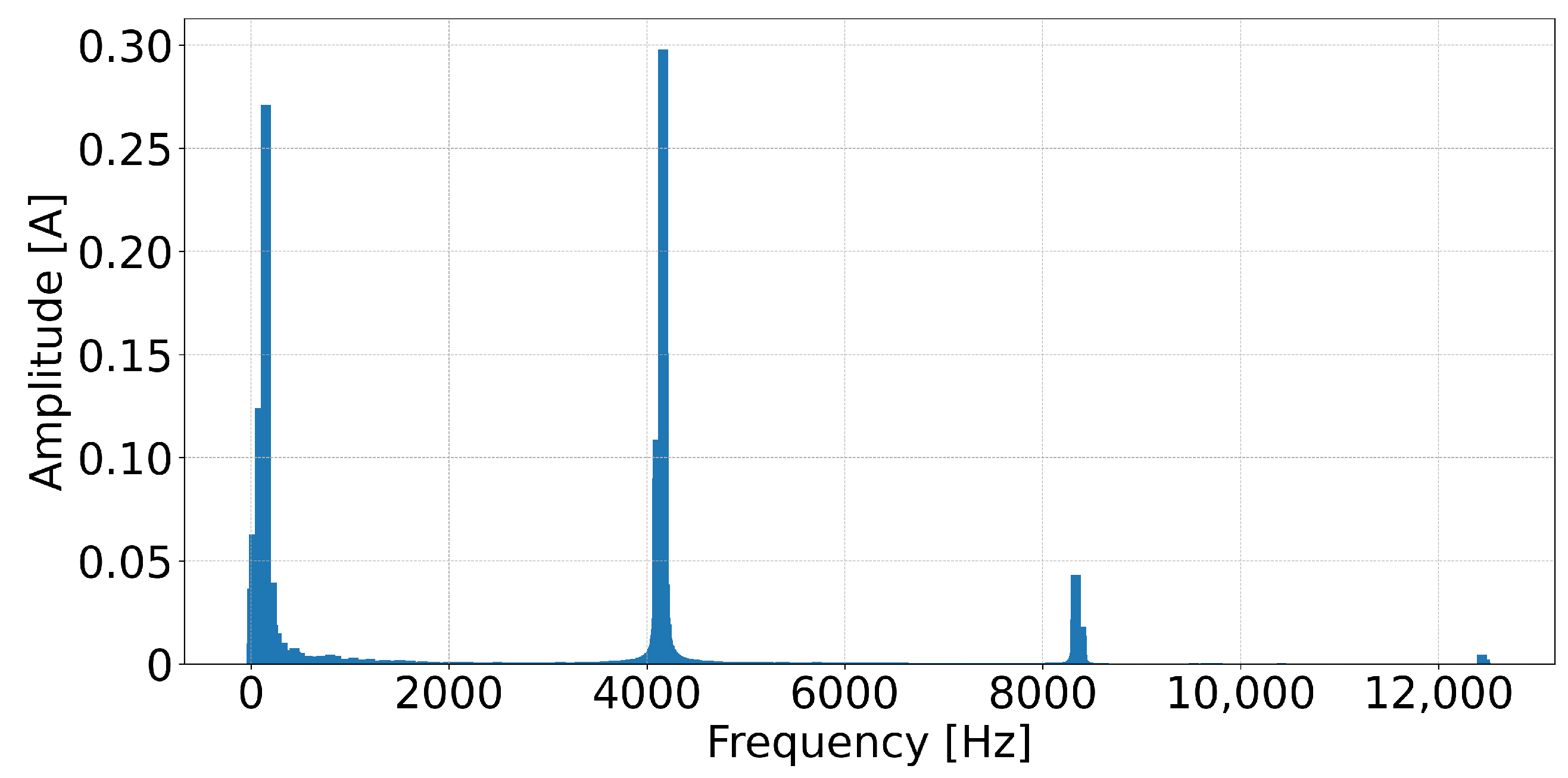
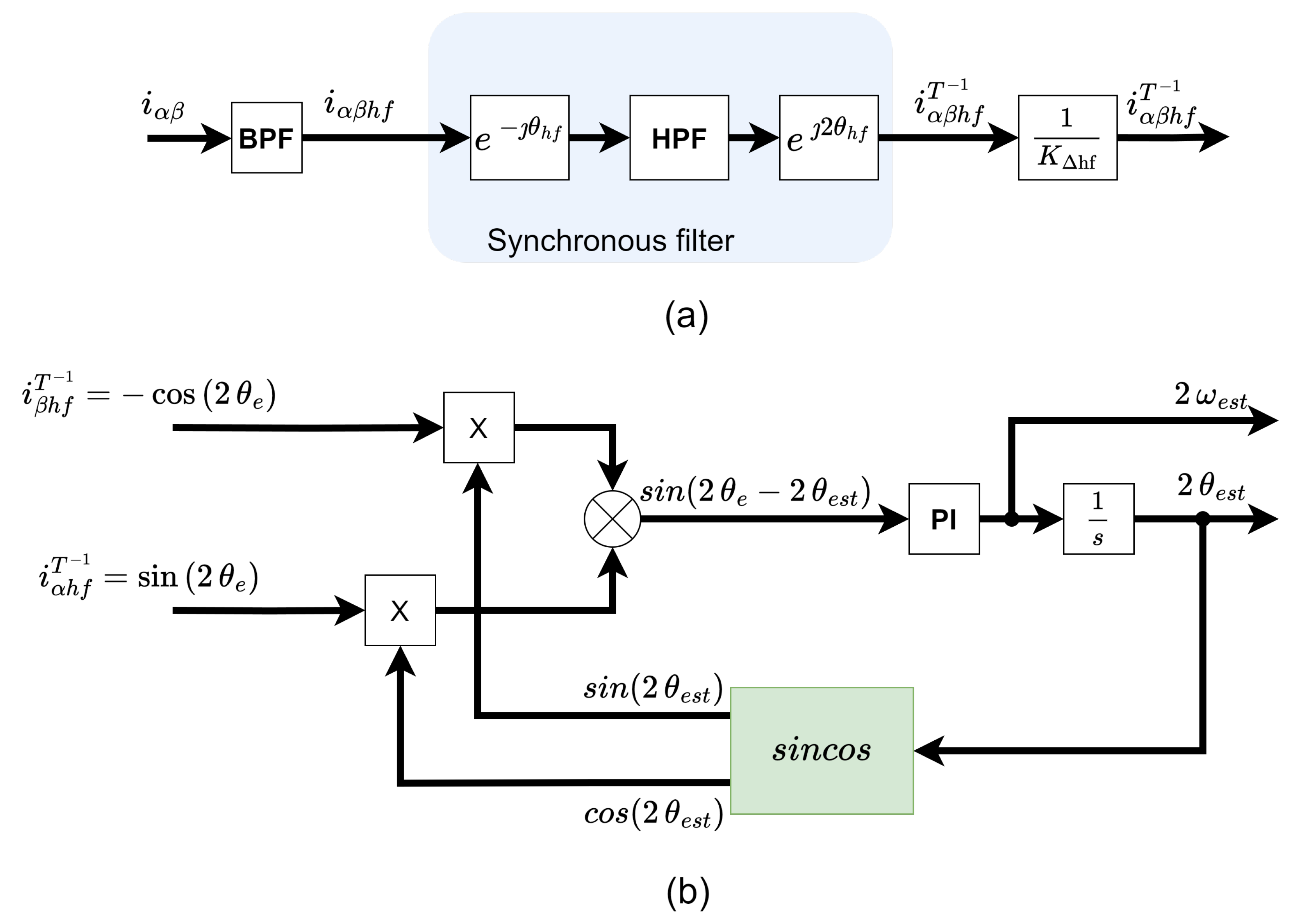
2.2. Demodulation of HF Current Response
2.3. Two-Interval Six-Segment HF Injection
2.3.1. Problem Statement
2.3.2. Proposed Solution
- The field-oriented control (FOC) structure is implemented and calculated every sampling period after samples of current, voltage, and other useful or mandatory quantities are taken.
- The sampling frequency is equal to the switching frequency .
- The DC-link current sensor is placed in the bottom current path between the DC-bus and the individual phases.
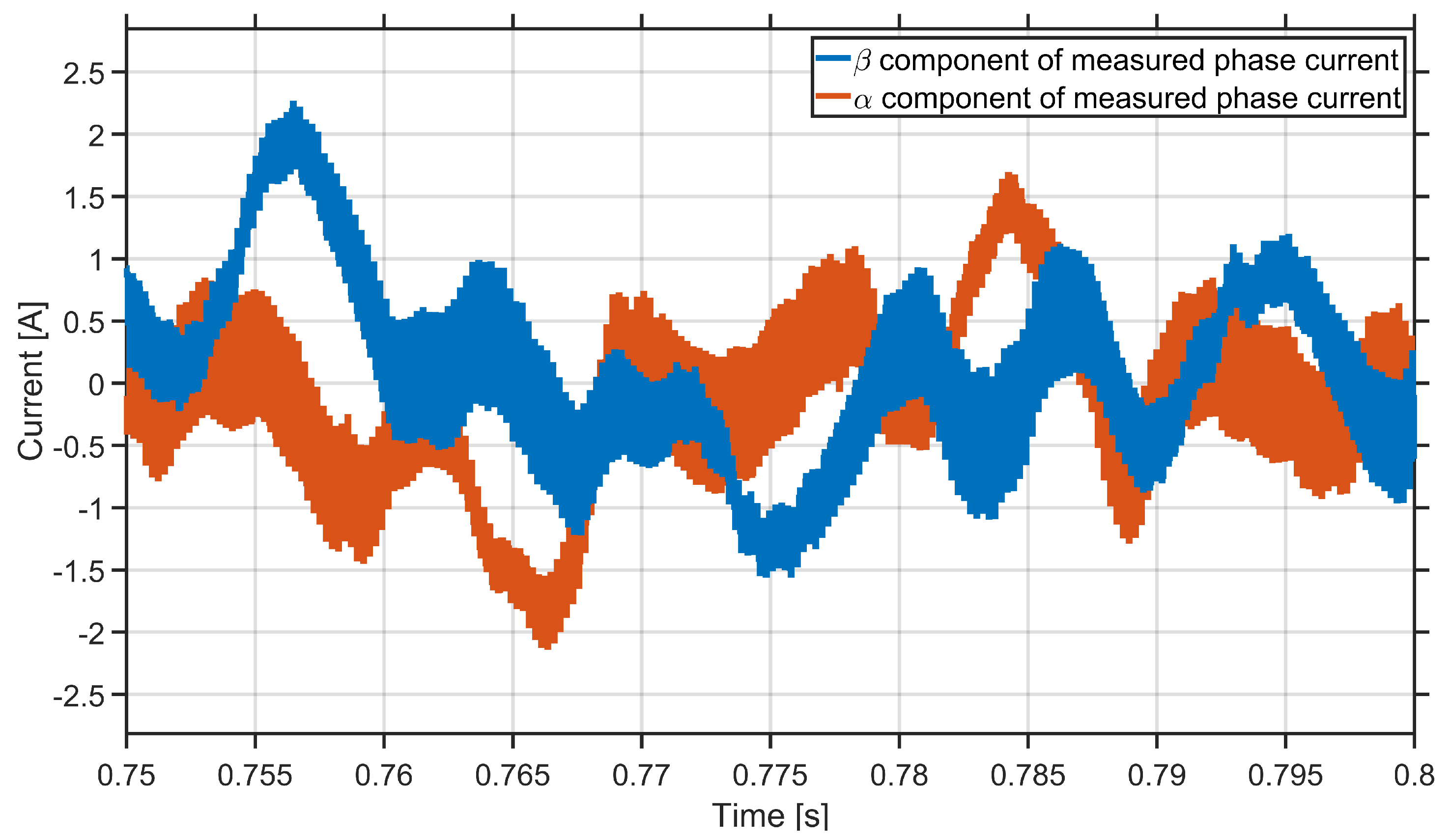
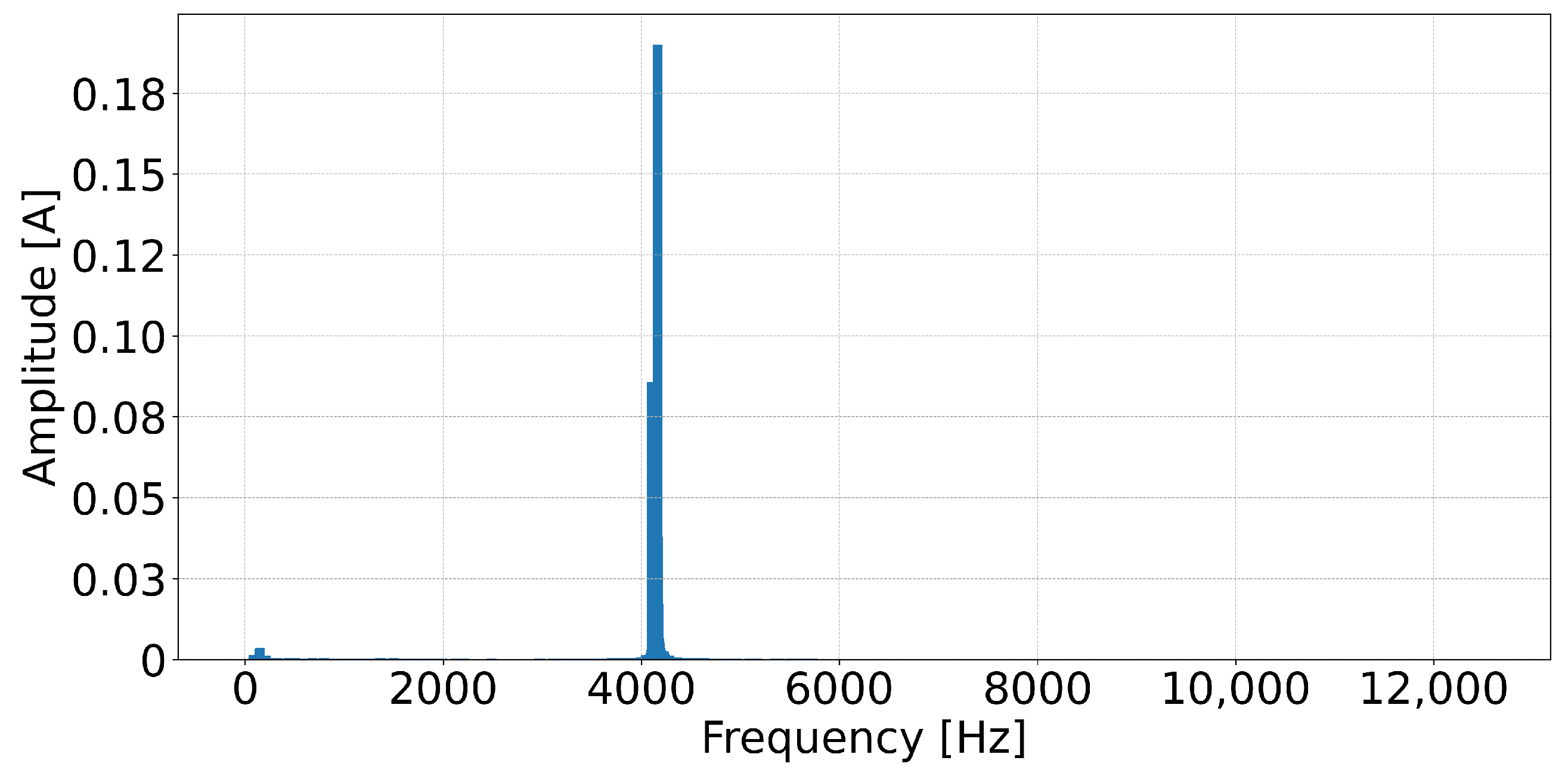
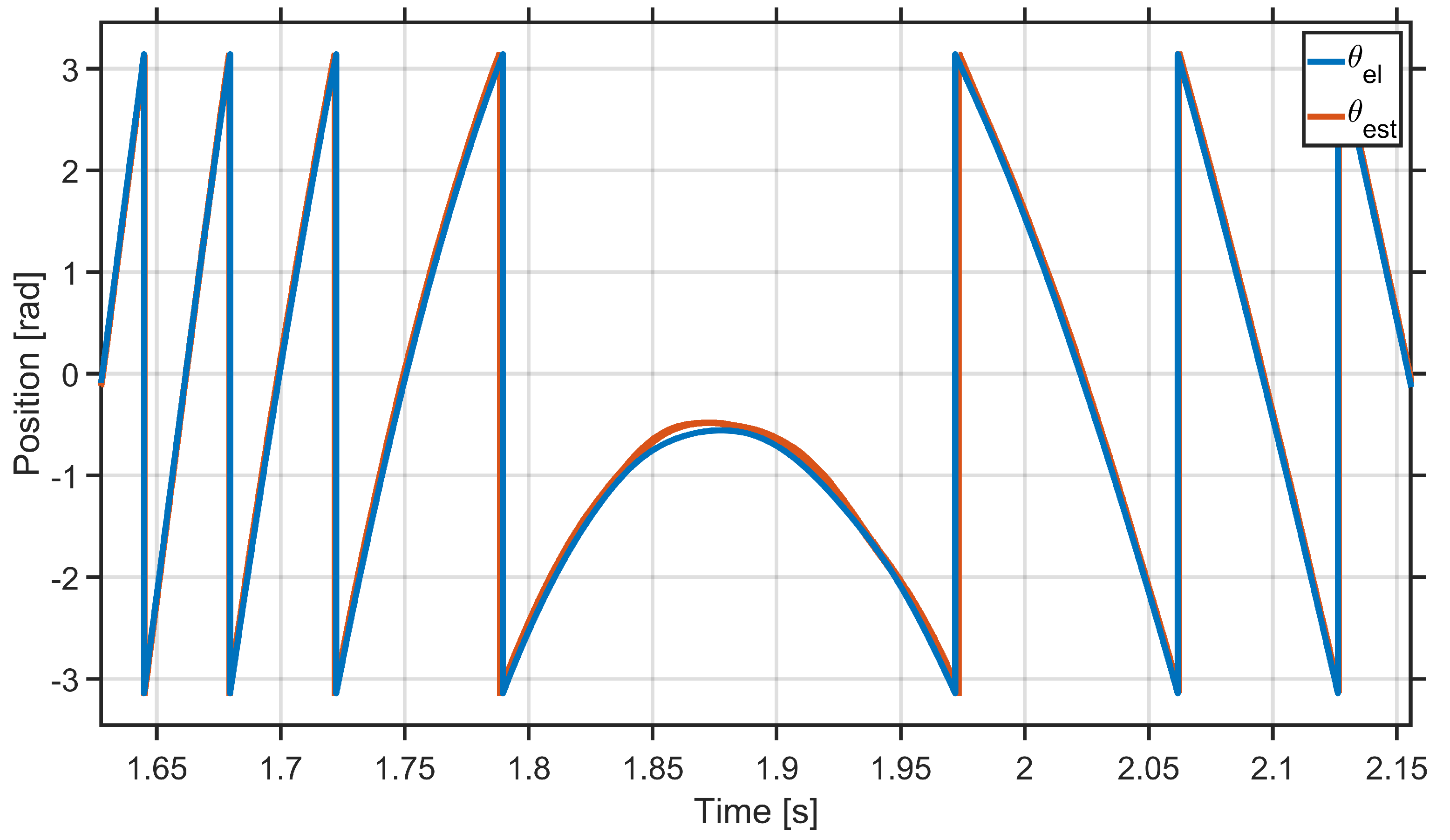
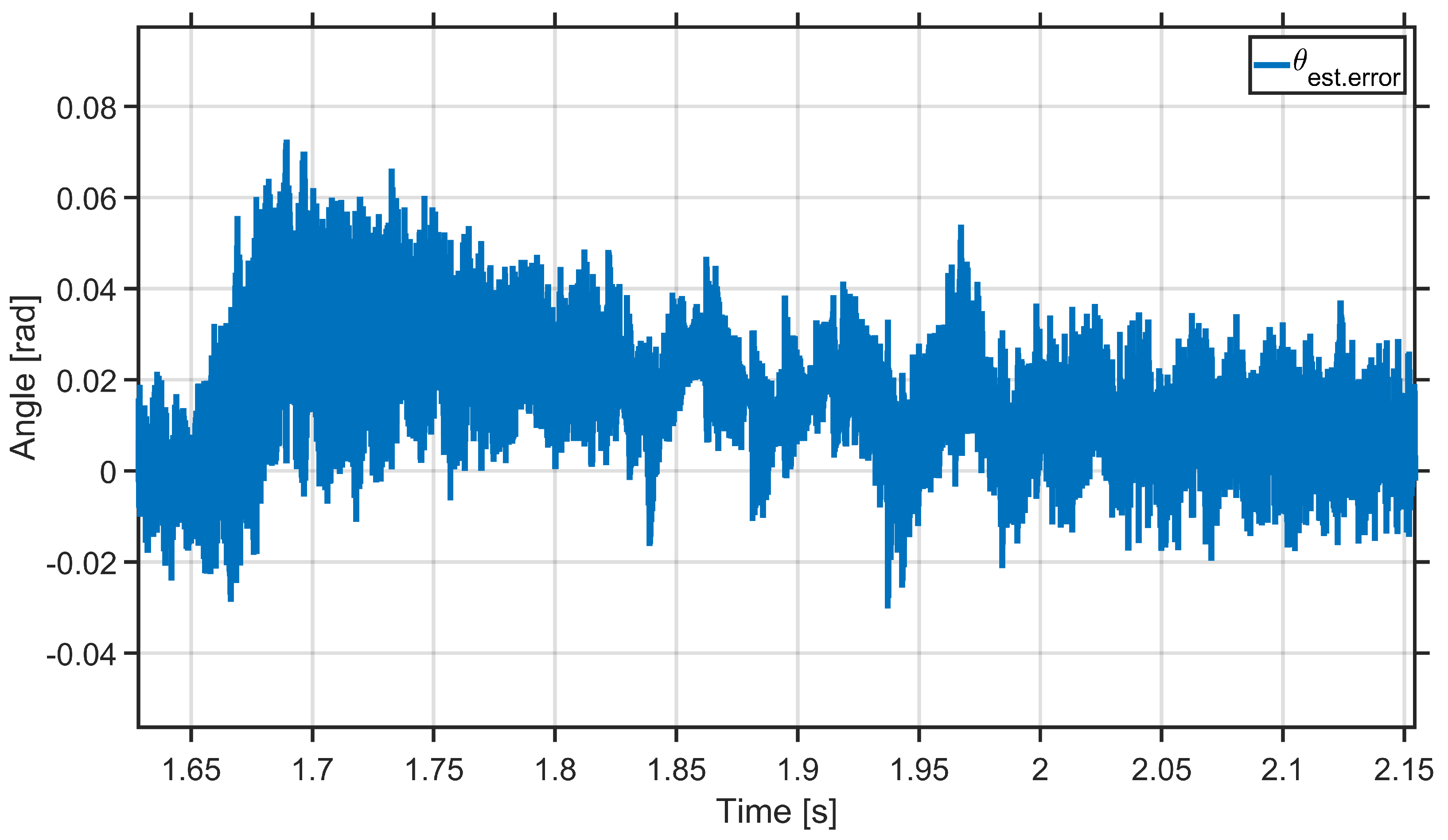
3. Simulation Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| IPMSM | Interior permanent magnet synchronous motor |
| HF | High frequency |
| PLL | Phase-locked loop |
| BPF | Band-pass filter |
| HPF | High-pass filter |
| PWM | Pulse-width modulation |
| FOC | Field-oriented control |
| ADC | Analog-to-digital converter |
| bEMF | back-EMF |
| SVM | Space Vector Modulation |
| VSI | Voltage Source Inverter |
References
- Schroedl, M. Sensorless control of AC machines at low speed and standstill based on the “INFORM” method. In Proceedings of the IAS ’96. Conference Record of the 1996 IEEE Industry Applications Conference Thirty-First IAS Annual Meeting, San Diego, CA, USA, 6–10 October 1996; Volume 1, pp. 270–277. [Google Scholar] [CrossRef]
- Ha, J.I.; Ohto, M.; Jang, J.H.; Sul, S.K. Design and selection of AC machines for saliency-based sensorless control. In Proceedings of the Conference Record of the 2002 IEEE Industry Applications Conference. 37th IAS Annual Meeting (Cat. No.02CH37344), Pittsburgh, PA, USA, 13–18 October 2002; Volume 2, pp. 1155–1162. [Google Scholar] [CrossRef]
- Niu, B.; Zhang, G.; Wang, S.; Zhu, L.; Zhao, N.; Huo, J.; Yang, H.; Wang, G.; Xu, D. Simultaneous MTPA and Sensorless Control Strategy for IPMSM Drives Based on High-Frequency Signal Injection. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Yoo, J.; Lee, Y.; Sul, S.K. Back-EMF Based Sensorless Control of IPMSM with Enhanced Torque Accuracy Against Parameter Variation. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 3463–3469. [Google Scholar] [CrossRef]
- Wang, W.; Yan, H.; Wang, X.; Xu, Y.; Zou, J. Analysis and Compensation of Sampling-Delay Error in Single Current Sensor Method for PMSM Drives. IEEE Trans. Power Electron. 2022, 37, 5918–5927. [Google Scholar] [CrossRef]
- Kim, M.; Sul, S.K.; Lee, J. Compensation of Current Measurement Error for Current-Controlled PMSM Drives. IEEE Trans. Ind. Appl. 2014, 50, 3365–3373. [Google Scholar] [CrossRef]
- Hu, M.; Hua, W.; Wu, Z.; Dai, N.; Xiao, H.; Wang, W. Compensation of Current Measurement Offset Error for Permanent Magnet Synchronous Machines. IEEE Trans. Power Electron. 2020, 35, 11119–11128. [Google Scholar] [CrossRef]
- Han, J.; Kim, B.H.; Sul, S.K. Effect of current measurement error in angle estimation of permanent magnet AC motor sensorless control. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017-ECCE Asia), Kaohsiung, Taiwan, 3–7 June 2017; pp. 2171–2176. [Google Scholar] [CrossRef]
- Lu, J.; Hu, Y.; Liu, J. Analysis and Compensation of Sampling Errors in TPFS IPMSM Drives with Single Current Sensor. IEEE Trans. Ind. Electron. 2019, 66, 3852–3855. [Google Scholar] [CrossRef]
- Jang, J.H.; Sul, S.K.; Son, Y.C. Current measurement issues in sensorless control algorithm using high frequency signal injection method. In Proceedings of the 38th IAS Annual Meeting on Conference Record of the Industry Applications Conference, Salt Lake City, UT, USA, 12–16 October 2003; Volume 2, pp. 1134–1141. [Google Scholar] [CrossRef]
- Zhao, J.; Nalakath, S.; Emadi, A. A High Frequency Injection Technique With Modified Current Reconstruction for Low-Speed Sensorless Control of IPMSMs With a Single DC-Link Current Sensor. IEEE Access 2019, 7, 136137–136147. [Google Scholar] [CrossRef]
- Gu, Y.; Ni, F.; Yang, D.; Liu, H. Switching-State Phase Shift Method for Three-Phase-Current Reconstruction With a Single DC-Link Current Sensor. IEEE Trans. Ind. Electron. 2011, 58, 5186–5194. [Google Scholar] [CrossRef]
- Shen, Y.; Zheng, Z.; Wang, Q.; Liu, P.; Yang, X. DC Bus Current Sensed Space Vector Pulsewidth Modulation for Three-Phase Inverter. IEEE Trans. Transp. Electrif. 2021, 7, 815–824. [Google Scholar] [CrossRef]
- Wu, C.; Zheng, L.; Shi, S.; Ying, W. A Quasi Edge Aligned Pulse-Width Modulation to Enhance Low-Speed Sensorless Control of PMSMs With a Single DC-Bus Current Sensor. IEEE Trans. Energy Convers. 2023, 38, 2919–2928. [Google Scholar] [CrossRef]
- Wang, W.; Yan, H.; Xu, Y.; Zou, J.; Buticchi, G. Improved Three-Phase Current Reconstruction Technique for PMSM Drive With Current Prediction. IEEE Trans. Ind. Electron. 2022, 69, 3449–3459. [Google Scholar] [CrossRef]
- Im, J.H.; Kim, R.Y. Improved Saliency-Based Position Sensorless Control of Interior Permanent-Magnet Synchronous Machines With Single DC-Link Current Sensor Using Current Prediction Method. IEEE Trans. Ind. Electron. 2018, 65, 5335–5343. [Google Scholar] [CrossRef]
- Zhao, J.; Nalakath, S.; Emadi, A. Observer Assisted Current Reconstruction Method with Single DC-Link Current Sensor for Sensorless Control of Interior Permanent Magnet Synchronous Machines. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 1228–1233. [Google Scholar] [CrossRef]
- Park, B.R.; Lim, G.C.; Han, Y.; Ha, J.I. Saliency-Based Sensorless Control Using Current Derivative in IPMSM Drives with Single DC-Link Current Sensor. IEEE Trans. Ind. Electron. 2024, 71, 3394–3404. [Google Scholar] [CrossRef]









| Parameter | Label | Value | Unit |
|---|---|---|---|
| Rated voltage | 48 | [V] | |
| Winding current | 48 | [A] | |
| Number of phases | m | 3 | [-] |
| Rated speed | 2300 | [RPM] | |
| Inertia | J | [] | |
| Number of pole-pairs | 3 | [-] | |
| EMF constant | [] | ||
| Stator winding resistance of one stator phase | [] | ||
| Three-phase synchronous inductance in d-axis | [mH] | ||
| Three-phase synchronous inductance in q-axis | [mH] | ||
| Ratio between q-axis and d-axis inductance | [-] | ||
| Stator inductance | [mH] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konvicny, D.; Makys, P.; Franko, A. Proposal of Low-Speed Sensorless Control of IPMSM Using a Two-Interval Six-Segment High-Frequency Injection Method with DC-Link Current Sensing. Energies 2024, 17, 5789. https://doi.org/10.3390/en17225789
Konvicny D, Makys P, Franko A. Proposal of Low-Speed Sensorless Control of IPMSM Using a Two-Interval Six-Segment High-Frequency Injection Method with DC-Link Current Sensing. Energies. 2024; 17(22):5789. https://doi.org/10.3390/en17225789
Chicago/Turabian StyleKonvicny, Daniel, Pavol Makys, and Alex Franko. 2024. "Proposal of Low-Speed Sensorless Control of IPMSM Using a Two-Interval Six-Segment High-Frequency Injection Method with DC-Link Current Sensing" Energies 17, no. 22: 5789. https://doi.org/10.3390/en17225789
APA StyleKonvicny, D., Makys, P., & Franko, A. (2024). Proposal of Low-Speed Sensorless Control of IPMSM Using a Two-Interval Six-Segment High-Frequency Injection Method with DC-Link Current Sensing. Energies, 17(22), 5789. https://doi.org/10.3390/en17225789







