Abstract
In 2019, more than 16% of the globe’s total production of electricity was provided by hydroelectric power plants. The core of a typical hydroelectric power plant is the turbine. Turbines are subjected to high levels of pressure, vibration, high temperatures, and air gaps as water passes through them. Turbine blades weighing several tons break due to this surge, a tragic accident because of the massive damage they cause. This research aims to develop predictive models to accurately predict the status of hydroelectric power plants based on real stored data for all factors affecting the status of these plants. The importance of having a typical predictive model for the future status of these plants lies in avoiding turbine blade breakage and catastrophic accidents in power plants and the resulting damages, increasing the life of these plants, avoiding sudden shutdowns, and ensuring stability in the generation of electrical energy. In this study, artificial neural network algorithms (RNN and LSTM) are used to predict the condition of the hydropower station, identify the fault before it occurs, and avoid it. After testing, the LSTM algorithm achieved the greatest results with regard to the highest accuracy and least error. According to the findings, the LSTM model attained an accuracy of 99.55%, a mean square error (MSE) of 0.0072, and a mean absolute error (MAE) of 0.0053.
1. Introduction
Human societies have been linked to their need for electrical energy as a fundamental factor in economic prosperity, and this need has increased in recent years with the tremendous development taking place in all aspects of life and the increase in population numbers [1]. The use of fossil resources in energy production, which has become the main ingredient for sustaining life, is high. In addition to increasing external dependence on energy, this leads to long-term and irreparable damage to the environment. Today, countries are making efforts to reduce the use of fossil energy sources to reduce global warming and create plans to raise the proportion of renewable energy sources [2]. Large-scale hydropower development for the production of electricity started in the early 20th century, and in the middle of that century, it was acknowledged as a renewable energy source [3,4]. Hydroelectric power plants (HEPPs) contribute more than 25% of the total electricity needs of many countries around the world. HEPPs also provide 50% of electricity demand in 65 countries, 80% in 32 countries, and nearly all electricity demand in 13 countries, with a total of 1307 gigawatts installed by 2019. Hydroelectric power plants accounted for 16% of global power generation in 2019 [5]. The total electricity generation from hydroelectric power plants is about 20% of the world’s electricity [6].
With this population expansion and the accompanying increase in demand for electrical power in various fields, to offset this increase, the generating units run in extremely harsh operating conditions and at maximum power. Hydroelectric power plants operate under poor operating conditions due to high dynamic load, especially turbines, which are subjected to severe vibrations in the structure and turbine blades, as well as high pressure and temperature, and air bubbles also occur. This leads to very high wear on turbine components such as blades and structure, in addition to affecting the power generator and transmission shaft, which is a common problem in dams such as Haditha Dam [7].
All dams suffer from similar problems due to the similar nature of their work, and these problems increase with the increasing demand for the energy generated from them and directly with the increasing population growth and the expansion of industries and factories, and this makes them work at their maximum capacity [8].
Dams cover a large proportion of the required amount of electrical energy, which is increasing at a time when hydroelectric stations are working to fill the deficit, which makes the dams operate at their maximum capacity to compensate for this deficiency.
HEPP turbines are sensitive to multiple parameters that continuously reduce their service life. Mechanical forces, material destruction, mechanical crushing, large temperature differences, cavitation, corrosion, and chemical forces can cause various types of damage to power plants. These difficulties are exacerbated by the increasing load to fill the energy deficit and by the harsh and unstable conditions experienced by some countries in the East Asian region in recent years [9,10].
One of the most important obstacles facing companies that produce electricity using hydropower is the lack of knowledge of the condition of the turbines, which are exposed to corrosion and the cracking of the blades due to increasing vibration and the accompanying rise in pressure and temperature. This leads to the breakage of blades that weigh several tons, and the resulting risks and catastrophic accidents in terms of the economy, living, and production, and endangers the lives of workers. The impact of this crash on the structure of the dam may expose it to destruction and endangers the lives of the population, especially since the turbines operate unstably due to the effect of water pressure and the accompanying air bubbles. This causes high vibration, high temperatures, and increased pressure inside the turbines [11,12,13,14].
Therefore, there was an urgent need for a highly reliable system to predict the condition of turbines to ensure that any dangerous condition is detected before it occurs to avoid it and avoid the serious damage resulting from it, and this model must be applicable to various dams in the world.
Figure 1 shows the most common malfunctions in hydraulic power plant generators and the root causes initiating these malfunctions [5,15].
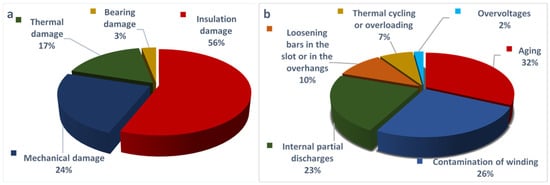
Figure 1.
(a) Damages to hydrogenerators and (b) root causes of failure [15].
Turkey, like most East Asian countries, contains many multi-purpose dams, the most important of which is generating electrical energy, as the technical production potential in Turkey amounts to 216 billion kilowatt-hours annually from hydroelectric energy sources. In addition, it is shown that Turkey has a potential of 128 billion kWh per year under current conditions. Hydropower plants constitute 31.8% of the total installed capacity in Turkey, with an installed capacity value of 29,916 MW [16]. Obruk Dam is one of the Turkish dams that aims to produce electric power. It generates total electric power of 210.8 megawatts and has an expected annual capacity of 473 million kilowatts per hour. The dam lake is 661 cubic meters, and the area of the lake is 50.21 square kilometers [17]. The Obruk Dam works in the same way as most dams; it contains turbines (Frances) that work vertically to generate electrical energy like most turbines use to generate electrical energy in various dams.
As computer technology has advanced, machine learning algorithms, like artificial neural networks [18,19], support vector machines [20], and extreme learning machines [21], have become increasingly prevalent in deformation prediction models, where the exceptional modeling and data processing capabilities of deep learning theories offer distinctive data analysis solutions for different machines [22,23]. Additionally, these algorithms contributed effectively to the field of diagnosing and identifying errors [24]. It also solves complex problems professionally, which are very challenging to solve using traditional analytical modeling. Deep learning and AI algorithms are known for their high accuracy, power, and excellent overall capabilities [25,26]. However, machine learning techniques suffer from various drawbacks, such as overfitting, easy local extrema, and difficulty in determining the model’s hyperparameters. With the advancement of deep learning technologies in recent years, by adding cell states and gates, LSTM successfully addresses the issues of gradient explosion, gradient disappearing, and long-term reliance on conventional recurrent neural network (RNN) models [27]. LSTM models have been extensively employed in numerous forecasts, including those related to vehicle trajectory [28], stream flow [29], well production [30], dam deformation [31,32], and other topics.
This work aims to create state prediction models for hydropower turbines and generators used in hydropower dams based on RNN and LSTM algorithms, based on the real data stored for various factors affecting the nature of turbines and generators operation, which was obtained from Obruk Dam in Turkey as a model for other dams.
The results indicate that the LSTM-based state forecasting model for turbines and generators has better forecasting performance, and the prediction accuracy of the single-layer LSTM model is higher than that of the RNN model without LSTM. Finally, due to its extreme accuracy compared to others, the single-layer LSTM model was used to predict the stability of turbines and generators in hydropower plants in the dam.
The importance of the turbine condition prediction model in Hydropower Plant (HPP) electricity generation can be illustrated by its contributions; the advantages of real-time turbine system status prediction for production equipment in HEPP plants can be listed as follows [5,33]:
- Major malfunctions that cause downtime are reduced to a minimum.
- Costs of operation and maintenance are decreased.
- The equipment is maintained based on the system parameters.
- It increases the equipment’s lifespan and effectiveness.
- Reduces the frequency of downtime.
- Risks to employees are reduced.
- The stations operate within vibration, pressure, and temperature limits.
With the HEPP forecasting system activated, the cost advantages listed are better than those listed below, depending on the system’s reliability [16,33]:
- The cost of maintenance drops by 50% to 80%.
- Equipment breakdowns are reduced by 50% to 80%.
- Reduces machine downtime by 50–80%.
- Overtime costs are reduced by 20% to 50%.
- Machine lifetime rises by 20% to 40%.
- Profits rise by 25% to 30%.
This section provides an overview of the systems used in hydropower plants and the prediction used in the field of electricity and dams. The paper’s subsequent sections are arranged as follows: The literature study and prior research are covered in Section 2; the process for developing deep learning models for hydropower prediction is presented in Section 3; Section 4 shows the experimental results of both models used; and Section 5 presents the conclusions.
2. Related Work
Hydropower plants have received little attention from academic studies on renewable energy (2.3 percent), despite the high proportion of hydropower generation in electricity [34]. Most studies have been conducted on dams to predict the generation of hydroelectric power considering climate change and the change in the level of water reservoirs, as well as predicting the dam infrastructure. The lowest percentage among these studies was for hydraulic turbines, although it is considered the core of the electric power plant, and at the same time, these studies relied on traditional control systems.
- Studies on Hydro Turbines
Zhong Liu and Lihua Zhou proposed a hydraulic turbine vibration control monitoring system based on LabVIEW and vibration wave display [35]. Rati Mohanta et al. studied the causes of vibrations in hydraulic turbines with all their fixed and rotating components considering vibration measurement criteria and presented a summary of the studies over 30 years [36]. Delphin Technology also provided a turbine vibration monitoring system; Femaris provided its system to help monitor the vibration of hydraulic turbines, and based on it, the fault diagnosis is ProfiSignal Basic and ProfiSignal Vibr [37]. To monitor temperature and smoke, Vijaya and Surender used an industrial robot using MATLAB GUI [38]. Puneet Bansal and Rajay Vedaraj suggested utilizing MATLAB GUI to create a vibration monitoring system for an electrical motor [39]. Omar Al-Hardanee et al. proposed a system for controlling and monitoring hydro turbines to predict and avoid errors; the process is performed by measuring vibration and temperature through sensors using the Arduino and displaying them using (GUI) in MATLAB; the system compares the signals captured from the sensors and compares them to the permissible limits [40].
- Using AI in the field of dams
Ali T.H. et al. applied artificial neural networks (ANNs) to predict the power generation capacity of the Hamrin Lake-Diyala Dam hydropower plant. The indicated results were that R2 is 0.96, and the root-mean-square value (RMSE) of the best performance achieved was 0.0032734 [41]. In order to estimate the temperature of a hydro-generating unit (HGU), Junyan Li et al. proposed a temporal series forecasting model based on Temporal Convolutional Network (TCN) and RNN. According to the study, the two forms of temperature forecasts for the TCN-RNN model had an average MSE increase of 42.2% and 48.3%, consecutively. The average increases in MAE were 26.5% and 16.4%, while the average increases in RMSE were 23.4% and 43.2% [42]. The authors, Fang Dao et al., presented a wear fault diagnosis approach for hydro turbines in hydropower units based on enhanced WT (wavelet threshold algorithm) preprocessing in conjunction with IWSO (Enhanced White Shark Optimizer) CNN-LSTM (Convolutional Neural Network Long Short Short-Term Memory); CNN-LSTM model hyperparameter adjustment using the IWSO technique. According to experimental results, the suggested approach’s accuracy is 96.2%, which is 8.9% greater than the accuracy of the IWSO-CNN-LSTM model without denoising [43]. Bi Yang et al. developed a framework based on a combined measure of feature selection and a bidirectional long short-term memory (BLSTM) network to obtain vibration direction prediction. A combined measure based on the Pearson correlation coefficient and distance is proposed to select appropriate working condition variables to make the prediction model more stable. The results obtained by the proposed method (WTD-Corr-BLSTM) are described as RMSE, and MAE are 0.42 and 0.31 [44].
Xin Gao et al. proposed a short-term electricity load forecasting method based on empirical mode decomposition-gated recurrent unit (EMD-GRU) with feature selection (FS-EMD-GRU). The findings demonstrated that the suggested method’s average prediction accuracy on four sets of data was 96.79%, 95.31%, 95.72%, and 97.17%, respectively. EMD-GRU, EMD-SVR, EMD-RF, random forest (RF), and support vector regression (SVR) models are contrasted with a single GRU model [45]. Mobarak Abumohsen et al. proposed a prediction model to estimate the electrical load based on the electricity company’s current electrical load measurements, and three model’s LSTM, GRU, and RNN were chosen. The GRU model performed the best in terms of accuracy and lowest error, with R-square of 90.228%, MSE of 0.00215, and MAE of 0.03266 [46]. Feifei He et al. created a hybrid short-load forecasting system that was optimized using the Bayesian optimization technique (BOA) and based on long short-term memory (LSTM) and variation mode decomposition (VMD) networks. The results of the suggested technique indicate that MAPE is 0.4186 percent and R-squared is 0.9945 when compared to SVR, multi-layered perceptron regression, LR, RF, and EMD-LSTM [47].
It is worth noting that the previously mentioned prediction systems that were proposed in the literature by previous researchers cannot be relied upon due to the radical difference in the way hydraulic turbines work and what was mentioned previously in all the different factors and energy sources.
To the best of the author’s knowledge, there is no artificial intelligence model that has been used to predict the status of hydroelectric power plants, including hydraulic turbines and electric power generators. The point that this research revolves around aims to use artificial intelligence to predict the status of hydroelectric power plants based on real data taken from the generation station in Obruk Dam in Turkey, where machine learning algorithms (LSTM, RNN) are used with the highest accuracy and lowest error rate, which will help solve the problem of hydroelectric power plants and power outages, save time and cost, and avoid disasters.
3. Materials and Methods
This section describes the model to which the study is applied, the case study’s characteristics and descriptive statistics, the second step of data exploration, and the third step of data preprocessing for machine learning. The RNN and LSTM algorithms, which are the main components of the model, are then presented (see Figure 2).
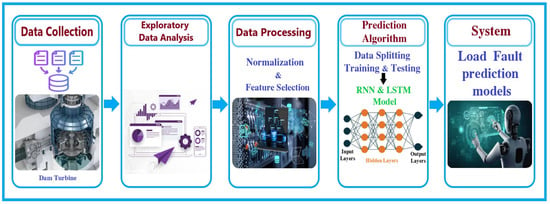
Figure 2.
Workflow system for dam station fault detection model.
Figure 2 illustrates the workflow, which goes through five basic steps. The first involves collecting data from different sensors, then the data analysis stage, after which it moves to data processing, which includes selecting some features, normalization, then preparing the prediction algorithm which includes data splitting training and testing and determining the typical model, and the last step is loading the algorithm to work on the prediction in an actual way.
3.1. Case Study
The Obruk Dam was built on the Kızılırmak River, which is 16 km from the Dudurga district of Çorum and 2 km from the Obruk village (Figure 2). It is a dam used for many purposes, the most important of which is the generation of electric power, with a total installed capacity of 210.8 MW for a total of 4 generators, each of which is 52.7 MW. The Obruk Dam entered service and began producing electricity in 2009. At its highest water level, the lake has a capacity of 661 hm3 and an area of 50.21 km2. The dam has four spillway covers and a 5000 m3/s discharge capacity (Figure 3).
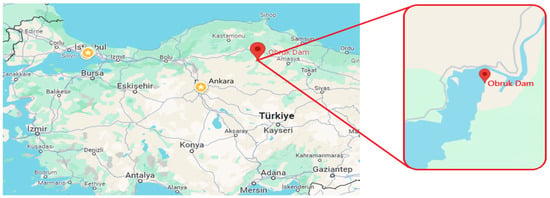
Figure 3.
The location of the Obruk hydroelectric power plant in Çorum Province, Turkey.
The dam’s main uses are hydroelectricity generation, urban drinking, and irrigation [17]. In addition, it is employed recreationally and for flood control.
3.2. Data Collection and Description
In this study, the data used in the forecasting process were obtained from the database stored by the monitoring program for the Obruk Dam hydroelectric power station. The system enters the new reading into the databases on a minute-by-minute basis. The dataset contains 523,373 rows and 45 columns of data obtained from 1 January 2020 to 31 December 2021. The main features in the dataset are the date, hour, day of the week, week number, month, year for all variables affecting the stability of the system, including frequency, temperature, pressure, volume of water in the dam, height, generation volume, and generator frequency.
The following tables show an example of a set of data used, such as vibration (Table 1), pressure (Table 2), and temperature (Table 3), which represents ten records.

Table 1.
A set of vibration data representing ten records is used in the forecast.

Table 2.
A set of pressure data representing ten records is used in the forecast.

Table 3.
A set of temperature data representing ten records is used in the forecast.
The limits set by the manufacturer for the values that are considered normal, a stable state, and critical, as well as those that represent a dangerous state, were adopted for all data and prepared to determine the final state of stability in the forecasting system. Table 2 shows descriptive measures for a group of data that have a direct impact on the stable state, such as pressure (Table 4), temperature (Table 5), and vibration (Table 6).

Table 4.
Pressure data limits.

Table 5.
Power, voltage, speed, level, and cos α data limits.

Table 6.
Temperature data limits.
The data taken from the dam for turbines and electric power generators, including the transmission shaft, are unstable and fluctuating and also differ in values from one sensor to another, as shown in Table 1, Table 2 and Table 3, and its limitations are shown clearly in Table 4, Table 5 and Table 6. Accordingly, the data will go through several stages of analysis, filtering, and preparation to be qualified to be used in the prediction process.
3.3. Exploratory Data Analysis (EDA)
In this section, all exploratory data related to variables influencing system stability are extracted and examined in this section. Analyzing exploratory data involves looking for various hidden patterns, connections, and features in the data. The data were analyzed and explored using a number of techniques, including box drawing, automatic correlation, and line drawing. One of the main features of EDA that is necessary for developing time series forecasting models is the capacity to visualize, examine, and uncover previously undiscovered patterns in the relationships between various variables [48].
3.3.1. Correlation
A statistical method known as correlation is used to measure the linear relationship between two or more variables. Correlation can be used to predict one variable based on another.
The theory behind using correlation analysis to choose features is that significant correlations between helpful factors and the outcome will be found. In order to determine whether there is sufficient connection to build a deep learning model that can anticipate the short-term load estimates and investigate the relationship between the dataset’s components, the heat map helps to comprehend the correlation ratio between the features. The seaborn package and Python matplotlib were used to build the heat map. Equation (1) is used to obtain the correlation coefficient (r) between the components [49].
where r = correlation coefficient, = values of the x-variable in a sample, = mean of the values of the x-variable, = values of the y-variable in a sample, and = mean of the values of the y-variable.
Figure 4 shows the set of correlations between features within the datasets, and it can be noted that there are correlations between a set of variables that have a direct impact on stability, such as the pressure variables themselves, vibration, and temperature themselves, as well as the sum of the variables together with respect to time throughout the days of the year. The interrelationship between the variables in the data is observed, as it ranges between a positive or negative relationship, while most of the data approach a positive or negative relationship.
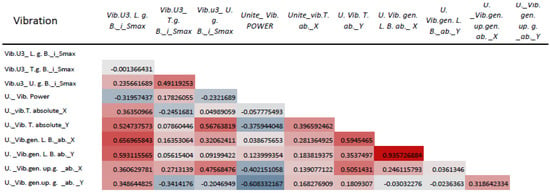
Figure 4.
Correlation coefficient for vibration features in the dataset.
It can be seen in the figure that there is a positive relationship between Unite vibration generator lower bearing absolute-X (U. Vib. gen. L. B. ab._ X) and the Unite vibration generator lower bearing absolute-Y (U._vib.gen. L. B. ab._Y) and close to it in the Unite vibration generator lower bearing absolute-X (U._Vib.gen. L. B._ab._X) and Unite3 vibration lower guide bearing_i_Smax (Vib.U3. L. g. B._i_Smax), there are negative relationships between Unite vibration power and Unite vibration generator upper guide absolute-Y, the rest of the values range between positive and negative relationships, according to the color gradation, as shown in Figure 4.
As can be seen in the figure, there is a positive relationship between Main tran. Water temp. and Main transformer oil temp. and also Generator stator temp. Z1 and Generator stator temp. Z11 and other values and a negative relationship between Thrust bearing shoe temp.2 and Thrust B shoe temp.1. The rest of the values range between positive and negative relationships, according to the color gradation, as shown in Figure 5.
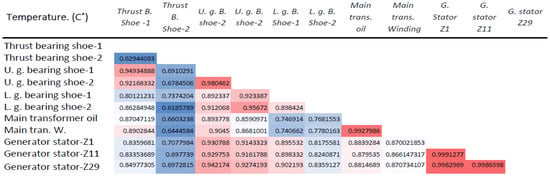
Figure 5.
Correlation coefficient for temperature features in the dataset.
As for pressure, through the interrelationship between variables, it is noted that pressure has less effect compared to the effect of vibration and temperature, as the values approach a positive relationship, such as the relationship between Water head diff. pressure and Spiral case exit pressure, and approach a negative relationship, such as the relationship between main shaft sealing pressure and butterfly valve oil pressure, as shown in Figure 6.
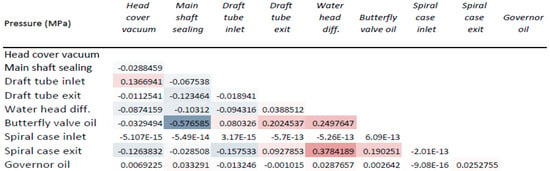
Figure 6.
Correlation coefficient for pressure features in the dataset.
As for the database of different variables combined, we notice a direct effect of the rise in the water level in the dam, no less important than vibration and temperature. It is noted here that there is a positive and negative relationship that is interconnected to the effect of water level in the dam and the other variables. It is noted that there is a positive relationship between the Dam Waterhead level and vibration unit 3 T. guide B, as well as a negative relationship between the Dam Waterhead level and Butterfly valve pressure, according to the color gradation, as shown in Figure 7.
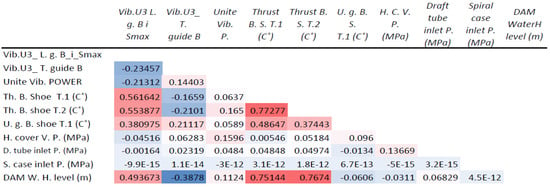
Figure 7.
The correlation coefficient for the database of different variables’ combined features in the dataset.
3.3.2. System Stability Behavior Analysis
Through the process of analyzing time series of system stability, times of stability and instability can be identified daily, weekly, monthly, and during the day.
Figure 8 and Figure 9 show the nature of the stability behavior over time. This makes it easier to determine if the data are repeated or random. In addition, a few statistical measures that illustrate the distribution of specific numbers in the dataset are provided.
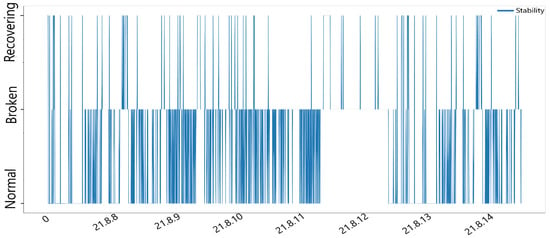
Figure 8.
System stability during the days of the week over time (8 August 2021 to 15 August 2021).
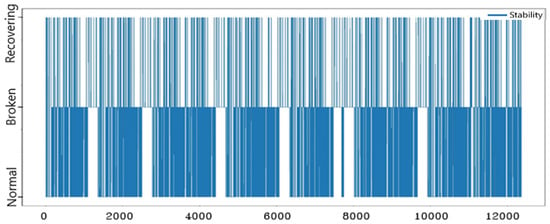
Figure 9.
The nature of the stability of the system.
3.3.3. Cleaning Data
Removing NaNs is the first step in data filtering after verifying the NaN values of the dataset. To make forecasting more effective and accurate, episodes in which the sensor did not send any data should not be confused with zero values, which might actually mean the value is zero (too many zeros in a dataset makes it a sparse dataset).
Figure 10 shows the data used, where no NaN values were observed, so the database is ready to be used for forecasting.
Figure 10.
NaNs for all the data.
3.3.4. Data Normalization
Data normalization is one of the most important preprocessing methods to prevent some features from outperforming all others, where data normalization is necessary if different input features (here sensors are used) have a different range in their amplitudes and values. Otherwise, the values will be skewed when using machine learning methods. The goal of data normalization is to assign equal importance to features that have the same scale: standardization and maximum–minimum normalization are among the many types of data normalization techniques available [50]. The linear transformation is performed on the data using (max–min), which is the normalization technique with the method of this normalization [51].
3.3.5. Hot Reconfiguration and Encryption
In the final step in data conditioning, the data must be resampled so that the LSTM (which is chosen) predicts the input to the model [samples, time steps, features]. Since we are looking for classification, we have to encode our target once before training so that the softmax activation interprets the categories correctly without misinterpreting the category order (0,1,2) as rating or importance. This is performed using the sklearn. preprocessing.OneHotEncode() function.
3.4. Forecasting Methodology
This section presents a method to predict the steady state of a dam turbine system using an RNN algorithm based on LSTM algorithms on the real dataset of the system, as shown in Figure 11. First, the dataset is created, and the preprocessing steps—such as feature selection and normalization—are described. Next, models are built and trained, using deep learning to predict short-term loads based on past data. These models are LSTM and RNN. The correctness of each machine learning model was then assessed using performance metrics and hyperparameter tweaking, which included the optimizer, activation function, learning rate, number of epochs, batch size, and number of hidden layers. Choose the most accurate forecasting model. Using Python and the Pandas, Seaborn, Sklearn, Matplotlib, TensorFlow, and NumPy libraries, all models in this paper were created.
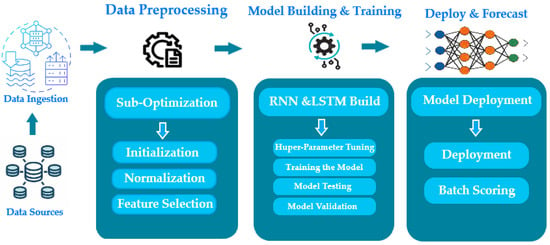
Figure 11.
Methodology for building hydropower station state prediction algorithms.
In LSTMs, the number of layers is more important than the number of memory cells with respect to time series analysis. The rule of thumb here is that the number of hidden units (memory cells) is less than the input features.
Two LSTM layers were used, each containing 42 hidden units and two output layers. You can use a simple single-output serial model here. We have two cases, and we want to show different use cases. Signal_out is a 1-unit dense layer that gives us an expected signal, while class_out is a 3-unit dense layer and activating softmax gives us the expected classes “Normal”, “Recovering”, and “Broken”.
3.4.1. Data Preprocessing
Preparing and processing data is the first step in training the machine learning model and helping it to use the data structure optimally. The machine learning model usually does not give high efficiency in prediction if the data are not prepared appropriately, and this is reflected in the results, as they are bad and fail. Different sub-optimization steps can be used to help in initialization and pre-processing [52]. Data normalization and removal of highly correlated features were used in the database, in addition to removing features with little correlation with the target feature, removing outliers, and evaluating to check for null values in the original data. The techniques will be fully described in the next section.
Figure 11 illustrates the methodology for building hydropower station condition prediction algorithms, which goes through three basic stages, where data must be collected and ingested from the source before that. The first step is concerned with data processing, which includes several sub-optimization steps such as initialization, normalization, and feature selection. Then, the model is built and trained in the second step, which includes Huber parameter tuning, training the model, testing the model, and finally, model validation. The third and final step is concerned with deployment, forecasting, and batch registration
3.4.2. Recurrent Neural Network and Long Short-Term Memory (LSTM)
RNN is one of the most promising DL models, and it works well as a learning model for sequential data processing applications like language processing and speech recognition. Through the neural network’s internal state memory of prior inputs, it acquires knowledge of the characteristics of time series data. RNN can also forecast data and readings for the future using historical and present data. However, in RNN architecture, data stored for a long time are difficult to learn due to the vanishing gradient problem or gradient explosion (vanishing) problem [53].
Recurrent Neural Networks (RNN)
Recurrent Neural Networks (RNNs) are a significant deep learning model that is well-suited for handling sequential data such as speech recognition and language processing. RNNs learn features from time series data by maintaining a memory of previous inputs within the neural network’s internal state. This capability allows RNNs to predict future information based on past and current data [54,55].
RNNs encounter a significant challenge known as the vanishing gradient problem, where the network has difficulty learning long-term dependencies. This issue leads to low efficiency in storing long-term data [56].
Long Short-Term Memory (LSTM)
To address the vanishing gradient problem, the Long Short-Term Memory (LSTM) network was proposed in 1997. LSTMs are designed to retain information for extended periods through a sophisticated architecture involving multiple gates [57], as shown in Figure 12.
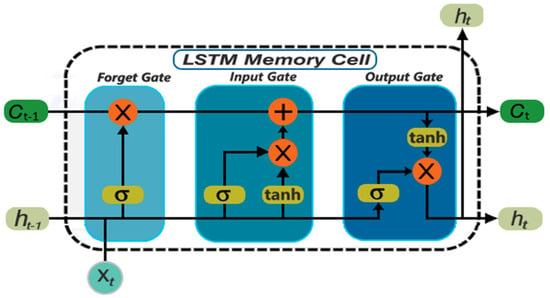
Figure 12.
A long short-term memory block diagram structure.
As shown in Figure 12, the LSTM architectures involves the memory cell which is controlled by three gates: the input gate, the forget gate, and the output gate. These gates decide what information to add to, remove from, and output from the memory cell
- Input Gate: Filters incoming information, allowing relevant data to enter the memory cell.
- Forget Gate: Helps the network forget previously stored information that is no longer needed, maintaining focus on new data.
- Output Gate: Decides whether the information in the memory cell should be outputted or retained.
These gates allow LSTM networks to selectively collect, remember, and discard information, making them highly efficient in dealing with time series data and long-term dependencies. Due to these capabilities, LSTMs are widely used in fields requiring sequential data analysis and future event prediction, such as language translation and speech recognition, and electrical load forecasting. In specific applications such as hydropower station condition prediction, LSTMs can learn the station condition from patterns of influencing factors such as vibration, pressure, and temperature, store these states in memory, and make predictions based on this acquired knowledge.
Key Advantages
- RNNs: Suitable for tasks involving short-term dependencies in sequential data.
- LSTMs: Overcome the limitations of RNNs by efficiently handling long-term dependencies, making them ideal for complex sequential data tasks.
RNNs and LSTMs are both essential tools in deep learning for sequential data processing. While RNNs provide a framework for understanding and predicting sequences, LSTMs offer a more advanced solution to the vanishing gradient problem, enabling the effective learning of long-term dependencies [58,59].
4. Results and Discussion
In this research, the stability state of the turbines of the Obruk Dam for generating electrical power in Turkey was simulated through the huge database obtained for the variables affecting their stability from the same dam as a model for simulating other hydroelectric power plants around the world, using various deep learning algorithms. The efficiency of the selected models (RNN and LSTM) is evaluated using efficiency performance metrics to ensure their high effectiveness and advanced performance.
4.1. Prediction Results
Prediction algorithms are built to obtain the highest and best prediction result that is close to ideal. The best methods were used and tested to obtain the ideal result among the results obtained from each model, taking into account choosing the best type of optimizer to obtain this result after testing. The test was also included based on several factors that affect prediction accuracy, such as the number of hidden layers, learning rate, type of activation function, and batch size.
Two prediction models (LSTM, RNN) were applied with different training and testing rates to obtain the result. It was found that the best value that can give the optimal result is training 67% and testing 33%. The best results were obtained after testing on selected types of optimizers and to achieve the greatest outcomes on each model with a distinct learning rate. The following sections discuss the results, choosing the best type of optimizers and the best types of loss calculation functions with different numbers of hidden layers and influencing factors.
4.1.1. Prediction Using RNN and LSTM Models with Adam Optimizer
This section will explain the methods used to obtain the most optimal result and discuss the results obtained from LSTM and RNN algorithms using hidden layers—both single and multiple—with Adam optimizer in addition to input and output layers in every model. The results are shown in the figures, which include two graphic lines, the first in blue, which represents the actual results, while the orange color represents the expected results from the forecast.
Figure 13 shows the prediction results obtained using the LSTM and RNN algorithms with one hidden layer. The training process showed the test results obtained for every learning rate.
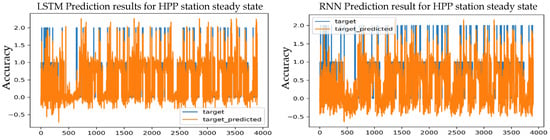
Figure 13.
Prediction results for an S-S HPP station using the Adam optimizer and 1 layer.
When the different test results for each learning rate in the LSTM and REN models were obtained and compared, the model that achieved the best predictive accuracy, which reached 99.55%, is the LSTM, which is a value that is largely identical to the expected value for training, which is 99.23%, this can also be seen clearly by comparing the error rates with the various methods and functions for calculating the error in predicting the stability state of the system. The peak was the minimum. It achieved the lowest loss value, which is MSE = 0.0072. The error rate in MAE was 0.0053, and the error rate was 0.001. The RMSE is 0.0551, at a learning rate of 0.001. These factors will contribute effectively to choosing the best model to be adopted.
The RNN model realized the best prediction accuracy value with one layer and learning rate of 0.001, which is 98.31%, and it was slightly closer to the expected value, which is 97.91%. It achieved the lowest loss value, which is MSE = 0.0513. The MAE error rate was 0.0175, and the RMSE error rate was 0.0846, at a learning rate of 0.001.
Figure 14 displays the real and predicted prediction results of the RNN model as well as the LSTM with two hidden layers. After obtaining the results of the various tests for both models with different learning rates and comparing them, the best result was found for the LSTM model, which achieved an accuracy of 99.40%; this value is close to the expected value for training, which is 98.24%. It achieved the lowest loss value, which is MSE = 0.0117, with a learning rate of 0.001. The error rate in MAE was 0.0058, where the RMSE was 0.0553, at a learning rate of 0.001.
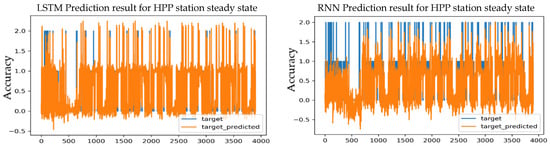
Figure 14.
Prediction results for an S-S HPP station using the Adam optimizer and 2 layers.
While the RNN model realized the best prediction accuracy value with one layer and learning rate of 0.001, which is 98.12%, and it was slightly closer to the expected value, which is 98.24%, it achieved the lowest loss value, which is MSE = 0.0603. The MAE error rate was 0.0251, and the RMSE error rate was 0.1007, at a learning rate of 0.001.
Figure 15 displays the real and predicted prediction results of the RNN model as well as the LSTM with Adam optimizer and three hidden layers.
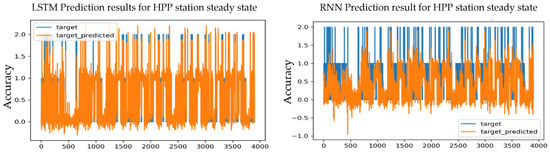
Figure 15.
Prediction results for an S-S HPP station using the Adam optimizer and 3 layers.
After obtaining the results of the various tests for both models with different learning rates and comparing them, the best result was found for the LSTM model, which achieved an accuracy of 99.34%; this value is close to the expected value for training, which is 99.01%. It achieved the lowest loss value, which is MSE = 0.0136, with a learning rate of 0.001. The error rate in MAE was 0.0057, where the RMSE was 0.0563, at a learning rate of 0.001.
While the RNN model realized the best prediction accuracy value with one layer and learning rate of 0.001, which is 98.12%, and it was slightly closer to the expected value, which is 91.54%, it achieved the lowest loss value, which is MSE = 0.1099. The MAE error rate was 0.0674, and the RMSE error rate was 0.1689, at a learning rate of 0.001.
The best result obtained with the highest accuracy and least amount of error was for the LSTM model with a learning rate of 0.001 and one layer. Therefore, it was concluded that this model with one layer gave the best results using the Adam optimizer, as shown in Table 7.

Table 7.
Prediction results for both models using Adam optimizer.
4.1.2. Prediction Using LSTM, and RNN Algorithms with RMSprop Optimizer
The second section deals with the LSTM and RNN algorithms with single, double, and triple layers, and the same loss calculation metrics that were used in the first section, with the RMSprop optimizer. After analyzing the results of the first section with the two models used and the different layers, it was found that the best result always had a learning rate of 0.001 in all cases for both models, LSTM and RNN.
In contrast, the results of a learning rate of 0.01 were negative in all cases, so the learning rate of 0.001 was adopted in the remaining sections.
Figure 16 shows the results of the training process obtained with a learning rate of 0.001 and one hidden layer. The test results values of the LSTM model are taken for each number of layers.
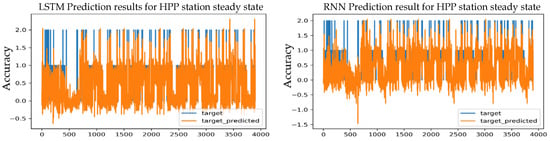
Figure 16.
Prediction results for an S-S HPP station using the RMSprop optimizer and 1 layer.
By taking the results from the testing process and analyzing them, it was found that the LSTM model with a learning rate of 0.001 with one layer achieved the highest prediction accuracy, which reached 97.93%, which is a value very close to the expected value for training, which is 95.05%, as well as the lowest loss value, MSE = 0.0494, MAE = 0.0279, and RMSE = 0.1207, which are the lowest values obtained.
Figure 17 shows the results of the two-layer LSTM model, which achieved a predictive accuracy of 96.94%, which is slightly lower than the accuracy value with a single layer.
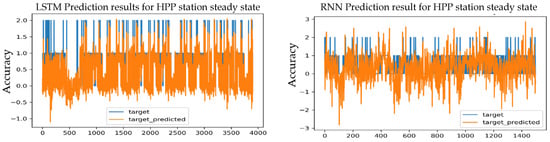
Figure 17.
Prediction results for an S-S HPP station using the RMSprop optimizer and 2 layers.
Figure 18 shows the results of the three-layer LSTM model, which achieved a predictive accuracy of 93.11%, which is slightly lower than the accuracy achieved with the single and double layers.
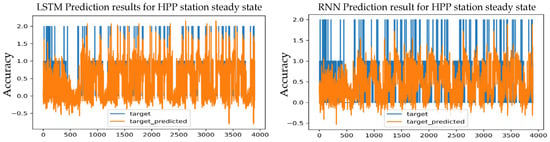
Figure 18.
Prediction results for an S-S HPP station using the RMSprop optimizer and 3 layers.
The above figures illustrate the results of the training process obtained with a learning rate of 0.001 for the RNN model with RMSprop optimizer. The values of the test results were taken from each number of layers in the RNN model. After comparing the test results, the single-layer RNN model achieves the highest results for prediction accuracy, which reached 96.82%, which is significantly higher than the training value, which is 95.82%. The loss values were as follows: MSE = 0.0734, MAE = 0.0302, and RMSE = 0.1504.
Meanwhile, the two-layer RNN model achieved a predictive accuracy of 94.27%, which is slightly lower than the accuracy value with a single layer. The three-layer RNN model also achieved a predictive accuracy of 93.39%, which is slightly lower than the accuracy achieved with the single and double layers.
Table 8 shows the different test results for each of the two models used (RNN, LSTM) with the RMSprop optimizer and single, binary, and triple layers, and using different loss calculation functions, adopting a training rate of 0.001.

Table 8.
Prediction results for both models using RMSprop optimizer.
The highest prediction accuracy was achieved with the LSTM model, which reached 97.93% using one layer as well as the lowest loss values, which is MSE = 0.0494, MAE = 0.0279, and RMSE = 0.1207, which are the lowest loss values obtained.
The RNN model achieved the best accuracy of 96.82%, with the loss values MSE = 0.0734, MAE = 0.0302, and RMSE = 0.1504, with a single layer.
The best result obtained with the highest accuracy and least amount of error was for the LSTM model with a learning rate of 0.001 and one layer.
4.1.3. Prediction Using LSTM and RNN Algorithms with Adagrad Optimizer
The third section deals with the LSTM and RNN algorithms with single, double, and triple layers, with the same loss calculation metrics that were used in the previous sections, with the Adagrad optimizer, using a learning rate of 0.001.
The figures (Figure 19, Figure 20 and Figure 21) below show the results of the training process obtained with a learning rate of 0.001 for the RNN and LSTM models with the Adagrad optimizer.
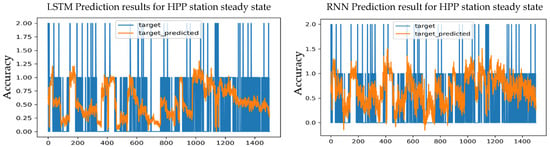
Figure 19.
Prediction results for an S-S HPP station using the Adagrad optimizer and 1 layer.
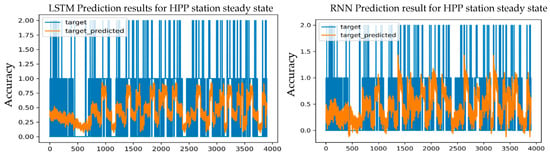
Figure 20.
Prediction results for an S-S HPP station using the Adagrad optimizer and 2 layers.
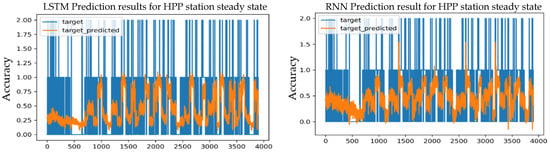
Figure 21.
Prediction results for an S-S HPP station utilizing Adagrad optimizer and three layers.
The different test results for the LSTM model were obtained and compared; the best predictive accuracy was achieved with one layer, which reached 73.47%, which is a value lower than the expected value for training, which is 75.21%, as well as the lowest loss value, MSE = 0.2291, MAE = 0.2844, and RMSE = 0.3668.
Whereas, the same model with two layers achieved a predictive accuracy of 72.70%, and it was the same accuracy value with three layers.
The RNN model also achieved the following results: it was found that the RNN model with one layer achieved the highest prediction accuracy, which reached 73.18%, which is lower than the training value of 75.21%. The loss values were as follows: MSE = 0.2081, MAE = 0.2458, and RMSE = 0.3521.
Whereas, the same model with two layers achieved a predictive accuracy of 72.01%, and with the three layers achieved a predictive accuracy of 69.33%, and these values are gradually lower than the prediction value of one layer.
Table 9 displays the various test outcomes for each of the two models used (RNN, LSTM) with the Adagrad optimizer and single, binary, and triple layers, and using different loss calculation functions, adopting a training rate of 0.001.

Table 9.
Prediction results for both models using Adagrad optimizer.
The highest prediction accuracy was achieved with the LSTM model, which reached 73.47% using one layer. As for the RNN model, it achieved the best accuracy of 73.18%, with a single layer.
As a result, the LSTM model with a learning rate of 0.001 and one layer is the best model that produced the maximum accuracy and lowest error rate.
4.1.4. Prediction Using LSTM and RNN Algorithms with Adadelta Optimizer
The third section deals with the LSTM and RNN algorithms with single, double, and triple layers, with the same loss calculation metrics that were used in the first and second sections, with the Adadelta optimizer, using a learning rate of 0.001.
The figures (Figure 22, Figure 23 and Figure 24) below illustrate the results of the training process obtained with a learning rate of 0.001 for the RNN and LSTM models with the Adadelta optimizer
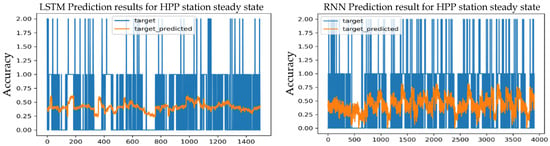
Figure 22.
Prediction results for an S-S HPP station using the Adadelta optimizer and 1 layer.
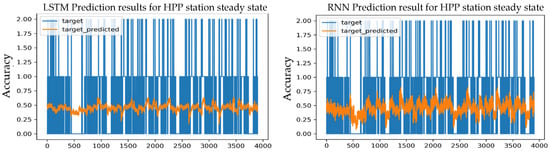
Figure 23.
Prediction results for an S-S HPP station using the Adadelta optimizer and 2 layers.
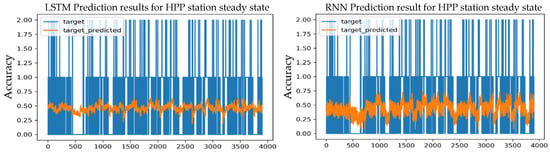
Figure 24.
Prediction results for an S-S HPP station using the Adadelta optimizer and 3 layers.
After comparing the test results obtained from the LSTM model with different numbers of layers, it was found that the LSTM model with a learning rate of 0.001 achieved the same predictive accuracy with single, double, and triple layers, which amounted to 56.39%, as well as the same expected values for training with each number of layers, which amounted to 53.25%, but the loss value varied, and the loss values were the lowest with a single layer and are as follows, MSE = 0.3027, MAE = 0.3336, and RMSE = 0.4134, which are the lowest values obtained.
While the training results of the RNN model with Adadelta optimizer and learning rate 0.001 show that the single-layer RNN model obtained the best prediction accuracy reaching 56.85% which is significantly higher than the training value of 54.02%. The loss values were as follows: MSE = 0.2640, MAE = 0.3353, and RMSE = 0.3980; it was the lowest among other loss values.
Whereas, the two-layer RNN model achieved a predictive accuracy of 56.39%, and the three-layer RNN model also achieved a predictive accuracy of 56.15%, and these values are gradually lower than the prediction value of one layer.
Table 10 shows the different test results for each of the two models used (RNN, LSTM) with the Adadelta optimizer and single, binary, and triple layers, and using different loss calculation functions, adopting a training rate of 0.001.

Table 10.
Prediction results for both models using Adadelta optimizer.
The highest prediction accuracy was achieved with the RNN model, which reached 56.85% using one layer as well as the lowest loss values, which are MSE = 0.2640, MAE = 0.3353, and RMSE = 0.3980, the lowest loss values obtained.
The RNN model achieved the best accuracy of 96.82%, with the loss values MSE = 0.0513, MAE = 0.0175, and RMSE = 0.0846, with a single layer.
Therefore, the RNN model, which has one layer and a learning rate of 0.001, is the best model that produced the highest accuracy and lowest error rate.
5. Conclusions
In this research, two deep learning models (LSTM and RNN) were employed to predict the stability state of the hydropower station based on the readings in the real database taken from Obruk Dam, Elektrik Uretim Anonim Sirketince electricity power production company in Turkey. Deep learning and forecasting are basic requirements for any country in the world to improve future planning. It is a science that contributes fundamentally to population, industrial, and economic stability, a major goal for any country where these models are as accurate, reliable, and meaningful as possible.
The best model that achieved the highest predictive accuracy among the different results as well as the lowest loss rate was discussed and identified by testing both models (LSTM and RNN) for the stability state of the Obruk Dam hydroelectric power station, taking into account the selection of the best types of optimizers, learning rates, number of layers, calculating the loss results using several ways.
Four different optimizers (Adam, RMSprop, Adadelta, and Adagrad) as well as three hidden layers (single, double, and triple) and three loss calculation methods (MAE, RMSE, and MSE) were used as auxiliary methods to identify the best-performing and most efficient model. The selected model will be eligible for use in all dams containing similar hydropower stations.
The LSTM model delivered the best results, as it was the most efficient and best performing, it achieved an accuracy of up to 99.55%, and the lowest loss value, which is MSE = 0.0072, and this value is clear with the rest of the loss calculation methods, which are MAE = 0.0053 and RMSE = 0.0551 at a learning rate of 0.001 by applying Adam optimizer and one hidden layer. The data used were split as follows, 67% training and 33% testing.
The proposed model will contribute to increasing the stability of hydropower plants, especially power generation turbines in dams, and will reduce the possibility of breakdowns and power outages for residents and industrial companies, reduce emergency maintenance costs, and plan for future maintenance.
Author Contributions
Conceptualization, O.F.A.-H. and H.D.; methodology, O.F.A.-H. and H.D.; software, O.F.A.-H.; validation, O.F.A.-H. and H.D.; formal analysis, O.F.A.-H.; investigation, O.F.A.-H. and H.D.; resources, O.F.A.-H.; data curation, O.F.A.-H.; writing—original draft preparation, O.F.A.-H.; writing—review and editing, O.F.A.-H. and H.D.; visualization, O.F.A.-H.; supervision, O.F.A.-H. and H.D.; project administration, O.F.A.-H. and H.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We would like to extend our sincere thanks and appreciation to the management of (Elektrik Üretim A.Ş.) EÜAŞ Company, Turkey, who provided me with the data and answered the inquiries I needed, especially İzzet Alagöz and Mehmet Bulut. We would also like to express our sincere thanks to Abdul Mutalib Mohsen, one of the engineers of Haditha Dam, Iraq, who provided us with valuable and required information that contributed to the completion of this study. We also express our sincere thanks to Huseyin Canbolat, Ankara Yıldırım Beyazıt University, who contributed to the completion of this study. Our sincere thanks to everyone who contributed to the completion of this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zolfaghari, M.; Golabi, M.R. Modeling and predicting the electricity production in hydropower using conjunction of wavelet transform, long short-term memory, and random forest models. Renew. Energy 2021, 170, 1367–1381. [Google Scholar] [CrossRef]
- Kartal, M.T.; Kılıç Depren, S.; Ayhan, F.; Depren, Ö. Impact of renewable and fossil fuel energy consumption on environmental degradation: Evidence from USA by nonlinear approaches. Int. J. Sustain. Dev. World Ecol. 2022, 29, 738–755. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, Y.; Zhang, R.; Ouyang, S.; Wang, X.; Liao, X. Integrated optimization of hydroelectric energy in the upper and middle Yangtze River. Renew. Sustain. Energy Rev. 2015, 45, 481–512. [Google Scholar] [CrossRef]
- Varol, M. CO2 emissions from hydroelectric reservoirs in the Tigris River basin, a semi-arid region of southeastern Turkey. J. Hydrol. 2019, 569, 782–794. [Google Scholar] [CrossRef]
- Alagöz, İ.; Bulut, M.; Geylani, V.; Yıldırım, A. Importance of real-time hydro power plant condition monitoring systems and contribution to electricity production. Turk. J. Electr. Power Energy Syst. 2021, 1, 1–11. [Google Scholar] [CrossRef]
- Nadeau, M.J.; Kim, Y.D. World Energy Resources Charting the Upsurge in Hydropower Development. Technical Report; World Energy Council: London, UK, 2015; Available online: https://www.worldenergy.org/assets/downloads/World-Energy-Resources_Charting-the-Upsurge-in-Hydropower-Development_2015_Report2.pdf (accessed on 1 June 2024).
- Muhsen, A.A.; Szymański, G.M.; Mankhi, T.A.; Attiya, B. Selecting the most efficient maintenance approach using AHP multiple criteria decisions making at haditha hydropower plant. Zesz. Nauk. Politech. Poznańskiej Organ. I Zarządzanie 2018, 78, 113–136. [Google Scholar]
- Yaseen, Z.M.; Ameen, A.M.S.; Aldlemy, M.S.; Ali, M.; Abdulmohsin Afan, H.; Zhu, S.; Sami Al-Janabi, A.M.; Al-Ansari, N.; Tiyasha, T.; Tao, H. State-of-the art-powerhouse, dam structure, and turbine operation and vibrations. Sustainability 2020, 12, 1676. [Google Scholar] [CrossRef]
- Al-Hadeethi, M.M.; Mustafa, M.W.B.; Muhsen, A.A. Exploiting Renewable Energy in Iraq to Conquer the Problem of Electricity Shortage and Mitigate Greenhouse Gas Emissions. In Proceedings of the 9th Virtual International Conference on Science, Technology and Management in Energy. Complex System Research Centre, Mathematical Institute of the Serbian Academy of Sciences and Arts, Belgrad, Serbia, 23–24 November 2023. [Google Scholar]
- Muhsen, A.A.; Al-Malik, A.A.; Attiya, B.H.; Al-Hardanee, O.F.; Abdalazize, K.A. Modal analysis of Kaplan turbine in Haditha hydropower plant using ANSYS and SolidWorks. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: London, UK, 2021; Volume 1105, p. 012056. [Google Scholar]
- Proske, D. Comparison of dam failure frequencies and failure probabilities. Beton-Und Stahlbetonbau 2018, 113, 2–6. [Google Scholar] [CrossRef]
- Cleary, P.W.; Prakash, M.; Mead, S.; Tang, X.; Wang, H.; Ouyang, S. Dynamic simulation of dam-break scenarios for risk analysis and disaster management. Int. J. Image Data Fusion 2012, 3, 333–363. [Google Scholar] [CrossRef]
- Reza, G.; Dziedzic, M. An Improved Conceptual Bayesian Model for Dam Break Risk Assessment. In World Environmental and Water Resources Congress; ASCE: Reston, VA, USA, 2024; pp. 1002–1018. [Google Scholar]
- Wang, S.; Yang, B.; Chen, H.; Fang, W.; Yu, T. LSTM-based deformation prediction model of the embankment dam of the danjiangkou hydropower station. Water 2022, 14, 2464. [Google Scholar] [CrossRef]
- CIGRE Study Committee SC11, EG11.02. Hydrogenerator Failures-Results of the Survey. 2003. Available online: https://www.e-cigre.org/publications/detail/392-survey-of-hydrogenerator-failures.html (accessed on 15 June 2024).
- TEIAŞ (Turkish Electricity Transmission Co.). Turkey Electricity Production and Transmission Statistics. 2020. Available online: https://www.teias.gov.tr/tr-TR/turkiye-elektrik-uretim-iletim-istatistikleri (accessed on 26 January 2020).
- OBRUK HEPP. Available online: https://www.euas.gov.tr/en-US/power-plants/obruk-hepp (accessed on 24 June 2024).
- Kao, C.Y.; Loh, C.H. Monitoring of long-term static deformation data of Fei-Tsui arch dam using artificial neural network-based approaches. Struct. Control Health Monit. 2013, 20, 282–303. [Google Scholar] [CrossRef]
- Ghiasi, B.; Noori, R.; Sheikhian, H.; Zeynolabedin, A.; Sun, Y.; Jun, C.; Hamouda, M.; Bateni, S.M.; Abolfathi, S. Uncertainty quantification of granular computing-neural network model for prediction of pollutant longitudinal dispersion coefficient in aquatic streams. Sci. Rep. 2022, 12, 4610. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Li, X.; Yang, B.; Wen, Z. Wavelet support vector machine-based prediction model of dam deformation. Mech. Syst. Signal Process. 2018, 110, 412–427. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, X.; Karimian, H.; Xiao, G.; Huang, J. A novel framework for prediction of dam deformation based on extreme learning machine and Lévy flight bat algorithm. J. Hydroinform. 2021, 23, 935–949. [Google Scholar] [CrossRef]
- Bhardwaj, S.; Wang, Y.; Yu, G.; Wang, Y. Information set supported deep learning architectures for improving noisy image classification. Sci. Rep. 2023, 13, 4417. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Song, M.M.; Xiong, Z.C.; Zhong, J.H.; Xiao, S.G.; Tang, Y.H. Research on fault diagnosis method of planetary gearbox based on dynamic simulation and deep transfer learning. Sci. Rep. 2022, 12, 17023. [Google Scholar] [CrossRef] [PubMed]
- Asutkar, S.; Tallur, S. Deep transfer learning strategy for efficient domain generalisation in machine fault diagnosis. Sci. Rep. 2023, 13, 6607. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Li, P. Research on gearbox temperature field image fault diagnosis method based on transfer learning and deep belief network. Sci. Rep. 2023, 13, 6664. [Google Scholar] [CrossRef]
- Ahmed, S.F.; Alam, M.S.B.; Hassan, M.; Rozbu, M.R.; Ishtiak, T.; Rafa, N.; Mofijur, M.; Shawkat Ali, A.B.M.; Gandomi, A.H. Deep learning modelling techniques: Current progress, applications, advantages, and challenges. Artif. Intell. Rev. 2023, 56, 13521–13617. [Google Scholar] [CrossRef]
- Dai, S.Z.; Li, L.; Li, Z.H. Modeling Vehicle Interactions via Modified LSTM Models for Trajectory Prediction. IEEE Access 2019, 7, 38287–38296. [Google Scholar] [CrossRef]
- Frame, J.M.; Kratzert, F.; Raney, A.; Rahman, M.; Salas, F.R.; Nearing, G.S. Post-processing the national water model with long short-term memory networks for streamflow predictions and model diagnostics. J. Am. Water Resour. Assoc. 2021, 57, 885–905. [Google Scholar] [CrossRef]
- Fan, D.Y.; Sun, H.; Yao, J.; Zhang, K.; Yan, X.; Sun, Z.X. Well production forecasting based on ARIMA-LSTM model considering manual operations. Energy 2021, 220, 119708. [Google Scholar] [CrossRef]
- Yang, S.; Han, X.; Kuang, C.; Fang, W.; Zhang, J.; Yu, T. Comparative study on deformation prediction models of Wuqiangxi concrete gravity dam based on monitoring data. Comput. Model. Eng. Sci. 2022, 131, 49–72. [Google Scholar] [CrossRef]
- Qu, X.D.; Yang, J.; Chang, M. A deep learning model for concrete dam deformation prediction based on RS-LSTM. J. Sens. 2019, 2019, 4581672. [Google Scholar] [CrossRef]
- Ahmad, I.; Rashid, A. On-line monitoring of hydro power plants in Pakistan. Inf. Technol. J. 2007, 6, 919–923. [Google Scholar] [CrossRef][Green Version]
- Lai, J.P.; Chang, Y.M.; Chen, C.H.; Pai, P.F. A survey of machine learning models in renewable energy predictions. Appl. Sci. 2020, 10, 5975. [Google Scholar] [CrossRef]
- Liu, Z.; Zou, S.; Zhou, L. Condition Monitoring System for Hydro Turbines Based on LabVIEW. In Proceedings of the 2012 Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Mohanta, R.K.; Chelliah, T.R.; Allamsetty, S.; Akula, A.; Ghosh, R. Sources of vibration and their treatment in hydro power stations-A review. Eng. Sci. Technol. Int. J. 2017, 20, 637–648. [Google Scholar] [CrossRef]
- CAS Dataloggers, (Vibration Monitoring System for Hydro Turbines). Available online: https://www.dataloggerinc.com/wp-content/uploads/2016/03/18-Vibration_Monitoring_System_for_Hydro_Turbines.pdf (accessed on 20 June 2024).
- Vijaya, K.K.; Surender, S. Industry Monitoring Robot using Arduino Uno with Matlab Interface. Adv. Robot. Autom. 2016, 5, 2–4. [Google Scholar] [CrossRef]
- Bansal, P.; Vedaraj, I.S.R. Monitoring and Analysis of Vibration Signal in Machine Tool Structures. Int. J. Eng. Dev. Res. 2014, 2, 2310–2317. [Google Scholar]
- Al-Hardanee, O.; Çankaya, İ.; Muhsen, A.; Canbolat, H. Design a control system for observing vibration and temperature of turbines. Indones. J. Electr. Eng. Comput. Sci. 2021, 24, 1437–1444. [Google Scholar] [CrossRef]
- Hammid, A.T.; Sulaiman, M.H.B.; Abdalla, A.N. Prediction of small hydropower plant power production in Himreen Lake dam (HLD) using artificial neural network. Alex. Eng. J. 2018, 57, 211–221. [Google Scholar] [CrossRef]
- Sun, L.; Liu, T.; Xie, Y.; Zhang, D.; Xia, X. Real-time power prediction approach for turbine using deep learning techniques. Energy 2021, 233, 121130. [Google Scholar] [CrossRef]
- Dao, F.; Zeng, Y.; Zou, Y.; Qian, J. Wear fault diagnosis in hydro-turbine via the incorporation of the IWSO algorithm optimized CNN-LSTM neural network. 2024; preprint. [Google Scholar]
- Yang, B.; Bo, Z.; Yawu, Z.; Xi, Z.; Dongdong, Z.; Yalan, J. The vibration trend prediction of hydropower units based on wavelet threshold denoising and bi-directional long short-term memory network. In Proceedings of the 2021 IEEE International Conference on Power Electronics, Computer Applications (ICPECA), Shenyang, China, 22–24 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 575–579. [Google Scholar]
- Gao, X.; Li, X.; Zhao, B.; Ji, W.; Jing, X.; He, Y. Short-term electricity load forecasting model based on EMD-GRU with feature selection. Energies 2019, 12, 1140. [Google Scholar] [CrossRef]
- Abumohsen, M.; Owda, A.Y.; Owda, M. Electrical load forecasting using LSTM, GRU, and RNN algorithms. Energies 2023, 16, 2283. [Google Scholar] [CrossRef]
- He, F.; Zhou, J.; Feng, Z.K.; Liu, G.; Yang, Y. A hybrid short-term load forecasting model based on variational mode decomposition and long short-term memory networks considering relevant factors with Bayesian optimization algorithm. Appl. Energy 2019, 237, 103–116. [Google Scholar] [CrossRef]
- Jaramillo, M.; Pavón, W.; Jaramillo, L. Adaptive Forecasting in Energy Consumption: A Bibliometric Analysis and Review. Data 2024, 9, 13. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, Z.; Wei, Z. Absolute logarithmic calibration for correlation coefficient with multiplicative distortion. Commun. Stat.-Simul. Comput. 2020, 52, 482–505. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Data Mining: The Textbook; Springer: Berlin/Heidelberg, Germany, 2015; Volume 1. [Google Scholar]
- Punyani, P.; Gupta, R.; Kumar, A. A multimodal biometric system using match score and decision level fusion. Int. J. Inf. Technol. 2022, 14, 725–730. [Google Scholar] [CrossRef]
- Yuan, B.; He, B.; Yan, J.; Jiang, J.; Wei, Z.; Shen, X. Short-term electricity consumption forecasting method based on empirical mode decomposition of long-short term memory network. IOP Conf. Ser. Earth Environ. Sci. 2022, 983, 12004. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A critical review of recurrent neural networks for sequence learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Dupond, S. A thorough review on the current advance of neural network structures. Annu. Rev. Control 2019, 14, 200–230. [Google Scholar]
- Graves, A. Supervised Sequence Labelling with Recurrent Neural Networks. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hochreiter, S. Untersuchungen zu dynamischen neuronalen Netzen. Diploma Tech. Univ. München 1991, 91, 31. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Fan, H.; Jiang, M.; Xu, L.; Zhu, H.; Cheng, J.; Jiang, J. Comparison of long short-term memory networks and the hydrological model in runoff simulation. Water 2020, 12, 175. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).