Clamping Pressure and Catalyst Distribution Analyses on PEMFC Performance Improvement
Abstract
1. Introduction
2. Mathematical Model
2.1. Model Assumptions
- The PEMFC is assumed to operate in steady state.
- Both the thermal and cyclic stress are ignored.
- The clamping pressure applied to the bipolar plate is uniform and equal everywhere.
- Only the elastic deformation of GDL is considered.
- Flows inside the PEMFC are assumed to be incompressible and laminar.
2.2. Solid Equations
2.3. Governing Equations
2.4. Boundary Condition
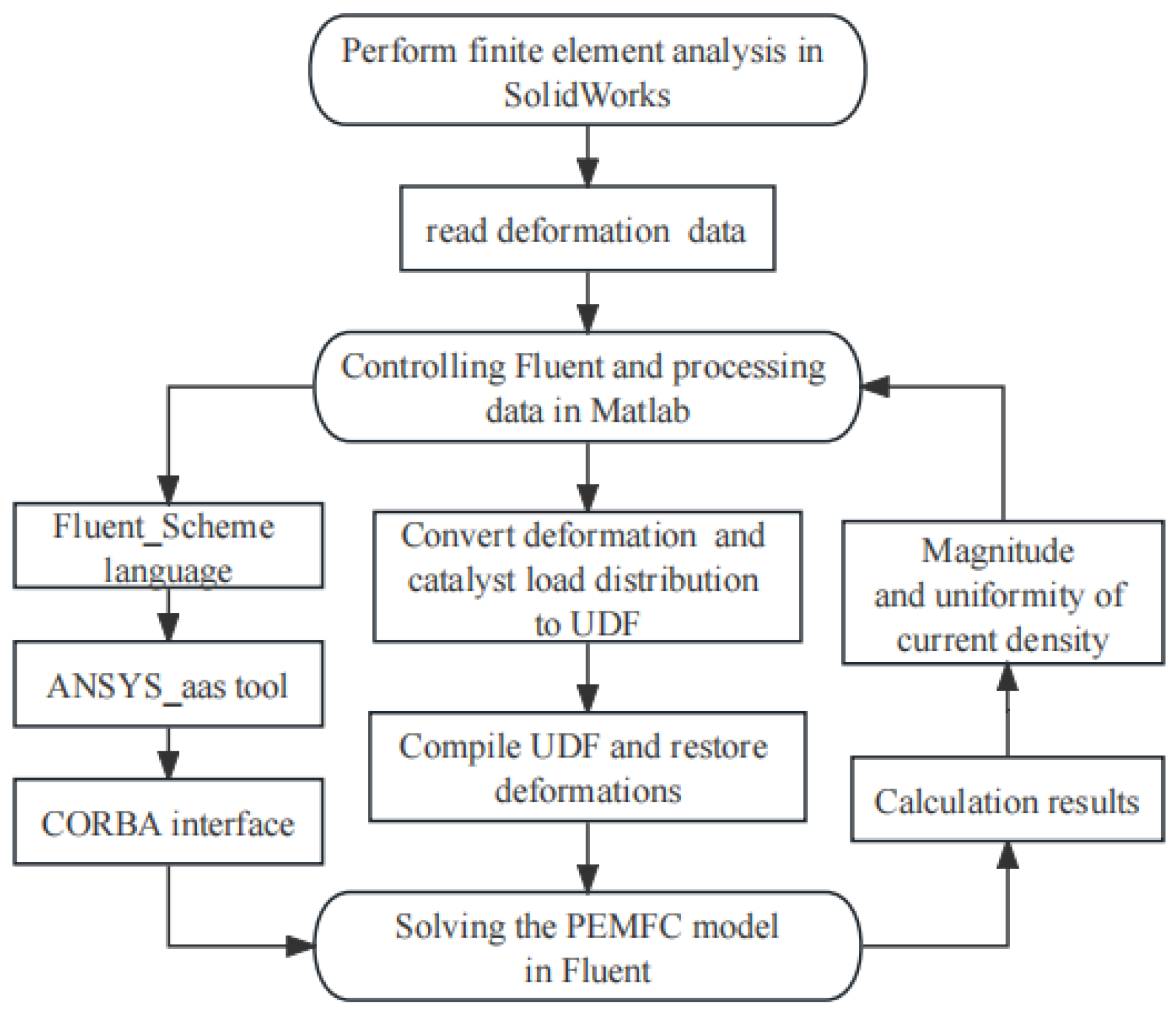
2.5. Numerical Simulation of Deformation
2.6. Model Validation
3. Results and Discussion
3.1. Deformation Analysis of Gas Diffusion Layer
3.2. Effects of Deformation on PEMFC Performance
3.3. Optimization of Cathode Catalytic Layer
4. Conclusions
- The GDL deformation is mainly caused by the clamping force from the rib, and the GDL deformation magnitude under the rib is much greater than that under the flow channel. Along the direction from BP to CL, the GDL deformation gradually decreases. Furthermore, the CL and PEM deformations are relatively smaller than GDL deformations.
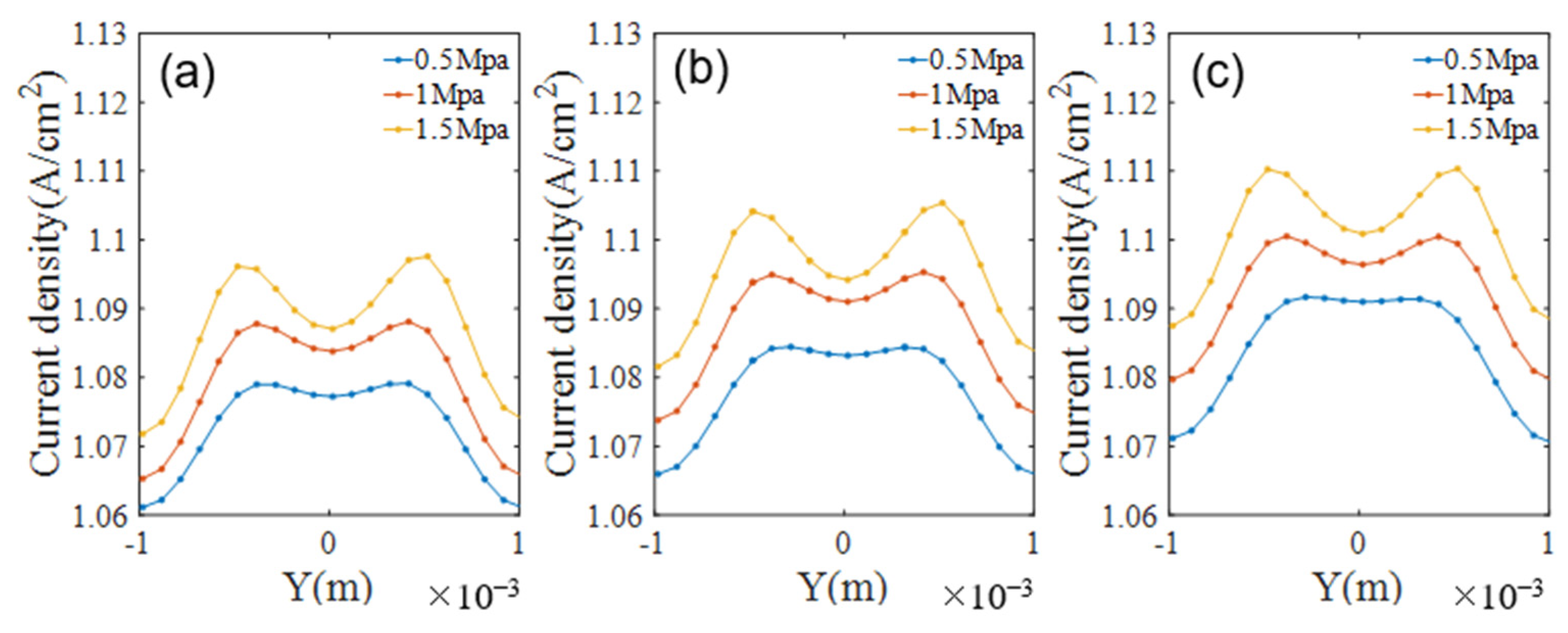
- The power output improved with increased clamping pressure. However, the distribution uniformities of reactants’ concentration, liquid water, heat, and current density deteriorated as the clamping pressure increased.
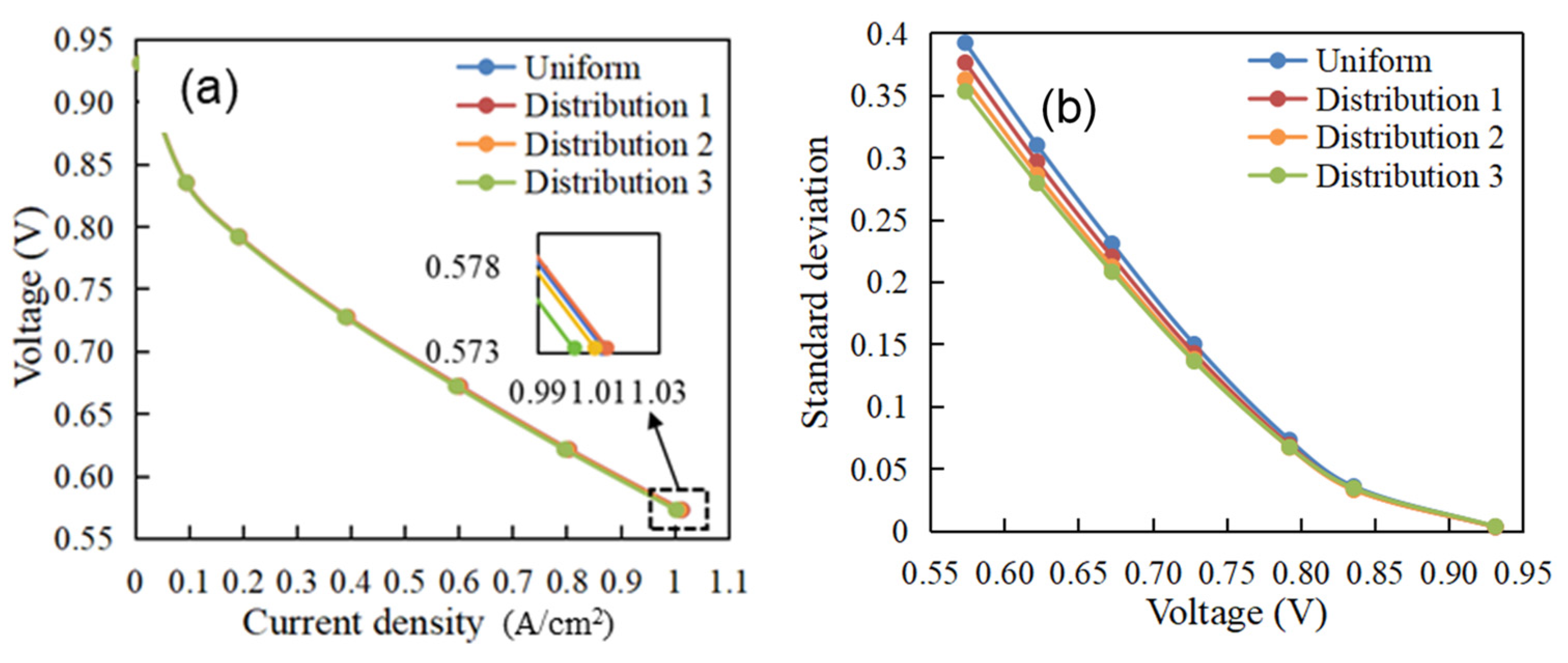
- Compared with uniform distribution under the premise of constant total cathode catalyst loading, the non-uniform distributions with reduced catalyst loading under the channel, along with increased catalyst loading under the rib, effectively improved the current density uniformity. A weighted objective function was constructed to evaluate the performance of different catalyst loading distributions. Compared with the uniform distribution, the optimal catalyst loadings under the channel and rib showed a change of −15% and 15%, respectively. The objective function of the above optimal distribution had a maximum value of 17.24%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Q.; Zhang, Z.; Xiao, G.; Xue, D. Hydrophobicity gradient optimization of fuel cell gas diffusion media for its application in vehicles. Fundam. Res. 2024, 4, 1036–1046. [Google Scholar] [CrossRef]
- Xiong, Z.; Meng, K.; Chen, K.; Chen, W.; Deng, Q.; Luo, Z.; He, D.; Zou, G.; Chen, B. Investigation of transport properties of gas diffusion layer of PEMFC with metallic bipolar plates based on mechanical compression. Int. J. Heat Mass Transf. 2024, 232, 125922. [Google Scholar] [CrossRef]
- Zhang, H.; Rahman, M.A.; Mojica, F.; Sui, P.C.; Chuang, P.Y.A. A comprehensive two-phase proton exchange membrane fuel cell model coupled with anisotropic properties and mechanical deformation of the gas diffusion layer. Electrochim. Acta 2021, 382, 138273. [Google Scholar] [CrossRef]
- Shi, Q.; Feng, C.; Ming, P.; Tang, F.; Zhang, C. Compressive stress and its impact on the gas diffusion layer: A review. Int. J. Hydrogen Energy 2022, 47, 3994–4009. [Google Scholar] [CrossRef]
- Li, W.Z.; Yang, W.W.; Zhang, W.Y.; Qu, Z.G.; He, Y.L. Three-dimensional modeling of a PEMFC with serpentine flow field incorporating the impacts of electrode inhomogeneous compression deformation. Int. J. Hydrogen Energy 2019, 44, 22194–22209. [Google Scholar] [CrossRef]
- Xiao, L.; Zhu, L.; Clökler, C.; Grünzweig, A.; Wilhelm, F.; Scholta, J.; Zeis, R.; Shen, Z.G.; Luo, M.; Sui, P.C. Experimental validation of pore-scale models for gas diffusion layers. J. Power Sources 2022, 536, 231515. [Google Scholar] [CrossRef]
- Zhang, Z.; He, P.; Dai, Y.J.; Jin, P.H.; Tao, W.Q. Study of the mechanical behavior of paper-type GDL in PEMFC based on microstructure morphology. Int. J. Hydrogen Energy 2020, 45, 29379–29394. [Google Scholar] [CrossRef]
- Aldakheel, F.; Ismail, M.S.; Hughes, K.J.; Ingham, D.B.; Ma, L.; Pourkashanian, M.; Cumming, D.; Smith, R. Gas permeability, wettability and morphology of gas diffusion layers before and after performing a realistic ex-situ compression test. Renew. Energy 2020, 151, 1082–1091. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, H.; Shao, X.; Zhan, Z.; Chen, B. A comparative numerical investigation of effect of mechanical compression on the transport properties of gas diffusion layer fabricated by wet and dry laid methods. Int. J. Heat Mass Transf. 2024, 234, 126064. [Google Scholar] [CrossRef]
- Chen, G.; Xu, Q.; Xuan, J.; Liu, J.; Fu, Q.; Shi, W.; Su, H.; Xing, L. Numerical study of inhomogeneous deformation of gas diffusion layers on proton exchange membrane fuel cells performance. J. Energy Storage 2021, 44, 103486. [Google Scholar] [CrossRef]
- Jing, G.; Hu, C.; Qin, Y.; Sun, X.; Ma, T. Complex mechanisms of PEMFC performance variations influenced by both structural deformation and contact resistance under the clamping force. Int. J. Hydrogen Energy 2024, 58, 137–148. [Google Scholar] [CrossRef]
- Movahedi, M.; Ramiar, A.; Ranjber, A.A. 3D numerical investigation of clamping pressure effect on the performance of proton exchange membrane fuel cell with interdigitated flow field. Energy 2018, 142, 617–632. [Google Scholar] [CrossRef]
- Liu, Y.; Kohrn, M.; Wick, M.; Pischinger, S. Optimization of the bipolar plate rib structure in proton exchange membrane fuel cells with an analytical method. Int. J. Hydrogen Energy 2022, 47, 17683–17698. [Google Scholar] [CrossRef]
- Zhang, H.; Xiao, L.; Chuang, P.Y.A.; Djilali, N.; Sui, P.C. Coupled stress–strain and transport in proton exchange membrane fuel cell with metallic bipolar plates. Appl. Energy 2019, 251, 113316. [Google Scholar] [CrossRef]
- Zheng, M.; Liang, H.; Bu, W.; Qu, C.; Hu, X.; Zhang, Z. Porosity and permeability optimization of PEMFC cathode gas diffusion layer based on topology algorithm. Int. J. Electrochem. Sci. 2024, 19, 100803. [Google Scholar] [CrossRef]
- Yu, R.; Guo, H.; Chen, H.; Ye, F. Segmented distribution of gas diffusion layer porosity and catalyst layer ionomer content in a polymer electrolyte membrane fuel cell. Chem. Eng. Res. Des. 2024, 209, 412–424. [Google Scholar] [CrossRef]
- Yu, R.J.; Guo, H.; Chen, H.; Ye, F. Heat and mass transfer at the interface between cathode catalyst layer and gas diffusion layer of a proton exchange membrane fuel cell. Int. Commun. Heat Mass Transf. 2023, 140, 106548. [Google Scholar] [CrossRef]
- Huang, X.; He, Y.; Sun, Y.; Sun, L.; Wang, T.; Zhang, X. Gradient ionomer designed cathode catalyst layer for proton exchange membrane fuel cells with enhanced performance. J. Power Sources 2024, 603, 234488. [Google Scholar] [CrossRef]
- Li, G.; Deng, C.; Ji, F.; Zheng, B.; Wang, X.; Wang, T. Balancing proton and mass transfers in cathode catalyst layer of high-temperature proton exchange membrane fuel cell via gradient porous structure design. J. Power Sources 2024, 593, 233807. [Google Scholar] [CrossRef]
- Shin, J.; Son, M.; Kim, S.I.; Song, S.A.; Lee, D.H. Design of multi-layered gradient catalysts for efficient proton exchange membrane fuel cells. J. Power Sources 2023, 582, 233546. [Google Scholar] [CrossRef]
- Yang, L.; Fu, K.; Jin, X.; Wang, S.; Gan, Q.; Zhang, Q.; Li, P.; Cao, C. Catalyst layer design with inhomogeneous distribution of platinum and ionomer optimal for proton exchange membrane fuel cell cold start. Chem. Eng. Sci. 2022, 263, 118132. [Google Scholar] [CrossRef]
- Sassin, M.B.; Garsany, Y.; Atkinson Iii, R.W.; Hjelm, R.M.E.; Swider-Lyons, K.E. Understanding the interplay between cathode catalyst layer porosity and thickness on transport limitations en route to high-performance PEMFCs. Int. J. Hydrogen Energy 2019, 44, 16944–16955. [Google Scholar] [CrossRef]
- Ansys Fluent Theory Guide. 2024. Available online: https://ansyshelp.ansys.com/Views/Secured/corp/v241/en/pdf/Ansys_Fluent_Theory_Guide.pdf (accessed on 15 August 2024).
- Giuseppe, C.; Stefano, F.; Alessandro, D. Methodology for PEMFC CFD Simulation Including the Effect of Porous Parts Compression. Int. J. Hydrogen Energy 2022, 47, 14658–14673. [Google Scholar]
- Zhou, Y.; Jiao, K.; Du, Q.; Yin, Y.; Li, X. Gas diffusion layer deformation and its effect on the transport characteristics and performance of proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2013, 38, 12891–12903. [Google Scholar] [CrossRef]
- Li, S.; Sundén, B. Effects of gas diffusion layer deformation on the transport phenomena and performance of PEM fuel cells with interdigitated flow fields. Int. J. Hydrogen Energy 2018, 43, 16279–16292. [Google Scholar] [CrossRef]
- Yablecki, J.; Bazylak, A. Determining the effective thermal conductivity of compressed PEMFC GDLs through thermal resistance modelling. J. Power Sources 2012, 217, 470–478. [Google Scholar] [CrossRef]
- Fan, R.; Chang, G.; Xu, Y.; Xu, J. Investigating and quantifying the effects of catalyst layer gradients, operating conditions, and their interactions on PEMFC performance through global sensitivity analysis. Energy 2024, 290, 130128. [Google Scholar] [CrossRef]
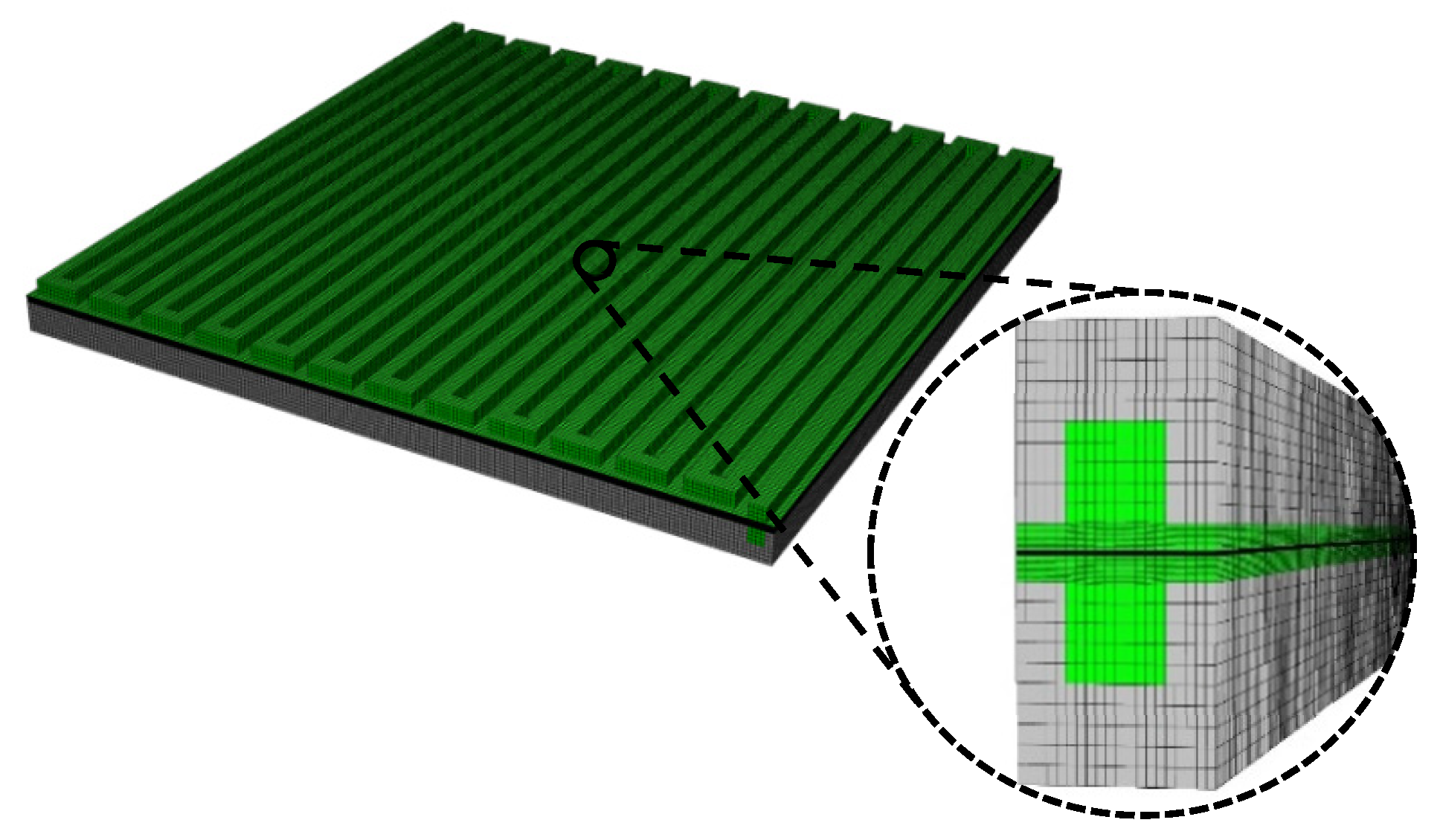







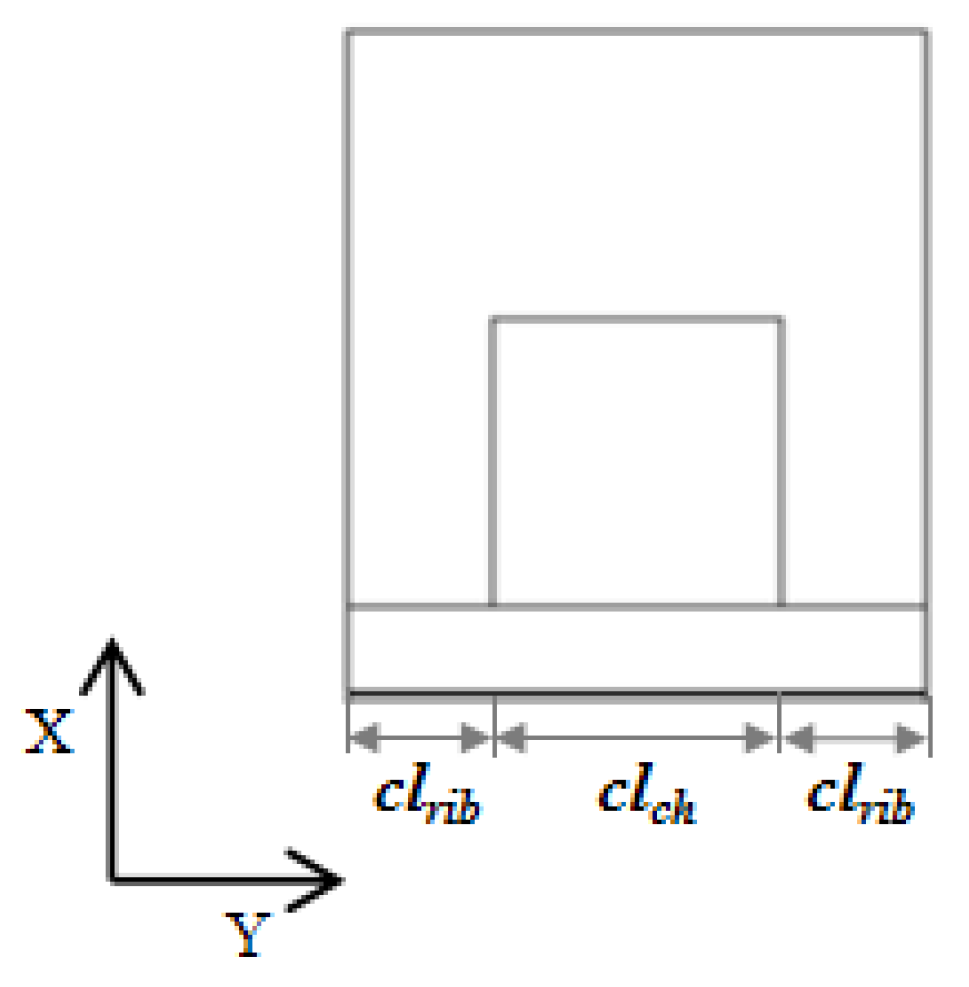



| Name | Value | Unit |
|---|---|---|
| Channel width | 0.001 | m |
| Channel height | 0.001 | m |
| Rib width | 0.001 | m |
| GDL thickness | 0.0003 | m |
| CL thickness | 0.00001 | m |
| PEM Thickness | 0.00003 | m |
| GDL porosity | 0.6 | - |
| CL porosity | 0.2 | - |
| Reaction area | 0.0002 | m2 |
| Physical Parameters | BP | GDL | PEM | CL |
|---|---|---|---|---|
| Young’s modulus (MPa) | 197,000 | 6.1 | 232 | 249 |
| Poisson’s ratio | 0.3 | 0.1 | 0.253 | 0.3 |
| Initial porosity | 0 | 0.6 | - | 0.2 |
| Density (kg/m3) | 7800 | 440 | 1980 | 2059 |
| Specific heat capacity (J/kg K) | 1580 | 568 | 833 | 3300 |
| Thermal conductivity (W/m K) | 20 | 1.0 | 0.95 | 1.0 |
| Conductivity coefficient (S/m) | 20,000 | 300 | - | 300 |
| Current (A) | Stoichiometry for Anode | Stoichiometry for Cathode | Gas Outlet Pressure (KPa) | Gas Relative Humidity | Gas Inlet Temperature (°C) |
|---|---|---|---|---|---|
| 0 | 14.34 | 12.03 | 60 | 100% | 80 |
| 5 | 43.02 | 36.11 | 60 | 100% | 80 |
| 10 | 21.51 | 18.05 | 60 | 100% | 80 |
| 15 | 14.34 | 12.03 | 60 | 100% | 80 |
| 20 | 10.75 | 9.03 | 60 | 100% | 80 |
| 22.5 | 9.56 | 8.02 | 60 | 100% | 80 |
| 25 | 8.6 | 7.22 | 60 | 100% | 80 |
| 27.5 | 7.82 | 6.56 | 60 | 100% | 80 |
| 30 | 7.17 | 6.02 | 60 | 100% | 80 |
| 35 | 6.15 | 5.16 | 60 | 100% | 80 |
| 40 | 5.38 | 4.51 | 60 | 100% | 80 |
| 45 | 4.78 | 4.01 | 60 | 100% | 80 |
| 50 | 4.3 | 3.61 | 60 | 100% | 80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Wang, X.; Xiao, G. Clamping Pressure and Catalyst Distribution Analyses on PEMFC Performance Improvement. Energies 2024, 17, 5223. https://doi.org/10.3390/en17205223
Yang Q, Wang X, Xiao G. Clamping Pressure and Catalyst Distribution Analyses on PEMFC Performance Improvement. Energies. 2024; 17(20):5223. https://doi.org/10.3390/en17205223
Chicago/Turabian StyleYang, Qinwen, Xu Wang, and Gang Xiao. 2024. "Clamping Pressure and Catalyst Distribution Analyses on PEMFC Performance Improvement" Energies 17, no. 20: 5223. https://doi.org/10.3390/en17205223
APA StyleYang, Q., Wang, X., & Xiao, G. (2024). Clamping Pressure and Catalyst Distribution Analyses on PEMFC Performance Improvement. Energies, 17(20), 5223. https://doi.org/10.3390/en17205223






