Proposal of Three Methods for Deriving Representative Mean Radiant Temperatures Considering Zone Spatial Distributions
Abstract
1. Introduction
2. Review of Existing MRT Derivation Methods
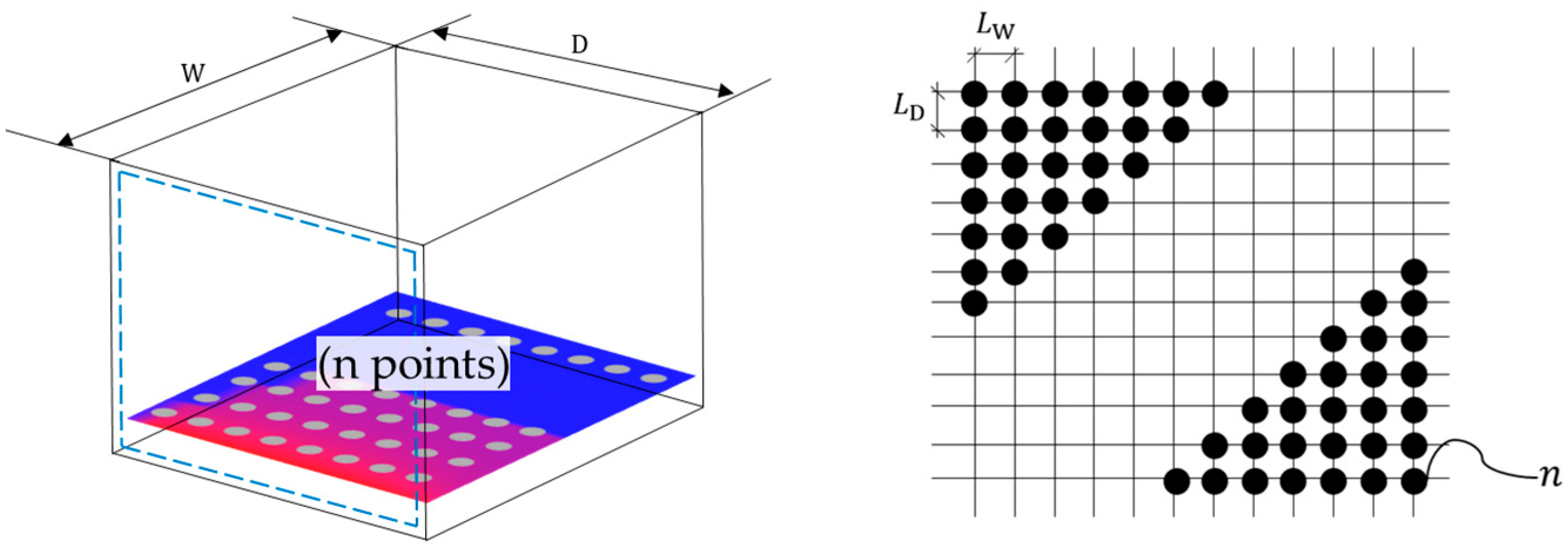
3. Derivation of Method
4. Experiment and Result
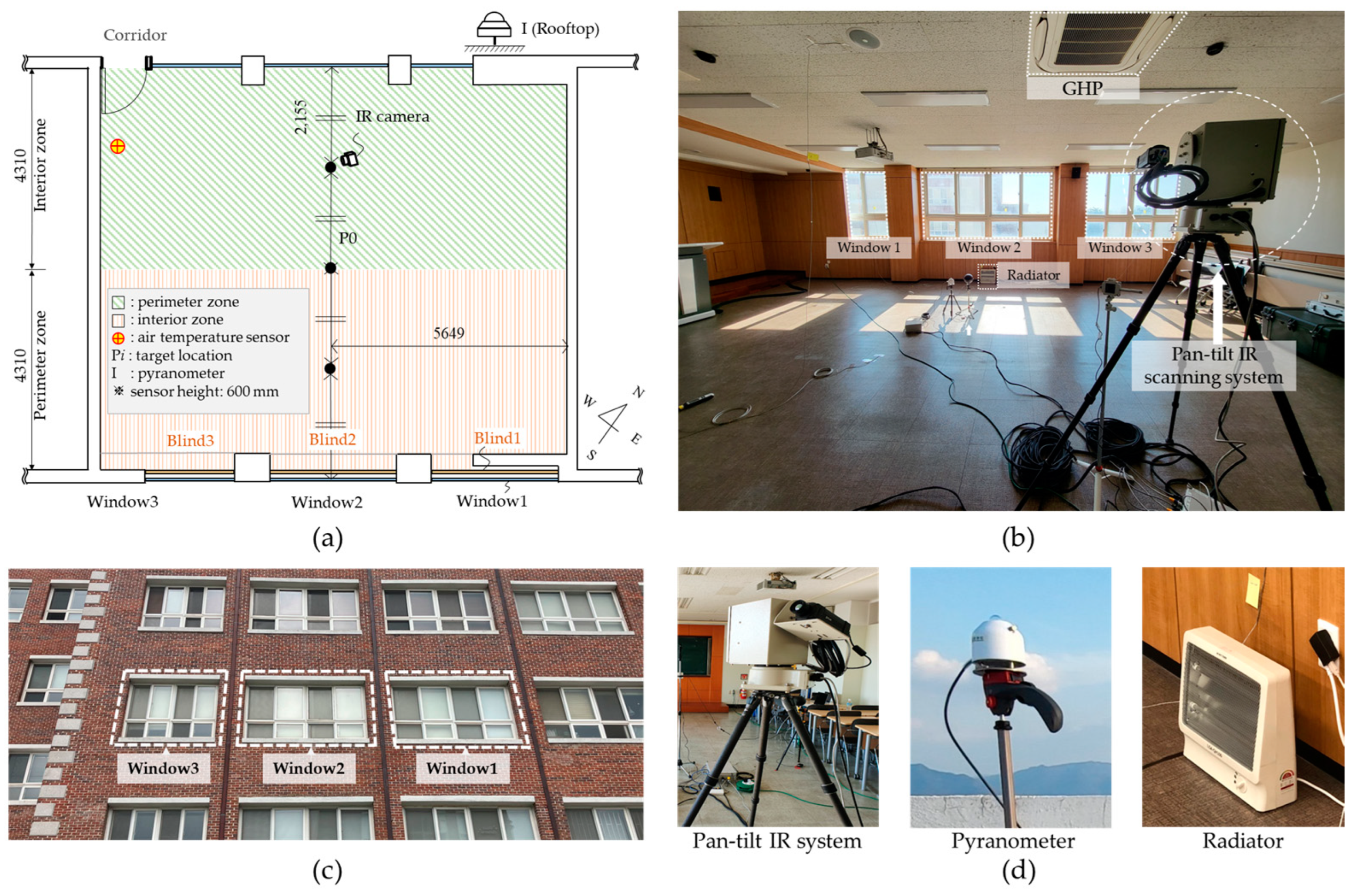
4.1. Experiment Set-Up
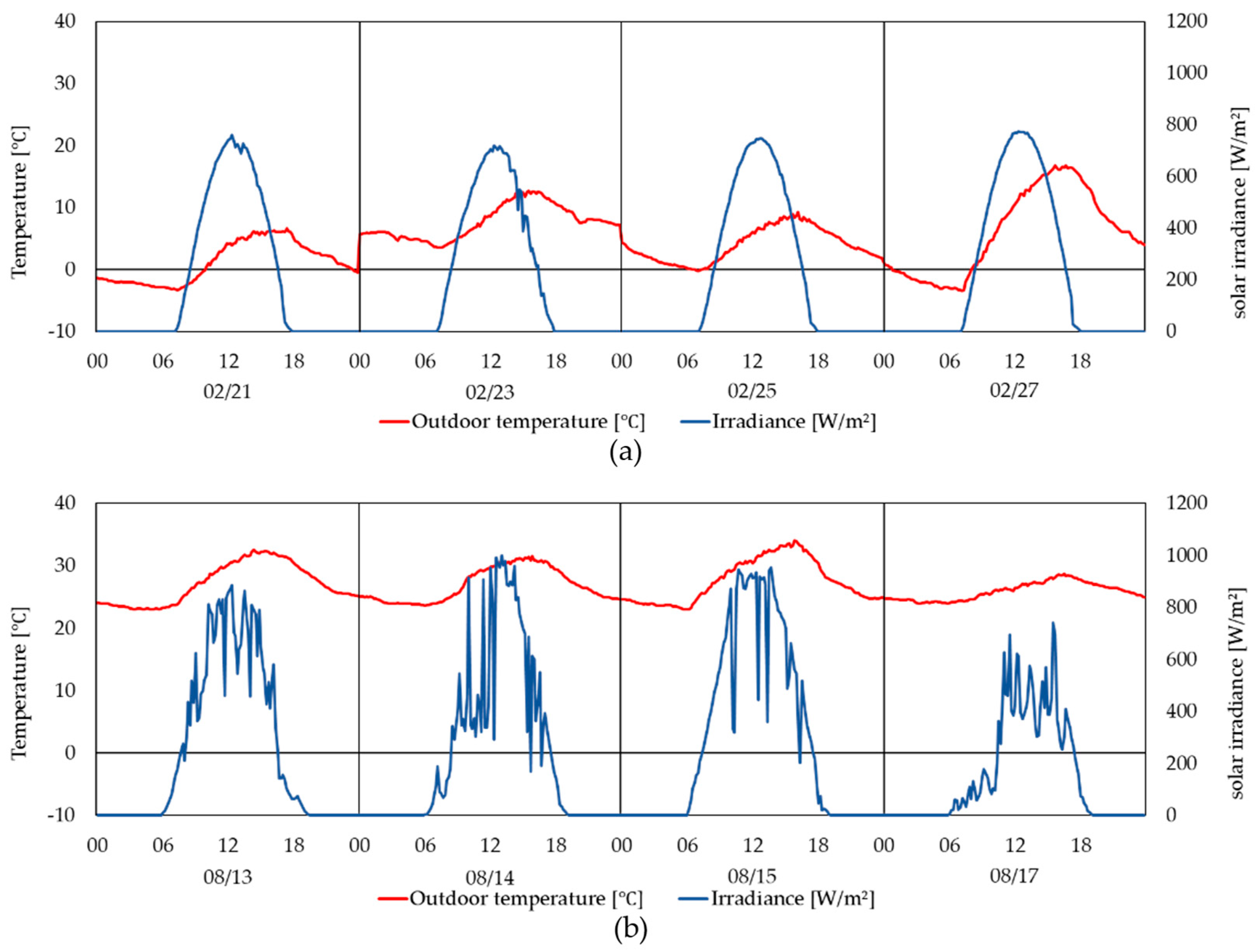
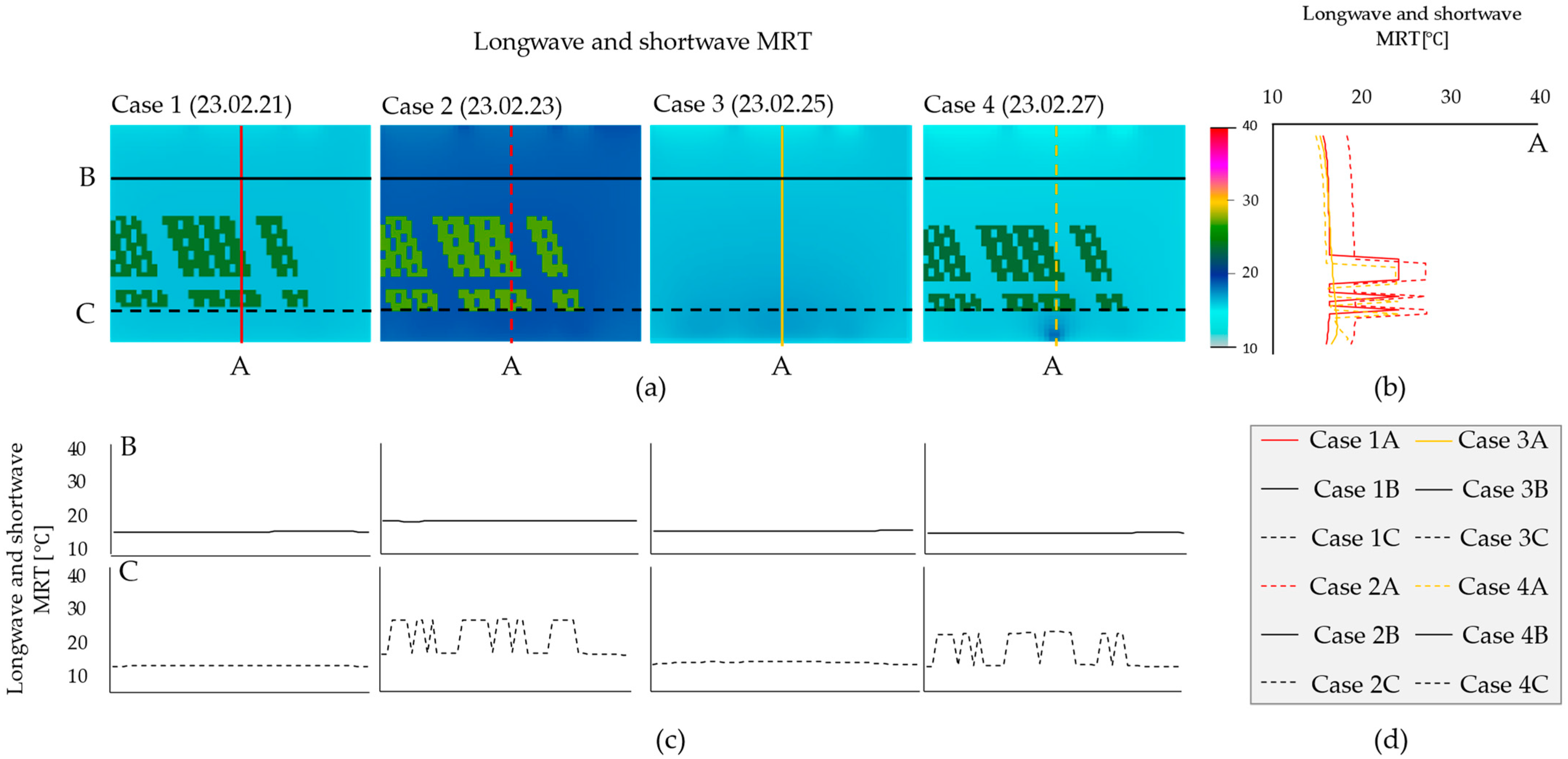
4.2. Result
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| mean radiant temperature (°C) | |
| j-th indoor surface temperature (°C) | |
| j-th indoor surface area () | |
| (,t) | absolute surface temperature of indoor surface j at time t |
| angle factor | |
| projected area factor of human body surface | |
| sunlit factor | |
| direct normal irradiance (W/m2) | |
| diffuse irradiance (W/m2) | |
| shortwave radiation absorption coefficient ( = 0.57) | |
| MRT calculation point | |
| t | time |
| n, | number of calculation points |
| perimeter zone | |
| interior zone | |
| width of calculation points | |
| depth of calculation points | |
| width of a target space | |
| depth of a target space | |
| permissible spacing between calculation points along both horizontal and vertical directions | |
| unshaded fraction | |
| solar transmittance | |
| Abbreviations and acronyms | |
| MRT | mean radiant temperature |
| PMV | predicted mean vote |
| GT | globe thermometer |
| CT | contact thermometer |
| IR | infrared |
| Win. | winter |
| Sum. | summer |
| S.L. | single location |
| A.W. | area weighted |
| S.Z. | sub-zonal |
| sMRT | single-zone averaged mean radiant temperature |
| mMRT | multi-zone averaged mean radiant temperature |
| pMRT | point-zone mean radiant temperature |
| HVF | horizontal view factor |
| SVF | sky view factor |
| GHP | gas heat pump |
| Greek letters | |
| emissivity | |
| Stefan–Boltzmann constant ( W/m2K4) |
References
- Park, J.; Kim, T.; Lee, C.-s. Development of Thermal Comfort-Based Controller and Potential Reduction of the Cooling Energy Consumption of a Residential Building in Kuwait. Energies 2019, 12, 3348. [Google Scholar] [CrossRef]
- Deng, Z.; Chen, Q. Artificial Neural Network Models Using Thermal Sensations and Occupants’ Behavior for Predicting Thermal Comfort. Energy Build. 2018, 174, 587–602. [Google Scholar] [CrossRef]
- Ku, K.L.; Liaw, J.S.; Tsai, M.Y.; Liu, T.S. Automatic Control System for Thermal Comfort Based on Predicted Mean Vote and Energy Saving. IEEE Trans. Autom. Sci. Eng. 2015, 12, 378–383. [Google Scholar] [CrossRef]
- Dogan, A.; Kayaci, N.; Demir, H.; Kemal, M. Energy & Buildings An Experimental Comparison of Radiant Wall and Ceiling Cooling System Integrated with Ground Source Heat Pump and Direct Expansion Fan Coil System in a Highly Glazed Office Room. Energy Build. 2023, 273, 112412. [Google Scholar] [CrossRef]
- Hwang, R.L.; Fang, P.L.; Chen, W.A. Impact of Solar Radiation on Indoor Thermal Comfort near Highly Glazed Façades in a Hot-Humid Subtropical Climate: An Experimental Evaluation. Build. Environ. 2023, 243, 110725. [Google Scholar] [CrossRef]
- Piasecki, M.; Fedorczak-cisak, M.; Furtak, M.; Biskupski, J. Experimental Confirmation of the Reliability of Fanger’ s Thermal Comfort Model—Case Study of a Near-Zero Energy Building (NZEB) O Ffi Ce Building. Sustainability 2019, 11, 2461. [Google Scholar] [CrossRef]
- Sung, S.H.; Yun, W.S.; Ryu, W.; Seo, H.; Hong, W.H. Development of Mean Radiant Temperature Virtual Sensor for Core and Perimeter Zones during the Summer Using Random Forest. J. Archit. Inst. Korea 2023, 39, 171–177. [Google Scholar] [CrossRef]
- Kubwimana, B.; Seyednezhad, M.; Najafi, H. Thermoelectric-Based Radiant Cooling Systems: An Experimental and Numerical Investigation of Thermal Comfort. Energies 2023, 16, 6981. [Google Scholar] [CrossRef]
- Huang, L.; John, Z. Critical Review and Quantitative Evaluation of Indoor Thermal Comfort Indices and Models Incorporating Solar Radiation Effects. Energy Build. 2020, 224, 110204. [Google Scholar] [CrossRef]
- Aparicio, P.; Salmerón, J.M.; Ruiz, Á.; Sánchez, F.J.; Brotas, L. The Globe Thermometer in Comfort and Environmental Studies in Buildings. Rev. Constr. 2016, 15, 57–66. [Google Scholar] [CrossRef][Green Version]
- Uribe, D.; Vera, S. Assessment of the Effect of Phase Change Material (PCM) Glazing on the Energy Consumption and Indoor Comfort of an Office in a Semiarid Climate. Appl. Sci. 2021, 11, 9597. [Google Scholar] [CrossRef]
- Wang, D.; Chen, G.; Song, C.; Liu, Y.; He, W.; Zeng, T.; Liu, J. Experimental Study on Coupling Effect of Indoor Air Temperature and Radiant Temperature on Human Thermal Comfort in Non-Uniform Thermal Environment. Build. Environ. 2019, 165, 106387. [Google Scholar] [CrossRef]
- Chang, H.; Park, S.-H.; Park, B. Analysis on Indoor Thermal Comfort of Buildings in Campus during Intermediate Season. J. Arch. Inst. Korea 2014, 16, 187–194. [Google Scholar]
- Arnesano, M.; Calvaresi, A.; Pietroni, F.; Zampetti, L.; Magnani, S.; Casadei, O.; Revel, G.M. A Sub-Zonal PMV-Based HVAC and Façade Control System for Curtain Wall Buildings. Proceedings 2018, 2, 1596. [Google Scholar] [CrossRef]
- Zampetti, L.; Arnesano, M.; Revel, G.M. Experimental Testing of a System for the Energy-Efficient Sub-Zonal Heating Management in Indoor Environments Based on PMV. Energy Build. 2018, 166, 229–238. [Google Scholar] [CrossRef]
- Park, J.; Choi, H.; Kim, D.; Kim, T. Development of Novel PMV-Based HVAC Control Strategies Using a Mean Radiant Temperature Prediction Model by Machine Learning in Kuwaiti Climate. Build. Environ. 2021, 206, 108357. [Google Scholar] [CrossRef]
- Chaudhuri, T.; Soh, Y.C.; Bose, S.; Xie, L.; Li, H. On Assuming Mean Radiant Temperature Equal to Air Temperature during PMV-Based Thermal Comfort Study in Air-Conditioned Buildings. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 7065–7070. [Google Scholar] [CrossRef]
- Guo, H.; Teitelbaum, E.; Houchois, N.; Bozlar, M.; Meggers, F. Revisiting the Use of Globe Thermometers to Estimate Radiant Temperature in Studies of Heating and Ventilation. Energy Build. 2018, 180, 83–94. [Google Scholar] [CrossRef]
- Lee, D.; Jo, J. Application of IR Camera and Pyranometer for Estimation of Longwave and Shortwave Mean Radiant Temperatures at Multiple Locations. Build. Environ. 2022, 207, 108423. [Google Scholar] [CrossRef]
- Kosiński, P.; Skotnicka-Siepsiak, A. Possibilities of Adapting the University Lecture Room to the Green University Standard in Terms of Thermal Comfort and Ventilation Accuracy. Energies 2022, 15, 3735. [Google Scholar] [CrossRef]
- Sung Jin, K.; Dong Seok, L. Method for Determining the Representative Mean Radiant Temperature for Heating and Cooling Control Application. J. Korean Inst. Archit. Sustain. Environ. Build. Syst. 2024, 18, 165–174. [Google Scholar]
- Lee, D.S.; Jo, J.H. Pan–Tilt Ir Scanning Method for the Remote Measurement of Mean Radiant Temperatures at Multi-Location in Buildings. Remote Sens. 2021, 13, 2158. [Google Scholar] [CrossRef]
- La Gennusa, M.; Nucara, A.; Rizzo, G.; Scaccianoce, G. The Calculation of the Mean Radiant Temperature of a Subject Exposed to the Solar Radiation—A Generalised Algorithm. Build. Environ. 2005, 40, 367–375. [Google Scholar] [CrossRef]
- Baker, N.; Steemers, K. Energy and Environment in Architecture a Technical Design Guide; Taylor & Francis: Abingdon, UK, 1998; p. 224. [Google Scholar]
- Choi, S.; Lee, D.; Jo, J. Method of Deriving Shaded Fraction According to Shading Movements of Kinetic Façade. Sustainability 2017, 9, 1449. [Google Scholar] [CrossRef]
- Lee, D.; Jo, J. Application of Simple Sky and Building Models for the Evaluation of Solar Irradiance Distribution at Indoor Locations in Buildings. Build. Environ. 2021, 197, 107840. [Google Scholar] [CrossRef]
- Lee, D.S.; Kim, E.J.; Cho, Y.H.; Kang, J.W.; Jo, J.H. A Field Study on Application of Infrared Thermography for Estimating Mean Radiant Temperatures in Large Stadiums. Energy Build. 2019, 202, 109360. [Google Scholar] [CrossRef]
- Kyung-soo, L.S.L. A Research on the Decomposition Model and Transposition Model Using the Measured Pyranometer Irradiation Data. J. Korean Sol. Energy Soc. 2018, 38, 1–20. [Google Scholar]
- Hawks, M.A.; Cho, S. Review and Analysis of Current Solutions and Trends for Zero Energy Building (ZEB) Thermal Systems. Renew. Sustain. Energy Rev. 2024, 189, 114028. [Google Scholar] [CrossRef]
- Guo, H.; Ferrara, M.; Coleman, J.; Loyola, M.; Meggers, F. Simulation and Measurement of Air Temperatures and Mean Radiant Temperatures in a Radiantly Heated Indoor Space. Energy 2020, 193, 116369. [Google Scholar] [CrossRef]
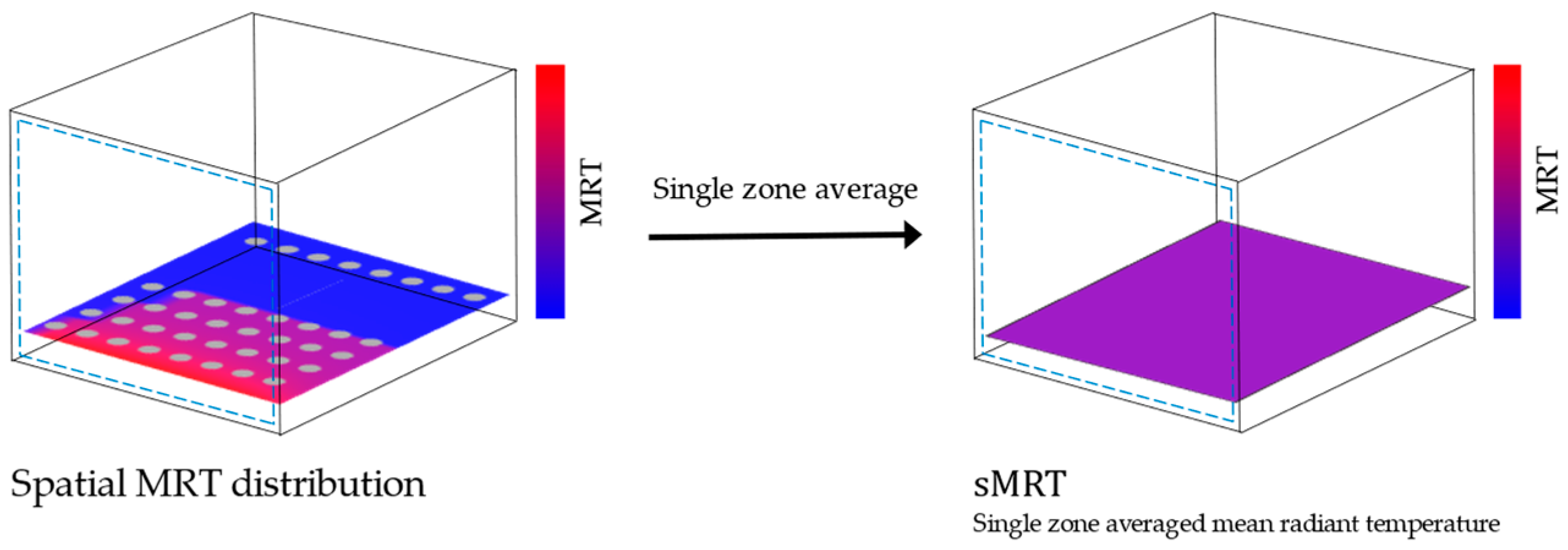
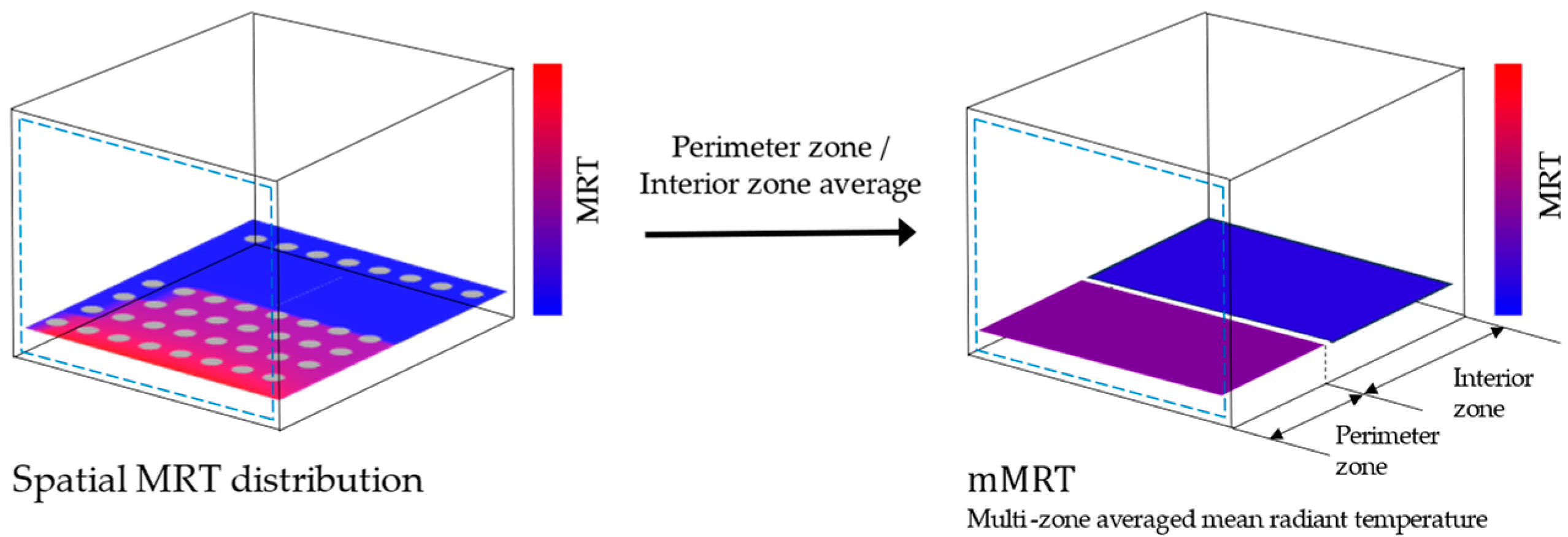
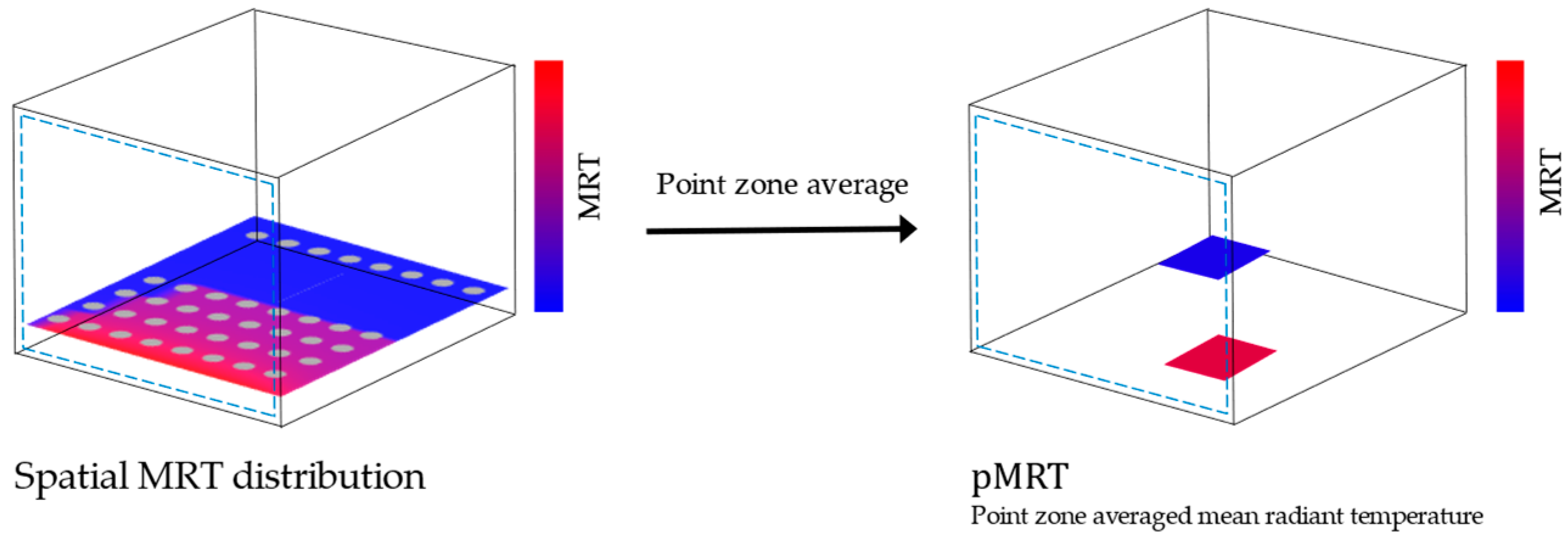
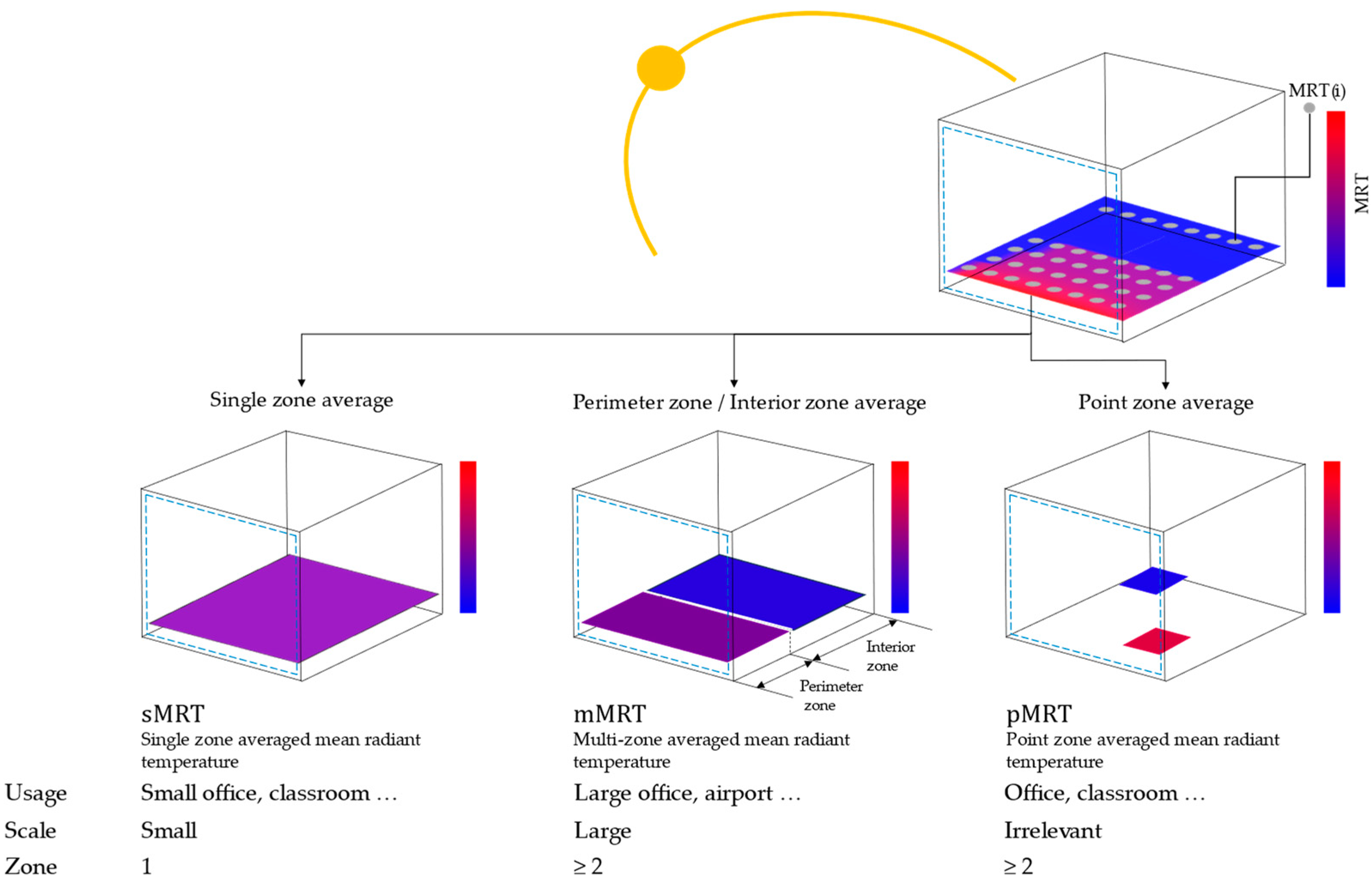
| Year | Bldg. Type | Season | Instrument | Representative MRT * | Radiant | Ref. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Air | GT | IR | CT | S.L. | A.W. | S.Z. | LW | SW | |||||
| 2018 | Office | Win. and sum. | x | x | [1] | ||||||||
| 2019 | Chamber | Sum. | x | x | [2] | ||||||||
| 2015 | Office | Sum. | x | x | [3] | ||||||||
| 2023 | Office | Sum. | x | x | x | x | [4] | ||||||
| 2023 | Chamber | Sum. | x | x | x | x | [5] | ||||||
| 2019 | Office | Win. | x | x | x | x | [6] | ||||||
| 2023 | Classroom | Sum. | x | x | x | x | [7] | ||||||
| 2023 | Chamber | Not presented | x | x | x | x | [8] | ||||||
| 2020 | Office | Win. | x | x | x | x | [9] | ||||||
| 2016 | Chamber | Sum. | x | x | x | x | [10] | ||||||
| 2021 | Office | Sum. | x | x | x | x | [11] | ||||||
| 2019 | Chamber | Sum. | x | x | x | [12] | |||||||
| 2014 | Office | Win. | x | x | x | [13] | |||||||
| 2020 | Office | Sum. | x | x | x | [14] | |||||||
| 2018 | Office | Win. | x | x | x | [15] | |||||||
| Season | Cases | System Type |
|---|---|---|
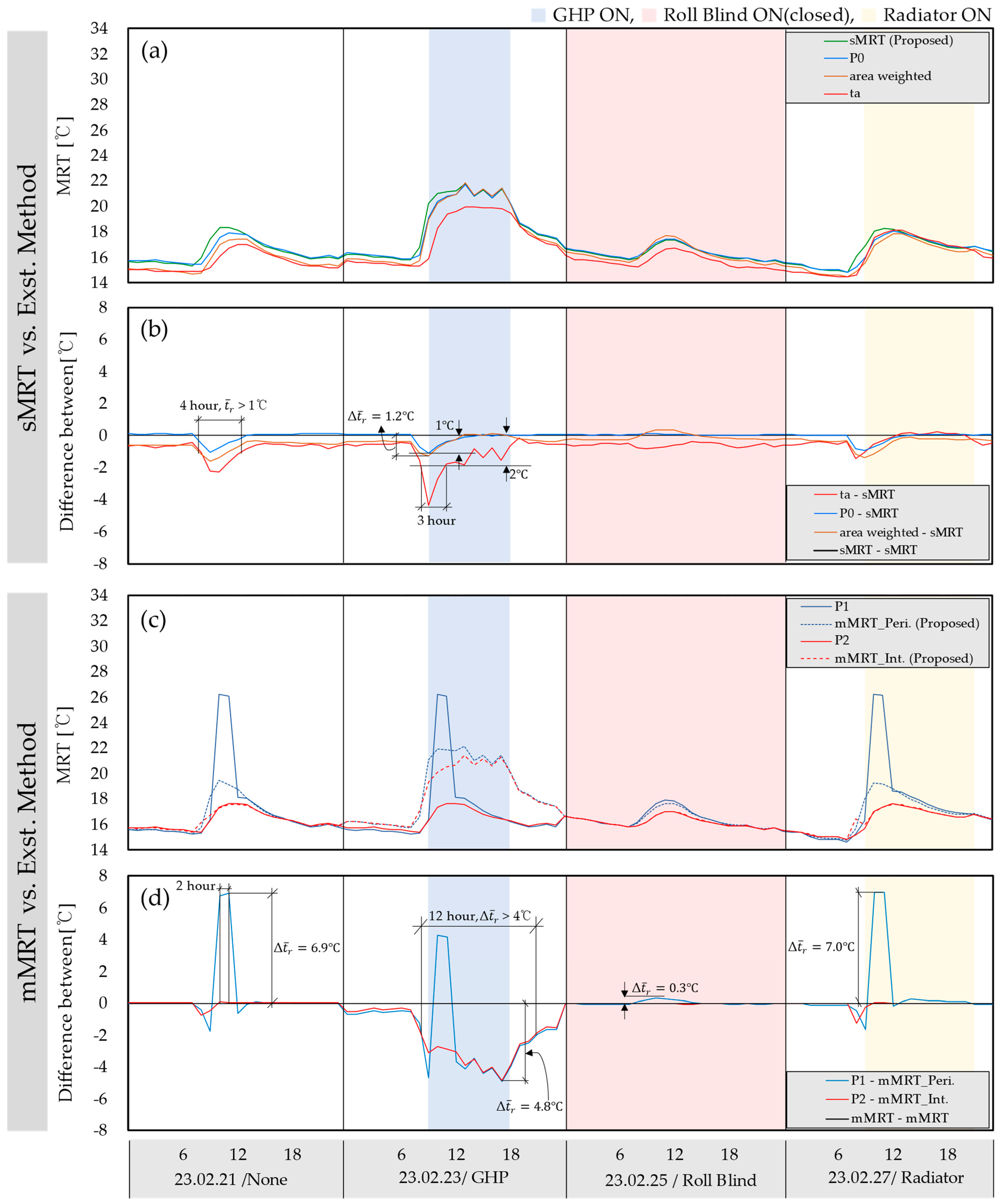
| Heating | Case 1 | None |
| Case 2 | GHP | |
| Case 3 | Roll Blind | |
| Case 4 | Radiator | |
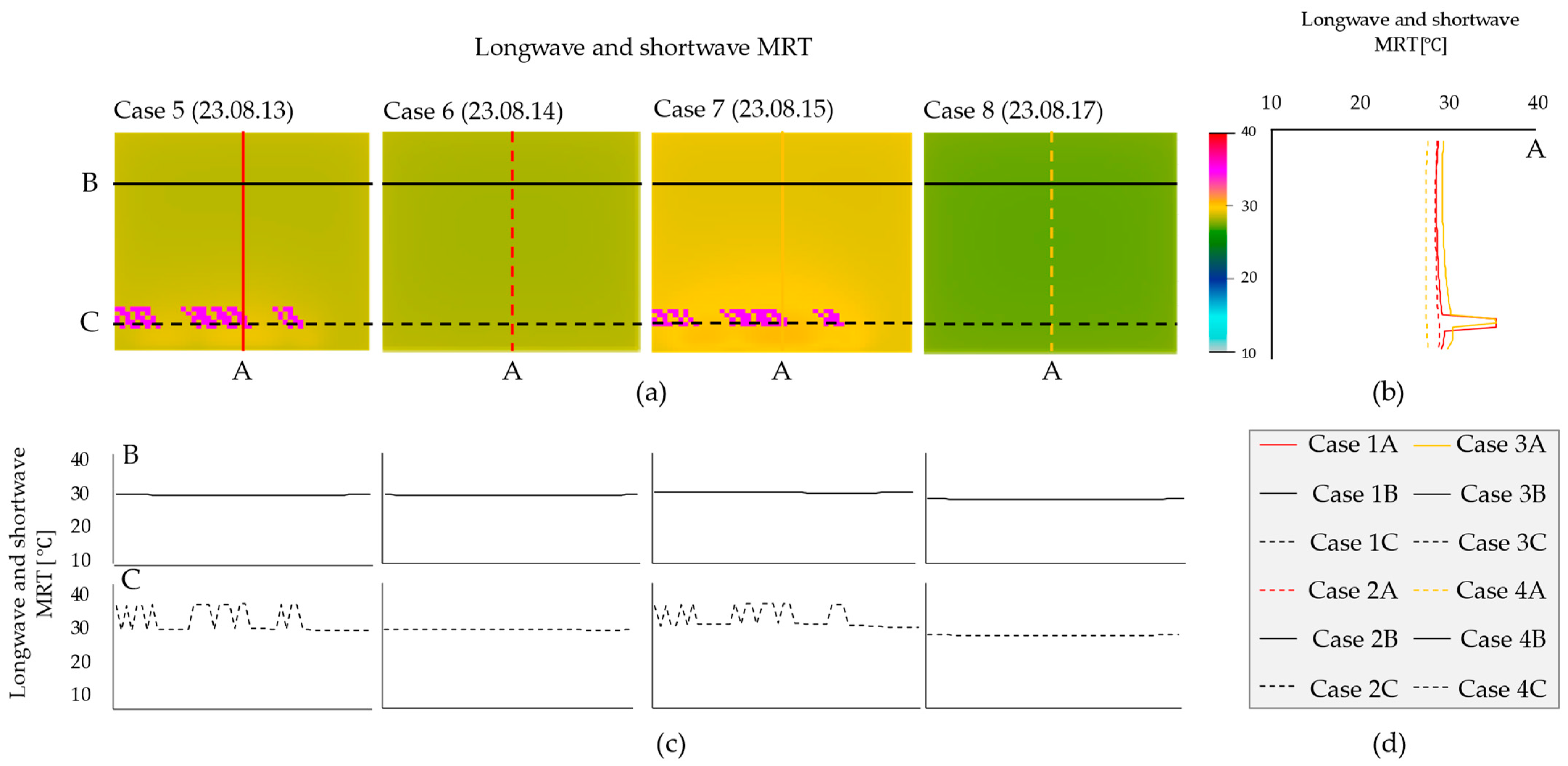
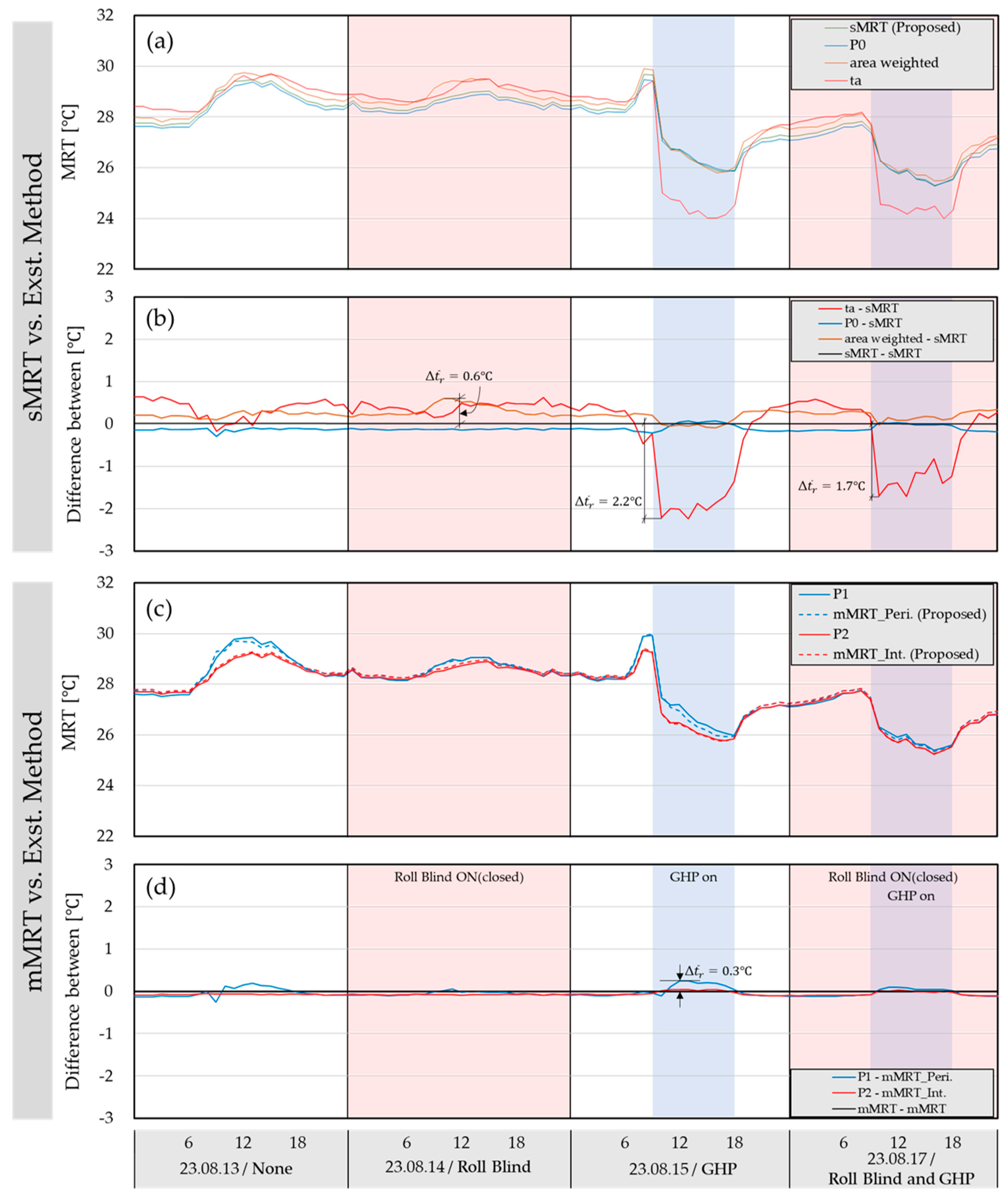
| Cooling | Case 5 | None |
| Case 6 | Roll Blind | |
| Case 7 | GHP | |
| Case 8 | Roll Blind and GHP |
| Device Name | Specifications | |
|---|---|---|
| Pan-tilt IR scanning system (developed by Lee et al., 2021 [22]) | Model | FLIR A310/±2 °C |
| Temperature range | −20 to 350 °C | |
| Accuracy | ±2% | |
| IR resolution | 320 × 240 pixels | |
| Pyranometer | Model | MS-40 |
| Irradiance range | 0 to 2000 W/m2 | |
| Accuracy | ±12 W/m2 | |
| Sensitivity | 7–14 µV/W/m2 | |
| Thermo-hygrometer | Model | Testo 174H |
| Operating temperature | −20 to 70 °C | |
| Accuracy | (T) ± 0.5 °C | |
| Resolution | 0.1 °C | |
| Cases System Type | Applied Methods * | Measured Representative MRT Values | |||||
|---|---|---|---|---|---|---|---|
| 09:05 | 12:05 | 15:05 | 18:05 | ||||
| Case 1 None | Measured data | Spatial MRT data |  |  |  |  | |
| Min–Max | 15.7–24.2 | 16.6–26.7 | 16.1–17.1 | 15.7–16.4 | |||
| Exst. | 15.2 | 17.0 | 16.4 | 15.6 | |||
| Single location | P0 | 16.4 | 17.9 | 17.0 | 16.4 | ||
| P1/P2 | 16.4/16.3 | 18.1/17.6 | 17.1/16.8 | 16.3/16.3 | |||
| Area-weighted | 15.8 | 17.5 | 16.5 | 15.8 | |||
| Prop. | 17.4 | 18.1 | 16.9 | 16.3 | |||
| Peri./Int. | 18.2/16.7 | 18.7/17.5 | 17.0/16.8 | 16.3/16.3 | |||
| Case 2 GHP | Measured data | Spatial MRT data |  |  |  |  | |
| Min–Max | 18.2–27.3 | 19.8–28.7 | 20.3–21.8 | 19.4–20.7 | |||
| Exst. | 15.9 | 19.6 | 19.9 | 19.5 | |||
| Single location | P0 | 19.1 | 21.0 | 21.4 | 20.2 | ||
| P1/P2 | 16.4/16.3 | 18.1/17.6 | 17.1/16.8 | 16.3/16.3 | |||
| Area-weighted | 19.0 | 21.0 | 21.3 | 20.1 | |||
| Prop. | 20.2 | 21.2 | 21.3 | 20.2 | |||
| Peri./Int. | 21.1/19.4 | 21.8/20.7 | 21.4/21.2 | 20.1/20.1 | |||
| Case 3 Roll Blind | Measured data | Spatial MRT data |  |  |  |  | |
| Min–Max | 15.2–17.3 | 16.2–18.2 | 15.7–16.7 | 15.4–16.1 | |||
| Exst. | 15.6 | 16.7 | 16.0 | 15.3 | |||
| Single location | P0 | 16.6 | 17.4 | 16.5 | 16.0 | ||
| P1/P2 | 17.0/16.2 | 17.9/17.0 | 16.6/16.3 | 16.0/15.9 | |||
| Area-weighted | 16.6 | 17.7 | 16.4 | 15.8 | |||
| Prop. | 16.4 | 17.3 | 16.5 | 16.0 | |||
| Peri./Int. | 16.7/16.2 | 17.6/17.0 | 16.6/16.4 | 16.0/15.9 | |||
| Case 4 Radiator (900 W) | Measured data | Spatial MRT data |  |  |  |  | |
| Min–Max | 14.8–24.3 | 16.5–27.5 | 16.4–20.2 | 16.0–19.3 | |||
| Exst. | 15.9 | 18.1 | 17.5 | 16.9 | |||
| Single location | P0 | 16.0 | 18.0 | 17.5 | 16.9 | ||
| P1/P2 | 16.3/15.7 | 18.7/17.6 | 17.9/17.2 | 17.0/16.7 | |||
| Area-weighted | 15.6 | 17.8 | 17.3 | 16.6 | |||
| Prop. | 17.0 | 18.2 | 17.5 | 16.8 | |||
| Peri./Int. | 18.0/15.9 | 18.8/17.6 | 17.7/17.3 | 16.9/16.7 | |||
| Cases System Type | Applied Methods * | Measured Representative MRT Values | ||||||
|---|---|---|---|---|---|---|---|---|
| 09:05 | 12:05 | 15:05 | 18:05 | |||||
| Case 5 None | Measured data | Spatial MRT data |  |  |  |  | ||
| Min–Max | 28.6–35.4 | 29.1–33.9 | 29.2–30.1 | 28.7–29.1 | ||||
| Exst. | 28.8 | 29.6 | 29.7 | 29.3 | ||||
| Single location | P0 | 28.7 | 29.3 | 29.3 | 28.7 | |||
| P1/P2 | 29.0/28.6 | 29.8/29.1 | 29.7/29.2 | 28.8/28.7 | ||||
| Area-weighted | 29.1 | 29.7 | 29.7 | 29.1 | ||||
| Prop. | 29.0 | 29.4 | 29.4 | 28.8 | ||||
| Peri./Int. | 29.3/28.7 | 29.7/29.2 | 29.6/29.3 | 28.8/28.8 | ||||
| Case 6 Roll Blind | Measured data | Spatial MRT data |  |  |  |  | ||
| Min–Max | 28.5–29.0 | 28.7–29.2 | 28.9–29.3 | 28.6–29.0 | ||||
| Exst. | 28.8 | 29.4 | 29.5 | 29.2 | ||||
| Single location | P0 | 28.5 | 28.7 | 28.9 | 28.6 | |||
| P1/P2 | 28.7/28.5 | 28.9/28.7 | 29.1/28.9 | 28.7/28.6 | ||||
| Area-weighted | 29.1 | 29.4 | 29.5 | 29.0 | ||||
| Prop. | 28.6 | 28.9 | 29.0 | 28.7 | ||||
| Peri./Int. | 28.7/28.6 | 28.9/28.8 | 29.1/29.0 | 28.7/28.7 | ||||
| Case 7 GHP | Measured data | Spatial MRT data |  |  |  |  | ||
| Min–Max | 29.2–35.3 | 26.1–31.8 | 25.7–26.6 | 25.8–26.1 | ||||
| Exst. | 29.4 | 24.7 | 24.0 | 24.5 | ||||
| Single location | P0 | 29.4 | 26.7 | 26.1 | 25.9 | |||
| P1/P2 | 29.9/29.3 | 27.2/26.5 | 26.4/26.0 | 26.0/25.8 | ||||
| Area-weighted | 29.9 | 26.7 | 26.0 | 26.0 | ||||
| Prop. | 29.6 | 26.7 | 26.1 | 25.9 | ||||
| Peri./Int. | 30.0/29.3 | 26.9/26.4 | 26.2/25.9 | 25.9/25.9 | ||||
| Case 8 Roll Blind and GHP | Measured data | Spatial MRT data |  |  |  |  | ||
| Min–Max | 27.4–27.8 | 25.6–26.0 | 25.4–25.8 | 25.5–25.7 | ||||
| Exst. | 27.7 | 24.4 | 24.3 | 24.3 | ||||
| Single location | P0 | 27.4 | 25.8 | 25.5 | 25.5 | |||
| P1/P2 | 27.4/27.4 | 25.9/25.7 | 25.6/25.5 | 25.6/25.5 | ||||
| Area-weighted | 27.7 | 25.8 | 25.7 | 25.7 | ||||
| Prop. | 27.5 | 25.7 | 25.5 | 25.6 | ||||
| Peri./Int. | 27.5/27.5 | 25.8/25.7 | 25.6/25.6 | 25.6/25.5 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, S.-J.; Jo, J.-H.; Lee, D.-S. Proposal of Three Methods for Deriving Representative Mean Radiant Temperatures Considering Zone Spatial Distributions. Energies 2024, 17, 5221. https://doi.org/10.3390/en17205221
Kwon S-J, Jo J-H, Lee D-S. Proposal of Three Methods for Deriving Representative Mean Radiant Temperatures Considering Zone Spatial Distributions. Energies. 2024; 17(20):5221. https://doi.org/10.3390/en17205221
Chicago/Turabian StyleKwon, Sung-Jin, Jae-Hun Jo, and Dong-Seok Lee. 2024. "Proposal of Three Methods for Deriving Representative Mean Radiant Temperatures Considering Zone Spatial Distributions" Energies 17, no. 20: 5221. https://doi.org/10.3390/en17205221
APA StyleKwon, S.-J., Jo, J.-H., & Lee, D.-S. (2024). Proposal of Three Methods for Deriving Representative Mean Radiant Temperatures Considering Zone Spatial Distributions. Energies, 17(20), 5221. https://doi.org/10.3390/en17205221






