A Method for Evaluating Demand Response Potential of Industrial Loads Based on Fuzzy Control
Abstract
1. Introduction
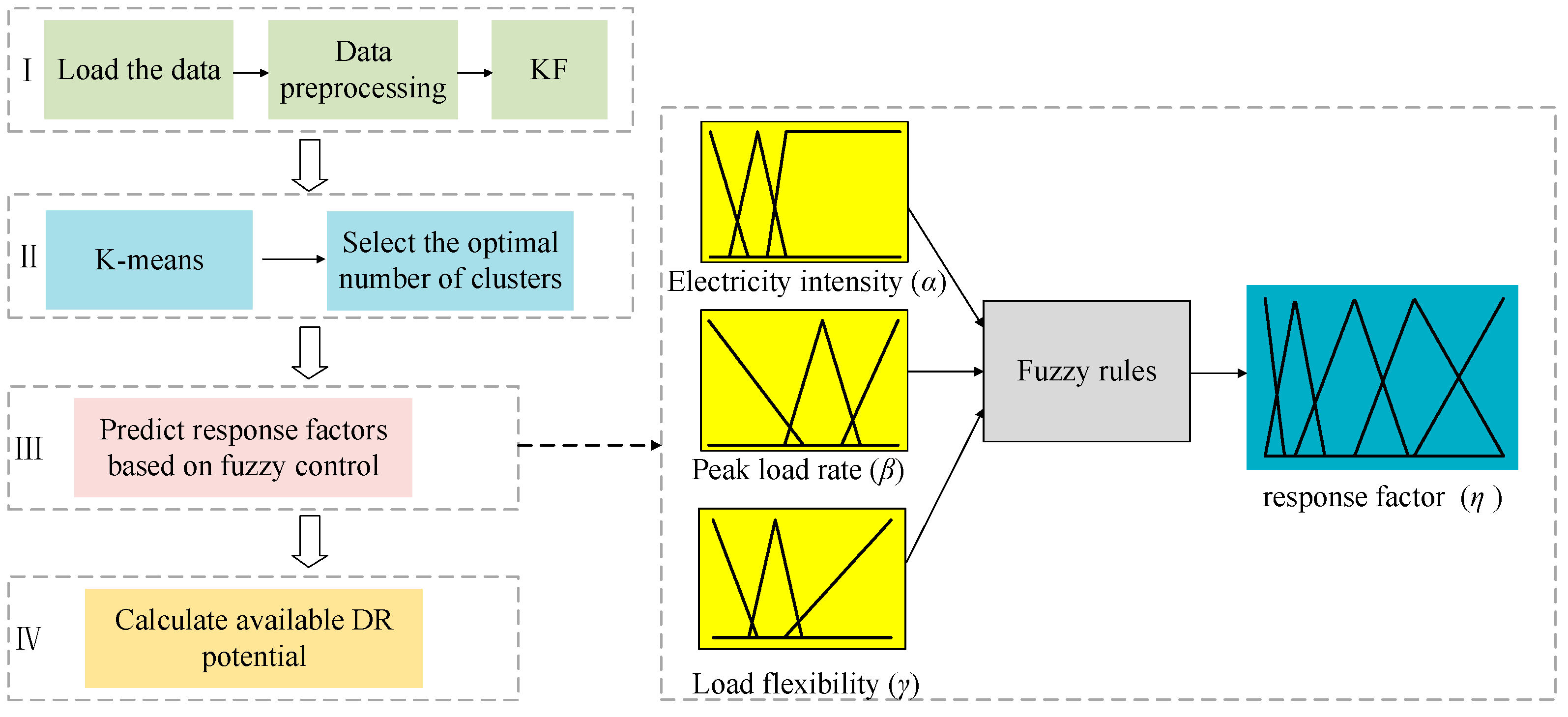
2. DR Potential Assessment Framework
3. Baseline Load Calculation
4. Response Factor Based on Fuzzy Controller
4.1. Input Data Analysis
- (1)
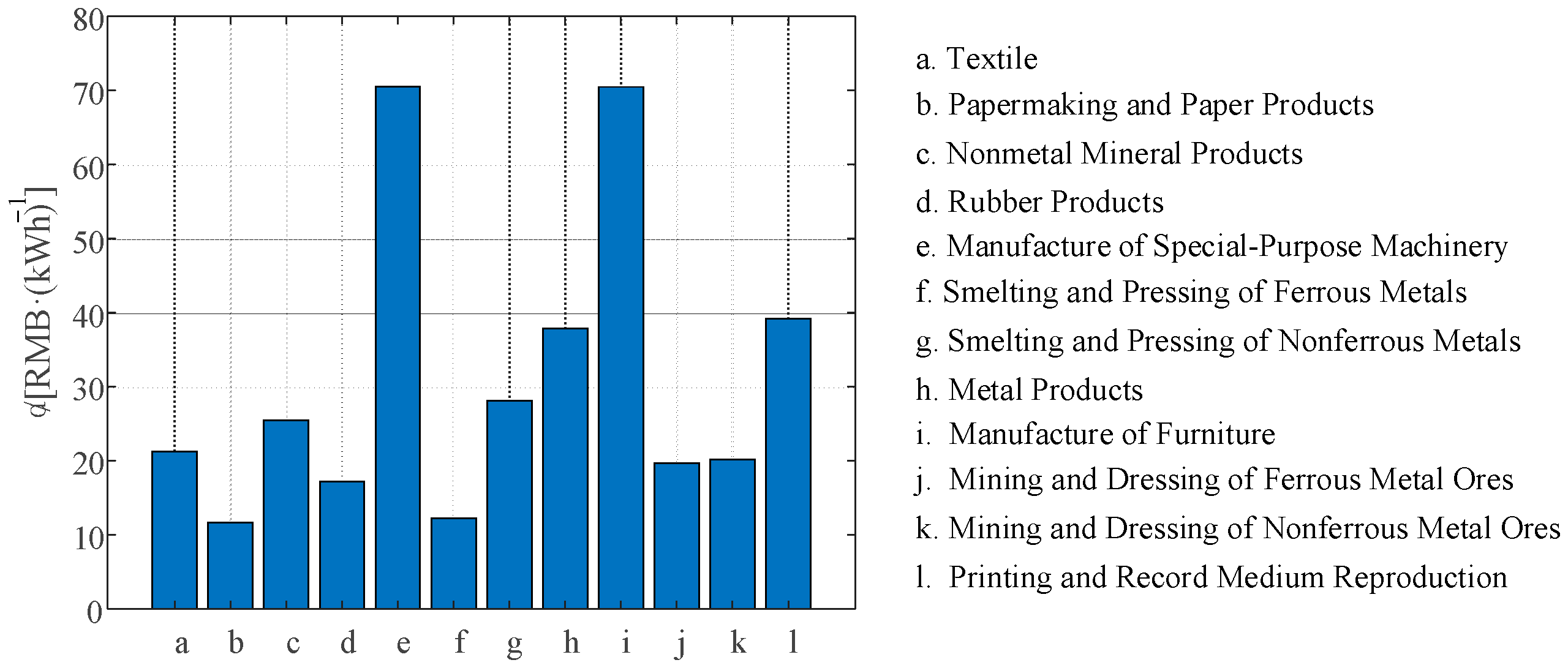
- Electricity Intensity
- (2)
- Peak load rate
- (3)
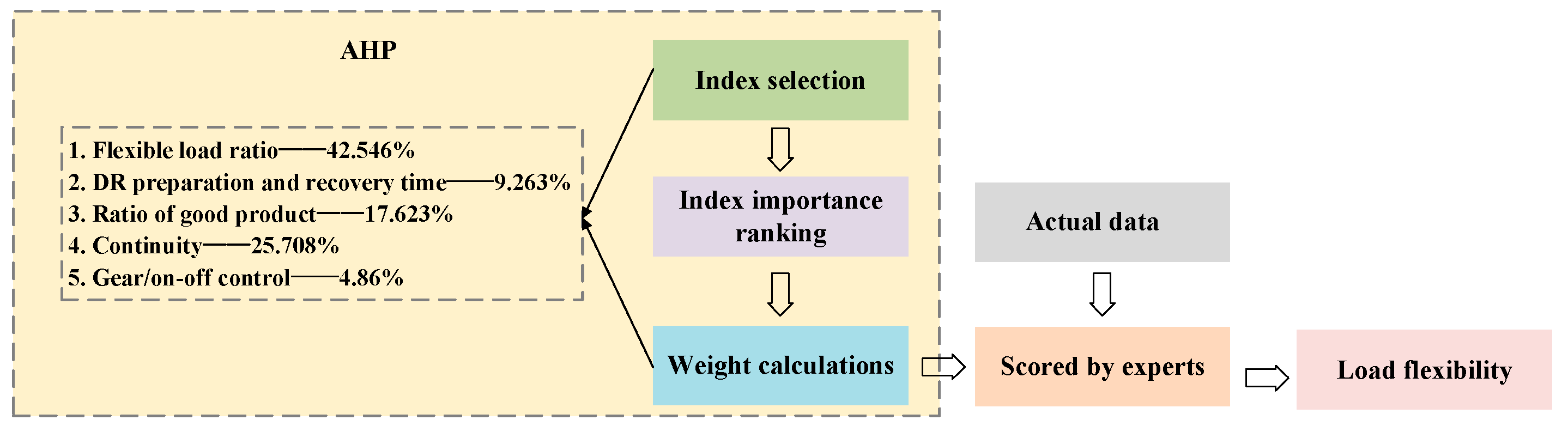
- Load flexibility
4.2. Fuzzy Control Design
4.2.1. Membership Function
- (1)
- Electricity Intensity
- (2)
- Peak load rate
- (3)
- Load flexibility
- (4)
- Response factor
4.2.2. Fuzzy Rule Design
- (1)
- If the electricity intensity is small (S1), the load flexibility is large (L3), and the peak load rate is large (L2), the response factor is very large (VL).
- (2)
- If the electricity intensity is medium (M1), the load flexibility is medium (M3), and the peak load rate is medium (M2), the response factor is medium (M).
- (3)
- If the electricity intensity is large (L1), the load flexibility is small (S3), and the peak load rate is small (S3), the response factor is very small (VS).
4.3. Process Summary
5. Calculation of Adjustable DR Potential
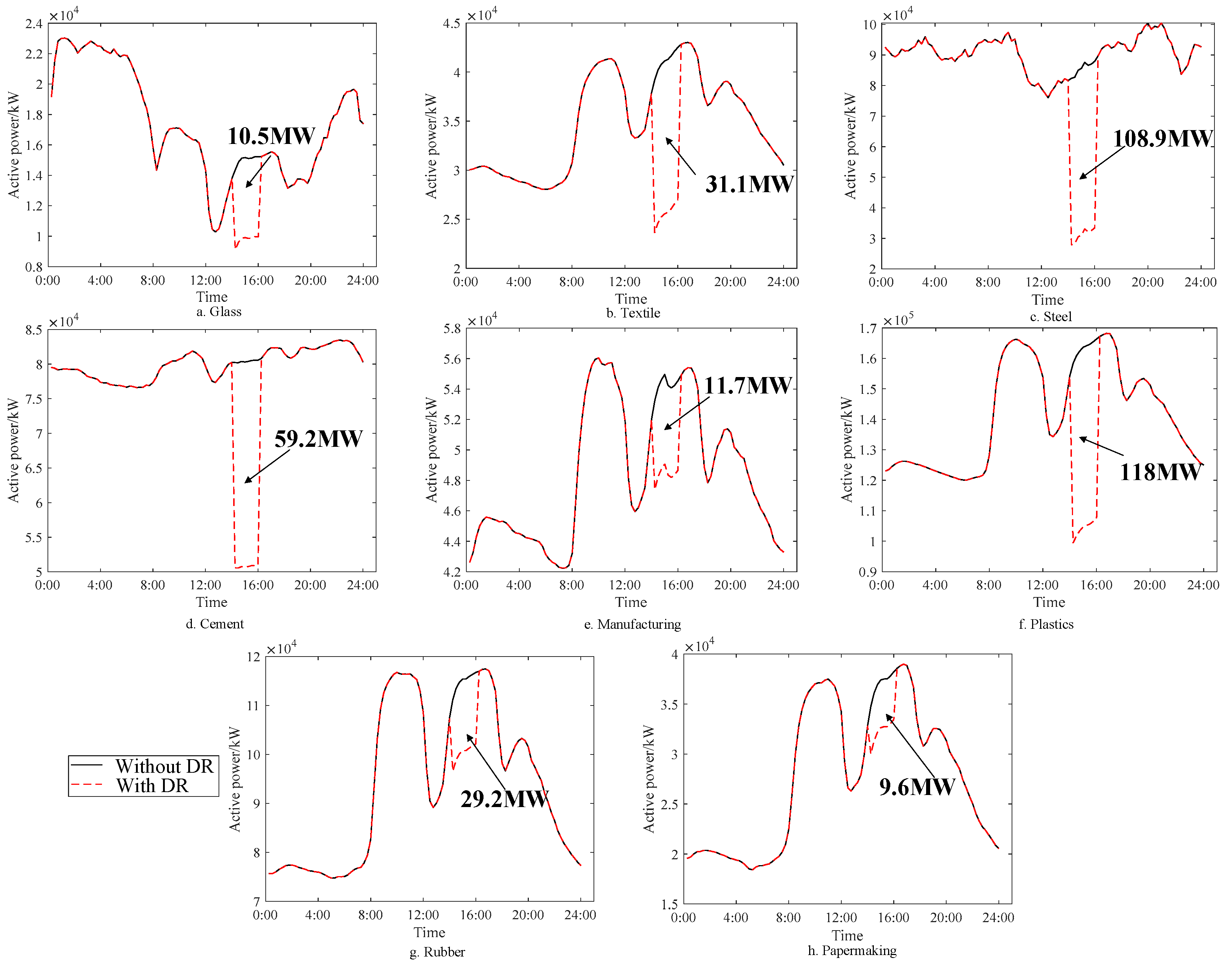
6. Case Study
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tong, J.L.; Liu, W.S.; Mao, J.B.; Ying, M.L. Role and development of thermal power units in new power systems. IEEE J. Radio Freq. Identif. 2022, 6, 837–841. [Google Scholar] [CrossRef]
- Wang, S.Y.; Zhao, C.Y.; Fan, L.; Bo, R. Distributionally Robust Unit Commitment with Flexible Generation Resources Considering Renewable Energy Uncertainty. IEEE Trans. Power Syst. 2022, 37, 4179–4190. [Google Scholar] [CrossRef]
- Wang, B.; Li, Y.; Ming, W.Y.; Wang, S.R. Deep Reinforcement Learning Method for Demand Response Management of Interruptible Load. IEEE Trans. Smart Grid 2020, 11, 3146–3155. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Benefits of Demand Response in Electricity Markets and Recommendations for Achieving Them; US Department of Energy: Washington, DC, USA, 2006.
- Emmanuel, B.; Chiu, M.C.; Hsu, H.W.; Lee, M.Y.; Wen, C.Y. Potential of Demand Response for Power Reallocation, a Literature Review. Energies 2022, 15, 863. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, B.; Wang, B.; Qiu, Y.; Shi, H.; Zhang, B.; Li, J.; Li, H.; Zhao, W. Incentive based emergency demand response effectively reduces peak load during heatwave without harm to vulnerable groups. Nat. Commun. 2023, 14, 6202. [Google Scholar] [CrossRef] [PubMed]
- Pang, Y.; He, Y.; Jiao, J.; Cai, H. Power load demand response potential of secondary sectors in China: The case of western Inner Mongolia. Energy 2020, 192, 116669. [Google Scholar] [CrossRef]
- Faruqui, A.; Sergici, S. Household response to dynamic pricing of electricity: A survey of 15 experiments. J. Regul. Econ. 2010, 38, 193–225. [Google Scholar] [CrossRef]
- Daniel, T.; Wallin, F. Potential and barriers for demand response at household customers. Energy Procedia 2015, 75, 1189–1196. [Google Scholar]
- Mishra, M.K.; Murari, K.; Parida, S. Demand-side management and its impact on utility and consumers through a game theoretic approach. Int. J. Electr. Power Energy Syst. 2022, 140, 107995. [Google Scholar] [CrossRef]
- Zhou, F.Q.; Deng, L.C.; Wang, J.; Wang, H.Y.; Lu, F.; Chen, J.Q.; Wang, L.; Li, S.W.; Wang, J.F.; Jiang, X.M.; et al. Demand Side Resource Potential Analysis Methods and Application—Case Study on the City of Huzhou in the Yangtze River Delta; Natural Resources Defense Council: Beijing, China, 2020. (In Chinese) [Google Scholar]
- Strobel, N.; Fuhrländer-Völker, D.; Weigold, M.; Abele, E. Quantifying the Demand Response Potential of Inherent Energy Storages in Production Systems. Energies 2020, 13, 4161. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Lee, Y.M. Deep transfer learning for thermal dynamics modeling in smart buildings. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data) 2019, Los Angeles, CA, USA, 9–12 December 2019; pp. 2033–2037. [Google Scholar]
- Kong, X.Y.; Kong, D.Q.; Yao, J.T.; Xiao, J. Online pricing of demand response based on long short-term memory and reinforcement learning. Appl. Energy 2020, 271, 114945. [Google Scholar] [CrossRef]
- Peirelinck, T.; Hermans, C.; Spiessens, F.; Deconinck, G. Domain randomization for demand response of an electric water heater. IEEE Trans. Smart Grid 2021, 12, 1370–1379. [Google Scholar] [CrossRef]
- Wohlfarth, K.; Klobasa, M.; Gutknecht, R. Demand response in the service sector-Theoretical, technical and practical potentials. Appl. Energy 2020, 258, 114089. [Google Scholar] [CrossRef]
- Kwon, P.S.; Østergaard, P. Assessment and evaluation of flexible demand in a Danish future energy scenario. Appl. Energy 2014, 134, 309–320. [Google Scholar] [CrossRef]
- Paulus, M.; Borggrefe, F. The potential of demand-side management in energy-intensive industries for electricity markets in Germany. Appl. Energy 2011, 88, 432–441. [Google Scholar] [CrossRef]
- Alkadi, N.; Starke, M.; Ma, O. Assessment of Industrial Load for Demand Response Across Western Interconnect; Oak Ridge National Lab.(ORNL): Oak Ridge, TN, USA, 2013.
- Jang, J.-S.R.; Sun, C.T. Neuro-fuzzy modeling and control. Proc. IEEE 1995, 83, 378–406. [Google Scholar] [CrossRef]
- Li, S.; Ahn, C.K.; Chadli, M.; Xiang, Z.R. Sampled-Data Adaptive Fuzzy Control of Switched Large-Scale Nonlinear Delay Systems. IEEE Trans. Fuzzy Syst. 2022, 30, 1014–1024. [Google Scholar] [CrossRef]
- Tong, S.C.; Min, X.; Li, Y.X. Observer-Based Adaptive Fuzzy Tracking Control for Strict-Feedback Nonlinear Systems with Unknown Control Gain Functions. IEEE Trans. Cybern. 2020, 50, 3903–3913. [Google Scholar] [CrossRef]
- Ding, S.H.; Zhang, B.B.; Mei, K.Q.; Park, J.H. Adaptive Fuzzy SOSM Controller Design with Output Constraints. IEEE Trans. Fuzzy Syst. 2022, 30, 2300–2311. [Google Scholar] [CrossRef]
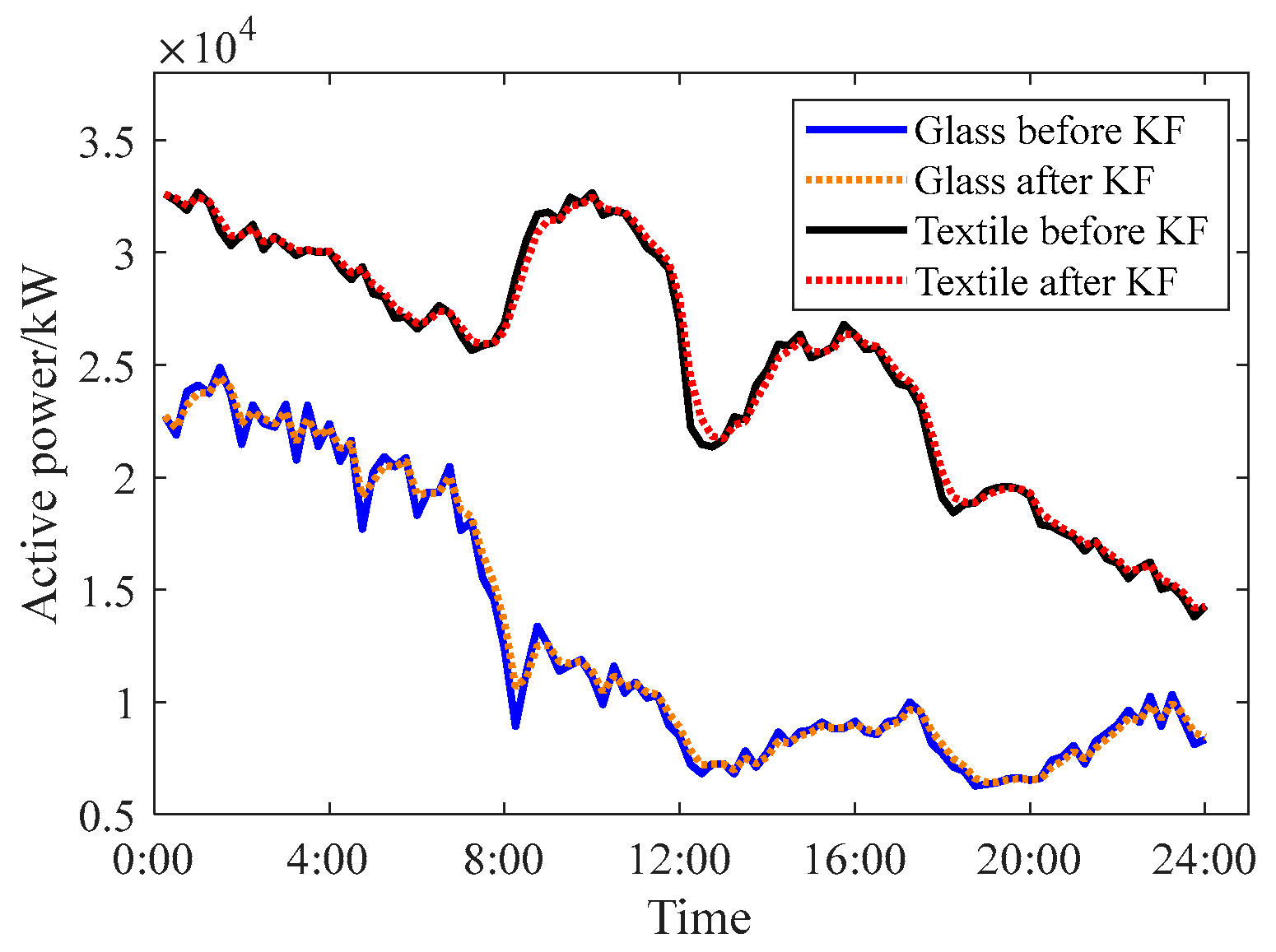
- Huang, Y.L.; Zhang, Y.G.; Wu, Z.M.; Li, N.; Chambers, J. A Novel Adaptive Kalman Filter with Inaccurate Process and Measurement Noise Covariance Matrices. IEEE Trans. Autom. Control 2018, 63, 594–601. [Google Scholar] [CrossRef]
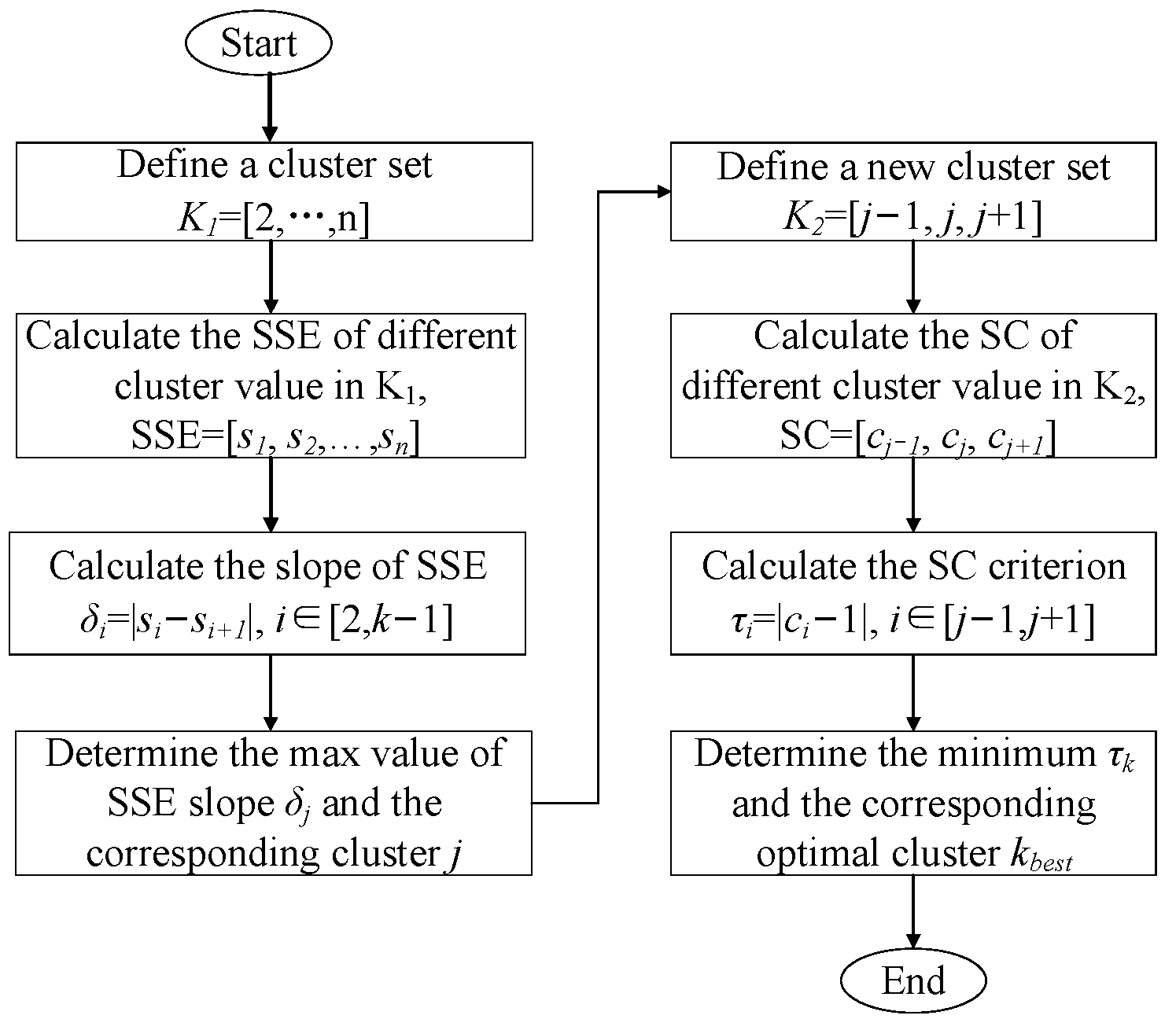
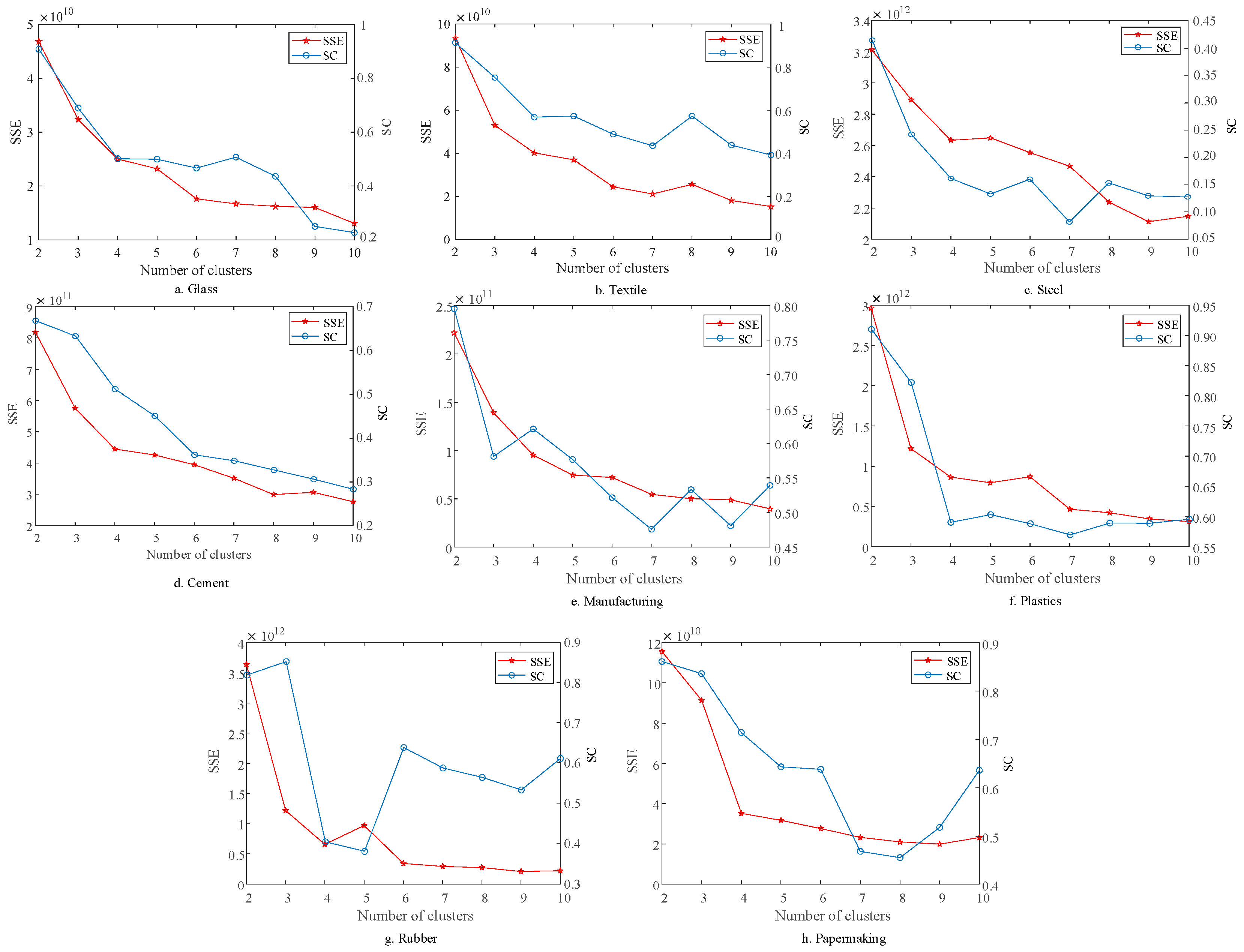
- Jeon, J.Y.; Choi, J.S.; Byun, H.G. Implementation of elbow method to improve the gases classification performance based on the RBFN-NSG algorithm. J. Sens. Sci. Technol. 2016, 25, 431–434. [Google Scholar] [CrossRef]
- Zhou, H.B.; Gao, J.T. Automatic method for determining cluster number based on silhouette coefficient. Adv. Mater. Res. 2014, 3244, 227–230. [Google Scholar] [CrossRef]
- Zhou, S.; Xu, Z.; Liu, F. Method for Determining the Optimal Number of Clusters Based on Agglomerative Hierarchical Clustering. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 3007–3017. [Google Scholar] [CrossRef] [PubMed]
- Peoples Government of Guangdong Province. Guangdong Statistical Yearbook; People’s Government of Guangdong Province: Guangzhou, China, 2022. (In Chinese)
- Cheng, Y.; Rao, R.; Ding, S. Potential analysis of power demand side adjustable load in industrial field. Energy Eng. 2023, 43, 72–78. (In Chinese) [Google Scholar]
- Feng, J.; Zhou, Y.F. The analysis of typical load characteristic and the ability of interruptible load of the electrical customer in Zhejiang province. Power Demand Side Manag. 2011, 13, 48–53. (In Chinese) [Google Scholar]
- Anand, A.; George, V.; Kanthi, R.; Tagore, M.; Padmashree, M. Basics on Categorizing Travel-Time-Based Degrees of Satisfaction Using Triangular Fuzzy-Membership Functions. Transp. Res. Procedia 2020, 48, 1555–1574. [Google Scholar] [CrossRef]
- Kompil, M.; Celik, H. Modelling trip distribution with fiuzzy and genetic fuzzy systems. Transp. Plan. Technol. 2013, 36, 170–200. [Google Scholar] [CrossRef]
- Kedia, A.; Saw, K.; Kati, B.K. Fuzzy Logic Approach in Mode Choice Modelling For Education Trips: A Case Study of Indian Metropolitan City. Transport 2015, 30, 286–293. [Google Scholar] [CrossRef]
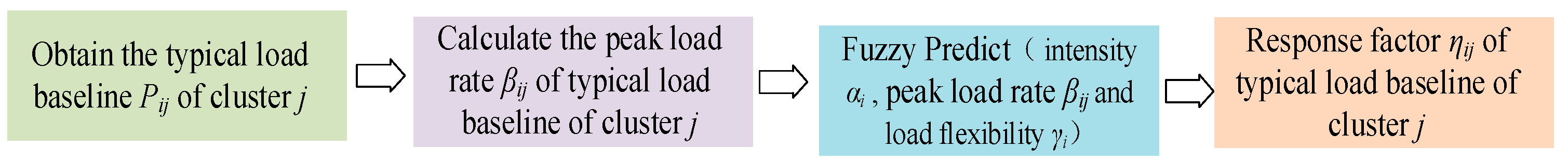
| Subscript i | Industrial User i | λij | the Weight of Cluster j |
| subscript j | j-th cluster | αi | electricity intensity |
| fi(t) | load dataset of industrial user i | ρi | GDP of industrial user i |
| k | clustering number | ζi | annual electricity consumption |
| Pij | j-th typical load baseline of user i | βij | peak load rate of cluster j |
| mi | total sample number | γi | load flexibility of industrial user i |
| nij | data number of the cluster j | ηij | response factor of cluster j |
| Industrial Type | Main Regulating Equipment | Flexible Load Ratio |
|---|---|---|
| Glass | glass melter; annealing furnace; air compressor; glass cutting machine; belt conveyor; toughening furnace | 25% |
| Textile | texturing machine; double-twisting machine; can tipper; loom machine; workshop lighting | 35% |
| Steel | electric furnace; bloomery; oxygenerator; steel rolling production line; bar production line; wire production line | 20% |
| Cement | rotary kiln; shaft kiln; raw mill; cement grinding mill; ball mill; air compressor; conveyor tape machine | 24% |
| Manufacturing | furnace for heat treatment; high-frequency furnace; melting furnace; blower; dryer; cooling pump; vetilator | 20% |
| Plastics | electric heaters; box mill; ultrasonic equipment; eyelet machine; wire press machine; high-velocity ram machine | 64% |
| Rubber | linard machine; motorshipengine; edger; conveyor; water washer | 33% |
| Papermaking | reeling machine; crane | 8% |
| L3 | M3 | S3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| L2 | M2 | S2 | L2 | M2 | S2 | L2 | M2 | S2 | |
| S1 | VL | VL | L | L | M | M | S | S | VS |
| M1 | L | L | M | M | M | S | S | VS | VS |
| L1 | M | S | S | M | S | S | VS | VS | VS |
| Industrial Type | Clustering Results | |
|---|---|---|
| k | n | |
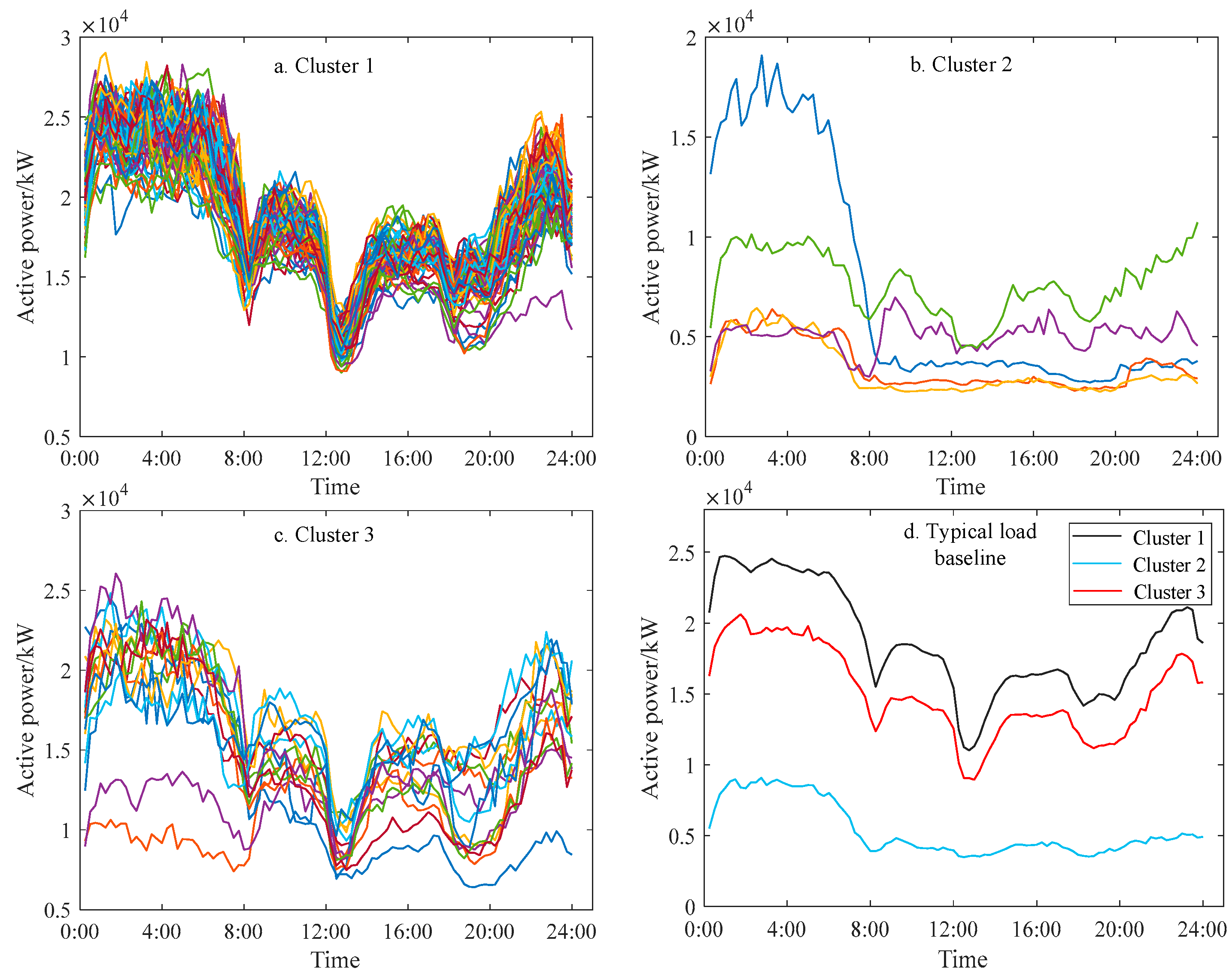
| Glass | k = 3 | n = [71, 5, 15] |
| Textile | k = 3 | n = [5, 67, 19] |
| Steel | k = 3 | n = [26, 34, 34] |
| Cement | k = 3 | n = [40, 43, 8] |
| Manufacturing | k = 4 | n = [25, 5, 47, 14] |
| Plastics | k = 5 | n = [38, 4, 12, 3, 34] |
| Rubber | k = 3 | n = [74, 1, 16] |
| Papermaking | k = 3 | n = [71, 4, 16] |
| Industrial Type | Peak Load Rate | Load Flexibility | Response Factor |
|---|---|---|---|
| Glass | γ1 = 0.663, γ2 = 0.481, γ3 = 0.659 | 2.57 | η1 = η3 = 0.348, η2 = 0.125 |
| Textile | γ1 = 0.971, γ2 = 0.988, γ3 = 0.991 | 3.03 | η1 = η2 = η3 = 0.366 |
| Steel | γ1 = 0.731, γ2 = 0.937, γ3 = 0.833 | 3.1 | η1 = η3 = 0.609, η2 = 0.611 |
| Cement | γ1 = 0.966, γ2 = 0.967, γ3 = 0.865 | 3.21 | η1 = η2 = 0.366, η3 = 0.365 |
| Manufacturing | γ1 = 0.98, γ2 = 0.928, γ3 = 0.98, γ4 = 0.963 | 2.15 | η1 = η2 = η3 = η4 = 0.11 |
| Plastics | γ1 = 0.991, γ2 = 0.849, γ3 = 0.961, γ4 = 0.982, γ5 = 0.985 | 3.13 | η1 = η2 = η3 = η4 = η5 = 0.463 |
| Rubber | γ1 = 0.995, γ2 = 1, γ3 = 0.976 | 1.85 | η1 = η2 = η3 = 0.125 |
| Papermaking | γ1 = 0.98, γ2 = 0.97, γ3 = 0.983 | 1.57 | η1 = η2 = η3 = 0.125 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Liu, Z.; Shao, C.; Lin, B.; Rong, J.; Dong, N.; Su, B.; Hong, Y. A Method for Evaluating Demand Response Potential of Industrial Loads Based on Fuzzy Control. Energies 2024, 17, 5146. https://doi.org/10.3390/en17205146
Li Y, Liu Z, Shao C, Lin B, Rong J, Dong N, Su B, Hong Y. A Method for Evaluating Demand Response Potential of Industrial Loads Based on Fuzzy Control. Energies. 2024; 17(20):5146. https://doi.org/10.3390/en17205146
Chicago/Turabian StyleLi, Yan, Zhiwen Liu, Chong Shao, Bingjun Lin, Jiayu Rong, Nan Dong, Buyun Su, and Yuejia Hong. 2024. "A Method for Evaluating Demand Response Potential of Industrial Loads Based on Fuzzy Control" Energies 17, no. 20: 5146. https://doi.org/10.3390/en17205146
APA StyleLi, Y., Liu, Z., Shao, C., Lin, B., Rong, J., Dong, N., Su, B., & Hong, Y. (2024). A Method for Evaluating Demand Response Potential of Industrial Loads Based on Fuzzy Control. Energies, 17(20), 5146. https://doi.org/10.3390/en17205146





