Abstract
Due to the rise of e-mobility applications, there is an increased demand to create more accurate control methods, which can reduce the loss in an e-drive system. The accurate modeling of the rotating machines needs to resolve a partial differential equation system that describes the thermal and mechanical behavior of the different parts in addition to the electromagnetic design. Due to these models’ limited resources and high computation demand, they cannot be used directly for real-time control. Model order reduction methods have been of growing interest in the past decades and offer solutions for this problem. According to the processed literature, many model order reduction-based methods are used for a wide range of problems. However, a paper has not been published that discusses a model order reduction-based real-time control model that is actually used in the industry. This paper aims to summarize and systematically review the model order reduction methods developed for rotating electrical machines in the last two decades and examine the possible usage of these methods for a real-time control problem.
1. Introduction
The numerical modeling of rotating electrical machines needs to resolve a complex and computationally demanding partial differential equation system. These modeling approaches have two very distinct main goals. One focuses on design—using large and accurate computations to find optimized geometries and parameters—and the other focuses on control —using real-time computations with limited computational resources. They are, therefore, limited in their scope and accuracy, generally supported by the on-line measurement of currents, rotor position, and temperature to increase their precision. This is a widely researched area since using more accurate models can significantly increase the performance and reduce the losses in the controlled electrical drive system, allowing the application of more sophisticated predictive or sensorless control methods [1,2,3,4,5].
The main goal during the development of real-time control models is to consider as many phenomena as possible to create more and more detailed models of the system. Control models cover flux and torque calculations—more accurate ones already including spatial harmonics, saturation, cross-coupling, losses, and the effects of changing temperature [6]. These novel methods enable the creation of high-fidelity models, which can be utilized for sensorless control [7] or facilitated to model the thermal behavior of the machine, enabling temperature-based power limitation [8].
Due to the increasing governmental [9] and customer demand, there are other parameters that should be controlled. One of the main challenges is to depict and reduce the noise, vibration, and harshness of an electrical drive system. The modeling and simulation of these parameters requires the solution of finite element method-based multiphysical models [10,11]. Model order reduction (MOR) techniques can make these complex models usable in small-scale real-time controls. MOR techniques are the subject of growing interest in electrical machine modeling [12]. There is particular interest for these techniques because they can consider multi-dimensional dependencies in future real-time control [13].
The current state-of-the art real-time control approaches are mainly supported by models based on lookup tables [14]. In these methods, the main limiting factor to the various additional considerations and increasing complexity is the relatively low computational power of an embedded controller [15]. Therefore, the parametric machine equations in the dq reference frame are still widely used as the basis for the real-time torque calculation of synchronous machines [16]. The , inductances are a function of , currents and are stored in lookup tables. In a control application, the currents , are the results of measurement and of Clarke and Park transformations.
The externally excited synchronous machines can be defined analogously with replaced by rotor winding and excitation current. It is, however, worth noting that the parametric , inductances are now a function of , , currents, adding a third dimension for the lookup. A three-dimensional lookup table has a huge memory need, which can significantly increase the cost of the embedded system. Moreover, adding an additional parameter is problematic since the highest-order interpolation available in AUTOSAR is the cuboid [17].
Nevertheless, this approach is also an actively researched area. By expanding Equation (1) to include all partial derivatives of flux linkages , Veeser et al. [18] created an online model and paired control that is capable of calculating and reducing cogging torque and torque ripples, which they demonstrated in a simulation. They avoided 3D lookups by using truncated Fourier series representations of the partial derivatives, as well as cogging torque that was dependent on and numerical differentiation that was dependent on currents. Di Tommasso [19] created multiple 3D lookups from FEM results to accurately depict torque ripple and iron loss effects in the dq reference frame of a PMSM.
Another modeling approach is using Magnetic Equivalent Circuits (MEC) [20,21,22], which utilize permeance networks on an electrical analogy: magnetic permeance is analogous to electrical conductance, magnetomotive sources are analogous to electrical voltage, and magnetic flux is analogous to electrical current. While magnetic circuits predate finite element modeling and were used historically for machine design, they offer a lower-complexity solution for the magnetic field than FEM, allowing online calculations [23]. Magnetic equivalent circuits acquiesce certain simplifications based on the modeler’s physical assumptions, such as neglecting the saturation of tooth tips as being irrelevant to the interesting electromagnetic quantities or limiting the elements to simple geometrical shapes. Seilmeier [24] tackled cross-coupling and geometrical and saturation-induced saliency effects in the fundamental wave scope using MECs. Faustner [25] created a static and dynamic nonlinear MEC of a permanent magnet synchronous machine (PMSM) and developed measurement-based parametrization for it. Forstner et al. [26] created a dynamic nonlinear real-time capable MEC for model predictive control purposes and fault-tolerant control strategies [27].
This paper provides a comprehensive review of MOR techniques, which, utilizing a finite element method (FEM)-based model as a starting point, derive a reduced-order model (ROM) that decreases solution time significantly (Figure 1). MOR techniques represent a new research direction in the area, with the possibility to consider more parameters during the operation, which would not be possible with a lookup table-based approach.
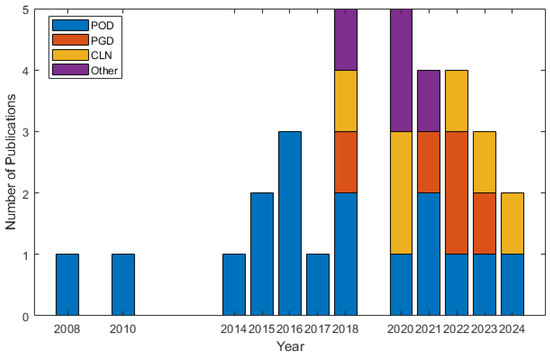
Figure 1.
MOR techniques are the subject of growing interest in rotating electrical machine modeling—a classification of reviewed papers.
The main goal of this paper is to find whether an MOR-based control model for electric machinery has already been reported in the literature. Additionally, it aims to summarize and describe the MOR methods developed or adjusted for magneto-quasi-static (MQS) simulations with nonlinear-parametered rotating machinery and assess their potential use for creating an MOR-based control model based on the reviewed content: how—or whether—they have addressed torque, torque ripple, localized and harmonic loss calculation, how accessible is their usage in terms of both software and required expertise, and whether they have been successfully scaled down to a real-time solution in any use case. After a brief introduction to the MQS FEM problem in Section 2, Section 3 focuses on various MOR methods developed over the past two decades. The review categorizes these methods based on their mathematical foundations, such as Singular-Value Decomposition (SVD), moment matching, and interpolation techniques. The paper also addresses the challenges associated with these methods, including handling nonlinearities in Section 4 and handling rotational movement in Section 5, before showing an overall view, future possibilities, and concluding remarks.
2. The Quasistatic Finite Element Problem
In order to gain a lightweight electromagnetic model, the computationally expensive finite element model serves as a starting point, which is required to be reduced. The governing equations for magneto-quasi-static fields are given by Maxwell’s equations, which, after applying the appropriate approximations and assuming quasi-static conditions, can be written as [28]
where is the magnetic vector potential, is the scalar electric potential, is the current density, is the magnetic reluctivity, is the electrical conductivity, and is the angular frequency. Applying finite element discretization to these equations, the system can be expressed in matrix form as
where and are the system matrices [29], is the vector of unknowns, is the source vector, and V is the input voltage. The coupling of the electromagnetic field with external circuits is described by the circuit equation:
where R and L are the external resistance and inductance, respectively, and is the magnetic flux. These equations form the basis for the finite element analysis of electromagnetic devices, allowing for the detailed simulation of their behavior under various conditions. By reducing the size of the system matrices using model order reduction techniques, significant computational efficiency improvement can be achieved; [30] performs an analysis of the feasibility for better time-domain- and possibly real-time applications. Rotating electromagnetic devices, however, introduce some complications. The model should consider nonlinearity due to the saturation of core material and the effects of the rotation and position dependence of the problem itself.
3. Model Order Reduction Methods
The roots of model order reduction lie in systems and control theory [30]. Systems of ever-increasing complexity are approximated with their input–output behavior, retaining only significant information. Most of these approximations are achieved through projections onto a lower-dimensional subspace: the original system is projected into an appropriately reduced basis in a computationally stable and efficient manner while maintaining a low approximation error and preserving system properties like stability and passivity [31]. The MOR methods are differentiated in how the appropriate basis is found. Antoulas et al. have written a general overview of model order reduction methods [31]. According to their classifications, the MOR methods can fit into two main categories: SVD and moment matching-based methods (Figure 2). Their general take on these categories is that SVD methods are computationally inefficient, give global error bounds, preserve stability and passivity, and behave better globally in frequency, while the moment-matching methods can be efficiently applied iteratively, but only conditionally preserve stability and passivity and show a better local behavior around their expansion point. Thus, an appropriate choice can be made depending on the modeling goal.
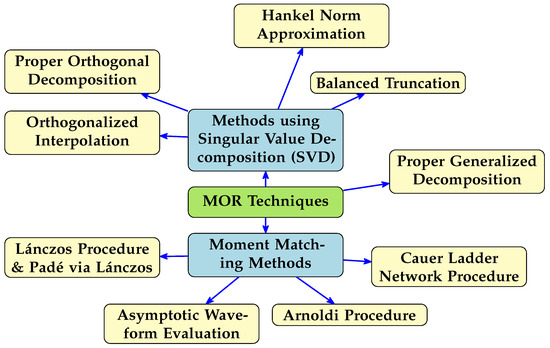
Figure 2.
Model order reduction methods.
Since their review, new MOR methods have been introduced, like the proper generalized decomposition [32] and the Cauer ladder network procedure [33], both used in MQS modeling. MOR methods are used for the widest variety of disciplines; this paper focuses on electromagnetic systems—specifically, rotating electrical machines—and their considerations.
3.1. Truncated Balanced Realization and Hankel-Norm Reduction
The method of truncated balanced realization (TBR) for system analysis via test signals was introduced by Moore [34]. Take a general linear dynamical system:
The matrix is the system matrix (or stiffness matrix), is the damping matrix, is the input vector, is the system input signal, is the system output vector, and and are the system output and state variables, respectively. One seeks to find a lower-dimensional system that approximates it by finding an appropriate T-projection operator, controllability Gramian P, and observability Gramian Q by solving the two corresponding Lyapunov equations:
In a balanced realization, the states to be found are the states that are both well-observable and well-controllable. Moore described that this is the case when the Gramians are equal and diagonal.
This can be achieved by finding using a balancing transformation. First, a Cholesky factorization is performed on . Then, the singular values of are found to create the transformation matrix [30]. The elements of , are the Hankel singular values. If , then the corresponding coordinate axis is more important, as well as better controllable and observable, than the axis . The balanced system can be reduced by omitting—truncating—the less important coordinate axes from [35]. The reduced system is then gained by
In 1984, Glover published his paper on the Hankel-norm reduction [36]. He defined the model-reduction problem as finding a surrogate system for an original of McMillan degree n given by its transfer function of McMillan degree , to minimize the norm of the error . His proposed norm is the Hankel norm.
Scherpen [37] extended the balanced realization to stable nonlinear systems based on the input–output energy functions, using a series of linearized coordinate transformations. This method only conditionally keeps a balanced reduced system, for which the author also described the conditions.
The balancing truncation methods are generally used to reduce RL- and RC-circuit equations. Kerler-Back and Stykel [38] regularized the linear electromagnetic FEM equations to gain a form similar to RC circuit equations, to which the TBR was applied. After describing the mathematical framework, they presented an iron core coil example with linear material characteristics. The 5-dimensional ROM followed the characteristics of the 3910-dimensional regularized FEM model with an error bound of . Using the TBR approach, however, no ROM of rotating electrical machines can be found in the literature.
3.2. Proper Orthogonal Decomposition
The previously shown MOR techniques are based on decomposing the system matrices, which is computationally intensive for large systems. For such systems, when building an ROM, considering the system response—or the system’s states—to some arbitrarily chosen excitations instead may be a more efficient choice. This method, called proper orthogonal decomposition (POD), uses snapshots. POD has its roots in probability theory and has multiple approaches like Karhunen–Loéve decomposition, principal component analysis, and SVD. Liang et al. proved that these three methods are equivalent [39]. Considering a static system with an n-by-n system matrix, the states are snapshotted in different input vectors or time steps, resulting in an n-by-m snapshot matrix, on which the singular value decomposition is performed [40].
The SVN separates the space and time functions. The n-by-n matrix is the link between the decomposition and the state distribution, the n-by-m matrix is the diagonal matrix of singular values ordered by size from largest to smallest, and the m-by-m matrix is the temporal—or input—dependency. By setting the last elements of to 0, a projection operator is gained: . The reduced system that approximates will be with the following definitions [41]:
The original x is obtained by
The finite element approximation of the magnetostatic field equations can be written in such a form [42], causing POD to be one of the most popular approaches for magnetostatic MOR [43,44,45,46,47]. POD reduction guarantees the best accuracy in the least squares sense, meaning that the highest energy modes are considered the most informative [41]. This, however, may be a disadvantage in systems that have important low-energy states, as POD would opt to ignore them. Hollaus et al. [48] considered DOE approaches to improve snapshot selection for the fast estimation of manufacturer deviation in permanent magnet remanence in a synchronous machine. They have found that the dimension of the reduced system has a decisive effect on the torque and torque ripple calculation accuracy, rather than the number and distribution of snapshots. Henneron et al. [49] introduced an error estimator for electromagnetic POD without any knowledge of the original function, dependent on the magnetic constitutive relation. They analyzed the weighted norm , which equals zero when the exact solution is found. The estimator can be used to optimize the number or distribution of snapshots.
3.3. SVD-Supported Interpolation
Boumesbah et al. [42] created a flux linkage cartography to control a switched reluctance machine (SRM) using POD. The authors stated that an interpolation-based method would increase calculation speed since nonlinear POD requires the recalculation of the full-order stiffness matrix at each step of the Newton–Raphson iteration. They proposed an orthogonal interpolation method (OIM), introduced by Far et al. [50]. OIM is also a snapshot-taking SVD technique, but it stores the right singular-vector matrix as a function of the snapshots. Each function can be a multidimensional polynomial or Fourier series.
where is the snapshot matrix, it its singular value decomposition, and is identified as a function of snapshots . Any new solution is created by interpolating the columns of the right singular-vector matrix for the new input set and using this new in the SVD. OIM reduces the solution time significantly, even considering nonlinearities, but it should be noted that OIM does not project back into a reduced subspace. Instead, it interpolates the SVD result directly. As such, it loses any resemblance to a physical model and is more similar to the lookup tables currently used in control applications. In [51], they have implemented a controller using the OIM method on a PSM machine. The method was tested to be better than the autocommissioning controller in terms of torque accuracy in the field weakening area. The OIM-based controller scheme increased the execution time from 6 s to 10 s.
Independently, Sakamoto [52] developed a similar interpolation method. However, instead of using , they interpolated , where was the quadrilateral FEM interpolation function and a coefficient vector, from which characteristic values like torque and losses could be directly evaluated. A third independent characteristic factor along the rotor position was independently calculated without increasing the dimensionality of the lookups above 2. The method was tested on a PMSM motor with less than 0.5% error in the local torque in comparison to FEM. In [53], it was shown that the method yields a speedup factor of 239 with accurate torque and radial force depiction.
3.4. Proper Generalized Decomposition
POD needs a priori knowledge of the solution vector—snapshots—to create a reduced basis approximation. The proper generalized decomposition (PGD) family of solvers was introduced by Ammar et al. [32] to handle multidimensional dependencies. It has been shown to efficiently deal with parametric models [54], allowing the “close to real-time” solution of boundary value problems. PGD approximates the parametric FEM solution by a sum of separable functions:
In an MQS case, represents the magnetic vector potential with m terms—or modes. Space modes, are dependent on space coordinates . Parameters that do not change the mesh —like magnet remanence, current amplitude, and angle—can also be separately considered. PGD is a generalization of POD and achieves a form in Equation (14) using various algorithmic iterative enrichment methods, as collected by Nuoy [55]. Henneron and Clénet applied PGD to an MQS problem [56], and, upon comparing it with POD, they found that PGD requires more modes and computational time to achieve the same error as POD. Soon, they extended their MQS PGD with the discrete empirical interpolation method (DEIM) to tackle nonlinearity [57] in a three-phase transformer model. They have confirmed PGD to be an attractive choice when multiple time steps need to be simulated. Montier et al. utilized PGD to create a PMSM metamodel [58]. They approximated the full-order model by , calculating a separate submodel for each current excitation. They remarked that the direct construction of was hindered by convergence issues in the PGD algorithm. Using circuit and mechanical coupling, they created a transient simulation for which adequate accuracy was reached at 80 PGD modes, resulting in an online speedup factor of 900. Sancarlos et al. [59] mapped the FE weak form into a new, prismatic coordinate system consisting of radial s and the tangential t dimension. This way, the real geometry was mapped to a separable domain (Figure 3).
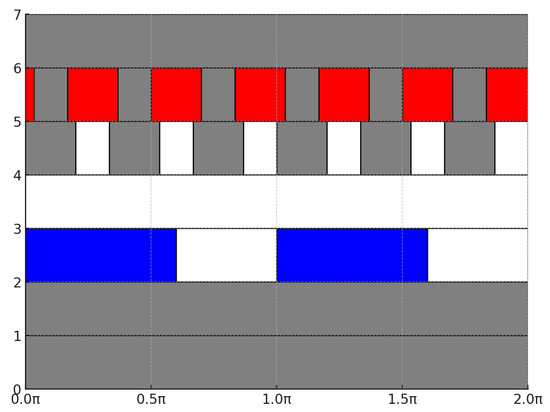
Figure 3.
Separable geometry in a prismatic coordinate system, created by Sancarlos et al. Grey is the core material, red represents the slot, blue the magnets. [59].
The finite sum was then created with the help of binary masking functions in both coordinates, realizing the separated representation characteristic to the PGD family. This realization allowed a stable joint consideration of all excitation currents in a single model, although it was limited to a linear system. Müller et al. [60] compared POD to PGD on an eddy current problem. They showed that PGD produces accurate results with fewer modes than the sequential POD, but the overall accuracy of the POD is linearly improving, while the PGD does not converge as smoothly as the POD methods. Recently, they created a parametric nonlinear PGD–DEIM model for a nonlinear parametric PMSM without considering rotor movement as a parameter [61], with their model parameters dependent on the electric angle and permanent magnet remanence. While a relatively low number of modes (seven modes for remanence variations and nine modes for current amplitude variations) achieved a residual accuracy of <1.5% in both cases, the torque error showed as an offset in the magnet remanence variation and a lower but varying error in the current amplitude variation. The computational effort reductions were 41% and 57%, respectively, although no remark was made whether the reduction in the computational effort included the MOR process itself. In [62], they included rotational motion. Without the application of DEIM and solving the nonlinear part of the system in full order, they found that the reference FOM solution has a lower computational effort if the number of NL iterations of the FOM is lower than m times the number of NL iterations of the ROM.
3.5. Moment-Matching Methods
The method of moments was first introduced in the field of statistics by P.L. Chebyshev (1874) and later used by Karl Pearson as an empirical tool for the estimation of population parameters, like expected value, variation, skewness, and kurtosis [63]. This method, used on the transfer function of a system, can be used to create a ROM, as published by Pillage and Rohrer [64] in their work about Asymptotic Waveform Evaluation (AWE), the first moment-matching method for reduced-order RLC circuit representation. The transfer function—the direct relation of input and output—of the linear system in Equation (6) in the Laplace domain can be expanded into a Taylor series around an expansion point . The coefficients of this series are called moments [65]. The transfer function of the linear system can be written and expanded as
where the matrices are the moments of the system. The Krylov-subspace methods—or moment-matching methods—aim to find an ROM whose moments match some of the moments of the original one by a recursive, iterative algorithm. The authors of the Padé via Lánczos (PVL) Process [66] provided an algorithm for the moment-matching method in circuit simulation. Pierquin [67] compared the Lánczos algorithm to POD in a simple MQS problem. While, at an equal number of modes, the POD has somewhat greater error, the moment-matching method underperforms in computation time. Lately, there have been advancements for these methods to reduce nonlinear systems [68,69], and a new moment-matching algorithm, tailored for electromagnetic problems, has surfaced: the Cauer ladder network method.
3.6. Cauer Ladder Networks
A relatively new MOR technique for electromagnetic problems, stemming from the 1D analysis of magnetic steel sheets, is the Cauer ladder network (CLN) representation [33]. Similarly to the previously discussed POD methods, the magnetic and electric field solutions are decomposed to spatial modes and corresponding time-dependent factors [70].
By omitting elements from r to ∞, an r-th-order approximation can be written as an R-L Cauer ladder network (Figure 4). The currents on the -th inductor and voltage drops on the -th resistor are the time-dependent factors of the field solutions in Equation (16).
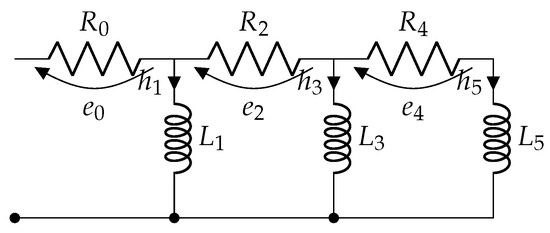
Figure 4.
Three-stage Cauer ladder network.
The first step represents a magnetostatic model, being the DC resistance and the low-frequency inductance. Higher steps represent the effect of eddy currents. In [33], the admittance function of the modeled system was written in a polynomial approximation, which was turned into a continous fraction by the Euclidean algorithm. Since the MOR methods, dependent on transfer functions, are usable for the reduction of linear systems, the authors proposed to consider the nonlinear behavior by substituting the first stage of the ladder with a current-dependent flux , considering the nonlinear dependency from the magnetostatic solution and ignoring it for the higher levels. Shindo et al. [71] introduced the CLN algorithm as a faster process to determine the spatial modes. The algorithm is based on the equivalence of the magnetic energy and Joule losses in the domain to that of the R-L components of the equivalent circuit.
where , is the modeled domain, and is the conductive domain. It was shown in [71] that the basis functions can be orthogonal without Gram–Schmidt orthogonalization when normalized by and , respectively, fulfilling
where is the Kronecker-delta, meaning that the operations in (18) give a nonzero value only when . Using (16)–(18), the following Algorithm 1 was proposed.
| Algorithm 1 The CLN algorithm for a linear system. |
For example, a SPICE solver can solve the gained circuit, and the field values can be reconstructed using (16) and (17).
Using algebraic topological methods [72] and a vector potential formulation on edge elements, Matsuo et al. showed a more efficient assembly of the Cauer ladder network [73] and compared the method with the PVL. They found that the CLN required n inversions instead of the required by PVL, yielded the circuit parameters without eigendecomposition, and derived an orthogonal expansion without the need for Gram–Schmidt orthogonalization while being as exact as the PVL. The later discussions of CLN mostly use this finite element formulation. Shindo et al. proved the capability of the method to calculate electromagnetic force from the input voltage in an electromagnet [71]. The higher-order stages were found to have an opposing force coefficient, as expected: the eddy currents diminish the effectiveness of the electromagnet. Considerations regarding inductive or resistive terminations were made. The former overestimates the force while underestimating the lag with increasing frequency, and vice versa. The number of stages also affects the highest frequency at which the force calculation is accurate. A lower bound for simple geometries and linear materials was given as . Accurate real-time force calculation was achieved on a PC up to 1 kHz supply.
This method’s handling of translational movement was first discussed in [74]. The CLN procedure was run in multiple discrete mover positions, and, in the online calculation, the circuit parameters were interpolated depending on a position input. Induced voltages due to movement were also included in the model. In [75], multiport CLN was introduced to handle M-phase systems, with modifications to the original algorithm. Initialization with source currents was described instead of the original source voltages. The network components and are matrices and the and basis vectors are also expanded to and . An advantage was reported in comparison with the block Lánczos method, since the matrices of the same CLN stages need not be orthogonal, increasing the stability of the solution while, in essence, not being more complicated than the original single-port method.
The first application of the CLN in a linear induction motor was reported in [76]. The stator and mover domains were reduced separately and joined with boundary conditions in the airgap. The multiport method was applied to the three-phase current excitation of the stator as well as the stator–mover interface, where the magnetic field, vector potential, and electric field at the boundary surface were considered to be expanded into spatial harmonic components on both the stator and rotor sides:
where and w is half the spatial period, while x is the coordinate along the boundary. The considered spatial harmonic coefficients and were joined by a rotation matrix :
with v being the velocity of the mover. Each considered harmonic component was a separate port in the multiport CLN. The CLN procedure was run for each input (three currents and harmonic components for the stator, considered harmonic components for the rotor). This way, a separate network was generated for the stator and rotor, connected by (20). Taking into account the air-gap flux up to the 17th harmonic component, the force and the Poynting vector were estimated with an error of less than 1%, the field solution agreed with the FEM solution under 198-fold acceleration, and it provided a good approximation of the effects of cogging harmonics in the time domain.
Eskandari et al. [77] proposed a two-level MOR: by connecting the machine-level and material-level models, they created a homogenized iron core model that allows the investigation of the effects of lamination properties during operation. They explained that the parameters of the CLN can be arbitrarily partitioned, and, by running the algorithm on complementary subdomains of the FEM simulation, it is possible to divide the coefficients into series resistances and parallel inductances. Thus, the stored magnetic energy and eddy current losses can be allocated spatially (e.g., in copper and laminated core regions).
They also researched multiple first-order approximation modes to define nonlinear reluctivity [78] and described a parameterized CLN that is capable of approximating nonlinear behavior, along with the algorithm that generates it [79]. The nonlinear CLN no longer creates the equivalent circuit for a unitary excitation state but considers multiple excitation states or coil currents. It searches for suitable circuit parameters based on the actual state for online computation. In 2022, Tobita et al. [80] applied the above techniques to create a nonlinear Cauer network description of a rotating induction motor. They emphasized that the parameterization based solely on excitation current and phase angle leads to inaccuracies due to the ignored effect of the rotor, and they recommended parameterization based on air-gap flux or coil flux. Both latter methods demonstrated transient behavior close to the FEM solution. A hysteretic loss-handling capability was recently added to the CLN in [81].
The collected previous works show that the CLN is a promising candidate as a lightweight time-domain modeling technique for induction machines. However, no reports on usage for synchronous machine types have yet been published.
Recently, the method has gained international interest. In [82], Hiruma and Clénet proposed and tested a guaranteed upper error bound estimation for the method. Köster et al. [83] combined the method with PGD to the double vector potential formulation and stressed the importance of the appropriate choice of inner conductive–nonconductive boundaries in order to keep the orthogonality of the modes. Ghnatios et al. [84] used the method to create a digital twin for a magnetic bearing, expanding it with a neural network-based correction to handle the nonlinearities better.
4. Handling Nonlinearity and Linearization Methods
In linear cases, it is not uncommon to achieve a reduction factor of a few hundreds to thousands while retaining calculation accuracy [30]. While linear model order reduction methods have a well-established framework and are even seeping into the modules of commercial FEM software [85,86], handling nonlinearity poses a greater challenge. Such reductions compartmentalize the original system to a linear and a nonlinear subsystem. The above-listed MOR techniques are limited to the linear part, needing to solve the nonlinear subsystem at its original size, which limits the computational advantage. Alternatively, an additional method is used to eliminate or further reduce the nonlinear part; this section endeavors to report on these additional methods. Nonlinearity can manifest as either a nonlinear dependence on the input or the states of the equation. Considering nonlinear dependence on states generalizes Equation (6) to
with , and being general state-dependent functions.
The linear projection operation in this system by itself cannot be executed anymore since the state-dependence causes and operations to need a high-dimensional solution. To reduce nonlinear models, an additional method is required, which may be decomposing the system to linear and nonlinear sub-blocks and reducing only the reducible linear part, using a hyperreduction technique, like the discrete empirical interpolation method (DEIM) or energy-conserving sampling and weighting (ECSW), or the piecewise linearization of the model to be reduced.
4.1. Piecewise Linearization
The original system of equations uses Taylor’s expansions for piecewise linearization (PWL) and trajectory piecewise linearization (TPWL). The accuracy of the linearization method used becomes the best achievable approximation accuracy of the reduced-order model. Rewieński and White [87] argued that higher-order Taylor polynomials are prohibitively expensive, and a linearized system model is feasible only for a weakly nonlinear system. They extended the first linearized reduced model around a state vector to a combination of linear models, which approximate the original with their weighted sum, approximating even highly nonlinear systems with adequate accuracy. Each linear part model has its validity range around its linearization point in the parameter space, and the approximation, dependent on the system state, is the weighted sum of the nearest valid part models. The sum of weights is always one, and the value of the corresponding weighting coefficient increases as the state variables vector approaches the i-th linearization point. The authors presented a weight-choosing algorithm. The accuracy of this technique increases with the number of chosen linearization points. They argued that it is not feasible to fill the whole parameter space with linearized part-models and proposed a training trajectory limited to the actual range of operation. With this approach, the number of used linearizations was reduced.
Qu et al. [88] presented a modified PWL technique on a 2D electromagnetic toroid FEM example with a Krylov-subspace-based MOR. Their modification lay in creating a separate local reduced-order model for each linearized system instead of a single global reduction step at . This resulted in a further reduction in model size. The full-order model was 1019-dimensional; the TPWL contained 220 elements, whereas the modified PWL was only 20, yielding a decrease in calculation time from 3.82 s to 0.00129 s. Notably, the toroid example exhibited strong symmetry. The authors mentioned that, even when the matrices are stable in the linearization points, a combination of these stable matrices may not guarantee stability. Additionally, their presented method generally yielded more accurate results using only the linearized model corresponding to the selected operating point. Thus, it is advisable to consider the TPWL model as a reduction to a certain linear system that, when approaching another linearization point, rapidly changes to its corresponding system, avoiding transfer states as much as possible.
It is also worth mentioning that only the exhibited U-I behavior was discussed. Internal states—in this case, the magnetic vector potential—are also interested in calculating forces and losses. A state-dependently different ROM may hinder such calculations.
Albunni [89] utilized TPWL with a global projection matrix and POD to model a nonlinear electromagnetic valve weakly coupled to a mechanical subsystem. The system to be reduced was more complex: not only the magnetic saturation caused a nonlinearity, but the change of mover position. The chosen EM-discretization was FEM with a coupled boundary element method (BEM–FEM). This method kept the number and the ordering of the EM field variables constant during component movement. With this approach, the nonlinearities could be decoupled, using a vector potential-dependent and a position-dependent stiffness matrix: , where a is the vector potential in the FEM discretization and x is the mover position. Force calculation was based on the Maxwell stress tensor on the boundary—ultimately, a vector–matrix–vector product of the states and a position-dependent matrix , which is a reducible analog to Equation (9). Considering both saturation and movement, the simulation time was reduced from the original 554 s to 11.65 s with virtually no error in calculated magnetic force and mover position. Later, the same method was used for the multiobjective optimization of the same valve and the ROM of a PMSM [90], also coupled with a rectifier model. Training trajectories were snapshotted at multiple rotational speeds. This coupled model was almost 1000 times faster than the full-order one in simulating a 90-degree rotation of the rotor. The method showed excellent interpolation properties regarding rotational speed, but poor accuracy at speeds not included in the original trajectory. A further advantage of this method was that additional linearizations could be added to the ROM without the need to regenerate already existing parts. While the solution time was drastically reduced, it remained in the domain of a few seconds. Calculating losses outside Joule losses in the winding was not in the scope of these works.
Trajectory-based linearization techniques for MOR have seen various uses since their introduction [91], but more recent studies focus on transmission lines and large NL circuits [92,93].
4.2. Discrete Empirical Interpolation Method
The discrete empirical interpolation method (DEIM), introduced in 2010 by Chaturantabut [94], considers the stiffness matrix in (21) to consist of linear and nonlinear parts, disregarding other possible nonlinearities. This reduced, k-dimensional system is
One can see that a projection can be found for linear , but the nonlinear term retains the computational complexity of the original, n-dimensional system.
DEIM approximates by its projection , which is defined to use only a fraction of elements of the original vector . The author proposed the following approximation:
The elements of are selected similarly to with the SVD of the nonlinear snapshots. The interpolation elements—the elements of —were chosen by a greedy DEIM algorithm.
Henneron and Clénet developed the DEIM–POD on a quasi-magnetostatic nonlinear 3D problem with edge element vector potential formulation and a single-phase AC input current [43]. Using the fixed-point technique [95] to split linear terms and residual nonlinearity in the magnetic field vector , they created a finite element discretization fitting for DEIM. Instead of SVD, they used the eigenvalue decomposition of the autocorrelation matrix of all snapshots in the snapshot matrix for the creation of the ROM in the following manner:
with the same notation as (10). This way, the created projection was considerably cheaper due to the number of snapshots being much lower than the vector of unknowns. The error was defined as the L2-norm of the relative current difference in the reference and reduced solution. The error disappeared at six POD modes with the POD method—where the nonlinear part needs a full-order solution—and eight POD modes and eight DEIM interpolation edges. The time-domain solution of s was achieved in 130 min with the full-order model, 24 min with POD, and 11 min with DEIM–POD. Thus, the final reduction factor is . Later, they extended their method to handle multiphase excitation [45] using the Newton–Raphson method and time-stepping on a three-phase 3D transformer model. Similarly to transformer tests, they used POD–DEIM on a no-load and a short-circuit configuration for building the ROM. They found that it accurately described the transformer behavior under loads that were not in the training data. Compared with the full-order model, the error in current was 0.6%, while the speedup factor was 16. Shimotani introduced block-MOR [96] for torque and loss calculation in a reluctance motor and a PMSM in a nonlinear 2D problem. The parameter space for POD was subdivided into m blocks for ranges along the rotor angle . The Newton–Raphson iteration was executed only at the corresponding -dependent block, reducing the size of the matrix–vector product. To further accelerate the calculation, a 1-D postprocessing step—introduced in [97]—was used to obtain machine torque and local losses. With an adequate choice of m, the speedup was over four times that of conventional POD with virtually no torque error and comparable losses for both methods. Actual computation times and a comparison to FEM were not disclosed. Building on Block-MOR, Sato et al. created an adaptive method for nonlinear MQS problems [98]. They developed an additional algorithm for determining the solution’s weakly and strongly nonlinear parts. The DEIM method was used for the weakly nonlinear parts, and the strongly nonlinear subdomains were solved in complete order. With this method, they achieved an accuracy equivalent to POD with a full-order nonlinear solution while still being 3–5 times faster than the FEM solution, demonstrated on an inductor and a reactor model. Montier et al. highlighted that the DEIM algorithm is prone to losing stability [44]. They suggested a structure-preserving DEIM variant where each type of Degree of Freedom (DoF) is reduced separately. In their later work, they [99] implemented the structure-preserving POD–DEIM method to reduce the transient simulation time of a synchronous machine. They used an empirical “offline/online” approach similar to [45], simulating no-load and short-circuit tests to create a ROM valid for the whole operating range.
They tested the method on a coupled circuit–EM–mechanical simulation. A 2D model of a nonlinear synchronous generator was studied. A total of time steps were used for transient simulation. They used a virtual no-load and a virtual short-circuit test for snapshot collection, both with steps. They found that an odd divisor of rotational-angle-dependent snapshots was required. An even number resulted in redundant, symmetrical information—the DEIM interpolation points gathered mostly near the air gap. The reduced bases were size 71 for POD and 160 for DEIM. They verified the ROM under an arbitrary constant load condition. The speedup of the calculation was given, including the snapshots computation. A factor of 35 was achieved with no error in the transient EMF and currents.
Petrov addressed the problem of the DEIM algorithm losing stability with an increasing number of interpolation points by improvements to the DEIM algorithm in the interpolation points selection to keep the norm (with the notation of Equation (25)) small [100]. Using a control-volume mixed FE scheme on a uniform quadrilateral grid, he also proposed handling the movement by multiplying the projection matrix with a shifting position-dependent permutation matrix . Focusing on the mathematics of the problem, he used an abstracted motor model consisting of core and coil material with a moving core part. Using a relatively large number of DEIM interpolation points, this method resulted in a minimum of 100 times reduction in computation time while keeping the -norm of the resulting potentials under 0.1 %. However, as mentioned, a tailored FE scheme with a sliding mesh approach was needed to achieve this. They have not reported loss calculation results.
4.3. Energy Conserving Sampling and Weighting
Recently, Maierhofer et al. called the DEIM approach non-symmetric and not necessarily stable [101]. Their proposed approach was the energy-conserving sampling and weighting (ECSW) method, introduced by Farhat [102]: weighting selected interpolation points so as to produce the same virtual work as the non-reduced system. The proposed method creates a symmetric and positive definite reduced stiffness matrix, which guarantees stability and allows the usage of a faster solver. However, a too-strict tolerance condition makes the ECSW algorithm fail. The authors presented the method using simple 2D and 3D solenoid geometry with nonlinear core material. Later, they demonstrated the method of simulating and reducing a coupled thermo-magneto-electric simulation of a magnetic bearing [103] for a digital twin monitoring use case. Although the ROM represented the FEM simulation adequately, their experimental validation showed differences. The measurement-based parametrization of the full-order model was needed to adjust the ROM. In [104], they introduced partial pECSW and configurational cECSW. The former reduced offline computational costs by domain decomposition and limiting the ECSW algorithm to the nonlinear subdomain. The latter used the ECSW method to create a separate goal-oriented postprocessing matrix for force calculation. Delagnes et al. [105] employed the POD–ECSW method in simulating a nonlinear induction motor case and compared it with another hyperreduction scheme. The POD–ECSW technique yielded a speedup factor of 40 within acceptable error, and it adequately simulated an error case of dropping terminal voltage.
5. Handling Position Dependence
While it is a highly relevant part of electrical machine modeling, the handling of changing positions in the reviewed literature was carried out in the FEM formulation itself before MOR. Position change can be achieved in multiple ways, as collected by [90,106]: with the meshing approach, a moving band approach that regenerates the airgap-mesh with geometry or position changes [107]; the sliding mesh approach, where the stationary and moving parts are connected with an equidistant array of interface nodes and a position change is achieved by permutation [108]; and coupled boundary approaches, where the subdomain of inner boundaries are joined algebraically.
5.1. Mesh Regeneration
In projection-based MOR, the projection operations require a constant number and ordering of discretization points, so the meshing approach is limited. In some interpolation-based approaches [42,50], it was applicable. Müller et al. [109] used different projection bases and switched between corresponding projections based on rotor position .
5.2. Permutation
The locked-step approach was used in [100,110]. The method splits the domain into stator and rotor subdomains and an inner boundary interface connected to both of them. The node distribution on the boundary is equidistant , and stator and rotor nodes match on the interface. A rotation of the rotor is then possible by turning the rotor mesh by steps . Figure 5 shows how the original rotor mesh (colored beige) alignment can only be changed in a manner that results in matching rotor and stator nodes (colored blue). A matrix representation of a domain adhering to this is in Equation (27).
where the indices refer to stator, rotor, interface, respectively. Only the submatrices marked with are position-dependent. A new rotor position is modeled by an index change operation—permutation—of the position-dependent parts. Petrov [100] multiplied the permutation matrix with the projection matrix to create a position-dependent projection, while Bontinck et al. [110] reduced the stator and rotor parts separately, leaving the interface at its original size. While it is a computationally cheap operation to reorganize the corresponding submatrices, the method limits the possible rotor positions, hence the name locked step. This would require one to have a small , which, in a real-time solution where matrix size is constrained, would limit achievable accuracy, and a nearest valid angle search would also be needed.
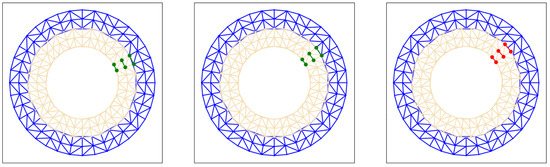
Figure 5.
Locked step approach. The original rotor mesh (left) can only be rotated in discrete steps, which results in matching stator (blue) and rotor (beige) nodes on the interface (middle). Achieveable positions are marked with green nodes. (Right) shows a rotor position that cannot be calculated with this method, marked with red nodes.
5.3. Algebraic Connection
Instead of changing the mesh or its topology, defining an algebraic connection between the interfaces keeps the number and order of the equations the same, eventually only changing the values inside the system matrices.
Albunni [89,90] used the BEM–FEM coupling method [111]. The system equation, considering the inner boundary in the air gap and eliminating the resulting algebraic variables, was written in the form
with the notation borrowed from Equation (6). Due to the magnetic linearity of the air gap, the position dependence of the stiffness matrix could be detached from the state-dependent nonlinear part modeled by FEM . While this allowed for an elegant handling of position dependence, it also introduced a position-dependence in the post-processing matrix for torque calculation in the air gap.
Montier et al. [58,99,112] considered movement by using the overlapping method, which Tsukerman introduced [113] and applied to vector potential formulation by Krebs et al. [114]. A thin non-meshed domain between the stator and rotor domain was created, and the finite element functions of both domains were extended into the non-meshed domain to ensure continuity properties. Since the overlapping domain was non-meshed, the number and position of unknowns did not change, only the stiffness matrix entries at the stator-rotor boundary. This way, a rotor position-dependent stiffness matrix was created. This method is applicable when material linearity on the interface is ensured, which was the case in the air gap. This method yields a similar decomposition of the stiffness matrix to Equation (28). They called the state-dependent—or saturation-dependent—part the permeability operator and the position-dependent part the angular operator. In [58], they proposed an approximation of the angular operator as
with
Müller et al. [61,62] employed a sliding interface method with a boundary mapping based on Lagrange multipliers [115].
The algebraic connection in the CLN method was applied for induction machines [76,80], using two multiport Cauer ladder networks for stator and rotor. Multiport CLN utilized matrix-valued impedances, one row for each port. The stator CLN consisted of the 3 phase ports and the considered spatial harmonics on the stator–rotor interface , while the rotor CLN had ports. The networks were connected by a position-dependent rotation matrix as a boundary operation described in Equation (20). The method used rotor position-dependent continuous functions from a truncated Fourier series, allowing the arbitrary choice of considered geometrical harmonics at the cost of increasing system size, each considered harmonic component increasing the port number of the CLNs (Figure 6).
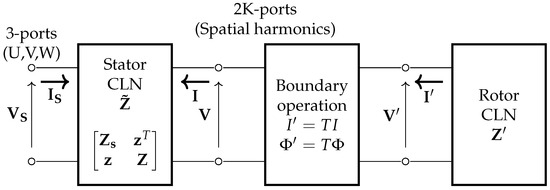
Figure 6.
Stator and rotor CLN submodels connected by a T rotation matrix. and defined in Equation (19), consisting of the Fourier coefficients of the circumferential magnetic field, and , defined similarly for the harmonic components of and the axial magnetic vector potential, and similarly for the harmonic components of the electric field [76].
6. Discussion
The methods presented previously have been developed or applied to the MQS use case recently. The momentum in this research started about a decade ago (see Figure 1). Until 2024, the only real-time control model that was designed using MOR was using the OIM method. After surveying the state-of-the-art, one of the most persistent challenges across all MOR techniques is managing nonlinearities without compromising accuracy or computational efficiency. Future work could explore more advanced hyper-reduction methods, such as ECSW, to provide stability and computational efficiency. CLN methods have shown promise for real-time applications due to their scalable nature, ability to model eddy currents, and magnetic saturation effects in detail. However, current research predominantly focuses on induction machines, leaving a gap in applying these methods to synchronous machines.
In this paper, the previously surveyed methods are compared and discussed by their following characteristics:
- 1.
- Scalability—is the reduced-order model accuracy adequate when the resource consumption is limited by real-time use?
- 2.
- Speedup ratio—given an error limit, how well does the method speed up the calculation?
- 3.
- Functionality—how many tools are available for or based on the method, how broad are their use cases, and how well does a method fulfill the stated goals of the paper?
- 4.
- Accessibility—how simple is it to integrate them into an existing framework, or how well are they already integrated?
6.1. On Accessibility
Projection-based MOR requires an available weak form, known stiffness, and damping matrices. Consequentially, commercial FEM software that grants limited access to their internal mathematical constructs has been developing their integrated MOR plugins, limiting them to linear—or linearized—and steady-state [86] cases. Research has given users the available FE-matrix frameworks for POD, TBR, AWE, and multiple methods not discussed here that are accessible in Matlab toolboxes [116,117] and Python libraries [118]; the case is similar for PGD [119]. The CLN algorithm is not yet found readily available in such a format. Most authors of papers on motor MOR have extensive previous academic work on electromagnetic FEM, underlining the assumption that the mathematical development of the methods themselves is still the main focus, and an entrance barrier for researchers aiming for practical use cases with limited theoretical immersion persists. The accessibility of these methods is also reliant on the available FE software and the chosen methods to consider movement and material nonlinearity. In comparison, orthogonal interpolation methods are more straightforward and require only the SVD of the finite element solution, which is an integral part of any mathematical toolkit.
6.2. On Scalability
The reviewed literature provided multiple use cases, but only a few cases reported real-time-capable solutions, the most prominent one being OIM, which has already been implemented in a controller [51]. The first real-time solution in CLN was reported in [71], albeit on a PC and with linear material characteristics as well as stationary parts, up to a 1 kHz switching frequency. Nevertheless, its unique way of handling nonlinear characteristics and movement allows unparalleled scalability.
The other discussed methods have yet to report a real-time solution with adequate accuracy for electrical machines. Although POD yields an L2-optimal reduced solution and defined error norm for ROM size, it struggles with parametric problems with more than two parameters. PGD offers a solution, but its algorithmic creation process does not grant a monotonic accuracy improvement by model size. This results in uncertainty regarding finding the optimal PGD model size. Both methods also rely on hyperreduction methods to increase their efficiency in handling nonlinear systems, limiting the achievable ROM size. In order to improve their downscale potential, further research in alternative methods is needed [62].
6.3. On Functionality
Despite being one of the oldest methods, TBR has yet to be explored in terms of its potential to reduce nonlinear MQS problems. In contrast, MOR methods such as POD, PGD, CLN, and SVD-supported interpolation have already been successfully used for rotating electrical machine simulation.
The CLN method was originally developed for electromagnetic problems in the time domain. Thus, the reported relevant functionalities of the CLN are the closest to the defined modeling goals. They efficiently handle geometrical and supply harmonic and hysteresis losses defined to any arbitrary subdomain and their effect on the electromagnetic force, enabling the instantaneous extraction of post-processing variables without projecting back to the original model space.
Interpolation-based methods have achieved torque and flux calculation, and, in [51], the authors mentioned that the method could also produce iron losses without additional loss tables. However, this was not presented in their work.
An overall view of functionalities and solutions in different methods are shown in Table 1.

Table 1.
Reduction methods and their reported functionalities.
6.4. On Speedup
Although it is the most essential aspect of assessment for MOR methods, a comparison of the speedup capabilities was problematic for the following three reasons. The reports employ different definitions for speedup factors. In many of them, the offline (reduction process) and online (reduced-order solution) parts are not handled separately, and a sum of these times is compared with the original solution time. The goal of the reduction governs that the optimization or deeper analysis [90] is more interested in the whole-time comparison, while a goal in control may neglect the time for decomposition since the online time is the critical factor. The original FE formulation plays a vital role in the speedup. An inefficient original model that can be represented ultimately by only a few modes can oversell the speedup of specific methods, as [100] showed by solving the same problem with different original mesh densities. The reduction error goals are also varying. Some papers opt for current, torque, or flux accuracy; others opt for the error norm of the vector potential, and different authors define a numerically different acceptable error bound.
The reviewed reports often show pairwise comparisons for specific modeling tasks. However, in order to rigorously assess each method’s speedup capabilities, a benchmark comparison where the above three aspects are well-defined and fixed will be needed. The authors plan to perform such an analysis later.
Table 2 shows that each method can speed up. The MOR process, calculated using the overall time, demonstrates that speedup is a function of the number of time steps. In these cases, an increased reduction factor when solving more time steps is observed. The table reports the results of online ROM vs. FOM wherever this information was available, highlighting the potential of these methods. Interpolation-based speedup refers to the computation effort of a single dependent value. The SVD-supported interpolation methods can reach the best speedup. A linear ROM can reach a factor of 900 [58], and a finely meshed original model inflates the speedup factor [100]. A significant reduction in speedup can be observed in cases where the sum of the reduction process and the online solution was compared to the original model.

Table 2.
Machine MOR methods and their reported speedup factor.
7. Conclusions
This review has covered developing and applying various model order reduction (MOR) methods to simulate and control rotating electrical machines. The primary focus has been on techniques like proper orthogonal decomposition (POD), proper generalized decomposition (PGD), and Cauer ladder network (CLN), highlighting their advantages, limitations, and computational efficiency improvements. Each method offers unique benefits, depending on the specific application requirements, such as time-domain simulation, design optimization, or multi-parameter sensitivity analysis. The study underscored the persistent challenges in handling nonlinearities, integrating dynamic effects like rotor movement, and maintaining stability while creating and selecting reduced-order models. The main research directions were shown from the state-of-the-art literature, and the methods were compared according to their functional adequacy for an online model, their accessibility, whether they have been succesfully scaled down to real-time in a use case, and their general capability for speedup. Overall, MOR techniques hold significant promise for advancing the efficiency and accuracy of electrical machine simulations, paving the way for more sophisticated and computationally feasible models.
Author Contributions
Conceptualization, K.L.K. and T.O.; methodology, K.L.K.; writing—original draft preparation, K.L.K.; writing—review and editing, K.L.K.; visualization, K.L.K.; supervision, T.O.; project administration, K.L.K. and T.O.; funding acquisition, T.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Research, Development, and Innovation Fund of Hungary—which was financed under the FK funding scheme: project no. 147030.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ASM | Asynchronous Machine |
| AWE | Asymptotic Waveform Evaluation |
| BEM | Boundary Element Method |
| CLN | Cauer Ladder Network |
| DEIM | Discrete Empirical Interpolation Method |
| DoF | Degree of Freedom |
| ECSW | Energy-Conserving Sampling and Weighting |
| EM | Electromagnetic |
| FEM | Finite Element Method |
| FOM | Full-Order Model |
| LUT | Lookup Table |
| MQS | Magneto-Quasi-Static |
| MOR | Model-Order Reduction |
| NL | Nonlinear |
| NVH | Noise, Vibration, Harshness |
| PC | Personal Computer |
| PGD | Proper Generalized Decomposition |
| PMSM | Permanent Magnet Synchronous Motor |
| POD | Proper Orthogonal Decomposition |
| PWL | Piecewise Linearization |
| RC | Resistor–Capacitor |
| RLC | Resistor–Inductor–Capacitor |
| ROM | Reduced-Order Model |
| SRM | Switched Reluctance Machine |
| SVD | Singular Value Decomposition |
| TPWL | Trajectory Piecewise Linearization |
References
- Rind, S.J.; Ren, Y.; Hu, Y.; Wang, J.; Jiang, L. Configurations and control of traction motors for electric vehicles: A review. Hin. J. Electr. Eng. 2017, 3, 1–17. [Google Scholar] [CrossRef]
- Merabet, A. Advanced control for electric drives: Current challenges and future perspectives. Electronics 2020, 9, 1762. [Google Scholar] [CrossRef]
- Bermúdez, M.; Martín, C.; González-Prieto, I.; Durán, M.J.; Arahal, M.R.; Barrero, F. Predictive current control in electrical drives: An illustrated review with case examples using a five-phase induction motor drive with distributed windings. IET Electr. Power Appl. 2020, 14, 1327–1338. [Google Scholar] [CrossRef]
- Zhong, Z.; Shao, Z.; Bao, Y. Real-Time Simulation of Permanent Magnet Synchronous Motor Considering Harmonic Currents Based on FPGA. J. Electr. Eng. Technol. 2021, 16, 3125–3134. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, Z. Low complexity model predictive current control for dual three-phase permanent magnet synchronous motor with extended control set and duty cycle modulation. Electr. Eng. 2024, in press. [CrossRef]
- Hu, D. Deriving a Fast and Accurate PMSM Motor Model from Finite Element Analysis Technical Report. 2017. Available online: https://www.mathworks.com/content/dam/mathworks/mathworks-dot-com/solutions/automotive/files/mac2017/deriving-fast-accurate-pmsm-motor-model-from-finite-element-analysis.pdf (accessed on 11 October 2024).
- Liu, C.; Luo, Y. Overview of advanced control strategies for electric machines. Chin. J. Electr. Eng. 2017, 3, 53–61. [Google Scholar] [CrossRef]
- Wallscheid, O. A Contribution to the Thermal Utilisation of Permanently Excited Synchronous Machines in Automotive Traction Applications—in German. Ph.D. Thesis, Universität Paderborn, Paderborn, Germany, 2017. [Google Scholar]
- United Nations Economic Commission for Europe (UNECE). UN/ECE Regulation No. 85: Uniform Provisions Concerning the Approval of Internal Combustion Engines or Electric Drive Trains Intended for the Propulsion of Motor Vehicles of Categories M and N with Regard to the Measurement of the Net Power and the Maximum 30 Minute Power of Electric Drive Trains; United Nations Economic Commission for Europe (UNECE): Geneva, Switzerland, 2023. [Google Scholar]
- Orosz, T.; Rassõlkin, A.; Kallaste, A.; Arsénio, P.; Pánek, D.; Kaska, J.; Karban, P. Robust Design Optimization and Emerging Technologies for Electrical Machines: Challenges and Open Problems. Appl. Sci. 2020, 10, 6653. [Google Scholar] [CrossRef]
- Katona, M.; Orosz, T. Circular Economy Aspects of Permanent Magnet Synchronous Reluctance Machine Design for Electric Vehicle Applications: A Review. Energies 2024, 17, 1408. [Google Scholar] [CrossRef]
- Zebari, R.; Abdulazeez, A.; Zeebaree, D.; Zebari, D.; Saeed, J. A Comprehensive Review of Dimensionality Reduction Techniques for Feature Selection and Feature Extraction. J. Appl. Sci. Technol. Trends 2020, 1, 56–70. [Google Scholar] [CrossRef]
- Suman, S.K.; Kumar, A. Investigation and Implementation of Model Order Reduction Technique for Large Scale Dynamical Systems. Arch. Comput. Methods Eng. 2022, 29, 3087–3108. [Google Scholar] [CrossRef]
- Benagri, I.; Haidi, T.; Derri, M.; Elmariami, F.; Mellouli, E.M.; Bouabdallaoui, D. Electric Motor Control Methods and Improvements Applied to Electric Vehicles: A State of the Art. In Proceedings of the 2024 4th International Conference on Innovative Research in Applied Science, Engineering and Technology, IRASET 2024, Fez, Morocco, 16–17 May 2024. [Google Scholar] [CrossRef]
- Texas Instruments C2000 Real-Time Microcontrollers. Available online: https://www.ti.com/microcontrollers-mcus-processors/c2000-real-time-control-mcus/products.html (accessed on 11 October 2024).
- Costin, M.; Lazar, C. Field-Oriented Predictive Control Structure for Synchronous Reluctance Motors. Machines 2023, 11, 682. [Google Scholar] [CrossRef]
- AUTOSAR. AUTOSAR CP Standard: Specification of Interpolation Functions Library, 2023. Available online: https://www.autosar.org/fileadmin/standards/R23-11/CP/AUTOSAR_CP_SWS_IFLLibrary.pdf (accessed on 11 October 2024).
- Veeser, F.; Braun, T.; Kiltz, L.; Reuter, J. Nonlinear modelling, flatness-based current control, and torque ripple compensation for interior permanent magnet synchronous machines. Energies 2021, 14, 1590. [Google Scholar] [CrossRef]
- Di Tommaso, A.O.; Miceli, R.; Nevoloso, C.; Scaglione, G.; Schettino, G. Improved High-Fidelity IPMSM mathematical model Including Saturation, Cross-Coupling, Torque Ripple and Iron Loss effects. In Proceedings of the 2022 International Conference on Electrical Machines, ICEM 2022, Valencia, Spain, 5–8 September 2022; pp. 21–27. [Google Scholar] [CrossRef]
- Tavana, N.R.; Dinavahi, V. Real-Time Nonlinear Magnetic Equivalent Circuit Model of Induction Machine on FPGA for Hardware-in-the-Loop Simulation. IEEE Trans. Energy Convers. 2016, 31, 520–530. [Google Scholar] [CrossRef]
- Asghari, B.; Dinavahi, V. Experimental validation of a geometrical nonlinear permeance network based real-time induction machine model. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–15. [Google Scholar] [CrossRef]
- Hemeida, A.; Lehikoinen, A.; Rasilo, P.; Vansompel, H.; Belahcen, A.; Arkkio, A.; Sergeant, P. A Simple and Efficient Quasi-3D Magnetic Equivalent Circuit for Surface Axial Flux Permanent Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2019, 66, 8318–8333. [Google Scholar] [CrossRef]
- Liu, J.; Dinavahi, V. Detailed Magnetic Equivalent Circuit Based Real-Time Nonlinear Power Transformer Model on FPGA for Electromagnetic Transient Studies. IEEE Trans. Ind. Electron. 2016, 63, 1191–1202. [Google Scholar] [CrossRef]
- Seilmeier, M.; Piepenbreier, B. Modeling of PMSM with multiple saliencies using a stator-oriented magnetic circuit approach. In Proceedings of the 2011 IEEE International Electric Machines & Drives Conference (IEMDC), Niagara Falls, ON, Canada, 15–18 May 2011; pp. 131–136. [Google Scholar] [CrossRef]
- Faustner, D.; Kemmetmüller, W.; Kugi, A. Magnetic equivalent circuit modeling of a saturated surface-mounted permanent magnet synchronous machine. IFAC-PapersOnLine 2015, 48, 360–365. [Google Scholar] [CrossRef]
- Forstner, G.; Kugi, A.; Kemmetmuller, W. A Magnetic Equivalent Circuit Based Modeling Framework for Electric Motors Applied to a PMSM with Winding Short Circuit. IEEE Trans. Power Electron. 2020, 35, 12285–12295. [Google Scholar] [CrossRef]
- Forstner, G.; Kugi, A.; Kemmetmüller, W. Fault-tolerant torque control of a three-phase permanent magnet synchronous motor with inter-turn winding short circuit. Control Eng. Pract. 2021, 113, 104846. [Google Scholar] [CrossRef]
- Shimotani, T.; Sato, Y.; Igarashi, H. Direct synthesis of equivalent circuits from reduced FE models using proper orthogonal decomposition. COMPE-Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 2035–2044. [Google Scholar] [CrossRef]
- Bossavit, A. Computational Electromagnetism: Variational Formulations, Complementarity, Edge Elements; Academic Press: Cambridge, MA, USA, 1998; p. 352. [Google Scholar]
- Schilders, W. Introduction to Model Order Reduction. In Model Order Reduction: Theory, Research Aspects and Applications; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–32. [Google Scholar] [CrossRef]
- Antoulas, A.C.; Sorensen, D.C.; Gugercin, S. A Survey of Model Reduction Methods for Large-Scale Systems. Contemp. Math. 2001, 280, 193–220. [Google Scholar] [CrossRef]
- Ammar, A.; Mokdad, B.; Chinesta, F.; Keunings, R.; Ammar, A.; Mokdad, B.; Chinesta, F.; Keunings, R. A New Family of Solvers for Some Classes of Multidimensional Partial Differential Equations Encountered in Kinetic Theory Modeling of Complex Fluids A New Family of Solvers for Some Classes of Multidimensional Partial Differential Equations Encountered in Kinetic Theory Modeling of Complex Fluids A new family of solvers for some classes of multidimensional partial differential equations encountered in kinetic theory modeling of complex fluids. J. Non-Newton. Fluid Mech. 2006, 139, 153–176. [Google Scholar] [CrossRef]
- Sato, Y.; Shimotani, T.; Igarashi, H. Synthesis of Cauer-Equivalent Circuit Based on Model Order Reduction Considering Nonlinear Magnetic Property. IEEE Trans. Magn. 2017, 53, 1100204. [Google Scholar] [CrossRef]
- Moore, B.C. Principal Component Analysis in Linear Systems: Controllability, Observability, and Model Reduction. IEEE Trans. Autom. Control 1981, 26, 17–32. [Google Scholar] [CrossRef]
- Fujimoto, K.; Scherpen, J.M.A. Singular Value Analysis and Balanced Realizations for Nonlinear Systems. In Model Order Reduction: Theory, Research Aspects and Applications; Springer: Berlin/Heidelberg, Germany, 2008; pp. 251–272. [Google Scholar] [CrossRef]
- Glover, K. All optimal Hankel-norm approximations of linear multivariable systems and their L∞ -error bounds. Int. J. Control 1984, 39, 1115–1193. [Google Scholar] [CrossRef]
- Scherpen, J.M.A. Balancing for nonlinear systems. Syst. Control Lett. 1993, 21, 143–153. [Google Scholar] [CrossRef]
- Kerler-Back, J.; Stykel, T. Balanced truncation model reduction for 3D linear magneto-quasistatic field problems. In Realization and Model Reduction of Dynamical Systems: A Festschrift in Honor of the 70th Birthday of Thanos Antoulas; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Liang, Y.C.; Lee, H.P.; Lim, S.P.; Lin, W.Z.; Lee, K.H.; Wu, C.G. Proper orthogonal decomposition and its applications-Part I: Theory. J. Sound Vib. 2002, 252, 527–544. [Google Scholar] [CrossRef]
- Chatterjee, A. An introduction to the proper orthogonal decomposition. Curr. Sci. 2000, 78, 808–817. [Google Scholar]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering Machine Learning, Dynamical Systems, and Control; Technical Report; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Boumesbah, A.E.; Martin, F.; Krebs, G.; Belahcen, A.; Marchand, C. Comparison of Model Order Reduction Methods for a Switched Reluctance Machine Characterization. IEEE Trans. Magn. 2021, 57, 7400906. [Google Scholar] [CrossRef]
- Henneron, T.; Clenet, S. Model order reduction of non-linear magnetostatic problems based on POD and DEI methods. IEEE Trans. Magn. 2014, 50, 33–36. [Google Scholar] [CrossRef]
- Montier, L.; Pierquin, A.; Henneron, T.; Clenet, S. Structure Preserving Model Reduction of Low-Frequency Electromagnetic Problem Based on POD and DEIM. IEEE Trans. Magn. 2017, 53, 7205204. [Google Scholar] [CrossRef]
- Henneron, T.; Clenet, S. Model-Order Reduction of Multiple-Input Non-Linear Systems Based on POD and DEI Methods. IEEE Trans. Magn. 2015, 51, 7207104. [Google Scholar] [CrossRef]
- Farzamfar, M.; Belahcen, A.; Rasilo, P.; Clenet, S.; Pierquin, A. Model Order Reduction of Electrical Machines With Multiple Inputs. IEEE Trans. Ind. Appl. 2017, 53, 3355–3360. [Google Scholar] [CrossRef]
- Paul, S.; Chang, J. Fast numerical analysis of electric motor using nonlinear model order reduction. IEEE Trans. Magn. 2018, 54, 8101404. [Google Scholar] [CrossRef]
- Hollaus, K.; Schöberl, J.; Schöbinger, M. MSFEM and MOR to Minimize the Computational Costs of Nonlinear Eddy-Current Problems in Laminated Iron Cores. IEEE Trans. Magn. 2020, 56, 7508104. [Google Scholar] [CrossRef]
- Henneron, T.; Mac, H.; Clénet, S. Error estimation of a proper orthogonal decomposition reduced model of a permanent magnet synchronous machine. IET Sci. Meas. Technol. 2015, 9, 172–177. [Google Scholar] [CrossRef]
- Farzam Far, M.; Martin, F.; Belahcen, A.; Montier, L.; Henneron, T. Orthogonal Interpolation Method for Order Reduction of a Synchronous Machine Model. IEEE Trans. Magn. 2018, 54, 8100506. [Google Scholar] [CrossRef]
- Far, M.F.; Martin, F.; Belahcen, A.; Rasilo, P.; Awan, H.A.A. Real-Time Control of an IPMSM Using Model Order Reduction. IEEE Trans. Ind. Electron. 2021, 68, 2005–2014. [Google Scholar] [CrossRef]
- Okamoto, K.; Sakamoto, H.; Igarashi, H. Implementation of Simplified Model Order Reduction Based on POD for Dynamic Simulation of Electric Motors. In Proceedings of the 2019 22nd International Conference on the Computation of Electromagnetic Fields (COMPUMAG), Paris, France, 15–19 July 2019; Volume 56, pp. 1–4. [Google Scholar] [CrossRef]
- Sakamoto, H.; Okamoto, K.; Igarashi, H. Fast Analysis of Rotating Machine Using Simplified Model-Order Reduction Based on POD. IEEE Trans. Magn. 2020, 56, 7506104. [Google Scholar] [CrossRef]
- Croft, T.L.D. Proper Generalised Decompositions: Theory and Applications. Doctoral Dissertation, Cardiff University, Cardiff, UK, 2015. [Google Scholar]
- Nouy, A. A priori model reduction through Proper Generalized Decomposition for solving time-dependent partial differential equations. Comput. Methods Appl. Mech. Eng. 2010, 199, 1603–1626. [Google Scholar] [CrossRef]
- Henneron, T.; Clenet, S. Model order reduction of quasi-static problems based on POD and PGD approaches. Eur. Phys. J. Appl. Phys. 2013, 64, 24514. [Google Scholar] [CrossRef]
- Henneron, T.; Clenet, S. Application of the PGD and DEIM to Solve a 3-D Non-Linear Magnetostatic Problem Coupled With the Circuit Equations. IEEE Trans. Magn. 2016, 52, 7202104. [Google Scholar] [CrossRef][Green Version]
- Montier, L.; Henneron, T.; Clenet, S.; Goursaud, B. Proper Generalized Decomposition Applied on a Rotating Electrical Machine. IEEE Trans. Magn. 2018, 54, 7202604. [Google Scholar] [CrossRef]
- Sancarlos, A.; Ghnatios, C.; Duval, J.L.; Zerbib, N.; Cueto, E.; Chinesta, F. Fast Computation of Multi-Parametric Electromagnetic Fields in Synchronous Machines by Using PGD-Based Fully Separated Representations. Energies 2021, 14, 1454. [Google Scholar] [CrossRef]
- Muller, F.; Crampen, L.; Henneron, T.; Clenet, S.; Hameyer, K. Model Order Reduction Techniques applied to Magnetodynamic Scalar Potential Formulation. In Proceedings of the 2019 19th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering (ISEF), Nancy, France, 29–31 August 2019; pp. 1–2. [Google Scholar] [CrossRef]
- Müller, F.; Baumanns, P.; Nell, M.M.; Hameyer, K. Nonlinear parametric simulation by proper generalized decomposition on the example of a synchronous machine. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2022, 41, 1171–1180. [Google Scholar] [CrossRef]
- Muller, F.; Hameyer, K. Consideration of Rotational Motion in the Proper Generalized Decomposition by a Sliding Interface Technique. IEEE Trans. Magn. 2022, 58, 7400904. [Google Scholar] [CrossRef]
- Prokhorov, A.V. Moment Encyclopedia of Mathematics. Available online: https://encyclopediaofmath.org/index.php?title=Moment&oldid=55270 (accessed on 11 October 2024).
- Pillage, L.; Rohrer, R. Asymptotic waveform evaluation for timing analysis. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 1990, 9, 352–366. [Google Scholar] [CrossRef]
- Bai, Z.; Li, R.C.; Su, Y. A Unified Krylov Projection Framework for Structure-Preserving Model Reduction. In Model Order Reduction: Theory, Research Aspects and Applications; Schilders, W., van der Vorst, H., Rommes, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 13, pp. 75–93. [Google Scholar] [CrossRef]
- Feldmann, P.; Freund, R. Efficient linear circuit analysis by Pade approximation via the Lanczos process. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 1995, 14, 639–649. [Google Scholar] [CrossRef]
- Pierquin, A.; Henneron, T.; Clénet, S.; Brisset, S. Model order reduction of magnetoquasi-static problems based on pod and Arnoldi-based Krylov methods. IEEE Trans. Magn. 2015, 51, 7206204. [Google Scholar] [CrossRef]
- Benner, P.; Feng, L. Model order reduction based on moment-matching. In System- and Data-Driven Methods and Algorithms; De Gruyter: Berlin, Germany, 2021; pp. 57–96. [Google Scholar] [CrossRef]
- Rafiq, D.; Bazaz, M.A. Model Order Reduction via Moment-Matching: A State of the Art Review. Arch. Comput. Methods Eng. 2022, 29, 1463–1483. [Google Scholar] [CrossRef]
- Kameari, A.; Ebrahimi, H.; Sugahara, K.; Shindo, Y.; Matsuo, T. Cauer Ladder Network Representation of Eddy-Current Fields for Model Order Reduction Using Finite-Element Method. IEEE Trans. Magn. 2018, 54, 7201804. [Google Scholar] [CrossRef]
- Shindo, Y.; Sugahara, K.; Kameari, A.; Matsuo, T. Dynamical model of an electromagnet using cauer ladder network representation of eddy-current fields. IEEJ J. Ind. Appl. 2018, 7, 305–313. [Google Scholar] [CrossRef]
- Sankaran, K. Beyond DIV, CURL and GRAD: Modelling electromagnetic problems using algebraic topology. J. Electromagn. Waves Appl. 2017, 31, 121–149. [Google Scholar] [CrossRef]
- Matsuo, T.; Kameari, A.; Sugahara, K.; Shindo, Y. Matrix Formulation of the Cauer Ladder Network Method for Efficient Eddy-Current Analysis. IEEE Trans. Magn. 2018, 54, 7205805. [Google Scholar] [CrossRef]
- Shindo, Y.; Yamamoto, R.; Sugahara, K.; Matsuo, T.; Kameari, A. Equivalent Circuit in Cauer Form for Eddy Current Field including a Translational Mover. IEEE Trans. Magn. 2020, 56, 8101807. [Google Scholar] [CrossRef]
- Matsuo, T.; Fujiwara, T.; Kuriyama, K.; Sugahara, K.; Kameari, A.; Tokumasu, T.; Shindo, Y. Multi-Port Model Order Reduction Using a Matrix Cauer Ladder Network. IEEE Trans. Magn. 2020, 56, 7506905. [Google Scholar] [CrossRef]
- Matsuo, T.; Sugahara, K.; Kameari, A.; Shindo, Y. Model Order Reduction of an Induction Motor Using a Cauer Ladder Network. IEEE Trans. Magn. 2020, 56, 7514704. [Google Scholar] [CrossRef]
- Eskandari, H.; Gyselinck, J.; Matsuo, T. Eddy-Current Field Analysis in Laminated Iron Cores Using Multi-Scale Model Order Reduction. IEEE Trans. Magn. 2021, 57, 6301004. [Google Scholar] [CrossRef]
- Eskandari, H.; Matsuo, T. Comparison Study of First-Order Approximations of Nonlinear Eddy-Current Field Using Cauer Ladder Network Method. IEEE Trans. Magn. 2021, 57, 6300704. [Google Scholar] [CrossRef]
- Eskandari, H.; Gyselinck, J.; Matsuo, T. Nonlinear Multi-Scale Model Order Reduction of Eddy-Current Problems. IEEE Trans. Magn. 2022, 58, 6300305. [Google Scholar] [CrossRef]
- Tobita, M.; Matsuo, T. Nonlinear Model Order Reduction of Induction Motors Using Parameterized Cauer Ladder Network Method. IEEE Trans. Magn. 2022, 58, 8205504. [Google Scholar] [CrossRef]
- Tobita, M.; Matsuo, T. A model order reduction of hysteretic eddy-current fields in electric machines using Cauer ladder network method. AIP Adv. 2023, 13, 025208. [Google Scholar] [CrossRef]
- Hiruma, S.; Clenet, S.; Igarashi, H.; Henneron, T.; Henneron Error Estimator for Cauer, T.; Clénet, S. Ladder Network Representation. IEEE Trans. Magn. 2022, 58, 7500904. [Google Scholar] [CrossRef]
- Koster, N.; Konig, O.; Biro, O. Proper Generalized Decomposition with Cauer Ladder Network Applied to Eddy Current Problems. IEEE Trans. Magn. 2021, 57, 6300904. [Google Scholar] [CrossRef]
- Ghnatios, C.; Rodriguez, S.; Tomezyk, J.; Dupuis, Y.; Mouterde, J.; Da Silva, J.; Chinesta, F. A hybrid twin based on machine learning enhanced reduced order model for real-time simulation of magnetic bearings. Adv. Model. Simul. Eng. Sci. 2024, 11, 3. [Google Scholar] [CrossRef]
- Comsol, A.B. Model Reduction in Comsol Multiphysics 6.0, 2021. Available online: https://doc.comsol.com/6.0/doc/com.comsol.help.comsol/comsol_ref_solver.32.009.html#1614687 (accessed on 11 October 2024).
- Pereira, S. How to Build Reduced Order Models of Computational Fluid Dynamics Simulations, Ansys blog. 2019. Available online: https://www.ansys.com/blog/how-to-build-reduced-order-model-cfd-simulations (accessed on 11 October 2024).
- Rewieński, M.; White, J. A trajectory piecewise-linear approach to model order reduction and fast simulation of nonlinear circuits and micromachined devices. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2003, 22, 155–170. [Google Scholar] [CrossRef]
- Qu, L.; Chapman, P. Extraction of low-order non-linear inductor models from a high-order physics-based representation. IEEE Trans. Power Electron. 2006, 21, 813–817. [Google Scholar] [CrossRef]
- Albunni, M.N.; Rischmuller, V.; Fritzsche, T.; Lohmann, B. Model order reduction of moving nonlinear electromagnetic devices. IEEE Trans. Magn. 2008, 44, 1822–1829. [Google Scholar] [CrossRef]
- Albunni, M.N. Model Order Reduction of Moving Nonlinear Electromagnetic Devices. Ph.D. Thesis, Technische Universitat München, Munchen, Germany, 2010. [Google Scholar]
- Nahvi, S.A.; Mashuq-un-Nabi; Janardhanan, S. Trajectory based methods for nonlinear MOR: Review and perspectives. In Proceedings of the 2012 IEEE International Conference on Signal Processing, Computing and Control, Solan, India, 15–17 March 2012; 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Kalra, S.; Nabi, M. TPWL Simulation of Large Nonlinear Circuits Using Subspace Angle-Based Adaptive Sampling. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 575–579. [Google Scholar] [CrossRef]
- Wang, C.; Yang, D.; Chen, Q. EI-MOR: A Hybrid Exponential Integrator and Model Order Reduction Approach for Transient Power/Ground Network Analysis. In Proceedings of the 2022 IEEE/ACM International Conference On Computer Aided Design (ICCAD), San Diego, CA, USA, 30 October–3 November 2022; pp. 1–8. [Google Scholar]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear model reduction via discrete empirical interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Chiampi, M.; Chiarabaglio, D.; Repetto, M. A Jiles-Atherton and fixed-point combined technique for time periodic magnetic field problems with hysteresis. IEEE Trans. Magn. 1995, 31, 4306–4311. [Google Scholar] [CrossRef]
- Shimotani, T.; Sato, Y.; Sato, T.; Igarashi, H. Fast Finite-Element Analysis of Motors Using Block Model Order Reduction. IEEE Trans. Magn. 2016, 52, 7207004. [Google Scholar] [CrossRef]
- Yamazaki, K.; Fukushima, N. Torque and loss calculation of rotating machines considering laminated cores using post 1-D analysis. In Proceedings of the Digests of the 2010 14th Biennial IEEE Conference on Electromagnetic Field Computation, Chicago, IL, USA, 9–12 May 2010; p. 1. [Google Scholar] [CrossRef]
- Sato, Y.; Clemens, M.; Igarashi, H. Adaptive Subdomain Model Order Reduction With Discrete Empirical Interpolation Method for Nonlinear Magneto-Quasi-Static Problems. IEEE Trans. Magn. 2016, 52, 1100204. [Google Scholar] [CrossRef]
- Montier, L.; Henneron, T.; Clénet, S.; Goursaud, B. Transient simulation of an electrical rotating machine achieved through model order reduction. Adv. Model. Simul. Eng. Sci. 2016, 3, 10. [Google Scholar] [CrossRef]
- Petrov, S. Model Order Reduction Algorithms in the Design of Electric Machines. In Large-Scale Scientific Computing; Lirkov, I., Margenov, S., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2020; Volume 11958. [Google Scholar] [CrossRef]
- Maierhofer, J.; Rixen, D.J. Model order reduction using hyperreduction methods (DEIM, ECSW) for magnetodynamic FEM problems. Finite Elem. Anal. Des. 2022, 209, 103793. [Google Scholar] [CrossRef]
- Farhat, C.; Chapman, T.; Avery, P. Structure-preserving, stability, and accuracy properties of the energy-conserving sampling and weighting method for the hyper reduction of nonlinear finite element dynamic models. Int. J. Numer. Methods Eng. 2015, 102, 1077–1110. [Google Scholar] [CrossRef]
- Maierhofer, J.; Dietz, C.; Zobel, O.M.; Rixen, D.J. Multiphysical Simulation, Model Order Reduction (ECSW) and Experimental Validation of an Active Magnetic Bearing. Actuators 2022, 11, 169. [Google Scholar] [CrossRef]
- Maierhofer, J.; Rixen, D.J. Computing Forces by ECSW-Hyperreduction in Nonlinear Magnetodynamic FEM Problems. IEEE Trans. Magn. 2024, 60, 7400113. [Google Scholar] [CrossRef]
- Delagnes, T.; Henneron, T.; Clenet, S.; Fratila, M.; Ducreux, J.P. Comparison of Hyper-Reduction Methods Combined with POD: Model Order Reduction of a Squirrel Cage Induction Machine in Nonlinear Case. IEEE Trans. Magn. 2024, 60, 7402010. [Google Scholar] [CrossRef]
- Marcsa, Z. Parallelized Finite Element Methods for Solving Coupled Electrodynamic Problems (in Hungarian). Ph.D. Thesis, Széchenyi István Egyetem, Győr, Hungary, 2018. [Google Scholar]
- Davat, B.; Ren, Z.; Lajoie-Mazenc, M. The Movement in Field Modeling. IEEE Trans. Magn. 1985, 21, 2296–2298. [Google Scholar] [CrossRef]
- Preston, T.W.; Reece, A.B.J.; Sangha, P.S. Induction Motor Analysis by Time-Stepping Techniques. IEEE Trans. Magn. 1988, 24, 471–474. [Google Scholar] [CrossRef]
- Muller, F.; Siokos, A.; Kolb, J.; Nell, M.; Hameyer, K. Efficient Estimation of Electrical Machine Behavior by Model Order Reduction. IEEE Trans. Magn. 2021, 57, 8105804. [Google Scholar] [CrossRef]
- Bontinck, Z.; Lass, O.; Rain, O.; Schöps, S. Model order reduction for rotating electrical machines. In Reduced-Order Modeling (ROM) for Simulation and Optimization: Powerful Algorithms as Key Enablers for Scientific Computing; Springer International Publishing: Cham, Switzerland, 2018; pp. 121–140. [Google Scholar] [CrossRef]
- Kurz, S.; Fetzer, J.; Lehner, G. Threedimensional transient BEM-FEM coupled analysis of electrodynamic levitation problems. IEEE Trans. Magn. 1996, 32, 1062–1065. [Google Scholar] [CrossRef]
- Montier, L.; Henneron, T.; Clenet, S.; Goursaud, B. Model Order Reduction Applied to a Linear Finite Element Model of a Squirrel Cage Induction Machine Based on POD Approach. IEEE Trans. Magn. 2021, 57, 8105204. [Google Scholar] [CrossRef]
- Tsukerman, I. Overlapping finite elements for problems with movement. In Proceedings of the 1992. Digests of Intermag. International Magnetics Conference, St. Louis, MO, USA, 13–16 April 1992; p. 70. [Google Scholar] [CrossRef]
- Krebs, G.; Henneron, T.; Clénet, S.; Le Bihan, Y. Overlapping finite elements used to connect non-conforming meshes in 3-D with a vector potential formulation. IEEE Trans. Magn. 2011, 47, 1218–1221. [Google Scholar] [CrossRef]
- Lange, E.; Henrotte, F.; Hameyer, K. A variational formulation for nonconforming sliding interfaces in finite element analysis of electric machines. IEEE Trans. Magn. 2010, 46, 2755–2758. [Google Scholar] [CrossRef]
- MORLab. sssMOR Toolbox. 2024. Available online: https://www.mathworks.com/matlabcentral/fileexchange/59169-sssmor-toolbox (accessed on 11 October 2024).
- MathWorks. Model Simplification. 2024. Available online: https://www.mathworks.com/help/control/model-simplification-1.html?s{_}tid=CRUX{_}lftnav (accessed on 11 October 2024).
- Milk, R.; Rave, S.; Schindler, F. pyMOR—Generic Algorithms and Interfaces for Model Order Reduction. SIAM J. Sci. Comput. 2016, 38, S194–S216. [Google Scholar]
- Zou, X.; Conti, M.; Díez, P.; Auricchio, F. A nonintrusive proper generalized decomposition scheme with application in biomechanics. Int. J. Numer. Methods Eng. 2018, 113, 230–251. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).