Abstract
Rapid advancements in electric vehicle (EV) technology have highlighted the importance of lithium-ion (Li) batteries. These batteries are essential for safety and reliability. Battery data show non-stationarity and complex dynamics, presenting challenges for current monitoring and prediction methods. These methods often fail to manage the variability seen in real-world environments. To address these challenges, we propose a Transformer model with a wavelet transform dynamic attention mechanism (WADT). The dynamic attention mechanism uses wavelet transform. It focuses adaptively on the most informative parts of the battery data to enhance the anomaly detection accuracy. We also developed a deep learning model with an improved Transformer architecture. This architecture is tailored for the complex dynamics of battery data time series. The model accounts for temporal dependencies and adapts to non-stationary behavior. Experiments on public battery datasets show our approach’s effectiveness. Our model significantly outperforms existing technologies with an accuracy of 0.89 and an AUC score of 0.88. These results validate our method’s innovation and effectiveness.
1. Introduction
With the rapid development of EV technology, the performance and safety of Li batteries as a core power source have received widespread attention [1,2,3]. The reliability of batteries directly affects the driving range, safety performance, and overall lifespan of EVs. Therefore, accurately monitoring the state of batteries and promptly detecting anomalies have become key technical challenges to ensure the safe operation of EVs. The non-stationarity and complex dynamics of battery charging data further increase the difficulty of monitoring, making traditional monitoring methods inadequate for practical applications [4,5].
Batteries exhibit non-stationarity and complex dynamics during the actual charging and discharging process. These characteristics reflect the complex processes of battery status changes over time, temperature, and usage conditions [6]. These nonlinear features make the monitoring and anomaly detection of the battery status extremely difficult [7,8]. Existing methods often fail to accurately identify minor changes and potential faults in batteries, leading to the ineffective prediction and prevention of battery failures.
In the field of battery state monitoring and anomaly detection, researchers have proposed numerous approaches, including methods based on physical modeling as well as strategies utilizing data-driven deep learning [9,10].
However, existing methods often fail to adequately consider the non-stationarity and complex dynamics of battery data. Physical models, which are constructed based on the chemical and physical laws of batteries, theoretically provide a basis for predicting and interpreting battery states [11,12]. Ref. [13] introduced an early soft internal short-circuit fault diagnosis method for lithium-ion battery packs in electric vehicles, utilizing incremental capacity curves and local outlier factor analysis to identify short-circuit faults at an early stage and accurately locate the faulty cells. Ref. [14] proposed a voltage correlation-based principal component analysis method, calculating the correlation coefficients between adjacent battery cells and setting thresholds for real-time fault monitoring, with an accumulative relative contribution plot algorithm to isolate and locate faulty cells. Ref. [15] presented a fault diagnosis method for lithium-ion batteries based on signal analysis and manifold learning, achieving earlier and more robust fault detection by eliminating the impact of state inconsistency and using clustering-based anomaly detection. Nevertheless, these models frequently demonstrate their limitations when confronted with the complexity of battery behavior in real-world applications. Specifically, physical models typically assume that battery behavior adheres to certain theoretical formulas, but under actual operating conditions, variations in battery performance can significantly deviate from these predictions due to a myriad of factors, such as changes in temperature, charging and discharging rates, and the effects of long-term cyclic use on battery performance.
Meanwhile, although data-driven deep learning methods have the potential to learn patterns and correlations from historical data, demonstrating prowess in handling complex nonlinear relationships, these methods face their own set of challenges when dealing with battery data [16,17]. Ref. [18] proposed a combined model-based and data-driven fault diagnosis method for lithium-ion batteries, using a sliding mode observer to estimate sensor faults and a data-driven gap metric approach to detect battery internal resistance faults, thereby reducing the communication resource consumption and improving fault detection accuracy. Ref. [19] proposed a real-time unsupervised learning diagnosis method for early battery faults, using improved principal component analysis to rotate the voltage sequence and achieve real-time fault location and traceability for lithium-ion battery cells. However, traditional deep learning models, especially those designed for processing time-series data like recurrent neural networks (RNNs) and their variants, often have limitations in capturing the long-term dependencies and non-stationary dynamic changes of battery data [15]. This is because the complexity of battery data arises not only from the long-term dependencies in the time series but also includes short-term dynamic variations and nonlinear characteristics, which are crucial for predicting battery states and detecting anomalies.
In addressing the complex challenges of battery data monitoring and anomaly detection, we introduced an innovative deep learning framework that merges wavelet transform with dynamic attention mechanisms, creating a novel WADT. Furthermore, the framework incorporates a convolutional wavelet Transformer model based on WADT, named WACformer, enhancing the extraction and analysis of time–frequency features of battery data, thus effectively tackling the non-stationarity and accurately capturing its complex dynamic changes. Further integrating this WADT with an improved Transformer model, we introduced a convolutional front-feed neural network for the extraction of temporal information. This convolutional wavelet Transformer model, based on WADT, not only inherits the advantages of the Transformer architecture in processing time-series data but also, through the WADT mechanism, enhances the model’s capability to detect anomalies in battery charging and discharging data, ensuring both accuracy and reliability of detection.
The main contributions of this paper are as follows:
- (1)
- We propose a dynamic attention mechanism integrated with wavelet transform that can adapt to the non-stationarity and complex dynamics of battery data, facilitating precise feature extraction from battery charging and discharging data.
- (2)
- We propose the use of a convolutional feed-forward neural network as a replacement for the traditional feed-forward neural network in the Transformer architecture, aimed at modeling temporal relationships within battery charging and discharging sequences.
- (3)
- We propose the WACformer model, which is built upon the WADT and a convolutional feed-forward neural network, to achieve accurate anomaly detection in EV Li batteries.
The rest of this paper is organized as follows: Section 2 presents the latest research related to anomaly detection in EV Li batteries. Section 3 describes the WADT designed in this paper. Section 4 shows the structure of WACformer. In Section 5, we show the classification results of the proposed model with the existing optimal models and baselines on the datasets, ablation experiments. Finally, Section 6 summarizes this manuscript.
2. Related Work
2.1. Battery Fault Detection
Battery data fault detection technology plays a crucial role in ensuring the safe and stable operation of batteries and effectively prolonging their lifespan [20]. With the rapid proliferation of EVs and the extensive deployment of renewable energy systems in recent years, the demand for and research interest in battery fault detection technologies have significantly increased [21]. As a vital component of these systems, the stability and safety of battery performance directly impact the reliability and economic efficiency of the entire system. Researchers have been dedicatedly analyzing changes in key parameters such as voltage, current, and temperature during the actual use of batteries, striving to predict the health status and potential fault types of batteries [22]. This analytical approach relies not only on traditional theoretical research based on physical and chemical models but also includes data-driven research utilizing advanced machine learning and signal processing technologies.
Through these methods, researchers are able to extract valuable information from complex battery data, thereby enabling the early warning and accurate diagnosis of potential battery faults [23]. Despite the research achievements and technological advancements made in the field of battery fault detection, the inherent non-stationarity of battery data and their complex dynamics under varying operational conditions continue to pose significant challenges to accurate monitoring and diagnosis of battery faults. Batteries may be affected by various factors during their usage, such as charging and discharging cycles, temperature changes, and aging, all of which can lead to changes in battery performance and potential fault risks. Therefore, the development of efficient fault detection methods capable of accurately identifying and predicting these complex dynamic changes is essential for enhancing the safety and reliability of battery systems.
2.2. Traditional Battery Fault Detection Methods
Traditional battery fault detection methods are fundamentally based on physical and chemical models that aim to replicate the battery’s internal mechanisms, thereby predicting its performance outcomes and pinpointing potential fault scenarios [24,25,26]. These models stand out for providing a solid theoretical basis and a high level of interpretability, which is crucial for understanding battery behaviors under diverse operational conditions. However, the reliance on precise model parameters and the requirements for elaborate mathematical formulations present significant challenges [27]. These challenges are particularly evident in their limited capacity to adapt and respond to the intricate and unpredictable nature of real-world battery data, which are characterized by their inherent non-stationarity and dynamic fluctuations.
Moreover, the application of these traditional methods in practical scenarios is further hindered by their inability to efficiently process and analyze large volumes of data generated by modern battery systems [28]. This limitation not only restricts their effectiveness in accurately detecting battery faults but also constrains their utility in rapidly evolving technological environments where batteries are subjected to a wide array of external stresses and operational demands.
2.3. Deep Learning-Based Battery Fault Detection Method
In recent years, the rapid advancement of deep learning technologies has led to their increasingly widespread application in the domain of battery fault detection [29,30,31]. Deep learning methods, capable of autonomously learning features from extensive datasets without relying on intricate physical or chemical models, have demonstrated significant superiority in handling nonlinear and high-dimensional data [32]. This is particularly evident in the analysis of time-series data, where deep learning models such as convolutional neural networks (CNNs), recurrent neural networks (RNNs), and long short-term memory networks (LSTMs) have proven to be highly effective in addressing the temporal dependencies inherent in battery data [33]. More recently, the Transformer model, renowned for its powerful sequence modeling capabilities, has been introduced into the realm of battery fault detection, showcasing its potential in managing complex dynamics and long-range dependencies within the data.
The introduction of the Transformer model further expands the toolbox available for battery fault detection, with its self-attention mechanism enabling the model to weigh the importance of different parts of the input data differently. This is especially beneficial in understanding the long-term dependencies and complex relationships that are often present in battery operational data, which can be crucial for the early detection and diagnosis of faults.
Despite these advancements, effectively integrating deep learning methods with the unique characteristics of battery data to enhance the accuracy and robustness of fault detection remains an open research challenge. This includes optimizing model architectures to better suit battery data’s specificities, addressing issues related to data quality and availability, and developing techniques to interpret the models’ predictions in a meaningful way. Furthermore, the integration of domain knowledge into deep learning models presents a promising avenue for research, potentially leading to more accurate and interpretable models that can effectively predict a wider range of battery faults.
3. Dynamic Attention Mechanism Based on Wavelet Transform
In this section, we propose a novel dynamic attention mechanism that utilizes the wavelet transform for feature extraction and employs a scoring function based on spectral energy to dynamically assess the importance of features. This method is aimed at optimizing signal processing tasks, such as battery state detection, by emphasizing the most critical features to enhance the accuracy and efficiency of predictions. The structure of WADT is shown in Figure 1.
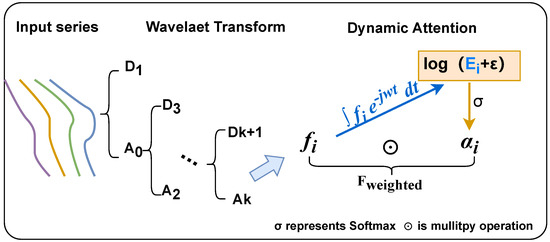
Figure 1.
The structure of WADT.
3.1. Feature Extraction
Firstly, we apply the discrete wavelet transform (DWT) to the input signal , to extract signal features at different time scales.
The DWT is used for feature extraction by decomposing a signal into its wavelet coefficients, which represent the signal at different scales and positions. The DWT of a signal can be mathematically represented as:
where:
- is the wavelet basis function, generated from the mother wavelet by scaling and translation: .
- j and k are integers that control the scale and translation of the wavelet, respectively.
- denotes the inner product of with , giving the wavelet coefficient at scale j and position k.
- is the complex conjugate of , assuming and can be complex-valued functions.
The wavelet coefficients obtained from DWT provide a multi-resolution analysis of the signal , capturing both its frequency and location information. This makes DWT an effective tool for feature extraction in signal processing tasks.
The step can be summarized as follows:
where represents a series of features extracted from the original signal through DWT.
3.2. Dynamic Attention Scoring
3.2.1. Spectral Energy Calculation
For each extracted feature , we first compute its spectral representation :
Then, the spectral energy of the feature is calculated by:
3.2.2. Scoring Function
Based on the spectral energy , we define the score function for each feature as:
where is a small constant to ensure numerical stability.
3.2.3. Dynamic Attention Weights
Using score , the dynamic attention weights for each feature are computed through the softmax function:
Thus, the weight for each feature reflects its relative importance in the current analysis task.
3.3. Attention-Weighted Feature Fusion
Finally, using the calculated dynamic attention weights , we perform a weighted fusion of all features to obtain the weighted feature representation :
This weighted feature representation emphasizes the most important features for the prediction task and can be directly used in subsequent classification or regression models to enhance model performance.
4. WACformer Model for Battery State Anomaly Detection
4.1. WACformer Overview
The WACformer model implements an advanced integrated architecture tailored for the specific analysis requirements of battery charge–discharge sequences. This architecture combines an encoder layer and a decoder layer, each enhanced with innovative strategies. The model extensively harnesses the previously described wavelet-based dynamic attention mechanism, which performs multi-scale analysis on the input sequences to efficiently extract information-rich features and dynamically assess their importance. This ensures focused attention on the most critical information. Additionally, WACformer introduces a novel design in the form of a convolutional feed-forward network (CFFN), which optimizes the model’s handling of temporal sequence data by capturing local temporal dependencies through convolutional layers. This approach, which combines efficient feature extraction with the precise modeling of temporal dependencies, demonstrates significant performance advantages in key applications such as battery state prediction. The model structure of WACformer is shown in Figure 2. To monitor the battery charge–discharge data, the WACformer model processes the voltage and current measurements from multiple EV samples as its primary input. By analyzing these parameters through its multi-scale wavelet-based attention mechanism, the model dynamically identifies deviations from normal operating patterns, enabling the early detection of potential faults and anomalies in the battery state.
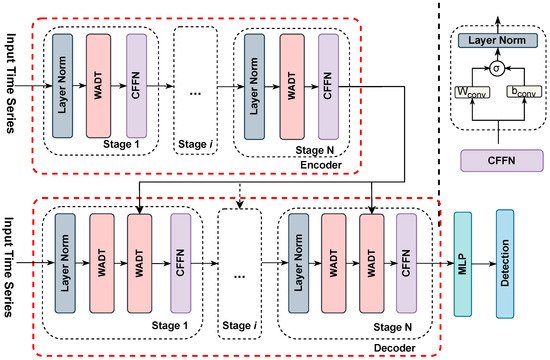
Figure 2.
The model structure of WACformer.
4.2. Encoder Layer
The encoder layer of WACformer processes the input sequence through a streamlined operation that encapsulates wavelet-based dynamic attention into a single comprehensive function:
Here, represents the wavelet-based attention Transformer function for the encoder, which encompasses both the discrete wavelet transform for feature extraction and the subsequent dynamic attention processing.
4.3. Decoder Layer
The decoder layer, tasked with interpreting the encoded features to generate predictions or analyses, similarly employs a wavelet-based attention mechanism, augmented with cross-attention to the encoder’s outputs:
In this formulation, is the wavelet-based attention Transformer function for the decoder, which integrates the encoded features with the decoder’s previous outputs to produce the final output sequence . The function seamlessly incorporates the dynamic attention mechanism and integrates information across the model via cross-attention.
4.4. Convolutional Feed-Forward Network (CFFN)
Integral to both the encoder and decoder architectures within the WACformer model, the convolutional feed-forward network (CFFN) plays a pivotal role in refining the representation of features, thereby capturing the temporal dynamics inherent in the sequence with enhanced precision. The mathematical formulation of the CFFN process is as follows:
Here, denotes the set of features that were processed by the wavelet-based dynamic attention mechanism within either the encoder or decoder, signifying an attention-modulated representation of the input sequence. The convolution operation * is applied between and a set of learnable convolutional filters , with representing the bias term. The function denotes a nonlinear activation function, commonly ReLU (rectified linear unit), which introduces nonlinearity into the feature processing, enabling the model to capture complex patterns within the data.
The convolutional layers within the CFFN are specifically designed to model temporal relationships by processing the sequence data in a manner that respects the locality of temporal features. This is achieved through the application of multiple convolutional filters that span different portions of the input, allowing the model to learn localized temporal features at various scales. The output represents the transformed feature set, which is subsequently fed into the next layer of the model.
This convolutional approach within the feed-forward network component of the WACformer model allows for a more nuanced understanding of the sequence data, leveraging spatial correlations to effectively model the temporal dependencies. This architectural innovation significantly enhances the model’s ability to process and interpret battery charge–discharge sequences, leading to more accurate predictions of battery states and other related outcomes.
Anomaly Detection Output Layer
After posting the decoder layer of the WACformer model, a specially devised output layer is utilized to discern anomalies in battery states, predicated on the processed sequence data. This output layer employs a deep learning-based classifier for predicting the presence of anomalies in battery states using the processed features emanating from the decoder layer:
Herein, signifies the model’s prognostication regarding the anomaly status of the battery state, inclusive of the probability distribution across disparate states. and , respectively, represent the weights and biases of the output layer, while the softmax function assures that the output values can be construed as probabilities.
The output layer not only furnishes direct predictions of the battery state but also ascertains potential anomaly patterns by learning intricate patterns within the sequence, thereby providing pivotal decision support for battery management systems.
In conclusion, the integration of the encoder and decoder layers combine with the innovative convolutional approach in the feed-forward layers, equips WACformer with the capability to model complex temporal relationships in battery charge–discharge sequences effectively. The model’s architecture, succinctly represented by and , offers a unified and efficient framework for processing sequential data, making it particularly suitable for applications requiring detailed temporal analysis, such as battery state prediction.
5. Experiments
In this section, we present a detailed assessment of the WACformer model’s capabilities by leveraging the publicly accessible EV dataset. We benchmark its detection efficacy against similar models. Furthermore, we offer a brief overview of the EV dataset, elucidate the rationale behind the choice of comparative models and baseline setups, detail the configuration of model parameters, and explain the conducted ablation studies. The outcomes of these experiments underscore WACformer’s enhanced performance relative to the models it was compared with.
5.1. Dataset
The dataset employed in this study encompasses EV data sourced from three distinct manufacturers, denote as Dahu, Socea, and Naobop. Each data point within the dataset represents the volume of data collected from a single vehicle over the span from its initial to its final charging record. Figure 3 illustrates typical features such as variations in battery voltage and current. The dataset used in this study is publicly available and validated for research purposes, accessible via the link (https://doi.org/10.6084/m9.figshare.23659323 (accessed on 20 September 2024)). The data were authentically collected from the vehicles, ensuring a realistic representation of real-world EV charging behaviors.
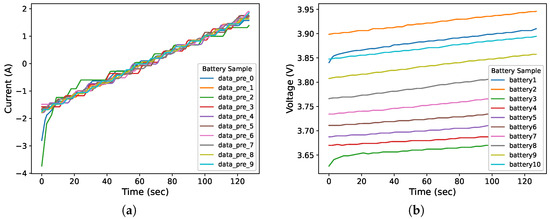
Figure 3.
Voltage and current variations during the charging of different batteries: (a) The voltage variation; and (b) The current variation.
5.2. Baselines and Evaluation Metrics
For the evaluation of the proposed WACformer model in detecting anomalies within EV battery datasets, we strategically selected a diverse set of 5 comparative models. These models encompass a broad spectrum of methodologies, including traditional machine learning as SVDD (support vector data description), GP (Gaussian process), deep learning as GDN (graph deviation network), AE (autoencoder), and domain-specific anomaly detection approaches as data-driven battery fault detection variant. Our selection criteria ensure a comprehensive comparison across various model architectures and capabilities. Each model is chosen based on its relevance to the task at hand and its potential to offer insightful comparisons with the WACformer model:
- GDN (graph deviation network): Introduces graph-based anomaly detection, well suited for relational data and capable of uncovering intricate patterns of deviations.
- AE (autoencoder): Serves as a baseline in many anomaly detection tasks, with its capacity to model normal behavior and identify outliers based on reconstruction errors.
- SVDD (support vector data description): Represents classical boundary-based anomaly detection, offering a strong comparison point for evaluating the sensitivity of WACformer in distinguishing outliers.
- GP (Gaussian process): Brings a probabilistic perspective to time-series modeling, valuable for assessing WACformer’s performance in capturing uncertainty and variability in battery data.
- Data-driven variant: Provides a domain-specific benchmark, reflecting the practical challenges and nuances of battery fault detection.
Through this comprehensive selection, our analysis aims not only to benchmark the performance of WACformer against established methods but also to underscore its advancements in the context of EV battery anomaly detection. Each model’s unique approach to handling time-series data and anomalies provides a robust framework for evaluating the effectiveness and innovation of WACformer within this specialized domain.
Metrics: In evaluating the model performance, especially in anomaly detection tasks, AUC (area under the curve) and ROC (receiver operating characteristic curve) serve as critical metrics. The essential calculations involved are as follows:
TPR (true positive rate) and FPR (false positive rate) form the foundation for constructing the ROC curve.
The ROC curve represents the model’s diagnostic ability by plotting TPR against FPR at various threshold settings. The area under the ROC curve (AUC) provides a single scalar value quantifying model performance.
5.3. Experimental Setup
The WACformer model has been developed using Python 3.7 and PyTorch 1.7 frameworks, with training conducted on an Nvidia RTX 3090 GPU for optimized performance. The initialization of all model weight parameters is performed utilizing the Xavier initialization method, with the gain parameter specifically adjusted to 1.2 for enhanced training stability. Detailed configurations of the model are outlined in Table 1, providing insights into the model’s setup and parameters.

Table 1.
Enhanced WACformer configuration.
5.4. Experimental Result
Comparison with existing methods: We performed a comprehensive evaluation of the WACformer model against a set of five comparative models on the EV battery dataset. The comparison focuses on anomaly detection accuracy and robustness, as quantified by AUC and ROC metrics. Table 2 presents the metrics of all models. Figure 4 shows the ROC curves of different models.

Table 2.
Revised performance metrics of comparative models with precision.
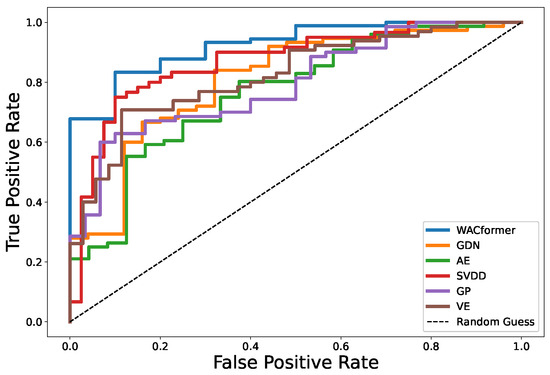
Figure 4.
ROC curves for different comparison models.
In our comprehensive evaluation of the WACformer model against a diverse set of comparative models on the EV battery dataset, focusing on anomaly detection accuracy and robustness, the performance metrics clearly highlight the superior capability of the WACformer model. As detailed in Table 2, the WACformer model outperforms all other models across the board, achieving the highest AUC score of 0.88, a TPR of 0.85, the lowest FPR of 0.08, and an impressive accuracy of 0.89.
GDN and AE models, while presenting as significant competitors, fall short with AUC scores of 0.70 and 0.72, respectively. The AE model, notably, shows a competitive edge with a TPR of 0.77 and an accuracy of 0.73, underlining its capacity as a reliable alternative for anomaly detection tasks. However, its performance does not reach the benchmark set by the WACformer model. The SVDD and GP models demonstrate moderate performance, with AUC scores of 0.51 and 0.66, respectively. Their lower TPR and higher FPR, compared to WACformer, indicate a reduced ability to accurately distinguish between normal and anomalous states within the EV battery dataset. The VE model, despite being a domain-specific anomaly detection approach, exhibits limited effectiveness with an AUC score of 0.55 and an accuracy of 0.62.
The analysis unequivocally establishes the WACformer model as the most proficient in identifying anomalies within EV battery datasets, underscoring its robustness and accuracy. The comprehensive metrics, including the AUC score, TPR, FPR, and accuracy, collectively affirm WACformer’s superior performance. This evaluation not only validates WACformer’s effectiveness in anomaly detection but also showcases its potential to set a new standard in the domain.
Ablation experiments: We conduct a thorough evaluation of the contributions of various components to its performance. The result of the ablation experiment is shown in Table 3. Figure 5 shows the ROC curves of ablation models.

Table 3.
Extended ablation study results including original transformer.
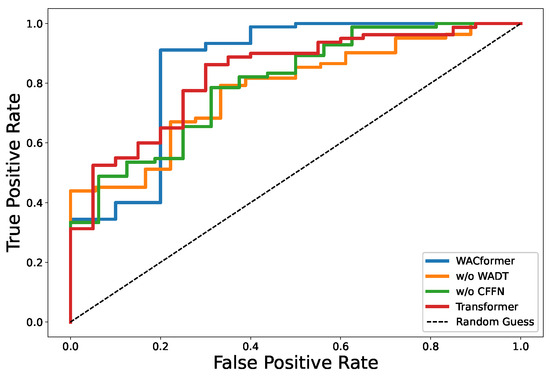
Figure 5.
ROC curves for different ablation models.
The extended ablation study meticulously evaluates the impact of various components within the WACformer model, focusing on anomaly detection in EV battery datasets. The results, as depicted in Table 3, offer insightful observations regarding the performance contributions of the WADT and the convolutional feed-forward network (CFFN), compared against the baseline performance of the original Transformer architecture.
The WACformer, showcasing an AUC score of 0.88, TPR of 0.85, FPR of 0.08, and an accuracy of 0.89, clearly outperforms the standard Transformer model. This indicates the effectiveness of the integrated components—WADT and CFFN—in enhancing the model’s ability to accurately detect anomalies within the dataset. The superior AUC and accuracy metrics highlight WACformer’s refined sensitivity and specificity in identifying true anomalies while minimizing false alarms, an essential aspect of robust anomaly detection systems.
Removing WADT from WACformer results in a notable decrease in performance, with AUC dropping to 0.82 and accuracy to 0.83. This suggests that WADT plays a crucial role in the model’s overall performance, likely due to its ability to efficiently capture and utilize the temporal and frequency domain information inherent in EV battery data for improved anomaly detection. Similarly, the exclusion of CFFN leads to a reduction in performance metrics, albeit to a lesser extent than removing WADT. With an AUC of 0.84 and accuracy of 0.85, the model still surpasses the original Transformer, suggesting that while CFFN contributes to enhancing model performance, its impact is somewhat less critical than WADT’s. The original Transformer model, without the specialized components tailored for EV battery anomaly detection, demonstrates the baseline performance with an AUC of 0.80 and accuracy of 0.81. While it serves as a solid foundation, the comparative analysis clearly illustrates the value added by WACformer’s custom components.
In conclusion, the ablation study underscores the significance of the WADT and CFFN components in the WACformer model, demonstrating their vital contributions to improving anomaly detection performance. The study not only validates the design choices made in developing WACformer but also showcases its superiority over conventional Transformer models in the context of EV battery anomaly detection.
Wavelet transform experiments: To assess the impact of different wavelet transforms on our model’s performance, we conducted an extensive evaluation. The results of these experiments are summarized in Table 4. Additionally, the ROC curves for models utilizing various wavelet transforms are depicted in Figure 6.

Table 4.
Performance comparison of different wavelet transforms in WACformer.
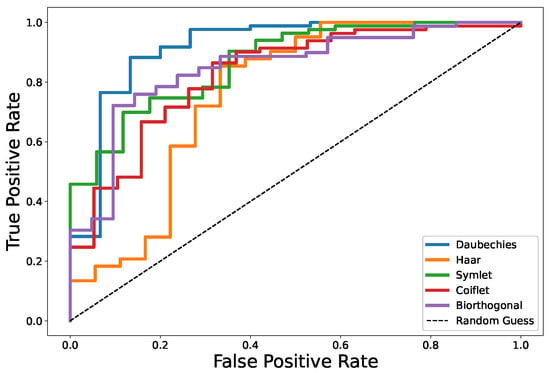
Figure 6.
ROC curves for different wavelet transforms.
In the evaluation of the WACformer model through the lens of various wavelet transforms, our experimental results elucidate the significant impact that the choice of wavelet transform has on the performance of anomaly detection in battery data. Among the wavelet transforms tested, the Daubechies wavelet transform exhibited a superior performance across all evaluated metrics, achieving an AUC score of 0.88, a TPR of 0.85, an FPR of 0.08, and an accuracy of 0.89. This result underscores the Daubechies wavelet’s adeptness at capturing the intricate balance between low-frequency components and high-frequency details inherent in battery data, thereby facilitating a more nuanced anomaly detection.
The Haar wavelet transform, characterized by its simplicity and direct approach to representing data changes, also demonstrated a commendable performance but was slightly outperformed by the Daubechies wavelet. With an AUC score of 0.85, a TPR of 0.82, an FPR of 0.10, and an accuracy of 0.86, the Haar wavelet proves effective yet slightly less nuanced in handling the complexities of battery data anomalies compared to the Daubechies wavelet.
Symlet, presenting a marginally smoother approach than the Haar and achieving a slightly better balance between waveform symmetry and transient feature capture, yielded an AUC of 0.86, a TPR of 0.83, an FPR of 0.09, and an accuracy of 0.87. This indicates a subtle improvement over the Haar wavelet, attributed to its enhanced ability to process the finer details within the time-series data.
Conversely, the Coiflet wavelet transform, despite its design for higher smoothness and detail capture, resulted in an AUC score of 0.84, a TPR of 0.81, an FPR of 0.11, and an accuracy of 0.85. Its performance suggests a slight compromise in effectively balancing anomaly detection against false positives compared to the leading Daubechies and Symlet wavelets.
Lastly, the biorthogonal wavelet transform, while still capable of identifying relevant features for anomaly detection, yielded the least favorable results with an AUC score of 0.82, a TPR of 0.79, an FPR of 0.14, and an accuracy of 0.83. This outcome highlights its relative inefficiency in maintaining an optimal balance between sensitivity and specificity in the detection process.
Collectively, these findings emphasize the critical role of selecting an appropriate wavelet transform in enhancing anomaly detection capabilities. The Daubechies wavelet transform, with its superior performance, emerges as the most effective for our WACformer model, particularly in the intricate task of battery anomaly detection. This comprehensive analysis not only validates the efficacy of incorporating wavelet transforms into the model architecture but also sheds light on the nuanced preferences that can further refine the accuracy and reliability of anomaly detection systems in complex time-series data applications.
6. Conclusions
In the evolving landscape of electric vehicle (EV) technology, our study introduces a novel approach for battery monitoring—a Transformer model with an integrated wavelet transform dynamic attention mechanism. This model adeptly handles the complexity and non-stationary nature of battery data, significantly enhancing anomaly detection. The integration of wavelet transform and dynamic attention within the Transformer architecture represents a groundbreaking advancement, offering unprecedented precision in monitoring and diagnosing battery states. Empirical evaluations on public datasets validate the superior performance of our model, showcasing substantial improvements in accuracy and AUC score over existing methods.
Author Contributions
Conceptualization, X.L.; Methodology, H.H.; Investigation, W.C. and Y.C.; Data curation, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This paper is supported by Regional Innovation and Development Joint Fund of the National Natural Science Foundation of China (U22A20225) and Major Science and Technology Project of Anhui Province (18030901064).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Wenjing Chang was employed by the State Grid Anhui Ultra High Voltage Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Romero, C.; Liu, Z.; Gordon, K.; Lei, X.; Joseph, K.; Broussard, E.; Gang, D.; Wei, Z.; Fei, L. FeS 2 deposited on 3D-printed carbon microlattices as free-standing electrodes for lithium-ion batteries. Chem. Commun. 2024, 60, 9085–9088. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Li, T.; Chang, C.; Yang, C.; Liao, L. Fault diagnosis method for lithium-ion batteries in electric vehicles based on isolated forest algorithm. J. Energy Storage 2022, 50, 104177. [Google Scholar] [CrossRef]
- Wang, Y.; Shang, Y.; Gu, X.; Li, J.; Zhang, C. An Incipient Multi-Fault Diagnosis Method for Lithium-Ion Battery Pack Based on Data-Driven with Incremental-Scale. IEEE Trans. Transp. Electrif. 2024; early access. [Google Scholar] [CrossRef]
- Sepasiahooyi, S.; Abdollahi, F. Fault Detection of New and Aged Lithium-ion Battery Cells in Electric Vehicles. Green Energy Intell. Transp. 2024, 3, 100165. [Google Scholar] [CrossRef]
- Li, Q.; Luo, H.; Cheng, H.; Deng, Y.; Sun, W.; Li, W.; Liu, Z. Incipient Fault Detection in Power Distribution System: A Time–Frequency Embedded Deep-Learning-Based Approach. IEEE Trans. Instrum. Meas. 2023, 72, 2507914. [Google Scholar] [CrossRef]
- Zhang, S.; Jiang, S.; Wang, H.; Zhang, X. A novel dual time-scale voltage sensor fault detection and isolation method for series-connected lithium-ion battery pack. Appl. Energy 2022, 322, 119541. [Google Scholar] [CrossRef]
- Jin, H.; Zhang, Z.; Ding, S.X.; Gao, Z.; Wang, Y.; Zuo, Z. Fault Diagnosis for Parallel Lithium-Ion Battery Packs with Main Current Sensor Fault and Internal Resistance Fault. IEEE Trans. Instrum. Meas. 2024, 73, 3521210. [Google Scholar] [CrossRef]
- Zhou, S.; Chen, Z.; Lin, T. Lithium-Ion Battery Cell Open Circuit Fault Diagnostics: Methods, Analysis, and Comparison. IEEE Trans. Power Electron. 2023, 38, 2493–2505. [Google Scholar] [CrossRef]
- Gan, N.; Sun, Z.; Zhang, Z.; Xu, S.; Liu, P.; Qin, Z. Data-Driven Fault Diagnosis of Lithium-Ion Battery Overdischarge in Electric Vehicles. IEEE Trans. Power Electron. 2022, 37, 4575–4588. [Google Scholar] [CrossRef]
- Shen, D.; Lyu, C.; Yang, D.; Hinds, G.; Ma, K.; Xu, S.; Bai, M. Concurrent multi-fault diagnosis of lithium-ion battery packs using random convolution kernel transformation and Gaussian process classifier. Energy 2024, 306, 132467. [Google Scholar] [CrossRef]
- Firoozi, R.; Sattarzadeh, S.; Dey, S. Cylindrical Battery Fault Detection under Extreme Fast Charging: A Physics-Based Learning Approach. IEEE Trans. Energy Convers. 2022, 37, 1241–1250. [Google Scholar] [CrossRef]
- Ma, M.; Li, X.; Gao, W.; Sun, J.; Wang, Q.; Mi, C. Multi-fault diagnosis for series-connected lithium-ion battery pack with reconstruction-based contribution based on parallel PCA-KPCA. Appl. Energy 2022, 324, 119678. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, L.; Deng, Z.; Xie, Y.; Couture, J.; Lin, X.; Zhou, J.; Hu, X. An Early Soft Internal Short-Circuit Fault Diagnosis Method for Lithium-Ion Battery Packs in Electric Vehicles. IEEE/ASME Trans. Mechatron. 2023, 28, 644–655. [Google Scholar] [CrossRef]
- Wang, G.; Yang, J.; Jiao, J. Voltage Correlation-Based Principal Component Analysis Method for Short Circuit Fault Diagnosis of Series Battery Pack. IEEE Trans. Ind. Electron. 2023, 70, 9025–9034. [Google Scholar] [CrossRef]
- Jiang, J.; Cong, X.; Li, S.; Zhang, C.; Zhang, W.; Jiang, Y. A Hybrid Signal-Based Fault Diagnosis Method for Lithium-Ion Batteries in Electric Vehicles. IEEE Access 2021, 9, 19175–19186. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, S.; Yang, Z.; He, Y. A multi-fault diagnosis method for lithium-ion battery pack using curvilinear Manhattan distance evaluation and voltage difference analysis. J. Energy Storage 2023, 67, 107575. [Google Scholar] [CrossRef]
- Shang, Y.; Wang, S.; Tang, N.; Fu, Y.; Wang, K. Research progress in fault detection of battery systems: A review. J. Energy Storage 2024, 98, 113079. [Google Scholar] [CrossRef]
- Jin, H.; Gao, Z.; Zuo, Z.; Zhang, Z.; Wang, Y.; Zhang, A. A Combined Model-Based and Data-Driven Fault Diagnosis Scheme for Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2024, 71, 6274–6284. [Google Scholar] [CrossRef]
- Gu, X.; Shang, Y.; Kang, Y.; Li, J.; Mao, Z.; Zhang, C. An Early Minor-Fault Diagnosis Method for Lithium-Ion Battery Packs Based on Unsupervised Learning. IEEECAA J. Autom. Sin. 2023, 10, 810–812. [Google Scholar] [CrossRef]
- Hardy, J.; Steggall, J.; Hardy, P. Rethinking lithium-ion battery management: Eliminating routine cell balancing enhances hazardous fault detection. J. Energy Storage 2023, 63, 106931. [Google Scholar] [CrossRef]
- Chatterjee, S.; Kumar Gatla, R.; Sinha, P.; Jena, C.; Kundu, S.; Panda, B.; Nanda, L.; Pradhan, A. Fault detection of a Li-ion battery using SVM based machine learning and unscented Kalman filter. Mater. Today Proc. 2023, 74, 703–707. [Google Scholar] [CrossRef]
- Ma, G.; Xu, S.; Cheng, C. Fault detection of lithium-ion battery packs with a graph-based method. J. Energy Storage 2021, 43, 103209. [Google Scholar] [CrossRef]
- Liu, X.; Wang, M.; Cao, R.; Lyu, M.; Zhang, C.; Li, S.; Guo, B.; Zhang, L.; Zhang, Z.; Gao, X.; et al. Review of abnormality detection and fault diagnosis methods for lithium-ion batteries. Automot. Innov. 2023, 6, 256–267. [Google Scholar] [CrossRef]
- Christensen, G.; Younes, H.; Hong, H.; Widener, C.; Hrabe, R.H.; Wu, J.J. Nanofluids as Media for High Capacity Anodes of Lithium-Ion Battery—A Review. J. Nanofluids 2019, 8, 657–670. [Google Scholar] [CrossRef]
- Zhang, S.; Li, J.; Li, R.; Zhang, X. Voltage sensor fault detection, isolation and estimation for lithium-ion battery used in electric vehicles via a simple and practical method. J. Energy Storage 2022, 55, 105555. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, C.; Li, J.; Xiong, R.; Pecht, M. Challenges and outlook for lithium-ion battery fault diagnosis methods from the laboratory to real world applications. eTransportation 2023, 17, 100254. [Google Scholar] [CrossRef]
- Sattarzadeh, S.; Roy, T.; Dey, S. Thermal fault detection and localization framework for large format batteries. J. Power Sources 2021, 512, 230400. [Google Scholar] [CrossRef]
- Qiu, Y.; Dong, T.; Lin, D.; Zhao, B.; Cao, W.; Jiang, F. Fault diagnosis for lithium-ion battery energy storage systems based on local outlier factor. J. Energy Storage 2022, 55, 105470. [Google Scholar] [CrossRef]
- Xue, Q.; Li, G.; Zhang, Y.; Shen, S.; Chen, Z.; Liu, Y. Fault diagnosis and abnormality detection of lithium-ion battery packs based on statistical distribution. J. Power Sources 2021, 482, 228964. [Google Scholar] [CrossRef]
- Zheng, Y.; Shen, A.; Han, X.; Ouyang, M. Quantitative short circuit identification for single lithium-ion cell applications based on charge and discharge capacity estimation. J. Power Sources 2022, 517, 230716. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Z.; Su, H. Fuzzy-kalman-filter-based short-circuit fault diagnosis design for lithium-ion battery. IEEE Trans. Ind. Electron. 2023, 71, 2883–2892. [Google Scholar] [CrossRef]
- Song, Y.; Yu, J.; Zhou, J.; Zhang, J.; Tang, D.; Yu, Z. Detection of Voltage Fault in Lithium-Ion Battery Based on Equivalent Circuit Model-Informed Neural Network. IEEE Trans. Instrum. Meas. 2024, 73, 1–10. [Google Scholar] [CrossRef]
- Xu, Y.; Ge, X.; Shen, W.; Yang, R. A Soft Short-Circuit Diagnosis Method for Lithium-Ion Battery Packs in Electric Vehicles. IEEE Trans. Power Electron. 2022, 37, 8572–8581. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).