Abstract
Existing single-stage planning and multi-stage non-rolling planning methods for distribution networks have problems such as low equipment utilization efficiency and poor investment benefits. In order to solve the above problems, this paper firstly proposes a multi-stage rolling planning method for distribution networks based on analyzing the limitations of the existing planning methods, which divides the planning cycle of the distribution network into multiple planning stages, and makes rolling amendments to the planning scheme of each stage according to the latest information during the planning cycle. Then, a multi-stage rolling planning model of distribution network taking into account conditional value at risk is established with the objective of minimizing the total investment and operation cost of the distribution network. On the one hand, the users’ electricity bill is taken into account in the objective function, and the necessity of this part of the benefits is demonstrated. On the other hand, the conditional value at risk is used to quantify the uncertainty of the operation cost in the process of the expansion planning of the distribution network, which reduces the operation cost risk of the distribution network. Next, this paper uses the rainflow counting method to characterize the capacity decay characteristics of energy storage in the distribution network, and proposes an iterative solution framework that considers energy storage capacity decay to solve the proposed model. Finally, the proposed method is applied to an 18-node distribution network planning case. This confirms that the multi-stage rolling planning method could improve the investment benefits and reduce the investment cost by approximately 27.27%. Besides, it will increase the total cost by approximately 2750 USD in the case if the users’ electricity bill is not taken into account. And the maximum capacity of energy storage may decay to 87.6% of the initial capacity or even lower during operation, which may cause the line current to exceed the limit if it is not taken into account.
1. Introduction
With the continuous growth of power load and the extensive access of distributed new energy resources, the traditional power distribution system has been developed significantly [1]. As an important part of the power system, scientific and reasonable planning of the distribution network is an important prerequisite to ensure its safe and economic operation [2]. However, on the one hand, with the continuous increase of distributed new energy resources in the distribution network, their uncertainty has brought great challenges to the grid expansion planning of the distribution network [3,4]. On the other hand, in the expansion planning of the distribution network, the existing single-stage planning and the multi-stage non-rolling planning methods have certain limitations, which limit the improvement of the investment benefits. Therefore, in order to improve the rationality and economy of distribution network construction, it is necessary to carry out an in-depth study on the expansion planning of distribution network based on the consideration of distributed new energy resources.
Depending on the number of planning stages, existing planning methods for distribution network expansion can be categorized into two types, namely single-stage planning methods [5,6,7] and multi-stage non-rolling planning methods [8,9,10]. The single-stage planning approach treats the entire planning cycle as one planning stage and develops a one-time planning program. For example, Yi et al. [5] established a joint expansion planning model of grid-storage for distribution network based on modified augmented relaxed optimal power flow, and determined the optimal planning scheme of grid-storage in the planning starting year. Xie et al. [6] took the distribution network planning cycle as a planning stage and established a coupled distribution system-transportation network (DS-TN) expansion planning model based on the coupling characteristics between the distribution system (DS) and the transportation network (TN), which optimized the planning scheme for DS and TN and improved the overall economy of the coupling system. The multi-stage non-rolling planning method divides the planning cycle into several planning stages and develops planning schemes for each stage separately. For example, Kabirifar et al. [8] divided the 15-year planning cycle of the distribution network into three planning stages, each of which is five years. Based on this, a multi-stage double-layer expansion planning model for the distribution network considering local energy market transactions is established, which realized the coordination of the various planning stages and improved the investment benefits. Feng et al. [9] divided the 21-year planning cycle of the distribution network into three planning stages on average. Based on this, a multi-stage expansion planning model of the distribution network considering the active management of distributed generation and network reconstruction was established, which improved the reliability and economy of the distribution network. However, the above methods have certain limitations. Although the single-stage planning method is widely used, the differentiated expansion demand in different planning years may lead to low equipment utilization efficiency and reduce the investment benefits. Furthermore, the investment benefits of the multi-stage non-rolling planning method is also subject to great uncertainty, as it is difficult for investors to accurately predict how various factors will change during the planning cycle. If rolling revisions can be made to the planning schemes of each stage based on the latest information during the planning cycle, it is expected to improve the utilization efficiency of equipment and improve investment benefits.
In addition, due to the strong coupling of planning and operation [11], the operation and scheduling of distribution networks is one of the core issues affecting their expansion planning. The operational objectives of distribution networks in existing studies include: maximizing the photovoltaic (PV) consumption rate [12], minimizing the total cost of expected energy not supplied [13], minimizing the total operating cost [14,15,16], etc. For example, Gao et al. [12] established a distribution network operation model with the objectives of maximum PV consumption rate and minimum standard deviation of line margin, which determined the operation strategy of the distribution network during the planning cycle, and provided a basis for the development of the distribution network planning scheme. Li et al. [15] established a distribution network operation model with the objective of minimizing total operating costs, taking into account multiple operating costs such as load shedding cost, the cost of purchasing power from the higher grid and PV abandonment cost. The power grid charges power transmission and distribution fee, called network fee, for providing power transmission and distribution services to users, which is an important part of the grid’s revenue. The network fee is roughly equal to the difference between the users’ electricity bill and the cost of purchasing power from the higher grid. However, when calculating the total operating costs, the existing studies often neglect the users’ electricity bill while taking into account the costs of purchasing power from the higher grid. If the active load shedding is not taken into account, the users’ electricity bill can be considered as a parameter and can be ignored. However, if the active load shedding is considered, the users’ electricity bill is related to the load shedding amount, which will affect the network fee, thus affecting the total operating cost of the distribution network and its expansion planning scheme. Therefore, the changes in network fee must be taken into account.
Energy storage plays an important role in the distribution network by using its energy transfer characteristics to peak shaving and valley filling, thereby delaying or avoiding the expansion of power lines. During the operation of energy storage, as the number of charge and discharge cycles increases, its maximum capacity will gradually decay, making its actual performance being lower than expected. However, existing researches on distribution network expansion planning [5,13,17] often overlook the capacity decay characteristics of energy storage and consider the maximum capacity of energy storage as a constant value. This may lead to investors overestimating the adjustment ability of energy storage, especially in the late stage of planning when the adjustment demand of energy storage is high and the capacity decay is severe, thereby affecting the distribution network expansion planning scheme and threatening the safe and economic operation of the distribution network. Therefore, it is necessary to consider the capacity decay characteristics of energy storage in the distribution network expansion planning research. Due to the complexity of the energy storage capacity decay process, it is difficult to include it in optimization models. Existing researches on energy storage planning and operation often does not consider the reduction of maximum energy storage capacity, but measures the loss caused by capacity decay through the capacity decay cost [18,19]. For example, Tang et al. [18] used a quadratic function of charge and discharge power to describe the loss caused by capacity decay. The method may play a good role in user side energy storage planning research, but it is not applicable to the distribution network expansion planning problem studied in this paper. Because the maximum energy storage capacity in this problem directly affects whether the line current exceeds the limit and determines the expansion planning scheme. It is difficult to calculate the loss caused by capacity decay through capacity decay cost. Therefore, it is necessary to consider the changes in the maximum energy storage capacity during the planning period.
To address the above problems, this paper analyses the limitations of the existing planning methods and proposes a multi-stage rolling planning method for distribution networks on this basis. Then, a multi-stage rolling planning model for distribution networks considering conditional value at risk (CVaR) is established with the objective of minimizing the total planning and operating cost of distribution network. The users’ electricity bill is included in the objective function. And the operating cost uncertainty in the distribution network expansion planning process is quantified by CVaR. The capacity decay characteristics of energy storage in the distribution network are characterized by rainflow counting method. Next, an iterative solution framework considering energy storage capacity decay is proposed to solve the proposed model. Finally, an 18-node distribution network is used as an example to verify the effectiveness of the proposed method. The comparison of the work of this paper with other works from the literature is shown in Table 1. And the research framework of this paper is shown in Figure 1.

Table 1.
The comparison of the work of this paper with other works.
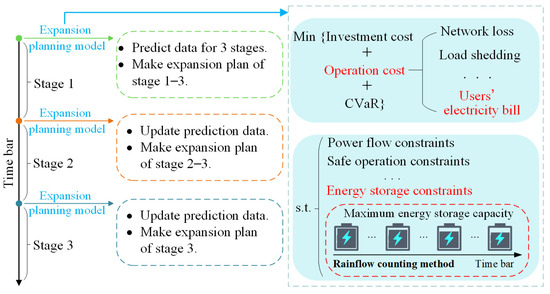
Figure 1.
Research framework.
The main innovation points of this paper are as follows.
- (1)
- For the problems of poor investment benefits and low equipment utilization efficiency of the existing distribution network expansion planning methods, this paper proposes a multi-stage rolling planning method for distribution networks, which can make rolling amendments to the planning scheme of each stage according to the latest information during the planning cycle and helps to improve the reasonableness and economy of the distribution network planning scheme.
- (2)
- For the problem that the existing distribution network expansion planning studies neglect the changes in network fee, this paper incorporates the users’ electricity bill into the objective function of the distribution network planning model and demonstrates the necessity of taking into account this part of the revenue. So that the operating cost of the distribution network can be calculated more accurately, and a more economic and reasonable expansion planning scheme can be formulated.
- (3)
- For the problem that the existing distribution network expansion planning studies neglect the capacity decay characteristics of energy storage, this paper uses the rainflow counting method to accurately characterize the capacity decay characteristics of energy storage and proposes an iterative solution framework that considers energy storage capacity decay to solve the proposed model, which helps optimize the distribution network expansion planning scheme and ensure the safe and economic operation of the distribution network.
The rest of this paper is structured as shown below. Section 2 analyses the limitations of existing single-stage planning and multi-stage non-rolling planning methods, and then proposes a multi-stage rolling planning method for distribution networks on this basis. Section 3 constructs a multi-stage rolling planning model for distribution networks taking into account CVaR. The model solving method is proposed in Section 4. Section 5 conducts numerical experiments on various cases to verify the feasibility and validity of the proposed method. In Section 5, several sets of simulations are carried out to verify the effectiveness of the proposed method. Finally, conclusions and future research directions are given in Section 6.
2. Multi-Stage Rolling Grid Expansion Planning for Distribution Networks
Most of the existing distribution network expansion planning uses single-stage planning or multi-stage non-rolling planning methods, this chapter first analyses the limitations of the existing planning methods and then introduces the multi-stage rolling planning method proposed in this paper.
2.1. Analysis of the Limitations of Existing Planning Methods
The single-stage planning method develops a one-time planning scheme in the starting year of planning, based on the prediction of various factors during the planning cycle, such as load growth and the capacity changes of wind turbine (WT), PV and energy storage. The single-stage planning is simple, effective and widely used, but there are some disadvantages when it is applied to distribution network expansion planning. Because the planning cycle of distribution network expansion planning is generally longer, customer loads may increase significantly during the planning cycle. Taking a certain line as an example, its annual maximum current during the planning cycle is shown in Figure 2. It can be seen that whether the line is expanded or not mainly depends on the maximum current in the late planning period. And if the line is expanded in the starting year of planning cycle accordingly, the line will always be in a low load rate state in the early and middle stages of planning periods, which leads to low equipment utilization efficiency and poor investment benefits.
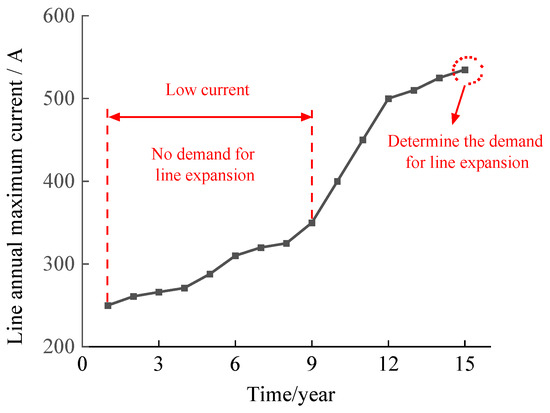
Figure 2.
Annual maximum current of a certain line during the planning period.
The multi-stage non-rolling planning method divides the planning cycle into several planning stages, and then formulates the planning scheme for each stage in the starting year of planning, based on the forecasting results of the various factors during the planning cycle. To a certain extent, multi-stage non-rolling planning can resolve the conflicts caused by the differentiated expansion needs in different planning years, increasing the efficiency of equipment utilization and improving the investment benefits. However, it is difficult for investors to accurately predict the changes of various factors over long-time scales. And when the development trends of various factors do not match the predicted results, the applicability of the planning schemes for each stage formulated in the starting year of planning will be greatly reduced.
2.2. Multi-Stage Rolling Planning Method
To address the limitations of the existing planning methods, this paper proposes a multi-stage rolling planning method for the distribution network, which divides the planning cycle of the distribution network into multiple stages and makes rolling amendments to the extended planning scheme in the initial year of each stage. The schematic diagram of the proposed method is shown in Figure 1. Distribution network expansion planning is typically defined over a planning horizon of 5–20 years. [20] In this paper, three planning stages are considered, and each planning stage is three years.
Multi-stage rolling planning makes it possible, on the one hand, to coordinate the differentiated needs for line expansion at different planning stages and to improve the efficiency of equipment utilization; on the other hand, it makes it possible to amend the expansion planning scheme as the changing characteristics of the factors become clearer and to improve the effectiveness of the investment.
3. Multi-Stage Rolling Grid Expansion Planning Model for Distribution Networks Considering CVaR
3.1. Objective Function
The multi-stage rolling planning model for the distribution network takes into account CVaR and minimizes the net present value of the total cost of planning and operating of the distribution network as the objective function, which determines the expansion planning scheme of the distribution network, the scheduling strategy for flexible resources such as WT, PV, and energy storage, the load shedding scheme, and the strategy for purchasing power from the higher grid. The total cost taking into account CVaR includes the investment cost of the expanded line, the operating cost of the distribution network, and CVaR, as shown in Equation (1).
where is the risk appetite coefficient, the value of which reflects the level of risk aversion of the decision-maker, and the larger its value, the higher the risk aversion level of the decision-maker.
- (1)
- The investment cost of the expanded lines is defined in Equation (2).
- (2)
- The operating cost of the distribution network consists of six parts, including network loss cost , load shedding cost , PV abandonment cost , WT abandonment cost , cost of purchasing electricity from the higher grid , and the users’ electricity bill , as shown in Equations (3)–(9).
At the same time, it is noted that both and in Equation (9) are input parameters in the model, so this part has no influence on the formation of the optimal expansion planning scheme for the distribution network. Equation (9) can be simplified and merged with Equation (5) to obtain a new objective function, as shown in Equation (10).
where is the simplified load shedding cost under scene w in year k.
According to Equations (9) and (10), if load shedding is not considered, the users’ electricity bill can be regarded as a parameter, which has no impact on the optimal solution of the model and can be ignored. However, if load shedding is taken into account, the users’ electricity bill is related to the load shedding amount, which can also be regarded as the unit cost of load shedding increases. It will have an impact on the total operating cost of the distribution network, thus affecting the formation of the expansion planning scheme. So, the users’ electricity bill must be included in the objective function.
3.2. Constraints
The development of expansion planning schemes and dispatch and operation strategies for distribution networks requires consideration of constraints such as investment constraints, nodal power balance constraints, power flow constraints, safe operation constraints, load shedding constraints, energy storage constraints, distributed power output constraints, and CVaR constraints.
- (1)
- Investment constraints
The line to be expanded is expanded only once in the planning cycle and only in the starting year of each planning stage, so the line investment constraint can be expressed by Equation (11).
- (2)
- Nodal power balance constraints
Each node of the distribution network should satisfy the nodal power balance constraints. The inflow power of each node is equal to the outflow power, as shown in Equations (12) and (13).
where and are the net active load and net reactive load of node i under scene w at time t in year k, respectively; and are the set of lines with node i as the head and end, respectively; and are the active power and reactive power flowing from node i to node j under scene w at time t in year k, respectively; and are the reactive load and the reactive power injected by the higher grid of node i under scene w at time t in year k, respectively; is the reactance of line ij; , , , and are the charging and discharging power of energy storage, and the reactive power of PV and WT of node i under scene w at time t in year k, respectively.
- (3)
- Power flow constraints
In this paper, the distribution network power flow is constrained by second-order cone relaxation [21,22], as shown in Equations (14)–(16).
where and are the auxiliary variables introduced by the second-order cone model related to the node voltage and line current; and are the voltage at node i and the current in line ij under scene w at time t in year k, respectively; (·)2 is the Euclidean norms.
- (4)
- Safe operation constraints
The normal operation of the distribution network needs to satisfy the security constraints. The node voltages, line currents, and power purchased from the higher grid need to be within a certain range, as shown in Equations (17)–(19).
where and are the squares of the upper and lower voltage limits at node i; and are the squares of the maximum current of line ij before and after the expansion; is the distribution capacity of the substation at node i.
- (5)
- Load shedding constraints
Some power users can participate in demand-side response by signing an agreement with the distribution network operator, who can reduce the user load to ensure the safe and stable operation of the power grid, and give the users a certain amount of economic compensation according to the amount of load shedding [23]. The amount of load shedding shall not exceed a certain percentage of the user load, as shown in Equation (20).
where is the maximum load shedding rate.
- (6)
- Energy storage constraints
The energy storage needs to comply with the safe operation conditions and satisfy the power constraints and state of charge constraints, as shown in Equations (21) and (23). In order to ensure that the energy storage in the next dispatch cycle has the same operating condition, this paper assumes that the initial value of the energy storage energy in this cycle is equal to the initial value in the next cycle, and both are equal to the lower limit value of the energy storage energy [24].
where is the stored energy of the energy storage at node i under scene w at time t in year k; and are the charging and discharging efficiency of the energy storage; is the 0–1 variable indicating the charging and discharging states of the energy storage; D is the maximum discharging depth of the energy storage; and are the maximum power and the maximum capacity of the energy storage at node i in year k, which is related to the health status of energy storage and can be obtained through Equation (24).
where is the health statue coefficient of energy storage at node i in year k obtained offline based on the rainflow counting method [25], which is the input parameter in this model.
- (7)
- Distributed power output constraints
Distributed power in this paper includes distributed PV and WT. The active and reactive power output constraints of distributed power are shown in Equations (25) and (26).
where and are the reactive power outputs of PV and WT at node i under scene w at time t in year k, respectively; and are the power factor angles of PV and WT at node i, respectively.
- (8)
- CVaR constraints
In this paper, the CVaR theory [26,27] is used to deal with the uncertainty of the operating cost in the distribution network expansion planning process. As a common risk measure method, CVaR can accurately measure the operational cost risk of a system by evaluating the probability and magnitude of system cost. For a discrete cost distribution, when the risk confidence is γ, CVaR is approximated as the expected cost corresponding to the set of scenes with higher costs with probability (1 − ). The CVaR constraints can be expressed in Equations (27)–(29):
where is an auxiliary decision variable introduced to calculate CVaR, whose optimal value is the value at risk (VAR); is the risk confidence; is the value of the operating cost under scene w exceeding VAR, which has a positive value.
4. Model Solution
The model proposed in this paper contains integer variables , and quadratic convex constraints, which is the second-order cone power flow constraints. It means that the proposed model belongs to the mixed integer second-order cone programming, which can be solved by the commercial solver Gurobi. On this basis, the proposed model could be simplified. The integer variable represents the charging and discharging states of the energy storage, which makes the energy storage not able to charge and discharge at the same time. When the objective function of the model is related to the cost, the integer variable could be omitted. Because the simultaneous charging and discharging of the energy storage will result in additional power loss and increase the total cost. Even if the charging and discharging states of the energy storage are not limited, the energy storage will not charge and discharge at the same time when the optimal solution of the distribution network expansion planning model is obtained. Therefore, Equation (22) can be replaced by Equation (30), which is one of the common simplification methods used in energy storage researches.
The capacity decay of energy storage is a nonlinear process that is difficult to be included in optimization models. Therefore, this paper refers to reference [28] and constructs an iterative solution framework. During each iteration, the health state coefficient of energy storage is calculated offline using Equation (31). The solution process is shown in Figure 3 (where n is the number of iterations).
where A, B, and C are parameters related to the maximum discharging depth of the energy storage D; is the number of cycles of the energy storage at node i at a certain discharging depth D in year k − 1. The type of energy storage battery in this paper is lithium iron phosphate battery.
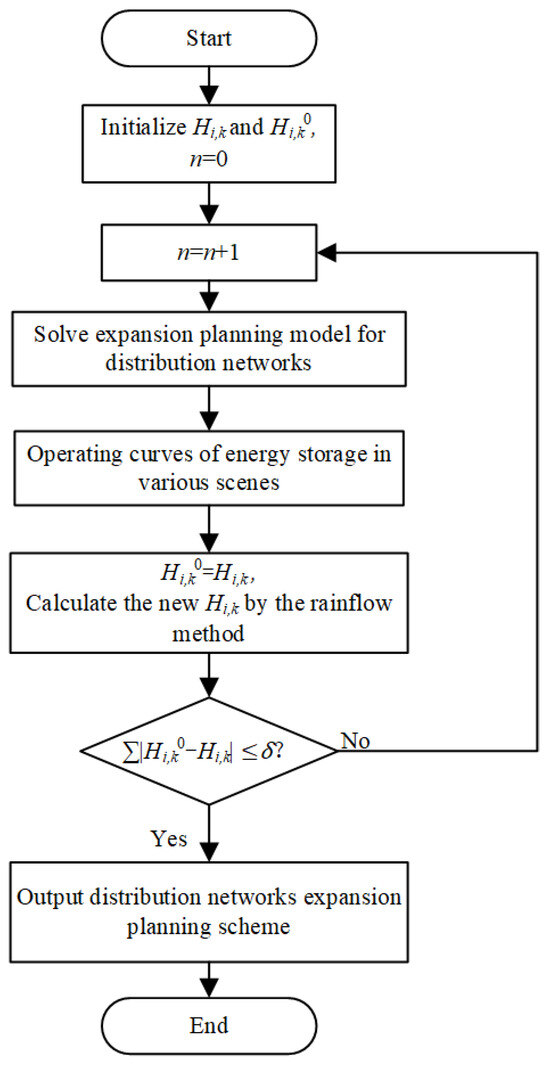
Figure 3.
Flow chart of iterative solution considering capacity decay.
5. Case Study
5.1. Case Settings
In this paper, an 18-node distribution system is used for the case study, and the initial network is shown in Figure 4. The reference voltage of this distribution system is 10 kV, with a total of 17 lines and a power reference value of 1 MVA. The data of existing lines and lines to be expanded are shown in the Table A1 and Table A2 of the Appendix A. For the distributed new energy resources output and customer load in the case, 4 typical daily scenes (3 general load scenes based on clustering and 1 peak load scene based on robust theory [29]) are considered, and each scene includes 24 time points. The capacity of both PV and WT is 500 kW. Node 6 is configured with energy storage with a capacity of 10 MWh and a maximum charging and discharging power of 5 MW. And node 14 is configured with energy storage with a capacity of 3 MWh and a maximum charging and discharging power of 1.5 MW. The set of load shedding nodes is {2, 4, 8, 11, 12, 13, 16, 17}. The rest of the key parameters in the case are shown in Table 2. The model in this paper is programmed in MATLAB-R2023a and solved by Gurobi-9.5.2.
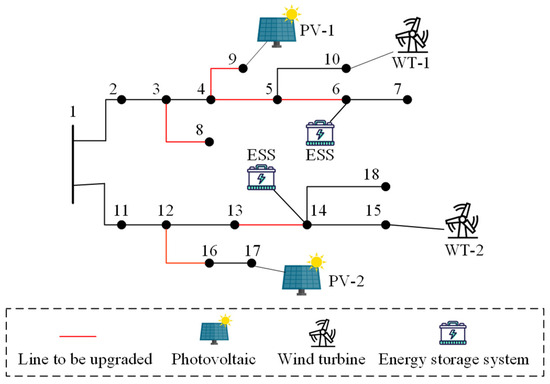
Figure 4.
A 18-node distribution system (The numbers in the figure are node numbers).

Table 2.
Key parameters.
5.2. Impact of Multi-Stage Rolling Planning
In order to compare and analyze the impact of the multi-stage rolling planning approach on the distribution network expansion planning scheme and the total investment and operation cost, this paper designs the following three cases, in which the capacity decay of energy storage is taken into account.
Case 1: The whole planning cycle is treated as a planning stage, and the single-stage planning method is used to develop the distribution network expansion planning scheme.
Case 2: The 9-year planning cycle is divided into three planning stages on average, and the planning scheme of each stage is developed in the start year of the planning period.
Case 3: The 9-year planning cycle is divided into three planning stages on average. Develop the planning scheme of each stage in the start year of the planning period, and make rolling amendments to the planning scheme in the start year of each stage.
This paper considers that the load at each node changes year by year during the planning cycle. The investor needs to formulate the planning scheme based on the annual load growth rate prediction results, assuming that the prediction results within 3 years are completely accurate. The longer the prediction time, the larger the prediction error. The annual load growth rate curve of each node is shown in Figure 5.
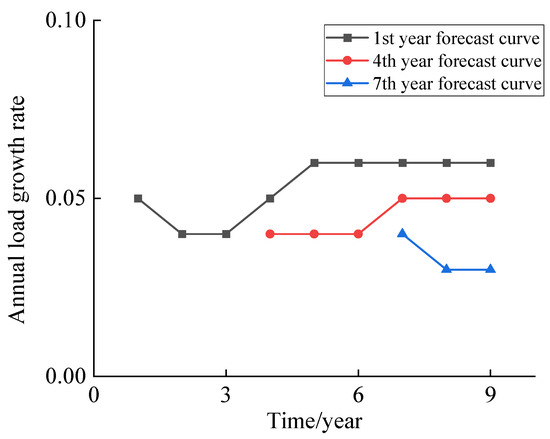
Figure 5.
Annual load growth rate curve.
On this basis, the results of the distribution network expansion planning in each case are shown in Table 3.

Table 3.
Distribution network planning results in different cases.
Comparing Case 1 and Case 2, it can be seen that the single-stage planning and the multi-stage non-rolling planning methods result in the same network structure at the end of the planning period, as the prediction results of the annual load growth rate are the same. The difference lies in the fact that the multi-stage non-rolling planning method carries out line expansion in stages according to the line expansion needs of each planning stage. On the one hand, after considering the time value of money, the method can reduce the investment cost of the line by 16.77%. On the other hand, the multi-stage non-rolling planning can improve the utilization efficiency of equipment, which extends the working life of equipment and improves the investment benefits.
The planning scheme in Case 2 is actually the same to the planning scheme developed in Case 3 in the 1st planning stage. As can be seen in Figure 5 and Table 3, over time the investor is able to more accurately predict the changes of the annual load growth rate and make rolling revisions to the planning scheme accordingly. Case 2 expands line 13–14 due to an overestimation of their expansion needs. While Case 3 more accurately predicts the expansion needs of the lines by continually revising the planning scheme based on the latest information, and finally avoids the expansion of line 13–14, which reduces the investment cost of the line by 27.27% and improves the investment benefits.
Then, in order to observe the utilization rate of the expanded lines during the planning cycle, the annual maximum line load rate curves of the expanded lines during the planning cycle are plotted in this paper, as shown in Figure 6.
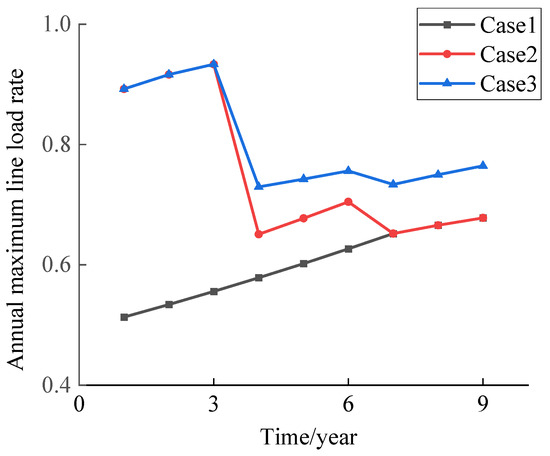
Figure 6.
Annual maximum line load rate curves of the expanded lines.
As can be seen in Figure 6, the single-stage planning method has a low equipment utilization rate. And by dividing the planning cycle into multiple planning stages, the multi-stage non-rolling planning method is able to alleviate the contradictions caused by the differentiated line expansion needs in different planning years and improve the utilization efficiency of equipment. On this basis, multi-stage rolling planning makes rolling amendments to the planning scheme on the basis of the latest information, which further enhances the utilization efficiency of equipment and improves the investment benefits.
5.3. Impact of the Users’ Electricity Bill
This paper points out that if the active load shedding is taken into account, the users’ electricity bill is related to the load shedding amount, which has an impact on the total operating cost of the distribution network, and thus affects the formation of the expansion planning scheme. Therefore, the users’ electricity bill must be included in the objective function. In order to study the impact of the users’ electricity bill on the distribution network expansion planning scheme, this paper designs Case 4 for simulation and analysis.
Case 4: The objective function is adjusted on the basis of Case 3, and the users’ electricity bill is no longer taken into account.
The simulation results are shown in Table 4.

Table 4.
Simulation results of Case 3 and Case 4.
Comparing Case 3 and Case 4 according to Table 4, it can be seen that the unit cost of load shedding in Case 4 is reduced after not taking into account the users’ electricity bill. As a result, Case 4 does not expand line 12–16, and control the line currents within a safe range by load shedding. However, the planning scheme is developed under the false underestimation of load shedding costs. In fact, the objective function value increases instead under this scheme, which means the investment benefits are reduced. Therefore, if the active load shedding is considered in the expansion planning of distribution network, the users’ electricity bill must be included in the objective function, otherwise the economics of the planning scheme will be affected and the investment benefits will be reduced.
5.4. Impact of the Energy Storage Capacity Decay
Energy storage can utilize its energy transfer characteristics to peak shaving and valley filling, thereby delaying or avoiding the expansion of power lines. The degree of capacity decay of energy storage directly affects whether the line current exceeds the limit and determines the expansion planning scheme. Therefore, in the research of distribution network expansion planning, the capacity decay characteristics of energy storage must be taken into account. In order to study the impact of energy storage capacity decay characteristics on distribution network expansion planning scheme, this paper designs Case 5 for simulation and analysis.
Case 5: On the basis of Case 3, the capacity decay of energy storage is not considered, which means the maximum capacity of energy storage will always be the same as the maximum capacity of the first year.
The simulation results are shown in Table 5.

Table 5.
Simulation results of Case 3 and Case 5.
The energy storage installed at node 6 can reduce the expansion demand of line 5–6 by peak shaving and valley filling. According to Table 5, it can be seen that without considering the capacity decay characteristics of energy storage, Case 5 believes that the current of line 5–6 will not exceed the limit under the effect of energy storage, so there is no need to expand line 5–6. But in fact, the capacity of energy storage will decay during the planning cycle, resulting in its actual performance being lower than expected. The capacity decay situation of energy storage at node 6 in Case 5 during the planning cycle is shown in Figure 7. According to Figure 7, it can be seen that the maximum capacity of energy storage at the end of the planning cycle is only 87.6% of the initial value, and the peak shaving and valley filling ability of energy storage is significantly reduced, resulting in current exceeding the limit of line 5–6 in Case 5. It will cause power accidents and threatens the safe operation of the power grid. Therefore, in the research of distribution network expansion planning, the capacity decay characteristics of energy storage must be taken into account, otherwise it will cause great safety hazards.
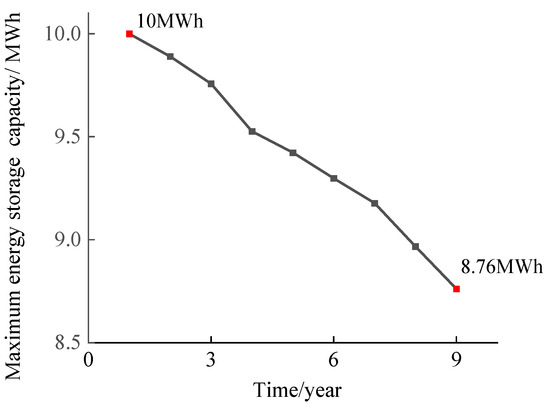
Figure 7.
The capacity decay situation of energy storage at node 6 in Case 5.
5.5. Impact of the Risk Appetite Coefficient
For investors with different levels of risk appetite, the generated distribution network grid expansion planning schemes will also be different. In order to study the impact of risk appetite coefficient on the distribution grid expansion planning scheme, this paper designs Case 6 for simulation and analysis.
Case 6: The risk appetite coefficient is adjusted on the basis of Case 3 to simulate investors with different levels of risk appetite.
The simulation results are shown in Table 6.

Table 6.
Simulation results of Case 3 and Case 6.
According to Table 6, it can be seen that as the risk appetite coefficient increases, investors’ decisions become more conservative. They tend to reduce the risk of high operating costs by expanding the lines more or earlier, and the value of CVaR gradually decreases. As the cost of reducing risk, the expected total cost of investors increases. When CVaR is not considered, it is equivalent to a risk appetite coefficient of 0. Investors will make very aggressive decisions, and they no longer consider the risk of high operating costs. Although the expected total cost is lower, the value of CVaR is large, which means high investment risks.
5.6. Robustness Analysis
The robustness of a model refers to its ability to resist errors in input data. A robust model can maintain stable performance and accurate results with various uncertainties in data. In order to study the robustness of the multi-stage rolling planning model, this paper designs Case 7 for simulation and analysis.
Case 7: On the basis of Case 3, it is assumed that the load growth rate prediction results within 3 years is no longer completely accurate, but there are some errors. A positive error rate means that the predicted value is greater than the actual value.
The simulation results are shown in Table 7.

Table 7.
Simulation results of Case 7.
According to Table 7, it can be seen that the multi-stage rolling planning model has good robustness when the error rate is within ±5%. The optimal solution of the model is the best expansion planning scheme. When the error rate is 10%, the accuracy of the results will be slightly affected, and the total cost will increase by 0.08%. When the error rate is −10%, underestimating user load will cause the line current to exceed the limit and threaten the safe operation of the power grid. Therefore, on the one hand, it is necessary to study load growth rate prediction methods to reduce prediction errors. On the other hand, the load growth rate should be avoided from being underestimated to reduce safety hazards.
6. Conclusions
Existing single-stage planning and multi-stage non-rolling planning methods suffer from low equipment utilization efficiency and poor investment benefits. Moreover, many researches of distribution network expansion planning often overlook the capacity decay characteristics of energy storage. To address the shortcomings of existing research, this paper proposes a multi-stage rolling planning method for distribution networks, and establishes a multi-stage rolling planning model for distribution networks taking into account CVaR with the goal of minimizing the total cost of investment and operation of distribution networks. Besides, this paper also uses the rainflow counting method to characterize the capacity decay characteristics of energy storage in the distribution network, and proposes an iterative solution framework that considers energy storage capacity decay to solve the proposed model. Finally, the following conclusions are obtained through the simulation of cases.
- (1)
- Compared to single-stage planning and multi-stage non-rolling planning, the multi-stage rolling planning method can not only develop the planning scheme based on the differentiated expansion demand in different planning years, but also make rolling amendments to the planning scheme of each stage according to the latest information during the planning cycle, which could improve the utilization efficiency of equipment and the investment benefits. As the result, the multi-stage rolling planning method could reduce the investment cost by approximately 27.27%.
- (2)
- In the establishment of the distribution network expansion planning model, if the active load shedding is considered, it is necessary to take into account the users’ electricity bill in the objective function. Otherwise, it will lead investors to underestimate the load shedding costs mistakenly and develop terrible planning scheme, which increases the total cost by approximately 2750 USD in Case 4.
- (3)
- The maximum capacity of energy storage will continuously decay during operation, reducing to 87.6% of the initial capacity or even lower. This directly affects whether the line current exceeds the limit and determines the expansion planning scheme. Therefore, the capacity decay characteristics of energy storage must be taken into account in the research of distribution network expansion planning, otherwise it will cause the line current to exceed the limit and threaten the safe operation of the power grid.
- (4)
- CVaR can be used to measure the risk of operating costs during the distribution network expansion planning. Different investors have varying risk appetite. A model that does not consider CVaR views investors as very aggressive. Instead, the proposed model considering CVaR can develop planning schemes based on investors’ risk appetite, balancing risks and earnings.
Currently, the way of dividing the planning stages in our work is subjective, which may not be the best way. Besides, when the scale of the distribution network is large or there are many scenes, the curse of dimensionality will make it difficult to solve the proposed mixed-integer program. In the future, research will be conducted on the division method of planning stages, developing a scientifical and reasonable stage division method based on the predicted information of load and cost of load shedding etc. In addition, the solution method of the proposed model will be further improved, increase the solving speed of the model, and enhance the applicability of the proposed method to large-scale and multi-scene distribution networks.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/en17205134/s1, Data S1: Load.mat; Data S2: Data_Instruction.pdf.
Author Contributions
Conceptualization, J.Z. (Junxiao Zhang), C.W. and J.Z. (Jing Zuo); Investigation, C.G. and S.Z.; Methodology, R.C. and Y.D.; Validation, Y.W.; Writing—original draft, J.Z. (Junxiao Zhang) and C.W.; Writing—review & editing, J.Z. (Jing Zuo), C.G. and S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by China Southern Power Grid Co., Ltd. Science and Technology Projects, grant number 030000KC23040067(GDKJXM20230379).
Data Availability Statement
The original contributions presented in the study are included in the article and Supplementary Material, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Junxiao Zhang, Jing Zuo, Chong Gao, Shurong Zheng, Ran Cheng and Yao Duan were employed by the Guangdong Power Grid Company Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A

Table A1.
Information of existing lines.
Table A1.
Information of existing lines.
| Number | Starting Point | End Point | Resistance/Ω | Reactance/Ω | Maximum Current/A |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 0.0181 | 0.0257 | 565 |
| 2 | 2 | 3 | 0.0164 | 0.0233 | 565 |
| 3 | 3 | 4 | 0.0165 | 0.0234 | 565 |
| 4 | 4 | 5 | 0.0243 | 0.0345 | 366 |
| 5 | 5 | 6 | 0.0211 | 0.0300 | 366 |
| 6 | 6 | 7 | 0.0217 | 0.0308 | 366 |
| 7 | 3 | 8 | 0.0209 | 0.0297 | 366 |
| 8 | 4 | 9 | 0.0211 | 0.0300 | 366 |
| 9 | 5 | 10 | 0.0220 | 0.0312 | 366 |
| 10 | 1 | 11 | 0.0188 | 0.0267 | 565 |
| 11 | 11 | 12 | 0.0173 | 0.0246 | 565 |
| 12 | 12 | 13 | 0.0177 | 0.0251 | 565 |
| 13 | 13 | 14 | 0.0250 | 0.0355 | 366 |
| 14 | 14 | 15 | 0.0214 | 0.0304 | 366 |
| 15 | 12 | 16 | 0.0237 | 0.0337 | 180 |
| 16 | 16 | 17 | 0.0255 | 0.0362 | 180 |
| 17 | 14 | 18 | 0.0229 | 0.0325 | 366 |

Table A2.
Information of lines to be expanded.
Table A2.
Information of lines to be expanded.
| Number | Starting Point | End Point | Resistance/Ω | Reactance/Ω | Expansion Cost/USD | Maximum Current/A |
|---|---|---|---|---|---|---|
| 1 | 4 | 5 | 0.0192 | 0.0272 | 31,625 | 565 |
| 2 | 5 | 6 | 0.0223 | 0.0317 | 50,875 | 565 |
| 3 | 3 | 8 | 0.0195 | 0.0277 | 38,500 | 565 |
| 4 | 4 | 9 | 0.0183 | 0.0260 | 27,500 | 565 |
| 5 | 13 | 14 | 0.0169 | 0.0240 | 34,375 | 565 |
| 6 | 12 | 16 | 0.0204 | 0.0290 | 45,375 | 565 |
References
- Wu, S.; Wang, Q.; Chen, Q.; Yu, C.; Tang, Y. Cyber-Physical Integrated Planning of Distribution Networks Considering Spatial-Temporal Flexible Resources. Prot. Control. Mod. Power Syst. 2024, 9, 142–156. [Google Scholar] [CrossRef]
- Li, Y.; Feng, B.; Wang, B.; Sun, S. Joint Planning of Distributed Generations and Energy Storage in Active Distribution Networks: A Bi-Level Programming Approach. Energy 2022, 245, 123226. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, G.; Li, K.; Li, B.; Chi, H.; Yao, Y.; Fan, Z. Reactive power optimization of a distribution network with high-penetration of wind and solar renewable energy and electric vehicles. Prot. Control. Mod. Power Syst. 2022, 7, 51. [Google Scholar] [CrossRef]
- Li, R.; Wong, P.; Wang, K.; Li, B.; Yuan, F. Power quality enhancement and engineering application with high permeability distributed photovoltaic access to low-voltage distribution networks in Australia. Prot. Control. Mod. Power Syst. 2020, 5, 18. [Google Scholar] [CrossRef]
- Yi, J.; Cherkaoui, R.; Paolone, M.; Shchetinin, D.; Knezovic, K. Expansion Planning of Active Distribution Networks Achieving Their Dispatchability via Energy Storage Systems. Appl. Energy 2022, 326, 119942. [Google Scholar] [CrossRef]
- Xie, S.; Hu, Z.; Wang, J. Two-stage robust optimization for expansion planning of active distribution systems coupled with urban transportation networks. Appl. Energy 2020, 261, 114412. [Google Scholar] [CrossRef]
- Moreira, A.; Heleno, M.; Valenzuela, A.; Eto, J.H.; Ortega, J.; Botero, C. A Scalable Approach to Large Scale Risk-Averse Distribution Grid Expansion Planning. IEEE Trans. Power Syst. 2024, 39, 2115–2128. [Google Scholar] [CrossRef]
- Kabirifar, M.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M.; Pourghaderi, N.; Dehghanian, P. A Bi-Level Framework for Expansion Planning in Active Power Distribution Networks. IEEE Trans. Power Syst. 2022, 37, 2639–2654. [Google Scholar] [CrossRef]
- Feng, C.; Liu, W.; Wen, F.; Li, Z.; Shahidehpour, M.; Shen, X. Expansion Planning for Active Distribution Networks Considering Deployment of Smart Management Technologies. IET Gener. Transm. Distrib. 2018, 12, 4605–4614. [Google Scholar] [CrossRef]
- Li, T.; Han, X.; Wu, W.; Sun, H. Robust expansion planning and hardening strategy of meshed multi-energy distribution networks for resilience enhancement. Appl. Energy 2023, 341, 121066. [Google Scholar] [CrossRef]
- Gao, H.; Wang, R.; He, S.; Wang, Z.; Liu, J. Bi-level stackelberg game-based distribution system expansion planning model considering long-term renewable energy contracts. Prot. Control. Mod. Power Syst. 2023, 8, 62. [Google Scholar] [CrossRef]
- Gao, L.; She, Y.; Zhu, L.; Zhang, J.; Wang, J.; Xu, W.; Cai, P.; Mi, Y. Research on Expansion Planning of Distributed Photovoltaic Distribution Network Including Energy Storage System and Line Load Margin. In Proceedings of the 2023 4th International Conference on Advanced Electrical and Energy Systems (AEES), Shanghai, China, 1–3 December 2023; pp. 1–10. [Google Scholar] [CrossRef]
- Zhou, S.; Han, Y.; Chen, S.; Yang, P.; Mahmoud, K.; Darwish, M.M.F.; Matti, L.; Zalhaf, A.S. A Multiple Uncertainty-based Bi-level Expansion Planning Paradigm for Distribution Networks Complying with Energy Storage System Functionalities. Energy 2023, 275, 127511. [Google Scholar] [CrossRef]
- Wang, S.; Dong, Z.; Chen, C.; Fan, H.; Luo, F. Expansion Planning of Active Distribution Networks with Multiple Distributed Energy Resources and EV Sharing System. IEEE Trans. Smart Grid 2020, 11, 602–611. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Q.; Strbac, G.; Hur, K.; Kang, C. Active Distribution Network Expansion Planning with Dynamic Thermal Rating of Underground Cables and Transformers. IEEE Trans. Smart Grid 2024, 15, 218–232. [Google Scholar] [CrossRef]
- Xiang, S.; Xu, D.; Wang, P.; Bai, Z.; Zeng, L. Optimal expansion planning of 5G and distribution systems considering source-network-load-storage coordination. Appl. Energy 2024, 366, 123372. [Google Scholar] [CrossRef]
- Pinto, R.S.; Unsihuay-Vila, C.; Tabarro, F.H. Coordinated Operation and Expansion Planning for Multiple Microgrids and Active Distribution Networks under Uncertainties. Appl. Energy 2021, 297, 117108. [Google Scholar] [CrossRef]
- Tang, C.; Liu, M.; Dai, Y.; Wang, Z.; Xie, M. Decentralized saddle-point dynamics solution for optimal power flow of distribution systems with multi-microgrids. Appl. Energy 2019, 252, 113361. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z.; Yu, T.; Yang, B.; Wang, H. Optimal mileage based AGC dispatch of a GenCo. IEEE Trans. Power Syst. 2020, 35, 2516–2526. [Google Scholar] [CrossRef]
- Hemmati, R. Dynamic expansion planning in active distribution grid integrated with seasonally transferred battery swapping station and solar energy. Energy 2023, 277, 127719. [Google Scholar] [CrossRef]
- Zare, A.; Chung, C.Y.; Zhan, J.; Faried, S.O. A Distributionally Robust Chance-Constrained MILP Model for Multistage Distribution System Planning with Uncertain Renewables and Loads. IEEE Trans. Power Syst. 2018, 33, 5248–5262. [Google Scholar] [CrossRef]
- Torbaghan, S.; Suryanarayana, G.; Hoschle, H.; D’Hulst, R.; Geth, F.; Caerts, C.; Van Hertem, D. Optimal Flexibility Dispatch Problem Using Second-Order Cone Relaxation of AC Power Flows. IEEE Trans. Power Syst. 2020, 35, 98–108. [Google Scholar] [CrossRef]
- Huang, C.; Li, K.; Zhang, N. Strategic joint bidding and pricing of load aggregators in day-ahead demand response market. Appl. Energy 2025, 377, 124552. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Xiang, Y.; Huo, D.; Liu, J. Optimal planning and investment benefit analysis of shared energy storage for electricity retailers. Int. J. Electr. Power Energy Syst. 2021, 126, 106561. [Google Scholar] [CrossRef]
- Yepes-Fernandez, H.; Restrepo, M.; Arango-Manrique, A. Lifetime Degradation Study of Batteries Operating as Community Energy Storage Systems. In Proceedings of the 11th IEEE Conference of the Andean Council, ANDESCON 2022, Barranquilla, Colombia, 16–19 November 2022. [Google Scholar]
- Xuan, A.; Shen, X.; Guo, Q.; Sun, H. A conditional value-at-risk based planning model for integrated energy system with energy storage and renewables. Appl. Energy 2021, 294, 116971. [Google Scholar] [CrossRef]
- Zhu, J.; Li, G.; Guo, Y.; Chen, J.; Liu, H.; Luo, Y.; Liu, W. Real-time risk-averse dispatch of an integrated electricity and natural gas system via conditional value-at-risk-based lookup-table approximate dynamic programming. Prot. Control. Mod. Power Syst. 2024, 9, 47–60. [Google Scholar] [CrossRef]
- Xie, Y.; Li, L.; Yang, K. Research on Shared Energy Storage Configuration Considering Energy Storage Battery Capacity Attenuation. Guangdong Electr. Power 2022, 35, 16–24. [Google Scholar] [CrossRef]
- Wang, Q.; Huang, C.; Wang, C.; Li, K.; Xie, N. Joint optimization of bidding and pricing strategy for electric vehicle aggregator considering multi-agent interactions. Appl. Energy 2024, 360, 122810. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).