Numerical Analysis of Hydrogen Behavior Inside Hydrogen Storage Cylinders under Rapid Refueling Conditions Based on Different Shapes of Hydrogen Inlet Ports

Abstract

In order to investigate the effects of different shapes of hydrogen inlet ports on the behavioral characteristics of hydrogen in Type IV hydrogen storage cylinders under rapid refueling conditions, a mathematical model of hydrogen temperature rise and a three-dimensional numerical analysis model were developed. The rectangular, hexagonal, triangular, Reuleaux triangular, circular, elliptical and conical inlet ports were researched by using computational fluid dynamics methods. The results showed that, for the same refueling flow rate and cross-sectional area, the hydrogen temperature inside a cylinder with a rectangular inlet port is higher and the jet tilt angle is larger than for a hexagonal port, while the thermal stratification phenomenon is not obvious. The hydrogen temperature inside a cylinder with a triangular inlet port is lower than that with a Reuleaux triangle port and the jet tilt angle is larger, and neither has significant thermal stratification. The hydrogen temperature inside a cylinder with a circular inlet port is higher than that with an ellipse port, the jets are not tilted on either one, and the phenomenon of thermal stratification is prominent. Further analysis indicated that enlarging the cross-sectional area and increasing the refueling flow rate results in a higher hydrogen temperature and intensified thermal stratification and an upward-angled jet can effectively reduce or eliminate thermal stratification.

1. Introduction

A hydrogen fuel cell vehicle is one of the mainstream directions for future development. A hydrogen storage cylinder is an indispensable component in the process of providing energy to hydrogen fuel cell vehicles. The sealing reliability of the mouth structure of a hydrogen storage cylinder is crucial for the safety of using hydrogen fuel vehicles [1]. In order to further highlight the convenience of the hydrogen refueling process for hydrogen fuel cell vehicles, the refueling time should be shortened as much as possible. However, because of the poor thermal conductivity of the plastic liner of Type IV hydrogen storage cylinders and the influence of the Joule–Thomson effect, the temperature inside a hydrogen storage cylinder will rise rapidly during the process of refueling and the internal temperature may exceed the 85 °C limit, which can create a safety hazard [2,3,4]. In order to minimize the hydrogen temperature increase during the refueling process, extended refueling times and pre-cooling of hydrogen are commonly employed. However, these methods have unavoidable problems in terms of time and cost. Therefore, improving the structure of hydrogen storage cylinders to explore a reduction in the internal temperature increase during refueling has become one of the most important ways to solve the problem of hydrogen temperature increases inside hydrogen storage cylinders [5,6].

In recent years, scholars from around the globe have been intensely studying the behavior of hydrogen temperature increases during rapid refueling processes, and some results have been achieved in this field. Firstly, in terms of the factors affecting hydrogen temperature increases, researchers have shown that the refueling rate, refueling pressure, refueling temperature, ambient temperature, initial pressure inside the cylinder, direction of the injector, thickness of the plastic inner liner, and the length-to-diameter ratio of the hydrogen storage cylinder all affect the hydrogen temperature increase. Notably, the refueling rate, pressure, and temperature are the main factors [7,8,9,10,11,12]. Secondly, in the cyclic fatigue study, a variety of methods for predicting the fatigue life of the plastic liner of the hydrogen storage cylinder and the carbon fiber layer under high temperature and high pressure have been proposed. Models combined with experimental data, theoretical analysis, thermodynamic properties of materials, and stress–strain relationships provide key support for the design and life assessment of hydrogen storage cylinders [13,14,15]. Thirdly, in controlling the temperature rise during hydrogen refueling, measures such as pre-cooling and graded refueling have been proposed, and tests have shown that pre-cooling the hydrogen to −40 °C or adopting a three-stage refueling can effectively reduce the final temperature of hydrogen while ensuring economy [16,17,18]. Finally, in the prediction of hydrogen temperature, various mathematical models have been established. These models predict the change in hydrogen temperature during the process of refueling and discharging of hydrogen storage cylinders, and they combine the heat conduction, convection, compression heat effect and the characteristics of hydrogen, effectively reflecting the change of the temperature of hydrogen under a high-pressure rapid refueling condition, providing theoretical support for the safety and efficiency of a hydrogen refueling system [19,20,21].

In summary, existing studies on the behavioral characteristics of hydrogen inside hydrogen storage cylinders mainly focus on hydrogen and the cylinder’s structures. The hydrogen inlet ports are also usually designed in a circular shape, but there are fewer studies on the effects of hydrogen storage cylinder mouth structures, including hydrogen inlet ports with different geometrical shapes, on the behavioral characteristics of the hydrogen inside hydrogen storage cylinders. Considering that the hydrogen inlet port is the necessary path for hydrogen to enter the hydrogen storage cylinder during the process of hydrogen refueling, the safety and rationality of its structure are crucial. Therefore, it is necessary to systematically investigate the effects of different hydrogen inlet port shapes and cross-sectional areas on the behavior of hydrogen in hydrogen storage cylinders. A series of studies were carried out in this paper to address this key issue.

2. Mathematical Model

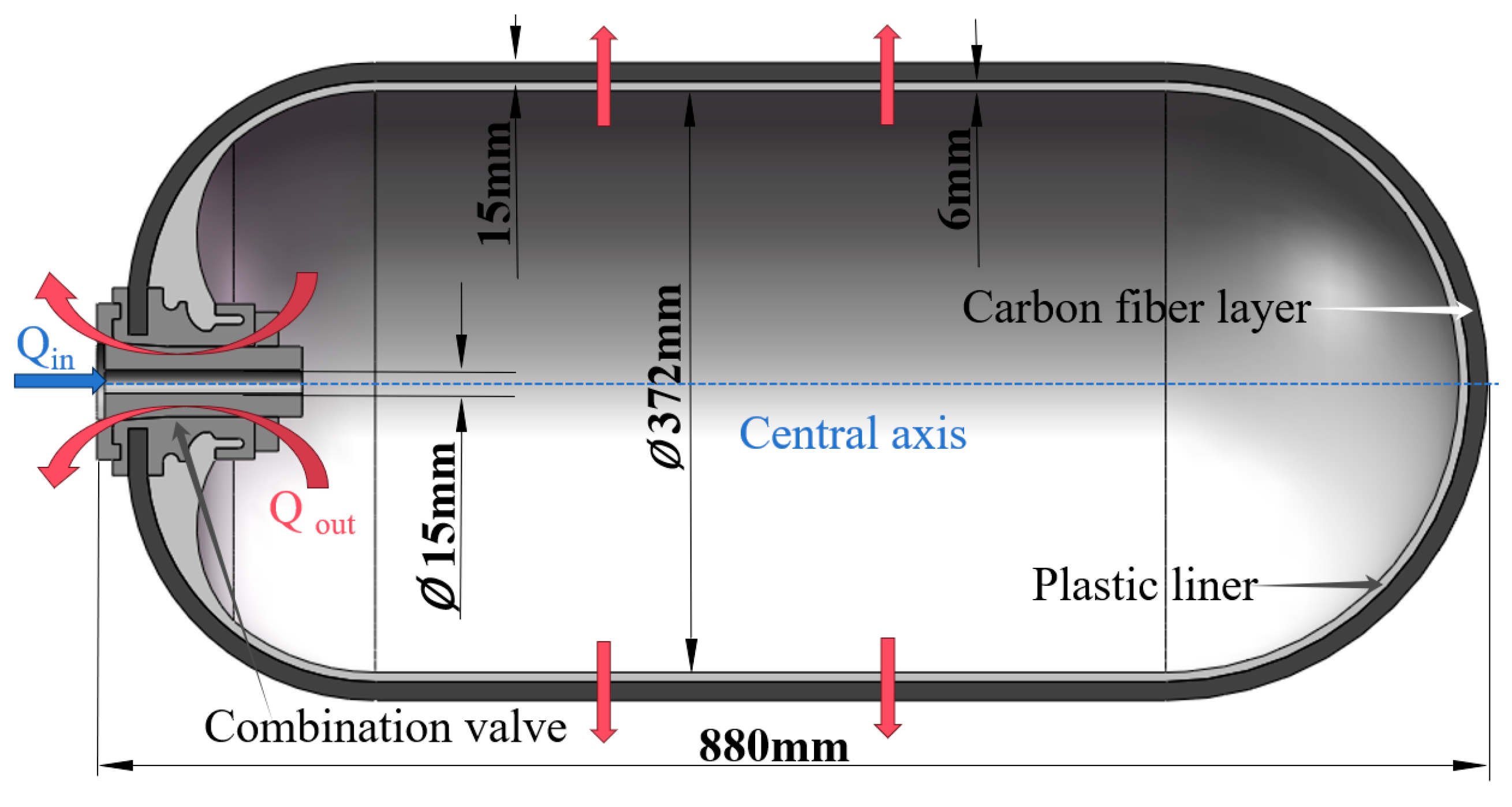
Figure 1 shows the structural dimensions of a hydrogen storage cylinder and the heat transfer process during refueling. According to the structure of the hydrogen storage cylinder, the heat transfer process can be divided into two parts: the first part is the heat exchange between the internal high temperature and the external environment through the plastic liner and carbon fiber layer, which is limited in heat exchange due to the poor thermal conductivity of the two; the second part is the heat exchange between the internal high temperature and the external environment through the combination valve, which is the main heat exchange pathway.

The following assumptions are made when analyzing the heat transfer mechanism for the hydrogen refueling and retention process:

(1)

It is assumed that there is no backflow or leakage of hydrogen during the refueling process;

(2)

It is assumed that the components of the hydrogen storage cylinder are rigid bodies and that no deformation occurs during the filling process;

(3)

It is assumed that the thermal conductivity of each material remains constant;

(4)

It is assumed that the refueling flow rate of hydrogen and the temperature of the gas source remain constant during the refueling process;

(5)

It is assumed that the flow in the hydrogen storage cylinder during the refueling process is axisymmetric and the effect of hydrogen buoyancy on the flow field is not considered [22];

(6)

It is assumed that the hydrogen temperature inside the hydrogen storage cylinder is uniformly distributed during the refueling process;

(7)

It is assumed that the internal temperature of the hydrogen storage cylinder does not exchange heat with the external environment through the plastic liner and carbon fiber layer;

(8)

It is assumed that the temperature of the combination valve is the same as the external environment temperature and uniformly distributed.

The energy conservation equation in the hydrogen region during refueling can be expressed as:

$${\displaystyle \frac{\mathrm{d}\left(\mathrm{mu}\right)}{\mathrm{dt}}}={\dot{\mathrm{m}}}_{\mathrm{in}}{\mathrm{h}}_{\mathrm{in}}+\Delta \mathrm{Q}$$

(1)

where m is the mass of hydrogen inside the hydrogen storage cylinder in kg; u is the specific internal energy of hydrogen in J/kg; t is the refueling time in s; ${\dot{\mathrm{m}}}_{\mathrm{in}}$ is the refueling rate of hydrogen in kg/s; ${\mathrm{h}}_{\mathrm{in}}$ is the specific enthalpy of hydrogen during refueling in J/kg; and $\Delta \mathrm{Q}$ is the amount of heat exchange between the hydrogen and the combination valve and wall of the cylinder in W.

The mass conservation equation for hydrogen can be expressed as:

$${\displaystyle \frac{\mathrm{dm}}{\mathrm{dt}}}={\dot{\mathrm{m}}}_{\mathrm{i}\mathrm{n}}$$

(2)

Considering the combination valve as a whole and assuming a uniform temperature distribution, the energy conservation equation in the region of the combination valve is, according to Newton’s law of cooling:

$${\displaystyle \frac{\mathrm{d}({\mathrm{m}}_{\mathrm{va}}{\mathrm{c}}_{\mathrm{va}}∆{\mathrm{T}}_{\mathrm{va}})}{\mathrm{dt}}}={\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{H}}{\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{H}}({\mathrm{T}}_{\mathrm{H}}-{\mathrm{T}}_{\mathrm{va}})-{\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{en}}{\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{en}}({\mathrm{T}}_{\mathrm{va}}-{\mathrm{T}}_{\mathrm{en}})-{\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{pl}}{\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{pl}}({\mathrm{T}}_{\mathrm{va}}-{\mathrm{T}}_{\mathrm{pl}})-{\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{CFRP}}{\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{CFRP}}({\mathrm{T}}_{\mathrm{va}}-{\mathrm{T}}_{\mathrm{CFR}\mathrm{P}})$$

(3)

where ${\mathrm{m}}_{\mathrm{va}}$ is the mass of the combination valve in kg; ${\mathrm{c}}_{\mathrm{va}}$ is the specific heat capacity of the material used in the combination valve in $\mathrm{J}/(\mathrm{kg}·\mathrm{K})$; $∆{\mathrm{T}}_{\mathrm{va}}$ is the temperature difference of the heat exchange process of the combination valve in K; ${\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{H}}$ is the convective heat transfer coefficient of the combination valve and hydrogen in $\mathrm{W}/({\mathrm{m}}^2·\mathrm{K})$; ${\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{H}}$ is the contact area of the combination valve and hydrogen in ${\mathrm{m}}^2$; ${\mathrm{T}}_{\mathrm{H}}$ is the temperature of the hydrogen in K; ${\mathrm{T}}_{\mathrm{va}}$ is the temperature of the combination valve in K; ${\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{en}}$ is the convective heat transfer coefficient of the combination valve and environment in $\mathrm{W}/({\mathrm{m}}^2·\mathrm{K})$; ${\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{en}}$ is the contact area of the combination valve and environment in ${\mathrm{m}}^2$; ${\mathrm{T}}_{\mathrm{en}}$ is the temperature of the environment in K; ${\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{pl}}$ is the thermal conductivity coefficient of the combination valve and plastic liner in $\mathrm{W}/({\mathrm{m}}^2·\mathrm{K})$; ${\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{pl}}$ is the contact area of the combination valve and plastic liner in ${\mathrm{m}}^2$; ${\mathrm{T}}_{\mathrm{pl}}$ is the temperature of the plastic liner in K; ${\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{CFRP}}$ is the thermal conductivity coefficient of the combination valve and carbon fiber layer in $\mathrm{W}/({\mathrm{m}}^2·\mathrm{K})$; ${\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{CFRP}}$ is the contact area of the combination valve and carbon fiber layer in ${\mathrm{m}}^2$; and ${\mathrm{T}}_{\mathrm{CFR}\mathrm{P}}$ is the temperature of the carbon fiber layer in K.

Similarly, the energy conservation equation for the plastic liner region is:

$${\displaystyle \frac{\mathrm{d}({\mathrm{m}}_{\mathrm{pl}}{\mathrm{c}}_{\mathrm{pl}}{∆\mathrm{T}}_{\mathrm{pl}})}{\mathrm{dt}}}={\mathrm{k}}_{\mathrm{pl}\text{-}\mathrm{H}}{\mathrm{A}}_{\mathrm{pl}\text{-}\mathrm{H}}({\mathrm{T}}_{\mathrm{H}}-{\mathrm{T}}_{\mathrm{pl}})+{\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{pl}}{\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{pl}}({\mathrm{T}}_{\mathrm{va}}-{\mathrm{T}}_{\mathrm{pl}})-{\mathrm{k}}_{\mathrm{pl}\text{-}\mathrm{CFRP}}{\mathrm{A}}_{\mathrm{pl}\text{-}\mathrm{CFRP}}({\mathrm{T}}_{\mathrm{pl}}-{\mathrm{T}}_{\mathrm{CFRP}})$$

(4)

where ${\mathrm{m}}_{\mathrm{pl}}$ is the mass of the plastic liner in kg; ${\mathrm{c}}_{\mathrm{pl}}$ is the specific heat capacity of the material used in the plastic liner in $\mathrm{J}/(\mathrm{kg}·\mathrm{K})$; $∆{\mathrm{T}}_{\mathrm{va}}$ is the temperature difference of the heat exchange process of the plastic liner in K; ${\mathrm{k}}_{\mathrm{pl}\text{-}\mathrm{H}}$ is the convective heat transfer coefficient of the plastic liner and hydrogen in $\mathrm{W}/({\mathrm{m}}^2·\mathrm{K})$; ${\mathrm{A}}_{\mathrm{pl}\text{-}\mathrm{H}}$ is the contact area of the plastic liner and hydrogen in ${\mathrm{m}}^2$; ${\mathrm{k}}_{\mathrm{pl}\text{-}\mathrm{CFRP}}$ is the thermal conductivity coefficient of the plastic liner and carbon fiber layer in $\mathrm{W}/({\mathrm{m}}^2·\mathrm{K})$; and ${\mathrm{A}}_{\mathrm{pl}\text{-}\mathrm{CFRP}}$ is the contact area of the plastic liner and carbon fiber layer in ${\mathrm{m}}^2$.

The energy conservation equation in the region of the carbon fiber layer is given by:

$${\displaystyle \frac{\mathrm{d}({\mathrm{m}}_{\mathrm{CFRP}}{\mathrm{c}}_{\mathrm{CFRP}}∆{\mathrm{T}}_{\mathrm{CFRP}})}{\mathrm{dt}}}={\mathrm{k}}_{\mathrm{pl}\text{-}\mathrm{CFRP}}{\mathrm{A}}_{\mathrm{pl}\text{-}\mathrm{CFRP}}({\mathrm{T}}_{\mathrm{pl}}-{\mathrm{T}}_{\mathrm{CFRP}})+{\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{CFRP}}{\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{CFRP}}({\mathrm{T}}_{\mathrm{va}}-{\mathrm{T}}_{\mathrm{CFRP}})-{\mathrm{k}}_{\mathrm{en}\text{-}\mathrm{CFRP}}{\mathrm{A}}_{\mathrm{en}\text{-}\mathrm{CFRP}}({\mathrm{T}}_{\mathrm{CFRP}}-{\mathrm{T}}_{\mathrm{en}})$$

(5)

where ${\mathrm{m}}_{\mathrm{CFRP}}$ is the mass of the carbon fiber layer in kg; ${\mathrm{c}}_{\mathrm{CFRP}}$ is the specific heat capacity of the material used in the carbon fiber layer in $\mathrm{J}/(\mathrm{kg}·\mathrm{K})$; $∆{\mathrm{T}}_{\mathrm{CFRP}}$ is the temperature difference of the heat exchange process of the carbon fiber layer in K; ${\mathrm{k}}_{\mathrm{en}\text{-}\mathrm{CFRP}}$ is the convective heat transfer coefficient of the environment and carbon fiber layer in $\mathrm{W}/({\mathrm{m}}^2·\mathrm{K})$; and ${\mathrm{A}}_{\mathrm{en}\text{-}\mathrm{CFRP}}$ is the contact area of the environment and carbon fiber layer in ${\mathrm{m}}^2$.

According to the assumption condition (7) that the plastic liner and carbon fiber layer are adiabatic, Equation (3) can be simplified as:

$${\displaystyle \frac{\mathrm{d}({\mathrm{m}}_{\mathrm{va}}{\mathrm{c}}_{\mathrm{va}}∆{\mathrm{T}}_{\mathrm{va}})}{\mathrm{dt}}}={\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{H}}{\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{H}}({\mathrm{T}}_{\mathrm{H}}-{\mathrm{T}}_{\mathrm{va}})-{\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{en}}{\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{en}}({\mathrm{T}}_{\mathrm{va}}-{\mathrm{T}}_{\mathrm{en}})$$

(6)

According to assumption condition (8), Equation (1) can be simplified as:

$${\displaystyle \frac{\mathrm{d}\left(\mathrm{mu}\right)}{\mathrm{dt}}}={\dot{\mathrm{m}}}_{\mathrm{in}}{\mathrm{h}}_{\mathrm{in}}-{\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{H}}{\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{H}}({\mathrm{T}}_{\mathrm{H}}-{\mathrm{T}}_{\mathrm{va}})$$

(7)

The equation for the mass change of hydrogen during refueling is:

$$\mathrm{m}={\mathrm{m}}_0+{\dot{\mathrm{m}}}_{\mathrm{in}}\mathrm{t}$$

(8)

where ${\mathrm{m}}_0$ is the mass of hydrogen inside the initial hydrogen storage cylinder in m.

Substituting Equation (8) into Equation (7) yields:

$$({\mathrm{m}}_0+{\dot{\mathrm{m}}}_{\mathrm{in}}\mathrm{t}){\displaystyle \frac{\mathrm{du}}{\mathrm{dt}}}+{\dot{\mathrm{m}}}_{\mathrm{in}}\mathrm{u}={\dot{\mathrm{m}}}_{\mathrm{in}}{\mathrm{h}}_{\mathrm{in}}-{\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{H}}{\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{H}}({\mathrm{T}}_{\mathrm{H}}-{\mathrm{T}}_{\mathrm{va}})$$

(9)

The specific internal energy $\mathrm{u}={\mathrm{c}}_{\mathrm{v}}{\mathrm{T}}_{\mathrm{H}}$, $\mathrm{h}={\mathrm{c}}_{\mathrm{p}}{\mathrm{T}}_{\mathrm{in}}$, where ${\mathrm{c}}_{\mathrm{v}}$ is the specific heat at constant volume, ${\mathrm{c}}_{\mathrm{p}}$ is the specific heat at constant pressure, and ${\mathrm{T}}_{\mathrm{in}}$ is the temperature of the gas source. Substituting in Equation (9) yields:

$${\mathrm{c}}_{\mathrm{v}}({\mathrm{m}}_0+{ \dot{\mathrm{m}}}_{\mathrm{in}}\mathrm{t}){\displaystyle \frac{\mathrm{d}{\mathrm{T}}_{\mathrm{H}}}{\mathrm{dt}}}={\dot{\mathrm{m}}}_{\mathrm{in}}({\mathrm{c}}_{\mathrm{p}}{\mathrm{T}}_{\mathrm{in}}-{\mathrm{c}}_{\mathrm{v}}{\mathrm{T}}_{\mathrm{H}})-{\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{H}}{\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{H}}({\mathrm{T}}_{\mathrm{H}}-{\mathrm{T}}_{\mathrm{en}})$$

(10)

Divide both sides of the equation by ${\dot{\mathrm{m}}}_{\mathrm{in}}{\mathrm{c}}_{\mathrm{v}}$, introduce the specific heat capacity ratio $\mathsf{\vartheta }={\mathrm{c}}_{\mathrm{v}}/{\mathrm{c}}_{\mathrm{p}}$, define ${\mathrm{t}}^{\prime }={\mathrm{m}}_0/{\dot{\mathrm{m}}}_{\mathrm{in}}$, $\mathsf{\varphi }={\mathrm{k}}_{\mathrm{va}\text{-}\mathrm{H}}{\mathrm{A}}_{\mathrm{va}\text{-}\mathrm{H}}/({\dot{\mathrm{m}}}_{\mathrm{in}}{\mathrm{c}}_{\mathrm{v}})$, substitute into Equation (10) and sort out:

$${\displaystyle \frac{\mathrm{d}{\mathrm{T}}_{\mathrm{H}}}{\mathrm{dt}}}={\displaystyle \frac{(\mathsf{\vartheta }{\mathrm{T}}_{\mathrm{in}}+\mathsf{\varphi }{\mathrm{T}}_{\mathrm{en}})-(1+\mathsf{\varphi }){\mathrm{T}}_{\mathrm{H}}}{{\mathrm{t}}^{\prime }+\mathrm{t}}}$$

(11)

Continuing to define ${\mathrm{T}}^{\prime }=\mathsf{\vartheta }{\mathrm{T}}_{\mathrm{in}}+\mathsf{\varphi }{\mathrm{T}}_{\mathrm{en}}/(1+\mathsf{\varphi })$ by substituting Equation (11) yields:

$${\displaystyle \frac{\mathrm{d}{\mathrm{T}}_{\mathrm{H}}}{\mathrm{dt}}}=(1+\mathsf{\varphi })({\displaystyle \frac{{\mathrm{T}}^{\prime }-{\mathrm{T}}_{\mathrm{in}}}{{\mathrm{t}}^{\prime }+\mathrm{t}}})$$

(12)

To solve Equation (12), which is a differential equation, define $\mathsf{\mu }=\mathrm{t}/{\mathrm{t}}^{\prime }$ and substitute the initial condition t = 0 before refueling, and obtain:

$${\mathrm{T}}_{\mathrm{H}}={\mathrm{T}}^{\prime }-({\mathrm{T}}^{\prime }-{\mathrm{T}}_{\mathrm{in}})({\displaystyle \frac{1}{1+\mathsf{\mu }}}{)}^{1+\mathsf{\varphi }}$$

(13)

This is the equation for the variation of the internal temperature of the hydrogen storage cylinder with time during the refueling process.

Combined with the constructed mathematical model, the temperature change history of hydrogen during the refueling process is plotted as shown in Figure 2. With the increase of refueling time, the temperature of the hydrogen gradually increases and tends to stabilize. The course diagram coincides with the temperature rise trend reflected in the simulation results.

3. Establishment of the Numerical Model

3.1. 3D Model

The 3D model of a Type IV hydrogen storage cylinder, which consists of a carbon fiber layer, a plastic liner and a combination valve, was created by using Solidworks. The design pressure of the cylinder is 70 MPa and the volume is 81 L. The specific structural and dimensional parameters are shown in Figure 1.

3.2. Validation of Calculation Methods

To ensure the accuracy and economy of the calculation, the number of grids was verified in this paper. The model was meshed by using the shared topology method, and the Body of Influence (BOI) technique was utilized to locally encrypt the grid in the intermediate regions of the combination valve and the fluid region where the hydrogen jet velocity is high [23]. Besides, boundary layer grids were also incorporated for more accurate simulation of near-wall flow and heat transfer phenomena [24].

Figure 3 displays the maximum temperature inside the hydrogen storage cylinder at the end of refueling for a different number of grids. As the grid count escalates from 207,000 to 1,032,000, there is a notable increase in simulation time. But the maximum temperature at the end of refueling leveled off as the number of grids increased. Considering the computational time and economy, 835,000 grids was considered to be the best choice that can guarantee the simulation accuracy and computational efficiency [25]. Consequently, the number of grids for all simulation models in this paper was divided into 835,000 grids.

Transient calculation was chosen for the simulation process and the turbulence model was the Realizable k-ε model [26]. In order to describe more accurately the pressure behavior of hydrogen under a high-pressure environment, the real gas equation of state (Redlich–Kwong) was applied [27]. The material properties were set as shown in

Table 1. Properties of materials used in hydrogen storage cylinders.

Name	Material	Thermal Conductivity	Density	Specific Heat Capacity
Combination valve	Aluminum alloy	170 W/m·K	2700 kg/m3	900 J/(kg·K)
Plastic liner	PA	0.42 W/m·K	952 kg/m3	2090 J/(kg·K)
Carbon fiber layer	T700s	5.95 W/m·K	1750 kg/m3	800 J/(kg·K)

. The time step was set to 0.01 s and the inlet boundary condition maintained a constant flow refueling at 10 g/s for a duration of 180 s [28]. Throughout this process, the temperature of the gas source was kept at 25 °C, while the initial pressure inside the hydrogen storage cylinder was set at 2 Mpa [29].

4. Results and Discussion

This paper focuses on the effect of different hydrogen inlet port shapes and their cross-sectional areas on the behavior of hydrogen in hydrogen storage cylinders under rapid refueling conditions. Utilizing FLUENT 2021R1, comparative research was carried out for rectangular, hexagonal, triangular, Reuleaux triangular, circular, elliptical and conical hydrogen inlet ports.

4.1. Rectangle and Hexagon

Figure 4 displays the shapes and dimensions of rectangular and hexagonal hydrogen inlet ports, both of which have the same cross-sectional area. CFD is taken to simulate the refueling process of the two under the same working conditions: hydrogen at 25 °C is refueled into the hydrogen storage cylinder at a constant rate of 10 g/s, the refueling time is 180 s, and the initial pressure and the initial temperature inside the cylinder are 2 MPa and 25 °C.

Figure 5 displays the temperature and streamlined distribution inside hydrogen storage cylinders with rectangular and hexagonal inlet ports at 180 s of refueling. In Figure 5a,b, the temperature distribution inside cylinders with rectangular and hexagonal inlet ports are displayed, while Figure 5c,d display their respective streamlined distribution. By comparing Figure 5a,c with Figure 5b,d, it can be observed that the hydrogen jet in the rectangular hydrogen inlet port is obviously upwardly inclined and the hydrogen flow rate increases significantly at the corners. This inclined jet phenomenon is closely related to the roundness and interior angle of the hydrogen inlet port. Larger roundness and interior angle provide a smoother flow path for hydrogen, allowing it to maintain a higher flow rate and a consistent streamline, which reduces the flow disturbance. As the roundness and interior angle decrease, the path of the hydrogen flow becomes more complex, and the sharp changes in the edges lead to an increase in momentum loss, which in turn affects the direction of the jet. The upward jet produced by the rectangular hydrogen inlet causes the overall vortex radius inside the hydrogen storage cylinder to increase, and the friction between the hydrogen is enhanced, resulting in a higher hydrogen temperature inside the cylinder than the hexagonal hydrogen inlet port. On the other hand, the angle between the hydrogen jet from the hexagonal hydrogen inlet port and the center axis is small, and the jet directly hits the bottom of the hydrogen storage cylinder, forming a local reflux. This phenomenon forces the refueled hydrogen to move toward the mouth of the hydrogen storage cylinder, resulting in insufficient mixing of hydrogen inside the cylinder and the formation of thermal stratification. Meanwhile, the hydrogen jet in the rectangular hydrogen inlet port, because of its upward inclination, can drive the hydrogen inside the hydrogen storage cylinder to rotate together to promote more uniform mixing, significantly reducing the appearance of thermal stratification.

4.2. Triangle and Reuleaux Triangle

Figure 6 displays the shapes and dimensions of the triangular and Reuleaux triangular inlet ports, and the simulation process of hydrogen refueling is completed with an equal cross-sectional area of both, following the above mentioned working conditions.

Figure 7 displays the temperature and streamlined distribution of hydrogen inside cylinders with triangular and Reuleaux triangular inlet ports at 180 s of the refueling process. Specifically, Figure 7a,c show the temperature distribution inside the cylinders with triangular and Reuleaux triangular inlet ports, respectively; Figure 7b,d show the streamlined distribution of them, separately; while Figure 7e is a localized zoomed-in view of the streamline inside the triangular inlet port. Although the hydrogen jets of both are tilted upward, more vortices are generated inside the cylinder with a Reuleaux triangle hydrogen inlet port than that inside the triangle, resulting in a higher temperature of the Reuleaux triangle hydrogen storage cylinder than the triangle at the end of the refueling, as shown in Figure 7b,d. Additionally, the collision of hydrogen with the walls of the hydrogen inlet port is more intense inside the triangle hydrogen inlet port as shown in Figure 7e, which leads to the initial energy dissipation, and the temperature change at the hydrogen inlet port of the cylinder is also reflected in Figure 7a. Since both the triangle and Reuleaux triangle have interior angles and small roundness, the hydrogen jets are tilted, and the smaller the interior angles and roundness, the larger the angle of the hydrogen jet to the center axis. The larger the tilted angle of the hydrogen jet, the higher the hydrogen flow rate. In addition, the internal thermal stratification phenomenon is not obvious in either one.

4.3. Circle, Ellipse and Cone

Figure 8 displays the shapes and dimensions of the circular, elliptical and conical inlet ports, where the cross-sectional area of the circular and elliptical ports is the same. The cross-sectional area of the conical inlet port gradually increases from the hydrogen inlet port inward. The refueling process simulations are conducted under the working conditions described in the previous section.

Figure 9 displays the temperature and streamlined distribution inside three different hydrogen storage cylinders with different hydrogen inlet ports at 180 s of refueling. Specifically, Figure 9a–c display the temperature distribution inside cylinders with circular, elliptical, and conical inlet ports, respectively; and Figure 9d–f display the corresponding streamlined distributions. From Figure 9a–c, it is observed that the temperature inside the cylinder with a conical inlet port is the highest and that with an elliptical inlet port is the lowest. Figure 9d–f show that more vortices are generated inside the cylinder with a conical inlet port than the other two cylinders, and the increased hydrogen chaos exacerbates the friction between the hydrogen, leading to an increase in temperature. In addition, as the cross-sectional area of the hydrogen inlet port increases, the hydrogen jet from the conical inlet port is longer and more diffuse under the same refueling flow rate, further exacerbating the degree of hydrogen chaos in the hydrogen storage cylinder and leading to more vortex generation. Since all three hydrogen inlet ports have a rounded shape without interior angles, the direction of the hydrogen jet is basically not tilted. Thermal stratification occurs in all three inside, and the cylinder with a conical inlet port is the most serious, while the elliptical one is at a relatively moderate level.

By comparing the final temperature inside the hydrogen storage cylinders with different geometries of hydrogen inlet ports as described above, it is found that the final temperature in the cylinders with triangular, hexagonal, and elliptical inlet ports are lower. In order to further research the effect of the shape of the hydrogen inlet port on the internal temperature increase and to shorten the refueling time, simulations of the refueling process of cylinders with triangular, hexagonal and elliptical inlet ports were conducted again by increasing the refueling flow rate from 10 g/s to 20 g/s and reducing the refueling time to 120 s, while all other conditions remained the same.

Figure 10 displays the temperature and streamlined distribution inside hydrogen storage cylinders with triangular, hexagonal, and elliptical inlet ports at 120 s during refueling. Figure 10a–c display the temperature distribution of the cylinders with triangular, hexagonal and elliptical inlet ports, respectively; while Figure 10d–f display the corresponding streamlined distribution. As the refueling flow rate increases, the hydrogen temperature inside the hydrogen storage cylinder increases significantly. The highest temperature is observed inside the cylinder with a triangular inlet port, while the lowest temperature is found inside the cylinder with an elliptical inlet port. From the streamlined distribution, it can be seen that this is mainly due to the fact that the upwardly tilted hydrogen jet from the triangular hydrogen inlet port results in the generation of a larger vortex radius inside the hydrogen storage cylinder than in the other two. Figure 10a displays that as the refueling flow rate increases, the hydrogen jet in the triangular inlet port is still tilted upward, and the collision of hydrogen with the wall of the hydrogen inlet port becomes more intense, leading to a further increase in the temperature inside the hydrogen inlet port. The direction of the hydrogen jet in the hexagonal and elliptical inlet ports is basically not inclined, but the jet velocity is increased. After increasing the refueling flow rate, the thermal stratification phenomenon inside cylinders with hexagonal and elliptical inlet ports becomes more serious, while there is almost no thermal stratification phenomenon or the phenomenon is lessened inside the cylinder with a triangular inlet port. Combined with the above analyses, this illustrates that an upward-tilted hydrogen jet can slow down or even eliminate the thermal stratification phenomenon.

By elevating the refueling flow rate, comparing the three hydrogen inlet port shapes of triangular, hexagonal and elliptical, and comprehensively analyzing the temperature rise and thermal stratification phenomenon in the hydrogen storage cylinder, the elliptical shape is considered to be the optimal shape of the hydrogen inlet port.

In order to research the effect of the roundness of an elliptical inlet port on the behavior of hydrogen inside the hydrogen storage cylinder, the long axis x of the elliptical inlet port was kept constant and the short axis y of the ellipse was shortened on the basis of Figure 8b, with the specific dimensions shown in Figure 11a,b. Then, the refueling was performed for 120 s while keeping the refueling flow rate of 20 g/s and other conditions unchanged, and the internal temperature and streamlined distribution were obtained.

The temperature and streamlined distribution inside the cylinders with two different elliptical hydrogen inlet ports during refueling at 120 s are shown in Figure 12. Figure 12a,b and Figure 12c,d display the temperature and streamlined distribution inside the cylinders with elliptical inlet ports having short axes of y = 10.3 mm and y = 8.3 mm, respectively. By combining Figure 10c,f with Figure 12, it can be seen that the temperature inside the hydrogen storage cylinder at the end of refueling first increases and then decreases as the roundness of the ellipse decreases, with the highest temperature observed inside the cylinder with an elliptical inlet port having a short axis of y = 10.3 mm. By comparing Figure 10f and Figure 12c,d, it is clear that the vortex radius inside the cylinder with an elliptical inlet port having a short axis of y = 10.3 mm is the largest, which leads to an increase in the degree of hydrogen friction and a significant temperature rise. When the elliptical roundness decreases, the hydrogen jets of the three types of cylinders basically do not tilt, and only the hydrogen jet inside the cylinder with an elliptical inlet port having a short axis y = 8.3 mm tilts slightly upward, but the angle is small and the thermal stratification phenomenon also increases first and then slows down. Because the elliptical hydrogen jet with the smallest roundness is slightly tilted upward, the thermal stratification inside its hydrogen storage cylinder is the most moderate. By combining the temperature rise and thermal stratification inside the hydrogen storage cylinder, the elliptical hydrogen inlet port with short axis y = 8.3 mm is found to be the best shape of hydrogen inlet port.

5. Conclusions

This paper is based on a three-dimensional finite element model of an on-board Type IV hydrogen storage cylinder. Research on the internal hydrogen behavior of hydrogen storage cylinders with different geometries of hydrogen inlet ports under rapid refueling was carried out. The specific conclusions are as follows:

• When the geometry of the hydrogen inlet port has interior angles, the smaller the roundness, the larger the angle between the hydrogen jet direction and the center axis. When the hydrogen inlet port geometry is rounded, the angle between the hydrogen jet direction and the center axis is small or even coincides with the center axis.
• When the roundness of the hydrogen inlet port geometry is small, the hydrogen inside the hydrogen storage cylinder forms an integral vortex below the center axis. As the roundness of the geometry increases, one vortex is formed on each side above and below the center axis.
• The greater the roundness of the hydrogen inlet port geometry, the more obvious the thermal stratification of hydrogen inside the cylinder, and the upward-tilted hydrogen jet can effectively slow down or even eliminate the thermal stratification phenomenon.
• To further enhance the sealing reliability of the hydrogen storage cylinder’s mouth, it is necessary to continue exploring the impact of the hydrogen inlet port’s roundness on the inflection points of the internal temperature, as well as the critical values of the hydrogen jet angles on the thermal stratification, and then to optimize the temperature suppression strategies.