Unconventional Fracture Networks Simulation and Shale Gas Production Prediction by Integration of Petrophysics, Geomechanics and Fracture Characterization
Abstract
1. Introduction
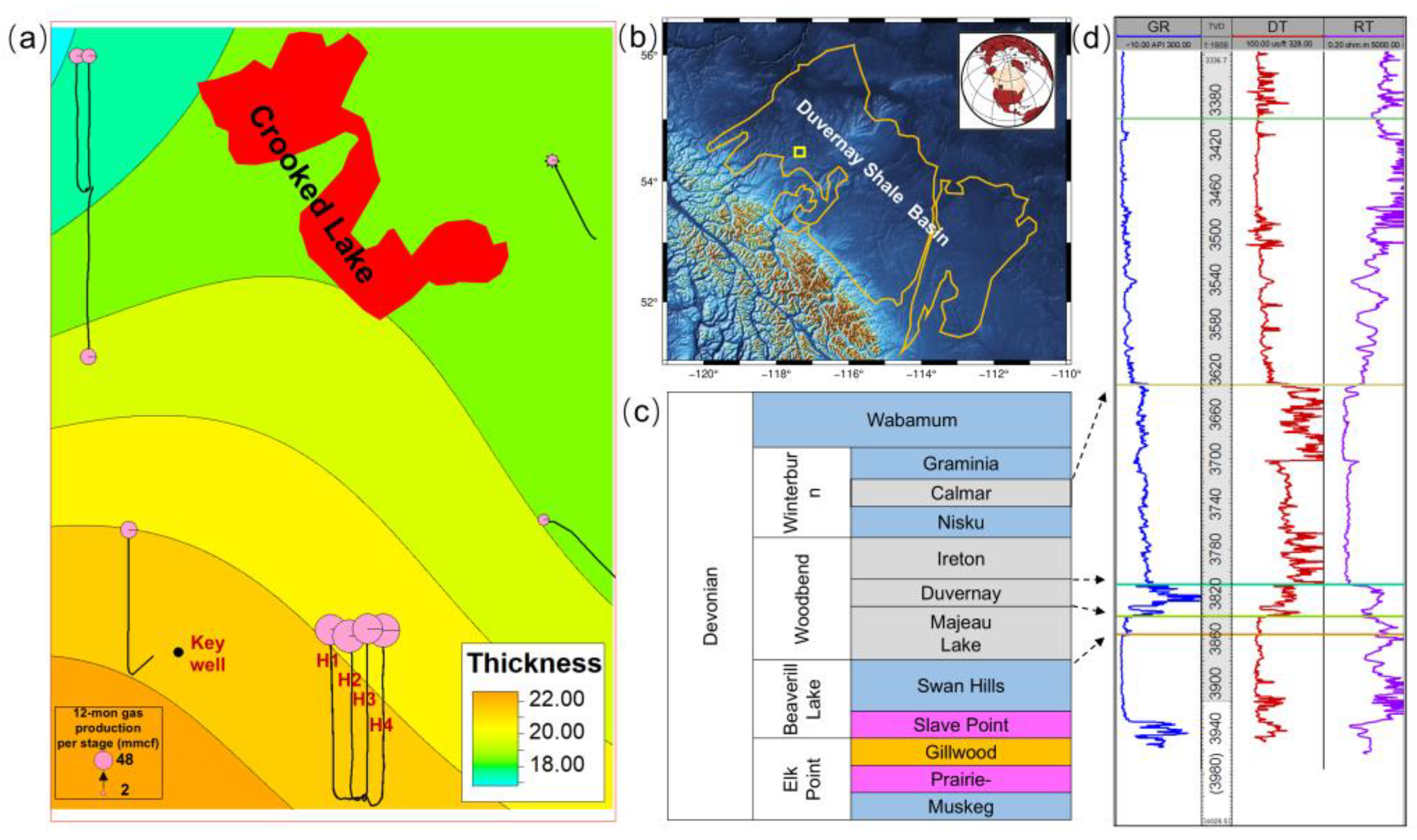
2. Field Background
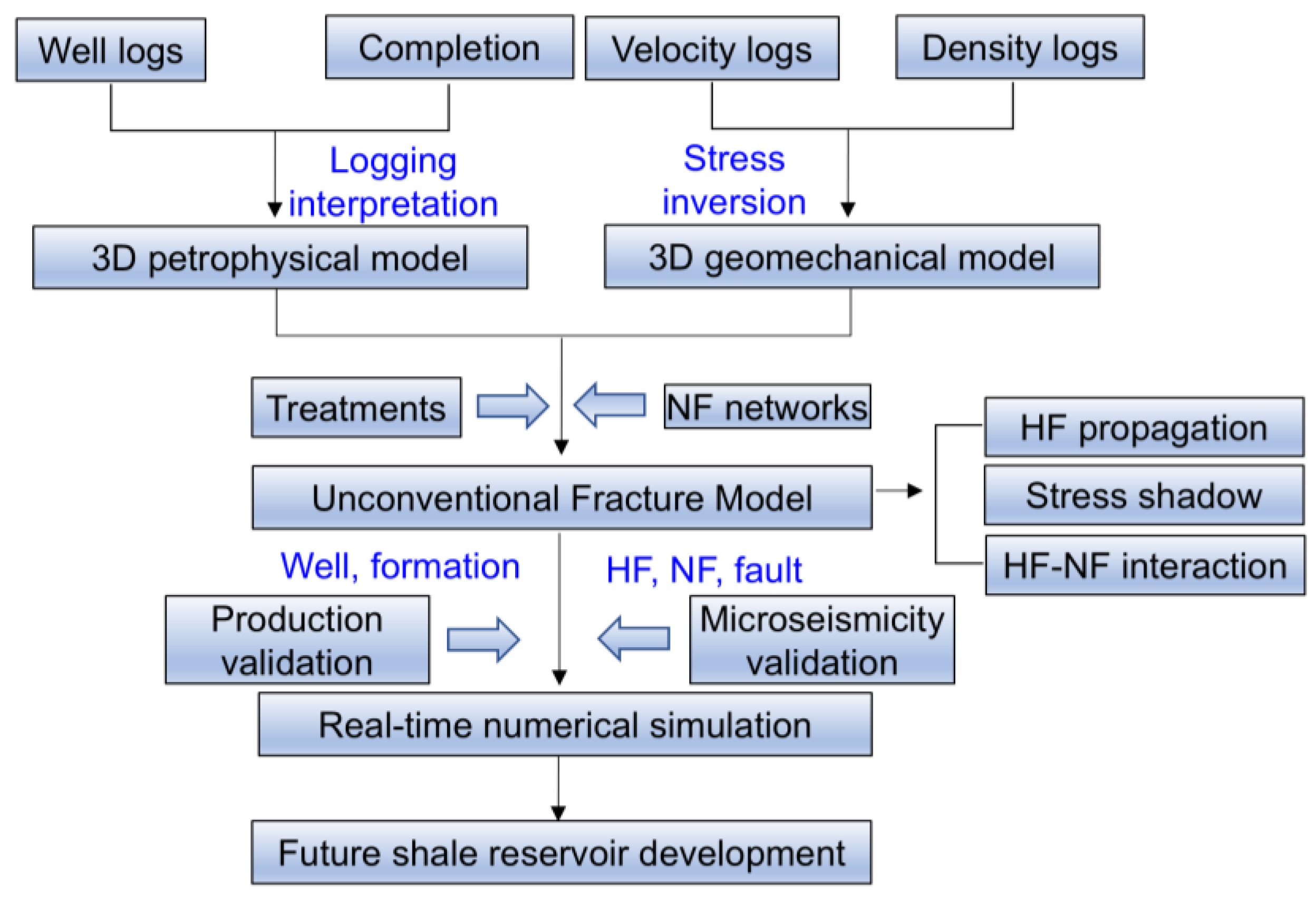
3. Methodology
3.1. Reservoir Petrophysics and Geomechanics Features
3.2. Unconventional Fracturing Modeling
3.3. Production Prediction via Reservoir Simulation
4. Results and Discussion
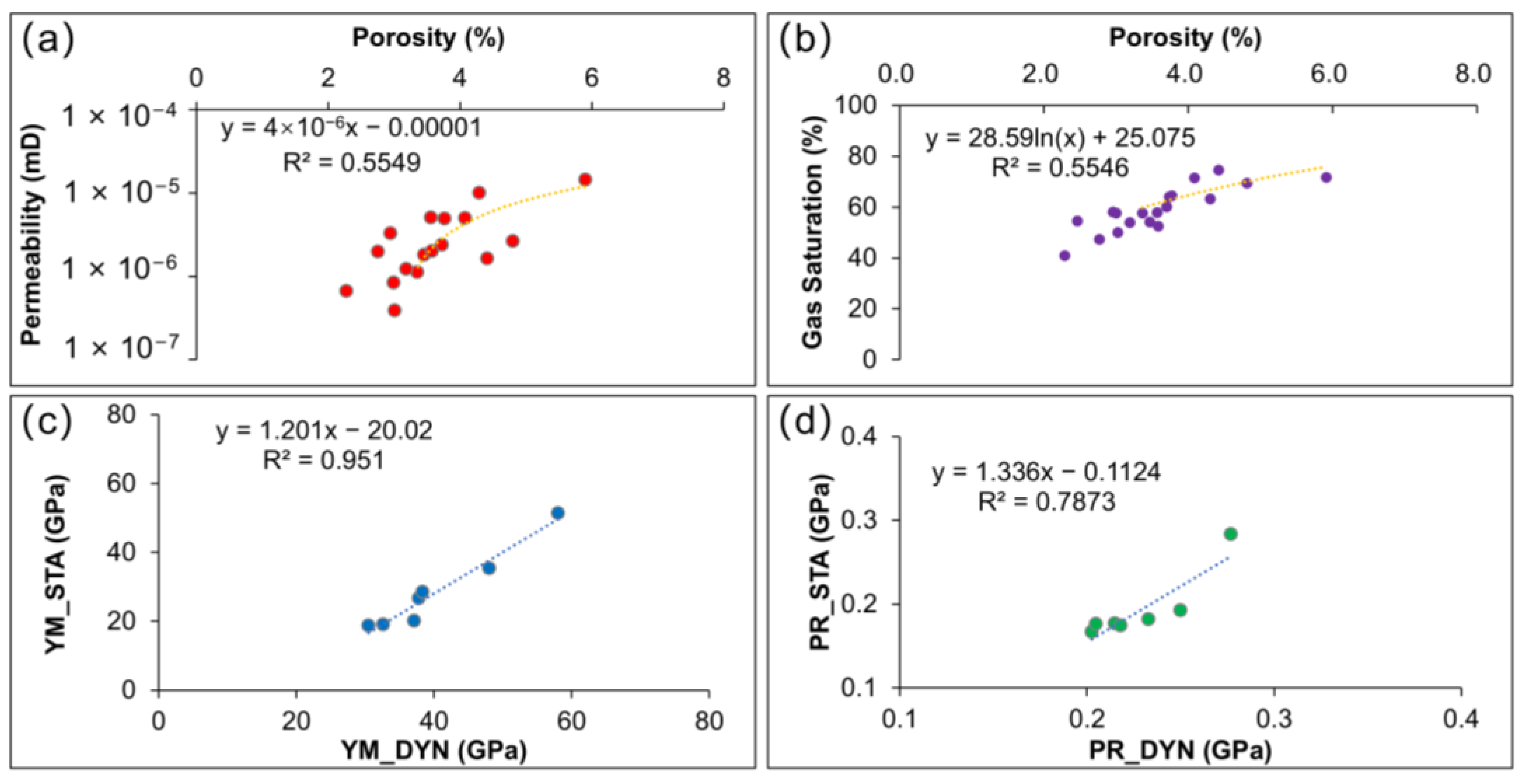
4.1. Reservoir Petrophysics and Geomechanics Characterization
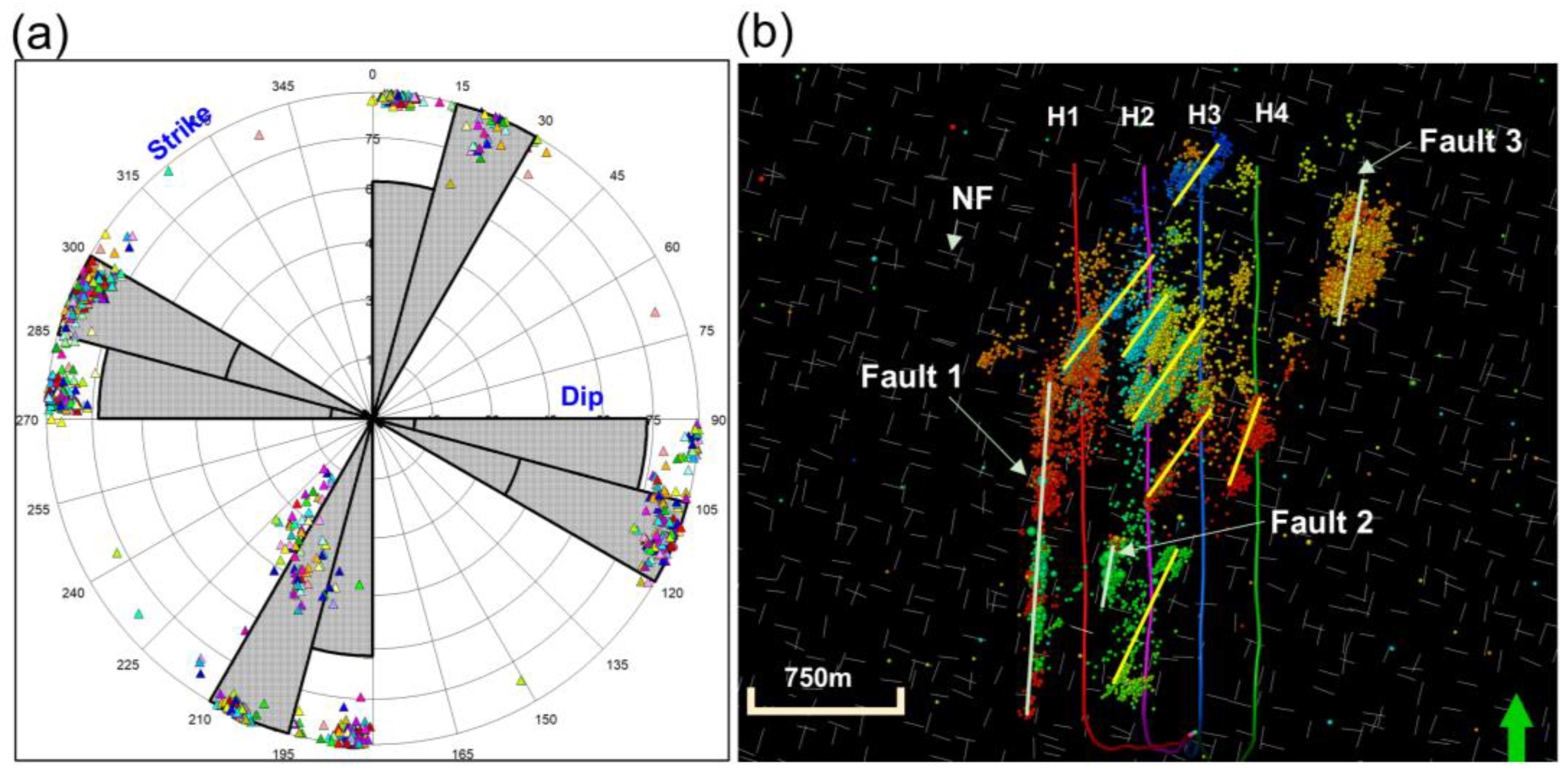
4.2. Unconventional Fracturing Model
4.3. UFM-Based Production Prediction Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA. Natural Gas Information: Overview; IEA: Paris, France, 2021; Available online: https://www.iea.org/reports/natural-gas-information-overview (accessed on 1 September 2024).
- Dunn, L.; Schmidt, G.; Hammermaster, K.; Brown, M.; Bernard, R.; Wen, E.; Befus, R.; Gardiner, S. The Duvernay Formation (Devo-nian): Sedimentology and reservoir characterization of a shale gas/liquids play in Alberta. In Proceedings of the GeoConvention 2012: Vision, Calgary, AB, Canada, 14–18 May 2012. [Google Scholar]
- Lyster, S.; Corlett, H.J.; Berhane, H. Hydrocarbon Resource Potential of the Duvernay Formation in Alberta—Update; AER/AGS Open-file Report 2017-02; Energy Resources Conservation Board: Edmonton, AB, Canada, 2017; 44p. [Google Scholar]
- Zhang, H.; Eaton, D.W.; Rodriguez, G.; Jia, S.Q. Source-Mechanism Analysis and Stress Inversion for Hydraulic-Fracturing-Induced Event Sequences near Fox Creek, Alberta. Bull. Seismol. Soc. Am. 2019, 109, 636–651. [Google Scholar] [CrossRef]
- Hui, G.; Chen, S.; He, Y.; Wang, H.; Gu, F. Machine Learning-Based Production Forecast for Shale Gas in Unconventional Reservoirs via Integration of Geological and Operational Factors. J. Nat. Gas Sci. Eng. 2021, 94, 104045. [Google Scholar] [CrossRef]
- Wang, S.; Chen, S. Insights to Fracture Stimulation Design in Unconventional Reservoirs Based on Machine Learning Modeling. J. Pet. Sci. Eng. 2019, 174, 682–695. [Google Scholar] [CrossRef]
- Li, Q.; Chen, M.; Fred, P.W.; Jin, Y.; Li, Z. Influences of engineering factors on shale gas productivity: A case study from the Haynesville shale gas reservoir in North America. Nat. Gas Ind. 2012, 32, 54–59. [Google Scholar]
- Kong, B.; Chen, S.; Chen, Z.; Zhou, Q. Bayesian Probabilistic Dual-Flow-Regime Decline Curve Analysis for Complex Production Profile Evaluation. J. Pet. Sci. Eng. 2020, 195, 107623. [Google Scholar] [CrossRef]
- Zhao, J.; Jin, L.; Azzolina, N.A.; Wan, X.; Yu, X.; Sorensen, J.A.; Kurz, B.A.; Bosshart, N.W.; Smith, S.A.; Wu, C.; et al. Investigating Enhanced Oil Recovery in Unconventional Reservoirs Based on Field Case Review, Laboratory, and Simulation Studies. Energy Fuels 2022, 36, 14771–14788. [Google Scholar] [CrossRef]
- Jiang, J.; Younis, R.M. Hybrid Coupled Discrete-Fracture/Matrix and Multicontinuum Models for Unconventional-Reservoir Simulation. SPE J. 2016, 21, 1009–1027. [Google Scholar] [CrossRef]
- Hui, G.; Chen, S.; Gu, F. Strike–Slip Fault Reactivation Triggered by Hydraulic-Natural Fracture Propagation during Fracturing Stimulations near Clark Lake, Alberta. Energy Fuels 2024, 38, 18547–18555. [Google Scholar] [CrossRef]
- Hui, G.; Chen, Z.; Wang, Y.; Zhang, D.; Gu, F. An integrated machine learning-based approach to identifying controlling factors of unconventional shale productivity. Energy 2023, 266, 126512. [Google Scholar] [CrossRef]
- Pawley, S.; Schultz, R.; Playter, T.; Corlett, H.; Shipman, T.; Lyster, S.; Hauck, T. The Geological Susceptibility of Induced Earthquakes in the Duvernay Play. Geophys. Res. Lett. 2018, 45, 1786–1793. [Google Scholar] [CrossRef]
- Hui, G.; Chen, Z.; Schultz, R.; Chen, S.; Song, Z.; Zhang, Z.; Song, Y.; Wang, H.; Wang, M.; Gu, F. Intricate Unconventional Fracture Networks Provide Fluid Diffusion Pathways to Reactivate Pre-Existing Faults in Unconventional Reservoirs. Energy 2023, 282, 128803. [Google Scholar] [CrossRef]
- Eaton, D.W.; Igonin, N.; Poulin, A.; Weir, R.; Zhang, H.; Pellegrino, S.; Rodriguez, G. Induced Seismicity Characterization during Hydraulic-Fracture Monitoring with a Shallow-Wellbore Geophone Array and Broadband Sensors. Seismol. Res. Lett. 2018, 89, 1641–1651. [Google Scholar] [CrossRef]
- Weir, R.; Lawton, D.; Lines, L.; Eyre, T.; Eaton, D. Application of Structural Interpretation and Simultaneous Inversion to Reservoir Characterization of the Duvernay Formation, Fox Creek, Alberta, Canada. Lead. Edge 2019, 38, 151–160. [Google Scholar] [CrossRef]
- Creaney, S.; Allan, J. Hydrocarbon Generation and Migration in the Western Canada Sedimentary Basin. Geol. Soc. Lond. Spec. Publ. 1990, 50, 189–202. [Google Scholar] [CrossRef]
- Li, G.; Luo, K.; Shi, D. Key Technologies, Engineering Management and Important Suggestions of Shale Oil/Gas Development: Case Study of a Duvernay Shale Project in Western Canada Sedimentary Basin. Pet. Explor. Dev. 2020, 47, 791–802. [Google Scholar] [CrossRef]
- Igonin, N.; Verdon, J.P.; Kendall, J.-M.; Eaton, D.W. Large-Scale Fracture Systems Are Permeable Pathways for Fault Activation During Hydraulic Fracturing. JGR Solid Earth 2021, 126, e2020JB020311. [Google Scholar] [CrossRef]
- Hui, G.; Chen, Z.; Chen, S.; Gu, F. Hydraulic fracturing-induced seismicity characterization through coupled modeling of stress and fracture-fault systems. Adv. Geo-Energy Res. 2022, 6, 269–270. [Google Scholar] [CrossRef]
- Chen, S.; Zhu, Y.; Wang, H.; Liu, H.; Wei, W.; Fang, J. Shale Gas Reservoir Characterisation: A Typical Case in the Southern Sichuan Basin of China. Energy 2011, 36, 6609–6616. [Google Scholar] [CrossRef]
- Tong, X.; Zhang, G.; Wang, Z.; Wen, Z.; Tian, Z.; Wang, H.; Ma, F.; Wu, Y. Distribution and Potential of Global Oil and Gas Resources. Pet. Explor. Dev. 2018, 45, 779–789. [Google Scholar] [CrossRef]
- Hui, G.; Chen, Z.; Yan, J.; Wang, M.; Wang, H.; Zhang, D.; Gu, F. Integrated Evaluations of High-Quality Shale Play Using Core Experiments and Logging Interpretations. Fuel 2023, 341, 127679. [Google Scholar] [CrossRef]
- Wozniakowska, P.; Eaton, D.W. Machine Learning-Based Analysis of Geological Susceptibility to Induced Seismicity in the Montney Formation, Canada. Geophys. Res. Lett. 2020, 47, e2020GL089651. [Google Scholar] [CrossRef]
- Weng, X.; Kresse, O.; Cohen, C.; Wu, R.; Gu, H. Modeling of Hydraulic-Fracture-Network Propagation in a Naturally Fractured Formation. SPE Prod. Oper. 2011, 26, 368–380. [Google Scholar]
- Weng, X.; Kresse, O.; Chuprakov, D.; Cohen, C.-E.; Prioul, R.; Ganguly, U. Applying Complex Fracture Model and Integrated Workflow in Unconventional Reservoirs. J. Pet. Sci. Eng. 2014, 124, 468–483. [Google Scholar] [CrossRef]
- Hui, G.; Chen, Z.-X.; Wang, H.; Song, Z.-J.; Wang, S.-H.; Zhang, H.-L.; Zhang, D.-M.; Gu, F. A Machine Learning-Based Study of Multifactor Susceptibility and Risk Control of Induced Seismicity in Unconventional Reservoirs. Pet. Sci. 2023, 20, 2232–2243. [Google Scholar] [CrossRef]
- Shen, L.W.; Schmitt, D.R.; Haug, K. Quantitative Constraints to the Complete State of Stress from the Combined Borehole and Focal Mechanism Inversions: Fox Creek, Alberta. Tectonophysics 2019, 764, 110–123. [Google Scholar] [CrossRef]
- Konstantinovskaya, E.; Li, Q.; Zhmodik, A.; Ibelegbu, C.; Schultz, R.; Shipman, T. Lateral Fluid Propagation and Strike Slip Fault Reactivation Related to Hydraulic Fracturing and Induced Seismicity in the Duvernay Formation, Fox Creek Area, Alberta. Geophys. J. Int. 2021, 227, 518–543. [Google Scholar] [CrossRef]
- Wang, R.; Wang, G.; Zhao, G.; Qian, M.; Liu, Y.; He, W.; Li, Z. Geological Characteristics and Resources Potential of Shale Oil in Chang 7 Member of Upper Triassic Yanchang Formation in Fuxian Area, Southern Ordos Basin, Western China. Unconv. Resour. 2023, 3, 237–247. [Google Scholar] [CrossRef]
- Valkó, P.; Economides, M.J. Performance of Fractured Horizontal Wells in High-Permeability Reservoirs. In Proceedings of the SPE Formation Damage Control Symposium, SPE, Lafayette, Louisiana, 14 February 1996; p. SPE-31149-MS. [Google Scholar]
- Wu, M.; Jiang, C.; Song, R.; Liu, J.; Li, M.; Liu, B.; Shi, D.; Zhu, Z.; Deng, B. Comparative Study on Hydraulic Fracturing Using Different Discrete Fracture Network Modeling: Insight from Homogeneous to Heterogeneity Reservoirs. Eng. Fract. Mech. 2023, 284, 109274. [Google Scholar] [CrossRef]
- Davies, R.J.; Mathias, S.A.; Moss, J.; Hustoft, S.; Newport, L. Hydraulic Fractures: How Far Can They Go? Mar. Pet. Geol. 2012, 37, 1–6. [Google Scholar] [CrossRef]
- Song, R.; Liu, J.; Yang, C.; Sun, S. Study on the Multiphase Heat and Mass Transfer Mechanism in the Dissociation of Methane Hydrate in Reconstructed Real-Shape Porous Sediments. Energy 2022, 254, 124421. [Google Scholar] [CrossRef]
- Du, J.; Liu, H.; Ma, D.; Fu, J.; Wang, Y.; Zhou, T. Discussion on Effective Development Techniques for Continental Tight Oil in China. Pet. Explor. Dev. 2014, 41, 217–224. [Google Scholar] [CrossRef]
- Guo, X.; Wu, K.; Killough, J.; Tang, J. Understanding the Mechanism of Interwell Fracturing Interference with Reservoir/Geomechanics/Fracturing Modeling in Eagle Ford Shale. SPE Reserv. Eval. Eng. 2019, 22, 842–860. [Google Scholar] [CrossRef]
- Hu, S.; Zhu, R.; Wu, S.; Bai, B.; Yang, Z.; Cui, J. Exploration and Development of Continental Tight Oil in China. Pet. Explor. Dev. 2018, 45, 790–802. [Google Scholar] [CrossRef]
- Wan, Y.; Li, Z.; Lu, B. The development of Fayetteville shale play and its implications. Nat. Gas Geosci. 2019, 30, 1655–1666. [Google Scholar]
- Zou, C.; Pan, S.; Jing, Z.; Gao, J.; Yang, Z.; Wu, S.; Zhao, Q. Shale oil and gas revolution and its impact. Acta Pet. Sin. 2020, 41, 1–12. [Google Scholar]
- Zhao, W.; Xia, M.; Zhang, Y.; Zhang, F.; Zhang, Y.; Zhu, H. Current situation and progress of shale gas exploration and development in Canada. Int. Pet. Econ. 2013, 21, 41–46. [Google Scholar]







| Well Name | Lateral Length (m) | Average TVD (m) | Number of Stages | HF Start Date | Frac Fluid Volume (m3) | Proppant Amount (t) | Max Injection Rate (m3/min) | Avg Treating Pressure (MPa) |
|---|---|---|---|---|---|---|---|---|
| H1 | 2638.6 | 3456.5 | 31 | 20 November 2016 | 38,303 | 4712 | 11.7 | 73.3 |
| H2 | 2640.0 | 3456.3 | 125 | 25 October 2016 | 50,232 | 5505 | 5.2 | 71.6 |
| H3 | 2678.7 | 3448.9 | 31 | 18 November 2016 | 44,309 | 4755 | 11.9 | 70.7 |
| H4 | 2626.4 | 3445.3 | 31 | 17 November 2016 | 46,773 | 4632 | 12.07 | 73.2 |
| Simulation Results | Fracture 1 | Fracture 2 | Fracture 3 | Fracture 4 |
|---|---|---|---|---|
| Propped Final Extension of HFN | 271.99 m | 136.37 m | 92.96 m | 227.88 m |
| Avg Propped Fracture Height | 18.84 m | 23.37 m | 27.26 m | 15.53 m |
| Avg Propped Fracture Aperture | 5.02 mm | 6.28 mm | 6.71 mm | 6.28 mm |
| Average Fracture Conductivity | 160.84 mD·m | 198.50 mD·m | 215.42 mD·m | 196.29 mD·m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Wang, P.; Hui, G.; Kong, X.; Jia, Y.; Huang, L.; Bai, Y.; Pi, Z.; Li, Y.; Yao, F.; et al. Unconventional Fracture Networks Simulation and Shale Gas Production Prediction by Integration of Petrophysics, Geomechanics and Fracture Characterization. Energies 2024, 17, 5084. https://doi.org/10.3390/en17205084
Huang W, Wang P, Hui G, Kong X, Jia Y, Huang L, Bai Y, Pi Z, Li Y, Yao F, et al. Unconventional Fracture Networks Simulation and Shale Gas Production Prediction by Integration of Petrophysics, Geomechanics and Fracture Characterization. Energies. 2024; 17(20):5084. https://doi.org/10.3390/en17205084
Chicago/Turabian StyleHuang, Wensong, Ping Wang, Gang Hui, Xiangwen Kong, Yuepeng Jia, Lei Huang, Yufei Bai, Zhiyang Pi, Ye Li, Fuyu Yao, and et al. 2024. "Unconventional Fracture Networks Simulation and Shale Gas Production Prediction by Integration of Petrophysics, Geomechanics and Fracture Characterization" Energies 17, no. 20: 5084. https://doi.org/10.3390/en17205084
APA StyleHuang, W., Wang, P., Hui, G., Kong, X., Jia, Y., Huang, L., Bai, Y., Pi, Z., Li, Y., Yao, F., Bao, P., & Zhang, Y. (2024). Unconventional Fracture Networks Simulation and Shale Gas Production Prediction by Integration of Petrophysics, Geomechanics and Fracture Characterization. Energies, 17(20), 5084. https://doi.org/10.3390/en17205084







