Multi-Objetive Dispatching in Multi-Area Power Systems Using the Fuzzy Satisficing Method
Abstract
1. Introduction
2. Background and Related Works
2.1. Electricity Demand Control and Coverage
2.2. Power System Operation Planning
Short-Term Projection (STP)
2.3. Economic Operation
2.3.1. Multiple Area Dispatch
2.3.2. Multi-Objective Economic Dispatch
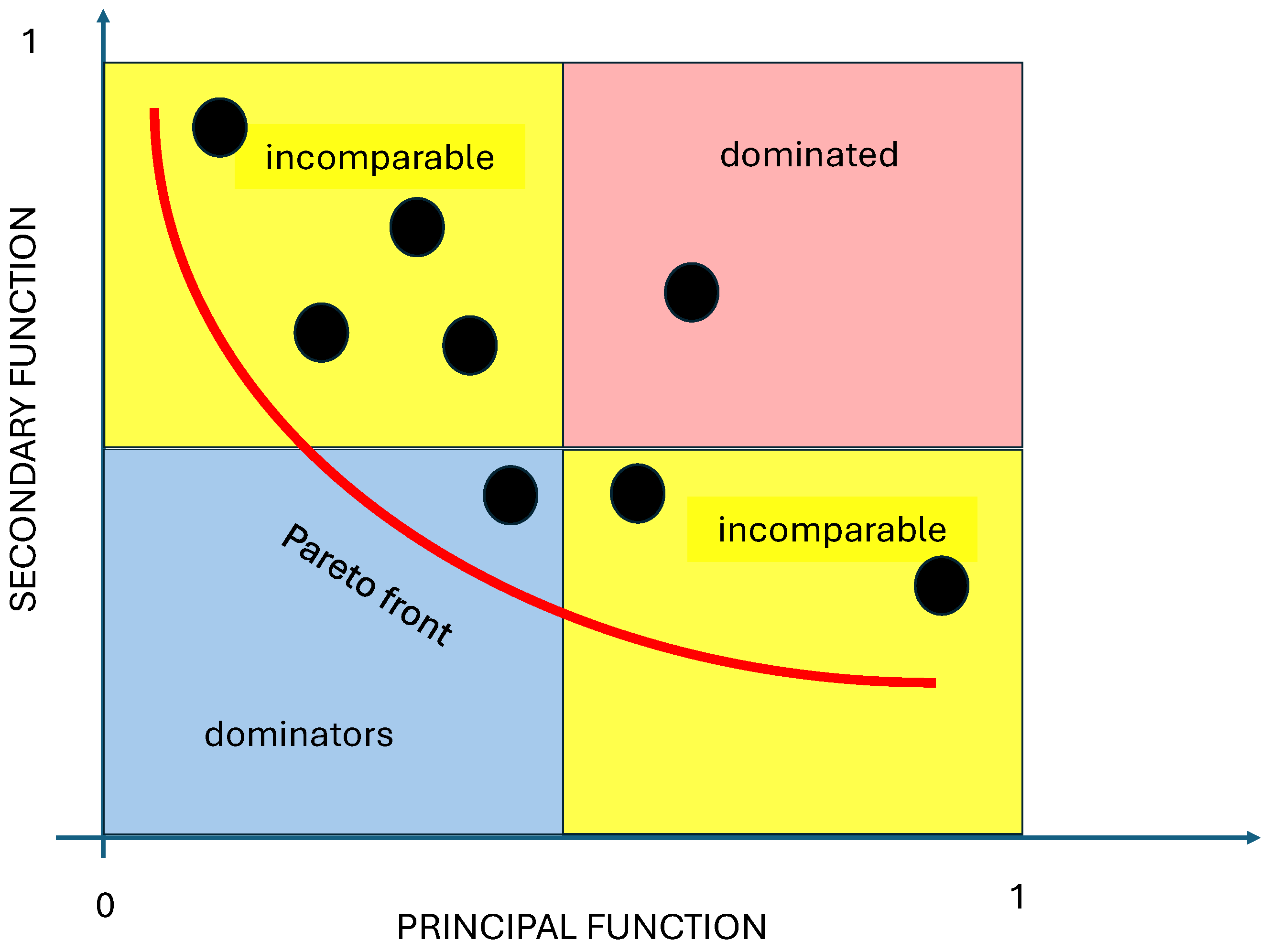
2.4. Pareto Front
Methodologies for Multi-Objective Dispatch Resolution
- a.
- Differential Evolution Method: Differential Evolution (DE) is a relatively recent population technique initially proposed by Storn and Price in 1995 as a heuristic method for minimizing nonlinear, nondifferentiable, continuous spatial functions. The DE algorithm has been applied to various fields of power system optimization [32]. Differential evaluation (DE) belongs to the class of evolutionary algorithms that include Evolutionary Strategies (ESs) and conventional genetic algorithms (CGAs). DE discerns the difference between two randomly chosen vectors from conventional genetic algorithms using perturbing vectors. Differential evolution is a scheme by which it generates test vectors from a set of initial populations. According to [32], when the differential evolution technique is applied to resolve DEMA and the results obtained with the same problem but using a conventional classical method (Newton–Raphson) and a classical heuristic method (Genetic Algorithm) are compared, remarkable benefits are observed.
- b.
- Particle swarm method: Particle swarm optimization (PSO) has been developed by simulating simplified social models. This algorithm is motivated by the behavior of organisms found in nature, such as flocks of birds or schools of fish, and uses a population-based search procedure. The algorithm probes a space by fitting the trajectories of individual vectors, which are referred to as particles since they are conceptualized as moving points in a multidimensional space. Individual particles are stochastically drawn to the positions of their previous best performance and the previous best performance of their neighbors [33]. The swarm method initializes with a set of random particles and then searches for optima by updating states. Each particle represents a feasible solution to the problem; in other words, each particle represents a point in the multidimensional search space, where the optimal point is to be determined. Each particle changes state around the multidimensional search space until a relatively immutable or optimal state is obtained. Using PSO for MAED solving is easy to implement and design compared to CGAs; however, the number of iterations increases significantly depending on the variables [33].
- c.
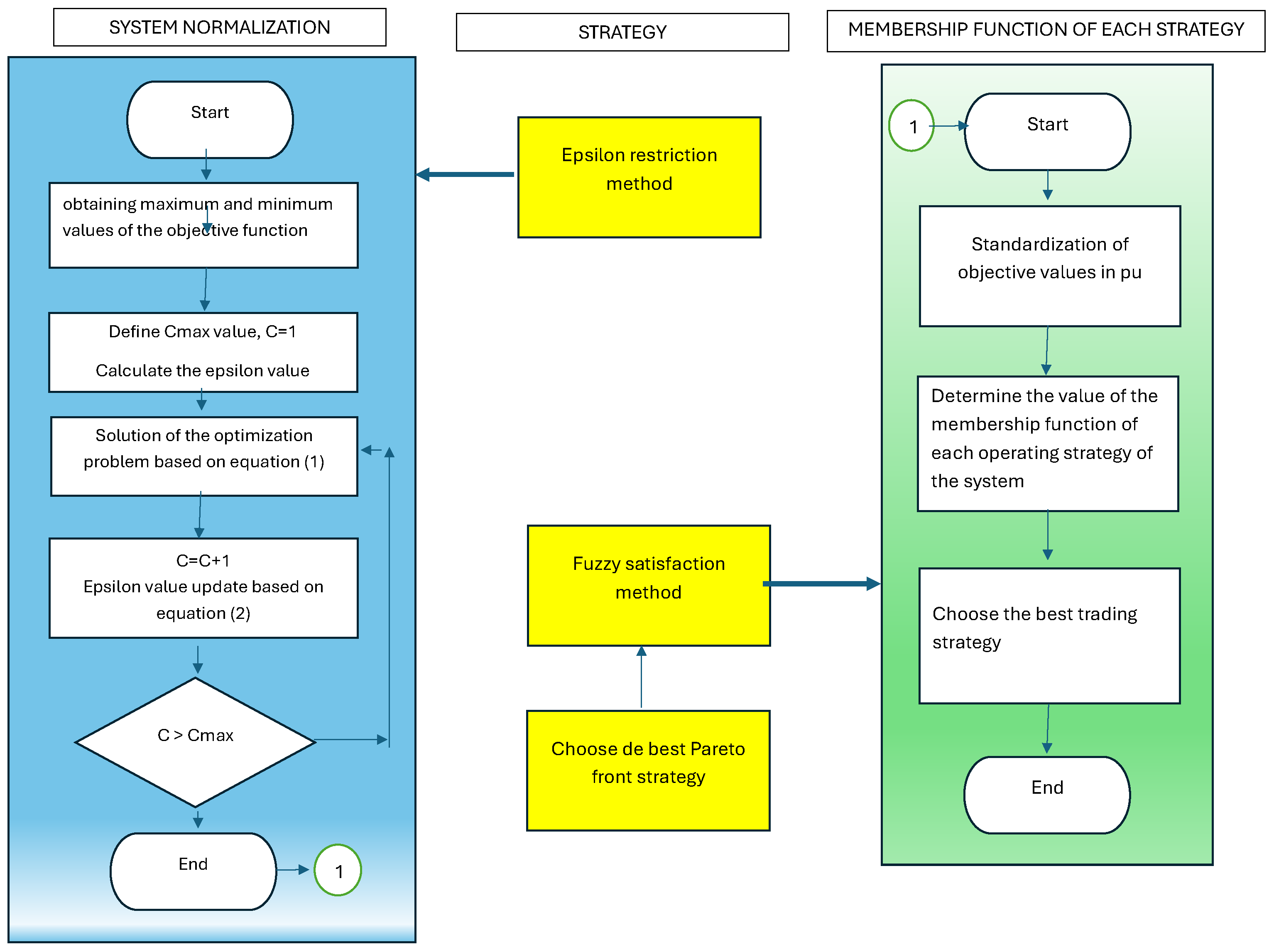
- constraint: The epsilon constraint () is one of the most used methodologies to solve multiobjective problems; it was proposed in 1975 by Lasdon, Wismer, and Haimes. This technique transforms a multiobjective model into a single-objective one by selecting a primary function and converting the others to constraints associated with epsilon parameters defined by each secondary objective function.
- d.
- Fuzzy satisficing approach: The fuzzy satisfying approach coordinates the multi-objective model, ensuring a precise trade-off between the preset objective functions. To achieve this, the objective values are first normalized in a unit system. We meticulously calculate the value of the membership function for each system operating strategy, leading us to select the best strategy from all the feasible options. This rigorous process is represented in Figure 3.
3. Mathematical Modeling
3.1. Objective Function Modeling
- Total operating cost of the system.
- Total cost for the production of the thermal generating park.
- Total cost for wind farm production.
- Total cost for the production of the photovoltaic generator farm.
- Index of modeled areas.
- Time period index.
- Index of thermal generators.
- Index of wind generators.
- Index of photovoltaic generators.
- Power generated by the thermal generator g located in area s in period p.
- Shape factor for the polynomial function of the cost function of the thermal generator g in area s.
- Factor of the displacement for the polynomial function of the cost function of the thermal generator g in area s.
- Constant for the polynomial function of the cost function of the thermal generator g in area s.
- Power generated by the wind generator w located in area s in period p.
- Power generated by photovoltaic generator r located in area s in period p.
- Selling price of energy from wind generator w located in area s.
- Selling price of energy from the photovoltaic generator r located in area s.
- Shape factor for the polynomial function of the emission function of the thermal generator g in area s.
- Factor of the displacement for the polynomial function of the emission function of the thermal generator g in area s.
- Constant for the polynomial function of the emission function of the thermal generator g in the area s.
3.2. Applicable Restrictions
- a.
- Demand supply: The restriction guarantees that the energy production, including the contributions of the exchanges between the areas, supplies the demand in each region and for each period.where:Demand in each period p for each area s.Flow exchanges between area s and area j in every period p.
- b.
- Flow exchanged between areas: The following inequality ensures that the flow between areas is within the technical limits of the link interconnecting them.where:Technical limit or capacity of the link interconnecting area s with area j.
- c.
- Bidirectional flow between areas: To model the flow exchange between areas, we establish mathematical formulations representing the bidirectional energy flow within a given hour and its relationship with link capacity. For this purpose, we develop the following restrictions.
- d.
- Technical limitation of generator production: The power dispatched by the generators depends on technical factors associated with their technology. For thermal generators, this means they are constrained by the maximum and minimum limits of their nominal capacity. Similarly, for generators using renewable energies, their production must stay within technical limits and consider the impact of resource utilization. The modeling for both cases is presented in the following formulation.where:Maximum limit of generator g located in area s.Maximum limit of generator r located in area s.Minimum limit of generator g located in area s.Maximum limit of generator w located in area s.Occurrence of the resource of generator w in area s.
- e.
- Increase and decrease in generated power: SavedGenerators with thermal technology must consider their technical limitations when increasing or reducing energy production during each hourly period analyzed. We establish the following equations for this purpose.where:Energy delivery limit of generator g located in area s for each of the periods of time.Energy reduction limit of generator g located in area s for each of the periods of time.
- f.
- System reserve: The supply of the demand in each area must be guaranteed, including the power reserve of each location, whose formulation corresponds to the following:where:Percentage of power reserve in area s.Maximum demand in area s.
3.3. Fuzzy Satisfaction and -Constraint
- 1
- Solve the optimization problem independently for each of the objective functions.
- 2
- Establish the minimum value of each one of the objective functions for each one of the resolutions carried out.
- 3
- Compute a constraint (-constraint) for each objective function.
- 4
- Vary from to , taking into account the number of events to simulate (n), maximizing in each event the , based on the following formulation.where:: Corresponding value of the counter to define a point of the Pareto front.: Total of the events evaluated in the counter.
- 5
- Each value obtained by solving each event using -constraint belongs to a solution of the optimization model.
- 6
- The Pareto front will be formed by the number of values obtained using -constraint.
3.4. Pseudocode
4. Model Application
4.1. Power Generating Plant
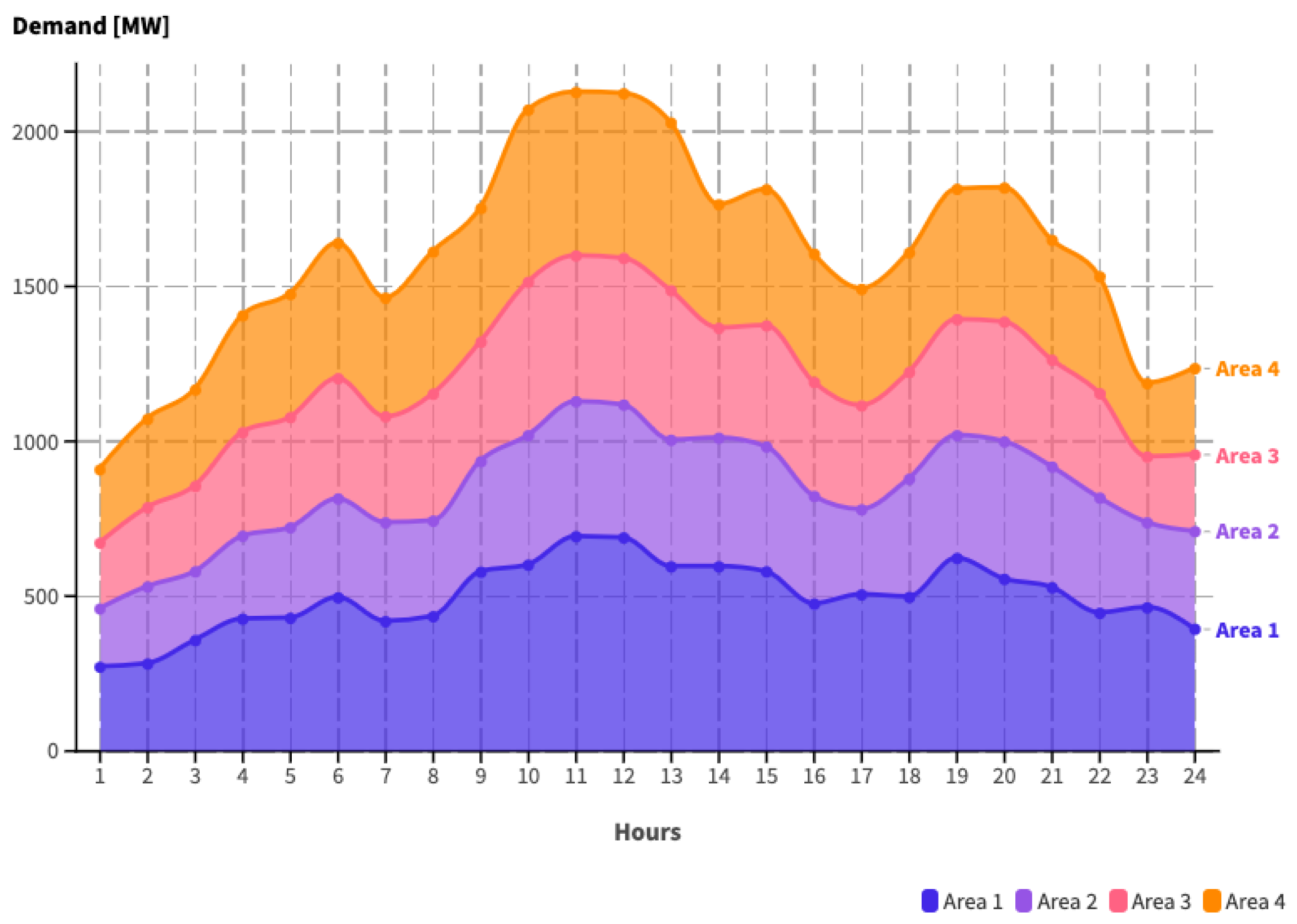
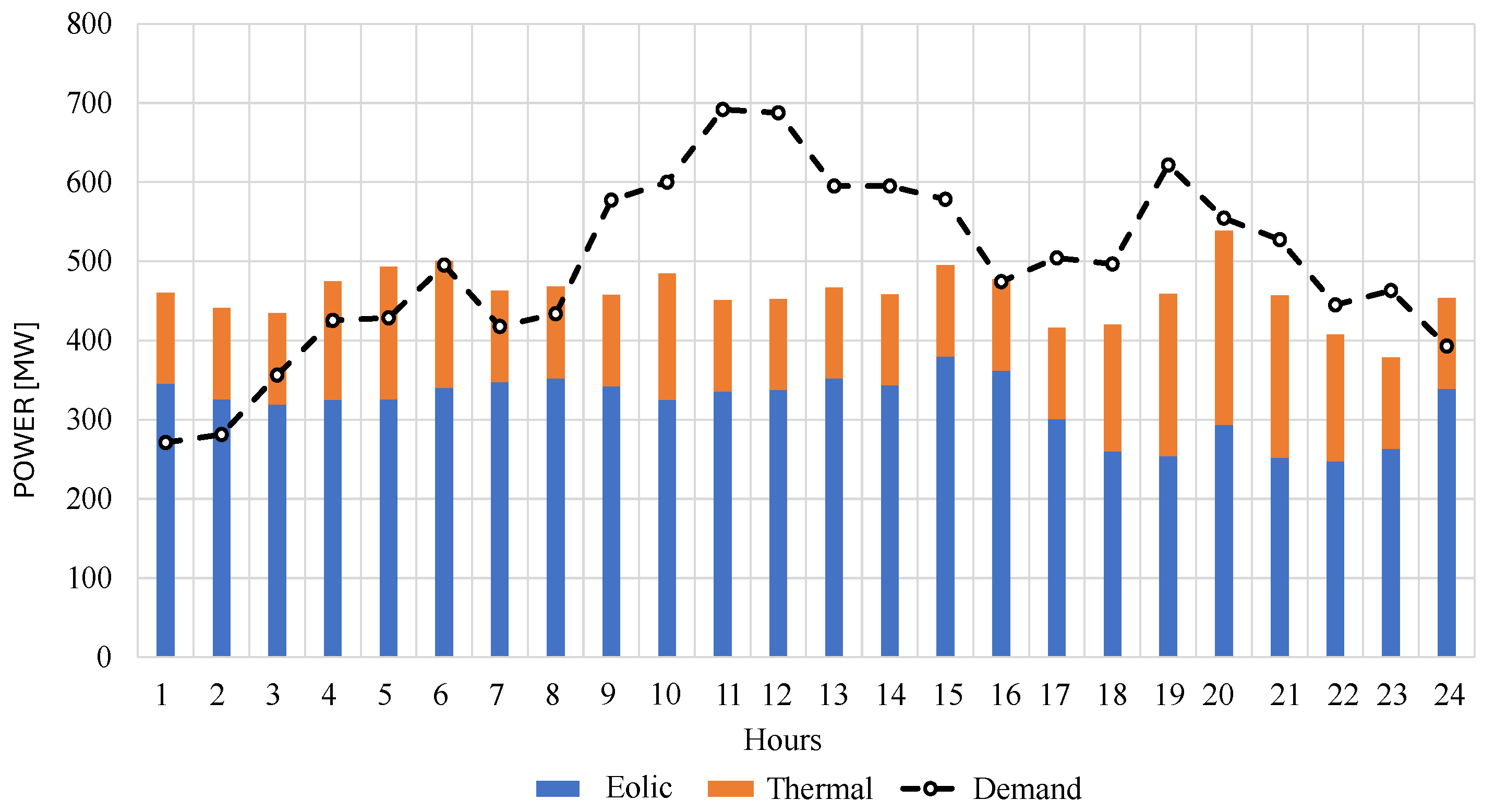
4.2. Demand
4.3. Links between Areas
4.4. Study Case
- i
- Case 1: In this study, we carry out energy dispatch in each area, allowing the generators to supply the demand autonomously and independently. Consequently, we do not model the interconnection of the areas. We will compare the resulting values of this study with those from the other two studies to validate the economic and technical parameters. We do not consider multi-objective modeling in this study.
- ii
- Case 2: In this case, we will model the interconnection of the different proposed areas, allowing us to understand the generators’ interaction in supplying demand in each area. We do not consider multi-objective modeling in this study. We will analyze and evaluate the economic and energy results by comparing them with cases 1 and 3, quantifying technical and economic variables.
- iii
- Case 3: This case will model the multi-objective problem, and additional areas will be interconnected; these premises’ interaction must guarantee each area’s global and individual demand. The results will be compared with those obtained in cases 1 and 2.
4.5. Parameters for Studies
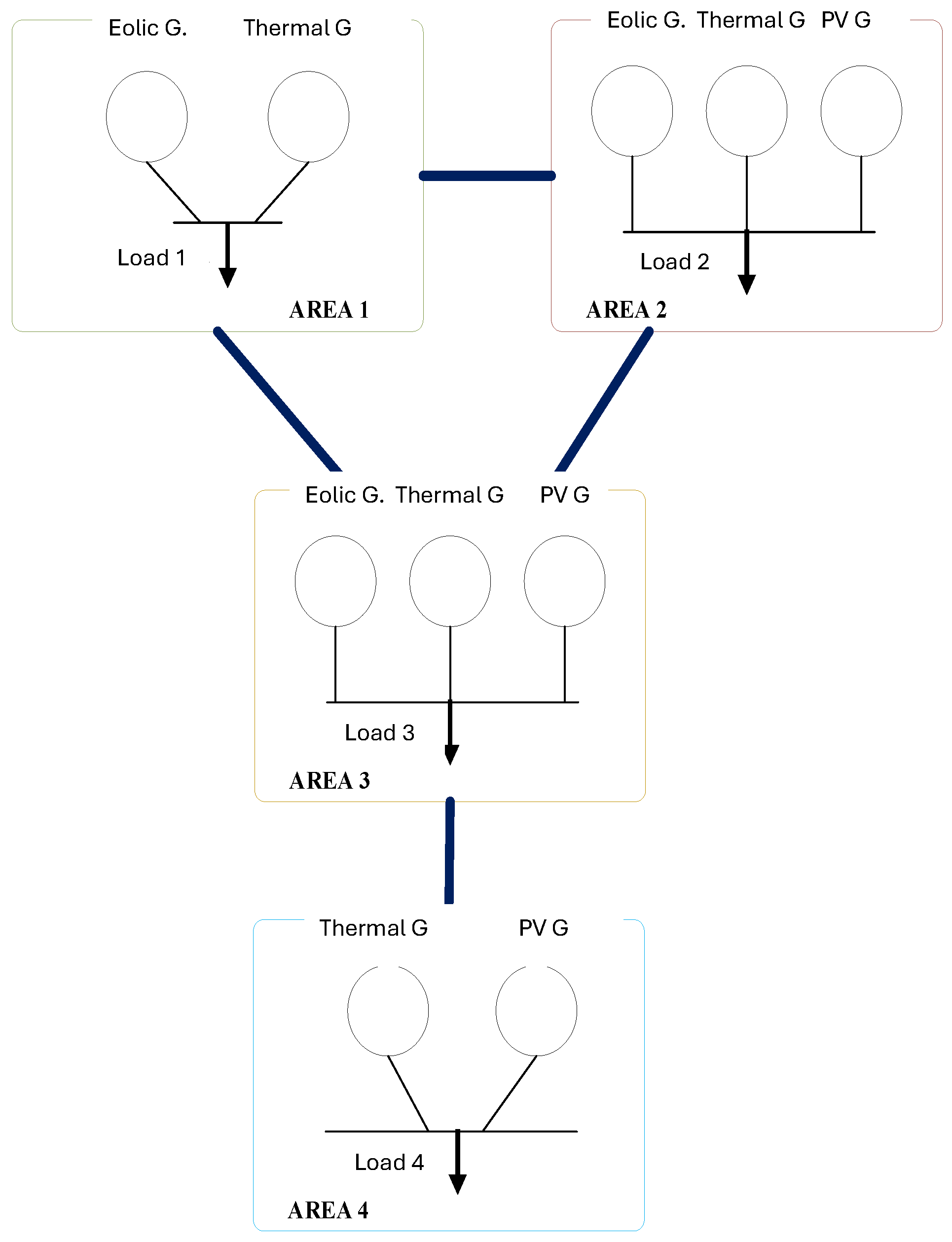
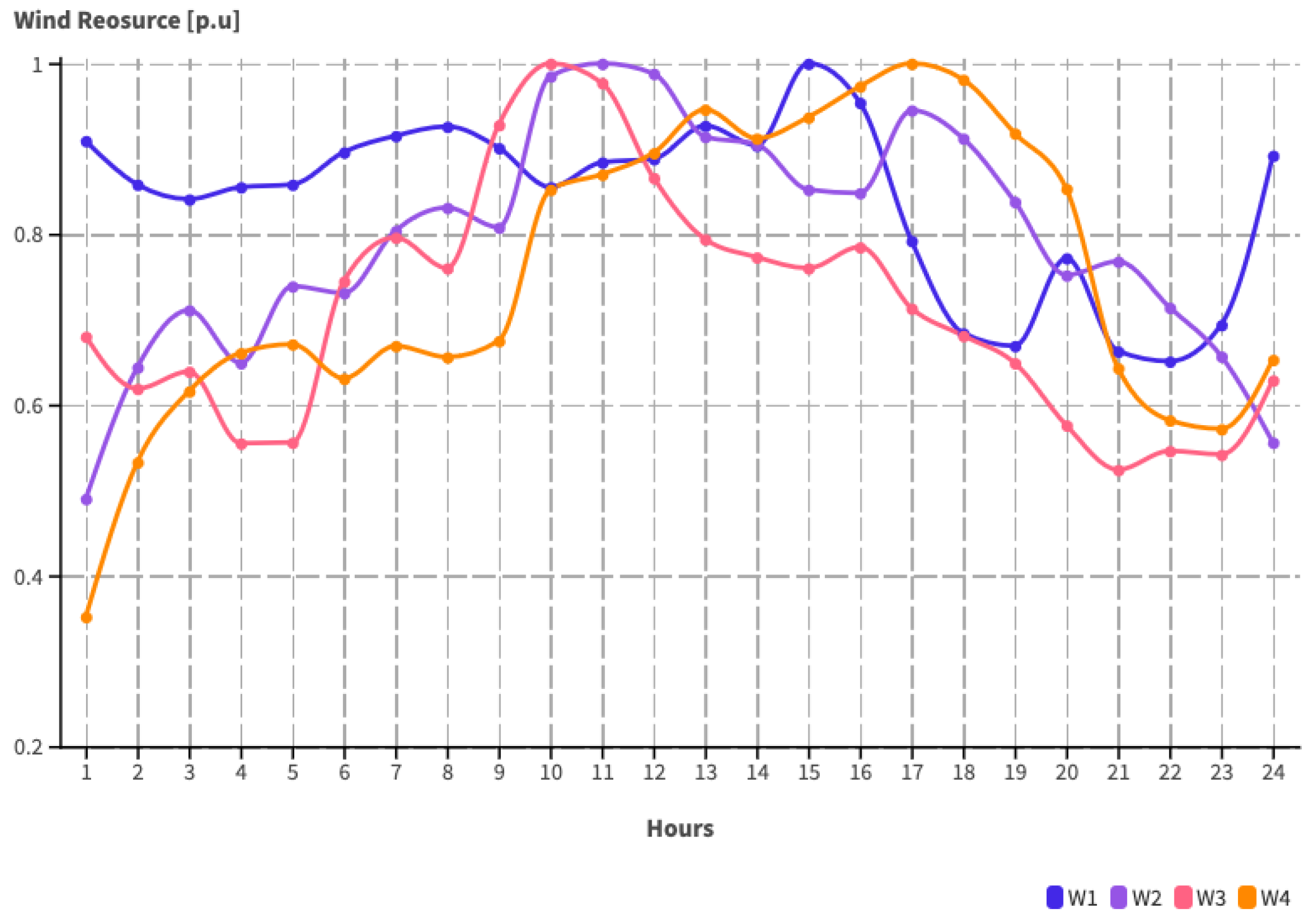
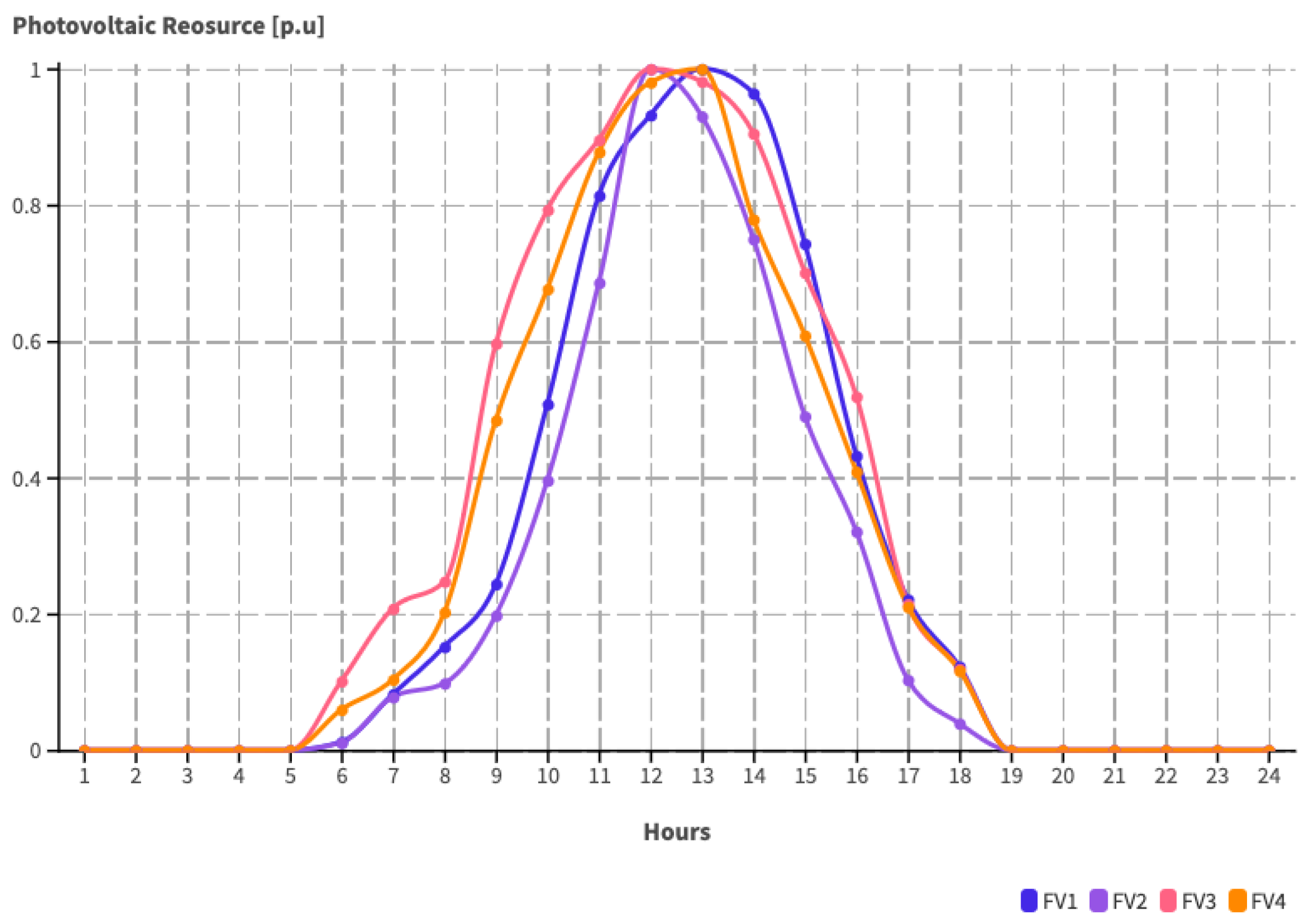
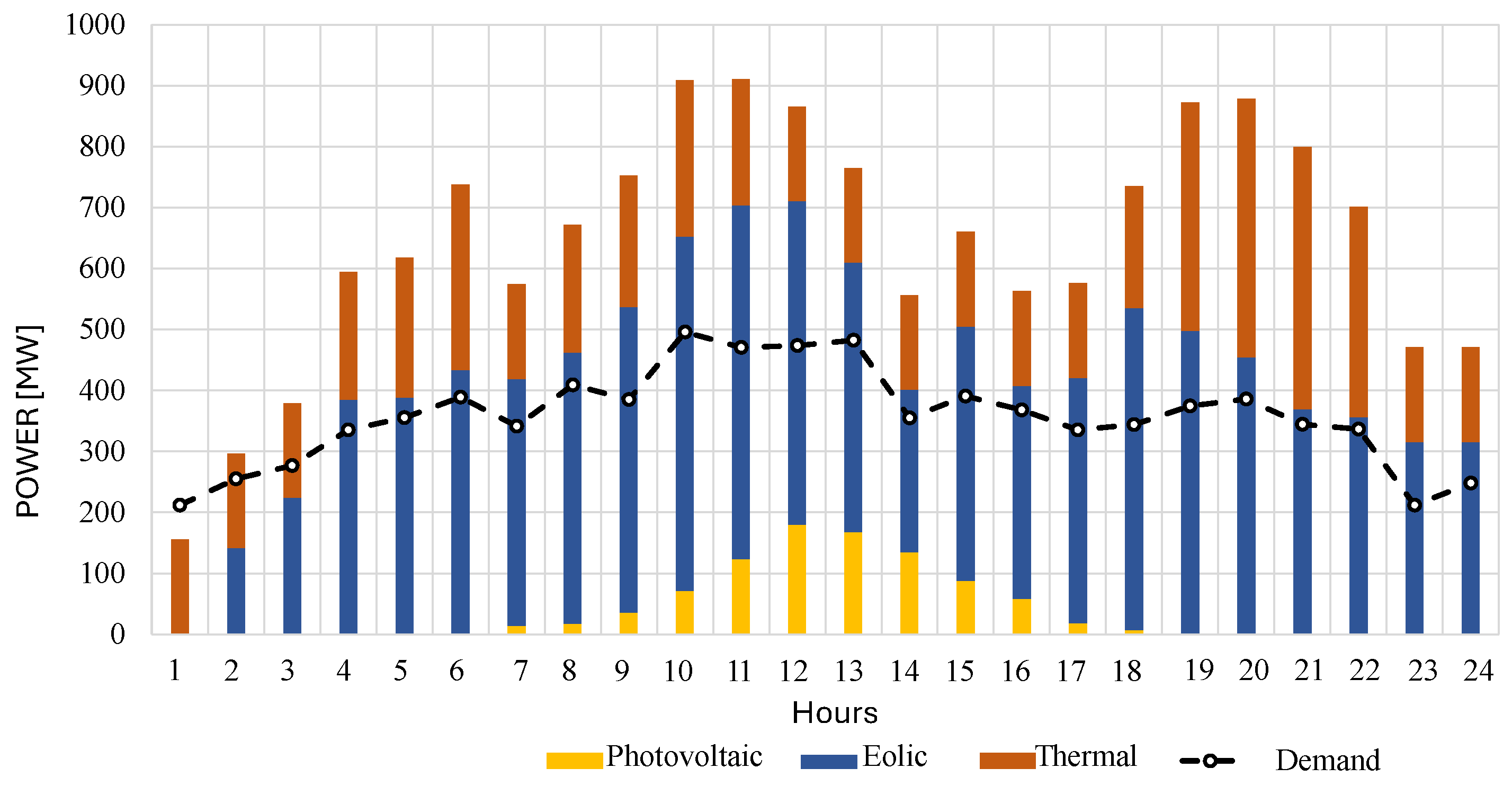
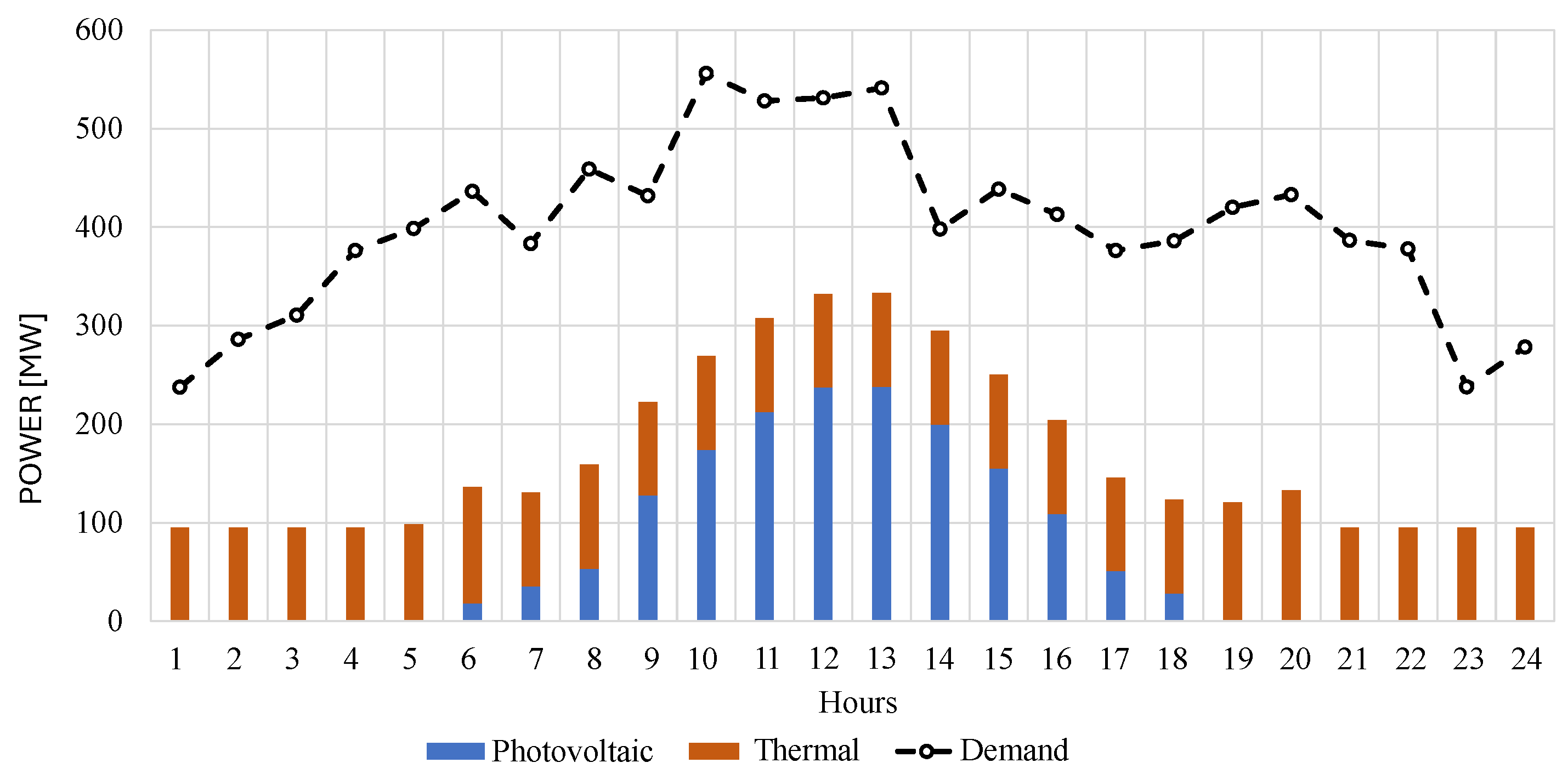
- Area 1 consists of four thermal-type generators with a total capacity of 870 MW and a wind unit with a capacity of 380 MW. It is interconnected with areas 2 and 3.
- Area 2 consists of three thermal generators with a total capacity of 630 MW, a photovoltaic generator with a capacity of 150 MW, and a wind generator with a capacity of 270 MW; it is interconnected with areas 1 and 3.
- Area 3 has a generator park with four thermal generators, each with a total capacity of 650 MW, two wind units, each with a capacity of 300 MW and 330 MW, and a 180 MW photovoltaic unit.
- Area 4 has a 680 MW generator park with thermal technology and two photovoltaic generators of 100 and 140 MW; it is interconnected only with area 3.
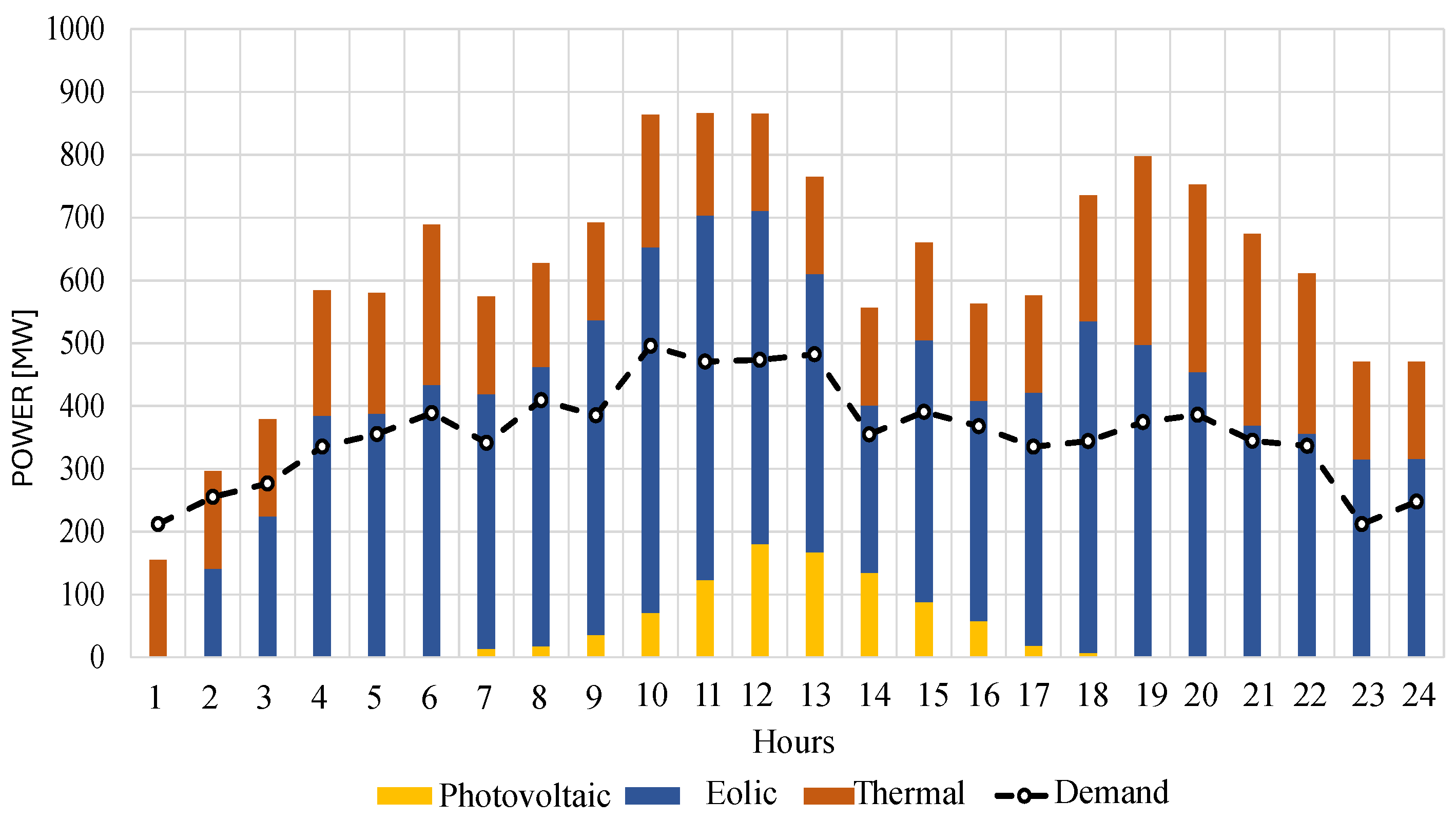
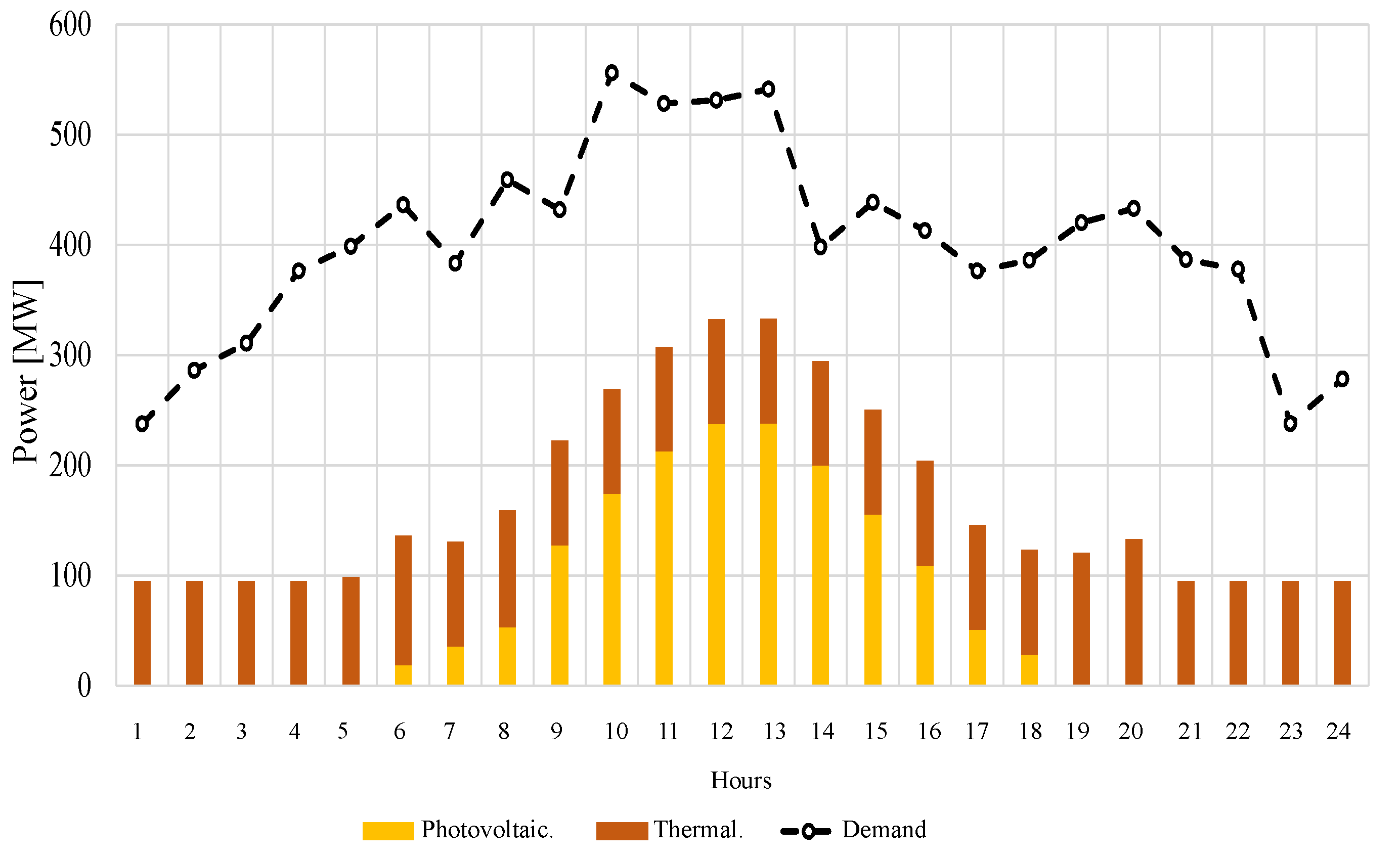
5. Analysis of Results
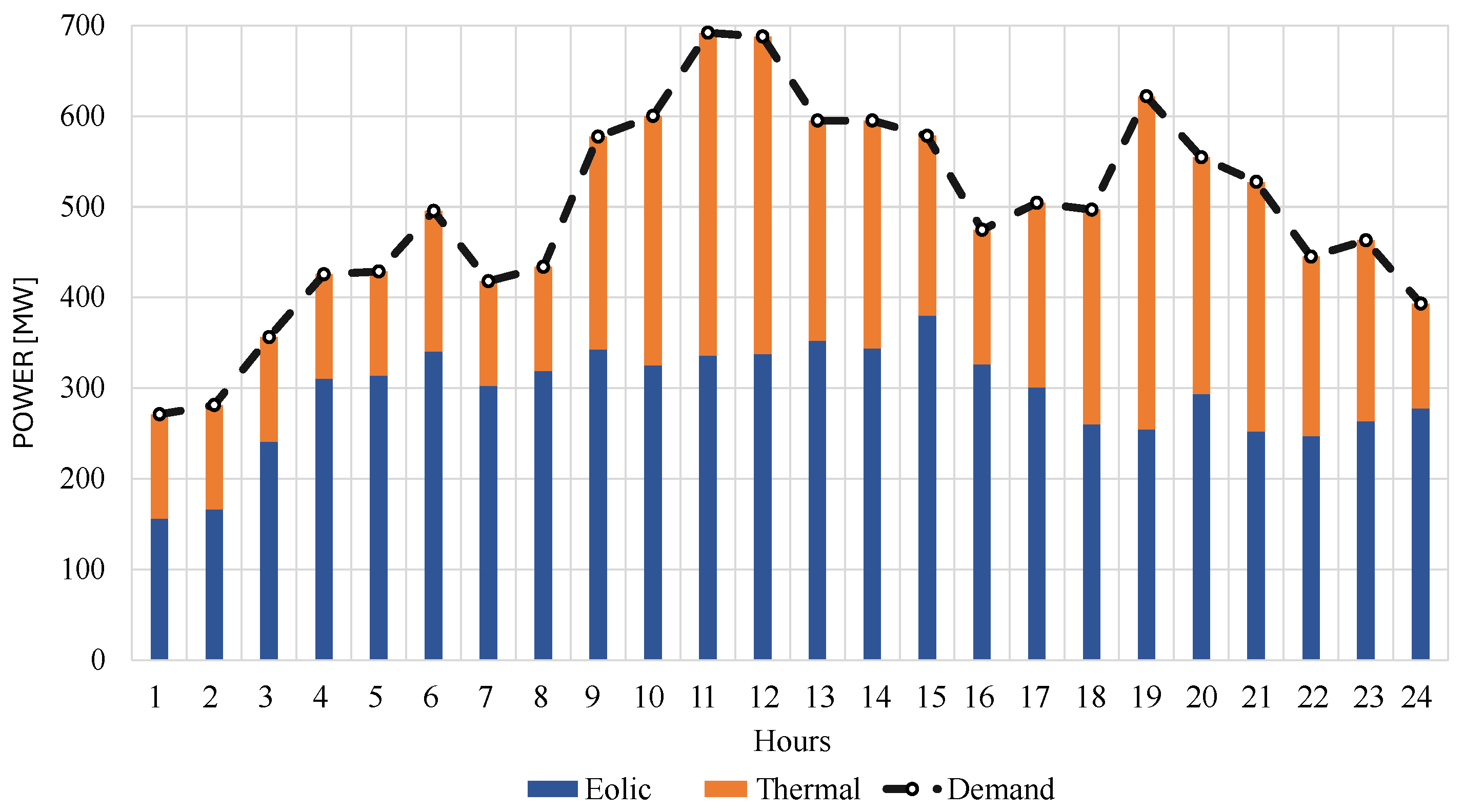
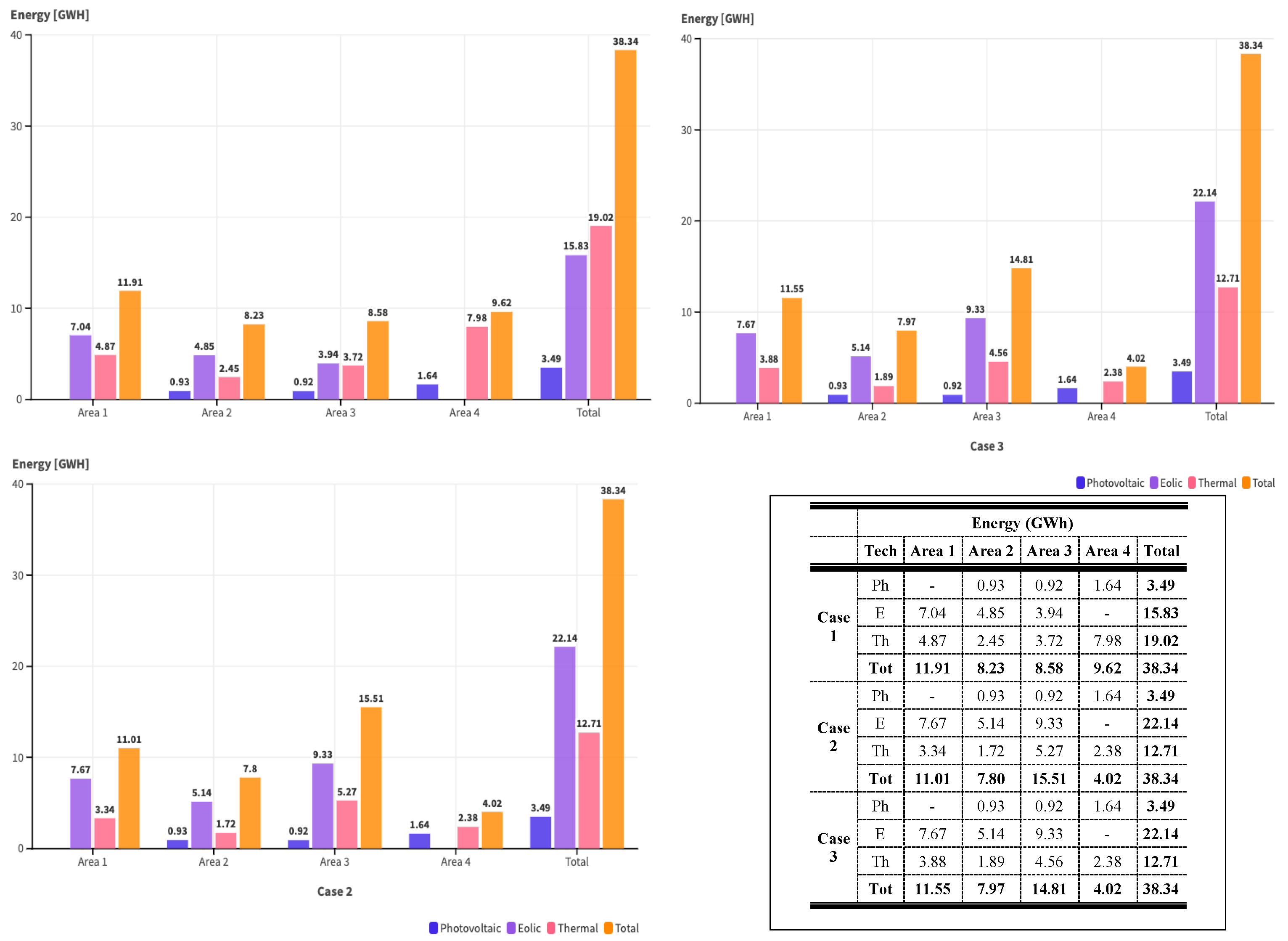
5.1. Case 1
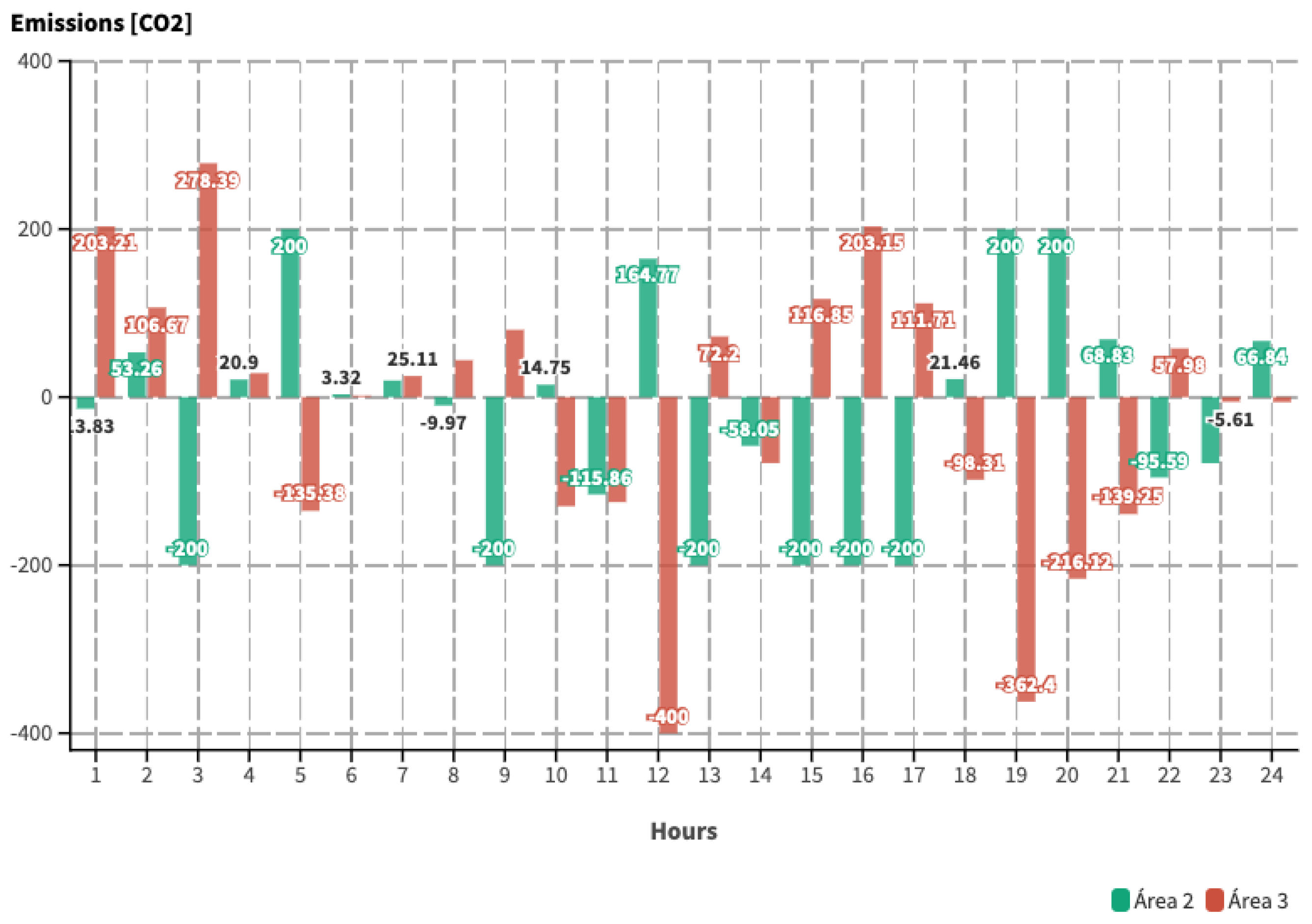
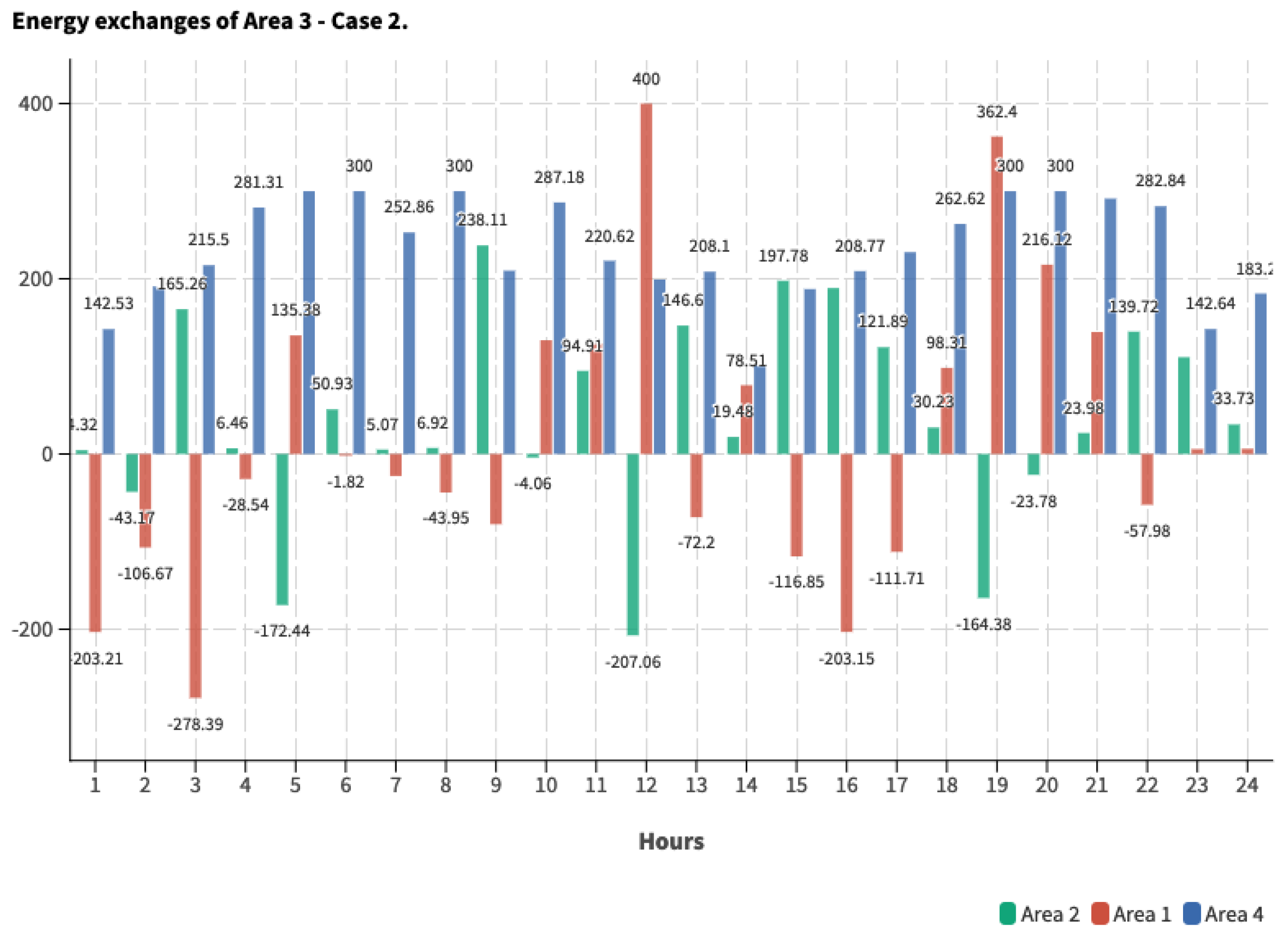
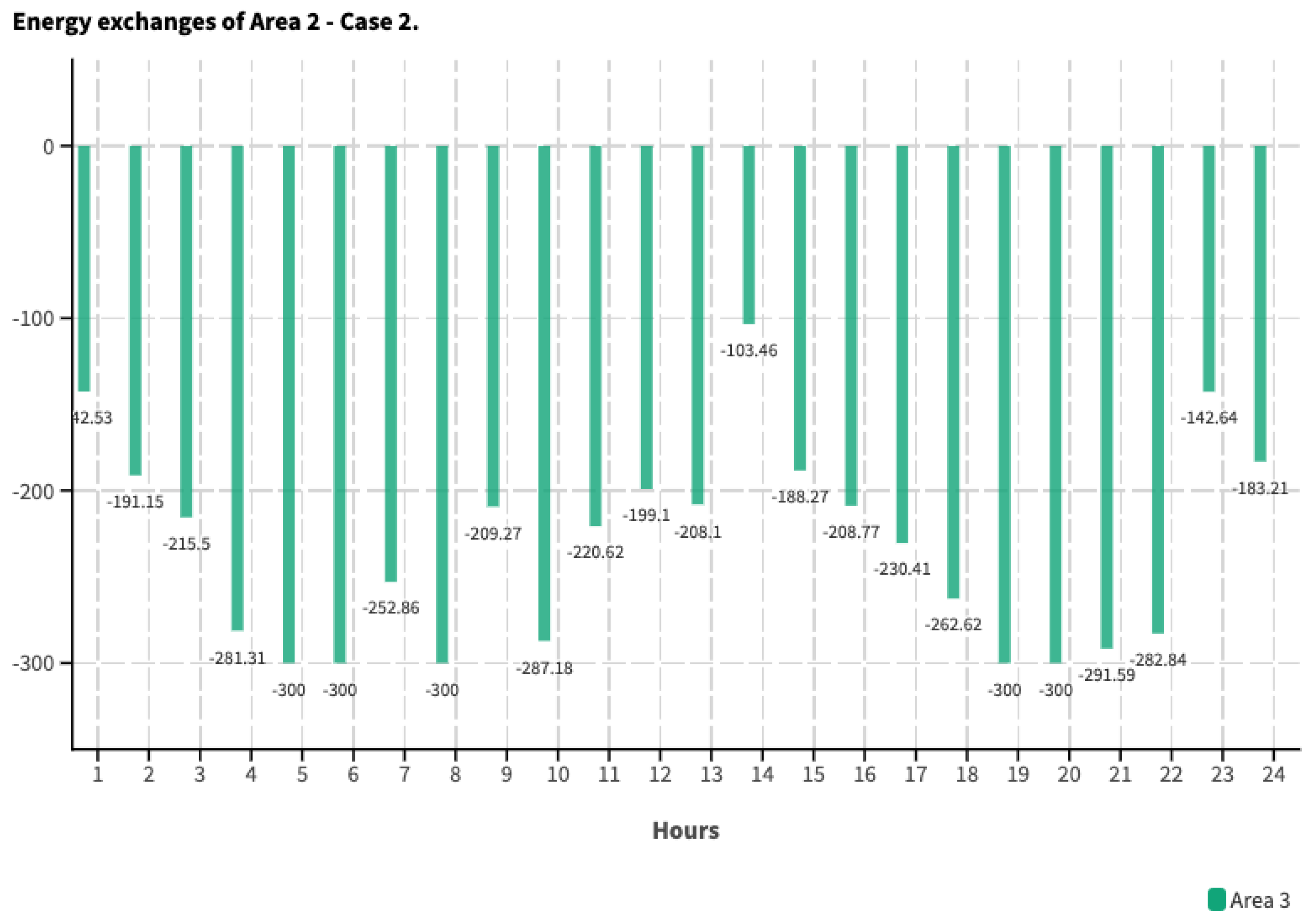
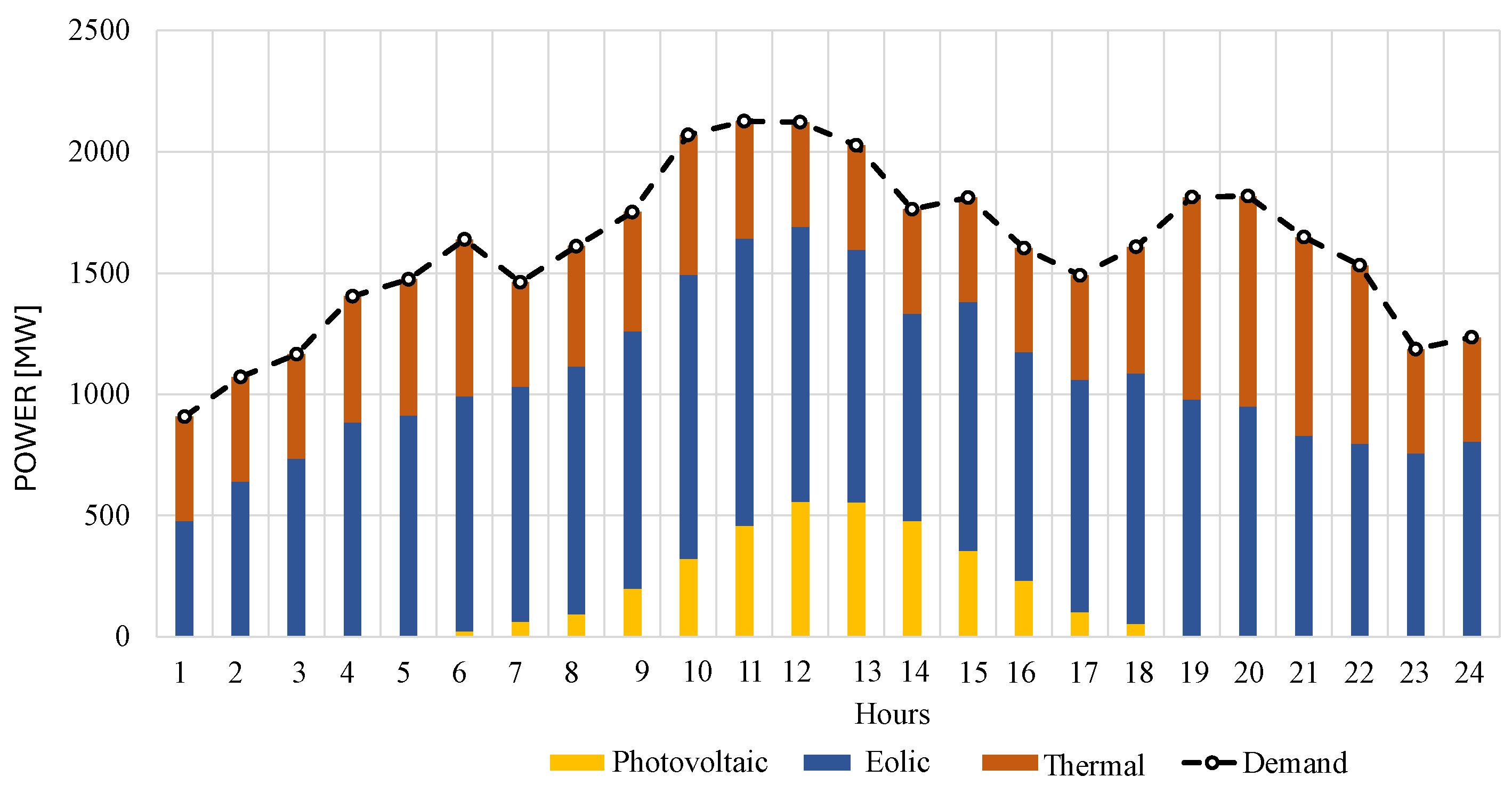
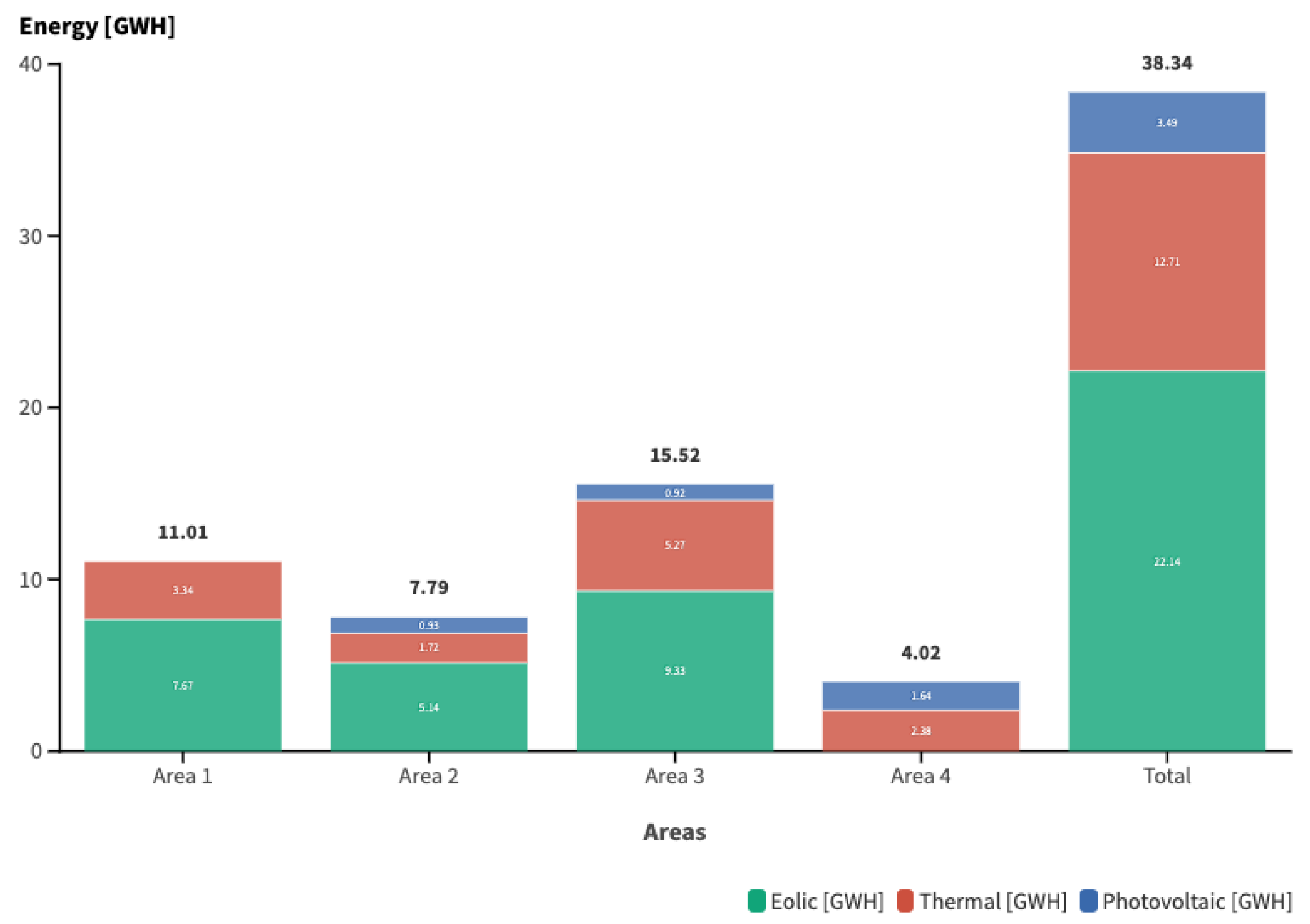
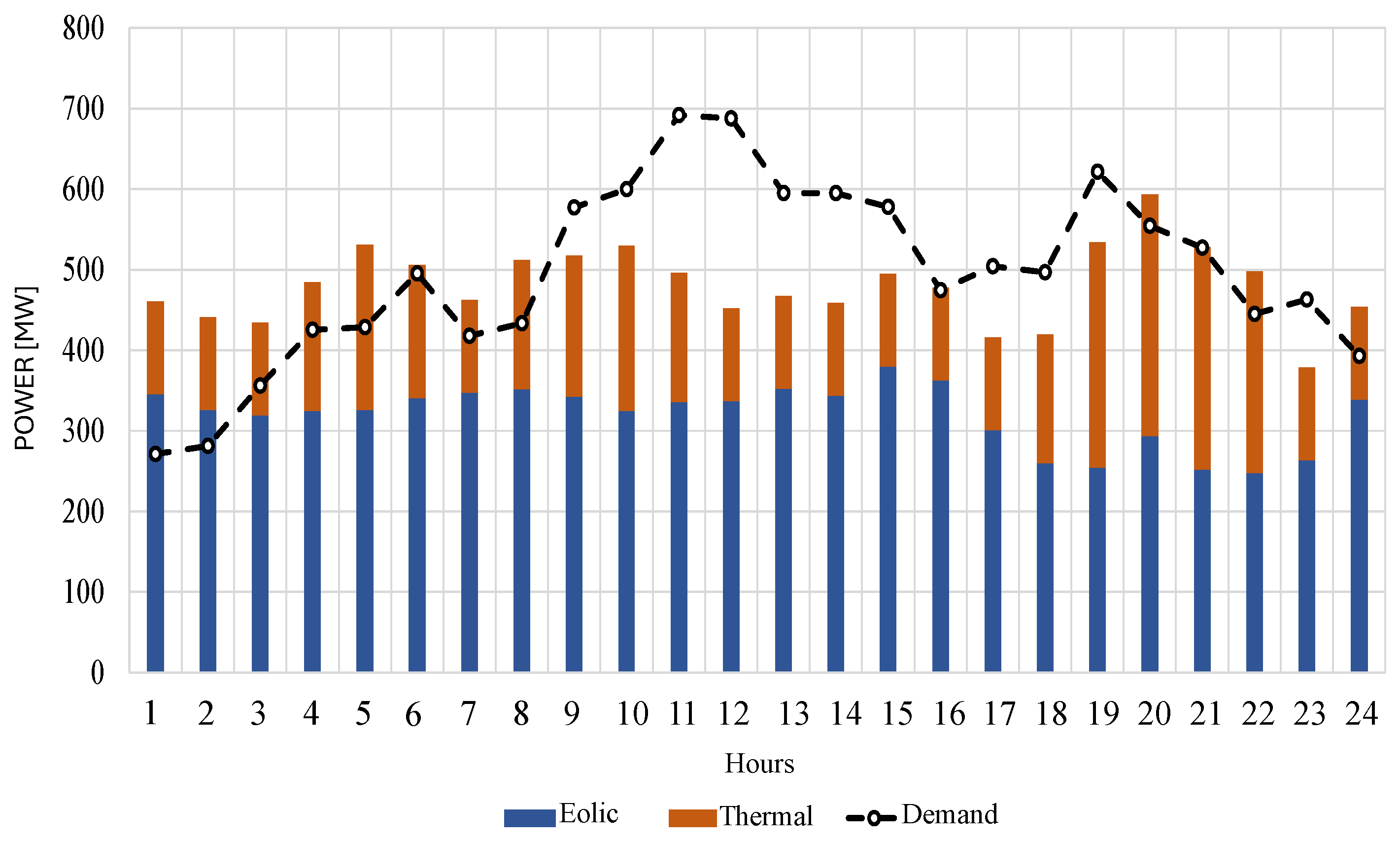
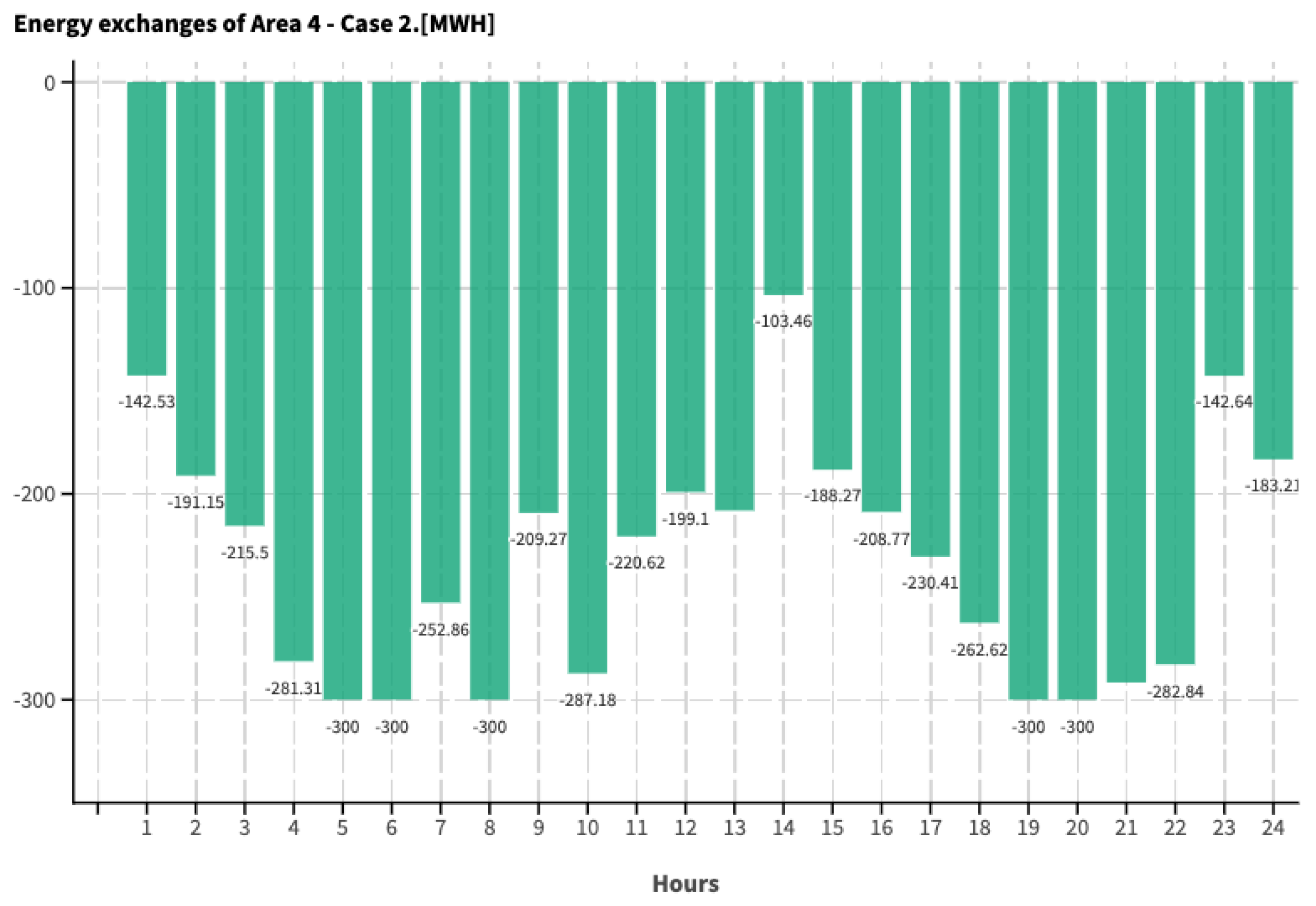
5.2. Case 2
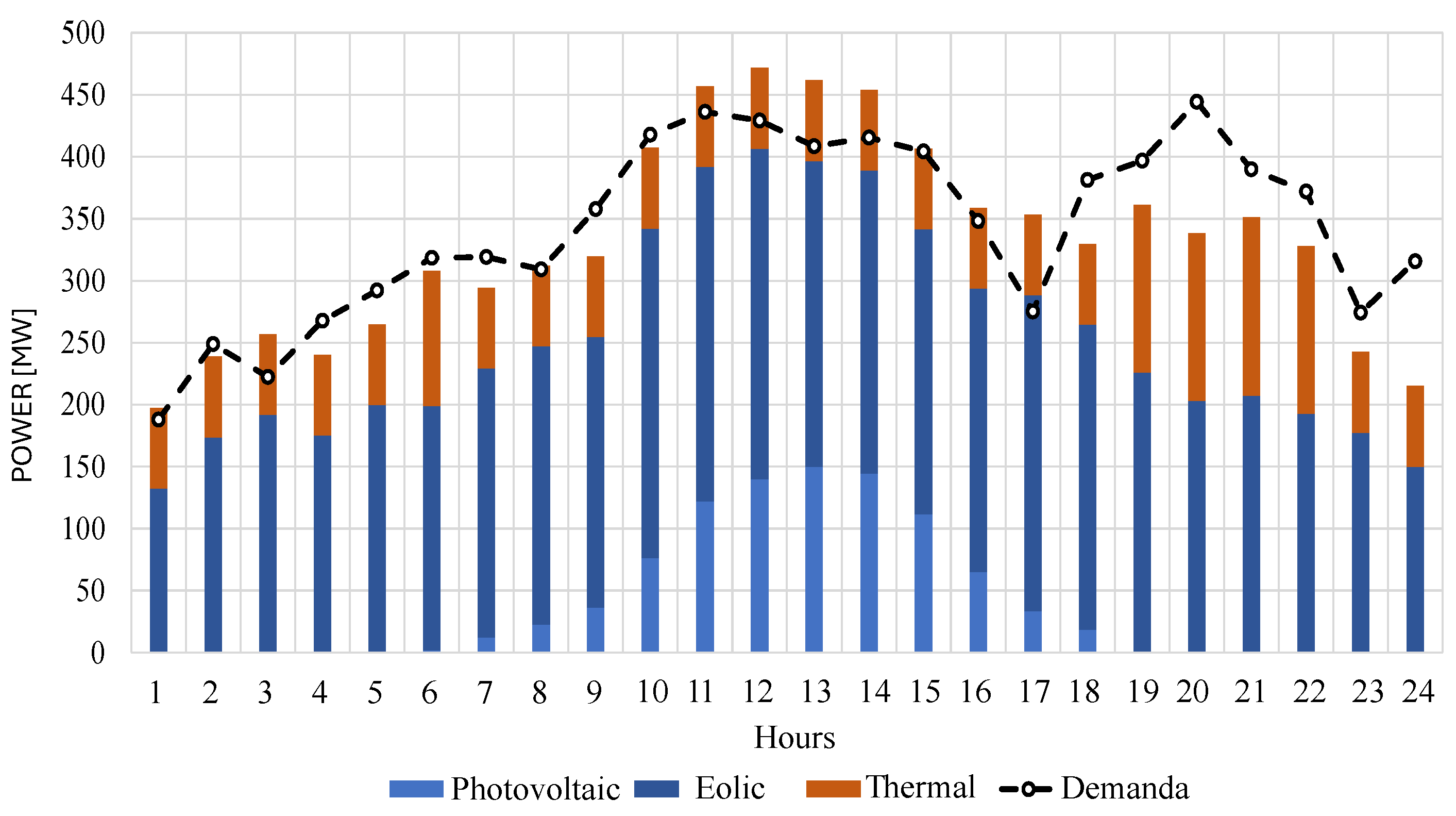
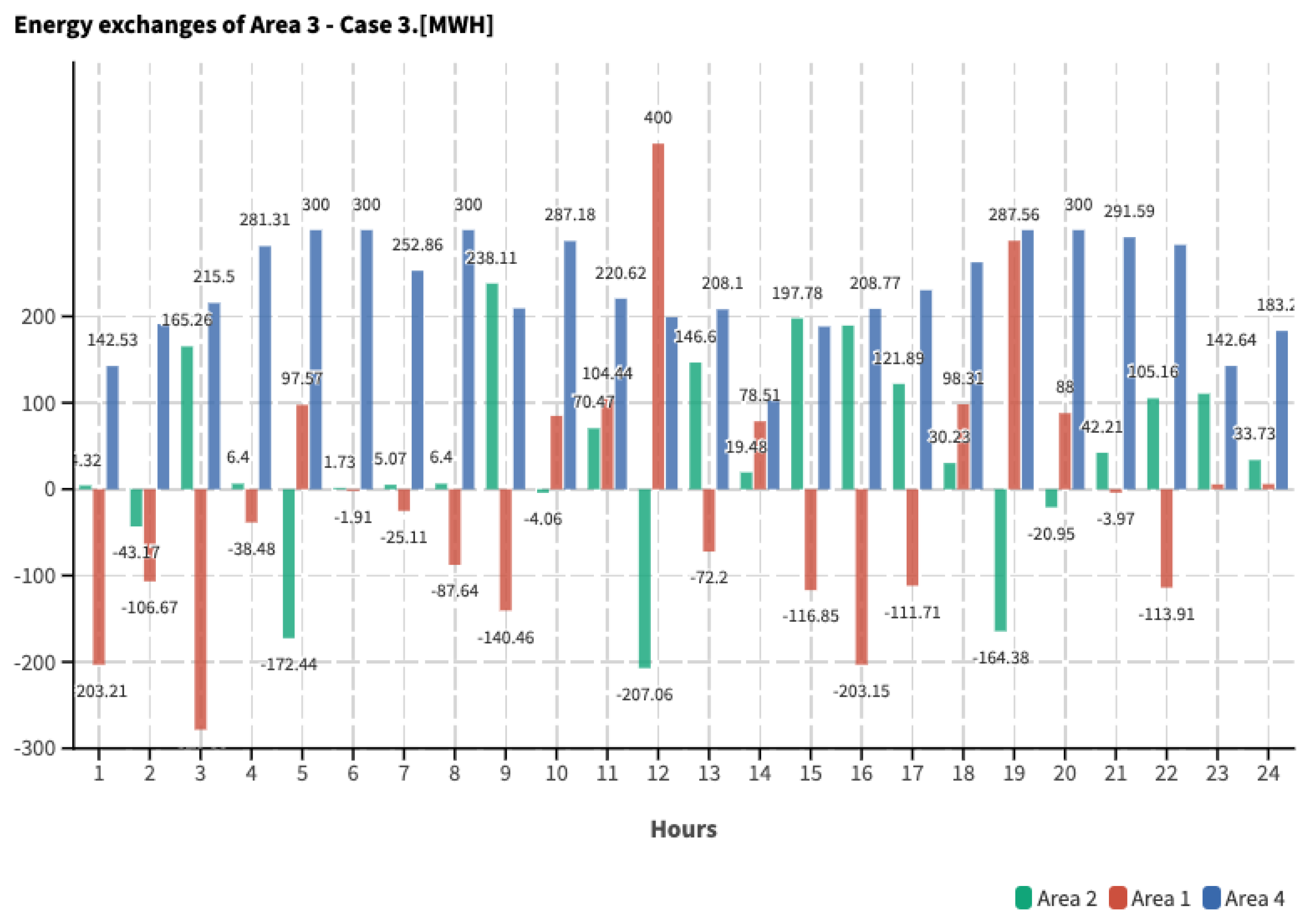
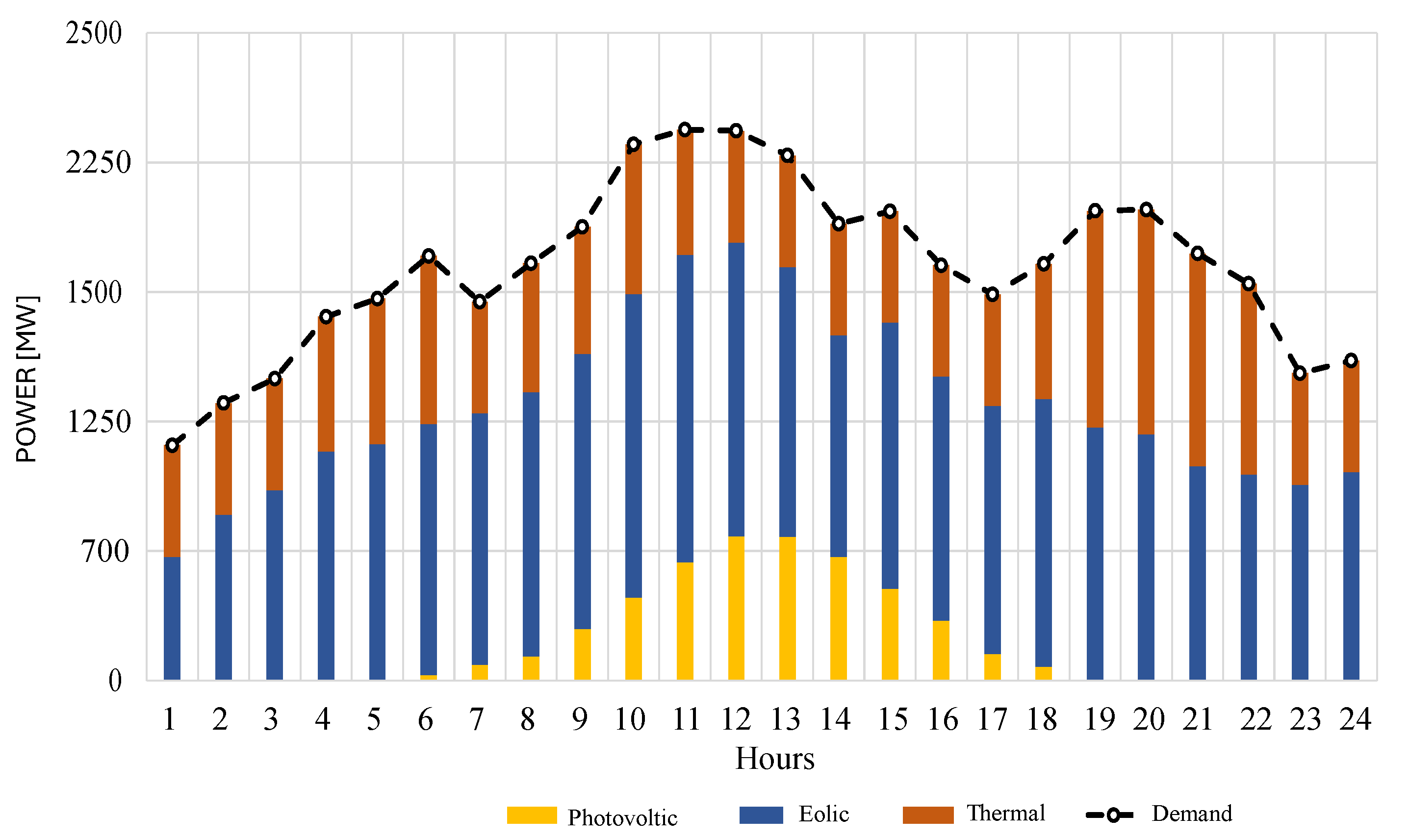
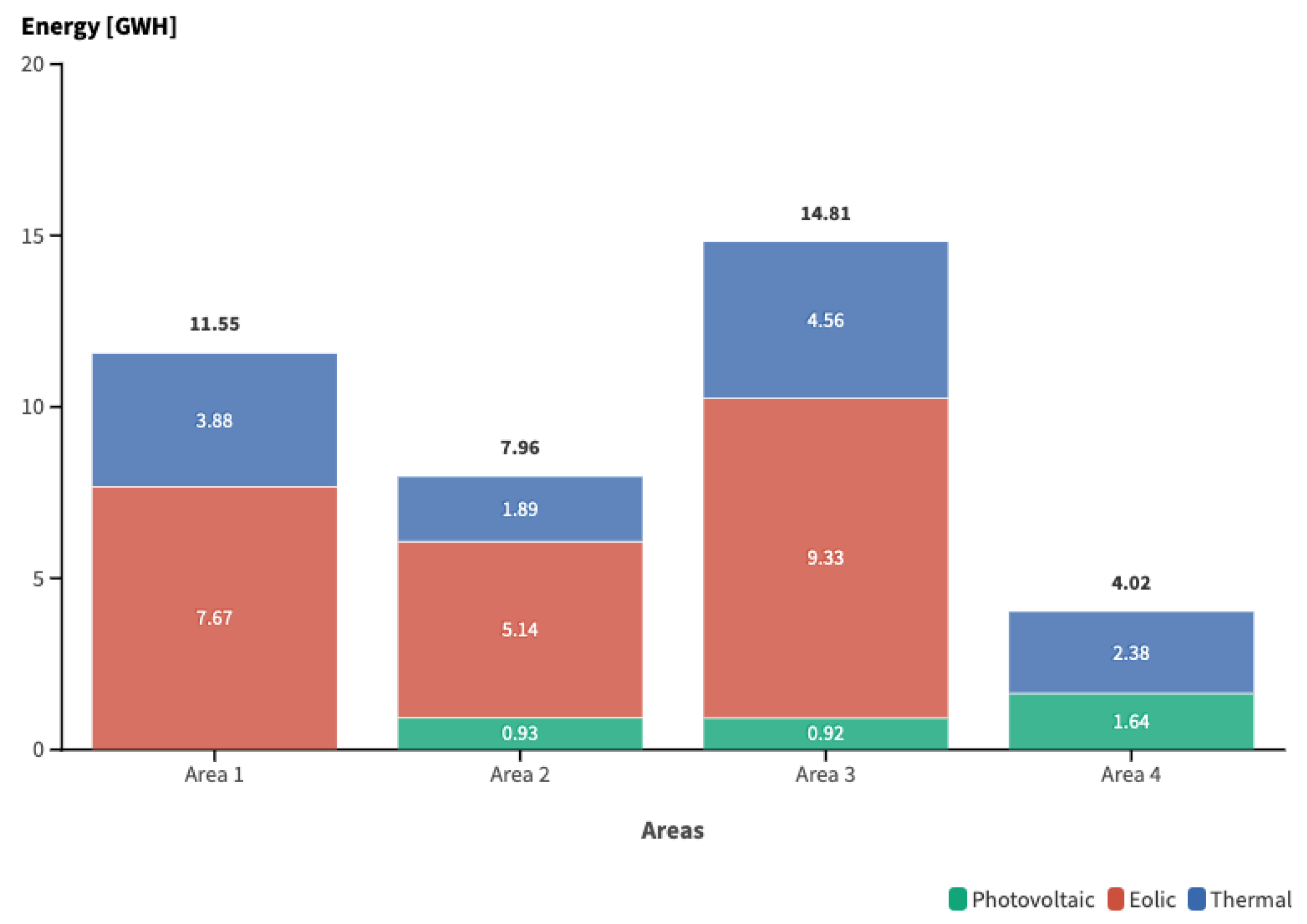
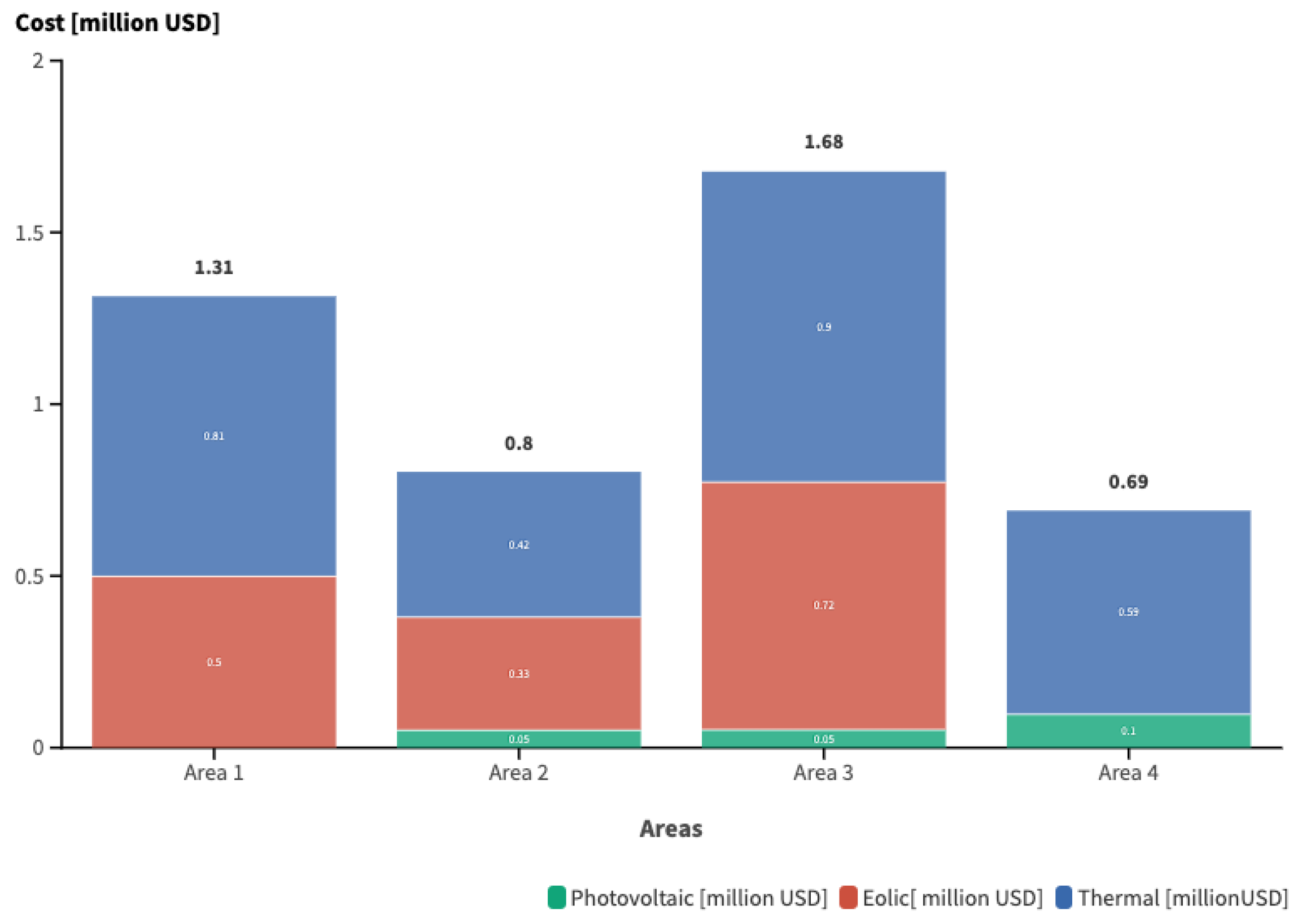
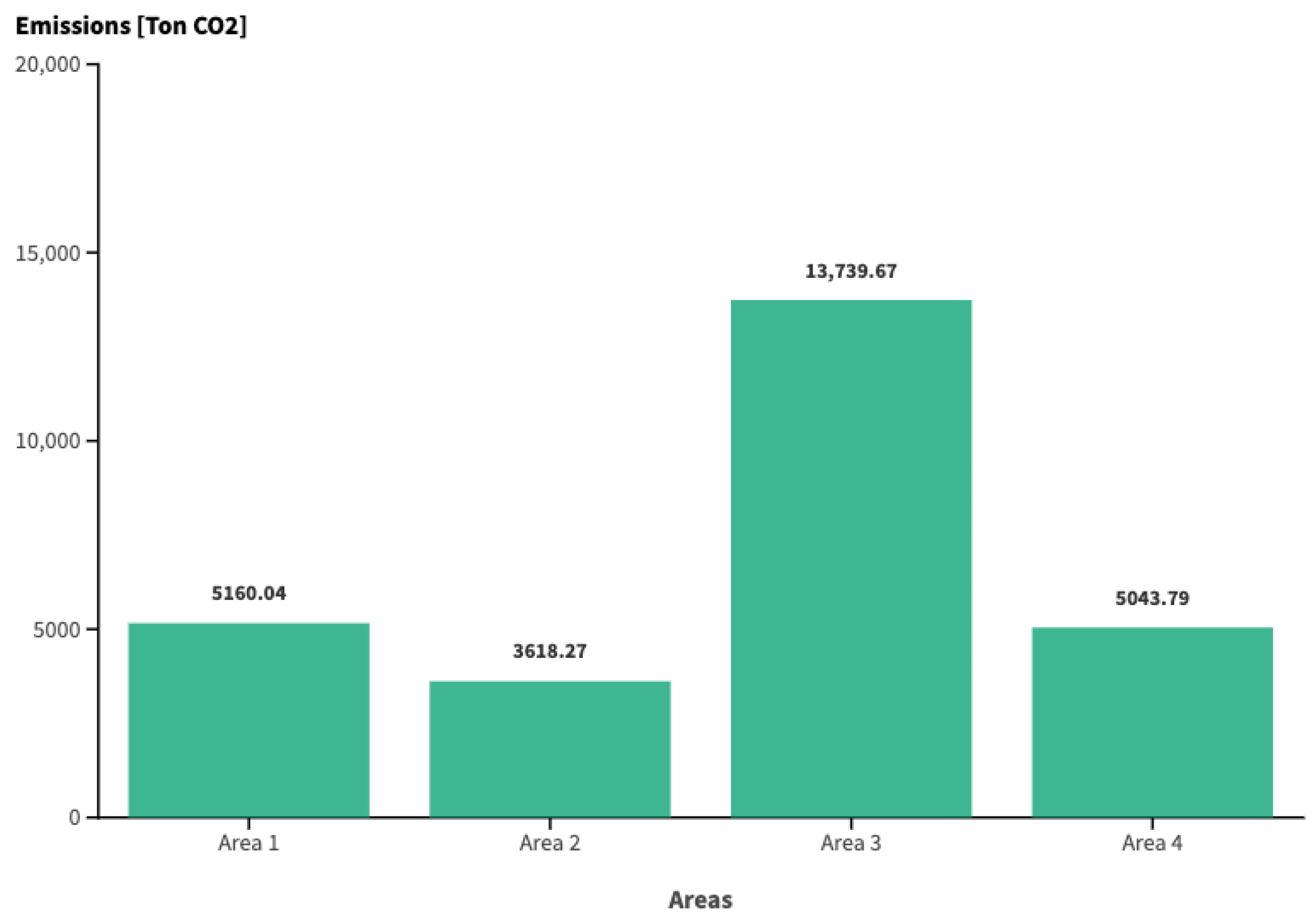
5.3. Study Case 3
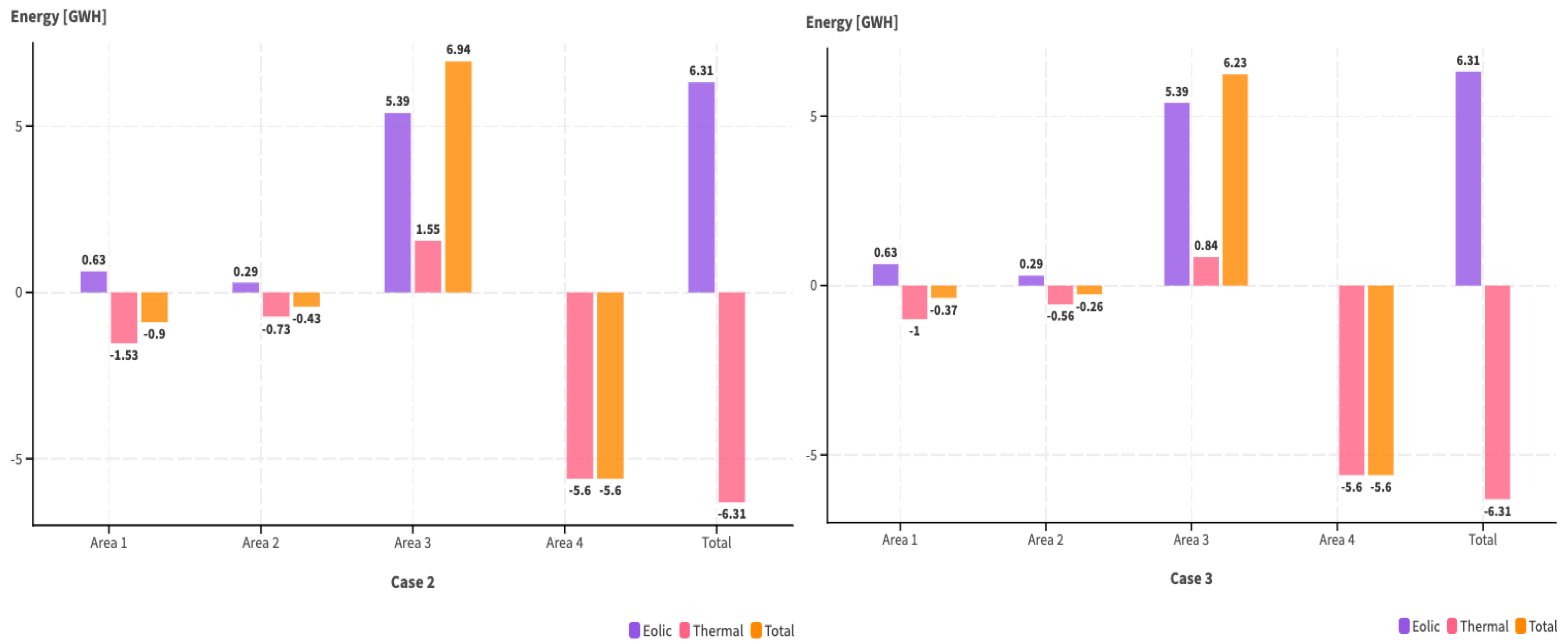
5.4. Comparative Analysis
6. Conclusions
Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prostejovsky, A.M.; Brosinsky, C.; Heussen, K.; Westermann, D.; Kreusel, J.; Marinelli, M. The future role of human operators in highly automated electric power systems. Electr. Power Syst. Res. 2019, 175, 105883. [Google Scholar] [CrossRef]
- Tong, K.; Ramaswami, A.; Feiock, R. Environmentally sustainable transitions of US district energy systems: Perspectives from infrastructure operators/designers through the co-evolutionary lens. J. Clean. Prod. 2020, 268, 121894. [Google Scholar] [CrossRef]
- Finkelman, R.B.; Wolfe, A.; Hendryx, M.S. The future environmental and health impacts of coal. Energy Geosci. 2021, 2, 99–112. [Google Scholar] [CrossRef]
- Moustakas, K.; Loizidou, M.; Rehan, M.; Nizami, A. A review of recent developments in renewable and sustainable energy systems: Key challenges and future perspective. Renew. Sustain. Energy Rev. 2020, 119, 109418. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, X.; Ma, J.; Wu, Y.; Liu, D.; Xie, W. System integration optimization for coal-fired power plant with CO2 capture by Na2CO3 dry sorbents. Energy 2020, 211, 118554. [Google Scholar] [CrossRef]
- Viviescas, C.; Lima, L.; Diuana, F.A.; Vasquez, E.; Ludovique, C.; Silva, G.N.; Huback, V.; Magalar, L.; Szklo, A.; Lucena, A.F.; et al. Contribution of Variable Renewable Energy to increase energy security in Latin America: Complementarity and climate change impacts on wind and solar resources. Renew. Sustain. Energy Rev. 2019, 113, 109232. [Google Scholar] [CrossRef]
- Wu, J.; Qiu, J.; Wang, X.; Ni, Y.; Han, X.; Dai, J.; Du, Z.; Xie, X. Study on Medium and Long-Term Generation Expansion Planning Method Considering the Requirements of Green Low-Carbon Development. In Proceedings of the 2018 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Kota Kinabalu, Malaysia, 7–10 October 2018; pp. 689–694. [Google Scholar] [CrossRef]
- Chen, Y.; Hou, J.; Chen, J.; Zheng, X.; Chen, H.; Liang, Z. A Novel Approach for Multi-Area Power System Day-ahead Scheduling under Uncertainties. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–9 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Narimani, H.; Razavi, S.E.; Azizivahed, A.; Naderi, E.; Fathi, M.; Ataei, M.H.; Narimani, M.R. A multi-objective framework for multi-area economic emission dispatch. Energy 2018, 154, 126–142. [Google Scholar] [CrossRef]
- Azizivahed, A.; Ghavidel, S.; Ghadi, M.J.; Li, L.; Zhang, J. Multi-area economic emission dispatch considering load uncertainty. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, Australia, 11–14 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Collins, S.; Deane, J.; Ó Gallachóir, B. Adding value to EU energy policy analysis using a multi-model approach with an EU-28 electricity dispatch model. Energy 2017, 130, 433–447. [Google Scholar] [CrossRef]
- Morris, J.; Farrell, J.; Kheshgi, H.; Thomann, H.; Chen, H.; Paltsev, S.; Herzog, H. Representing the costs of low-carbon power generation in multi-region multi-sector energy-economic models. Int. J. Greenh. Gas Control 2019, 87, 170–187. [Google Scholar] [CrossRef]
- Basu, M. Multi-area dynamic economic emission dispatch of hydro-wind-thermal power system. Renew. Energy Focus 2019, 28, 11–35. [Google Scholar] [CrossRef]
- Cheng, F.; Yang, M.; Han, X.; Liang, J. Real-time dispatch based on effective steady-state security regions of power systems. In Proceedings of the 2014 IEEE PES General Meeting | Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Basu, M. Multi-region dynamic economic dispatch of solar–wind–hydro–thermal power system incorporating pumped hydro energy storage. Eng. Appl. Artif. Intell. 2019, 86, 182–196. [Google Scholar] [CrossRef]
- Solaun, K.; Cerdá, E. Climate change impacts on renewable energy generation. A review of quantitative projections. Renew. Sustain. Energy Rev. 2019, 116, 109415. [Google Scholar] [CrossRef]
- Lei, Y.; Wang, D.; Jia, H.; Chen, J.; Li, J.; Song, Y.; Li, J. Multi-objective stochastic expansion planning based on multi-dimensional correlation scenario generation method for regional integrated energy system integrated renewable energy. Appl. Energy 2020, 276, 115395. [Google Scholar] [CrossRef]
- Sakawa, M.; Kato, K. An interactive fuzzy satisficing method for multiobjective structured linear programs and its application. In Proceedings of the 1995 IEEE International Conference on Systems, Man and Cybernetics, Intelligent Systems for the 21st Century, Vancouver, BC, Canada, 22–25 October 1995; Volume 5, pp. 4045–4050. [Google Scholar] [CrossRef]
- Huang, Y.; Hou, W.; Huang, Y.; Li, J.; Li, Q.; Wang, D.; Zhang, Y. Multi-Objective Optimal Operation for Steam Power Scheduling Based on Economic and Exergetic Analysis. Energies 2020, 13, 1886. [Google Scholar] [CrossRef]
- Khanna, M.; Rao, N.D. Supply and Demand of Electricity in the Developing World. Annu. Rev. Resour. Econ. 2009, 1, 567–596. [Google Scholar] [CrossRef]
- Jiyun, J.; Hu, C. Supply and Demand Conflict in Supply Chain Based on Principal-Agent Theory. In Proceedings of the 2009 Second International Conference on Intelligent Computation Technology and Automation, Changsha, China, 10–11 October 2009; pp. 11–14. [Google Scholar] [CrossRef]
- Armendáriz, M.; Heleno, M.; Cardoso, G.; Mashayekh, S.; Stadler, M.; Nordström, L. Coordinated microgrid investment and planning process considering the system operator. Appl. Energy 2017, 200, 132–140. [Google Scholar] [CrossRef]
- Gaur, A.S.; Das, P.; Jain, A.; Bhakar, R.; Mathur, J. Long-term energy system planning considering short-term operational constraints. Energy Strategy Rev. 2019, 26, 100383. [Google Scholar] [CrossRef]
- Wyrwa, A.; Suwała, W.; Pluta, M.; Raczyński, M.; Zyśk, J.; Tokarski, S. A new approach for coupling the short- and long-term planning models to design a pathway to carbon neutrality in a coal-based power system. Energy 2022, 239, 122438. [Google Scholar] [CrossRef]
- Carrillo-Galvez, A.; Flores-Bazan, F.; Parra, E.L. An Analytical Approach to the Environmental/Economic Dispatch Problem. In Proceedings of the 2019 IEEE CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Valparaiso, Chile, 13–27 November 2019; pp. 1–5. [Google Scholar] [CrossRef]
- He, L.; Lu, Z.; Zhang, J.; Geng, L.; Cai, Y.; Li, X. Economic dispatch of multi-area integrated electricity and natural gas systems considering emission and hourly spinning reserve constraints. Int. J. Electr. Power Energy Syst. 2021, 132, 107177. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, S.; Cheng, H.; Zhang, C. Joint Generation, Transmission and Energy Storage Systems Expansion Planning in Multi-area Power Systems Considering Detailed Modeling of Tie lines. In Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Weihai, China, 13–16 July 2020; pp. 720–726. [Google Scholar] [CrossRef]
- Wang, X.; Shi, X.; Zhang, H.; Wang, F. Multi-objective optimal dispatch of wind-integrated power system based on distributed energy storage. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 2788–2792. [Google Scholar] [CrossRef]
- Sakthivel, V.; Suman, M.; Sathya, P. Combined economic and emission power dispatch problems through multi-objective squirrel search algorithm. Appl. Soft Comput. 2021, 100, 106950. [Google Scholar] [CrossRef]
- Lombardi, P.; Schwabe, F. Sharing economy as a new business model for energy storage systems. Appl. Energy 2017, 188, 485–496. [Google Scholar] [CrossRef]
- Singhal, P.K.; Naresh, R.; Sharma, V.; N, G.K. Enhanced lambda iteration algorithm for the solution of large scale economic dispatch problem. In Proceedings of the International Conference on Recent Advances and Innovations in Engineering (ICRAIE-2014), Jaipur, India, 9–11 May 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Gubin, P.Y.; Oboskalov, V.P.; Mahnitko, A.; Gavrilovs, A. An Investigation into the Effectiveness of the Differential Evolution Method for Optimal Generating Units Maintenance by EENS Criteria. In Proceedings of the 2020 IEEE 61th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 5–7 November 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Saw, B.K.; Bohre, A.K. Multi DG Planning with Impact of Mixed-Load Models using Intelligent Methodologies: BF-PSO, PSO and GA. In Proceedings of the 2023 IEEE 3rd International Conference on Smart Technologies for Power, Energy and Control (STPEC), Bhubaneswar, India, 10–13 December 2023; pp. 1–5. [Google Scholar] [CrossRef]
- del Ambiente, M. Factor de Emision de CO2 del Sistema Nacional Interconectado de Ecuador. 2024. Available online: https://www.recursosyenergia.gob.ec/wp-content/uploads/2023/08/wp-1692720103183.pdf (accessed on 10 June 2024).
- Ministerio de Energía y Recursos Naturales No Renovables. Plan Maestro de Electricidad. Available online: https://www.recursosyenergia.gob.ec/plan-maestro-de-electricidad/ (accessed on 21 June 2024).
- Melgar-Dominguez, O.D.; Pourakbari-Kasmaei, M.; Mantovani, J.R.S. Robust Short-Term Electrical Distribution Network Planning Considering Simultaneous Allocation of Renewable Energy Sources and Energy Storage Systems. In Robust Optimal Planning and Operation of Electrical Energy Systems; Mohammadi-Ivatloo, B., Nazari-Heris, M., Eds.; Springer International Publishing: Cham, Germany, 2019; pp. 145–175. [Google Scholar] [CrossRef]
- Zhu, J. Optimization of Power System Operation; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar] [CrossRef]






| step 1 | set → Areas and load curves |
| Demand periods | |
| Data Area | |
| Input → Technical Data generators | |
| step 2 | Emissions data |
| Productions cost | |
| step 3 | Input → netting Data |
| Area interconnection | |
| set | |
| Objetive function | |
| step 4 | |
| Objetive Function 2: | |
| Set → restrictions | |
| step 5 | Model execute |
| step 6 | -constraint application |
| step 6 | execution of the fuzzy satisfaction method |
| step 7 | Optimum Pareto |
| step 8 | End |
| Name | Technology | Locate |
|---|---|---|
| T1 | Thermal | |
| T2 | Thermal | |
| T3 | Thermal | Area 1 |
| T4 | Thermal | |
| W1 | Eolic | |
| T5 | Thermal | |
| T6 | Thermal | |
| T7 | Thermal | Area 2 |
| W2 | Eolic | |
| FV1 | Photovoltaic | |
| T8 | Thermal | |
| T9 | Thermal | |
| T10 | Thermal | |
| T11 | Thermal | Area 3 |
| W3 | Eolic | |
| W4 | Eolic | |
| FV2 | Photovoltaic | |
| T12 | Thermal | |
| T13 | Thermal | |
| T14 | Thermal | Area 4 |
| T15 | Thermal | |
| FV3 | Photovoltaic |
| [MW] | [MW] | [MW/h] | [MW/h] | |
|---|---|---|---|---|
| T1 | 20 | 150 | 45 | 45 |
| T2 | 35 | 140 | 90 | 90 |
| T3 | 30 | 230 | 100 | 100 |
| T4 | 30 | 350 | 110 | 110 |
| T5 | 10 | 130 | 35 | 35 |
| T6 | 20 | 250 | 70 | 70 |
| T7 | 35 | 250 | 100 | 100 |
| T8 | 30 | 100 | 50 | 50 |
| T9 | 60 | 200 | 75 | 75 |
| T10 | 25 | 100 | 55 | 55 |
| T11 | 40 | 250 | 100 | 100 |
| T12 | 10 | 130 | 55 | 55 |
| T13 | 20 | 250 | 100 | 100 |
| T14 | 35 | 200 | 80 | 80 |
| T15 | 30 | 100 | 50 | 50 |
| [USD/MWh2] | [cts/kWh] | [USD] | |
|---|---|---|---|
| T1 | 0.00519 | 16.554 | 557.43 |
| T2 | 0.00732 | 21.078 | 444.92 |
| T3 | 0.00648 | 22.140 | 436.86 |
| T4 | 0.00398 | 20.009 | 887.62 |
| T5 | 0.00908 | 21.536 | 661.56 |
| T6 | 0.00860 | 18.708 | 435.30 |
| T7 | 0.00602 | 20.113 | 972.88 |
| T8 | 0.00459 | 22.195 | 610.92 |
| T9 | 0.00372 | 19.883 | 578.02 |
| T10 | 0.00201 | 15.775 | 480.31 |
| T11 | 0.00535 | 17.074 | 574.94 |
| T12 | 0.00784 | 22.590 | 476.83 |
| T13 | 0.00695 | 23.728 | 468.20 |
| T14 | 0.00427 | 21.444 | 951.29 |
| T15 | 0.00944 | 22.378 | 687.41 |
| MBTU/MWh2 | MBTU/kWh | MBTU | |
|---|---|---|---|
| T1 | 0.0043 | 6.120 | 421.83 |
| T2 | 0.0021 | 6.778 | 220.77 |
| T3 | 0.0061 | 6.845 | 132.12 |
| T4 | 0.0044 | 6.948 | 144.45 |
| T5 | 0.0050 | 6.950 | 158.85 |
| T6 | 0.0031 | 7.033 | 224.37 |
| T7 | 0.0013 | 7.169 | 192.42 |
| T8 | 0.0012 | 8.221 | 129.60 |
| T9 | 0.0161 | 8.625 | 157.59 |
| T10 | 0.0002 | 9.192 | 66.96 |
| T11 | 0.0046 | 7.334 | 152.48 |
| T12 | 0.0053 | 7.336 | 167.68 |
| T13 | 0.0032 | 7.423 | 236.84 |
| T14 | 0.0014 | 7.567 | 203.11 |
| T15 | 0.0012 | 8.677 | 136.80 |
| Item | Item | ||
|---|---|---|---|
| lb/MBTU | lb/MBTU | ||
| T1 | 1.577 | T8 | 4.133 |
| T2 | 1.568 | T9 | 3.781 |
| T3 | 2.860 | T10 | 4.627 |
| T4 | 2.698 | T11 | 2.860 |
| T5 | 2.328 | T12 | 2.698 |
| T6 | 2.622 | T13 | 2.328 |
| T7 | 2.964 | T14 | 2.622 |
| T15 | 2.964 |
| Rate | ||
|---|---|---|
| [MW] | [cts/kWh] | |
| W1 | 380 | 6.5 |
| W2 | 270 | 6.4 |
| W3 | 300 | 7.3 |
| W4 | 330 | 8.2 |
| FV1 | 150 | 5.5 |
| FV2 | 180 | 5.7 |
| FV3 | 100 | 4.4 |
| FV4 | 140 | 7.1 |
| Link | Capacity [MW] |
|---|---|
| Area 1–Area 2 | 200 |
| Area 1–Area 3 | 400 |
| Area 2–Area 3 | 600 |
| Area 4–Area 3 | 300 |
| Area 2 [MWH] | Area 3 [MWH] | Total [MWH] | |
|---|---|---|---|
| Delivery | 1033.89 | 1329.70 | 2363.58 |
| Reception | −1571.94 | −1696.43 | −3268.36 |
| Netting | −538.05 | −366.73 | −904.78 |
| Area 2 [MWH] | Area 3 [MWH] | Total [MWH] | |
|---|---|---|---|
| Delivery | 614.89 | 1571.94 | 2186.83 |
| Reception | −1585.33 | −1033.89 | −2619.22 |
| Netting | −970.44 | 538.05 | −432.39 |
| Area 1 [MWH] | Area 2 [MWH] | Area 4 [MWH] | Total | |
|---|---|---|---|---|
| Delivery | 1585.33 | 1696.43 | 5601.44 | 8883.20 |
| Reception | −614.89 | −1329.70 | 0.0 | −1944.59 |
| Netting | 970.44 | 366.73 | 5601.44 | 6938.61 |
| Area 4 | Total | |
|---|---|---|
| Delivery | 0.00 | 0.00 |
| Reception | −5601.44 | −5601.44 |
| Netting | −5601.44 | −5601.44 |
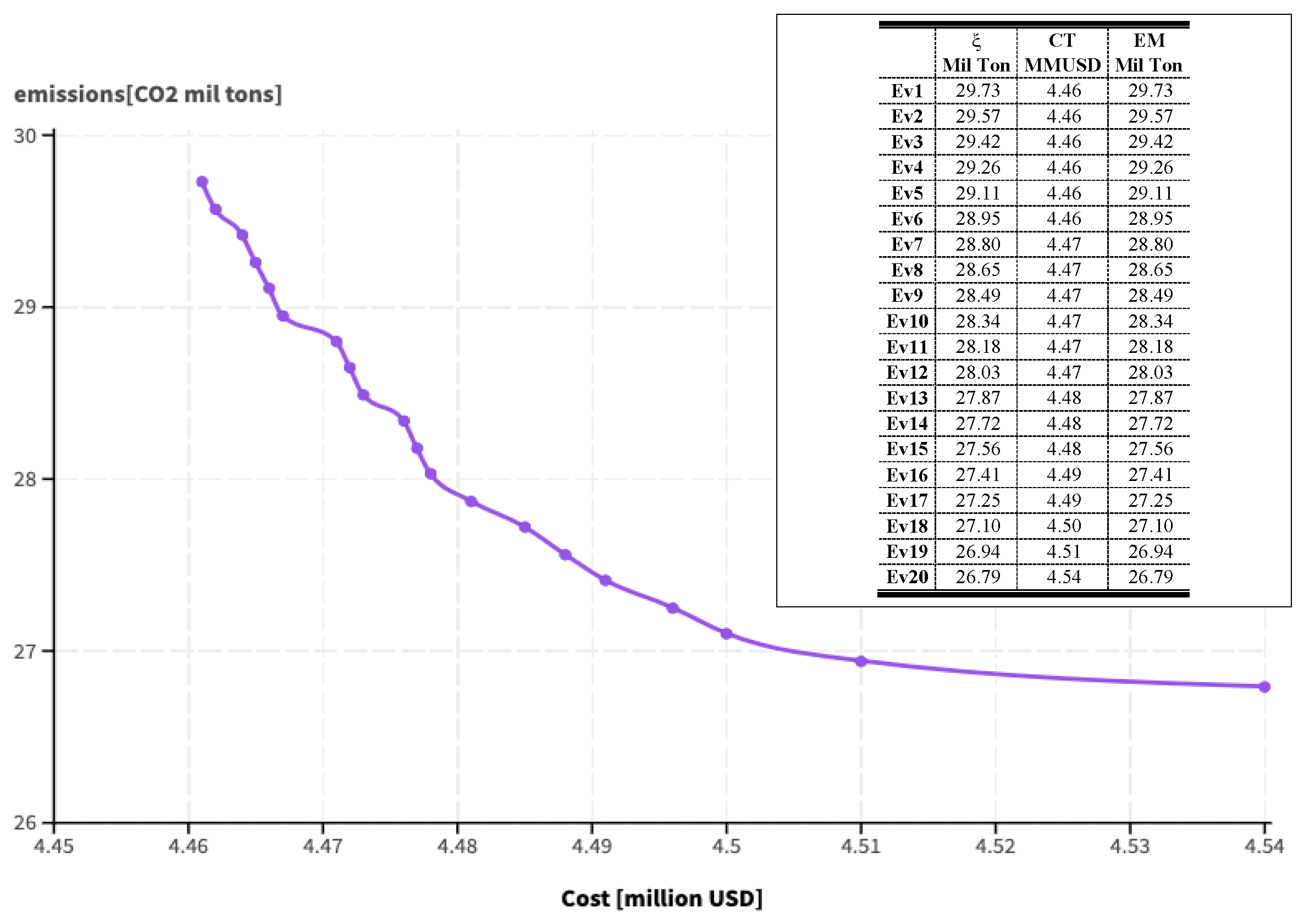
| Events | Min | ||
|---|---|---|---|
| Ev1 | 1.0000 | 0.000 | 0.000 |
| Ev2 | 0.9978 | 0.053 | 0.053 |
| Ev3 | 0.9945 | 0.105 | 0.105 |
| Ev4 | 0.9894 | 0.158 | 0.158 |
| Ev5 | 0.9842 | 0.211 | 0.211 |
| Ev6 | 0.9789 | 0.263 | 0.263 |
| Ev7 | 0.9682 | 0.316 | 0.316 |
| Ev8 | 0.9552 | 0.368 | 0.368 |
| Ev9 | 0.9418 | 0.421 | 0.421 |
| Ev10 | 0.9199 | 0.474 | 0.474 |
| Ev11 | 0.8940 | 0.526 | 0.526 |
| Ev12 | 0.8677 | 0.579 | 0.579 |
| Ev13 | 0.8361 | 0.632 | 0.632 |
| Ev14 | 0.8009 | 0.684 | 0.684 |
| Ev15 | 0.7587 | 0.737 | 0.737 |
| Ev16 | 0.6927 | 0.789 | 0.693 |
| Ev17 | 0.6128 | 0.842 | 0.613 |
| Ev18 | 0.5263 | 0.895 | 0.526 |
| Ev19 | 0.3918 | 0.947 | 0.392 |
| Ev20 | - | 1.000 | 0.000 |
| Area 2 [MWH] | Area 3 [MWH] | Total | |
|---|---|---|---|
| Delivery | 893.74 | 1499.69 | 2393.42 |
| Reception | −1512.41 | −1246.87 | −2759.28 |
| Netting | −618.67 | 252.81 | −365.86 |
| Area 2 [MWH] | Area 3 [MWH] | Total | |
|---|---|---|---|
| Delivery | 612.06 | 1512.41 | 2124.47 |
| Reception | −1494.77 | −893.74 | −2388.51 |
| Netting | −882.71 | 618.67 | −264.04 |
| Area 1 [MWH] | Area 2 [MWH] | Area 4 [MWH] | Total | |
|---|---|---|---|---|
| Delivery | 1494.77 | 1246.87 | 5601.44 | 8343.09 |
| Reception | −612.06 | −1499.69 | 0.0 | −2111.75 |
| Netting | 882.71 | −252.81 | 5601.44 | 6231.35 |
| Area 4 | Total | |
|---|---|---|
| Delivery | 0.00 | 0.00 |
| Reception | −5601.44 | −5601.44 |
| Netting | −5601.44 | −5601.44 |
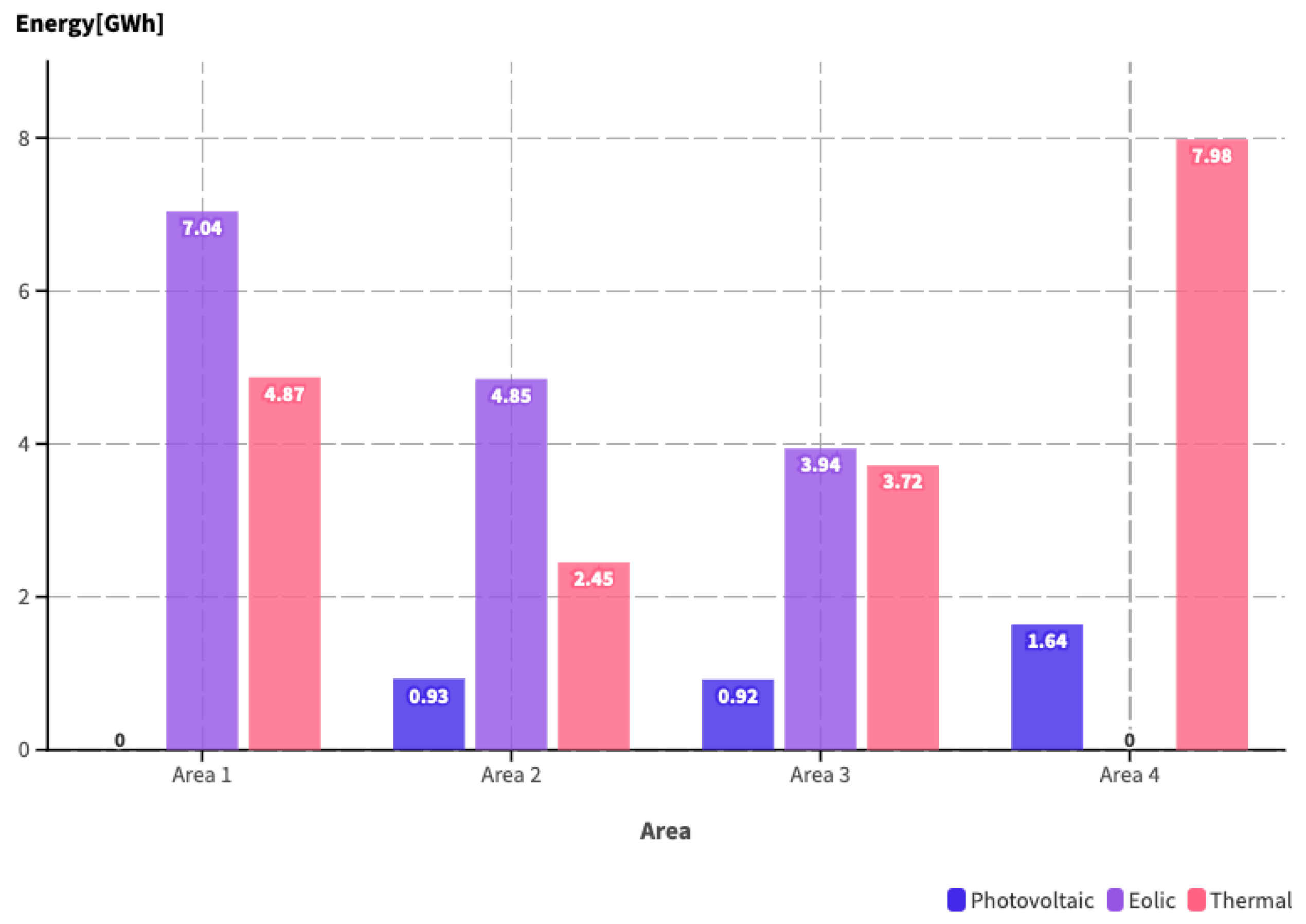
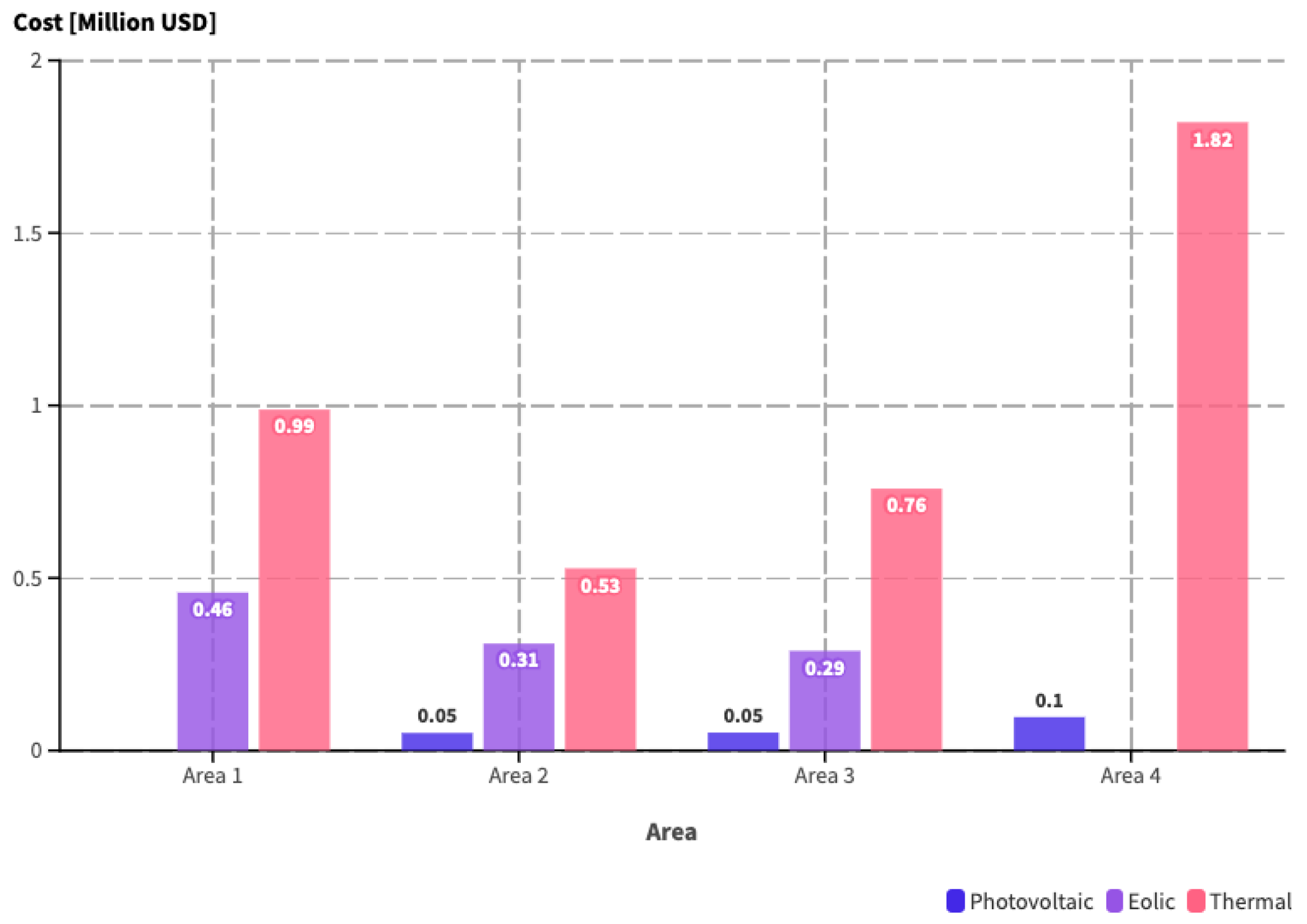
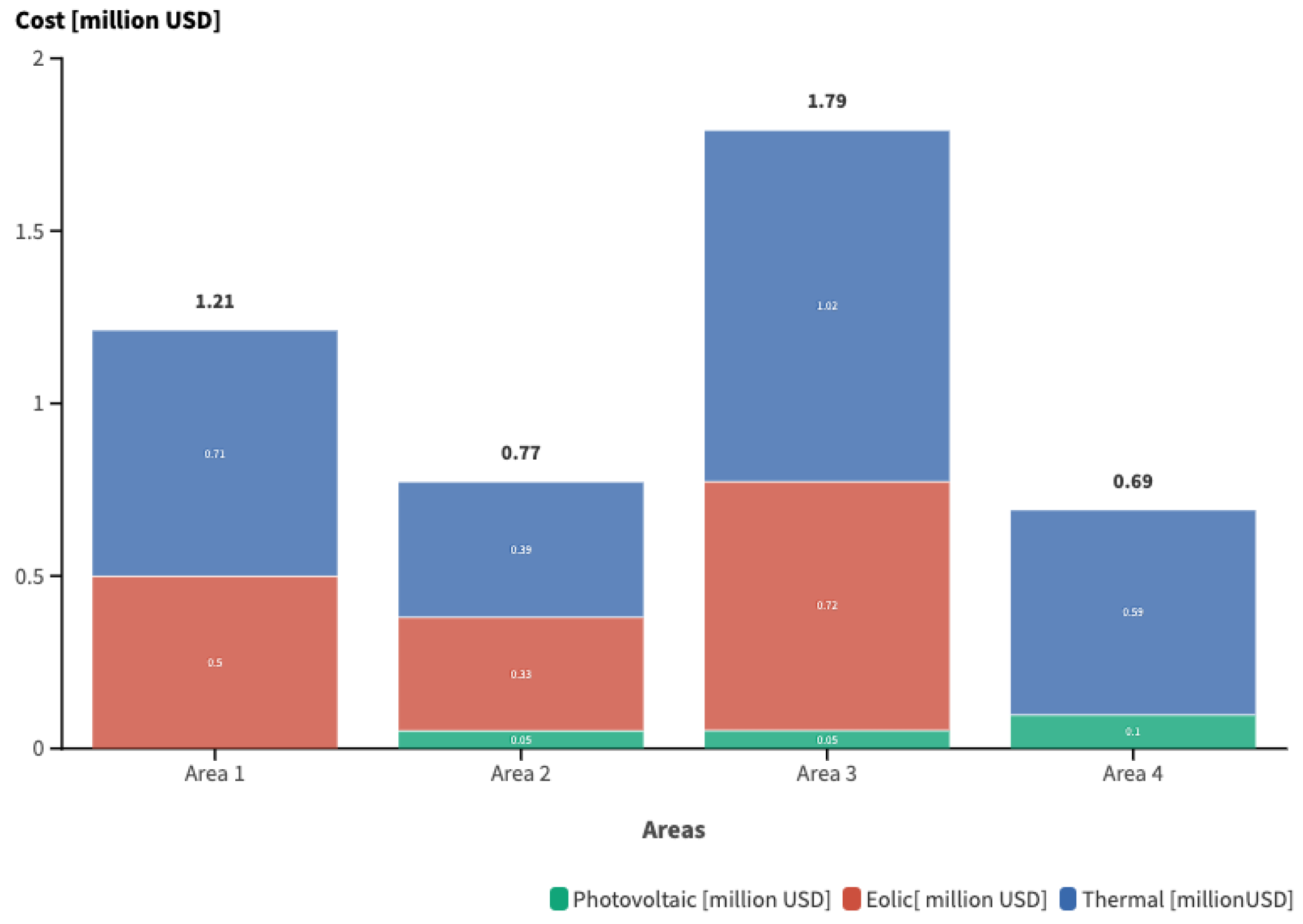
| Case | Areas | Photovoltaic | Eolic | Thermal | Total |
|---|---|---|---|---|---|
| Area 1 | - | 0.458 | 0.988 | 1.446 | |
| Case 1 | Area 2 | 0.051 | 0.310 | 0.528 | 0.890 |
| Area 3 | 0.052 | 0.289 | 0.759 | 1.101 | |
| Total | 0.200 | 1.057 | 4.097 | 5.354 | |
| Area 1 | - | 0.499 | 0.712 | 1.211 | |
| Area 2 | 0.051 | 0.329 | 0.391 | 0.772 | |
| Case 2 | Area 3 | 0.052 | 0.721 | 1.017 | 1.790 |
| Area 4 | 0.097 | - | 0.593 | 0.690 | |
| Total | 0.200 | 1.549 | 2.714 | 4.463 | |
| Area 1 | - | 0.499 | 0.815 | 1.314 | |
| Area 2 | 0.051 | 0.329 | 0.423 | 0.803 | |
| Case 3 | Area 3 | 0.052 | 0.721 | 0.904 | 1.677 |
| Area 4 | 0.097 | - | 0.593 | 0.690 | |
| Total | 0.200 | 1.549 | 2.735 | 4.485 |
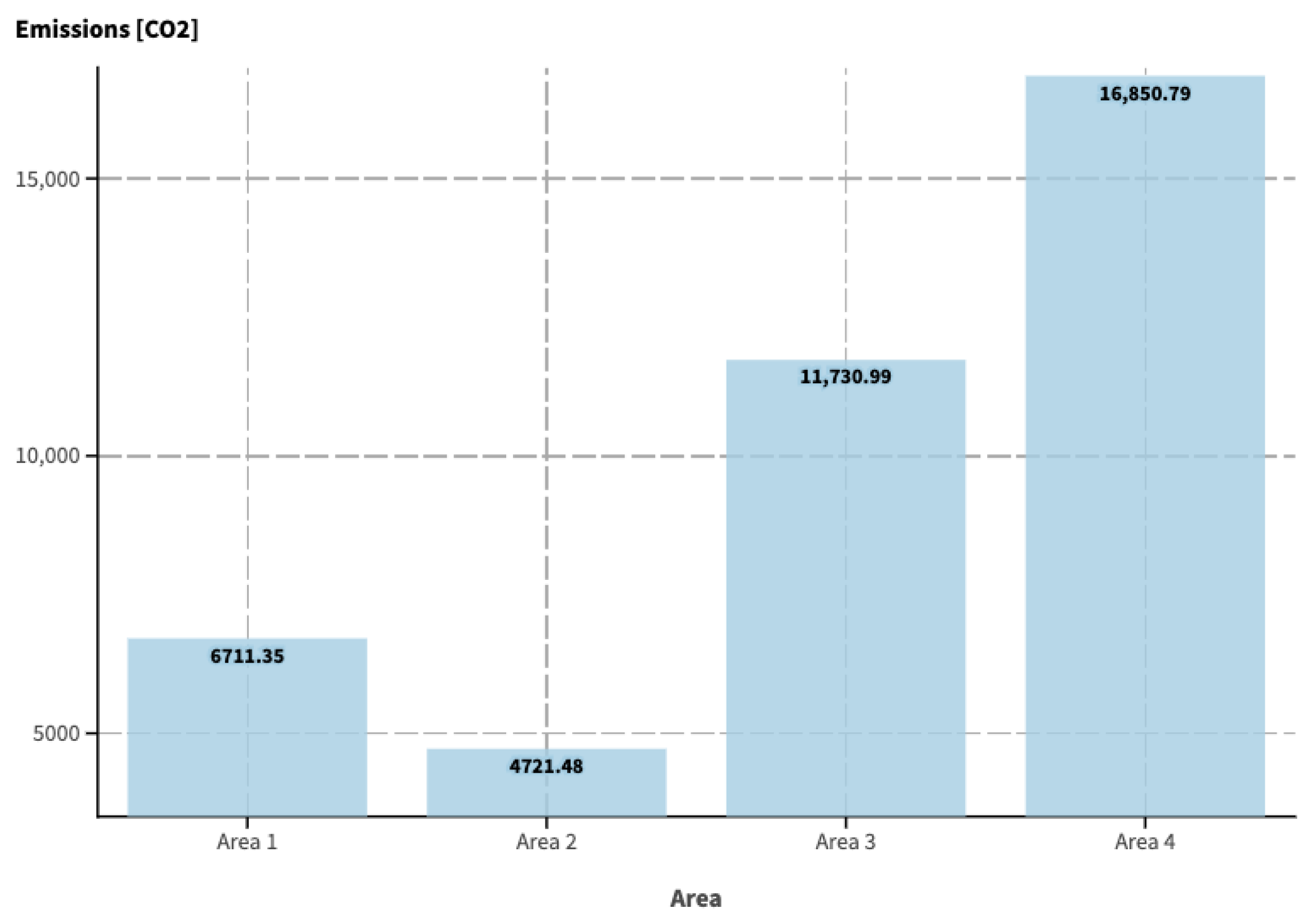
| Area | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
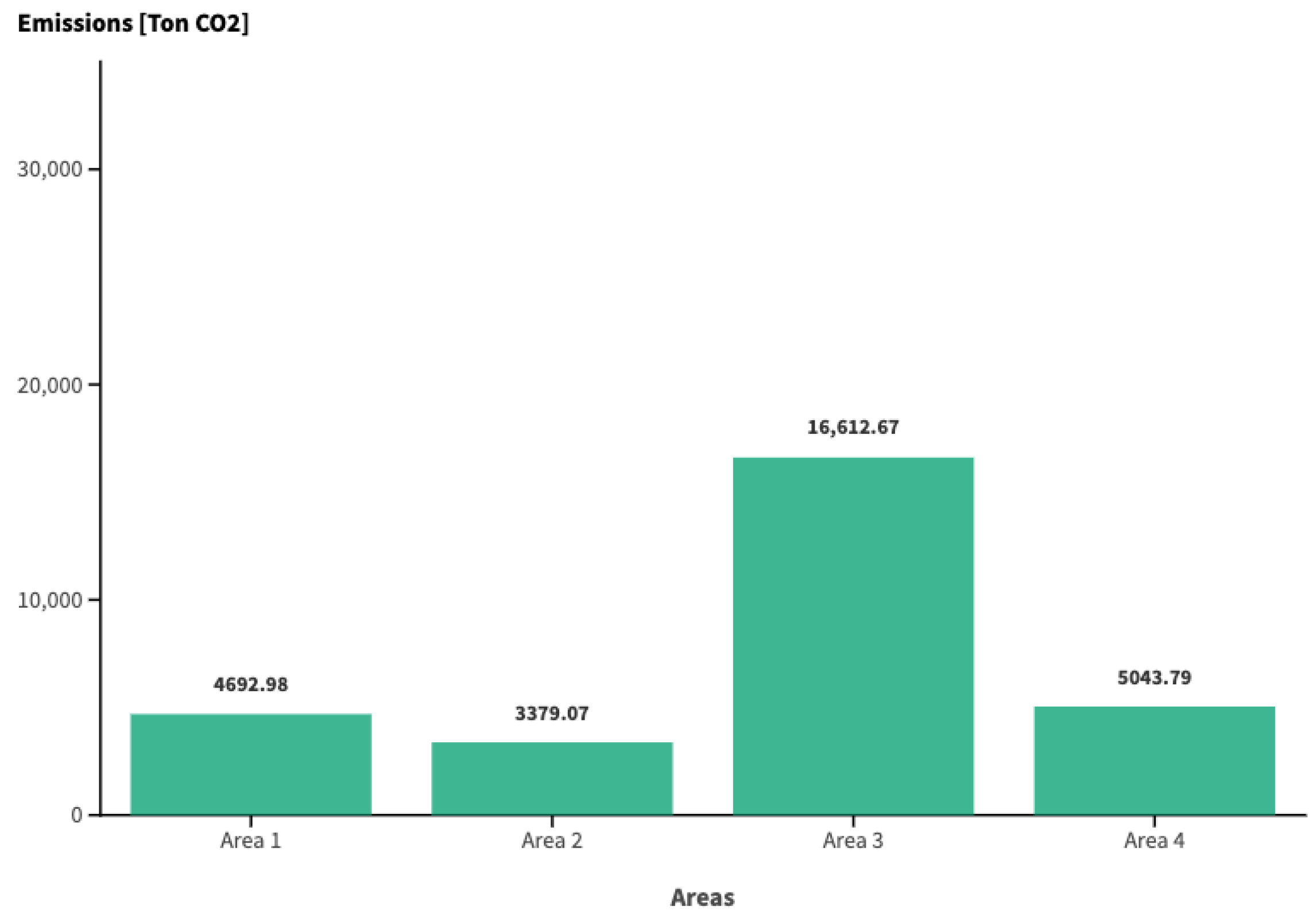
| Area 1 | 6711.35 | 4692.98 | 5160.04 |
| Area 2 | 4721.48 | 3379.07 | 3618.27 |
| Area 3 | 11,730.99 | 16,612.67 | 13,739.67 |
| Area 4 | 16,850.79 | 5043.79 | 5043.79 |
| Total | 40,014.60 | 29,728.50 | 27,561.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cristian, P.; Tipán, L. Multi-Objetive Dispatching in Multi-Area Power Systems Using the Fuzzy Satisficing Method. Energies 2024, 17, 5044. https://doi.org/10.3390/en17205044
Cristian P, Tipán L. Multi-Objetive Dispatching in Multi-Area Power Systems Using the Fuzzy Satisficing Method. Energies. 2024; 17(20):5044. https://doi.org/10.3390/en17205044
Chicago/Turabian StyleCristian, Paspuel, and Luis Tipán. 2024. "Multi-Objetive Dispatching in Multi-Area Power Systems Using the Fuzzy Satisficing Method" Energies 17, no. 20: 5044. https://doi.org/10.3390/en17205044
APA StyleCristian, P., & Tipán, L. (2024). Multi-Objetive Dispatching in Multi-Area Power Systems Using the Fuzzy Satisficing Method. Energies, 17(20), 5044. https://doi.org/10.3390/en17205044








