Appendix A
Methodology of the Data Bank Construction for the Petrochemical Demand Models.
The three main steps used to construct the data bank are described in detail below.
Step 1—Construction of the quantity demanded of the four main dependent variables
The data set is at the annual frequency and starts from 1971 until 2019. As mentioned, we aim to model the oil demand from different petrochemical feedstocks, namely naphtha, ethane, liquified petroleum gas (LPG), and other petrochemical feedstocks. To this end, we specify four dependent variables. These dependent variables measure the demand for petrochemical feedstocks for each region i. Therefore, the dependent variables are as follows:
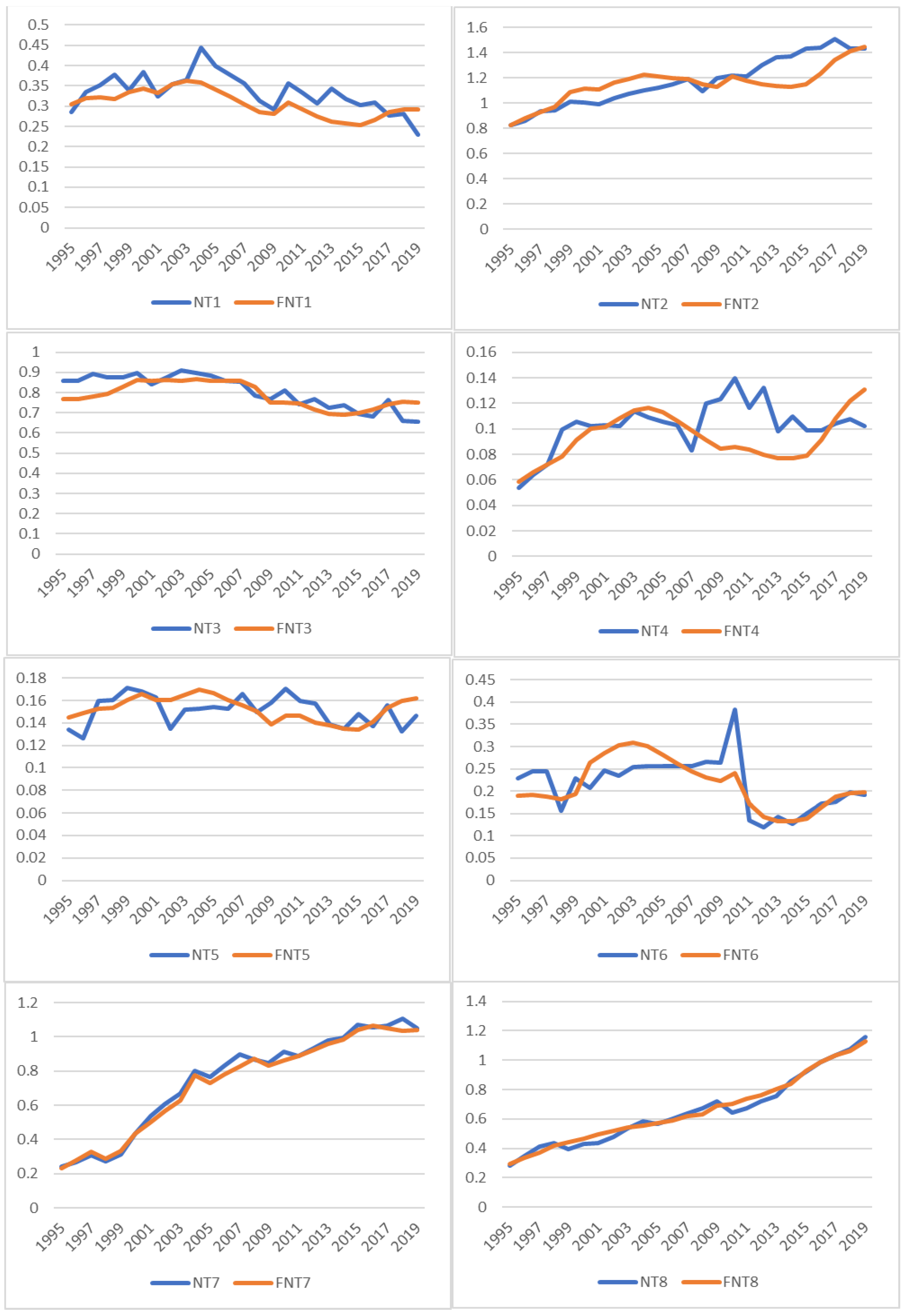
The demand for naphtha, denoted as NTi.
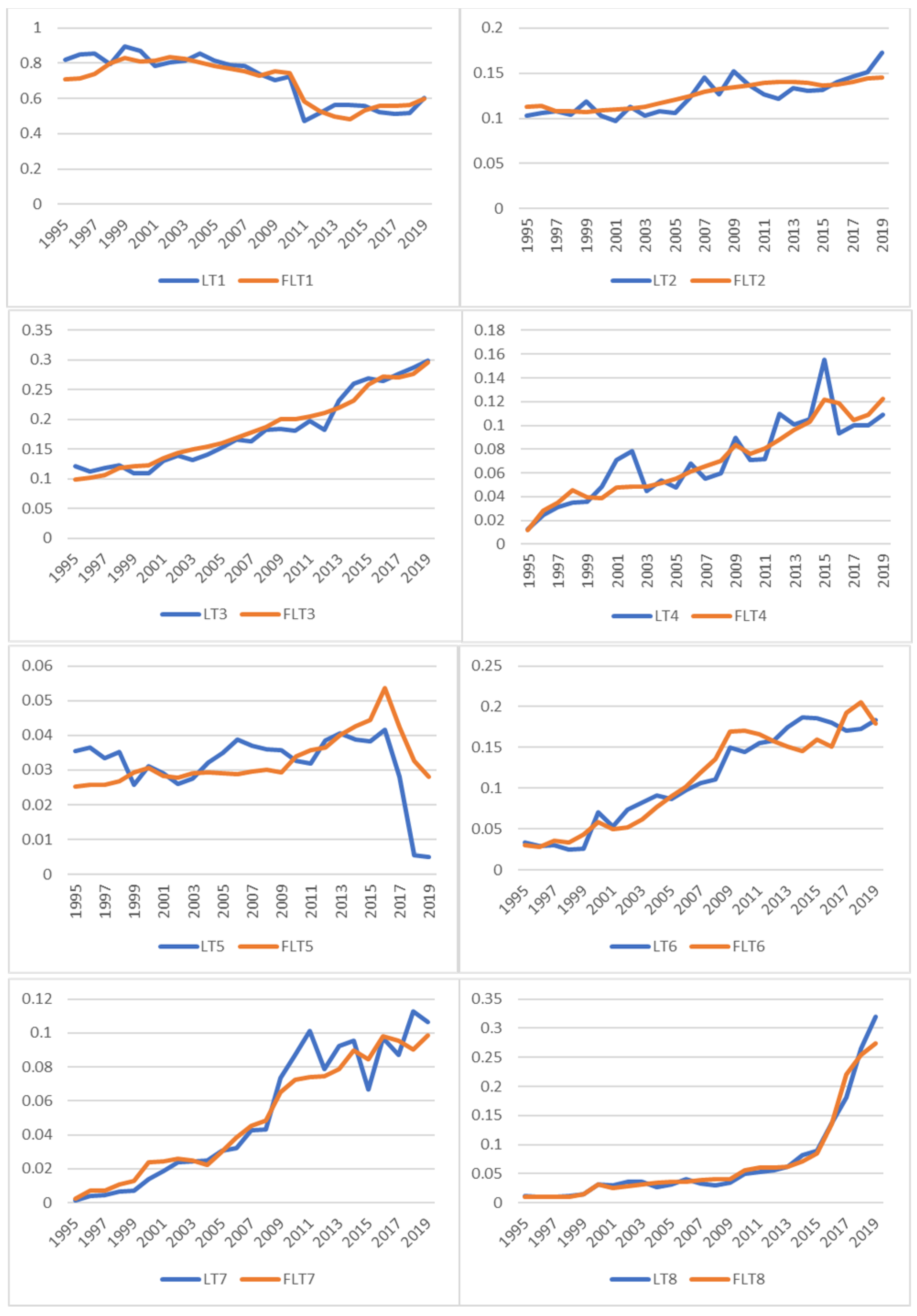
The demand for LPG, denoted as LTi.
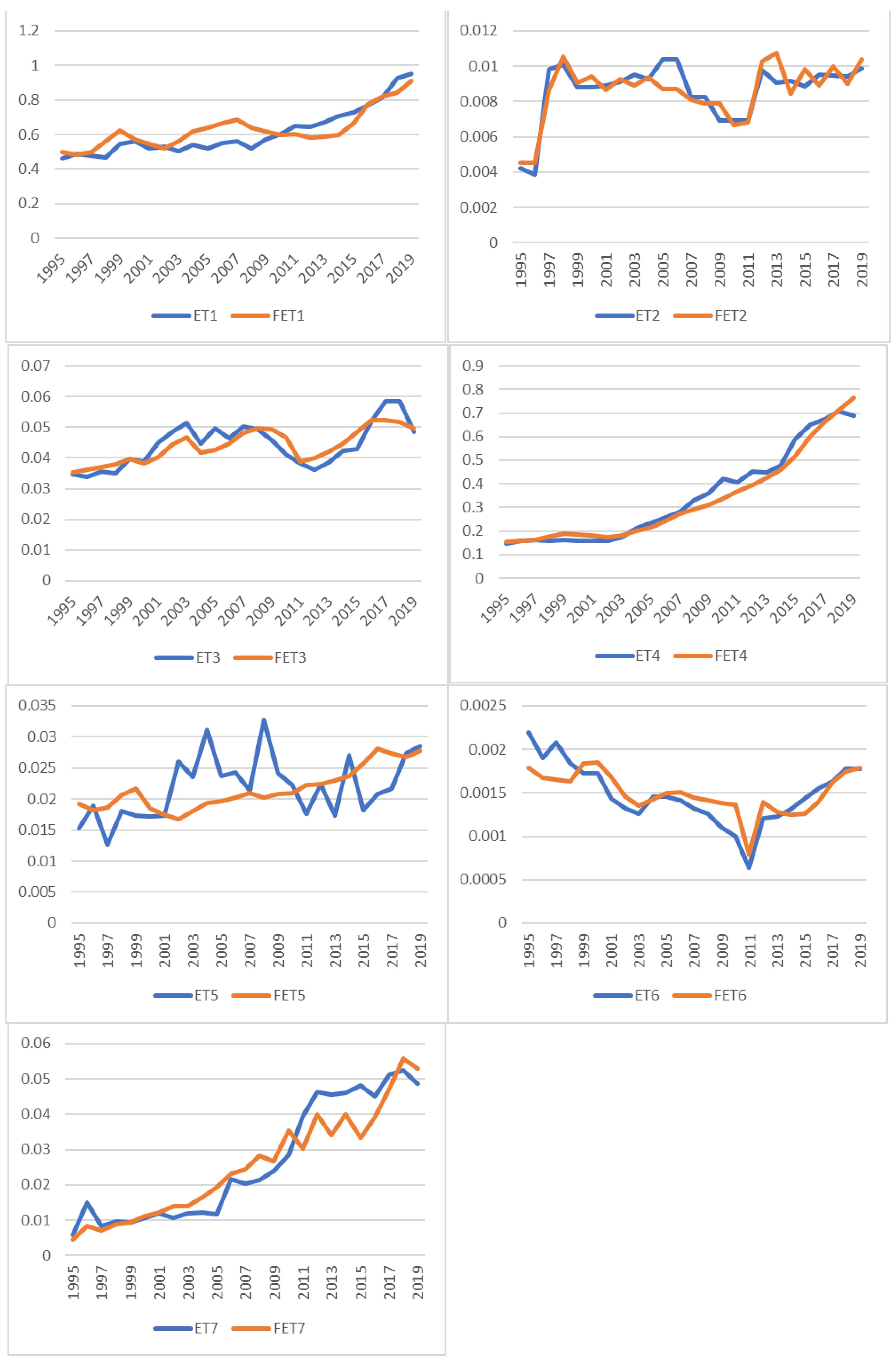
The demand for ethane, denoted as ETi.
Finally, the demand for other petrochemical feedstocks used in petrochemical plants is denoted as OTi.
All the demand is from petrochemical plants for the production of intermediate and final petrochemical products.
The aforementioned dependent variables are measured in our econometric models in million barrels of oil equivalent per day (MMboe/d). The reason for using this unit of measurement is to estimate the daily demand for oil from the petrochemical industry.
Furthermore, not only do we aim to forecast global demand, but we also estimated several regressions for each region of the world. Our estimation of demand has been developed for the following regions:
0-World
1-OECD America.
2-OECD Europe.
3-OECD Asia and Oceania.
4-Middle East and Africa.
5-Latin America.
6-Eurasia.
7-Asia, excluding China.
8-China.
The letter ‘i’ as a subscript to the previously mentioned variables (NT
i, LTi, ET
i, OT
i) will be equal to 0, 1, 2, 3, 4, 5, 6, 7, and 8. Again, this means that there will be an estimated demand regression for each petrochemical feedstock for each ‘i’th region. The aforementioned dependent variables were collected from the International Energy Agency’s (IEA’s) World Energy Balances database, through a subscription [
17,
18], and measured in terms of kilotons of oil equivalent. The data set was converted from kilotons of oil equivalent to million barrels of oil equivalent per day by multiplying by 0.00714 and dividing by 365 days.
Step 2—Construction of the macroeconomic and socioeconomic explanatory variables
The second step involved the construction of the data set for the macroeconomic and socioeconomic variables, with data taken from the World Bank’s World Development Indicators [
19] so as to have a homogeneous set of data. Data are at an annual frequency from 1971 to 2019 and were collected for the following variables:
Nominal gross domestic product (GDP) in United States (U.S.) dollars (USD).
Real GDP in USD (base = 2015).
Real GDP per capita.
Population in millions.
Percentage of population living in urban areas.
We have taken the data available at the country level for about 180 countries.
The aggregation is performed at the regional level, by summing GDP values in dollars, population in millions, and urban population in millions. We have taken the regional average GDP per capita by dividing GDP values by the population, and the percentage of the population living in urban areas is derived by dividing the urban population by the total population.
Step 3—Construction of the prices of the four dependent variables at the regional level
Step three involved the construction of the data set for the prices of the four petrochemical feedstocks (naphtha, ethane, LPG, and other petrochemical feedstocks), which were taken and assembled from two main sources, Platts and the United Nations Comtrade database [
20]. From now on, we abbreviate this data source as UNCOMtrade. The Platts data are time series of prices expressed in USD per unit of measurement.
The UNCOMtrade data are a time series of exports and imports of values and quantities at the country level, from which it is possible to recover a measure of import and export unit values. These data have been used as a proxy for the price developments for certain time periods and regions missing in the Platts data. Accordingly, the data sources are as follows:
- -
Platts Data Bank, considering prices of leading products in leading areas according to their classification (see
Table A1).
- -
UNCOMtrade United Nation Trade Data Bank, considering the SITC classification at the three- and four-digit level. Adapting this level of classification is essential for the purpose of capturing the exports, import values, and quantities of the four petrochemical feedstocks mentioned in this paper.
The SITC series taken as a proxy of the prices of the four products are the following:
Naphtha: proxy of price—product 3321, motor spirit, gasoline, and other light oils.
Ethane: proxy of price—product 271,111, natural gas, liquefied.
LPG: proxy of price—product proxy, product 3324, residual fuel oils.
Other oil: proxy of price—product proxy, product 3323, distillate fuels.
Data for the import and export unit values have been computed as dollar values divided by quantity for each product and each region.
The Platts price data are available for different regions and time periods. The elementary prices available from Platts are listed in
Table A1. These data report prices for propane, butane, naphtha, gasoil, fuel oil, and gasoline for Asia, the Americas, Europe, and the Middle East. For some regions, different prices were reported.
Table A1.
Platts price definitions.
Table A1.
Platts price definitions.
| Platts Code | Name of Price Assessment | Date Availability | Region | Petrochemical Feedstock |
|---|
| PMAAV00 | Propane Refrigerated CFR North Asia 30–60 days cargo | 1982 | Asia | Propane |
| PMAAF00 | Butane Refrigerated CF North Asia 30–60 DAYS CARGO | 1985 | Asia | Butane |
| PAAAD00 | Naphtha c+f Japan Cargo USD/mt (NextGen MOC) | 1983 | Asia | Naphtha |
| PAAAG00 | Naphtha c+f Japan Cargo 60–75 Days (NextGen MOC) | 1991 | Asia | Naphtha |
| PAAAF00 | Naphtha c+f Japan Cargo 45–60 Days (NextGen MOC) | 1991 | Asia | Naphtha |
| PAAAE00 | Naphtha c+f Japan Cargo 30–45 Days (NextGen MOC) | 1991 | Asia | Naphtha |
| POABC00 | Gasoil FOB Spore Cargo | 1983 | Asia | Gasoil |
| PUABE00 | FO 180 CST FOB ARAB GULF Cargo | 1978 | Asia | Fuel oil |
| PMAAT00 | Propane Conway Pipeline | 1983 | Americas | Propane |
| PMAAD00 | Butane Conway spot | 1983 | Americas | Butane |
| POAED00 | Gasoil No.2 USGC Prompt Pipeline | 1979 | Americas | Gasoil |
| POAEE00 | Gasoil No.2 USGC Prompt waterborne | 1979 | Americas | Gasoil |
| POAEG00 | Gasoil No.2 New York Harbor Barge | 1979 | Americas | Gasoil |
| PUAFZ00 | USGC HSFO Waterborne (NextGen MOC) | 1979 | Americas | Fuel oil |
| PAAAL00 | Naphtha CIF NEW Cargo USD/mt | 1990 | Europe | Naphtha |
| PAAAM00 | Naphtha FOB Rdam Barge USD/mt | 1990 | Europe | Naphtha |
| PMABA00 | Propane CIF NEW Large Cargo | 1985 | Europe | Propane |
| PMAAS00 | Propane FOB ARA | 1985 | Europe | Propane |
| PMAAK00 | Butane CIF NWE Large Cargo | 1985 | Europe | Butane |
| PMAAC00 | Butane FOB ARA | 1985 | Europe | Butane |
| PUAAL00 | FO 1% S CIF NEW Cargo | 1979 | Europe | Fuel oil |
| PUAAP00 | FO 1% S FOB Rdam Barge | 1979 | Europe | Fuel oil |
| PAAAI00 | naphtha FOB Med Cargo | 1979 | Africa | Naphtha |
| PMABF00 | Propane FOB AG 20–40 DAYS CARGO vs. SAUDI PROPANE cp m1 | 1994 | ME | Propane |
| PMABG00 | BUTANE FOB AG 20–40 DAYS CARGO vs. SAUDI BUTANE CP M1 | 1994 | ME | Butane |
| PAAAA00 | Naphtha FOB Arab Gulf Cargo | 1978 | ME | Naphtha |
| POAAT00 | Gasoil FOB Arab Gulf Cargo | 1983 | ME | Gasoil |
| PUABE00 | FO 180 CST FOB ARAB GULF Cargo | 1978 | ME | Fuel oil |
| PUADV00 | FO 180 CST 3.5% S FOB SPORE CARGO | 1980 | Asia | Fuel oil |
| PGACT00 | Gasoline Unl 87 USGC Prompt Pipeline | 1979 | U.S. | Gasoline |
In
Table A2, we associate the original Platts prices with the paper’s classification of regions.
The first crucial point to note is that Platts prices are available for different products for six regions of the world: Asia, the Americas, Europe, Africa, the Middle East, and the U.S. In
Table A2, we show the correspondence between Platts’ and this paper’s regions. Platts data cover four main regions, and these have been attributed to the paper’s regional classifications. For instance, Platts’ Asia region corresponds to three regions of the paper’s classifications: OECD Asia, Asia excluding China, and China. Platts’ America region has been attributed to two of the paper’s regional classifications: OECD Americas and Latina America.
Table A2.
Platts’ and this paper’s regional correspondence.
Table A2.
Platts’ and this paper’s regional correspondence.
| Platts’ Regions | This Paper’s Regional Classifications | | |
|---|
| Asia | 2 OECD Asia | 7 Asia excl. China | 8 China |
| America | 1 OECD Americas | 5 Latin America | |
| Europe | 3 OECD Europe | 6 Eurasia | |
| Africa and ME | 4 Africa and Middle East | | |
The second point to note is that Platts’ product classification is different from this paper’s regional classification. Therefore, we used the Platts product prices for each region, as shown in
Table A3. We used propane and butane for LT, naphtha for NT, gasoil, and fuel oil for OT. For instance, PMAAV00 and PMAAF00 are the prices that are used to construct a weighted average to proxy the price of LT for Asia.
Table A3.
Definitions.
| | Prices | | |
|---|
| Region | LT | NT | OT |
|---|
| Asia | PMAAV00 | PAAAD00 | PUABE00 |
| | PMAAF00 | PAAAG00 | POABC00 |
| | | PAAAF00 | |
| | | PAAAE00 | |
| America | PMAAT00 | PGACT00 | PUAFZ00 |
| | PMAAD00 | | |
| Europe | PMABA00 | | PUAAL00 |
| | PMAAS00 | | PUAAP00 |
| | PMAAK00 | | |
| | PMAAC00 | | |
| ME and Africa | PMABF00 | PAAAI00 | POAAT00 |
| | PMABG00 | PAAAA00 | PUABE00 |
We then aggregated the prices for the countries, regions, and years available from the United Nations Comtrade database [
20] according to our regional classification. We used a procedure with the function VLOOKUP to select the available data for the eight regions. This procedure is necessary because the data may contain a different number of reporting countries within each region for a given year. In other words, the data include varying numbers of countries for every year. The procedure avezzzyraged the country values for every year to obtain a time series with an average regional value for every year. Given the existing variability of the number of reporting countries in different years, with some reporting data on an intermittent basis, and some data clearly misreported, we decided to exclude the outlier countries from the yearly averages if the values deviate by more than one sigma from the regional average. Some of the misreported data were typically an underreporting of the quantity, which could give rise to excessive and implausible unit values (the division of a dollar value by a misreported quantity could result in a too high a unit value).
The data resulting from the above, for every region:
Time series with 52 observations 1971–2021 for naphtha ethane and LPG.
Time series with 39 observations 1971–2008 for other oil.
We then used the UNCOMTRADE unit values to estimate the missing data in the Platts data.
Table A1 gives Platts data for different time periods. We averaged the UNCOMTRADE price indicators to match the Platts prices according to the correspondence shown in
Table A2. Then we made a backward interpolation of the missing values for the Platts prices with the growth rates of the UNCOMTRADE price indicators for naphtha, LPG, and other petrochemical feedstocks. By doing this, we obtain a complete data set of Platts prices for the period 1971–2019. We used UNCOMTRADE data directly for ethane because Platts data do not report ethane prices.
The last phase was the construction of the time series for the four product prices for the eight regions used in the estimation. As explained above, we used the complete Platts data set to construct this paper’s regional prices, according to the correspondence shown in
Table A2. We labeled the prices with the product suffix and the region suffix, as shown below:
PNT0 PNT1 PNT2 PNT3 PNT4 PNT5 PNT6 PNT7 PNT8
PET0 PET1 PET2 PET3 PET4 PET5 PET6 PET7 PET8
PLT0 PLT1 PLT2 PLT3 PLT4 PLT5 PLT6 PLT7 PLT8
POT0 POT1 POT2 POT3 POT4 POT5 POT6 POT7 POT8
For instance, PNT1 is the price of naphtha in region 1 (OECD Americas), PET2 is the price of ethane in region 2 (OECD Europe), and so on.