Mean Droplet Size Prediction of Twin Swirl Airblast Nozzle at Elevated Operating Conditions

Abstract

This study introduces a novel predictive model for atomization droplet size, developed using comprehensive data collected under elevated temperature and pressure conditions using a twin swirl airblast nozzle. The model, grounded in flow instability theory, has been meticulously parameterized using the Particle Swarm Optimization (PSO) algorithm. Through rigorous analysis, including analysis of variance (ANOVA), the model has demonstrated robust reliability and precision, with a maximum relative error of 19.3% and an average relative error of 6.8%. Compared to the classical atomization model by Rizkalla and Lefebvre, this model leverages theoretical insights and incorporates a range of interacting variables, enhancing its applicability and accuracy. Spearman correlation analysis reveals that air pressure and the air pressure drop ratio significantly negatively impact droplet size, whereas the fuel–air ratio (FAR) shows a positive correlation. Experimental validation at ambient conditions shows that the model is applicable with a reliability threshold of We₁/Re₁ ≥ 0.13 and highlights the predominance of the pressure swirl mechanism over aerodynamic atomization at higher fuel flow rates (q > 1.25 kg/h). This research effectively bridges theoretical and practical perspectives, offering critical insights for the optimization of airblast nozzle design.

1. Introduction

Modern aeroengines predominantly utilize liquid fuels due to their exceptional energy density per unit volume. The efficient atomization and subsequent evaporation of liquid fuel are critical for combustion [1,2,3]. As performance demands on combustion chambers increase, it has become evident that conventional single-pressure swirl nozzles are increasingly inadequate. This limitation has prompted the development and widespread adoption of airblast nozzles, which combine a pressure swirl nozzle or a prefilming nozzle with multiple concentric swirlers. These advanced nozzles leverage aerodynamic forces to achieve superior atomization and rapid air–fuel mixing [4,5,6,7,8].

Extensive research has been conducted on the flow field structure [9,10,11,12,13], spray distribution [14,15,16], and atomized particle size [17,18,19,20] of airblast nozzles, offering essential insights for nozzle design. The particle size of atomized liquid fuel has been identified as a vital factor, with a direct impact on ignition and extinction performance, combustion efficiency, and outlet temperature distribution. A thorough examination of the literature on the subject of atomization particle size reveals a clear focus on the question of its determinants [21,22,23]. The geometric parameters of the nozzle have a direct impact on the atomization particle size [24,25,26]. Additionally, more studies focus on the operating conditions. In particular, air velocity and pressure is of great importance due to its impact on aerodynamic forces, thereby playing a crucial role in airblast atomization dynamics [27]. Viscosity, a critical property of fuel, is significantly influenced by temperature and plays a crucial role in the break-up mechanism [28,29,30]. Mir et al. have conducted a comprehensive analysis of the interplay between multiple influencing variables, which encompass the air-to-liquid ratio, pressure drop ratio, and surface tension, providing valuable insights for guiding engineering applications [31].

The Sauter mean diameter (SMD) is a commonly employed metric for assessing the quality of atomization, as it provides an indication of the surface area of liquid fuel particles of equal mass. A variety of approaches have been employed for the purpose of predicting the SMD, including the utilization of numerical simulation methods [32,33,34,35]. Furthermore, some studies have integrated theoretical analysis with experimental techniques. For example, Liu et al. [22] introduced the finite stochastic breakage model (FSBM), which offers a novel perspective on atomization mechanisms. Other researchers, including Senecal et al. [36], Su et al. [37], and Reitz et al. [38], have simplified the atomization process to a two-dimensional planar problem, developing theoretical models based on flow instability theory and validating their models through experimental data. Their studies have provided researchers with robust mathematical frameworks, enhancing the capability for in-depth analysis of atomization mechanisms and the development of atomization models [39,40,41,42]. Chen et al. [21] and Rizkalla et al. [27] develop a comprehensive multi-factor model for predicting the SMD based on extensive experimental data, respectively. Although these model offers several advantages, including simplicity and high accuracy, they lack a detailed representation of atomization mechanisms and provide limited physical insight.

The combustion chamber of an aeroengine, distinguished by its confined space, extreme temperatures, pressures, and high-velocity flows, exhibits complex flow characteristics that are significantly different from ambient conditions. The research conducted by Zhang et al. [43] and Varga et al. [44], which closely simulates extreme conditions, reveals that the aerodynamic Weber number is the primary factor determining atomization droplet size. Varga’s findings indicate that the breakup mechanism of liquid jets in high-speed air flows is analogous to that of droplets subjected to sudden exposure to high-speed gas streams. Given the difficulties inherent in spray testing under elevated pressure, there is a dearth of experimental research on atomization particle size in pressurized environments. It is noteworthy that there is a limited number of studies providing data on droplet sizes under heating and pressurization conditions, such as those by Rizkalla [27] and Zheng [45]. This scarcity underscores the urgent need for a comprehensive modeling study that examines droplet size in twin swirl airblast nozzles operating under heated and pressurized conditions, encompassing various influencing factors.

This study adopted a combined method of theoretical analysis and atomization experiments to investigate the prediction model of nozzle atomization particle size. The primary goal of the present paper is to establish a physics-based prediction model for the atomization particle size of twin swirl airblast nozzles operating under pressurized conditions. The comprehensive effects of various factors, including air pressure, temperature, pressure drop ratio, fuel properties, and fuel-to-air ratio, on the atomization particle size of kerosene have been obtained. Notably, the maximum air pressure reached up to 0.8 MPa. Furthermore, a thorough evaluation of the rationality and applicability of the prediction model was conducted.

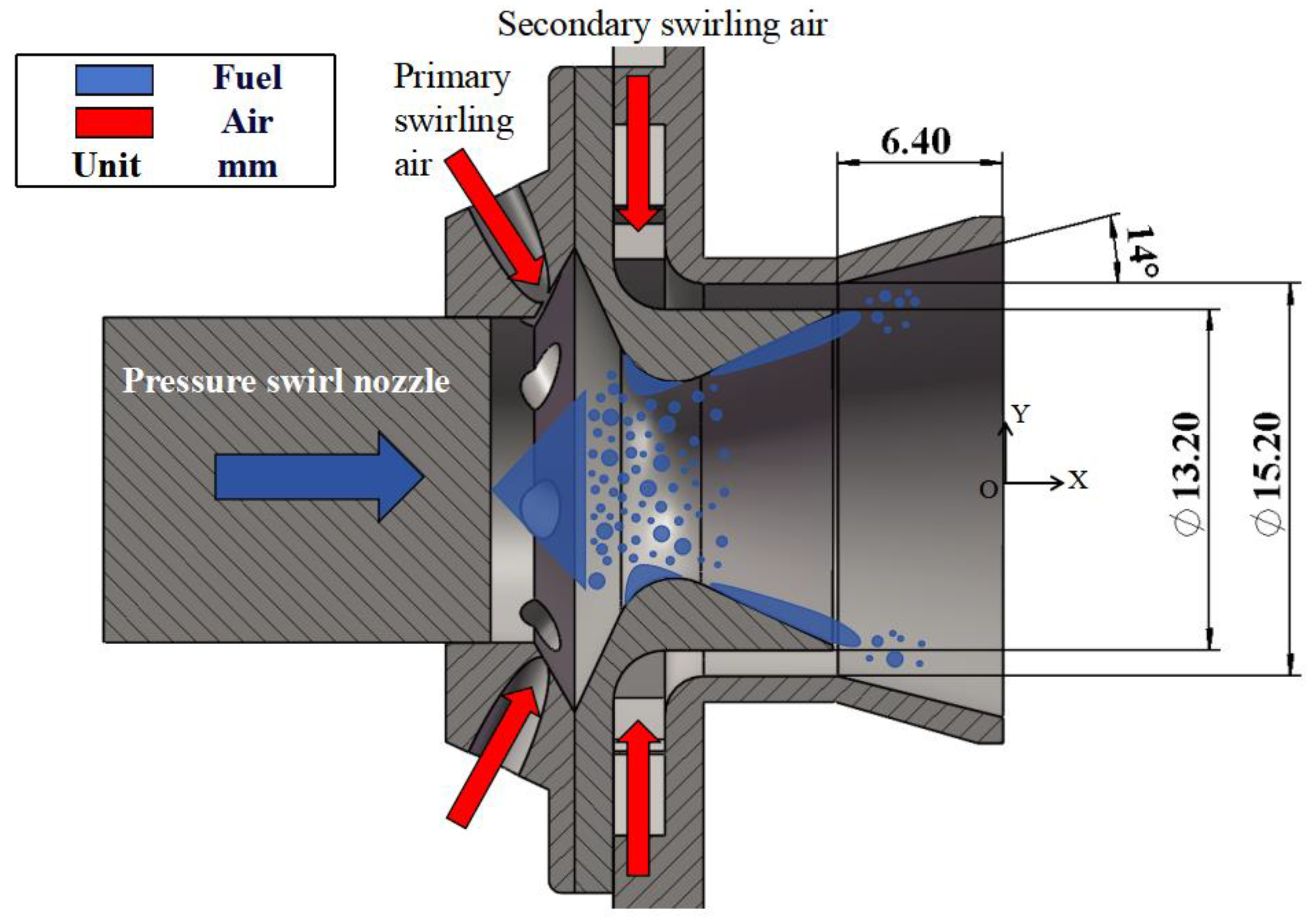
2. Experimental Setup

2.1. Test System

The schematic diagram of the experimental system is presented in Figure 1. An adjustable air compressor (Kaishan, JNV160, Quzhou, China) supplies the air, with its flow rate measured by a vortex shedding flowmeter, achieving an accuracy of 1% of the reading value. Subsequently, the air is heated by an electric heater situated downstream of the flowmeter. The temperature of the air is gauged using a K-type thermocouple at the inlet measurement section, with an associated margin of error of 1 °C. Furthermore, the air pressure is monitored via a total pressure sensor at the inlet measurement section, thereby ensuring a pressure measurement error of 1%. In order to ascertain the pressure drop ratio across the airblast nozzle, the differential pressure is gauged between two pressure sensors situated at the inlet measurement and outlet measurement sections. The pressure drop ratio, denoted mathematically as $\mathsf{\Delta }P/P_a$, is recognized as being intimately linked to air flow velocity and has been studied as a crucial parameter influencing atomized particle size. In the outlet measurement section, water spray nozzles are used to cool down the mixture, facilitating the sedimentation of fuel components within it. Prior to discharge, the liquid phase is separated by a cyclone separator.

Chinese RP-3 aviation kerosene was used in the experiment, which has similar physical and chemical properties to Jet-A. The fuel supply is facilitated by an adjustable plunger pump. To reduce the fluctuation of fuel flow, a buffer tank filled with small steel balls is set up on the fuel line. The fuel mass flow rate is accurately measured by a Coriolis flowmeter, with an error of 0.5% of the reading value. The fuel-to-air ratio (FAR) is calculated with an error of 1.12% by relative error propagation. Prior to the experiment, a temperature-controlled cabinet holding 8 L of fuel is pre-set to the desired temperature. Upon activation of the fuel pump, the preheated fuel is gently propelled into the nozzle. To effectively reduce heat exchange between the incoming hot air and the fuel within the test chamber fuel line, multiple layers of thermal insulation wrap the outside of the fuel line. The fuel temperature measurement point is strategically located at the end of the fuel line to be as close as possible to the nozzle outlet.

The double swirl air blast nozzle is shown in Figure 2. The nozzle consists of a central pressure swirl nozzle, a two-stage air swirler, a venturi tube, and a sleeve. The venturi tube has an outlet diameter of 13.20 mm, while the sleeve has an initial diameter of 15.20 mm, a length of 6.40 mm, and a half-cone angle of 14°. The primary swirler is designed with eight slanted apertures, each 2.2 mm in diameter, while the secondary swirler has ten radial vortex channels. The swirl number (SN), a quantitative measure of the swirl intensity generated by the swirler, is calculated for the radial swirlers according to the method originally developed by Sheen et al. [46].

$$\mathrm{SN}=\frac{{\int }_0^{R_0}\rho U_y{U}_{\theta }2\pi r^{2}dr}{R{\int }_0^{R_0}\rho U_y^{2}2\pi rdr}$$

(1)

where $U_y$ is axial velocity; $U_{\theta }$ is the tangential velocity; and $R_0$ is the outer radius of the venturi exit. The SN of the inner and outer swirlers is 1.800 and 1.146, respectively.

The Malvern Laser Particle Size Analyzer (Spraylink 2.0, Zhuhai, China), using a 20 mW 638 nm laser with a 15 mm beam diameter, is designed to accurately measure spray particle diameters from 0.1 μm to 2080 μm. Strategically placed on either side of a viewing window, the analyzer aligns the central axis of its laser 30 mm downstream of the nozzle outlet, perpendicular to the central axis of the fuel spray cone, as shown in Figure 1. A review of the literature reveals that fuel atomization is sufficient at 30 mm [12]. Using laser diffraction, it efficiently captures scattering patterns from the beam as it passes through the sample, facilitating particle size determination. For large sample volumes, this method outperforms Phase Doppler Particle Analyzer (PDPA) systems in efficiency and convenience. Specifically, the SMD represents the diameter of a sphere that reflects the same volume-to-surface-area ratio as the particle distribution. It could be calculated based on Reference [7].

Prior to the initiation of the experiments, the Malvern instrument undergoes a thorough calibration process. Three standard particles with sizes of 400 nm, 1 µm, and 9 µm were used for calibration. The relative measurement error for these three standard particles is within 1%. Therefore, it is concluded that the reading error of this instrument is within 1%. Next, multiple tests are performed for each operating condition, and the final results are averaged across these tests to reduce the influence of random errors and improve the accuracy of the results.

2.2. Experimental Conditions

The experimental design encompasses a comprehensive range of conditions based on the operational range and pre-experimental data outlined in

Table 1. The experimental conditions from 1 to 40.

S/N	Pa (MPa)	∆P/Pa (%)	Ta (K)	Tl (K)	FAR
1	0.3	4	450	316	0.04
2	0.3	4	450	346	0.04
3	0.3	6	450	316	0.04
4	0.3	4	450	316	0.02
5	0.3	4	450	316	0.06
6	0.1	4	450	316	0.04
7	0.4	6	490	331	0.02
8	0.4	6	490	331	0.06
9	0.2	6	490	331	0.06
10	0.4	2	490	301	0.02
11	0.4	6	410	301	0.02
12	0.2	2	410	301	0.06
13	0.4	2	490	301	0.06
14	0.2	2	410	301	0.02
15	0.4	2	410	331	0.06
16	0.4	2	410	301	0.06
17	0.2	2	490	301	0.06
18	0.2	6	490	301	0.06
19	0.4	2	490	331	0.02
20	0.4	6	410	301	0.06
21	0.4	6	410	331	0.02
22	0.2	2	490	331	0.02
23	0.2	2	410	331	0.06
24	0.2	6	490	301	0.02
25	0.4	6	490	301	0.06
26	0.4	2	490	331	0.06
27	0.2	2	410	331	0.02
28	0.4	2	410	301	0.02
29	0.1	4	303	316	0.04
30	0.2	4	340	316	0.04
31	0.45	4	500	316	0.04
32	0.25	4	450	316	0.04
33	0.5	4	450	316	0.04
34	0.3	4	350	316	0.04
35	0.3	2	450	316	0.04
36	0.4	6	410	331	0.06
37	0.2	6	410	301	0.02
38	0.2	6	490	331	0.02
39	0.2	2	490	331	0.06
40	0.4	2	410	331	0.02

. The study specifically investigates seven intake air pressure settings (0.1 MPa, 0.2 MPa, 0.25 MPa, 0.3 MPa, 0.4 MPa, 0.45 MPa, 0.5 MPa), three swirler pressure drop ratio conditions (2%, 4%, 6%), five air temperature settings (303 K, 340 K, 350 K, 410 K, 450 K), four fuel temperature conditions (301 K, 316 K, 331 K, 346 K) and three FAR conditions (0.02, 0.04, 0.06). Taking into account the cross-effects of these parameters on the atomization particle size, 40 experimental conditions were designed, as presented in Table 1. It is noteworthy that the prediction model for particle size is calibrated based on data from these 40 experimental conditions. Additionally, experimental conditions 41–46 were designed in subsequent research to evaluate the generalization of the model, with the actual maximum air pressure reaching up to 0.8 MPa.

3. Semi-Empirical Prediction Model for SMD

3.1. Atomization Process of Twin Swirl Airblast Nozzle

The atomization process within a twin swirl airblast nozzle is distinguished by a complex interplay of flow and fragmentation dynamics. In the initial phase, fuel is expelled from the pressure swirl nozzle, with a portion of it impacting and fragmenting into droplets upon collision with the surface of the venturi. The remaining fuel adheres to the wall of the venturi. The fuel that adheres to the wall is subsequently discharged as a liquid film at the venturi exit. Subsequently, the liquid film interacts with the surrounding gas, resulting in the induction of Kelvin–Helmholtz instabilities and Rayleigh–Taylor ring waves on its surface, which are influenced by inertial centrifugal forces. Concurrently, the film is subjected to shear and disruptive forces from the high-speed swirling air generated by the dual-stage swirlers. The combined effect of these factors results in the fragmentation of the liquid film into liquid belts, thereby initiating the primary stage of atomization. As these liquid belts progress downstream, aerodynamic forces exert further deformation and fragmentation, ultimately resulting in the formation of fine liquid droplets through secondary atomization.

In the context of this study, which was conducted under conditions of elevated temperature and pressure, the aerodynamic influence of swirling air plays a pivotal role in the atomization process. Accordingly, the theoretical modelling presented herein focuses on the analysis of the liquid film in proximity to the venturi outlet, deliberately excluding a detailed analyzation of the pressure swirl nozzles and the film-forming flow along the venturi wall. The impact of droplet clustering resulting from collisional fragmentation at the wall surface will be addressed in future work through the optimization of relevant parameters.

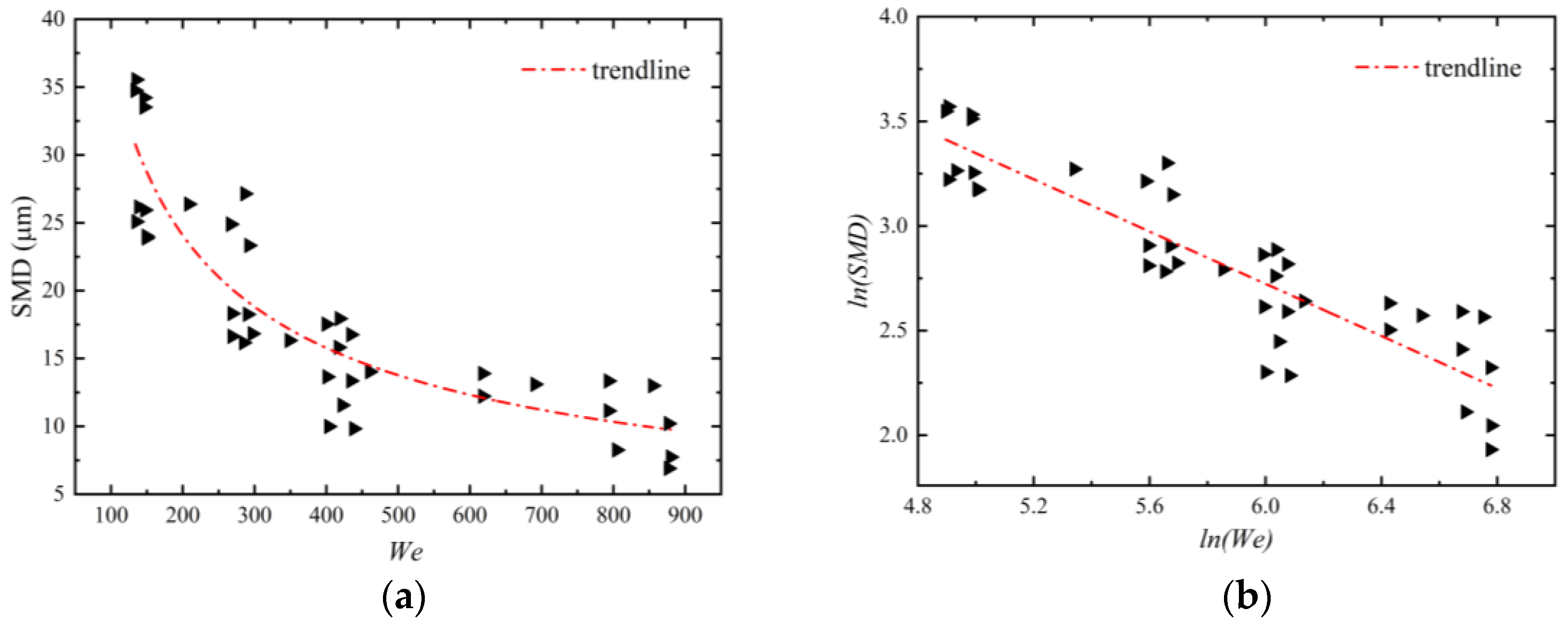
3.2. Semi-Empirical Prediction Models

In the atomization process of a twin swirl airblast nozzle, the liquid film of fuel ejected through the venturi is fragmented into liquid belts as a result of surface instabilities and aerodynamic shear forces. In a two-dimensional planar analysis, the dimensions of these liquid belts are primarily determined by the wavelength of the surface waves at rupture [36] and the thickness of the liquid film [47]. In consideration of the fact that the maximum unstable wave number is directly correlated with the wavelength, the assessment of dimensionless parameters is based on the maximum unstable wave number at rupture and the liquid film thickness. Although the aerodynamic impact is clearly significant, it is also considered in order to enhance the overall understanding of the atomization process.

Firstly, a two-dimensional viscous jet liquid film with a thickness of 2 h is considered, being injected into a static inviscid incompressible air medium with a velocity of $U_l$. The liquid film has a density of ${\rho }_l$, a kinematic viscosity of ${\mu }_l$, and a surface tension coefficient of $\sigma$. The density of the air is ${\rho }_a$. The liquid kinematic viscosity $v_l$ is defined as ${\mu }_l/{\rho }_l$. The surface wave dispersion equations for a high-speed viscous jet are mainly based on the study of Senecal [36].

$${\omega }^2\left[tanh\left(kh\right)+\epsilon \right]+\omega \left[4v_l{k}^{2}tanh\left(kh\right)+2i\epsilon k{U}_l\right]+4v_l^2{k}^{4}tanh\left(kh\right)-4v_l^2{k}^3\gamma tanh\left(\gamma h\right)-\epsilon U_l^2{k}^2+\frac{\sigma k^3}{{\rho }_l}=0$$

(2)

where the complex growth rate $\omega ={\omega }_r+i{\omega }_i$, wave number $k=2\pi /\lambda$,$\lambda$ represents the surface wave wavelength, ${\gamma }^2=k^2+\frac{\omega }{v_l}$, $\epsilon ={\rho }_a/{\rho }_l \left(\epsilon \ll 1\right)$ represents the ratio of gas–liquid density. High-speed jet condition surface waves will be dominated by short waves, that is $\epsilon \ll kh$, so one can obtain the simplified solution of Equation (2):

$${\omega }_r=-2v_l{k}^2+\sqrt{4v_l^2{k}^4+\epsilon U_l^2{k}^2-\frac{\sigma k^3}{{\rho }_l}}$$

(3)

When ${\omega }_r$ has a maximum value, the liquid film ruptures. At this time, there is a corresponding maximum unstable wave number $K_S$ and maximum unstable wavelength ${\lambda }_s$, which satisfies $K_s=2\pi /{\lambda }_s$.

The form of the solution of Equation (3) under the inviscid condition is deterministic:

$$K_{s,inviscid}=\frac{{\rho }_a{U}_l^2}{\sigma }$$

(4)

Let $\frac{\partial {\omega }_r}{\partial k}=0$ be obtained as follows:

$$-8v_l\sqrt{4v_l^2{k}^4+q{U}_l^2{k}^2-\frac{\sigma k^3}{{\rho }_l}}+16v_l^2{k}^2+2\epsilon U_l^2-\frac{3\sigma k}{{\rho }_l}=0$$

(5)

Since the analytical solution of Equation (5) is too complex to be used for modeling, the $K_s$ model with viscous conditions is constructed on the basis of Equations (4) and (5):

$$K_s\propto {\left(\frac{{\rho }_a{U}_l^2}{\sigma }\right)}^{\alpha }{\left(\frac{{\rho }_l{\rho }_a{U}_l^2}{{\mu }_l^2}\right)}^{\frac{1-\alpha }{2}}$$

(6)

Considering the thickness $h_s$ and breaking length $L_b$ at the liquid film breakup, the model of Xiao’s [26] mass conservation is chosen:

$$h_s=\frac{d_{0}t}{2L_{b}sin\theta }$$

(7)

While t is the fuel film thickness at the outlet of the venturi, the relation can be obtained from Kim’s [48] equation:

$$\frac{t}{d_0}\propto {\left(\frac{q{\mu }_l}{{\rho }_l\Delta P_l{d}_0^3}\right)}^{0.25}$$

(8)

The $\Delta P_l$ is the fuel pressure meeting $\Delta P_l\approx \frac{1}{2}{\rho }_l{U}_l^2$. The $d_0$ is the pressure swirl nozzle diameter. The semi-liquid spray cone angle θ can be calculated using Lefebvre’s [7] results:

$$\theta \propto {\left(\frac{\Delta P_l{\rho }_l{d}_0^2}{{\mu }_l^2}\right)}^{0.11}$$

(9)

They can be roughly assumed as follows:

$$sin\theta \propto {\left(\frac{\Delta P_l{\rho }_l{d}_0^2}{{\mu }_l^2}\right)}^{0.11}$$

(10)

$$cos\theta \propto {\left(\frac{\Delta P_l{\rho }_l{d}_0^2}{{\mu }_l^2}\right)}^{-0.11}$$

(11)

Han’s [40] research includes the following equation:

$$L_b\propto {\left(\frac{{\rho }_l\sigma tcos\theta }{{\rho }_a^2{U}_l^2}\right)}^{0.5}$$

(12)

The following equation can be obtained by making $q={\rho }_l{U}_l{S}_e$, where $S_e$ denotes the effective area of the nozzle:

$$\frac{h_s}{d_0}\propto {\left(\frac{{\rho }_a{U}_l^2{d}_0}{\sigma }\right)}^{-0.5}{\epsilon }^{-0.5}{\left(\frac{{\rho }_l{U}_l{d}_0}{{\mu }_l}\right)}^{-0.94}{d}_0^{0.5}{S}_e^{0.25}$$

(13)

To summarize, the size $d_L$ model of the liquid blocks formed by the breaking of the liquid film is consistent with the following equation:

$$d_L\propto \sqrt{\frac{h_s}{K_s}}$$

(14)

Then the following equation can be obtained:

$$d_L\propto \sqrt{\frac{{\left(\frac{{\rho }_a{U}_l^2{d}_0}{\sigma }\right)}^{-0.5}{\left(\frac{{\rho }_l{U}_l{d}_0}{{\mu }_l}\right)}^{-0.94}{\epsilon }^{-0.5}{d}_0^{1.5}{S}_e^{0.25}}{{\left(\frac{{\rho }_a{U}_l^2}{\sigma }\right)}^{\alpha }{\left(\frac{{\rho }_l{\rho }_a{U}_l^2}{{\mu }_l^2}\right)}^{\frac{1-\alpha }{2}} }}$$

(15)

In the preceding discussion, the stationary air environment was considered due to the inherent difficulty of solving control equations for viscous jets subjected to high-velocity air. The complex swirling flow generated by the swirler represents an additional challenge in deriving analytical solutions for these equations. Consequently, the impact of the swirling airflow is examined from a macroscopic standpoint. Figure 3a demonstrates a notable power function relationship, and linearization yields a Pearson’s correlation coefficient of r = −0.882 (Figure 3b).

This indicates a robust correlation between the Weber number (We), which characterizes the air–liquid interaction, and the SMD. Consequently, a dimensionless number is introduced to directly represent the aerodynamic impact.

$$W{e}_1=\frac{{\rho }_a{U_a}^2{d}_0}{\sigma }$$

(16)

Based on Equation (15), the following three dimensionless factors can be extracted:

$$W{e}_2=\frac{{\rho }_a{U}_l^2{d}_0}{\sigma }$$

(17)

$$R{e}_1=\frac{{\rho }_a{U}_l{d}_0}{{\mu }_l}$$

(18)

$$R{e}_2=\frac{{\rho }_l{U}_l{d}_0}{{\mu }_l}$$

(19)

In addition, because the dimensionless factor will form the model as a product of power functions, the relationship between air density ${\rho }_a$ and fuel density ${\rho }_l$ is already included. Also, for the sake of simplicity and unity of the model, the density ratio $\mathsf{\epsilon }$ is not included as a factor in the model. Based on the test data, the velocity $U_a$ could be calculated by $\Delta P_a={\rho }_a{U}_a^2/2$.

Build the model as follows:

$$\frac{d_L}{d_0}=a{\left(W{e}_1\right)}^b{\left(W{e}_2\right)}^c{\left(R{e}_1\right)}^d{\left(R{e}_2\right)}^e$$

(20)

Dombrowski and Johns’ study [49] includes the following equation:

$$d_D=1.88d_L{\left(1+3O{h}_1\right)}^{\frac{1}{6}}$$

(21)

$O{h}_1={\mu }_l/{\left({\rho }_l\sigma d_L\right)}^{1/2}$ is the Ohnesorge number. Because of the significant positive correlation between the SMD and the initial size of droplets formed by the breaking of liquid belts, and also for ease of differentiation, the SMD is rewritten by substituting (22):

$$SMD=1.88D_L{\left(1+3O{h}_2\right)}^{\frac{1}{6}}$$

(22)

Similarly, they can be obtained by changing $d_L$ into $D_L$:

$$\frac{D_L}{d_0}=A{\left(W{e}_1\right)}^B{\left(W{e}_2\right)}^C{\left(R{e}_1\right)}^D{\left(R{e}_2\right)}^E$$

(23)

$$O{h}_2=\frac{{\mu }_l}{{\left({\rho }_l\sigma D_L\right)}^{\frac{1}{2}}}$$

(24)

where the five, A, B, C, D, and E, are coefficients to be determined.

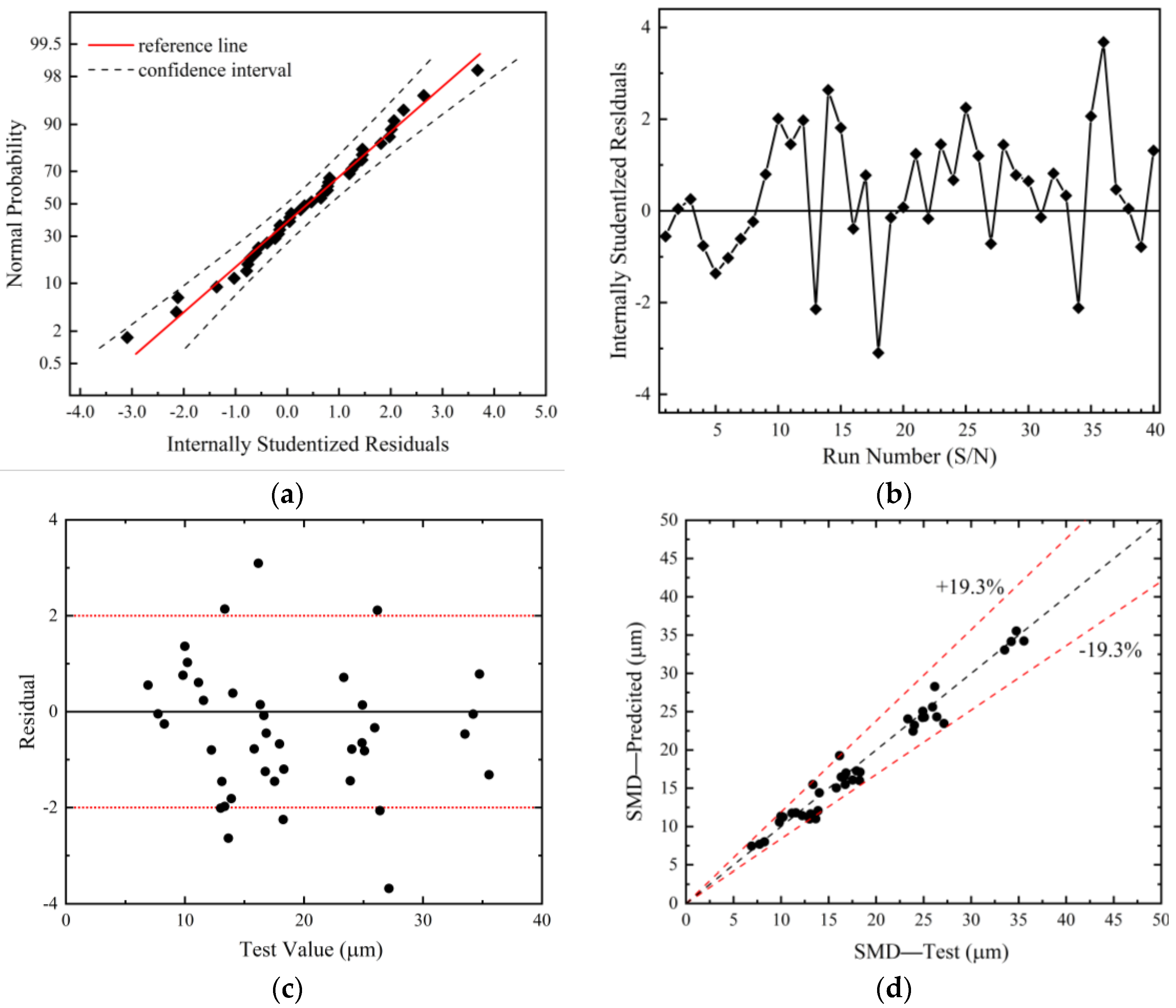
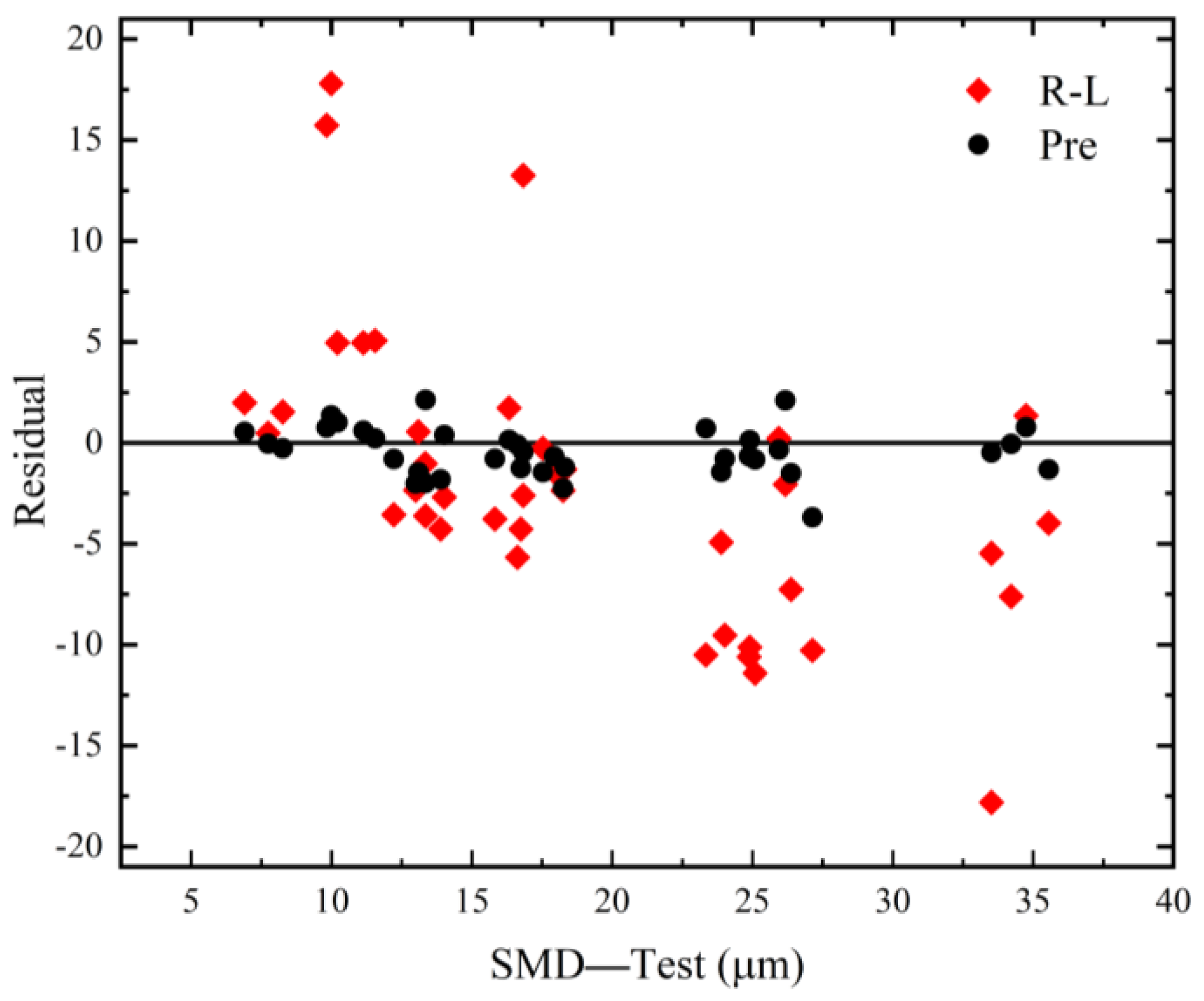
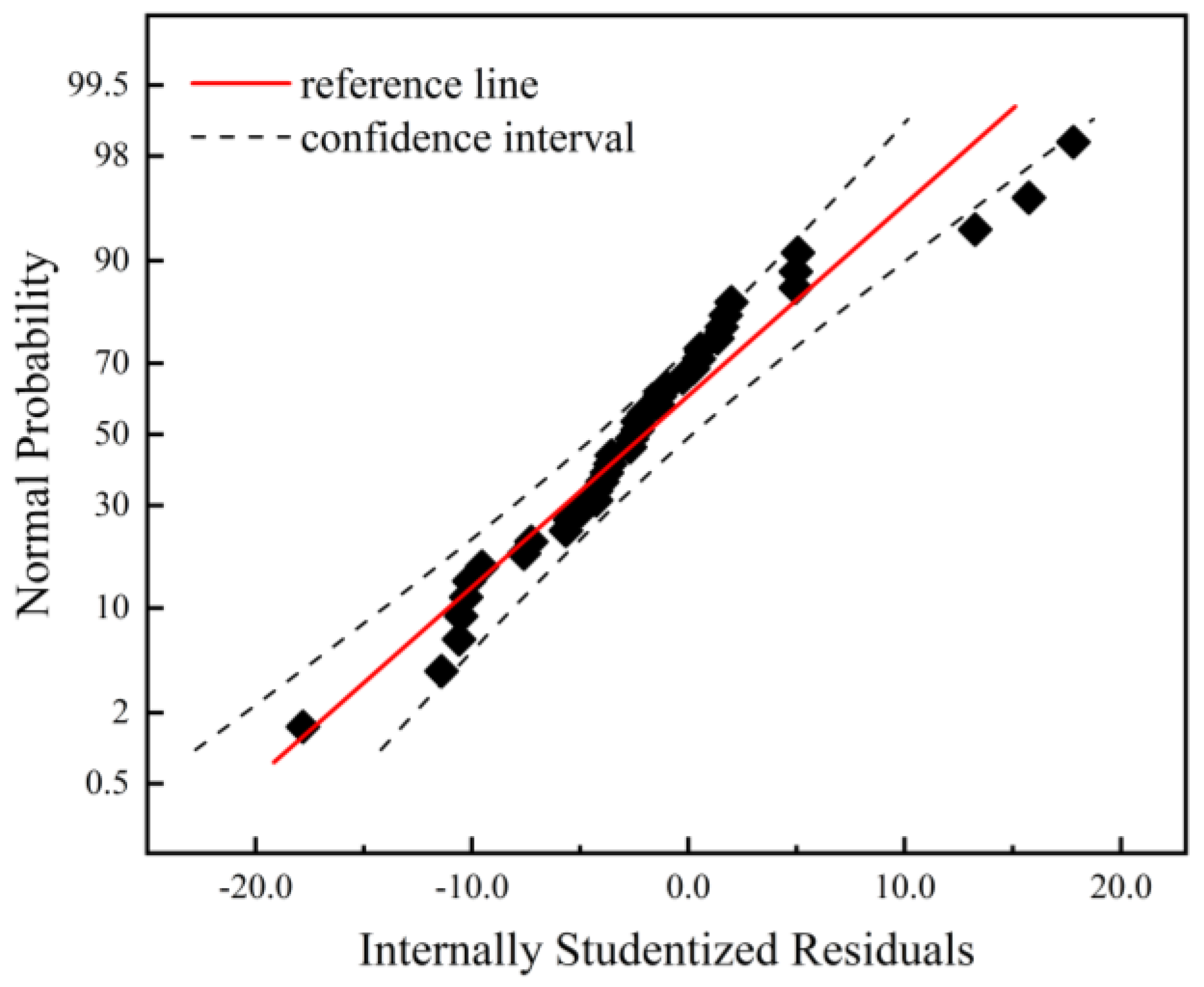
4. Evaluation of the Model

4.1. The Validation of the Predictive Model

Based on Equations (22)–(24) and using the 40 experimental data sets listed in Table 1, the five unknown coefficients were determined in

Table 2. Values of the parameters and the variance, $R^2$.

A	B	C	D	E	R2
1249	−0.8645	0.1551	−0.0113	0.0148	0.967

through optimization via the Particle Swarm Optimization (PSO) algorithm.

In multiple regression models, the analysis of multicollinearity is crucial for identifying high correlations among independent variables, thereby preventing unstable coefficient estimates and facilitating interpretability. Similarly, the analysis of autocorrelation ensures the independence of residuals, enhancing the accuracy of parameter estimates and the validity of hypothesis testing. Both analyses are essential for ensuring the reliability and predictive power of the model. In the analysis of the model, the Variance Inflation Factor (VIF) was employed to assess multicollinearity, while the Durbin–Watson test was utilized to evaluate autocorrelation. It is generally accepted that a VIF value within the range of [1, 5] is considered acceptable, and a Durbin–Watson statistic in the interval of [1.5, 2.5] is deemed reasonable. As presented in

Table 3. VIF values and Durbin–Watson statistic.

$\mathit{V}\mathit{I}{\mathit{F}}_{\mathit{W}{\mathit{e}}_1}$	$\mathit{V}\mathit{I}{\mathit{F}}_{\mathit{W}{\mathit{e}}_2}$	$\mathit{V}\mathit{I}{\mathit{F}}_{\mathit{R}{\mathit{e}}_1}$	$\mathit{V}\mathit{I}{\mathit{F}}_{\mathit{R}{\mathit{e}}_1}$	D-W
1.259	2.335	3.560	3.355	1.706

, all analyzed values fall within the acceptable ranges. Favorable results from multicollinearity and autocorrelation analyses indicate stable parameter estimates and valid hypothesis testing, thereby enhancing the model’s predictive power and reliability.

In an ideal scenario, model residuals should exhibit a normal distribution of random variation, which can be attributed to the experimental process. In order to assess the validity of the model, a normal probability plot of the residuals was constructed. Figure 4a illustrates this plot for the SMD residuals, with data points situated within the 0.95 confidence interval and exhibiting a distribution that closely aligns with a normal distribution. This conformity provides evidence that the predictive model is valid.

In order to ascertain whether the model is subject to any systematic influence as a result of the sequence of experimental runs, an examination was conducted of the relationship between model residuals and run order. Figure 4b illustrates the correlation between the SMD residuals and the order of the experimental runs. The analysis indicates an absence of significant grouping or discernible trends, thereby suggesting that the residuals are not subject to any systematic effects resulting from the sequence of runs.

In order to evaluate the efficacy of the regression model, residuals for the SMD were plotted against the corresponding experimental SMD values. This plot allows for a visual assessment of the model’s unbiasedness and adherence to constant error assumptions. Figure 4c illustrates that the data points are randomly distributed around the horizontal line (residual value = 0), which indicates an absence of systematic bias. The predictions neither consistently exceed nor fall below the experimental values. Furthermore, the residuals do not display a notable trend with increasing experimental values, indicating that the error variance remains constant and thus satisfying the assumption of homoskedasticity in regression analysis. Furthermore, the absence of a discernible pattern in the residuals serves to confirm the suitability of the predictive model.

Figure 4d presents a linear plot of model predictions in comparison to experimental values. The plot demonstrates that all model predictions fall within a relative error band of 19.3%, with an average relative error of 6.8%. These findings corroborate those of the analysis of variance (ANOVA) section, indicating that the prediction model is an accurate estimator of the SMD.

It is crucial to assess the predictive model’s performance on operating points that lie outside the training set but within the operational range. This allows for the assessment of overfitting, the model’s generalization capability, and its overall reliability. Overfitting occurs when a model captures noise rather than the underlying data patterns, which renders it ineffective if it performs well on the training set but fails to generalize to new data. The model was evaluated using six data sets from

Table 4. The experimental conditions 41–46 are designed to verify the model’s generalization.

S/N	Pa (MPa)	∆P/Pa (%)	Ta (K)	Tl (K)	FAR
41	0.8	4	550	316	0.02
42	0.4	6	490	301	0.02
43	0.3	4	550	316	0.04
44	0.3	4	450	286	0.04
45	0.2	6	410	301	0.06
46	0.2	2	490	301	0.02

as the test set. As shown in Figure 5, the model shows optimal performance on the test set, with no evidence of overfitting, and has robust generalization capabilities, confirming its reliability. Moreover, the results of tests 41 and 43 in Table 4 demonstrate that the model retains its robustness in high-temperature (550 K) and high-pressure (0.8 MPa) conditions, thereby extending its applicability beyond the original training data.

4.2. Comparison with Other SMD Prediction Model

The study by Rizkalla and Lefebvre [27], which incorporated multiple influencing factors into a pneumatic atomization prediction model and performed experimental validation under heated and pressurized conditions, provides a suitable basis for comparison with the prediction model developed in this work.

$$SMD=F\frac{{\left(\sigma {\rho }_l{D}_P\right)}^{0.5}}{{\rho }_a{U}_a}\left(1+FAR\right)+G{\left(\frac{{{\mu }_l}^2}{\sigma {\rho }_l}\right)}^{0.425}{D_P}^{0.575}{\left(1+FAR\right)}^2$$

(25)

The coefficients F and G for the model are determined using a PSO algorithm to complete. $D_P$ is the geometric feature size, taking the same value as $d_0$. For clarity, the model developed in this study is designated as the “Pre” model, while the model (25) investigated by Rizkalla and Lefebvre is referred to as the “R-L” model. The “R-L” model’s coefficient of determination is 0.816.

Figure 6 elucidates two salient issues pertaining to the residual distributions of the “R-L” model. Firstly, the residual values demonstrate a decreasing trend as the true SMD increases, thereby exhibiting a clear negative correlation. Secondly, the residuals are predominantly positive when the true SMD is below 15 $\mathsf{\mu }\mathrm{m}$ and predominantly negative when it exceeds 15 $\mathsf{\mu }\mathrm{m}$. These issues, analogous to those identified in the “Pre” model in the preceding section, indicate the presence of substantial systematic errors in the “R-L” model. In light of these findings, it can be concluded that the current “R-L” model structures are unsuitable for the study presented here.

Figure 7 illustrates the normal probability distributions for the “R-L” model, accompanied by a 0.95 confidence interval that is consistent with the findings for the “Pre” model. However, it should be noted that not all data points lie within the confidence interval boundaries. Furthermore, the overall slope of the data points is steeper than that of the reference line, indicating the presence of outliers and a skewed data distribution. In comparison to Figure 4, this suggests that the “R-L” model’s validity is questionable, while the “Pre” model exhibits markedly superior performance.

The data presented in Figure 8a,b demonstrate that the “Pre” model exhibits a lower relative prediction error and higher prediction accuracy in comparison to the “R-L” model. In particular, the “Pre” model demonstrates superior performance to the classical “R-L” model in regression analysis, offering a significant improvement in the precision of SMD forecasting.

The preceding analysis indicates that the overall performance of the “R-L” model is suboptimal. In consideration of the preceding research by Rizkalla and Lefebvre on this model [50], the issues can be broadly attributed to two main categories. Firstly, the structure of the “R-L” model was not derived from theoretical analysis, but rather based on empirical data. Secondly, the experimental setup did not take into account the interactions between the experimental variables. This reliance on empirical data has resulted in structural deficiencies in the model, which has led to poor performance in multivariate predictions. In contrast, the model presented in this study, “Pre”, is derived from theoretical foundations and incorporates aspects of the Design of Experiments (DOE) methodology in its experimental design, thereby accounting for the interactions between variables.

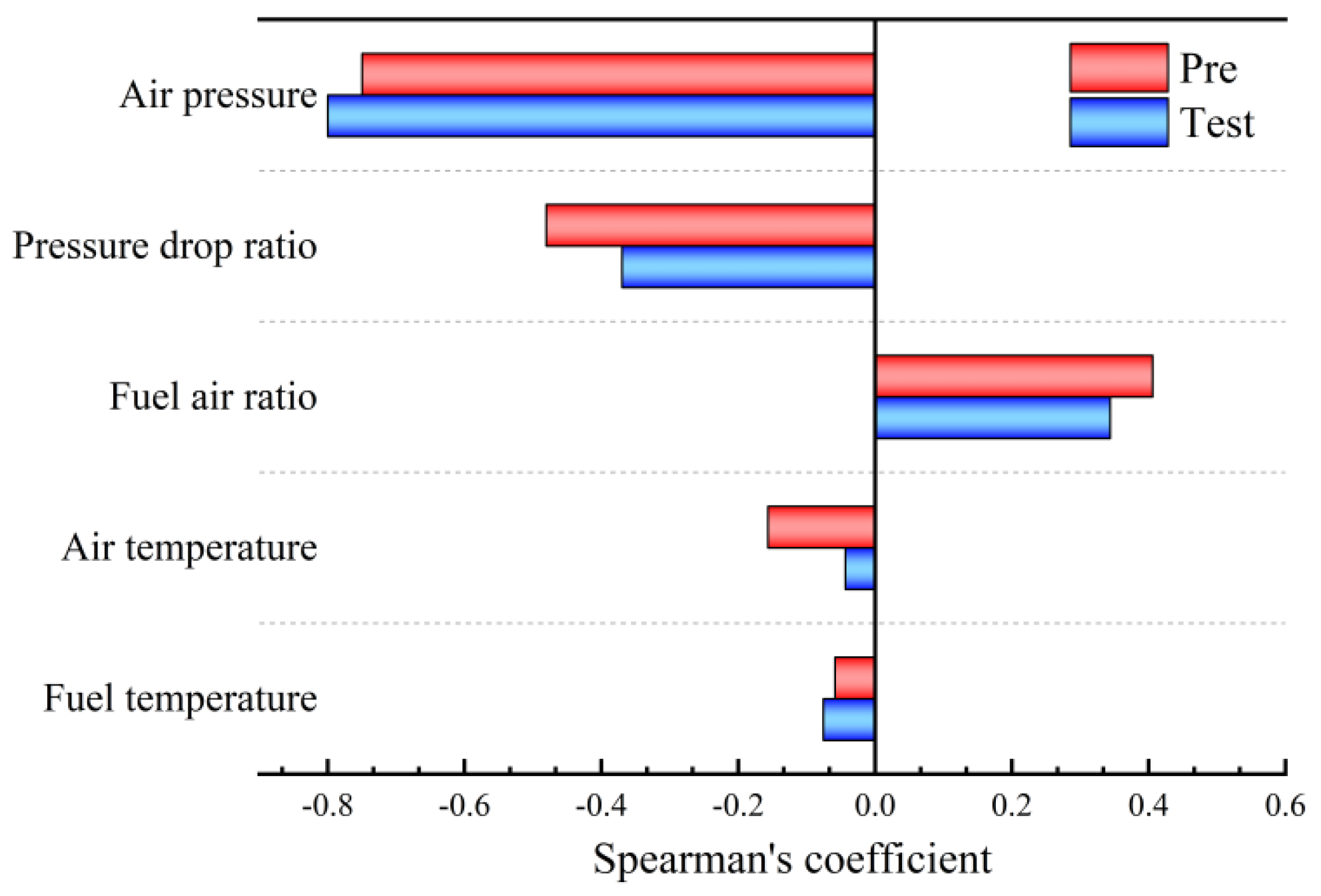
4.3. The Spearman Analysis of the Experimental Variables

Spearman’s rank correlation analysis was employed to examine the relationship between the SMD and the experimental variables. As illustrated in Figure 9, the analysis reveals that the swirler pressure drop ratio exerts the most substantial influence on the SMD, followed by inlet air pressure. These findings are in accordance with those of previous aerodynamic modeling, which indicate that both the pressure drop ratio and inlet pressure are negatively correlated with the atomized SMD. An increase in the swirler pressure drop ratio has a significant effect on airflow velocity, which in turn enhances the interaction between the gas and liquid phases, thereby reducing the SMD. This process can be characterized by the dimensionless number $W{e}_1$.

The impact of fuel temperature on atomization, as a consequence of its influence on fuel viscosity and surface tension, has been the subject of considerable debate in the literature [28,29,30]. The intake air temperature exerts an indirect influence on the physical properties of the fuel by modifying the ambient temperature during atomization. Although the effect of inlet air temperature is relatively minor, it affects gas density primarily through the mechanisms of heat transfer. The aforementioned temperature variation exerts an influence on fuel temperature during the atomization process, thereby enhancing evaporation pressure within the fine droplets. As a result, these effects play a significant role in droplet evaporation, which in turn leads to a reduction in the SMD.

In the experiment, the FAR was controlled by maintaining a constant airflow while varying the fuel mass rate. In these circumstances, the unchanging airflow ensures that the aerodynamic forces remain relatively stable. The increase in fuel flow rate enhances the fuel jet’s resistance to aerodynamic breakup while simultaneously increasing the spatial density of droplets, thereby raising the probability of droplet collision and coalescence. Consequently, there is a positive correlation between the SMD and the FAR, as indicated by a positive Spearman correlation coefficient. In the study by Lefebvre [7], a constant fuel flow rate was maintained while varying the air intake to adjust the fuel–air ratio, resulting in outcomes comparable to those presented here. This phenomenon can be approximately characterized by the ratio $W{e}_1/R{e}_1$. The relationship between aerodynamic effects and fuel flow rate will be discussed in further detail in the following section.

The predictive model not only accurately captures the qualitative effects of each experimental variable on the SMD but also exhibits a strong correlation with the experimental data. This agreement serves to reinforce the model’s robust physical properties and its reliability in reflecting the underlying phenomena.

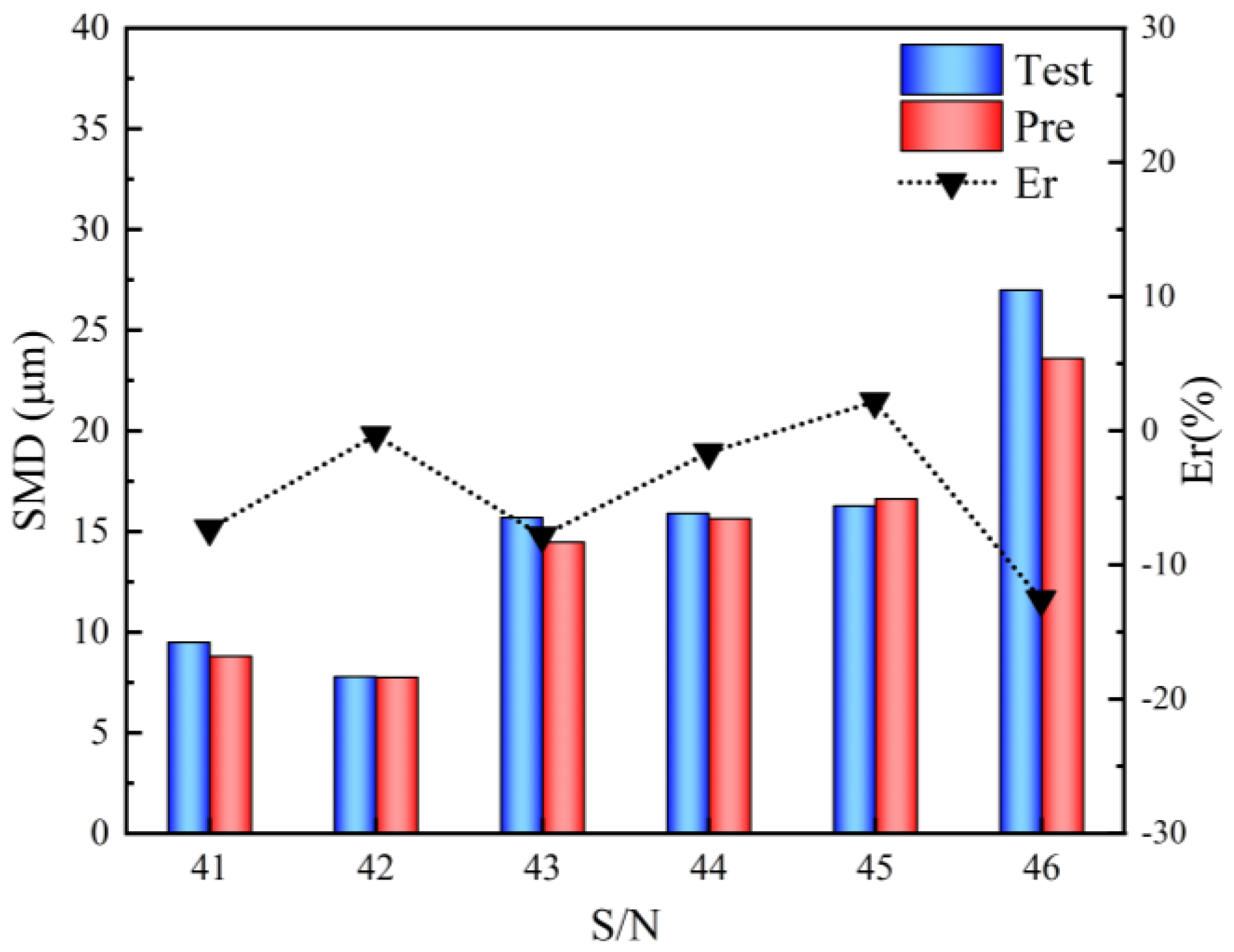
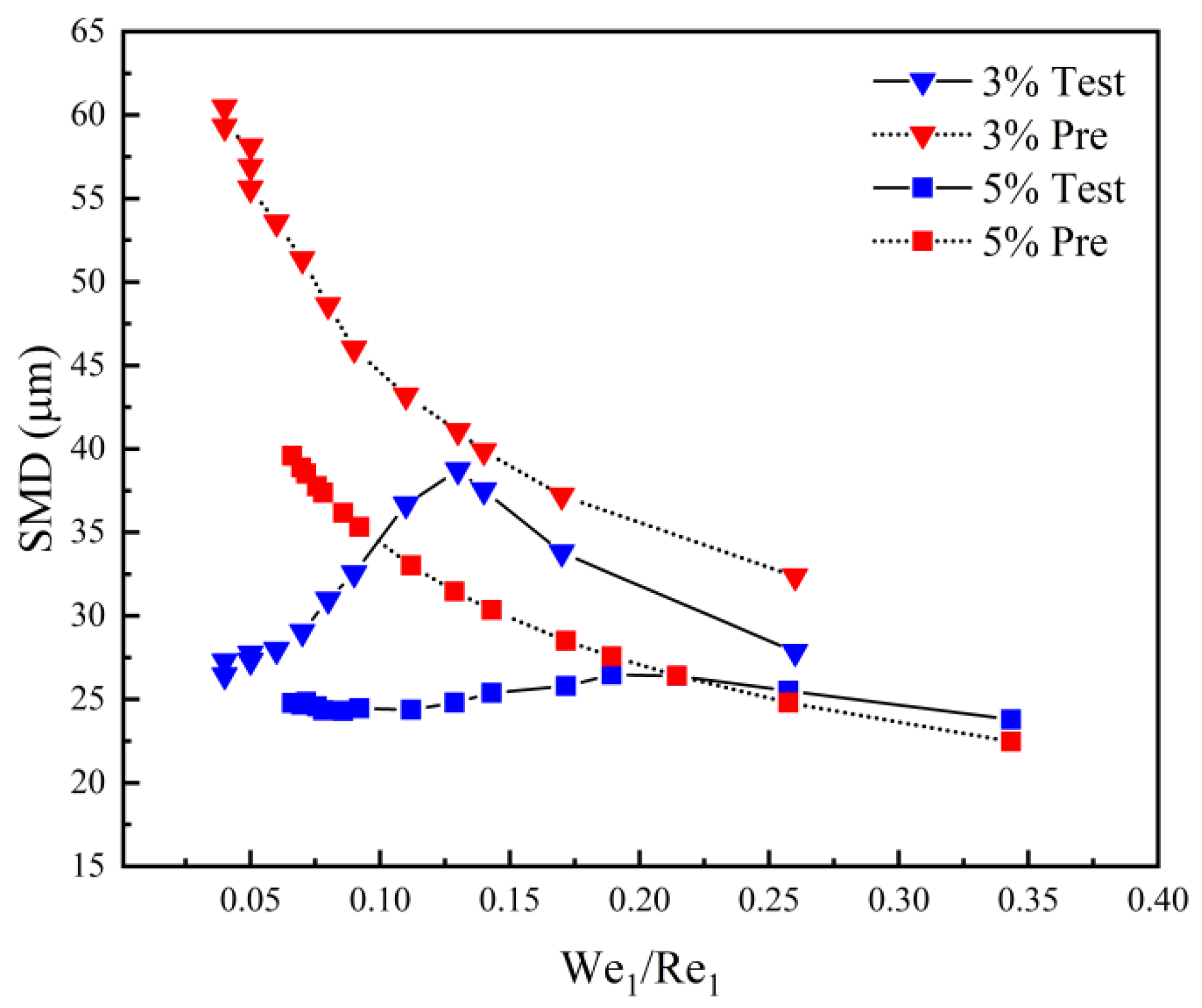
4.4. The Discussion at Ambient Temperature and Pressure Conditions

Figure 9 demonstrates that the predictive model “Pre” markedly overestimates the impact of the pressure drop ratio across the swirl injector. Figure 3 suggests a robust inverse relationship between the SMD and ${\mathit{We}}_1$ in the present predictive model. It is anticipated that these issues will significantly impair, or even render unsuitable, the performance of the model under standard ambient conditions (101 kPa, 295 K). It is thus necessary to provide an adequate explanation of the model’s scope and to offer a reasonable account of the phenomenon in question.

As previously discussed, the ratio $W{e}_1/R{e}_1$ is employed as a preliminary indicator of the relationship between aerodynamic effects and fuel flow rate. Figure 10 presents a comparison between experimental and model-predicted values under pressure drop ratio conditions of 3% and 5%. It is observed that when $W{e}_1/R{e}_1$ ≥ 0.13, the discrepancy between the model predictions and experimental values is within an acceptable range, thereby indicating the validity of the model. However, when $W{e}_1/R{e}_1$ < 0.13, the experimental values do not diverge with decreasing $W{e}_1/R{e}_1$ as the predictions suggest; instead, they exhibit a turning point and a converging trend. In the preceding analysis, the atomization model was simplified under pressurized conditions by neglecting the influence of the central pressure swirl nozzle. However, this simplification is not valid under atmospheric pressure conditions, where the impact of the pressure swirl nozzle becomes critical for maintaining effective atomization. Furthermore, elevated temperatures can facilitate the evaporation of droplet clusters, leading to a slight expansion in the applicability range of the predictive model with respect to $W{e}_1/R{e}_1$.

Lefebvre [7] demonstrated that increasing fuel pressure enhances atomization efficiency in pressure swirl nozzles by increasing the fuel flow rate and thus enhancing the inertial centrifugal forces. Accordingly, the inflection point observed in Figure 10 is attributed to the dominance of the pressure swirl nozzle in atomization. To ascertain the fuel flow rate at which the pressure swirl nozzle becomes the dominant factor in atomization under ambient temperature and pressure conditions, experiments were conducted varying the fuel flow rate under 1%, 3%, and 5% swirler pressure drop ratio conditions, as illustrated in Figure 11. A noteworthy inflection in the SMD was observed at a fuel flow rate of q = 1.25 kg/h. This suggests that, at ambient temperature and pressure, a fuel flow rate of q = 1.25 kg/h attains a critical fuel pressure, beyond which the rise in SMD due to aerodynamic decay is counterbalanced, and further increases the fuel flow rate result in enhanced atomization.

The twin swirl airblast nozzle, which incorporates both pressure swirl and aerodynamic impact atomization mechanisms, achieves a synergistic enhancement of the respective strengths and weaknesses of each atomization method. This results in superior atomization performance across a broad operational range. Consequently, this type of nozzle is extensively used in aerospace engine combustion chambers to accommodate complex and variable operational environments. Due to the potential issue of viewport contamination under ambient temperature and pressure conditions, this study has conducted only a limited set of experiments to illustrate this phenomenon. Further research is needed to refine predictive models for ambient conditions and to explore the competitive mechanisms between the two atomization modes.

5. Conclusions

This study presents a predictive model for atomization droplet size derived from data collected under conditions of elevated temperature and pressure using a twin swirl airblast nozzle, incorporating multi-parameter cross-influences. The model is founded upon the principles of flow instability theory and has been parameterized with the assistance of the PSO algorithm. The principal conclusions are as follows:

• The results of the ANOVA, etc., indicate that the model structure is both reliable and reasonable, demonstrating a high prediction accuracy and robust generalization capabilities. The maximum relative error in predictions is 19.3%, while the average relative error is 6.8%.
• In comparison to the classic atomization model proposed by Rizkalla and Lefebvre, the model presented here is founded upon theoretical analysis and incorporates the effects of various interacting variables that were considered during the experimental design. This results in superior applicability and precision.
• The results of the Spearman analysis indicate that the model accurately reflects the qualitative impacts and correlations of variables on atomization droplet size. Among the variables, the most significant negative impact on droplet size is observed for air pressure and the air pressure drop ratio, while the FAR shows a positive correlation with droplet size.
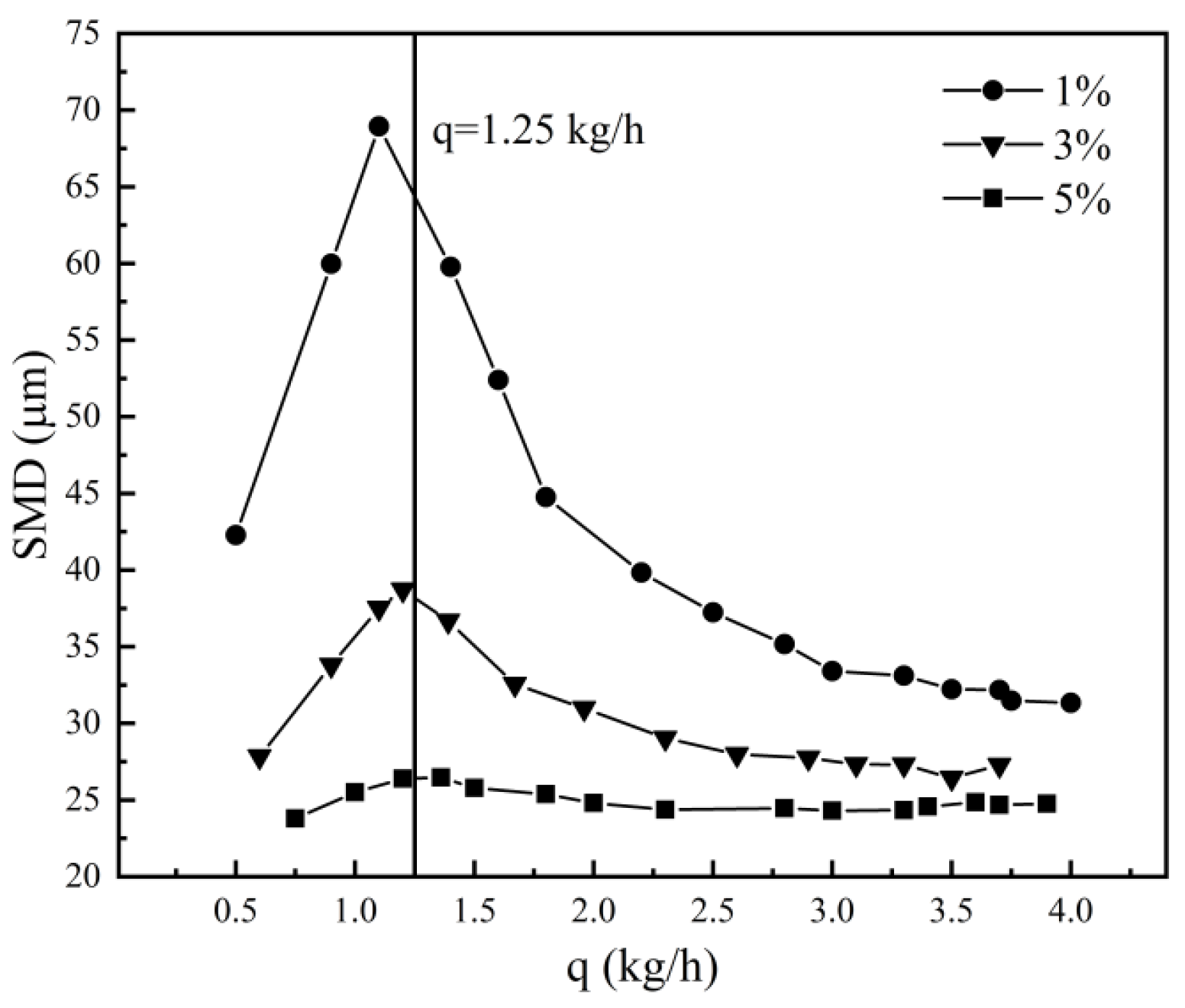
• Experiments conducted at ambient temperature and pressure indicate that the model’s applicability falls within the range defined by We₁/Re₁ ≥ 0.13. The twin swirl airblast nozzle exhibits competing mechanisms of aerodynamic and pressure swirl atomization. At ambient conditions and a fuel flow rate of q > 1.25 kg/h, the pressure swirl mechanism is observed to predominate over the aerodynamic mechanism.

This study integrates theoretical analysis with experimental data to develop a predictive model that accounts for real-world engineering conditions and the interaction of multiple variables. The findings offer significant insights that can inform the design of airblast nozzles.