Abstract
In the context of the green energy transition, the rapid expansion of flexible resources such as distributed renewable energy, electric vehicles (EVs), and energy storage has significantly impacted the operation of distribution networks. This paper proposes a multi-objective optimization approach for active distribution networks (ADNs) based on analytical target cascading (ATC). Firstly, a dynamic optimal power flow (DOPF) calculation method is developed using second-order conic relaxation (SOCR) to address power flow and voltage issues in the distribution network, incorporating active management (AM) elements. Secondly, this study focuses on aggregating the power of flexible resources within station areas connected to distribution network nodes and incorporating these resources into demand response (DR) programs. Finally, a two-layer model for collaborative multi-objective scheduling between station areas and the active distribution network is implemented using the ATC method. Case studies demonstrate the model’s effectiveness and validity, showing its potential for enhancing the operation of distribution networks amidst the increasing integration of flexible resources.
1. Introduction
Under the guidance of the “dual carbon” goal and driven by the construction of a new power system, the role of distribution networks as key energy infrastructure is becoming increasingly prominent. With the explosive growth and large-scale integration of distributed photovoltaics (DPV), electric vehicles (EVs), and new energy storage technologies, the distribution network is undergoing a profound transformation from passive to active and from one-way radiation to two-way interaction, facing unprecedented transformation pressure and innovation opportunities [1]. Against this backdrop, the active distribution network has emerged, tasked not only with ensuring the basic responsibility of power supply but also with enhancing carrying capacity, achieving intelligent operation and maintenance, promoting clean energy transition, and optimizing the efficient allocation of source-grid-load-storage resources.
The distributed nature, intermittency, and volatility of distributed photovoltaic power generation systems present challenges such as system peak regulation and may cause reverse power flow, leading to large fluctuations in grid voltage and power factors, thus reducing the stability of the power system [2,3,4,5,6]. Additionally, the high penetration of distributed photovoltaics can complicate the net load characteristics of the distribution network, affecting net load forecasting and source-load balance [7,8,9,10]. By effectively utilizing active management elements in the active distribution network, such as on-load tap changers (OLTCs), capacitor banks (CBs), static VAR compensators (SVCs), and energy storage systems (ESSs), reverse power flow and node voltage deviation can be reduced, optimizing power flow distribution. However, linear modeling of these elements poses a significant challenge.
Traditional distribution networks primarily rely on centralized control for power dispatch. However, with the large-scale integration of distributed resources, the number of points that need to be monitored and controlled has surged, making centralized control insufficient to handle the massive energy and information interactions at numerous nodes. Consequently, as distributed generation and diverse flexible loads grow explosively and are integrated on a large scale, directly controlling each distributed device is no longer feasible. Research has increasingly focused on analyzing the aggregation characteristics of various distributed resources and controlling them as a whole. The literature [11] analyzes the matching relationship between different types of power output and load based on the degree of inconsistency and complementarity between multiple power sources and load power changes, constructing an evaluation index for source-load cluster operation. The literature [12] analyzes the complementary characteristics of distributed power sources such as wind and solar, energy storage, and conventional loads, proposing a cluster partitioning method based on fuzzy clustering algorithms that consider the complementarity between nodes and electrical distance. Simulation results show that the integration of distributed resources helps reduce the reverse power flow problem. However, the study does not fully consider the intermittency and randomness of distributed power sources such as wind and solar, which present significant challenges to the security and stability of the grid. While the complementarity between power sources and loads is analyzed, the literature does not specify how to address these random and uncertain factors, especially under extreme weather conditions or significant load fluctuations, making the cluster partitioning and operational evaluation indicators potentially unable to accurately reflect the actual operating state.
At the regional power system level, particularly in the distribution network and feeder areas, managing the energy usage of controllable resources among different types of users in the feeder area is a key method to improve operational stability, economic efficiency, and the proportion of renewable energy integration. Many scholars, domestically and internationally, have studied the reasonable extraction and effective aggregation of controllable resources on the user side. The literature [13] aggregates air conditioner models, analyzing the relationship between aggregated air conditioning power and parameters such as indoor and outdoor environments. The literature [14,15,16] uses a 0–1 description of water heater operating modes to construct a water heater load aggregation model and analyze its aggregation effectiveness. The literature [17,18,19] establishes aggregated charging power models for electric vehicles based on the initial state of charge and initial charging time of different types of electric vehicles. However, these studies all focus on aggregating models for single, homogeneous loads, which are not suitable for the diverse load characteristics of feeder areas. For multiple types of controllable resources, the literature [20] introduces the concept of load aggregators to aggregate various user loads and optimize them based on economic cost. The literature [21] considers user energy satisfaction to establish physical dynamic models of controllable resources and develops multi-level aggregation algorithms. Currently, research on the aggregation and scheduling of diverse user-side resources in feeder areas is limited, and there is a lack of reasonable strategies for effective energy management in feeder areas.
To address this, this paper proposes a multi-objective optimization operation method for multi-agent active distribution networks based on the analytical target cascading (ATC) method. This method aggregates flexible resources such as distributed renewable energy, electric vehicles, and energy storage to participate in demand response, improving power flow and voltage in the distribution network. The paper first proposes a dynamic optimal power flow calculation method based on second-order cone relaxation, incorporating active management elements for control. Then, using the ATC method, a multi-objective collaborative optimization scheduling model for feeder areas and the distribution network is constructed, forming a two-level optimization model. Case studies validate the rationality and effectiveness of this model, demonstrating the advantages of the proposed method in improving photovoltaic absorption, reducing line losses, and optimizing the operation of the distribution network. This study establishes a demand response model for various flexible resources within the feeder area, achieving optimal economic efficiency and user comfort through coordinated scheduling.
This paper makes three main contributions:
- (1)
- For the impact of distributed photovoltaic integration on distribution network operation, considering the operational constraints of various active management elements, a multi-objective optimization model for dynamic optimal power flow based on mixed-integer second-order cone programming (MISOCP) is established with the goal of minimizing reverse power flow, node voltage deviation, line active power loss, and photovoltaic curtailment penalties, achieving optimized scheduling for the distribution network.
- (2)
- For various flexible resources within the feeder area, a power aggregation and demand response model is established, constructing a mixed-integer linear programming (MILP) model with the objective of optimizing the economic efficiency and energy comfort of load aggregators, achieving optimal scheduling for the feeder area.
- (3)
- A two-level hierarchical optimization scheduling model is established, with the MISOCP-DOPF model for the distribution network as the upper layer and the MILP model for the feeder area as the lower layer. The ATC method is used for model decoupling, achieving coordinated optimization of the distribution network and feeder area operations.
2. Active Distribution Network Modeling
In the distribution network, AM elements include on-load tap changers (OLTCs) for voltage regulation, discrete reactive power compensation with capacitor banks (CBs), continuous reactive power adjustment with static VAR compensators (SVCs), active power regulation with energy storage systems (ESSs), and both active and reactive power regulation with photovoltaic inverters (PVIs).
2.1. Objective Function
To minimize reverse power flow and node voltage deviations while also considering operational efficiency, the objective is to minimize the sum of reverse power flow, node voltage deviations, active power losses in lines, and penalties for reducing photovoltaic active power. Normalization is performed using the ideal point method, resulting in a multi-objective optimization model aimed at the safe and economical operation of the distribution network. The model can be expressed as follows:
where is the reverse power flow; is the node voltage deviations; is the active power losses in lines; is the penalties for reducing photovoltaic active power; , , , and are the objective values before optimization; , , , and are the ideal points for each objective after optimization; , , , and are the weights of each objective, satisfying ; and are the active and reactive power injections at nodes, respectively; and are node identifiers; is the set of nodes with reverse power flow; t is the time period; is the set of periods with reverse power flow; is the time interval; is the node voltage; is the reference voltage for the OLTC primary side, set to 1 p. u.; is the set of all nodes; is the total number of periods; is the set of all branches; ij identifies the branch; is the branch current; is the branch resistance; is the set of nodes containing distributed generators (DGs); is the active power output of DGs; and is the forecasted DG output.
2.2. Constraints
2.2.1. System Flow Constraints
The optimal power flow (OPF) model for the distribution network, based on the branch flow model (BFM), is a nonlinear model (see Appendix B for details). To facilitate computation, capacity constraints in the quadratic terms need to be linearized. Therefore, angle relaxation (AR) and second-order cone relaxation (SOCR) are used for convexification. By applying , and extending single-period flow calculations to multiple periods, the basic dynamic optimal power flow (DOPF) model is constructed. The SOCR-DOPF model is as follows:
where is the objective function; P and Q are the active and reactive power of the branches, respectively; x is the branch reactance; and are the constraints related to the active and reactive power injections at nodes, respectively; k is the node identifier; is the set of end nodes for branches starting at node j; is the set of starting nodes for branches ending at node j; and are the upper and lower limits of branch currents, respectively; and are the upper and lower limits of node voltages, respectively; is the branch capacity; is the capacity of the node (or substation); and is the 2-norm.
2.2.2. OLTC Operating Constraints
2.2.3. CB and SVC Operating Constraints
The constraints for CBs are established as follows:
where is the set of nodes containing CBs; is the reactive power compensation provided by the CBs; is the reactive power compensation of a single CB unit; is the number of CB units in operation; is the maximum allowable number of CB units in operation; is a binary variable indicating whether a CB unit is in operation; and are binary variables for adjacent time periods, respectively, where is a decrease in the number of CB units in operation from period t − 1 to period t; and is the maximum allowable number of CBs switching operations within period T.
The model for SVCs is established as follows:
where is the set of nodes containing SVCs; is the reactive power compensation provided by the SVCs; and and are the lower and upper limits of the SVC’s reactive power compensation, respectively.
2.2.4. Constraints for DG Operation
The model for DG is established as follows:
where is the real power output of the DG; is the predicted power output; is the ratio of the DG’s power output to its maximum capacity; stands for the reactive power output; and corresponds to the impedance angle associated with the DG’s minimum power factor.
3. Modeling of Distribution Feeder Areas
3.1. System Architecture
Figure 1 illustrates the control structure of flexibility resources in the distribution network’s substation areas. In certain substations, there are significant flexibility resources, such as electric vehicles, temperature-controlled loads, energy storage, and distributed photovoltaics. Due to the high willingness of users to participate in demand response, these flexibility resources are aggregated through a substation aggregation center. Building on this, the substation management center interacts with the distribution network via tie-line power and adjusts user electricity consumption habits through demand response. This approach balances economic efficiency and user comfort within the substation area, achieving power balance and increasing the photovoltaic absorption rate. In the distribution network, nodes have decentralized photovoltaic integration. Given the impact of renewable energy integration on the distribution network, AM elements are additionally integrated at the nodes to actively adjust voltage and power flow. The distribution network control center can adjust these AM elements to optimize the technical parameters of the network.
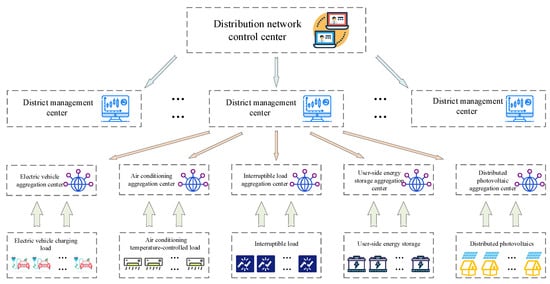
Figure 1.
Schematic diagram of hierarchical regulation and control of “distribution network-station area-flexible resources”.
3.2. Objective Function
To effectively encourage user participation in demand response and support photovoltaic integration while considering user comfort, this section develops an objective function based on both economic efficiency and user temperature satisfaction. This forms a multi-objective optimization scheduling model for the distribution feeder area. Because the objective functions have different units, normalization is required. The process is as follows:
where is the normalized value of the economic indicator; is the actual cost value before normalization; is the maximum possible value of the economic indicator before normalization; and is the minimum possible value before normalization. The user temperature satisfaction indicator is expressed as a percentage, so it does not require additional normalization. Therefore, the overall objective function can be expressed as follows:
where and are the weight coefficients for the two objective functions, respectively (); and is the user satisfaction indicator.
3.2.1. Economic Indicators
The economic indicator is viewed from the perspective of the district management center and considers the control costs of various flexible resources over period T. Its expression is as follows:
where is the fee paid by the district management center to the distribution network at time t; is the demand response cost at time t; refers to the penalty for curtailed solar power at time t; and is the operation and maintenance cost of energy storage within the district at time t.
where and are the power purchased and sold by the district to the distribution network at time t, respectively; and and are the unit prices for purchasing and selling electricity from the district management center to the distribution network, respectively.
where is the total number of interruption levels; is the compensation price for interruptible load at level m; is the amount of interruptible load at level m at time t; is the compensation price for air conditioning load; is the compensation price for EV charging load; is the air conditioning load before response at time t; is the air conditioning load after response at time t; is the electric vehicle charging load after response at time t; and is the electric vehicle charging load before response at time t.
where is the penalty cost per unit of curtailed solar power, and is the amount of curtailed solar power in the area at time t.
where and are the discharge and charge power of the energy storage system at time t, respectively; and is the maintenance cost per unit of discharge and charge power for the energy storage system.
3.2.2. User Temperature Satisfaction Indicator
During demand response, air conditioners in the distribution area adjust the temperature set by users, leading to a difference between the actual indoor temperature and the users’ expectations. This discrepancy can impact users’ daily lives and may lead to dissatisfaction. Therefore, it is important to model user temperature satisfaction. First, calculate the percentage deviation between the indoor temperature after response and the ideal temperature:
where is the indoor temperature at time t; and and are the maximum and minimum indoor temperatures, respectively.
User temperature satisfaction can then be expressed as follows:
where is the state of the air conditioning cluster at time t, which is a binary variable where a value of 0 indicates that the air conditioning cluster is in a standby state, and a value of 1 signifies that the cluster is operating at its rated capacity.
3.3. Constraints
3.3.1. EV Constraints
Unlike traditional loads, EV charging loads exhibit significant uncertainty. To accurately predict changes in EV load, it is necessary to model its key characteristics and describe its dynamic behavior. Based on traditional vehicle travel patterns, the following describes the charging and behavior characteristics of EVs.
Research typically assumes that the daily driving distance of an EV follows a log-normal distribution, with its probability density function expressed as follows:
where and are the mean and standard deviation of the , respectively.
For a one-day period, the initial state of charge of an EV before travel follows a uniform distribution, with its probability density function expressed as follows:
where a and b are the lower and upper limits of , respectively.
Based on Equations (16) and (17), the state of charge of the EV from the end of the trip to the charging station can be determined as follows:
where is the battery capacity of the EV; and is the energy consumption per 100 km.
The initial charging time of the EV when it connects to the grid follows a normal distribution, with the probability density function expressed as follows:
where and are the mean and standard deviation of , respectively.
Based on Equations (18) and (19), the time required for the EV to complete charging can be calculated as follows:
where is the EV charging efficiency; and is the EV’s rated changing power.
Therefore, the end time of EV charging is given by the following:
The end time of EV charging is processed, and the charging load power for a single EV is represented by time intervals as follows:
After conducting number of simulations, the average is computed to determine the original charging load power for the EVs:
where is the charging load power of the j EV at time t during the i simulation. This describes how the EV’s charging load varies over time.
According to psychology and economics theories, adjusting electricity prices can influence user consumption behavior. By implementing a time-of-use pricing strategy, the scheduling department can maximize the potential of flexible resources and guide the basic flexible resource loads to align with system scheduling requirements.
The time-of-use pricing periods for a typical day are determined using K-means clustering on the net load within the distribution area. Peak, shoulder, and off-peak periods are then matched with their respective electricity prices. The net load model for the distribution area is as follows:
where is the net load of the distribution area at time t; and is the forecasted load at time t.
The impact of electricity prices on user consumption behavior is quantified using the price elasticity of demand. The expression is as follows:
where and are the changes in EV charging load and electricity price, respectively; and is the original EV charging load and original price, respectively. The equation, thus, is the ratio of load transfer rate to price transfer rate at time t.
The demand elasticity matrix is composed of demand elasticity coefficients and is expressed as follows:
By guiding changes in user electricity consumption through adjustments in electricity prices, the goal of “peak shaving and valley filling” can be achieved. The expression for this time-of-use pricing response model in the context of EV applications is as follows:
where , , and are the user electricity loads for the peak, flat, and off-peak periods after the response, respectively; , , and is the original user electricity loads for the peak, flat, and off-peak periods before the response, respectively; and , , and and , , and are the original electricity prices and their changes for the peak, flat, and off-peak periods.
where is the proportion of EV charging load participating in the demand response. This describes the model for price-based demand response participation by EVs.
3.3.2. Air Conditioning Constraints
With the ongoing development of smart appliances, temperature-controlled loads are becoming increasingly prevalent within distribution networks. The scheduling department can manage these temperature-controlled loads as a collective group. Given that most of these loads are air conditioners, they are used as a representative example. Building thermal resistance and air thermal capacity are modeled as electrical resistance and capacitance, respectively. Light and ambient temperature are represented as electrical sources. An equivalent thermal parameter model is used to simulate the heat exchange process of air conditioners, thereby establishing a power aggregation model.
Air conditioners are electrical devices that depend on ambient temperature. To describe the indoor temperature controlled by air conditioners, an equivalent thermal parameter model (ETP) is often used. The expression for this model is as follows:
where is the outdoor temperature at time t; is the actual operating power of the air conditioner at time t; R is the thermal resistance of the air conditioner; and C is the thermal capacitance of the air conditioner.
The energy consumption of an air conditioner is closely related to its operating mode. The logic for determining the operating state of the air conditioner is expressed as follows:
where is the temperature hysteresis range for air conditioner state transitions; and is the simulation period. When the actual indoor temperature exceeds the sum of the air conditioner’s set temperature and the hysteresis temperature, the air conditioner must operate at its rated capacity. Conversely, when the actual indoor temperature falls below the difference between the set temperature and the hysteresis temperature, the air conditioner stops operating. In all other scenarios, the air conditioner maintains the same operational state as in the previous time step. Consequently, the actual operating power of the air conditioner can be expressed as follows:
where is the operating power of the i air conditioner within the area; is the rated operating power of the air conditioner; and is the total number of air conditioners in the area.
Although different air conditioning units share the same operating mechanism for temperature control, their equivalent thermal resistance, thermal capacity, and energy efficiency ratios vary. Under a common temperature control target, all air conditioning units in the area can be connected in parallel to create an aggregated equivalent thermal parameter model. By increasing the average set temperature of the air conditioners, the total power of the temperature control load cluster can be reduced, enabling incentive-based demand response. The model is expressed as follows:
where is the equivalent thermal resistance after aggregating the air conditioners; is the thermal resistance of the i air conditioner; signifies the equivalent thermal capacity after aggregation; is the thermal capacity of the i air conditioner; is the equivalent energy efficiency ratio after aggregation; and is the energy efficiency ratio of the i air conditioner.
where and are the equivalent indoor and outdoor temperatures at time t, respectively; and is the equivalent cooling power of the aggregated air conditioners at time t.
where is the equivalent rated cooling power of the aggregated air conditioners; is the equivalent original set temperature after aggregation; is the original set temperature of the i air conditioner; G is the air conditioner’s temperature adjustment level; is the maximum adjustment level; and and are the maximum and minimum indoor temperatures, respectively. The following is an improved version of Equation (30):
where is the set temperature of the air conditioners after participating in demand response; and is the real-time operating status of the air conditioners in the aggregated model at time t.
3.3.3. Constraints on Interruptible Loads
Based on the impact of load interruptions on users’ daily lives and production activities, interruptible loads are typically categorized into three types.
where is the total amount of interruptible load for the entire area at time t.
Different interruption ratios and compensation prices are set according to the interruptible load level. The higher the interruption level, the lower the ratio coefficient and the higher the compensation price. The interruptible load demand response model is established as follows:
where is the maximum amount of level m interruptible load over two consecutive periods; is the upper limit of the interruptible load ratio for level within a continuous period; and is the upper limit of the interruptible load ratio for level at time t.
3.3.4. Constraints for Energy Storage and Distributed Photovoltaics
For user-side energy storage and distributed photovoltaics, we assume that the parameters of each device follow a uniform distribution within a certain range. We use the Monte Carlo method to approximate and generate data by analyzing the power characteristics of individual devices and then aggregating the power of all devices to develop a model for the power aggregation of the cluster. The energy storage system model is described as follows:
where and are the maximum and minimum storage capacities of the energy storage system, respectively; and are the maximum and minimum storage capacities of the d storage unit within the distribution area, respectively; and are the discharge and charge powers of the energy storage system at time t, respectively; and refer to the discharge and charge powers of the d storage unit at time t, respectively; and are the discharge and charge efficiencies of the energy storage system at time t, respectively; is the storage amount of the energy storage system at time t; and are the maximum discharge and charge powers of the energy storage system, respectively; and are the discharge and charge states of the energy storage system, respectively; and is the time step.
To ensure that the actual consumption of PV energy does not exceed the generated PV energy, the following constraint applies to the consumption of rooftop PV within the distribution area:
where is the actual PV output power at time t; is the total PV generation within the distribution area at time t; is the total generation of the d distributed PV unit within the distribution area at time t; and is the total number of distributed PV units in the distribution area.
3.3.5. Overall Constraints of the Distribution Area
In addition to the flexible resources within the distribution area, the primary power supply for the area is also sourced from power purchased by load aggregators from the distribution network. The internal power balance model for the distribution area is described as follows:
where and are the original fixed load power and interruptible load power at time t, respectively; and and are the power purchased from and sold to the distribution network at time t.
The constraints on power purchases and sales within the distribution area are as follows:
where and are binary variables (0–1) indicating the status of power purchase and sale to the distribution network at time t, respectively; and and are the maximum power that can be purchased from or sold to the distribution network at time t, respectively, as determined by the capacity of the interconnection line between the distribution area and the grid.
4. Solution Methodology for the Bi-Level Model
4.1. Model Preprocessing
As described earlier, the bi-level model for the coordinated scheduling of the distribution network and the distribution area consists of two layers. The upper layer focuses on the active distribution network, which includes AM (active management) elements. This layer establishes constraints related to power flow and the operation of AM elements, evaluating aspects such as reverse power flow, node voltage, line active power loss, and curtailed solar energy. The lower layer focuses on the distribution area, which includes various flexible resources. It sets operational constraints for these resources and overall constraints for the area, assessing the economic performance of the distribution area’s management center and the temperature satisfaction of its users. The bi-level model for coordinated scheduling between the distribution network and the distribution area is illustrated in Figure 2.
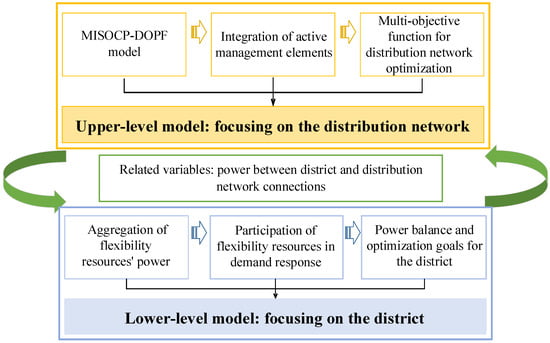
Figure 2.
Two-layer model of distribution network-station area cooperative dispatching.
4.2. Solving the Bi-Level Model Using ATC
Based on the established objective functions and constraints for both the upper and lower layers, the global optimization model is formulated as follows:
where and are the weighting coefficients for the optimization objectives of the lower-level distribution area and the upper-level distribution network, respectively; and and are the normalization factors corresponding to these objectives.
To simplify the resolution of the complex coupled model involving multiple stakeholders, the ATC algorithm is used to decouple the aforementioned global optimization model. The power transactions between the distribution area and the distribution network are treated as linkage power, and the augmented Lagrangian function is employed as the penalty function. This transforms the global optimization model in Equation (42) into the following bi-level optimization model.
Upper-level:
Lower-level:
where and are the first- and second-order Lagrange multipliers corresponding to the linkage power of the i transmission line at time t, respectively; is the difference between the upper-level linkage power and the lower-level optimized linkage power at time t on the i transmission line; is the value that needs to be optimized at the lower level and is communicated to the upper level; is the difference between the upper-level optimized linkage power and the lower-level linkage power; is the value that needs to be optimized at the upper level, and this value is passed from the upper to the lower level.
The convergence criteria for the iterative solution of the bi-level optimization model are as follows:
where and are the linkage power on the i transmission line at time t for the upper and lower levels during the k iteration, respectively; and are the objective function values for the distribution network and the i district in the k iteration, respectively; and and are the convergence tolerances, respectively.
The Lagrange multiplier update criterion is as follows:
The relevant solving process is shown in Algorithm 1.
| Algorithm 1: Analysis target cascading. |
| Step 1: Initialize parameters, . |
| Step 2: Given the expected values of tie-line power from the lower-level model, solve the upper-level model and record the resulting values of tie-line power , denoted as , respectively. |
| Step 3: Given the expected values of tie-line power from the upper-level model, solve the lower-level model and record the resulting values of tie-line power , denoted as , respectively. |
| Step 4: Determine convergence based on the convergence criterion given in Equation (45). If convergence is achieved, terminate the iteration. |
| Step 5: , update the Lagrange multipliers according to the update rule in Equation (46). Return to Step 2. |
5. Case Studies
This study uses the IEEE 33-node model as the research subject to validate the model’s effectiveness. Some nodes in the distribution network are integrated with AM elements, with specific parameters detailed in Appendix A, Table A1 [22]. The power generation and load power of photovoltaic systems are predicted using the K-means++ algorithm, as shown in Appendix B, Figure A1. The topology connecting the substation area, AM elements, and the active distribution network is illustrated in Figure 3. The model is coded with the YALMIP toolbox 20230622 in MATLAB R2024a for Windows environment and solved by commercial optimization software GUROBI 11.0.
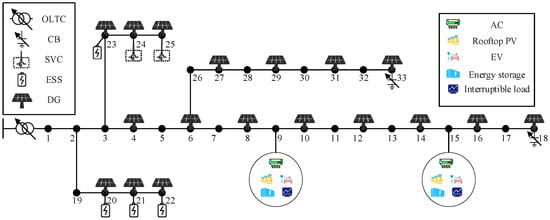
Figure 3.
Topology diagram of station area, AM element, and distribution network connection.
5.1. Analysis of Active Distribution Network Optimization Dispatch Results
According to relevant industry standards, a reverse power flow exceeding 80% of the transformer capacity is considered a reverse heavy overload, and a node voltage exceeding 107% of the reference voltage is classified as node overvoltage. The dispatch results of various AM elements within the active distribution network are shown in Figure 4, Figure 5, Figure 6 and Figure 7. During midday, when photovoltaic generation is high and the load is low, power back feed and node overvoltage frequently occur in the distribution network. Around 12:00 to 13:00, both the SVC and ESS absorb a significant amount of active power, and the OLTC tap ratio decreases, which helps reduce the “source” power in the network and effectively increases the “load” power.
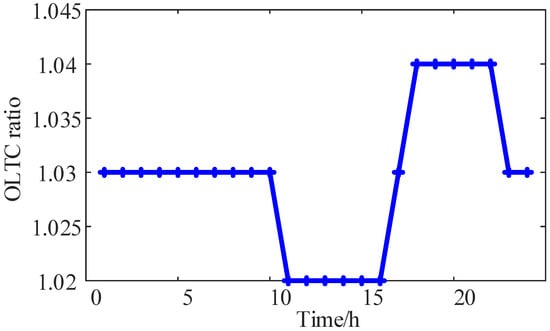
Figure 4.
OLTC scheduling results.
Figure 5.
CB scheduling results.
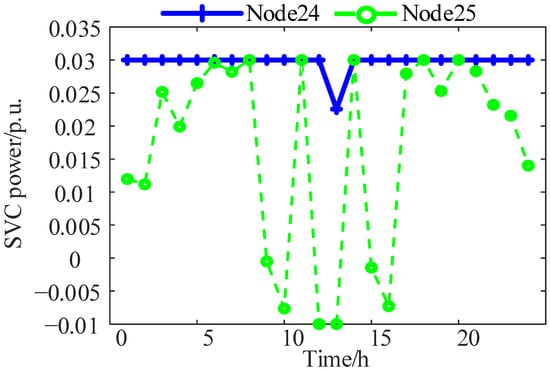
Figure 6.
SVC scheduling results.
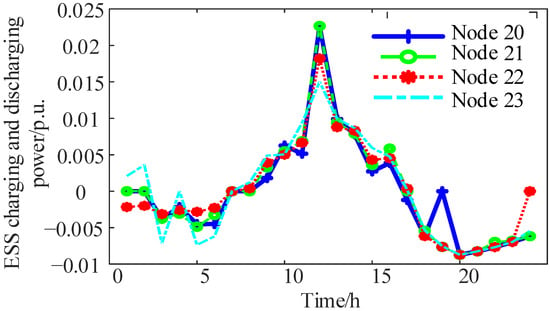
Figure 7.
ESS scheduling results.
Table 1 presents a comparison of the simulation results for various scenarios in the active distribution network. The comparison confirms that large-scale photovoltaic (PV) integration causes reverse power flow and increases node voltage deviation but reduces active power losses in the lines. However, the integration of AM elements can effectively mitigate the reverse power flow and the increased node voltage deviation caused by PV integration while further reducing active power losses in the lines. Figure 8 illustrates the voltage levels at various nodes in the distribution network: (a) without PV integration, (b) after the integration of high-percentage PV, and (c) after the integration of AM elements into a network with high penetration of distributed PV. A comparison between Figure 8a and Figure 8b clearly shows that significant distributed PV generation can lead to overvoltage for distribution network users. A comparison with Figure 8c demonstrates that the integration of AM elements results in a flatter voltage distribution, significantly improving system voltage quality and effectively mitigating overvoltage at distribution network nodes. Analysis of Figure 9 reveals that some nodes still have an abandoned light at certain times, and the photovoltaic consumption rate is still not 100%, indicating that the photovoltaic carrying capacity of these nodes with an abandoned light has reached its limit. This observation can be used to evaluate the large-scale distributed photovoltaic consumption capacity of different nodes.

Table 1.
Comparison of simulation results.
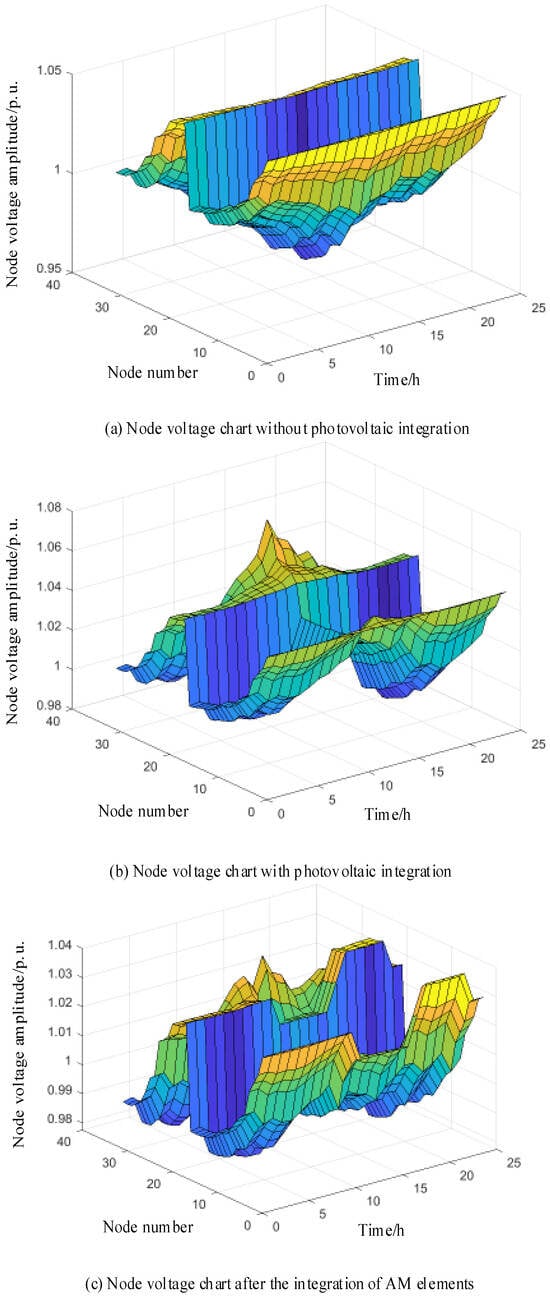
Figure 8.
Node voltage in the distribution network.
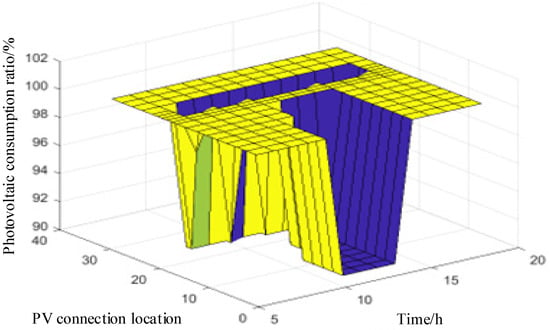
Figure 9.
Proportion of distributed PV consumption in the distribution network.
5.2. Analysis of Distribution Substation Optimization Dispatch Results
The parameters of various flexible resources integrated into the substation area are listed in Appendix A, Table A2, Table A3, Table A4, Table A5 and Table A6 [23]. Before dispatch, the peak, flat, and valley periods are determined based on netload, and the corresponding electricity prices are matched, as shown in Appendix B, Figure A3. The overall dispatch results for the substation area are presented in Figure 10, and the dispatch results for each flexible resource are shown in Figure 11, Figure 12, Figure 13 and Figure 14. Analysis of Figure 10 indicates that the substation area primarily relies on flexible resources for dispatch without selling electricity back to the distribution network. The energy storage dispatch results are shown in Figure 11. During valley price periods, energy storage charges as much as possible to build reserves, and during flat and peak price periods, it discharges to meet the substation area’s load demand, thereby reducing electricity costs. The stored energy increases during charging and decreases during discharging, which aligns with its operational requirements.
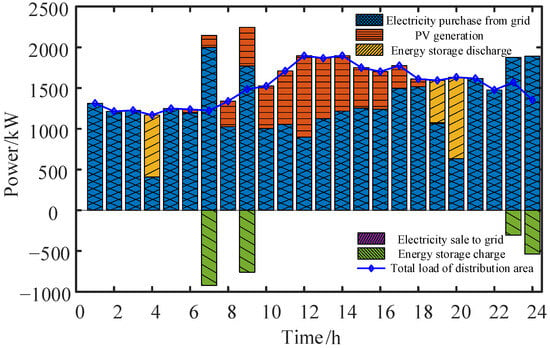
Figure 10.
Station scheduling results.
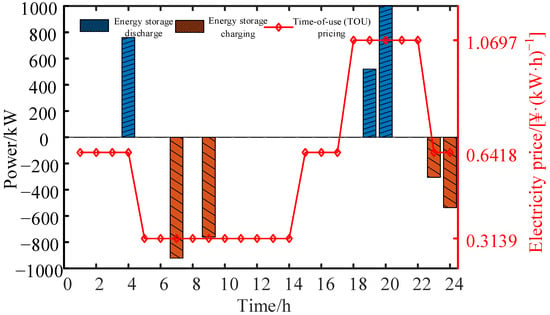
Figure 11.
Station ESS scheduling results.
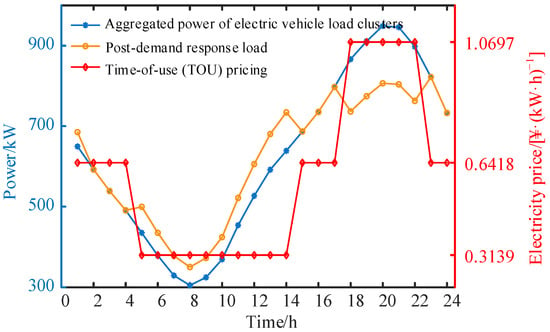
Figure 12.
Station EV scheduling results.
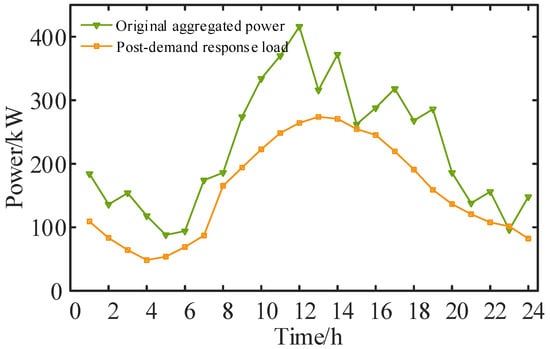
Figure 13.
Station air conditioning scheduling results.
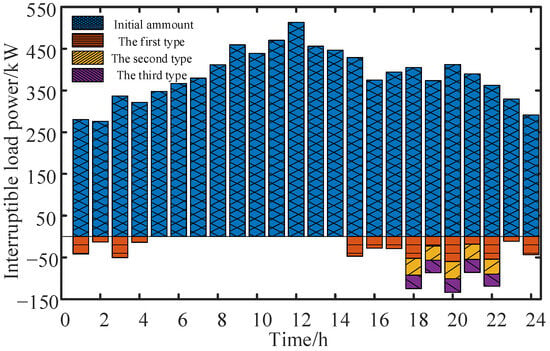
Figure 14.
Station interruptible load scheduling results.
The EV dispatch results for the substation area are shown in Figure 12. During peak price periods, the EV charging load decreases and shifts to valley price periods, while it remains unchanged during flat price periods, meeting the requirements of price-based demand response. The air conditioning dispatch results for the substation area are shown in Figure 13. It is evident that the air conditioning load decreases throughout the 24 h period. The control center increases the air conditioning set temperature to reduce the electric load while ensuring that the maximum indoor temperature requirement is not exceeded, thus minimizing electricity costs. The dispatch results for interruptible loads are shown in Figure 14. During peak price periods, the control center first interrupts the first category of interruptible loads to minimize user impact. However, to ensure that the interruption time for the same category of loads does not exceed constraints within continuous periods, the center does not continuously interrupt the first category. Instead, it switches to interrupting the second and third categories of loads. No loads are interrupted during flat and valley price periods. The results of the objective functions after dispatch are shown in Table 2. The total electricity cost for the substation area is 19,817 RMB, with 18,330 RMB spent on purchasing electricity from the distribution network, representing the primary expense. The curtailment penalty is 0 RMB, indicating that all the PV energy is fully utilized. The energy comfort index is 0, meaning that after dispatch, the indoor temperature in the substation area is as close as possible to the most comfortable level, which is the average of the maximum and minimum indoor temperature standards.

Table 2.
Objective function results.
5.3. Analysis of Algorithm Solving Performance
Figure 15 shows the convergence error values corresponding to the two convergence conditions of Equation (45).
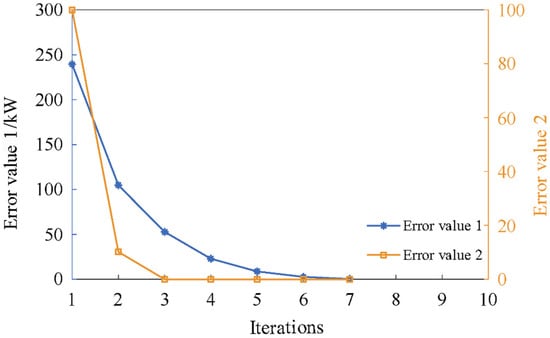
Figure 15.
Convergence error values.
As can be seen from Figure 15, the error value 2 satisfies the convergence accuracy after three iterations, and the error value 1 satisfies the convergence accuracy after 7 iterations. The algorithm exhibits fast convergence speed and high computational accuracy. The calculation time for the collaborative optimization scheduling of the distribution transformer area is around 40 s, indicating high computational efficiency that can meet the operational requirements of the system.
6. Conclusions
This paper presents a multi-objective dispatch optimization model for an active distribution network involving multiple entities. The upper layer focuses on the active distribution network, while the lower layer targets the distribution substation area. The power exchanged between these two layers serves as the linking power for iterative, coordinated optimization, ultimately leading to convergence. This study aggregates the power of various flexible resources within the substation area, enabling unified control of each type of load and collective participation in demand response. This approach ensures efficient and unified multi-objective dispatch, balancing the interests of both the substation management center and the users while maintaining operational flexibility. Simulation results demonstrate that the two-layer optimization model effectively addresses the coordinated optimization of the active distribution network and the substation area, improving PV utilization and enhancing user-side dispatch flexibility. The limitation of this paper lies in the fact that the proposed method is only applicable to a certain scale of distribution systems. For future research, we plan to extend this method to larger-scale distribution systems to further validate its engineering application value.
Author Contributions
Y.Z.: conceptualization, methodology, formal analysis, writing—original draft, writing—review and editing, visualization, and project administration. Y.X.: software, validation, investigation, resources, data curation, and writing—review and editing. R.Z.: conceptualization, methodology, formal analysis, investigation, and funding acquisition. J.Y.: investigation and methodology. Y.Y.: validation and data curation. Y.C.: resources and supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the “Science and Technology Service Project of State Grid Henan Electric Power Company Xixia County Power Supply Company ‘High-Quality Power Supply and Consumption Technology and Application in Distribution Area under the Background of Distributed Photovoltaic Large-Scale Development’”, grant No. SGHANYXXYWJS2310144.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The authors gratefully acknowledge the support of the Science and Technology Service Project of State Grid Henan Electric Power Company Xixia County Power Supply Company and thank the anonymous reviewers and editors for their valuable review comments on this manuscript.
Conflicts of Interest
Author Yiran Zhao and Yong Xue were employed by the company State Grid Henan Electric Power Company Xixia County Power Supply Company, The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A

Table A1.
Parameters of AM elements.
Table A1.
Parameters of AM elements.
| Name | Parameter Values | Name | Parameter Values |
|---|---|---|---|
| OLTC tap ratio range | 1 ± 6% | ESS charge and discharge power range/MW | 0~0.3 |
| Reactive power compensation capacity per single CB Bank/Mvar | 0.1 | ESS state of charge (SOC) range/MW h | 0.15~0.8 0.3 (initial) |
| SVC reactive power compensation range/Mvar | −0.1~0.3 | ESS charge and discharge efficiency | 0.9 (charge) 0.85 (discharge) |
| DG power limit ratio | 0.9 | DG power factor range | 0.95 (lead)~0.95 (lag) |

Table A2.
Parameters of EV and DR.
Table A2.
Parameters of EV and DR.
| Name | Parameter Values | Name | Parameter Values |
|---|---|---|---|
| 3.2 | 0.88 | ||
| 0 | 1 | ||
| /kW·h | 80 | /kW·h | 18.89 |
| 10.50, 19.00 | 2.14, 3.14 | ||
| /kW | 7 | 0.90 | |
| 30 | 1000 | ||
| [−0.040, 0.032, 0.024; 0.032, −0.032, 0.004; 0.024, 0.004, −0.024] | |||
| /% | 15 | /[¥·(kW·h)−1] | 0.3 |

Table A3.
Parameters of AC and DR.
Table A3.
Parameters of AC and DR.
| Name | Parameter Values | Name | Parameter Values |
|---|---|---|---|
| /[°C·(kW)−1] | [6, 16] | /[kW·h·(°C)−1] | [0.525, 0.57] |
| [2.6, 3.6] | /kW | 2 | |
| /°C | [21, 28] | /°C | 3 |
| /°C | 27.68 | /°C | 24.77 |
| /°C | 3 | 1000 | |
| /[¥·(kW·h)−1] | 0.3 |

Table A4.
Parameters of interruptible load and DR elements.
Table A4.
Parameters of interruptible load and DR elements.
| Name | Parameter Values | Name | Parameter Values |
|---|---|---|---|
| 3 | /% | 15, 10, 8 | |
| /% | 20, 20, 20 | /[¥·(kW·h)−1] | 0.5, 0.7, 0.8 |

Table A5.
Parameters of ESS elements.
Table A5.
Parameters of ESS elements.
| Name | Parameter Values | Name | Parameter Values |
|---|---|---|---|
| /kW | 1000 | /kW | 1000 |
| 0.95 | 0.95 | ||
| /kW·h | 1900 | /kW·h | 300 |
| 1000 | /[¥·(kW·h)−1] | 0.02 |

Table A6.
Parameters of DG elements.
Table A6.
Parameters of DG elements.
| Name | Parameter Values | Name | Parameter Values |
|---|---|---|---|
| 1000 | /[¥·(kW·h)−1] | 1.2 |
Appendix B
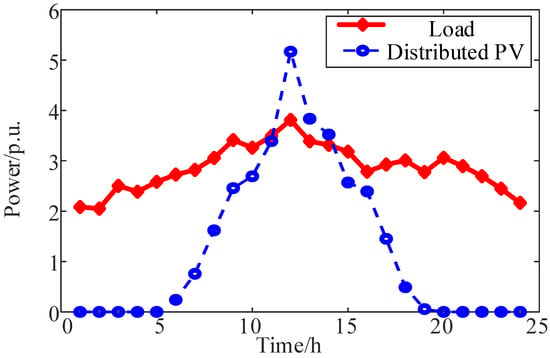
Figure A1.
PV and load power prediction curves.
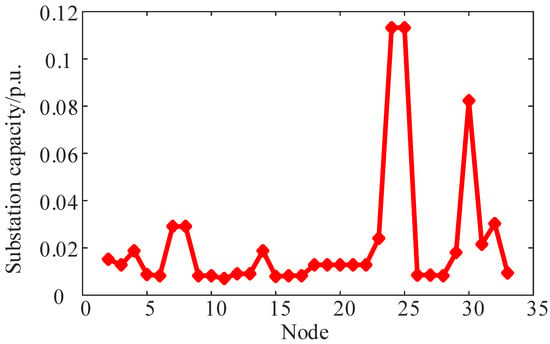
Figure A2.
Capacity of the substation.
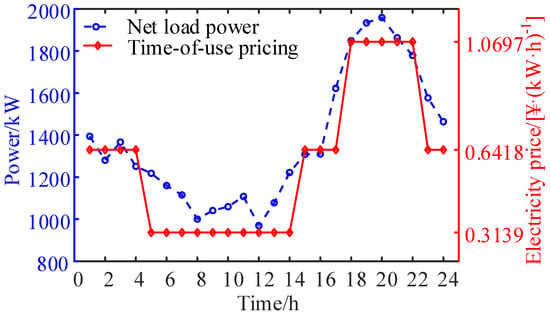
Figure A3.
Netoad power and time-of-use electricity price in the station area.
References
- National Development and Reform Commission; National Energy Administration. Guidance on High-Quality Development of Distribution Networks under New Circumstances. Available online: https://www.gov.cn/zhengce/zhengceku/202403/content_6935790.htm (accessed on 6 February 2024).
- Zhang, C.; Zhao, S.; Yang, H. Research on withstand performance test of internal short circuit fault of photovoltaic grid-connected inverter. High Volt. Appar. 2022, 58, 28–33. [Google Scholar]
- Huang, X.; Wu, H.; Li, M. Study on key factors affecting power supply performance of outdoor photovoltaic power. High Volt. Appar. 2021, 57, 36–42. [Google Scholar]
- Sansawat, T.T.; O’Donnell, J.; Ochoa, L.F.; Yao, X.; Zhu, Y. Decentralized voltage control for active distribution networks. In Proceedings of the 44th International Conference, Pittsburgh, PN, USA, 21–29 May 2022. [Google Scholar]
- Viawan, F.A.; Sannino, A.; Dalder, J. Voltage control with on-load tap changers in medium voltage feeders in the presence of distributed generation. Electr. Power Syst. Res. 2007, 77, 1314–1322. [Google Scholar] [CrossRef]
- Lu, J.; Ling, C. Analysis on lightning transient characteristics of PV module and array grounding system. Insul. Surge Arresters 2021, 4, 166–170. [Google Scholar]
- Xing, L.; Zhong, C.; Lijie, C.; Shengnan, R.; Xinyu, H. Local distributed voltage control in distribution networks with high permeability of PVs. Power Capacit. React. Power Compens. 2021, 42, 268–275. [Google Scholar]
- Rui, H.; Zhengang, X.; Yushu, C. Research on autonomous control method of photovoltaic inverter with active fault ride-through capability. High Volt. Appar. 2022, 58, 101–110. [Google Scholar]
- Angelim, J.H.; Affonso, C.M. Impact of distributed generation technology and location on power system voltage stability. IEEE Lat. Am. Trans. 2016, 14, 1758–1765. [Google Scholar] [CrossRef]
- Masoum, A.S.; Deilami, S.; Moses, P.S.; Masoum, M.A.; Abu-Siada, A. Smart load management of plug-in electric vehicles in distribution and residential networks with charging stations for peak shaving and loss minimization considering voltage regulation. IET Gener. Transm. Distrib. 2011, 5, 877–888. [Google Scholar] [CrossRef]
- Ye, L.; Qu, X.; Yao, Y. Analysis of intra-day time scale operation characteristics of wind-solar-hydro multi-energy complementary power generation system. Autom. Electr. Power Syst. 2018, 42, 158–164. [Google Scholar]
- Hu, D.; Ding, M.; Bi, R.; Liu, X.; Rong, X. Sizing and placement of distributed generation and energy storage for a large-scale distribution network employing cluster partitioning. J. Renew. Sustain. Energy 2018, 10, 25–31. [Google Scholar] [CrossRef]
- Chen, X.Y.; Wang, J.X.; Xie, J.; Xu, S.; Yu, K.; Gan, L. Demand response potential evaluation for residential air conditioning loads. IET Gener. Transm. Distrib. 2018, 12, 4260–4268. [Google Scholar] [CrossRef]
- Pourmousavi, S.A.; Patrick, S.N.; Nehrir, M.H. Real-time demand response through aggregate electric water heaters for load shifting and balancing wind generation. IEEE Trans. Smart Grid 2014, 5, 769–778. [Google Scholar] [CrossRef]
- Li, H.C.; Wang, X.W.; Yuan, Y.B.; Su, W.; Gong, Y. Simulation and analysis of electric water heater load regulation model based on direct load control. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–5. [Google Scholar]
- Zeng, L.K.; Sun, Y.; Ye, Q.Z.; Qi, B.; Li, B. A centralized demand response control strategy for domestic electric water heater group based on appliance cloud platform. IEEJ Trans. Electr. Electron. Eng. 2017, 12, S16–S22. [Google Scholar] [CrossRef]
- Zhou, N.C.; Xiong, X.C.; Wang, Q.G. Simulation of charging load probability for connection of different electric vehicles to distribution network. Electr. Power Autom. Equip. 2014, 34, 1–7. [Google Scholar]
- Zhang, L.; Yan, Z.; Feng, D.H.; Xu, S.; Li, N.; Jing, L. Two-stage optimization model based coordinated charging for EV charging station. Power Syst. Technol. 2014, 38, 967–973. [Google Scholar]
- Wang, C.H.; Tian, L.T.; Zhang, F.; Cheng, L. Optimal sizing of photovoltaic and battery energy storage of electric vehicle charging station based on two-part electricity pricing. In Proceedings of the 2020 IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China, 23–25 November 2020; pp. 1379–1384. [Google Scholar]
- Sun, Y.P. Research on Dynamic Aggregation Model and Scheduling Mechanism of Demand Side Resources for Urban Power Grid. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2018. [Google Scholar]
- Zhao, B.Y.; Xiong, C.; Zhang, P.C. Aggregation method of load virtual power plant based on cyber-physical system. Power Demand Side Manag. 2020, 22, 15–20, 27. [Google Scholar]
- Yibing, L.; Wenchuan, W.; Boming, Z.; Zhengshuo, L.; Zhigang, L. Multi-period Optimal Operation of Active and Reactive Power Coordination in Active Distribution Networks Based on Mixed-Integer Second-Order Cone Programming. Proc. CSEE 2014, 34, 2575–2583. [Google Scholar] [CrossRef]
- Feng, W.; Zhiqiang, L.; Keyong, Z.; Wang, G.; Yin, H.; Jia, Z.; Zhao, H.; Mi, Y. Aggregation and Scheduling of Controllable Resources in Distribution Areas Based on Time-of-Use Electricity Prices and Energy Storage Charging and Discharging Strategies. Energy Storage Sci. Technol. 2023, 12, 1204–1214. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).